Adolescent development of multiscale structural wiring and functional interactions in the human connectome

Significance

The current study charted longitudinal adolescent brain development in 199 typically developing youth based on an advanced in vivo model of corticocortical wiring. Our findings revealed that the structural wiring of multiple cortical networks continues to mature during adolescence, and findings were observed in both sensory as well as higher-order transmodal systems. Using task-free functional MRI in the same subjects, we could furthermore show ongoing and correlated changes in functional network architecture, particularly an increased differentiation between sensory and default mode networks. By showing coordinated development of structural and functional brain networks, our findings provide insights into human brain maturation from childhood to adulthood.

Abstract

Adolescence is a time of profound changes in the physical wiring and function of the brain. Here, we analyzed structural and functional brain network development in an accelerated longitudinal cohort spanning 14 to 25 y (n = 199). Core to our work was an advanced in vivo model of cortical wiring incorporating MRI features of corticocortical proximity, microstructural similarity, and white matter tractography. Longitudinal analyses assessing age-related changes in cortical wiring identified a continued differentiation of multiple corticocortical structural networks in youth. We then assessed structure–function coupling using resting-state functional MRI measures in the same participants both via cross-sectional analysis at baseline and by studying longitudinal change between baseline and follow-up scans. At baseline, regions with more similar structural wiring were more likely to be functionally coupled. Moreover, correlating longitudinal structural wiring changes with longitudinal functional connectivity reconfigurations, we found that increased structural differentiation, particularly between sensory/unimodal and default mode networks, was reflected by reduced functional interactions. These findings provide insights into adolescent development of human brain structure and function, illustrating how structural wiring interacts with the maturation of macroscale functional hierarchies.

In adolescence, increasing evidence suggests that ongoing maturation of structural and functional brain networks underpins broad cognitive development (1–9). Prior MRI literature has assessed regional changes in brain structure in youth (1–3, 10–16), showing age-related widespread decreases in cortical thickness (1, 13) as well as changes in surrogates of intracortical myelin content (15–17). Complementing these regional changes, diffusion and functional MRI (fMRI) studies have shown that adolescence is a period of ongoing maturation of the microstructure of interconnecting white matter tracts as well as large-scale developmental changes in functional organization, indicative of shifts in brain connectivity toward a more distributed network topology (18–20). Utilizing multimodal longitudinal MRI analyses, we explored how adolescent structural network development gives rise to potential shifts in functional network architecture.

Core to our work was a comprehensive and recently introduced in vivo model of cortical wiring, which integrates several neuroimaging features of structural connectivity (i.e., diffusion MRI tractography, corticocortical geodesic distance mapping, and microstructural covariance analysis) (21). Diffusion MRI tractography maps white matter fibers and is useful for characterizing deeper tracts, but it is limited to the approximate distance between regions of cortical gray matter (22, 23). On the other hand, geodesic distance analysis measures spatial proximity of areas across the cortical sheet, tapping into short-range corticocortical connectivity and wiring cost (24). Finally, a recent extension of structural covariance analysis (25, 26), labeled microstructural profile covariance analysis, identifies networks with similar myelin-sensitive imaging characteristics across cortical depths in a subject-specific manner (27, 28). By integrating these complementary measures from diffusion MRI tractography, geodesic distance, and microstructural covariance via unsupervised pattern learning, we are able to generate a coordinate system that allows cortical regions to be arranged based on the similarity in their anatomical connections (21). In a prior evaluation in healthy adults, we demonstrated that this approach captures spatial gradients of 1) cortical cytoarchitecture, 2) cell type–specific gene expression, and 3) intrinsic functional connectivity and signal flow measured from resting-state fMRI (rs-fMRI) and intracranial electrical recordings (21), supporting neurobiological and functional validity. Here, we adopted this wiring model to chart adolescent development of cortical structural networks longitudinally.

Adolescence is a period of rapid change in social and cognitive processes (5, 7). As brain structure ultimately scaffolds brain function (29–35), it is not surprising that multiple functional networks also change throughout adolescence. Prior rs-fMRI connectivity analyses in youth have shown shifts in the functional connectivity patterns of multiple networks, often situated in transmodal systems such as the default mode and frontoparietal networks (3, 36, 37). On the other hand, several studies have emphasized a marked contribution of head motion to age-related changes in structural and functional connectivity (38–42), motivating careful consideration and adequate control of head motion in neurodevelopmental connectomics. Ongoing increases in the availability of multimodal datasets have allowed recent studies to examine how brain structure and function comature. For example, structural network modules are known to become more segregated with advancing age, and this process reflects ongoing development of executive function from 8 to 22 y (43). In other studies, it has been established that structure–function coupling changes with age, particularly in terms of the difference between transmodal vs. sensory and motor networks (3, 44). Based on these emerging results, our study aimed to adopt a multimodal anatomical coordinate space to allow us to establish how adolescent changes in cortical wiring are reflected in the maturation of functional networks.

Our study was based on the Neuroscience in Psychiatry Network (NSPN) 2400 cohort, an accelerated longitudinal dataset that enrolled healthy individuals between 14 and 25 y (16, 45). Structural wiring models were derived for each participant at two time points based on multimodal neuroimaging and unsupervised machine learning (46), and we estimated longitudinal trajectories in structural network maturation using linear mixed effect models. In addition to assessing whether age effects on structural wiring were similar to cortical thickness changes in the same subjects (1, 11, 13, 47), we examined how structural wiring changes reflect adolescent functional network maturation based on parallel rs-fMRI acquisitions. Multiple sensitivity analyses assessed the robustness of our findings with respect to several analysis parameter variations.

Results

We studied 199 healthy participants obtained from the NSPN 2400 cohort who were part of the accelerated longitudinal design and had imaging data available (16, 45) (Fig. 1A). All participants included in our study had measures at two time points (mean inter-scan interval was 0.94 y, range = 0.5 to 1), with a mean age of 18.84 y (range = 14 to 25) at baseline and 19.96 y (range = 15 to 26) at follow-up. Participants were uniformly distributed across the entire age range, with a similar sex ratio (52/48% males/females). Participant demographics, image processing, and analysis are further detailed in Methods.

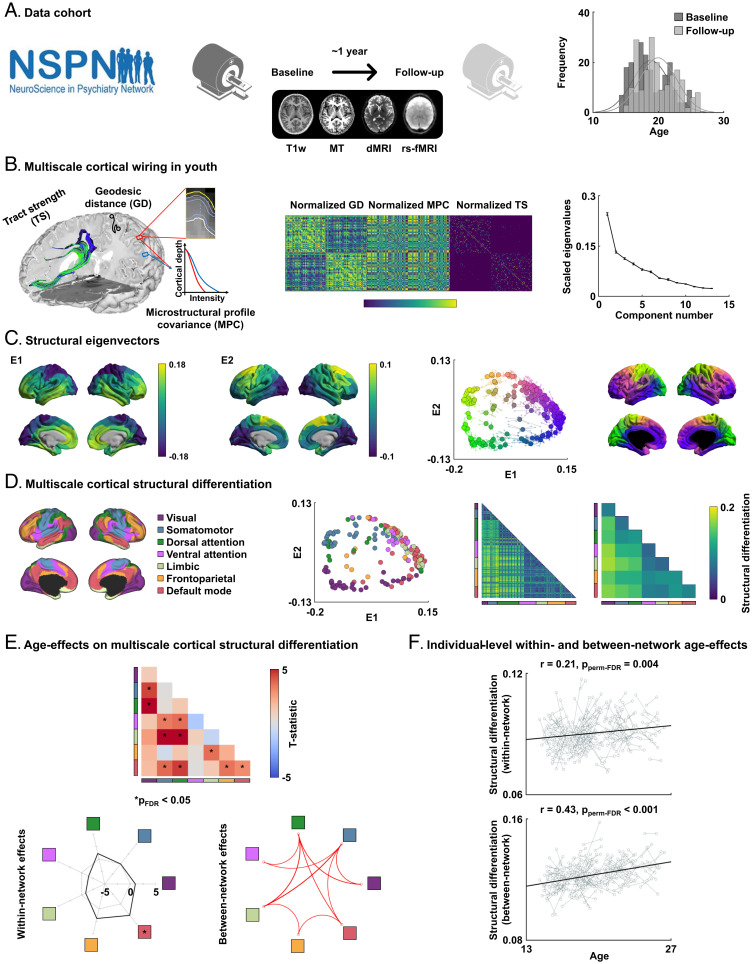
Fig. 1.

Adolescent development of multiscale cortical wiring. (A) We studied the multimodal MRI dataset from the NSPN 2400 cohort, examining both baseline and follow-up scans. Age at both visits is represented in the histograms. (B) Our in vivo model of corticocortical wiring combined three cortical neuroimaging features (i.e., geodesic distance, microstructural profile covariance, and tract strength). Matrices were normalized and concatenated prior to applying nonlinear manifold learning, which identifies a coordinate system informed by cortical wiring. The scree plot shows eigenvalues of each estimated component, with error bars indicating the SD across 10 repetitions. (C) We estimated two eigenvectors (E1 and E2) from cortical wiring features. Averaged maps across 10 repetitions are reported. The scatterplot represents each brain region projected onto the two-dimensional wiring space with different colors mapped onto the cortical surface. Solid big dots indicate mean results across 10 repetitions, and small transparent dots linked to the solid dots with lines indicate the results from each repetition. (D) Nodes in the wiring space were assigned to seven intrinsic functional communities. Multiscale cortical structural differentiation (i.e., the Euclidean distance between different nodes in the wiring space) was calculated at a node level and summarized for intrinsic functional communities. (E) The t statistics of age effects on structural differentiation within and between networks are reported, with significant (p_FDR < 0.05) results marked by asterisks. Within-network effects are represented by a radar plot, and a significant network is indicated by an asterisk. Significant between-network effects are reported by a circular plot, where the red lines indicate increases in structural differentiation. (F) The scatterplots show age-related changes in within-network (Upper) and between-network (Lower) structural differentiation of each individual in the identified networks. dMRI, diffusion magnetic resonance imaging; GD, geodesic distance; MPC, microstructural profile covariance; TS, tract strength; T1w, T1-weighted.

Multiscale Cortical Wiring in Youth.

Following a recently developed approach in healthy adults (21), we built a comprehensive in vivo model of corticocortical wiring for every subject time point (Fig. 1B). Models combined MRI-based measures of geodesic distance, microstructural profile covariance, and diffusion MRI tract strength. We integrated these three complementary features into a common space using diffusion map embedding, a nonlinear dimensionality reduction technique (Methods) (46). Two eigenvectors (eigenvector 1 [E1] and eigenvector 2 [E2]) were identified that collectively explained ∼37.8 ± 0.01% (mean ± SD) of information and averaged across 10 iterations with different nonoverlapping subsets within the NSPN cohort (Fig. 1 B and C and Methods). The first eigenvector (E1) depicted a gradient running from sensory/motor networks toward transmodal networks, such as the default mode and frontoparietal networks. The second eigenvector (E2) differentiated anterior and posterior cortices. We calculated the Euclidean distance between all brain regions in the wiring-derived low-dimensional space to provide a measure of structural differentiation (Fig. 1D and Methods). While within-network connectivity showed overall low structural differentiation, connections between sensory and transmodal regions showed high values. In other words, nodes in the same network showed less structural differentiation (indicating integration), while differentiation was greater between regions in different networks, particularly between sensory vs. transmodal cortices, a pattern indicative of segregation. Findings were furthermore summarized according to seven intrinsic functional networks (48) by assigning each brain region to the nearest networks (SI Appendix, Fig. S1).

Tracking Adolescent Changes in Multiscale Cortical Structural Differentiation.

We assessed age effects on this structural differentiation using linear mixed effect models. In adolescence, several prior studies have reported robust age-related changes in cortical thickness (1, 11, 13, 47), and we confirmed similar age effects in our NSPN cohort. Indeed, cortical thickness decreased in widespread cortical regions with advancing age (false discovery rate [FDR]; [p_FDR] < 0.05) (SI Appendix, Fig. S2A). Running a spatial correlation analysis between longitudinal thickness and structural differentiation effects while controlling for spatial autocorrelation (49), we only observed a weak spatial association to changes in structural differentiation, with no correlation to within-network structural differentiation (r = −0.02 ± 0.05, p_spin-FDR = 0.27) and a trend-level association to between-network structural differentiation (r = −0.12 ± 0.04 across 10 repetitions, p_spin-FDR = 0.06) (SI Appendix, Fig. S2B). We then assessed age effects on structural differentiation after controlling for sex, measurement site, head motion, and subject-specific random intercepts as well as cortical thickness (50). With increasing age, structural differentiation increased within and between multiple networks (p_FDR < 0.05) (Fig. 1E). Specifically, among the seven large-scale communities, the default mode network showed the greatest within-network changes (Fig. 1E). We also observed increased structural differentiation between several networks, particularly between nodes of default mode and attention networks, frontoparietal regions, as well as between sensory and attention, limbic networks (p_FDR < 0.05) (Fig. 1E). Investigating changes in structural differentiation for each individual in the identified networks, we established small but significant increases with within-network structural differentiation with age (r = 0.21, p_perm-FDR = 0.004) as well as a moderate association between age and between-network structural differentiation (r = 0.43, p_perm-FDR < 0.001) (Fig. 1F).

We additionally assessed age effects on each cortical feature (i.e., geodesic distance, microstructural profile covariance, and tract strength) to quantify how structural differentiation captures age-related changes in cortical organization relative to changes in single features (SI Appendix, Fig. S3). When analyzing structural differentiation, the effect size (i.e., the mean absolute t statistic across network pairs) was 32.07 ± 17.88% higher than when studying only geodesic distance across 10 repetitions (Methods), 15.45 ± 6.53% higher than when studying microstructural profile covariance, and 14.65 ± 11.58% higher than when studying tract strength, indicating that structural differentiation describes adolescent cortical reorganization more sensitively than each modality separately. When associating age effects on structural differentiation with those on each feature, structural differentiation increases were strongly related to reductions in microstructural profile covariance (r = −0.58, p_FDR = 0.001) but not very much to changes in tract strength (r = −0.25, p_FDR = 0.21) nor geodesic distance (r = 0.22, p_FDR = 0.27), supporting the notion that increases in multiscale structural differentiation reflected mostly a decreased similarity of intracortical microstructure. Furthermore, as the overall manifold size (i.e., mean of structural differentiation across all networks) was significantly associated with age (r = 0.19 ± 0.02, P < 0.001 across 10 repetitions), we repeated linear mixed effect models after additionally controlling for mean structural differentiation (SI Appendix, Fig. S4). Despite decreases in the effect size, we observed overall consistent patterns, confirming that age effects on structural differentiation were not driven by the expansion in manifold space itself.

Associations with Macroscale Functional Network Maturation.

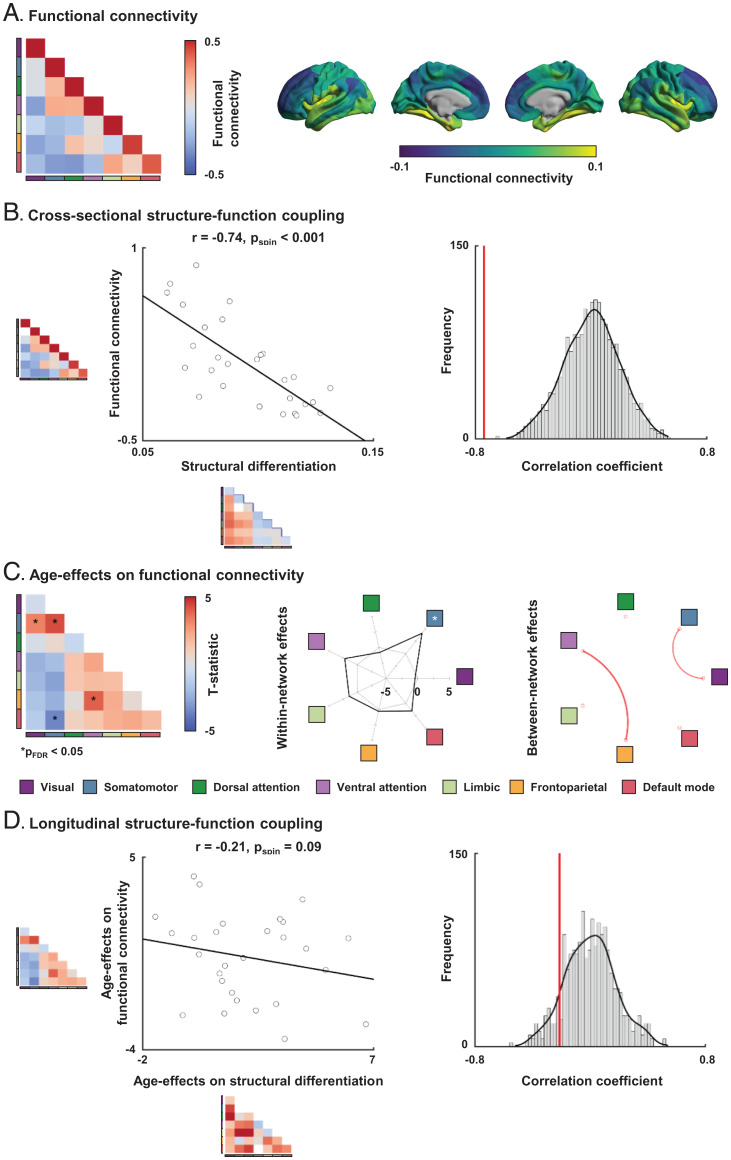
To evaluate functional associations of the changes in multiscale cortical wiring, we first generated functional connectivity based on rs-fMRI obtained in the same subjects at equivalent time points (Fig. 2A). At a cross-sectional level, we found strong negative associations between structural differentiation and functional connectivity across intrinsic functional networks (r = −0.74, p_spin < 0.001) (Fig. 2B). In other words, regions with increased structural differentiation generally show weaker functional connectivity. We then charted the development of functional connectivity across age, and we found decreases in sensory–default mode network connectivity and increases in connectivity between sensory networks (p_FDR < 0.05) (Fig. 2C). To assess how the age-related changes in structural and functional measures were inter-related, we correlated the age effects on structural differentiation with the age effects on functional connectivity. Here, we found a tendency for a negative association (r = −0.21, p_spin = 0.09) (Fig. 2D). The negative relationship between structural differentiation and functional connectivity indicates that regions/networks with stronger structural differentiation show reduced functional connectivity.

Fig. 2.

Association between functional connectivity and structural differentiation. (A) The functional connectivity matrix was summarized according to intrinsic functional communities (Left) and projected onto brain surfaces (Right). (B) Cross-sectional structure–function coupling between functional connectivity and structural differentiation. The histogram indicates a null distribution of correlation coefficients generated based on 1,000 spin tests, and the actual r value is represented by a red bar. (C) Age effects on functional connectivity. The t statistics of age effects are reported. The within-network effects are represented with a radar plot, and a significant network is reported with an asterisk. Significant between-network effects are reported with a circular plot, where the red/blue lines indicate increases/decreases in structural differentiation. (D) Longitudinal structure–function coupling between age effects on functional connectivity and structural differentiation.

We furthermore assessed structure–function coupling across different age bins using data from the Human Connectome Project (HCP)—Development dataset (focusing on participants younger than 14 y of age), the current NSPN dataset (14 y ≤ age < 26 y), and the HCP—Young Adults dataset (focusing on individuals older than 26 y of age), and we observed largely consistent results (SI Appendix, Fig. S5). We additionally assessed inter-individual differences in structure–function coupling, focusing on the connections that showed significant age effects on both structural differentiation and functional connectivity (Figs. 1E and 2C). We observed a negative association between sensorimotor and default mode networks (p_perm = 0.01) at the cross-sectional level and a similar, albeit weaker effect at the longitudinal level (p_perm = 0.05) (SI Appendix, Fig. S6). These results confirm the findings between sensory and default mode networks at the level of the individual.

Sensitivity Analysis.

We assessed whether our findings were robust with respect to several methodological variations.

• a)Parcellation scales. We repeated assessing age effects using different parcellation scales (i.e., 100 and 300 regions) and revealed consistent results (SI Appendix, Fig. S7), indicating the robustness of our findings across different scales.
• b)Structural eigenvector generation using principal component analysis. Our main analysis estimated structural eigenvectors using diffusion map embedding (51), in keeping with a previous approach to study structural eigenvectors in healthy young adults (21, 52). We repeated our analysis after alternatively estimating structural eigenvectors using principal component analysis (53), and the eigenvectors and age effects were similar (SI Appendix, Fig. S8), confirming robustness.
• c)Parcellation scheme. We generated connectome eigenvectors and assessed adolescent remodeling using a functional (i.e., Schaefer) parcellation (54) instead of the structural parcellation scheme (55) used for our principal analysis and found consistent results (SI Appendix, Fig. S9), indicating the robustness of our analyses across different parcellations. Moreover, the age effects on structural differentiation were more similar between 200 functional parcels of the Yeo 7 network (54) and 200 structural parcels compared with the similarity between 100 and 200 structural parcels, showing the correspondence between different parcellation schemes.
• d)Age effects based on low–head motion participants. To assess the effects of head motion on age-related changes in both structural differentiation and functional connectivity, we assessed age effects using participants with very low head motion only (50% of participants with the lowest frame-wise displacement). We observed consistent findings (SI Appendix, Fig. S10).
• e)Cortical wiring in age-stratified participant subgroups. Comparing the spatial maps of eigenvectors generated in younger (age < 17) and older (age ≥ 21) participants from the NSPN dataset with those of the HCP—Young Adults datasets (21, 56), we observed higher similarity for older (r = 0.92/0.80, p_spin < 0.001/0.001 for E1/E2) than for younger participants (r = 0.91/0.78, p_spin < 0.001/0.004) (SI Appendix, Fig. S11). We furthermore performed cell type–specific transcriptomic association and enrichment analyses (Methods). Specifically, we correlated structural eigenvectors of younger participants (age < 17) and older participants (age ≥ 21) subdivided within our dataset as well as young adults from the HCP—Young Adults database, with post mortem gene expression maps provided by the Allen Human Brain Atlas (57–59), where the significance of the association was determined based on 1,000 spin tests. We tested the identified genes for any cell type–specific genes (60, 61) by calculating the overlap ratio between them after 1,000 random permutations of the cell type–specific gene lists. As expected from the above increase in similarity in wiring spaces, we also observed higher transcriptomic associations between HCP young adults and older adolescents from NSPN than between HCP young adults and younger adolescents from NSPN (SI Appendix, Fig. S12), suggesting that cell type–specific enrichment approaches adult-like patterns with increasing age of adolescent samples.

Discussion

The current work assessed adolescent maturation of cortical networks based on an advanced in vivo model of cortical wiring (21). Charting typical development from late childhood to early adulthood using the longitudinal NSPN cohort (16, 45), we observed marked increases in within- and between-network structural differentiation in both sensory and transmodal association networks. Moreover, associating cortical structural wiring features with intrinsic functional connectivity obtained from parallel rs-fMRI analysis performed in the same subjects, we observed that functional networks reconfigure alongside the marked reorganization of corticocortical wiring. Collectively, our work offers a perspective on how structural brain networks reconfigure and how these changes give rise to ongoing functional maturation in typically developing youth.

Our work centered on an advanced in vivo model of structural wiring that integrates multiple dimensions of corticocortical connectivity (21), namely diffusion MRI tractography strength, geodesic distance, and microstructure profile covariance. Each feature taps into different aspects of corticocortical connectivity, grounded in foundational neuroanatomical studies on the multiple facets of the cortical wiring scheme (62). Synergistic integration of these features is hypothesized to describe structural connectivity more comprehensively and to thus provide insights into structure–function relationships in the developing brain. In fact, tract strength is an established measure of short- and long-range white matter fibers (63, 64), whereas geodesic distance computed within the cortical ribbon has been proposed to index horizontal connectivity between adjacent cortical regions (24, 65). Similarity of intracortical microstructural profiles, quantified as microstructural profile covariance (28), is generally recognized as an indicator of inter-regional connectivity (21, 27, 66, 67). In fact, the structural model of brain connectivity, initially formulated in nonhuman animals, predicts that areas with similar microstructure are more likely to be connected than areas with different connectivity profiles (68). These findings were recently extended to human neuroanatomy by relating microstructural similarity to diffusion MRI–derived streamline strength (67, 69) and to resting-state functional connectivity (28, 70). By translating the approach previously formulated in adults (21) to typically developing adolescents in the current work, we demonstrated that the wiring space in youth overall resembles the one previously seen in adults. Indeed, the two principal dimensions of the wiring space differentiated unimodal from transmodal cortex and anterior from posterior regions—two major axes of adult macroscale cortical topography (71–75). On the other hand, we also showed how the structural networks increasingly reconfigure into those seen in adults. The NSPN dataset was acquired using an accelerated longitudinal design, enrolling individuals aged from late childhood to young adulthood with a 1-y follow-up on average (16, 45). Compared with cross-sectional studies, longitudinal designs are sensitive to intraindividual changes in cortical features, allowing developmental trajectories to be charted directly (3, 20, 76–78). Our multiscale approach gathered evidence for developmental shifts in cortical wiring, indicative of increased structural differentiation in multiple systems, with the highest effects in default mode and ventral attention networks. These findings indicate that differentiation of corticocortical structural networks, in particular transmodal systems at the apex of the cortical hierarchy (3, 37, 79, 80), continues into early adulthood.

Our findings on cortical wiring changes need to be contextualized within a well-established literature on developmental changes in cortical morphology during adolescence, which indicates widespread cortical thickness reductions with advancing age, a finding likely reflecting ongoing synaptic pruning and cortical myelination (10, 16, 81, 82). Here, by analyzing longitudinal cortical thickness changes in the same NSPN participants, we could confirm widespread cortical thinning in youth with advancing age. In addition, we showed that wiring space changes were only partially attributable to these changes in cortical thickness, however, suggesting that age-related structural wiring changes likely occurred above and beyond maturational effects on cortical morphology per se. In prior work in healthy adults (21), we could identify associations between in vivo cortical wiring space organization and intracortical factors, specifically cell type–specific gene expression as well as externopyramidization. Although these associations were indirect and based on separate datasets (in vivo MRI and histology-based post mortem gene expression information), they nevertheless supported a link between multiscale wiring and internal cortical microcircuitry that goes beyond the changes measurable by cortical thickness measures alone. Such interactions between different scales of cortical organization during typical development could be further explored in studies obtaining wiring space data and gene expression in the same subjects.

An increasing body of studies has provided insights into age-related changes in structural and functional connectivity in adolescence, which help to further contextualize the current findings. First, multiple studies assessing structural or functional changes separately have shown spatiotemporal variations in developmental change patterns. At the level of structural connectivity, diffusion MRI–based studies showed continued microstructural changes in multiple fiber tracts in late childhood and adolescence (83), likely underpinning a continuous integration of long-range hub-to-hub connectivity (16, 20, 84, 85). In particular, a relative strengthening of long-range anterior–posterior tracts in adolescence has been reported, implicating tracts between posterior cingulate and medial prefrontal cortex (79). Studies examining developmental connectome reconfigurations also supported increases in hub-to-hub connectivity in adolescents, particularly frontal–subcortical and frontal–parietal connections (84, 85). Our findings based on a multiscale wiring model recapitulated these findings, showing increased structural differentiation in higher-order association and transmodal systems. Considering intrinsic function, prior work has suggested age-related reductions in short-range functional interactions between default mode and sensory/motor systems along with strengthening of long-range interactions within default mode networks, suggesting increased coherence of such transmodal systems (37, 86–88). Such conclusions are in line with a longitudinal graph theoretical rs-fMRI analysis focusing on the default mode network (89) and a work indicating that longitudinal functional trajectories differ between sensory/motor networks on the one hand and association systems on the other hand (37). Our work also showed a relative strengthening of functional connectivity within primary networks with simultaneous weakening of sensory–default mode interactions, which likely reflects ongoing functional segregation of primary and heteromodal systems. Second, our work adds evidence on how functional and structural changes may converge. We observed overall associations between structural differentiation and functional connectivity at baseline and revealed that adolescent decreases in functional connectivity between sensory and association systems are marginally reflected in increased structural differentiation between these systems, consistent with prior cross-sectional (79, 86, 87, 90) and longitudinal findings (91, 92). Based on these prior findings, the developmental processes would likely culminate in increased structural differentiation of heteromodal association systems from other brain networks. Ultimately and as our work shows, these findings may also affect functional organization and be compatible with work on the development of structure–function coupling in adolescence and changes in cognitive functions (3, 79). Finally and beyond the findings in our work that focused on changes between 14 and 25 y, it remains to be investigated as to which connections do already exist at the beginning of a given neurodevelopmental time window. Our supporting analyses based on the HCP—Development and HCP—Young Adults datasets along with the NSPN cohort suggest that while cortical wiring patterns are overall already quite similar to an adult configuration in younger NSPN participants and younger children from the HCP—Development dataset, similarity further increases throughout adolescence. It will be important for future exploration to track a wider developmental time span longitudinally, ideally from early childhood until adulthood. This will also allow for the identification of potentially nonlinear age-related changes in structure–function coupling in the first decades of life and the comparison of age-related changes during adolescence with those in early childhood and adulthood, respectively.

Numerous neurodevelopmental connectomics studies have shown an effect of head motion, motivating its consideration as a potential confounding factor as well as strategies for its control (38–42). Considering age-related changes in functional network organization, prior work has shown that adequate control for head motion changes connectivity within and between networks substantially (38–42). Indeed, controlling for head motion in rs-fMRI connectivity analysis has been shown to diminish the age effects, in particular for long-range connections (41, 42). Considering structural connectivity estimated from diffusion MRI, head motion has similarly been shown to affect both short- and long-range connectivity strength (93), suggesting that it is also an important confounder for structural brain network analyses. In the current study, we controlled for head motion effects during image preprocessing and statistical analysis, and furthermore, we confirmed the robustness of age effects on structural differentiation as well as functional connectivity within the 50% of participants with the lowest in-scanner head motion estimates.

Our multimodal wiring space analysis established how features of brain anatomy can change in tandem, a perspective that would not arise from the analysis of single features. Of note, the applied model of corticocortical wiring can be generated at the level of the group as well as individual subjects. As such, our model and approach can have practical value for the understanding and monitoring of typical as well as atypical brain development. Atypical corticocortical wiring at different spatial scales has been implicated in numerous neurological and neuropsychiatric conditions, notably autism, epilepsy, and schizophrenia (94–98). In fact, each of these conditions is characterized by a complex combination of atypical cortical microstructure, wiring, and geometry (99–102). The findings support the potential value of our approach to inform prognostic and diagnostic applications in future work and to better understand factors contributing to shared and syndrome-specific functional anomalies.

To conclude, we longitudinally tracked development of structural brain networks in adolescence and showed an ongoing differentiation based on an advanced model of corticocortical wiring across multiple brain networks, in particular an increased differentiation between uni- and transmodal systems that was also found to mirror ongoing functional network reconfigurations. Our multimodal framework, thus, provides insights into structural and functional brain development in adolescence and points to an inherent coupling of developmental trajectories across both domains.

Methods

Participants.

We obtained imaging and phenotypic data from the NSPN 2400 cohort (openly available at https://nspn.org.uk/) (103), which contains questionnaire data on 2,402 individuals (with MRI data in a subset of ∼300) from adolescence to young adulthood in a longitudinal setting (16, 45). In this study, we included 199 participants who completed quality-controlled (Data Preprocessing) multimodal MRI scans consisting of T1 weighted, magnetization transfer (MT), diffusion MRI, and rs-fMRI for at least two time points (48% female; mean ± SD; age = 18.84 ± 2.83 y [between 14 and 25] at baseline and 19.96 ± 2.84 y [between 15 and 26] at follow-up with an inter-scan interval of 0.94 ± 0.17 y [between 0.5 and 1]) (Fig. 1A). Data were collected from three different sites: the Wolfson Brain Imaging Centre, the Medical Research Council (MRC) Cognition and Brain Sciences Unit in Cambridge, and the University College London. Participants provided informed written consent for each aspect of the study, and parental consent was obtained for those aged 14 to 15 y old. Ethical approval was granted for this study by the National Health Service Research Ethics Service (NHS NRES) Committee East of England–Cambridge Central (project ID 97546). The authors assert that all procedures contributing to this work comply with the ethical standards of the relevant national and institutional committees on human experimentation and with the Helsinki Declaration of 1975, as revised in 2008.

MRI Acquisition.

Imaging data were obtained using a Siemens Magnetom TIM Trio 3T scanner at all sites. The T1-weighted and MT sequences were acquired using a quantitative multiparameter mapping sequence (repetition time [TR]/flip angle = 18.7 ms/20° for T1 weighted and 23.7 ms/6° for MT; six equidistance echo times [TE] = 2.2 to 14.7 ms; voxel size = 1 mm³; 176 slices; field of view [FOV] = 256 × 240 mm; matrix size = 256 × 240 × 176) (104). The diffusion MRI data were acquired using a spin-echo echo-planar imaging (EPI) sequence (TR = 8,700 ms; TE = 90 ms; flip angle = 90°; voxel size = 2 mm³; 70 slices; FOV = 192 × 192 mm²; matrix size = 96 × 96 × 70; b value = 1,000 s/mm²; 63 diffusion directions; six b0 images). The rs-fMRI data were collected using a multiecho EPI sequence with three different TEs (TR = 2.43 ms; TE = 13.0/30.55/48.1 ms; flip angle = 90°; voxel size = 3.75 × 3.75 × 4.18 mm³; 34 slices; FOV = 240 × 240 mm²; matrix size = 64 × 64 × 34; 269 volumes).

Data Preprocessing.

T1-weighted data were processed using the fusion of neuroimaging preprocessing pipeline integrating AFNI, FSL, FreeSurfer, ANTs, and Workbench (https://gitlab.com/by9433/funp) (105–109), which is similar to the minimal preprocessing pipeline for the HCP (110). Gradient nonlinearity and b0 distortion correction, nonbrain tissue removal, and intensity normalization were performed. The white and pial surfaces were generated by following the boundaries between different tissues (107, 111–113). The midthickness surface was generated by averaging the white and pial surfaces, and it was used to generate an inflated surface. Quality control involved visual inspection of the surface reconstructions from T1-weighted data, and cases with suboptimal cortical segmentation were excluded. We generated 14 equivolumetric cortical surfaces within the cortex, especially between inner white and outer pial surfaces, and sampled MT intensity along these surfaces (28). The diffusion MRI data were processed using MRtrix3 (23), including correction for susceptibility distortions, head motion, and eddy currents. The rs-fMRI data were processed using the multiecho independent component analysis pipeline (https://github.com/ME-ICA/me-ica) (114, 115). The first six volumes were discarded to allow for magnetic field saturation, and slice timing was corrected. Motion correction parameters were estimated from the middle TE data by aligning all volumes to the first volume using rigid-body transformation. The coregistration transformation parameters from functional to structural images were estimated by registering the skull-stripped spatially concatenated multiecho functional data to the skull-stripped anatomical image using affine transformation. The estimated parameters from motion correction and anatomical coregistration procedures were applied to each slice-timing corrected TE data and then, temporally concatenated. The noise components were removed using principal component analysis followed by independent component analysis (114, 115). The processed fMRI data were mapped to the standard gray ordinate space (i.e., 32k Conte69) with a cortical ribbon-constrained volume-to-surface mapping algorithm. Finally, data were surface smoothed with 5-mm full width at half-maximum.

Multiscale Cortical Wiring Features.

We calculated complementary cortical wiring features from different imaging sequences, namely geodesic distance from T1 weighted, microstructural profile covariance from MT, and tract strength from diffusion MRI (Fig. 1B). Geodesic distance is a physical distance represented by the shortest paths between two points along the cortical surface (24, 52, 65). To calculate the geodesic distance matrix, we first matched each vertex to the nearest voxel in volume space. We then calculated the distance to all other voxels traveling through a gray/white matter mask using a Chamfer propagation (https://github.com/mattools/matImage/wiki/imGeodesics) (116). Unlike a previously introduced approach that calculates only intrahemispheric distance (24, 52, 65), this approach allows for estimating inter-hemispheric projections (21). We mapped geodesic distance to a 200–cortical nodes parcellation scheme, which preserves the boundaries of the Desikan Killiany atlas (55) (SI Appendix, Fig. S1). Following our prior study in adults (28), the microstructural profile covariance matrix was constructed by calculating linear correlations between cortical depth–dependent intensity profiles of different nodes, controlling for the average whole-cortex intensity profile based on the 200 parcels. The microstructural profile covariance matrix was thresholded at zero and log transformed. We generated the tract strength matrix from preprocessed diffusion MRI data using MRtrix3 (23). Anatomical constrained tractography was performed using different tissue types derived from the T1-weighted image, including cortical and subcortical gray matter, white matter, and cerebrospinal fluid (117). We coregistered the T1-weighted and diffusion MRI data using a boundary-based registration and applied the transformation to different tissue types to align them onto the native diffusion MRI space. The multishell and multitissue response functions were estimated (118), and constrained spherical deconvolution and intensity normalization were performed (119). Seeding from all white matter voxels, the tractogram was generated using a probabilistic approach (23, 120) with 40 million streamlines, a maximum tract length of 250, and a fractional anisotropy cutoff of 0.06. Subsequently, we applied spherical-deconvolution informed filtering of tractograms to optimize an appropriate cross-section multiplier for each streamline (121) and reconstructed whole-brain streamlines weighted by cross-section multipliers. Reconstructed cross-section streamlines were mapped onto the 200 parcels to build tract strength matrix and log transformed (122, 123).

Structural Eigenvector Identification.

We estimated structural eigenvectors based on the multiscale cortical features calculated above using an openly accessible normative manifold map approach (https://github.com/MICA-MNI/micaopen/tree/master/structural_manifold) (21), which is now integrated in BrainSpace (https://github.com/MICA-MNI/BrainSpace) (46). First, we ranked the normalized nonzero entries of the input matrices, and the less sparse matrices (i.e., geodesic distance and microstructural profile covariance) were rescaled to the same numerical range as the sparsest matrix (i.e., tract strength) to balance the contribution of each input measure (Fig. 1B). Notably, we rank normalized the inverted geodesic distance matrix to represent closer regions with larger values. We horizontally concatenated the normalized geodesic distance, microstructural profile covariance, and tract strength matrices and constructed an affinity matrix with a normalized angle kernel with 10% density, which quantifies the strength of cortical wiring between two regions. We applied diffusion map embedding (51), a nonlinear dimensionality reduction technique that is robust to noise and computationally efficient, to generate corticocortical wiring spaces (124, 125) (Fig. 1C). Diffusion map embedding applies singular value decomposition to the corticocortical affinity matrix that was transformed via a diffusion kernel, where regions with more similar connectivity have small diffusion times, while dissimilar regions have larger diffusion times. It is controlled by two parameters α and t, where α controls the influence of the density of sampling points on the manifold (α = 0, maximal influence; α = 1, no influence) and t controls the scale of eigenvalues of the diffusion operator. We set α = 0.5 and t = 0 to retain the global relations between data points in the embedded space, following prior applications (17, 20, 28, 46, 52, 99, 126). Cortical regions with more similar interregional patterns are more proximal in this structural manifold space. To assess robustness, we repeated estimating structural eigenvectors 10 times with different sets of participants. Specifically, we split the dataset into nonoverlapping template (1 of 10) and non-template (9 of 10) partitions with similar distributions of age, sex, and site. The template eigenvector was generated using the averaged concatenated matrix of the template dataset, and individual-level eigenvectors were estimated from the non-template dataset and aligned to the template eigenvector via Procrustes alignment (46, 127). We repeated generating connectome eigenvectors 10 times with different template and non-template datasets.

Age Effects on Structural Eigenvectors.

To chart age effects on structural eigenvectors, we first calculated multiscale cortical structural differentiation, which is the Euclidean distance between different brain regions in the manifold space (Fig. 1D) (21, 128), and stratified the node-level structural differentiation based on intrinsic functional communities (48). It has been shown that cortical thickness shows significant changes across age (1, 11, 13, 47). We first replicated these morphological findings by assessing age effects on cortical thickness measured using T1-weighted MRI (SI Appendix, Fig. S2A). Next, we linearly correlated time-related changes in structural differentiation and those in cortical thickness to assess spatial similarity across the cortex (SI Appendix, Fig. S2B). The significance of the similarity was assessed based on 1,000 spin tests that account for spatial autocorrelation (46, 49) and was FDR corrected across within- and between-network correlations. We then assessed age effects on network-level structural differentiation using a linear mixed effect model (50). The model additionally controlled for sex, site, head motion (i.e., frame-wise displacement measured from diffusion MRI), and cortical thickness and included a subject-specific random intercept. We corrected for multiple comparisons across all pairs of functional communities with p_FDR < 0.05 (129). We repeated the age modeling 10 times with different non-template individuals and reported only those network pairs showing significant effects across all repetitions (Fig. 1E). To assess individual-level changes in structural differentiation across the age, we calculated linear correlations between mean age and within- and between-network structural differentiation in the identified networks between baseline and follow-up, where the significance was determined based on 1,000 permutation tests randomly assigning subjects (Fig. 1F). We additionally implemented mixed effect models for each cortical wiring feature separately (i.e., geodesic distance, microstructural profile covariance, and tract strength) to assess how much the age effects improved when we considered multiscale cortical structural differentiation (SI Appendix, Fig. S3). The age effect t statistics of each feature were correlated with those of structural differentiation to assess which features are strongly related to adolescent development in structural differentiation. To assess the association between global wiring effects and age, we calculated linear correlation between age and mean structural differentiation across the whole network. We also implemented a linear mixed effect model that additionally controlled for mean structural differentiation to assess whether the age effects on structural differentiation are affected by global changes in the size of manifold space (SI Appendix, Fig. S4).

Association between Structural Differentiation and Functional Connectivity.

Structure–function coupling analyses assessed how multiscale cortical wiring related to functional connectivity. First, we constructed the functional connectivity matrix by calculating linear correlations of resting-state functional time series between different brain regions, controlling for average whole-cortex signals (Fig. 2A). After row-wise thresholding with remaining 10% of values for each row in the connectivity matrix, we assessed structure–function correspondence via linear correlations between the z-transformed functional connectivity and structural differentiation measures at the network level (48) (Fig. 2B). To assess the relationship between age effects on multiscale cortical wiring and those on functional connectivity, we first calculated the age effects t statistic on functional connectivity for all node pairs (Fig. 2B). Then, we calculated linear correlations between the age effect t statistics of functional connectivity and structural differentiation (Fig. 2D). We assessed the significance of these using 1,000 spin tests (46, 49). To assess the consistency of structure–function coupling across age, we evaluated cross-sectional structure–function coupling at different age bins: 1) age < 14 using the HCP—Development dataset (130); 2) 14 ≤ age < 17, 3) 17 ≤ age < 20, 4) 20 ≤ age < 23, and 5) 23 ≤ age < 26 using the current NSPN cohort; and 6) age ≥ 26 using the HCP—Young Adults dataset (56) (SI Appendix, Fig. S5). To examine inter-individual variations in the association between structural differentiation and functional connectivity, we additionally assessed structure–function coupling focusing on the networks that showed significant age effects on both structural differentiation and functional connectivity (SI Appendix, Fig. S6).

Sensitivity Analysis.

• a)Parcellation scales. Our main analyses were based on a 200–cortical node subparcellation of the Desikan Killiany atlas (55). To assess robustness across parcellation scales, we repeated out analysis eigenvectors using structural atlases with 100 and 300 parcels (SI Appendix, Fig. S7).
• b)Structural eigenvector generation using principal component analysis. Instead of relying on diffusion map embedding (51), we generated structural eigenvectors using principal component analysis (53). Then, we repeated calculating multiscale cortical structural differentiation and assessed age effects to evaluate consistency of our findings (SI Appendix, Fig. S8).
• c)Functional parcellation. We also repeated structural eigenvector generation and age modeling using the functional Schaefer parcellation scheme with 200 parcels (54) (SI Appendix, Fig. S9).
• d)Age effects based on low–head motion participants. We assessed age effects on both network-level structural differentiation and functional connectivity using a linear mixed effect model (50) fit to data from participants with low head motion (50% of participants with the lowest frame-wise displacement for both structural differentiation and functional connectivity) (SI Appendix, Fig. S10). The multiple comparisons were corrected using FDR (129).
• e)Cortical wiring in age-stratified participant subgroups. To assess the development of cortical structures, we generated eigenvectors in younger (age < 17 y) and older (age ≥ 21 y) participants separately (SI Appendix, Fig. S11). We calculated linear correlations between the generated eigenvectors with those estimated from the HCP—Young Adults dataset (21, 56), and the significance of correlations was assessed using 1,000 spin tests that account for spatial autocorrelation (49). In addition, we aimed to decode multiscale cortical wiring of younger and older adolescence from the current NSPN cohort as well as young adults from the HCP—Young Adults database, respectively, based on cell type–specific gene expressions (SI Appendix, Fig. S12). We associated the structural eigenvectors with the post mortem gene expressions provided by the Allen Human Brain Atlas. Specifically, among all genes from the Allen Human Brain Atlas, we selected genes consistently expressed across donors using the abagen toolbox (https://github.com/rmarkello/abagen) (59, 131, 132). For each gene, we correlated the whole-brain gene expression map between all pairs of donors and considered genes with an average inter-donor r > 0.5 for subsequent analyses. We spatially correlated the eigenvector maps with the gene expression maps to assess which genes were associated with the macroscale findings. For each gene, we performed the correlation analysis 1,000 times with spin-rotated eigenvectors to construct a null distribution (49). If the real correlation coefficient between eigenvectors and gene expression maps did not belong to the 95% of the null distribution, we considered that the gene was significantly associated with the eigenvectors. We further corrected the P values using FDR < 0.05 (129). To address cell type–specific gene enrichment, we compared the identified genes with cell type–specific genes proposed in prior work, which includes excitatory and inhibitory neuronal subtypes in the cortex and nonneuronal cells, such as endothelial cells, pericytes, astrocytes, oligodendrocytes and their precursor cells, and microglia (60, 61). We calculated overlap ratios to assess how many genes expressed for eigenvectors are included in each cell type–specific gene list. To assess the significance of the overlap ratio, we performed 1,000 permutation tests. For each cell type, we randomly assigned genes among all cell type–specific genes with the same gene length. Then, we calculated the overlap ratio between the genes expressed for eigenvector differences and the permuted cell type–specific genes. For each cell type, we constructed a null distribution using the overlap ratio; if the real overlap ratio did not belong to 95% of the null distribution, it was deemed significant, and the P value was corrected using FDR < 0.05 (129).

Data Availability

Codes for multimodal connectome manifold generation and codes for structural differentiation calculation have been deposited in GitHub [https://github.com/MICA-MNI/micaopen/tree/master/structural_manifold (133), https://github.com/MICA-MNI/BrainSpace (134), and https://github.com/MICA-MNI/micaopen/tree/master/manifold_features (135)]. The imaging and phenotypic data were provided by the NSPN 2400 cohort, and openly available at https://nspn.org.uk/ (103).