Abstract
In the analysis of observational studies, inverse probability weighting (IPW) is commonly used to consistently estimate the average treatment effect (ATE) or the average treatment effect in the treated (ATT). The variance of the IPW ATE estimator is often estimated by assuming that the weights are known and then using the so-called “robust” (Huber-White) sandwich estimator, which results in conservative standard errors (SEs). Here we show that using such an approach when estimating the variance of the IPW ATT estimator does not necessarily result in conservative SE estimates. That is, assuming the weights are known, the robust sandwich estimator may be either conservative or anticonservative. Thus, confidence intervals for the ATT using the robust SE estimate will not be valid, in general. Instead, stacked estimating equations which account for the weight estimation can be used to compute a consistent, closed-form variance estimator for the IPW ATT estimator. The 2 variance estimators are compared via simulation studies and in a data analysis of the association between smoking and gene expression.
Keywords: confounding, estimating equations, exposure effect, Huber-White sandwich variance estimator, inverse probability weighting, observational data, treatment effect, variance estimation
Abbreviations
- ATE
average treatment effect
- ATT
average treatment effect in the treated
- IPW
inverse probability weighting
- METSIM
Metabolic Syndrome in Men
- SE
standard error
- SEE
stacked estimating equations
Observational studies are often used to draw inference about the effect of a treatment (or exposure) on an outcome of interest, especially in settings where randomized trials are not feasible. Common estimands for these types of analyses are the average treatment effect (ATE) and the average treatment effect in the treated (ATT). These estimands answer different causal questions, so it is critical to first establish the motivation and goals of inference when choosing a target estimand. Smoking, for example, is a commonly studied exposure where investigators may be interested in the ATT (1). With smoking as the exposure, the ATT considers the effect of smoking only among those who smoke. On the other hand, the ATE contemplates the counterfactual scenario where everyone in the population smokes versus when no one smokes, which may not be of interest from a public health perspective. The ATT is also often of interest in pharmacoepidemiology, where the effect of a certain drug in users of that drug is often the most relevant estimand for public health research (2–4). The ATT has utility across a range of areas within epidemiology where there is interest in effect of an exposure in the exposed population (5–7). Other contexts in which the ATT is often the target of inference include health behavior and policy (8–11), ecology and environmental management (12–14), criminology (15–17), and economics and public policy (18–21).
Inverse probability weighting (IPW) is often used for estimation of treatment effects from observational data, where confounding is expected in general. IPW estimators of the ATE and ATT can be computed by regressing the outcome on the exposure using weighted least squares, where the weights are functions of estimated propensity scores. The variance of the IPW ATE estimator is often estimated by assuming that the weights are known and then using the so-called “robust” (Huber-White) sandwich estimator, hereafter referred to as the naive estimator, which results in conservative standard errors (SEs) (22–25). Likewise, the variance of the IPW ATT estimator is sometimes estimated by assuming that the weights are known (2, 14, 26). Herein we prove that such an approach can produce either conservative or anticonservative SE estimates for the IPW ATT estimator. Consequently, confidence intervals derived using this approach will not be valid, in general. Instead, stacked estimating equations which account for the weight estimation can be used to compute a consistent, closed-form variance estimator for the IPW ATT estimator.
This paper is organized as follows. In the Methods section, we describe the IPW estimator for the ATT, and the corresponding variance estimators. The Results section includes asymptotic calculations and simulation studies of the variance estimators for 4 simple example scenarios, where we show that the robust variance estimator with the weights assumed known can be conservative or anticonservative. We also present an analysis of data from the Metabolic Syndrome in Men (METSIM) Study using the IPW ATT estimator and the variance estimators from the Methods section. Finally, we conclude with a discussion of the implications of these findings, limitations, and areas for future work. Derivations and software code for replicating the results presented in the main text are provided in Web Appendices 1–3 (available at https://doi.org/10.1093/aje/kwac014).
METHODS
IPW ATT estimator
Consider an observational study where the goal is to draw inference about the effect of a binary exposure A on an outcome Y. For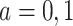 
, let 
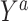denote the potential outcome had, possibly counter to fact, the exposure level been a. Let Y denote the observed outcome, such that 
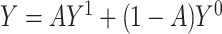. The ATT, the estimand of interest, is defined as 
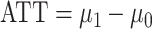, where 
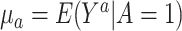for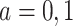 
denotes the mean potential outcome under treatment a among the treated individuals. For the case of a binary outcome, the ATT can be interpreted as the causal risk difference in the treated.
With observational data, there is potential for confounding because individuals are not randomized to exposure A. IPW can be used to adjust for confounding of the relationship between the exposure and the outcome. In particular, weights for each individual are estimated by first fitting a logistic regression model of A with predictors L based on a set of measured preexposure variables; then the IPW ATT estimator (27) equals
 |
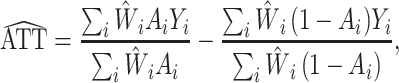(1) |
where the estimated weight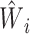 
for individual i is computed based on the estimated propensity score from the fitted logistic model as described in Web Appendix 1 and 
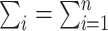. The 2 ratios in equation 1 are sometimes referred to as Hajek or modified Horvitz-Thompson estimators (25). Note that no outcome model for Y given A or L is assumed.
A convenient way to compute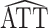 
using standard software entails fitting a simple linear regression model of Y on A by weighted least squares. The variance of 
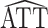is sometimes then estimated by assuming that the weights are known and computing the naive variance estimator, which is easily computed in standard software (e.g., sandwich in R (R Foundation for Statistical Computing, Vienna, Austria) or the REG procedure with the WHITE option in the MODEL statement in SAS (SAS Institute, Inc., Cary, North Carolina)). While computationally convenient, this estimator will not generally result in valid inference, as we show below.
Variance estimators of the ATT estimator
The asymptotic distribution of the IPW ATT estimator in equation 1 can be derived using standard estimating equation theory. In particular, in Web Appendix 1,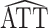 
is shown to be consistent and asymptotically normal. The asymptotic variance 
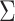of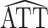 
and a corresponding simple closed-form consistent estimator 
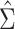are also given in Web Appendix 1. Thus, in large samples the variance of 
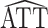can be approximated by 
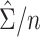, which below is referred to as the stacked estimating equations (SEE) variance estimator. The estimator 
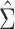of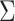 
is also often referred to as the empirical sandwich variance estimator (28).
The derivation of the result above considers the usual scenario in observational studies where the weights are estimated. Now suppose instead that the weights are assumed to be known, and therefore the propensity score need not be estimated. Let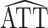 
* denote the estimator in equation 1 with 
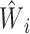replaced by 
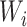(as defined in Web Appendix 1). Then, similar to the above, it is straightforward to show that 
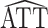* is consistent and asymptotically normal with asymptotic variance 
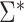. Likewise, a simple, closed-form, consistent estimator 
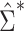of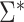 
is given in Web Appendix 1, where 
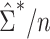denotes the naive variance estimator discussed at the end of the previous section. In Web Appendix 1, it is shown that 
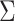and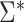 
differ by a constant that can be either positive or negative. Therefore, 
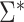can be either larger or smaller than 
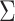, as we show via 4 simple examples in the next section. This suggests that using 
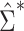may result in conservative or anticonservative inference.
Asymptotic calculations
In the Results section,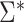 
and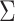 
are compared for 4 simple data-generating processes. Table 1 contains variable definitions and relationships for the variable L, the exposure A, and the potential outcomes 
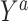, in each of 4 examples. In scenarios 1 and 2 the variable L is binary, and in scenarios 3 and 4, L is continuous (normal). In all 4 scenarios, the exposure A is binary and 
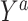given L is normally distributed with a standard deviation of 0.5. The marginal exposure probability 
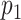and the population ATT value are also given in Table 1; these scenarios were chosen because they do not involve rare exposures or extreme effect sizes.
Table 1.
Distribution of L, Exposure A, and Potential Outcome Ya for 4 Different Hypothetical Scenarios of a Confounded Exposure-Outcome Relationship, Along With the Marginal Probability of Exposure and the ATT
| Scenario | L | Logit{P(A = 1|L = l)} | E(Ya|L = l) | p 1 a | ATT |
|---|---|---|---|---|---|
| 1 | Bern(0.5)b |
|
|
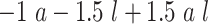
0.16 | −0.78 |
| 2 | Bern(0.3)b |
|
|
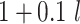
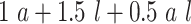
0.74 | 1.15 |
| 3 | N(0, 1)c |
|
|
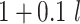
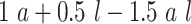
0.73 | 0.96 |
| 4 | N(1, 1)c |
|
|
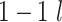
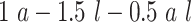
0.50 | 0.71 |
Abbreviation: ATT, average treatment effect in the treated.
a
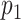= Pr(A = 1).
b Bern(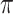
) = Bernoulli distribution with expectation 
.
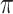c N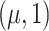
= normal distribution with mean μ and variance 1.
RESULTS
Asymptotic calculations
The asymptotic variances of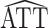 
and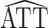 
* for scenarios 1–4 are shown in Table 2; software code for replicating the scenario 1 results is provided in Web Appendix 2. The ratio of asymptotic standard deviations, i.e., 
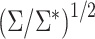, is also reported in Table 2 for the sake of comparison with the empirical results reported in the section below. Note from Table 2 that 
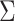may be substantially smaller or larger than 
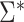. These asymptotic results suggest that 
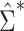will tend to yield anticonservative inferences in scenarios 1 and 3 and conservative inferences in scenarios 2 and 4. This is demonstrated empirically in the next section.
Table 2.
Asymptotic Variance of the ATT Estimator When Weights Are Unknown (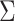
) and Known (
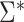) and the Ratio (Unknown:Known) of the Asymptotic Standard Deviations
| Scenario |
|
|
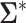
SD Ratio |
|---|---|---|---|
| 1 | 3.90 | 2.26 | 1.31 |
| 2 | 1.36 | 4.33 | 0.56 |
| 3 | 4.37 | 3.59 | 1.10 |
| 4 | 11.28 | 24.50 | 0.68 |
Abbreviations: ATT, average treatment effect in the treated; SD, standard deviation.
Simulation studies
For each scenario shown in Table 1, n = 1,000 independent and identically distributed copies of the variables L, A, and Y were generated for each of 1,000 data sets. For each simulated data set,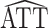 
was calculated using weights estimated by fitting propensity score model 1 in Web Appendix 1. Standard errors were estimated using both 
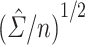and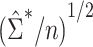 
. The former can be obtained with the geex package in R (29) or the CAUSALTRT procedure in SAS (30), and the latter is widely available in various R packages (e.g., sandwich, geeglm) or using SAS procedures (e.g., REG, GENMOD). The simulation study presented here and the data analysis described in the following section were conducted in R, version 3.6.3 (31), with variance estimates computed using the geex package; detailed example code is provided in Web Appendix 2. For each simulated data set, Wald 95% confidence intervals were constructed using each SE estimate.
Results from the simulation study are presented in Table 3. In all scenarios, 95% confidence intervals based on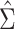 
achieved nominal coverage, whereas confidence intervals constructed using 
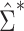either under- or overcovered. These results are in agreement with the asymptotic derivations in the Methods section. The average estimated SE (
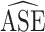) for both of the SE estimators was computed over the 1,000 simulated data sets for each scenario. The 
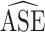ratios are reported in Table 3; as expected, these ratios are very similar to the asymptotic standard deviation ratios in Table 2. Additional simulation studies were conducted with the sample sizes 
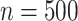and n = 2,000; the results, given in Web Table 1 of Web Appendix 3, were similar to those in Table 3.
Table 3.
Empirical Standard Error, Average Estimated Standard Error Using the SEE and Naive Variance Estimates, 95% Confidence Interval Coverage, and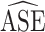 
Ratio (SEE:Naive) for Each Simulated Scenario
| Variance Estimator | ||||||
|---|---|---|---|---|---|---|
| SEE | Naive | |||||
| Scenario | ESE |
|
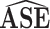
95% CI
Coverage |
|
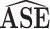
95% CI
Coverage |
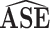
Ratio |
| 1 | 0.06 | 0.06 | 0.95 | 0.05 | 0.87 | 1.31 |
| 2 | 0.04 | 0.04 | 0.95 | 0.07 | 1.00 | 0.56 |
| 3 | 0.07 | 0.07 | 0.95 | 0.06 | 0.93 | 1.10 |
| 4 | 0.11 | 0.10 | 0.94 | 0.15 | 1.00 | 0.65 |
Abbreviations: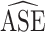 
, average estimated standard error; CI, confidence interval; ESE, empirical standard error; SEE, stacked estimating equations.
METSIM data analysis
The METSIM Study has been described and analyzed previously (32, 33). Participants in this population-based study were Finnish men aged 45–73 years, a subset of whom had RNA expression data recorded from an adipose tissue biopsy (
) (34). The exposure of interest A is current smoking (yes/no), and the outcomes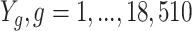 
, are normalized adipose tissue expression levels for each of 18,510 genes. Each of these gene expression outcomes will be analyzed separately. The target of inference is the ATT for each gene, that is, the average effect of current smoking on that gene’s expression in smokers. The set of variables L considered sufficient for satisfying the conditional exchangeability assumption (defined in Web Appendix 1) was age, alcohol consumption, body mass index (weight (kg)/height (m)2), exercise level, and vegetable consumption.
Logistic regression model 1 (Web Appendix 1), a model of current smoking on the set of variables L, was fitted to estimate the weights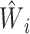 
for each individual. It is good practice to check that the mean of the estimated weights is close to its expected value. For the ATT weights, the expected value is 
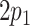; see Web Appendix 1 for details. The probability 
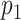is unknown here, but it can be estimated by 
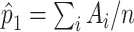. For the METSIM data, the mean of the estimated weights and the estimated expected value of the weights were both 0.34. The IPW estimator of the ATT for each gene was computed by fitting a separate linear regression model 
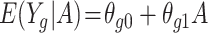via weighted least squares using the estimated weights. The same set of individuals and weights was used for each model. SEs for the estimated 
were estimated using both 
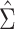and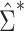 
.
Figure 1A shows the ratio of the 2 estimated SEs for each of the 18,510 genes, where the gray dashed line indicates equality of the 2 SE estimates. While most of the SE estimates using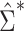 
were conservative (ratio < 1), there were hundreds of genes for which the estimates were anticonservative relative to 
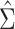. The difference in SE estimates was modest for most genes, but even small differences in SE estimates can substantially affect the P values. Figure 1B shows raw (i.e., unadjusted for multiple testing) P values for Wald tests of the null hypothesis
H0: 
using either SE estimate. Only the 50 genes with the smallest P values are shown. The top 50 genes as ranked by smallest P value differed between the 2 approaches, so there are 54 genes in total represented in Figure 1B. Neithe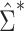r 
nor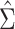 
always resulted in larger raw P values, which aligns with the results displayed in Figure 1A. In fact, P values were often 2–3 times larger or smaller when using 
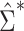compared with 
.
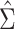Figure 1.
Comparison of stacked estimating equations (SEE) and naive standard error (SE) estimates for each gene in the Metabolic Syndrome in Men (METSIM) Study, 2005–2010. A) Ratio of estimated SEs, computed using 
and 
, for the average treatment effect in the treated (ATT) for each gene in an analysis of METSIM Study data. The vertical dashed line at 0 denotes equality of the 2 SE estimates. B) P values (unadjusted) for both methods of SE estimation for each of the top 50 genes as ranked by either method (54 genes are depicted in total).
DISCUSSION
In the context of variance estimation for the ATT estimator when using IPW, assuming the weights are known can result in either a conservative or an anticonservative variance estimate. This finding is contrary to the well-known result regarding variance estimation for the ATE—namely, that assuming that the weights are known results in conservative variance estimates (22–25). Four simple examples are provided demonstrating that SE estimates may be substantially larger or smaller depending on whether the weights are treated as known or estimated. Haneuse and Rotnitzky (35) derived a similar result in the continuous treatment (exposure) setting.
The variance estimator using stacked estimating equations is consistent, has a closed form, and can be easily computed using the geex package in R or the CAUSALTRT procedure in SAS. R code for the asymptotic calculations is provided in Web Appendix 2, along with a workflow for analyzing a simulated data set. The bootstrap is another approach to estimating the variance of the IPW ATT estimator (11, 21, 36). Performance of the bootstrap for the simulation study scenarios and the METSIM data analysis is illustrated in Web Table 2 and Web Figure 1 of Web Appendix 3. The bootstrap SE estimator performed similarly to the SEE estimator in the simulation studies, although the bootstrap estimator does not have a closed form and therefore is more computationally intensive than the SEE estimator.
The IPW ATT estimator and corresponding SEE variance estimator can be applied in settings where the outcome is continuous or binary. As we noted above, in the latter case the ATT can be interpreted as the casual risk difference in the treated. For binary outcomes, the causal risk ratio in the treated, that is,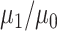 
, may also be of interest and can be consistently estimated by the ratio of Hajek estimators from equation 2. The results in this paper immediately apply to the ratio estimator as well. That is, the ratio estimator variance can be consistently estimated using SEE, whereas the robust variance estimator computed assuming that the weights are known may be conservative or anticonservative; this is illustrated in Web Tables 3–5 in Web Appendix 3 for 2 binary outcome examples.
The IPW ATT estimator has certain limitations which should be kept in mind when it is being used in analyses. The estimator is only valid (consistent) under the identifiability conditions described in Web Appendix 1, namely the stable unit treatment value assumption, positivity, and conditional exchangeability. Violations of these assumptions can lead to bias of the IPW estimator and under- or overcoverage of corresponding Wald confidence intervals. Positivity violations may be assessed by examining covariate overlap between treated and untreated individuals. Empirical results demonstrating variance estimator bias and confidence interval undercoverage when there is lack of covariate overlap are presented in Web Table 6 and Web Figure 2 of Web Appendix 3. In instances where there are positivity violations, analysis may be restricted (37) to strata of individuals where there is covariate overlap or may use methods other than IPW (such as g-estimation (38)) that are better suited for such settings.
In addition to the identifiability conditions, validity of the IPW ATT estimator relies on a correctly specified, finite dimensional parametric propensity score model. Recent extensions of M-estimation theory (39–41) could be utilized to study the large-sample behavior of ATT estimators in the presence of high-dimensional covariates. Future work could also compare different variance estimators of doubly robust estimators of the ATT that permit misspecification of the propensity score model.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics, Gillings School of Global Public Health, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States (Sarah A. Reifeis, Michael G. Hudgens). Dr. Sarah A. Reifeis is currently affiliated with Eli Lilly and Company, Indianapolis, Indiana.
This work was supported by the Chancellor’s Fellowship from the Graduate School at the University of North Carolina at Chapel Hill and by National Institutes of Health grant R01 AI085073.
The data that support the findings of this study are openly available in Gene Expression Omnibus (GEO) under accession number GSE70353 (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE70353).
We thank Dr. Michael Love for helpful comments.
This work was presented at the 2020 Joint Statistical Meetings conference (virtual), August 2–6, 2020, and at the 2021 Eastern North American Region Spring Meeting (virtual), March 14–17, 2021.
The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Conflict of interest: none declared.
REFERENCES
- 1. Moodie EEM, Saarela O, Stephens DA. A doubly robust weighting estimator of the average treatment effect on the treated. Stat. 2018;7(1):e205. [Google Scholar]
- 2. Brookhart MA, Wyss R, Layton JB, et al. Propensity score methods for confounding control in nonexperimental research. Circ Cardiovasc Qual Outcomes. 2013;6(5):604–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Taylor A, Westveld AH, Szkudlinska M, et al. The use of metformin is associated with decreased lumbar radiculopathy pain. J Pain Res. 2013;6:755–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Nduka CU, Stranges S, Bloomfield GS, et al. A plausible causal link between antiretroviral therapy and increased blood pressure in a sub-Saharan African setting: a propensity score-matched analysis. Int J Cardiol. 2016;220:400–407. [DOI] [PubMed] [Google Scholar]
- 5. Fink DS, Keyes KM, Calabrese JR, et al. Deployment and alcohol use in a military cohort: use of combined methods to account for exposure-related covariates and heterogeneous response to exposure. Am J Epidemiol. 2017;186(4):411–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Richardson DB, Keil AP, Kinlaw AC, et al. Marginal structural models for risk or prevalence ratios for a point exposure using a disease risk score. Am J Epidemiol. 2019;188(5):960–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Richardson DB, Keil AP, Edwards JK, et al. Standardizing discrete-time hazard ratios with a disease risk score. Am J Epidemiol. 2020;189(10):1197–1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Rawat R, Kadiyala S, McNamara PE. The impact of food assistance on weight gain and disease progression among HIV-infected individuals accessing AIDS care and treatment services in Uganda. BMC Public Health. 2010;10:316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Austin PC. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar Behav Res. 2011;46(3):399–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Boulay M, Lynch M, Koenker H. Comparing two approaches for estimating the causal effect of behaviour-change communication messages promoting insecticide-treated bed nets: an analysis of the 2010 Zambia Malaria Indicator Survey. Malar J. 2014;13:342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Were LPO, Were E, Wamai R, et al. The association of health insurance with institutional delivery and access to skilled birth attendants: evidence from the Kenya Demographic and Health Survey 2008–09. BMC Health Serv Res. 2017;17:454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Gross K, Rosenheim JA. Quantifying secondary pest outbreaks in cotton and their monetary cost with causal-inference statistics. Ecol Appl. 2011;21(7):2770–2780. [DOI] [PubMed] [Google Scholar]
- 13. Tamini LD. A nonparametric analysis of the impact of agri-environmental advisory activities on best management practice adoption: a case study of Québec. Ecol Econ. 2011;70(7):1363–1374. [Google Scholar]
- 14. Ramsey DS, Forsyth DM, Wright E, et al. Using propensity scores for causal inference in ecology: options, considerations, and a case study. Methods Ecol Evol. 2019;10(3):320–331. [Google Scholar]
- 15. Apel RJ, Sweeten G. Propensity score matching in criminology and criminal justice. In: Piquero AR, Weisburd D, eds. Handbook of Quantitative Criminology. New York, NY: Springer Publishing Company; 2010:543–562. [Google Scholar]
- 16. Morris RG. Exploring the effect of exposure to short-term solitary confinement among violent prison inmates. J Quantit Criminol. 2016;32(1):1–22. [Google Scholar]
- 17. Widdowson AO, Siennick SE, Hay C. The implications of arrest for college enrollment: an analysis of long-term effects and mediating mechanisms. Criminology. 2016;54(4):621–652. [Google Scholar]
- 18. Heckman JJ, Vytlacil E. Policy-relevant treatment effects. Am Econ Rev. 2001;91(2):107–111. [Google Scholar]
- 19. Addai KN, Owusu V, Danso-Abbream G. Effects of farmer-based-organization on the technical efficiency of maize farmers across various agro-ecological zones of Ghana. J Econ Dev Stud. 2014;2(1):141–161. [Google Scholar]
- 20. Marcus J. Does job loss make you smoke and gain weight? Economica. 2014;81(324):626–648. [Google Scholar]
- 21. Jawid A, Khadjavi M. Adaptation to climate change in Afghanistan: evidence on the impact of external interventions. Econ Anal Policy. 2019;64:64–82. [Google Scholar]
- 22. Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some regressors are not always observed. J Am Stat Assoc. 1994;89(427):846–866. [Google Scholar]
- 23. Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Stat Med. 2004;23(19):2937–2960. [DOI] [PubMed] [Google Scholar]
- 24. Wal WM, Geskus RB. ipw: an R package for inverse probability weighting. J Stat Softw. 2011;43(13):1–23. [Google Scholar]
- 25. Hernán M, Robins J. Causal Inference: What If. Boca Raton, FL: Chapman & Hall/CRC Press; 2020. [Google Scholar]
- 26. Pirracchio R, Carone M, Rigon MR, et al. Propensity score estimators for the average treatment effect and the average treatment effect on the treated may yield very different estimates. Stat Methods Med Res. 2016;25(5):1938–1954. [DOI] [PubMed] [Google Scholar]
- 27. Sato T, Matsuyama Y. Marginal structural models as a tool for standardization. Epidemiology. 2003;14(6):680–686. [DOI] [PubMed] [Google Scholar]
- 28. Stefanski L, Boos D. The calculus of M-estimation. Am Stat. 2002;56(1):29–38. [Google Scholar]
- 29. Saul BC, Hudgens MG. The calculus of M-estimation in R with geex. J Stat Softw. 2020;92(2):1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. SAS Institute Inc. The CAUSALTRT procedure. In: SAS/STAT 15.1 User’s Guide. Cary, NC: SAS Institute Inc.; 2018:2365–2423. [Google Scholar]
- 31. R Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2020. [Google Scholar]
- 32. Civelek M, Wu Y, Pan C, et al. Genetic regulation of adipose gene expression and cardio-metabolic traits. Am J Hum Genet. 2017;100(3):428–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Reifeis SA, Hudgens MG, Civelek M, et al. Assessing exposure effects on gene expression. Genet Epidemiol. 2020;44(6):601–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Laakso M, Kuusisto J, Stančáková A, et al. The Metabolic Syndrome in Men study: a resource for studies of metabolic and cardiovascular diseases. J Lipid Res. 2017;58(3):481–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Haneuse S, Rotnitzky A. Estimation of the effect of interventions that modify the received treatment. Stat Med. 2013;32(30):5260–5277. [DOI] [PubMed] [Google Scholar]
- 36. Imbens GW. Nonparametric estimation of average treatment effects under exogeneity: a review. Rev Econ Stat. 2004;86(1):4–29. [Google Scholar]
- 37. Westreich D, Cole SR. Invited commentary: positivity in practice. Am J Epidemiol. 2010;171(6):674–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Vansteelandt S, Joffe M. Structural nested models and g-estimation: the partially realized promise. Stat Sci. 2014;29(4):707–731. [Google Scholar]
- 39. Wolfson J. EEBoost: a general method for prediction and variable selection based on estimating equations. J Am Stat Assoc. 2011;106(493):296–305. [Google Scholar]
- 40. Johnson BA, Lin D, Zeng D. Penalized estimating functions and variable selection in semiparametric regression models. J Am Stat Assoc. 2008;103(482):672–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. He X, Shao Q-M. On parameters of increasing dimensions. J Multivar Anal. 2000;73(1):120–135. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.