Prediction of the trans-stenotic pressure gradient with arteriography-derived hemodynamic features in patients with idiopathic intracranial hypertension

Abstract

The pathogenesis of idiopathic intracranial hypertension (IIH) is attributed to segmental stenosis of the venous sinus. The current treatment paradigm requires a trans-stenotic pressure gradient of ≥8 mmHg or ≥6 mmHg threshold. This study aimed to develop a machine learning screening method to identify patients with IIH using hemodynamic features. A total of 204 venous manometry instances (n = 142, training and validation; n = 62, test) from 135 patients were included. Radiomic features extracted from five arteriography perfusion parameter maps were selected using least absolute shrinkage and selection operator and then entered into support vector machine (SVM) classifiers. The Thr8-23-SVM classifier was created with 23 radiomic features to predict if the pressure gradient was ≥8 mmHg. On an independent test dataset, prediction sensitivity, specificity, accuracy, and AUC were 0.972, 0.846, 0.919, and 0.980, respectively (95% confidence interval: 0.980–1.000). For the 6 mmHg threshold, thr6-28-SVM incorporated 28 features, and its sensitivity, specificity, accuracy, and AUC were 0.923, 0.956, 0.935, and 0.969, respectively (95% confidence interval: 0.927–1.000). The trans-stenotic pressure gradient result was associated with perfusion pattern changes, and SVM classifiers trained with arteriography perfusion map-derived radiomic features could predict the 8 mmHg and 6 mmHg dichotomized trans-stenotic pressure gradients with favorable accuracy.

Introduction

Patients with idiopathic intracranial hypertension (IIH) present an elevation in intracranial pressure (ICP) without a definite etiology. Common symptoms vary from headaches and pulsatile tinnitus to the most feared visual loss due to chronic papilledema. The standard treatment paradigm usually starts with oral acetazolamide and weight management, but many patients fail to respond. This treatment is followed by more aggressive procedures such as ventriculoperitoneal shunting and optic nerve fenestration. ¹ As the exploration of the underlying pathophysiology advances, more data suggest that elevated ICP is associated with lateral sinus stenosis and its elimination may lead to a significant reduction in ICP.^2,3 Since the first endovascular attempt to resolve IIH symptoms by Higgins et al., numerous studies^{4 –6} as well as our own registry study ⁷ have proven the efficacy and safety profile of venous sinus stenting for IIH. According to a recent review, over 90% of treated patients experienced significant papilledema improvement, and the major complication rate was as low as 1.5%. ⁸

However, venous sinus stenting is not a panacea for all IIH cases; it is only indicated for patients with a gradient of at least 6–8 mmHg obtained using venous manometry according to the guidelines and established conventions. ⁹ Experimental data suggested that a correction of 0.7 mmHg gradient pressure in the superior sagittal sinus lowers the opening pressure (OP) by 1 cmH₂O. ¹⁰ The current Dandy’s diagnostic criteria for IIH require an OP of greater than or equal to 25 cmH₂0; thus, an OP of 5–7 cmH₂0 or a gradient of 3.5–4.9 mmHg should be resolved. Since a gradient residual of 0–2 mmHg exists after stenting, setting 6 mmHg or 8 mmHg as the threshold for stenting is reasonable.^11,12 However, venous manometry procedures require femoral venous puncture, local anesthesia, ⁵ pressure guidewire, and microcatheter, which add pain, extra radiation exposure, and extra costs to the patients. In addition, the Dandy criteria are not a good calibration tool to identify patients with a large pressure gradient. In a recent study including 104 patients with IIH, only 58% of patients were found to have a pressure gradient of ≥8 mmHg. ¹³

Therefore, developing less aggressive tools that can identify patients with IIH with a significant pressure gradient without venous manometry is clinically useful. This study aimed to construct machine learning classifiers trained on arteriography-derived hemodynamic features that can predict the trans-stenotic pressure gradient at an appropriate level of accuracy.

Materials and methods

Patient enrollment

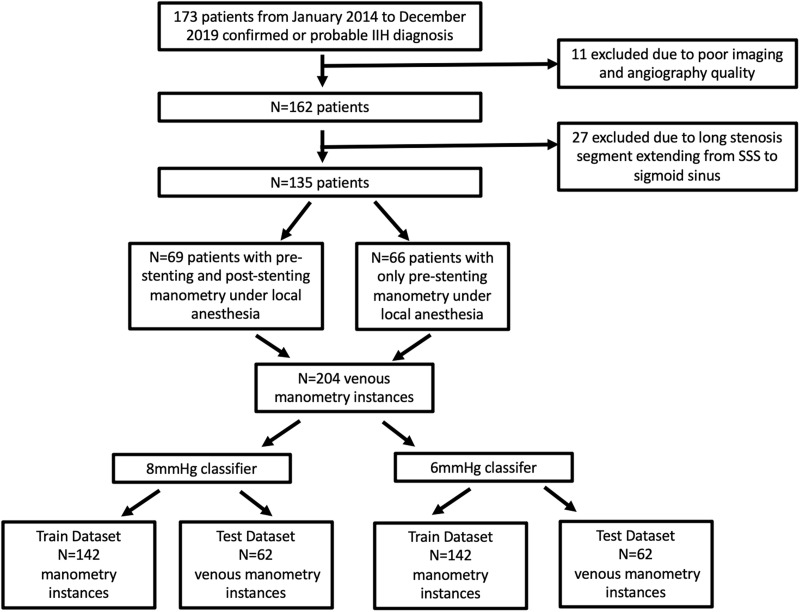
In the cohort of our trial, we retrospectively selected 135 out of 173 patients from our registry named safety and efficacy of endovascular stenting for idiopathic intracranial hypertension with venous sinus stenosis ⁷ (Figure 1). Eleven patients were excluded due to poor imaging and angiography quality and 27 due to long stenosis segment extending from the SSS to the sigmoid sinus. According to the Helsinki Declaration of 1975, written informed consent was obtained from all patients, and the study was approved by the ethical committee of Beijing Tiantan Hospital, Capital Medical University (ethical statement number: KY2016-039-02). 66 patients had only pre-stenting manometry obtained under local anesthesia and 69 of them had also post stenting manometries under local anesthesia. A total of 204 manometry instances were included. The inclusion and exclusion criteria for these patients were based on the trial protocol. In brief, venous stenting is only indicated for patients with IIH with a definite localized lateral sinus stenosis on digital subtraction angiography (DSA), and the pressure gradient across the stenotic segment should be equal to or greater than 8 mmHg under local anesthesia. The entire dataset was randomly split into a training dataset and an independent test dataset at a ratio of 7:3.

Figure 1.

Flowchart of inclusion and exclusion of manometry instances.

Manometry

For each patient, pressure gradients were defined as the difference in pressure between the distal and proximal segment of the transverse sinus. All manometries were performed under local anesthesia via femoral vein access using a microcatheter Rebar-27 (ev3 Neurovascular, Irvine, CA, USA). The hub of Rebar-27 was connected to the pressure monitoring kit DELTRAN II, 3 cc/hr Flow Rate (Utah Medical Products, Midvale, Utah, USA).

Arteriography image acquisition, preprocessing, and time density curve (TDC) parameter calculation

DSA images were acquired on the Artis station (Siemens, Germany), Terra Station (GE, United States), AW6302 Station (GE, United States), and 722038-153 Station (Philips, Netherlands) at Towne’s position and anteroposterior view. Each DSA run was obtained during a 4-mL/s injection of Vispaque (GE Healthcare Ireland Limited, Carrigtohill, Munster, Ireland) through a 5 F angiographic catheter at the cervical segment of the ICA, with a total volume of 6 mL. Acquisition parameters for the majority of DSA sequences were as follows: pixel spacing, 0.217 × 0.217; median peak tube voltage, 81.2 kV [interquartile range (IQR): 77.9–83.8]; window center, 2047; window width, 4095; cine rate, 4; median of frames for each DICOM, 49.0 (IQR: 41–58); and row and column size of each frame, both 1024. The mask and bolus frames were registered before subtraction. To eliminate the index hemisphere opacification during the arterial and venous phases, we injected contrast in the contralateral ICA.

For each DSA run, we calculated the following five contrast flow-related parameters from a TDC at each pixel: cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT), time to peak (TTP), and maximum contrast media concentration (MAX) (Figure 1). We used a simplified gamma variate function to fit the TDC, ¹⁴ and codes for image preprocessing and TDC fitting were written in Python (version 3.6.1), as detailed in our previous publication. ¹⁵ TTP and MAX were defined as the time when the TDC reached its maximum value and the maximum value per se, respectively. MTT was obtained by measuring the average residence time of the contrast and was calculated as β (α + 1). CBV was a relative index of the blood flow volume and was calculated by integrating the TDC over 10 s. CBF was calculated by dividing the CBV by MTT.

Radiomic feature extraction and stable feature selection

To extract the radiomic features, we initially created a two-dimensional map, on which the pixel value represented the maximum intensity value across all the frames at each coordinate. Two interventional neuroradiologists delineated the region of interest (ROI) on the stenosed transverse sinus separately, and both were blinded to the true pressure gradient. On each parameter map, we extracted 18 first-order statistic features, 22 gray-level co-occurrence matrix (GLCM) texture features, 16 gray-level run-length matrix (GLRLM) texture features, 280 Laplacian of Gaussian filtered image features (LoG) and 224 wavelet features. On the TTP map, we extracted nine two-dimensional shape features. A total of 2809 radiomic features were extracted from each DSA run using an open-source Python package called PyRadiomics (version 3.0). ¹⁶ For gray-level discretization, a fixed bin width of 0.02 was used. The pixel spacing of each map was resampled to 0.4 mm by 0.4 mm. The stability of radiomic features was tested using intraclass coefficient correlation (ICC) between two ROI contours; only features with ICC equal to or greater than 0.8 were considered stable and were entered into the following classifier construction. The nomenclature of radiomic features includes parameter map, image type, feature class, and feature name. For example, “TTPwavelet.LH_firstorder_Kurtosis” was the feature Kurtosis belonging to the first order class, extracted on a wavelet-transformed TTP map.

Machine learning modeling and statistics

We built an SVM model with a radial kernel to predict the 6 mmHg dichotomized pressure gradient and another SVM model to predict the 8 mmHg dichotomized pressure gradient. Informative radiomic features were selected using the least absolute shrinkage and selection operator (LASSO) algorithm with five-fold cross validation. The lambda value that gave the maximum cross-validated area under the curve (AUC) of LASSO fit was chosen, and features with non-zero coefficients were then selected. The hyperparameters of the SVM classifier were tuned using a grid-search method. Two hyperparameters were tuned, and both the gamma value and cost parameter C were tested for 0.0001, 0.001, 0.01, 0.1, 1.0, 10, and 100. The combination of gamma and parameter C, which maximized the prediction accuracy of the SVM classifier, was finally chosen. Classifier performance was evaluated on the training, test, and test-2 datasets drawn by a junior neurointerventionalist. Performance metrics, including sensitivity, specificity, accuracy, F1-score, and AUC, were calculated. To improve the interpretability of our SVM classifier, we computed feature importance using the “permutation importance” method. The importance of the explanatory variable was ranked using the mean variable importance of over 1000 permutations. The study process is summarized in Figure 2.

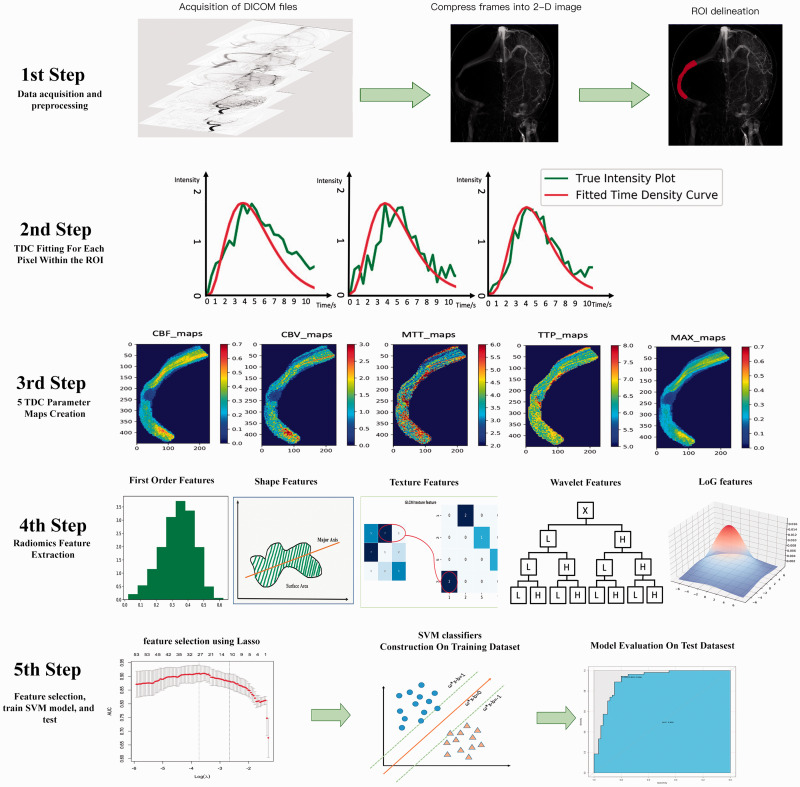
Figure 2.

Illustration of the study process. DICOM files were compressed into one frame, so that all pixels opacified by the contrast agent could be shown on the two-dimensional image, then ROIs were delineated by two neurointerventionalists blinded to each other’s result (1st step). A pixel-wise calculation of the time density curve (TDC) was performed (2nd step), and five perfusion parameters were derived from the TDC for each pixel. Five perfusion maps were then generated for each patient (3rd step). On each map, we extracted five group perfusion-related radiomic features, including first-order statistical features, shape features, texture features, wavelet features, and LoG features (4th step). Informative features were then selective using LASSO, and these features were entered into the SVM model to predict the pressure gradient, and model’s performance was further tested on an independent test dataset (5th step).

For continuous variables, after assessing normality (Shapiro-Wilk test), the difference between groups was calculated using Student’s t-test or Wilcoxon rank-sum test, as appropriate. For categorical variables, Fisher’s exact test was used. For descriptive statistics, continuous variables were represented as medians with interquartile range or mean with standard error, and categorical variables as the number of events with frequencies. Statistical significance was set at p < 0.05. All statistical analyses were conducted using R software (version 3.6.1; R Foundation for Statistical Computing, Vienna, Austria). Packages used for classifier construction and feature importance calculation were “e1071,” “caret,” “DALEX,” and “pROC.”

Results

Baseline demographics

In total, 204 manometry instances from 135 patients were included in the study, of which 69 (33.8%) were measured after venous sinus stenting. Females were predominant in the population, and 82.4% (168/204) of the pressure recordings were obtained from them. The median age at manometry and body mass index were 36.0 years (IQR: 28.0–44.0) and 26.9 kg/m² (IQR: 24.0–30.0), respectively. The median pressure gradient was 10.0 mmHg (IQR: 3.00–15.5), and the maximum gradient measured was 39.0 mmHg. A total of 118 (57.8%) and 128 (62.7%) pressure gradients were higher than 8 mmHg and 6 mmHg, respectively. All manometry instances were randomly split into a training dataset (n = 142) and a test dataset (n = 62) at a ratio of 7:3. As shown in Table 1, the baseline characteristics showed no statistical differences between the two datasets.

Table 1.

Baseline clinical and manometry characteristics.

Characteristics	Training data (n = 142)	Test data (n = 62)	P value
8 mmHg model
Sex (male/female)	23/119 (19.3%)	13/49 (26.5%)	0.429
Pressure gradient <8 mmHg (yes/no)	60/82 (73.2%)	26/36 (72.2%)	1.000
Age at manometry, years	36.0 (28.0, 44.0)	35.5 (29.0, 44.8)	0.990
Body mass index, kg/m2	26.2 (23.6, 30.0)	27.9 (25.7, 29.9)	0.118
Pressure gradient, mmHg	10.8 (3.00, 15.9)	10.0 (3.00, 14.0)	0.627
6 mmHg model
Sex (male/female)	26/116 (22.4%)	10/52 (19.2%)	0.842
Pressure gradient <6 mmHg (yes/no)	53/89 (59.6%)	23/39 (59.0%)	1.000
Age at manometry, years	36.0 (29.0, 44.0)	33.5 (27.0, 44.0)	0.202
Body mass index, kg/m2	27.5 (24.0, 30.0)	26.20 (23.8, 30.0)	0.343
Pressure gradient, mmHg	10.0 (3.00, 15.88)	8.00 (3.00, 13.00)	0.542

Radiomic feature extraction and informative feature selection

In each feature class, the percentage of stable features exceeded 90%. Detailed percentages of stable features in each perfusion map are summarized in Supplementary Table 1. For the 8 mmHg threshold model, the LASSO algorithm selected 23 informative features with non-zero coefficients, including one shape feature named sphericity, two features from the CBF map, three from the CBV map, eight from the MAX map, one from the MTT map, and eight from the TTP map. For the 6 mmHg model, 28 features, including one shape feature named sphericity, two features from the CBF map, seven from the CBV map, six from the MAX map, two from the MTT map, and 10 from the TTP map, were selected (Supplementary Table 2).

Model performance evaluation and feature ranking

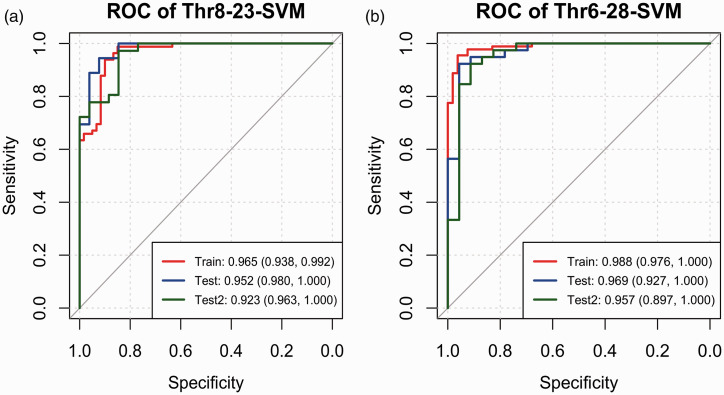
Using the informative features selected by LASSO, we created the thr8-23-SVM model to predict if the gradient was below the 8 mmHg threshold and the thr6-28-SVM model to predict the 6 mmHg dichotomized pressure gradient. Both models were trained on the training dataset, tested on the test dataset, and further validated on the test dataset (denoted as test-2) calculated from ROIs delineated by a junior neurointerventionalist. The tuning of the hyperparameters is plotted in Supplementary Figure 1. The confusion matrix-derived model performance metrics (Table 2) and AUC values (Figure 3) for both models all exceeded 0.900, except that the specificity of the thr8-23-SVM model was approximately 0.850 for the three datasets.

Table 2.

Model performance metrics.

Metrics	Thr8-23-SVM			Thr6-28-SVM
	Train	Test	Test-2a	Train	Test	Test-2a
Sensitivity	0.976	0.972	0.944	0.966	0.923	0.923
Specificity	0.850	0.846	0.846	0.925	0.956	0.913
Accuracy	0.923	0.919	0.903	0.950	0.935	0.919
F1-score	0.936	0.933	0.919	0.961	0.947	0.935
AUC (95% CI)	0.965	0.980	0.963	0.988	0.969	0.957

^aTest-2 is the dataset of radiomic features extracted from ROIs drawn by a junior neurointerventionalist.

Figure 3.

ROC curve for thr8-23-SVM (a) and thr6-28-SVM models (b) on the training dataset (red line), test dataset (blue line) and test 2 dataset (dark green line). The AUC values and 95% confidence intervals are listed on the bottom right corner.

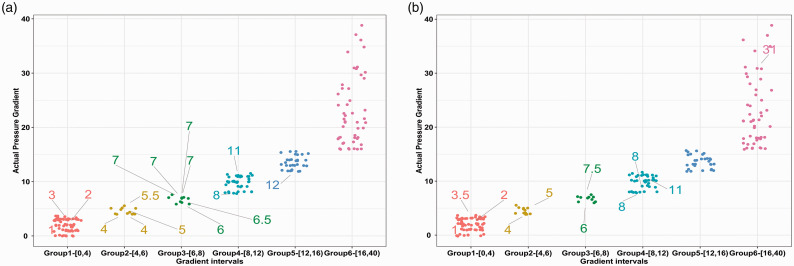
We then divided the pressure gradient instances into six intervals to further explore the distribution of misclassified cases. As shown in Figure 4(a), thr8-23-SVM had most of its false positive predictions in the 6–8 mmHg subgroup (6/10, 60.0%), followed by the 4–6 mmHg subgroup (4/12, 33.3%). This finding was similar for the thr6-28-SVM model, but the number of misclassified cases was much lower in both intervals (Figure 4(b)). For both models, the false positive prediction rate was 4.69% in the 0–4 mmHg interval.

Figure 4.

Scatterplot of misclassified pressure gradient recordings for the thr8-23-SVM (a) and thr6-28-SVM models (b). The X axis was subdivided into six intervals, and the Y axis denoted the actual pressure gradient for each manometry instance in each group. False predictions were labeled with their true pressure gradient value, and the line did not point exactly to the dot; thus, the dots were jittered to avoid overlapping. For example, in Figure a (Group 2), there were four false predictions; the true gradient values were 5 mmHg, 5.5 mmHg, 4 mmHg, and 4 mmHg, but these 4 instances were predicted to be over the 8 mmHg threshold; therefore, they were false-positive predictions.

In Table 3, we list the top five important features ranked using the “permutation method” for both models. Notably, the shape feature sphericity was ranked second in the thr6-28-SVM model and ranked 18th in the thr8-23-SVM model, and its absence alone resulted in an accuracy loss of 0.864%.

Table 3.

Top 5 features of the two models.

Feature ranking	Accuracy loss
Thr8-23_SVM model
TPoriginal_glrlm_RunLengthNonUniformityNormalized	3.68%
MAXwavelet.LL_firstorder_skewness	3.03%
TTPlog.sigma.3.0 mm_glcm_MaximumProbability	2.60%
CBFwavelet.LL_glcm_Correlation	2.60%
MAXlogsigma.5.0 mm_glcm_MaximumProbability	2.49%
Thr6-28_SVM model
CBFwavelet.LL_glcm_Correlation	4.42%
TTPoriginal_shape2D_Sphericity	3.36%
CBFlog.sigma.4.0 mm_glrlm_LowGrayLevelRunEmphasis	2.73%
MAXlog.sigma.3.0 mm_glcm_Imc2	2.73%
CBVwavelet.HL_glrlm_GrayLevelNonUniformity	1.89%

Discussion

In this study, we created two SVM classifiers based on DSA perfusion radiomic features that could predict both the 8 mmHg dichotomized and the 6 mmHg dichotomized venous pressure gradients with adequate accuracy for patients with IIH. These models offer a new tool to identify candidate patients with IIH who may benefit from venous sinus stenting.

The rationale of our method is rooted in the fact that, on trans-stenotic images, intensity attenuation metrics represent a functional assessment of the stenosis beyond the numeric percent stenosis. Similar to percutaneous coronary intervention, fractional flow reserve serves as the gold standard hemodynamic evaluation of coronary stenosis, ¹⁷ which measures the ratio of distal coronary pressure of the stenosis to the aortic pressure in an invasive manner using a pressure wire. However, this pressure measurement can be accurately simulated from CTA images using the computational flow dynamic technique.^18,19 For intracranial arterial stenosis, estimating trans-stenotic hemodynamics can also be achieved using intensity-based metrics as a relative index of blood flow. In its simplest form, Liebeskind et al. used the distal/proximal signal intensity ratio (SIR) on TOF-MRA images to identify high-risk intracranial lesions. ²⁰ SIR was reproducible with high interobserver agreement, ²¹ and their results indicated that SIR <0.9 predicted an elevated stroke risk in the territory for patients with intracranial artery stenosis and was independently associated with downstream cerebral hypoperfusion as evidenced on CTP maps.^20,22 Compared with SIR, which only measures the trans-stenotic intensity change, a more robust approach was the addition of time parameters by tracking the contrast bolus and extracting perfusion features from a TDC. Perfusion features, including the time to peak, MTT, cerebral blood flow, and CBV, can be derived from MRI perfusion images and DSA images.^23,24 The application of these features has expanded to clinical settings, such as the prediction of aneurysm occlusion, ²⁵ AVM rupture ²⁶ and AVM embolization outcome. ²⁷ Most of the studies focused on flow estimation on arteries, but not until very recently, this method was translated into the venous sinus.

Almadidy et al. first derived the venous stenosis index (VSI) from color-coded DSA images to classify hemodynamically significant stenosis using the 8 mmHg criteria. ²⁸ Smaller VSI values have been observed in less stenosed and post-stented sinuses. In a cohort of 11 patients, VSI ≥1.36 had a sensitivity of 72.7% and an AUC of 0.82 in predicting whether the gradient pressure was above 8 mmHg. ²⁸ By definition, VSI represents the cerebral blood flow reduction rate across the sinus stenosis, which is equivalent to the CBV value. This study proved that the contrast flow pattern change existed in patients with IIH and served as a good measure of pressure gradient. However, the color-coded DSA software cannot calculate the MTT and CBF parameters in a pixel-wise manner. ²⁹ The proposed VSI used a mean value calculated on a manually selected ROI, and the choice of the ROI size and location seemed arbitrary, which may lead to poor interrater reliability. ³⁰

To ease the problem of ROI placement and take advantage of the pattern change information hidden in the pixel-wise calculated perfusion maps, we adopted a radiomic approach to decode the flow patterns within an ROI that incorporated the stenosed sinus segment as a whole. Similar to the VSI, which calculated the mean value of CBV, our two SVM models also incorporated mean value formed perfusion parameters, namely, MAXwavelet.HH_firstorder_Mean for thr8-23-SVM model and TTPwavelet.LH_firstorder_Median for thr6-28-SVM model. In contrast to VSI, which could predict the gradient group very accurately, these two features ranked 20th and 19th places in their models, and their absence can only cause a slight accuracy loss. A pivotal role in both models was features that represented the pixel distribution and feature map textures. These features were able to represent flow changes due to focal stenosis, but the interpretation of their true clinical relevance was difficult. The only instinctively comprehensible feature incorporated into both models was the shape feature called sphericity.

Sphericity was the second most important explanatory feature in the thr6-28-SVM model, and its absence led to a 3.36% decrease in prediction accuracy. Focal stenosis of the venous sinus can be identified in up to 33% of patients in a general population and in more than 90% in patients with IIH. Visually rated stenosis has been proven to be able to identify patients with IIH with a sensitivity and specificity of 93%,^31,32 the influence of stenosis rate on the pressure gradient has not been completely elucidated. Our two-dimensional shape feature sphericity was the first index to quantify stenosis severity; it is the ratio of the perimeter of the ROI to the perimeter of a circle with the same surface area as the ROI. Therefore, smaller sphericity values denote more severe stenosis, which is in accordance with our result that patients with IIH with higher pressure gradients had smaller sphericity values. Of note, sphericity ranked 18th place in the thr8-23-SVM model. Its decreasing importance in models with a higher threshold may indicate that morphological change was the initiating factor of elevated pressure, but as the pressure increased, more hemodynamic changes were involved to further accelerate the disease progression. The drawback of sphericity lies in its two-dimensional nature. Although the Towne’s position best delineated the stenosis in most patients, stenosis was most evident on the lateral oblique view in some cases. Therefore, we speculate that numeric shape features extracted from the three-dimensional image are promising for further improving the classifier’s performance.

In our study, we trained a binary model to predict two dichotomized gradients, rather than a regression model that estimated the continuous pressure gradient. This was mainly because clinical decision-making was based on these two thresholds. Theoretically, a correction of a 7 mmHg gradient decreases the ICP of 9–10 cmH₂O, and the consensus now is that venous stenting should be reserved for patients with IIH with a minimum pressure gradient of 6–8 mmHg.^9,33 For the 8 mmHg threshold model, most of the misclassified instances were adjacent to the threshold. For these borderline gradient values, because both catheter manometry had a certain degree of fluctuation of approximately 2 mmHg in measurements, the clinical significance of these mispredictions needs to be further explored in a clinical setting. In other words, even though we predicted the gradient instances within the 6–8 mmHg interval false positively as above the threshold, if sinus stenting was performed following the prediction result, those patients might still expect a symptom improvement. However, the 4.69% false-positive predictions in the 0–4 mmHg intervals for both models lead to excess treatment. This reflected in our classifiers that had some limitations because gradients below 4 mmHg generally required no venous stenting.

We failed to make our models totally non-invasive because current imaging protocols did not include CT or MRI images that could be used to calculate the TDC. Other approaches capable of realizing non-invasive manometry include computational hemodynamic modeling techniques and four-dimensional (4D) flow MRI techniques. The pioneering work by Levitt et al. first reported that the flow and wall shear stress throughout the sinuses were higher in patients with pathologic pressure gradients than in those without them. ³⁴ However, these differences are not sufficient to predict the 8 mmHg or 6 mmHg dichotomized pressure status. Moreover, two factors restrict it from becoming totally non-invasive and accurate. First, patient-specific pressure boundary conditions cannot be obtained without venous manometry. As reported by many studies, the pressure values of venous sinuses are quite variable, and the standard deviation of pressure recordings at the transverse sinus was reported to be over 8 mmHg. ³³ Second, patient-specific anatomic models should not be simplified into a tubular form, because in the settings of IIH, the collected occipital emissary vein and vein of Labbe are major outflow channels. ³⁵ In our unpublished 4D flow data, venous sinuses proximal to the stenosis had a much larger flow than the distal segment, indicating the existence of tributary venous outflows proximal to the stenosis. Recently, 4D flow has been applied to explore the pressure distribution in venous sinus lesions. Ding et al. reported a significant correlation between the trans-stenotic velocity difference and pressure gradient (R = 0.675). ³⁶ However, as reported in literature and our own data, the current 4D flow MRI-derived venous sinus pressure, which is calculated using the Navier–Stokes equation, is an order of magnitude smaller than venous manometry data. The development of a 4D flow MRI-based substitute for venous manometry requires additional data and experimental modeling.

Conclusion

In conclusion, the two SVM binary classifiers with hemodynamic radiomic features derived from the DSA perfusion maps were able to predict the trans-stenotic pressure gradient at an acceptable accuracy. This result suggests that analysis of the contrast hemodynamics on arterial DSA images may be a good surrogate for retrograde venography and manometry. Our classifiers lacked external validation, and a test set from DSA images acquired at different centers is warranted to further validate their generalizability.