Significance
The spatial structure of microbial communities can influence their ecological and evolutionary dynamics. Gut bacteria in particular experience large variations in growth conditions along the colon. However, little is known about how these spatial growth processes influence the long-term genetic turnover of the gut community. Here we develop a mathematical framework to predict how stochastic evolutionary forces emerge from simple models of bacterial growth in the intestinal lumen. This framework describes how fluid flow and growth combine to shape the frequencies of mutations at different spatial locations. We show that over longer timescales, these mutation dynamics can often be captured by coarse-grained models that lack explicit spatial structure, even when there is strong spatial variation in species-level composition.
Keywords: natural selection, genetic drift, spatial structure, separation of timescales
Abstract
The genetic composition of the gut microbiota is constantly reshaped by ecological and evolutionary forces. These strain-level dynamics are challenging to understand because they depend on complex spatial growth processes that take place within a host. Here we introduce a population genetic framework to predict how stochastic evolutionary forces emerge from simple models of microbial growth in spatially extended environments like the intestinal lumen. Our framework shows how fluid flow and longitudinal variation in growth rate combine to shape the frequencies of genetic variants in simulated fecal samples, yielding analytical expressions for the effective generation times, selection coefficients, and rates of genetic drift. We find that over longer timescales, the emergent evolutionary dynamics can often be captured by well-mixed models that lack explicit spatial structure, even when there is substantial spatial variation in species-level composition. By applying these results to the human colon, we find that continuous fluid flow and simple forms of wall growth alone are unlikely to create sufficient bottlenecks to allow large fluctuations in mutant frequencies within a host. We also find that the effective generation times may be significantly shorter than expected from traditional average growth rate estimates. Our results provide a starting point for quantifying genetic turnover in spatially extended settings like the gut microbiota and may be relevant for other microbial ecosystems where unidirectional fluid flow plays an important role.
The human gut harbors a diverse microbial ecosystem that plays an important role in maintaining health and reducing susceptibility to disease (1, 2). The composition of the gut microbiota is shaped by interactions between hundreds of different species (3, 4), which must continually reproduce in order to balance their daily excretion in feces (5, 6). These high rates of cell turnover create enormous opportunities for rapid evolutionary change: the trillions of bacteria within a single human colon produce more than a billion new mutations every day (7), and tens of thousands of bacterial generations will typically elapse within a single human lifetime (1, 8). Consistent with these estimates, a growing number of empirical studies, ranging from experimental evolution in mouse models (9–12) to longitudinal sequencing of human subjects (7, 13–20), have shown that genetic variants can sweep through resident populations of gut bacteria on timescales of weeks and months. The causes and consequences of this genetic turnover could play an important role in mediating the stability and resilience of this diverse microbial ecosystem (21).
A central challenge in understanding these dynamics stems from the complex structure of the gut environment. While the frequencies of genetic variants are usually measured in homogenized fecal samples, most microbial growth occurs in the spatially extended setting of the large intestine. However, little is currently known about how this spatial structure influences the dynamics that are observed in sequenced fecal samples. This makes it difficult to draw quantitative conclusions from existing genetic data: What does it mean if the frequency of a variant increases dramatically over a few days or if it eventually declines in frequency a few weeks later? Is it reasonable to interpret these coarse-grained measurements using well-mixed models from population genetics, or are spatially explicit models necessary for quantitative comparisons with data?
Previous studies of gut microbial biogeography have shown that the underlying growth conditions vary over a huge range of length scales, from the micrometer scales of intercellular interactions (22–24) to macroscopic compartments like the mucosa, lumen, and intestinal crypts (25). Even within the comparatively simpler environment of the central lumen—thought to be the primary site of growth for some of the most abundant Bacteroides and Firmicutes species (26)—significant longitudinal gradients are established by the basic anatomy of the intestinal tract: primary nutrients are supplied at one end of the colon, where microbial densities are relatively low, and are rapidly consumed by bacteria in the ascending colon (27). The constant influx of fluid, along with additional mixing from contractions of the intestinal walls (26, 28), causes both the bacteria and their metabolic by-products to drift toward lower regions of the colon, where they are eventually excreted in feces. These physical processes combine to produce large gradients in nutrient concentrations, pH, and excretion rates across the longitudinal axis of the large intestine (27–29), which can have important consequences for the relative growth rates and abundances of different species (28, 30–34).
The evolutionary implications of these spatial gradients are less well understood since the details will depend on the phenotypic differences that exist among more closely related strains. However, even in the absence of any phenotypic differences, the longitudinal structure of the lumen will generate physical consequences that can be appreciated by revisiting our back-of-the-envelope calculation for the production rate of new mutations. While billions of mutations may be produced each day, not all of them emerge on equal footing. A mutation that occurs near the lower end of the colon is very likely to be excreted in feces before it can produce viable offspring. Conversely, a mutation that occurs near the entrance of the colon is significantly more likely to produce descendants that can persist and grow within the host over many generations.
These physical considerations suggest that only a subset of the luminal population will tend to contribute to its long-term genetic composition. Similar arguments apply for estimates of the effective generation time, which can vary substantially in different regions of the colon (27, 35, 36). These arguments suggest that the relevant evolutionary parameters must average over this existing longitudinal structure. However, the weights in this average will be determined not by the current bacterial densities and growth rates but rather by their long-term contribution to the future population. Our limited understanding of these evolutionary weights—even in the simplest models of luminal growth—leaves many important questions unresolved: Can fluid flow alone generate sufficient population bottlenecks that would allow large fluctuations in mutant frequencies within a host? How do absolute growth rate differences map onto the frequency trajectories that can be observed in vivo? How do the answers to these questions depend on the physical properties of the gut environment, which vary dramatically across host species and can be modulated by drugs or other dietary perturbations?
In this study, we introduce a mathematical framework for predicting how stochastic evolutionary forces emerge from simple models of microbial growth in spatially extended environments like the intestinal lumen. Building on earlier work in refs. 37–41, we show that the emergent evolutionary dynamics can often be captured by spatially homogeneous models with an appropriate set of effective parameters, even when the ecological effects of spatial structure are very strong. We derive analytical expressions to show how the effective selection coefficients, generation times, and population sizes are related to the underlying growth rates and flow profiles across the population. By applying this framework to the human colon (28), we find that fluid flow alone is unlikely to generate large fluctuations in the frequencies of sequenced mutations, while the diffusion of slowly growing cells can still have a large impact on the long-term evolution of the population. These results provide a framework for understanding how spatial structure influences the genetic composition of the gut microbiota and may be relevant for other microbial ecosystems (e.g., hot springs and acid mine drainage systems) where unidirectional flow is thought to play an important role (42, 43).
Analysis
We consider the dynamics of mutant lineages in a spatial model of luminal growth that incorporates continuous fluid flow, growth, and active mixing from contractions of the intestinal walls (26, 28). A key assumption of our model is that the mixing process is strong enough to destroy any cross-sectional spatial structure within the lumen (28), yielding an effective diffusion process in the longitudinal dimension (denoted by x) with an effective flow rate v(x) and an effective diffusion coefficient D(x) (Fig. 1A). The local density of species μ at position x and time t can then be described by a reaction–diffusion equation,
| [1] |
where is a function that describes the net growth rate of species μ. We assume that this net growth rate depends on a set of local environmental variables , which could represent local nutrient concentrations, pH, or the abundances of other species. These environmental variables will generally be described by their own set of reaction–diffusion equations, which are coupled to the species densities . For the remainder of this work, we will assume that the ecosystem has approached a nonequilibrium steady state, in which the species densities and environmental variables can be described by time invariant profiles and . This is a crucial simplification as it means that the growth rates can be replaced by simple spatially varying growth functions , which are conditionally independent of the surrounding community. These steady-state growth functions are uniquely determined by the steady-state density profiles of each species,
| [2] |
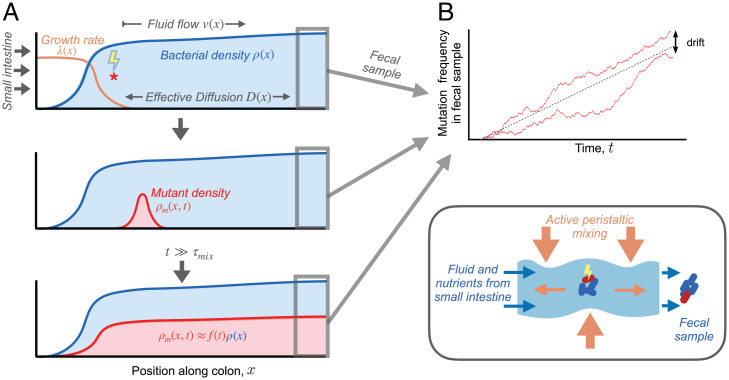
Fig. 1.
Dynamics of a genetic variant in a spatially extended population in the intestinal lumen. (A) Schematic of spatial growth model. Nutrients enter the colon from the small intestine (on the left), and fecal samples are generated at the distal end (on the right). Intestinal wall contractions mix contents of lumen (Bottom Right), producing effective diffusion in the axial direction (26, 28). Continuous fluid flow through the colon generates longitudinal gradients in steady-state bacterial growth rates [, orange line] and population densities [, shaded blue region]. Mutation events (red star) find new lineages that begin to grow and spread out in space [, shaded red region]. After generations, the spatial distribution of the mutant lineage approaches that of the wild-type population but with a smaller overall size. (B) Mutation frequencies observed in fecal samples over time. Two hypothetical trajectories are shown (red lines), illustrating the stochastic fluctuations that arise due to genetic drift.
which implies that the realized growth rates can in principle be determined from static snapshots of the community’s spatial composition.
Dynamics of Mutant Lineages.
We wish to understand the dynamics of genetic variants within species in the steady-state communities described above. Since these variants may initially be present in just a small number of cells, the deterministic dynamics in Eq. 1 must be augmented to account for stochastic fluctuations in cell numbers in both space and time. As long as the frequency of the mutant lineage is sufficiently rare, we expect it to have a negligible influence on the steady state values of and , which implies that the growth function of the mutant can be described its own steady state growth profile . In SI Appendix, section 1, we use a microscopic birth-and-death model to show that the density profile of the mutant lineage can be described by the coarse-grained stochastic differential equation
| [3] |
where and are independent Brownian noise terms with (44), and is the variance in offspring number of the local birth–death process. In the absence of explicit cell death, will be proportional to the local growth rate ; we expect this to be a reasonable approximation in the human gut, where live cells compose a large fraction of the total excreted biomass (5, 45, 46).
Eq. 3 is a stochastic variant of the familiar Fisher-Kolmogorov-Petrovsky-Piskunov equation (47, 48), which is frequently used to model the spread of species or genetic variants through space (47–50). An important difference in our setting is that the expansion velocity v(x) is now set by the fluid flow in the surrounding environment, such that the mutant and wild-type populations are continuously “treadmilling” in place. We show below that this typically leads to pushed rather than pulled expansions (51, 52), which will have important implications for the stochastic dynamics of genetic drift in this system (53, 54).
Eq. 3 provides a quantitative model for predicting the spread of a genetic variant within a resident gut community under the combined action of fluid flow, mixing, and spatially varying growth rates. While the spatiotemporal dynamics of Eq. 3 are complex in the most general case, further simplifications arise in scenarios where the emergent evolutionary forces (e.g., natural selection and genetic drift) are much slower than the ecological processes of growth, flow, and mixing. These ecological forces will combine to produce a characteristic mixing timescale , which represents the time required for the descendants of a mutant lineage to disperse across space (Fig. 1A). For times much larger than , the shape of the mutant density profile will approach the steady-state population profile,
| [4] |
but with a prefactor f(t) that depends on the mutant growth rate , the stochastic noise terms in Eq. 3, and the initial density profile . This prefactor f(t) also coincides with the relative frequency of the mutant lineage in a simulated fecal sample (Fig. 1B). Thus, the dynamics of f(t) provide a crucial connection between the spatial growth dynamics in Eq. 3 and the frequencies of mutant lineages that can be observed in metagenomic sequencing data.
Much of the relevant behavior can be understood by considering a perfectly neutral lineage [] founded by a single individual position x0 (Fig. 1A). In SI Appendix, section 2, we show that the distribution of f(t) at intermediate times () can be captured by a well-mixed Wright–Fisher model,
| [5] |
with an effective initial frequency
| [6] |
and an effective rate of genetic drift
| [7] |
that is independent of x0. Eq. 5 implies that this new mutation will require a time of order to drift to frequency in future fecal samples (55, 56). These dynamics will be consistent with the separation of timescales assumption as long as , which requires that . Since Λ is inversely proportional to the bacterial density, and is independent of density (SI Appendix, section 2), we expect these results to apply for a broad range of frequencies when the population size is sufficiently large.
At intermediate times (), the descendants of the mutant lineage will be approximately evenly distributed across the population (Fig. 1A), so the conditional fixation probability of the entire lineage is simply f(t). Averaging over the random values of f(t) using Eq. 5, we find that
| [8] |
which implies that Eq. 6 has a simple interpretation as the fixation probability of a neutral mutation that arises at position x0 (37). Similarly, the product represents the spatial distribution of future common ancestors of the population (37), regardless of whether they have a mutation or not. In this way, g(x) provides a quantitative measure of the spatial locations that have an outsized influence on the genetic composition of the future population. In SI Appendix, section 3, we show that by modeling the long-term accumulation of neutral mutations within these populations, we obtain a simple prediction for the effective generation time,
| [9] |
where d(x) is the local death rate at position x. This result allows us to reexpress the “wall clock” rate of genetic drift in Eq. 7 as a more traditional effective population size:
| [10] |
which is proportional to the total bacterial density as expected. When cell death is negligible [], these effective parameters are completely determined by the steady state density profile .
Analytical Solutions for a Minimal Model of Bacterial Growth.
We can gain more intuition for these results by examining a minimal model of bacterial growth that yields analytical solutions for the growth and density profiles in Eqs. 9 and 10. We assume that flow and diffusion are uniform in space, such that there is a characteristic length scale that sets the transition between diffusive and advective motion. We further assume that growth depends on a single limiting nutrient with a step-like dose–response curve (Fig. 2A). These assumptions produce a spatial growth profile with a sharp transition at a critical position (Fig. 2B), whose location depends on the relative magnitudes of λ, v, and D. In SI Appendix, section 4, we obtain analytical expressions for the resulting population density profiles, which are illustrated in Fig. 2 C and D.
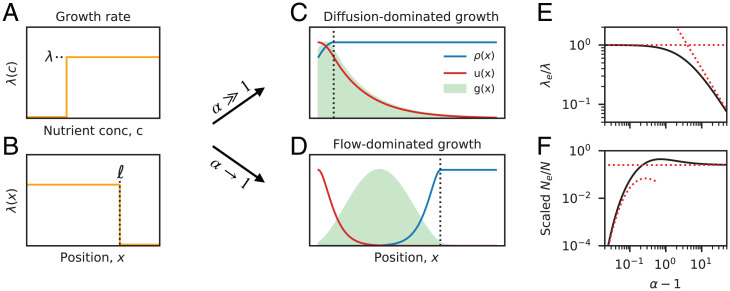
Fig. 2.
Analytical solutions for a minimal model of bacterial growth. (A and B) Schematic of bacterial growth rates. A step-like growth response curve (A) leads to a sharp transition between high growth () and no growth () at a critical position (B). (C and D) Spatial profiles of population density, (blue line), neutral fixation probability, u(x) (red line), and distribution of future common ancestors, (green shaded region), for examples of (C) diffusion-dominated growth () and (D) flow-dominated growth (). In both cases, the dashed black lines indicate the boundary of the growth region in B. (E) Scaled effective growth rate, , and (F) scaled effective population size, , as a function of the washout parameter . Black lines denote the analytical predictions in SI Appendix, section 2, while the red lines illustrate the asymptotic behavior in the and limits.
We observe two characteristic regimes that depend on the value of the dimensionless parameter , which compares the characteristic timescales of growth () and local dilution (). When , growth is not sufficient to overcome the constant loss of individuals due to fluid flow, and the population cannot permanently establish itself in the gut—a scenario we refer to as “washout” (26). At the opposite extreme (), growth is sufficiently rapid that the nutrients are depleted long before flow is relevant (, where diffusive mixing is still the dominant form of motion. This diffusion-dominated growth produces a nearly uniform population density profile and a distribution of future ancestors [] that is primarily composed of slowly growing cells with (Fig. 2C). This leads to a reduced effective growth rate, (Fig. 2E), and an effective population size, , that is independent of the length of the colon (Fig. 2F).
Between these two extremes, we also observe an intermediate regime close to the washout threshold (), where flow dominates over diffusion throughout most of the growth region (). This produces a strong spatial gradient in the density profile and a distribution of future ancestors [] that is primarily concentrated within the growth region (Fig. 2D). The effective growth rate therefore approaches its maximum value (Fig. 2E), while the effective population size is dramatically reduced (Fig. 2F). By examining the contributions to Eq. 10, we find that these lower effective population sizes are driven by fluctuations in a narrow region near the entrance of the colon (), rather than the comparatively larger subpopulation of dividing cells (). This shows how long-term lineage dynamics can have a major impact on the emergent evolutionary parameters in our model.
While the enhanced fluctuations are most pronounced near the washout threshold (), we note that washout itself does not play a major role in this behavior. In SI Appendix, section 3, we show that the results in Fig. 2 are robust to the addition of a washed out region at the proximal end of an otherwise established population. This suggests that it is the accumulated growth over many diffusion lengths—rather than washout per se—that is the primary cause of the reduced effective population size when . It also suggests that our qualitative results do not depend on the specific nature of the boundary between the large and small intestine, since the small number of cells that diffuse into this low-growth region do not dramatically change the dynamics that occur downstream.
Dynamics of Selected Mutations.
We can use a similar separation of timescales approach to analyze the fates of selected mutations as well (SI Appendix, section 3). Provided that the growth rate differences are sufficiently small (see below), we find that the emergent dynamics on timescales can again be mapped onto a well-mixed Wright–Fisher model,
| [11] |
with an effective selection coefficient
| [12] |
This equation encapsulates the relevant growth rate differences across the ancestral region . For a global increase in growth rate [], the effective selection coefficient se is proportional to s as expected. However, Eq. 12 also allows us to account for tradeoffs in growth rate that emerge at different spatial locations. The relative weights of the fitness effects in these different microenvironments are determined by the product , which biases the effective selection coefficients toward regions with higher local growth rates.
The mapping in Eq. 11 allows us to obtain a precise picture of the dynamics a beneficial mutation as observed in simulated fecal samples. When , the dynamics of the selected lineage will be identical to the neutral mutations described in Eq. 5 above. With probability , the mutant lineage will eventually establish and grow deterministically as and will fix within the population on a characteristic timescale (55, 56). These dynamics will be consistent with the separation of timescales assumption as long as .
For stronger selection strengths (), the separation of timescales assumption will eventually break down, and growth rate differences will start to play an important role during the mixing process itself. In this case, we show in SI Appendix, section 1, that an analogous fixation probability can still be obtained numerically by solving the ordinary differential equation
| [13] |
which gives the fixation probability of a beneficial mutation that arises at a given position x. Eq. 13 is similar to existing branching process models of fixation in spatially or genetically subdivided populations (57–59) but with an additional nonlinearity that accounts for the conservative noise of spatial diffusion. The total fixation probability can be obtained from Eq. 13 by averaging w(x) over the local production rate of new mutations, , yielding
| [14] |
When , we recover the linear relation predicted by the separation of timescales approximation. Deviations from this behavior at larger values of se can therefore provide insight into the mixing timescale , which we have so far treated as an implicit parameter.
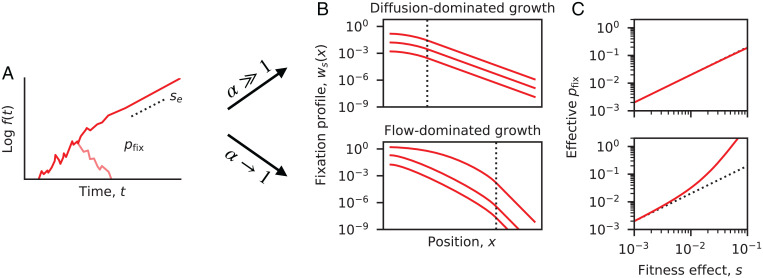
In Fig. 3, we compute these fixation probabilities numerically for the minimal model in Fig. 2, assuming a global increase in growth rate [] and a replication-dominated mutation rate []. We find good agreement with the separation of timescales prediction at sufficiently low values of s. This shows that is primarily determined by the ancestral region [] rather than the total length of the colon (). For diffusion-dominated growth (), this linear approximation remains accurate for growth rate advantages as large as , demonstrating the broad utility of the separation of timescales approach in this regime. In contrast, we find that deviations can emerge at much lower values of s in the flow-dominated growth regime (), such that the fixation probabilities are often much larger than expected under the separation of timescales approximation (Fig. 3C). The spatial profiles in Fig. 3B show that this increase is primarily driven by enhanced fixation probabilities in lower regions of the colon (Fig. 3C), which acts to expand the range of production of successful beneficial mutations. These deviations can be rationalized by the longer times required for lineages to migrate across the ancestral region , which implies that even small growth rate advantages can produce larger numbers of additional offspring before complete mixing is achieved. However, despite these enhanced fixation probabilities, we find that the long-term growth rates of established mutations continue to match the separation of timescales prediction above. By solving a related equation for the average density profile (SI Appendix, section 5), we find that the exponential growth rates eventually approach even when . This shows that finite mixing can have a differential impact depending on the timescales of the corresponding evolutionary processes (e.g., establishment vs. fixation).
Fig. 3.
Dynamics of selected mutations. (A) Schematic trajectory of a beneficial mutation, which either establishes and grows exponentially at rate se (dashed line) or else goes extinct (light red line). (B) The spatially resolved fixation probability of a beneficial mutation that originates at position x. Red lines denote the numerical solutions of Eq. 13 for the minimal model in Fig. 2 with a constant growth rate advantage (SI Appendix, section 4). The dashed lines indicate the transition from to . (Top) A population in the diffusion-dominated growth regime () and (Bottom) a population in the flow-dominated growth regime (). In both cases, fixation profiles were calculated for , and . (C) The effective fixation probability obtained by averaging , the range of initial positions. (Top and Bottom) The same populations as in B. Dashed lines indicate the separation-of-timescales prediction, . Deviations from this prediction emerge in the flow-dominated growth regime, due to the enhanced fixation probability of mutations that originate at larger x values (illustrated in B).
Application to the Human Colon
Our analytical results show that the effective evolutionary parameters in our minimal model can strongly depend on the relative magnitudes of growth, flow, and mixing across the large intestine. How do these results extend to bacteria growing in the human colon? While direct measurements of the growth rates and density profiles are difficult to obtain in this system, rough estimates for many of the key parameters were recently obtained by Cremer et al. (28) using a generalization of the model in Eq. 1. By explicitly modeling the consumption and production metabolites along the length of the human colon (), Cremer et al. (28) obtained predictions for the steady-state growth rates and density profiles for a pair of representative species from the Bacteroides and Firmicutes phyla (Fig. 4A).
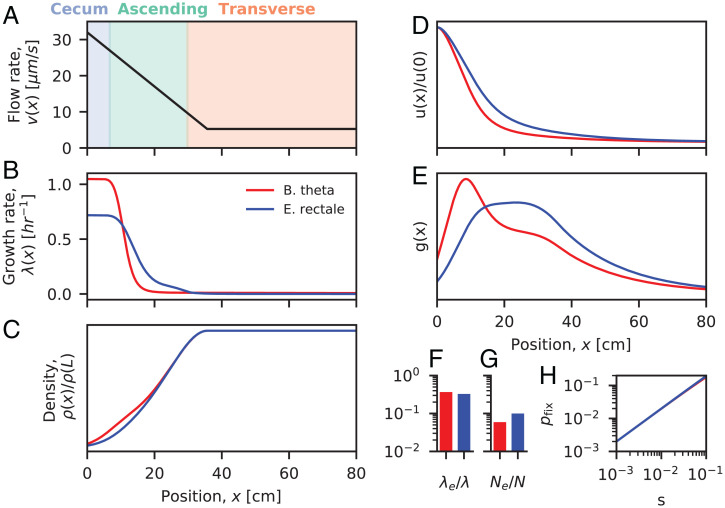
Fig. 4.
Applications to bacteria in the human colon. (A) Estimates of the flow velocity along the first 80 cm of the human colon (28). Colors indicate the positions of different colonic segments. (B and C) Steady-state growth rate and density profiles estimated for two representative species using the results of ref. 28. Growth rate profiles were extracted from the figures in ref. 28, and the corresponding density profiles were calculated from Eq. 2 using the methods described in SI Appendix, section 5. (D and E) Predictions for the neutral fixation profile u(x) (D) and distribution of common ancestors g(x) (E) obtained from the estimated parameters in A–C (SI Appendix, section 5). In both cases, the predicted ancestral distributions contain a large contribution from regions with low growth rates. (F–H) Predictions for the effective growth rate, effective population size, and the net fixation probability of beneficial mutations (SI Appendix, section 5).
An important feature of this model is the presence of a spatially varying flow rate, which is caused by the absorption of water by the colonic epithelium. Cremer et al. (28) estimated that this effect causes the flow rate to decline from to over the length of the proximal colon ( cm). Given an estimated mixing rate of , the effective diffusion length scales range from 3 to 20 cm, and the corresponding timescales range from min to 11 h. These estimates suggest that the in vitro growth rates of the representative strains ( 0.6 to 1 h–1) will be close to washout at the highest flow rates but far from washout elsewhere, making it difficult to directly apply the results from our minimal model in Figs. 2 and 3.
To overcome this challenge, we developed a numerical approach for calculating the effective evolutionary parameters in Eqs. 9, 10, and 14 using the steady-state density profiles estimated by Cremer et al. (28) (SI Appendix, section 5). The results are shown in Fig. 4. In both cases, we find that the flow rate decreases sufficiently rapidly across the proximal colon that the corresponding ancestral regions [] include a substantial contribution from slowly growing cells. For example, the Bacteroides thetaiotaomicron curves in Fig. 4E predict that about a third of the future common ancestors will come from regions where growth rates are /d, while another third will come from nutrient-rich regions where growth rates are /h. This suggests that these resident populations will lie on the boundary between diffusion-dominated and flow-dominated growth in Figs. 2 and 3. This has several implications for the emergent evolutionary dynamics.
Fig. 4F shows that the effective growth rates are about 3 times smaller than the maximum growth rates attained at the entrance of the colon. This corresponds to about nine generations per day for the B. theta example and about 5 generations per day for Eubacterium rectale. These predictions are 5 to 10 times higher than the traditional /d estimates based on the daily biomass excreted in feces (60, 61), which reflects the higher-than-average growth rates experienced by evolutionarily relevant lineages. Interestingly, these higher growth rates are more consistent with direct measurements of B. theta generation times in germ-free mice (62), suggesting that some of the emergent evolutionary parameters may be similar in these environments despite vast differences in host physiology.
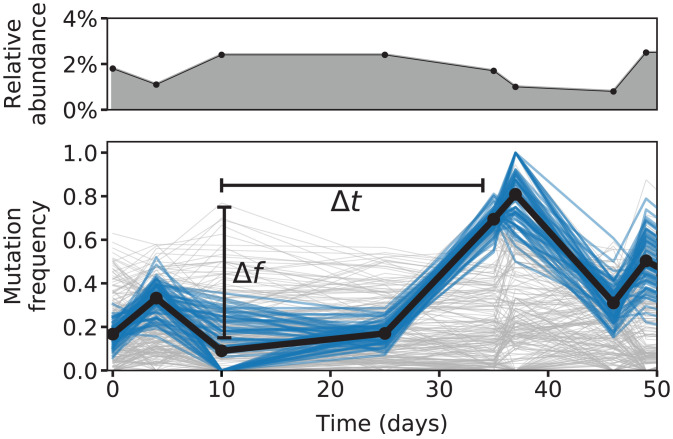
In addition to these shortened generation times, Fig. 4G shows that corresponding effective population sizes are about 10 to 20 times smaller than the total number of bacterial cells in the colon. This leads to elevated rates of genetic drift but not at the levels necessary to drive large changes in the frequencies of genetic variants over a single host lifetime. Given the large number of bacteria in the human gut [ (63)], these estimates predict that a species with 1% relative abundance would have an absolute rate of genetic drift of about per day. At this rate, genetic drift would require more than a hundred years to generate even a 1% shift in the frequency of a common genetic variant. This stands in contrast to the rapid shifts in frequency that are observed for some mutations in sequenced human fecal samples (Fig. 5). This quantitative discrepancy suggests that other factors, like natural selection or temporal bottlenecks, are required to explain these observations.
Fig. 5.
Mutation frequencies within a Bacteroides massiliensis population from a single human subject. (Top) Relative abundance of B. massiliensis and (Bottom) the frequencies of single nucleotide variants in this species inferred from longitudinally sequenced fecal samples from a previous study (15) (SI Appendix, section 5). Blue trajectories highlight a cluster of mutations that experienced a large shift in frequency during the study (), despite relatively small changes in the overall relative abundance of B. massiliensis (approximately twofold; Top). The timescale of this genetic shift ( d) is many orders of magnitude faster than our predicted timescale of genetic drift (; Fig. 4 and Eq. 16), even after accounting for the observed fluctuations in overall relative abundance.
Finally, Fig. 4H shows that the mixing timescales in the human colon are sufficiently rapid that the establishment probabilities of beneficial mutations are well approximated by the linear prediction () across a wide range of physiologically relevant fitness benefits. These results show that our separation of timescales approach can apply even for human-relevant conditions, yielding quantitative estimates for a number of key evolutionary parameters.
Extensions to Wall Growth and Other Spatial Refugia.
So far, we have assumed that the emergent evolutionary forces are dominated by the dynamics within the luminal fluid. However, our basic mathematical framework can also be extended to incorporate certain forms of wall growth (or other spatial refugia), which are known to play an important role in a variety of microbial ecosystems (23, 25, 43, 64, 65). While a complete analysis of this case is beyond the scope of the present paper, many of the key features can already be appreciated within a simple model, in which a well-mixed luminal compartment is connected to a large number of protected subpopulations on the walls of the large intestine (SI Appendix, Fig. S1 and section 6). By mitigating the effects of fluid flow, these wall-bound populations have an advantage in contributing genetic material to the future population. In extreme cases, these wall-bound populations can help recolonize the lumen after strong perturbations like diarrhea. However, their influence on the steady-state dynamics of genetic turnover is less well understood.
Previous work has argued that wall growth composes a small fraction of the daily biomass production in the human gut since the effective linear density in the wall () is much smaller than the corresponding density in the lumen () (26, 28). By generalizing our separation of timescales approach to this regime, we find that the long-term rates of genetic turnover critically depend on the engraftment rate ε, which represents the per-generation probability for a luminal cell to successfully migrate into one of the subpopulations on the wall (SI Appendix, section 6). When wall growth composes a small fraction of the total biomass production (), we find even tiny rates of engraftment,
| [15] |
are sufficient to ensure that genetic drift is dominated by the luminal compartment (). This suggests that there is a broad parameter regime where our previous results still apply. When , fluctuations within the wall population start to become more important, and the long-term rate of genetic drift is amplified by a factor of
| [16] |
At even smaller engraftment rates, the separation of timescales approximation eventually breaks down, and the long-term dynamics start to be dominated by the sequential spread of strains across many isolated refugia (SI Appendix, section 6). These slow spreading dynamics can lead to apparent rates of genetic drift that are even weaker than the lumen (), despite the fact that the relevant population of cells is significantly smaller. This highlights how the dynamics of many distinct refugia can be qualitatively different from a single refuge on its own.
This nonmonotonic behavior illustrates the importance of the engraftment rate ε, which is currently poorly constrained by experimental data. Previous estimates in the human gut suggest that the total wall growth is bounded by (26). Using these estimates as a guide, our model predicts that wall growth should have a negligible impact on genetic drift as long as and that engraftment rates of order are required to enhance the rate of drift by a factor of . These values are still too small to explain the rapid shifts in frequency observed in sequenced fecal samples (Fig. 5).
Our analysis also highlights the importance of the underlying timescales of these dynamics: while smaller engraftment rates can produce higher rates of genetic drift, these fluctuations still require at least generations to propagate back into the lumen before they are eventually sampled in feces (SI Appendix, section 6). On shorter timescales, we expect that wall-dominated genetic drift will generate autocorrelated fluctuations in sequenced fecal samples, similar to the background selection scenario analyzed in ref. 40. Understanding the dynamics of these lagged fluctuations—and the signatures they leave in genetic data like Fig. 5—could provide a promising approach for measuring the impact of wall growth from bulk metagenomic sequencing data.
Discussion
The spatial organization of microbial communities can strongly influence their ecological and evolutionary dynamics (66–71). Here we sought to quantify these effects in the human gut microbiota, whose long-term composition is shaped by lineages that manage to evade dilution in feces. We have developed a mathematical framework for predicting how stochastic evolutionary forces emerge from simple models of bacterial growth in the intestinal lumen and how they give rise to the genetic variation that can be observed in simulated fecal samples.
While our simplified models neglect many important features of microbial and host physiology, they make several key predictions about the role of spatial structure for the within-host evolution of the gut microbiota. Chief among these is the finding that the emergent evolutionary dynamics can often be captured by effective models that lack explicit spatial structure, even in cases where longitudinal gradients have a large effect on local species composition. Similar results are implicit in earlier studies that focused on neutral fixation and heterozygosity (37–39, 41, 72). Here we showed that this equivalence extends to wider range of evolutionary phenomena, including the establishment and spread of beneficial mutations. This suggests that well-mixed models from population genetics might have broader utility for modeling the dynamics of genetic variants in sequenced fecal samples, despite the explicit spatial structure that is present within the gut. In these cases, our results provide a basis for connecting the inferred parameters (e.g., effective selection coefficients and population sizes) with specific weighted averages over the underlying growth and density profiles.
Consistent with previous intuition, we found that unidirectional fluid flow can have a large impact on the emergent evolutionary parameters in our model. Populations that are close to the washout threshold experience dramatically elevated rates of genetic drift—much larger than would be predicted by the absolute number of dividing cells (SI Appendix, section 2). This shows how long-term lineage dynamics can play an essential role in extrapolating evolutionary parameters from absolute growth and density measurements.
By applying our results to recent estimates from the human colon, we found that continuous fluid flow (and simple forms of wall growth) are unlikely to lower effective population sizes to the point where we would expect large fluctuations in genetic composition within a host lifetime. This suggests that additional factors, such as natural selection or temporal bottlenecks, are necessary to explain the rapidly changing mutation frequencies that have been observed in sequenced human fecal samples (7, 13–20). We also found that the spatial gradients generated by fluid flow can cause the effective generation time to be about 5 to 10 times shorter than the traditional /d estimates obtained from the average growth rate across the colon (60, 61). This suggests that the human gut microbiota may experience substantially more evolution than previously expected over the course of a given year. It also suggests that relatively small fitness advantages ( 1 to 10%) may be sufficient to drive large changes in the frequencies of genetic variants over daily and weekly timescales. We note that our precise estimates should be treated with a degree of caution since they are currently derived from relatively rough estimates of the underlying growth rates and density profiles in the gut (28). Our framework provides a flexible approach for refining these estimates using future measurements of spatially resolved growth rates (73) or microbial abundances (32) in human subjects.
Future experiments could test these predictions quantitatively using genetic barcoding techniques (74–76), both in animal models (12) and potentially even in humans (77). For example, by introducing libraries of barcoded strains and tracking their relative fluctuations in later fecal samples, it should be possible to directly measure the effective rate of genetic drift in Eq. 5 and thereby test the theoretical predictions in Fig. 4. Even stronger tests are possible if the strain labeling events could be coupled to local environmental conditions (e.g., pH and mucin) (78–80). By tracking the frequencies of these labeled lineages as they spread out across the colon—and potentially into the intestinal walls (32)—one could directly measure the weighting function u(x) and its associated mixing timescales. Our results provide a framework for interpreting these spatiotemporal measurements and for using them to extract key unknown parameters like the engraftment rate ε (SI Appendix, section 6).
The limitations of our simple growth model create many additional directions for future work. For example, our results suggest that it will be critical to understand how temporal variation in growth conditions—either from regular circadian rhythms (81, 82) or larger perturbations like antibiotics (15)—might alter the emergent evolutionary forces we have studied here. It would also be interesting to examine how more complex forms of wall growth or other spatial refugia (62, 83, 84) might contribute to long-term genetic turnover within the gut. While the details of these models will necessarily differ from the ones studied here, our results suggest that similar separation of timescales approaches may continue to be useful for analyzing these additional scenarios as well. By integrating out variation over shorter length scales and timescales, these coarse-graining approaches can provide a promising route for modeling evolutionary dynamics in complex natural settings (85).
Supplementary Material
Acknowledgments
This work was supported in part by an NSF Graduate Research Fellowship, the Alfred P. Sloan Foundation grant FG-2021-15708, and a Terman Fellowship from Stanford University. B.H.G. is a Chan Zuckerberg Biohub Investigator.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2114931119/-/DCSupplemental.
Data Availability
Source code for the data analysis and figure generation have been deposited in GitHub (https://github.com/bgoodlab/spatial_gut_evolution) (86). All other study data are included in the article and/or SI Appendix. Previously published data were used for this work (15, 28).
References
- 1.Cho I., Blaser M. J., The human microbiome: At the interface of health and disease. Nat. Rev. Genet. 13, 260–270 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gilbert J. A., et al., Current understanding of the human microbiome. Nat. Med. 24, 392–400 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eckburg P. B., et al., Diversity of the human intestinal microbial flora. Science 308, 1635–1638 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huttenhower C., et al.; Human Microbiome Project Consortium, Structure, function and diversity of the healthy human microbiome. Nature 486, 207–214 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stephen A. M., Cummings J. H., The microbial contribution to human faecal mass. J. Med. Microbiol. 13, 45–56 (1980). [DOI] [PubMed] [Google Scholar]
- 6.Cummings J. H., Bingham S. A., Heaton K. W., Eastwood M. A., Fecal weight, colon cancer risk, and dietary intake of nonstarch polysaccharides (dietary fiber). Gastroenterology 103, 1783–1789 (1992). [DOI] [PubMed] [Google Scholar]
- 7.Zhao S., et al., Adaptive evolution within gut microbiomes of healthy people. Cell Host Microbe 25, 656–667.e8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shoemaker W. R., Chen D., Garud N. R., Comparative population genetics in the human gut microbiome. Genome Biol. Evol. 14, evab116 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barroso-Batista J., et al., The first steps of adaptation of Escherichia coli to the gut are dominated by soft sweeps. PLoS Genet. 10, e1004182 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lescat M., et al., Using long-term experimental evolution to uncover the patterns and determinants of molecular evolution of an Escherichia coli natural isolate in the streptomycin-treated mouse gut. Mol. Ecol. 26, 1802–1817 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yilmaz B., et al., Long-term evolution and short-term adaptation of microbiota strains and sub-strains in mice. Cell Host Microbe 29, 650–663.e9 (2021). [DOI] [PubMed] [Google Scholar]
- 12.Vasquez K. S., et al., Quantifying the interplay between rapid bacterial evolution within the mouse intestine and transmission between hosts. Cell Host Microbe 29, P1454–1468.E4 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ghalayini M., et al., Evolution of a dominant natural isolate of Escherichia coli in the human gut over the course of a year suggests a neutral evolution with reduced effective population size. Appl. Environ. Microbiol. 84, e02377–e17 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garud N. R., Good B. H., Hallatschek O., Pollard K. S., Evolutionary dynamics of bacteria in the gut microbiome within and across hosts. PLoS Biol. 17, e3000102 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roodgar M., et al., Longitudinal linked-read sequencing reveals ecological and evolutionary responses of a human gut microbiome during antibiotic treatment. Genome Res. 31, 1433–1446 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yaffe E., Relman D. A., Tracking microbial evolution in the human gut using Hi-C reveals extensive horizontal gene transfer, persistence and adaptation. Nat. Microbiol. 5, 343–353 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Poyet M., et al., A library of human gut bacterial isolates paired with longitudinal multiomics data enables mechanistic microbiome research. Nat. Med. 25, 1442–1452 (2019). [DOI] [PubMed] [Google Scholar]
- 18.Zlitni S., et al., Strain-resolved microbiome sequencing reveals mobile elements that drive bacterial competition on a clinical timescale. Genome Med. 12, 50 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Verster A. J., et al., The landscape of type vi secretion across human gut microbiomes reveals its role in community composition. Cell Host Microbe 22, 411–419.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jiang X., et al., Invertible promoters mediate bacterial phase variation, antibiotic resistance, and host adaptation in the gut. Science 363, 181–187 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ferreiro A., Crook N., Gasparrini A. J., Dantas G., Multiscale evolutionary dynamics of host-associated microbiomes. Cell 172, 1216–1227 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Earle K. A., et al., Quantitative imaging of gut microbiota spatial organization. Cell Host Microbe 18, 478–488 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mark Welch J. L., Hasegawa Y., McNulty N. P., Gordon J. I., Borisy G. G., Spatial organization of a model 15-member human gut microbiota established in gnotobiotic mice. Proc. Natl. Acad. Sci. U.S.A. 114, E9105–E9114 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shi H., et al., Highly multiplexed spatial mapping of microbial communities. Nature 588, 676–681 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Donaldson G. P., Lee S. M., Mazmanian S. K., Gut biogeography of the bacterial microbiota. Nat. Rev. Microbiol. 14, 20–32 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cremer J., et al., Effect of flow and peristaltic mixing on bacterial growth in a gut-like channel. Proc. Natl. Acad. Sci. U.S.A. 113, 11414–11419 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cummings J. H., Macfarlane G. T., The control and consequences of bacterial fermentation in the human colon. J. Appl. Bacteriol. 70, 443–459 (1991). [DOI] [PubMed] [Google Scholar]
- 28.Cremer J., Arnoldini M., Hwa T., Effect of water flow and chemical environment on microbiota growth and composition in the human colon. Proc. Natl. Acad. Sci. U.S.A. 114, 6438–6443 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Evans D. F., et al., Measurement of gastrointestinal pH profiles in normal ambulant human subjects. Gut 29, 1035–1041 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Friedman E. S., et al., Microbes vs. chemistry in the origin of the anaerobic gut lumen. Proc. Natl. Acad. Sci. U.S.A. 115, 4170–4175 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sheth R. U., et al., Spatial metagenomic characterization of microbial biogeography in the gut. Nat. Biotechnol. 37, 877–883 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zmora N., et al., Personalized gut mucosal colonization resistance to empiric probiotics is associated with unique host and microbiome features. Cell 174, 1388–1405.e21 (2018). [DOI] [PubMed] [Google Scholar]
- 33.Tropini C., Earle K. A., Huang K. C., Sonnenburg J. L., The gut microbiome: Connecting spatial organization to function. Cell Host Microbe 21, 433–442 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Montassier E., et al., Probiotics impact the antibiotic resistance gene reservoir along the human GI tract in a person-specific and antibiotic-dependent manner. Nat. Microbiol. 6, 1043–1054 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Poulsen L. K., Licht T. R., Rang C., Krogfelt K. A., Molin S., Physiological state of Escherichia coli BJ4 growing in the large intestines of streptomycin-treated mice. J. Bacteriol. 177, 5840–5845 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Riglar D. T., et al., Bacterial variability in the mammalian gut captured by a single-cell synthetic oscillator. Nat. Commun. 10, 4665 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hallatschek O., Nelson D. R., Gene surfing in expanding populations. Theor. Popul. Biol. 73, 158–170 (2008). [DOI] [PubMed] [Google Scholar]
- 38.Nagylaki T., Geographical invariance and the strong-migration limit in subdivided populations. J. Math. Biol. 41, 123–142 (2000). [DOI] [PubMed] [Google Scholar]
- 39.Wilkins J. F., A separation-of-timescales approach to the coalescent in a continuous population. Genetics 168, 2227–2244 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cvijović I., Good B. H., Desai M. M., The effect of strong purifying selection on genetic diversity. Genetics 209, 1235–1278 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Whitlock M. C., Barton N. H., The effective size of a subdivided population. Genetics 146.1, 427–441 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Crump B. C., Hopkinson C. S., Sogin M. L., Hobbie J. E., Microbial biogeography along an estuarine salinity gradient: Combined influences of bacterial growth and residence time. Appl. Environ. Microbiol. 70, 1494–1505 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cohan F. M., Ward D., Microbial Diversity in Hot Spring Cyanobacterial Mats: Pattern and Prediction (Thermal Biology Institute, 2005). [Google Scholar]
- 44.Gardiner C., Handbook of Stochastic Methods (Springer, New York, 1985). [Google Scholar]
- 45.Ben-Amor K., et al., Genetic diversity of viable, injured, and dead fecal bacteria assessed by fluorescence-activated cell sorting and 16S rRNA gene analysis. Appl. Environ. Microbiol. 71, 4679–4689 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Maurice C. F., Haiser H. J., Turnbaugh P. J., Xenobiotics shape the physiology and gene expression of the active human gut microbiome. Cell 152, 39–50 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fisher R. A., The wave of advance of advantageous genes. Ann. Eugen. 7, 355–369 (1937). [Google Scholar]
- 48.Kolmogorov A., Petrovsky I., Piskunov N., Investigation of the equation of diffusion combined with increasing of the substance and its application to a biology problem. Bull. Mosc. State Univ. Ser. A: Math. Mech 1, 1–25 (1937). [Google Scholar]
- 49.Skellam J. G., Random dispersal in theoretical populations. Biometrika 38, 196–218 (1951). [PubMed] [Google Scholar]
- 50.Hastings A., et al., The spatial spread of invasions: New developments in theory and evidence. Ecol. Lett. 8, 91–101 (2005). [Google Scholar]
- 51.Van Saarloos W., Front propagation into unstable states. Phys. Rep. 386, 29–222 (2003). [Google Scholar]
- 52.Wang C. H., Matin S., George A. B., Korolev K. S., Pinned, locked, pushed, and pulled traveling waves in structured environments. Theor. Popul. Biol. 127, 102–119 (2019). [DOI] [PubMed] [Google Scholar]
- 53.Birzu G., Hallatschek O., Korolev K. S., Fluctuations uncover a distinct class of traveling waves. Proc. Natl. Acad. Sci. U.S.A. 115, E3645–E3654 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Birzu G., Matin S., Hallatschek O., Korolev K. S., Genetic drift in range expansions is very sensitive to density dependence in dispersal and growth. Ecol. Lett. 22, 1817–1827 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Fisher D. S., “Evolutionary dynamics” in Complex Systems, Jean-Philippe Bouchaud M. M., Dalibard J. (Les Houches, Elsevier, 2007), vol. 85, pp. 395–446. [Google Scholar]
- 56.Good B. H., PhD thesis, Harvard University, Cambridge, MA (2016).
- 57.Hallatschek O., The noisy edge of traveling waves. Proc. Natl. Acad. Sci. U.S.A. 108, 1783–1787 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fisher D. S., Asexual evolution waves: Fluctuations and universality. J. Stat. Mech. Theory Exp. 2013, P01011 (2013). [Google Scholar]
- 59.Good B. H., Desai M. M., Deleterious passengers in adapting populations. Genetics 198, 1183–1208 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Savageau M. A., Escherichia coli habitats, cell types, and molecular mechanisms of gene control. Am. Nat. 122, 732–744 (1983). [Google Scholar]
- 61.Gibbons R. J., Kapsimalis B., Estimates of the overall rate of growth of the intestinal microflora of hamsters, guinea pigs, and mice. J. Bacteriol. 93, 510–512 (1967). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Li H., et al., The outer mucus layer hosts a distinct intestinal microbial niche. Nat. Commun. 6, 8292 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sender R., Fuchs S., Milo R., Revised estimates for the number of human and bacteria cells in the body. PLoS Biol. 14, e1002533 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Mark Welch J. L., Rossetti B. J., Rieken C. W., Dewhirst F. E., Borisy G. G., Biogeography of a human oral microbiome at the micron scale. Proc. Natl. Acad. Sci. U.S.A. 113, E791–E800 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Dodge R., et al., A gut commensal niche regulates stable association of a multispecies microbiota. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.09.30.462663v1.
- 66.Hallatschek O., Hersen P., Ramanathan S., Nelson D. R., Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. U.S.A. 104, 19926–19930 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Coyte K. Z., Schluter J., Foster K. R., The ecology of the microbiome: Networks, competition, and stability. Science 350, 663–666 (2015). [DOI] [PubMed] [Google Scholar]
- 68.Baym M., et al., Spatiotemporal microbial evolution on antibiotic landscapes. Science 353, 1147–1151 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Nadell C. D., Drescher K., Foster K. R., Spatial structure, cooperation and competition in biofilms. Nat. Rev. Microbiol. 14, 589–600 (2016). [DOI] [PubMed] [Google Scholar]
- 70.Dal Co A., van Vliet S., Kiviet D. J., Schlegel S., Ackermann M., Short-range interactions govern the dynamics and functions of microbial communities. Nat. Ecol. Evol. 4, 366–375 (2020). [DOI] [PubMed] [Google Scholar]
- 71.Conwill A., et al., Anatomy promotes neutral coexistence of strains in the human skin microbiome. Cell Host Microbe 30, 171–182.e7 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Labavić D., Loverdo C., Bitbol A. F., Hydrodynamic flow and concentration gradients in the gut enhance neutral bacterial diversity. Proc. Natl. Acad. Sci. U.S.A. 119, e2108671119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Korem T., et al., Growth dynamics of gut microbiota in health and disease inferred from single metagenomic samples. Science 349, 1101–1106 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Levy S. F., et al., Quantitative evolutionary dynamics using high-resolution lineage tracking. Nature 519, 181–186 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Nguyen Ba A. N., et al., High-resolution lineage tracking reveals travelling wave of adaptation in laboratory yeast. Nature 575, 494–499 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Jasinska W., et al., Chromosomal barcoding of E. coli populations reveals lineage diversity dynamics at high resolution. Nat. Ecol. Evol. 4, 437–452 (2020). [DOI] [PubMed] [Google Scholar]
- 77.Maldonado-Gómez M. X., et al., Stable engraftment of bifidobacterium longum ah1206 in the human gut depends on individualized features of the resident microbiome. Cell Host Microbe 20, 515–526 (2016). [DOI] [PubMed] [Google Scholar]
- 78.Naydich A. D., et al., Synthetic gene circuits enable systems-level biosensor trigger discovery at the host-microbe interface. mSystems 4, e00125-19 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Merk L. N., Shur A., Pandey A., Murray R. M., Green L. N., Engineering logical inflammation sensing circuit for modulating gut conditions. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.11.10.377085v1.
- 80.Loveless T. B., et al., Molecular recording of sequential cellular events into DNA. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.11.05.467507v1.
- 81.Thaiss C. A., et al., Transkingdom control of microbiota diurnal oscillations promotes metabolic homeostasis. Cell 159, 514–529 (2014). [DOI] [PubMed] [Google Scholar]
- 82.Leone V., et al., Effects of diurnal variation of gut microbes and high-fat feeding on host circadian clock function and metabolism. Cell Host Microbe 17, 681–689 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Lourenço M., et al., The spatial heterogeneity of the gut limits predation and fosters coexistence of bacteria and bacteriophages. Cell Host Microbe 28, 390–401.e5 (2020). [DOI] [PubMed] [Google Scholar]
- 84.Donaldson G. P., et al., Spatially distinct physiology of Bacteroides fragilis within the proximal colon of gnotobiotic mice. Nat. Microbiol. 5, 746–756 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bergelson J., Kreitman M., Petrov D. A., Sanchez A., Tikhonov M., Functional biology in its natural context: A search for emergent simplicity. eLife 10, e67646 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Ghosh O. M., Good B. H., Source code for “Emergent evolutionary forces in spatial models of luminal growth and their application to the human gut microbiota.” GitHub. https://github.com/bgoodlab/spatial_gut_evolution. Deposited 17 June 2021. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source code for the data analysis and figure generation have been deposited in GitHub (https://github.com/bgoodlab/spatial_gut_evolution) (86). All other study data are included in the article and/or SI Appendix. Previously published data were used for this work (15, 28).