Simultaneous Detection of Signal Regions Using Quadratic Scan Statistics With Applications to Whole Genome Association Studies

Abstract

We consider in this paper detection of signal regions associated with disease outcomes in whole genome association studies. Gene- or region-based methods have become increasingly popular in whole genome association analysis as a complementary approach to traditional individual variant analysis. However, these methods test for the association between an outcome and the genetic variants in a pre-specified region, e.g., a gene. In view of massive intergenic regions in whole genome sequencing (WGS) studies, we propose a computationally efficient quadratic scan (Q-SCAN) statistic based method to detect the existence and the locations of signal regions by scanning the genome continuously. The proposed method accounts for the correlation (linkage disequilibrium) among genetic variants, and allows for signal regions to have both causal and neutral variants, and the effects of signal variants to be in different directions. We study the asymptotic properties of the proposed Q-SCAN statistics. We derive an empirical threshold that controls for the family-wise error rate, and show that under regularity conditions the proposed method consistently selects the true signal regions. We perform simulation studies to evaluate the finite sample performance of the proposed method. Our simulation results show that the proposed procedure outperforms the existing methods, especially when signal regions have causal variants whose effects are in different directions, or are contaminated with neutral variants. We illustrate Q-SCAN by analyzing the WGS data from the Atherosclerosis Risk in Communities study.

1. Introduction

An important goal of human genetic research is to identify the genetic basis for human diseases or traits. Genome-Wide Association Studies (GWAS) have been widely used to dissect the genetic architecture of complex diseases and quantitative traits in the past ten years. GWAS uses an array technology that genotypes millions of Single Nuclear Polymorphisms (SNPs) across the genome, and aims at identifying SNPs that are associated with traits or disease outcomes. GWAS has been successful for identifying thousands of common genetic variants putatively harboring susceptibility alleles for complex diseases (Visscher et al., 2012). However, these common variants only explain a small fraction of heritability (Manolio et al., 2009) and the vast majority of variants in the human genome are rare (The 1000 Genomes Project Consortium, 2010). A rapidly increasing number of Whole Genome Sequencing (WGS) association studies are being conducted to identify susceptible rare variants, for example the Genome Sequencing Program of the National Human Genome Research Institute, and the Trans-Omics for Precision Medicine Program of the National Heart, Lung, and Blood Institute.

A limitation of GWAS is that it only genotypes common variants. A vast majority of variants in the human genome are rare (The 1000 Genomes Project Consortium, 2010; Tennessen et al., 2012). Whole genome sequencing studies allow studying rare variant effects. Individual variant analysis that is commonly used in GWAS is however not applicable for analyzing rare variants in WGS due to a lack of power (Bansal et al., 2010; Kiezun et al., 2012; Lee et al., 2014). Gene-based tests, as an alternative to the traditional single variant test, have become increasingly popular in recent years in GWAS analysis (Li and Leal, 2008; Madsen and Browning, 2009; Wu et al., 2010). Instead of testing each SNP individually, these gene based tests evaluate the cumulative effects of multiple variants in a gene, and can boost power when multiple variants in the gene are associated with a disease or a trait (Han et al., 2009; Wu et al., 2010). There is an active recent literature on rare variant analysis methods which jointly test the effects of multiple variants in a variant set, e.g., a genomic region, such as burden tests (Morgenthaler and Thilly, 2007; Li and Leal, 2008; Madsen and Browning, 2009), and non-burden tests (Wu et al., 2011; Neale et al., 2011; Lin and Tang, 2011; Lee et al., 2012), e.g., Sequence Kernel Association Test (SKAT) (Wu et al., 2011). The primary limitation of these gene-based tests is that it needs to pre-specify genetic regions, e.g., genes, to be used for analysis. Hence these existing gene-based approaches are not directly applicable to WGS data, as analysis units are not well defined across the genome, because of a large number of intergenic regions. It is of substantial interest to scan the genome continuously to identify the sizes and locations of signal regions.

Scan statistics (Naus, 1982) provide an attractive framework to scan the whole genome continuously for detection of signal regions in whole genome sequencing data. The classical fixed window scan statistics allow for overlapping windows using a moving window of a fixed size, which “shifts forward” a window with a number of variants at a time and searches for the windows containing signals. A limitation of this approach is that the window size needs to be pre-specified in an ad hoc way. In cases where multiple variants are independent in a sequence, Sun et al. (2006) proposed a region detection procedure using a scan statistic that aggregates the p-values of individual variant tests. However this is not applicable to WGS due to the linkage disequilibrium (LD), i.e,. correlation, among nearby variants. Recently, McCallum and Ionita-Laza (2015) proposed likelihood-ratio-based scan statistic procedure to refine disease clustering region in a gene, but not for testing associations across the genome. Furthermore, this method does not allow for covariates adjustment (e.g., age, sex and population structures), and can be only used for binary traits.

The mean-based scan statistic procedures have been used in DNA copy number analysis. Assuming all variants are signals with the same mean in signal regions, several authors have proposed to use the mean of marginal test statistics in each candidate region as a scan statistic. Specifically, Arias-Castro et al. (2005) proposed a likelihood ratio-based mean scan procedure in the presence of only one signal region. Zhang et al. (2010) described an analytic approximation to the significance level of this scan procedure, while Jeng et al. (2010) showed this procedure is asymptotically optimal in the sense that it separates the signal segments from the non-signals if it is possible to consistently detect the signal segments by any identification procedure. This setting is closely related to the change-point detection problem. Olshen et al. (2004) developed an iterative circular binary segmentation procedure to detect change-points, whereas Zhang and Siegmund (2007, 2012) proposed a BIC-based model selection criterion for estimating the number of change-points. However, the key assumption of these mean scan procedures that all observations have the same signals in signal regions generally does not hold in genetic association studies.

Indeed, although the mean based scan statistics are useful for copy number analysis, these procedures have several limitations for detecting signal regions in whole genome array and sequencing association studies. Specifically, they will lose power due to signal cancellation in the presence of both trait-decreasing and trait-increasing genetic variants, or the presence of both causal and neural variants in a signal region. Both situations are common in practice. Besides, these procedures assume the individual variant test statistics are independent across the whole genome. However, in practice, the variants in a genetic region are correlated due to linkage disequilibrium.

In this paper, we propose a quadratic scan statistic based procedure (Q-SCAN) to detect the existence and locations of signal regions in whole genome association studies by scanning the whole genome continuously. Our procedure can consistently detect an entire signal segment in the presence of both trait-increasing and trait-decreasing variants and mixed signal and neutral variants. It also accounts for the correlation (LD) among the variants when scanning the genome. We derive an empirical threshold that controls the family-wise error rate. We study the asymptotic property of the proposed scan statistics, and show that the proposed procedure can consistently select the exact true signal segments under some regularity conditions. We propose a computationally efficient searching algorithm for the detection of multiple non-overlapping signal regions.

We conduct simulation studies to evaluate the finite sample performance of the proposed procedure, and compare it with several existing methods. Our results show that, the proposed scan procedure outperforms the existing methods in the presence of weak causal and neutral variants, and both trait-increasing and trait-decreasing variants in signal regions. We applied the proposed procedure to the analysis of WGS lipids data from the Atherosclerosis Risk in Communities (ARIC) study to identify genetic regions which are associated with lipid traits.

The remainder of the paper is organized as follows. In Section 2, we introduce the hypothesis testing problem and describe our proposed scan procedure and a corresponding algorithm to detect multiple signal regions. In Section 3, we present the asymptotic properties of the scan statistic, as well as the statistical properties of identifiable regions. In Section 4, we compare the performance of our procedure with other scan statistic procedures in simulation studies. In Section 5, we apply the proposed scan procedure to analyze WGS data from the ARIC study. Finally, we conclude the paper with discussions in Section 6.

2. The Statistical Model and the Quadratic Scan Statistics for Signal Detection

2.1. Summary Statistics of Individual Variant Analysis Using Generalized Linear Models

Suppose that the data are from n subjects. For the ith subject (i = 1, ⋯, n), Y_i is an outcome, X_i = (X_i1, …, X_iq)^T is a vector of q covariates, and G_ij is the jth of p variants in the genome. Under the global null model, there is no genetic effect. One constructs individual variant test statistics in GWAS and WGS studies by regressing Y_i on each variant G_ij adjusting for the covariates X_i. Conditional on (X_i, G_ij), Y_i is assumed to follow a distribution in the exponential family with the density f(Y_i) = exp{Y_iθ_i − b(θ_i) / a_i(ϕ) + c(Y_i, ϕ)}, where a_i(·), b(·) and c(·) are some known functions, and θ_i and ϕ are the canonical parameter and the dispersion parameter, respectively (McCullagh and Nelder, 1989). Denote by η_ij = E(Y_i | X_i, G_ij) = b′(θ_i).

Under the global null model, there is no genetic effect across the genome and hence η_ij = η_i for j = 1, …, p. We consider the null Generalized Linear Model (GLM) $g\left({\eta }_i\right)=X_i^T\alpha$, where g(·) is a monotone link function. For simplicity, we assume g(·) is a canonical link function. Under the global null model, the variance of Y_i is var(Y_i) = a_i(ϕ)v(η_i), where v(η_i) = b″(θ_i) is a variance function. Let ${\widehat{\eta }}_{0i}=g^{-1}\left(X_i^T\alpha \right)$, where α is the Maximum Likelihood Estimator (MLE) of α, and $\widehat{\varphi }$ is the MLE of ϕ, both under the global null model. Assume $\Lambda =\text{diag}\left\{a_1(\widehat{\varphi })v\left({\widehat{\eta }}_{01}\right),\dots ,a_n(\widehat{\varphi })v\left({\widehat{\eta }}_{0n}\right)\right\}$ and P = Λ⁻¹ − Λ⁻¹ X (X^T Λ⁻¹ X)⁻¹ X^T Λ⁻¹.

The test statistic for the jth variant is constructed using the working marginal model $g\left({\eta }_i\right)=X_i^T\alpha +G_{ij}{\beta }_j$, and the marginal score test statistic for β_j of the jth variant is

$$U_j=G_{\cdot j}^T\left(Y-{\eta }_0\right)/\sqrt{n},$$

where G_j = (G_{1 j}, ⋯, G_nj)^T denotes the jth variant data of n subjects, ${\eta }_0={\left({\widehat{\eta }}_{10},\cdots ,{\widehat{\eta }}_{n0}\right)}^T$ and Y = (Y₁, ⋯, Y_n)^T. These individual variant test statistics are asymptotically jointly distributed as U ~ N(μ, Σ), where U = (U₁, ⋯, U_p)^T, μ = E(U). Note that μ = 0 under the global null of all β_j being 0, and Σ_jj′ can be estimated by

$${\Sigma }_{j{j}^{\prime }}=G_j^{T}P{G}_{j^{\prime }}/n.$$ (1)

These individual SNP summary statistics U_j are often available in public domains or provided by investigators to facilitate meta-analysis of multi-cohorts.

Genetic region-level analysis has become increasingly important in GWAS and WGS rare variant association studies (Li and Leal, 2008; Lee et al., 2014). The existing region-based tests require pre-specification of regions using biological constructs, such as genes. For a given region, region-level analysis aggregates the marginal individual SNP test statistics U_j across the variants in the region to test for the significance of the region (Li and Leal, 2008; Madsen and Browning, 2009; Wu et al., 2011). However, whole genome array and sequencing studies consist of many intergenic regions. Hence, analysis based on genes or prespecified regions of a fixed length, e.g., a moving window of 4,000 base pairs (bp), are not desirable for scanning the genome to detect signal segments. This is because region-based tests will lose power if a pre-specified region is too big or too small. Indeed, it is of primary interest in whole genome association analysis to scan the whole genome to detect the sizes and locations of the regions that are associated with diseases and traits. We tackle this problem using the quadratic scan statistic.

2.2. Detection of Signal Regions Using Scan Statistics

Let a sequence of p marginal test statistics be U = {U₁, …, U_p}, where U_i is the marginal test statistic at location i and p is the total number of locations, e.g., the total number of variants in GWAS or WGS. We assume that the sequence U follows a multivariate normal distribution U ~ N(μ, Σ), where μ is an unknown mean of U and Σ = cov(U). Under the global null hypothesis of no signal variant across the genome, we have μ = 0. Under the alternative hypothesis of non-overlapping signal regions, there exist signals at certain non-overlapping regions I₁, …, I_r satisfying ${\mu }_{I_j}\ne 0$, where ${\mu }_{I_j}={\left\{{\mu }_i\right\}}_{i\in I_j}$ and j = 1, …, r. Note the lengths of the signal regions are allowed to be different. Besides, the signal region I_j satisfies that in a large area that contains I_j, there is no signal point (μ = 0) outside I_j and the edges of I_j are signal points. Denote a collection of the non-overlapping signal regions by $\mathcal{I}=\left\{I_1,\dots ,I_r\right\}$. Our goal is to detect whether signal segments exist, and if they do exist, to identify the location of these segments. Precisely, we wish to first test

$$H_0:\mathcal{I}=\varnothing \text{ against }{H}_1:\mathcal{I}\ne \varnothing ,$$ (2)

and if H₀ is rejected, detect each signal region in $\mathcal{I}$.

A scan statistic procedure solves the hypothesis testing problem (2) by using the extreme value of the scan statistics of all possible regions,

$$Q_{\text{max}}=\underset{L_{\text{min}}\le \left|I\right|\le L_{\text{max}}}{\text{max}}Q(I)$$ (3)

where Q(I) is the scan statistic for region I, | I | denotes the number of variants in region I, and L_min and L_max are the minimum and maximum variants number in searching windows, respectively. A large value of Q_max indicates evidence against the null hypothesis. If the null hypothesis is rejected and results in only one region, the selected signal region is $\widehat{I}={\text{argmax}}_{L_{\text{min}}\le |I|\le L_{\text{max}}}Q(I)$.

Jeng et al. (2010) and Zhang et al. (2010) proposed a scan procedure based on the mean of the marginal test statistics of a candidate region (M-SCAN). The mean scan statistic for region I is defined as

$$M(I)=\sum _{i\in I}{Z}_i/\sqrt{\left|I\right|},$$ (4)

where $Z_i=U_i/\sqrt{var\left(U_i\right)}$ is the standardized score statistics. When the test statistics Z_i are independent (Σ = I_n) with a common mean in a signal region (μ_i = μ for all i ∈ I_j), Arias-Castro et al. (2005) and Jeng et al. (2010) showed that the mean scan procedure is asymptotically optimal in the sense that it separates the signal segments from the non-signals as long as the signal segments are detectable.

However, in whole genome association studies, the assumptions that marginal tests Z_i are independent and have the same mean in signal regions often do not hold. This is because, first, marginal test statistics in a region are commonly correlated due to the LD of variants; second, signal variants in a signal region are likely to have effects in different directions and be mixed with neutral variants in the signal regions. Hence application of the existing mean scan statistics (4) for detecting signal regions in whole genome association studies is likely to not only yield invalid inference due to failing to account for the correlation between the Z_i’s across the genome, but also more importantly lose power due to cancellation of signals in different directions in signal regions.

2.3. The Quadratic Scan Procedure

To overcome the limitations of the mean scan procedure, we propose a quadratic scan procedure (Q-SCAN) that selects signal regions based on the sum of quadratic marginal test statistics, which is defined as,

$$Q(I)=\frac{\sum _{i\in I}{U}_i^2-\text{E}\left(\sum _{i\in I}{U}_i^2\right)}{var\left(\sum _{i\in I}{U}_i^2\right)}=\frac{\sum _{i\in I}{U}_i^2-\sum _{i=1}^{\left|I\right|}{\lambda }_{I,i}}{\sqrt{2\sum _{i=1}^{\left|I\right|}{\lambda }_{I,i}^2}},$$ (5)

where λ_I = (λ_I,1, λ_I,2, ⋯ λ_I,|I|)^T is the eigenvalues of ${\Sigma }_I=G_I^{T}P{G}_I/n$ and Σ_I is the covariance matrix of test statistics U_I. In the presence of correlation among the test statistics Z’s, the null distribution of Q(I) is a centered mixture of chi-squares $\sum _{j=1}^{|I|}\left({\lambda }_{I,j}/\sqrt{2\sum _{i=1}^{|I|}{\lambda }_{I,i}^2}\right)\times \left({\chi }_{1j}^2-1\right)$, where the ${\chi }_{1j}^2$ are independent chi-square random variables with one degree of freedom. When signals have different directions, the proposed quadratic scan statistic avoids signal cancellation that will result from using the mean scan statistic (4). By using the standardization of the sum of quadratic marginal test statistics in region I, the scan statistics Q(I) handles different LD structure across the genome and are comparable for different region lengths.

We reject the null hypothesis (2) if the scan statistic of a region is larger than a given threshold h(p, L_min, L_max, α). The threshold h(p, L_min, L_max, α) is used to control the family-wise error rate at exact α level. If this results in only one region, the estimated signal region is $\widehat{I}={\text{argmax}}_{L_{\text{min}}\le |I|\le L_{\text{max}}}Q(I)$. If this results in multiple overlapping regions, we estimated the signal region as the interval whose test statistic is greater than the threshold and achieves the local maximum in the sense that the test statistic of that region is greater than the regions that overlap with it. We propose a searching algorithm to consistently detect true signal regions in the next section.

We propose to use Monte Carlo simulations to determine h(p, L_min, L_max, α) empirically. Specifically, we generate samples from N(0, Σ) and calculate Q_max. We repeat this for N times and use the 1 – α quantile of the empirical distribution as the data-driven threshold. Section 2.5 presents details on calculating the empirical threshold.

2.4. Searching Algorithm for Multiple Signal Regions

In general, there might be several signal regions in a whole genome. We now describe an algorithm for detecting multiple signal regions. Motivated by GWAS and WGS, we assume the signal regions are short relatively to the size of the whole genome, and are reasonably well separated. Hence intuitively, the test statistic for proper signal region estimation should achieve a local maximum. Following Jeng et al. (2010) and Zhang et al. (2010), our proposed searching algorithm first finds all the candidate regions with the quadratic scan statistic greater than a pre-specified threshold h(p, L_min, L_max, α). Then we select the intervals from the candidate sets that has the largest test statistic than the other overlapped intervals in the candidate set as the estimated signal regions. The detailed algorithm is given as follows:

Step 1. Set the minimum number of variants of searching windows as L_min and the maximum number of variants of searching windows as L_max, and calculate Q(I) for the intervals with the number of variants between L_min and L_max.

Step 2. Pick the candidate set

$${\mathcal{I}}^{(1)}=\left\{I:Q(I)>h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right),L_{\text{min}}\le \left|I\right|\le L_{\text{max}}\right\}$$

for some threshold h(p, L_min, L_max, α). If ${\mathcal{I}}^{(1)}\ne \varnothing$, we reject the null hypothesis, set j = 1 and proceed with the following steps.

Step 3. Let ${\widehat{I}}_j={\text{argmax}}_{I\in {\mathcal{I}}^{(j)}}Q(I)$, and update ${\mathcal{I}}^{(j+1)}={\mathcal{I}}^{(j)}\backslash \left\{I\in {\mathcal{I}}^{(j)}:I\cap {\widehat{I}}_j\ne \varnothing \right\}$.

Step 4. Repeat Step 3 and Step 4 with j = j + 1 until ${\mathcal{I}}^{(j)}$ is an empty set.

Step 5. Define ${\widehat{I}}_1,{\widehat{I}}_2,\cdots$ as the estimated signal regions.

After the test statistic Q(I) is calculated for each region L_min ≤| I |≤ L_max, we can estimate the null distribution of Q_max. A threshold h(p, L_min, L_max, α) is set based on the null distribution of Q_max. Specifically, the threshold h(p, L_min, L_max, α) is calculated to control for the family-wise error rate at a desirable level α by adjusting for multiple testing of all searched regions. Section 2.5 provides detailed discussions on calculating h(p, L_min, L_max, α) and Section 3.1 discussed the bound of h(p, L_min, L_max, α).

Steps 3–4 are used to search for all the local maximums of the scan statistic Q(I) by iteratively selecting the intervals from the candidate set with the largest scan statistics Q(I), and then deleting a selected signal interval and any other intervals overlapping with it from the candidate set before moving on to select the next signal interval. Step 5 collects all the local maximums as the set of selected signal regions. The intuition of this algorithm is as follows. Since we assume the signal segments are well separated in the sequence, for a signal region, no region with variants number between L_min and L_max overlaps with more than one signal region. Thus the test statistic of a signal region I is larger than the other intervals that overlap with it. It follows that a local maximum provides good estimation of a signal region.

Selection of the minimum and maximum variants numbers in searching windows, i.e., L_min and L_max, is an important issue in scan procedures. Specifically, to ensure that each signal region will be searched, L_min and L_max should be smaller and larger than the variants number in all signal regions, respectively. In the meantime, L_max should be smaller than the shortest gap between signal regions to ensure that no candidate region I with L_min ≤| I |≤ L_max overlaps with two or more signal regions. These two parameters L_min and L_max also determine computation complexity. A smaller range between L_min and L_max requires less computation. Instead of setting the range of moving window sizes on the basis of the number of base pairs, we specify a range of moving window sizes on the basis of the number of variants. In practice, we recommend to choose L_min = 40 and L_max = 200. Different from the fact that the observed rare variants number in a given window increases with a fixed number of base pairs as sample size increases, such a range specification on the basis of the number of variants is independent of sample sizes.

2.5. Threshold for Controlling the Family-Wise Error Rate

Although the theorems in Section 3 shows that the family-wise error rate can be asymptotically controlled, it is difficult to use a theoretical threshold for an exact α – level test in practice. The standard Bonferroni correction for multiple-testing adjustment is also too conservative for the Q-SCAN procedure, because the candidate search regions overlap with each other and the scan statistics for these regions are highly correlated. Therefore, we propose to use Monte Carlo simulations to determine an empirical threshold to control for the family-wise error rate at the α – level. For each step, we estimate Σ using (1) and generated samples from N(0, Σ). Specifically, we first generate u ~ N(0, I_n) and calculate the pseudo-score vector by $U=G{P}^{1/2}u/\sqrt{n}$ where $G=\left(G_1^T,\cdots ,G_n^T\right)$ is the p × n genotype matrix, n is the number of subjects in the study, and P is the n × n projection matrix of the null GLM. Then we calculate the extreme value Q_max of the test statistic Q(I) using (3) and (5) across the genome based on the pseudo-score U and the estimated covariance matrix Σ = GPG^T / n. We repeat this for a large number of times, e.g, 2, 000 times, and use the 1 – α quantile of the empirical distribution of Q_max as the empirical threshold h(p, L_min, L_max, α) for controlling the family-wise error rate at α. Both the calculation and the Q-SCAN procedure have been implemented in the R package QSCAN, available on github (https://github.com/zilinli1988/QSCAN).

3. Asymptotic Properties of the Quadratic Scan Procedure

In this section, we present two theoretical properties of the quadratic scan procedure. The first property shows the convergence rate of the extreme value Q_max and gives a bound of the empirical threshold h(p, L_min, L_max, α). The second property shows that, under certain regularity conditions, the quadratic scan procedure consistently detects the exact signal regions. The proofs of the theorems are provided in the online supplementary materials.

3.1. Bound of the Empirical Threshold

We first provide a brief summary of notation used in the paper. For any vector a, set $\Vert a{\Vert }_1=\sum _i\left|a_i\right|$, $\Vert a{\Vert }_2=\sqrt{\sum _i{a}_i^2}$ and $\Vert a{\Vert }_{\infty }=\underset{i}{\text{sup}}\left|a_i\right|$. For two sequences of real numbers a_p and b_p, we say a_p ≪ b_p or a_p = o (b_p), when limsup a_p / b_p → 0. Recall that $U_i=G_i^T(Y-\mu )/\sqrt{n}$ is the score statistic for variant i (i = 1,2, ⋯, p). Under the null hypothesis, $U_i~N\left(0,{\sigma }_i^2\right)$ with ${\sigma }_i^2=G_i^{T}P{G}_i/n$ for all i = 1,2, ⋯, p, where P is the projection matrix in the null model. Assume there exists a constant c > 0 such that ${\sigma }_i^2\ge c$. The following theorem gives the convergence rate of Q_max.

Theorem 1 If the following conditions (A)-(C) hold,

(A) ${\text{max}}_{|I|=L_{\text{max}}}{\Vert {\lambda }_I\Vert }_{\infty }\le K_0$, where K₀ is a constant,

(B) $\frac{L_{\text{min}}}{\text{log}(p)}\to \infty$ and $\frac{\text{log}\left(L_{\text{max}}\right)}{\text{log}(p)}\to 0$,

(C) ${\left\{U_i\right\}}_{i=1}^p$is M_p-dependent and $\frac{\text{log}\left(M_p\right)}{\text{log}(p)}\to 0$, then

$$\frac{\underset{L_{\text{min}}\le \left|I\right|\le L_{\text{max}}}{\text{max}}Q(I)}{\sqrt{2\text{\hspace{0.17em}log}(p)}}\stackrel{p}{\to }1,$$

as p → ∞ under the global null hypothesis.

Condition (A) holds when the lower bound of the minor allele frequency of variants is a constant that is greater than 0. In GWAS and WGS, the number of variants p is large, e.g., from hundreds of thousands to hundreds of millions. However, log(p) grows much slower and is comparable to the length of genes and of LD blocks, so that the condition (B) of L_min and L_max is reasonable in practice. Further, since two marginal test statistics are independent when two variants are sufficiently far apart in the genome, the assumption of M_p dependence in Condition (C) is reasonable in reality.

Note the empirical threshold h (p, L_min, L_max, α) is the (1 – α) th quantile of Q_max, that is,

$$\mathbb{P}\left(Q_{\text{max}}>h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right)\right)=\alpha .$$

By Theorem 1, for any ϵ > 0, when p is sufficiently large, we have $(1-ϵ)\sqrt{2\text{ log}(p)}\le h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right)\le (1+ϵ)\sqrt{2\text{ log}(p)}$. Next we give a more accurate upper bound of h (p, L_min, L_max, α).

Theorem 2 If conditions (A) and (B) in Theorem 1 hold, for p sufficiently large, we have

$$h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right)\le \sqrt{2\left[\text{log}\left\{p\left(L_{\text{max}}-L_{\text{min}}\right)\right\}-\text{log}(\alpha )\right]}+\frac{\sqrt{2}\left[\text{log}\left\{p\left(L_{\text{max}}-L_{\text{min}}\right)\right\}-\text{log}(\alpha )\right]}{{\left\{L_{\text{min}}\text{ log}(p)\right\}}^{\frac{1}{4}}}.$$

By Theorems 1 and 2, for p sufficiently large, we give the bound of the empirical threshold as follows,

$$(1-ϵ)\sqrt{2\text{\hspace{0.17em}log}(p)}\le h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right)\le \sqrt{2{\gamma }_p}+\frac{\sqrt{2}{\gamma }_p}{{\left\{L_{\text{min}}\text{ log}(p)\right\}}^{\frac{1}{4}}},$$

where ϵ is a small constant and γ_p = log{p(L_max − L_min)} − log(α).

3.2. Consistency of Signal Region Detection

In this section, we show the results of power analysis. We first show that the proposed Q-SCAN procedure could consistently select a signal region that overlaps with the true signal region. Let μ_I = {μ_i}_i∈I for any region I. Assume I* is the signal region with ${\mu }_{I^{*}}\ne 0$ and L_min ≤| I* |≤ L_max. Denote the signal region by $I^{*}=\left({\tau }_1^{*},{\tau }_2^{*}\right]$ that satisfies certain regularity conditions on its norm and edges, e.g., the L₂ norm measuring the overall signal strength of I* is sufficiently large and the edges of I* are signal points, that is, ${\mu }_{{\tau }_1^{*}+1}\ne 0$ and ${\mu }_{{\tau }_2^{*}}\ne 0$. We also assume there is no signal point (μ ≠ 0) outside I* in a large area that contains I*, that is, there exists τ ≥ L_max, such that ${\mu }_{I_1}={\mu }_{I_2}=0$, where $I_1=\left({\tau }_1^{*}-\tau ,{\tau }_1^{*}\right]$ and $I_2=\left({\tau }_2^{*},{\tau }_2^{*}+\tau \right]$ are the non-signal regions of length τ on the left and right of the signal regions I*. We formally present these in Conditions (D) and (E) in the following two theorems.

Theorem 3 Assume conditions (A)-(C) in Theorem 1 and the following condition (D) hold,

$$(D)\frac{{\Vert {\mu }_{I^{*}}\Vert }_2^2}{{\Vert {\lambda }_{I^{*}}\Vert }_2}\ge 2\left(1+{ϵ}_0\right)\sqrt{\text{log}(p)}\text{ for some constant }{ϵ}_0>0\text{, }$$

then there exists constant C > 0, such that

$$\mathbb{P}\left\{Q\left(I^{*}\right)>h\left(p,L_{\text{min}},L_{\text{max}},\alpha \right)\right\}\ge 1-2p^{-C{ϵ}_0^2}\to 1.$$

as p → ∞.

Condition (D) imposes on the signal strength of the signal region. This condition is similar to the condition assumed in Jeng et al. (2010) and ensures that the signal region I* will be selected in the candidate set ${\mathcal{I}}^{(1)}$. For each signal variant i, by our definition, μ_i = E(U_i) has the same convergence rate as $\sqrt{n}$, where n is the sample size. In GWAS or WGS, the sample size is often large and thus condition (D) is reasonable in reality. Theorem 3 could consistently select a signal region that overlaps with the true signal region whose overall signal strength in sense of L₂ norm is sufficiently large.

To show the consistency of signal region detection, we first introduce a quantity to measure the accuracy of an estimator of a signal segment. For any two regions I₁ and I₂, define the Jaccard index between I₁ and I₂ as J(I₁, I₂) = | I₁ ∩ I₂ | / | I₁ ∪ I₂ |. It is obvious that 0 ≤ J(I₁, I₂) ≤ 1, and J(I₁, I₂) = 1 indicating complete identity and J(I₁, I₂) = 0 indicating disjointness. Let $\mathcal{I}=\left\{{\widehat{I}}_1,{\widehat{I}}_2,\cdots \right\}$ be a collection of estimated signal regions, we define region I* is consistently detected if for some η_p = o(1), there exists $\widehat{I}\in \mathcal{I}$ such that

$$\mathbb{P}\left(J\left(\widehat{I},I^{*}\right)\ge 1-{\eta }_p\right)\to 1,$$

as p → ∞. The following theorem shows that the proposed Q-SCAN could consistently detect existence and locations of the signal region I* under some regularity conditions.

Theorem 4 Assume conditions (A)-(D) in Theorem 3 and the following condition (E) hold,

$$(E)\underset{I⊊I^{*}}{\text{inf}}\frac{\text{log}\left({\Vert {\mu }_{I^{*}}\Vert }_2^2\right)-\text{log}\left({\Vert {\mu }_I\Vert }_2^2\right)}{\text{log}\left({\Vert {\lambda }_{I^{*}}\Vert }_2\right)-\text{log}\left({\Vert {\lambda }_I\Vert }_2\right)}>1,$$

then there exists constant C > 0, such that

$$\mathbb{P}\left(J\left(\widehat{I},I^{*}\right)\ge 1-{\eta }_p\right)\ge 1-p^{-C{ϵ}_0^2}-p^{-C{\eta }_p^2}\to 1,$$

for any η_p that satisfies ${\left\{\frac{\text{log}\left(L_{\text{max}}\right)}{\text{log}(p)}\right\}}^{\frac{1}{2}}\ll {\eta }_p\ll 1$ as p → ∞.

Condition (E) specifies the properties of the overall signal strength that a signal region needs to satisfy in order for it to be consistently detected by the Q-SCAN procedure. This definition allows a signal region to consist of both signal and neutral variants, which is more realistic and commonly the case in GWAS and WGS. This condition is implicitly assumed when signals have the same strength and tests are independent. However this common strength assumption that is suitable for copy number variation studies is inappropriate for GWAS and WGS. Condition (E) also holds when the tests are independent and the sparsity parameter is constant in the signal region. To be specific, let s(I) be the number of signals in region I, that is, the number of μ_i’s that are not zero in region I. Assume s(I) = | I |^ξ(I), where ξ(I) = ξ* is the sparsity parameter of region I. Although signals are sparse across the genome, we assume that signals are dense in the signal region (Donoho and Jin, 2004; Wu et al., 2011) and hence ξ* >1 / 2. Then, for any I ⊊ I*, we have $\{\text{log}({\Vert {\mu }_{I^{*}}\Vert }_2^2\}-\text{log}\left({\Vert {\mu }_I\Vert }_2^2\right))/\left\{\text{log}\left({\Vert {\lambda }_{I^{*}}\Vert }_2\right)-\text{log}\left({\Vert {\lambda }_I\Vert }_2\right)\right\}=2{\xi }^{*}>1$ and thus condition (E) holds.

The results in Theorem 4 show that the proposed quadratic scan procedure is consistent for estimating a signal region, and its consistency depends on the signals only through their L₂ norm. This indicates that the direction and sparsity of the signals in a signal region do not affect the consistency of the proposed scan procedure. When marginal test statistics are independent and signals have the same strength in the signal region, i.e., μ_i = μ for all i ∈ I*, Jeng et al. (2010) developed a theoretically optimal likelihood ratio selection procedure based on the mean scan statistic (4). For the likelihood ratio selection procedure to consistently detect the signal region I*, the condition on μ is $\mu \ge \sqrt{2\left(1+{\delta }_p\right)\text{log}(p)}/\sqrt{\left|I^{*}\right|}$ for some δ_p such that ${\delta }_p\sqrt{\text{log}p}\to \infty$. It means that ${\Vert {\mu }_{I^{*}}\Vert }_2^2\ge 2\left(1+{\delta }_p\right)\text{log}(p)$. Because | I* | / log(p) → ∞, this condition is weaker than condition (D) in Theorem 4, which is ${\Vert {\mu }_{I^{*}}\Vert }_2^2\ge 2\left(1+{ϵ}_0\right)\sqrt{\left|I^{*}\right|\text{log}(p)}$ for this situation. However, it is obvious that the quadratic procedure has more power than the mean scan procedure (Jeng et al., 2010) in the presence of both trait-increasing and trait-decreasing variants in the signal region. The quadratic scan procedure is also more powerful in the presence of weak or neutral variants in the signal region. We will illustrate this in finite sample simulation studies in Section 4.

4. Simulation Studies

4.1. Family-wise Error Rate for Quadratic Scan Procedure

In order to validate the proposed quadratic scan procedure in terms of protecting family-wise error rate using the empirical threshold, we estimated the family-wise error rate through simulation. To mimic WGS data, we generated sequence data by simulating 20,000 chromosomes for a 10-megabase (Mb) region on the basis of the calibration-coalescent model that mimics the linkage disequilibrium structure of samples from African Americans using COSI (Sanda et al., 2008). The simulation used the 10-Mb sequence to represent the whole genome and focused on low frequency and rare variants with minor allele frequency (MAF) less than 0.05. The total sample size n is set to be 2, 500, 5, 000 or 10, 000 and the corresponding number of variants in the sequence are 189, 597, 242, 285 and 302, 737, respectively.

We first consider the continuous phenotype generated from the model:

$$Y=0.5X_1+0.5X_2+\mathit{ϵ},$$

where X₁ is a continuous covariate generated from a standard normal distribution, X₂ is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, and ϵ follows a standard normal distribution. We selected the minimum searching window length L_min = 40 and the maximum searching window length L_max = 200. We scan the whole sequence for controlling the family-wise error rate at 0.05 and 0.01 level by using the 2,000 Monte Carlo simulations based empirical threshold that introduced in Section 2.5. The simulation was repeated for 10, 000 times.

We also conducted the family-wise error rate simulations for dichotomous phenotypes using similar settings except that the dichotomous outcomes were generated via the model:

$$\text{logit}\left\{\mathbb{P}\left(Y_i=1\right)\right\}=-4.6+0.5X_1+0.5X_2,i=1,\cdots ,n,$$

which means the prevalence is set to be 1%. Case-control sampling was used and the numbers of cases and controls were equal. The sample sizes were the same as those used for continuous phenotypes.

For both continuous and dichotomous phenotype simulations, we applied the proposed Q-SCAN procedure and M-SCAN procedure to each of the 10, 000 data sets. To control for LD, the mean scan statistic for region I is defined as

$$M(I)={\left(\sum _{i\in I}{U}_i\right)}^2/var\left(\sum _{i\in I}{U}_i\right).$$ (6)

The empirical family-wise type I error rates estimated for Q-SCAN and M-SCAN are presented in Table 1 for 0.05 and 0.01 levels, respectively. The family-wise error rate is accurate at both two significance levels and all the empirical family-wise error rate fall in the 95% confidence interval of the 10,000 Bernoulli trials with probability 0.05 and 0.01. These results showed that both Q-SCAN procedure and M-SCAN procedure are valid methods and protect the family-wise error rate.

Table 1.

Simulation Studies of Family-Wise Error Rates. The family-wise error rate of the Q-SCAN procedure is estimated with 10, 000 simulated data sets. In each data set, we considered three sample sizes n = 2, 500, n = 5, 000 or n = 10, 000, and the corresponding numbers of variants in the sequence are 189,597, 242,285 and 302,737. The minimum and maximum searching window lengths are set to be L_min = 40 and L_max = 200, respectively. Q-SCAN refers to the scan procedures using the scan statistics $Q(I)=\sum _{i\in I}{U}_i^2-\text{E}\left(\sum _{i\in I}{U}_i^2\right)/var\left(\sum _{i\in I}{U}_i^2\right)$ for region I, where U_i is the score statistic of ith variant. M-SCAN refers to the scan procedures using the scan statistics $M(I)={\left(\sum _{i\in I}{U}_i\right)}^2/var\left(\sum _{i\in I}{U}_i\right)$ for region I. The 95% confidence interval of 10, 000 Bernoulli trials with probability 0.05 and 0.01 are [0.0457,0.0543] and [0.0080,0.0120].

		Continuous Phenotypes			Dichotomous Phenotypes
Total Sample Size	Size	n = 2500	n = 5000	n = 10000	n = 2500	n = 5000	n = 10000
Q-SCAN	0.05	0.0485	0.0475	0.0514	0.0414	0.0481	0.0488
	0.01	0.0098	0.0100	0.0101	0.0077	0.0104	0.0092
M-SCAN	0.05	0.0453	0.0525	0.0494	0.0485	0.0501	0.0492
	0.01	0.0097	0.0123	0.0083	0.0094	0.0085	0.0100

4.2. Power and Detection Accuracy Comparisons

In this section, we performed simulation studies to investigate the power of the proposed Q-SCAN procedure in finite samples, and compared its performance with the M-SCAN procedure using scan statistic (6) and the SKAT (Wu et al. 2011) conducted using a sliding window approach with fixed window sizes. Genotype data was generated in the same fashion as Section 4.1. The total sample sizes were set as n = 2, 500, n = 5, 000 and n = 10, 000. We generated continuous phenotypes by

$$Y=0.5X_1+0.5X_2+G_1^c{\beta }_1+\cdots +G_s^c{\beta }_s+\mathit{ϵ},$$

where X₁, X₂ and ϵ are the same as those specified in the family-wise error rate simulations, $G_1^c,\cdots ,G_s^c$ are the genotypes of the s causal variants and βs are the log odds ratio for the causal variants. We randomly selected two signal regions across the 10-Mb sequence in each replicate and repeated the simulation 1,000 times. The number of variants in each signal region p₀ was randomly selected from 50 to 80. Causal variants were selected randomly within each signal region. Assume ξ is the sparsity index, that is, $s=p_0^{\xi }$. We assumed signals are dense in the signal region (ξ > 1 / 2) and considered two sparsity settings ξ = 2 / 3 and ξ = 3 / 4. Each of causal variant has an effect size as a decreasing function of MAF, β = −c log₁₀ (MAF). We set c = 0.185 for ξ = 2 / 3 and c = 0.14 for ξ = 3 / 4. We also considered three settings of effect direction: the sign of β_i’s are randomly and independently set as 100% positive (0% negative), 80% positive (20% negative), and 50% positive (50% negative).

We applied Q-SCAN to simulated datasets, and we compared its performance with the sliding-window procedure using SKAT wherein the sliding-window size was set to be fixed at 3 kilobase (kb), 4 kb and 5 kb. We controlled the family-wise type I error rate at the 0.05 level by using the proposed empirical threshold for Q-SCAN and M-SCAN and the Bonferroni correction for sliding window procedures. We set the minimum and maximum numbers of variants in searching windows of Q-SCAN and M-SCAN as (L_min, L_max) = (40,200) and (L_min, L_max) = (50,80).

To evaluate power for these methods, we considered two criteria, the signal region detection rate and the Jaccard index as performance measurements. Let I₁ and I₂ be the two signal regions and $\left\{{\widehat{I}}_j\right\}$ be a collection of signal regions. The signal region detection rate is defined as

$$\frac{1}{2}\left[1\left\{I_1\cap \left(\cup {\widehat{I}}_j\right)\ne \varnothing \right\}+1\left\{I_2\cap \left(\cup {\widehat{I}}_j\right)\ne \varnothing \right\}\right],$$

where 1(·) is an indicator function. Here we define the signal region as detected if it is overlapped with one of the detected regions. For the Jaccard index, we define it as

$$\frac{1}{2}\left\{\underset{j}{\text{max }}J\left(I_1,{\widehat{I}}_j\right)+\underset{j}{\text{max }}J\left(I_2,{\widehat{I}}_j\right)\right\},$$

where J(·,·) is defined in Section 3.2.

Figure 1 summarizes the simulation results when the sparsity index ξ = 2 / 3. In this situation, the Q-SCAN procedure had a better performance for detecting signal regions than M-SCAN and the sliding window procedure using SKAT with a fixed window size, when the effects of causal variants are in different direction. Its performance was comparable to the M-SCAN procedure when the effects of causal variants were in same direction. Specifically, when the effects of causal variants were in different directions, Q-SCAN had a higher signal region detection rate and Jaccard index than that of the M-SCAN and the sliding window procedure using SKAT. The difference between Q-SCAN and M-SCAN was more appreciable when the proportion of variants with negative effects increased from 20% to 50%. When the effects of causal variants were in the same direction, both Q-SCAN and M-SCAN had a higher power than the sliding window procedure using SKAT both in terms of signal region detection rate and Jaccard index. Although M-SCAN had a highest signal region detection rate and Jaccard index, the performance of Q-SCAN was comparable to that of the M-SCAN and the difference decreased as the sample size increased. When the range of searching window was closer to the size of signal regions, both Q-SCAN and M-SCAN had better power, but the difference was small.

Fig. 1.

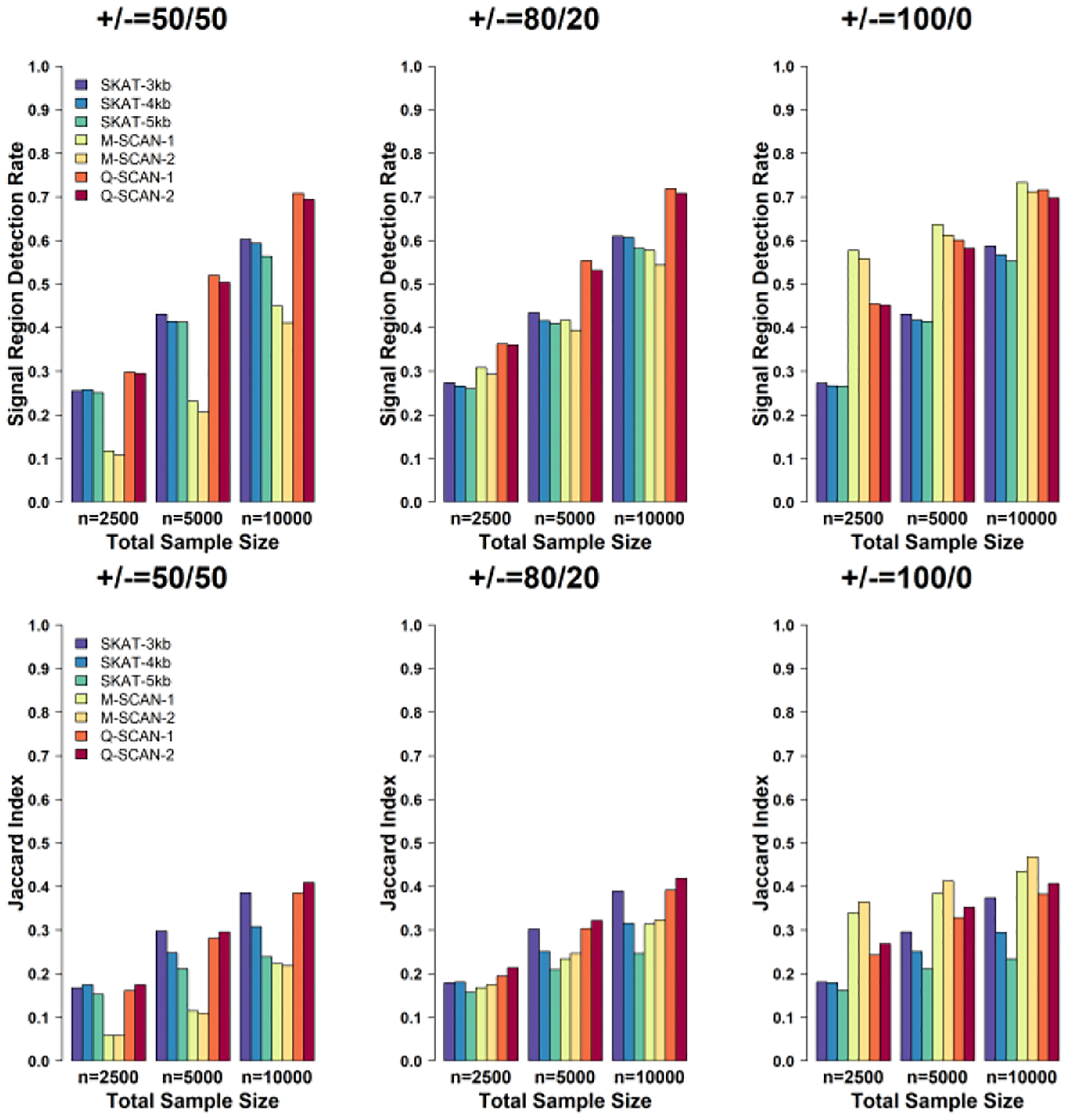
Power and accuracy of estimated signal region comparisons using Q-SCAN, M-SCAN and sliding window procedure using SKAT for the setting with the sparsity index ξ = 2 / 3. We evaluated power via the signal region detection rate and the Jaccard index defined in the simulation section. Both criteria were calculated at the family-wise error rate at 0.05 level. The number of variants in signal region p₀ was randomly selected between 50 and 80 and $s=p_0^{\xi }$ causal variants were selected randomly within each signal region. Each causal variant has an effect size that is set as a decreasing function of MAF, β = −clog₁₀ (MAF) and c = 0.185. From left to right, the plots consider settings in which the coefficients for the causal rare variants are 100% positive (0% negative), 80% positive (20% negative), and 50% positive (50% negative). We repeated the simulation for 1,000 times. Q-SCAN and M-SCAN refer to the scan procedures using the scan statistics $\sum _{i\in I}{U}_i^2-\text{E}\left(\sum _{i\in I}{U}_i^2\right)/var\left(\sum _{i\in I}{U}_i^2\right)$ and ${\left(\sum _{i\in I}{U}_i\right)}^2/var\left(\sum _{i\in I}{U}_i\right)$, respectively. In both two scan procedures, “−1” and “−2” represents the range of the numbers of variants in searching windows (L_min, L_max) = (40,200) and (L_min, L_max) = (50,80), respectively. The sliding window length was set as 3 kb, 4 kb and 5 kb.

Although Q-SCAN and M-SCAN with (L_min, L_max) = (50,80) were three times faster than those with (L_min, L_max) = (40,200), the computation time for Q-SCAN with (L_min, L_max) = (40,200) to perform whole genome analysis on 10,000 simulated samples only required 75 minutes for 100 2.90 GHz computing cores with 3 gigabyte (Gb) memory. Further, setting L_max = 200 also ensured that promoters are covered in the Q-SCAN procedure, since promoters are often defined as a 6-kb region which contains +/− 3-kb windows of the transcription starting site, and 90% of 6-kb sliding windows of simulated genomes for 10,000 individuals have less than 200 variants. Figure 2 summarizes the simulation results when the sparsity index ξ = 3 / 4. The simulation results were qualitatively similar and showed that Q-SCAN outperformed M-SCAN and the sliding window procedure using SKAT with a pre-fixed window size.

Fig. 2.

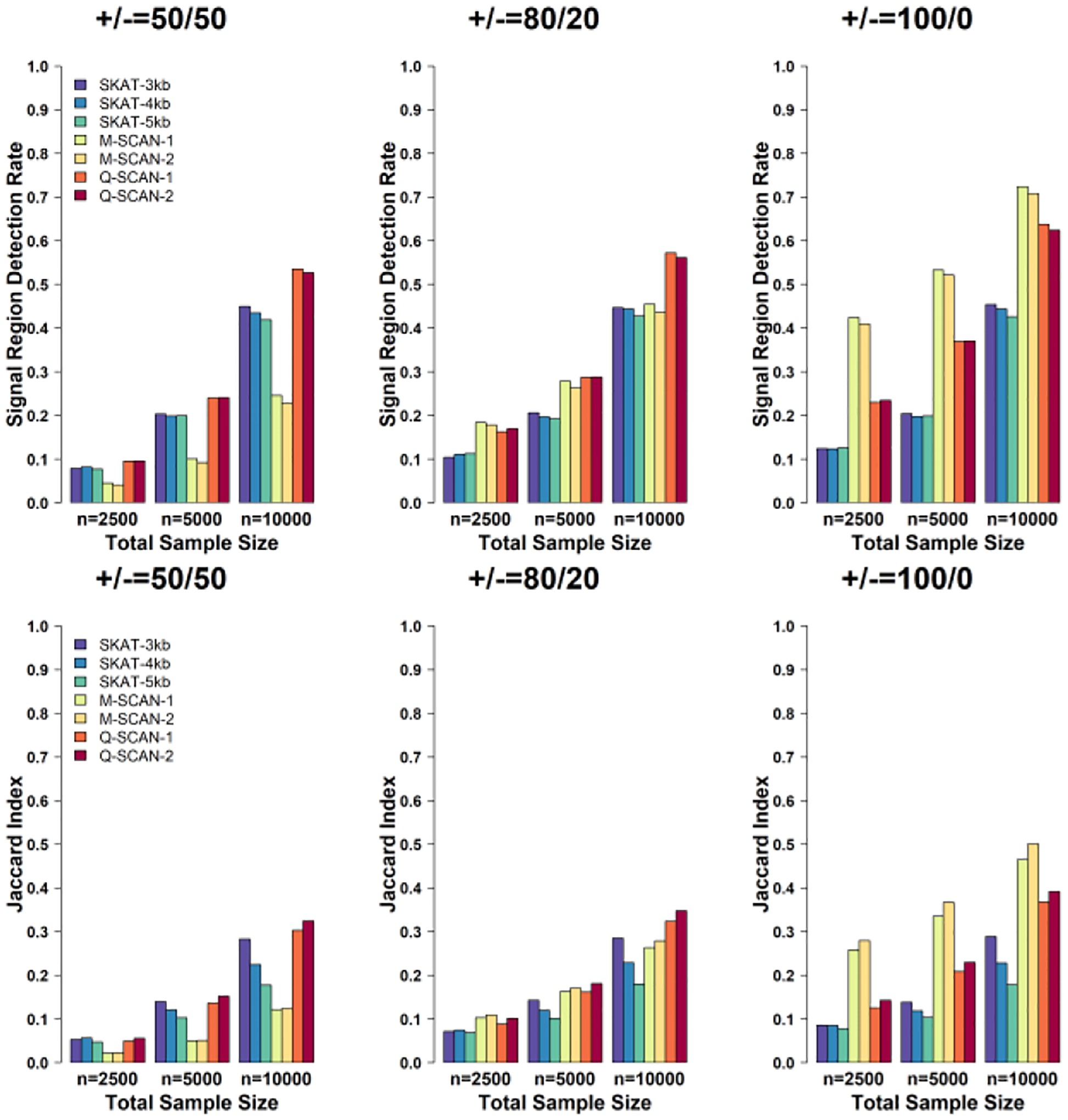
Power and accuracy of estimated signal region comparisons using Q-SCAN, M-SCAN and sliding window procedure using SKAT assuming the sparsity index ξ = 3 / 4. We evaluated power via the signal region detection rate and the Jaccard index defined in the simulation section. Both criteria were calculated at the family-wise error rate at 0.05 level. The number of variants in signal region p₀ was randomly selected between 50 and 80. The $s=p_0^{\xi }$ causal variants were selected randomly within each signal region. Each causal variant has an effect size that is set as a decreasing function of MAF, β = −clog₁₀ (MAF) and c = 0.14. From left to right, the plots consider settings in which the coefficients for the causal rare variants are 100% positive (0% negative), 80% positive (20% negative), and 50% positive (50% negative). We repeated the simulation for 1,000 times. Q-SCAN and M-SCAN refer to the scan procedures using the scan statistics $\sum _{i\in I}{U}_i^2-\text{E}\left(\sum _{i\in I}{U}_i^2\right)/var\left(\sum _{i\in I}{U}_i^2\right)$ and ${\left(\sum _{i\in I}{U}_i\right)}^2/var\left(\sum _{i\in I}{U}_i\right)$, respectively. In both two scan procedures, “−1” and “−2” represents the range of the numbers of variants in searching windows (L_min, L_max) = (40,200) and (L_min, L_max) = (50,80), respectively. The sliding window length was set as 3 kb, 4 kb and 5 kb.

In summary, our simulation study illustrates that Q-SCAN has an advantage for identifying signal regions over M-SCAN and the sliding window procedure using SKAT with a pre-specified fixed window size, in the sense that Q-SCAN had a higher signal region detection rate and Jaccard index, regardless of signal directions and signal sparsity. We also conducted power simulations for different effect sizes, and the pattern was similar. These results could be found in the Supplementary Materials (Figure S1–Figure S2).

5. Application to the ARIC Whole Genome Sequencing Data

In this section, we analyzed the ARIC WGS study conducted at the Baylor College of Medicine Human Genome Sequencing Center. DNA samples were sequenced at 7.4-fold average depth on Illumina HiSeq instruments. We were interested in detecting genetic regions that were associated with two quantitative traits, small, dense, low-density lipoprotein cholesterol (LDL) and lipoprotein(a) (Lp(a)), both of which are risk factors of cardiovascular disease. After sample-level quality control (Morrison et al., 2017), there were 33 million variants observed in 1,705 European Americans (EAs). Among these variants, 80% were low-frequency and rare variants (MAF <5%). For this analysis, since the sample size is not large, we analyzed these low-frequency and rare variants across the whole genome.

To illustrate the proposed Q-SCAN procedure, we compared the performance of the Q-SCAN procedure with the Mean scan procedure M-SCAN and SKAT (Wu et al., 2011) conducted using a sliding window approach with fixed window sizes. Following Morrison et al. (2017), for the sliding window approach, we used the sliding window of length 4 kb and began at position 0 bp for each chromosome, utilizing a skip length of 2 kb, and we tested for the association between variants in each window and the phenotype using SKAT with equal weights. We adjusted for age, sex, and the first three principal components of ancestry in the analysis for both traits and additionally adjusted for current smoking status in the analysis of Lp(a), consistent with the procedure described in Morrison et al. (2017). Because the distribution of both LDL and Lp(a) are markedly skewed, we transformed them using the rank-based inverse normal-transformation following the standard GWAS practice (Barber et al., 2010), see Figure S3.

For both Q-SCAN and M-SCAN procedures, we set the range of searching window sizes by specifying the minimum and maximum numbers of variants L_min = 40 and L_max = 200. We controlled the family-wise error rate (FWER) at the 0.05 level in both Q-SCAN and M-SCAN analyses using the proposed empirical threshold based on 2,000 Monte Carlo simulations. For the sliding window procedure, following Morrison et al. (2017), we required a minimum number of 3 minor allele counts in a 4-kb window with a skip of length of 2 kb, which results in a total of 1, 337, 382 overlapping windows in EAs. As around 1.3 million windows were tested using the sliding window procedure, we used the Bonferroni method to control for the FWER at the 0.05 level in the sliding window method following the GWAS convention. We hence set the region-based significance threshold for the sliding window procedure at 3.75 × 10⁻⁸ (approximately equal to 0.05 / 1,337,000). We note that both Q-SCAN and M-SCAN directly control for the FWER without the need of further multiple testing adjustment.

Q-SCAN detected a signal region of 4, 501 basepairs (from 45, 382, 675 to 45, 387, 175 bp on chromosome 19) consisting of 58 variants that had a significant association with LDL among EAs with the family-wise error rate 0.005. This region resides in NECTIN2 and covers three uncommon variants with individual p-values less than 1 × 10⁻⁶, including rs4129120 with p = 8.47 × 10⁻⁹ and MAF = 0.036, rs283808 with p = 5.71 × 10⁻⁷ and MAF=0.042, and rs283809 with p = 5.71 × 10⁻⁷ and MAF = 0.042. Although the variant rs4129120 had a small p-value, it was not significant after adjusting for multiple comparisons of 9, 367, 575 variants with MAF ≥ 0.01 across the genome, giving the family-wise error rate estimated by Bonferroni correction as 0.079. This was marginally significant and much larger than the family-wise erorr rate of the region detected by Q-SCAN 0.005. Several common variants in NECTIN2 have been found to have significant associations with LDL in previous studies (Talmud et al., 2009; Postmus et al., 2014).

The M-SCAN procedure did not detect any signal segment associated with LDL to reach genome-wide significance when we controlled for the FWER at 0.05. Examination of the data showed that the variant effects had different directions and were mixed with neutral variants in the signal region detected by Q-SCAN (the region from 45, 382, 675 to 45, 387, 175 bp on chromosome 19). The 4-kb sliding window approach using SKAT, which was used in previous study (Morrison et al., 2017), detected two significant sliding windows. However, both two windows did not cover all of the three variants rs4129120, rs283808 and rs283809, and the SKAT p-values of the two sliding windows that cover variant rs4129120 were 1.15 × 10⁻⁸ and 1.17 × 10⁻⁸, respectively. In contrast, the SKAT p-value of the signal region detected by Q-SCAN was 1.87 × 10⁻⁹. This indicated that our procedure increased the power for detecting signal regions by estimating the locations and the sizes of signal regions more accurately. These results explain why our Q-SCAN procedure is more powerful than the M-SCAN procedure and the sliding window procedure using a fixed window size in the analysis of LDL in ARIC WGS data.

We next performed WGS association analysis of Lp(a) among EAs in the ARIC study using Q-SCAN, M-SCAN and the SKAT-based sliding window method with a fixed window length of 4 kb. Compared to the existing methods, Q-SCAN was able to detect four significant novel intergenic regions associated with lipoprotein(a) (Lp(a)). These four significant regions resided in a 519-kb region on chromosome 6 from 160,595,533 bp to 161,114,514 bp, including an intergenic region between SLC22A1 and SLC22A2, an intergenic region between SLC22A2 and SLC22A3, an intergenic region between LPAL2 and LPA, and an intergenic region between LPA and PLG. Among these four associations, one was not found using the sliding window procedure, and three were not found using the M-SCAN procedure. No additional association in intergenic regions was detected using the SKAT-based sliding window with fixed window sizes and the M-SCAN procedure (Figure 3). In summary, compared to the existing methods, the Q-SCAN procedure not only enables obtaining more significant findings, but also is less likely to miss important signal regions.

Fig. 3.

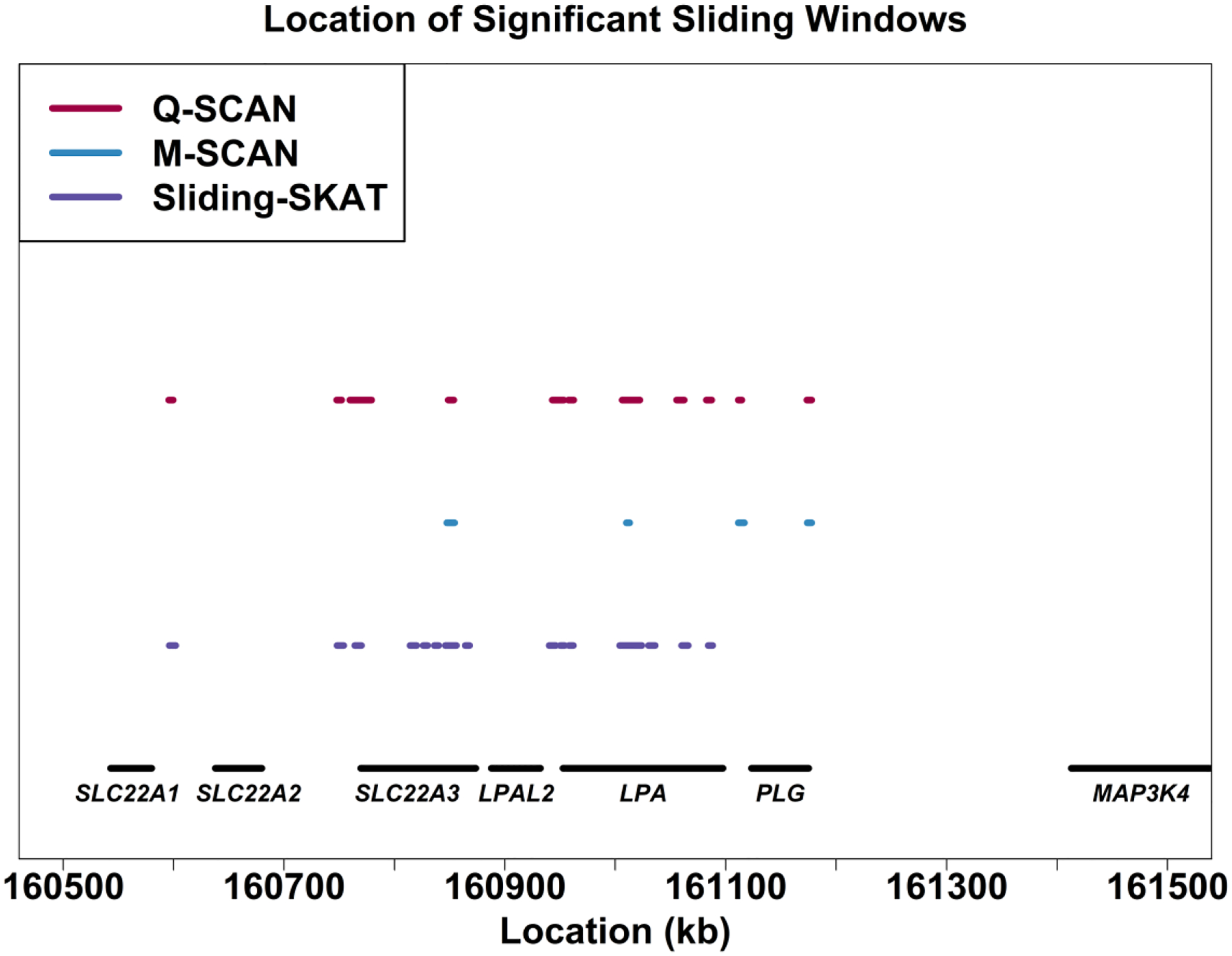
Genetic landscape of the windows that were significantly associated with lipoprotein(a) on chromosome 6 among European Americans in the ARIC Whole Genome Sequencing Study. Three methods were compared: Q-SCAN, M-SCAN and 4 kb sliding window procedures using SKAT with equal weights. A dot means that the sliding window at this location is significant using the method the color of the dot represents. The physical positions of windows are based on build hg19.

6. Discussions

In this paper, we propose a quadratic scan procedure to detect the existence and the locations of signal regions in whole genome array and sequencing studies. We show that the proposed quadratic scan procedure could control for the family-wise error rate using a proper data-driven threshold. Under regularity conditions, we also show that our procedure can consistently select the true signal segments and estimate their locations. Our simulation studies demonstrate that the proposed procedure has a better performance than the mean-based scan method in the presence of variants effects that are in different directions, or mixed signal variants and neutral variants in signal regions. An analysis of WGS and heart-and blood-related traits from the ARIC study illustrates the advantages of the proposed Q-SCAN procedure for rare-variant WGS analysis, and demonstrates that Q-SCAN detects the locations and the sizes of signal regions associated with LDL and Lp(a) more powerfully and precisely.

The computation time of Q-SCAN is linear in the number of variants in WGS and the range of the number of variants in searching windows, and hence is computationally efficient. To analyze a 10 Mb region sequenced on 2,500, 5,000 or 10,000 individuals, when we selected the number of variants in searching windows between 40 and 200, the proposed Q-SCAN procedure took 15, 19 and 25 minutes, respectively, on a 2.90GHz computing cores with 3 Gb memory. Using the same computation core, Q-SCAN took 20 hours to analyze the whole genome sequencing data of EA individuals in the ARIC study. The Q-SCAN procedure also works for parallel computing. For example, analysis of the whole genome for 10,000 individuals only requires 75 minutes if using 100 computation cores.

Specification of the minimum and maximum searching window lengths L_min and L_max is an important issue in the Q-SCAN procedure. Specifically, the range of the searching window lengths determines computation complexity. In the meantime, the range of the searching window length should be wide enough to cover different true signal regions across the genome, including the important functional masks of non-coding regions, such as promoters and enhancers. Based on our simulation results, we recommend to set L_min = 40 and L_max = 200 when the sample size is less than 20,000.

We derived an empirical threshold based on Monte Carlo simulations to control for the family-wise error rate at an exact α – level and gave the asymptotic bound of the proposed threshold. This step costs additional computational time in applying our procedure. Future research is needed to develop an analytic approximation to the significance level for the proposed Q-SCAN statistics. We allow in this paper individual variant test statistics to be correlated, and assume M_p – dependence. This is a reasonable assumption in WGS association studies, because two marginal test statistic are independent when two variants are far apart in the genome. It is of future research interest to extend our procedure to more general correlation structures. Moreover, the proposed Q-SCAN procedure worked well when signals were dense in signal regions. An interesting problem for future research is to develop a scan procedure for very sparse signal regions (Donoho and Jin, 2004).

We assume in this paper all the variants have the same weight in constructing the quadratic scan statistic. In WGS studies, upweighting rare variants and functional variants could boost power when causal variants are likely to be more rare and functional. It is of great interest to extend our proposed scan procedure by weighting individual test statistics using external bioinformatic and evolutionary biology knowledge, such as variant functional information when applying to WGS studies. We assume individual variant test statistics are asymptotically jointly normal. However, when most of variants are rare variants in the sequence, this normal assumption might not hold in finite samples for binary traits. An interesting problem of future research is to extend the results to the situation where individual variant test statistics are not normal and use the exact or approximate distributions of individual test statistics to construct scan statistics.

7. Software

The Q-SCAN procedure was implemented in the R package QSCAN, which is freely available at (https://github.com/zilinli1988/QSCAN). A numerical example of the Q-SCAN procedure is available at https://github.com/zilinli1988/QSCAN.