Toward an artificial intelligence‐assisted framework for reconstructing the digital twin of vertebra and predicting its fracture response

Abstract

This article presents an effort toward building an artificial intelligence (AI) assisted framework, coined ReconGAN, for creating a realistic digital twin of the human vertebra and predicting the risk of vertebral fracture (VF). ReconGAN consists of a deep convolutional generative adversarial network (DCGAN), image‐processing steps, and finite element (FE) based shape optimization to reconstruct the vertebra model. This DCGAN model is trained using a set of quantitative micro‐computed tomography (micro‐QCT) images of the trabecular bone obtained from cadaveric samples. The quality of synthetic trabecular models generated using DCGAN are verified by comparing a set of its statistical microstructural descriptors with those of the imaging data. The synthesized trabecular microstructure is then infused into the vertebra cortical shell extracted from the patient's diagnostic CT scans using an FE‐based shape optimization approach to achieve a smooth transition between trabecular to cortical regions. The final geometrical model of the vertebra is converted into a high‐fidelity FE model to simulate the VF response using a continuum damage model under compression and flexion loading conditions. A feasibility study is presented to demonstrate the applicability of digital twins generated using this AI‐assisted framework to predict the risk of VF in a cancer patient with spinal metastasis.

A new artificial intelligence‐enabled modeling platform, relying on a deep convolutional generative adversarial network, image processing, and shape optimization is introduced for virtual reconstruction of a highly realistic geometrical model of human vertebra. A high fidelity finite element model of the resulting digital twin is then generated to simulate the vertebra fracture response using a continuum damage model. A feasibility study is presented that showcases the application of this integrated computational framework for analyzing the impact of tumor and loading conditions on the risk of vertebral fracture in cancer patients with spinal metathesis.

1. INTRODUCTION

More than 1.6 million cases of cancer are diagnosed in the United States every year. ¹ Symptomatic spinal metastases are estimated to occur in up to 10% of all cancer patients. ² Majority of the spinal metastasis cases occur in the extradural compartment, most frequently presenting within the vertebral bodies. ³ Most of the metastatic burden (70%) is within the thoracic spine, followed by the lumbar spine (20%), cervical spine, and sacrum. ⁴ Vertebral fracture (VF) is a major clinical concern during the treatment of cancer patients with spinal metastasis (SM). These fractures are directly related to the effect of tumor metastasis on the anatomical integrity and internal structure of the bone tissue. ⁵ , ⁶ Stereotactic radiotherapy (SRT) is an effective treatment modality that has shown significant improvement in local tumor control and pain in SM patients. However, loss of stability due to the treatment of tumor cells and possible weakening of the bone tissue due to SRT may further increase the risk of VF, which may cause severe pain and spinal instability. ⁷ , ⁸ This often necessitates additional surgical interventions such as vertebroplasty to treat post‐fracture complications. As patients continue to live longer with improved systemic therapies for metastatic cancer, the utilization of SRT will continue to grow given its association with longer local control. This will likely lead to more VFs, which can severely impact the quality of life for patients. Therefore, predicting the risk of VF in metastatic spine cancer patients is crucial for informed decision‐making and design of better treatment strategies to benefit these patients.

While biomechanical loads are believed to play a major role in the initiation of VF, the correlation between spinal loads and morphological changes to the vertebral body (due to tumor lesion or radiation) that lead to bone fracture is not well understood. Note that, in addition to its macroscopic shape, the fracture response of vertebra is highly dependent on microstructural features of the trabecular region. In‐vitro studies can provide fundamental knowledge on the mechanical behavior of vertebral structure but they cannot accurately measure relevant biomechanical parameters such as in‐vivo internal stresses that play a crucial role in damage initiation and failure. Computational modeling is a viable alternative for studying such parameters, which has gained more attention due to recent advances in numerical techniques, computing power, and 3D imaging technology. ⁹

In the current manuscript, we introduce a new computational framework capable of creating realistic digital twins of vertebral bodies to assess the risk of VF in patients with SM. The concept of digital twin is borrowed from engineering principles, where the in silico representation of a complex system (here, vertebra) serves as a virtual model to analyze the current condition and predict its future performance based on real‐time data characterizing the system condition. ¹⁰ Digital twins utilization in orthopedics is revolutionizing surgical procedures by helping surgeons study new therapies and medical implants. ¹¹ , ¹² , ¹³ For example, in a recent study, the digital twin of a patient's fractured tibia was used to simulate different stabilization scenarios and provide post‐operative information on the risk of fracture. ¹³

Majority of numerical studies presented in the literature on the mechanical behavior of vertebra do not incorporate the intricate microstructure of the trabecular bone and instead use a computational homogenization approach relying on effective properties of this region. ¹⁴ , ¹⁵ , ¹⁶ However, an accurate prediction of the initiation and evolution of damage during the VF process requires taking into account he trabecular microstructure and the variation of material properties within that in the FE model. This requires the ability to generate a highly realistic geometrical models of vertebral body that captures such microstructural details. However, incorporating the trabecular bone microstructure in the FE model of a patient's vertebra could be a grand challenge, as diagnostic CT scans lack the resolution needed to characterize these features. Micro‐CT devices can provide a high resolution visualization of the 3D bone microstructure, with a voxel size that could even reach sub‐micron scale. ¹⁷ , ¹⁸ On the other hand, obtaining high‐resolution micro‐CT scans would practically be impossible in‐vivo due to sample preparation requirements. Thus, micro‐CT imaging is only feasible for cadaveric samples (often a small portion of the trabecular bone) and cannot be used to create a patient‐specific model of the whole vertebra. Consequently, only a few FE studies are presented that investigate the biomechanics of human vertebra from the microstructural perspective. ¹⁹ , ²⁰

The challenges outlined above have motivated the development of an AI‐enhanced framework in this work, coined ReconGAN, to create realistic vertebra geometric models by virtually reconstructing the trabecular bone microstructure and integrating that with the macroscopic shape of vertebra obtained from a patient's CT scans. Note that several algorithms have been introduced for virtual reconstruction of porous materials, among which we can mention the Gaussian random fields, ²¹ optimization‐based methods, ²² multi‐point statistics (MPS), ²³ direct sampling (DS) ²⁴ and cross‐correlation simulation (CCSIM). ²⁵ However, microstructural models reconstructed using such algorithms are often too simplistic to replicate the complex architecture of the trabecular bone, which in addition to a tortuous porous microstructure has a significant variation of material properties within each trabecula. Note that it is crucial to realistically capture such variations in a synthesized microstructure used for FE damage analysis, as they can have a notable impact on the damage response of bone tissue.

Deep learning (DL) algorithms such as convolutional neural networks (CNN) and generative models can be used as an alternative to conventional reconstruction algorithms to synthesize realistic virtual microstructures from imaging data. ²⁶ , ²⁷ For example, a CNN‐based transfer learning approach equipped with encoding and decoding layers is employed to generate statistically equivalent two‐dimensional (2D) microstructures based on an arbitrary target image of the sample. ²⁶ A variational auto‐encoder (VAE) generative model, ²⁸ combined with style transfer, ²⁹ is utilized in ²⁷ to synthesize sandstone samples. However, one of the main challenges toward using these algorithms for medical applications is the lack of a sufficiently large and diverse set of training data. ³⁰ While a number of medical image repositories such as SpineWeb are publicly available, ³¹ , ³² majority of these data sets correspond to the organ‐level (macroscale). Creating similar repositories of micro‐CT images for biological tissues (e.g., for the trabecular bone microstructure) is a complex and expensive process that requires a collaborative effort between multiple research organizations. ³³

A class of DL algorithms that can overcome the challenges associated with scarcity of training data is generative adversarial networks (GANs). ³⁴ Inspired by game theory, GANs consist of two adversarial networks working simultaneously, where a generator network is tasked to create synthetic images while a second network, the discriminator, serves as a binary classifier to distinguish between actual and synthetic images. The two networks practically play a minimax game to reach Nash equilibrium, ³⁵ where the goal of the generator is to maximize the probability of fooling the discriminator while the discriminator is trained to minimize the cross‐entropy loss between real and fake images. GANs have extensively been used in the computer vision community for image synthesis, image segmentation, and cross‐modality translations. ³⁶ , ³⁷ , ³⁸ For example, Deep Convolutional GANs (DCGANs) ³⁹ are employed to generate synthetic 2D images of liver lesions to assist training other DL models for lesion classification. ⁴⁰ A patch‐based GAN learning algorithm is trained to provide a cross‐modality framework for translation between CT and MRI images of brain. ³⁷ Also, 3D GANs have been employed to synthesize volumetric object models, ⁴¹ although their application compared to 2D GANs is limited.

The ReconGAN framework introduced in this work relies on a 3D DCGAN to generate gray‐scale microstructural models of the trabecular bone after being trained with quantitative micro‐CT (micro‐QCT) images obtained from cadaveric samples. We utilize a data augmentation approach to enable training this model using a limited set of imaging data extracted from a single cadaveric vertebra. The ability of DCGANs to generate realistic virtual bone microstructures is validated by comparing a number of statistical microstructural descriptors with those of micro‐QCT data. Note that the main reason for using DCGANs to synthesize the trabecular bone microstructure rather than directly reconstructing this microstructure from micro‐QCT data is the scalability of the former, that is, the ability of the generator network to virtually enlarge the model. Given the small size of cadaveric samples used for preparing these imaging data, this capability is essential for creating a sufficiently large model of the trabecular bone microstructure that can subsequently be incorporated in a whole vertebra geometrical model. A set of image processing steps is employed to engrave the trabecular microstructure generated using DCGAN and embed that within the cortical shell extracted from the patient's CT scans to build this whole vertebra model. An FE‐based shape optimization simulation aimed at minimizing stress concentrations is then carried out to obtain a realistic (smooth) transition between trabecular and cortical regions. This step is inspired by the Wolff's law, ⁴² which considers a direct correlation between bone formation and mechanical stresses during the remodeling process.

Next, the whole vertebra model generated using ReconGAN is converted to a high‐fidelity FE model to simulate its damage response and predict the risk of VF. The damage initiation in the bone tissue is associated with the nucleation of voids, for example, debonding of the collagen‐hydroxyapatite interfaces at the ultrastructural level ⁴³ or slipping of lamellae along cement lines at the microscale. ⁴⁴ The next stage involves the growth and coalescence of these voids, which results in strain localization bands at the tissue level. ⁴⁵ , ⁴⁶ In continuum mechanics, this damage mechanism is mainly driven by stress‐triaxiality, that is, the ratio of hydrostatic stress to the von‐Mises stress. ⁴⁷ It is well‐known that incorporating the stress‐triaxility in a damage model accounts for tension‐compression asymmetry, as well as the loading‐mode dependency of the bone strength. ⁴⁸ Several studies have suggested that tissue damage in the trabecular bone is strongly correlated with the applied strain. ⁴⁸ , ⁴⁹ In this work, we implement the phenomenological strain‐based ductile damage model presented in Reference 50 to capture these phenomena in the vertebral body during VF simulations.

The remainder of this article is structured as follows: The constitutive models used for simulating the damage response of the bone are presented in Section 2. In Section 3, after describing the process used for preparing micro‐QCT images of the trabecular bone, we introduce the ReconGAN framework and different steps of this algorithm for synthesizing realistic geometrical models of vertebra. Section 4 presents a feasibility study relying on ReconGAN on the effect of microstructural and morphological changes in the vertebra tissue due to metastatic tumors on its VF response. Final concluding remarks are summarized in Section 5.

2. CONSTITUTIVE MODELS AND MATERIAL PROPERTIES

Several correlation functions between the elastic modulus (E) and the bone density are presented in the literature. ⁵¹ , ⁵² Defining the apparent bone density as

$${\rho }_{\mathrm{app}}=\frac{\mathrm{BV}}{\mathrm{TV}}\rho ,$$ (1)

where $\frac{\mathrm{BV}}{\mathrm{TV}}$ is the bone volume fraction, many studies have suggested that the relationship between E and ρ _app is best represented by

$$E=K{\rho }_{\mathrm{app}}^n.$$ (2)

In this power law equation, scalar coefficients K and n depend on various parameters such as the tissue type (cortical vs. trabecular), anatomical location of the bone, age group, and external loading conditions. In this work, we adopt these coefficients from Reference 53 for the trabecular bone as K = 24.53 GPa and n = 1.3, which are calibrated for vertebral trabecular specimens subjected to compression. Also, the elastic modulus and the Poisson's ratio of the vertebra cortical bone is set to E _cor = 10 GPa and ν _cor = 0.3, respectively. ⁵⁴ , ⁵⁵

A phenomenological ductile damage model is implemented to track the initiation and progression of damage in the bone tissue. ⁵⁰ , ⁵⁶ In this model, the von‐Mises yield criterion, together with an isotropic hardening law, is employed to characterize the bone elastoplastic response as

$$\mathrm{Y}={\sigma }_{\mathrm{vm}}-{\sigma }_Y\left({\epsilon }_{\mathrm{eq}}^{\mathrm{pl}}\right)=0,$$ (3)

where σ _vm is the von‐Mises stress, ε _eq ^pl is the equivalent plastic strain, and σ _Y (ε _eq ^pl) is the yield stress function calibrated based on experimentally measured stress–strain response of the bone. To simulate progression of damage in the bone tissue, we first define the effective stress tensor σ _eff as

$${\mathit{\sigma }}_{\mathrm{eff}}=\frac{\mathit{\sigma }}{1-D}$$ (4)

where σ is the FE stress tensor and D is a scalar parameter representing damage, which ranges from 0 to 1 during progressive failure. Damage initiation is triggered based on a strain‐driven criterion given by

$$Y_D={\epsilon }_{\mathrm{eq}}^{\mathrm{pl}}-{\epsilon }_0^{\mathrm{pl}}\left(\eta \right)=0,$$ (5)

where ${\epsilon }_0^{\mathrm{pl}}\left(\eta \right)$ is a threshold function for stress triaxiality η = −p/σ _vM (p is the hydro‐static stress) determined based on micromechanical tests on trabecular bone. ⁴⁶ Note that incorporating η in the damage models allows for capturing the loading‐mode dependent damage response of the bone. After detecting the micro‐damage initiation, progressive failure is governed by an exponentially evolving damage parameter $D=D\left({\overline{u}}^{\mathrm{pl}}\right)$, which is a function of the effective plastic displacement. The rate of damage evolution is given by

$${\dot{\overline{u}}}^{\mathrm{pl}}=L{\dot{\epsilon }}_{\mathrm{eq}}^{\mathrm{pl}}$$ (6)

where L is a scalar parameter estimated based on the mesh size and ${\dot{\epsilon }}_{\mathrm{eq}}^{\mathrm{pl}}$ is the rate of equivalent plastic strain.

The yield function used in this work is estimated based on a well‐established linear hardening law with 0.05E tangent modulus and a yield strain of 0.9%. ⁴⁸ The load‐dependent damage threshold values for equivalent plastic strains under tension, compression, and torsion are set to ${\epsilon }_0^{\mathrm{pl}}\left(\eta \right)$= 0.6%, 0.7%, and 1.4%, respectively. ⁴⁶ More details regarding the implementation of this model and the process of calibrating parameters used in this damage model are presented in. ⁵⁰ , ⁵⁷

3. RECONGAN: AI‐ENHANCED MICROSTRUCTURE RECONSTRUCTION

In this section, we introduce the ReconGAN framework for the virtual reconstruction of a realistic geometrical models of vertebra. This algorithm consists of three main phases: (i) synthesizing the trabecular bone microstructure using a 3D DCGANs trained with micro‐QCT images obtained from cadaveric samples; (ii) extracting the cortical shell of the vertebra from diagnostic CT scans of the patient's spine; (ii) infusing the virtually reconstructing trabecular microstructure into the cortical shell, which requires image processing tasks and performing an FE‐based shape optimization to obtain a realistic transition between the two regions. These phases are described in more detail next.

3.1. Micro‐QCT imaging and characterization

In order to prepare micro‐QCT scans of the trabecular bone tissue, a cadaveric specimen (cf. Figure 1A) was collected in collaboration with the cooperative human tissue network at the Ohio State University (OSU). All procedures were reviewed and given an exemption approval by the OSU's investigation review board. The autopsy subject was a 57‐year old female with no history of infectious disease. Five cuboid trabecular bone specimens with dimensions 6 mm × 6 mm × 10 mm were extracted in the principal direction from the cadaveric vertebra using a precision saw machine. The specimens were collected from the T1 to T2 vertebrae, both from the core and peripheral regions, and later fixed in 70% ethanol and stored in 4°C to eliminate the risk of infection. The whole procedure of cutting and storing the specimen until performing micro‐QCT scans lasted 3 days.

FIGURE 1.

(A) Cadaveric vertebral sample and the micro‐quantitative computed tomography (QCT) images associated with one of the cuboid specimens extracted from its trabecular region; (B) Specimens setup and CaHA calibration phantoms within the micro‐QCT scanner tube

The samples were scanned using a Bruker SkyScan 1276 device with spatial resolution of 20 μm, while setting the voltage for X‐ray to 40 KV (cf. Figure 1B). The samples were scanned with a camera exposure time of 350 ms, resulting in a scan time of approximately 4 h. The primary output from micro‐QCT data is a voxelated gray‐scale (GS) field, which is then converted to equivalent bone mineral density (BMD) distribution. Figure 1A shows the reconstructed GS microstructure of the trabecular bone obtained from micro‐QCT data for one of the cubic specimens.

During the scans, a pair of Bruker calibration phantoms with known concentrations of calcium hydroxyapatite (CaHA) were also scanned with the specimens. The known mass concentrations of these two phantoms (0.25 and 0.75 g/cm³) were calibrated with their measured GS values from micro‐QCT images. Using these two data points, a linear relationship was established between the BMD and the scanned GS as

$$\rho =\alpha +\beta \mathrm{GS},$$ (7)

where α and β are calibration coefficients and the bone density, ρ, is given in [g/cm³]. In this study, α and β are evaluated as −5.53 and 0.013, respectively. It must be noted that due to beam hardening effects, the size of the phantoms slightly affects the measured density, meaning it is important to use a phantom with a similar cross‐sectional area as trabecular bone samples.

We use two statistical microstructural descriptors to characterize morphological features of the trabecular microstructures reconstructed from micro‐QCT data. A two‐point correlation function S ₂(r) is used to determine the probability of finding two points at distance r, x ₁ = x and x ₂ = x + r, belonging to the same material phase p _i. ⁵⁸ This probability distribution function (PDF) statistically quantifies both the local and global morphological distributions of the bone within the trabecular microstructure, which can be expressed as

$$S_2\left(r\right)=\mathrm{P}\left(x_1,x_2\in p_i\right).$$ (8)

It is also worth noting that at r = 0, the two‐point correlation function yields the phase volume fraction.

The bone microstructures reconstructed from micro‐QCT data can also be characterized based on image quality metrics such as the pixel intensity, contrast, and brightness. Note that it is highly important that the microstructural models created using DCGANs (Section 3.2) properly replicate these features. This is due to the fact that, according to (7), the bone density is directly linked to the GS associated with each pixel (pixel intensity), which in turn determines the distribution of elastic modulus of the bone using (2) in the FE mesh. In this work, the similarity metric between actual and virtual images is determined based on the image histogram, ⁵⁹ h(g). This histogram shows the GS range, i.e., the number of pixels/voxels within a given range of GS values. For instance, in an 8‐bit grayscale image, h(g) displays the distribution of 256 different possible pixel intensity values.

3.2. Reconstruction of trabecular microstructure

The micro‐QCT data obtained from cadaveric samples are used for training a 3D DCGAN to virtually reconstruct realistic microstructural models of the trabecular bone. Original GAN models (vanilla‐GAN) rely on training two independent networks, known as generator and discriminator, in an adversarial manner. The generator G learns to map an n_d‐dimensional random input latent vector z ∼ p _z (z) (usually sampled from a standard normal distribution) to realistically looking fake samples G(z) ∼ p _fake. The discriminator D simultaneously learns to distinguish between fake samples G(z) created by the generator and samples from real data x ∼ p _real. In this adversarial game, the discriminator is tasked to determine the probability D(G(z)) that the fake data belong to the real dataset, while the generator learns to create more realistic samples that are not recognized as fake by the discriminator. Mathematically speaking, the two networks play a two‐player minmax game with the cost function

$$\underset{\mathrm{G}}{\min }\underset{\mathrm{D}}{\max }{\mathrm{\ell }}_{\mathrm{GAN}},$$ (9)

where ℓ _GAN is the adversarial loss function given by

$${\mathrm{\ell }}_{\mathrm{GAN}}={\mathbb{E}}_{\mathbf{x}\sim {\mathrm{p}}_{\text{real}}}\left[\text{logD}\left(\mathbf{x}\right)\right]+{\mathbb{E}}_{\mathbf{z}\sim {\mathrm{p}}_{\mathrm{z}}}\left[\log \left(1‐\mathrm{D}\left(\mathrm{G}\left(\mathbf{z}\right)\right)\right)\right].$$ (10)

In this equation, D(x) is the probability that x is from the real dataset. The generator is trained to minimize

$${\mathrm{\ell }}_{\mathrm{GAN}}^G={\mathbb{E}}_{\mathbf{z}\sim {\mathrm{p}}_{\mathrm{z}}}\left[\log \left(1‐\mathrm{D}\left(\mathrm{G}\left(\mathbf{z}\right)\right)\right)\right],$$ (11)

while the discriminator tries to maximize

$${\mathrm{\ell }}_{\mathrm{GAN}}^D={\mathbb{E}}_{\mathbf{x}\sim {\mathrm{p}}_{\text{real}}}\left[\text{logD}\left(\mathbf{x}\right)\right]+{\mathbb{E}}_{\mathbf{z}\sim {\mathrm{p}}_{\mathrm{z}}}\left[\log \left(1‐\mathrm{D}\left(\mathrm{G}\left(\mathbf{z}\right)\right)\right)\right].$$ (12)

In a vanilla‐GAN, each network is trained using a gradient‐based approach while keeping parameters of the other network fixed. In practice, the discriminator outperforms the generator and reaches a stage of vanishing gradients for D, which leads to no more useful feedback to further train G. To stabilize the training process, several heuristic solutions such as label‐smoothing, ⁶⁰ two time‐scale learning rule (TTUR), ⁶¹ and addition of continuous noise to the input of discriminator ⁶² are proposed.

Main building blocks of vanilla‐GANs are fully connected layers, which are replaced by deep convolutional layers in DCGANs ³⁹ to specifically target imaging data. This also leads to a better training stability by utilizing convolutions and transposed‐convolutions (fractionally‐strided convolution) for down‐sampling and up‐sampling operations. Moreover, DCGANs utilize batch normalization (BatchNorm) ⁶³ to regulate the input to each unit and leaky rectifier linear units (LeakyRelu) ⁶⁴ to prevent vanishing gradients. In the generator, the last transposed convolution layer is followed by a hyperbolic tangent function to synthesize images in a bounded pixel space. Further, the last convolutional layer of the discriminator is accompanied by a Sigmoid function for the classification task.

In this study, a 3D DCGAN with the architecture shown in Figure 2 is implemented to synthesize the trabecular bone microstructure. Note that no fully connected or pooling layer is used in this model and hyper‐parameters of each network are optimized via back‐propagation. Also, convolutions are performed using strided 4 × 4 × 4 kernels. To further stabilize the training process on the volumetric (voxel‐based) imaging data obtained from micro‐QCT, we used a least square form of the loss function (LSGAN) given by Mao et al. ⁶⁵

$$\begin{array}{ll}{\mathrm{\ell }}_{\text{LSGAN}}^D& =\frac{1}{2}\mathbb{E}\left[{\left(\mathrm{D}\left(\mathbf{x}\right)-b\right)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim {\mathrm{p}}_{\mathrm{z}}}\left[{\left(\mathrm{D}\left(\mathrm{G}\left(\mathbf{z}\right)\right)-a\right)}^2\right],\\ {\mathrm{\ell }}_{\text{LSGAN}}^G& =\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim {\mathrm{p}}_{\mathrm{z}}}\left[{\left(\mathrm{D}\left(\mathrm{G}\left(\mathbf{z}\right)\right)-c\right)}^2\right].\end{array}$$ (13)

FIGURE 2.

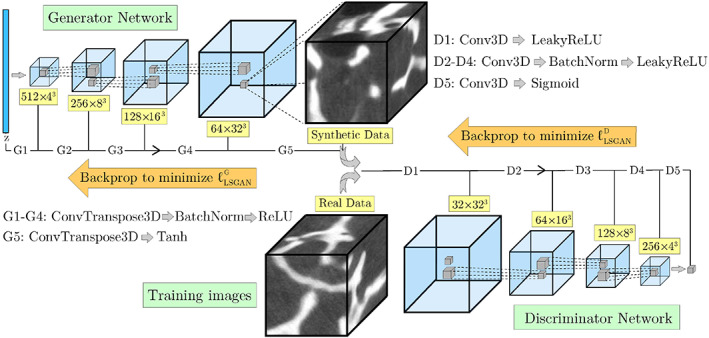
Architecture of the 3D deep convolutional generative adversarial network model used for the virtual reconstruction of trabecular microstructure

In the equation above, a and b are labels of fake and real data, respectively, and c is the label used by the generator to fool the discriminator. In the current DCGAN model, a = 0.9 and b = 0 are employed for labeling fake and real data. The LSGAN is supplemented with TTUR for further stabilization and to avoid mode collapse. Both the generator and the discriminator are then trained via mini‐batch stochastic gradient‐descent (SGD) based optimizer ADAM. ⁶⁶ To stabilize the training for the volumetric images used in this study, several trial and error runs were performed to determine an optimal set of hyper‐parameters.

Unlike classic stochastic microstructure reconstruction algorithms, DCGANs do not require an a priori objective function to replicate target statistical microstructural descriptors. Instead, the objective function is encoded in the convolutional layers and evolves as the two adversarial networks train to outperform one another. Therefore, pre‐training this model could serve as a baseline to facilitate fine‐tuning (transfer learning) for trabecular tissue synthesis in other organs such as femur as supplementary data is introduced. Despite all these advantages, one of the main challenges for training this model is the difficulty associated with acquiring a diverse and sufficiently large set of data, which requires preparing multiple micro‐QCT images. Note that training deep networks such as DCGANs with a limited number of data (images) could substantially increase the risk of overfitting. Given that the only micro‐QCT data available in this work are from two cadaveric samples, a data augmentation approach ⁶⁷ was utilized to address this issue.

Classic data augmentation techniques for grayscale images typically involve image manipulations such as translation, rotation, scaling, flipping, random noise addition, and shearing. ⁶⁸ In this work, transformations causing shape deformation such as shearing must be avoided during the augmentation process to preserve important characteristics of micro‐QCT images that affect the underlying trabecular microstructure. To achieve this, each image was transformed to eight new images, each rotated at a random angle of θ = [0^°, …, 180^°], followed by flipping that three times (up–down, right–left, front–back). Inspired by the sliding window approach in object detection algorithms, ⁶⁹ for each augmented image, the moving cuboid sampling technique was implemented to create cubic training images with l _t  × l _t  × l _t voxels and partial overlap. The size of training images was determined by comparing the average porosity of cubic samples of different sizes (32³, 64³, 128³) with the porosity of the original micro‐QCT imaging data. This assumption was later justified, as training the DCGAN model using smaller images created checkerboard artifacts and reflections in the generated microstructures. Therefore, a size of 128 × 128 × 128 voxels was selected for volumetric images used for training the model. This DCGAN algorithm was developed in the Pytorch library ⁷⁰ and then trained on two V100 NVIDIA GPUs with 32 GB of memory using the computing resources at the Ohio Supercomputer Center (average training time: 16 h).

As noted previously, the main motivation for using DCGANs to virtually reconstruct the trabecular microstructure is its ability to scale‐up the size of synthesized microstructures compared to the size of training data. This capability is crucial for the reconstruction of a realistic geometrical model of vertebra, as it allows creating a sufficiently large trabecular microstructure that can be embedded in the vertebra cortical shell extracted from the patient's CT scan (cf. Section 3.3). Creating an enlarged synthetic image using DCGANs can theoretically be achieved by adding more convolution layers to the generator network. However, altering the DCGAN architecture in this approach requires retraining that at a much higher computational cost due to using a deeper generator network. Alternatively, one can control the size of synthesized images without retraining the DCGAN by modifying dimensions of the input vector. In this approach, which was employed in this work, while training is performed using images of size l ₀ with an input vector of size n _z , an arbitrary‐sized image of size l _i could be generated using a different input dimensionality of (a × b × c)n _z , where a, b, and c represent scaling factors in x, y, and z directions, respectively.

Figure 3 illustrates four trabecular bone microstructures with different sizes generated using the DCGAN model described above. Note that, according to (2) and (7), the pixel intensity in these grayscale volumetric images is first used to evaluate the density and then the elastic modulus of the bone. Figure 3 shows the distribution of the elastic modulus evaluated using this approach in these synthesized microstructure, showing the ability of DCGAN to simulate the increasing stiffness of the bone from external surface to central regions of trabecula. Clearly, this qualitative observation is not sufficient to confirm the ability of this DCGAN model for reconstructing realistic trabecular microstructures. To verify that these synthetic microstructures are statistically equivalent to those directly reconstructed from micro‐QCT data, we have compared their two‐point correlation functions and voxel‐based histograms in Figure 4. Both plots show a good agreement between statistical microstructural descriptors corresponding to the synthesized (varying sized) and actual (fixed size) microstructures. In particular, the error associated with two‐point correlation functions are <2% regardless of the size of the synthesized microstructure. The comparison of voxel‐based histograms shows that, although there is a small mismatch in the porous region (which is not incorporated in the FE model), the virtual and actual microstructures are fairly similar within the bone tissue region.

FIGURE 3.

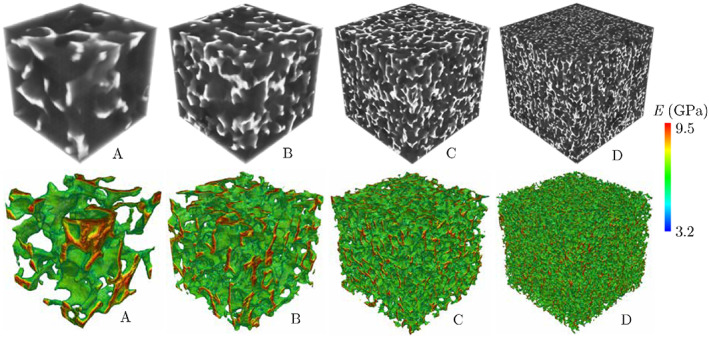
Four trabecular bone microstructures synthesized using DCGAN with voxel sizes l _A  = 256, l _B  = 512, l _C  = 1024, and l _D  = 2048 and corresponding distributions of the elastic modulus evaluated based on GS values. DCGAN, deep convolutional generative adversarial network; GS, gray‐scale

FIGURE 4.

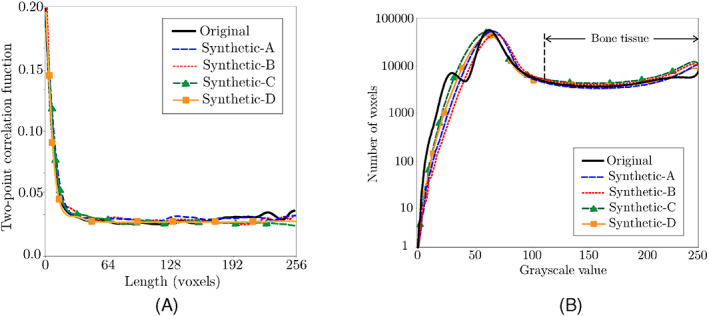
Comparison between (A) two‐point correlation functions and (B) grayscale histograms of synthetic microstructures A–D generated using DCGAN (cf. Figure 3) and the actual microstructure directly obtained from micro‐QCT data. DCGAN, deep convolutional generative adversarial network; QCT, quantitative computed tomography

It is worth mentioning that reconstructing a patient‐specific model of the trabecular bone using the DCGAN model introduced in this work requires access to a massive library of micro‐QCT images obtained from a diverse set of cadaveric samples in terms of the age, sex, pre‐existing disease, etc. This will allow creating an enlarged trabecular microstructure using micro‐QCT data that best resembles a patient's morphometric data and their bone BMD determined from diagnostic CT scans. As described in the following section, this trabecular model is then integrated with the cortical shell extracted from a CT scan to create a patient‐specific geometrical model of the vertebra. Note that the trabecular microstructures synthesized in Figure 3 and subsequently used for creating a whole vertebra model are based on a single set of micro‐QCT data (cf. Section 3.1) and a full library of these imaging data is currently under development by the authors. Therefore, the vertebral model reconstructed next should not be regarded as an actual patient‐specific model, as the main objective of this work is to demonstrate the feasibility of this approach for creating such models.

3.3. Creating whole vertebra models

Figure 5 illustrates the process of creating a geometrical model of the whole vertebra by engraving the cubic trabecular microstructure generated using DCGAN to fill the cortical shell extracted from patient's CT scans. The initial thickness of the cortical shell approximated from CT data is about 0.6 mm, which is compatible to measurements reported in the literature. ⁷¹ Engraving and embedding the trabecular microstructure in the cortical shell was accomplished using an open‐source python library named scikit‐image. ⁷² The engraving process involves the subtraction of the cortical geometry from the enlarged trabecular microstructure, followed by filtering out unnecessary trabecular regions that fall outside the cortical shell periphery. Next, the subtracted trabecular microstructure is embedded in the cortical shell geometry to create a realistic model of the vertebra (cf. Figure 5C). More details regarding different steps of this process are provided in Figure 6. However, while the resulting microstructure might seem realistic (cf. Figure 5C), there is an abrupt transition between sculpted trabecular region and the cortical shell, which could lead to sharp angles between the two regions. This seemingly small flaw could lead to exceedingly high and unrealistic stress concentrations in this interfacial region during a VF simulation, which in turn causes premature damage nucleation and thereby under‐prediction of the vertebra strength. The bone structure in an actual vertebral body is designed by nature such that there is a smooth transition (tapered zone) between trabecular and cortical regions to eliminate such sites of stress concentrations.

FIGURE 5.

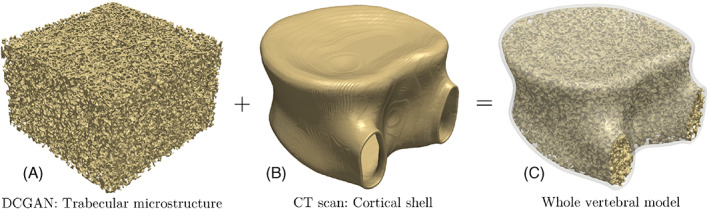
Creating the geometrical model of the whole vertebra by engraving the trabecular microstructure generated using deep convolutional generative adversarial network to fill the cortical shell extracted from the patient's CT scan

FIGURE 6.

Process of engraving the trabecular microstructure generated using deep convolutional generative adversarial network to fill the cortical shell geometry extracted from the patient's CT scan using the scikit‐image library

In order to eliminate a sharp transition between cortical and trabecular regions in the whole vertebra model, we perform a shape optimization simulation ⁷³ inspired by the Wolff's law ⁴² to minimize stress concentrations in these regions. It must be noted that the assumption of the self‐optimal design of the bone microstructure, that is, a remodeling rate dependent on mechanical stimuli, has been utilized in several studies, see for example. ⁷⁴ , ⁷⁵ As a prelude to this FE‐based shape optimization, we must first generate a high‐fidelity conforming mesh to create an FE model for the virtual vertebral body. Given the low elastic modulus of the bone marrow within the trabecular region relative to that of the bone tissue, the former is considered as pores in this model. Figure 7A illustrates a small portion of the conforming mesh used in this analysis, which was generated after the segmentation of voxel‐based geometric model of the vertebra using the software Simpleware ⁷⁶ (total number of elements: ≈7.7 million).

FIGURE 7.

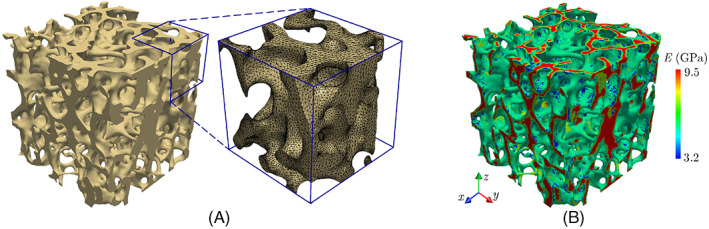
(A) Small portion of the conforming finite element mesh and (B) variation of the elastic modulus in the trabecular region of the vertebra model

In the FE model of the vertebral body, we must also take into account the variation of the trabecular bone material properties by mapping its elastic modulus calculated based on GS values in the voxelated microstructure (cf. Figure 7B) to mesh elements. Note that these elements are not necessarily aligned with original image voxels after image segmentation. Therefore, an average GS for each element was first evaluated as

$${\mathrm{GS}}_{\mathrm{ave}}=\frac{1}{V}{\int }_V\mathrm{GS}\left(x,y,z\right)\mathrm{d}V,$$ (14)

where V is the element volume and GS(x, y, z) is the grayscale corresponding to its Gauss quadrature point approximated using a trilinear interpolation between eight voxels confining (x, y, z). This average GS was then utilized to calculate the bone density and subsequently the elastic modulus assigned to each element using (7) and (2).

A non‐parametric shape optimization algorithm was implemented using the software TOSCA ⁷³ to evolve the bone architecture in the vicinity of the trabecular‐cortical interface into a more realistic architecture by minimizing von‐Mises stresses in this region. The zone in which the bone architecture is modified is limited to a close proximity of the cortical shell to have a minimal impact on statistical microstructural descriptors of the trabecular bone away from this region. In this non‐parametric shape optimization, mesh nodes on the surface of bone are chosen as implicit parameters (design nodes), which are iteratively updated (relocated) based on results of a linear elastic FE approximation to minimize stress concentrations. The objective function is defined as

$$\mathrm{maximize}\mid {\sigma }_{\mathrm{vm}}\left({\mathbf{x}}_{\mathrm{des}}\right)-{\sigma }_{\mathrm{vm}}^0\left({\mathbf{x}}_{\mathrm{des}}\right)\mid \text{subject to}\sum ^{N_e}{V}_e=\sum ^{N_e}{V}_e^0,$$ (15)

where σ _vm and σ _vm ⁰ are current and initial von‐Mises stresses at design nodes, x_des, respectively. Note that the optimization is carried out subject to the constraint of no volumetric change, that is, the sum of element volumes, V _e , remains unchanged.

During the shape optimization process, design nodes are modified using a heuristic re‐design rule given by

$$\mathrm{\Delta }{\mathbf{x}}_{\mathrm{des}}=\alpha \left({\sigma }_{\mathrm{vm}}\left({\mathbf{x}}_{\mathrm{des}}\right)-{\sigma }_{\mathrm{vm}}^0\left({\mathbf{x}}_{\mathrm{des}}\right)\right).$$ (16)

In this equation, α is the distance in the search direction evaluated using the line‐search method. ⁷⁷ The constrained Laplacian smoothing algorithm ⁷⁸ was employed to preserve the FE mesh quality while relocating design nodes. Additional quality metrics such as element aspect ratios, dihedral angles, volume skewness, and shape factors were also monitored to ensure the quality of the mesh is not deteriorated throughout the simulation. Figure 8 illustrates how minimizing σ _vm in the cortical‐trabecular interfacial zone results in a tapered transition in this region to eliminate unrealistic sites of stress concentrations.

FIGURE 8.

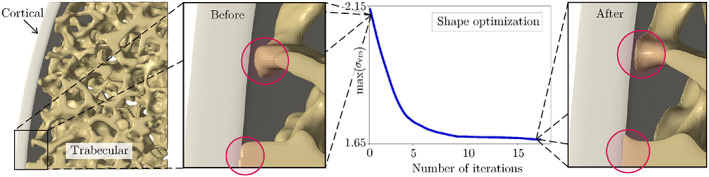
Performing finite element‐based shape optimization to obtain a tapered transition from cortical to trabecular bone in the virtual vertebra model, which avoid unrealistic stress concentrations in these regions during Vertebral Compression Fracture (VCF) simulations

4. RESULTS AND DISCUSSION

In this section, we employ the whole vertebral model synthesized using ReconGAN to perform a feasibility study on the impact of metastatic tumors on the VF response. Metastatic tumors are often categorized as osteolytic and osteoblastic, where the former is caused by metastatic cancerous cells built up in the bone marrow. This phenomenon disrupts the bone remodeling process, which significantly reduces the bone stiffness/strength and makes it more vulnerable to fracture. ⁷⁹ These softened regions often appear as voids or loss of mineralization in a CT scan due to significant destruction of the bone tissue. Furthermore, lytic metastases are accompanied by thinning of the trabecular network through the entire vertebra. ⁸⁰ Blastic lesions, on the other hand, result from an uncontrolled formation of immature tissue with an unorganized collagenous structure around the trabecular bone due to tumor‐induced growth factors. ⁸¹ , ⁸²

Figure 9A illustrates a slice of co‐registered CT‐MRI scans, from which the tumor morphology is extracted for the current study and incorporated in the FE model (cf. Figure 9B). The retrospective CT/MRI scans belong to a lung cancer patient (51 years old, female), who had been admitted to the Ohio State University James Comprehensive Cancer Center. As shown in Figure 9C, we assumed two versions of this tumor in the FE models, that is, fully lytic and fully blastic to better study their impact on the mechanical stability of vertebra. Note that to model a lytic tumor, the bone tissue within the lesion area is removed due to its negligible stiffness and strength. Because blastic lesions are accompanied by the deterioration of the bone stiffness in the affected area, according to Reference 83, the elastic modulus of the trabecular bone is reduced by 19% in this region. Note that the elastic modulus reported for tumor cells in the literature is orders of magnitude lower than that of the bone tissue, although it could have a wide range of variation between 0.1 to 200 KPa. ⁸⁴ , ⁸⁵ In this work, we have assumed E _tumor = 0.56 KPa and ν _tumor = 0.4. ⁸⁵

FIGURE 9.

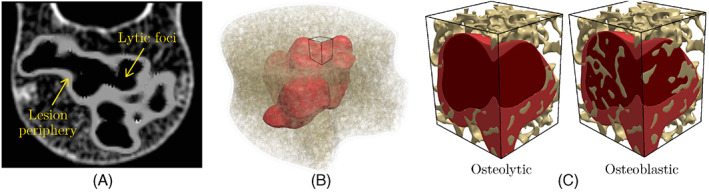
(A) Co‐registered CT‐MRI scan of a vertebra with a metastatic tumor; (B) 3D reconstruction of tumor morphology added to the virtual vertebral model generated using ReconGAN; (C) comparing lytic and blastic tumors in a small portion of the trabecular bone

Figure 10 shows the setup and boundary conditions of the FE model of the vertebra to simulate its VF response under combined compression and bending loads (flexion). As shown in this figure, portions of the intervertebral disc (IVD) with effective properties E _IVD = 17 MPa and ν _IVD = 0.45 ⁸⁶ are also incorporated in the FE model (modeled as a linear elastic material) to more realistically simulate the in‐vivo loadings applied to the vertebra. The boundary conditions consist of constraining the displacement degrees of freedom along the bottom surface of the lower IVD, while a uniform downward displacement with the rate ${\dot{u}}_z=0.05$ mm/s (in the middle) and a tilt angle with the rate ${\dot{\theta }}_z$ are applied on the upper IVD. In this work, we study five flexion loading case scenarios denoted by C₁ to C₅, which in order correspond to ${\dot{\theta }}_z=0.0,0.1,0.2,0.4$, and 0.5^°/s. Note that the first loading case scenario, C₁: ${\dot{\theta }}_z=0.0$, corresponds to applying a uniform compression on the vertebra (no bending).

FIGURE 10.

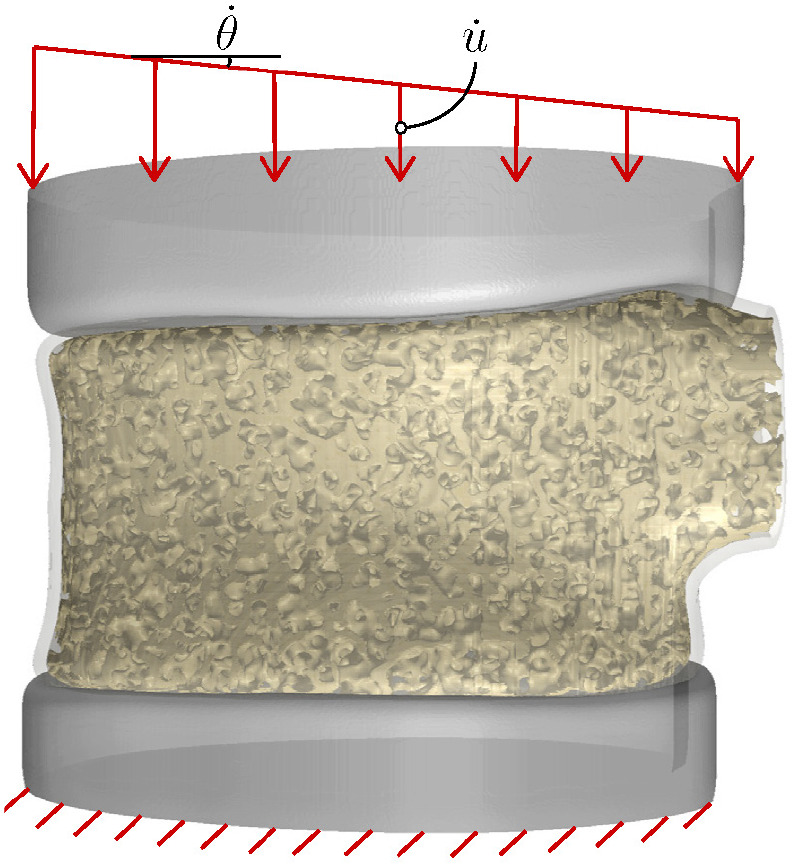
Model setup and applied boundary conditions for performing vertebral fracture simulations

The VF simulations were conducted in Abaqus using the continuum damage model described in Section 2 for approximating the initiation and evolution of damage in the bone tissue. The element deletion strategy was employed to avoid convergence issues associated with fully damaged elements, which otherwise would be highly distorted due to their zero stiffness. A self‐contact model was also employed to avoid the inter‐penetration of disconnected segments of fractured bone under compression. Given the large number of elements in the FE models (healthy: 7.7 million, lytic: 6.5 million, and blastic: 9.8 million), the VF simulations were carried out in parallel using 48 processors, with run times varying between 16 and 45 h depending on the mesh size.

Figure 11A illustrates the simulated force‐displacement responses of healthy, lytic, and blastic vertebrae under the C₁ loading condition (uniform compression). Damage patterns in the healthy vertebra at different loading stages are depicted in Figure 11B–F, showing that the damage initiates from weak regions of the trabecular bone and propagates toward the cortical shell to form a macro‐crack. We have also shown side and top views of damage patterns after failure in all vertebral models in Figure 12. Note that the resulting fracture pattern in the healthy vertebra is compatible with experimental observations from VF tests under a compression in Reference 87. Moreover, according to Figure 11A, the peak load capacity (∼3.9 kN) is within the physiological range for similar vertebral bodies. ⁸⁸ , ⁸⁹ The figure also shows a notable drop in the maximum load sustained by the vertebra in the presence of lytic (∼28%) and blastic (∼13%) tumors. As expected, significant destruction of the bone tissue in the former case scenario leads to the most devastating impact on strength. It is worth noting that the maximum displacement at fracture for the metastatic vertebrae remained nearly unchanged despite their lower load bearing capacity, which is compatible with results of a recent in‐vitro study on vertebral bodies with lytic and blastic lesions. ⁸⁰

FIGURE 11.

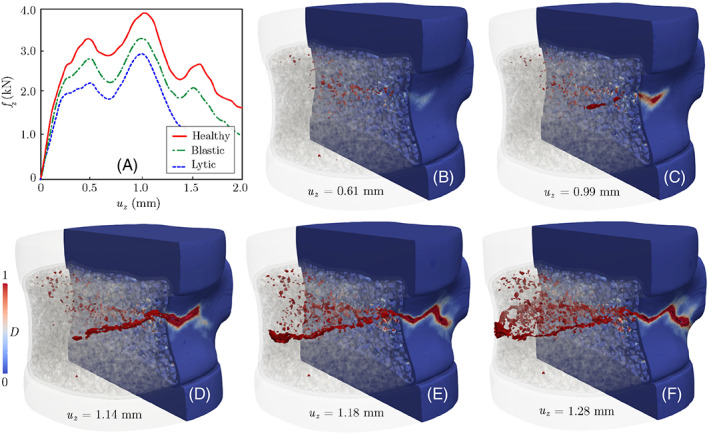
(A) Force‐displacement responses of healthy, lytic, and blastic vertebra subjected to uniform compression. (B–F) Damage pattern at different loading stages, which initiates from the trabecular regions and propagates toward and eventually along the cortical shell. Note that u _z is the applied displacement boundary condition in the z direction, while f _z refers to the resultant reaction force along the top (or bottom) surface of the vertebra

FIGURE 12.

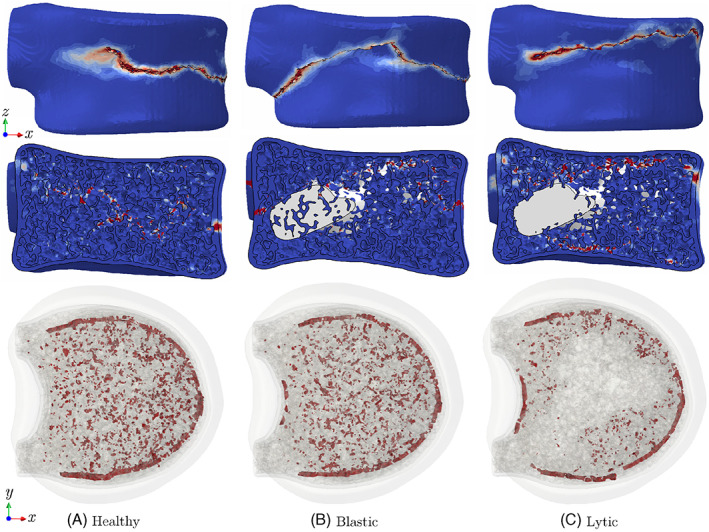
Fracture patterns in healthy, blastic, and lytic vertebra under uniform compression (C₁)

We have further studied the impact of metastatic tumor on the VF response of the lytic vertebra under flexion loads C₂ to C₅. Figure 13A shows the resulting force‐displacement responses of the vertebra under these loading conditions and their comparison with the case of uniform compression, C₁. Damage patterns after failure subjected to C₁, C₃, and C₅ loadings are illustrated in Figures 13B–D. Note the nonlinear behavior (yielding and strain hardening) observed after the initial linear force‐displacement response of the vertebra under different loading conditions corresponds to the plastic behavior of the trabecular region. However, this nonlinear zone keeps shrinking by increasing the bending load, such that a semi‐brittle failure response is observed for the C₅ loading condition. As shown in Figure 13A, this behavior corresponds to damage accumulation in the anterior region of the vertebra due to magnified compressive stresses caused by the bending load. The accelerated damage accumulation in this region facilitates its propagation in the cortical shell and causes a brittle failure response accompanied by a significant drop in the vertebra height in the anterior cortical shell. Note that the damage pattern shown in Figure 13D is compatible with wedge‐shaped fractures reported in osteoporotic patients. ⁹⁰ This observation also highlights the importance of measuring the anterior height of the vertebra for clinical assessment of VF. ⁹¹

FIGURE 13.

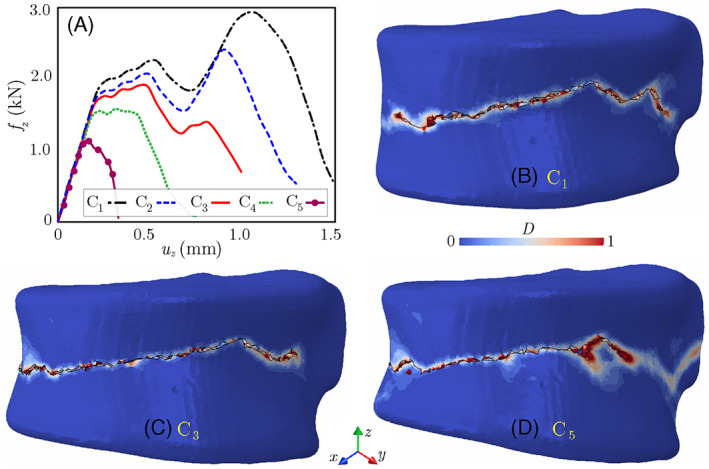
(A) Force‐displacement responses of the lytic vertebra subject to uniform compression and flexion loads; (B–D) damage patterns after failure under loadings C₁, C₃, and C₅. Note that u _z is the applied displacement boundary condition in the z direction, while f _z refers to the resultant reaction force along the top (or bottom) surface of the vertebra

The reason for the brittle versus ductile failure responses of the lytic vertebra under C₁ and C₅ loadings, respectively, can better be understood by analyzing corresponding elastic stress fields and cortical damage evolutions in Figure 14. While the vertebra still yields an elastic load‐displacement response, as shown in Figure 14, a uniform compressive load (C₁) causes sites of high‐stress concentrations in the trabecular region, meaning the damage first nucleates in this region when increasing the load. On the other hand, the flexion load gives rise to high‐stress concentrations in the anterior cortical bone, which accelerates the damage initiation in that. Comparing the damage patterns at two stages of loading for each case (C₁ and C₅) in Figure 14B verifies this hypothesis, as it shows C₅ loading leads to damage nucleation in the anterior region of the cortical shell. Note that, the amplified stress concentrations in these regions under the C₅ loading lead to damage initiation in the cortical bone at ${\overline{u}}_z=0.23$ mm, while for the case of C₁ loading the cortical shell does not experience a notable damage until ${\overline{u}}_z=0.65$ mm. Instead, under the C₁ loading, the damage accumulates in the trabecular region before propagating toward the cortical shell, which allows trabecula to absorb a significant amount of energy before the development of a macro‐crack.

FIGURE 14.

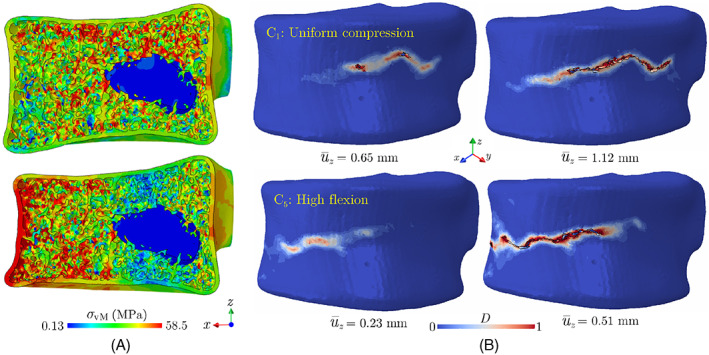
(A) von‐Mises stress distribution in the elastic zone on a cross‐section of the lytic vertebra and (B) damage pattern in the cortical shell of this vertebra under C₁ (uniform compression) and C₅ (high flexion) loading case scenarios

5. CONCLUSIONS

An AI‐assisted framework, coined ReconGAN, was developed for synthesizing realistic digital twins of the human vertebra and predicting its fracture response. ReconGAN enables integrating diagnostic imaging data (e.g., CT scans) with virtual microstructural models of the trabecular bone, reconstructed using a 3D DCGAN model, to create realistic geometrical models of the whole vertebra. The DCGAN model was trained using grayscale images of the trabecular bone tissue obtained via micro‐QCT and its accuracy was verified by comparing statistical microstructural descriptors of actual and synthesized microstructures. An FE‐based shape optimization approach was implemented to infuse the trabecular microstructure generated using this DCGAN model into the vertebra cortical shell extracted from patient's CT scans by minimizing stress concentrations to provide a smooth transition between these regions. A feasibility study relying on virtual geometrical models of the whole vertebra synthesized using ReconGAN was then carried out on the impact of metastatic tumors on the risk of VF. A phenomenological continuum damage model, together with a self‐contact model for fragmented bone pieces, were employed to predict the VF response. The main outcomes of the study are summarized below:

• Under uniform compression, the damage initiates from weak regions of the trabecular bone and propagates toward the cortical shell to form a macro‐crack (failure). The energy absorbed by the trabecular region during this process leads to a ductile failure response, which highlights the crucial impact of the trabecular microstructure on the mechanical stability of vertebra under this loading condition.

• Incorporating two metastatic tumors confined within the trabecular region, both with identical shapes but modeled as lytic and blastic lesions, led to ∼28% and ∼13% reduction in the vertebra strength, respectively.

• Under high flexion loads, amplified compressive stresses in the anterior cortical shell lead to accelerated damage nucleation in this region, which in turn facilitates the formation of a macro‐crack and a significant drop in the load bearing capacity of vertebra. This fracture mode is also accompanied with a notable reduction in the vertebra height in the anterior region, which is qualitatively confirmed by clinical observations.

It must be noted that the main purpose of the feasibility study presented here was to demonstrate the crucial impact of the vertebra macroscopic shape and microstructural details, synthesized using ReconGAN, on the VF response. A more comprehensive study aimed at linking the vertebra geometrical features to its mechanical stability, especially for patients with SM, requires significant further developments beyond the scope of this work. For example, in addition to experimentally calibrating and validating the FE model, mechano‐biological factors must also be taken into account in simulating the VF response in cancer patients. Moreover, considering the intricate microstructure and the nonlinear material behavior of the intervertebral discs will provide a more realistic load transfer to the vertebra. Nevertheless, the AI‐enhanced computational framework introduced in this manuscript is a promising first step toward establishing such patient‐specific models for the assessment of the risk of VF and designing potential preventive therapeutic interventions accordingly.

Ahmadian H, Mageswaran P, Walter BA, et al. Toward an artificial intelligence‐assisted framework for reconstructing the digital twin of vertebra and predicting its fracture response. Int J Numer Meth Biomed Engng. 2022;38(6):e3601. doi: 10.1002/cnm.3601

DATA AVAILABILITY STATEMENT

Research data are not shared.