Deep learning‐based microarray cancer classification and ensemble gene selection approach

Abstract

Malignancies and diseases of various genetic origins can be diagnosed and classified with microarray data. There are many obstacles to overcome due to the large size of the gene and the small number of samples in the microarray. A combination strategy for gene expression in a variety of diseases is described in this paper, consisting of two steps: identifying the most effective genes via soft ensembling and classifying them with a novel deep neural network. The feature selection approach combines three strategies to select wrapper genes and rank them according to the k‐nearest neighbour algorithm, resulting in a very generalisable model with low error levels. Using soft ensembling, the most effective subsets of genes were identified from three microarray datasets of diffuse large cell lymphoma, leukaemia, and prostate cancer. A stacked deep neural network was used to classify all three datasets, achieving an average accuracy of 97.51%, 99.6%, and 96.34%, respectively. In addition, two previously unreported datasets from small, round blue cell tumors (SRBCTs)and multiple sclerosis‐related brain tissue lesions were examined to show the generalisability of the model method.

1. INTRODUCTION

Microarray data structures are critical for diagnosing and classifying various types of malignant tissues and diseases; however, the high dimension of the genes and the limited number of samples are effective at overcoming the challenges of gene expression and classification [1, 2, 3]. It is difficult and time‐consuming to interpret disease‐causing genes since only a small number of genes accurately characterise the disease biologically [4]. When diseases such as cancer are detected early, effective medications can be developed. Moreover, discovering efficient genes in a laboratory is difficult, time‐consuming, and expensive. By automating the separation of genes from microarray data, it is possible not only to reduce the classification errors, but also to reduce the time factor involved in completing the processing to the desired level [5]. A feature selection in machine learning aims to obtain the smallest possible subset of problem space features while still achieving the highest level of recognition and classification [6, 7, 8]. Also for many approaches for selecting features, such as filter models, wrapper models, and embedded procedures, an optimization strategy can give acceptable results. Nevertheless, they are time consuming and have a low potential for universal optimization. The computational cost of filter models is lower than that of wrapper and integrated models [8, 9]. Filtering and wrapper are commonly used strategies for gene selection. According to the filtering methods, each feature is assigned a value based on its association with a class label and a single variable scoring criterion. Consequently, the genes with the highest ranking are selected and classified. In contrast, wrapper techniques require a collection of classifications to assess each gene's performance during the ranking process. Thus, the optimal subcategory of the genes is determined based on the performance rankings/scoring in all discovered subcategories. Although filtering methods cannot quantify genomic relationships, wrapper strategies may be limited by their high processing costs [10, 11]. Combining wrapper methods with quick classification models enables ranking of features even when microarray data is associated with a large number of genes. A properly modified classifying parameter establishes the foundation for achieving the desired accuracy and precision, which is why various studies have investigated k‐nearest neighbour (k‐NN) bracing adjustment [12]. Along with the selection of features in microarray data, efficient classifications improve accuracy and efficiency. In fact, artificial neural networks (ANNs) are a class of efficient algorithms that, with appropriate adjustment and learning, can produce optimal results regardless of the complexity of the problem domain. There are maximum‐learning‐potential neural networks [13], border class regression classification [14], logistic regression [15], random decision trees [16], and Bayesian theory [17]. Breast cancer, colon cancer, lymph node cancer, and lung cancer can all be diagnosed using gene expression analysis. Machine learning techniques and feature selection in gene expression are recommended for the detection of lung cancer [18].

Machine learning (especially deep learning (DL)) has become a popular tool among studies for classification in many applications [19]. Recently, DL has had a significant impact on microarray data processing. With the recent availability of these datasets, DL approaches can be used to speed up the analysis of data and improve the accuracy of cancer diagnosis, prognosis, and treatment response. There seems to be an urgent need for accurate and fast approaches to automatically model gene expression using microarray data. By combining fastening methods with fast binding classes, we can increase the time and rank selected genes at the same time. Furthermore, by implementing an efficient DL model, it is possible to significantly and easily improve the accuracy of gene expression.

Using a soft homogenization method and three wrapper strategies, the present study provided a successful combination technique of gene expression for a variety of diseases. When selecting effective genes subsets, the k‐NN method can be used for decision‐making in the features selection part. The purpose of this paper is to provide a unique method of classifying with a reasonable amount of error as a generalizable approach to creating gene expression models. Using the soft search strategy, the effective genes from the microarray dataset can be identified. Another component of the suggested method's originality is the stacked autoencoder (SAE). The following contributions are made by this work:

• (1)Using supervised learning with a K‐NN classifier to evaluate the weights of the genes, we propose a modification approach to gene selection. The improved gene selector and stacked auto‐encoder (SAE) classifier combine the statistical findings of relevant genes using an objective ranking technique, which eliminates the need for potentially inept and biased expert knowledge.
• (2)We present a deep stacked auto‐encoder model that achieves robust classification with low computational consumption while maintaining accuracy under severe test conditions.
• (3)The methods for disease classification outlined earlier are very dependent on the selection strategy for genes and the classifier used. Consequently, the fundamental objective of this research is to construct a generalisable and precise method for studying genes using microarray data.

The rest of the paper is structured as follows: Related work is discussed in Section 2 of this paper. Section 3 describes the proposed strategy for identifying diseases based on the genes selected and DL approach. Section 4 explains the dataset used in our study, as well as the results and discussion. Section 5 presents the investigation's findings and possible strategies.

2. RELATED WORK

A review of the recent machine and DL‐based cancer prediction and biomarker gene identification studies will be conducted. Utilising data on cancer gene expression from highlighted resources, researchers will be able to evaluate and assess their proposed analytical approaches.

2.1. Classical gene selection and learning

As described in their study, Nguyen et al. [20] selected features for microarray data, selected genes, and classified the data using a fuzzy standard additive model in combination with correction of the analytic hierarchy process [21]. Furthermore, they used genetic algorithm optimization to enhance and change the parameters of the unsupervised classification structure.

Momenzadeha et al. [22] used Markov's hidden model and t‐test of two samples, entropy test, receiving agent characteristic curve, and Wilcoxon test to choose features based on wrapper approaches.

Using a graph‐embedded deep feed forward network (GEDFN), Kong et al. [23] created a gene expression model. Lu et al. [24] proposed an adaptive genetic and mutual information maximization (MIM) algorithm algorithm for microarray data on colorectal, leukaemia, prostate, lung, breast, and small, round blue cell tumor (SRBCT). By selecting a feature from many data arrays, Sun et al. [25] quantified uncertainty using neighbour entropy. Sayed et al. [26] used the Nested Genetic Algorithm (NGA) to select features from a large volume of microscopic data in order to identify the condition. Deng et al. [27] developed a two‐step system for cancer classification that combines the XGBoost method with a multi‐objective evolutionary algorithm.

Using an optimised gene subset selection method, Tavasoli et al. [28] introduced a modified approach for microarray data classification. According to their study, five microarray datasets were classified using an optimised support vector machine using a modified Water Cycle Algorithm (WCA).

2.2. Deep learning

Using the stacked deep autoencoder algorithm, a DL technique has been proposed for identifying genes that can be used for identifying malignant tissue from healthy tissue. Gene expression analysis using RNA‐Seq data has been conducted [29].

The authors of the study [30] used multi‐model ensembles based on DL to investigate three cancer types (Stomach, Breast, and Lung).

In Matsubara et al. [31], gene expression data and a protein interaction network were used to classify 639 lung cancer samples (487 malignant, 152 benign).

To assess data from eight different malignancies, Zeebaree et al. [32] proposed a DL approach using Convolutional Neural Networks.

The multimodal deep neural network algorithm developed by Sun et al. [33] allows early detection of breast cancer. Based on microRNA (miRNA) gene expression data and classifiers such as the long short‐term memory (LSTM) and Matthews correlation coefficient (MCC), five distinct subtypes of kidney cancer were identified [34].

Anika et al. [35] suggested a CNN‐based approach for predicting the presence of 20 various types of cancer using gene expression data (from The Cancer Genome Atlas [TCGA]). The researchers evaluated 60,383 genes in all, using 1881 samples from each of the 20 cancers.

Using TCGA RNA‐Seq data, a new Deep Flexible Neural Forest (DFNForest) approach was evaluated [36] to replace deep neural networks in the classification of three distinct tumour subtypes (Glioblastoma multiforme, Breast, and Lung).

To predict the outcome of liver cancer, a differential regulatory network integrated deep neural network (DRE‐DNN) was constructed using a standard DNN (hepatocellular carcinoma) [37].

Several approaches use the feature selection and classification procedure to classify microarrays. Since gene selection is crucial to gene expression analysis, a number of studies have been conducted on the various aspects of this fundamental problem. Microarray data may contain a significant number of genes that are redundant or unsuitable for predictive design. However, given the volume of data in microarray data, a small number of related genes may provide more benefits for learning. Previous studies have sought to identify genes that are related to each other based on their significant class correlations.

3. PROPOSED METHOD

The suggested approach is shown in Figure 1. Pre‐processing, Feature (gene) selection, and classification are the main steps of the proposed method.

FIGURE 1.

Schematic diagram of the proposed algorithm in gene selection and classification

3.1. Pre‐processing

During pre‐processing, we shuffled the data in order to prevent the automatic classification model from becoming over‐trained. Although the samples are mixed randomly, the label positions can vary depending on the classes represented by each analysed sample. The combination of samples and adjusting the label corresponding to the sample’s position during the validation stage allow the learning algorithm to adjust to only one class of genes or a subset of them. This method improves classification accuracy by avoiding over‐fitting [38, 39]. The positions of the corresponding samples are shifted at random, and the labels are shifted as well. Each gene in each dataset is naturally highly dispersed and utilises a diverse set of genes, so they must be normalised in the preprocessing stage. Gene normalisation reduces processing costs and optimises gene expression. The appropriate normalising range is (0–1) based on the min‐max normalisation. Hence, the minimum‐maximum method is applied for normalisation as follows:

$$Y_{\text{norm}}=\left(Y_s-Y_{s_{\min }}\right)\times {\left(Y_{s_{\max }}-Y_{s_{\min }}\right)}^{-1}$$ (1)

This indicates that all numbers are scaled between 0 and 1. While the variables Y _smin and Y _smax reflect the values of the minimum and maximum, a normalised value is called Y _norm. In addition, Y _s denotes the gene's current expression level.

3.2. Gene selection

Three methods are used to choose features: Signal‐to‐noise ratio (SNR), Wilcoxon method, and receiver operating characteristic (ROC). The ROC curves are representations of the true positive rate versus the false positive rate in the first approach. The area under the curve (AUC) may be determined using this illustration using Equation (2) [40]:

$$AUC={\displaystyle \underset{0}{\overset{1}{\int }}{T}_1\left(T_2^{-1}\left(t\right)\right)}dt\Rightarrow t\in \left(\mathrm{0,1}\right)$$ (2)

T is a complement/supplement to F _i , where F ₁ (x) and F ₂ (x) are the distribution functions of x in two different statistical communities F _i (x). Only genes with a higher AUC are consisted in the gene selection vector because their high AUC value indicates that the labels containing the gene in the samples have a low degree of overlap. The Mann‐Whitney test, which determines if two populations are comparable statistically, is an analogue of the Wilcoxon test. While the null hypothesis asserts that the distribution functions of the two populations are identical, the alternative hypothesis asserts that the distribution functions of the two populations are not same. This test is preferred in many practical scenarios since it does not need a basic assumption about the difference between the two samples. Here's how to do the Wilcoxon test:

• (1)Superimposing all observations from both groups and putting them in an ascending order based on their total number.
• (2)Wilcoxon's statistic is based on the total of all the ranks included in smaller groups.
• (3)Based on the overall distribution table, p‐values are calculated and used to make assumptions.

For gene selection, the absolute values of the standardized Wilcoxon statistic are more effective and beneficial in the Wilcoxon test than the Wilcoxon coefficients.

The SNR methodology, which measures the difference between gene labels expressed in terms of connection (3), is a third method used [41].

$$SNR\left(f_i,c\right)=\left({\mu }_1-{\mu }_2\right)\times {\left({\sigma }_1+{\sigma }_2\right)}^{-1}$$ (3)

where μ ₁ and μ ₂, as well as σ ₁ and σ ₂, denote the mean and standard deviation of the samples, respectively. The variables and f_i are regarded as vectors containing the gene labels and the ith characteristic vector, respectively. SNRs are expected to select a feature from each gene in order to solve the gene selection problem and classify the microarray data [42]. Finally, during the training phase, the genes that earn the most votes among the three related classes are chosen as the most relevant traits. The training data is divided into new and validation and training sets using the K‐fold method (CV = 10) and the most often occurring feature is used to represent the selected gene. The primary gene predicts the classification class, and k is the closest picked neighbour, which is fast and delivers a good response for the huge data gene set. The proposed method was used to improve the performance of k‐NNs in this study [12], utilising a query and k‐d algorithm to minimise calculations and improve class performance. The trend of gene selection is revealed in Figure 2 in a gentle method, taking into account the precision gained during the training phase.

FIGURE 2.

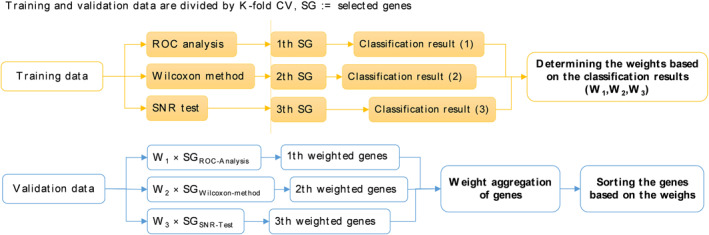
In our soft ensembling method between selected genes, the following three methods are applied: receiver operating characteristic (ROC), Wilcoxon, and SNR; the classification accuracy of the training data is multiplied by the gene weight, and the best genes are then selected based on their weighted average among all the weighted genes

3.3. Stacked auto‐encoder

Stacked Auto‐encoders (SAE) are constructed using auto‐encoders. Each auto‐encoder's hidden layer is connected to the hidden layer of the next auto‐encoder in a neural network. Throughout the training phase, the hidden layer of the prior auto‐encoder must be used as input to the subsequent one. Figure 3 depicts the SAE architecture employed in this experiment.

FIGURE 3.

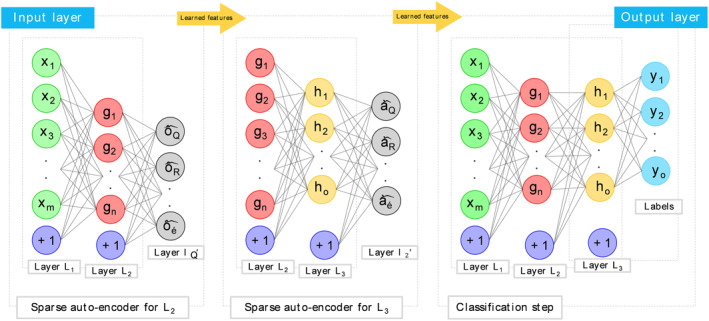
The configuration of the proposed Stacked Auto‐encoder

Using the SAE, you may create new abstractions by layering them on top of existing ones. When rebuilding, the final hidden layer output contains the high‐level attributes of the gene data. In the object field, an object's properties define its conductivity distribution. We used the Logistic Regression layer to determine the conductivity distribution.

We feed the DNN with normalised gene selections. It is denoted by the symbol U = {G⁽¹⁾, G⁽²⁾,…, G^(M)}, where M denotes the number of training sets and G^(k) ∈ [0,1]^m denotes the number of normalised genes. The letter m indicates that there are an unknown number of gene values in a collection of randomly chosen gene sequences.

Internal conductivity distribution sample (U = {σ⁽¹⁾, σ⁽²⁾,…, σ^(M)}), where σ^(k) ∈ [0,1]ⁿ and n denote the probability of each class. To seed the weight and bias matrices and vectors, unsupervised layer‐by‐layer learning is used. The DNN is entrusted with the duty of digesting the gene with the value U = {G⁽¹⁾, G⁽²⁾,…, G^(M)}. The entire technique is summarised below: It is important to train the first hidden layer first, using the previous one's output. The same procedure is repeated until all concealed layers are taught. To initialise the whole DNN during the supervised fine‐tuning phase, the pre‐trained network parameters from the final hidden layer of a DNN are fed into a Logistic Regression model. The network takes its name from a representative sample of the real conductivity distribution. The top‐down approach to fine‐tuning network parameters is based on a back‐propagation algorithm based on the technique of gradient optimization. A more generalisable model can be enhanced by reducing overfitting through the use of “dropout.” 0.5% of the network's hidden units are randomly deleted from the network's network during each training session. Simplifying neuronal coadaptation enables the construction of a more resilient network. The dropout layer performs admirably when trained on huge datasets. As seen in a typical auto‐encoder, dropout has an effect on Equations (4) and (5).

$$y_i=f\left({\displaystyle {\sum }_{j=1}^m{w}_{ij}}Bernoulli\left(p\right)\ast x_i+b_i\right)$$ (4)

$$z_j=f\left({\displaystyle {\sum }_{j=1}^m{w^T}_{ij}}Bernoulli\left(p\right)\ast y_i+{b^{\prime }}_i\right)$$ (5)

Bernoulli() is defined as a function that generates a random vector of either zero or one with a probability of p equal to 0.50.

4. RESULTS

This section describes the outcomes of the gene selection and classification scheme, as well as the outcomes of the proposed DL model that was implemented.

4.1. Datasets

The study is descriptive‐analytical investigation in which data are gathered from library‐library databases, mostly gene descriptions. These records are frequently accessible via a free online medical search portal equipped with dynamic search and browse features. The authors collected gene expression data through laboratory operations such as microsurgery chip fabrication, sample collection of various samples including cancer and healthy specimens, RNA extraction, and DNA supplementation. The experiments were conducted using three sets of data: diffuse large B‐cell lymphomas (DLBCL) [43], leukaemia [42], and prostate cancer [44]. Each data sample in the dataset contains information about the sampling technique and reliability of the instrument, and there are two types of malignancies classified in relation to DLBCL and follicular lymphoma (FL). The DLBCL dataset contains 7070 genes from 77 samples, of which 58 were positive for DLBCL and the remaining samples were positive for FL. To differentiate the two lymphomas, classification models are developed utilising gene expression data. The leukaemia dataset contains bone marrow and blood samples from patients with acute lymphoblastic leukaemia (ALL) and acute myeloid leukaemia (AML). This data collection contains 72 samples (47 ALL and 25 AML), each of which had 7129 gene samples. The third dataset contains 102 samples (50 from natural sources and 52 from prostate tissue), each of which contains 125,333 genes. In the cross‐section, all gene data are normalised [45].

4.2. Setting

Data analysis took place in the 2022 MATLAB programing environment, and statistical tests include quantitative and qualitative results that follow the simulation of a software model. The system used for modelling has properties with Intel (R), Core (TM) and Core i7 processors with 8 gigabyte of RAM and a 64‐bit operating system.

In the feature selection stage, a range of settings were considered and by selecting a much smaller number of initial features with the aim of reducing the processing cost of the initial data set and without changing the initial features, the appropriate set was selected. To compare the proposed feature selection model and other methods of selecting a feature,certain number of features (from 5 to 45 genes) are given to the k‐NN classification each time the accuracy is evaluated. To prevent overfitting, we utilized the algorithm to find the least Mean Square Error (MSE) through multiple repetitions (among all the tested structures). Its performance for the sample data was such that if the mean error square factor is less than the specified value (0.05), the corresponding network is selected as the base network, otherwise, the minimum MSE and the corresponding structure are selected.

The number of hidden layers in the DNN model has a significant effect on the model's capacity to learn. Generally, we'll adjust the learning rates and number of iterations for each layer to fine‐tune our model. Three to five layer neural networks have been constructed. Each layer contained 208 nodes in the input layer, 812 in the output layer, and 150 in the hidden layer. Between 0.1 and 0.01, rates of learning varied from pre‐to in‐training. The fine‐tuning method consisted between one and five hundred iterations. Additionally, the following network configurations were used: The pre‐training session was divided into 10 groups of 10 persons each, with each group receiving a 100‐epoch training epoch. At this point, the batch size was lowered to 40. The MSE was used to evaluate the network's performance.

4.3. Assessments

In Tables 1, 2, 3 to 1, 2, 3, the results of the simulation for 5 folds (each fold include 10 divisions) are shown for DLBCL data, leukaemia and prostate cancer, respectively, and the outputs are calculated for the experimental data.

TABLE 1.

Estimation of the accuracy of the gene expression test for diffuse large B‐cell lymphomas (DLBCL) data under different conditions of gene selection and classification

Data dividing	No. Layers	Feature selection by wrapper method			Feature selection by ensemble model
		Max	Mean	Min	Max	Mean	Min
10‐fold (1)	Low	0.90 ± (0.045)	0.87 ± (0.078)	0.85 ± (0.118)	0.92 ± (0.021)	0.90 ± (0.056)	0.89 ± (0.072)
	Med	0.95 ± (0.022)	0.91 ± (0.034)	0.89 ± (0.044)	100	0.97 ± (0.011)	0.95 ± (0.016)
	High	0.93 ± (0.034)	0.90 ± (0.042)	0.87 ± (0.078)	0.95 ± (0.034)	0.94 ± (0.032)	0.93 ± (0.036)
10‐fold (2)	Low	0.92 ± (0.036)	0.88 ± (0.064)	0.86 ± (0.084)	0.93 ± (0.029)	0.92 ± (0.043)	0.91 ± (0.065)
	Med	0.94 ± (0.032)	0.89 ± (0.051)	0.88 ± (0.064)	100	0.98 ± (0.017)	0.96 ± (0.026)
	High	0.94 ± (0.029)	0.92 ± (0.038)	0.89 ± (0.060)	0.96 ± (0.027)	0.98 ± (0.042)	0.94 ± (0.051)
10‐fold (3)	Low	0.91 ± (0.045)	0.85 ± (0.084)	0.83 ± (0.096)	0.94 ± (0.018)	0.92 ± (0.033)	0.90 ± (0.065)
	Med	0.95 ± (0.025)	0.89 ± (0.041)	0.87 ± (0.085)	0.99 ± (0.007)	0.96 ± (0.014)	0.94 ± (0.022)
	High	0.92 ± (0.037)	0.87 ± (0.055)	0.84 ± (0.086)	0.95 ± (0.026)	0.93 ± (0.035)	0.92 ± (0.044)
10‐fold (4)	Low	0.89 ± (0.073)	0.85 ± (0.089)	0.82 ± (0.124)	0.96 ± (0.028)	0.94 ± (0.054)	0.91 ± (0.075)
	Med	0.94 ± (0.031)	0.90 ± (0.046)	0.88 ± (0.067)	100	0.98 ± (0.013)	0.96 ± (0.024)
	High	0.93 ± (0.048)	0.88 ± (0.076)	0.84 ± (0.109)	0.95 ± (0.031)	0.93 ± (0.044)	0.91 ± (0.056)
10‐fold (5)	Low	0.90 ± (0.045)	0.87 ± (0.078)	0.85 ± (0.118)	0.94 ± (0.034)	0.92 ± (0.051)	0.91 ± (0.078)
	Med	0.95 ± (0.043)	0.93 ± (0.068)	0.90 ± (0.074)	0.98 ± (0.022)	0.97 ± (0.030)	0.95 ± (0.046)
	High	0.94 ± (0.051)	0.90 ± (0.077)	0.88 ± (0.092)	0.96 ± (0.028)	0.94 ± (0.048)	0.93 ± (0.053)

TABLE 2.

Estimation of the accuracy of gene expression for leukaemia cancer data in different conditions of gene selection and classification

Data dividing	No. Layers	Feature selection by wrapper method			Feature selection by ensemble model
		Max	Mean	Min	Max	Mean	Min
10‐fold (1)	Low	0.92 ± (0.025)	0.91 ± (0.032)	0.89 ± (0.056)	0.96 ± (0.014)	0.94 ± (0.025)	0.95 ± (0.048)
	Med	0.96 ± (0.021)	0.94 ± (0.027)	0.92 ± (0.35)	100	0.99 ± (0.009)	0.98 ± (0.018)
	High	0.92 ± (0.031)	0.91 ± (0.044)	0.89 ± (0.076)	0.97 ± (0.026)	0.96 ± (0.027)	0.94 ± (0.024)
10‐fold (2)	Low	0.94 ± (0.024)	0.93 ± (0.036)	0.91 ± (0.051)	0.97 ± (0.013)	0.95 ± (0.026)	0.94 ± (0.028)
	Med	0.96 ± (0.021)	0.94 ± (0.024)	0.92 ± (0.036)	100	0.98 ± (0.011)	0.97 ± (0.021)
	High	0.93 ± (0.034)	0.91 ± (0.054)	0.89 ± (0.067)	0.97 ± (0.016)	0.96± (0.023)	0.95 ± (0.041)
10‐fold (3)	Low	0.92 ± (0.028)	0.91 ± (0.035)	0.88 ± (0.070)	0.98 ± (0.011)	0.96 ± (0.017)	0.94 ± (0.034)
	Med	0.97 ± (0.018)	0.94 ± (0.022)	0.92 ± (0.044)	100	0.99 ± (0.008)	0.98 ± (0.010)
	High	0.95 ± (0.035)	0.93 ± (0.037)	0.92 ± (0.056)	0.98 ± (0.018)	0.97 ± (0.018)	0.95 ± (0.037)
10‐fold (4)	Low	0.95 ± (0.037)	0.93 ± (0.041)	0.90 ± (0.065)	0.98 ± (0.018)	0.97 ± (0.026)	0.95 ± (0.032)
	Med	0.98 ± (0.020)	0.94 ± (0.027)	0.93 ± (0.039)	100	0.99 ± (0.006)	0.98 ± (0.011)
	High	0.94 ± (0.029)	0.92 ± (0.039)	0.90 ± (0.041)	0.98 ± (0.023)	0.97 ± (0.026)	0.95 ± (0.041)
10‐fold (5)	Low	0.94 ± (0.031)	0.92 ± (0.036)	0.88 ± (0.086)	0.98 ± (0.014)	0.96 ± (0.019)	0.95 ± (0.039)
	Med	0.97 ± (0.023)	0.96 ± (0.031)	0.93 ± (0.053)	100	0.98 ± (0.012)	0.95 ± (0.039)
	High	0.96 ± (0.032)	0.94 ± (0.042)	0.92 ± (0.078)	0.98 ± (0.015)	0.97 ± (0.025)	0.96 ± (0.028)

TABLE 3.

Estimation of the accuracy of the gene expression test for prostate cancer data under different conditions of gene selection and classification

Data dividing	No. Layers	Feature selection by wrapper method			Feature selection by ensemble model
		Max	Mean	Min	Max	Mean	Min
10‐fold (1)	Low	0.89 ± (0.046)	0.86 ± (0.071)	0.85 ± (0.141)	0.91 ± (0.032)	0.88 ± (0.048)	0.86 ± (0.132)
	Med	0.94 ± (0.033)	0.90 ± (0.060)	0.88 ± (0.073)	0.98 ± (0.026)	0.96 ± (0.031)	0.93 ± (0.056)
	High	0.90 ± (0.057)	0.86 ± (0.058)	0.85 ± (0.129)	0.94 ± (0.044)	0.91 ± (0.058)	0.89 ± (0.108)
10‐fold (2)	Low	0.90 ± (0.068)	0.86 ± (0.092)	0.83 ± (0.121)	0.93 ± (0.045)	0.90 ± (0.063)	0.87 ± (0.119)
	Med	0.94 ± (0.053)	0.92 ± (0.064)	0.90 ± (0.070)	100	0.97± (0.024)	0.94 ± (0.051)
	High	0.91 ± (0.073)	0.89 ± (0.084)	0.87 ± (0.113)	0.95 ± (0.034)	0.93 ± (0.055)	0.90 ± (0.095)
10‐fold (3)	Low	0.90 ± (0.056)	0.88 ± (0.094)	0.86 ± (0.118)	0.92 ± (0.035)	0.90 ± (0.044)	0.87 ± (0.093)
	Med	0.94 ± (0.034)	0.90 ± (0.056)	0.88 ± (0.096)	0.98 ± (0.025)	0.95 ± (0.035)	0.92 ± (0.048)
	High	0.91 ± (0.076)	0.89 ± (0.073)	0.87 ± (0.108)	0.94 ± (0.042)	0.91 ± (0.057)	0.88 ± (0.084)
10‐fold (4)	Low	0.89 ± (0.067)	0.87 ± (0.075)	0.86 ± (0.123)	0.93 ± (0.035)	0.91 ± (0.067)	0.87 ± (0.083)
	Med	0.95 ± (0.048)	0.93 ± (0.041)	0.91 ± (0.087)	100	0.97 ± (0.024)	0.94 ± (0.041)
	High	0.89 ± (0.074)	0.87 ± (0.085)	0.86 ± (0.106)	0.94 ± (0.041)	0.91 ± (0.051)	0.89 ± (0.072)
10‐fold (5)	Low	0.89 ± (0.056)	0.85 ± (0.074)	0.84 ± (0.143)	0.92 ± (0.033)	0.88 ± (0.061)	0.85 ± (0.128)
	Med	0.94 ± (0.041)	0.92 ± (0.060)	0.90 ± (0.082)	0.98 ± (0.020)	0.95 ± (0.049)	0.91 ± (0.086)
	High	0.91 ± (0.050)	0.89 ± (0.071)	0.88 ± (0.113)	0.96 ± (0.039)	0.93 ± (0.064)	0.90 ± (0.096)

In Figure 4, the box‐plot of the feature selection method and its analogies for duplication are demonstrated in all the three data models. The minimum and maximum distance to find the optimal subset of soft genes in all the three models of gene expression data possess a smaller width. In these tables, the dynamics of the network in case of changing the number of layers and also the change in the number of neurons are assumed and different corresponding accuracies are estimated. In most cases, adjustment based on low and high neurons has led to good accuracy, and the scattering of accuracy is less.

FIGURE 4.

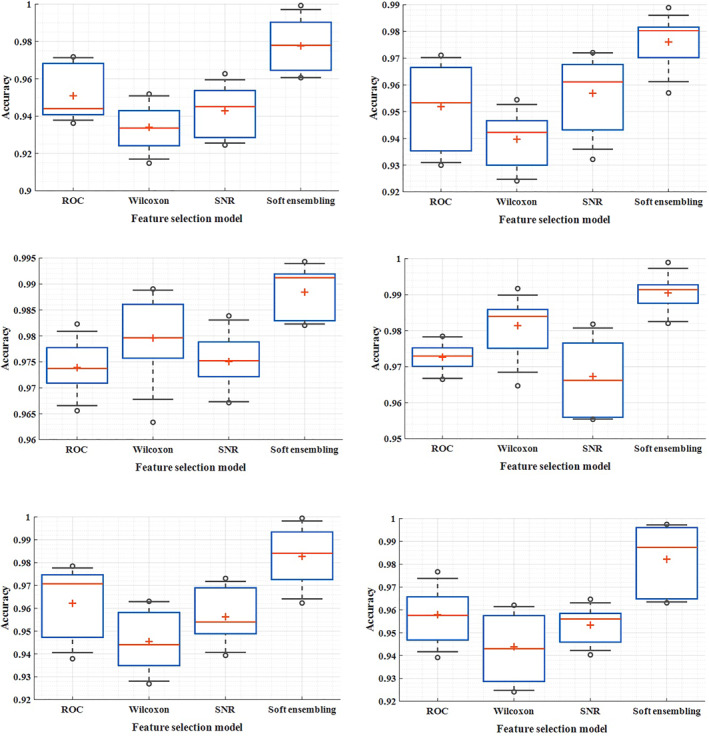
Box plot of different methods of selecting features and comparing them with double repetition in diffuse large B‐cell lymphomas (DLBCL), leukaemia and data, respectively

The number of low layers is assumed to be one to three hidden layers for the network, and the large number of layers varies from 4 to 8 layers. The low number of neurons varies from 5 to 15 neurons and the large number from 20 to 30 neurons, and the process of layer and neuron stabilisation was performed according to the incremental‐estimation method. The number of input and output layer nodes was adjusted based on the number of genes selected and the number of classes related to gene expression, respectively. To compare the performance of the feature selection, the proposed method at this stage is compared with a single wrapper method. In addition to reducing the scatter between the accuracy, the output is also significantly improved. On average, the application of a soft homogenisation method has resulted in optimization at a distance of 4%–6%, and among the results for all three gene data models, 100% accuracy can be observed. The lowest levels of distribution in leukaemia gene expression and the highest distribution are estimated for prostate cancer data.

In addition, the method of selecting the proposed feature in selecting the effective genes owns accuracy values less than the confidence interval. There is no significant difference between the expert's opinion on gene expression and the label obtained by the proposed algorithm in each sample (p‐Value <0.02); and the standard deviation of the outputs was negligible.

5. DISCUSSION

The proposed method in different subjects of classification and various data brings functional comprehensiveness. A number of the proposed solutions in the field of gene expression are obtained by spending countless time in limited repetitions, highly distributed classification results, and intolerance uncertainty ranges. To assess the influence of gene selection through the proposed method, we evaluated 5–45 optimal genes with accuracy criteria presented in Figure 5. All three forms reveal reproducibility of the algorithm as well as its robustness.

FIGURE 5.

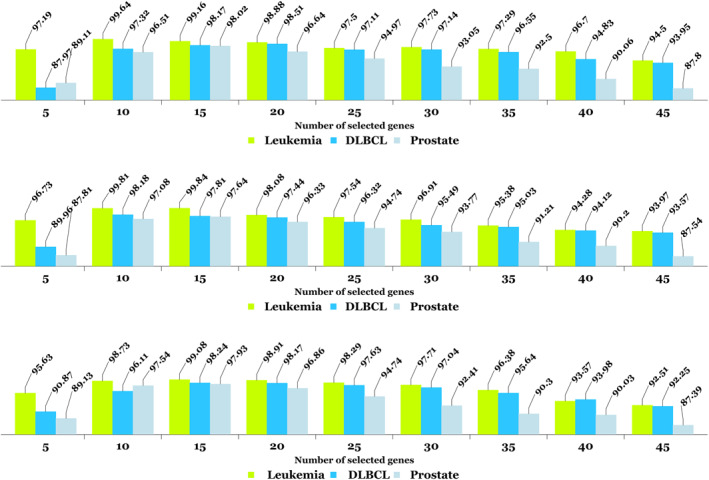
For each of the three microarray datasets, results (per percent) for automatic gene selection and classification are presented via soft ensembling and SAE methods with the fewest number of effective genes in the first, second, and third iterations in row 1, row 2, and row 3, respectively

It also manifests that the minimum accuracy of the gene (from 10 genes to 20 genes) can be accurately determined and classified. It is interesting to note that the previous algorithms have already selected the gene (feature), however, they have skipped analysing the minimum number of effective genes [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34]. In the proposed method, using the cross‐validation method, and K‐fold with variable K values adopted as 5, 10, 15 and 20, criteria were estimated. Generally, the output is at the maximal value in case the number of selected genes is neither too high nor too low. On the other hand, data such as DLBCL and prostate cancer were accurately implemented in the algorithm by applying an average number of genes. Nevertheless, for data such as leukaemia, which is inherently satisfactory, even by applying a small number of selected genes, the outputs are acceptable. In most similar methods, the minimum amount of gene selected is abandoned; this is highly important since it can directly affect the reduction of processing the volume and increase the speed of achieving the optimal output.

In contrast to prior methodologies [24, 25, 26], the generalisability of the model for gene expression in microarray data has received less attention. Indeed, generalisability can be asserted if a model demonstrates the required robustness and reliability when classifying previously unseen data. Two more additional datasets with features distinct from the initial microarray dataset were used to assess generalisability. The first microarray is a collection of SRBCTs obtained from children. These tumours represent four distinct subtypes of neuroblastoma (NB), rhabdomyosarcoma (RMS), non‐lymphoma Hodgkin's (NHL), and the Ewing family of malignancies (EWS). Each class has 23 samples (EWS), 20 samples (RMS), 12 samples (NB), and 8 samples (NHL), totalling 63 samples containing 2308 genes. The primary distinction between this data and the previously described data is that the previously unknown microarray data has four separate classes of gene expression (four‐class mode), whereas the previously discussed data contains only two classes (presence or absence of the disease).

The second data is a collection of transcript profiles of multiple sclerosis including 44 microarray samples with 27,336 genes; 26 sections from its 44 samples showed multiple sclorosis (MS) with progressive stages of the disease and 18 samples without any neurological complications [46, 47]. Little research has been performed on this type of data due to the low classification accuracy of the solutions along with the differences in their transcription process to create a microarray molecular chain [48]. In Figures 6 and 7, classification accuracy is expressed in terms of the number of effective features or genes selected in both SRBCTs and MS unseen data.

FIGURE 6.

The results of classification (per percent) for small, round blue cell tumors’ (SRBCTs) unseen data with different number of genes. At each stage of applying selected genes, the K‐fold cross validation test is performed to create training and test data, and the highest, lowest, and average values of folds are displayed

FIGURE 7.

The results of classification (per percent) for multiple sclorosis (MS) unseen data with different number of genes. At each stage of applying selected genes, the K‐fold cross validation test is performed to create training and test data, and the highest, lowest, and average values of folds are displayed

Un‐like the research method proposed in this study, which uses soft ensembling among the filtering methods to find effective genes, several swarm intelligence‐based learning algorithms are in fact based on searching the answer space. These algorithms have the chance of getting stuck in the local optima while searching for the general ones [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 49, 50]. As classifiers are generally more suitable in the process of learning parameters using different algorithms, hence, improving the classification recognition should not be limited to gene expression. Our future plans include implementing the model with improved deep LSTM networks [51] and effective feature selection [52] for more accurate classification and using platforms such as Internet of Things (IoT) [53, 54] for fast data processing.

6. CONCLUSION

For feature selection and classification, a new hybrid approach based on soft ensembling and stacked auto‐encoders was proposed that assigns rankings to the five effective genes of the microarray data. Combining the three methods of soft wrapper with classification using the k‐NN algorithm led to the minimum number of genes needed for final classification. When compared to filtering methods and optimization algorithms that are associated with low accuracy and slow data processing, the combination method based on three wrapping methods speeds up the process of selecting the suitable subset while maintaining a high level of accuracy. Despite the relatively small number of samples, the novel stacked auto‐encoder avoided almost entirely the complexity of over‐fitting, which could have led to high classification error. Apart from the robustness and simplicity of the proposed method, the generalisability of the model is another critical aspect that can be adjusted to increase the accuracy while minimising the classification error. A more powerful and time‐consuming method will be developed in the future. In the future, we will focus on finding the best genes and improving the structure of SAE.

CONFLICT OF INTEREST

The author declares that there is no conflict of interest that could be perceived as prejudicing the impartiality of the research reported.

Rezaee, K. , et al.: Deep learning‐based microarray cancer classification and ensemble gene selection approach. IET Syst. Biol. 16(3‐4), 120–131 (2022). 10.1049/syb2.12044

DATA AVAILABILITY STATEMENT

All the data and codes are available through corresponding authors.