Comparison between estimated and measured myopia progression in Hong Kong children without myopia control intervention

Abstract

Purpose

To compare myopia progression estimated by the Brien Holden Vision Institute (BHVI) Myopia Calculator with cycloplegic measures in Hong Kong children wearing single‐vision distance spectacles over a 1‐ and 2‐year period.

Methods

Baseline age, spherical equivalent refraction (SER) and ethnicity of control participants from previous longitudinal myopia studies were input into the BHVI Myopia Calculator to generate an estimate of the SER at 1 and 2 years. Differences between the measured and estimated SER (116 and 100 participants with 1‐ and 2‐year subjective refraction data, respectively, and 111 and 95 participants with 1‐ and 2‐year objective refraction, respectively) were analysed, and the measured SER compared with the 95% confidence interval (CI) of the estimated SER.

Results

In children aged 7–13 years, 36% progressed within the 95% CI of the Myopia Calculator's estimate, whereas 33% became less myopic than predicted (range 0.31 to 1.92 D less at 2 years) and 31% became more myopic than predicted (range 0.25 to 2.33 D more myopic at 2 years). The average difference between the estimated and measured subjective or objective SER at 1 and 2 years of follow‐up was not clinically significant (<0.25 D).

Conclusions

On average, the BHVI Myopia Calculator estimated SER was in close agreement with measured cycloplegic SER after 1 and 2 years of follow‐up (mean differences < 0.25 D). However, the measured myopia progression only fell within the 95% CI of the estimated SER for 32%–38% of children, suggesting that the BHVI ‘without management’ progression data should be interpreted with caution. The inclusion of additional data, modified to include axial elongation, from longitudinal studies of longer duration with larger sample sizes and a range of racial backgrounds may improve the Calculator's ability to predict future myopia progression for individual children.

Key points.

• The extent of myopia progression over 1–2 years corrected with single‐vision spectacles was accurately predicted by the Brien Holden Vision Institute Myopia Calculator in 32%–38% of 7–13‐year‐old Hong Kong children.

• Including the use of biometric data from longitudinal studies may improve estimates of future myopia progression or axial eye growth in children.

• Practitioners should be aware that modelling of myopia progression data might not provide an accurate estimate of future myopia progression for each individual child.

INTRODUCTION

Myopia is currently a global concern because of its rapidly increasing prevalence, especially in Asia. ¹ , ² , ³ , ⁴ It is projected that 50% of the world population will be myopic by 2050 (−0.50 D or worse), including 10% with high myopia (worse than −5.00 D). ⁵ Increasing myopia and axial length is associated with a higher risk of ocular disease ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ and visual impairment. ⁸ , ¹¹ , ¹² In recent years, numerous interventions such as orthokeratology, ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ atropine, ²² , ²³ , ²⁴ , ²⁵  multifocal soft contact lenses, ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ various spectacle designs ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ and combination treatments ⁴² , ⁴³  have demonstrated an ability to slow the progression of myopia in children to varying extents, compared to control groups of children wearing single‐vision spectacles or contact lenses.

Given the range of environmental and genetic factors linked with refractive error development, ⁴⁴ it is difficult to confidently predict future myopia development, myopia progression and axial elongation for an individual child. However, understanding the likely extent of myopia progression without an intervention can assist practitioners and parents to determine if a myopia control treatment is appropriate, and may be used as a tool to educate children and adult caregivers to communicate the importance of myopia control. Cross‐sectional studies can provide some insight into temporal variations in refractive error and axial length across large cohorts ⁴⁵ , ⁴⁶ ; however, because each age group examined includes a different sample of children, these datasets are potentially not as useful for estimating future refractive error change for an individual child as longitudinal data sets following the same cohort of children. Since detailed longitudinal datasets of paediatric myopia progression with large sample sizes are limited, Donovan et al. ⁴⁷ conducted a weighted meta‐analysis of 20 longitudinal data sets that included automated cycloplegic refraction in children from urban regions. Six of the studies in the meta‐analysis included children of predominantly European descent (i.e., studies conducted in the USA) and the other 14 studies included children of predominantly Asian descent (i.e., studies conducted in Hong Kong, Singapore, China, Japan and Thailand). This meta‐analysis revealed higher rates of myopia progression in younger children, females, and Asian compared to European children.

The Brien Holden Vision Institute (BHVI) Myopia Calculator (bhvi.org/myopia‐calculator‐resources/) is a web‐based resource that allows the user to estimate potential myopia progression without a myopia control intervention (based on annual progression data obtained from children aged 6 to 16 years, described in Donovan et al. ⁴⁷ ) and with various myopia control interventions (based on published peer‐reviewed journal articles and conference presentations). The user can modify some input parameters for each individual child including ethnicity (Caucasian or Asian), age (6–16 years old in 1‐year increments) and current refractive error (−5.00 to −0.50 D in 0.50 D increments). It then provides an estimated spherical equivalent refraction (SER) up to 17 years of age, and plots the mean estimated SER with the 95% confidence interval (CI). From these data, the estimated myopia progression can be determined. The graphical representation of myopia progression with and without an intervention can be a useful educational tool for eye care practitioners when discussing myopia management with patients and adult caregivers.

The purpose of this study was to compare the measured amount of myopia progression in Hong Kong children wearing single‐vision distance spectacles ¹³ , ²⁰ , ⁴⁸ , ⁴⁹ over a follow‐up period of 1‐ and 2‐years with the amount of myopia progression estimated by the BHVI Myopia Calculator for individual children without a myopia control intervention, based on their age, ethnicity and baseline refractive error.

METHODS

In this retrospective study, refractive data of the control participants wearing single‐vision distance spectacles in four orthokeratology clinical trials were retrieved (Retardation of Myopia in Orthokeratology (ROMIO) Study: A 2‐Year Randomized Clinical Trial, ¹³  Myopia Control Using Toric Orthokeratology (TO‐SEE Study), ²⁰ Relative peripheral refraction in children: a changes in eyes with different ametropias (PR study) ⁴⁸ and Orthokeratology with increased compression factor (OKIC): study design and preliminary results). ⁴⁹ In these investigations, participants in the control groups were prescribed single‐vision distance spectacles, and the prescription was updated if the monocular visual acuity (VA) was worse than 0.18 logMAR or refractive error (either myopia, astigmatism or SER) had progressed by more than 0.50 D at any visit. All children were Chinese between 7 to 13 years old at the beginning of the study, with refractive sphere between −5.00 D and −0.50 D and refractive cylinder not more than 1.50 D. Exclusion criteria included strabismus, amblyopia, any other ocular pathologies, abnormal functional conditions and any long‐term systemic conditions.

Cycloplegic subjective and objective SER obtained at the baseline, 1‐ and 2‐year visits (if available) were retrieved. Cycloplegia was achieved by applying either one drop of 0.5% ¹³ , ²⁰ or 0.4% proparacaine hydrochloride ⁴⁸ followed by one drop of 1% tropicamide and one drop of 1% cyclopentolate 5 min apart, or two drops of 1% cyclopentolate (without application of an anaesthetic) 5 min apart. ⁴⁹ Cycloplegic refraction was performed at least 30 min after instillation when the amplitude of accommodation was <2.00 D with no pupillary response. The minimum available data for inclusion in this analysis was either subjective or objective refraction from the baseline and 1‐year follow up visits.

Subjective refraction was performed using a trial frame and trial lenses with maximum plus for maximum visual acuity technique. Objective refraction was performed by masked examiners using the Shin‐Nippon SRW‐5001 open‐field auto‐refractor (shin‐nippon.jp). The average of the first three or five sets of readings with differences in spherical and cylindrical power ≤ 0.25 D were used for analysis.

Estimated change in spherical equivalent refraction by the Brien Holden Vision Institute Myopia Calculator

The baseline SER, age and ethnicity (Asian) of each participant were input into the BHVI Myopia Calculator. Since the BHVI Calculator uses an age increment of 1 year and a SER increment of 0.50 D, the baseline age and SER entered required rounding. For the baseline age, children between 6.5 to 7.49 years of age were entered as 7 years old and children between 7.5 to 8.49 years were entered as 8 years of age (and so on). The same approach was used for the baseline SER; a SER between −0.74 D to −0.25 D was entered as −0.50 D, a SER between −1.24 to −0.75 D was entered as −1.00 D and so on.

The BHVI Calculator provides an estimate of the mean SER, and a 95% confidence interval (CI) around this estimate, presented graphically. In order to extract the 95% CI of the estimated SER for each participant, WebPlotDigitizer (automeris.io/WebPlotDigitizer/) was used. The measured progression of each participant was categorised with reference to the 95% CI of the BHVI Calculator's estimated progression as: (1) in agreement (within the estimated 95% CI); (2) underestimation of the SER (actual progression greater than estimated by the Calculator and outside the estimated 95% CI) or (3) overestimation of the SER (actual progression less than estimated by the Calculator and outside the estimated 95% CI). The estimated SER data were extracted from the BHVI Myopia Calculator in December 2020.

Statistical analysis

The eye selected in this study was the right eye from all four studies. ¹³ , ²⁰ , ⁴⁸ , ⁴⁹ Statistical analysis was performed using IBM SPSS Predictive Analytics Software version 26 (ibm.com). The Shapiro‐Wilk tests and the Kolmogorov‐Smirnov tests were used to determine the normality of each parameter where the sample size was either smaller or larger than 50 in each group/category, respectively. Normally distributed data were described using the mean and standard deviation, and non‐normally distributed data were described using the median and range.

Bland‐Altman analysis was used to evaluate the agreement between the estimated and measured SER using both subjective and objective measurements. ⁵⁰ , ⁵¹ Pearson's correlation coefficient was used to quantify the relationship between the average of the measured and estimated SER, and the difference between the means over 2 years. Paired t‐tests and related‐sample Wilcoxon signed rank tests were used to compare subjective and objective refraction at baseline, and 1‐ and 2‐year follow‐up visits. Probability (p) values < 0.05 were considered statistically significant.

RESULTS

Baseline characteristics

The demographic and refractive characteristics of the participants at baseline are summarised in Table  1 . A total of 116 participants had 1‐year subjective refraction data, comprising 53 males and 63 females, with a median [range] subjective baseline SER of −2.25 [−4.50, −0.25] D (Table  1 ), while 100 participants (49 males, 51 females) had 2‐year subjective refraction data available, with a median [range] baseline SER of −2.25 [−4.50, −0.25] D. The measured median [range] subjective SER at the 1‐ and 2‐year follow‐ up visits was −3.00 [−5.50, −0.63] and −3.63 [−6.25, −0.50] D, respectively.

TABLE 1.

Demographics and baseline data (median [range]) of participants wearing single‐vision distance spectacles from four studies (ROMIO, ¹³ OKIC, ⁴⁹ PR ⁴⁸ and TO‐SEE ²⁰ )

	All	ROMIO 13	OKIC 49	PR 48	TO‐SEE 20
Participants with subjective refraction data
Age (years)	9 [7, 13]	9 [7, 11]	10 [8, 11]	8 [7, 10]	9 [7, 13]
Subjective SER (D)	−2.25 [−4.50, −0.25]	−2.38 [−4.13, −0.75]	−2.25 [−3.75, −1.00]	−1.38 [−4.25, −0.25]	−3.00 [−4.50, −0.63]
Rounded subjective SER (D)	−2.50 [−4.50, −0.50]	−2.50 [−4.00, −1.00]	−2.50 [−4.00, −1.00]	−1.50 [−4.50, −0.50]	−3.00 [−4.50, −0.50]
One‐year sample size	116	41	23	29	23
Actual SER (D)	−3.00 [−5.50, −0.63]	−3.38 [−4.75, −0.88]	−3.00 [−4.50, −1.13]*	−2.50 [−5.50, −0.63]	−3.38 [−5.26, −1.13]
Estimated SER (D)	−3.07 [−5.42, −1.27]	−3.25 [−4.81, −1.59]	−3.35 [−4.61, −1.68]*	−2.50 [−5.30, −1.27]	−3.74 [−5.42, −1.27]
Two‐year sample size	100	41	11	25	23
Actual SER (D)	−3.63 [−6.25, −0.50]	−3.75 [−5.13, −1.00]	−3.75 [−5.25, −1. 88]	−2.75 [−4.88, −0.50]	−4.00 [−6.25, −1.50]
Estimated SER (D)	−3.71 [−6.17, −1.95]	−3.88 [−5.50, −2.11]	−4.04 [−4.66, −2.44]	−2.92 [−4.30, −1.95]	−4.36 [−6.17, −1.95]
Participants with objective refraction data
Age (years)	9 [7, 13]	9 [7, 11]	10 [8, 11]	8 [7, 10]	9 [7, 13]
Objective SER (D)	−2.33 [−5.23, −0.26]	−2.75 [−4.62, −0.69]	−2.56 [−3.38, −1.00]	−1.65 [−4.58, −0.26]	−2.77 [−5.23, −0.72]
Rounded objective SER (D)	−2.50 [−5.00, −0.50]	−3.00 [−4.50, −0.50]	−2.50 [−3.50, −1.00]	−1.50 [−4.50, −0.50]	−3.00 [−5.00, −0.50]
One‐year sample size	111	36	23	29	23
Actual SER (D)	−3.12 [−5.81, −0.87]	−3.47 [−4.88, −0.88]	−3.06 [−4.50, −1.13]	−2.61 [−5.60, −0.87]	−3.43 [−5.81, −1.31]
Estimated SER (D)	−3.15 [−5.49, −1.10]	−3.56 [−5.19, −1.10]	−3.35 [−4.33, −1.68]	−2.50 [−5.30, −1.27]	−3.64 [−5.49, −1.38]
Two‐year sample size	95	36	11	25	23
Actual SER (D)	−3.75 [−6.77, −1.01]	−3.90 [−5.44, −1.06]	−3.75 [−5.25, −1.62]	−2.92 [−5.46, −1.01]	−4.43 [−6.77, −1.14]
Estimated SER (D)	−3.83 [−6.17, −1.62]	−4.08 [−5.76, −1.62]	−4.04 [−5.02, −2.26]	−3.23 [−4.30, −1.95]	−4.18 [−6.17, −1.95]

Abbreviations: D, dioptre; SER, spherical equivalent refraction.

*Statistically significant between 1‐year actual and estimated SER in OKIC project (p = 0.01).

A total of 111 participants had 1‐year objective refraction data, consisting of 48 males and 63 females, whereas 2‐year data were available from 44 males and 51 females. Since the objective SER was slightly more myopic than the subjective SER at baseline (mean −0.11 ± 0.27 D, p < 0.001), and at the 1‐ and 2‐year follow‐up (mean −0.10 ± 0.31 D and −0.17 ± 0.31, p = 0.001 and <0.001, respectively), both the measured subjective and objective refraction data were compared with the estimated SER from the BHVI Calculator.

Comparison between the estimated and measured objective refraction

The distribution of the estimated objective SER at 1 and 2 years of follow‐up, respectively, were: (1) 32.4% and 36.8% within the estimated 95% CI; (2) 36% and 27.4% greater than the upper bound of the estimated 95% CI (Calculator underestimates progression); (3) 31.5% and 35.8% less than the lower bound of the estimated 95% CI (Calculator overestimates progression) (Table  2 ). This indicates that the measured objective refraction at 1 and 2 years of follow‐up was within the 95% CI of the estimated SER for approximately 34% of participants, and the Calculator overestimated and underestimated progression in approximately 34% (range 0.20 to 1.39 D overestimate at 1 year and 0.36 to 1.86 D at 2 years) and 32% (range 0.18 to 1.08 D underestimate at 1 year and 0.30 to 2.33 D at 2 years) of participants, respectively.

TABLE 2.

Summary of differences between Brien Holden Vision Institute (BHVI) Myopia Calculator estimates and measured spherical equivalent refraction (SER)

SER	Visit	Differences (estimated minus measured, (D))			Distribution of observations relative to BHVI estimated 95% CI (% of sample)
		Mean ± SD	Lower, upper bound of 95% LoA	p‐value	Within	Underestimation	Overestimation
Subjective	1‐year	−0.03 ± 0.46	−0.93, 0.86	0.44	37.1% (43/116)	31.9% (37/116)	31.0% (36/116)
	2‐year	−0.12 ± 0.70	−1.48, 1.24	0.09	38.0% (38/100)	28.0% (28/100)	34.0% (34/100)
Objective	1‐year	−0.02 ± 0.45	−0.91, 0.87	0.69	32.4% (36/111)	36.0% (40/111)	31.5% (35/111)
	2‐year	−0.05 ± 0.75	−1.51, 1.42	0.53	36.8% (35/95)	27.4% (26/95)	35.8% (34/95)

Abbreviations: D, dioptre; LoA, limits of agreement; p‐value, probability value for difference between BHVI estimates and measured SER, one‐sample t test.

Table  2 displays the mean difference ± SD between the estimated and measured objective refraction at 1 year (−0.02 ± 0.45 D, n = 111, p = 0.69) and 2 years of follow‐up (−0.05 ± 0.75 D, n = 95, p = 0.53). These mean differences are small and would not be considered clinically significant, or likely to affect patient management. However, the Bland‐Altman plots (Figure  1 ) highlight the number of participants for whom the actual measured SER was outside the 95% CI of estimated SER at both 1 year (67.6% outside the estimated CI) and 2 years (63.2% outside the estimated CI). There were no significant correlations between the differences of the estimated and measured objective SER and their means at 1 year (Pearson's r = −0.09, p = 0.37), whereas this relationship was statistically significant for the 2‐year data (Pearson's r = −0.32, p = 0.002). That is, for a less myopic SER, the Calculator tended to overestimate the measured SER.

FIGURE 1.

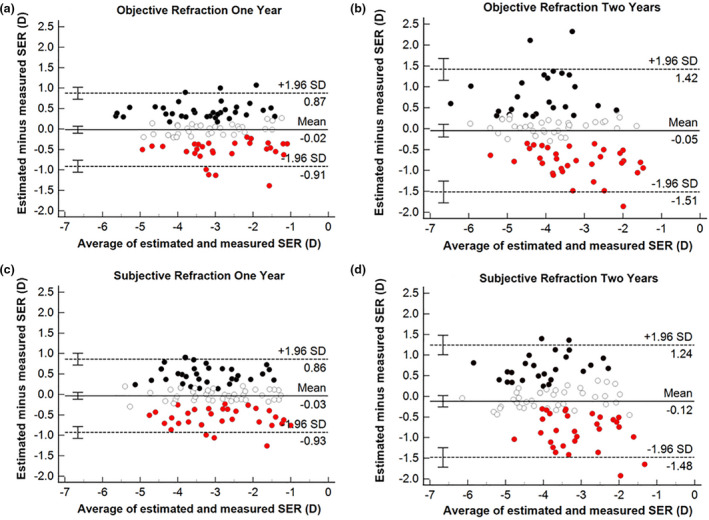
Bland‐Altman plots of the mean differences (Brien Holden Vision Institute (BHVI) estimates minus measured SER) versus their means, and the lower, upper bound of 95% CI at (a) 1 and (b) 2 years by objective refraction, and (c) 1 and (d) 2 years by subjective refraction. The solid line represents the mean difference and the dashed lines represent the upper and lower limits of agreement. Each error bar represents the 95% CI for the mean difference and limits of agreement. The data points in different colours denote when the measured SER was within the 95% CI of the estimated SER (white), was greater than the upper bound of the 95% CI of the estimated SER (Calculator prediction underestimates progression) (black), and was less than the lower bound of the 95% CI of the estimated SER (Calculator prediction overestimates progression) (red). (CI, confidence interval; SER, spherical equivalent refraction)

Comparison between estimated and measured subjective refraction

The distribution of the estimated subjective SER at 1 and 2 years of follow‐up, respectively, were: (1) 37.1% and 38.0% within the estimated 95% CI; (2) 31.9% and 28.0% greater than the upper bound of the estimated 95% CI (Calculator underestimates progression); (3) 31.0% and 34.0% less than the lower bound of the estimated 95% CI (Calculator overestimates progression) (Table  2 ). This indicates that the measured subjective refraction at 1 to 2 years of follow‐up was within the estimated SER 95% CI for approximately 38% of participants, and the Calculator overestimated and underestimated progression in approximately 32% (range 0.24 to 1.26 D underestimate at 1 year and 0.31 to 1.92 D at 2 years) and 30% (range 0.14 to 0.90 D overestimate at 1 year and 0.25 to 1.40 D at 2 years) of participants, respectively.

On average, there was no significant difference between the estimated and measured subjective SER at 1 (−0.03 ± 0.46 D, n = 116, p = 0.44) or 2 years of follow‐up (−0.12 ± 0.69 D, n = 100, p = 0.09). While the group average for the differences between the estimated and measured SER was small and would not be considered clinically significant, the 95% CI were ±0.90 D for 1 year and ±1.36 D for 2 years. There was a significant association between the differences of the estimated and measured subjective SER and their means at 2 years (Pearson's r = −0.27, p = 0.006), indicating that for a less myopic SER, the Calculator tended to overestimate the measured myopia progression.

DISCUSSION

This is the first study to examine the agreement between the estimated future SER (i.e., estimated myopia progression) obtained from the BHVI Myopia Calculator with the measured cycloplegic objective and subjective refraction in Hong Kong children wearing single‐vision distance spectacles over a follow‐up period of 1 and 2 years. The main finding from this analysis was that, when averaged across the entire sample of children, only small differences were observed between the estimated and measured refraction (mean differences < 0.25 D). However, comparison of the measured refraction to the 95% CI of the estimated SER for each individual child (consistent with how the BHVI Myopia Calculator is utilised in clinical practice) revealed that the measured refraction fell within the 95% CI of the estimated SER for only around 36% of individuals. For the cohort of children examined in the current study, the BHVI Myopia Calculator underestimated the extent of myopia progression in about 31% of children and overestimated the extent of myopia progression in about 33% of children (i.e., the measured refraction was outside the 95% CI of the estimated SER for about 64% of children), averaged across the 1‐ and 2‐year objective and subjective data (overestimate 0.31 to 1.92 D, underestimate 0.25 to 2.33 D at 2 years).

The measured refractive data used in the current analysis consisted of subjective and objective measurements obtained under cycloplegia, which provided similar outcomes when compared to the BHVI Myopia Calculator at the 1‐ and 2‐year follow‐up visits (Table  2 ). Based on the information provided on the BHVI Myopia Calculator website, the ‘progression curve with standard correction was generated based on annual progression data obtained from children from urban Asia aged 6 to 16 years (Brien Holden Vision Institute database),’ it is not clear whether the single‐vision distance progression data is based on objective/subjective or cycloplegic/non‐cycloplegic measures of refraction. However, given the strong correlation between the 1 year predicted progression data obtained from the BHVI Myopia Calculator for the participants in the current analysis and the predicted annual progression for the same participants calculated using the estimated annual progression equation for Asian children in Figure  1 of Donovan et al. ⁴⁷ (r = 0.99, mean absolute difference 0.05 D), it appears that the single‐vision distance progression data is based on objective measures of refraction obtained under cycloplegia. Practitioners should be aware that the calculator is based on cycloplegic objective refraction measures and estimates of myopia progression beyond 3 years may be derived from extrapolations of data included in the meta‐analysis of Donovan et al. ⁴⁷ (range of study durations included 10 months to 3 years).

Another limitation of the BHVI Myopia Calculator is the lack of consideration of biometric data. Since an overarching goal of myopia control interventions is to minimise potential vision impairment later in life due to ocular pathologies associated with excessive axial elongation (e.g., retinal detachment ⁵² and myopic maculopathy ¹² ), it has been suggested that axial length should be monitored in addition to refractive progression throughout childhood, ⁵³ particularly since vision impairment is more strongly correlated with axial length than refractive error. ⁵⁴  The inclusion of ocular biometrics, such as axial length and corneal curvature within a predictive model (in addition to age, sex and race), may help to improve future estimates of myopia progression or the likelihood of potential vision impairment later in life.

In terms of the duration of follow‐up, the 95% limits of agreement between the estimated and measured refraction increased by approximately 58% between 1 and 2 years from ±0.89 D to ±1.46 D, and ±0.90 D to ±1.36 D for the objective and subjective refraction data, respectively. This may be due in part to the slightly smaller sample size for the 2‐year measured data. However, the proportion of individual cases where the measured refraction was within the 95% CI of the BHVI estimated SER was relatively stable between the 1‐ and 2‐year visits (only about 4% variation). This was most likely because the 95% CI of the BHVI estimated SER increases with increasing duration of follow‐up.

Saunders et al. ⁵⁵ compared the BHVI Myopia Calculator SER estimates with cycloplegic objective refraction data obtained from Caucasian children followed for either 3 or 6 years in a population‐based sample from the UK (The Northern Ireland Childhood Errors of Refraction (NICER) study ⁵⁶ ). Similar to the current study, the BHVI Myopia Calculator overestimated myopia progression in about 38% of Caucasian children aged 12–13 years (n = 61) and about 58% of children aged 9–10 years (n = 19). In the UK population examined, the BHVI Myopia Calculator was more likely to overestimate the magnitude of progression for children with lower baseline SER, consistent with the trend observed for the Hong Kong children in the current study (Figure  1 ). The current study, and the previous analysis by Saunders et al., ⁵⁵  highlight that the BHVI Myopia Calculator may not provide reliable estimates of myopia progression for children from all races.

The main limitations of the current study were the relatively short follow‐up period of 1 to 2 years, and the restricted age range and level of myopia at baseline since the children were participants in control groups of orthokeratology studies. Future studies that include refractive progression data from children aged 6–16 years with baseline refractive errors ranging from −5.00 to −0.50 D (the range of input parameters in the BHVI Myopia Calculator) followed for several years may provide a greater understanding of the accuracy of estimated myopia progression provided by the BHVI Myopia Calculator. However, given the mounting evidence supporting early intervention for progressive myopia in children to prevent ocular complications later in life, ⁵⁷ it may not be ethically justifiable to conduct long‐term prospective studies of myopic children wearing single‐vision distance spectacles, particularly in Asian countries.

In conclusion, on average, the estimated SER data obtained from the BHVI Myopia Calculator using the baseline refraction, sex and ethnicity of Hong Kong children wearing single‐vision distance spectacles was in close agreement with the measured cycloplegic subjective and objective refraction data over 1 and 2 years of follow‐up (mean differences < 0.25 D). However, the extent of myopia progression measured under cycloplegia only fell within the 95% CI of the estimated SER for 32%–38% of individual children depending on the method of refraction and duration of follow up. Although the BHVI Myopia Calculator can be a useful educational tool when discussing myopia management with children and adult caregivers, practitioners should be aware that the progression data for a standard single‐vision correction (the ‘without management’ option) used in the BHVI Myopia Calculator may not provide an accurate estimate of the extent of myopia progression for all children and should be used with caution. The inclusion of additional data, potentially including axial length, from longitudinal studies of longer duration with larger sample sizes and a range of racial backgrounds may improve the Calculator's ability to predict future myopia progression for children accurately on an individual basis.

CONFLICT OF INTEREST

All authors have no proprietary interest in any of the products mentioned.

AUTHOR CONTRIBUTIONS

Yajing Yang: Conceptualization (supporting); Data curation (lead); Formal analysis (lead); Investigation (lead); Methodology (supporting); Visualization (lead); Writing‐original draft (lead); Writing‐review & editing (equal). Sin Wan Cheung: Conceptualization (supporting); Data curation (supporting); Formal analysis (supporting); Investigation (supporting); Methodology (supporting); Visualization (supporting); Writing‐review & editing (equal). Pauline Cho: Conceptualization (lead); Data curation (supporting); Formal analysis (supporting); Funding acquisition (lead); Investigation (supporting); Methodology (lead); Project administration (lead); Supervision (supporting); Visualization (supporting); Writing‐review & editing (equal). Stephen J Vincent: Conceptualization (lead); Data curation (supporting); Formal analysis (lead); Investigation (supporting); Methodology (lead); Supervision (lead); Visualization (lead); Writing‐review & editing (equal).

Yang Y, Cheung SW, Cho P, Vincent SJ. Comparison between estimated and measured myopia progression in Hong Kong children without myopia control intervention. Ophthalmic Physiol Opt. 2021;41:1363–1370. 10.1111/opo.12895