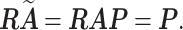Summary
High-throughput sequencing technology provides unprecedented opportunities to quantitatively explore human gut microbiome and its relation to diseases. Microbiome data are compositional, sparse, noisy, and heterogeneous, which pose serious challenges for statistical modeling. We propose an identifiable Bayesian multinomial matrix factorization model to infer overlapping clusters on both microbes and hosts. The proposed method represents the observed over-dispersed zero-inflated count matrix as Dirichlet-multinomial mixtures on which latent cluster structures are built hierarchically. Under the Bayesian framework, the number of clusters is automatically determined and available information from a taxonomic rank tree of microbes is naturally incorporated, which greatly improves the interpretability of our findings. We demonstrate the utility of the proposed approach by comparing to alternative methods in simulations. An application to a human gut microbiome data set involving patients with inflammatory bowel disease reveals interesting clusters, which contain bacteria families Bacteroidaceae, Bifidobacteriaceae, Enterobacteriaceae, Fusobacteriaceae, Lachnospiraceae, Ruminococcaceae, Pasteurellaceae, and Porphyromonadaceae that are known to be related to the inflammatory bowel disease and its subtypes according to biological literature. Our findings can help generate potential hypotheses for future investigation of the heterogeneity of the human gut microbiome.
Keywords: Bayesian nonparametric prior, Compositional data analysis, Feature allocation, Mixture model, Phylogenetic Indian buffet process
1. Introduction
Microbes parasitic on various parts of the human body are inseparable from the well-being of their hosts. Recent studies have shown that microbiota have profound effects on the formation, development, and progression of numerous diseases like psoriasis (Benhadou and others, 2018), obesity (Castaner and others, 2018), inflammatory bowel disease (IBD, Franzosa and others, 2019), preterm birth (Fettweis and others, 2019), and diabetes (Tilg and Moschen, 2014). In this article, we focus on IBD, a chronic and complex disease that features heterogeneity at the microbiome level. As Lloyd-Price and others (2019) pointed out, the disease activity is accompanied by molecular disruptions in microbial transcription, variations with taxonomic shifts, and other genomic activities. The seemingly strong association between gut microbes and IBD urges scientists to investigate microbial composition profiles in patients, which can improve our understanding of disease etiology and potentially lead to personalized treatments.
The emergence of high-throughput sequencing technology such as deep metagenomic sequencing has generated a plethora of data that have enabled researchers to quantitatively study both taxonomic and functional effect of microbiota on hosts (Turnbaugh and others, 2007). However, due to the compositional, sparse, heterogeneous, and noisy nature of the microbiome abundance data, they pose serious challenges in statistical modeling.
Composition. Microbiome abundance data are inherently compositional (Gloor and others, 2017), in the sense that individual counts are restricted by a sum constrain due to tissue size or sequencing depth. The abundance of each microbial component is only coherently interpretable relative to others within that sample. As a consequence, models that treat microbial taxa as independent variables may lead to substantial biases (Buccianti, 2013).
Sparsity. Microbial counts are sparse. Taking our IBD data as an example, more than 45% of the observations are exact zeros, which greatly complicates the sampling distribution. Excessive zeros occur mainly for two reasons: (i) bacteria are not present in tested hosts and hence the zeros are true biological zeros and (ii) the sequencing depth is not enough to capture rare bacteria which is referred to as technical zeros. Often, approaches need to explicitly differentiate between these two types of zeros to reduce estimation biases, which are addressed by the two-part model, the tobit model, and their combination (Liu and others, 2019).
Heterogeneity. The composition of microbiota is heterogeneous and drastically different across hosts. Methods based on iid sampling are deemed unsuitable for microbiome data analysis. Individualized characterization is necessary to unravel genuine information and avoid spurious conclusions derived from a homogeneous modeling assumption.
Noisiness. Measurements from sequencing platforms contain high levels of noises due to the technical instability, which inevitably confounds with the biological variation that researchers strive to investigate. Methods that ignore the experimental noises are susceptible to false discoveries which will be propagated to downstream analysis and hinder scientific advancement.
Current statistical methodologies in the analysis of microbiome data are largely focused on the supervised learning framework. For example, in regression analysis where covariates are compositional, the linear log-contrast model with  regularization was adopted in Lin and others (2014) and Shi and others (2016) to select relevant covariates in the analysis of metagenomic data. However, they do not explicitly take into account the excessive zeros but replace them with arbitrary small numbers. When treating compositional data as response, a sparse Dirichlet-multinomial regression model was employed in Chen and Li (2013) to associate microbiome composition with environmental covariates. The method is able to account for over-dispersion of observed counts and select important covariates. Xia and others (2013) introduced an additive logistic normal multinomial regression model and selected significant covariates via a group
regularization was adopted in Lin and others (2014) and Shi and others (2016) to select relevant covariates in the analysis of metagenomic data. However, they do not explicitly take into account the excessive zeros but replace them with arbitrary small numbers. When treating compositional data as response, a sparse Dirichlet-multinomial regression model was employed in Chen and Li (2013) to associate microbiome composition with environmental covariates. The method is able to account for over-dispersion of observed counts and select important covariates. Xia and others (2013) introduced an additive logistic normal multinomial regression model and selected significant covariates via a group 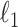 penalty. Chen and Li (2016) proposed a zero-inflated Beta regression model. The model includes a logistic regression component to model presence or absence of microbes in samples and a Beta regression component to model non-zero microbiome abundance. Wadsworth and others (2017) developed a Bayesian Dirichlet-multinomial regression model combined with spike-and-slab priors to select important covariates that are predictive of microbial abundances. Grantham and others (2020) proposed a Bayesian mixed-effects model for capturing the effects of treatment, covariates, and latent factors on microbial responses.
penalty. Chen and Li (2016) proposed a zero-inflated Beta regression model. The model includes a logistic regression component to model presence or absence of microbes in samples and a Beta regression component to model non-zero microbiome abundance. Wadsworth and others (2017) developed a Bayesian Dirichlet-multinomial regression model combined with spike-and-slab priors to select important covariates that are predictive of microbial abundances. Grantham and others (2020) proposed a Bayesian mixed-effects model for capturing the effects of treatment, covariates, and latent factors on microbial responses.
There are also a rising number of models focusing on revealing microbiome interactions. For example, Friedman and Alm (2012) proposed to estimate the Pearson correlations between log-transformed components of compositional data under the assumption of sparsity, which is later implemented more efficiently with parallel computing by Watts and others (2018). A composition-adjusted thresholding was proposed by Cao and others (2019) to obtain a sparse correlation estimate. More recently, Cai and others (2019) developed a Markov random field model to detect differential microbial networks. A key step in their approach is to dichotomize microbial compositions into a binary matrix. However, the dichotomization in their approach is based on a fixed quantile, the choice of which is somewhat arbitrary and sensitive.
While the majority of microbiome data analyses are performed in a supervised manner, in this paper we focus on an unsupervised learning task, namely, the probabilistic matrix factorization of microbiome data which can also be interpreted as overlapping biclustering. Many matrix factorization techniques have been proposed to handle continuous matrices (Bhattacharya and Dunson, 2011; Ročková and George, 2016), non-negative matrices (Lee and Seung, 2000; Hoyer, 2004), count matrices (Zhou and others, 2012; Gopalan and others, 2014), and binary matrices (Meeds and others, 2007; Ni and others, 2019; Wu and others, 2019). However, none of these methods is directly applicable to compositional microbiome data. To account for both sparsity and heterogeneity of microbiome data, a matrix factorization approach based on Dirichlet prior and low-dimensional representation was proposed in Shafiei and others (2015). Ren and others (2017) developed a Bayesian nonparametric ordination approach to capture the high-dimensional microbial dependencies via low-dimensional latent factors. Recently, a low rank approximation method was proposed by Cao and others (2019) which minimizes the multinomial likelihood-based loss function combined with a nuclear norm regularization on the composition matrix. They focused on recovering the composition and matrix factorization rather than inferring latent clustering structure which is the main objective of this article. Xu and others (2020) developed a zero-inflated Poisson factor model with Poisson rates negatively related to inflated zero occurrences. Again, their main focus was on reducing the dimensionality of the microbiome data and a separate clustering algorithm is required to identify the clusters.
In this article, we propose a Bayesian multinomial matrix factorization (MMF) model that infers the latent clustering structure from compositional, sparse, heterogeneous, and noisy microbiome data. The proposed MMF introduces a mixture model representation of observations through a set of latent variables to indicate the relative abundance of taxa. In essence, this simple formulation of the sampling model adaptively dichotomizes the multinomial observations into a binary matrix, which is more robust to noise and does not require a separate treatment of excessive zeros. Given the binary indicator matrix, priors are imposed hierarchically to characterize the heterogeneity via latent features. Specifically, we construct the hierarchical model with a combination of latent logit model, phylogenetic Indian buffet process prior (pIBP, Miller and others, 2008; Chen and others, 2016), and beta-Bernoulli prior. Using pIBP, we are able to infer an unknown number of overlapping clusters/communities of the taxa. pIBP also takes into account the taxonomic relationships among the taxa, which gives rise to more interpretable and reliable results. Conditional on the clusters of taxa, the beta-Bernoulli prior are assigned to cluster hosts, again allowing overlaps. Moreover, the sparse nature of the pIBP and beta-Bernoulli priors leads to an identifiable matrix factorization under a mild condition. Using simulations, we demonstrate that the proposed MMF has favorable performance compared to competing methods and is relatively robust to the choice of hyperparameters and misspecified tree information. We then apply MMF to an IBD microbiome data set (Qin and others, 2010), which reveals interesting clusters containing bacteria families Bacteroidaceae, Bifidobacteriaceae, Enterobacteriaceae, Fusobacteriaceae, Lachnospiraceae, Ruminococcaceae, Pasteurellaceae, and Porphyromonadaceae that are known to be related to the IBD and its subtypes according to biological literature. Despite the exploratory nature of this study, our findings can help generate hypotheses for further investigation of the heterogeneity of the human gut microbiome.
The rest of this article is organized as follows. We introduce the proposed MMF model in Section 2. Posterior inference based on Markov chain Monte Carlo (MCMC) sampling is described in Section 3. In Sections 4 and 5, we respectively illustrate our approach with simulation studies and the analysis of an IBD data set. This article is concluded with a brief discussion in Section 6.
2. Model
2.1. Classifying taxon abundance via adaptive dichotomization
Let 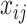 denote the observed count of taxon
denote the observed count of taxon 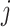 in host
in host 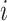 ,
, 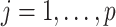 and
and 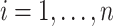 . Let
. Let 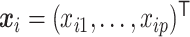 and
and 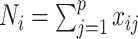 . We assume
. We assume 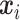 follows a Dirichlet-multinomial distribution,
follows a Dirichlet-multinomial distribution,
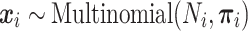 |
with host-specific relative abundances,
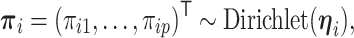 |
where 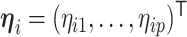 . Note that the Dirichlet-distributed relative abundances
. Note that the Dirichlet-distributed relative abundances 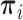 can be equivalently represented as normalized gamma random variables
can be equivalently represented as normalized gamma random variables 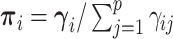 with unnormalized relative abundances
with unnormalized relative abundances 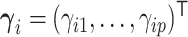 and
and 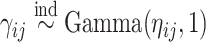 , where the gamma distribution is parameterized as
, where the gamma distribution is parameterized as 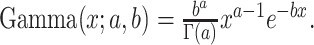
We introduce a latent indicator variable 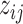 to classify whether a taxon
to classify whether a taxon 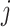 is significantly present or absent in host
is significantly present or absent in host 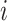 . However, there is no consensus on the classification of taxa based on absolute or relative abundances. In supervised tasks, the classification rule may be chosen to minimize certain objective functions. For example, when the goal is to predict a response variable with microbiome covariates, one can potentially find an optimal dichotomization that minimizes the prediction error. Lack of such gold standard in matrix factorization, we propose a mixture model to probabilistically classify raw taxa counts into states of high presence versus low presence and absence,
. However, there is no consensus on the classification of taxa based on absolute or relative abundances. In supervised tasks, the classification rule may be chosen to minimize certain objective functions. For example, when the goal is to predict a response variable with microbiome covariates, one can potentially find an optimal dichotomization that minimizes the prediction error. Lack of such gold standard in matrix factorization, we propose a mixture model to probabilistically classify raw taxa counts into states of high presence versus low presence and absence,
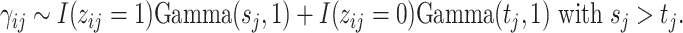 |
(2.1) |
In words, due to the constraint 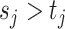 ,
, 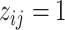 indicates high relative abundance and
indicates high relative abundance and 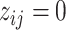 indicates low relative abundance. The choice of the two-component mixture model is motivated by the fact that the distribution of microbial abundances tend to be overdispersed and bi-modal (Koren and others, 2013; Lahti and others, 2014). If we further constrain
indicates low relative abundance. The choice of the two-component mixture model is motivated by the fact that the distribution of microbial abundances tend to be overdispersed and bi-modal (Koren and others, 2013; Lahti and others, 2014). If we further constrain 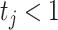 , the prior (2.1) becomes a spike-and-slab prior with Gamma
, the prior (2.1) becomes a spike-and-slab prior with Gamma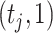 as the spike distribution, assigning an infinite mass at zero. Through the multinomial sampling and adaptive discretization, the zero counts would naturally fall into the category of low abundance with high probability. Therefore, we do not need an extra zero-inflated component to explicitly deal with the zero counts in our model. In addition, the adaptive dichotomization also accounts for sequencing errors as in Parmigiani and others (2002). The induced distribution of
as the spike distribution, assigning an infinite mass at zero. Through the multinomial sampling and adaptive discretization, the zero counts would naturally fall into the category of low abundance with high probability. Therefore, we do not need an extra zero-inflated component to explicitly deal with the zero counts in our model. In addition, the adaptive dichotomization also accounts for sequencing errors as in Parmigiani and others (2002). The induced distribution of 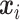 is a discrete mixture of Dirichlet-multinomial distributions with
is a discrete mixture of Dirichlet-multinomial distributions with 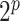 components, with each component corresponding to one configuration of
components, with each component corresponding to one configuration of 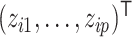 . The latent variable
. The latent variable 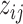 can be viewed as a denoised version of the raw observations
can be viewed as a denoised version of the raw observations 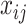 . A similar idea of denoising was recently used by Cai and others (2019) where they assumed that taxa with relative abundances lower than 0.001% are due to noise or sequencing errors and adopted the 0.25 quantile as a hard cutoff for more abundant taxa. Our approach differs from theirs in that we do not need to fix a cutoff and the proposed method adaptively dichotomizes the data. We assign hyperpriors on the unknown parameters
. A similar idea of denoising was recently used by Cai and others (2019) where they assumed that taxa with relative abundances lower than 0.001% are due to noise or sequencing errors and adopted the 0.25 quantile as a hard cutoff for more abundant taxa. Our approach differs from theirs in that we do not need to fix a cutoff and the proposed method adaptively dichotomizes the data. We assign hyperpriors on the unknown parameters  ,
,
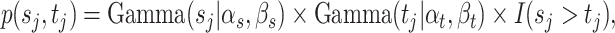 |
(2.2) |
with 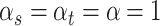 and
and 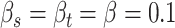 . Sensitivity analyses will be performed on the choice of all the hyperparameters in Section 4 and Section B of the Supplementary material available at Biostatistics online.
. Sensitivity analyses will be performed on the choice of all the hyperparameters in Section 4 and Section B of the Supplementary material available at Biostatistics online.
The mixture model in (2.1) can reliably classify taxa with well separated relative abundances into two states. However, the classification can have greater uncertainties for taxa with less variable relative abundances across observations. In Section 2.2, we will introduce latent structures on 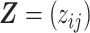 that stabilize uncertain classifications, reduce the dimensionality, and induce overlapping cluster structure for both hosts and microbial taxa.
that stabilize uncertain classifications, reduce the dimensionality, and induce overlapping cluster structure for both hosts and microbial taxa.
2.2. Biclustering taxa and hosts via binary matrix factorization
We introduce lower-dimensional matrices to characterize the heterogeneity of both rows and columns of  . In particular, we let
. In particular, we let 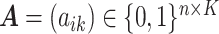 and
and 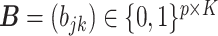 denote the host-cluster and taxon-cluster matrices with
denote the host-cluster and taxon-cluster matrices with 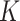 clusters. The clustering interpretations of
clusters. The clustering interpretations of 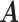 and
and 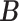 will be elaborated in Section 2.3. The number
will be elaborated in Section 2.3. The number 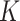 of columns of
of columns of 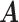 and
and 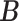 is usually much smaller than the dimensions of the original data (
is usually much smaller than the dimensions of the original data (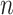 and
and 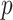 ). We link
). We link 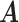 and
and 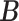 to
to 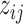 by a latent logit model
by a latent logit model
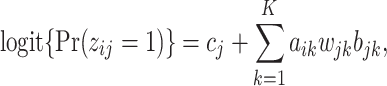 |
(2.3) |
where 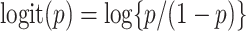 . If a group of hosts have a common activated biological pathway (related to normal body functions or diseases) that involves a common set of taxa, then these taxa are likely to have significant presence in those host samples. Therefore, we choose to constrain
. If a group of hosts have a common activated biological pathway (related to normal body functions or diseases) that involves a common set of taxa, then these taxa are likely to have significant presence in those host samples. Therefore, we choose to constrain 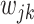 to be positive, although in principle they can take any values; similar considerations in a different context were made in Wood and others (2006). Parameter
to be positive, although in principle they can take any values; similar considerations in a different context were made in Wood and others (2006). Parameter 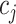 represents the log odds ratio of baseline probability of the presence of taxon
represents the log odds ratio of baseline probability of the presence of taxon 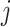 . We assume weakly informative priors on
. We assume weakly informative priors on 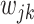 and
and 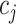 ,
, 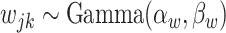 , and
, and 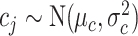 , with
, with 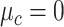 ,
, 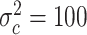 ,
, 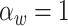 , and
, and 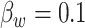 .
.
2.3. Indian buffet process and taxonomic rank tree
The host–cluster matrix 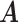 and taxon–cluster matrix
and taxon–cluster matrix 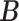 can be interpreted as clustering of rows and columns of
can be interpreted as clustering of rows and columns of 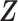 , respectively. Host
, respectively. Host 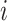 (taxon
(taxon 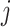 ) belongs to cluster
) belongs to cluster 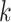 if the corresponding
if the corresponding 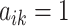 (
(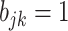 ). Since we do not constrain
). Since we do not constrain 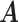 and
and 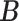 to having unit row sums, clusters can have overlaps. This is useful in microbiome applications because a taxon can be active in multiple communities and likewise a host can also belong to more than one group. To make inference on these two matrices, we will impose a Bayesian nonparametric prior on
to having unit row sums, clusters can have overlaps. This is useful in microbiome applications because a taxon can be active in multiple communities and likewise a host can also belong to more than one group. To make inference on these two matrices, we will impose a Bayesian nonparametric prior on  that can automatically determine the number
that can automatically determine the number 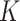 of clusters.
of clusters.
The Indian buffet process (IBP, Griffiths and Ghahramani, 2005) has been widely used as a Bayesian nonparametric prior on binary matrices with potentially unbounded number of columns. IBP assumes the rows of the binary matrix are exchangeable. This assumption becomes a limitation when the rows (taxa) are seemingly dependent as in our case. For instance, the relationships between taxa are commonly organized as a taxonomic rank tree. Taxa with smaller distances on the tree tend to have similar biological functions and therefore are expected to have higher probability of being in the same cluster. To incorporate this prior knowledge, we adopt the phylogenetic IBP (pIBP, Miller and others, 2008) to encourage taxonomically similar taxa to form clusters.
To describe the generating process of pIBP, we first assume a fixed and finite number 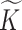 of clusters and will later relax it. Conditional on
of clusters and will later relax it. Conditional on 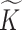 , we associate a parameter
, we associate a parameter 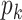 to each column of
to each column of 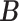 , which is assigned a
, which is assigned a 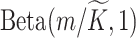 prior. We put a
prior. We put a 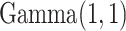 prior on
prior on 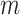 to infer its value from data. While the columns of
to infer its value from data. While the columns of 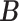 are still independent as in IBP, entries within each column are generated jointly, with the pattern of dependence characterized by a stochastic process on a taxonomic rank tree. The tree has
are still independent as in IBP, entries within each column are generated jointly, with the pattern of dependence characterized by a stochastic process on a taxonomic rank tree. The tree has 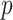 taxa of interest as leaves and higher taxonomic ranks as internal/root nodes. Assume the path from every leaf up to the root contains
taxa of interest as leaves and higher taxonomic ranks as internal/root nodes. Assume the path from every leaf up to the root contains 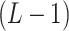 internal nodes, and each edge has length
internal nodes, and each edge has length 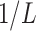 so that the total length of the path from every leaf to the root is 1. This implies that the marginal prior probability of
so that the total length of the path from every leaf to the root is 1. This implies that the marginal prior probability of 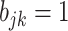 is the same across taxa
is the same across taxa 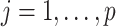 .
.
To generate the entries of the 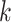 th column, we proceed as follows: (i) assign value zero to the root node of the tree; (ii) along any path from the root to a leaf, let the value change to one with an exponential rate
th column, we proceed as follows: (i) assign value zero to the root node of the tree; (ii) along any path from the root to a leaf, let the value change to one with an exponential rate 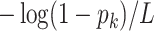 ; (iii) once the value has changed to one along a path from the root, all leaves below that change point are assigned value one; and (iv) set the entries in the
; (iii) once the value has changed to one along a path from the root, all leaves below that change point are assigned value one; and (iv) set the entries in the 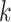 th column of
th column of 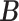 to the values of the corresponding leaves. By construction, leaves that are closer on the tree tend to receive identical values (of zeros or ones) in each column and therefore the corresponding taxa are more likely to fall in the same cluster. Note that the marginal prior probability of
to the values of the corresponding leaves. By construction, leaves that are closer on the tree tend to receive identical values (of zeros or ones) in each column and therefore the corresponding taxa are more likely to fall in the same cluster. Note that the marginal prior probability of 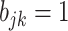 is
is 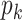 , as given in the original paper of Miller and others (2008). To remove the dependency of the generating process from a fixed
, as given in the original paper of Miller and others (2008). To remove the dependency of the generating process from a fixed 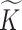 , we let
, we let 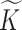 go to infinity and obtain the pIBP. Hereafter, we omit empty columns and denote the number of non-empty columns by
go to infinity and obtain the pIBP. Hereafter, we omit empty columns and denote the number of non-empty columns by 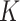 .
.
Conditional on taxon-cluster matrix 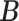 (only via
(only via 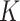 ), each element
), each element 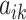 in
in 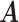 follows an independent beta-Bernoulli distribution
follows an independent beta-Bernoulli distribution 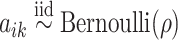 , and
, and 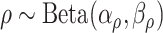 with
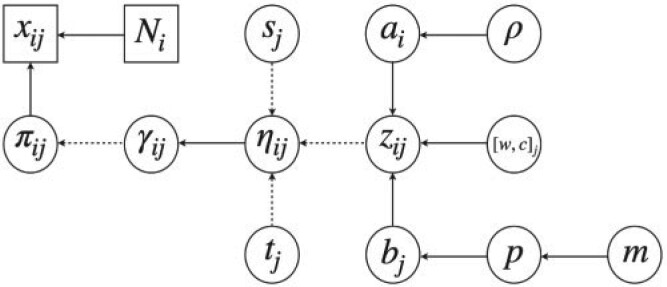
with 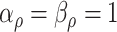 . The complete hierarchical model is represented as directed acyclic graph in Figure 1.
. The complete hierarchical model is represented as directed acyclic graph in Figure 1.
Fig. 1.
A graphical representation of the model. Dashed edges and squares are deterministic, and solid edges and circles are stochastic.
Our choice of the nonparametric pIBP prior allows for flexible modeling of the latent structures. First, the number of clusters is potentially unbounded (i.e., it can increase as the sample size grows) and can be inferred from data. Second, given the number of clusters, the prior model assigns positive mass on any taxon-cluster matrix 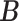 (via pIBP) and any host-cluster matrix
(via pIBP) and any host-cluster matrix 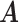 (via independent Bernoulli’s conditional on
(via independent Bernoulli’s conditional on 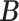 ). Third, through the logit link, the prior model on
). Third, through the logit link, the prior model on 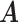 and
and 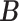 also induces a flexible prior on the latent abundance matrix
also induces a flexible prior on the latent abundance matrix 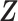 .
.
2.4. Identifiability of the proposed model
Matrix factorization is often non-identifiable without additional assumptions. For example, model (2.3) can be written in a matrix form,
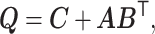 |
where 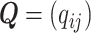 with
with 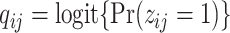 ,
, 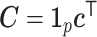 with
with 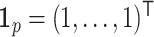 and
and 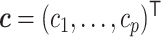 , and, slightly abusing the notation,
, and, slightly abusing the notation, 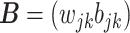 absorbs the weights
absorbs the weights 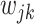 . Let
. Let 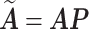 and
and 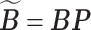 for any
for any 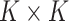 orthogonal matrix
orthogonal matrix 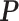 . It is obvious that
. It is obvious that 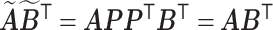 . Consequently,
. Consequently, 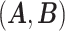 and
and 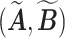 would lead to the same
would lead to the same  and the same sampling distribution and are therefore non-identifiable in general. However, the fact that
and the same sampling distribution and are therefore non-identifiable in general. However, the fact that 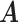 is binary makes the proposed matrix factorization identifiable up to column permutations under a mild condition.
is binary makes the proposed matrix factorization identifiable up to column permutations under a mild condition.
Proposition 1
If
is a binary matrix and there exists an integer matrix
such that
, then
and
is uniquely identifiable up to column permutation.
Proof. Let
with an orthogonal matrix
. We will show that
must be a permutation matrix if
is a binary matrix. We have
Since both
and
are integer matrices,
must be an integer matrix. This implies that each row of
is a unit vector and
is therefore a permutation matrix.
The condition is, in our opinion, mild. For example, it is satisfied if for any 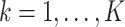 , there exists
, there exists 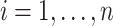 such that
such that 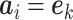 where
where 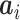 is the
is the 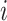 th row of
th row of 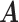 and
and 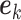 is a unit vector with 1 at its
is a unit vector with 1 at its 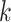 th entry (in this case
th entry (in this case 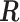 would simply be a binary matrix that acts to select those
would simply be a binary matrix that acts to select those 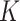 rows of
rows of 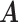 ). In words, the proposed model is identifiable if for any cluster
). In words, the proposed model is identifiable if for any cluster 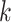 , there exists at least one member of this cluster that does not belong to any other clusters. Below, for completeness, we give a non-identifiable example when the condition of Proposition 1 is not met.
, there exists at least one member of this cluster that does not belong to any other clusters. Below, for completeness, we give a non-identifiable example when the condition of Proposition 1 is not met.
EXAMPLE 1
Suppose
Then, the matrix
satisfies
but is not a permutation matrix.
3. Posterior inference
The proposed MMF is parameterized by 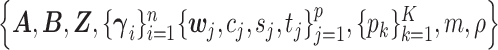 . We carry out the posterior inference by MCMC simulation. To improve mixing, we marginalize out unnormalized relative abundance parameters
. We carry out the posterior inference by MCMC simulation. To improve mixing, we marginalize out unnormalized relative abundance parameters 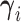 ’s. While other parameters are trivial to update with Gibbs or Metropolis–Hastings (M–H), care must be taken in updating
’s. While other parameters are trivial to update with Gibbs or Metropolis–Hastings (M–H), care must be taken in updating 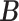 and
and 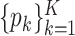 , details of which are provided below. The updating procedures of other parameters are presented in Section A of the Supplementary material available at Biostatistics online. We let
, details of which are provided below. The updating procedures of other parameters are presented in Section A of the Supplementary material available at Biostatistics online. We let 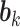 and
and 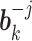 respectively denote the
respectively denote the 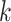 th column of
th column of 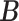 and the
and the 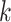 th column of
th column of 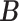 without the
without the 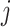 th entry. Sequentially for
th entry. Sequentially for 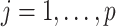 , we cycle through the following three steps.
, we cycle through the following three steps.
-
Step i. Update existing (non-empty) columns
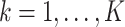 of
of 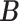 . For
. For 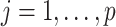 , we sample the binary
, we sample the binary 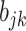 from the full conditional distribution,
from the full conditional distribution,
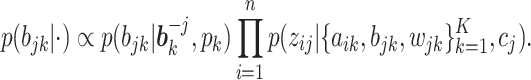
While an analytic form of
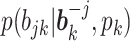 is hard to obtain, it can be computed by the sum-product algorithm exactly and efficiently. Details of the sum-product algorithm can be found in Bishop (2006). Importantly, if a column becomes all zeros after update, we delete that column and reduce
is hard to obtain, it can be computed by the sum-product algorithm exactly and efficiently. Details of the sum-product algorithm can be found in Bishop (2006). Importantly, if a column becomes all zeros after update, we delete that column and reduce 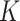 by 1.
by 1. -
Step ii. Update
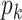 for existing columns of
for existing columns of 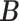 . Suppose
. Suppose 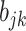 is any non-zero entry in the
is any non-zero entry in the 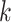 th column. The full conditional of
th column. The full conditional of 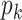 is given by
is given by
where the first factor is a standard uniform distribution (Miller and others, 2008) and the second factor can be efficiently computed by decomposing it into a series of univariate conditional distributions using the chain rule. For example, without loss of generality, assuming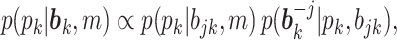
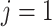 , then
, then
where each factor can be computed again using the sum-product algorithm. Since we only know the full conditional up to a normalization constant, we draw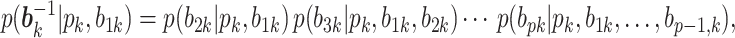
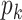 by a M-H step, where a new value is proposed from
by a M-H step, where a new value is proposed from 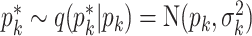 and is accepted with probability
and is accepted with probability
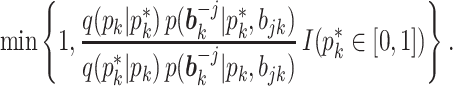
Following the default choice in Miller and others (2008), we choose
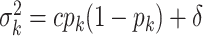 , with
, with 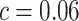 and
and 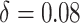 .
. - Step iii. Propose new columns. After all the existing columns are updated, we propose to add new columns. We first draw
where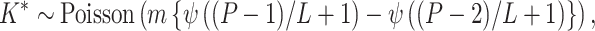
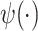 is the digamma function and
is the digamma function and 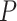 is the total number of nodes in the tree. If
is the total number of nodes in the tree. If 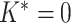 , we will go to the next step. Otherwise, we propose a set of new parameters
, we will go to the next step. Otherwise, we propose a set of new parameters 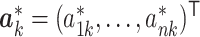 and
and 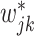 from their prior distributions,
from their prior distributions, 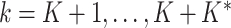 . We accept new columns and the associated new parameters with probability
. We accept new columns and the associated new parameters with probability
where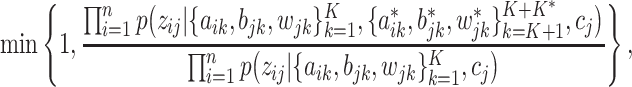
 . Lastly, if new columns are accepted, we increase
. Lastly, if new columns are accepted, we increase 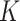 by
by 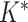 and sample
and sample 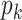 for the new columns by a M–H step,
for the new columns by a M–H step,
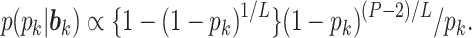
To summarize the posterior distribution based on the Monte Carlo samples, we proceed by first calculating the maximum a posteriori estimate 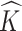 of
of 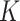 from the marginal posterior distribution. Conditional on
from the marginal posterior distribution. Conditional on 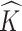 , we find an estimate of
, we find an estimate of 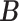 by the following procedure. For any matrices
by the following procedure. For any matrices 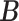 ,
, 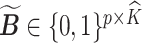 , we define a distance
, we define a distance
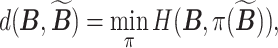 |
(3.4) |
where 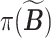 denotes a permutation of the columns of
denotes a permutation of the columns of 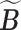 and
and 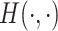 is the Hamming distance between two binary matrices, i.e., counting the number of different entries between the two matrices. A point estimator
is the Hamming distance between two binary matrices, i.e., counting the number of different entries between the two matrices. A point estimator 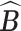 of
of  is then obtained as
is then obtained as
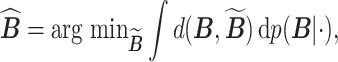 |
where 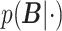 denotes the marginal posterior distribution of
denotes the marginal posterior distribution of 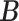 given
given 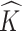 . Empirically, both the integration and the optimization can be approximated using the available Monte Carlo samples. Specifically, we define the posterior mode
. Empirically, both the integration and the optimization can be approximated using the available Monte Carlo samples. Specifically, we define the posterior mode 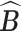 as
as
 |
where 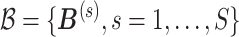 is the set of posterior samples of
is the set of posterior samples of 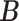 and the distance function is given in (3.4). Conditional on
and the distance function is given in (3.4). Conditional on 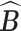 , we continue to run the Markov chain for a while. Then, the point estimates of other parameters are obtained as the posterior means computed from the new Monte Carlo samples.
, we continue to run the Markov chain for a while. Then, the point estimates of other parameters are obtained as the posterior means computed from the new Monte Carlo samples.
4. Simulation
In our simulation study, we considered a dataset with 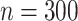 hosts,
hosts, 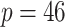 taxa, and
taxa, and 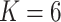 true clusters; similar in size to the later application. For
true clusters; similar in size to the later application. For 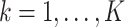 , we first set
, we first set 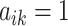 ,
, 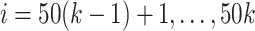 , and
, and 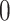 all the others. Then, we randomly changed 10% of zero entries in the host-cluster matrix
all the others. Then, we randomly changed 10% of zero entries in the host-cluster matrix 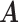 to one. We used the same taxonomic rank tree as in later application to generate the taxon-cluster matrix
to one. We used the same taxonomic rank tree as in later application to generate the taxon-cluster matrix 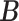 , which had
, which had 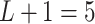 levels. Furthermore, cluster-specific probability parameters
levels. Furthermore, cluster-specific probability parameters 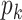 were all set to 0.3. The resulting true
were all set to 0.3. The resulting true 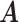 and
and 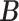 , along with the phylogenetic tree are shown in Figure S.1 of the Supplementary material available at Biostatistics online. By construction, each taxon or host was allowed to belong to multiple clusters. Latent indicators
, along with the phylogenetic tree are shown in Figure S.1 of the Supplementary material available at Biostatistics online. By construction, each taxon or host was allowed to belong to multiple clusters. Latent indicators 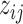 were generated from the logit model (2.3) with
were generated from the logit model (2.3) with 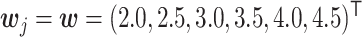 and
and 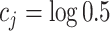 . For the unnormalized relative abundance
. For the unnormalized relative abundance 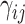 , we simulated them from the gamma mixture model (2.1) with varying degrees of separation of mixture components,
, we simulated them from the gamma mixture model (2.1) with varying degrees of separation of mixture components, 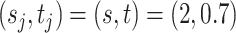 ,
, 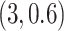 , and
, and 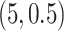 . Among these three simulation scenarios,
. Among these three simulation scenarios, 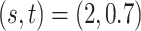 was the most difficult as it induced the least separation between the two mixture component. The observations were finally generated from the multinomial sampling model for which the total counts were drawn from the discrete uniform distribution
was the most difficult as it induced the least separation between the two mixture component. The observations were finally generated from the multinomial sampling model for which the total counts were drawn from the discrete uniform distribution 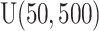 .
.
We ran the MCMC algorithm of MMF for 5000 iterations with 10 random initial clusters. The first 2500 iterations were discarded as burn-in and posterior samples were retained every 5th iteration after burn-in. On average, it took 3.8 h on a 2.3 GHz Quad-Core Intel Core i7 laptop. To evaluate the recovery accuracy, we calculated the estimation errors for both 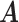 and
and 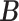 . Specifically, we computed the Hamming distance between the estimated and true
. Specifically, we computed the Hamming distance between the estimated and true 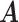 and
and 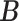 , normalized by the respective total number of elements. When the estimated number of clusters was different from the truth, we padded the smaller matrix with columns of zeros, making the resulting matrices comparable in dimension.
, normalized by the respective total number of elements. When the estimated number of clusters was different from the truth, we padded the smaller matrix with columns of zeros, making the resulting matrices comparable in dimension.
Method evaluation. The results under three sets of true values of 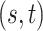 are summarized in Table 1 based on 50 repeated simulations. As expected, the performance improved as the two mixture components in (2.2) became more separated, from
are summarized in Table 1 based on 50 repeated simulations. As expected, the performance improved as the two mixture components in (2.2) became more separated, from 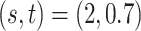 to
to 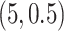 . The proposed MMF was able to identify the correct number
. The proposed MMF was able to identify the correct number 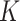 of clusters at least 95% of the time. Figure S.1 of the Supplementary material available at Biostatistics online depicts the estimated host-cluster and taxon-cluster matrices
of clusters at least 95% of the time. Figure S.1 of the Supplementary material available at Biostatistics online depicts the estimated host-cluster and taxon-cluster matrices 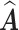 and
and 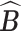 of the proposed MMF from one simulation result with the worst error rate in the scenario
of the proposed MMF from one simulation result with the worst error rate in the scenario 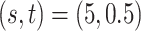 after adjusting for label switching and dropping redundant columns. They are visually quite close to the truth, indicating that the proposed method was able to consistently and accurately identify the clusters of hosts and taxa.
after adjusting for label switching and dropping redundant columns. They are visually quite close to the truth, indicating that the proposed method was able to consistently and accurately identify the clusters of hosts and taxa.
Table 1.
Simulation results of the proposed MMF and competing methods. Average errors in estimating 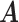 and
and 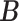 are quantified as the Hamming distance between the estimated and true matrices, normalized by the respective total number of elements. The numbers in the parentheses are standard deviations. The smallest errors are in boldface. The competing methods are low rank approximation (LRA), non-negative matrix factorization (NNMF), zero-inflated Poisson factor model (ZIPFM), and two-step multinomial matrix factorization (TSMF)
are quantified as the Hamming distance between the estimated and true matrices, normalized by the respective total number of elements. The numbers in the parentheses are standard deviations. The smallest errors are in boldface. The competing methods are low rank approximation (LRA), non-negative matrix factorization (NNMF), zero-inflated Poisson factor model (ZIPFM), and two-step multinomial matrix factorization (TSMF)
|
(2, 0.7) | (3, 0.6) | (5, 0.5) | |||
|---|---|---|---|---|---|---|
Error 
|
Error 
|
Error 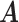
|
Error 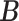
|
Error 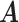
|
Error 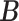
|
|
| MMF | 0.373 | 0.167 | 0.171 | 0.055 | 0.117 | 0.057 |
| (0.062) | (0.029) | (0.022) | (0.021) | (0.023) | (0.028) | |
| LRA | 0.298 | 0.269 | 0.205 | 0.185 | 0.203 | 0.165 |
| (0.042) | (0.023) | (0.052) | (0.017) | (0.058) | (0.021) | |
| NNMF | 0.351 | 0.279 | 0.288 | 0.247 | 0.256 | 0.208 |
| NNMF | (0.049) | (0.030) | (0.062) | (0.021) | (0.059) | (0.014) |
| ZIPFM | 0.425 | 0.258 | 0.291 | 0.249 | 0.246 | 0.232 |
| (0.014) | (0.031) | (0.008) | (0.023) | (0.002) | (0.022) | |
| TSMF | 0.382 | 0.253 | 0.325 | 0.132 | 0.237 | 0.089 |
| TSMF | (0.092) | (0.033) | (0.057) | (0.043) | (0.092) | (0.018) |
Comparisons with competing methods. Matrix factorization has been studied extensively in the literature. We compared the proposed MMF with three existing alternative matrix factorization methods, the low rank approximation (LRA, Cao and others 2019), the non-negative matrix factorization (NNMF, Cai and others 2017), and the zero-inflated Poisson factor model (ZIPFM, Xu and others 2020).
In order to compare the performance of biclustering, the overlapping clustering method, fuzzy c-means (Bezdek and others, 1984), was applied to the latent factors or low rank matrices obtained from the competing methods. The dimension of latent factors was chosen by their default optimization procedure. The number of clusters was set to the truth 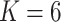 for competing methods whereas it was estimated for the proposed MMF. The estimation errors were defined by first converting clustering results to binary host–cluster or taxon–cluster matrix, and then calculating the distance between the estimated and true matrices as was done for the proposed method. In addition, we also considered a two-step approach that was similar to the proposed MMF, denoted by TSMF. Specifically, instead of joint modeling, the two-step approach first dichotomized observations using a default cutoff as suggested in Cai and others (2019) and then applied the same Bayesian nonparametric binary matrix factorization method as in MMF to the binary data. The results of all the methods are reported in Table 1. The proposed MMF consistently outperformed the competing methods in most settings (keeping in mind that the number of clusters was set to truth for LRA, NNMF, and ZIPFM), especially for the taxon-cluster matrix
for competing methods whereas it was estimated for the proposed MMF. The estimation errors were defined by first converting clustering results to binary host–cluster or taxon–cluster matrix, and then calculating the distance between the estimated and true matrices as was done for the proposed method. In addition, we also considered a two-step approach that was similar to the proposed MMF, denoted by TSMF. Specifically, instead of joint modeling, the two-step approach first dichotomized observations using a default cutoff as suggested in Cai and others (2019) and then applied the same Bayesian nonparametric binary matrix factorization method as in MMF to the binary data. The results of all the methods are reported in Table 1. The proposed MMF consistently outperformed the competing methods in most settings (keeping in mind that the number of clusters was set to truth for LRA, NNMF, and ZIPFM), especially for the taxon-cluster matrix 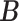 . Although when
. Although when 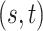 was specified to be
was specified to be 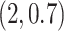 , the estimation error of
, the estimation error of 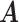 in LRA was smaller, the significantly more accurate result of estimating
in LRA was smaller, the significantly more accurate result of estimating 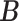 in the proposed MMF shows the benefit of using the phylogenetic tree information.
in the proposed MMF shows the benefit of using the phylogenetic tree information.
Additional simulations with different values of 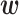 . We performed additional simulation for
. We performed additional simulation for 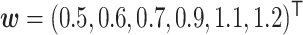 and
and 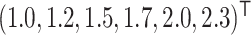 in Section B of the Supplementary material available at Biostatistics online, which led to similar conclusion as above.
in Section B of the Supplementary material available at Biostatistics online, which led to similar conclusion as above.
Misspecified model. For fairer comparison, we mimicked the generating process of microbial metagenomic sequencing data, which was different from the proposed model. In this experiment, 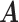 and
and 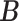 were first generated as before. Then, the true counts
were first generated as before. Then, the true counts 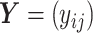 were simulated from a negative binomial model,
were simulated from a negative binomial model,
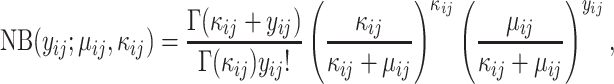 |
where 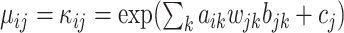 such that
such that 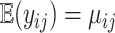 and
and 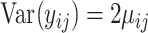 . The counts were then proportionally down-sampled from a multinomial distribution with sequencing depth uniformly chosen from
. The counts were then proportionally down-sampled from a multinomial distribution with sequencing depth uniformly chosen from 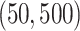 . We subsequently applied the proposed MMF and the competing methods to the down-sampled dataset. The results based on 50 repetitions are summarized in Table 2, which show the overall competitive performance of the proposed MMF over the alternatives, especially in estimating
. We subsequently applied the proposed MMF and the competing methods to the down-sampled dataset. The results based on 50 repetitions are summarized in Table 2, which show the overall competitive performance of the proposed MMF over the alternatives, especially in estimating 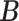 .
.
Table 2.
Simulation results of the misspecified model. Average errors in estimating 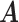 and
and 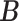 are quantified as the Hamming distance between the estimated and true matrices, normalized by the respective total number of elements. The numbers in the parentheses are standard deviations. The competing methods are low rank approximation (LRA), non-negative matrix factorization (NNMF), zero-inflated Poisson factor model (ZIPFM), and two-step multinomial matrix factorization (TSMF).
are quantified as the Hamming distance between the estimated and true matrices, normalized by the respective total number of elements. The numbers in the parentheses are standard deviations. The competing methods are low rank approximation (LRA), non-negative matrix factorization (NNMF), zero-inflated Poisson factor model (ZIPFM), and two-step multinomial matrix factorization (TSMF).
| MMF | LRA | NNMF | ZIPFM | TSMF | |
|---|---|---|---|---|---|
Error rate 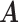
|
0.323 | 0.301 | 0.351 | 0.368 | 0.329 |
| (0.072) | (0.044) | (0.062) | (0.015) | (0.083) | |
Error rate 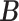
|
0.157 | 0.293 | 0.319 | 0.382 | 0.191 |
| (0.036) | (0.032) | (0.023) | (0.019) | (0.047) |
Sensitivity analyses. We performed two sets of sensitive analyses regarding the choice of all the hyperparameters as well as the impact of misspecified tree information. The inference under MMF was relatively robust, in our opinion. Details are provided in Section B of the Supplementary material available at Biostatistics online. In practice, if no prior knowledge is available, we recommend to use the default non-informative prior specification in Sections 2.1–2.3.
5. Real data
Gut microbes actively interact with their hosts and have profound relevance to inflammatory bowel disease (IBD) which is a very heterogeneous disease at the microbiome level. The goal of this case study was to investigate the heterogeneous microbial profiles in relation to IBD in an unsupervised data-driven manner. We applied the proposed MMF to an IBD microbiome dataset (Qin and others, 2010). The data were obtained by sequencing fecal specimens collected from IBD patients as well as healthy adult controls using the Illumina’s Genome Analyzer (metagenomic sequencing); details of the data generating procedure can be found in Qin and others (2010). The dataset contained 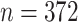 observations with 240 healthy hosts and 132 IBD patients, and provided information on microbial compositions at various taxonomic levels (kingdom, phylum, class, order, family, genus, and species) of these samples. We chose to work with the family level counts because lower levels (e.g., the specie level) had extremely large number of zeros (more than 80% elements in the count matrix were zeros). In addition, we filtered out families that appear in less than 10% of samples (i.e., taxa with more than 90% of zeros) and preserved only families belonging to kingdom bacteria. The resulting data had
observations with 240 healthy hosts and 132 IBD patients, and provided information on microbial compositions at various taxonomic levels (kingdom, phylum, class, order, family, genus, and species) of these samples. We chose to work with the family level counts because lower levels (e.g., the specie level) had extremely large number of zeros (more than 80% elements in the count matrix were zeros). In addition, we filtered out families that appear in less than 10% of samples (i.e., taxa with more than 90% of zeros) and preserved only families belonging to kingdom bacteria. The resulting data had 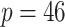 taxa for subsequent analysis. The relationships of taxa can be naturally represented by a taxonomic rank tree. Taxa that are closer on the tree tend to have similar activities and functions. We depict the tree of 46 taxa along with their higher taxonomic ranks, kingdom, phylum, class, and order in Figure 2. This taxonomic rank tree was used as prior information to encourage the clustering of taxa that are taxonomically similar.
taxa for subsequent analysis. The relationships of taxa can be naturally represented by a taxonomic rank tree. Taxa that are closer on the tree tend to have similar activities and functions. We depict the tree of 46 taxa along with their higher taxonomic ranks, kingdom, phylum, class, and order in Figure 2. This taxonomic rank tree was used as prior information to encourage the clustering of taxa that are taxonomically similar.
Fig. 2.
Real data. Heatmaps of estimated clusters using the proposed MMF. Colored cells are ones and black cells are zeros. Rows of 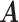 are hosts arranged in a block-diagonal-liked form. Rows of
are hosts arranged in a block-diagonal-liked form. Rows of 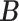 are taxa which are arranged according to the taxonomic rank tree. Each column represents a cluster with overlaps. The red/green cells in the heatmap of
are taxa which are arranged according to the taxonomic rank tree. Each column represents a cluster with overlaps. The red/green cells in the heatmap of 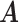 represents patients/controls with ones.
represents patients/controls with ones.
We ran two separate Markov chains of MMF for 10 000 iterations. The first 5000 iterations were discarded as burn-in and posterior samples were retained every 5th iteration after burn-in. It took 8.2 h on a 2.3 GHz Quad-Core Intel Core i7 laptop. To monitor the MCMC convergence, we computed the Gelman and Rubin’s potential scale reduction factor (PSRF, Gelman and Rubin, 1992) for key parameters. The MCMC diagnostic did not show a sign of lack of convergence: the PSRF was 1.01 for number 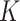 of clusters and the median PSRF was
of clusters and the median PSRF was 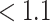 (with stdev 0.1) for
(with stdev 0.1) for 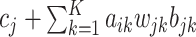 , the quantity on the right-hand side of (2.3). The Monte Carlo samples from the two Markov chains were combined for subsequent analysis.
, the quantity on the right-hand side of (2.3). The Monte Carlo samples from the two Markov chains were combined for subsequent analysis.
To check the model fit adequacy (measure of “lack-of-fit”), we performed within-sample prediction that compared the observed composition (i.e., 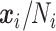 ) with the posterior predictive mean. The scatter plot of predicted versus observed relative abundance of taxa is given in Figure S.2(a) of the Supplementary material available at Biostatistics online showing that the within-sample prediction was accurate. The correlation between two matrices was 0.94, which indicated an adequate model fit.
) with the posterior predictive mean. The scatter plot of predicted versus observed relative abundance of taxa is given in Figure S.2(a) of the Supplementary material available at Biostatistics online showing that the within-sample prediction was accurate. The correlation between two matrices was 0.94, which indicated an adequate model fit.
Figure S.2(b) of the Supplementary material available at Biostatistics online shows the posterior distribution of the number  of clusters. The posterior mode occurred at
of clusters. The posterior mode occurred at 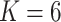 . Conditional on
. Conditional on 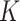 , the posterior estimates of
, the posterior estimates of 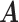 and
and 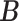 are shown in Figure 2. In Figure 2a, black cells are 0, green cells are 1 for controls, and red cells are 1 for patients. Samples that did not belong to any clusters are omitted in the figures.
are shown in Figure 2. In Figure 2a, black cells are 0, green cells are 1 for controls, and red cells are 1 for patients. Samples that did not belong to any clusters are omitted in the figures.
Cluster 1 contained predominantly IBD patients (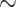 70%). The biclustering nature of the proposed MMF allowed us to investigate the corresponding subset of taxa that were related to these IBD patients. For example, the cluster 1 contains family Enterobacteriaceae, part of class Gammaproteobacteria, which have been reported to increase in relative abundance in patient with IBD (Lupp and others, 2007). The fact that it exclusively belonged to patient-dominated cluster 1 is consistent with its biological relevance to IBD. Moreover, genus Fusobacterium, a member of the family Fusobacteriaceae, have been found to be at a higher abundance in patients with ulcerative colitis (UC, a subtype of IBD) relative to control subjects (Ohkusa and others, 2002). Fusobacteriaceae family was also contained in cluster 1 only, which again signified the importance of this family with relevance to IBD. Generally, phyla Proteobacteria and Actinobacteria are expected to increase in IBD patients (Matsuoka and Kanai, 2015), which is consistent with our result in cluster 1. Apart from the findings that were confirmed by the existing literature, cluster 1 includes some families in phylum Firmicutes, which are known to play major anti-inflammatory roles and therefore their abundances are expected to decrease in IBD patients. Further biological investigation is required to validate this new finding.
70%). The biclustering nature of the proposed MMF allowed us to investigate the corresponding subset of taxa that were related to these IBD patients. For example, the cluster 1 contains family Enterobacteriaceae, part of class Gammaproteobacteria, which have been reported to increase in relative abundance in patient with IBD (Lupp and others, 2007). The fact that it exclusively belonged to patient-dominated cluster 1 is consistent with its biological relevance to IBD. Moreover, genus Fusobacterium, a member of the family Fusobacteriaceae, have been found to be at a higher abundance in patients with ulcerative colitis (UC, a subtype of IBD) relative to control subjects (Ohkusa and others, 2002). Fusobacteriaceae family was also contained in cluster 1 only, which again signified the importance of this family with relevance to IBD. Generally, phyla Proteobacteria and Actinobacteria are expected to increase in IBD patients (Matsuoka and Kanai, 2015), which is consistent with our result in cluster 1. Apart from the findings that were confirmed by the existing literature, cluster 1 includes some families in phylum Firmicutes, which are known to play major anti-inflammatory roles and therefore their abundances are expected to decrease in IBD patients. Further biological investigation is required to validate this new finding.
Likewise, most hosts in cluster 6 were IBD patients as well. This cluster shared quite a few taxa with cluster 1, which was not surprising as they both contained predominantly IBD patients. However, they also had distinct taxa that are biologically meaningful. On the one hand, cluster 6 uniquely contained the family Pasteurellaceae, of which the abundances tend to increase in patients with Crohn’s disease (CD, Gevers and others, 2014), another subtype of IBD. This suggested the possibility of these patients belonging to the CD subtype. On the other hand, cluster 1, as discussed earlier, uniquely contained the family Fusobacteriaceae, which suggested the possibility of these patients belonging to the UC subtype (Ohkusa and others, 2002).
Cluster 2 was dominated by control samples (healthy hosts). It was associated with families Bifidobacteriaceae and Ruminococcaceae. Their members, genera Bifidobacterium and Faecalibacterium, have been shown to be protective of the host from inflammation via several mechanisms (Sokol and others, 2008), including the stimulation of the anti-inflammatory cytokine and down-regulation of inflammatory cytokines. A reduced abundance of genus Odoribacter, which belongs to family Porphyromonadaceae, has been discovered in the most severe form of UC called pancolitis (Morgan and others, 2012). It also contained families in class Betaproteobacteria, whose relationship with IBD is yet to be established.
Clusters 3, 4, and 5 had a mix of patients and controls. They contained families Bacteroidaceae and Lachnospiraceae. Their members, genera Bacteroides and Roseburia, have been shown to decrease in IBD patients (Machiels and others, 2014; Zhou and Zhi, 2016).
We have reported results that were confirmed by the biological literature. Our biclustering results also provided novel insights into the relationships between microbial abundances and IBD, which need to be further verified by biological experiments. Our discoveries were potentially useful as a guidance to design and conduct more targeted and focused experiments.
For comparison, we applied MMF without the tree information (i.e., using the ordinary IBP prior) to this dataset. The result is shown in Figure S.3 of the Supplementary material available at Biostatistics online. It identified four clusters, and most clusters were dominated by control samples. Without tree information, we failed to identify the cluster associated with IBD patients and two IBD-related bacteria families Enterobacteriaceae and Fusobacteriaceae, which were successfully discovered when prior knowledge regarding the taxonomic ranks were incorporated in the analysis. Additionally, taxa from the same cluster were much less similar taxonomically: the log probability of generating this matrix from the taxonomic tree was  119.95, whereas the log probability of generating the matrix inferred from the pIBP was
119.95, whereas the log probability of generating the matrix inferred from the pIBP was  91.48, which indicated that the results from the pIBP prior were substantially more consistent with the taxo- nomic rank tree. Without using the tree information, the lack of taxonomic similarity within the identified clusters made it hard to interpret the results biologically. Although pIBP imposed structures on taxa only, the interpretation of the clusters of hosts was significantly enhanced as we have demonstrated earlier.
91.48, which indicated that the results from the pIBP prior were substantially more consistent with the taxo- nomic rank tree. Without using the tree information, the lack of taxonomic similarity within the identified clusters made it hard to interpret the results biologically. Although pIBP imposed structures on taxa only, the interpretation of the clusters of hosts was significantly enhanced as we have demonstrated earlier.
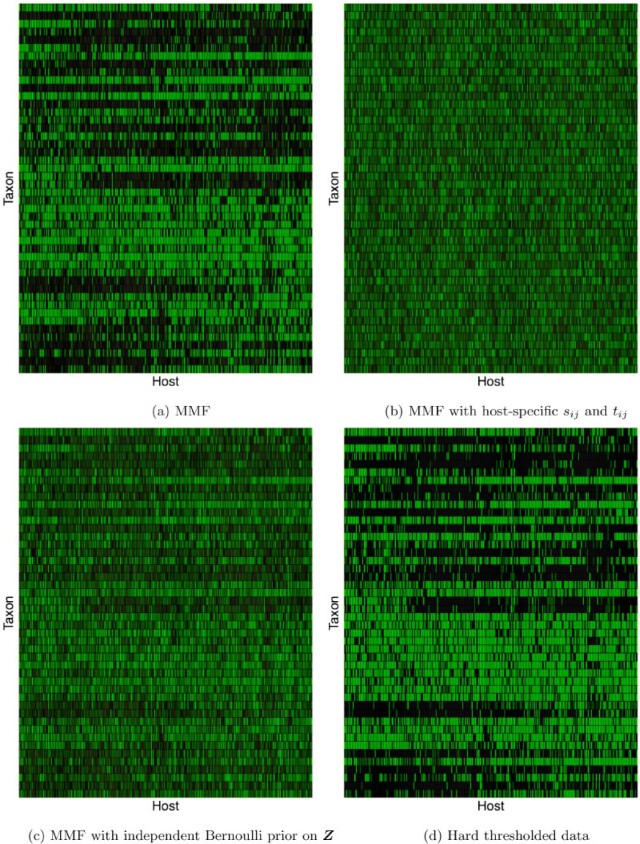
As suggested by an anonymous referee, in Figure 3, we report the posterior mean of 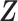 from (a) the proposed MMF, (b) modified MMF with host-specific
from (a) the proposed MMF, (b) modified MMF with host-specific 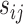 and
and 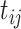 rather than
rather than 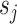 and
and 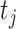 , and (c) modified MMF with independent Bernoulli prior on
, and (c) modified MMF with independent Bernoulli prior on 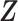 instead of pIBP. Additionally, as a reference, we also plot the thresholded data in Figure 3(d) by following the rule in Cai and others (2019). While there is no gold standard in unsupervised learning, we found that the posterior mean of
instead of pIBP. Additionally, as a reference, we also plot the thresholded data in Figure 3(d) by following the rule in Cai and others (2019). While there is no gold standard in unsupervised learning, we found that the posterior mean of 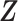 from the proposed MMF captures the latent abundance pattern better than (b) and (c) by comparing with the deterministic reference (d).
from the proposed MMF captures the latent abundance pattern better than (b) and (c) by comparing with the deterministic reference (d).
Fig. 3.
The posterior mean of the latent binary matrix 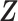 obtained from (a) MMF, (b) modified MMF with host-specific
obtained from (a) MMF, (b) modified MMF with host-specific 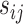 and
and 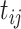 , and (c) modified MMF with independent Bernoulli prior on
, and (c) modified MMF with independent Bernoulli prior on 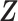 . The hard thresholded data are given in (d). Colors change from black to green indicating 0 to 1.
. The hard thresholded data are given in (d). Colors change from black to green indicating 0 to 1.
6. Discussion
In this article, we have developed a novel identifiable sparse MMF method to simultaneously cluster microbes and hosts. The proposed approach accounts for the compositional, sparse, heterogeneous, and noisy nature of microbiome data, and describes the data generating process by a hierarchical Bayesian model, which allows for probabilistic characterization of latent structures (i.e., overlapping clusters) through full posterior inference. The incorporation of taxonomic knowledge can facilitate the interpretability and reproducibility of the inferred clusters when the prior information resembles the truth. Our simulation results demonstrate the advantage of utilizing prior information to assist inference on latent clusters. In analyzing a human gut microbiome dataset, we find latent microbial communities that are closely related to IBD and its subtypes.
There are four directions that can be taken to extend this work. First, zero-inflation exists in other data types such as single-cell RNA-seq data. It is far less common to treat single-cell data as multinomial counts and therefore the proposed MMF cannot be directly applied. However, with a minor modification of the sampling distribution (e.g., zero-inflated Poisson distribution), the method can be generalized for biclustering single-cell data. Second, the joint modeling approach can be used for many other tasks beyond matrix factorization. For example, microbial networks can be inferred by replacing the matrix factorization model with a graphical model such as Markov random fields and Bayesian networks on the latent binary indicators  . Third, MCMC allows for full posterior inference but is not scalable to large and high-dimensional data. The current inference algorithm can be substantially accelerated by using consensus Monte Carlo algorithms for big-data clustering (Ni and others, 2019; Ni and others, 2020) without sacrificing much accuracy. Fourth, the overlapping clusters can be restricted to non-overlapping clusters if desired by considering random partition models including various extensions of the Dirichlet process (Lijoi and others, 2007; Favaro and Teh, 2013; De Blasi and others, 2015).
. Third, MCMC allows for full posterior inference but is not scalable to large and high-dimensional data. The current inference algorithm can be substantially accelerated by using consensus Monte Carlo algorithms for big-data clustering (Ni and others, 2019; Ni and others, 2020) without sacrificing much accuracy. Fourth, the overlapping clusters can be restricted to non-overlapping clusters if desired by considering random partition models including various extensions of the Dirichlet process (Lijoi and others, 2007; Favaro and Teh, 2013; De Blasi and others, 2015).
7. Software
R code, together with a complete documentation, is available on request from the first author (fangtingzhou@tamu.edu). The data that support the findings of this study are openly available in the R package curatedMetagenomicData which can be downloaded at https://github.com/waldronlab/curatedMetagenomicData/.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Fangting Zhou, Department of Statistics, Texas A&M University, College Station, TX, USA and Institute of Statistics and Big Data, Renmin University of China, Beijing, China.
Kejun He, Center for Applied Statistics, Institute of Statistics and Big Data, Renmin University of China, Beijing, China.
Qiwei Li, Department of Mathematical Sciences, The University of Texas at Dallas, Dallas, TX, USA.
Robert S Chapkin, Department of Nutrition and Food Science, Texas A&M University, College Station, TX, USA.
Yang Ni, Department of Statistics, Texas A&M University, College Station, TX, USA.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
National Natural Science Foundation of China (No. 11801560 to K.H.), in part; Texas AgriLife Research, the Sid Kyle Chair Endowment, the Allen Endowed Chair in Nutrition & Chronic Disease Prevention, the Cancer Prevention Research Institute of Texas (RP160589), and the National Institutes of Health (R01-ES025713, R01-CA202697, and R35-CA197707) to R.S.C., in part; The National Science Foundation (NSF DMS-1918851 to Y.N.).
References
- Benhadou, F., Mintoff, D., Schnebert, B. and Thio, H. B. (2018). Psoriasis and microbiota: a systematic review. Diseases 6, 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezdek, J. C., Ehrlich, R. and Full, W. (1984). FCM: the fuzzy c-means clustering algorithm. Computers & Geosciences 10, 191–203. [Google Scholar]
- Bhattacharya, A. and Dunson, D. B. (2011). Sparse Bayesian infinite factor models. Biometrika 98, 291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop, C. (2006). Pattern Recognition and Machine Learning. Springer-Verlag, New York. [Google Scholar]
- Buccianti, A. (2013). Is compositional data analysis a way to see beyond the illusion? Computers & Geosciences 50, 165–173. [Google Scholar]
- Cai, T., Li, H., Ma, J. and Xia, Y. (2019). Differential Markov random field analysis with an application to detecting differential microbial community networks. Biometrika 106, 401–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai, Y., Gu, H. and Kenney, T. (2017). Learning microbial community structures with supervised and unsupervised non-negative matrix factorization. Microbiome 5, 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao, Y., Lin, W. and Li, H. (2019a). Large covariance estimation for compositional data via composition-adjusted thresholding. Journal of the American Statistical Association 114, 759–772. [Google Scholar]
- Cao, Y., Zhang, A. and Li, H. (2019b). Multisample estimation of bacterial composition matrices in metagenomics data. Biometrika 107, 75–92. [Google Scholar]
- Castaner, O., Goday, A., Park, Y.-M., Lee, S.-H., Magkos, F., Shiow, S.-A. T. E., and Schröder, H. (2018). The gut microbiome profile in obesity: a systematic review. International Journal of Endocrinology 2018, 4095789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, E. Z. and Li, H. (2016). A two-part mixed-effects model for analyzing longitudinal microbiome compositional data. Bioinformatics 32, 2611–2617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, J. and Li, H. (2013). Variable selection for sparse Dirichlet-multinomial regression with an application to microbiome data analysis. Annals of Applied Statistics 7, 418–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, M., Gao, C. and Zhao, H. (2016). Posterior contraction rates of the phylogenetic Indian buffet processes. Bayesian Analysis 11, 477–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Blasi, P., Stefano, F., Antonio, L., Mena, R. H., Prünster, I. and Ruggiero, M. (2015). Are Gibbs-type priors the most natural generalization of the Dirichlet process? IEEE Transactions on Pattern Analysis and Machine Intelligence 37, 212–229. [DOI] [PubMed] [Google Scholar]
- Favaro, S. and Teh, Y. W. (2013). MCMC for normalized random measure mixture models. Statistical Science 28, 335–359. [Google Scholar]
- Fettweis, J. M., Serrano, M. G.Brooks, J. P., Edwards, D. J., Girerd, P. H., Parikh, H. I., Huang, B., Arodz, T. J., Edupuganti, L., Glascock, A. L., and others. (2019). The vaginal microbiome and preterm birth. Nature Medicine 25, 1012–1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franzosa, E. A., Sirota-Madi, A.Alexandra, A.-P., Julian, F., Nadine, H., Henry J., Reinker, S., Vatanen, T., Hall, A. B., Mallick, H., and others. (2019). Gut microbiome structure and metabolic activity in inflammatory bowel disease. Nature Microbiology 4, 293–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman, J. and Alm, E. J. (2012). Inferring correlation networks from genomic survey data. PLoS Computational Biology 8, e1002687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A. and Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science 7, 457–472. [Google Scholar]
- Gevers, D., Kugathasan, S.Denson, L. A., V‘azquez-Baeza, Y., Van T. W., Ren., B., Schwager, E., Knights, D., Song, S. J., Yassour, M., and others. (2014). The treatment-naive microbiome in new-onset Crohn’s disease. Cell Host & Microbe 15, 382–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gloor, G. B., Macklaim, J. M.Pawlowsky-Glahn, V. and Egozcue, J. J. (2017). Microbiome datasets are compositional: and this is not optional. Frontiers in Microbiology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopalan, P., Ruiz, F. J. R., Ranganath, R. and Blei, D. M. (2014). Bayesian nonparametric Poisson factorization for recommendation systems. In: Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, Vol. 33. pp. 275–283. [Google Scholar]
- Grantham, N. S., Guan, Y., Reich, B. J., Borer, E. T. and Gross, K. (2020). Mimix: a Bayesian mixed-effects model for microbiome data from designed experiments. Journal of the American Statistical Association 115, 599–609. [Google Scholar]
- Griffiths, T. L. and Ghahramani, Z. (2005). Infinite latent feature models and the Indian buffet process. In: Proceedings of the 18th International Conference on Neural Information Processing Systems. MIT Press. pp. 475–482. [Google Scholar]
- Hoyer, P. O. (2004). Non-negative matrix factorization with sparseness constraints. Journal of Machine Learning Research 5, 1457–1469. [Google Scholar]
- Koren, O., Knights, D., Gonzalez, A., Waldron, L., Segata, N., Knight, R., Huttenhower, C. and Ley, R. E. (2013). A guide to enterotypes across the human body: meta-analysis of microbial community structures in human microbiome datasets. PLoS Computational Biology 9, e1002863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahti, L., Salojärvi, J., Salonen, A., Scheffer, M. and De Vos, W. M. (2014). Tipping elements in the human intestinal ecosystem. Nature Communications 5, 4344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, D. D. and Seung, H. S. (2000). Algorithms for non-negative matrix factorization. In: Algorithms for Non-negative Matrix Factorization. MIT Press. pp. 535–541. [Google Scholar]
- Lijoi, A., Mena, R. H. and Prünster, I. (2007). Controlling the reinforcement in Bayesian non-parametric mixture models. Journal of the Royal Statistical Society: Series B 69, 715–740. [Google Scholar]
- Lin, W., Shi, P., Feng, R. and Li, H. (2014). Variable selection in regression with compositional covariates. Biometrika 101, 785–797. [Google Scholar]
- Liu, L., Shih, Y.-C. T., Strawderman, R. L., Zhang, D., Johnson, B. A. and Chai, H. (2019). Statistical analysis of zero-inflated nonnegative continuous data: a review. Statistical Science 34, 253–279. [Google Scholar]
- Lloyd-Price, J., Arze, C.Ananthakrishnan, A. N., Schirmer, M., Avila-Pacheco, J., Poon, T. W., Andrews, E., Ajami, N. J., Bonham, K. S., Brislawn, C. J., (2019). Multi-omics of the gut microbial ecosystem in inflammatory bowel diseases. Nature 569, 655–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lupp, C., Robertson M. L.Wickham, M. E, Sekirov, I., Champion, O. L, Gaynor, E. C. and Finlay, B B. (2007). Host-mediated inflammation disrupts the intestinal microbiota and promotes the overgrowth of enterobacteriaceae. Cell Host & Microbe 2, 119–129. [DOI] [PubMed] [Google Scholar]
- Machiels, K., Joossens, M.. and others. (2014). A decrease of the butyrate-producing species Roseburia hominis and Faecalibacterium prausnitzii defines dysbiosis in patients with ulcerative colitis. Gut 63, 1275–1283. [DOI] [PubMed] [Google Scholar]
- Matsuoka, K. and Kanai, T. (2015). The gut microbiota and inflammatory bowel disease. In: Seminars in Immunopathology, Vol. 37. pp. 47–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meeds, E., Ghahramani, Z., Neal, R. M. and Roweis, S. T. (2007). Modeling dyadic data with binary latent factors. In: Proceedings of the 19th International Conference on Neural Information Processing Systems. MIT Press. pp. 977–984. [Google Scholar]
- Miller, K. T., Griffiths, T. L. and Jordan, M. I. (2008). The phylogenetic Indian buffet process: a non-exchangeable nonparametric prior for latent features. In: Proceedings of the 24th Conference on Uncertainty in Artificial Intelligence. UAI’08. Arlington, Virginia, USA: AUAI Press. pp. 403–410. [Google Scholar]
- Morgan, X. C., Tickle, T. L, and others. (2012). Dysfunction of the intestinal microbiome in inflammatory bowel disease and treatment. Genome Biology 13, R79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni, Y., Ji, Y. and Müller, P. (2020). Consensus monte carlo for random subsets using shared anchors. Journal of Computational and Graphical Statistics, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni, Y., Müller, P., Diesendruck, M., Williamson, S., Zhu, Y. and Ji, Y. (2019a). Scalable Bayesian nonparametric clustering and classification. Journal of Computational and Graphical Statistics 29, 53–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni, Y., Müller, P. and Ji, Y. (2019b). Bayesian double feature allocation for phenotyping with electronic health records. Journal of the American Statistical Association, 115, 1620–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohkusa, T., Sato, N.Ogihara, T., Morita, K., Ogawa, M. and Okayasu, I. (2002). Fusobacterium varium localized in the colonic mucosa of patients with ulcerative colitis stimulates species-specific antibody. Journal of Gastroenterology and Hepatology 17, 849–853. [DOI] [PubMed] [Google Scholar]
- Parmigiani, G., Garrett, E. S., Anbazhagan, R. and Gabrielson, E. (2002). A statistical framework for expression-based molecular classification in cancer. Journal of the Royal Statistical Society: Series B 64, 717–736. [Google Scholar]
- Qin, J., Li, R.Raes, J., Arumugam, M., Burgdorf, K. S., Manichanh, C., Nielsen, T., Pons, N., Levenez, F., Yamada, T., and others. (2010). A human gut microbial gene catalogue established by metagenomic sequencing. Nature 464, 59–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren, B., Bacallado, S., Favaro, S., Holmes, S. and Trippa, L. (2017). Bayesian nonparametric ordination for the analysis of microbial communities. Journal of the American Statistical Association 112, 1430–1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ročková, V. and George, E. I. (2016). Fast Bayesian factor analysis via automatic rotations to sparsity. Journal of the American Statistical Association 111, 1608–1622. [Google Scholar]
- Shafiei, M., Dunn, K. A., Boon, E., MacDonald, S. M., Walsh, D. A., Gu, H. and Bielawski, J. P. (2015). Biomico: a supervised Bayesian model for inference of microbial community structure. Microbiome 3, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi, P., Zhang, A. and Li, H. (2016). Regression analysis for microbiome compositional data. The Annals of Applied Statistics 10, 1019–1040. [Google Scholar]
- Sokol, H.Pigneur, B., Watterlot, L., Lakhdari, O., Bermúdez-Humarán, L. G., Gratadoux, J.-J., Blugeon, S., Bridonneau, C., Furet, J.-P., Gérard, G., and others. (2008). Faecalibacterium prausnitzii is an anti-inflammatory commensal bacterium identified by gut microbiota analysis of Crohn disease patients. Proceedings of the National Academy of Sciences Unites States of America 105, 16731–16736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilg, H. and Moschen, A. R. (2014). Microbiota and diabetes: an evolving relationship. Gut 63, 1513–1521. [DOI] [PubMed] [Google Scholar]
- Turnbaugh, P. J., Ley, R. E.Hamady, M., Fraser-Liggett, C. M., Knight, R. and Gordon, J. I. (2007). The human microbiome project. Nature 449, 804–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wadsworth, W. D., Argiento, R., Guindani, M., Galloway-Pena, J., Shelburne, S. A. and Vannucci, M. (2017). An integrative Bayesian dirichlet-multinomial regression model for the analysis of taxonomic abundances in microbiome data. BMC Bioinformatics 18, 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts, S. C., Ritchie, S. C., Inouye, M. and Holt, K. E. (2018). FastSpar: rapid and scalable correlation estimation for compositional data. Bioinformatics 35, 1064–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood, F., Griffiths, T. L. and Ghahramani, Z. (2006). A non-parametric Bayesian method for inferring hidden causes. In: Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence. UAI’06. Arlington, Virginia, USA: AUAI Press. pp. 536–543. [Google Scholar]
- Wu, Z., Casciola-Rosen, L., Rosen, A. and Zeger, S. L. (2019). A Bayesian approach to restricted latent class models for scientifically-structured clustering of multivariate binary outcomes. Biometrics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia, F., Chen, J., Fung, W. K. and Li, H. (2013). A logistic normal multinomial regression model for microbiome compositional data analysis. Biometrics 69, 1053–1063. [DOI] [PubMed] [Google Scholar]
- Xu, T., Demmer, R. T. and Li, G. (2020). Zero-inflated poisson factor model with application to microbiome read counts. Biometrics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, M., Hannah, L., Dunson, D. and Carin, L. (2012). Beta-negative binomial process and Poisson factor analysis. In: Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics. pp. 1462–1471. [Google Scholar]
- Zhou, Y. and Zhi, F. (2016). Lower level of bacteroides in the gut microbiota is associated with inflammatory bowel disease: a meta-analysis. BioMed Research International. 2016, 5828959. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.