Abstract
Clinical research often focuses on complex traits in which many variables play a role in mechanisms driving, or curing, diseases. Clinical prediction is hard when data is high‐dimensional, but additional information, like domain knowledge and previously published studies, may be helpful to improve predictions. Such complementary data, or co‐data, provide information on the covariates, such as genomic location or P‐values from external studies. We use multiple and various co‐data to define possibly overlapping or hierarchically structured groups of covariates. These are then used to estimate adaptive multi‐group ridge penalties for generalized linear and Cox models. Available group adaptive methods primarily target for settings with few groups, and therefore likely overfit for non‐informative, correlated or many groups, and do not account for known structure on group level. To handle these issues, our method combines empirical Bayes estimation of the hyperparameters with an extra level of flexible shrinkage. This renders a uniquely flexible framework as any type of shrinkage can be used on the group level. We describe various types of co‐data and propose suitable forms of hypershrinkage. The method is very versatile, as it allows for integration and weighting of multiple co‐data sets, inclusion of unpenalized covariates and posterior variable selection. For three cancer genomics applications we demonstrate improvements compared to other models in terms of performance, variable selection stability and validation.
Keywords: clinical prediction, empirical Bayes, omics, penalized generalized linear models, prior information
1. INTRODUCTION
High‐dimensional data is increasingly common in clinical research in the form of omics data, for example, data on gene expressions, methylation levels and copy number alterations. Omics are used in clinical applications to predict various outcomes, in particular binary and survival, possibly using clinical covariates like age and gender in addition to omics in the predictor. Examples in cancer genomics include diagnosis of cancer, predicting therapy response and time to recurrence of a tumor.
Unfortunately, many clinical omics studies are hampered by small sample size (eg, ), either due to budget or practical constraints. In addition to the main data, however, auxiliary information on the covariates usually exists, in the form of domain knowledge and/or results from external studies. In cancer genomics, acquired domain knowledge is made available in published disease related signatures and online encyclopedia containing gene ontology or pathway information. External, similar studies are available in repositories like The Cancer Genome Atlas (TCGA), 1 from which summary statistics like P‐values can be derived. In general we use the term co‐data, for complementary data , to refer to any data that complements the main data by providing information on the covariates. Figure 1 depicts some examples. Moreover, Section 5 details an example on treatment benefit prediction for colorectal cancer with microRNA data, using various sources of co‐data.
FIGURE 1.

Examples of different types of co‐data in cancer genomics. (A) Chromosomes: non‐overlapping groups of genes on the same chromosome. (B) Pathways: overlapping groups of interacting genes or molecules. (C) Gene ontology: groups structured in a directed acyclic graph (DAG) representing relationships in for example biological function. (D) P‐values: continuous P‐values derived from an external study
One would like to build upon all relevant existing knowledge when learning predictors and selecting covariates for the main data, thus learn from multiple and various co‐data sets. Co‐data vary in relevance and type of data. How much, if anything at all, can be learnt from co‐data depends on the application and data at hand, and is in general unknown. The type of co‐data may be continuous or discrete, for example, external P‐values or group membership, possibly further constrained or structured, for example, hierarchical groups.
Various methods have been developed which focus on predicting a specific type of response combined with one source of co‐data. 2 , 3 Extending these methods to different types of response or co‐data is not always straightforward, as approximation or optimization algorithms often do not generalize trivially. Typically, co‐data or, more general, prior information is included in statistical prediction models by letting it guide the choice for a specific penalty (or prior) that penalizes (or shrinks) model parameters. As this choice highly affects the model fit in high‐dimensional data, the ability of the fitted prediction model to generalize well to new samples heavily relies on a carefully tuned penalty or prior. Penalties for group lasso 4 and for latent overlapping group lasso 5 penalize covariates in groups to favor group sparse solutions, selecting groups of covariates. While being able to use these group penalties to incorporate additional structure on the group level such as grouped trees 6 and hierarchical groups, 7 only one overall hyperparameter is used to tune the penalty. This makes the penalty unable to adapt locally to the main data when part of the groups or structure is non‐informative for, or in disagreement with the main data, leading to sub‐optimally performing prediction models.
Recent work has focused on group adaptive penalties, 8 , 9 , 10 in which groups of covariates share the same prior or penalty parameterized by a group‐specific hyperparameter. The hyperparameters are learnt from the data, effectively learning how informative the co‐data is and how important each covariate group is for the prediction problem at hand. Whereas these penalties or priors are able to adapt locally on the group level, these methods do not allow for including any structure on the groups. Moreover, the methods tend to overfit in the number of hyperparameters for an increasing number of groups.
Here we present a method for ridge penalized generalized linear models that is the first to combine adaptivity on the group level with the ability to handle multiple and various types of co‐data. While the main data still drives the regression parameter estimation, the co‐data can impact the penalties which act as inverse weights in the regression. By adequately learning penalties from valuable co‐data, prediction and covariate selection for omics improve. The method is termed ecpc, for empirical Bayes Co‐data learnt Prediction and Covariate selection. A moment‐based empirical Bayes approach is used to estimate the adaptive group ridge penalties efficiently, opening up the possibility to introduce an extra layer of shrinkage on the group level. Any type of shrinkage can be used in this layer, rendering a unique, flexible framework to improve predictions because:
much as a penalty on the covariate level shrinks regression coefficients towards 0 to counter overfitting and improve parameter estimates, a penalty on the group level shrinks adaptive group penalties to an ordinary, non‐adaptive ridge penalty. Therefore, the method is able to learn how informative co‐data is, ranging from no shrinkage for informative, stable co‐data, to full shrinkage for non‐informative co‐data;
instead of including group structure on the covariate level, a structured penalty is included on the group level directly. The method utilizes this facet to incorporate known structure of overlapping groups, to handle hierarchically structured groups and to handle continuous co‐data by using a data‐driven adaptive discretization.
Multiple co‐data are handled by first combining each co‐data set with a penalty suitable for that specific co‐data source, then integrating various co‐data by learning co‐data weights with the same moment‐based empirical Bayes approach. Interpretation of the estimated hyperparameters yields extra information on importance of groups of covariates and co‐data sources. Lastly, the framework allows for unpenalized covariates and posterior variable selection. Our approach to use a dense model (ridge regression) plus posterior selection is motivated by a 2‐fold argument: i) biology: for complex traits such as cancer most of the genome is likely to have an effect; 11 ii) statistics: even in sparse settings dense modeling plus posterior selection can be rather competitive to sparse modeling, 12 while better facilitating to shift on the grey‐scale from sparse to dense. For an overview of functionality we refer to Table 1, which highlights the versatility of our method as contrasted with other group (adaptive) methods.
TABLE 1.
Overview of properties of co‐data learnt methods compared in Section 5: group lasso obtains group sparsity by penalizing the regression coefficients with a group lasso penalty governed by one global penalty parameter; GRridge uses empirical Bayes moment estimation to obtain group‐adaptive ridge penalties; graper employs a full Bayes model with group‐specific spike‐and‐slab priors; gren uses an empirical‐variational Bayes approach for group‐adaptive elastic net penalties; ecpc combines empirical Bayes moment estimation for group‐adaptive ridge penalties with shrinkage on the group level to account for various co‐data
| Method | ||||||
|---|---|---|---|---|---|---|
| Property | group lasso 4 , 5 , 7 | GRridge 8 | graper 9 | gren 10 | ecpc | |
| Group‐adaptive | ‐ | v | v | v | v | |
| Type of covariate model: | Dense | ‐ | v | v | v | v |
| Group‐sparse | v | ‐ | ‐ | ‐ | v | |
| Sparse | v/‐ | v/‐ | v | v | v/‐ | |
| Type of co‐data: | Non‐overlapping groups | v | v | v | v | v |
| Overlapping groups | v | v | ‐ | ‐ | v | |
| Hierarchical groups | v | ‐ | ‐ | ‐ | v | |
| Multiple co‐data sources | ‐ | v | ‐ | v | v | |
| Hyperparameter shrinkage (many groups) | ‐ | ‐ | v/‐ | ‐ | v | |
| Type of response model: | Linear | v | v | v | ‐ | v |
| Binary | v | v | v | v | v | |
| Survival | v | v | ‐ | ‐ | v | |
The article is outlined as follows. Section 2 elaborates on generic types of co‐data. Section 3 then presents the model and methods to estimate the model parameters. Here, we present the penalized estimator for adaptive group penalties using an extra layer of any type of shrinkage, which forms the basis for handling various types of co‐data. Several model extensions are presented in Section 3.4. Section 4 summarizes a simulation study that illustrates how the extra layer of shrinkage enables the method to learn to shrink group weights when needed. Section 5 then demonstrates the method on three cancer genomics applications using multiple co‐data, showing that ecpc improves or matches benchmark methods in terms of predictive performance, variable selection stability and validation. Finally, Section 6 concludes and discusses the method.
2. CO‐DATA
Co‐data complements the main data from which the predictor has to be learnt. Whereas the main data contain information about the samples, the co‐data contain information about the covariates. Co‐data can be retrieved from external sources, for example, from public repositories, or derived from the main data, as long as the response is not used. To exemplify different types of co‐data, we show some prototypical examples in Figure 1. Here we describe the generic structures of co‐data underlying the examples.
Non‐overlapping groups of covariates: the covariates are grouped in non‐overlapping groups. An example in cancer genomics is groups of genes located on the same chromosome.
Overlapping groups: the covariate groups are overlapping, for example, groups representing pathways, that is, for some biological process all genes involved are grouped. As genes often play a role in multiple processes, the resulting groups are overlapping.
Structured groups: relations between groups are represented in a graph. Gene ontology, for example, represents groups of genes in a directed acyclic graph. Each node in the graph represents a biological function corresponding to a group of genes that (partly) fulfill that function. Nodes at the top of the hierarchy represent general biological functions and are refined downwards in the graph. Each node represents a subset of genes of its parent nodes.
Continuous co‐data: as opposed to the discrete groups in the previous examples, the co‐data are continuous. Examples are P‐values derived from a previously published, similar study, and standard deviations of each covariate computed from the data.
3. METHOD
3.1. Notation
We denote the response vector by and the observed high‐dimensional data matrix by , . We use D different co‐data sources to define groups of covariates. The collection of all groups of the dth co‐data source is called a group set, for example, one group set for all pathways and one for all chromosomes. We denote a group set d by , containing groups. We denote a group g in group set d by , containing covariates. Figure 2 illustrates the notation of groups and group sets. Each covariate belongs to at least one group in each group set. Covariates with missing co‐data should preferably be grouped in a separate group as the missingness might be informative. The groups can possibly be overlapping or structured as in a hierarchical tree, illustrated in Figure 3.
FIGURE 2.
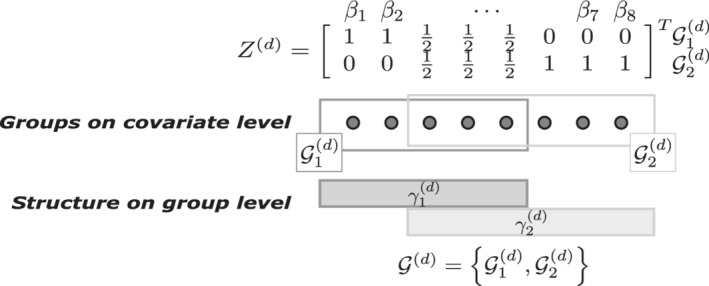
Illustration of notations and definitions. Balls represent covariates, rectangles groups of covariates. Group set consists of overlapping groups, and , of sizes and . The group set defines the co‐data matrix . Each group corresponds to a weight on the group level
FIGURE 3.
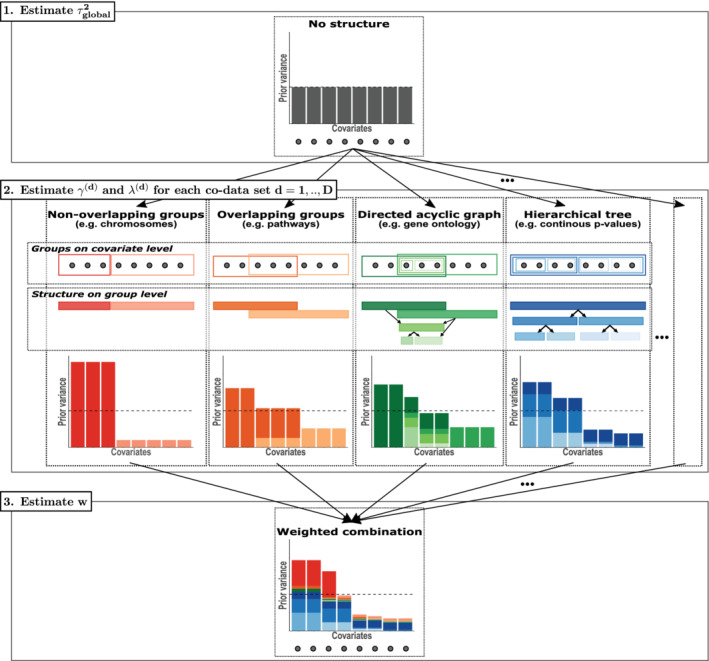
Schematical overview of estimating the hyperparameters. Step 1: the global prior variance is estimated. Step 2: group weights and hyperpenalties , are estimated for each co‐data set separately using appropriate shrinkage. Step 3: group set weights are estimated to combine the co‐data sets. The estimated hyperparameters are used to estimate the regression coefficients as given in Equation 3 [Colour figure can be viewed at wileyonlinelibrary.com]
Next, we define D design matrices to represent group membership information of the co‐data group sets. Suppose that covariate k is a group member of groups in group set d, with the set of indices of the groups in group set d containing k. We define the design matrix, or co‐data matrix, , as follows, illustrated in Figure 2:
Definition 1
The co‐data matrix corresponding to group set d is the design matrix with element for the kth covariate and gth group given by:
(1) Effectively, will be used to pool the information from the groups in group set d that covariate k belongs to.
3.2. Model
We regress on X using a generalized linear model (GLM) with regression coefficient vector . We impose a normal prior on with a global prior variance and local prior variance . The local prior variances are regressed on the co‐data , , with each of the D group weight vectors modeling the relative importance of the groups in group set d, and the group set weight the relative importance of group set d. The model is then as follows:
| (2) |
with some exponential family distribution with corresponding link function , denoting the ith row of X, and denoting the expectation with respect to the probability density/mass function , where we leave out dependence on since we consider X as fixed. Note that when some groups are overlapping and say belongs to different groups, we average the group weights.
We adopt the Bayesian formulation in Equation 2 to estimate the prior parameters with an empirical Bayes approach explained in Section 3.3. We may interpret the empirical Bayes estimates to link , and to the a priori expected effect size globally, in groups and in group sets respectively. Details are included in Section A9 in the Supporting Information. For the final predictor, we make use of the equivalence between the maximum a posteriori estimate for , , and the penalized maximum likelihood estimate (MLE), and predict the response for new samples in a frequentist manner: .
The prior is similar to the prior used in the method GRridge, 8 but has additional group set weights, such that multiple group sets (called partitions in GRridge 8 ) can be evaluated simultaneously instead of iteratively. Moreover, whereas GRridge tends to overfit for many co‐data groups, we introduce an extra level of shrinkage on the prior parameter level to counter this. This extra level has a substantial practical impact as it opens up the possibility of using the wealth of existing shrinkage literature to handle various types of co‐data to improve predictions, as explained in Section 3.3.1.
3.3. Estimation
The unknown model parameters are the regression coefficients and the prior parameters, also called hyperparameters, , where the local variances are omitted as those relate directly to and via Equation 2. We use an empirical Bayes approach: 13 estimate the hyperparameters and plug those in the prior to find the penalized maximum likelihood estimate for :
| (3) |
Note that this is just ordinary ridge regression with a weighted penalty, which can easily be solved with existing software, for example, with the R‐package glmnet. Hence, the main task is to estimate the hyperparameters. We do so in a hierarchical fashion in three steps, illustrated in Figure 3. These steps can be summarized as follows, details given below:
Overall level of regularization : for linear regression, we maximize the marginal likelihood directly as it is analytical, setting all local variances to 1. For other types of regression (for now, logistic and Cox), we use the canonical approach of cross‐validation, which can be computed efficiently. 14
Group weights for each group set, , given : we use penalized moment‐based estimates based on an initial, ordinary ridge estimate using the ridge penalty related to . The regularization of the moment‐based estimating equations accounts for structure in the groups and overfitting when the number of groups approaches or exceeds the number of samples. Various penalty functions can be used for various types of co‐data. The penalty functions are parameterized by hyperpenalties , which are estimated in a data‐driven way using splits of the groups.
Group set weights , given and : we use moment‐based estimates for the group set weights.
3.3.1. Group weights for each group set,
We use the empirical Bayes method of moments (MoM) to estimate the group weights for each group set separately. 13 GRridge 8 implements the moment‐based estimates for the prior variance for linear and logistic regression. Here, we first repeat the main steps and provide details for the MoM estimating equations for linear, logistic and Cox regression in Section A in the Supporting Information. After, we explain the new, extra level of shrinkage, used to obtain stable local variance estimates. Below, we sometimes refer to the extra level of shrinkage as hypershrinkage, to clearly distinguish shrinking regression coefficients on the covariate level from shrinking hyperparameters on the group level. As a last note, throughout this article we assume a zero prior mean, as given in Equation 2. The MoM can easily be extended to include estimates for a prior mean , , in case should be shrunk to a non‐zero target . Details are given in Section A in the Supporting Information.
Let the estimate be given, estimated as explained above. The ordinary ridge MLE corresponding to this level of regularization, , is a function of the data Y. Consider one group set , . The MoM equates empirical moments to theoretical moments over all covariates in one group , where the theoretical moments are taken with respect to the marginal likelihood . Setting up the moment equation for all groups in the group set , we obtain the following equations:
| (4) |
| (5) |
| (6) |
with a function of the unknown parameters .
The theoretical moments on the right‐side of the equation above are analytic for linear regression and are approximated by using a second order Taylor approximation for the inner expectation in Equation 5 for logistic 15 and Cox regression, after which the outer expectation is analytic. The function h (or its approximation) in Equation 6 is linear in , that is, solving the moment estimating equations boils down to solving a linear system of equations and unknowns :
| (7) |
with and depending on the data X and initial estimate . Details are given in Section A.
In case of few, non‐overlapping groups of equal size, it suffices to solve the linear system directly, truncating negative group weight estimates, potentially resulting from approximation or numerical errors, to 0. However, often we have many groups, potentially unequal in size, or structured in another, potentially hierarchical, way, which demands penalization of the system. For example, Section 4 demonstrates how ridge hypershrinkage may be used to prevent overfitting in too many groups and how hierarchical lasso hypershrinkage may be used to select groups in a group set of hierarchical, overlapping groups. Hence we propose to replace the solution of Equation 7, which can be cast as a least squares minimization, by :
| (8) |
where denotes the element‐wise truncation of the elements of a vector at 0, and where , the estimate for the hyperpenalty parameter , is obtained as explained below. Note that solving Equation 8 corresponds to solving a penalized linear regression with penalty function . So for most well‐known penalties, such as ridge and lasso, software exists to obtain estimates for . Otherwise, a general purpose gradient‐based solver may be used, which suffices, because is generally not a very large dimensional vector.
The modular approach of decoupling group shrinkage from direct covariate shrinkage not only relieves the computational burden for , but also accommodates generalizing to any other group shrinkage scheme. As a default hyperpenalty, we propose to use a weighted ridge penalty with target 1 and weighted hyperpenalty parameter governing the amount of group shrinkage. The target of 1 embodies the prior assumption that the group set is not informative: all group weights are shrunk towards 1. Then, the weighted ridge prior on the covariate level is shrunk to an ordinary ridge prior. The hyperpenalty is weighted such that the local variances on the covariate level are a priori independent of the group sizes. Details are given in Section A5 in the Supporting Information. A ridge penalty on the covariate level is used to improve regression coefficient estimates when there are many, possibly correlated covariates. In a similar sense, the ridge penalty on the group level improves the group parameter estimates when there are many groups or overlapping and therefore correlated groups.
Instead of truncating the group weight estimates at 0, one could employ a penalty that has support on the positive real numbers only, such as the logarithm of the inverse gamma distribution, as it naturally models variance parameters. Use of an inverse gamma penalty leads, however, to inferior results in our applications. An intuitive explanation for this is, while models variance parameters on the covariate level, it does not enter the least squares error criterion in a similar fashion on the group level.
3.3.2. Hyperpenalties
We would like to find an estimate such that the penalized moment‐estimates are stable and follow any constraints imposed by known group structure. Instead of using a computationally intensive approach of cross‐validation (CV) on the samples, we use random splits of the covariate groups. This approach relates to previously used techniques, 16 in which moment equations are perturbed to retrieve estimates invariant for those perturbations.
The approach is as follows: split each group randomly in two parts, and . Use only all in‐parts in the MoM‐equations in Equation 4 to compute a linear system as in Equation 7, with matrix and vector depending on which covariates belong to the in‐part. Similarly, one retrieves a linear system for only out‐parts with corresponding matrix and vector denoted by and . Any stable estimate that adheres to the imposed group structure should fit both the linear systems corresponding to the in‐part and the out‐part well, as both parts belong to the same groups. Therefore we use the estimate for which the penalized estimate of the in‐part best fits the linear system of the out‐part, averaged over multiple random splits , that is, the estimate minimizes the following mean residual sum of squares (RSS):
| (9) |
Using cross‐validation on the samples would require solving the regression for from Equation 3, setting up the linear system from Equation 7 and solving the penalized regression for from Equation 8, for each fold. Using splits of the groups only requires the latter two, now not for each fold but for each split. The computational cost associated with splitting groups is therefore far lower than that associated with cross‐validating samples, as p is generally of a much larger order of magnitude than .
3.3.3. Group set weights
After estimating all group weights , for each group set separately, we combine the group sets in a linear combination with group set weights . Similarly as for , a linear system is derived by setting up moment equations as in Equation 4 for all groups. By plugging in the estimates and rearranging the equations, we obtain a linear system of equations and D unknowns. The group set weights estimate is then the ordinary least squares estimate truncated at 0. Details are given in Section A3 in the Supporting Information.
3.4. Model extensions
We strive for a uniquely generic approach that can handle a wide variety of primary data (covariates and response) and co‐data. The extensions below support this aim and are all accommodated by the ecpc software.
3.4.1. Continuous co‐data
In principle, one could model a covariate specific prior variance as a (parsimonious) function of continuous co‐data. However, such a function is likely non‐linear, and needs to be very flexible. We choose to approximate this function by adaptive discretization, resulting in a piece‐wise constant function. Adaptivity is necessary because the effect sizes are unknown, so for a continuous co‐data set it might not be clear how fine a discretization should be, if the discretization should be evenly spaced, and if not, where on the continuous scale the discretization should be finer.
The approach is as follows. First define hierarchical groups, representing varying grid sizes: i) define the first group as the group including all covariates, ordered according to the continuous co‐data. When the co‐data is not informative, using this group only would suffice. The group weight corresponding to the first group is defined to be the top node in the hierarchical tree; ii) recursively split each group g at the median co‐data value of group g into two groups of half the size. The group weights of these latter two groups are defined as child nodes of the parent node for group weight in the hierarchical tree, illustrated in Figure S1 in the Supporting Information. We obtain a tree in which each node corresponds to a group weight. So, denote the adaptive discretization by the set of nested intervals corresponding to group weights : . The proposed approach leads to for p‐quantile of the continuous co‐data. The hierarchy of the groups is summarized in the following group set on group level by the ancestor set: 7 , with . The prior weight of a covariate k with continuous co‐data value is then estimated by the following piecewise linear function:
The hierarchy is then used in a hierarchical lasso penalty using a latent overlapping group penalty, 5 , 7 which is used as extra level of shrinkage in Equation 8 to select hierarchical groups, illustrated in Figure S1:
| (10) |
The hierarchical lasso penalty can select a node only if all its parent nodes are selected. Applied here, each selection of nodes corresponds to a selection of hierarchical groups, hence discretization. For some hyperpenalty large enough, only the top node, corresponding to the group weight for the group of all covariates, is selected. For smaller values of , nodes lower in the hierarchy corresponding to large group weight estimates (ie, small penalties) are selected first. Use the estimate for given in Equation 9 to select group weights that correspond to a discretization that fits the data well.
Each selected group corresponds to one moment equation in (7), enabling small groups deep in the hierarchy to have much larger weights than others. These moment equations are endowed with a ridge penalty as in Equation 8 to stably estimate the final group weights.
3.4.2. Group selection
Group lasso and hierarchical lasso are popular methods to select groups of covariates on the covariate level, 5 , 7 possibly shrinking covariates according to some given hierarchy. An alternative for obtaining a group sparse model is to use the proposed method in combination with a (hierarchical) sparse penalty on the group level; by setting group weights to 0, all covariates in that group are set to 0. When the number of covariates is much larger than the number of groups, it can be beneficial in terms of computational cost to use the (hierarchical) sparse penalization on the group level. A similar two‐step approach as for continuous co‐data described above can be used; first, we select groups on the group level by using a hierarchical lasso penalty (Equation 10 for the hierarchy defined in some ancestor set ) or lasso penalty: . Second, a ridge penalty is used to estimate the group weights of the selected groups. The software accommodates both the hierarchical lasso penalty and lasso penalty as hypershrinkage.
3.4.3. Covariate selection for prediction
In the applications that we consider, covariates may be (highly) correlated and the outcome might be predicted correctly only by a large group of interacting and correlated covariates. For example in genetics, gene expression is often correlated as many genes interact via complex networks of pathways. Moreover, predicting complex diseases might not always be as easy as finding few genes with large effects, as complex diseases may be associated with a shift in the entire system, and therefore potentially explained only by many small effects. 11 Penalties leading to dense predictors or group sparse predictors are well‐known to handle correlated variables better than penalties leading to sparse predictors.
In practice, however, it might be desirable to find a well‐performing parsimonious predictor, for example, due to budget constraints for practical implementation of the predictor. Various approaches have been proposed for sparsifying predictors.
First, perform variable selection based on (marginal) penalized credible regions, which was shown to render consistent selection. 12 Second, a similar post‐hoc selection strategy using an additional L1 penalty as performed in GRridge 17 was shown to perform well in terms of prediction for a number of cancer genomics applications. 17 Third, decoupling shrinkage and selection 18 approximates the linear predictor by a sparsified version using adaptive lasso. For completeness, we provide technical details of these approaches in Section A7 in the Supporting Information, and have included these three options in the ecpc software.
After selecting covariates, the regression coefficients are re‐estimated using the weighted ridge prior to obtain the final predictor. Whether or not it is better to recalibrate the overall level of regularization depends on the, unknown, underlying sparsity. If the best possible model is dense, the weighted ridge prior found in the first step should be used to prevent overestimation of the regression coefficients. If the best possible model is in fact sparse, it would be better to recalibrate and set group weights to 1 to undo overshrinkage due to noise variables. We include both approaches as an option in the software, which may be compared by considering predictive performance.
3.4.4. Unpenalized covariates
Sometimes one wishes to include unpenalized covariates, for example clinical covariates like tumor size or age of a patient. It can be shown that, conveniently, the moment estimates for penalized groups are independent of the group parameters for the group of unpenalized covariates. Details are given in Section A8 in the Supporting Information. Then, in the model given in Equation 2, the Gaussian prior is only imposed on those covariates which are to be penalized.
4. SIMULATION STUDY
In Section 5, we apply the method, termed ecpc: Empirical Bayes Co‐data learnt Prediction and Covariate selection, to three cancer genomics applications and compare it with other methods. Here, the purpose of the simulations is to show the benefit of using an extra level of shrinkage on the group weights for estimation of the prior group variances and group set weights and for prediction of new samples. Details and results are given in Section B in the Supporting Information. Figure and table numbers in the Supporting Information are referred to with a prefix S, for example, Figure S1. First, we compare ecpc with and without ridge hypershrinkage to ordinary ridge in linear regression with informative or random co‐data consisting of non‐overlapping groups. The group prior variances estimated by ecpc cluster around the maximum prior estimates (Figure S2), that is, the values that maximize the prior distribution given the true, simulated regression coefficients. Figure S3 illustrates that for random co‐data, ecpc without hypershrinkage predicts worse than ordinary ridge, as it overfits the group weights of the random groups. With hypershrinkage, however, ecpc predicts as well as ordinary ridge, as the group weights are shrunk towards 1. For informative co‐data, ecpc with hypershrinkage shrinks little, thereby performing similarly to ecpc without hypershrinkage, and outperforming ordinary ridge as it benefits from the co‐data. Figure S4 shows that when the random and informative co‐data are combined, ecpc with hypershrinkage retrieves better group set weight estimates than ecpc without hypershrinkage. Second, we compare to the method graper, 9 which is based on a full Bayes model with vague hyperprior on the prior parameters. As the vague hyperprior is fixed and cannot be adapted to the data, graper performs similarly to ecpc without hypershrinkage and overfits for random co‐data (Figure S5). Lastly, we illustrate ecpc in a hierarchical co‐data setting. Figures S7 and S8 show the benefit of (hierarchical) hypershrinkage for informative co‐data in terms of estimation and prediction. This benefit disappears when co‐data is random, although the predictive performance is maintained with respect to ordinary ridge.
5. APPLICATION
We apply the ecpc method to three data applications in cancer genomics, for which we have multiple co‐data sources available. We are interested in the added value of flexibly learning from co‐data. Therefore we first discuss interpretation of the estimated hyperparameters (described in Section A9 in the Supporting Information). Second, we discuss prediction performance and covariate selection. We compare ecpc to widely used predictors as benchmarks, and with other methods that can handle multiple co‐data sources as this is what we have available for the applications. Below, we present the main results. Additional results are provided in Section C in the Supporting Information.
5.1. Predicting therapy response in colorectal cancer
We apply ecpc to microRNA (miRNA) expression data from a study on colorectal cancer. 19 The data contain measured miRNA expression levels for independent individuals, for whom we would like to predict whether a specific therapy 19 will have clinical benefit (coded 1) or not (progressed disease, coded 0). In a previous study, 20 tissue was collected from primary and metastatic tumors plus adjacent normal tissue from a different set of non‐overlapping samples. The miRNA expression levels were measured and compared in a pairwise fashion, comparing metastatic or primary tumor to adjacent normal, to obtain Bayesian false discovery rates (BFDRs) and local false discovery rates (lfdrs). miRNAs that are expressed differentially in the tumor compared to the adjacent normal tissue are potentially relatively important for predicting the therapy response. The false discovery rates have been shown to be indeed informative for the prediction 10 where gren, a group‐regularized logistic elastic net regression is used. Unlike ecpc, gren requires non‐adaptive partitioning of the lfdrs, using fairly arbitrary thresholds. In addition, it combined the two lfdrs to limit the number of groups, as it does not allow for hyperparameter shrinkage as in ecpc. So, we use partly the same co‐data as gren, but add others as this can easily be handled by ecpc.
We use five co‐data sets: 1) (abun, 10 groups): abundance, that is, prestandardised average expression, of the miRNAs, discretized in 10 non‐overlapping, equally‐sized groups; 2) (sd, 10 groups): standard deviation of the (prestandardised) miRNA expression, discretized in 10 non‐overlapping, equally‐sized groups. As we expect weights to change at most gradually with abundance and standard deviation, this non‐adaptive discretization should be sufficient to estimate the weights. Changing the number of groups to 5 or 20 leads to similar performance as presented below (Figure S11); 3) (TS, 2 groups): one group with tumor specific miRNAs (BFDR in the primary and/or metastatic tumor) and one group with the rest; 4) (lfdr1, continuous): continuous lfdrs from the comparison metastatic vs adjacent normal non‐colorectal tissue; 5) (lfdr2, continuous): continuous lfdrs from the comparison primary vs normal colorectal tissue. We generate a hierarchy of groups by recursively splitting the continuous co‐data , illustrated in Figure 4.
FIGURE 4.
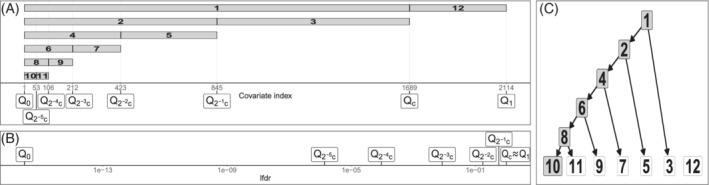
Illustration of the lfdr2 group set used in the miRNA expression data. (A) covariates are ordered by lfdr. Covariates are first split at in two groups for the cut‐off value c such that BFDR. The lower lfdr group is then recursively split at the median into two new groups, as this group is expected to be of more importance. The lfdr1 group set is obtained in the same way; (B) the lfdr values corresponding to the quantiles; (C) the hierarchy of the groups, which is used in the extra level of shrinkage to find a discretization that fits the data well as described in Section 3.4.1. White groups are not selected when fit on the data
We use the default ridge penalty for the first three co‐data group sets and the combination of the hierarchical lasso and ridge described in Section 3.4.1 for the last two. We use the default strategy using an additional L1‐penalty for posterior selection in a dense setting, as described in Section 3.4.3. This either matched or outperformed other posterior selection strategies (Figure S13). We perform a 10‐fold cross‐validation to compare several dense and sparse methods. Different folds rendered similar results as shown below.
Interpretation of estimated hyperparameters. The group set lfdr2 obtains on average the largest group set weight, in particular larger than lfdr1 (Figure 5A). This suggests that differences between primary tumor and adjacent normal tissue are more important for predicting clinical benefit than differences between metastasis and adjacent normal tissue. This may be explained by the fact that the comparison between the metastasis and adjacent normal tissue is between different cell types, in contrast to the comparison between the primary tumor and adjacent tissue. TS, abun and sd also contribute to the prior variance weight albeit less than lfdr2 for most folds. None of the group weights are fully shrunk in any of the co‐data sources (Figures 5B and S9), indicating that all co‐data contain some relevant information. Considering the group weight estimates of lfdr2, we observe that, unsurprisingly, the groups in the hierarchy up till the smallest lfdr group are selected (Figure 4). Covariates with a smaller lfdr obtain a larger prior variance (Figure 5B). The median group weight for a covariate in the lfdr2 group with smallest lfdr values is 75, indicating that a priori, we expect the magnitude of a covariate in this group to be times as large as the global average.
FIGURE 5.
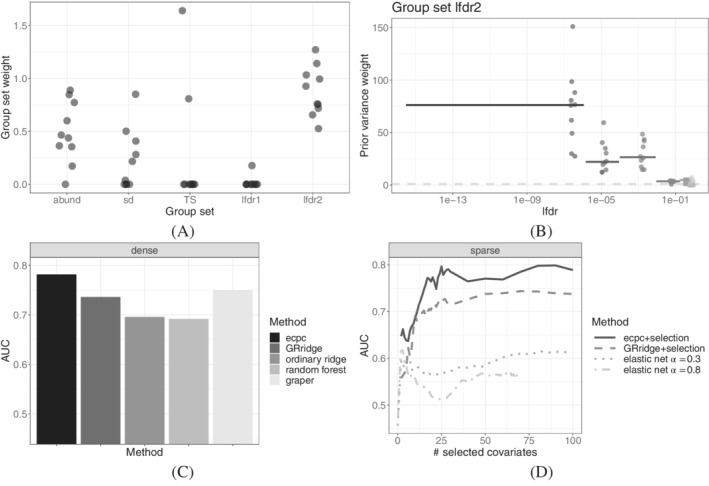
Results of 10‐fold CV in miRNA data example. (A) Estimated co‐data group set weights across folds; (B) estimated local prior variance weight in lfdr2 for different continuous lfdr values across folds. The horizontal line segments indicate the median local prior variance in the leaf groups of the hierarchical tree illustrated in Figure 4, ranging from the minimum to maximum lfdr‐value in that group. The points indicate the estimates across folds, jittered along the median lfdr‐value in the leaf groups. The dashed line at 1 corresponds to ordinary ridge weights for non‐informative co‐data. A larger prior variance corresponds to a smaller penalty; (C) AUC in various dense models; (D) AUC in various sparse models
Performance. Dense ecpc outperforms GRridge, random forest and the dense benchmark ordinary ridge in terms of cross‐validated AUC (Figure 5C). The benchmark AUC increases by nearly 0.1 by learning from co‐data. GRridge also benefits from co‐data, but less so than ecpc, as the latter is more flexible in two aspects (illustrated in Figure S19); first, whereas GRridge iterates over multiple co‐data, ecpc explicitly models and estimates co‐data weights, thereby enabling to focus relatively more on the relevant co‐data source lfdr2. Second, GRridge only uses the leaf groups of Figure 4 to represent the continuous co‐data, whereas ecpc is able to represent the lfdrs with an adaptive sparse hierarchical model. The latter is able to assign a larger weight to groups with smaller lfdr values.
The sparse ecpc selects a prespecified number of covariates in each fold. In the sparse setting, too, ecpc outperforms the benchmark elastic net and GRridge with the same posterior selection (Figure 5D). The benchmark AUC improves maximally by 0.23 at 25 covariates. Besides, ecpc is combined with a lasso penalty on the group level to obtain a group sparse model. It outperforms group lasso and hierarchical lasso (Figure S12).
Furthermore, we compare to two other recent group‐adaptive methods, gren and graper. 9 The results of gren on this data set are presented in fig. 1B in Reference 10. These are competitive to ours, with an AUC around 0.8, but only for gren using the elastic net parameter , which is not automatically chosen; other values of render worse results. Besides, the number of covariates selected by gren is around 75, which is much larger than the approximate 25 covariates required by ecpc (Figure 5D). graper cannot include overlapping (hierarchical) groups or multiple group sets. Therefore, as ecpc showed group set lfdr2 to be informative (Figure 5A), graper was applied to the leaf groups of this hierarchical group set. This resulted in an AUC of 0.74 (sparse setting) or 0.75 (dense setting), hence somewhat lower than ecpc (Figure 5C,D). Note that the sparse setting of graper does not select covariates; it only provides inclusion probabilities.
Covariate selection. A comparison of the estimated regression coefficients of ecpc to ordinary ridge shows a more heavy‐tailed distribution of the first (Figure S15). This facilitates and stabilizes posterior selection as the difference between small‐sized regression coefficients and large‐sized ones is larger. Comparing ecpc to elastic net on subsamples of the data indeed shows a larger overlap between selections of 25 or 50 covariates (Figure S16) with a better performance (Figure S17) when ecpc is used.
Our data come from an observational study with clinical benefit as primary outcome and survival as, likely related, secondary outcome. 19 To assess the broader use of the four sets of 25 markers, selected by either ecpc, GRridge, or elastic net (), we study their association with overall survival (OS). First, on the same samples, then on an independent validation set. The ecpc markers validated as well as GRridge and better than elastic net for the first, and better than both for the second. Full descriptions of both analyses are included in Section C1 in the Supporting Information.
5.2. Classifying cervical cancer stage
The goal in the second application is to use methylation data to classify samples as normal tissue or CIN3 tissue, a stage with a high risk of progressing to cervical cancer. The methylation levels are measured in independent, self‐taken samples of cervical tissue of women with normal tissue (control) or CIN3 tissue (case). After prefiltering, the data consist of methylation levels of probes corresponding to unique locations in the DNA. The full analysis and two available co‐data sources are described in Section C2 in the Supporting Information. Here we summarize the main findings.
Both co‐data sources are relevant, as ecpc does not fully shrink group parameters (Figure S21). Co‐data learning neither benefits nor harms the performance of ecpc and GRridge in the dense setting, compared to the benchmark ordinary ridge. In the sparse setting, both outperform elastic net, though elastic net is competitive to ecpc for models with 10‐75 selected covariates. The maximum added benefit of ecpc is an increase in the AUC of 0.12 for a model with four selected covariates (Figure S22). Lastly, ecpc shows a stabilized covariate selection, as the overlap between selections of covariates on subsamples is larger when compared to elastic net for and (Figure S26).
5.3. Classifying lymph node metastasis
In the last application, the goal is to classify the presence of lymph node metastasis (LNM). The data consist of RNA sequencing gene expression profiles from HPV negative samples for probes. The data, three co‐data sources and full analysis are further described in Section C3 in the Supporting Information. Again, all co‐data sets are relevant, as ecpc does not fully shrink group parameters (Figure S28). The method ecpc outperforms other dense methods and is competitive to other sparse methods in terms of prediction performance tested on an independent data set (Figure S29). Moreover, the benefit of learning from co‐data is reflected in the substantially larger overlap between selections of 25 or 50 covariates on subsamples of the data when compared to elastic net with or (Figure S30), with better performance in terms of classification when using covariate selection (Figure S31).
6. DISCUSSION
We presented a method, termed ecpc, to learn from multiple and various types of co‐data to improve prediction and covariate selection for high‐dimensional data, by adapting multi‐group penalties in ridge penalized generalized linear models. The method allows for missing co‐data, unpenalized covariates and posterior variable selection. We introduced an extra level of shrinkage on the group level, rendering a unique, flexible framework that accommodates a wide variety of co‐data. Our default ridge hypershrinkage accounts for multiple, possibly overlapping groups. Combined with lasso‐type penalties, it can handle group‐sparsity, hierarchical co‐data and continuous co‐data.
On top of learning from co‐data to improve performance, the method also provides hyperparameter estimates that may be interpreted to quantify the predictive strength on group level and co‐data source level. This opens up new possibilities for researching structures of variables on a higher level, for example, to assess which biological functions, corresponding to particular gene sets, are most predictive, or to assess which definition of gene sets, for which multiple proposals exist, benefits the prediction most.
The method may be extended by including different types of hypershrinkage, such as fusion penalties for graphically group‐structured co‐data. Besides fusion penalties on the group level, the method may also be extended to include fusion penalties on the covariate level. The latter is, however, less straightforward, as this changes the moment estimating equations non‐trivially.
We account for potential differences in group sizes by using prior ‘null’ group weights derived under the assumptions that i) groups are non‐overlapping, and; ii) a priori, the group set is not informative (the ‘null’; see Section A5 in the Supporting Information). Potential group overlap could be accounted for by a generalized ridge hyperpenalty matrix with non‐zero off‐diagonal elements, although this may be time‐consuming. While the prior ‘null’ weights protect against overfitting (on the group level), they may not be optimal when the groups are informative. An interesting extension is to replace these ‘null’ weights by hierarchical weights parsimoniously modeled from co‐data on the group level, for example, groups of, or test statistics for, groups of covariates. This essentially adds another level to our model.
The framework integrates multiple co‐data by learning co‐data weights. Alternatively, one could merge multiple co‐data and consider the merged set as one co‐data source. Group weight estimates of groups of different co‐data sources are independent given the data in the first approach, but dependent in the latter approach due to overlap in the groups. One advantage of the first approach is that non‐informative co‐data may be deselected, such that including non‐informative groups does not worsen the estimates of informative co‐data groups. Also, the latter approach does not allow for interpretation of importance of co‐data sources. Besides, estimating group weights per co‐data source independently has computational advantages, as it can be done in parallel. Moreover, it again supports flexibility, as different types of hypershrinkage can be used for different co‐data varying in type or importance. Interactions between groups of different co‐data sources are, however, not explicitly modeled. If desired, co‐data sources may be merged and expanded with interaction terms. This could be combined with additional (hierarchical) constraints on the group level.
The proposed model includes one global prior variance parameter to govern the overall level of regularization. For multi‐omics data, in which different sources of data are combined in one predictor, an omics type specific global prior variance parameter may be preferable in order to set different omics types to the same scale. 21 Multiple global prior variances can easily be included by rescaling the data matrix by the associated global variance weight. 8
The proposed empirical Bayes approach utilizes the Bayesian formulation with the normal prior as given in Equation 2 to estimate the hyperparameters (or prior parameters). Hybrid versions of empirical and full Bayes approaches were demonstrated to leverage a good trade‐off between the computational burden and ability to propagate model errors. 13 Hence, this is an interesting future direction.
The degree of improvement in other applications depends on the quality and relevance of available co‐data, but also on the level of sparseness of the “true” underlying data generating mechanism. Our method accommodates data ranging from group sparse to dense underlying distributions. As demonstrated in the data applications, use of co‐data facilitates posterior selection. Yet for truly sparse settings, sparse penalties may outweigh the benefits of including co‐data and borrowing information using dense penalties. Most omics prediction problems, however, are unlikely to be truly sparse, 11 although a parsimonious predictor can still predict well. Others have argued for “decoupling shrinkage and selection” in dense 12 and sparse 18 settings. We follow their reasoning, although with a different implementation, namely by adding an L1 penalty to the ridge penalties, which performed superior for our applications.
The R‐package ecpc is available on CRAN. We provide R scripts and data to reproduce analyses and figures, and a script demonstrating the package on https://github.com/Mirrelijn/ecpc. Currently, ecpc accommodates linear, logistic and Cox survival response, and multiple discrete or continuous co‐data, using a ridge penalty as default hypershrinkage, possibly combined with a lasso penalty for group selection, or hierarchical lasso constraints for hierarchical group selection.
Supporting information
Data S1: Supporting Information
ACKNOWLEDGEMENTS
The first author is supported by ZonMw TOP grant COMPUTE CANCER (40‐ 00812‐98‐16012). The authors would like to thank Soufiane Mourragui (Netherlands Cancer Insitute) for the many fruitful discussions and Magnus Münch (Amsterdam UMC) for preparation of the microRNA data.
van Nee MM, Wessels LF, van de Wiel MA. Flexible co‐data learning for high‐dimensional prediction. Statistics in Medicine. 2021;40(26:5910–5925. 10.1002/sim.9162
Funding information ZonMw, 40‐00812‐98‐16012
DATA AVAILABILITY STATEMENT
We provide R‐scripts and data to reproduce analyses and figures, and a script demonstrating the package on https://github.com/Mirrelijn/ecpc.
REFERENCES
- 1. Tomczak K, Czerwińska P, Wiznerowicz M. The Cancer Genome Atlas (TCGA): an immeasurable source of knowledge. Contemp Oncol. 2015;19(1A):A68‐A77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Boonstra PS, Taylor JM, Mukherjee B. Incorporating auxiliary information for improved prediction in high‐dimensional datasets: an ensemble of shrinkage approaches. Biostatistics. 2013;14(2):259‐272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Tai F, Pan W. Incorporating prior knowledge of predictors into penalized classifiers with multiple penalty terms. Bioinformatics. 2007;23(14):1775‐1782. [DOI] [PubMed] [Google Scholar]
- 4. Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J R Statist Soc, B. 2006;68(1):49‐67. [Google Scholar]
- 5. Jacob L, Obozinski G, Vert JP. Group lasso with overlap and graph lasso. Paper presented at: Proceedings of the 26th Annual International Conference on Machine Learning; 2009: 433–440.
- 6. Liu J, Ye J. Moreau‐Yosida regularization for grouped tree structure learning. Paper presented at: Proceedings of the 23rd International Conference on Neural Information Processing Systems; 2010: 1459–1467.
- 7. Yan X, Bien J. Hierarchical sparse modeling: a choice of two group lasso formulations. Stat Sci. 2017;32(4):531‐560. [Google Scholar]
- 8. van de Wiel M, Lien T, Verlaat W, van Wieringen WN, Wilting SM. Better prediction by use of co‐data: adaptive group‐regularized ridge regression. Stat Med. 2016;35:368‐381. [DOI] [PubMed] [Google Scholar]
- 9. Velten B, Huber W. Adaptive penalization in high‐dimensional regression and classification with external covariates using variational Bayes. Biostatistics. 2019;22(2):348‐364. 10.1093/biostatistics/kxz034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Münch MM, Peeters CF, Van Der Vaart AW, Van De Wiel MA. Adaptive group‐regularized logistic elastic net regression. Biostatistics. 2019;kxz062. 10.1093/biostatistics/kxz062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Boyle EA, Li YI, Pritchard JK. An expanded view of complex traits: from polygenic to omnigenic. Cell. 2017;169(7):1177‐1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Bondell HD, Reich BJ. Consistent high‐dimensional Bayesian variable selection via penalized credible regions. J Am Stat Assoc. 2012;107(500):1610‐1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. van de Wiel MA, Te Beest DE, Münch MM. Learning from a lot: Empirical Bayes for high‐dimensional model‐based prediction. Scand Stat Theory Appl. 2019;46(1):2‐25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hastie T, Tibshirani R. Efficient quadratic regularization for expression arrays. Biostatistics. 2004;5(3):329‐340. [DOI] [PubMed] [Google Scholar]
- 15. Le Cessie S, Van Houwelingen JC. Ridge estimators in logistic regression. J R Stat Soc, C. 1992;41(1):191‐201. [Google Scholar]
- 16. Wu Y, Yang P. Optimal estimation of Gaussian mixtures via denoised method of moments; 2018. arXiv preprint arXiv:1807.07237.
- 17. Novianti PW, Snoek BC, Wilting SM, van de Wiel MA. Better diagnostic signatures from RNAseq data through use of auxiliary co‐data. Bioinformatics. 2017;33(10):1572‐1574. [DOI] [PubMed] [Google Scholar]
- 18. Hahn PR, Carvalho CM. Decoupling shrinkage and selection in Bayesian linear models: a posterior summary perspective. J Am Stat Assoc. 2015;110(509):435‐448. [Google Scholar]
- 19. Neerincx M, Poel D, Sie DL, et al. Combination of a six microRNA expression profile with four clinicopathological factors for response prediction of systemic treatment in patients with advanced colorectal cancer. PLoS One. 2018;13(8):e0201809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Neerincx M, Sie D, Van De Wiel M, et al. MiR expression profiles of paired primary colorectal cancer and metastases by next‐generation sequencing. Oncogenesis. 2015;4(10):e170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Boulesteix AL, De Bin R, Jiang X, Fuchs M. IPF‐LASSO: Integrative L1‐penalized regression with penalty factors for prediction based on multi‐omics data. Comput Math Methods Med. 2017;2017:7691937. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1: Supporting Information
Data Availability Statement
We provide R‐scripts and data to reproduce analyses and figures, and a script demonstrating the package on https://github.com/Mirrelijn/ecpc.


