A guide to choosing and implementing reference models for social network analysis

ABSTRACT

Analysing social networks is challenging. Key features of relational data require the use of non‐standard statistical methods such as developing system‐specific null, or reference, models that randomize one or more components of the observed data. Here we review a variety of randomization procedures that generate reference models for social network analysis. Reference models provide an expectation for hypothesis testing when analysing network data. We outline the key stages in producing an effective reference model and detail four approaches for generating reference distributions: permutation, resampling, sampling from a distribution, and generative models. We highlight when each type of approach would be appropriate and note potential pitfalls for researchers to avoid. Throughout, we illustrate our points with examples from a simulated social system. Our aim is to provide social network researchers with a deeper understanding of analytical approaches to enhance their confidence when tailoring reference models to specific research questions.

I. INTRODUCTION

Individuals interact with each other in many ways but determining why they interact and uncovering the function of social patterns, i.e. the social network, is challenging. Network theory has provided useful tools to quantify patterns of social interactions (Wasserman & Faust, 1994; Croft, James & Krause, 2008; Borgatti et al., 2009). The analysis of social networks is complicated by the fact that applying statistical inference using standard methods is often not appropriate because of the inherent dependence of individuals within a network (for example, the actions of one individual are linked to the actions of another) (Croft et al., 2011). Network methods have emerged as a powerful set of tools with which to analyse social systems (Butts, 2008; Wey et al., 2008; Pinter‐Wollman et al., 2014; Farine & Whitehead, 2015; Cranmer et al., 2017; Fisher et al., 2017; Silk et al., 2017a , b ; Sosa, Sueur & Puga‐Gonzalez, 2020). Using network tools can often be difficult because important assumptions can be cryptic and do not apply universally across all suites of research questions or data types. Network analyses have been used to address many diverse questions in social and behavioural sciences (Clauset, Arbesman & Larremore, 2015; Croft, Darden & Wey, 2016; Crabtree, Vaughn & Crabtree, 2017; Power, 2017; Sih et al., 2018; Bruch & Newman, 2019; Ripperger et al., 2019; Webber & Vander Wal, 2019). This diversity of questions and approaches, especially in an interdisciplinary field like network science, has led many researchers to develop tools customized to a particular use case. Careful consideration of the maths underlying each approach can help understand the similarities and differences between alternative methods, can ensure that researchers are correctly testing their hypothesis, and can help researchers avoid violating the assumptions of particular methods.

Herein, we describe methods for drawing statistical inferences about patterns of sociality, focusing on the underlying maths and using simulated examples to illustrate each approach (see online Supporting Information, Appendix S1). We begin by explaining the concept of a reference (null) model, outlining when these reference models are required, discussing the key considerations facing researchers when using them, and outlining some of the potential pitfalls that may arise. We then introduce different approaches to creating reference models. We highlight the benefits of each approach and provide typical research questions for which different reference models are appropriate. We detail particular pitfalls of using the different approaches, illustrating potential questions and pitfalls using examples and simulations. We base our simulations on the social system of a mythical animal, the burbil (Section II.2). Our paper is targeted at those who have some experience in social network analysis and are looking for ways to make statistical inferences about the social systems they are studying. Whitehead (2008), Croft et al. (2008), Farine & Whitehead (2015), Krause et al. (2015), and Newman (2018) provide excellent introductions to the study of social networks.

II. REFERENCE MODELS FOR STATISTICAL INFERENCE IN NETWORK DATA

The essence of any statistical inference is to determine whether empirical observations are meaningful or whether they are the outcomes of chance alone. When data do not meet the assumptions of traditional statistical methods, as is often the case with network data (Croft et al., 2011; Cranmer et al., 2017), researchers can compare their data against chance distributions, i.e. distributions of values that are generated in a random process.

Traditionally, the likelihood of an observation occurring by chance has been referred to as a null model (Croft et al., 2011; Good, 2013). However, the term ‘null’ might incorrectly suggest that no patterns of interest are present. While it is correct to assume for statistical inference purposes that nothing is happening in relation to the phenomenon that is being observed, many other processes can still be acting on, or otherwise limiting, the system. For this reason, we advocate using the term reference models (Gauvin et al., 2020) rather than null models or chance distributions. The use of the term ‘reference’ highlights the notion that we are not comparing observations to a completely random scenario that contains no predictable patterns but rather to a system in which certain features of interest are preserved and others are randomized.

To perform statistical inference using reference models, the two most important questions a researcher needs to ask are: ‘how can empirical data be sampled in an unbiased way?’ and ‘what is the likelihood that a given pattern is present by chance?’ These questions are linked because chance could be different depending on the sampling approach. For example, if one samples only females, the chance distribution should not include males because the mechanisms that underlie the observed processes could differ between males and females. Identifying the appropriate chance distribution that observations should be compared to is critical for avoiding straw‐man hypotheses. Much previous research and development of tools has focused on sampling data in an unbiased way for network analysis or attempting to account for biases in data collection to conduct statistical inference (e.g. Croft et al., 2008, 2011; James, Croft & Krause, 2009; Franks, Ruxton & James, 2010; Farine & Strandburg‐Peshkin, 2015; Farine, 2017; Farine & Carter, 2020). However, more methodological development is needed to expand our statistical inference possibilities and tune computational methods to better answer specific questions, especially when the generating process of the observed social pattern may be complicated or multifaceted.

Importantly, there are inherent differences between observed biological networks and the mathematical constructs that underlie reference distributions. Observed biological networks are finite and therefore may not embody mathematical properties that are guaranteed to hold asymptotically, e.g. after infinite sampling. Therefore, it is important not to attribute meaning to differences between observed networks and reference models that emerge from the difference between the finite nature of the observed network and the general mathematical construct that describes the reference model. Instead, inference of meaning should come from consideration of agreement with, or deviation from, appropriately chosen patterns that reflect the real‐world processes that generate and/or constrain them.

(1). The construction, use, and evaluation of reference models

The effective use of a reference model hinges on four key steps, which focus on answering a biological question by comparing empirical observations to randomized or synthetic constructs. In sequence, we suggest that researchers (a) clearly articulate the biological question, (b) choose an appropriate test statistic, (c) generate a reference distribution, and (d) evaluate whether the biological question was addressed and whether the model behaved as intended. By identifying these discrete steps, we can scrutinize the analysis process to avoid methodological pitfalls (see Section IV).

(a). Step 1: articulate the research question and specify the feature of the reference model to be randomized

A reference model answers a question by connecting an observation to a distribution of hypothetical observations in which some aspect of the data has been shuffled, resampled, or otherwise stochastically altered. Creating a reference distribution by randomizing some aspect of the observed data is an alternative to an experimental manipulation, where an experimental treatment would create a distribution of observations of the system. Choosing which observed feature(s) to randomize in a reference model is as important as designing a carefully controlled experiment: both require combining the research question, domain knowledge, and accessible data to determine what should be held constant and what should be manipulated. Thus, the outcome of Step 1 is a list of network or data properties that are to be (i) randomized or (ii) maintained. Networks are interesting precisely because they capture complex interdependencies between nodes, which means that choosing what to manipulate and what to hold constant is not always trivial.

Although all reference models randomize some aspect of the data while fixing other aspects, both randomization and fixation can be done at different levels of abstraction: (Level 1) permutation, in which observations are swapped by sampling without replacement; (Level 2) resampling, in which observations are sampled from the observed data with replacement; (Level 3) distribution sampling, in which observations are drawn from a fixed distribution; and (Level 4) generative processes, in which synthetic data or networks are constructed from stochastic rules (Fig. 1). These levels of model abstraction can be applied to the observed data at different stages of analysis.

Fig 1.

Methods for creating reference models increase in level of abstraction. Methods progress from reference models that rely strongly on the empirical observations of sociality (left, Level 1) to methods that make assumptions about the generative processes that underlie the observed sociality and do not use the observed social associations when producing a reference model (right, Level 4).

(b). Step 2: choose a test statistic

The test statistic is the quantity that will be calculated from both the empirical data and from the reference model. Many summary measures can be used as test statistics [see summaries in Sosa et al. (2020) and Wey et al. (2008)]. The test statistic should quantify the network feature, or the relationship between features, that is tied directly to the biological question (see Table 1 for an example).

Table 1.

Example of two research teams and their approach to studying burbil sociality

Step 1a. Articulate research question.

Team 1: do burbils socially associate by nose colour? Team 2: do burbils associate at random?

Step 1b. Develop a reference model.

Team 1: to determine if burbils associate based on nose colour, the researchers decide to preserve the observed network structure (Fig. 2A), i.e. who associates with whom, but randomize it with respect to nose colour. Note that this choice maintains all aspects of burbil social structure – except for nose colour – which is the variable the researchers are interested in examining. Team 2: to determine if burbils associate at random, the researchers generate random networks with the same number of nodes and edges and then, for each random network, they draw edge weights from a normal distribution with the same mean and standard deviation as the observed adjacency matrix.

Step 2. Choose a test statistic.

Team 1: the researchers use a weighted assortativity coefficient to measure the tendency of burbils to associate with those of the same nose colour. Team 2: the researchers choose a measure of variance of the weighted degree (strength) distribution – coefficient of variance (CV) – as the test statistic to compare the observed and reference networks.

Step 3. Generate a reference distribution.

Both teams generate a reference distribution by running 9999 iterations of their randomization procedure to which they compare the observed test statistic. Using 9999 iterations means their full reference data set (including the observed value) is n = 10000. They use their different algorithms to generate their reference distributions. Both research teams plot the distribution of the 9999 reference test statistics as a histogram and the observed value as a line for visualization (see Fig. 2B for Team 1's histogram). They then use a two‐tailed comparison to examine if the observed test statistics falls inside or outside the 95% confidence interval (CI) of the reference distribution (i.e. between the 2.5 and 97.5% quantiles or outside this range).

Step 3a. Network randomization and generating reference test statistic.

Team 1: after each shuffle of nose colour, the weighted assortativity coefficient is calculated to obtain 9999 reference values to compare with the observed value. Team 2: after the creation of each new interaction network, the CV of the weighted degree distribution is calculated for each simulation to obtain 9999 reference values of simulated weighted degree CV to compare with the observed value.

Step 3b. Compare reference and observed test statistics.

Step 3c. Draw inferences from comparison between observed and reference values.

Team 1: the observed assortativity coefficient falls higher than the 95% confidence interval of the reference distribution indicating that burbils do indeed assort by nose colour – tending to associate more with burbils with the same colour noses (Fig. 2B). Team 2: the observed weighted degree CV falls inside the 95% interval of the reference distribution, indicating that the network is not different from random with regard to this particular network measure.

Step 4. Evaluate the process and adjust the reference model approach as needed.

Team 1 asked a specific question, used a permutation procedure that shuffled only the one aspect of burbil society that was of interest, and they chose a test statistic that was well matched to their question. Team 2 asked a vague question (what does it mean for a network to be non‐random? What is the biological meaning of ‘random’ and how is it measured?). They found it difficult to define a satisfactory reference model and they chose a test statistic that was not as directly linked to their question. Team 2 is therefore uncertain about the biological conclusions they can draw. Most importantly, they failed to determine how the way in which they generated their reference distribution matches their research question. This failure stems from the lack of specificity of their biological question. Further, they missed the fact that they included zero values for self‐loops in their calculation of the mean and standard deviation of the edge weights when generating their reference networks. These edge weights had a biased representation and inflated their importance compared to the observed edge weights.

(c). Step 3: generate a reference distribution

Samples from a reference model constitute a reference data set and applying the test statistic to each randomized sample in the reference data set creates a reference distribution. In this way, the samples from the reference model can be compared to the empirical data through the lens of the test statistic. If the test statistic from the observed data is indistinguishable from the distribution of test statistics in the reference distribution, a researcher would not be able to reject their hypothesis. If the test statistic from the observed data falls outside or at the extremities of the reference distribution, then a researcher would conclude that the feature, or relationship, of interest is unlikely to occur by chance and would reject their hypothesis.

(d). Step 4: evaluate the process and adjust the reference model approach as needed

Researchers must carefully evaluate whether the reference model they have built is in alignment with their research question of interest. Researchers also need to determine whether the reference model behaves as intended or whether a different process is needed to test the question of interest. As we show in this review, there are many ways in which reference models may have hidden biases that can result in misleading outcomes. In evaluating reference models, it is beneficial to separate Step 1 (choosing which features to randomize and which to preserve, and at what level of abstraction) from Step 2 (choosing a test statistic). Such separation will allow researchers to diagnose pitfalls associated with a test statistic versus pitfalls related to the data randomization procedure. Reference models may need several iterations of the construction/evaluation steps to settle on a model that is well aligned with the research question and biological question and which behaves as intended.

(2). A tangible example of reference model use

To illustrate and provide examples for the different randomization procedures and to summarize some of the key pitfalls that each approach is susceptible to, we created an imaginary social network data set of the mythical burbils. We will refer to this imaginary society throughout this review and provide supporting code for all the examples in Appendix S1. Briefly, burbils live in open habitats and exhibit two unique nose‐colour morphs (red and orange). Individual burbils can be uniquely identified and their sex (male or female) and age (adults, subadults and juveniles) are known. Burbils form fission–fusion societies characterized by large groups that roost together at night but fission into smaller subgroups when foraging during the day. The number of subgroups each day is drawn from a Poisson distribution (λ = 5) and we suspect that subgroup membership may be assorted by nose colour (see example in Section II.2a). Foraging subgroups from different roosting groups occasionally meet and intermingle, creating opportunities for between‐group associations These between‐group associations are more likely if the two burbil groups belong to the same ‘clan’ (similar to the vocal clans of killer whales; Yurk et al., 2002). Burbil groups differ in size, and groups of different sizes might have different social network structures. Within their social groups, burbils are involved in both dominance interactions and affiliative interactions with groupmates and we suspect that these are influenced by age and sex. These interactions can only occur between individuals in the same subgroups with the number of interactions recorded in each subgroup varying based on the number of individuals recorded. Further information on burbil societies, social network generation, and example analyses are provided in Appendix S1.

(a). Illustration of several pitfalls in reference model construction and use

To illustrate the need for carefully considering various pitfalls when constructing reference models, we provide an example that compares two reference models, one resulting in more specific outcomes than the other. Specifically, we highlight in this example that carefully articulating the research question (Step 1) has important cascading effects onto the entire analysis. One of the more detrimental cascading effects is a mismatch between the research question and the resulting conclusions. In our example, two teams of researchers (Team 1 and Team 2) set out to study burbil association networks. Both teams have association data from a single group of burbils. Based on these association data, they build a weighted, undirected network (Fig. 2A). The researchers have information on the attributes of the burbils, such as age, sex, and nose colour. Team 1 immediately notices that individual burbils differ from one another in their nose colour and ask a specific research question related to that trait. Team 2 overlooks the natural history of the burbils and asks a much more general question about burbil social structure. We analyse the process that both teams went through in Table 1, highlighting the pitfalls they each encounter related to the way they defined their research question (R code for both analyses provided in Appendix S1, Section 3.1.1).

Fig 2.

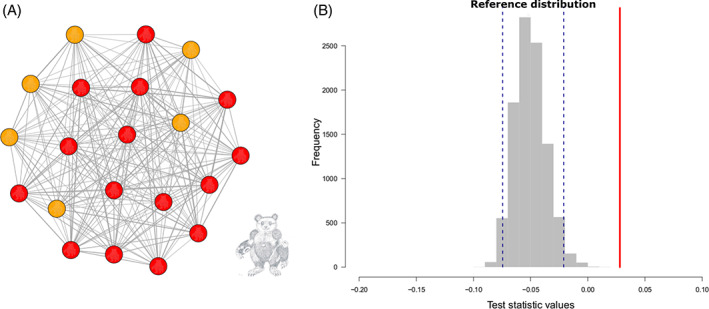
An example of study approaches: do burbils socially assort by nose colour? (A) Association network of burbils, with nodes colour‐coded by nose colour and (B) distribution of values based on the permutation procedure of Team 1; observed value of the test statistic shown as a red solid line and the 2.5 and 97.5% quantiles of the reference distribution as blue dashed lines.

III. DO YOU NEED A REFERENCE MODEL? THE IMPORTANCE OF DISTINGUISHING BETWEEN EXPLORATION‐ AND HYPOTHESIS‐DRIVEN INVESTIGATION

A reference model functions, in a computational sense, as a control against the observed outcomes in a system. The ‘null hypothesis’ would be that no meaningful differences exist between the calculated reference and the measured results. Our goal in constructing an appropriate reference model is therefore to know confidently when to reject that null hypothesis.

Although we focus on selecting appropriate reference models against which to contrast hypothesized processes or outcomes (i.e. an appropriate control for an observational experiment), the idea of a test against a reference model itself relies implicitly on the existence of a known and concrete alternative hypothesis describing either the process from which the observations emerged or describing features of the observed data/structures themselves. One potential (and common) point of complication in the analysis of social networks is that hypothesis generation (i.e. data exploration) and hypothesis testing may be easily conflated. In exploration‐driven investigations it is impossible to design an appropriate reference model because it is impossible to decouple a hypothesis from the observations themselves.

There is often a temptation to randomize each pattern of interest in a network with the hope that finding the correct reference model for contrast can allow meaningful interpretation from observations that may not be rich enough, or well understood enough yet, to support it. This is not at all to suggest that exploratory data analysis is inappropriate. It is critical to differentiate purposefully between the exploration phase of research (when pattern discovery may itself be the goal and does not require statistical departure from a constructed reference model) and the hypothesis‐testing phase of research (when appropriate reference models are necessary).

(1). Exploration versus hypothesis testing – a case study

Consider the case in which a researcher suspects that individual risk of infection from a contagious disease circulating in a population may be correlated with some measure of the centrality of individuals in the network. There are three potential cases that are all included in this general description.

Case 1: the mode of transmission of the pathogen is known (e.g. sexually transmitted). In this case, the network of contacts among individuals that may provide the means for disease transmission is well defined (in the same example, an edge is drawn between two individuals who have engaged in sexual contact with each other). Given that network, we may hypothesize that a particular centrality measure may correlate with infection risk (for example, eigenvector or betweenness centrality). Calculating the individual centralities of each node in the network and their respective correlation with observed disease burden is a valid endeavour and requires the construction of an appropriate reference model to be able to infer meaning and make appropriate interpretations of the outcome.

Case 2: the researchers are interested in finding the correlation of one particular centrality measure with disease risk, but the mode of transmission for the infection is not known. For example, it might transmit by sexual transmission or be transmitted via inhalation of droplets from the respiratory system, so close contact with anyone coughing/sneezing/exhaling while infected is sufficient for potentially successful transmission. In this case the researchers may construct two potential networks: one from observed sexual contact and the other from some spatial proximity index that would reflect exposure to exhaled droplets from others. Here again, calculating the betweenness of the individuals in each of these two different networks and their respective correlations with observed disease burden is also valid and requires an appropriate reference model.

Case 3: the researchers are unsure of the mode of transmission of the pathogen, nor do they know which centrality measure might correlate with infection risk. In this case, selecting the combination of network structure and centrality measure that yields the highest correlation with observed disease burden may not be a well‐formed question, but an exploratory approach would be appropriate. Therefore, a reference model is not necessary, and no matter how carefully constructed, it would not be able to provide a valid context for interpretation. Because the centrality calculation does not exist in the absence of the structure of the selected network, the ‘pair’ of measure and network that produces the greatest fit to the observed transmission pattern is the logical equivalent of over‐fitting a regression. Unfortunately, unlike a simple regression, because the centralities of individuals depend on the network structure (i.e. factors that are extrinsic to the node itself), validation by sensitivity of the correlation under iterative removal and recalculation (or other common techniques) is not possible.

IV. COMMON PITFALLS WHEN USING REFERENCE MODELS

When using reference models to analyse network data, researchers should keep in mind the pitfalls that can arise at each of the above steps. We provide a broad overview here and link these general pitfalls to specific examples that are related to the different approaches to generating reference models, which we detail below.

(1). Pitfalls in matching a reference model to the research question

The most important step when designing a randomization procedure is ensuring that the research question is directly addressed. Researchers may set out to examine a particular question but then randomize the network in a way that misses the question and results in misleading conclusions (see Table 1 for an example). Designing an appropriate randomization procedure can be challenging because changing one property of a network can often change others and imposing too many constraints may lead to computational issues or prevent researchers from answering the desired question. Therefore, having a clear understanding of the types of constraints that can be imposed is important.

Reference models for social networks can be constructed to preserve both or either non‐social or social aspects of the animals’ biology. Non‐social constraints are properties of the biological system that are extrinsic to the social processes that underlie the social network but might influence whether or not an interaction occurs. Such constraints might shape how the reference distribution is generated, for example by providing restrictions on possible permutations or resampling. Restricting permutations (or resampling) to specific time windows, for example, could prevent creating interactions between individuals that had not been born yet and ones that have already died or immigrated away from the study site. Similarly, including spatial constraints in reference models recognizes that some individuals can never meet, for example terrestrial organisms that are separated by a river they cannot cross. Failing to prevent the generation of samples in the reference model that are not naturally feasible may lead to false positive results. Often, imposing these constraints will require knowledge of the study system. Social constraints are emergent properties of the network that might be important to maintain when testing particular hypotheses (e.g. the degree distribution, the number of network components or clusters, etc.). These properties are easier to maintain using some approaches to generating reference models than others. For example, data stream permutation methods overlook the importance of maintaining specific properties of the social network (discussed in more detail in Section V.2) (Weiss et al., 2021), which can be important when developing reference models to answer some questions. Not accounting for social constraints can result in reference data sets (networks) that fall within the non‐social constraints imposed but which have substantial differences between some key properties of the emergent network structure in the reference data set and the observed social network. A failure to include social constraints can result in errors in inference (Weiss et al., 2021).

Both social and non‐social constraints can cause unintended changes, resulting in a reference model that no longer addresses the original research question or addresses a similar but not identical research question (see Section V.2). For example, randomization of movement data can alter the social networks constructed from those movements, which may in turn, introduce undesired changes in reference networks that could not be foreseen from the movement data permutations. Thus, randomizing away correlations at one scale (e.g. movement) may introduce correlations at another scale (e.g. social).

Further, while it is important to consider both network social and non‐social constraints on the reference data sets, a reference model can include too many constraints (see Section V.2). In some cases, these constraints may prevent the production of a reference model (too few possible configurations) or make the process too computationally intensive. Applying constraints may also lead to a narrow reference distribution. While this does not have to be a pitfall (and might just be the nature of the biological question), a pitfall arises if these restrictions stop a researcher from randomizing the aspects of the data that are the focus of the research question. Sometimes creating a wide enough reference model is not possible using less abstract approaches (permutations and resampling, see Fig. 1), for example, very small networks have a small, finite number of possible edge permutations. In such a situation, it might be beneficial to change the randomization approach. We discuss in Section VII a randomization procedure that can allow researchers to produce wider distributions than those that are obtained by permutation.

(2). Pitfalls in test statistic choice

We cannot emphasize enough the importance of choosing a biologically appropriate test statistic. The data, network structure, or properties of the test statistic may constrain decisions about test statistic use. Understanding the biological meaning of the test statistic that is being compared between observed and reference data will determine whether or not the biological question can be answered. Researchers might be familiar with particular network measures (e.g. degree, strength, betweenness, density, modularity) and use only those to answer all their questions about network structure. However, not all measures are appropriate for answering every research question, and each measure has a different biological meaning that can depend also on the network structure (Wey et al., 2008; Brent, 2015; Farine & Whitehead, 2015; Silk et al., 2017a ; Sosa et al., 2020). Therefore, it is important to understand the biological meaning of the test statistic. Understanding the biological meaning of the test statistic will prevent testing too many measures (Webber, Schneider & Vander Wal, 2020). The more test statistics one measures, the more hypotheses are being tested and so the greater the need to account for multiple testing (to prevent false‐positive errors). Additionally, it is important to consider correlation between test statistics. For example, a researcher might be interested in uncovering the centrality of individuals in a network and would like to use degree, strength, and betweenness. However, it is possible that these three measures are highly correlated with one another (e.g. Borgatti, 2005; Farine & Whitehead, 2015; Silk et al., 2017a ), and some test statistics may be correlated in unexpected ways (e.g. centrality measures can be correlated with community structure). An additional pitfall is that for some research questions, the randomization procedure can affect the test statistic in unexpected ways, especially if comparing networks of different sizes. There might be ways to adjust a test statistic, but such adjustments can lead to subtle changes in the research question being asked and therefore to new inferences (see Appendix S1, Section 3.2.1).

A related pitfall when comparing networks of different sizes is that the most appropriate normalization approach can depend on the behavioural rules that generate the network. Determining effects of network size on the choice of test statistics may require conducting simulations and/or examination of the literature. We show in Appendix S1 (Section 3.2.1) how the generative process that underlies the network can impact the ability to compare networks of different sizes. For example, if we ask how network size influences the average connectivity of individuals, we could compare the mean degree of burbils in huddling networks of two different‐sized groups. In both cases the same rules underlie network structure. We consider two situations, a random graph or a small‐world process, in which individuals are typically connected to nearby nodes with only occasional long‐distance connections. When comparing the mean degree of two networks of different sizes a sensible normalization is to divide raw degree values by the number of individuals in the group minus one (i.e. the number of individuals it is possible to be connected to). However, the outcome of doing this depends on whether the network is generated as a random graph or a small‐world process. In the former, the normalized mean degree is much more similar between the two groups than the mean of the raw degree values. However, when we do the same for a small‐world network the mean of the raw degrees is similar, while the mean of normalized degree values is very different. This example highlights the challenges in testing the similarity of different‐sized networks without knowledge of the behaviour that generated them. A similar caveat applies when using resampling‐based reference models to compare networks of different sizes.

(3). Pitfalls in generating the reference distribution

The process of generating the reference distribution holds a number of potential pitfalls for the unwary. First, the reference model does not always sample the full parameter space. There might be values that will never appear in the reference distribution because of the structure of the data or the algorithm of the randomization. Under‐representation of values in the reference distribution might be important to maintain but could also be an unwanted side‐product that could be resolved by using a different randomization procedure, as we explain in Section IV.1. We provide an example of how sampling from different distributions yields different ranges of values in Section VII. Second, the parameter space needs to be sampled in an unbiased manner. When generating a reference distribution, certain values might be over‐ or under‐represented if the procedure used to generate the model does not explore the entire parameter space or explores it naively. Ideally, the randomization procedure will produce a reference distribution in which values are uniformly distributed or follow a distribution that is appropriate for the network structure. It is important to understand the constraints of the randomization procedure that is being used to determine if such biased distributions may emerge. We provide a detailed example in Section V.2.

Third, generating a reference distribution can be computationally intensive, to the point that it is not feasible to generate a large enough reference distribution. We offer a range of approaches, some of which (like sampling from distributions, Section VII) are less computationally intensive than others (such as permutations in Section V). If computational constraints influence the choice of methods, it is important to evaluate carefully what concessions are being made regarding the ability of the randomization procedure to answer the biological question. For example, when using permutations, conducting too few swaps can lead to problems with statistical inference (see Section V).

(4). Pitfalls in failing to evaluate the process comprehensively and adjust the reference model approach as needed

Many of the general pitfalls identified here can be detected by carefully evaluating the approach used to make sure that the reference model is tuned to the research question and is behaving as expected. This step can help identify further potential pitfalls. One important point to consider is whether the reference model is being used to answer a statistically motivated question (i.e. to test a hypothesis) rather than to explore the data in search of significant deviations from the model (as discussed in Section III). A second potential pitfall is that agreement between observed data and reference model outcomes does not necessarily imply similar causality. If the observed data are similar to the randomized data, this does not necessarily mean that the algorithm underlying the randomization is the same as the biological process that underlies the observed network; with a close match, the algorithm is a plausible generating mechanism for the observed patterns but must be tested further. For example, many observed social networks are characterized by a heavy‐tailed degree distribution, such that the network has few individuals with much higher degree than the rest of the individuals, i.e. they can be considered as hubs. Often, researchers model the heavy‐tailed degree distribution of such networks as a power law, in which the frequency of nodes with a certain degree k is proportional to k^−α. Although the algorithm of degree‐based preferential attachment (i.e. the Barabási–Albert model; Barabási & Albert, 1999) yields a network with a power law degree distribution, so do other algorithms (e.g. the ‘copy model’; Kleinberg et al., 1999). It is therefore clear that inferring the process by which a network results in a power law degree distribution cannot uniquely rely on agreement with the emergent structure itself. We provide further examples of this pitfall in Section VIII.

Finally, not all network analysis requires the use of reference models (see also Section III). While the use of reference models is often necessary when analysing features of individuals that are linked to others in a network because of the dependency between individuals, there are questions and methods that do not require the use of reference models. For example, one might use network measures to characterize many groups in a society. Researchers might want to ask if a network measure, for example density, increases with the size of the group. In this case a simple correlation between group size and density would address the research question. If, however, the researchers are interested in the process that underlies the relationship between group size and network density they might use generative models (Section VIII) or sample from distributions (Section VII) to produce groups of different sizes using different engagement rules. Note, however, that the second approach addresses the question: ‘what are the underlying causes of the observed relationship between group size and density?’ rather than answering the original research question: ‘is there a relationship between group size and density’?

V. PERMUTATION‐BASED REFERENCE MODELS

Permutation‐based reference models take observed data and shuffle it to produce reference data sets (Good, 2013). The resulting reference models preserve certain attributes of the observed data set, such as distributions of key network measures or features of the raw data, such as group size. Because data are shuffled and observations are swapped, new values are not necessarily introduced in the reference models (although new values of some measures can be calculated). The most conceptually simple permutation‐based methods randomize a single feature of the observed data while preserving all other observed features. Statistically, this approach breaks correlations that are shaped by the permuted feature. Permutations can be applied either to the network structure itself (e.g. nodes and edges, or features of them) or to the raw data that underlies the network structure (e.g. movement data, group membership, etc.).

(1). Feature permutation

Permutations can be used on both node features and edge features. In both cases, these permutations involve swapping attributes among either the nodes or the edges. Attributes can be any feature of the nodes or the edges. Common node attributes are individual identity (often referred to as the node's label), sex, body size, age, colour, or other features. Attributes of edges can be the types of edges connecting two nodes, for example, different types of relationships or interactions, such as aggression and affiliation, or the direction of the edge for asymmetric relationships or for directed interactions.

Node feature permutation‐based reference models swap attributes among nodes in the network. Node feature swaps preserve the structure of the observed networks but break potential correlations between the structure of the network and node attributes. Comparing observed networks to node attribute permutation reference models allows researchers to test if the attributes of interest are associated with observed patterns of interactions or associations (for an example, see Table 1).

Node feature swaps frequently have been used as reference models in social network analysis (Johnson et al., 2017; Snijders et al., 2018; Hamilton et al., 2019; Wilson‐Aggarwal et al., 2019). They are used most often to test associations between measures of social network position and phenotypic traits of individuals (e.g. Keiser et al., 2016; Ellis et al., 2017; Johnson et al., 2017; Hamilton et al., 2019; Wilson‐Aggarwal et al., 2019). We provide an example in Appendix S1 (Section 3.1.2) in which we test the relationship between sex and out‐strength in burbil dominance networks. Inference from node swap permutations can be complex if there are underlying processes (e.g. differences in sampling) that may generate patterns of interest. For example, in Appendix S1 (Section 3.1.2) we swap a node attribute, nose colour, to test if burbils socially assort by nose colour when they interact in an affiliative manner. These node swap permutations show that burbil affiliative networks are indeed assorted by nose colour. However, interactions can only occur when individuals are associating within the same group, therefore, without taking into account patterns of subgroup formation in the population in the permutation, we are unable to answer whether affiliative interactions are assorted for nose colour within subgroups.

Edge feature permutation‐based reference models swap attributes of the edges, leaving the node identities, node metadata, and the connections among them intact. Edge feature swaps can involve shuffling the following: (i) labels of edges – swapping one type of interaction for another, like aggression to affiliation, (ii) edge directions – swapping which individual directs a behaviour to which recipient in an interaction, swapping an edge from A to B to go from B to A (Miller et al., 2017; de Bacco, Larremore & Moore, 2018), or (iii) edge weights – swapping the values that represent the strength, frequency, or duration of interactions among individuals, such as swapping a strong relationship between A and B with a weak relationship between C and D). Note that permuting edge weights can only involve swaps between pairs with non‐zero weighted edges otherwise it would become edge rewiring as detailed in Section V.2. We provide an example of edge direction swaps in Appendix S1 (Section 3.1.3) where we test the hypothesis that adult burbils have higher out‐strength in networks of dominance interactions than younger individuals (subadults and juveniles). We swap edge directions at random in an iterative process where we generate a Markov chain (see Section V.2). Permuting edge weights can be useful for answering questions about the strength of social ties. We provide an example in which we test the hypothesis that burbils of different sexes have different out‐strengths in the network of affiliative interactions (Appendix S1, Section 3.1.3). The affiliative network is highly connected (has a high density of edges and few or no zero‐weighted edges) making it suitable to use edge weight permutations in this way. In an iterative process we select pairs of dyads and swap the number of affiliative interactions between them to randomise which edges are associated with which weights, breaking down the correlation between edge weights and node attribute, in this case sex.

Edge feature swaps could be used on raw temporal data in edge list form if each interaction between two individuals is labelled with the time at which the interaction occurred. A possible edge label swap would be to randomize the time at which each interaction occurred (changing the time label but keeping the identities of the pairs that interacted). If edges have further information about the type of interactions (e.g. the type of behaviour, such as grooming or fighting) one could also randomize the type of interaction that occurred at each particular time, thus, changing the type of interactions but keeping the individuals involved and the timing or order of the interactions the same as observed. In both these examples, the edge label swaps would not lead to reference models that are different from the observed data set if all time points or all types of social interactions are aggregated. However, network measures that are sensitive to temporal dynamics or to the type of interactions [such as multilayer measures (Kivelä et al., 2014; Finn et al., 2019)] can be affected by these feature swaps.

(2). Edge rewiring with permutation

Edge rewiring involves swapping the edges that represent interactions or associations in raw data streams or swapping edges that connect nodes in a network in an adjacency matrix. For example, edge rewiring may swap the edges ab and cd to replace them with edges ad and cb. Edge rewiring results in what is known in network science as the configuration model (Bollobás, 1980).

The configuration model is a graph that is sampled uniformly from all graphs of a given degree sequence (with some key technicalities). The degree sequence is the list of all observed degrees in a network, which can be summarized as a degree distribution. Configuration models require appropriate care when making decisions about the specifications of the underlying model (Fosdick et al., 2018). Like edge feature swaps, edge rewiring breaks correlations between the node metadata and the structure of the network to test whether the observed edge arrangement leads to a network structure that is different from a structure that would be achieved by chance, while preserving group size and the metadata of nodes. Edge rewiring can be conducted at different stages, from modifying the raw data (in what are often known as pre‐network permutations or data stream permutations; Farine, 2017) to modifying the group's network structure directly by manipulating the adjacency matrix. In general, rewiring models form what mathematicians call a Markov chain, such that drawing samples by rewiring is equivalent to sampling from a distribution of networks by Markov chain Monte Carlo (MCMC) (Fosdick et al., 2018).

Edge rewiring on raw data is often used in animal social network analysis (data stream permutations, where edges often represent each single interaction or association rather than a summarized version of an edge's strength). Importantly, when data stream permutations are used on this raw form of the data, the configuration model that is generated is related to the current format of the data rather than the projected social network that is subsequently analysed. Biologists often use a rewiring approach for association data in group‐by‐individual matrices, also known as gambit of the group data formats (e.g. Bejder, Fletcher & Bräger, 1998; Croft et al., 2005, 2006; Poirier & Festa‐Bianchet, 2018; Zeus, Reusch & Kerth, 2018; Brandl et al., 2019). In this data format, each individual is recorded as present in a particular group and ‘group’ is often defined as an aggregation of animals that are present at the same time and the same place (Whitehead & Dufault, 1999; Franks et al., 2010). This data format is a bipartite network with edges that connect individuals to the groups in which they were observed, i.e. it is a bipartite version of the configuration model that respects the bipartition. When such data stream permutations are applied to group‐by‐individual matrices the edge‐rewiring step takes place on this bipartite network rather than on the projected social network that is created subsequently. Similarly, when edge rewiring is used for raw data on behavioural interactions (e.g. Webber et al., 2016; Miller et al., 2017), it is the multigraph that contains all interactions (i.e. a network with multiple rather than weighted edges between nodes) that is rewired, while the network analysed is subsequently treated as a weighted network (with single edges between nodes).

Elaborate rewiring procedures can be used to impose both social and non‐social constraints. For example, researchers may constrain rewiring to only swap individuals between groups that occur in the same location or on the same day (non‐social constraints). Researchers may further want to impose network constraints, such as forcing the re‐wired reference models to preserve the degree distribution of the observed network. The R package igraph (Csardi & Nepusz, 2006) can rewire social networks while maintaining a fixed degree sequence, while Chodrow (2019) shows how to preserve both event size (the number of individuals in each grouping event) and the degree of each individual if using data stream permutations to analyse data on animal groups (or equivalent bipartite networks in other fields) and Farine & Carter (2020) propose a double permutation test to help avoid elevated type I errors. Another example of an elaborate rewiring procedure is disconnecting either just one or both end(s) of an edge and re‐connecting it to a new individual (or individuals) (e.g. Hobson & DeDeo, 2015; Formica et al., 2016; Hobson, Mønster & DeDeo, 2021). For example, an edge connecting A to B can be disconnected from B and re‐wired to connect A to C. This kind of rewiring results in some changes to both the dyadic relationships between individuals and the network structure, but preserves other features of the networks, such as eigenvector centrality, and can be used to generate reference data sets that are consistent with a desired network constraint (Hobson & DeDeo, 2015; Hobson et al., 2021). This edge‐rewiring procedure is different from the configuration model, as it does not generally preserve the degree sequence. If the network is directed, this type of rewiring can be used to preserve the sequence of out‐degrees, but not in‐degrees (or vice versa). As the complexity of the rewiring procedures and the constraints imposed on them increase, these rewiring procedures become more similar to generative models, which we detail in Section VIII.

We provide examples of data stream permutations for both association (Section 3.1.4.1) and interaction (Section 3.1.4.2) data in Appendix S1. For associations, we generate two reference distributions to test the hypotheses that burbil associations are non‐random with or without accounting for assortativity by nose colour. Our permutations conduct edge rewiring in the group‐by‐individual matrix and in both reference models we constrain swaps to occur within the same burbil group and to be between two subgroups observed on the same day. The first reference model is naive as we already know the burbils are assorted by nose colour (Table 1). However, when we additionally constrain swaps so that edges can only be rewired between burbils with the same nose colour, we see that association patterns are random between burbils with the same nose colour within a subgroup. This example demonstrates the potential power of using multiple reference models in concert. For interactions, we ask what explains burbil affiliative interactions. Using edge rewiring in the raw interaction data we find that there is no evidence for assortativity by nose colour when controlling for subgroup membership. We show this by rewiring interactions within each subgroup so that the nose colour of each dyad is randomized. Affiliative interactions are assorted by nose colour only because each subgroup tends to be dominated by one nose colour or the other (rather than being an unbiased sample of individuals in the group).

(3). Key pitfalls for permutation‐based reference models

For permutation‐based methods, a first major potential pitfall to watch for is failing to impose the correct constraints on swaps. In feature swaps (conducted on the adjacency matrix itself), it may not always be possible to constrain swaps as desired. For example, swaps can be constrained to occur only between individuals recorded at the same location (e.g. Shizuka et al., 2014), in the same group (e.g. Ellis et al., 2017), or that are alive at the same time (e.g. Shizuka & Johnson, 2020). However, it can be challenging to incorporate some constraints. If we test for assortment by nose colour in the burbil network of affiliative interactions then there is no natural way to restrict swaps on the adjacency matrix to account for burbils only interacting with others in the subgroups they occur in (Appendix S1, Section 3.1.2). However, using an edge‐rewiring approach we can constrain permutations within each subgroup (Appendix S1, Section 3.1.4.2). For reference models generated by edge rewiring, it is critical to consider both the non‐social and social constraints because decisions about which constraints to build into the rewiring procedure affect the resulting configuration model. In many common animal social network rewiring methods, researchers control for unwanted structure in non‐social constraints (e.g. sampling biases, differences in gregariousness, etc.). It is less common for researchers to consider social constraints, such as forcing the rewired networks to conform to a particular degree distribution. However, without social constraints, the reference model will approach a random network as the number of rewiring steps increases and can result in misleading, false‐positive inference (Weiss et al., 2021). Chodrow (2019) shows how one can preserve both the size of interactions (number of animals in each interaction) and the degree of each individual to produce a permutation of the data stream that preserves the degree distribution.

A second pitfall of using permutation‐based reference models are computational limitations and potential for biased sampling. Permutation‐based approaches are often computationally intensive (e.g. as seen when running the code in Appendix S1, Section 3.1). Computational constraints can be exacerbated when increasing the number of constraints on the permutation (social or non‐social) because many of the attempted swaps will be rejected. In some cases, over‐specifying constraints on the randomization can result in a configuration model with insufficient acceptable states, making it impossible to generate a reference model, especially when examining small networks. Furthermore, it is important to sample from the configuration model in an unbiased manner. This pitfall is especially likely when sampling from a distribution of networks by MCMC, as is often done in edge‐rewiring approaches. When a swap is rejected (i.e. a suggested swap is not possible within the set of constraints imposed) it is important to resample the current reference network as the next iteration of the Markov chain (Krause et al., 2009). If such resampling is not done, then the configuration model will be sampled in a biased way (Fig. 3), which could lead to errors in inference. Such rejection of swaps will arise more frequently when there are more constraints imposed on the permutations, and then other potential pitfalls arise: the Markov chain will (i) take longer to become stationary, and (ii) be slower to mix, which could lead to further errors in inference. Addressing this pitfall requires a burn‐in period during which the permuted networks are not used in the reference distribution and a thinning interval that equates to permuted networks only being saved as reference data sets after so many iterations in the Markov chain (e.g. every 10th iteration). We provide examples of these in Appendix S1 (Sections 3.1.3 and 3.1.4).

Fig 3.

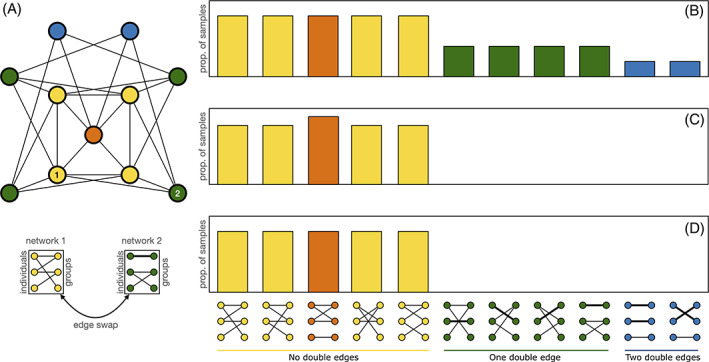
An illustration of how incorrect use of Markov chain Monte Carlo (MCMC) methods can lead to biased sampling from the configuration model when using data stream permutations. When permuting a bipartite group‐by‐individual network there are 11 possible configurations, depicted at the bottom of the figure. Of these possibilities, five (coloured yellow and orange) are acceptable because they do not contain double edges (as shown in the green and blue possibilities as a thick edge). Double edges indicate that the same individual occurred in the same grouping event twice – which is impossible. (A) The ‘graph of graphs’, or the Markov chain. (B) The distribution of samples obtained when permutations are conducted and every state, including those that are impossible (green and blue) are accepted. (C) The distribution of samples obtained when rejecting swaps that result in double edges and then rewiring a randomized network. Note that a sampling bias arises here – the orange state is oversampled – because it has more routes to other acceptable states as seen in A. (D) The distribution of the samples obtained when swaps that make double edges are resampled (i.e. the correct unbiased sampling approach). Note that in D the sampling of the five acceptable states is uniform – as it should be.

A third potential pitfall of permutation‐based approaches is that they are often prone to having unanticipated effects on network structure, especially when permutations are conducted on the raw data stream. Consequently, failing to properly evaluate the computational approach is a particularly important pitfall for permutation‐based approaches. For example, a completely uniform random rewiring might make the data too ‘unrealistic’ or mean the distribution of the response variable is changed considerably (Weiss et al., 2021). Edge rewiring of the group‐by‐individual matrices (as explained above) typically alters degree and edge weight distributions, which can lead to false positive errors because the reference model does not address the question originally asked. Incorporating constraints imposed on the rewiring possibilities (e.g. Chodrow, 2019) could help resolve this problem.

VI. RESAMPLING‐BASED REFERENCE MODELS

Resampling of network data is a bootstrapping procedure that generates reference models which can be further from the observed data (Fig. 1) than the permutation‐based methods we have discussed thus far. While generating reference models using permutations permits each observation to appear only once in the reference model (i.e. sampling without replacement), creating reference models using resampling (i.e. sampling with replacement) results in observations appearing more than once, or not at all, in each simulation iteration. This difference between the two approaches can change which features of the data are maintained and which ones are randomized. For example, if a researcher decides that an important feature of the social structure is the degree distribution, rather than the exact dyadic interactions between individuals, one can produce reference models by resampling from the observed degree sequence (i.e. the list of all observed degrees). Resampling from the degree sequence will produce reference networks with a similar degree distribution to the observed network, but the observed and reference networks might differ in the degree sequence and potentially also in the number of nodes and/or edges. One potential use of resampling‐based reference models is the ability to draw reference networks of different sizes and compare them (see Appendix S1, Section 3.2.1 for more details and caveats to using this approach). Resampling can be an effective tool when used with the raw data, however the only network‐level properties that can be sampled with replacement are the degree sequence and edge weights (e.g. Appendix S1, Section 3.2.1). Thus, a resampling approach is more specific and more limited than other approaches we present.

(1). Resampling raw data

An important utility of the resampling approach in behavioural studies is to resample the raw data that is the foundation of the network, rather than the network itself. For example, researchers of animal social networks often use the spatial positions of animals to infer interactions from co‐localization of individuals [two individuals being in the same place at the same time (e.g. Pinter‐Wollman et al., 2011; Mersch, Crespi & Keller, 2013; Robitaille, Webber & Vander Wal, 2019; Schlägel et al., 2019). A raw data resampling procedure could sample with replacement individuals’ locations from the observed locations, thus preserving the physical constraints on these locations. This approach restricts the sampling to biologically feasible locations so, for example, a terrestrial animal could not be resampled in the middle of a lake. We provide an example in Appendix S1 (Section 3.2.2) of resampling the foraging location of burbil subgroups separately for each of the 16 groups in our main study population. The resulting reference models maintain the observed subgroup memberships and locations are only sampled from within each group's home range.

The way in which the data are resampled could have a large influence on the reference model. For example, restricting the resampling of locations of particular individuals to only their own set of locations (e.g. Spiegel et al., 2016) will maintain home range sizes and average travel distances, and therefore, it might maintain the number and identity of individuals that each individual interacts with. Such a resampling procedure is more likely to result in reference models that are closer to the observed network structure, especially if non‐social rather than social considerations are important in generating this structure. Conversely, if individuals seek out conspecifics to interact with preferentially, then not having network constraints in the resampling procedure means that the resampling will break the temporal overlap between interacting individuals. Consequently, well‐designed resampling of locations can be useful to teasing apart non‐social and social explanations for network structure (Spiegel et al., 2016). Alternatively, one could allow resampling an individual's position from all observed positions of all individuals in the population. Such a resampling approach would require that it is biologically feasible for animals to move from one position to any other location in which animals were observed. Resampling that breaks the link between the identity of an individual and its movement patterns can produce reference models that differ considerably from the observed networks, for example, in the number of interactions among individuals. These reference models could be used to test the relative importance of non‐social factors that may drive interactions.

(2). Pitfalls for resampling‐based reference models

The first important pitfall to watch for when resampling network data is that certain resampled degree sequences cannot produce a network because they include too many edges or too many nodes. For example, if the sum of all degrees in a network ends up being an odd number after resampling the degree sequence of an unweighted network, a network cannot be generated. Next, when resampling the raw data that underlies the network, it is important to make sure that the resulting network is biologically feasible. For example, resampling of spatial locations could allow an individual to interact simultaneously with two individuals that are at opposite ends of the study site if not conducted with appropriate caution.

Finally, pitfalls of resampling‐based approaches also include over‐ or under‐sampling certain values and deviating from the observed network in unexpected ways. Such biased sampling is likely to be a particular issue for small networks in which the observed degree sequence represents a small sample from the degree distribution. For example, resampling from small degree sequences could lead to repeated sampling of a particular degree value that is an outlier in the observed degree sequence.

Alternatively, rare values of degree might be omitted in the reference model, leading to substantial changes in certain network measures. These biases could result in very broad or even multimodal reference distributions in some contexts, and potentially cause problems with inference. Test statistics that are based on edge strength could be highly impacted by resampling from the degree sequence, especially if the observed strength distribution is skewed. For example, resampling could alter the strength distribution of the reference network by omitting the tail of the distribution. The effects of resampling on different types of measures could become part of the research question if thought through carefully, otherwise it risks leading to erroneous inferences.

VII. DISTRIBUTION‐BASED REFERENCE MODELS

Reference models can emerge from general processes that shape a network rather than from the data itself. One can generalize the features of the observed network, as we detail in this section, or the processes that underlie the formation of the network, as we discuss in Section VIII. In Section VI we discussed resampling from the observed data; a further generalization of this approach is to create reference models based on inferences of the probabilistic description of the observed data, such as the degree distribution. Distribution‐based approaches can result in reference data sets that diverge from some of the specific characteristics of observed networks that are often preserved in permutation‐based reference model approaches (such as group size, or the number of interactions), making distribution‐based approaches a method for generating reference data sets which are more abstracted from observed data sets (Fig. 1).

There are a number of technical approaches for implementing distribution‐based randomization. To maintain the observed degree distribution in the reference models, researchers can either permute the network edges so that the reference network will have the exact same degree sequence as the observed network but is otherwise random (as described in Section V). Alternatively, researchers could create a reference network by resampling (with replacement) a new degree sequence from the observed degrees (as described in Section VI) or generate a network from the configuration model (as described in Section VIII). Resampling from the degree sequences is equivalent to drawing random samples from an empirical degree sequence defined as

$$P_k=\frac{\text{number of nodes with degree}k}{\text{total number of nodes}}$$

However, if the functional form of the underlying degree distribution is unknown, it is possible to draw random samples from a fitted distribution to obtain a new degree sequence and subsequently generate a network (Fig. 4). For example, in many social networks there are right‐skewed degree distributions in which most individuals have few interactions, and few individuals have many interactions. Such a degree distribution often fits a geometric distribution. Therefore, if researchers are interested in maintaining the shape of the distribution, but not necessarily the exact number of times each degree was observed, then reference models can be generated by resampling from a geometric distribution that has the same parameters as the observed data. Sampling from a fitted distribution can result in sampling nodes with degree k that were not present in the observed network, unlike the resampling approach detailed in Section VI. Sampling from a fitted distribution imposes fewer restrictions on the reference model, which can have both statistical and computational advantages.

Fig 4.

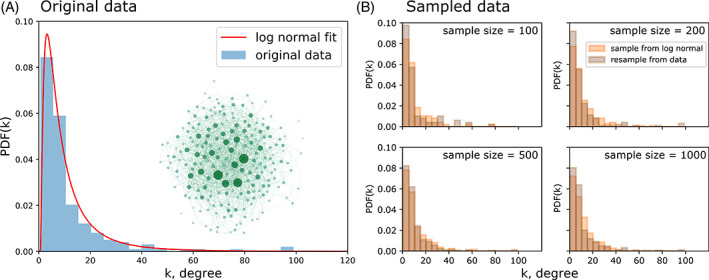
Drawing random degree sequences from the distribution‐based model. (A) Histogram of the degree sequence of the network shown in the inset and a fitted lognormal distribution (red line). (B) Random samples of different sizes (100, 200, 500, 1000 randomization iterations) drawn from the fitted lognormal distribution (orange) and by resampling the original degree sequence (grey). Network visualization was done using Gephi (Bastian, Heymann & Jacomy, 2009) with force atlas, a force‐directed layout. Node colour and size correspond to degree.

Drawing from a distribution can be thought of as sampling from a ‘smoothed’ version of the observed network. The biggest challenge is to find an appropriate statistical model for the fit. In many cases, finding an appropriate model can be done by fitting a parametric distribution to the data (for example, using maximum likelihood estimation) and drawing random samples from that distribution (e.g. Rozins et al., 2018). It is more convenient to fit continuous distributions, even when describing a discrete behaviour, and one should be conscious of the implications of various rounding procedures to turn the sample into whole numbers (Clauset, Shalizi & Newman, 2009). In some cases, there are efficient stochastic processes that can be used for the distributions‐based randomization approach. For example, to generate a network with the same degree distribution as the observed network, researchers can use the Chung‐Lu model, which draws an edge between every pair of nodes i, j, with probability proportional to k _i · k _j where k _i and k _j are the degrees of node i and j, respectively. Using this process would generate networks with degrees that were not present in the observed network, despite having similar degree distributions to the observed network.

Distribution‐based models can offer flexibility and robustness. They are especially useful when other randomization procedures result in too few unique reference networks that satisfy all the randomization constraints, i.e. there are not enough unique random samples to compare the observed with (e.g. in small networks, see Section V.3). Furthermore, the inferences from a distribution‐based randomization approach emerge from the statistical features of the observed data and therefore may uncover inherent patterns in the underlying social processes. However, selecting appropriate distribution‐based reference models can also come with challenges, which we outline below.

(1). Key pitfalls for distribution‐based reference models

An important potential pitfall when sampling from a distribution is failing to fit the correct distribution to the observed data and therefore simulating a reference data set that differs from the observed one in key parameters. For example, a uniform random network has a Poisson degree distribution. However, many real‐world social networks have overdispersed (right‐skewed) degree distributions (e.g. Rozins et al., 2018) and failing to account for this overdispersion in a distribution‐based reference model will lead to errors in inference.

A second potential pitfall arises when sampling independently from two distributions that co‐vary. For example, consider a theoretical distribution‐based reference model that preserves both the degree distribution and the distribution of clustering coefficients of an observed network. The clustering coefficient of a node measures the fraction of pairs of neighbours of that node that share a link. This quantity tends to co‐vary with degree, often in a negative direction, especially in networks with an assortative community structure (e.g. Fig. 5). The negative relationship between degree and clustering coefficient emerges from the fact that high‐degree nodes tend to connect different communities and therefore their friends are not tightly connected to each other because they belong to many different communities. In Fig. 5 we show a burbil association network with an assortative community structure in which node size corresponds to degree and node colour corresponds to clustering coefficient (see Appendix S1, Section 3.3). If a researcher ignored correlations between degree and clustering coefficient and sampled two sequences of numbers independently from the distribution in A and B respectively, the resulting distributions would mimic the data set individually but not jointly. We illustrate another example of failing to account for the correlation between two distributions (degree and mean edge weight) in Appendix S1 (Section 3.3). For some correlations there may be easy solutions to this co‐variance, for example if degree distributions differed between two sexes then they could be simulated separately for each sex. For other distributions (of network measures or in the raw data) it will be necessary to draw simulations from the appropriate multivariate distribution.

Fig 5.

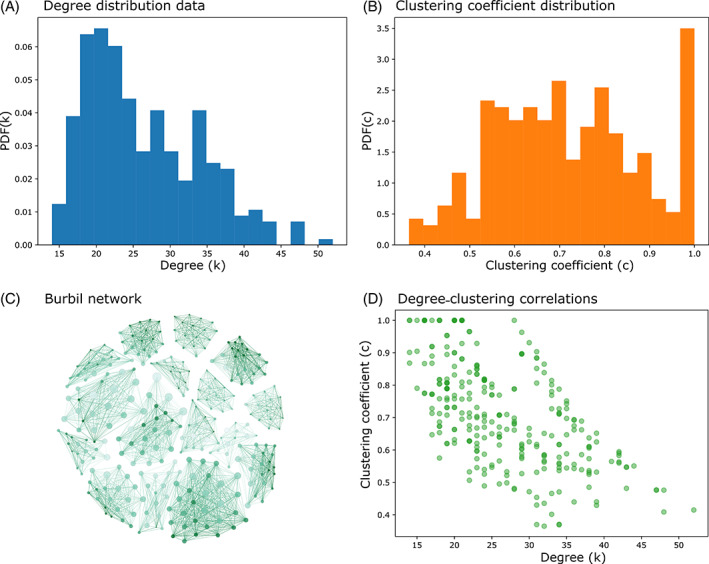
An illustration of covariance between two network properties in a burbil association network generated in Appendix S1, Section 3.3. (A) The degree distribution of the network. (B) The distribution of the clustering coefficient – the fraction of a node's friends that are friends with each other. (C) A visualization of the network where node size corresponds to degree and node colour corresponds to clustering coefficient [network visualization was done using Gephi (Bastian et al., 2009) with force atlas, a force‐directed layout]. (D) The correlation between clustering coefficient and degree in the network.

A third pitfall of using distribution‐based reference models is that it is not (currently) possible to simulate networks with fixed distributions of many social network measures, one example being clustering coefficient (as per the example above). For a fixed number of nodes and edges, or for a fixed degree distribution, we know how to sample a network uniformly over all networks with such properties. However, conducting such uniform sampling can be done for very few other network properties.

Researchers often use reference models that do not sample uniformly from the space of all networks with a given property, but rather use reference models that happen to have properties that are close to the network in question (like the generative models in Section VIII). It is important to understand the difference between sampling uniformly over all networks with a given property and sampling from a set of networks that tend to have the property while also having other constraints on their structure, because of the influence that these sampling methods will have on the inference process. These potential pitfalls of generating distribution‐based reference models limits the contexts in which such randomization can be applied.

VIII. GENERATIVE REFERENCE MODELS

Generative models produce a set of reference networks according to stochastic rules or processes which encode assumptions about how the network was formed. Thus, generative models are like recipes for creating networks from scratch. For instance, a researcher might know the behavioural rules that typically underlie the formation of interactions and might therefore create a network‐forming generative model that instantiates those rules. However, care must be taken when modelling networks using such general rules about interaction formation because they have the potential to produce reference networks that are very different from those observed, despite sharing the same number of nodes, links, or other high‐level features. In particular, when a generative process is fundamentally non‐biological, that generative model may be a poor reference model because it differs too dramatically – and implausibly – from the observed network.

One example of a common but usually implausible reference model used in studies of animal behaviour is the uniform model G(n, p) (Gilbert, 1959), also referred to as the Erdős–Rényi (ER) model. This model produces reference networks according to a simple recipe: begin with n nodes, and then place a link between each pair of nodes with probability p, independently of other pairs. While this model has the potential to create any simple network, i.e. a network without self loops or multiedges, it is designed to maximize entropy and uniformity, and is therefore unlikely to mimic any of the features of a network arising from animal behaviour. Indeed, even animals following a Brownian motion rule in space will encounter each other in a way that is constrained by physical distance and barriers (Pinter‐Wollman, 2015) meaning that even random encounters are poorly captured by the uniform reference model. Another example of a common reference model is the configuration model, introduced in Section V. While the configuration model is commonly associated with the degree‐preserving permutation of edges via rewiring, it is also simply a modified uniform model with more constraints: it chooses uniformly from all networks with a given degree sequence. The configuration model differs from G(n,p) in two key ways, by (i) having a fixed and non‐random degree sequence and number of edges, and (ii) potentially containing self‐loops and multi‐edges. The configuration model is a generative reference model, for which there are a large number of different variations (Fosdick et al., 2018).

There is no shortage of generative models for networks. In fact, many common statistical models of networks, which we may usually think of as models to fit to data, are generative, including exponential random graph models (ERGMs: Lusher, Koskinen & Robins, 2013; Robins et al., 2007; Snijders et al., 2006) and stochastic block models [SBMs (Bollobás, 1980; Snijders & Nowicki, 1997). Just as with other classes of reference models, generative reference models require the careful consideration of the research question and hypothesis to inform the choice of the generative rules. For instance, ERGMs are dyadic models that can be used to test hypotheses about which features of dyads affect the presence or strength of edges. By including sex as an explanatory variable in an ERGM, it becomes possible for there to be differences between the likelihood of edges between female–female, female–male and male–male dyads. We illustrate some simple examples of the use of these models in our burbil case study. In Appendix S1 (Section 3.4.1) we fit an ERGM to a within‐group dominance network simultaneously to test hypotheses about the role of individual traits in explaining dominance relationships and an SBM to a population‐level association network to examine how well the community structure of the association network is explained by group membership.

A class of system‐specific generative reference models are agent‐based models (ABMs). In network analysis, ABMs can be spatially explicit or socially explicit. Spatially explicit models can help reveal the role of spatial behaviour in explaining social network structure. For example, a generative model in which the movement of individuals is constrained by the spatial organization of the environment could be used to test whether spatial constraints are sufficient to explain social structure. Researchers could further include differences in spatial behaviour between individuals within such an ABM (Pinter‐Wollman, 2015). In Appendix S1 (Section 3.4.2) we use a spatially explicit agent‐based model to test whether the space use of burbils can explain patterns of between‐group associations. Note that if we do not include any social component in the model then while our reference network is correlated with the observed network, it predicts far too many between‐group associations.

Socially explicit ABMs incorporate social behaviour (e.g. interaction preferences). One example of a socially explicit ABM in the study of animal behaviour is the social inheritance model, in which offspring are likely to form connections with friends of their parents while avoiding parents’ enemies (Ilany & Akçay, 2016). While such a mechanism is highly likely, and indeed has been supported in some social systems, such as spotted hyenas, Crocuta crocuta (Ilany, Holekamp & Akçay, 2020), this model requires knowledge about relatedness and historical interactions, or long‐term relationships, that are not available in all study systems. In our burbil case study in Appendix S1 (Section 3.4.2) we develop two socially explicit agent‐based models that build on our spatially explicit model. The first uses knowledge about burbil subgroup size to simulate burbils moving within groups rather than independently. The reference network generated is much more similar to the observed network than the previous version, which was only spatially explicit. We then test the hypothesis that ‘clan’ membership (burbil groups belong to three distinct clans) can help explain patterns of between‐group associations. When we include clan membership in our ABM, the reference model produces a network that is very similar to the observed one, suggesting that clan membership can indeed explain the observed social interactions. In reality we would replicate these ABMs 1000 or more times to generate a full reference distribution rather than providing a single comparison, which we did to reduce computational time.

(1). Key pitfalls for generative reference models

Comparing observed data with generative reference models provides insights about what processes might underlie observed interactions, and what processes might not. However, as a note of caution, it is possible to create the same types of networks with multiple generative processes – multiple recipes can generate similar patterns. Therefore, when observed data match a generative reference model, it does not necessarily mean that the modelled generative process is indeed the biological process that actually generated the observed network. Instead, it means that the modelled generative process is a plausible hypothesis that needs to be tested mechanistically.

Further, as generative models become more and more complicated, constraints on one property that is being modelled can have cascading effects on other properties. Complicated generative models with many parameters can result in one desirable property while other properties of the model remain poorly understood. Furthermore, complicated models require the specification of many parameters, which, if mis‐specified, can produce reference distributions that differ significantly from observations, leading to spurious conclusions. Uniform and configuration models have enjoyed much usage because their complete distributions, constraints, and correlations among their properties are well understood. However, these simple models might not encapsulate all the biological complexities a researcher might be interested in. As we experiment with more exotic and complex generative models, which capture more realistic aspects of observed behaviour, it is increasingly important to check carefully for the unintentional creation of fundamentally unrealistic patterns and behaviours in our reference models. Such unrealistic patterns can be identified through an iterative approach, for example, by going back to the study system and asking if patterns observed in the reference models are feasible in real life.

IX. CONCLUSIONS

1. We provide an overview of the process and caveats of using reference models when analysing social networks. We detail common approaches to generating reference distributions that increase in level of abstraction with respect to the observed data set.

2. We highlight the strengths and weaknesses of each approach, drawing attention to common pitfalls that can arise when using them.

3. Our goal is to provide a guide for researchers using social network analysis for hypothesis testing in diverse study systems. We anticipate that our overview will help researchers appreciate the similarities and differences between different analytic approaches better and also encourage greater confidence in designing appropriate reference models for their research questions.

4. Our key message is that the construction of reference models should depend closely on both the research question and study system and that the use of generic approaches applied without careful evaluation as to their suitability can lead to incorrect inferences.

Supporting information

Appendix S1. A guide to choosing and implementing reference models for social network analysis.

Appendix S2. Supporting Information