Diversity begets diversity during community assembly until ecological limits impose a diversity ceiling

Abstract

Microbial communities are hugely diverse, but we do not yet understand how species invasions and extinctions drive and limit their diversity. On the one hand, the ecological limits hypothesis posits that diversity is primarily limited by environmental resources. On the other hand, the diversity‐begets‐diversity hypothesis posits that such limits can be easily lifted when new ecological niches are created by biotic interactions. To find out which hypothesis better explains the assembly of microbial communities, we used metabolic modelling. We represent each microbial species by a metabolic network that harbours thousands of biochemical reactions. Together, these reactions determine which carbon and energy sources a species can use, and which metabolic by‐products—potential nutrients for other species—it can excrete in a given environment. We assemble communities by modelling thousands of species invasions in a chemostat‐like environment. We find that early during the assembly process, diversity begets diversity. By‐product excretion transforms a simple environment into one that can sustain dozens of species. During later assembly stages, the creation of new niches slows down, existing niches become filled, successful invasions become rare, and species diversity plateaus. Thus, ecological limitations dominate the late assembly process. We conclude that each hypothesis captures a different stage of the assembly process. Species interactions can raise a community's diversity ceiling dramatically, but only within limits imposed by the environment.

1. INTRODUCTION

Bacterial life on Earth is extraordinarily diverse. Our planet is inhabited by an estimated 1.4–1.9 million bacterial lineages (Louca et al., 2018), and every gram of soil hosts between 2000 and 18,000 distinct such lineages (Daniel, 2005). Understanding how Earth holds all this biodiversity is a fundamental challenge to ecology and evolution. Part of the difficulty in meeting this challenge is that planet Earth offers limited resources, which may impose a ceiling on biodiversity. In this vein, the prominent “ecological limits” hypothesis of biodiversity (Rabosky & Hurlbert, 2015; Schluter & Pennell, 2017) posits that rates of diversification should decrease as diversity increases and fills available ecological niches. In contrast, the “diversity begets diversity” hypothesis posits that diversity could stimulate further diversification (Calcagno et al., 2017; Whittaker, 1972) as species–species interactions get more complex and novel niches are created (Erwin, 2008; Laland et al., 1999), or as existing niches are partitioned more and more finely as a result of competition (Bailey et al., 2013; Dieckmann & Doebeli, 1999).

Evidence for either hypothesis in bacteria, animals and plants is mixed. For example, a combination of field work and phylogenetic analysis of Himalayan songbirds suggests that an observed slowdown in their speciation rate is explained by niche filling. Their species distributions are well explained by resource abundance (Price et al., 2014). Two evolution experiments with Pseudomonas fluorescens strains also support the ecological limits hypothesis (Brockhurst et al., 2007; Gómez & Buckling, 2013). In these experiments a strain's diversification slowed down as more strains were included in a coculture. Conversely, similar experiments with different strains of P. fluorescens support the “diversity begets diversity” perspective. These experiments tracked the diversification of a focal lineage of P. fluorescens in bacterial communities that harboured from one to eight lineages of P. fluorescens. More novel morphotypes evolved when communities were initially more diverse (Jousset et al., 2016). Further support for the “diversity begets diversity” hypothesis comes from experiments with crops and weeds, which show that weed diversity is high whenever crop diversity is high (Palmer & Maurer, 1997). It also comes from data on plant and arthropod diversity on the Canary and Hawaiian islands, where the proportion of endemic species increases with increasing species numbers (Emerson & Kolm, 2005). It also comes from inferences of microbial diversification rates from several taxonomic ratios, such as the species to genus ratio (Madi et al., 2020). In addition, theoretical modelling using adaptive dynamics also suggests that some initial diversity can facilitate further diversification (Calcagno et al., 2017).

The diversity of a community may increase both through ecological processes, as species disperse and invade a community, or through evolutionary processes, as existing member species diversify and speciate. Pertinent evidence on the ecological limits and diversity‐begets‐diversity hypotheses comes in part from experiments or field work that only quantify diversification rates, making it difficult to disentangle ecological from evolutionary limitations. However, the hypotheses should ideally be distinguished by considering both evolutionary and ecological processes. In a scenario where one can control the appearance of new species in a community, either because they evolve in the community or disperse into the community, will environmental resources constrain community diversity, or will species–species interactions promote ever‐increasing diversity? This is the question we aim to answer here.

To this end, we used a very simple community assembly strategy inspired by the environmental filter metaphor (Levy & Borenstein, 2013; Thakur & Wright, 2017) and by trait‐based models (Mcgill et al., 2006). Such models organize ecological processes around traits—species properties that impact species survival. Typically, species show trade‐offs in these traits, and a trait that gives a species an advantage in one environment might be disadvantageous in another. The environment selects (filters) species according to their traits. This modelling strategy has been widely successful, for example to predict community composition along environmental gradients (Allison, 2012; Laughlin et al., 2012; Litchman & Klausmeier, 2008; Mcgill et al., 2006; Thakur & Wright, 2017). Here, we use it to model the assembly of microbial communities, where a trait refers to a species’ ability to thrive on a specific source of carbon and energy.

We simulated the assembly of microbial communities in which we represent each individual species by a metabolic network that comprises thousands of metabolic reactions needed for an organism's survival in a given chemical environment. The advantage of this approach is that it allows fundamental metabolic traits to emerge from first biochemical principles, which are embodied in the metabolic reaction network of an organism. Especially important traits for our purpose include the ability to survive on a given source of carbon and energy, and on the ability to excrete specific by‐products of metabolism. Traits like these can be computationally predicted with flux balance analysis (FBA; Orth et al., 2010), an experimentally validated (Orth et al., 2011; Varma & Palsson, 1994) computational method that can determine the flux of matter through every reaction in a metabolic network when cells are in a metabolic steady‐state, and when they grow their biomass is at the maximum possible rate given the biochemical reactions they can catalyse. FBA has been successfully used to predict growth and by‐product secretion of bacteria in different media (Edwards et al., 2001; Ibarra et al., 2002; Varma & Palsson, 1994).

Metabolic networks have been characterized for hundreds of organisms (Gu et al., 2019a). They are highly valuable to understand metabolic biology and evolution because they reflect an organism's evolutionary history. For the same reason, however, they are of limited use for studies like ours, which aim to understand how community assembly may be affected by specific metabolic properties of the assembled species, such as the number of biochemical reactions any one species harbours, and the number of carbon sources it can utilize. For this purpose, one needs to vary these properties systematically, but in the network of any one organism, they are fixed. To circumvent this limitation, we started our community assembly not from previously characterized metabolic networks of microbial species. Instead, we randomly sampled (with a Markov chain Monte Carlo [MCMC] method) thousands of metabolic networks from a much larger “universe” or “pan‐metabolism” of biochemical reactions, such that each network fulfilled specific requirements. These requirements include the ability to sustain life on specific carbon sources such as glucose, while containing an otherwise random complement of chemical reactions. We refer to such metabolic networks as random viable networks. For the purpose of our analysis, each such network represents a different “species,” and we used these “species” to simulate the assembly of a community in a well‐mixed chemostat‐like environment where resources are supplied by the environment at a constant rate.

Our community assembly procedure consists of three iterated steps (Figure 1). First, a random species invades the environment/community. Second, the environment acts as a filter that selects those species that persist in the community. Third, the persisting species may change the environment by excreting metabolic by‐products. We repeated these three assembly steps for thousands of species invasions in any one community, and simulated hundreds of community assemblies in environments with different amounts of resources and varying strengths of competition.

FIGURE 1.

Modelling community assembly. (a) The three steps we used to model community assembly. (I) Species (modelled as random viable metabolisms) are added at random to a standing community. (II) The environment acts as a filter, selecting successful species, that is those best at growing on at least one of the carbon sources available in the environment. Successful species persist in the community. (III) The species that comprise the community modify the environment through the excretion of metabolites that can serve as carbon sources for other species. (b) Example assembly trajectory of one community up to the invasion of the fourth species. Simulations begin by initializing the composition of the environment, shown as a purple rectangle at the top. The presence of each of the 223 potential carbon sources is represented as a purple vertical bar, such that each location on the horizontal x‐axis corresponds to one carbon source. In this example and in most of our simulations (unless otherwise stated), the initial environment contains glucose as the sole carbon source, which is indicated in the top rectangle by the single vertical purple line. After establishing the initial environment, we perform the first invasion with “species 1” chosen at random from our MCMC‐derived sample of random viable networks. The species’ ability to grow on each potential carbon source (whether or not the carbon source is present in the environment) is shown in the green rectangle by a green line in the x‐position that corresponds to the specific carbon source. Darker green lines indicate higher growth. Species 1 can grow on the only available carbon source (glucose), and because no other species is yet present, we consider species 1 successful. Species 1 modifies the environment with the excretion of by‐products of its growth on glucose, as shown in the second purple rectangle from the top. These by‐products are available as potential nutrients for the second round of assembly. In this round, a randomly chosen species 2 invades the community. Its growth rate on each carbon source is shown below that of species 1. Species 2 cannot grow faster than species 1 on any of the available carbon sources. It therefore goes extinct and only species 1 persists in the community. The carbon sources it excretes are available for the third assembly step. Each such step consists of a new round of (I) species invasion, (II) environmental filtering and (III) niche construction

During community assembly, we found that many persisting species excrete metabolic by‐products, which can sustain species that invade later through cross‐feeding interactions in which one organism consumes the excretion of another. In other words, species create opportunities for cross‐feeding, which begets further diversity. Further, we find that communities grow more diverse when competition among species is stronger. Together, these two observations show that biotic interactions between species are critical to establishing diverse communities. At the same time, communities show limits in the number of species they accommodate. As community richness increases, the probability that a new species successfully invades a community decreases. The reason is that by‐product excretion cannot create new niches ad infinitum. Eventually all new niches have been created, and subsequent invasions mostly fill the existing niches. At this late stage, the assembly dynamics enters an “ecological limits” regime.

2. METHODS

2.1. Flux balance analysis

FBA is a computational method to predict metabolic flux—the rate at which chemical reactions convert substrates into products—through all biochemical reactions that make up the organism's metabolic network (Orth et al., 2010). FBA requires information about the stoichiometry of all chemical reactions in the metabolic network, which is mathematically represented in the stoichiometric matrix S of size m × r. The integer m denotes the number of metabolites, and the integer $r$ denotes the number of reactions in the network. Each entry S_ij of the stoichiometric matrix contains the stoichiometric coefficient with which metabolite i participates in reaction j. FBA makes two central assumptions. The first is that cells effectively optimize some metabolic property such as growth rate (v _growth). The second is that cells (metabolisms) are in a metabolic steady state. Additional constraints can be incorporated into the optimization problem that FBA solves by setting lower bounds l_i and upper bounds u_i to individual reaction fluxes v_i , in order to account for the thermodynamic and enzymatic properties of a biochemical reaction (Orth et al., 2010). The optimization problem that FBA solves can be formalized as a linear programming problem (Orth et al., 2010; Varma & Palsson, 1994) in the following way:

$$\begin{array}{cc}& \text{Maximize}{v}_{\text{growth}}\hfill \\ \hfill & \mathrm{s}\text{.t}.Sv=0\hfill \\ \hfill & l_i\le v_i\le u_i\hfill \end{array}$$

We performed FBA with cobrapy (Ebrahim et al., 2013).

2.2. Modelling species with random viable networks

We sampled random viable networks with a computational variant of MCMC sampling, which permits efficient sampling of the large space containing all possible metabolic reaction, that is, the pan‐metabolism. For our work, we used a pan‐metabolic network comprising 5625 metabolites and 7222 biochemical reactions (Barve & Wagner, 2013; San Roman & Wagner, 2018). To sample random viable networks, we began with a specification of desired metabolic characteristics. For example, for many of our analyses, we wanted to create networks that are at least viable on glucose as a sole carbon source, and that comprise as many reactions as Escherichia coli (i.e., 2583 reactions in the widely used E. coli metabolic model iJO1366). To identify a single initial network fulfilling these requirements, we first performed FBA on the pan‐metabolic network (Barve & Wagner, 2013; San Roman & Wagner, 2018) in a chemically minimal environment with glucose as the only source of carbon. Of all reactions in this pan‐metabolic network, 1263 reactions showed nonzero metabolic flux. We included all these reactions in the initial network, which ensured the network's viability on glucose. We then chose the remaining (1320) reactions needed to arrive at an equal number of reactions as the E. coli metabolism at random (with a uniform distribution) from the pan‐metabolic network.

This initial network was the starting point of MCMC sampling from the space of all possible metabolic networks. The MCMC procedure performs a long random walk through this space. Each step in this walk consists of a reaction swap, in which a reaction from the current network is randomly chosen for deletion, while a randomly chosen reaction from the pan‐metabolism but absent in the current network is added to the current network (without changing reaction reversibility or stoichiometry). If the modified network remains viable after this reaction swap, the swap is accepted, and the network is modified with a further reaction swap. In contrast, if the reaction swap disrupts viability on the desired carbon source(s), such as glucose, the swap is rejected and a new swap is tried. Modifying metabolic networks through reaction swaps ensures that the number of reactions in the network remains constant and equal to the number of reactions in the initial network.

This MCMC procedure creates a long sequence of metabolic networks, all of them viable on the desired carbon sources. As the number of reaction swaps increases, the number of reactions that the altered network shares with the initial network becomes smaller and smaller, until its complement of reactions becomes effectively randomized, which occurs after ~5000 successful swaps (Samal et al., 2010). We stored such a randomized network for further analysis after 5000 successful swaps, and repeated this procedure from the initial network to create 1000 random networks viable on specific carbon sources, such as glucose. During this process we did not alter the exchange reactions of the starting network, which ensures that in the randomized networks the same metabolites can be exchanged with the environment as in E. coli. Furthermore, we used the biomass reaction from E. coli iJO1366 to assess the viability of networks during MCMC sampling. The random viable networks used in this study are available in GitHub at https://doi.org/10.5281/zenodo.5206841.

2.3. Potential carbon sources

We performed FBA to examine all metabolites that the pan‐metabolic network could use as a sole carbon source (San Roman & Wagner, 2018). To this end, we considered those carbon‐containing metabolites which have an exchange reaction in the E. coli model iJO1366, and we used the biomass reaction of the same E. coli model in the pan‐metabolic network. We performed FBA with the pan‐metabolism in a simulated environment in which one candidate carbon source was available at a time and assumed that ammonium, calcium, chloride, cobalt, copper, iron, magnesium, manganese, molybdate, nickel, oxygen, phosphate, potassium, protons, sodium, sulphate and zinc were available in the environment in nonlimiting amounts. We considered a metabolite a “potential” carbon source if it allowed biomass production of the pan‐metabolism. We identified 223 potential carbon sources. Any metabolism sampled from the pan‐metabolic network will be viable on a subset of these carbon sources.

2.4. Identifying species traits with FBA

For every random viable metabolic network (“species”) we considered, we used FBA to determine its viability on all 223 potential carbon sources. To this end, we performed FBA in a minimal environment where only one potential carbon source was available at a time, as explained in the previous section. The result was a predicted biomass growth flux for each species on each of the 223 potential carbon sources. We used these predicted growth rates in the second step of our simulation of community assembly (i.e., in the environmental filtering step).

We also used FBA to analyse the niche construction potential of every species. We were interested in those metabolites that could be excreted by one species, and thus potentially serve as carbon sources for some other species. Therefore, we identified those metabolites from the list of potential carbon sources that could be produced as a by‐product of growth when a species consumes a given carbon source. To this end, we allowed consumption of this carbon source (with a maximal uptake rate of 10 mmol gDW⁻¹ h⁻¹) in an otherwise minimal environment, and maximized the production of each potential carbon source, while constraining the species’ biomass production to be greater than zero. If a potential carbon source could be produced at a rate greater than zero under this constraint, we considered that the carbon source was excreted into the environment.

This modelling decision is motivated by two kinds of experimental observations. First, microbes modify their environment by secreting multiple metabolites. For instance, targeted metabolomics experiments show that Saccharomyces cerevisiae, E. coli, Bacillus licheniformis and Corynebacterium glutamicum excrete 30–40 metabolites due to overflow metabolism (Paczia et al., 2012). (Untargeted metabolomics might reveal an even greater diversity of secreted metabolites.) Second, metabolic modelling tends to underestimate secretions found experimentally, regardless of whether it maximizes microbial growth rate (Pinu et al., 2018).

3. RESULTS

3.1. Modelling community assembly

We first created a pool of 1000 species, from which we sample individual species for community assembly. Each species is represented by a metabolic network that we require to be viable—it can synthesize all essential biomass molecules such as amino acids, lipids and nucleotides (see Section 2)—on a specific carbon source, but that contains an otherwise random complement of biochemical reactions from a much larger universe (“pan‐metabolism”) of biochemical reactions known to take place in the biosphere. To create this species pool, we used an MCMC sampling procedure, which allows us to create random viable metabolic networks with specific characteristics (see Section 2). For most of our analysis these characteristics are that, first, all species (metabolic networks) contain the same number of 2583 metabolic reactions as the well‐established and widely used metabolic model iJO1366 of Escherichia coli (Orth et al., 2011). Second, all species are permeable to the same 330 metabolites that E. coli cells can import or export (Orth et al., 2011). Third, we require all species to be viable on the same carbon source, glucose. We note that as a result of metabolism's complex and reticulate structure, species required to be viable on one carbon source are usually also viable on multiple others (Barve & Wagner, 2013). (We relax these constraints in later analyses (Figures S4 and S6)

We used FBA (see Methods) to determine viability for each of our 1000 species on 223 potential carbon sources (see Section 2), and found that one species is viable on an average of 32 ± 10 different carbon sources (Figure S1). We consider the carbon sources on which any one species is viable as the species’ fundamental ecological niche. Together, all 1000 species are viable on 220 different carbon sources. On average, 15 ± 13% of the species are viable on each carbon source. In addition to viability, we also determined the metabolic by‐products of growth that any one species excretes when growing on any one carbon source. We found that on average each of our species excretes 23 ± 4 metabolic by‐products when growing on glucose, which is comparable to the number of secretions found in microbes such as E. coli or Saccharomyces cerevisiae (Methods; Paczia et al., 2012).

We began our community assembly process with a deliberately simple chemical environment, which supplies only one carbon source—glucose—at a constant rate. In other words, in this initial environment only one metabolic niche exists. Community assembly then consisted of multiple iterations of the following three steps (Figure 1):

1. Species invasion: a species is introduced into the environment/community. This step simulates the invasion of the community by a species, or the evolutionary origin of a new species within a community. Each such species is selected at random from our species pool with equal probability. The same species can be selected multiple times in the course of assembling one community.

2. Environmental filtering: the environment serves as a filter selecting those species from the community that can persist in the environment. Specifically, we assume that those species that persist achieve the highest biomass growth among all present species, when consuming at least one of the available carbon sources in the environment. All other species go extinct. This modelling decision is based on the competitive exclusion principle (Hardin, 1960), which states that species cannot coexist if they compete for the same limiting resources. This second step embodies competition between species in the community (Levy & Borenstein, 2013). We apply this filtering method because simulating the population dynamics of all species in each community is computationally infeasible, given that we simulate thousands of invasion steps in each of the hundreds of communities we assemble for each analysis.

3. Niche construction: all species that make up the community at a given time modify the environment by excreting by‐products of metabolizing the carbon sources they use for growth.

We repeated this three‐step process for 5000 invasions, at which point the number of species in the communities no longer increases. In addition, we repeated the entire process of community assembly 500 times.

Figure 2a shows the assembly dynamics for 50 randomly chosen communities out of a total of 500 assembled communities, where each community had experienced up to 5000 individual species invasion events. Figure 2a shows that the number of persisting species (community richness, akin to alpha‐diversity; Krebs, 2014) increases rapidly until it plateaus before 5000 species invasions. A final assembled community harbours on average 35.9 ± 0.4 species (based on 500 assembled communities). Final species richness varies somewhat, and ranges from 33 to 38 species. Collectively, the final 500 communities harbour 64 different species, which implies extensive overlap in the species making up different communities. This suggests that the order in which species invade the community has little effect on the community composition.

FIGURE 2.

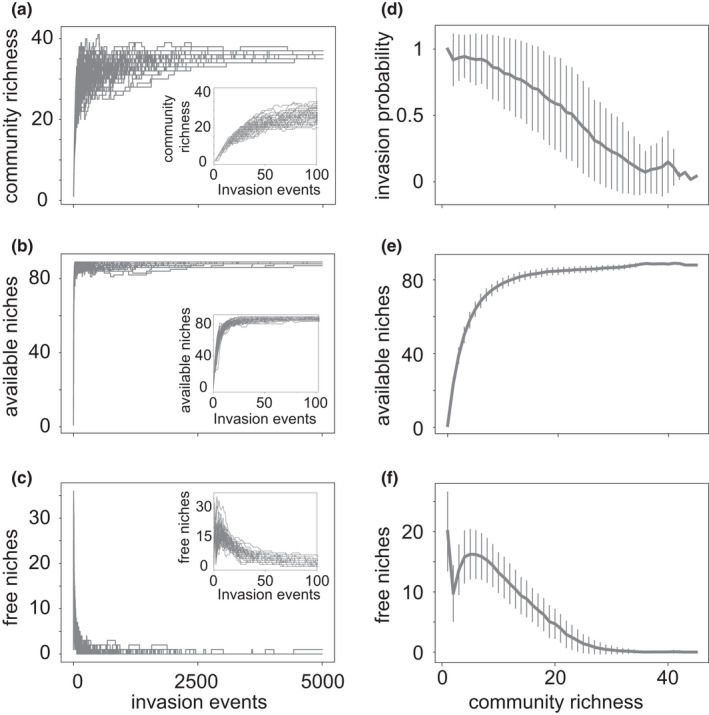
Species and niche dynamics during community assembly. (a–c) The horizontal axis shows time (number of species invasion events) during community assembly. The vertical axes show (a) community richness (number of species), (b) number of available niches (carbon sources in the environment) and (c) number of free niches (carbon sources present in the environment and not consumed by any species in the community). The insets show the same data but for up to 100 invasions. (d–f) The horizontal axis shows community richness. The vertical axes show (d) invasion probability (number of trials before a successful invasion), (e) the number of available niches (carbon sources) and (f) the number of free niches as a function of community richness. The plots show data from 50 (a–c) or 500 (d–f) assembled communities. During assembly, each community was subject to 5000 species invasion events. Error bars in (d)–(f) indicate one standard deviation

Figure 2b shows that the number of available metabolic niches (i.e., the number of carbon sources present in the environment) also increases rapidly. This increase results from the excretion of an increasing number of metabolic by‐products as a community comes to host more and more species. At the same time, an increasing number of species also consume an increasing number of carbon sources. This is why the number of free niches (i.e., the number of carbon sources that are not consumed by any species in the community) only rises early during community assembly (Figure 2c). It reaches a peak after approximately six species invasions, and then declines slowly to zero. In other words, late in the assembly process, newly invading species are more likely to consume existing carbon sources (which are excreted by resident species) than they are to lead to the excretion of new carbon sources.

We determined the probability that a new species invasion is successful (i.e., that the invading species persists) as the number of invasion events that take place before a successful event occurs. Figure 2d shows that this probability declines monotonically with the number of species in a community. Figure 2e,f show the number of available and free niches as a function of community richness, averaged over 500 communities. The underlying data show that merely 12 ± 2 species are needed to construct 90% of the maximal number of available niches (Figure 2e). When a community hosts more than 6 ± 2 species, a successful species invasion begins to create fewer niches than it fills (i.e., the number of newly excreted carbon sources becomes smaller than the additional number of carbon sources consumed). As a consequence, the number of free niches stops increasing and starts decreasing (see peak in Figure 2f).

Together, the data in Figure 2 demonstrate how important biotic interactions and in particular the construction of new metabolic niches is to the assembly process we studied. In the absence of niche construction, our environment could have only accommodated the single species that is best suited for growth on the only carbon source initially available in the environment (Hardin, 1960). However, the construction of new niches does not continue throughout the assembly process. Towards the end of this process, newly invading species are more likely to fill existing niches than to help create new ones.

3.2. More complex environments lead to more diverse communities

Thus far, we had assembled communities starting from the simplest possible environment, which contains only a single carbon and energy source. We next wanted to find out how abiotic environmental complexity (i.e., the number of resources in the environment) affects community assembly. We hypothesized that more complex environments sustain richer communities, because they harbour more niches that are independent of any one species’ metabolic excretions. To validate this hypothesis, we assembled communities in environments that contained one, five, 10, 15 or 20 carbon sources. All these environments contained glucose, and we selected the remaining carbon sources at random from the list of 223 potential carbon sources (see Section 2).

Indeed, environments offering more resources lead to more diverse final communities (Figure 3). However, the complexity of the environment does not translate one‐to‐one into final community richness. For example, an environment that offers 20 times more resources than the simplest environment results in communities that sustain only 4.0 ± 0.1 additional species (Figure 3). We also found that the invasion probability as a function of community richness is modestly but consistently higher for the most complex environment (Figure S3a). We also observed more available and free niches in the initially complex environment than in the simple one (Figure S3b,c).

FIGURE 3.

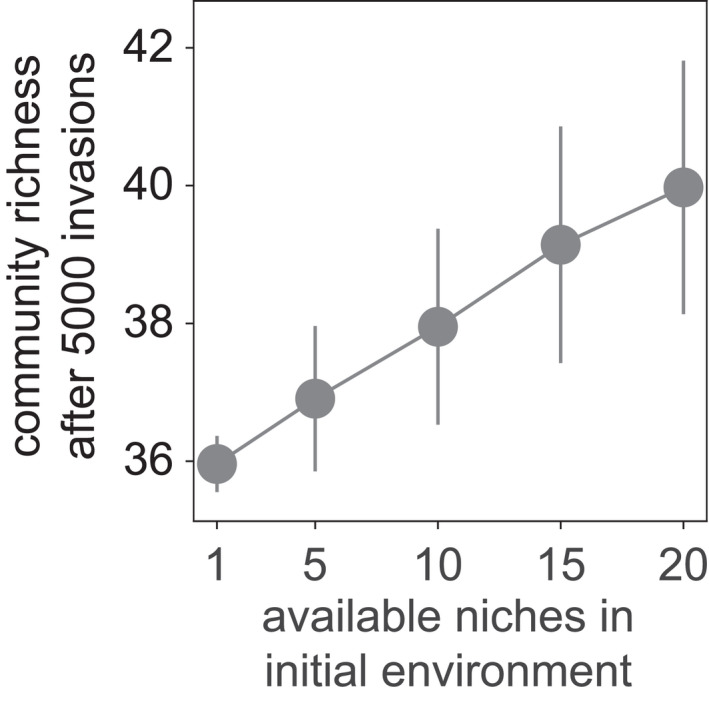
Richer initial environments lead to richer final communities. We simulated the assembly of communities in environments that offered between one and 20 carbon sources (horizontal axis) at the beginning of community assembly. The vertical axis shows the number of species (community richness) at the end of a community assembly process consisting of 5000 species invasions. Circles show means obtained from the assembly of 500 communities. Bars indicate one standard deviation

3.3. Competition narrows the realized niche of species

Classical competition theory (Hutchinson, 1959) argues that competition is the major biological process controlling the structure of natural communities. Quantifying competition is generally difficult (Krebs, 2014) but our method allows us to quantify and manipulate competition strength in two ways. In this section, we explore how competition affects community richness. Specifically, we model exploitative competition (Tilman, 1982) for limiting carbon sources, and do so in two complementary ways. First, we change the number of species that compete for the available resources. Second, we change the species’ fundamental niche width. We next describe both approaches in more detail.

We first varied the strength of competition by changing the number of species that can invade a community (i.e., by changing the size of the species pool). In the previous section, we had assembled communities through iterative species invasions, where we had chosen invading species from a pool of 1000 species. To strengthen competition, we now changed the pool size to 250, 500 or 750 species, sampled at random from the original set of 1000 species.

As the size of a species pool becomes larger, the likelihood that any one species is the fastest‐growing among all species on any one carbon source is lower, which means that competition for resources gets stronger. In Figure 4a we show how increasing the species pool size does indeed decrease the likelihood that any one species from the pool is the fastest‐growing. To calculate this likelihood we first computed the average number of resources on which a species showed the highest growth. This quantity varies between zero (if the species grows worse than any other species from the pool on all carbon sources) and one (if the species grows better than all other species on all carbon sources). We repeated this calculation for every species in a pool, and calculated the average for all species in the pool. We then repeated this analysis 500 times, each time for a different random pool of species (that comprised 250, 500 or 750 species). Figure 4a reports the average over these 500 replicates.

FIGURE 4.

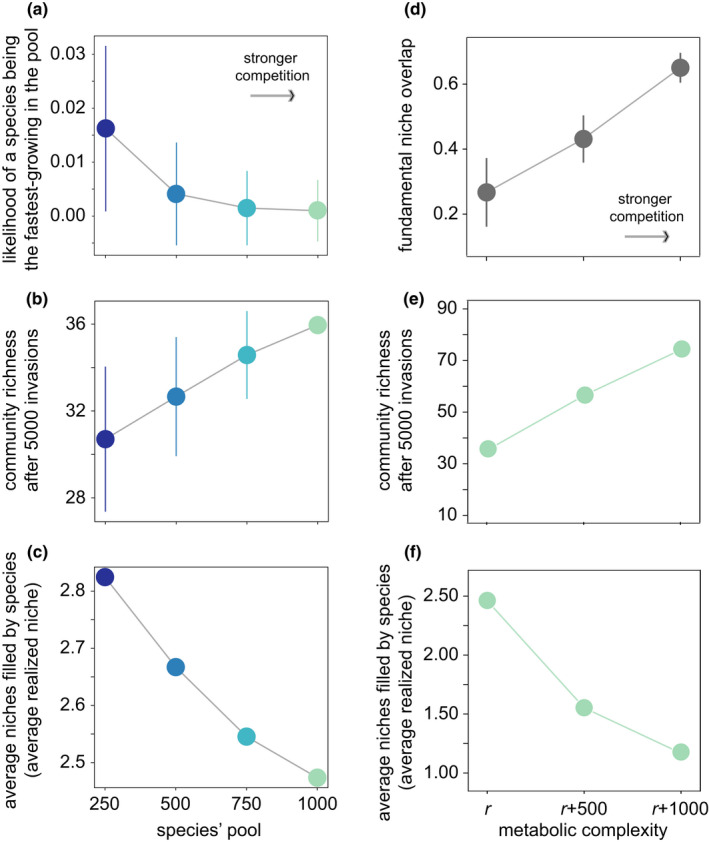
Competition causes a narrower division of available niches. (a–c) The horizontal axis shows the number of species in the species pool from which communities are assembled. Larger species pools imply higher competition among species. Vertical axes show (a) the probability of a species to be the fastest growing on a carbon source, averaged across carbon sources and across the whole pool, (b) community richness (number of species) and (c) average number of niches filled by each species (average realized niche, quantified as the number of available niches minus the number of free niches and divided by the total number of species in a community). (d–f) The horizontal axis shows the metabolic complexity of the species used for community assembly, that is their total number of biochemical reactions relative to the reference r = 2583 of Escherichia coli model iJO1366. (d) The vertical axis shows the average overlap in fundamental niche between two species pairs, quantified as the number of carbon sources on which both species can grow, divided by the union of carbon sources on which either species can grow. Higher metabolic complexity resulted in higher niche overlap between species, which increases the potential for competitive interactions between species. (e) Community richness and (f) average realized niche breadth (quantified as in c). Arrows in (a) and (d) indicate the direction in which competition gets stronger. Circles in (b), (c), (e) and (f) show averages over 500 assembled communities after simulating 5000 invasion events per community. Circle colours indicate the size of the species pool used to assemble the communities (a colour change from blue to green corresponds to an increase in the pool size from 250 to 1000 species). Bars show one standard deviation

The stronger competition embodied in larger species pools results in more diverse communities (Figure 4b). This higher community richness is explained by two factors. First, as competition gets stronger, we observe a modest increase in the total number of niches available after 5000 species invasions (86.9 ± 1.6 and 88.9 ± 0.2 available niches for species pools of 250 and 1000 species, respectively, Figure S4b) while the number of free niches after 5000 invasions is not affected (all available niches are filled, Figure S4c). In other words, more niches are filled when competition is stronger. Second, we observe that stronger competition causes a reduction of the realized niche (Figure 4c). That is, individual persisting species consume, on average, fewer carbon sources. (To determine the average realized niche we divided the number of filled niches by community richness.) Altogether, the larger community richness observed when competition is stronger results from more niches being available and filled, and from the fact that each species occupies fewer niches (consumes fewer resources).

A second way to vary competition strength is to alter the degree of overlap in the fundamental niches that two species occupy (i.e., the number of carbon sources that they can thrive on). Species with more similar fundamental niches show more intense competition (Bailey et al., 2013). We can manipulate this niche overlap by altering the metabolic complexity of the species that we assemble into communities, that is by altering the number of biochemical reactions in each metabolic network, which is possible with our sampling approach (see Section 2). To this end, we created pools of metabolic networks that had 500 or 1000 more reactions than the E. coli model we used as a reference (“r”, iJO1366; Orth et al., 2011). We designated members of these pools as having metabolic complexity “r+500” and “r+1000,” respectively. We used species of equal metabolic complexity to assemble communities, selecting species from a pool of 1000 species. (Figure S4 shows analogous results for pool sizes of 250, 500 and 750 species.)

Species in these pools are on average viable on more carbon sources—they have a broader fundamental niche—than species with lower complexity (Figure S1). In addition, species pairs in these pools also overlap to a greater extent in their fundamental niches. We quantified this niche overlap by enumerating the number of carbon sources on which both species can grow, and divided this number by the total number of carbon sources on which at least one of the species can grow (Figure 4d). In sum, increased metabolic complexity increases competition among species by increasing their niche overlap.

We found that communities assembled from species with high metabolic complexity are more species‐rich (Figure 4e). However, the number of available or free niches does not change when increasing metabolic complexity above that of r (“r+500” and “r+1000” in Figure S4b,c). Instead, the larger community diversity observed at high metabolic complexity results from a narrower partition of niche space among the species (Figure 4f).

We also explored the consequences of reducing metabolic complexity below that of r. We assembled communities with species that contain 500 or 1000 fewer reactions than the reference model (pools designated “r+500” and “r+1000”). The results are more difficult to interpret than those for metabolic complexity higher than r (see Figure S4 and Text S2). However, just as in the analysis where we changed the species’ pool, a combination of two factors explains community richness. These are the total number of niches filled and the average realized niche (see Text S2 for a more detailed explanation).

In sum, we observe that strong competition results in a division of niche space into more and narrower niches that are occupied by the resident species. Everything else being equal, this results in more diverse communities.

4. DISCUSSION

The “ecological limits” and “diversity begets diversity” hypotheses were proposed to explain the forces that shape biodiversity on Earth. Several analyses aiming to validate these hypotheses have examined the rate of evolutionary diversification to provide support for one or other hypothesis (Brockhurst et al., 2007; Gómez & Buckling, 2013; Jousset et al., 2016). However, evolution is not the only means by which community diversity can increase, because new species can also increase diversity by invading a community. We therefore feel that the hypotheses should be distinguished by considering a scenario that considers the contributions of both ecological and evolutionary processes to community diversity. A modelling approach like ours is well suited for this, because the species we simulate could be thought as being new evolved species or species that invade a community as they disperse from elsewhere. With these considerations in mind, we here simulate the assembly of thousands of communities in which we can control the number of new species allowed to invade a community and monitor the community's response to each invasion.

Our results suggest that the dichotomy between the diversity‐begets‐diversity and the ecological limits hypothesis is a false one. Both hypotheses capture important aspects of diversification. At initial stages of community assembly, species–species interactions in the form of cross‐feeding and competition facilitate diversification. Species “construct” new niches through their metabolic excretions, which creates opportunities for the invasion of new species that thrive on these excretions (Figure 2). Competition helps partition niche space into more and narrower niches, which can result in larger diversity (Figure 4). At later stages in the assembly process, no new niches can be created, niche space cannot be partitioned further, successful species invasions become rare and diversity reaches a ceiling. In sum, the diversity‐begets‐diversity and the ecological limits scenarios best capture different stages—early vs. late—of community assembly. Community diversity has limits, but these limits are not just externally imposed. They can be modified by the species themselves.

Two other conclusions emerge from our results. First, even when all niches have become filled during community assembly, diversity may not have reached its ceiling. Competition can further increase community richness even in this case, because it can help narrow the realized niche of individual species (Figure S2). Second, our conclusions reinforce the argument that it is best to consider ecological processes separately from evolutionary processes when studying diversification. The reason is that the probability of successful invasions decreases even early during community assembly, while species are still creating new niches during the “diversity begets diversity” regime (Figure 2d; Figures S3, S5). This observation, which agrees with existing theory (Case, 1990; Tilman, 2004; Vila et al., 2019), experimental observations (Fargione et al., 2003; Stachowicz et al., 1999) and the empirical observation that diversification also slows down on evolutionary timescales (Condamine et al., 2019), implies that a slowdown in diversification (or speciation) is by itself not sufficient proof for the ecological limits hypothesis.

Competition is commonly thought to stimulate the diversification of species (Abrams, 2006; Bailey et al., 2013; Dieckmann & Doebeli, 1999; Meyer et al., 2016; Meyer & Kassen, 2007; Yoder et al., 2010), although it can also prevent such diversification (Bailey et al., 2013; Brockhurst et al., 2007; Gómez & Buckling, 2013). In our work, a successful invasion increases competition, because available resources have to be shared between more species. After such an invasion, communities may show an increase, no change or a net decrease in diversity if multiple species go extinct as a result of the invasion (Figure 2a), in agreement with empirical observations from the literature (Abrams, 2006; Bailey et al., 2013; Brockhurst et al., 2007; Dieckmann & Doebeli, 1999; Gómez & Buckling, 2013; Meyer et al., 2016; Meyer & Kassen, 2007; Yoder et al., 2010). However, such varying short‐term consequences of competition for individual invasions need to be distinguished from the long‐term consequences for an entire assembly process. At the end of this process (once community richness no longer increases), we find that communities with stronger competition have become more diverse (Figure 4). In other words, our work predicts that increased competition results in a net increase of diversity.

In an organism, many traits are interconnected. Traits that are advantageous for one aspect of fitness may trade‐off with traits that affect other aspects. Such trade‐offs are thought to be important for determining community structure (Begon et al., 2006; Johnson et al., 2012; Litchman & Klausmeier, 2008; Tilman, 1982). Our results also suggest—albeit indirectly—that trade‐offs in resource use are important for the communities we assemble. If there were no such trade‐offs, we would expect that one or a few species consume all available resources. Instead, we find a great diversity of species, which suggests the presence of trade‐offs in resource use. It is important to point out that our modelling framework does not assume such trade‐offs to exist. They arise from elementary biochemical principles embodied in the set of biochemical reactions that constitute a metabolic reaction network.

Our work has several limitations. Addressing them offers opportunities for future research. First, we study a very constrained subspace of Hutchinsonian niche space, the multidimensional space comprising all environmental factors required for the survival of a species (Hutchinson, 1957). Specifically, we only consider the sources of carbon and energy that sustain heterotrophic organisms, because they are frequently cross‐fed between bacteria (D’Souza et al., 2018; McNally & Borenstein, 2018). Our modelling framework does not account for other abiotic factors, such as temperature and pH, nor does it account for non‐nutrient‐mediated species interactions, such as those that arise from cell‐to‐cell communication, or the secretion of toxic molecules. Community richness could increase above the limit we observe if such interactions help create even more niches. In addition, our knowledge about pan‐metabolism is increasing, and newly characterized metabolic reactions could further increase a community's predicted potential to create more niches and diverse communities.

Second, we observe that different species grow on similar sets of carbon sources–their fundamental niches are similar—which may result from the method we used to create metabolic networks for community assembly. Specifically, we constrained these networks to be viable on glucose, which may have increased their niche similarity, because these networks must share subsets of biochemical reactions required for growth on glucose (Barve et al., 2012). To explore how this choice may have affected our analysis, we performed two complementary analyses. In a first analysis, we compared how the fundamental niche overlap of random viable networks compares to that in real organisms. For that, we used bacteria from the human gut (Magnúsdóttir et al., 2017). Specifically, we identified in the metabolic networks of 818 species those metabolites that could serve as sources of carbon, and quantified fundamental niche overlap based on the results. We found that the fundamental niche overlap between these species can range from zero (no overlap) and up to one (full overlap), like the range of overlap explored with random viable networks (see Text S1, Figures S7, S8). In a second analysis, we created random metabolic networks required to be viable on carbon sources other than glucose (acetate, pyruvate, serine, alanine and lactose) (Figure S6). Communities assembled using these networks differed little in community diversity, even when we assembled communities from species required to be viable on different carbon sources. Therefore, this limitation is not likely to affect our observations dramatically.

Third, we observed that communities can be composed of up to 80 species whose persistence depended, directly or indirectly, on the species consuming the initial resource, glucose. Unfortunately, our current modelling approach cannot answer how abundant these species are, and how much glucose would be required to sustain a highly diverse community. To answer these questions remains an important task for future work.

Fourth, we use the growth rate of species on single carbon sources to predict growth in a complex environment with multiple carbon sources. In such an environment, a microbial species growing in isolation may either consume a single (preferred) carbon source, several carbon sources, or all available carbon sources. Which of these strategies it pursues depends on multiple factors, including the species, the cultivation method (batch or chemostat) and the similarity between the carbon sources (Aidelberg et al., 2014; Egli et al., 1993; Kovárová‐Kovar & Egli, 1998). The picture is even more complex in cocultures, where species interactions may affect consumption patterns. Our decision to use maximal growth on a single carbon source to model a species’ persistence is motivated by recent experiments which show that the assembly of communities in mixtures of nutrients can be predicted from assembly in single‐nutrient environments (Estrela, Sanchez‐Gorostiaga et al., 2020; Fu et al., 2020). For example, the taxonomic structure of a community assembled in glucose medium (Goldford et al., 2018) can be explained by the growth of its constituent species in isolation, either on the externally provided glucose, or on the cross‐fed metabolites acetate, succinate and lactate (Estrela, Vila, et al., 2020).

Metabolic modelling is a powerful modelling framework. It has been successfully used to study microbial physiology (Notebaart et al., 2008; Segrè et al., 2002; Shlomi et al., 2005; Varma & Palsson, 1994), to design strains for industrial and medical applications (Gu et al., 2019b; Lun et al., 2009; Mishra et al., 2018), and to explore questions in the field of evolution (Bajić et al., 2018; Barve & Wagner, 2013; William Harcombe et al., 2013; Ibarra et al., 2002; Notebaart et al., 2014; San Roman & Wagner, 2018, 2020; Sandberg et al., 2017) and ecology (Estrela, Sanchez‐Gorostiaga et al., 2020; Harcombe et al., 2014; Levy & Borenstein, 2013; Machado et al., 2021; McNally & Borenstein, 2018; Zelezniak et al., 2015), as reviewed previously (García‐Jiménez et al., 2021; Gu et al., 2019b; Mardinoglu & Nielsen, 2012). Though outside the scope of our work, the modelling framework used here can in principle also be used to study other ecological phenomena, such as successional dynamics (Bell & Pascual, 2020; Chase, 2003; Dini‐Andreote et al., 2014; Lockwood et al., 1997; Nemergut et al., 2007), and the role of historical contingency (or priority effects) in the assembly process (Chase, 2003; Fukami, 2015). What is more, whole‐community genome sequencing, together with semi‐automatic methods for metabolic reconstruction, facilitate the creation of genome‐scale metabolic models for not just one organism, but for multiple organisms in a community (DeJongh et al., 2007; Dias et al., 2015; Mendoza et al., 2019; Wang et al., 2018). Thus, it may soon be possible to conduct an analysis like ours with metabolic networks characterized in a community from the wild. While such an analysis cannot control all the variables that our computational work can control, it can go beyond a proof of principle, explain actual limits on community diversity and identify rules of community assembly important in nature. It will be especially suited for the analysis of those complex communities where cross‐feeding interactions are important, such as that of the human gut (Magnúsdóttir et al., 2017), the soil (Baran et al., 2015) or planktonic organisms (Enke et al., 2019).

CONFLICT OF INTEREST

The authors declare no competing interests.

AUTHOR CONTRIBUTIONS

Conceived and designed the analyses: M.S.R., A.W. Performed the analyses: M.S.R. Analysed the data: M.S.R., A.W. Wrote the paper: M.S.R., A.W.

Supporting information

Supplementary Material

San Roman, M. , & Wagner, A. (2021). Diversity begets diversity during community assembly until ecological limits impose a diversity ceiling. Molecular Ecology, 30, 5874–5887. 10.1111/mec.16161

Data Availability Statement

The data that support the findings of this study are openly available in GitHub at https://doi.org/10.5281/zenodo.5206841.