Abstract
Dynamic Bayesian networks (DBNs) can be used for the discovery of gene regulatory networks (GRNs) from time series gene expression data. Here, we suggest a strategy for learning DBNs from gene expression data by employing a Bayesian approach that is scalable to large networks and is targeted at learning models with high predictive accuracy. Our framework can be used to learn DBNs for multiple groups of samples and highlight differences and similarities in their GRNs. We learn these DBN models based on different structural and parametric assumptions and select the optimal model based on the cross-validated predictive accuracy. We show in simulation studies that our approach is better equipped to prevent overfitting than techniques used in previous studies. We applied the proposed DBN-based approach to two time series transcriptomic datasets from the Gene Expression Omnibus database, each comprising data from distinct phenotypic groups of the same tissue type. In the first case, we used DBNs to characterize responders and non-responders to anti-cancer therapy. In the second case, we compared normal to tumor cells of colorectal tissue. The classification accuracy reached by the DBN-based classifier for both datasets was higher than reported previously. For the colorectal cancer dataset, our analysis suggested that GRNs for cancer and normal tissues have a lot of differences, which are most pronounced in the neighborhoods of oncogenes and known cancer tissue markers. The identified differences in gene networks of cancer and normal cells may be used for the discovery of targeted therapies.
Keywords: dynamic Bayesian networks, time series, gene expression, Bayesian learning, classification, MCMC
Introduction
Learning gene regulatory networks (GRNs) from gene expression data has been the focus of much research in the last decades [7, 10, 38, 62]. The precise knowledge of GRNs can help to understand the molecular mechanisms driving diseases and facilitate the search for targeted therapies [3, 32]. Multiple computational methods can be used to learn GRNs from observational data, including correlation analysis [20, 29, 34], Boolean networks [31, 36], Bayesian networks [5, 12, 59], differential equation models [60, 61] and machine learning approaches [19]. A recent benchmarking study [63] revealed no clear winner among different methods for GRN reconstruction, with different methods demonstrating advantages in different settings.
A Bayesian network is a probabilistic graphical model representing dependencies between random variables via a directed acyclic graph (DAG). Due to its probabilistic nature, this model is well suited to describe noisy biological data. However, static Bayesian networks do not allow directed cycles, rendering it impossible for them to model feedback loops. The Dynamic Bayesian Network (DBN) model overcomes this problem by including dependencies between nodes at different time points and accommodating the possibility of cycles [28, 39, 50].
DBN models were used to learn biological networks [35], including GRNs [2, 6, 15, 30, 59, 64] and multi-omics networks [48]. Learning DBN structures from data is computationally challenging because the number of possible network topologies grows exponentially with the number of nodes. Some methods solve this issue by employing a greedy search [48, 59], others restrict the network topology by prohibiting instantaneous dependencies between genes or limiting the number of possible incoming edges per each node [18, 35, 57]. However, topological restrictions may potentially result in the discovery of suboptimal models [41].
Another limitation of most network learning methods lies in the assumption that all samples in the dataset represent the same GRN, however this assumption may be violated. For example, it has been shown experimentally that protein–protein interactions differ drastically between tumor and normal cell lines [23]. Hence the discovery of context-specific GRNs can facilitate the discovery of targeted therapies [56]. Only limited research was devoted to learning DBNs from distinct but related contexts [24, 42, 43]. However, none of the methods was applied to networks with more than  nodes, and all suggested approaches utilized limited DBN topologies that assume no instantaneous dependencies between genes.
nodes, and all suggested approaches utilized limited DBN topologies that assume no instantaneous dependencies between genes.
The goal of this study was to create a scalable framework for learning DBN models that provide high predictive accuracy and can be used for learning GRNs for multiple subgroups of samples, defined, for example, by molecular, histological or clinical phenotypes. We employed a Bayesian approach [26] for learning DBNs that is scalable to networks with hundreds of nodes and implemented in the R-package BiDAG [52]. BiDAG was previously used for context-specific learning of static gene networks [27, 51]. This package allows selecting from a wide range of network topologies, including prior information from public gene interaction databases and modeling gene interactions whose strength changes over time. In addition, the Bayesian approach to structure learning implemented in the package is well equipped to prevent overfitting, a known problem occurring in the analysis of high-dimensional biological data.
Apart from BiDAG, we found five R-packages for learning DBNs, namely G1DBN [28], dbnlearn [8], dbnR [44], ebdbNet [45] and bnstruct [9]. Only dbnR and bnstruct are able to learn DBNs with the same range of topologies as BiDAG. However, these packages can only learn models whose parameters are constant over time, while BiDAG can be used for learning both constant and time-varying models. We compared BiDAG with these tools in simulation studies to determine which tool best reconstructs network structures.
Apart from BiDAG, none of the mentioned DBN learning tools includes functions enabling classification. For this reason, for classification comparison, we chose standard classification tools that cannot perform network reconstruction. In addition, we compared our results with the DBN-based classifier reported in [24] for the same datasets, however the code of this classifier is not available.
To demonstrate the applications of the described approach, we identified time-series datasets in the Gene Expression Omnibus (GEO) database [1], which included gene expression data for at least two different phenotypic groups of the same tissue and comprised at least 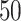 observations in each of two consecutive time slices. We found two datasets (GSE5462 and GSE37182) that satisfied these criteria. To inform model selection in the absence of ground truth, we used a cross-validated measure of predictive accuracy that was previously used to perform DBN model selection [35, 48]. In addition, we used cross-validated classification accuracy to assess the different models’ ability to distinguish between the analyzed phenotypic groups. Concerning applications, the suggested framework helped to understand if the phenotypic groups in each dataset could be better represented by GRNs with the same structure (but not parameters) or if gene regulation differs substantially so that different structures more accurately represent the analyzed subgroups. In addition, our analysis demonstrated that the range of modeling possibilities offered by BiDAG is helpful for the discovery of models that reach the highest predictive accuracy, while the DBN-based classifier demonstrated competitive classification accuracy.
observations in each of two consecutive time slices. We found two datasets (GSE5462 and GSE37182) that satisfied these criteria. To inform model selection in the absence of ground truth, we used a cross-validated measure of predictive accuracy that was previously used to perform DBN model selection [35, 48]. In addition, we used cross-validated classification accuracy to assess the different models’ ability to distinguish between the analyzed phenotypic groups. Concerning applications, the suggested framework helped to understand if the phenotypic groups in each dataset could be better represented by GRNs with the same structure (but not parameters) or if gene regulation differs substantially so that different structures more accurately represent the analyzed subgroups. In addition, our analysis demonstrated that the range of modeling possibilities offered by BiDAG is helpful for the discovery of models that reach the highest predictive accuracy, while the DBN-based classifier demonstrated competitive classification accuracy.
Methods and data
A DBN is a probabilistic graphical model for the joint distribution of random variables 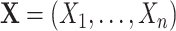 observed at time points
observed at time points 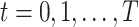 . The DBN model uses a directed graph to encode a factorization of the joint distribution of
. The DBN model uses a directed graph to encode a factorization of the joint distribution of 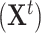 along the time slices
along the time slices 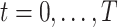 (Figure 1A). Here, we consider DBNs in which structures are identical for all time slices. We also assume that variables in time slice
(Figure 1A). Here, we consider DBNs in which structures are identical for all time slices. We also assume that variables in time slice 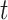 can depend on other variables in time slice
can depend on other variables in time slice 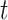 and on variables in time slice
and on variables in time slice 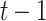 , i.e.
, i.e.
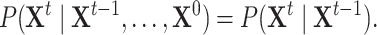 |
(1) |
Figure 1.
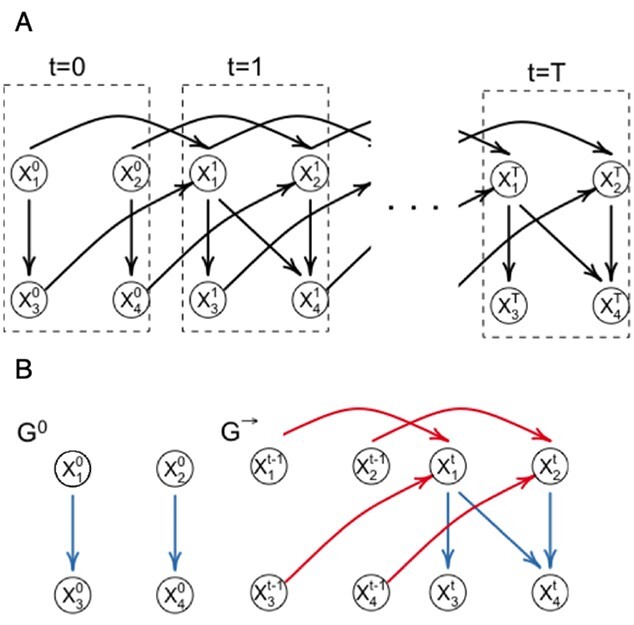
DBN graphical representation. (A) The unfolded structure of the first-order DBN model consisting of 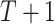 time slices can be represented by initial and transition structures. (B) The edges between time slices are highlighted in red and called inter-edges. The edges within time slices are highlighted in blue and called intra-edges.
time slices can be represented by initial and transition structures. (B) The edges between time slices are highlighted in red and called inter-edges. The edges within time slices are highlighted in blue and called intra-edges.
Such DBN models are referred to as first-order DBNs.
The joint probability distribution of a DBN with 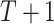 time slices is
time slices is
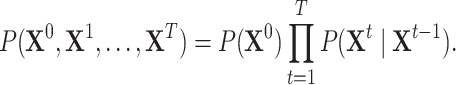 |
(2) |
With these assumptions, the unfolded structure of a DBN (Figure 1A) can be represented in a compact way with two DAGs 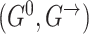 which are referred to as initial structure and transition structure, respectively (Figure 1B). The initial structure contains only edges in the first time slice. The transition structure describes relationships between gene expression levels in all other time slices,
which are referred to as initial structure and transition structure, respectively (Figure 1B). The initial structure contains only edges in the first time slice. The transition structure describes relationships between gene expression levels in all other time slices, 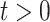 . The edges within one time slice are called intra-edges and edges between time slices are called inter-edges. In
. The edges within one time slice are called intra-edges and edges between time slices are called inter-edges. In 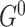 , only intra-edges are present, while
, only intra-edges are present, while 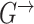 contains both intra and inter-edges. We are primarily interested in discovering the transition structure because it describes both instantaneous dependencies (represented by intra-edges) and dependencies between gene expression levels at different time points (represented by inter-edges).
contains both intra and inter-edges. We are primarily interested in discovering the transition structure because it describes both instantaneous dependencies (represented by intra-edges) and dependencies between gene expression levels at different time points (represented by inter-edges).
Within each time slice 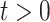 the joint distribution of
the joint distribution of 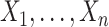 is factorized according to a Bayesian network model:
is factorized according to a Bayesian network model:
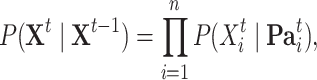 |
(3) |
where 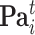 denotes the set of parents of node
denotes the set of parents of node 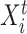 in time slices
in time slices 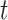 and
and 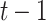 in
in 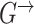 . For
. For 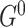 the parent sets
the parent sets 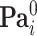 are used instead to factorize
are used instead to factorize 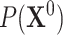 .
.
To fully specify a DBN, we also need parameters 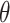 which describe probabilistic dependencies between each node
which describe probabilistic dependencies between each node 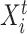 and its parents in a DBN structure. We assume that
and its parents in a DBN structure. We assume that 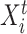 are jointly normally distributed. This results in the distribution of each node
are jointly normally distributed. This results in the distribution of each node  being a linear regression on its parents [14]:
being a linear regression on its parents [14]:
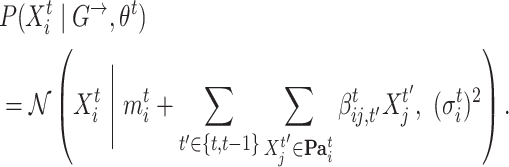 |
(4) |
For each time slice 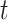 , we have the parameters
, we have the parameters 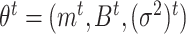 , where
, where 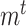 is a vector of regression intercepts,
is a vector of regression intercepts, 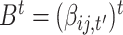 a set of all regression coefficients and
a set of all regression coefficients and 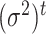 a vector of variances. For
a vector of variances. For  , the sum over parents in the previous time slice is dropped. We consider two cases, namely stationary DBNs where parameters stay constant over time
, the sum over parents in the previous time slice is dropped. We consider two cases, namely stationary DBNs where parameters stay constant over time 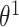 =
= 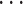 =
= 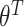 =:
=: 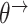 and time-varying DBNs, where
and time-varying DBNs, where  ,
, 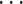 ,
, 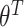 are generally different. The parameters
are generally different. The parameters 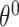 and
and 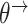 are different even for a stationary model. In a time-varying model, we assume time-varying parameters, while the structure
are different even for a stationary model. In a time-varying model, we assume time-varying parameters, while the structure 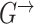 is assumed to be the same across time slices
is assumed to be the same across time slices 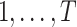 .
.
We also consider a special case where the initial structure 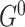 is the same as the internal structure of the transition structure
is the same as the internal structure of the transition structure 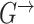 , i.e. for all nodes, all intra-slice edges in
, i.e. for all nodes, all intra-slice edges in  are the same as these edges in
are the same as these edges in 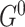 .
.
For learning the DBN structure from observational data 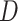 , we employ the Bayesian approach implemented in the R package BiDAG [26, 52], and use the BGe score for learning and sampling the structures of Bayesian networks [14, 25]. The BGe score of a graph
, we employ the Bayesian approach implemented in the R package BiDAG [26, 52], and use the BGe score for learning and sampling the structures of Bayesian networks [14, 25]. The BGe score of a graph 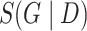 is derived from its posterior probability that is proportional to its marginal likelihood and graph prior:
is derived from its posterior probability that is proportional to its marginal likelihood and graph prior:
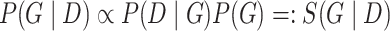 |
(5) |
As was shown in [11, 14], when some technical assumptions are fulfilled, the score 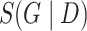 decomposes in terms, each depending on a single node and its parents (see details in Supplementary data):
decomposes in terms, each depending on a single node and its parents (see details in Supplementary data):
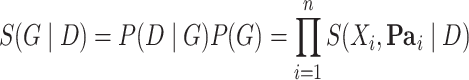 |
(6) |
The BGe score assumes a normal-Wishart prior on parameters [14] that satisfies the assumptions required for score decomposition in Equation(6).
For DBNs, the dataset 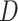 consists of
consists of 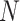 observations from
observations from 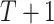 time slices. To learn a time-varying DBN, we divide
time slices. To learn a time-varying DBN, we divide 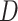 in
in 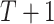 parts and define the BGe score of a DBN structure as
parts and define the BGe score of a DBN structure as
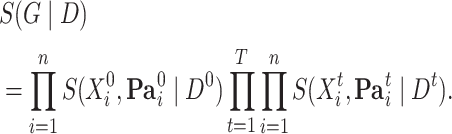 |
(7) |
To perform structure learning for a stationary model we divide the data into two parts: 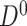 and
and 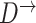 , where
, where 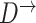 contains observations from all pairs of neighboring time slices. Equation (7) then simplifies to
contains observations from all pairs of neighboring time slices. Equation (7) then simplifies to
 |
(8) |
We use the iterative order Markov chain Monte Carlo (MCMC) scheme [26] to estimate the a posteriori (MAP) structures 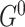 and
and 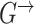 . In addition, we estimate consensus structures by averaging over a sample of graphs from the posterior distribution and composing consensus structures of edges whose posterior probability is higher that 0.9 [26, 52].
. In addition, we estimate consensus structures by averaging over a sample of graphs from the posterior distribution and composing consensus structures of edges whose posterior probability is higher that 0.9 [26, 52].
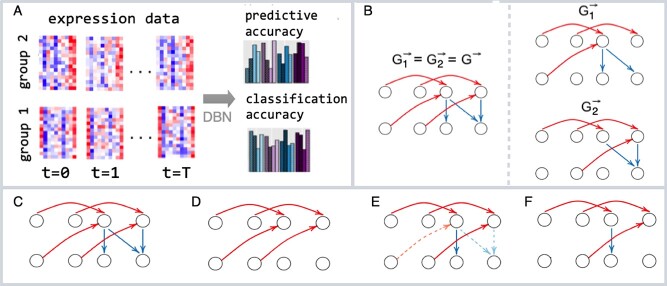
Learning DBN models for phenotypic subgroups
In the proposed framework, each sample 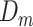 contains gene expression levels of one patient from all time points and is assigned to a phenotypic subgroup
contains gene expression levels of one patient from all time points and is assigned to a phenotypic subgroup 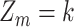 ,
, 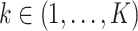 . In this work, we analyzed two datasets, each comprising gene expression from
. In this work, we analyzed two datasets, each comprising gene expression from 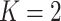 subgroups (Figure 2A), however the model can be extended to an arbitrary number of groups.
subgroups (Figure 2A), however the model can be extended to an arbitrary number of groups.
Figure 2.
DBN learning and classification framework. (A) We learn DBN-based classification models from the time-series gene expression data of two phenotypic groups (group 1 and group 2) with various structural and parametric assumptions and assess the predictive accuracy and classification accuracy of these models using leave-one-out cross-validation. (B) We evaluate models where phenotypic groups are represented by the same or different DBN structures. For each model we consider a set of four structural restrictions/prior assumptions: (C) no restrictions, (D) model without intra-edges (E) model that penalizes non-STRING edges (dashed) (F) model where non-STRING edges are blacklisted.
Since the analyzed subgroups of samples in each dataset are related, we propose considering two models: one which assumes that DBN structures are subgroup-specific and the other one that represents all subgroups by a single DBN structure (Figure 2B). In the latter case, the differences between subgroups can be explained by differences in DBN parameters. From a biological perspective, it is interesting to understand to which extent the interaction networks of different subgroups, for example, defined by different phenotypes, differ from each other.
To inform the choice between different structural and parametric model assumptions, we suggest computing mean absolute error (MAE) as a measure of predictive accuracy, which was already used in previous applications of DBN to biological datasets [35, 48]. MAE reflects how well the model predicts the changes in gene expression levels in time.
To avoid overfitting, we estimated MAE using leave-one-out cross-validation (CV). In each CV run, we removed one sample 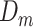 from the data
from the data 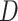 and used the remaining data
and used the remaining data 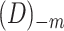 to learn DBN structure and parameters. After that, we plugged in the values
to learn DBN structure and parameters. After that, we plugged in the values 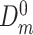 containing gene expression levels of the test sample from the first time slice and predicted gene expression levels in all other time slices iteratively according to the learned model. Finally, we computed MAE for each node and time slice and averaged it across all genes, slices and test samples.
containing gene expression levels of the test sample from the first time slice and predicted gene expression levels in all other time slices iteratively according to the learned model. Finally, we computed MAE for each node and time slice and averaged it across all genes, slices and test samples.
In addition to the predictive accuracy, we measured cross-validated classification accuracy to evaluate how well the DBN-based classifier can discriminate between the analyzed subgroups.
Other DBN learning tools do not provide functions for classification. For this reason, we compared our DBN-based classifier against random forest and naive Bayes classifiers [17, 33]. We ran the CV 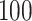 times for the random forest classifier to average out randomness in the results.
times for the random forest classifier to average out randomness in the results.
Structural assumptions
Including prior biological knowledge can improve network learning [65], so we consider two different ways to include such knowledge: by penalizing the edges that cannot be found in public protein–protein interaction databases, such as, e.g. the STRING database [53] (Figure 1E) and by excluding these edges completely from the search space (Figure 1F). Penalization is implemented by imposing a nonuniform prior over structures:
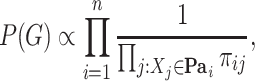 |
(9) |
where 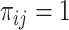 if the interaction between genes
if the interaction between genes 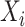 and
and 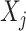 can be found in the STRING database with a confidence level of at least
can be found in the STRING database with a confidence level of at least 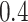 , and
, and 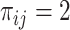 otherwise.
otherwise.
Most DBN models and tools prohibit intra-edges. We do not assume the presence or absence of intra-edges by default. Instead, we include the model without intra-edges in the set of investigated models (Figure 2D) and compare its predictive accuracy with other models, including the model without any structural restrictions (Figure 2C).
Work steps of the model
Our goal is to evaluate DBN models using all possible combinations of structural assumptions depicted in Figure 2B and Figure 2C:F. In addition, we consider models with time-varying and constant parameters for datasets where more than two time slices are present. For each combination of structural and parametric assumptions we perform the following CV procedure:
| Leave-one-out CV procedure for DBNs. |
|---|
| Input: |
Time series gene expression data 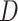 and class membership and class membership |
assignments of each sample (row of 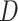 ): ): 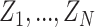
|
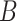 —blacklist matrix,
—blacklist matrix, 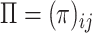 —penalization matrix, parameter —penalization matrix, parameter |
assumptions, 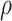 —posterior probability threshold —posterior probability threshold |
| Output: |
| Cross-validated clustering accuracy of MAP and consensus models |
| Cross-validated MAE of MAP and consensus models |
For 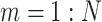
|
1. Define training data 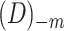 and test sample and test sample 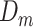
|
| 2. Learn MAP and consensus structures and parameters |
Given 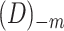 , ,  , ,  : : |
For 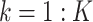
|
Learn MAP DBN structure 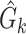
|
| Obtain a sample of DBN structures from the posterior |
distribution 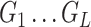
|
Given 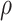 and and 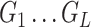 estimate consensus structure estimate consensus structure 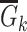
|
Given 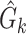 and and 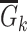 estimate MAP parameters estimate MAP parameters 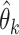 , , 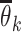
|
Compute class posteriors 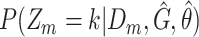 and and |
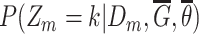
|
| END For |
| 3. Assign membership and compute MAE |
| Assign class memberships given MAP and consensus models |
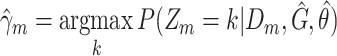
|
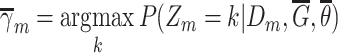
|
Given 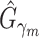 , , 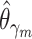 , ,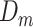 compute MAE (MAP model) compute MAE (MAP model) |
Given 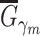 , , 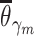 , , 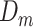 compute MAE (consensus model) compute MAE (consensus model) |
| END For |
| 4. Compute clustering accuracy and global MAE of MAP and |
| consensus models |
Compute clustering accuracy by comparing 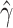 , , 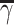 and and 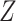
|
| Compute global MAE by averaging over all test samples |
Posterior probabilities of class memberships 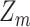 of observations
of observations 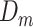 are computed as follows:
are computed as follows:
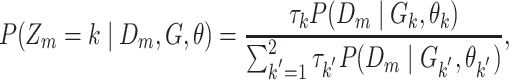 |
(10) |
where likelihoods 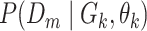 are computed according to the learned DBN structures and parameters:
are computed according to the learned DBN structures and parameters:
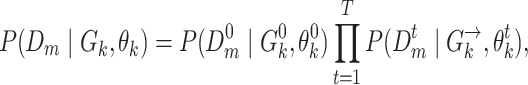 |
(11) |
and 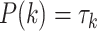 are estimated from the training data.
are estimated from the training data.
When the same structure for the analyzed subgroups is assumed, the graphs in step 2 need to be learned only once instead of 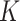 times separately for each subgroup.
times separately for each subgroup.
BiDAG package
The R-package BiDAG [52] implements a collection of MCMC methods that can be used for learning and sampling of static Bayesian network structures as well as DBNs. To implement the work steps of the model described in Section 2.3, we used the following functions:
iterativeMCMC implements a hybrid MCMC approach introduced in [26] and was used for MAP structure search
orderMCMC was used for sampling from the posterior distribution
modelp was used for model averaging
scoreagainstDBN was used to compute likelihoods from Equation (11)
compareDBNs was used for model comparison
Data
We applied the described framework to two biological datasets, each containing time-series gene expression data of two phenotypic subgroups of the same tissue type (Section 4).
The dataset GSE5462 contains gene expression data of 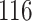 biopsies from
biopsies from 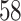 breast cancer patients at two time points: pre-treatment and
breast cancer patients at two time points: pre-treatment and 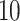 –
–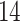 days after treatment with letrozole [37]. We log2-transformed and normalized the raw data using robust multiarray averaging (RMA, R-package affy, [13]) for subsequent DBN analysis.
days after treatment with letrozole [37]. We log2-transformed and normalized the raw data using robust multiarray averaging (RMA, R-package affy, [13]) for subsequent DBN analysis.
The second dataset, GSE37182, contains expression data of  biopsies from
biopsies from 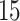 colorectal cancer patients, totaling 88 normal tissue biopsies and
colorectal cancer patients, totaling 88 normal tissue biopsies and 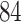 tumor tissue biopsies [40]. The samples were obtained during surgery and left at room temperature at four time points: 20 min (
tumor tissue biopsies [40]. The samples were obtained during surgery and left at room temperature at four time points: 20 min (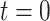 ), 60 min (
), 60 min (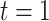 ), 180 min (
), 180 min (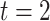 ) and 360 min (
) and 360 min (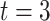 ). Afterwards, the samples were stored at
). Afterwards, the samples were stored at 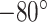 C until RNA extraction. The data from the repository were already normalized separately within each group (tumor and non-tumor). To make samples between two conditions comparable, we used the package NormalyzerDE [58] and performed median normalization.
C until RNA extraction. The data from the repository were already normalized separately within each group (tumor and non-tumor). To make samples between two conditions comparable, we used the package NormalyzerDE [58] and performed median normalization.
Gene filtering
To select genes to be included in the DBNs we performed DGE analysis using the R package limma [46]. We considered genes as differentially expressed between conditions if their false discovery rate (FDR)-adjusted P-value was smaller than 0.05. We did not apply a log2-fold-change cutoff.
Simulation studies
We generated 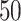 two-step DBNs structures. For each DBN structure, we generated
two-step DBNs structures. For each DBN structure, we generated 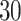 training samples from four consecutive time slices and two test samples. We learned MAP and consensus structures corresponding to posterior thresholds of
training samples from four consecutive time slices and two test samples. We learned MAP and consensus structures corresponding to posterior thresholds of 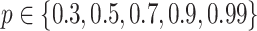 using the Bayesian approach implemented in BiDAG ([52], Section 2.4). We also learned best-scoring structures using greedy hill climbing and the BIC score from the R-package bnlearn [49] with the limits on the number of parents of
using the Bayesian approach implemented in BiDAG ([52], Section 2.4). We also learned best-scoring structures using greedy hill climbing and the BIC score from the R-package bnlearn [49] with the limits on the number of parents of 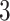 and
and 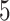 . For each limit, we also learned consensus structures based on bootstrap support levels of
. For each limit, we also learned consensus structures based on bootstrap support levels of 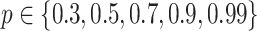 . Finally, we learned DBN structures using the R-packages dbnR and bnstruct. dbnR implements the MMHC approach for DBNs [54]. The package bnstruct implements hill climbing as well, however it automatically discretizes continuous data.
. Finally, we learned DBN structures using the R-packages dbnR and bnstruct. dbnR implements the MMHC approach for DBNs [54]. The package bnstruct implements hill climbing as well, however it automatically discretizes continuous data.
We compared the learned structures with the ground truth using true positive rate (TPR), FDR and structural Hamming distance (SHD). SHD is defined as the number of edge additions, deletions and reversals needed to make the two graphs match [54].
Results
Simulated data
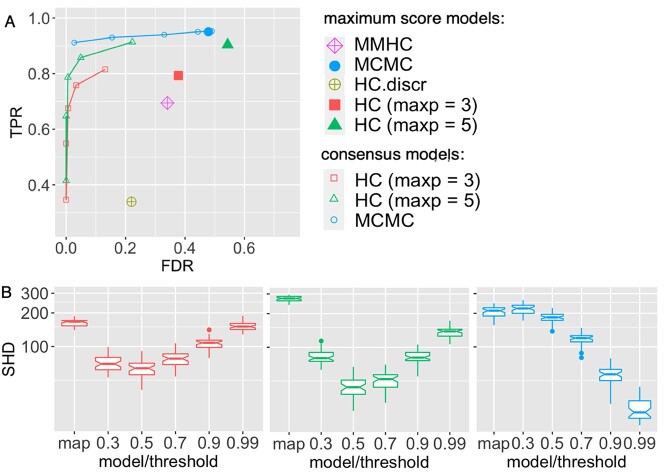
In the simulation studies (Section 2.7), we generated 50 random DBNs and data from these DBNs, followed by network reconstruction using available software packages. We explored the situation when the number of observations between neighboring time points is smaller than the number of nodes.
The MCMC approach reached the highest TPR, followed by hill climbing and MMHC (Figure 3A). However, hill climbing applied to discretized data showed the worst result discovering less than 40% of true positives. Such a poor performance likely demonstrates the effect of information loss due to data discretization. Notably, all best-scoring structures resulted in a high FDR. Structural overfitting of maximum score structures in the high-dimensional setting was previously demonstrated in [26] and Bayesian model averaging proved to be effective for decreasing the FDR.
Figure 3.
Comparison of performance of DBN structure learning algorithms on simulated data. A total of 50 random two-step DBN structures were generated with 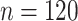 nodes and three parents on average for each node in the transition structure. The training datasets contained 30 samples from four consecutive time slices, the test datasets included two samples each. MCMC (blue, R-package BiDAG), hill climbing (HC, red and green, R-package bnlearn), MMHC (violet, R-package dbnR) and hill climbing applied to discretized data (HC.discr, yellow, R-package bnstruct) were used to learn the DBN structures and compare them with the ground truth using (A) the TPR and FDR and (B) SHD. The performance of the hill climbing was evaluated for two limits for the parent set size:
nodes and three parents on average for each node in the transition structure. The training datasets contained 30 samples from four consecutive time slices, the test datasets included two samples each. MCMC (blue, R-package BiDAG), hill climbing (HC, red and green, R-package bnlearn), MMHC (violet, R-package dbnR) and hill climbing applied to discretized data (HC.discr, yellow, R-package bnstruct) were used to learn the DBN structures and compare them with the ground truth using (A) the TPR and FDR and (B) SHD. The performance of the hill climbing was evaluated for two limits for the parent set size: 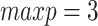 (red) and
(red) and 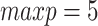 (green). Consensus models for MCMC and hill climbing were learned using a range of posterior thresholds and bootstrap support levels of
(green). Consensus models for MCMC and hill climbing were learned using a range of posterior thresholds and bootstrap support levels of 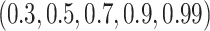 .
.
Only bnlearn and BiDAG provide tools for model averaging. Hence we did not include other approaches in the comparison of consensus graphs. We observed that consensus structures contained fewer false-positive edges but also fewer true positives. SHD, which sums all differences (TP, FP and errors in directions of edges), was lower for consensus than for MAP structures (Figure 3B). The lowest SHD was achieved with the MCMC scheme at the posterior threshold of 0.99, demonstrating an advantage of using BiDAG for DBN structure learning.
The better performance of BiDAG comes at the cost of longer runtimes. BiDAG needed 14 min to find the MAP structure and perform the sampling from the posterior distribution. Hill climbing required 4.5 min, including 100 bootstrap runs needed to estimate consensus structures. Hill climbing applied to discretized data required the longest time of 68 min to learn the best scoring graph.
Analysis of time-series gene expression data
We applied the proposed approach to two transcriptomic datasets from the GEO repository (Section 2.5, Section 4): the colorectal cancer dataset GSE37182 and the breast cancer dataset GSE5462. For each dataset, we learned several DBN models (Sections 2.1–2.2) using the Bayesian approach and measured, via leave-one-out cross-validation (CV), how they perform with regard to predictive accuracy and classification accuracy (Section 2.3).
For the colorectal cancer dataset, we learned a DBN with time-varying parameters and compared it with a DBN assuming parameters that stay constant across all time slices 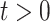 . A time-varying DBN can describe the underlying process with higher precision. However, it can also lead to overfitting.
. A time-varying DBN can describe the underlying process with higher precision. However, it can also lead to overfitting.
Analysis of breast cancer time-series gene expression data
The GSE5462 dataset contains gene expression measurements for two groups of breast cancer patients: responders and non-responders to treatment (Section 2.5). We selected the genes that were either differentially expressed between responders and non-responders or differentially expressed in post-treatment compared with pre-treatment samples (Section 2.6). In addition, we included all transcription factors of the identified genes found in the database Omnipath [55].
The best model learned by BiDAG yielded a higher classification accuracy than naive Bayes and random forest (Table 2). We further noted that all models in this work outperformed the highest classification accuracy of DBN models reported in [24] as well as the ML approaches that the authors used for comparison.
Table 1.
Cross-validated classification accuracy demonstrated by DBN-based and standard classification tools
The lowest MAE was reached for DBNs learning the same DBN structure for both subgroups (Table 3). This finding aligns well with the differential gene expression and pathway enrichment analysis. Since out of 22 283 genes, only 19 were differentially expressed, we can assume that the GRNs are very similar in responders and non-responders. However, the highest classification accuracy of 0.85 was reported for models that learned DBN structures independently for responders and non-responders (Table 2).
Table 2.
Ten DBN models with the lowest cross-validated MAE learned by BiDAG for the breast cancer dataset
| Model | intra_edges | blacklist | prior | init_trans | class_structures | MAE |
|---|---|---|---|---|---|---|
| MAP | + | non-STRING | - | sharing intra | same | 0.428 |
| MAP | + | non-STRING | - | sharing intra | different | 0.436 |
| MAP | + | non-STRING | - | no sharing | different | 0.437 |
| consensus | + | non-STRING | - | sharing intra | same | 0.438 |
| consensus | - | - | - | sharing intra | same | 0.438 |
| consensus | + | non-STRING | - | sharing intra | different | 0.44 |
| consensus | + | - | - | sharing intra | same | 0.448 |
| consensus | + | non-STRING | - | no sharing | different | 0.448 |
| MAP | + | - | STRING | sharing intra | same | 0.450 |
| consensus | + | - | STRING | sharing intra | same | 0.452 |
We chose the MAP model for the downstream analysis that learned the same DBN structure for responders and non-responders and blacklisted all non-STRING interactions. Even though the classification accuracy of this model was only the second highest, the lower MAE suggests that it better predicts the changes in post-treatment gene expression levels and hence is more appropriate for the analysis of gene expression dynamics.
Pathway enrichment analysis showed that no KEGG [21] pathway was enriched in the differentially expressed genes. However, when we assessed the set of all parent nodes of these genes in the estimated DBN structure (Supplementary data, Figure S1), three KEGG pathways (p53 signaling, cellular senescence and cell cycle) were enriched (FDR 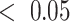 ). Thus, the DBN model connected genes found to be important for treatment response to genes from major cancer-related pathways. Among these genes, the most connected node was CDK1 (Cyclin Dependent Kinase 1), which is a known target for treating breast cancer [22]. Interestingly, Cdk inhibitors are already approved for treating breast cancer as the first-line treatment in combination with letrozole (used in the analyzed dataset) [47] which confirms the discovered link.
). Thus, the DBN model connected genes found to be important for treatment response to genes from major cancer-related pathways. Among these genes, the most connected node was CDK1 (Cyclin Dependent Kinase 1), which is a known target for treating breast cancer [22]. Interestingly, Cdk inhibitors are already approved for treating breast cancer as the first-line treatment in combination with letrozole (used in the analyzed dataset) [47] which confirms the discovered link.
Analysis of colorectal cancer time-series gene expression data
For the colorectal cancer dataset GSE37182, we performed the DGE analysis at three consecutive time points, using 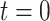 as a reference (Section 2.6). The number of differentially expressed genes increased with time. In total, we identified 58 genes that were differentially expressed over all time points in cancer and tumor biopsies.
as a reference (Section 2.6). The number of differentially expressed genes increased with time. In total, we identified 58 genes that were differentially expressed over all time points in cancer and tumor biopsies.
We proceeded with the identification of transcription factors that may be involved in regulating the identified genes using the Omnipath database. We combined them with the first set of genes and used their union for the DBN analysis with BiDAG. We learned multiple DBN models using various structural and parametric assumptions (Sections 2.1–2.2) and performed cross-validation as described above to select the best model (Section 2.3).
The classification accuracy was 100% for all models and higher than the accuracy of the best model reported in [24] (98.5%). The MAE was clearly the lowest for DBNs assuming time-varying parameters (Table 4) as none of the 10 best models assumed constant parameters. From a biological perspective, the time-varying model is also plausible. First, the time lags between the measurements were nonuniform. Second, the tissue was left at room temperature, and the process of degradation likely led to changes in the strengths of dependencies between genes. Among the time-varying models, the lowest MAE was reached for models where intra-edges were prohibited.
Table 3.
Ten DBN models with the lowest cross-validated MAE learned by BiDAG for the colorectal cancer dataset
| Model | parameters | intra_edges | blacklist | prior | class_structures | MAE |
|---|---|---|---|---|---|---|
| consensus | time-varying | - | - | - | different | 0.210 |
| MAP | time-varying | - | - | - | different | 0.214 |
| MAP | time-varying | + | - | - | different | 0.221 |
| consensus | time-varying | - | - | - | same | 0.222 |
| MAP | time-varying | - | - | - | same | 0.224 |
| MAP | time-varying | + | - | - | different | 0.226 |
| MAP | time-varying | + | non-STRING | - | different | 0.228 |
| MAP | time-varying | + | - | - | same | 0.230 |
| consensus | time-varying | + | - | - | different | 0.233 |
| MAP | time-varying | + | non-STRING | - | same | 0.233 |
Finally, we observed that DBN models that learn structures for tumor and normal subgroups independently resulted in the lowest MAE. Consequently, for the downstream analysis, we selected a consensus DBN model which learns structures separately for normal and tumor samples and blacklists intra-slice edges. Despite being learned independently, the DBN models for cancer and normal subgroups shared 60% of edges. Such a high overlap suggests that a lot of underlying processes in cancer and normal cells can be described by the same dependencies between genes.
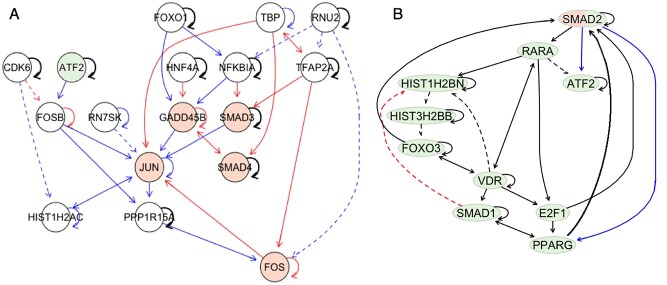
To highlight the differences and similarities between the analyzed phenotypic groups, we identified the nodes with the most different and similar interaction partners in networks representing tumor and normal subgroups. There were 18 nodes that had neighborhoods with empty intersections in two networks. Out of these, three genes (FOS, JUN, GADD45B) belong to the KEGG colorectal cancer pathway. Two genes from this set, namely FOSB and JUN, were identified and validated as markers for colorectal tumor tissue degradation [40](Figure 4A). Out of 20 nodes with most similar neighborhoods 10 can be found of a generic transcription pathway (Figure 4B, Supplementary data, Figure S2, [4]).
Figure 4.
Subnetworks of DBN transition structures discovered for the GSE37182 dataset. Structures of time-varying DBN models without intra-edges were learned independently for normal and tumor subgroups. The blue edges denote the edges which are specific to the normal model; red edges are specific to the tumor model. Black edges are present in both models. The solid lines correspond to edges between genes which were found as interactors in the STRING database. Genes from the colorectal cancer pathway (KEGG) are highlighted in orange. (A) Most differently connected genes (FOSB, JUN, FOS, GADD45B) in DBN transition structures of cancer and normal DBN models that are either enriched in the colorectal cancer signaling pathway or were previously validated as biomarkers of cancer and their parents in the learned DBN models. (B) Most similarly connected genes, which were also found on the generic transcription pathway [4] (highlighted in green).
Discussion
DBNs are powerful models for analyzing time-series gene expression data because they allow us to shed light on the GRNs that orchestrate molecular processes. Recently, a lot of research has focused on learning context-specific gene networks [23, 27, 42, 51]. In this work, we proposed a framework for learning DBNs for multiple phenotypic groups. This framework employs the Bayesian approach to structure learning of DBNs implemented in the R-package BiDAG and provides a broad range of modeling options, including various DBN topologies, constant and time-varying parameters, the inclusion of priors as well as Bayesian model averaging. We demonstrated in simulation studies that BiDAG outperforms other available tools for DBN structure learning.
We applied the proposed framework to two time-series gene expression datasets, each comprising data from two subgroups of samples. The GSE5462 dataset included gene expression data of breast tumor biopsies taken before and after treatment with letrozole. Our analysis suggested that GRNs do not differ substantially between responders and non-responders. However, the analysis of the learned DBN structure suggested that differences in the signaling pathways of the subgroups might lie at the phosphoproteome level since the kinase CDK1 appeared to be densely connected to a few genes that were differentially expressed between the responders and non-responders. Even with only a few differences detected at the gene expression level between the subgroups, the classification accuracy was higher than reported in the previous study [24].
For the colon cancer dataset, the best predictive accuracy was reached for the model assuming different DBN structures for tumor and normal samples. This finding indicates that GRNs differ considerably in normal and tumor cells and aligns well with experimental results obtained from the analysis of normal and tumor cell lines in [23]. At the same time, in our analysis, the DBN structures for normal and cancer groups overlapped by 60%. This finding corresponds to the common understanding that many housekeeping pathways work similarly in tumor and healthy cells. The biggest differences between networks were identified in the neighborhoods of genes from the colorectal cancer pathway as well as genes that were previously validated as markers stratifying cancer and normal tissue [40].
In both analyzed datasets, the range of modeling options available with BiDAG helped to learn the models with the highest predictive accuracy. Models with time-varying parameters demonstrated the best results for the colon cancer dataset, and the presence of intra-edges resulted in the highest predictive accuracy for the breast cancer data. No other DBN tool includes both of these options. In the case of the colon cancer dataset, the consensus model resulted in the lowest MAE, demonstrating the advantage of the Bayesian approach.
Despite clear advantages, this work has some limitations. BiDAG requires longer runtimes than other methods for structure learning and much longer runtimes than standard classification methods. However, BiDAG is still feasible for relatively large networks and longer runtimes are compensated with better performance. Specific model choices, namely the assumption of normal distributions of the random variables and linearity of the dependencies of their means, may also be considered as a limitation of the model. However, BiDAG also implements the BDe score for categorical variables and it allows users to define their own scoring functions. Hence the model can be extended to other distributions.
Key Points
The proposed strategy for learning GRNs of multiple phenotypic groups unifies the efficient method of DBN structure learning and the versatile approach to model selection, enabling the discovery of models with high predictive and classification accuracy.
The efficient Bayesian approach to structure learning is better equipped to prevent overfitting than greedy hill climbing coupled with other conventional techniques.
Application of the proposed method to the real transcriptomic data revealed differences and similarities between the regulatory networks of cancer and normal cells that aligned well with previous findings and can be used to facilitate the discovery of targeted therapies.
Author contributions statement
P.S. and J.K. conceived the research project. N.B. supervised the research project. P.S. and J.K. designed and implemented the computational framework and conducted the analyses. P.S. and N.B. wrote the manuscript. N.B. and J.K. reviewed and edited the manuscript.
Data and code availability
The unprocessed data is available at the public GEO repository under identifiers GSE5462 and GSE37182. The datasets can be accessed at https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE5462 https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE37182 The reproducible code and the results are available at the GitHub repository https://github.com/cbg-ethz/DBNclass. The latest version of the BiDAG package including implemented updates is available at CRAN repository https://cran.r-project.org/web/packages/BiDAG
Supplementary Material
Acknowledgments
The authors thank the anonymous reviewers for their valuable suggestions. Part of this research was supported by the European Research Council (ERC) Synergy Grant 609883 and SystemsX.ch Research, Technology and Development (RTD) Grant 2013/150.
Author Biographies
Polina Suter She is a biotech investment manager at Magnetic Capital. Her research interests include context-specific network learning and multi-omics data integration. This work was primarily conducted while the author was a PhD candidate at ETH Zurich.
Jack Kuipers He is a senior scientist at ETH Zurich. His research is focused on cancer evolution modelling, phylogenetic tree inference, probabilistic graphical models and single-cell sequencing analysis.
Niko Beerenwinkel He is a professor at ETH Zurich. His research is at the interface of mathematics, statistics, and computer science with biology and medicine.
Contributor Information
Polina Suter, Department of Biosystems Science and Engineering, ETH Zurich, Matternstrasse 26, 4058 Basel, Switzerland; SIB Swiss Institute of Bioinformatics, Switzerland.
Jack Kuipers, Department of Biosystems Science and Engineering, ETH Zurich, Matternstrasse 26, 4058 Basel, Switzerland; SIB Swiss Institute of Bioinformatics, Switzerland.
Niko Beerenwinkel, Department of Biosystems Science and Engineering, ETH Zurich, Matternstrasse 26, 4058 Basel, Switzerland; SIB Swiss Institute of Bioinformatics, Switzerland.
References
- 1. Barrett T, Wilhite SE, Ledoux P, et al. NCBI GEO: archive for functional genomics data sets—update. Nucleic Acids Res 2012;41(D1):D991–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ajmal HBE, Madden MG. Dynamic Bayesian network learning to infer sparse models from time series gene expression data. IEEE/ACM Trans Comput Biol Bioinform 2021;1–1. doi: 10.1109/TCBB.2021.3092879. [DOI] [PubMed] [Google Scholar]
- 3. Cangiano M, Grudniewska M, Salji MJ, et al. Gene regulation network analysis on human prostate orthografts highlights a potential role for the JMJD6 regulon in clinical prostate cancer. Cancer 2021;13(9):2094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Caudy M. Generic transcription pathway. Reactome - a curated knowledgebase of biological pathways 2008;24:R-HSA-212436. [Google Scholar]
- 5. de Campos LM, Cano A, Castellano JG, et al. Combining gene expression data and prior knowledge for inferring gene regulatory networks via Bayesian networks using structural restrictions. Stat Appl Genet Mol Biol 2019;18(3):20180042. [DOI] [PubMed] [Google Scholar]
- 6. de Luis Balaguer MA, Sozzani R. Inferring gene regulatory networks in the arabidopsis root using a dynamic Bayesian network approach. In: Kerstin Kaufmann and Bernd Mueller-Roeber (eds) Methods in Molecular Biology. New York: Springer, 2017, 331–48. [DOI] [PubMed] [Google Scholar]
- 7. Emmert-Streib F, Dehmer M, Haibe-Kains B. Gene regulatory networks and their applications: understanding biological and medical problems in terms of networks. Frontiers in Cell and Developmental Biology 2014;2:38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Fernandes R. dbnlearn: Dynamic Bayesian Network Structure Learning, Parameter Learning and Forecasting, 2020. https://cran.r-project.org/web/packages/dbnlearn/index.html.
- 9. Sambo AFF. bnstruct: Bayesian Network Structure Learning from Data with Missing Values, 2022. https://cran.r-project.org/web/packages/bnstruct/index.html.
- 10. Friedman N. Inferring cellular networks using probabilistic graphical models. Science 2004;303(5659):799–805. [DOI] [PubMed] [Google Scholar]
- 11. Friedman N, Koller D. Being bayesian about network structure. a bayesian approach to structure discovery in bayesian networks. Machine Learning 2003;50(1/2):95–125. [Google Scholar]
- 12. Friedman N, Linial M, Nachman I, et al. Using Bayesian networks to analyze expression data. J Comput Biol 2000;7(3-4):601–20. [DOI] [PubMed] [Google Scholar]
- 13. Gautier L, Cope L, Bolstad BM, et al. affy–analysis of affymetrix GeneChip data at the probe level. Bioinformatics 2004;20(3):307–15. [DOI] [PubMed] [Google Scholar]
- 14. Geiger D, Heckerman D. Parameter priors for directed acyclic graphical models and the characterization of several probability distributions. The Annals of Statistics 2002;30(5):1412–1440. [Google Scholar]
- 15. Grzegorczyk M, Husmeier D. Improvements in the reconstruction of time-varying gene regulatory networks: dynamic programming and regularization by information sharing among genes. Bioinformatics 2010;27(5):693–9. [DOI] [PubMed] [Google Scholar]
- 16. Grzegorczyk M. An Introduction to Gaussian Bayesian Networks. Totowa, NJ: Humana Press, 2010, 121–47. [DOI] [PubMed] [Google Scholar]
- 17. Ho TK. Random decision forests. In: Proceedings of 3rd international conference on document analysis and recognition, Vol. 1. IEEE, 1995, 278–82. [Google Scholar]
- 18. Husmeier D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics 2003;19(17):2271–82. [DOI] [PubMed] [Google Scholar]
- 19. Huynh-Thu VA, Geurts P. dynGENIE3: dynamical GENIE3 for the inference of gene networks from time series expression data. Sci Rep 2018;8(1):3384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Jeong D, Lim S, Lee S, et al. Construction of condition-specific gene regulatory network using kernel canonical correlation analysis. Front Genet 2021;12:652623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kanehisa M, Furumichi M, Sato Y, et al. KEGG: integrating viruses and cellular organisms. Nucleic Acids Res 2020;49(D1):D545–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kang J, Sergio CM, Sutherland RL, et al. Targeting cyclin-dependent kinase 1 (CDK1) but not CDK4/6 or CDK2 is selectively lethal to MYC-dependent human breast cancer cells. BMC Cancer 2014;14(1):32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kim M, Park J, Bouhaddou M, et al. A protein interaction landscape of breast cancer. Science 2021;374(6563):eabf3066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Kourou K, Rigas G, Papaloukas C, et al. Cancer classification from time series microarray data through regulatory dynamic Bayesian networks. Comput Biol Med 2020;116:103577. [DOI] [PubMed] [Google Scholar]
- 25. Kuipers J, Moffa G, Heckerman D. Addendum on the scoring of gaussian directed acyclic graphical models. The Annals of Statistics 2014;42(4):1689–1691. [Google Scholar]
- 26. Kuipers J, Suter P, Moffa G. Efficient sampling and structure learning of Bayesian networks. J Comput Graph Stat 2022;0:1–12. [Google Scholar]
- 27. Kuipers J, Thurnherr T, Moffa G, et al. Mutational interactions define novel cancer subgroups. Nat Commun 2018;9(1):4353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Lèbre S. Inferring dynamic genetic networks with low order independencies. Stat Appl Genet Mol Biol 2009;8(1):1–38. [DOI] [PubMed] [Google Scholar]
- 29. Lee HK. Coexpression analysis of human genes across many microarray data sets. Genome Res 2004;14(6):1085–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Li H, Wang N, Gong P, et al. Learning the structure of gene regulatory networks from time series gene expression data. BMC Genomics 2011;12(S5):S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Li P, Zhang C, Perkins EJ, et al. Comparison of probabilistic boolean network and dynamic Bayesian network approaches for inferring gene regulatory networks. BMC Informatics 2007;8(S7):S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Madhamshettiwar PB, Maetschke SR, Davis MJ, et al. Gene regulatory network inference: evaluation and application to ovarian cancer allows the prioritization of drug targets. Genome Med 2012;4(5):41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Majka M. naiveBayes: High Performance Implementation of the Naive Bayes Algorithm in R. R package version 0.9.7, 2019. [Google Scholar]
- 34. Margolin AA, Nemenman I, Basso K, et al. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics 2006;7(S1):S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. McGeachie MJ, Sordillo JE, Gibson T, et al. Longitudinal prediction of the infant gut microbiome with dynamic Bayesian networks. Sci Rep 2016;6(1):20359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Melkman AA, Cheng X, Ching W-K, et al. Identifying a probabilistic boolean threshold network from samples. IEEE Transactions on Neural Networks and Learning Systems 2018;29(4):869–81. [DOI] [PubMed] [Google Scholar]
- 37. Miller WR, Larionov A. Changes in expression of oestrogen regulated and proliferation genes with neoadjuvant treatment highlight heterogeneity of clinical resistance to the aromatase inhibitor, letrozole. Breast Cancer Res 2010;12(4):R52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Mochida K, Koda S, Inoue K, et al. Statistical and machine learning approaches to predict gene regulatory networks from transcriptome datasets. Front Plant Sci 2018;9:1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Murphy K, Mian S. Modelling gene expression data using dynamic Bayesian networks. Technical report, Computer Science Division. Berkeley, CA: University of California, 1999. [Google Scholar]
- 40. Musella V, Verderio P, Reid JF, et al. Effects of warm ischemic time on gene expression profiling in colorectal cancer tissues and normal mucosa. PLoS ONE 2013;8(1):e53406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Nair A, Chetty M, Wangikar PP. Improving gene regulatory network inference using network topology information. Mol Biosyst 2015;11(9):2449–63. [DOI] [PubMed] [Google Scholar]
- 42. Oates CJ, Korkola J, Gray JW, et al. Joint estimation of multiple related biological networks. The Annals of Applied Statistics 2014;8(3):1892–1919. [Google Scholar]
- 43. Penfold CA, Millar JBA, Wild DL. Inferring orthologous gene regulatory networks using interspecies data fusion. Bioinformatics 2015;31(12):i97–i105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Quesada D. dbnR: Dynamic Bayesian Network Learning and Inference 2022. https://cran.r-project.org/web/packages/dbnR/index.html, version 0.7.5. [Google Scholar]
- 45. Rau A. ebdbNet: Empirical Bayes Estimation of Dynamic Bayesian Networks, 2022. https://cran.r-project.org/web/packages/ebdbNet/index.html, version 1.2.6.
- 46. Ritchie ME, Phipson B, Di W, et al. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res 2015;43(7):e47–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Roskoski R. Cyclin-dependent protein kinase inhibitors including palbociclib as anticancer drugs. Pharmacol Res 2016;107:249–75. [DOI] [PubMed] [Google Scholar]
- 48. Ruiz-Perez D, Lugo-Martinez J, Bourguignon N, et al. Dynamic Bayesian networks for integrating multi-omics time series microbiome data. mSystems 2021;6(2):e01105–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Scutari M. Learning Bayesian networks with the bnlearn R package. J Stat Softw 2010;35(3):1–22. [Google Scholar]
- 50. Scutari M. Bayesian network models for incomplete and dynamic data arXiv:1906.06513, 2019:1–24.
- 51. Suter P, Dazert E, Kuipers J, et al. Multi-omics subtyping of hepatocellular carcinoma patients using a Bayesian network mixture model bioRxiv:2021.12.16.473083, 2021:1–25. [DOI] [PMC free article] [PubMed]
- 52. Suter P, Kuipers J, Moffa G, et al. Bayesian structure learning and sampling of Bayesian networks with the R package BiDAG. arXiv:2105.00488. 2021:1–29.
- 53. Szklarczyk D, Gable AL, Lyon D, et al. STRING v11: protein–protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res 2018;47(D1):D607–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Tsamardinos I, Brown LE, Aliferis CF. The max-min hill-climbing Bayesian network structure learning algorithm. Machine Learning 2006;65(1):31–78. [Google Scholar]
- 55. Türei D, Korcsmáros T, Saez-Rodriguez J. OmniPath: guidelines and gateway for literature-curated signaling pathway resources. Nat Methods 2016;13(12):966–7. [DOI] [PubMed] [Google Scholar]
- 56. van der Wijst MGP, de Vries DH, Brugge H, et al. An integrative approach for building personalized gene regulatory networks for precision medicine. Genome Med 2018;10(1):96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Werhli AV, Husmeier D. Reconstructing gene regulatory networks with Bayesian networks by combining expression data with multiple sources of prior knowledge. Stat Appl Genet Mol Biol 2007;6(1):15. [DOI] [PubMed] [Google Scholar]
- 58. Willforss J, Chawade A, Levander F. NormalyzerDE: Online tool for improved normalization of omics expression data and high-sensitivity differential expression analysis. J Proteome Res 2018;18(2):732–40. [DOI] [PubMed] [Google Scholar]
- 59. Xing L, Guo M, Liu X, et al. An improved Bayesian network method for reconstructing gene regulatory network based on candidate auto selection. BMC Genomics 2017;18(S9):844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Yang B, Bao W. RNDEtree: Regulatory network with differential equation based on flexible neural tree with novel criterion function. IEEE Access 2019;7:58255–63. [Google Scholar]
- 61. Zhang Q, Yao Y, Zhang J, et al. Using single-index ODEs to study dynamic gene regulatory network. PLOS ONE 2018;13(2):e0192833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Zhang X, Zhao X-M, He K, et al. Inferring gene regulatory networks from gene expression data by path consistency algorithm based on conditional mutual information. Bioinformatics 2011;28(1):98–104. [DOI] [PubMed] [Google Scholar]
- 63. Zhao M, He W, Tang J, et al. A comprehensive overview and critical evaluation of gene regulatory network inference technologies. Brief Bioinform 2021;22(5):1–15. [DOI] [PubMed] [Google Scholar]
- 64. Zhu J, Chen Y, Leonardson AS, et al. Characterizing dynamic changes in the human blood transcriptional network. PLoS Comput Biol 2010;6(2):e1000671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Zou M, Conzen SD. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics 2004;21(1):71–9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The unprocessed data is available at the public GEO repository under identifiers GSE5462 and GSE37182. The datasets can be accessed at https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE5462 https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE37182 The reproducible code and the results are available at the GitHub repository https://github.com/cbg-ethz/DBNclass. The latest version of the BiDAG package including implemented updates is available at CRAN repository https://cran.r-project.org/web/packages/BiDAG