Significance
DNA functions in living cells are crucially affected by the three-dimensional genome structure and dynamics. We analyze the whole genome of human cells by developing a polymer model of interphase nuclei. The model reveals the essential importance of the unfolding process of chromosomes from the condensed mitotic state for describing the interphase nuclei; through the unfolding process, heterogeneous repulsive interactions among chromatin chains induce phase separation of chromatin, which quantitatively explains the experimentally observed various genomic data. We can use this model structure as a platform to analyze the relationship among genome structure, dynamics, and functions.
Keywords: genome organization, A/B compartments, chromatin domains, lamina-associated domains, nucleolus-associated domains
Abstract
Three-dimensional genome structure and dynamics play critical roles in regulating DNA functions. Flexible chromatin structure and movements suggested that the genome is dynamically phase separated to form A (active) and B (inactive) compartments in interphase nuclei. Here, we examine this hypothesis by developing a polymer model of the whole genome of human cells and assessing the impact of phase separation on genome structure. Upon entry to the G1 phase, the simulated genome expanded according to heterogeneous repulsion among chromatin chains, which moved chromatin heterogeneously, inducing phase separation of chromatin. This repulsion-driven phase separation quantitatively reproduces the experimentally observed chromatin domains, A/B compartments, lamina-associated domains, and nucleolus-associated domains, consistently explaining nuclei of different human cells and predicting their dynamic fluctuations. We propose that phase separation induced by heterogeneous repulsive interactions among chromatin chains largely determines dynamic genome organization.
Three-dimensional genome structure and its dynamics play crucial roles in regulating eukaryotic DNA functions (1–3). The recent development of techniques, such as high-throughput chromosome conformation capture (Hi-C and related methods) (4–6), electron microscopy (7), and superresolution microscopy (8–11), has enhanced our understanding of genome organization. For further clarifying the mechanisms of genome organization, it is necessary to develop reliable computational models that can bridge these different experimental paradigms. Computational polymer models of individual chromosomes and their complexes were developed using the Hi-C data of global chromatin contacts as the input to deduce the knowledge-based forces on chromatin (12–15). More refined input data such as the global genome-wide contact pattern in the single-cell Hi-C data were necessary for modeling the whole-genome structure of mouse and human cells (16–18). For further elucidating the principles of genome organization, it is highly desirable to develop a physical model of the whole genome using straightforward assumptions instead of fitting the model to the vast amount of experimental data on the global genome conformation.
In physical modeling of the whole genome, the important subject is examination of the possible phase separation of chromatin and assessment of its impact on genome structure. Chromatin shows flexible configuration (7–9) and movements (10, 11, 19), suggesting that chromatin in interphase nuclei is dynamically phase separated to determine the genome structure (20–23). In the present study, we tested this hypothesis by examining the mechanism of phase separation. A previously proposed mechanism, which is still under debate (24), is the droplet-like condensation of factors such as HP1; these condensates may mediate attraction between heterochromatin regions, leading to phase separation of heterochromatin from euchromatin (25, 26). Following this idea, the previous whole-genome models assumed attractive interactions, but these interactions spontaneously gathered heterochromatin toward the nuclear center, leading to the unusual genomic configuration. This anomalous chromatin distribution was remedied in the models by assuming counteracting attractive interactions between chromatin and the nuclear lamina (22, 27). However, the mechanism to establish such a balance among competitive interactions in the nucleus was unclear. In the present study, we resolved this difficulty by focusing on repulsion rather than attraction in chromatin interactions. We consider a polymer model, which describes heterogeneously distributed physical properties of chromatin. With heterogeneous repulsive interactions among chromatin regions, the simulated genome unfolded from the mitotic chromosomes, which generated heterogeneous movement of chromatin chains, leading to phase separation of chromatin in the G1 phase. This repulsion-driven phase separation quantitatively explains the genome organization of human fibroblast (IMR90) and lymphoblastoid (GM12878) cells and predicts dynamic fluctuations residing after the genome reached the G1 phase.
Results
Neighboring Region Contact Index.
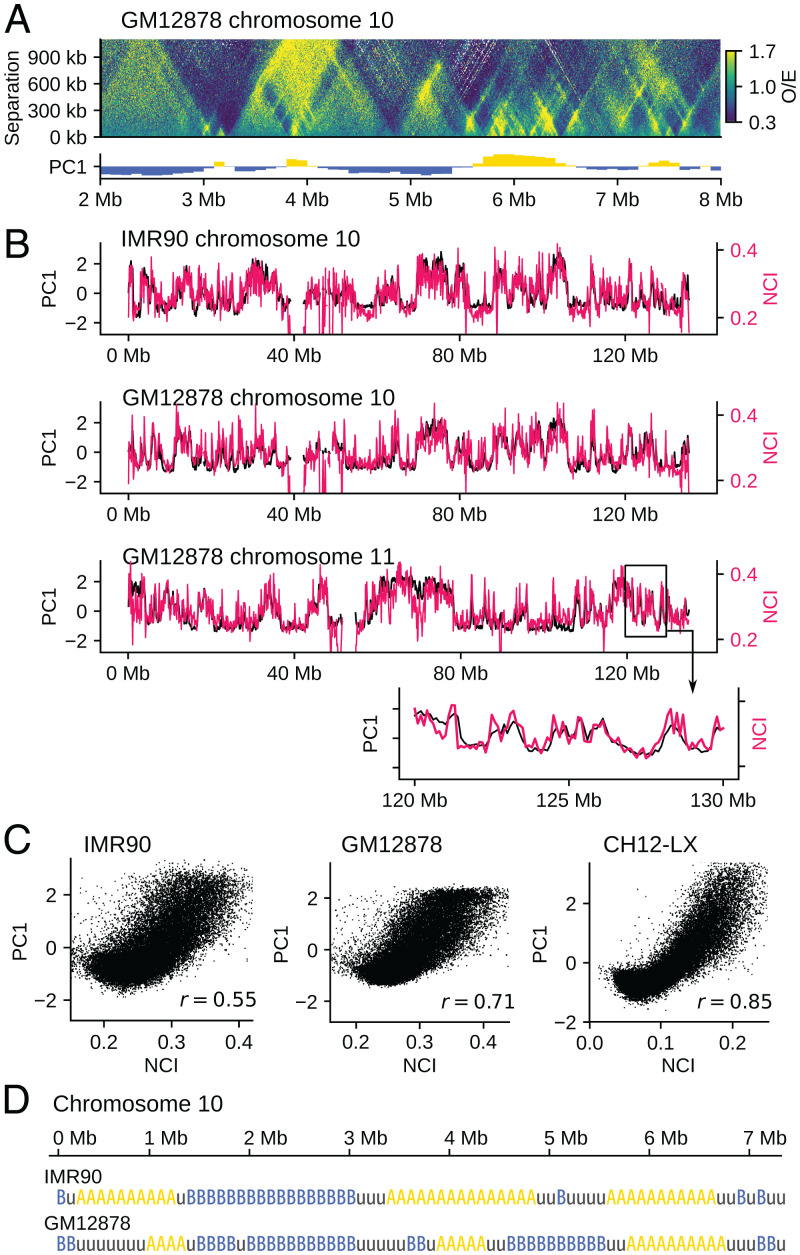
The interactions between chromatin regions depend on the local physical properties of chromatin. We inferred these physical properties from the local chromatin contacts. Fig. 1A shows a distribution of the ratio of observed/expected contact frequencies obtained from the Hi-C data (5), , where is the observed contact frequency between kth and k + sth positions along the sequence, and F(s) is the mean contact frequency for the sequence separation s. Contacts between chromatin loci with the sequence separation s < 300 kb are more frequent in compartment A than compartment B, while contacts with s > 300 kb are more frequent in compartment B (Fig. 1A). Here, compartment A/B was identified by principal component analysis (PCA) of the Hi-C contact matrix of the genome (4). In other words, the properties of chromatin at a few hundred kilobase scale are correlated to the compartments defined in hundreds of megabases or the larger scale. We quantified this correlation by defining the neighboring region contact index (NCI), , where is a sum of the frequency of contacts between 50-kb chromatin regions labeled i and j along the sequence. As shown in Fig. 1 B and C, NCI correlates to the compartment signal defined by PCA. This finding suggests that the A/B compartmentalization originates from the heterogeneity of local chromatin properties as captured by NCI. We examined this hypothesis by performing the whole-genome polymer simulation.
Fig. 1.
Correlation between the local contact frequency and the global compartment signal. (A) The ratio of observed/expected Hi-C contact frequencies plotted on the plane of the position along the sequence k and the sequence separation s for chromosome 10 of GM12878 (Top) is compared with the first principal component vector (PC1) of of the whole genome (5), which is the compartment signal (4) distinguishing compartments A and B (Bottom). The compartment signal shows compartment A when it is positive (yellow) and compartment B when it is negative (blue). (B) The NCI, W(i) (red), is superposed on the compartment signal PC1 (black) for chromosome 10 of (Upper) IMR90 and (Upper Middle) GM12878 and (Lower Middle) chromosome 11 of GM12878. (Lower) A close-up view of an example 10-Mb region. (C) Scattered plots for comparing the whole genome data of NCI and the compartment signal PC1 of IMR90, GM12878, and CH12-LX (5). Each dot is a 100-kb segment. Pearson’s correlation coefficient is r = 0.55 (IMR90), 0.71 (GM12878), and 0.85 (CH12-LX). (D) According to the NCI value, we annotated each 100-kb region of human chromosomes with three labels: type A, type B, and type u.
First, we define the property of each chromatin region using NCI; the 100-kb region with is called the type-A region, where Zw is the Z score of NCI. The region with is called the type-B region, and the region with is called the type-u region. Type-A (type-B) regions are abundant in euchromatin (heterochromatin). Because the typical size of the loop domain is kb (5), larger NCI in a type-A region implies more-frequent intradomain contacts. These intradomain contacts may arise from DNA–protein complexes organized for transcription or replication (28, 29), and cohesin molecules off the CTCF-bound sites can associate with these complexes (30, 31) to reinforce contacts and enhance NCI. A type-u region represents either the region showing the intermediate feature between euchromatin and heterochromatin as was identified by clustering the Hi-C contact data (32) or the mosaic of type-A and type-B regions averaged over a 100-kb interval.
We use the type-A/B/u sequence (Fig. 1D), derived from the local Hi-C data, as the input into our whole-genome polymer simulation. We consider heteropolymer chains connecting type-A, type-B, and type-u beads by springs, with each bead representing a 100-kb chromatin region. Then, we compare the predicted results from the polymer simulation with the experimentally observed global Hi-C contact data. These global data have a much larger size than the input; therefore, this comparison between the simulated and observed data should give a stringent test of the physical assumptions adopted in the simulation. We note that the other definitions of the sequence of chromatin properties, such as the histone modification patterns (21, 33, 34), are compatible with the present polymer model as the alternative input into the simulation. In the present study, we use the type-A/B/u sequence instead of the other definitions to restrict ourselves to using only the local physical chromatin properties as the input.
Effective Interactions between Chromatin Regions.
Interactions between type-A/B/u regions should reflect their physical and molecular properties. In particular, the H3K9 methylated nucleosomes in heterochromatin-like type-B regions bind HP1 proteins, which glue nucleosomes to induce the effective attraction between nucleosomes (35, 36). Hence, the previous computational models assumed attractive interactions between coarse-grained (CG) heterochromatin-like regions (12–15, 22, 27). However, the effective interactions between CG regions consisting of hundreds of nucleosomes may differ from those between individual nucleosomes. Indeed, analyses of polymer systems showed that CG interactions largely depend on density (37–39); in high polymer density, the CG interactions between polymer chains can be repulsive, even with attractive interactions between polymer segments (39). Therefore, care should be taken to model the interactions between CG chromatin regions, particularly when chromatin density is high.
Here, we estimated the effective interactions between 100-kb type-A/B/u regions by modeling chromatin with bead-and-spring chains with a 1-kb resolution. We considered type-A (type-B) chains in which all beads are type A (B). Each chain has a 500-kb length, and each bead in the chain represents a 1-kb chromatin segment. We considered the system consisting of 8 to 30 chains in a box with the periodic boundary condition (Fig. 2 A and B) with the potential
| [1] |
where represents springs connecting neighboring beads in each chain, and represents the repulsive volume-excluding interactions between beads.
Fig. 2.
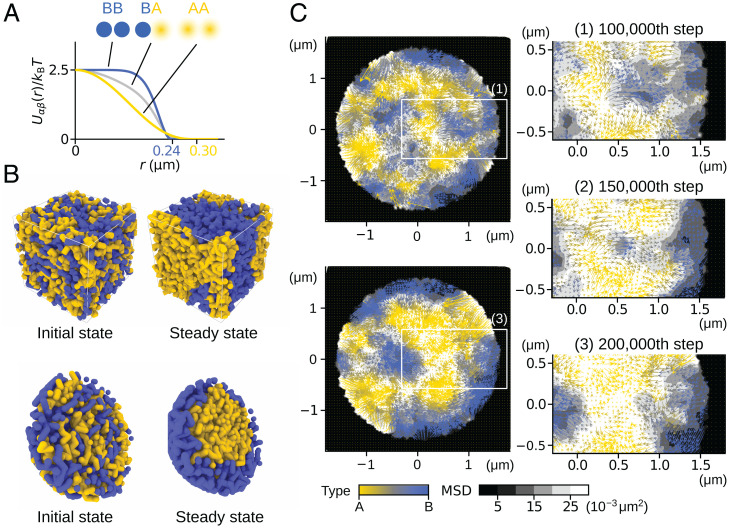
The 1-kb resolution polymer model to estimate the CG interactions between 100-kb chromatin regions. (A) Eight (Left) and 30 (Right) chains of 500-kb type-B chromatin are confined in periodic boxes of different size. (Left) Chains in chromatin density in units of number density of beads (, with bead diameter ), showing chromatin condensation. (Right) Chains in (), showing repulsion in a crowded system. Cohesin and HP1 are absent in both simulations. Different chains are colored differently. (B) Example configurations of 500-kb type-A (Left) and type-B (Right) chains picked out from the simulated system. Cohesin molecules bundle loops in each chain (magenta). (C) The simulated radius of gyration, , of type-A (red) and type-B (blue) chains is plotted as a function of the length l (in units of kilobases) of subdomain used for measuring . Inset is the log–log plot of the same data. A dashed line is , showing that of type-B chains is not fitted to a single exponent curve. (D) The CG interaction potential between 100-kb type-A regions obtained with the PRISM theory (solid lines) and the PMF (dashed line) in various chromatin densities (shown in the legend in units of number density of beads). (E and F) The CG interaction potentials between 100-kb type-B regions obtained with the PRISM theory (solid lines) and PMF (dashed lines) in various chromatin densities (shown in the key in units of number density of beads). Cohesin and HP1 are absent in E and present in F. (G) between type-A regions (red) and between type-B regions (blue) are superposed. In D–G. noise was smoothed out by the Gaussian filter of the size (SI Appendix, SI Text and Fig. S1). In B, C, and G, . Cohesin is present in the system shown in B–D, F, and G and is absent in A and E.
We assumed the short-range bead–bead attraction arising from the interactions between nucleosomes. These interactions depend on the stochastically varying configuration of nucleosomes (40) having a lifetime of (35). When HP1 binds, such nucleosome–nucleosome association is stabilized with the extended lifetime of (35), enhancing the attractive interactions. in Eq. 1 represents these stochastic attractive interactions in type-B chains. On the other hand, in type-A chains, histone tails are often acetylated, diminishing the attractive nucleosome–nucleosome interactions (41), and HP1 proteins should avoid binding to the acetylated histone tails; therefore, we put in type-A chains. We further considered the effects of the binding of cohesin to chromatin chains. Cohesin can bundle the chain into a loop, inducing effectively attractive interactions between the bundled regions. We represented this effect with by assuming that cohesin stochastically moves along the chain, extruding a loop of the chromatin chain. In type-A chains, various functional complexes should block the cohesin movement (30, 31) as found in the large NCI (Fig. 1), while the cohesin movement is less disturbed in type-B chains (32). We modeled such a difference in cohesin movement along chromatin chains in the 1-kb resolution model. We simulated the thermally fluctuating ensemble of chains with 1-kb resolution to derive the CG interactions between 100-kb chromatin regions. See SI Appendix, SI Text for detailed explanations of the simulations.
When we assume the binding of cohesin to chromatin chains and the bead diameter , the calculated spatial distribution of chains shows the radius of gyration, () for 200-kb type-A (B) regions (Fig. 2 B and C). Importantly, of type-A chains is scaled as for the length l of subdomain for measurement in the chain, while of type-B chains is not fitted to a single exponent curve, showing a saturating behavior as a function of l (Fig. 2C). These behaviors of are consistent with the microscope observations of active and repressed chromatin regions (8).
From the calculated radial distribution g(r) between 100-kb regions in the 1-kb resolution model, we obtained the potential of mean force (PMF), . When the chromatin density is sufficiently low, PMF represents the CG interaction between chromatin regions separated by a distance r. However, in high chromatin density, many-body effects modulate the PMF. We eliminated these many-body effects by calculating the direct correlation function with the polymer reference interaction site model (PRISM) theory (42), from which we derived the intrinsic pairwise potential . Therefore, the CG interactions with a 100-kb resolution are approximated by in low density and in high density. See SI Appendix, SI Text for the application of the PRISM theory.
In Fig. 2 D–F, we show calculated in various chromatin densities ρ. For type-A regions with cohesin (Fig. 2D), has a Gaussian-like form showing the repulsive interaction between type-A regions. Without cohesin, the type-A regions are more extended, leading to a milder repulsion with the smaller amplitude of . This repulsive interaction is consistent with the observation that chromatin does not condense in vitro when histone tails are acetylated (23). For type-B regions in the absence of cohesin and HP1 (Fig. 2E), showed a distinctly attractive interaction for density (), consistent with the in vitro observation that chromatin is condensed and phase separated from solvent when histone tails are unacetylated (23). This attractive interaction is due to the nucleosome–nucleosome interaction, which is further enhanced when HP1 binds to type-B chains. However, in high chromatin density with showed a mildly repulsive interaction.
Type-B chains with cohesin and HP1 showed attractive for , while becomes dominantly repulsive in () and repulsive in () (Fig. 2F). Cohesin binding to type-B chains compacts each loop domain with effective intraloop attraction (Fig. 2B). For inducing attractive interdomain interactions, domain conformation needs to be loosened with some free-energy cost to allow interdomain HP1 bridging. This effect is particularly evident when domains are compacted in high chromatin density. Therefore, tighter domain compaction with cohesin binding in high chromatin density diminishes interdomain attraction, emphasizing repulsive interaction. The repulsive slope of the potential becomes steeper as cohesin density is larger (SI Appendix, Fig. S1B). Density of chromatin in human cells, , is high enough to exhibit repulsive interactions. Thus, with the cohesin and HP1 binding, repulsive interaction between type-B regions arises.
In our whole-genome simulation, we used mathematically convenient forms of potentials and (Methods), which capture the main features of the interactions obtained with the 1-kb resolution model and the PRISM theory (Fig. 2G); the interaction between type-A regions and the interaction between type-B regions are both repulsive, with the steeper slope in . We set the potential width of and as similar to the calculated values in ; as two chromatin regions approach, start to rise at for type-A regions and for type-B regions (Fig. 2G). The calculated height of the potential was between two type-A regions. Accordingly, we set the potential height . between two type-B regions was considerably larger than that between two type-A regions. We did not use this large value in the whole-genome model, because the PRISM theory only derives the interchain potential, but we used the same potential functions for the intrachain and interchain type-B interactions in the whole-genome model. For explaining the intrachain structure consistently, we assumed a lower height of than that of . Later in this paper, we discuss the effects of varying , by comparing the calculated results with the experimental Hi-C data (SI Appendix, Fig. S11). Fig. 3A shows the functional forms of the potentials used in the whole-genome model; is Gaussian-like, and is a harder repulsive interaction. The repulsion between two type-u regions was assumed to be , and we set with α and β being A, B, or u.
Fig. 3.
Heterogeneous repulsive interactions and phase separation. (A) Potential functions between type-A, type-B, or type-u regions in distance r; , and . (B and C) A polymer-blend system was simulated to demonstrate the phase separation induced by heterogeneous repulsive interactions; 100 chains, each composed of 20 segments of type-A (yellow), and 100 chains, each composed of 20 segments of type-B (blue), were mixed and subjected to the Brownian motion. (B) Polymer chains mixed in a box with the periodic boundary condition (Top) and in a spherical container shown with the semisphere view (Bottom). (Left) The initial configuration. (Right) A snapshot after the system reached a steady state. (C) (Left) Cross-section of the sphere at the th step (Top) and the th step (Bottom). (Right) Close-up views of the rectangular areas in Left. Fluctuation (gray-scaled background, the 10-step MSD) and flow (arrow, the 10-step displacement) of polymer segments averaged within each 0.12-m region around the mesh points are shown. Colors of flows represent the ratio of A/B density. The images were rendered using OVITO (43).
Phase Separation Driven by the Repulsive Interactions.
The interactions induce phase separation of type-A and type-B regions when we confine them in a high-density space. We demonstrate this behavior by using a simple model of the polymer blend consisting of polymers of type-A segments and polymers of type-B segments. The Brownian motion of these mixture polymers induces phase separation (Fig. 3B). The mean-square displacement (MSD) analysis (grayscale in Fig. 3C) shows that the type-B segments are packed in a more solid-like manner, whereas the type-A segments show a more fluid behavior. The large fluctuations of type-A segments allow the type-A segments to merge into the phase-A domain. In particular, in the system confined in a rigid sphere, the type-A segments occupy the inner region to acquire the volume allowing the motion while the type-B segments are packed at the periphery analogously to the heterochromatin/euchromatin separation in cells (Fig. 3 B and C).
The Whole-Genome Simulation.
We simulated the whole-genome structure and dynamics of human cells by using the annotated sequence of type A/B/u (Fig. 1D) and the repulsive potentials Uαβ with (Fig. 3A).
During interphase in the human nucleus, a chromosome is displaced at most m (44), a much shorter distance than the nuclear size; the system is neither stirred nor equilibrated during interphase. Therefore, to explain genome organization in interphase, the process of structure formation at the entry to the G1 phase needs to be carefully considered (45). We simulated an anatelophase genome by pulling a centromere locus of each condensed chromosome chain toward one direction in the model space (Fig. 4A). Then, from the thus obtained configuration, we started the simulation of decompression by assuming the disappearance of the condensin constraints at this stage, which allowed chromosomes to expand with repulsion among chromatin chains (Fig. 4A and Movies S1–S3). The nuclear envelope forms during this expansion (48). We simulated this envelope formation by assuming a spheroid (IMR90) or sphere (GM12878) surface, whose radii varied dynamically by balancing the pressure from outside the nucleus and the one arising from the repulsion among chromatin chains. We repeated this simulation 200 times with different random number realizations. These 200 trajectories represent an ensemble of different 200 cells.
Fig. 4.
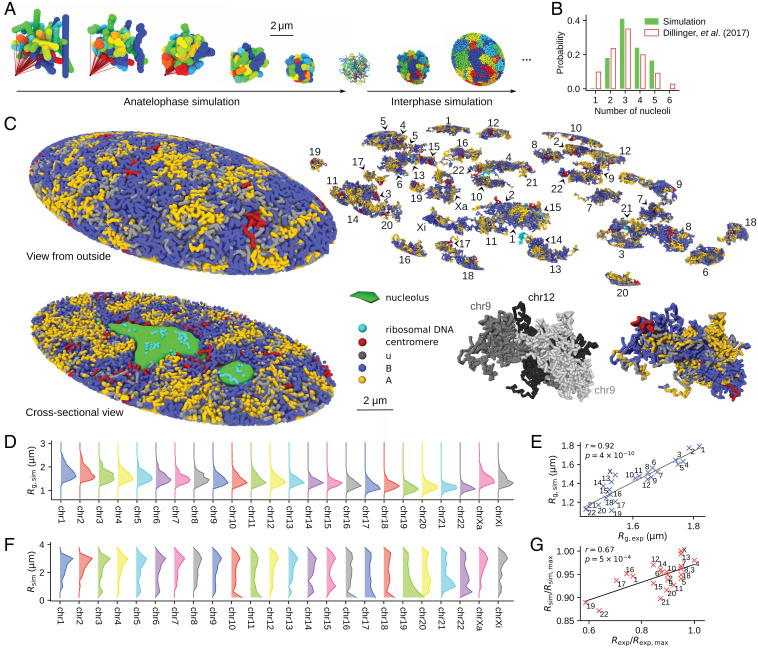
The simulated human genome. (A) The anatelophase simulation of the genome and the subsequent expansion of the nucleus at the entry to interphase; 46 chromosome chains are colored differently. From left to right: Chromosomes were represented by 46 rods placed in random orientations; the centromere locus of each chromosome was dragged by a spring (red line), whose end was anchored to a point in the space (leftmost); chromosome chains with a 10-Mb resolution were subjected to the thermal fluctuations during this dragging process (2nd to 5th from the left); the chains were fine grained to 100-kb resolution and equilibrated (6th from the left); and expansion of the genome was simulated as the entry process to G1 (7th and 8th from the left). (B) Distribution of the population fraction of cells having the number of nucleoli designated on the x axis. Comparison of the simulated 200 cells (green) (SI Appendix, SI Text and Fig. S2) and the experimental data (white bars with red outlines) (46) is shown. (C) A snapshot of the simulated G1 nucleus of IMR90. A view from the outside, the cross-section view, individual chromosomes, and the close-up view of three associated chromosomes are shown. A homologous pair of chromosome 9 and chromosome 12 occasionally associated in this simulated cell, showing an example case that the compartments spread across chromosomes. The genome is phase separated into type-A (yellow), type-u (gray), and type-B (blue) chromatin regions and the nucleoli (green). Centromeres (red) are found near the type-B regions, and rDNA loci (cyan) are near the type-B regions or buried in the nucleoli. (D) Distribution of Rg of chromosomes in GM12878 cells, sampled from 200 simulated cells. (E) Rg averaged over the distribution in D is compared with the microscope data (9). The correlation coefficient is r = 0.92, with . (F) Distribution of the radial position of the center of mass of chromosomes in GM12878 cells, sampled from 200 simulated cells. (G) The two-dimensional radial positions of the center of mass of chromosomes are compared with the microscopy data (47). The simulated chromosomes were projected onto a two-dimensional plane to calculate the two-dimensional radial positions. The correlation coefficient is r = 0.67, with . In A and C, the images were rendered using OVITO (43).
The nucleoli also form during this expansion (49). We represented the nucleoli by assemblies of particles adhering to ribosomal DNA (rDNA), into which the transcription products and the related factors are condensed. The weak short-range, attractive interactions arising from the exchange of diffusive molecules were assumed between the particles, which spontaneously assembled to form nucleoli through the genome expansion process. The number distribution of the resultant nucleoli per cell shows a peak at three and fluctuates around two to five, showing agreement with the microscope observation (46) (Fig. 4B). Each chromosome gained a V-shaped conformation during anatelophase, whose effects remained through the expansion process, leading to the long-range contacts between p and q arms of chromosomes in interphase. The nonequilibrium nature or the memory of the mitotic phase in the interphase genome architecture is consistent with the correlation between the chromosome configuration in the mitotic phase and that in the interphase observed among vastly different organisms (50).
Fig. 4C shows a snapshot of the simulated structure obtained after the nucleus reached a stationary size. In this state, the genome is phase separated into type-A, type-B, and type-u regions and nucleoli, where the type-u regions reside at the boundary of the type-A and type-B regions. Phase-separated A/B regions are formed in each chromosome and across chromosomes. We should note that this state is a nonequilibrium stationary state obtained by keeping the balance of pressures from outside and inside the nucleus. In this state, chromosomes were not mixed significantly but formed territories because the pressure balance was acquired before the slow entangling and mixing of chromosomes proceed. Size of chromosome territories was measured by the radius of gyration Rg of chromosomes. Distribution of Rg of each chromosome in the stationary 200 cells is plotted in Fig. 4D, showing the extent of cell-to-cell fluctuation. The mean Rg of the distribution agrees with the microscopy data (9), with the correlation coefficient r = 0.92 (Fig. 4E). Distribution of the radial position of chromosome territories, that is, the radial position of the center of mass of chromosomes, also fluctuates from cell to cell, but the distribution shows a distinct tendency for chromosomes with smaller size to reside in the inner region of the nucleus, and, particularly, chr19 tends to be buried inside the nucleus (Fig. 4F). The averaged radial position is compared with the microscopy data (47), showing correlation coefficient r = 0.67 (Fig. 4G).
Genome Organization Generated through Phase Separation of Chromatin.
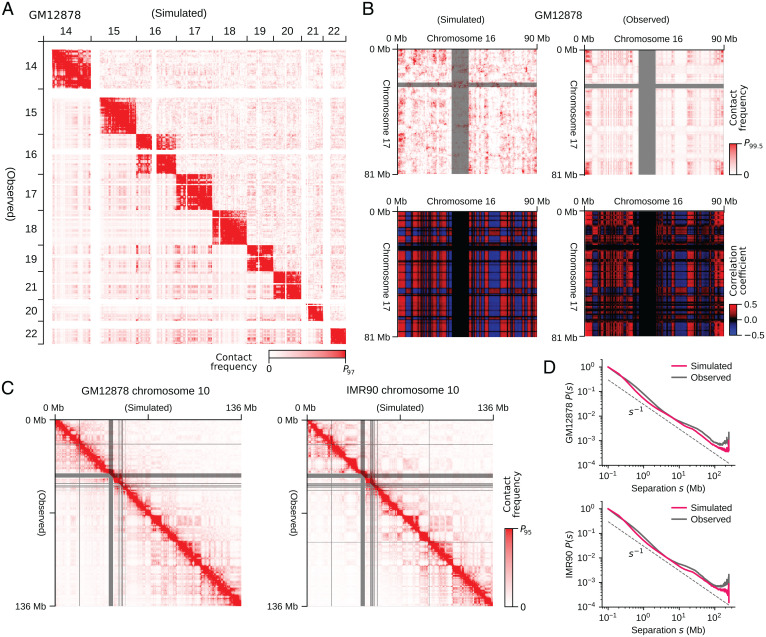
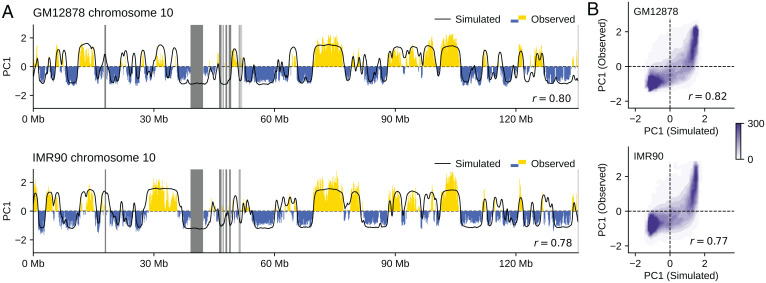
We analyzed the generated structures by comparing the experimentally observed (5) and simulated Hi-C contact matrices. The simulated data reproduces the observed features of contacts among several chromosomes (Fig. 5A) and in the whole genome (SI Appendix, Fig. S3), while the noise arising from the small sample size (n = 200) of simulated cells remains, reflecting the intense cell-to-cell fluctuation in interchromosome contacts. The noise was removed by enhancing the signal-to-noise ratio with the correlation coefficient representation of the contact matrix (4), clarifying the agreement between the simulated and observed results (Fig. 5B). Comparisons for the intrachromosome contacts show a further agreement between the simulated and observed results (Fig. 5C and SI Appendix, Figs. S4–S7). Diagonal blocks in the intrachromosomal matrices represent chromatin domains with several megabases or larger size. The simulated and observed block patterns agree with each other, suggesting these chromatin domains arise from phase separation (Movies S4 and S5). The observed dependence of the contact frequency P(s) on the sequence distance s is well reproduced in the simulation (Fig. 5D), showing that the simulation explains both the global and local chromosome structures in a balanced way. The plaid pattern of the interchromosomal (Fig. 5 A and B) and intrachromosomal (Fig. 5C) contact matrices represents A/B compartmentalization. This A/B compartmentalization was quantified using the compartment signal. The compartment signals derived from the simulated data were superposed with the observed data, with a Pearson’s correlation coefficient of (Fig. 6A). The genome-wide compartment signals for IMR90 and GM12878 show that the simulation reproduces the genome-wide data (Fig. 6B). Therefore, our model explains the A/B compartments and the other features of the intrachromosome and interchromosome Hi-C contacts in different cells using the same single set of model parameters. These features were lost when type-A, type-B, and type-u loci were randomly assigned along the polymer chains (SI Appendix, Fig. S8), showing that the arrangement of local properties along the chromatin chain is essential for proper phase separation and genome organization. Results in Figs. 4–8 were obtained by sampling the data from the calculated 200 trajectories, each having a length of h. Results were not much altered when we sampled the data from the trajectories of h (SI Appendix, Fig. S9). The results were robust against the change in the definition of the type-A/B/u annotation. In SI Appendix, Fig. S10, we show the results obtained by categorizing chromatin regions into two types, A and B, as type A for and type B . Effects of varying the functional form of are shown in SI Appendix, Fig. S11. The gentler slope of the repulsive potential with the higher value of also gave the phase-separated genome structure, but the contrast of phase separation was weakened with the gentle repulsive force between type-B regions; the distinct heterogeneity of repulsive force, that is, soft between type-A regions and hard between type-B regions, is a driving force of phase separation of chromatin.
Fig. 5.
Comparisons of the simulated and experimentally observed chromatin contact frequencies. (A) The simulated (upper right) and observed (lower left) contact matrix among several chromosomes of GM12878. (B) The simulated (Left) and observed (Right) interchromosome contacts between chromosomes 16 and 17 of GM12878 (Top) and those represented with the correlation coefficient matrix (4) (Bottom). (C) The simulated (upper right) and observed (lower left) intrachromosome contact matrix of chromosome 10. (D) The simulated (red) and observed (black) contact frequency P(s) averaged over the genome for the sequence separation s. Data are plotted in 1-Mb resolution in A and B, and 100-kb resolution in C. In B and C, the experimental data are lacking in the regions designated by gray bars. The experimental data are from ref. 5.
Fig. 6.
Comparisons of the simulated and experimentally observed compartment signals. (A) The simulated (black) and observed (yellow and blue) compartment signals of chromosomes 10 of GM12878 (r = 0.80) and IMR90 (r = 0.78). The experimental data are lacking in the regions designated by gray bars. (B) Contour plot of the density of compartment signals of the whole genome on the plane of the simulated and observed signal values for GM12878 (r = 0.82) and IMR90 (r = 0.77). Density is the number of 100-kb chromatin segments in a bin of square on the plane. The experimental data are from ref. 5. Compartment signal is the first principal component (PC1) of the simulated or observed chromatin contact matrix.
Fig. 7.
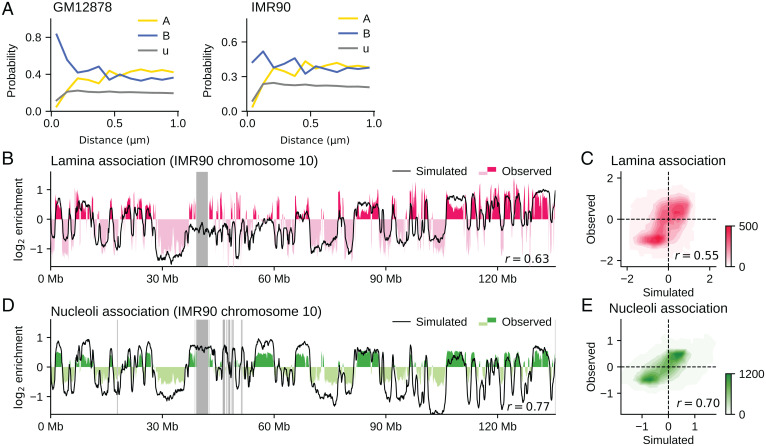
Comparisons of the simulated and experimentally observed data of association of chromatin with nuclear structures. (A) The probability of finding the type-α chromatin with A (yellow), u (gray), and B (blue) is plotted as a function of distance from the nuclear envelope (Methods). GM12878 (Left) and IMR90 (Right). The data from B to E are for IMR90. (B) The simulated (black) and observed (red and pink) lamina–chromatin association for chromosome 10; r = 0.63. (C) Contour plot of the density of the genome-wide lamina–chromatin association on the plane of the simulated and observed values; r = 0.55. (D) The simulated (black) and observed (green and thin green) nucleoli–chromatin association for chromosome 10; r = 0.77. (E) Contour plot of the density of the genome-wide nucleoli–chromatin association on the plane of the simulated and observed values; r = 0.70. In C and E, density is the number of 100-kb chromatin segments in a bin of square on the plane. In B and D, the experimental data are lacking in the regions designated by gray bars. The experimental data of B and C are the chromatin immunoprecipitation sequencing data for Lamin B1 (51). The experimental data of D and E are from ref. 46.
Fig. 8.
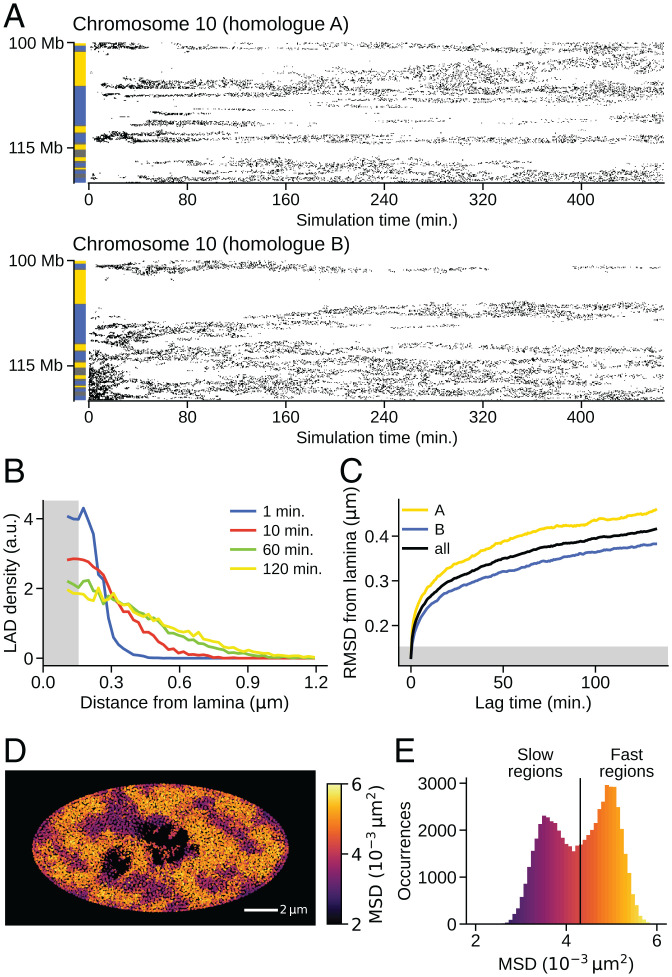
Dynamic fluctuations of the genome structure. The data are for the simulated IMR90 nucleus. (A) Time-dependent contact development between lamina and chromatin is plotted as points of contact on the plane of time and the sequential position. A pair of homologs of chromosome 10 are compared. Bars on the left show the NCI annotation to distinguish type-A, (yellow), type-B (blue), and type-u (gray) regions. (B) Temporal change of the normalized distribution (Methods) of distance between lamina and the chromatin loci, where the time duration was measured as time passed after each locus attached to the lamina. (C) Temporal change of the RMSD between lamina and the chromatin loci after each locus attached to the lamina. Type-A chromatin (yellow), type-B chromatin (blue), and the average (black) are shown. In B and C, the chromatin locus was regarded to be in contact with the lamina when it is in a gray hatched area. (D) A snapshot of the cross-section with the square displacement of each 100-kb region during s designated by colors. The dark regions near the center are nucleoli. (E) Distribution of the MSD of each 100-kb region during s. Colors in E are the same as in D.
We further analyzed the generated genome structure by examining the lamina–chromatin association. Fig. 7A shows that type-B chromatin accumulates, while type-A chromatin depletes near the nuclear envelope (Methods). The specific lamina–chromatin attractive interactions are not considered in the present model; therefore, this accumulation was not due to the tethering of type-B chromatin to the lamina but was induced dynamically similarly to the simulated polymer-blend system (Fig. 3 B and C). Fig. 7B compares the simulated and experimentally observed (51) lamina–chromatin association data for an example chromosome. The loci showing a large frequency of association, that is, the lamina-associated domains (LADs), are reproduced by the present simulation. LADs in the other chromosomes are shown in SI Appendix, Fig. S12. Fig. 7C compares the genome-wide data, showing an agreement between the simulated and observed (51) lamina–chromatin association, with r = 0.55. Specific factors that tether the LADs to the lamina should delay the dissociation kinetics of the LADs from the lamina, but our simulation revealed that the lamina–LAD association resulted as a consequence of the dynamic genome-wide phase separation process. We found similar results around the nucleoli. The simulation reproduced the observed (46) nucleolus-associated domains (NADs), although the chromatin chains, except for the rDNA loci, were not tethered to the nucleoli in the model (Fig. 7D). NADs in the other chromosomes are shown in SI Appendix, Fig. S13. The simulated and observed genome-wide nucleoli–chromatin associations show an agreement, with r = 0.70 (Fig. 7E). We note that the A/B compartments were well reproduced even when the system was simulated with the absence of nucleoli (SI Appendix, Fig. S14), showing that the nucleoli are not the driving force of phase separation of chromatin but a perturbation to the genome structure.
Dynamic Fluctuations of the Genome
After the simulated genome reached a stationary G1 phase, there remained fluctuations in genome movement such as the dynamic feature of the simulated lamina–chromatin interactions (Fig. 8A). The lamina–chromatin contacts spread as the genome expanded from t = 0 min. After the genome became stationary at min, dynamic fluctuations including association, dissociation, and positional shift of lamina–chromatin contacts continued to take place. A pair of homologous chromosomes showed differing fluctuating patterns from each other. We analyzed these fluctuations by plotting the temporal change of the normalized spatial distribution of chromatin loci after they adhered to the lamina (Fig. 8B and Methods). The distribution became broad over time, reflecting the dynamic dissociation of chromatin from the lamina as observed in the single-cell experiment (52). The root-mean-square distance (RMSD) of chromatin loci from the lamina is plotted as a function of time passed after each chromatin locus attached to the lamina, showing RMSD with for both type-A and type-B chromatin but with larger RMSD for the type-A chromatin (Fig. 8C). With this small α, once the loci were attached to the lamina, they stayed within m of the lamina for a long time, as experimentally observed (52). This reflects the tendency of the phase-separated compartment to retain LADs near the lamina.
Dynamic fluctuations were found in the entire nucleus. Fig. 8D shows a snapshot of the distribution of square displacement of each 100-kb chromatin region during s. The distribution is heterogeneous, with slow movement at the nuclear periphery and fast movement in the inner regions. Similar heterogeneous distributions were observed using live-cell imaging (10, 11, 53). Fig. 8E is the distribution of MSD of each chromatin region during s. The distribution was bimodal, as observed with live-cell imaging (54), showing contributions from the fast and slow components. The fast chromatin is mostly type A, whereas the slow chromatin tends to be type B (SI Appendix, Fig. S15). The pair-correlation functions showed that the positions of fast chromatin are correlated within m, constituting the fast-moving domains (SI Appendix, Fig. S16).
The difference in the movements between type-A and type-B regions was a driving force of phase separation during the genome expansion process at the entry to the G1 phase. This difference remained in fluctuations of dynamic association/dissociation of chromatin to/from the lamina after the genome reached the G1 phase and in the heterogeneity of the genome-wide dynamic fluctuations of chromatin in interphase nuclei. Coupling of these fluctuations with DNA functions such as transcription (55) and replication (56, 57) is an important issue for which the present model should provide a basis for the analyses.
Discussion
The simulated results showed that the present whole-genome model helps bridge different experimental analyses, including Hi-C and other high-throughput measurements, as well as live-cell imaging. The model explained various genomic data quantitatively, suggesting that the repulsion-driven phase separation largely determines the genome organization.
The analyses of cohesin-depleted cells with the Hi-C methods (58, 59) and theoretical modeling (60) have shown that A/B compartmentalization discussed in the present study and formation of the submegabase cohesin-bound loop domains of chromatin chains or topologically associating domains are two independent mechanisms that characterize genome organization. In the present whole-genome model, the NCI annotation of local chromatin property represents the effect of loop domain formation, which should cooperatively determine the intraloop physical property (61, 62). However, for analyzing the structure and dynamics of loop domains with their typical size being kb (5), the genome needs to be modeled with a higher resolution than the present 100-kb resolution. Incorporation of the 1-kb resolution model into the present phase-separated whole-genome structure should provide insights into this problem, helping to clarify the interplay between compartmentalization and loop domain formation/dissolution.
On the other hand, in a larger structure than a 100-kb scale, the determinant role of the phase separation mechanism implies that tethering of chromatin chains to the lamina, nucleoli, and other droplet-like condensates such as mediator droplets at superenhancers (55, 63) or nuclear speckles should work as perturbations to the genome structure/dynamics. The present model structure is usable as a starting structure for analyzing these chain-constraining effects and other perturbative effects.
Thus, the repulsion-driven phase-separated structure of the genome provides a platform for analyzing the effects of both small- and large-scale structural effects for comprehensive analyses of the genome organization.
Methods
Outline of the Interphase Genome Simulation.
We modeled the human genome with 46 heteropolymers; each polymer was a beads-on-a-string chain with a single bead representing a 100-kb chromatin region, which amounts to beads in the genome. The nucleoli were represented by assemblies of beads. Chromatin and nucleolar beads were confined in a spherical (GM12878) or spheroidal (IMR90) nuclear envelope, whose size was dynamically varied to adjust the balance of pressures inside and outside the nucleus. Dynamical movements of chromatin and nucleolar beads were simulated by numerically solving the overdamped Langevin equation with a discretization time step of in time units of . The initial genome conformation was prepared by simulating the anatelophase genome, and the subsequent genome expansion was simulated as the entry process to interphase. The nucleus reached a stationary size after ∼200,000 steps, and we sampled the genome structure until the 700,000th step. Each simulation run corresponds to a single cell simulation, and we performed independent simulation runs using different random number implementation. See SI Appendix, SI Text for a detailed explanation.
Potential Functions for Repulsive Interactions between 100-kb Chromatin Regions.
Repulsive potentials shown in Fig. 3A are
| [2] |
and
| [3] |
where r is the distance between two 100-kb chromatin regions, ε is a measure of the free-energy cost of overlapping of two regions, and and are typical of the spreading of type-A and type-B repulsive forces. The functional form of in Eq. 2 was used because this algebraic form well approximates a Gaussian function, while showing higher computational efficiency than the Gaussian. The functional form of Eq. 3 was used as an extension of the form in Eq. 2. We set to allow overlapping of chromatin regions with thermal fluctuation, , and to reproduce chromatin density in nuclei, where A(t) is a scaling factor that monotonously increases from 0.5 as the genome size increases at the entry to the G1 phase (SI Appendix, SI Text), and after the genome reaches the G1 phase (Fig. 4C).
Hi-C Data of Chromatin Contacts.
Simulated Hi-C data.
Instantaneous contact matrix was sampled at time t in the kth simulation run. A pair of chromatin beads i and j were considered to be in contact if the beads were closer than a scaled threshold distance,
| [4] |
where A(t) is a scaling factor explained in SI Appendix, SI Text, and is the threshold distance. We set , because the simulated functions of pair correlation in distance peaked at for all bead types of A, B, and u. was sampled every 20 steps from the 20,000th step to the 70,000th step. We write this set of sampling time points as . was summed into
| [5] |
Here, the population contact matrix defined above differentiates the alleles on two homologous chromosomes. In order to compare the results with the conventional Hi-C experimental data, we averaged out the homologous contact frequency. With sites and denoting the homologous copies of sites i and j, respectively, we calculated a smaller contact matrix,
| [6] |
Deriving Hi-C Contact Matrix and Compartment Signal from the Simulated or the Experimentally Observed Data.
From the experimentally observed (5) or simulated raw contact matrix, mij, the ratio was calculated as described in ref. 4. Here, mij is the observed or simulated Hi-C contact counts, and pij is the expected contact counts between i and j. For intrachromosome contacts, is the mean contact counts for the sequence separation with its average taken over the genome. For interchromosome contacts, we used . Here, is the total number of interchromosome contact counts in the genome, and is the fraction of contacts involving site i, with , where the interchromosomal sum over k was taken genome-wide, excluding intrachromosome sites. is the number of chromosome loci in the genome.
In Fig. 5B, the interchromosome contacts were analyzed by showing the normalized correlation coefficient matrix,
| [7] |
where . The compartment signal shown in Figs. 1 and 6 is the first principal component vector (PC1) of the whole-genome contact matrix, that is, the eigenvector for the largest eigenvalue of the whole-genome matrix Rij. The amplitude of the compartment signal was normalized to make its dispersion unity, and its sign was defined as positive for compartment A and negative for compartment B.
Data of Simulated Lamina–Chromatin Association.
Simulated probability distribution of chromatin residence near the nuclear envelope.
We counted the number
| [8] |
of beads of type X (= A, B, u, or no) lying within a range of distance from the nuclear envelope of the kth cell. Here, beads of type A, B, and u are chromatin beads, and beads of type no are nucleolar beads; is the number of elements in the set , and is the shortest distance of the ith bead from the nuclear envelope in the kth cell at the 700,000th step. We collected these numbers from 10 cells and calculated the sum . Then, we normalized the frequency at each distance d to get the distribution of each type of bead,
| [9] |
For small enough d, in GM12878, whereas is nonnegligible in IMR90 because of the flat shape of the ellipsoidal IMR90 nucleus. Because we modeled each 100-kb chromatin segment as a sphere with soft-core repulsions, exhibits an oscillatory pattern with a period corresponding to the diameter of the sphere. The overall trend of the distribution is the essential prediction, and the oscillation is an artifact of this coarse graining in the simulation. Hence, we calibrated the bin width to so that the oscillatory component is smoothed out. The thus obtained is shown in Fig. 7A.
Simulated frequency of lamina–chromatin association.
Instantaneous lamina–chromatin contact at the ith bead of the kth cell was sampled at time t as
| [10] |
where δi is the distance between the ith chromatin bead and the nuclear envelope, and is the threshold distance. We sampled every 1,000 steps from the 500,000th to 700,000th step. Writing this set of sampling instances as , the population lamina–chromatin contact was calculated from simulation runs as
| [11] |
The profile was normalized to its genome-wide average and log-transformed,
| [12] |
In Fig. 7 B and C, the resulting profile is compared with the experimental data.
Dynamic Chromatin Dissociation from the Nuclear Envelope.
We analyzed a spatiotemporal chromatin distribution near the nuclear envelope in an example single simulated cell. We sampled chromatin configuration every 1,000 steps from the 450,000th to 700,000th step. We write this set of time instances as . Let ti be the time when the bead i made first contact with the nuclear envelope;
| [13] |
where is the distance between bead i and the nuclear envelope, and is the threshold distance. We assumed if the ith bead did not approach to the nuclear envelope within the simulated duration; means that the ith bead was in contact with the lamina at time ti and stayed at the lamina or diffused away from the lamina thereafter. We counted the number
| [14] |
of chromatin beads lying within a range of distance from the nuclear envelope in the time interval . Here, is the shortest distance of the ith bead from the nuclear envelope at time t. We also computed the spatial distribution of all the chromatin beads in all the time steps as a reference,
| [15] |
Then, we normalized the frequency by the reference frequency to get the normalized spatiotemporal distribution of chromatin once attached to the lamina at τ = 0,
| [16] |
We used the spatial bin size and the temporal bin size (i.e., 1,000 steps) to show in Fig. 8B.
Data of Simulated Nucleoli–Chromatin Association.
Simulated frequency of nucleoli–chromatin association.
Nucleoli were represented as droplets formed by the assemblies of nucleolar beads in the present model. The frequency of nucleoli–chromatin association was calculated by contact counts between chromatin beads and nucleolar beads in the model. Instantaneous nucleoli–chromatin contact was calculated in the same way as the instantaneous chromatin–chromatin contact of Mij and summed over time and cells. From the obtained contact with and , the population nucleoli–chromatin contact profile was derived as
| [17] |
where bead is a homologous copy of chromatin bead i. Then, the profile was normalized to its genome-wide average and log-transformed,
| [18] |
In Fig. 7 D and E, the resulting profile is compared with the experimental data.
Supplementary Material
Acknowledgments
We are grateful to Dr. Kazuhiro Maeshima for critical reading of the manuscript. This work was supported by Core Research for Evolutionary Science and Technology (CREST) Grant JPMJCR15G2 of Japan Science and Technology Agency; the Riken Pioneering Project; Nagoya University Research Fund and KAKENHI Grants 20H05530, 21H00248, and 22H00406 of Japan Society for the Promotion of Science.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2109838119/-/DCSupplemental.
Data Availability
Codes have been deposited in GitHub (https://github.com/snsinfu/2022a-genome-dynamics).
References
- 1.Bickmore W. A., The spatial organization of the human genome. Annu. Rev. Genomics Hum. Genet. 14, 67–84 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Misteli T., The self-organizing genome: Principles of genome architecture and function. Cell 183, 28–45 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Maeshima K., Tamura S., Hansen J. C., Itoh Y., Fluid-like chromatin: Toward understanding the real chromatin organization present in the cell. Curr. Opin. Cell Biol. 64, 77–89 (2020). [DOI] [PubMed] [Google Scholar]
- 4.Lieberman-Aiden E., et al., Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326, 289–293 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rao S. S., et al., A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159, 1665–1680 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hsieh T. S., Fudenberg G., Goloborodko A., Rando O. J., Micro-C XL: Assaying chromosome conformation from the nucleosome to the entire genome. Nat. Methods 13, 1009–1011 (2016). [DOI] [PubMed] [Google Scholar]
- 7.Ou H. D., et al., ChromEMT: Visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science 357, eaag0025 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boettiger A. N., et al., Super-resolution imaging reveals distinct chromatin folding for different epigenetic states. Nature 529, 418–422 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Su J. H., Zheng P., Kinrot S. S., Bintu B., Zhuang X., Genome-scale imaging of the 3D organization and transcriptional activity of chromatin. Cell 182, 1641–1659.e26 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nozaki T., et al., Dynamic organization of chromatin domains revealed by super-resolution live-cell imaging. Mol. Cell 67, 282–293.e7 (2017). [DOI] [PubMed] [Google Scholar]
- 11.Shaban H. A., Barth R., Recoules L., Bystricky K., Hi-D: Nanoscale mapping of nuclear dynamics in single living cells. Genome Biol. 21, 95 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang B., Wolynes P. G., Topology, structures, and energy landscapes of human chromosomes. Proc. Natl. Acad. Sci. U.S.A. 112, 6062–6067 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pierro M. Di, Zhang B., Aiden E. L., Wolynes P. G., Onuchic J. N., Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. U.S.A. 113, 12168–12173 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Oliveira Junior A. B., Contessoto V. G., Mello M. F., Onuchic J. N., A scalable computational approach for simulating complexes of multiple chromosomes. J. Mol. Biol. 433, 166700 (2021). [DOI] [PubMed] [Google Scholar]
- 15.Shi G., Thirumalai D., From Hi-C contact map to three-dimensional organization of interphase human chromosomes. Phys. Rev. X 11, 011051 (2021). [Google Scholar]
- 16.Tan L., Xing D., Chang C. H., Li H., Xie X. S., Three-dimensional genome structures of single diploid human cells. Science 361, 924–928 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qi Y., et al., Data-driven polymer model for mechanistic exploration of diploid genome organization. Biophys. J. 119, 1905–1916 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tan L., et al., Changes in genome architecture and transcriptional dynamics progress independently of sensory experience during post-natal brain development. Cell 184, 741–758.e17 (2021). [DOI] [PubMed] [Google Scholar]
- 19.Maeshima K., Ide S., Hibino K., Sasai M., Liquid-like behavior of chromatin. Curr. Opin. Genet. Dev. 37, 36–45 (2016). [DOI] [PubMed] [Google Scholar]
- 20.Cook P. R., Marenduzzo D., Entropic organization of interphase chromosomes. J. Cell Biol. 186, 825–834 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pierro M. Di, Cheng R. R., Lieberman Aiden E., Wolynes P. G., Onuchic J. N., De novo prediction of human chromosome structures: Epigenetic marking patterns encode genome architecture. Proc. Natl. Acad. Sci. U.S.A. 114, 12126–12131 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Falk M., et al., Heterochromatin drives compartmentalization of inverted and conventional nuclei. Nature 570, 395–399 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gibson B. A., et al., Organization of chromatin by intrinsic and regulated phase separation. Cell 179, 470–484.e21 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Erdel F., et al., Mouse heterochromatin adopts digital compaction states without showing hallmarks of HP1-driven liquid-liquid phase separation. Mol. Cell 78, 236–249.e7 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Larson A. G., et al., Liquid droplet formation by HP1α suggests a role for phase separation in heterochromatin. Nature 547, 236–240 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Strom A. R., et al., Phase separation drives heterochromatin domain formation. Nature 547, 241–245 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Paulsen J., et al., Chrom3D: Three-dimensional genome modeling from Hi-C and nuclear lamin-genome contacts. Genome Biol. 18, 21 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schmitt A. D., et al., A compendium of chromatin contact maps reveals spatially active regions in the human genome. Cell Rep. 17, 2042–2059 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dequeker B. J. H., et al., MCM complexes are barriers that restrict cohesin-mediated loop extrusion. bioRxiv [Preprint] (2020). 10.1101/2020.10.15.340356 (Accessed 17 May 2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu Y., Dekker J., Biochemically distinct cohesin complexes. bioRxiv [Preprint] (2021). 10.1101/2021.08.24.457555 (Accessed 17 May 2022). [DOI] [Google Scholar]
- 31.Banigan E. J., et al., Transcription shapes 3D chromatin organization by interacting with loop-extruding cohesin complexes. bioRxiv [Preprint] (2022). 10.1101/2022.01.07.475367 (Accessed 17 May 2022). [DOI] [Google Scholar]
- 32.Spracklin G., et al., Heterochromatin diversity modulates genome compartmentalization and loop extrusion barriers. bioRxiv [Preprint] (2021). 10.1101/2021.08.05.455340 (Accessed 17 May 2022). [DOI] [Google Scholar]
- 33.Jost D., Carrivain P., Cavalli G., Vaillant C., Modeling epigenome folding: Formation and dynamics of topologically associated chromatin domains. Nucleic Acids Res. 42, 9553–9561 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Qi Y., Zhang B., Predicting three-dimensional genome organization with chromatin states. PLOS Comput. Biol. 15, e1007024 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kilic S., et al., Single-molecule FRET reveals multiscale chromatin dynamics modulated by HP1α. Nat. Commun. 9, 235 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bryan L. C., et al., Single-molecule kinetic analysis of HP1-chromatin binding reveals a dynamic network of histone modification and DNA interactions. Nucleic Acids Res. 45, 10504–10517 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dinpajooh M., Guenza M. G., On the density dependence of the integral equation coarse-graining effective potential. J. Phys. Chem. B 122, 3426–3440 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Carbone P., Varzaneh H. A. K., Chen X., Müller-Plathe F., Transferability of coarse-grained force fields: The polymer case. J. Chem. Phys. 128, 064904 (2008). [DOI] [PubMed] [Google Scholar]
- 39.Krakoviack V., Hansen J. P., Louis A. A., Influence of solvent quality on effective pair potentials between polymers in solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 041801 (2003). [DOI] [PubMed] [Google Scholar]
- 40.Perišić O., Schlick T., Dependence of the linker histone and chromatin condensation on the nucleosome environment. J. Phys. Chem. B 121, 7823–7832 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Winogradoff D., Echeverria I., Potoyan D. A., Papoian G. A., The acetylation landscape of the H4 histone tail: Disentangling the interplay between the specific and cumulative effects. J. Am. Chem. Soc. 137, 6245–6253 (2015). [DOI] [PubMed] [Google Scholar]
- 42.Schweizer K. S., Curro J. G., Integral-equation theory of the structure of polymer melts. Phys. Rev. Lett. 58, 246–249 (1987). [DOI] [PubMed] [Google Scholar]
- 43.Stukowski A., Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2010). [Google Scholar]
- 44.Walter J., Schermelleh L., Cremer M., Tashiro S., Cremer T., Chromosome order in HeLa cells changes during mitosis and early G1, but is stably maintained during subsequent interphase stages. J. Cell Biol. 160, 685–697 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stefano M. Di, Nützmann H. W., Marti-Renom M. A., Jost D., Polymer modelling unveils the roles of heterochromatin and nucleolar organizing regions in shaping 3D genome organization in Arabidopsis thaliana. Nucleic Acids Res. 49, 1840–1858 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dillinger S., Straub T., Németh A., Nucleolus association of chromosomal domains is largely maintained in cellular senescence despite massive nuclear reorganisation. PLoS One 12, e0178821 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Boyle S., et al., The spatial organization of human chromosomes within the nuclei of normal and emerin-mutant cells. Hum. Mol. Genet. 10, 211–219 (2001). [DOI] [PubMed] [Google Scholar]
- 48.Güttinger S., Laurell E., Kutay U., Orchestrating nuclear envelope disassembly and reassembly during mitosis. Nat. Rev. Mol. Cell Biol. 10, 178–191 (2009). [DOI] [PubMed] [Google Scholar]
- 49.Hernandez-Verdun D., Assembly and disassembly of the nucleolus during the cell cycle. Nucleus 2, 189–194 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hoencamp C., et al., 3D genomics across the tree of life reveals condensin II as a determinant of architecture type. Science 372, 984–989 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sadaie M., et al., Redistribution of the Lamin B1 genomic binding profile affects rearrangement of heterochromatic domains and SAHF formation during senescence. Genes Dev. 27, 1800–1808 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kind J., et al., Single-cell dynamics of genome-nuclear lamina interactions. Cell 153, 178–192 (2013). [DOI] [PubMed] [Google Scholar]
- 53.Zidovska A., Weitz D. A., Mitchison T. J., Micron-scale coherence in interphase chromatin dynamics. Proc. Natl. Acad. Sci. U.S.A. 110, 15555–15560 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ashwin S. S., Nozaki T., Maeshima K., Sasai M., Organization of fast and slow chromatin revealed by single-nucleosome dynamics. Proc. Natl. Acad. Sci. U.S.A. 116, 19939–19944 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nagashima R., et al., Single nucleosome imaging reveals loose genome chromatin networks via active RNA polymerase II. J. Cell Biol. 218, 1511–1530 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Miura H., et al., Single-cell DNA replication profiling identifies spatiotemporal developmental dynamics of chromosome organization. Nat. Genet. 51, 1356–1368 (2019). [DOI] [PubMed] [Google Scholar]
- 57.Klein K. N., et al., Replication timing maintains the global epigenetic state in human cells. Science 372, 371–378 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Rao S. S. P., et al., Cohesin loss eliminates all loop domains. Cell 171, 305–320.e24 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schwarzer W., et al., Two independent modes of chromatin organization revealed by cohesin removal. Nature 551, 51–56 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nuebler J., Fudenberg G., Imakaev M., Abdennur N., Mirny L. A., Chromatin organization by an interplay of loop extrusion and compartmental segregation. Proc. Natl. Acad. Sci. U.S.A. 115, E6697–E6706 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Xie W. J., Zhang B., Learning the formation mechanism of domain-level chromatin states with epigenomics data. Biophys. J. 116, 2047–2056 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Katava M., Shi G., Thirumalai D., Chromatin dynamics controls epigenetic domain formation. bioRxiv [Preprint] (2021). 10.1101/2021.01.18.427115 (Accessed 17 May 2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Boija A., et al., Transcription factors activate genes through the phase-separation capacity of their activation domains. Cell 175, 1842–1855.e16 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Codes have been deposited in GitHub (https://github.com/snsinfu/2022a-genome-dynamics).