Differences in ion-RNA binding modes due to charge density variations explain the stability of RNA in monovalent salts

Abstract

The stability of RNA increases as the charge density of the alkali metal cations increases. The molecular mechanism for this phenomenon remains elusive. To fill this gap, we performed all-atom molecular dynamics pulling simulations of HIV-1 trans-activation response RNA. We first established that the free energy landscape obtained in the simulations is in excellent agreement with the single-molecule optical tweezer experiments. The origin of the stronger stability in sodium compared to potassium is found to be due to the differences in the charge density–related binding modes. The smaller hydrated sodium ion preferentially binds to the highly charged phosphates that have high surface area. In contrast, the larger potassium ions interact with the major grooves. As a result, more cations condense around phosphate groups in the case of sodium ions, leading to the reduction of electrostatic repulsion. Because the proposed mechanism is generic, we predict that the same conclusions are valid for divalent alkaline earth metal cations.

All-atom simulations of RNA unfolding highlight the critical role(s) played by charge density.

INTRODUCTION

RNA folding is a complex process that is not only determined by the nucleotide sequence but also driven by cations that are needed to soften the electrostatic repulsive interactions between the negatively charged phosphate groups (1, 2). Although there are exceptions (3–5), in general, independently stable secondary structures form first, followed by consolidation of tertiary interactions that stabilize the folded state. Several studies (6–12) have shown that RNA undergoes marked compaction during folding as the salt concentration is increased. The entropy loss due to secondary structure formation is primarily compensated by the gain in hydrogen bonding and base stacking interactions involving the nucleotides. Condensation of cations onto the phosphate groups is required for RNA to fold (1, 13–17). Thus, the formation of a stable folded RNA involves an interplay of a number of factors (RNA conformations; size, shape, and valence of cations; and hydration effects), which makes it difficult to decipher the principles governing the folding of RNA (2).

Analyses of RNA structures and simulations have shown that cations bind to discrete sites on RNA rather than nonspecifically (18–24). Optical melting experiments, small-angle x-ray scattering (SAXS), nuclear magnetic resonance, and gel electrophoretic studies suggest that there is a complicated interplay between RNA conformations and charge density (25–33). In addition, single-molecule optical and magnetic tweezer experiments (34–38) and atomic force microscopy (39) reported a cation size–dependent stabilization of RNA hairpins (34). These experiments show higher RNA stability in NaCl solution than in KCl solution. Experimental and theoretical studies suggest that the smaller hydrated monovalent cations are more effective in RNA stabilization. A conclusion of general validity is that cation charge density is a dominant factor in affecting RNA stability (26, 27).

Various mechanisms have been proposed to explain the charge density–induced stability in RNA folding (10, 16, 26, 40–42). If RNA is more flexible in KCl than in NaCl, then the entropic stabilization of the unfolded state would result in a smaller free energy difference between the native and unfolded states in K⁺ ion. Another possibility is that the smaller size of Na⁺ ions leads to stronger binding to the RNA surface. This could induce further compaction of RNA, which would be consistent with SAXS experiments on a ribozyme (10). However, the molecular basis of the postulated charge density, ρ_c, hypothesis remains unclear. Because the results of a large number of experiments on RNA stability hinge on the use of ρ_c as the primary factor in determining RNA stability, providing a molecular explanation would greatly advance our understanding of ion-RNA interactions. Doing so would require atomically detailed simulations that quantitatively account for the coupling between RNA conformations and fluctuations in the fields created by the cations.

Here, we use all-atom simulations in explicit water to investigate the impact of Na⁺ and K⁺, with markedly different ρ_c values, on RNA folding. For illustration purposes, we consider the mechanical stability of HIV-1 TAR, a ubiquitous RNA that forms a helix-junction-helix structure. Using mechanical force (f) to unfold the hairpin, as was done in single-molecule pulling experiments (34), we monitor the interactions between the cation and RNA as it unfolds. We first show that the simulations capture the results obtained in experiments (34), which showed that HIV-1 TAR is more stable in Na⁺ than in K⁺. We then determined the microscopic basis of the impact on the stability of HIV-1 TAR in the presence of the two cations. There are marked differences between the binding preferences of the cations to the RNA surface depending on their size and hence ρ_c. Potassium ions predominantly bind to the major grooves with high affinity. In sharp contrast, the smaller sodium ions, with higher charge density, are localized on the phosphate backbone. These differences in the preferential binding resulted in different coordination numbers. Sodium ions, which are exposed to a larger surface, have a higher number of cation coordination and hence result in higher thermodynamic stability of the RNA. A broader principle that emerges from this study is that, for given ion valence and ion shape, the cation with the highest charge density can bind most tightly to the negatively charged phosphate groups and therefore impart the greatest stability on the folded RNA.

RESULTS

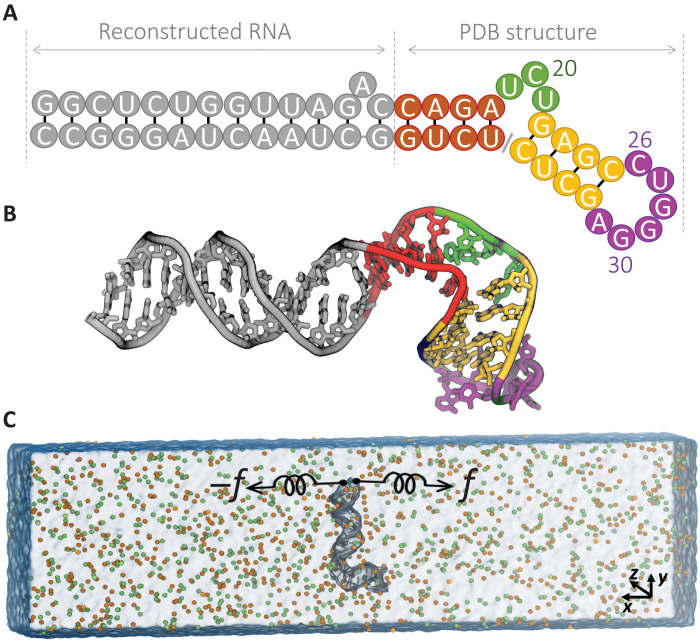
To investigate the energy landscape of RNA subject to mechanical force and to study the role of monovalent cation size in RNA stabilization, we chose the HIV-1 TAR RNA hairpin, which was the subject of investigation in the pulling experiments by Vieregg et al. (34) and Li et al. (36). In Fig. 1 (A and B), we show the sequence and structure of the 52–nucleotide (nt)–long HIV-1 TAR RNA. The structure consists of a 26-nt extended stem (gray), connected to a 4-nt lower stem (red) with a 3-nt apical loop (green), followed by a 4–base pair upper stem (yellow) that is bridged by a 6-nt bulge region (purple). The simulation box with the direction of the pulling coordinate is shown in Fig. 1C. This construct enabled us to directly compare our findings to mechanical pulling experiments. Direct comparison of available experimental data allowed us to assess the validity of the theoretical findings.

Fig. 1. Schematic of molecular simulation setup for HIV-1 TAR hairpin.

(A) RNA sequence. (B) The structure of the HIV-1 TAR hairpin under study consists of an extended stem (gray), connected to lower stem (red) with apical loop (green), followed by upper stem (yellow) that is bridged by bulge region (purple). (C) Setup for the MD simulation in 400 mM KCl, K⁺ (orange) and Cl⁻ (green). The RNA hairpin (gray) is aligned perpendicular to the x axis, and the terminus nucleotides are pulled.

Cation-dependent energy landscapes

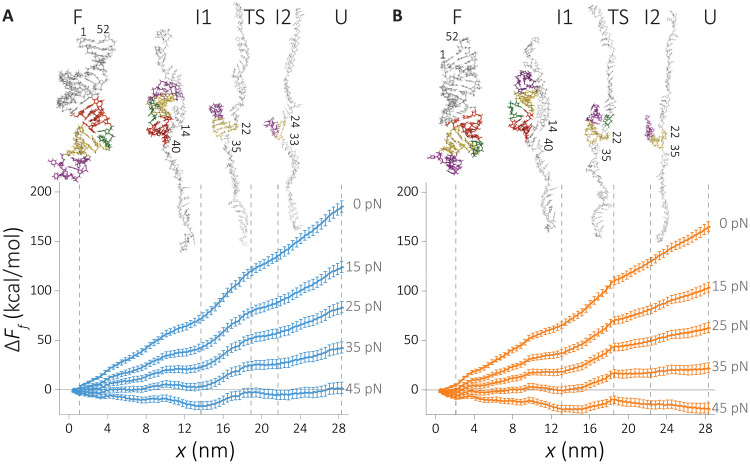
We constructed the energy landscape along the mechanical pulling coordinate using the umbrella sampling approach (detailed in Methods) (43). The effect of applied force, f, on the relative free energy, projected onto the molecular extension ΔF_f(x) is calculated using ΔF_f(x) = ΔF₀(x) − fx, where ΔF₀(x) is the relative free energy at zero force. Our results, plotted in Fig. 2 (A and B), display a staircase-like energy landscape, where the intermediate states become visible only if f ≠ 0. Our simulations show the mechanical unfolding process of HIV-1 TAR as an unzipping process with some minor deviation depending on solvent conditions. The picture that emerges from the all-atom simulations is consistent with our earlier works (44–46). In accord with the experimental findings (34), the RNA has higher stability in Na⁺, thus confirming the charge density hypothesis. A systematic difference in the magnitude of the free energy is found between Na⁺ and K⁺ ions at all f values, as revealed in the free energy profiles (Fig. 2, A and B).

Fig. 2. Force-induced unfolding energy landscape of HIV-1 TAR hairpin.

Free energy profiles are computed by umbrella sampling molecular dynamics (MD) simulations. (A) RNA in NaCl and (B) in KCl. The reaction coordinate, x, is the displacement along the pulling direction. The effect of force (f) on the landscape F_f is estimated by F_f(x) = F₀(x) − fx. Vertical lines indicate major intermediate states along the RNA unfolding: F, folded state; I1, intermediate state 1; TS, transition state; I2, intermediate state 2; and U, unfolded state. The snapshots from simulations representing the intermediate states are shown in the insets with the last base-paired hairpin that is marked.

On the basis of the location of the local minima, which appear at f ≠ 0, we monitor the unfolding mechanism. The insets in Fig. 2 (A and B) summarize the changes in the secondary structures as RNA transitions from the folded state to the unfolded one. States labeled F, I1, TS, I2, or U represent the major points along the energy landscape. The F is the fully folded state. I1 is the early intermediate where the apical loop and lower stem are formed. TS is the putative transition state for the unfolding transition that marks the rupture of the upper stem. I2 is the last intermediate state where only the upper stem and bulge are folded. Last, U is the extended state where no secondary structure remains.

Transition state

On the basis of the computed energy landscape, we locate the transition state for the unfolding transition to be Δx^* = x_N − x^* ≈ 17.5 nm, where, x_N and x^* correspond to the native (F) and transition state (TS), respectively. Unexpectedly, the value of the calculated Δx^* compares favorably well with the value (≈17 nm) measured experimentally in KCl (36). As noted before, the simulations show that HIV-1 TAR RNA has higher stability in NaCl solution compared to that in KCl. The difference in the stability between the two cations, ΔΔF = ΔF_Na⁺(x_I2) − ΔF_K⁺(x_I2) ≈ 9 kcal/mol, where F(x_I2) is the free energy value in state I2, compares well with a measured stability of 7 kcal/mol (34). Given the approximations in the simulations and the use of high loading rates, we believe that the agreement between simulations and experiments is very good. In this state, we found an additional non-native bond formation that facilitates a higher stability of this intermediate state compared to the unfolded state (Fig. 2 and fig. S1). In this region, additional hydrogen bonds are formed between the unzipped single-stranded and the remaining folded segment of the hairpin structure (see fig. S2), primarily between the guanines of the single strand and the phosphate backbone of the helix, and between the adenines or uracils of the single strand and the 2′-hydroxyl group (Fig. 2, inset, and fig. S2).

The determining factor in HIV-1 TAR RNA stability in monovalent cations

The good agreement between simulations and experiments is used as a rationale for determining the microscopic mechanism using atomically detailed simulations. Our goal is to decipher the physical principles that explain the cation size–dependent stability. To test the molecular origin of the charge density hypothesis (10, 26, 34), we monitor the changes in (i) conformational entropy of RNA, (ii) the degree of RNA compaction, (iii) the energetic factors, and (iv) solvent structuring during the unfolding process. The calculation of these quantities is described in Methods.

Both the conformational entropy and the degree of compaction (measured by radius of gyration) show an increase in unfolding with a sharp transition in entropy near the transition state (fig. S3). However, no difference between Na⁺ and K⁺ ions is evident that can explain the observed change in stability. We examined the number of water molecules released during unfolding (fig. S4). The radial distribution function (RDF) associated with water shows that the hydration shell is more structured in the unfolded state. The number and binding affinity of water molecules decrease as RNA folds. However, none of the aforementioned factors show a notable cation size dependence that can distinguish between the different effects that the two cations have on RNA stability.

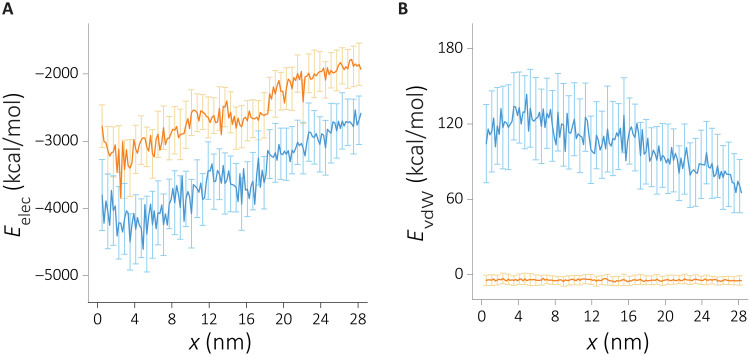
To investigate the effect of the cation size, we turned our attention to RNA-ion interactions. We compute the nonbonded interaction energy as a function of the molecular extension. We also partitioned the nonbonded energy terms into electrostatic and van der Waals terms. The results, displayed in Fig. 3, show that the magnitude of the electrostatic energy far exceeds the van der Walls in both cation types, suggesting that the electrostatic interactions are dominant. Unlike the previous analysis (figs. S3 and S4), the nonbonded ion-RNA interaction energy shows marked differences between the two cations. RNA-Na⁺ interactions are energetically more favorable compared to RNA-K⁺ interactions.

Fig. 3. The change in the intermolecular nonbonded interaction terms as a function of extension when RNA is in Na⁺ (blue) or in K⁺ (orange).

(A) The electrostatic energy component. (B) The van der Waals energy component.

Cation size–dependent ion solvation

The stark difference between the cations in the electrostatic energy offers a plausible explanation for the higher stability in NaCl. To understand the differences in the electrostatic interactions, we first investigate the cation distributions around the RNA along the mechanical unfolding pathway. Using the midpoint of the unfolding force, f_1/2, we divide the RNA population into folded and unfolded states (fig. S1). On the basis of the free energy landscape, we select state I2 to represent the unfolded state. In Fig. 4 (A and B), we show RNA-cation distance distributions in the two basins, representing the folded and unfolded state ensembles. Note that our conclusions are general and not dependent on the precise choice of a particular unfolded state. To demonstrate that we show the RNA-cation distributions when state U is taken as the unfolded state (fig. S5).

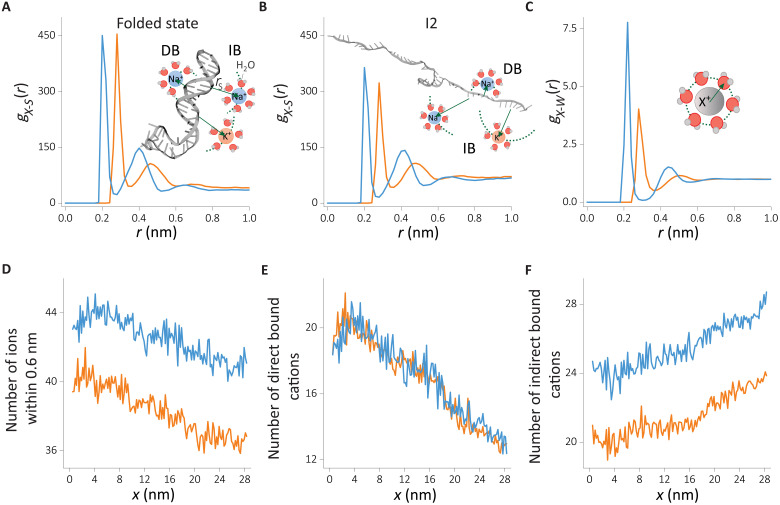
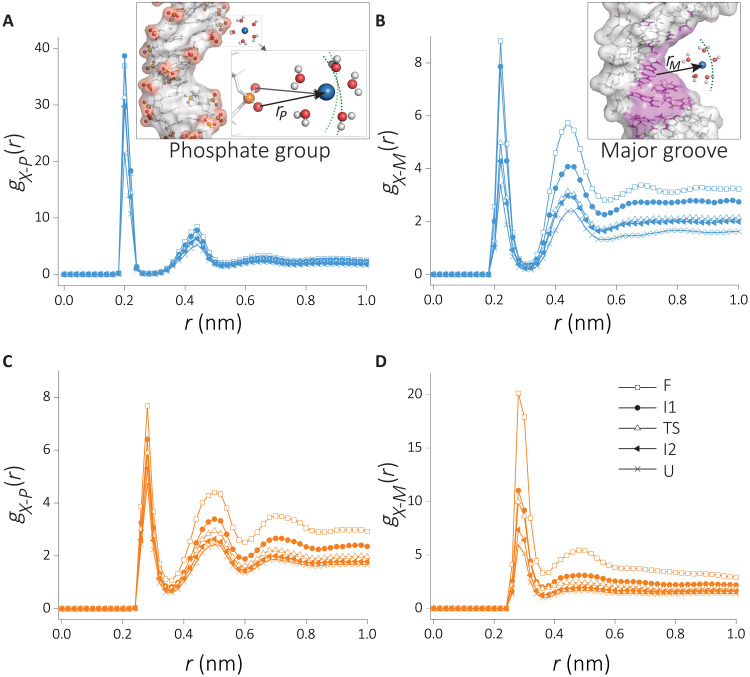
Fig. 4. Cation distributions around the HIV-1 TAR hairpin in the folded and unfolded states.

RDFs are computed from the surface of the RNA to the cation. (A and B) RDF of cation-RNA, g_{X − S}(r), (A) in the folded state and (B) in the unfolded intermediate state I2. Schematics in (A) and (B) illustrate the two binding modes: direct binding (DB) and indirect binding (IB). (C) RDF of cations (X⁺) with the oxygen atom of water, g_{X − W}(r). (D to F) Changes in the number of Na⁺ and K⁺ coordination computed from cumulative distribution (see Methods for details), (D) the total number of ions within 0.6-nm influence radius from the RNA surface, (E) the directly bound cations, and (F) the number of indirectly binding cations. Data for Na⁺ and K⁺ are given in blue and orange, respectively

The RDF of cations reflects their preferential binding propensities and their binding strengths (Fig. 4, A and B). We first focus on the cation distributions in the folded state (Fig. 4A). The first peak at 2.0 Å corresponds to direct binding (DB) of Na⁺ cations, while for K⁺, this peak shifts further to 2.8 Å. In the DB mode, cations exchange one of the water molecules in the solvation shell with the RNA surface atom. Despite the proximity of the Na⁺ ion to the negatively charged RNA surface, the peak height in the RDFs is the same as in the K⁺ ion. Although RNA-Na⁺ interactions are electrostatically favored, the smaller radius of Na⁺ relative to K⁺ also results in a stronger hydration shell. This is evidenced by the RDF of cations with water (Fig. 4C). The higher amplitude of RDF in the case of sodium suggests a stronger hydration shell. The Na⁺ ions disfavor dehydration of water more than K⁺. Hence, Na⁺ ions less frequently engage in DB (Fig. 4C) to the RNA surface. The larger size of K⁺ ions, on the other hand, leads to a weaker electrostatic interaction with the RNA surface. The weaker hydration shell of K⁺ ions also promotes DB of K⁺ ions to the RNA surface. As a result, the smaller size of Na⁺ does not provide an obvious advantage over K⁺ ions in terms of binding affinity to the first hydration shell. The second peak in Fig. 4A corresponds to the indirect binding (IB) of cations. Here, we observe a higher affinity for Na⁺ ions, reflecting the small hydrodynamic radius. Hydrated K⁺ ion that is about Δr ≈ 0.8 Å larger in radius than sodium ion results in a weaker electrostatic interaction and hence a smaller amplitude in the RDF.

A similar picture emerges when we analyze the unfolded state (Fig. 4B and fig. S5), suggesting that the two binding modes are common in the RNA conformational states. There is a general trend of weakening the cation binding affinities in the unfolded state, reflected in a reduction of RDF peak amplitudes. This is in accord with the reduced charge density of the backbone ρ_c ∝ (1/R_g) reported in fig. S3B. The DB of K⁺ ions is disfavored in the unfolded state, implying a correlation between cation binding mode and the degree of folding/compaction. Such a correlation is not evident for Na⁺ ions.

The coordination number, obtained from RDFs, could be used to assess the degree of cation association. In addition, the coordination number allows us to benchmark our findings with the mean-field theories and enables monitoring of the coupling between the RNA conformations and counterion association as the RNA unfolds under tension. In Fig. 4 (D to F), we plot the x-dependent changes in the total, DB, and IB cation coordination, respectively. A strong coupling between RNA conformation and cation association is evident for all the binding modes. At small x, corresponding to the folded state, cations accumulate near RNA (Fig. 4D). The number of Na⁺ cations shows about ≈10% higher condensation. The cation size–dependent difference in cation occupancy was reported in the ion competition experiments for double-stranded DNA (dsDNA) at ≈50 mM monovalent salt concentrations (47). Higher salt concentrations studied here and dsRNA instead of dsDNA are expected to result in a bigger difference, which accords well with our findings. DB shows a steeper change in condensation in Fig. 4E. The number of cations that are directly bound decreases about twofold during the unfolding process, while the total number of ions condensed on the RNA decreases only about 10%. The dependence of the number of bound cations to RNA as a function of x is independent of the cation size. In sharp contrast, the number of cations that are bound indirectly to RNA shows marked differences between Na⁺ and K⁺ ions. Our data suggest that hydrated Na⁺ cations accumulate more onto the RNA surface than hydrated K⁺ ions. The number of IB ions increases as x increases (transition to the folded from the unfolded state), suggesting a migration from the directly bound cation atmosphere to the indirectly bound state as the RNA charge density decreases.

As a result of the cation size–dependent condensation, Na⁺ ions neutralize ≈79% of the RNA charges, whereas K⁺ ions shield only about ≈73% when HIV-1 TAR RNA is in the folded state. These values are in reasonable accord with the counterion condensation theory (CCT) (15). However, CCT predictions do not readily account for cation size dependence. This implies that the subtle roles that K⁺ and Na⁺ play in affecting RNA stability require a more nuanced picture, which we discuss below.

Cation size–dependent spatial distributions

Our analysis suggests that Na⁺ ions condense more onto the RNA. What are the molecular details of increased localization of Na⁺ ions relative to K⁺ ions around the RNA? To answer this question, we divide the RNA surface into two groups following previous studies (48,49). We focus on the major groove and the phosphate group of the RNA backbone. We plot in Fig. 5 the partitioning of cations into these groups.

Fig. 5. RDF of cations with the two major binding sites of RNA at the defined states along the unfolding path.

The RDF of (A) Na⁺, phosphate group; (B) Na⁺, major groove; (C) K⁺, phosphate group; and (D) Na⁺, major groove.

Similar to Fig. 4 (A and B), the RDFs of the subgroups show two peaks corresponding to the DB and IB (Fig. 5). Binding to the phosphate group is favored for Na⁺ ions, whereas binding to the major grooves is favored by K⁺ ions. When the RDFs are compared along the reaction coordinate, there is a clear correlation between the charge density of the RNA backbone (fig. S3B) and RDF peak amplitudes (Fig. 5, A and B). In the case of Na⁺ ions, the major difference in the RDFs is in the DB to the phosphate groups and in the IB to the major groove. In the case of K⁺ ions, DB to the major groove shows the strongest dependence on the conformations. The folded state shows a marked difference in the peak heights, suggestive of strong dependence on the RNA conformations.

To investigate the effect of cation size–dependent partitioning on charge neutrality, we compute the cumulative number of charges within 6 Å from each group. On the basis of this, Na⁺ binding to the backbone compensates for about 63.7% of RNA charge, while the major groove neutralizes about 15.1%. These numbers are 16.4% (backbone) and 56.7% (major) for K⁺. Preferential cation binding at short range does not provide enough cations to fully neutralize the RNA. The RNA neutralization happens at longer distances (≈9 Å from the RNA surface) where preferential binding loses its meaning.

Residue-level cation localization along RNA folding/unfolding pathway

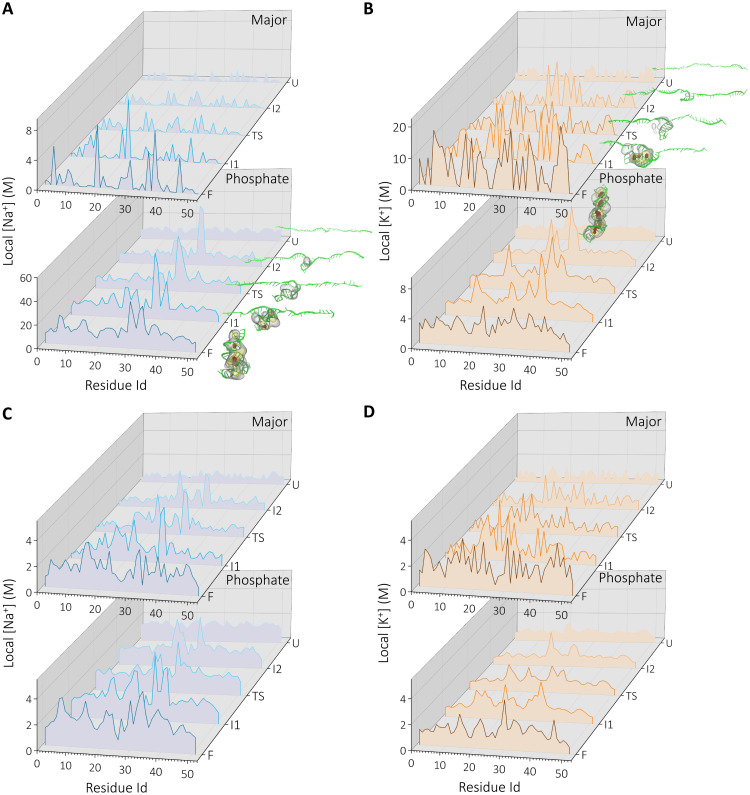
In Fig. 5, we show the differences in the partitioning of the cations averaged over the whole RNA surface. To gain a more detailed understanding of how the cations are localized, we zoomed in on the residue level differences and we monitor them as RNA unfolds. To quantify the ionic environment, we compute local cation concentrations at the residue level (see Methods for details). As in the previous section, we partition the binding into phosphate and major groove subgroups. The DB and IB are considered here separately. We monitor the local cation concentration as RNA undergoes structural transitions. The results for Na⁺ and K⁺ distributions are compared in Fig. 6 (A to D).

Fig. 6. Residue-level cation concentration at the defined states along the RNA unfolding pathway.

(A and B) the concentration of DB cations to major and phosphate backbone and (C and D) the indirectly bound cations for Na⁺ (blue) and K⁺ (orange). Insets show local concentration in 3D density profiles at each state (see Methods for details). Only the high-density regions are shown: ρ > 11ρ_bulk (red), ρ > 7ρ_bulk (yellow), and ρ > 3ρ_bulk (gray).

Although the number of DB cations is similar between K⁺ and Na⁺ (Fig. 4E), their partitions among the major groove/backbone show marked differences. The localization of K⁺ ions around the phosphate group is weaker compared to their binding to the major groove. In addition, K⁺ localization shows differences when compared with Na⁺ ions, despite the strong similarity between the RNA structures sampled in each cation.

In accord with the results in Fig. 5, Na⁺ shows weak localization in the major groove with few discrete binding pockets along the chain. The high cation density regions in the concentration plots coincide well with the three-dimensional (3D) ion densities computed for each intermediate state (Figs. 2 and 6, bottom). As the RNA unfolds, the cations leave the DB mode on the surface of the RNA. Almost all DB cations disappeared at (state I1) (Fig. 5A). DB to the phosphates shows similar patterns with higher local concentration and specific localization around residues 30 to 36 that correspond to the bulge region. A major difference between major and phosphate DB is that the latter remains intact on the RNA surface until the late stages (state I2).

In contrast, K⁺ ions show strong DB to the major groove, as reflected in (Fig. 6B). The cation localization at the major groove remains visible until state (state I2). In K⁺, the secondary structure formation and major groove cation localization are concomitant along the unfolding pathway. Nearly every secondary structure element has a K⁺ ion binding site at the major groove. The structures representing the intermediate states and 3D cation density profiles, reflecting the cation atmosphere, also highlight the unique discrete binding properties of K⁺ (Fig. 6B, top).

In Fig. 6 (C and D), we plot the local ion concentrations around the residues for indirectly bound cations. Here, the concentrations are smaller compared with DB (Fig. 6, A and B). This is due to the higher volume available to the outer-sphere cations. Similar to the DB mode, Na⁺ shows a higher affinity to the phosphate groups; however, the contrast between the two binding modes is minor. Secondary structure formation enhances cation localization in the case of Na⁺. The difference between the two cations lies in the way at which they associate with the phosphate groups. Na⁺ shows a structure-dependent discrete binding, while K⁺ ions form a uniform distribution surrounding the residues at early stages of folding. However, the discrete nature of the major groove binding is still evident in the later stages of the folding process in the case of K⁺.

Sequence effects on cation localization

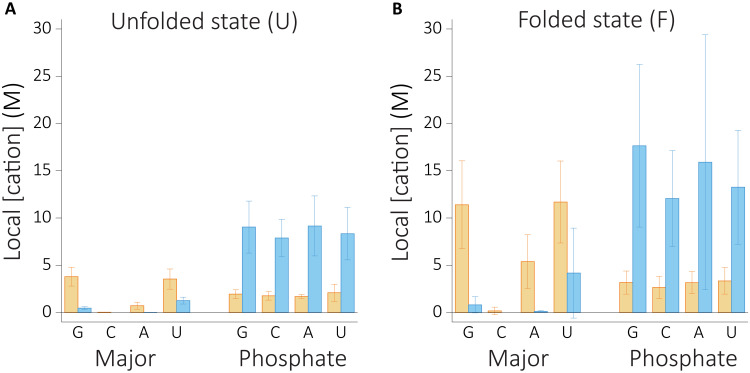
To quantify the sequence dependence of cation binding, we calculated local cation concentration for each type of nucleobases (Fig. 7). We observe a structure-dependent relationship for sequence dependence. Phosphate binding shows weak specificity both in the folded and unfolded states. Na⁺ ions interact stronger with phosphates, and binding gets stronger as phosphate charge density increases at the folded state. K⁺ ions, on the other hand, do not show any specific binding when the RNA is in the unfolded state. In contrast, binding of K⁺ ions to the major groove shows stronger dependence at the folded state, showing sequence specificity, favoring G, U, and A nucleotides.

Fig. 7. Local cation concentrations of Na⁺ (blue) and K⁺ (orange) as a function of sequence at the unfolded and folded states.

(A) The unfolded state. (B) The folded state.

DISCUSSION

By using all-atom simulations, we found a clear difference in the stability of HIV-1 TAR hairpin in KCl versus NaCl solutions (Fig. 2), which accords well with the experimental findings (34). After having identified that ion size–dependent electrostatic interactions are the main cause of the RNA structural stabilization, we dissected the molecular mechanism, leading to the observed stability in Na⁺ compared to K⁺. The major finding that explains the stability difference is that the smaller-size Na⁺ ions with higher charge density bind preferably to the backbone phosphates, whereas larger-size K⁺ ions with a smaller charge density prefer the major grooves. The first is an electrostatic phenomenon, while the latter is a size or excluded volume effect. While Na⁺ condensation depends on RNA charge density, K⁺ ion association depends on the secondary structure and sequence identity.

The difference between the number of bound Na⁺ and K⁺ ions to RNA is due to the stronger interactions involving hydrated Na⁺ ions, as well as the bigger surface area that these ions can access. To demonstrate that this is the case, we compute the average solvent accessible surface area (SASA) available for each subgroup. The results, summarized in fig. S6, show that Na⁺ ions that bind to phosphate groups have access to an area of 76 nm² in the unfolded state. This number reduces only by about 3% when RNA folds. Although the SASA remains similar, the RNA charge density increases because of compaction. In contrast, the SASA for K⁺ ions that primarily bind to the major groove is 55 nm² in the unfolded state. This number shows a marked reduction (∼35 %) upon compaction. In the folded state, the SASA becomes 37 nm², which is nearly half of the SASA available to Na⁺ ions. As a result of preferential binding that is dictated by the cation size, Na⁺ ions have larger entropy by exploring a bigger area of binding compared to K⁺ ions. Moreover, this binding mode cannot compensate for the weaker (compared to Na⁺) interaction with RNA.

Together, we propose a novel molecular mechanism for explaining the enhanced stability of the HIV-1 TAR RNA in Na⁺ compared to K⁺. The Na⁺ ions preferentially bind to the phosphate groups, whereas the K⁺ ions are localized near the major grooves. The very notable changes in the binding modes between the ions to RNA are sufficiently different, which readily explains the observed stability differences. There are two additional predictions that arise from our study. (i) Although the study focused on HIV-1 TAR, the mechanism should hold for other RNA molecules and DNA because it depends on generic properties of cations and the structures of nucleic acids that are stabilized by monovalent cations. (ii) Because charge density of the cations determines the binding modes to RNA, we predict that the stability of RNA should decrease as one goes down the alkali metals in group I of the periodic table. RNA stability should be maximum in Na⁺ solution and decrease as the radius of the alkali metal ions increases.

METHODS

Molecular dynamics simulations

We model the starting structure of the 52-nt-long HIV-1 TAR RNA, with the sequence 5′-GGCUCUGGUUAGACCAGAUCUGAGCCUGGGAGCUCUCUGGCUAACU AGGGCC-3′, by extending the crystal structure of HIV-1 TAR RNA [Protein Data Bank (PDB) entry: 1ANR; residues 19 to 43] (50). The dsRNA construct comprising the sequences of 5′-GGCUCUGGUUAGAC-3′ and 5′-GCUAACUAGGGCC-3′ was built using the Nucleic Acid Builder (51). We joined the two units manually and minimized the energy to refine the structure. For this and all other calculations, we used GROMACS 5.05 program with ff99-parmbsc0 force field (52) due to its success in capturing the HIV-1 TAR dynamics in the previous study (53).

The energy-minimized HIV-1 TAR hairpin structure was aligned along the x axis of a periodic box with dimensions of 42 nm by 6.5 nm by 12.5 nm. The dimension along the long axis is chosen to ensure that the RNA does not interact with the periodic images after it is fully stretched, which is technically important in performing the pulling simulations. The RNA molecule was solvated in water and ions (Fig. 1C). Details of molecular dynamics (MD) simulation setup are explained in the Supplementary Materials.

Steered MD simulations

The last frame in the equilibrated trajectory for each cation condition was used to generate the unfolding pathway of the HIV-1 TAR upon application of the mechanical force. In particular, 300-ns-long steered MD (SMD) simulations (54) were performed to pull the 3′ and 5′ termini of the RNA (Fig. 1C). For the reaction coordinate, we used the molecular extension, which is the x component of the center of mass distance between the two terminus nucleotides. To realize as slow a pulling speed as possible in the MD simulations, we used a pulling rate of 0.1 nm/ns with a force constant of 1000 kJ/(mol×nm²).

Free energy calculations

Using the conformations along the force-induced unfolding pathway of the SMD, we construct the free energy profile of RNA as a function of the pulling coordinate, x, using umbrella sampling MD simulations (43). Each conformation picked was restrained using a harmonic biasing potential U = (k/2)(x − x_i)², where k = 1000 kJ/(mol×nm²), and x_i is the reference distance of the ith window. We used about 142 windows with a 2-Å interwindow spacing, and we sampled conformations for about 100 ns in each umbrella, giving rise to an aggregate simulation time of ≈14 microseconds for each solvent condition. The sampled conformations were saved every 10 ps for data analyses.

The free energy landscape was constructed by calculating the potential of mean force (PMF) using the GROMACS-implemented weighted histogram analysis method (55, 56). Statistical errors were estimated using the bootstrap analysis with 200 bootstrap samples. From the PMF, we estimated the force-dependent free energy change along x at various applied forces.

Intermolecular interaction energy

We used a NAMDEnergy analysis tool (www.ks.uiuc.edu) implemented in visual molecular dynamics (VMD) to calculate the nonbonded intermolecular interaction energy for each umbrella window. Coordinates of the atoms were extracted every 1000 ps. The data in each umbrella are divided to equal pieces to estimate the SE presented as means±SD.

Surface-bound water and ion numbers

RDF of group X around group Y, g_X−Y(r), was calculated to gain insights into ion and water distributions. The cumulative number of cations on the RNA surface (S) up to distance R, N_X−S(R), is computed as

$$N_{X-S}(R)=\frac{N_{\text{cation}}}{V}{\displaystyle {\int }_0^R}4\mathrm{\pi }{r}^2{g}_{X-S}(r)\mathit{dr}$$ (1)

where N_cation is the total number of cations in the simulation box volume V and R is the cutoff distance beyond which the cation is deemed to be unbound. To find the number of inner-sphere (NIS) cations, we chose R to be the minimum between the first two peaks in the RDFs. Note that this number depends on the cation size. For outer-sphere cations, we integrate the equation to the second minimum and subtract the value the from NIS. Similarly, water molecules around RNA surface (S-W) or cation (X-W) were investigated. All atoms of water were considered for water-RNA interactions, whereas, for the investigation of cation-water, we used the oxygen atom of the water.

Configurational entropy

We applied principal components analysis (PCA) to elucidate collective motions from simulation. All heavy atoms of the RNA were used in performing the PCA. We diagonalized the covariance matrix of atomic fluctuations along the folding pathway. The RNA chain entropy, S, is estimated by analyzing the resulting eigenvalues, σ, using the Schlitter’s formula (57)

$$S_{\text{abs}}<S=(1/2)\text{ln det} [1+(k_{\mathrm{B}}T{e}^2/{\hslash }^2)\mathbf{M}\mathrm{\sigma }]$$ (2)

where k_B is the Boltzmann’s constant, ℏ is the Planck’s constant, T is the absolute temperature, e is the Euler value, and M is the diagonal mass matrix of rank 3N.

Local ion concentration profiles

To provide further details on cation localization around RNA, we compute local cation concentration. For that, we divided RNA into two subgroups: cations around the phosphate backbone and cations around major grooves. The concentration around each group is estimated as (58)

$$c(X_i)=g_{\mathit{Xi}}(r_{\text{max}})c_{\text{bulk}}$$ (3)

where X_i≡{phosphate group, major groove} represents the two subgroups for residue i. We used O1P and O2P atoms to represent the backbone phosphate group. The major groove atoms are nucleotide dependent. We chose for A(N6, N7), C(N4), G(N7, O6), and U(O4). g_Xi(r_max) is the maximum peak height of the normalized RDF of the cation and atom(s) on the RNA subgroup, and c_bulk is the bulk solution concentration.

Cation density profiles

To visualize the cation cloud around the RNA, we computed the cation density in Cartesian coordinates. For an arbitrary point in space r ≡ (x, y, z), the average cation number density ϕ(x, y, z) is computed from the trajectory using

$$\mathrm{\varphi }(\mathbf{r})=⟨\frac{1}{V}\sum _i\mathrm{\delta }(\mathbf{r}-{\mathbf{r}}_i)⟩$$ (4)

where the sum goes over the cation index i in the simulation box of volume V. δ(x) is the Kronecker delta, and ⟨…⟩ represents the ensemble average.

Supplementary Materials

This PDF file includes:

Section S1

Figs. S1 to S6

References

View/request a protocol for this paper from Bio-protocol.