Abstract
Calibration is a vital aspect of the performance of risk prediction models, but research in the context of ordinal outcomes is scarce. This study compared calibration measures for risk models predicting a discrete ordinal outcome, and investigated the impact of the proportional odds assumption on calibration and overfitting. We studied the multinomial, cumulative, adjacent category, continuation ratio, and stereotype logit/logistic models. To assess calibration, we investigated calibration intercepts and slopes, calibration plots, and the estimated calibration index. Using large sample simulations, we studied the performance of models for risk estimation under various conditions, assuming that the true model has either a multinomial logistic form or a cumulative logit proportional odds form. Small sample simulations were used to compare the tendency for overfitting between models. As a case study, we developed models to diagnose the degree of coronary artery disease (five categories) in symptomatic patients. When the true model was multinomial logistic, proportional odds models often yielded poor risk estimates, with calibration slopes deviating considerably from unity even on large model development datasets. The stereotype logistic model improved the calibration slope, but still provided biased risk estimates for individual patients. When the true model had a cumulative logit proportional odds form, multinomial logistic regression provided biased risk estimates, although these biases were modest. Nonproportional odds models require more parameters to be estimated from the data, and hence suffered more from overfitting. Despite larger sample size requirements, we generally recommend multinomial logistic regression for risk prediction modeling of discrete ordinal outcomes.
Keywords: calibration, discrete ordinal outcome, predictive performance, proportional odds, risk prediction, simulation
1. INTRODUCTION
Risk prediction modeling is ubiquitous in the medical literature. Most of these prediction models are developed for dichotomous outcomes, estimating the risk that a condition is present (diagnostic) or will develop within a certain time horizon (prognostic). However, several clinically important outcomes are ordinal in nature, with a finite and often limited number of ordered categories. One example is the extent of coronary artery disease in symptomatic patients, for which Edlinger et al recently developed a risk prediction model. 1 The diagnosis can be any of five increasingly severe conditions: no coronary artery disease, nonobstructive stenosis, one‐vessel disease, two‐vessel disease, or three‐vessel disease. Another example is the modified Rankin scale to assess function recovery after stroke, as in a model by Risselada et al. 2 This scale has seven ordered categories: death, severe disability, moderately severe disability, moderate disability, slight disability, no significant disability despite symptoms, or no symptoms at all. Such outcomes are often dichotomized, although we would generally not recommend that for the following reasons: (1) it leads to a loss of information, (2) the merged categories may require different clinical management, and (3) merging categories may result in an extremely heterogeneous “supercategory”.
The default statistical model for ordinal outcomes is the cumulative logit model with proportional odds (CL‐PO), which is commonly referred to as “ordinal logistic regression”. Several alternative logistic models for ordered categories exist, such as the adjacent category, continuation ratio, and stereotype models, which make different assumptions about the structure of ordinality. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 Alternatively, the multinomial logistic regression (MLR) can be used for modeling ordinal and other multicategory outcomes, ignoring the ordinality of the outcome.
For dichotomous outcomes, there is a large body of methodological literature and guidance on how prediction models should be constructed and how their performance should be evaluated in terms of discrimination and calibration. 11 , 12 , 13 , 14 , 15 , 16 , 17 Methods to assess discrimination and calibration have been extended to models for nominal outcomes. 18 , 19 , 20 For ordinal outcomes, discrimination measures have been proposed but calibration has been barely addressed. 21 , 22 , 23 , 24 Harrell and colleagues discussed the development of a risk prediction model for an ordinal outcome using CL‐PO. 21 Calibration was assessed for a dichotomized version of the outcome, such that the standard methods for binary outcomes could be applied. More research on calibration is required, in particular because calibration is the Achilles heel of prediction modeling. 25
In this article, we study the performance of a variety of regression algorithms to develop prediction models for discrete ordinal outcomes. We (1) evaluate different approaches to investigate calibration, (2) study the impact of the proportional odds assumption on risk estimates and calibration statistics, and (3) explore the impact on overfitting when using simpler models that assume proportional odds vs more complex models without assuming proportional odds.
This article is structured as follows. Regression models for discrete ordinal outcomes are described in Section 2, and measures for predictive performance in Section 3. Section 4 presents a simulation study to assess the impact of model choice on estimated risks, model calibration, and overfitting, and to compare approaches to quantify model calibration. Section 5 presents a case study, and in Section 6 we discuss our findings.
2. REGRESSION MODELS FOR DISCRETE ORDINAL OUTCOMES
2.1. Regression models
We predict an outcome Y with K categories () using Q predictors X q (), . For simplicity, we will assume in notation that the models are modeling the predictors as linear and additive effects, but our work can easily be generalized to allow for alternative functional forms and interaction terms.
2.1.1. Multinomial logistic regression
A generic model for categorical outcomes is multinomial logistic regression (MLR), which ignores the ordinality of the outcome. MLR models the outcome as follows 10 :
| (1) |
for and where and where is called a linear predictor. One outcome category is used as the reference, and all other categories are contrasted with this reference category. We use as the reference, but the choice does not affect the estimated risks.
2.1.2. Cumulative logit models
The likely most commonly used regression model for ordinal outcomes is the cumulative logit with proportional odds (CL‐PO) 10 :
| (2) |
for and where . Due to the proportional odds assumption, every predictor effect is modeled using only one parameter, irrespective of k. This means that predictor effects are assumed constant over k on the log‐odds scale. The model has intercepts.
The cumulative logit model can also be formulated without the proportional odds assumption, leading to the CL‐NP model 10 :
| (3) |
for and where . Here, the predictor effects depend on k, such that parameters are estimated for each predictor. Note that CL‐NP may lead to invalid models where the estimated risk that is higher than the estimated risk that . 8 , 10
2.1.3. Adjacent category models
An alternative method to model ordinality is to target pairwise probabilities of adjacent categories, rather than cumulative probabilities. Assuming proportional odds, the adjacent category with proportional odds model (AC‐PO) model is 10
| (4) |
for and where . Proportional odds in this setup refers to identical effects for moving up one category, instead of identical effects for every dichotomization of Y.
The adjacent model setup can also be applied without the proportional odds assumption, leading to the adjacent category without proportional odds model (AC‐NP):
| (5) |
for and where . This model is equivalent to MLR.
2.1.4. Continuation ratio models
Instead of cumulative or pairwise probabilities, conditional probabilities can be targeted. Continuation ratio models estimate the probability of a given outcome category conditional on the outcome being at least that category. The continuation ratio model with proportional odds assumptions (CR‐PO) is 10
| (6) |
for and where . Without proportional odds, the continuation ratio model is (CR‐NP):
| (7) |
for and where .
2.1.5. Stereotype logistic model
Anderson introduced a model that finds a compromise between MLR and AC‐PO, by relaxing the proportional odds assumption on the level of the equations rather than on the level of each predictor separately. 7 The stereotype logistic model (SLM) is written as:
| (8) |
for and where and is used as the reference. The model estimates one coefficient per predictor, but estimates scaling factors . Every predictor coefficient is multiplied by . To avoid identifiability problems, a constraint has to be imposed on the scaling factors, which typically is that . In principle, the model is an ordered model if the scaling factors are monotonically increasing or decreasing. While this could be imposed as an additional constraint during model fitting, it is not necessary and may cause computational problems. 3 , 7
2.2. A comparison of the number of parameters
For any particular application, the number of parameters (regression model coefficients including intercepts) of the above defined models varies. The models without a proportional odds assumption (MLR, CL‐NP, AC‐NP, CR‐NP) require parameters, models with proportional odds (CL‐PO, AC‐PO, CR‐PO) require parameters. SLM falls in between with parameters. Table 1 presents the number of parameters for illustrative values of and .
TABLE 1.
Number of parameters to be estimated for some values of and
| Number of parameters | ||||||
|---|---|---|---|---|---|---|
|
|
|
Proportional odds models | Stereotype logistic model | Nonproportional odds models | ||
| 3 | 3 | 5 | 6 | 8 | ||
| 3 | 5 | 7 | 8 | 12 | ||
| 3 | 10 | 12 | 13 | 22 | ||
| 5 | 3 | 7 | 10 | 16 | ||
| 5 | 5 | 9 | 12 | 24 | ||
| 5 | 10 | 14 | 17 | 44 | ||
| 10 | 3 | 12 | 20 | 36 | ||
| 10 | 5 | 14 | 22 | 54 | ||
| 10 | 10 | 19 | 27 | 99 | ||
Abbreviations: K, number of outcome categories; Q, number of predictors.
3. PREDICTIVE PERFORMANCE MEASURES FOR DISCRETE ORDINAL OUTCOMES MODELS
The estimated risk of category k is denoted by , with the estimated risk for individual i in a data set of size N () denoted as . These risks are model‐specific, conditional on and the estimated model parameters. Hence , where includes all parameters estimated from the model of choice (Equations ((1), (2), (3), (4), (5), (6), (7), (8))). For example, includes all estimated intercepts, model coefficients and scaling factors. The Appendix provides more details on how to calculate the risks for the different types of models. Analogously, the estimated risk that the outcome category has at least value k is denoted as , with the estimated risk for individual i denoted as .
3.1. Calibration of risk models for ordinal outcomes
3.1.1. Calibration intercepts and slopes per outcome category or dichotomy
A simple approach that capitalizes on the well‐known calibration tools for binary outcomes, is to evaluate risk model calibration for every outcome category separately by defining a binary outcome that equals 1 if and 0 otherwise. 26 The calibration intercept and calibration slope can be computed by the following binary logistic calibration model:
| (9) |
The calibration slope equals , the calibration intercept equals when is fixed to 1.
Alternatively, the outcome can be dichotomized as (1 if and 0 otherwise), and a calibration model for the dichotomized outcome can be defined as:
| (10) |
Calibration intercepts and slopes can be obtained as for .
Due to the ordinal nature of the outcome, may appear more sensible than , although this may depend on the actual clinical decisions that the model is intended to support.
3.1.2. Model‐specific calibration intercepts and calibration slopes
When making a prediction model for a binary outcome using standard maximum likelihood logistic regression, the calibration intercept and calibration slope are by definition 0 and 1 when evaluated on the development dataset (ie, the exact same dataset that was used to develop the prediction model). 26 A model with intercept of 0 and slope of 1 has been defined as “weak calibration”. 26 Thus, maximum likelihood binary logistic regression for a binary outcome is by definition weakly calibrated on the development dataset. When making a prediction model for an ordinal outcome, and assessing calibration per outcome category () or per outcome dichotomy () (Equations ((9), (10))), calibration intercepts and slopes are no longer 0 and 1 on the development dataset. Procedures with intercept 0 and slope 1 on the development dataset are possible, but depend on the regression model used to develop the prediction model for the ordinal outcome. Such procedures are therefore not generic, and we describe them for each ordinal regression model separately.
For MLR, the model‐specific calibration model is of the following form 18 :
| (11) |
for and are the linear predictors from the fitted MLR prediction model (Equation (1)). The calibration intercepts equal , when fixing the corresponding calibration slope to 1 and the remaining slopes to 0. The calibration slopes equal , when fixing the remaining slopes to 0. When this model is used to evaluate calibration of the MLR model on the development dataset, weak calibration holds: the calibration slopes are equal 1 and the calibration intercepts equal 0. See Van Hoorde and colleagues for further elaboration in the context of prediction models for nominal outcomes. 18
For CL‐PO, the linear predictors are identical except for the intercepts (Equation (2)). Hence for each linear predictor , , separate CL‐PO calibration models are fit as follows:
| (12) |
The calibration slopes equal , and the calibration intercepts equal when is fixed to 1. Similarly, for fitted AC‐PO and CR‐PO prediction models (Equations (4) and (6)), separate AC‐PO or CR‐PO calibration models are fit for each linear predictor , :
| (13) |
| (14) |
Calibration intercepts and slopes are calculated as for the CL‐PO model (Equation (12)). For fitted prediction models based on AC‐NP, CR‐NP, and SLM (Equations (5), (7), and (8)), the setup is analogous to that for prediction models based on MLR. Calibration models are as follows:
| (15) |
| (16) |
| (17) |
Calibration intercepts and slopes are calculated as for the MLR calibration model (Equation (11)). For every model, weak calibration holds on the development dataset: calibration intercepts are 0 and calibration slopes are 1.
3.1.3. Flexible multinomial calibration plots
To generate flexible calibration curves for risk models with multicategory outcomes based on any model, Van Hoorde and colleagues suggested a flexible recalibration model that is extended from the MLR recalibration model. 18 The model is as follows:
| (18) |
where , obtained from the fitted model, and a vector spline smoother. 27 , 28 The probabilities resulting from this flexible recalibration model are labeled the observed proportions , with , and where are the estimated values for and are the fitted spline smoothers . For individual i, the observed proportions are denoted as . See Section 6 and Data S1 for information about alternative flexible recalibration models.
For each outcome category k, a calibration plot can be constructed that relates the estimated model‐based risks (horizonal axis) to the observed proportion (vertical axis). Contrary to binary outcomes, there is no one‐to‐one relationship between and for ordered or unordered multicategory outcomes. 18 Either the result can be plotted as a calibration scatter plot, or the scatter plot can be smoothed to present the results as calibration plots. Using and , it is also possible to make calibration plots per outcome dichotomy, should that be of interest.
Flexible calibration curves for an outcome category may be obtained more simply by replacing in Equation (9) with a splines or loess fit, as described elsewhere for binary outcomes. 26 Because this approach ignores the multicategory nature of the outcome, it cannot be used to generate calibration scatter plots but may approximate smoothed calibration scatter plots based on Equation (18).
3.1.4. Estimated calibration index
Single‐number summaries of calibration plots exist for binary outcomes, such as Harrell's E statistics. 11 The estimated calibration index (ECI) was introduced as a single‐number summary of calibration for nominal outcomes, but can also be used for ordinal or binary outcomes. 29 The ECI is the average squared difference between and , where the latter are based on a flexible recalibration model (Equation (18)). Originally, ECI was defined as follows:
| (19) |
The second part of the formula ensures that ECI is scaled between 0 and 100. Here, 0 indicates that for all i and k and 100 the theoretical worst‐case scenario where for each case the estimated risk of one outcome category is 1 and the observed proportion of another outcome category is 1. This is an extreme scaling; in the current work we use a different one, where the maximal value of ECI refers to a model that has no predictive ability. In that case, all equal the event rate of outcome category k (). If we set the maximal value to 1 instead of 100, this rescaled ECI is defined as follows:
| (20) |
3.2. Discrimination
To evaluate model discrimination, we used the ordinal C statistic (ORC). 24 Despite being designed for ordinal outcomes, the ORC equals the average C statistic for all pairs of outcome categories, and is interpreted as the probability to separate two cases from two randomly chosen outcome categories. As with the binary C statistic, ORC = 0.5 implies no and ORC = 1 perfect discriminative performance. To calculate pairwise C statistics, we have to express the prediction of the outcome through a single number. For proportional odds models, this can be based on . For any model, we can also use the expected value of the outcome prediction, . For all pairs of outcome categories, a pairwise C statistic is calculated as the standard binary C statistic for cases belonging to one of the two outcome categories using the single number prediction.
4. MONTE CARLO SIMULATION STUDY
4.1. Methods
We use the aims‐data‐estimands‐methods‐performance (ADEMP) structure to provide a structured overview of the simulation study. 30
Aims: The aims are to (1) study the impact of the choice of model on estimated risks and model calibration, (2) study the impact of the model choice on model overfitting, and (3) evaluate different approaches to calculate calibration slopes for regression models predicting an ordinal outcome.
Data generating mechanism: We simulate data assuming a true model that has either MLR or CL‐PO form. Under CL‐PO proportional odds holds for cumulative logits only. For data under MLR form, we specified four main scenarios involving a model with continuous predictors and an outcome with categories. For simplicity, every predictor is independently normally distributed conditional on the outcome category, that is, . . The four scenarios vary by outcome prevalence (balanced or imbalanced) and whether the means of each predictor are equidistant between outcome categories or not, in a full factorial approach (Tables 2 and S1). Equidistant means imply that proportional odds hold for adjacent category logits, but not for cumulative logits. The true ORC for these scenarios is 0.74. For data under CL‐PO form, we specified three main scenarios with 4 continuous predictors, 3 outcome categories (, ), and an ORC of 0.74 under the data generating model (Tables 2 and S2). The scenarios vary by outcome prevalence (balanced, imbalanced, highly imbalanced). We identified additional scenarios by varying factors nonfactorially in an effort to maximize the effect on miscalibration and on differences between models. We investigated the effect of having (and ), highly nonequidistant means (only for data under MLR form), highly imbalanced outcome distribution, and low discrimination (ORC = 0.66). Finally, we added scenarios with only binary predictors and scenarios in which noise predictors are included.
TABLE 2.
Overview of simulation scenarios
| Scenario | Q | K | ORC | Outcome distribution | Means of a |
|---|---|---|---|---|---|
| True model has MLR form | |||||
| Basic | |||||
| 1 | 4 continuous | 3 | 0.74 | Balanced | Equidistant |
| 2 | 4 continuous | 3 | 0.74 | Imbalanced | Equidistant |
| 3 | 4 continuous | 3 | 0.74 | Balanced | Nonequidistant |
| 4 | 4 continuous | 3 | 0.74 | Imbalanced | Nonequidistant |
| Additional | |||||
| 5 | 4 continuous | 3 | 0.74 | Imbalanced | Highly nonequidistant |
| 6 | 3 continuous | 4 | 0.74 | Imbalanced | Highly nonequidistant |
| 7 | 3 continuous | 4 | 0.66 | Imbalanced | Highly nonequidistant |
| 8 | 3 continuous | 4 | 0.66 | Highly imbalanced | Highly nonequidistant |
| 9 | 4 binary | 3 | 0.74 | Imbalanced | Nonequidistant |
| 10 | 3 binary | 4 | 0.74 | Imbalanced | Highly nonequidistant |
| 11 | 8 continuous (4 true + 4 noise) | 3 | 0.74 | Imbalanced | Nonequidistant |
| True model has CL‐PO form | |||||
| Basic | |||||
| 1 | 4 continuous | 3 | 0.74 | Balanced | NA |
| 2 | 4 continuous | 3 | 0.74 | Imbalanced | NA |
| 3 | 4 continuous | 3 | 0.74 | Highly imbalanced | NA |
| Additional | |||||
| 4 | 3 continuous | 4 | 0.74 | Imbalanced | NA |
| 5 | 3 continuous | 4 | 0.66 | Imbalanced | NA |
| 6 | 3 continuous | 4 | 0.66 | Highly imbalanced | NA |
| 7 | 4 binary | 3 | 0.74 | Imbalanced | NA |
| 8 | 3 binary | 4 | 0.74 | Imbalanced | NA |
| 9 | 8 continuous (4 true + 4 noise) | 3 | 0.74 | Balanced | NA |
Abbreviations: CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; ORC, ordinal C statistic.
For binary predictors, equidistance does not refer to means per outcome category, but to logit(prevalence) per outcome category.
Estimands/targets of analysis: The focus in this simulation is on large sample and out‐of‐sample calibration performance, but we also assess discrimination and prediction error.
Methods: We focus on the MLR, CL‐PO, AC‐PO, and SLM models to limit the amount of results (Equations (1), (2), (4), and (8)). To approach true model coefficients and performance, a large dataset with 200 000 observations was simulated for each scenario. Models were fitted (developed) and performance evaluated (validated) on this single large dataset. Next, to assess the impact of overfitting, we simulated 200 new datasets of size 100 and 500 for all main scenarios, developed the models on each dataset, and evaluated performance on the large dataset with size 200 000. We report the mean value for each performance measure. The chosen sample sizes are partly arbitrary, but see Data S1 for further explanation.
Performance measures: We report the calibration intercepts and slopes by outcome category, by outcome dichotomy, and by linear predictor (ie, algorithm‐specific). Further, we report the root mean squared prediction error (rMSPE) and ORC. For rMSPE we use the true risks in each scenario (which are known under the data generating model):
| (21) |
The ECI was only reported for the large sample evaluation, not for evaluating overfitting. The statistical analyses were performed using the R statistical software, version 4.0.1. The package for fitting the logistic regression models was VGAM, using functions vglm and rrvglm for SLM. 31 The complete R code is available on GitHub (https://github.com/benvancalster/OrdinalCalibration).
4.2. Results
4.2.1. MLR truth—main scenarios
In the large sample simulations, when true predictor means were equidistant (scenarios 1‐2), risk estimates corresponded almost perfectly with true risk for the MLR, AC‐PO, and SLM models (Figures 1, 2). When the true predictor means were nonequidistant (scenarios 3‐4), only MLR obtained risk estimates that corresponded closely to the true risks (Figures 3, 4). Regarding calibration intercepts and slopes (Table 3), we observed that these were near perfect for MLR. For the SLM model, the scaling factors also resulted in near perfect calibration intercepts and slopes even though estimated risks deviated from the true risks for scenarios 3 and 4. For AC‐PO, calibration slopes per outcome category and per outcome dichotomy were off for scenarios 3‐4. Scenarios 1‐2 did not pose problems for AC‐PO, because the equidistant means imply that proportional odds hold in terms of adjacent categories. For CL‐PO, calibration intercepts were fine but calibration slopes per outcome category or per outcome dichotomy were off for all scenarios. Interestingly, the model‐specific calibration intercepts and slopes were 0 and 1, respectively, for all models and scenarios. Hence, the miscalibration problems for CL‐PO and AC‐PO were not reflected in these measures. The reason is that these calculations are model‐specific, and thus that they quantify calibration under the assumption that proportional odds hold (for cumulative logits in case of CL‐PO, or for adjacent category logits in case of AC‐PO). Flexible calibration curves are presented in Figures S1‐S4.
FIGURE 1.
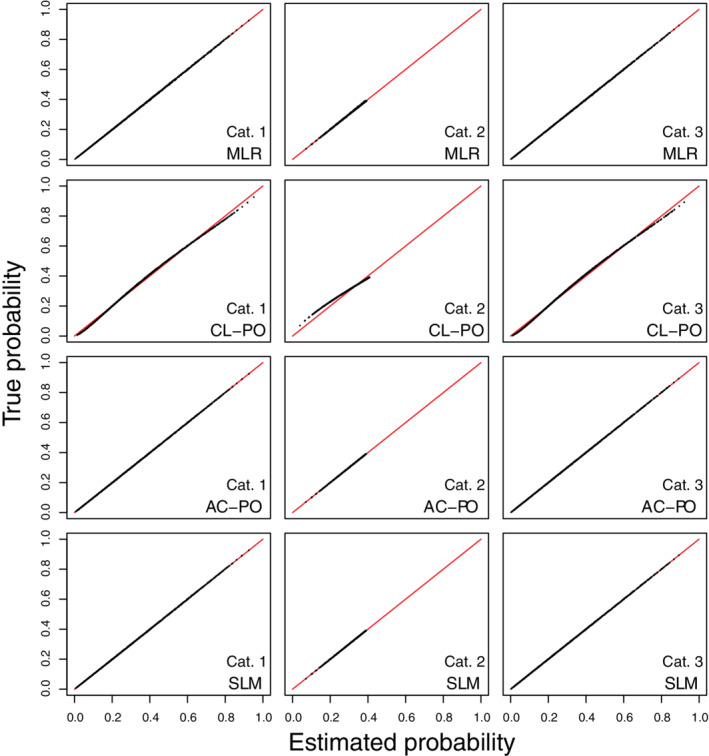
Scatter plots of true risks vs estimated risks for simulation scenario 1 when the true model has the form of a multinomial logistic regression. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 2.
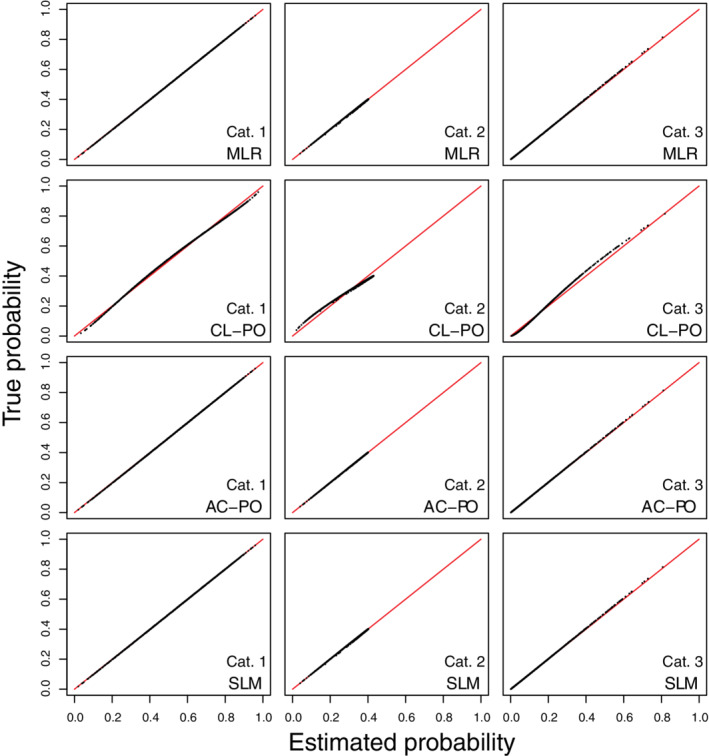
Scatter plots of true risks vs estimated risks for simulation scenario 2 when the true model has the form of a multinomial logistic regression. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 3.
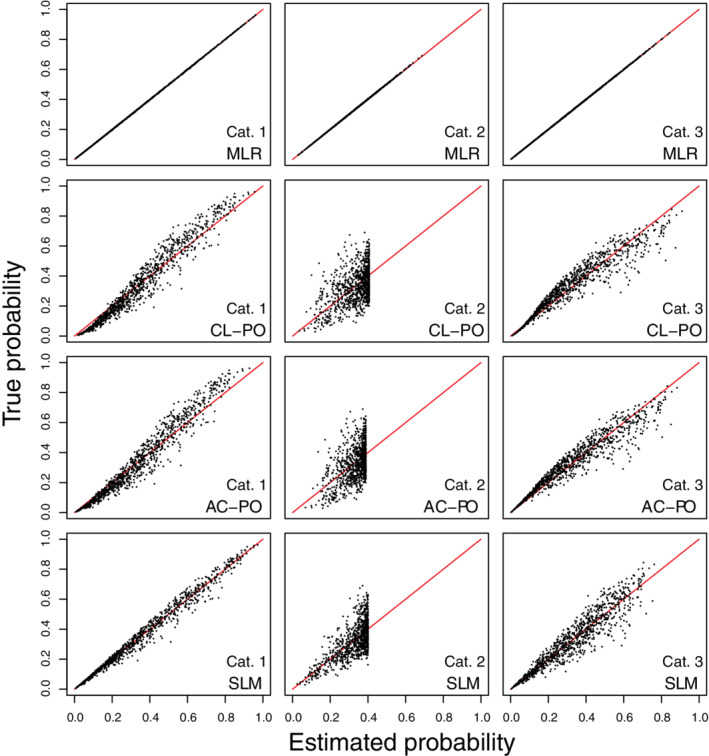
Scatter plots of true risks vs estimated risks for simulation scenario 3 when the true model has the form of a multinomial logistic regression. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 4.
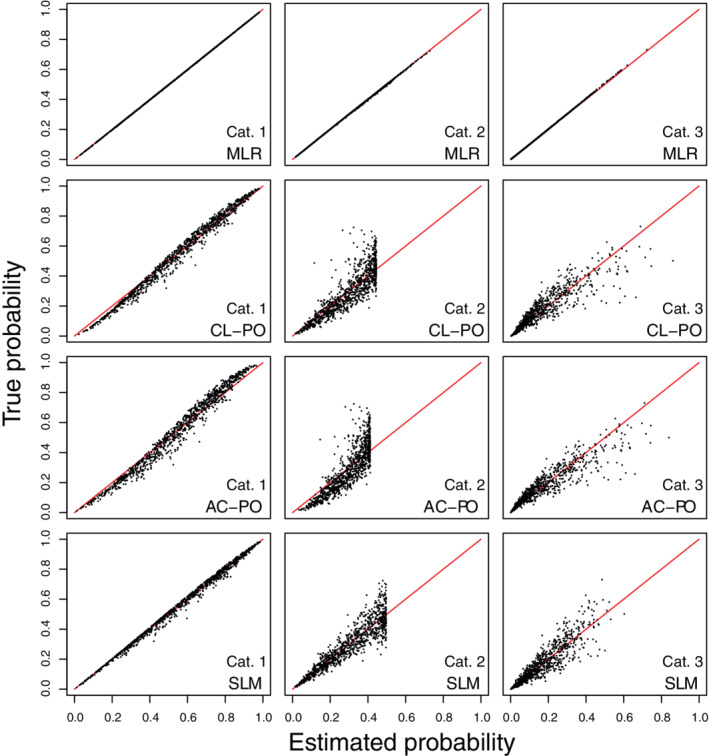
Scatter plots of true risks vs estimated risks for simulation scenario 4 when the true model has the form of a multinomial logistic regression. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
TABLE 3.
Apparent performance based on a large dataset of n = 200 000 for the main simulation scenarios
| Calibration intercepts/Calibration slopes | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Per outcome category | Per outcome dichotomy | Model‐specific | Single number metrics | ||||||||||||
| Model |
|
|
|
|
|
LP1 | LP2 | ECI | rMSPE | ORC | |||||
| MLR truth scenario 1: balanced outcome, equidistant means | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.741 | |||||
| CL‐PO | 0.00/1.02 | −0.01/0.75 | 0.00/1.02 | 0.00/1.02 | 0.00/1.02 | 0.00/1.00 | 0.00/1.00 | 0.006 | 0.012 | 0.741 | |||||
| AC‐PO | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.001 | 0.741 | |||||
| SLM | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.001 | 0.741 | |||||
| MLR truth scenario 2: imbalanced outcome, equidistant means | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.740 | |||||
| CL‐PO | 0.01/0.96 | −0.01/0.79 | −0.01/1.14 | −0.01/0.96 | −0.01/1.14 | 0.00/1.00 | 0.00/1.00 | 0.010 | 0.016 | 0.740 | |||||
| AC‐PO | 0.00/1.00 | 0.00/1.01 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.740 | |||||
| SLM | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.740 | |||||
| MLR truth scenario 3: balanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.741 | |||||
| CL‐PO | −0.03/1.21 | −0.01/0.75 | 0.03/0.86 | 0.03/1.21 | 0.03/0.86 | 0.00/1.00 | 0.00/1.00 | 0.049 | 0.075 | 0.738 | |||||
| AC‐PO | 0.00/1.19 | 0.00/0.95 | 0.00/0.84 | 0.00/1.19 | 0.00/0.84 | 0.00/1.00 | 0.00/1.00 | 0.046 | 0.074 | 0.738 | |||||
| SLM | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.063 | 0.738 | |||||
| MLR truth scenario 4: imbalanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.737 | |||||
| CL‐PO | −0.02/1.11 | 0.01/1.13 | 0.03/0.85 | 0.02/1.11 | 0.03/0.85 | 0.00/1.00 | 0.00/1.00 | 0.032 | 0.058 | 0.735 | |||||
| AC‐PO | 0.00/1.17 | 0.00/1.47 | 0.00/0.76 | 0.00/1.17 | 0.00/0.76 | 0.00/1.00 | 0.00/1.00 | 0.059 | 0.064 | 0.736 | |||||
| SLM | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.047 | 0.733 | |||||
| CL‐PO truth scenario 1: balanced outcome | |||||||||||||||
| MLR | 0.00/0.99 | 0.00/1.38 | 0.00/0.99 | 0.00/0.99 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.006 | 0.014 | 0.740 | |||||
| CL‐PO | 0.00/1.00 | 0.00/1.01 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.003 | 0.740 | |||||
| AC‐PO | 0.00/1.00 | 0.00/1.38 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.006 | 0.014 | 0.740 | |||||
| SLM | 0.00/0.99 | 0.00/1.38 | 0.00/0.99 | 0.00/0.99 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.006 | 0.014 | 0.740 | |||||
| CL‐PO truth scenario 2: imbalanced outcome | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/1.09 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.005 | 0.013 | 0.740 | |||||
| CL‐PO | 0.00/1.00 | 0.00/1.01 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.003 | 0.740 | |||||
| AC‐PO | 0.00/1.07 | 0.00/1.34 | 0.00/0.88 | 0.00/1.07 | 0.00/0.88 | 0.00/1.00 | 0.00/1.00 | 0.012 | 0.018 | 0.740 | |||||
| SLM | 0.00/1.00 | 0.00/1.09 | 0.00/0.99 | 0.00/1.00 | 0.00/0.99 | 0.00/1.00 | 0.00/1.00 | 0.006 | 0.013 | 0.740 | |||||
| CL‐PO truth scenario 3: highly imbalanced outcome | |||||||||||||||
| MLR | 0.00/1.00 | 0.00/1.02 | 0.00/0.98 | 0.00/1.00 | 0.00/0.98 | 0.00/1.00 | 0.00/1.00 | 0.004 | 0.009 | 0.742 | |||||
| CL‐PO | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.000 | 0.002 | 0.742 | |||||
| AC‐PO | 0.00/1.08 | 0.00/1.22 | 0.00/0.77 | 0.00/1.08 | 0.00/0.77 | 0.00/1.00 | 0.00/1.00 | 0.015 | 0.017 | 0.742 | |||||
| SLM | 0.00/1.00 | 0.00/1.02 | 0.00/0.98 | 0.00/1.00 | 0.00/0.98 | 0.00/1.00 | 0.00/1.00 | 0.004 | 0.009 | 0.742 | |||||
Abbreviations: AC‐PO, adjacent category logit model with proportional odds; CAD, coronary artery disease; CL‐PO, cumulative logit model with proportional odds; ECI, estimated calibration index; LP, linear predictor; MLR, multinomial logistic regression; ORC, ordinal C statistic; rMSPE, root mean squared prediction error; SLM, stereotype logit model.
The ECI and rMSPE results were lowest (ie, best) for the MLR model throughout, and substantially higher for CL‐PO and AC‐PO under nonequidistant means, and slightly increased for CL‐PO even under equidistant means (Table 3). For SLM, ECI was low throughout, but rMSPE was increased under nonequidistant means. The discrimination differed only slightly, with ORC providing slightly higher values for MLR in scenarios 3 and 4. For completeness, the large‐sample estimated model coefficients are given in Table S3.
The results of the small sample simulations were in line with expectations (Tables 4, 5). When comparing the large sample performance to the average validation performance of models developed on small samples (N = 100), the MLR models had the strongest decrease in performance, CL‐PO and AC‐PO the least. MLR models, which have the highest number of parameters, even had worse validation performance than the three other types of models. The effects of overfitting were smaller when development datasets had a sample size of 500.
TABLE 4.
Validation performance based on small development datasets of n = 100 for the main simulation scenarios (reported as the average performance on a large validation dataset for 200 simulated development datasets)
| Calibration intercepts/Calibration slopes | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Per outcome category | Per outcome dichotomy | Model‐specific | Single number metrics | ||||||||||||
| Model |
|
|
|
|
|
LP1 | LP2 | rMSPE | ORC | ||||||
| MLR truth scenario 1: balanced outcome, equidistant means | |||||||||||||||
| MLR | 0.00/0.78 | 0.03/0.31 | −0.02/0.80 | 0.00/0.78 | −0.02/0.80 | 0.02/0.73 | −0.03/0.76 | 0.104 | 0.727 | ||||||
| CL‐PO | 0.00/0.86 | 0.03/0.55 | −0.02/0.86 | 0.00/0.86 | −0.02/0.86 | 0.02/0.84 | 0.00/0.84 | 0.080 | 0.728 | ||||||
| AC‐PO | 0.00/0.84 | 0.03/0.73 | −0.02/0.85 | 0.00/0.84 | −0.02/0.85 | 0.02/0.83 | −0.04/0.83 | 0.077 | 0.728 | ||||||
| SLM | 0.00/0.85 | 0.03/0.56 | −0.02/0.85 | 0.00/0.85 | −0.02/0.85 | 0.02/1.04 | −0.02/0.82 | 0.085 | 0.728 | ||||||
| MLR truth scenario 2: imbalanced outcome, equidistant means | |||||||||||||||
| MLR | −0.01/0.80 | 0.03/0.45 | 0.01/0.73 | 0.01/0.80 | 0.01/0.73 | 0.02/0.82 | −0.01/0.58 | 0.104 | 0.724 | ||||||
| CL‐PO | 0.00/0.80 | 0.02/0.64 | 0.00/0.96 | 0.00/0.80 | 0.00/0.96 | 0.00/0.84 | −0.04/0.84 | 0.079 | 0.726 | ||||||
| AC‐PO | −0.01/0.84 | 0.03/0.82 | 0.01/0.83 | 0.01/0.84 | 0.01/0.83 | 0.02/0.83 | −0.01/0.83 | 0.077 | 0.725 | ||||||
| SLM | −0.01/0.84 | 0.02/0.70 | 0.01/0.88 | 0.01/0.84 | 0.01/0.88 | 0.02/0.92 | 0.02/0.82 | 0.085 | 0.725 | ||||||
| MLR truth scenario 3: balanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.03/0.85 | −0.03/0.56 | 0.02/0.79 | −0.03/0.85 | 0.02/0.79 | −0.04/0.83 | 0.03/0.67 | 0.105 | 0.725 | ||||||
| CL‐PO | −0.01/1.07 | −0.03/0.60 | 0.06/0.76 | 0.01/1.07 | 0.06/0.76 | 0.04/0.89 | −0.04/0.89 | 0.110 | 0.725 | ||||||
| AC‐PO | 0.02/1.05 | −0.02/0.76 | 0.03/0.75 | −0.02/1.05 | 0.03/0.75 | −0.03/0.87 | 0.03/0.87 | 0.108 | 0.725 | ||||||
| SLM | 0.03/0.86 | −0.03/0.65 | 0.02/0.90 | −0.03/0.86 | 0.02/0.90 | −0.03/0.89 | 0.00/0.86 | 0.109 | 0.722 | ||||||
| MLR truth scenario 4: imbalanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.02/0.83 | 0.01/0.69 | 0.00/0.70 | −0.02/0.83 | 0.00/0.70 | 0.00/0.84 | 0.00/0.54 | 0.101 | 0.724 | ||||||
| CL‐PO | −0.02/0.95 | 0.03/0.94 | 0.02/0.73 | 0.02/0.95 | 0.02/0.73 | 0.02/0.86 | −0.02/0.86 | 0.095 | 0.724 | ||||||
| AC‐PO | 0.00/0.99 | 0.02/1.20 | −0.01/0.65 | 0.00/0.99 | −0.01/0.65 | 0.01/0.84 | −0.02/0.84 | 0.097 | 0.724 | ||||||
| SLM | 0.01/0.85 | 0.02/0.83 | −0.01/0.86 | −0.01/0.85 | −0.01/0.86 | 0.01/0.89 | −0.01/0.90 | 0.096 | 0.721 | ||||||
| CL‐PO truth scenario 1: balanced outcome | |||||||||||||||
| MLR | 0.01/0.79 | 0.00/0.38 | 0.02/0.80 | −0.01/0.79 | 0.02/0.80 | 0.00/0.75 | 0.01/0.73 | 0.108 | 0.726 | ||||||
| CL‐PO | 0.00/0.87 | 0.01/0.75 | 0.01/0.86 | 0.00/0.87 | 0.01/0.86 | 0.03/0.86 | −0.03/0.86 | 0.080 | 0.728 | ||||||
| AC‐PO | 0.01/0.85 | 0.01/1.01 | 0.01/0.85 | −0.01/0.85 | 0.01/0.85 | 0.00/0.84 | 0.00/0.84 | 0.079 | 0.728 | ||||||
| SLM | 0.01/0.85 | 0.01/0.75 | 0.01/0.88 | −0.01/0.85 | 0.01/0.88 | 0.00/0.68 | 0.00/0.83 | 0.089 | 0.727 | ||||||
| CL‐PO truth scenario 2: imbalanced outcome | |||||||||||||||
| MLR | 0.02/0.84 | −0.01/0.63 | 0.03/0.73 | −0.02/0.84 | 0.03/0.73 | −0.02/0.86 | 0.03/0.54 | 0.103 | 0.724 | ||||||
| CL‐PO | 0.02/0.87 | 0.00/0.85 | 0.00/0.87 | −0.02/0.87 | 0.00/0.87 | 0.03/0.87 | −0.03/0.87 | 0.080 | 0.726 | ||||||
| AC‐PO | 0.02/0.92 | 0.00/1.12 | 0.01/0.76 | −0.02/0.92 | 0.01/0.76 | −0.01/0.85 | 0.01/0.85 | 0.081 | 0.725 | ||||||
| SLM | 0.02/0.87 | −0.01/0.92 | 0.03/0.88 | −0.02/0.87 | 0.03/0.88 | −0.02/0.91 | 0.01/0.84 | 0.087 | 0.725 | ||||||
| CL‐PO truth scenario 3: highly imbalanced outcome | |||||||||||||||
| MLR | −0.02/0.77 | 0.07/0.69 | −0.04/0.46 | 0.02/0.77 | −0.04/0.46 | 0.05/0.80 | 0.01/0.23 | 0.100 | 0.723 | ||||||
| CL‐PO | −0.03/0.82 | 0.06/0.83 | −0.04/0.83 | 0.03/0.82 | −0.04/0.83 | −0.02/0.82 | −0.01/0.82 | 0.075 | 0.726 | ||||||
| AC‐PO | −0.03/0.87 | 0.06/1.00 | −0.05/0.64 | 0.03/0.87 | −0.05/0.64 | 0.05/0.81 | −0.08/0.81 | 0.077 | 0.726 | ||||||
| SLM | −0.03/0.81 | 0.06/0.83 | −0.01/0.72 | 0.03/0.81 | −0.01/0.72 | 0.05/0.82 | 0.01/0.75 | 0.085 | 0.725 | ||||||
Abbreviations: AC‐PO, adjacent category logit model with proportional odds; CAD, coronary artery disease; CL‐PO, cumulative logit model with proportional odds; ECI, estimated calibration index; LP, linear predictor; MLR, multinomial logistic regression; ORC, ordinal C statistic; rMSPE, root mean squared prediction error; SLM, stereotype logit model.
TABLE 5.
Validation performance based on small development datasets of n = 500 for the main simulation scenarios (reported as the average performance on a large validation dataset for 200 simulated development datasets)
| Calibration intercepts/Calibration slopes | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Per outcome category | Per outcome dichotomy | Model‐specific | Single number metrics | ||||||||||||
| Model |
|
|
|
|
|
LP1 | LP2 | rMSPE | ORC | ||||||
| MLR truth scenario 1: balanced outcome, equidistant means | |||||||||||||||
| MLR | 0.01/0.97 | −0.01/0.67 | 0.00/0.97 | −0.01/0.97 | 0.00/0.97 | −0.01/0.95 | 0.01/0.97 | 0.047 | 0.738 | ||||||
| CL‐PO | 0.01/1.00 | −0.01/0.72 | 0.01/1.00 | −0.01/1.00 | 0.01/1.00 | 0.01/0.98 | −0.01/0.98 | 0.038 | 0.738 | ||||||
| AC‐PO | 0.01/0.98 | −0.01/0.95 | 0.00/0.98 | −0.01/0.98 | 0.00/0.98 | −0.01/0.98 | 0.01/0.98 | 0.034 | 0.738 | ||||||
| SLM | 0.01/0.98 | −0.01/0.87 | 0.00/0.99 | −0.01/0.98 | 0.00/0.99 | −0.01/0.99 | 0.00/0.98 | 0.037 | 0.738 | ||||||
| MLR truth scenario 2: imbalanced outcome, equidistant means | |||||||||||||||
| MLR | 0.00/0.95 | 0.00/0.83 | 0.00/0.95 | 0.00/0.95 | 0.00/0.95 | 0.00/0.95 | 0.00/0.93 | 0.044 | 0.736 | ||||||
| CL‐PO | 0.02/0.92 | −0.01/0.75 | −0.01/1.10 | −0.02/0.92 | −0.01/1.10 | 0.01/0.96 | −0.01/0.96 | 0.038 | 0.737 | ||||||
| AC‐PO | 0.00/0.96 | 0.00/0.97 | 0.00/0.96 | 0.00/0.96 | 0.00/0.96 | 0.00/0.96 | 0.00/0.96 | 0.033 | 0.737 | ||||||
| SLM | 0.00/0.96 | 0.00/0.95 | 0.00/0.97 | 0.00/0.96 | 0.00/0.97 | 0.00/0.96 | 0.00/0.96 | 0.036 | 0.737 | ||||||
| MLR truth scenario 3: balanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.00/0.97 | −0.01/0.88 | 0.01/0.97 | 0.00/0.97 | 0.01/0.97 | −0.01/0.97 | 0.01/0.94 | 0.045 | 0.738 | ||||||
| CL‐PO | −0.03/1.19 | −0.01/0.72 | 0.05/0.84 | 0.03/1.19 | 0.05/0.84 | 0.01/0.98 | −0.01/0.98 | 0.082 | 0.736 | ||||||
| AC‐PO | 0.00/1.17 | −0.01/0.92 | 0.01/0.83 | 0.00/1.17 | 0.01/0.83 | −0.01/0.98 | 0.01/0.98 | 0.081 | 0.736 | ||||||
| SLM | 0.00/0.98 | −0.01/0.92 | 0.01/1.00 | 0.00/0.98 | 0.01/1.00 | −0.01/0.98 | 0.00/0.98 | 0.073 | 0.735 | ||||||
| MLR truth scenario 4: imbalanced outcome, nonequidistant means | |||||||||||||||
| MLR | 0.01/0.97 | −0.01/0.94 | 0.00/0.94 | −0.01/0.97 | 0.00/0.94 | −0.01/0.98 | 0.00/0.87 | 0.043 | 0.735 | ||||||
| CL‐PO | −0.01/1.08 | 0.00/1.10 | 0.02/0.83 | 0.01/1.08 | 0.02/0.83 | 0.01/0.98 | 0.00/0.98 | 0.067 | 0.733 | ||||||
| AC‐PO | 0.01/1.14 | 0.00/1.42 | 0.00/0.75 | −0.01/1.14 | 0.00/0.75 | −0.01/0.97 | 0.00/0.97 | 0.072 | 0.733 | ||||||
| SLM | 0.01/0.98 | 0.00/0.99 | 0.00/0.99 | −0.01/0.98 | 0.00/0.99 | −0.01/0.98 | −0.01/0.97 | 0.060 | 0.730 | ||||||
| CL‐PO truth scenario 1: balanced outcome | |||||||||||||||
| MLR | 0.02/0.94 | 0.00/0.90 | −0.02/0.96 | −0.02/0.94 | −0.02/0.96 | −0.01/0.94 | −0.02/0.96 | 0.048 | 0.738 | ||||||
| CL‐PO | 0.02/0.97 | 0.00/0.96 | −0.02/0.96 | −0.02/0.97 | −0.02/0.96 | 0.02/0.97 | 0.02/0.97 | 0.034 | 0.738 | ||||||
| AC‐PO | 0.02/0.96 | 0.00/1.30 | −0.02/0.96 | −0.02/0.96 | −0.02/0.96 | −0.01/0.96 | −0.02/0.96 | 0.036 | 0.738 | ||||||
| SLM | 0.02/0.95 | 0.01/1.19 | −0.02/0.97 | −0.02/0.95 | −0.02/0.97 | −0.01/0.97 | −0.03/0.96 | 0.039 | 0.738 | ||||||
| CL‐PO truth scenario 2: imbalanced outcome | |||||||||||||||
| MLR | 0.00/0.97 | −0.01/0.97 | 0.03/0.91 | 0.00/0.97 | 0.03/0.91 | 0.00/0.98 | 0.03/0.84 | 0.046 | 0.737 | ||||||
| CL‐PO | 0.00/0.97 | −0.01/0.97 | 0.03/0.96 | 0.00/0.97 | 0.03/0.96 | 0.00/0.97 | −0.03/0.97 | 0.034 | 0.738 | ||||||
| AC‐PO | 0.00/1.03 | −0.01/1.27 | 0.03/0.85 | 0.00/1.03 | 0.03/0.85 | 0.00/0.96 | 0.03/0.96 | 0.038 | 0.737 | ||||||
| SLM | 0.00/0.97 | −0.01/1.07 | 0.03/0.94 | 0.00/0.97 | 0.03/0.94 | 0.00/0.98 | 0.03/0.95 | 0.038 | 0.738 | ||||||
| CL‐PO truth scenario 3: highly imbalanced outcome | |||||||||||||||
| MLR | −0.02/0.96 | 0.02/0.96 | 0.01/0.87 | 0.02/0.96 | 0.01/0.87 | 0.02/0.98 | 0.00/0.64 | 0.041 | 0.739 | ||||||
| CL‐PO | −0.02/0.96 | 0.02/0.97 | 0.01/0.97 | 0.02/0.96 | 0.01/0.97 | −0.01/0.96 | −0.02/0.96 | 0.033 | 0.739 | ||||||
| AC‐PO | −0.02/1.04 | 0.02/1.17 | 0.01/0.74 | 0.02/1.04 | 0.01/0.74 | 0.02/0.96 | −0.01/0.96 | 0.037 | 0.739 | ||||||
| SLM | −0.02/0.96 | 0.02/0.99 | 0.01/0.97 | 0.02/0.96 | 0.01/0.97 | 0.02/0.97 | 0.02/0.97 | 0.035 | 0.739 | ||||||
Abbreviations: AC‐PO, adjacent category logit model with proportional odds; CAD, coronary artery disease; CL‐PO, cumulative logit model with proportional odds; ECI, estimated calibration index; LP, linear predictor; MLR, multinomial logistic regression; ORC, ordinal C statistic; rMSPE, root mean squared prediction error; SLM, stereotype logit model.
4.2.2. MLR truth—additional scenarios
In the additional scenarios, the above findings show a similar pattern (Table S4 and Figures S5‐S18). MLR continued to provide near perfect risk estimates, but risk estimates for other models were clearly distorted. For CL‐PO and AC‐PO, it was not difficult to find scenarios where calibration slopes for intermediate outcome categories ( if , or if ) are highly problematic. In scenario 8, the calibration slope for was even negative for CL‐PO and AC‐PO. In scenarios 6‐8, with and , one can clearly see how SLM's scaling factors helped to ascertain good calibration intercepts, slopes, and plots, despite distorted individual risk estimates. Having binary predictors or a number of noise predictors did not change the findings.
4.2.3. CL‐PO truth—main and additional scenarios
We present results for the main scenarios in the main text (Figures 5, 6, 7), and for all other scenarios in Data S1 (Figures S19‐S33). In the large sample situations, risk estimates corresponded almost perfectly with true risks for CL‐PO (Figures 5, 6, 7 and S19‐S24). Other models had distorted risk estimates, but the distortion was generally modest. Calibration intercepts and slopes were near perfect for CL‐PO, but not for the other models (Tables 3 and S5). For MLR, calibration slopes of around 1.3‐1.4 were observed for category 2 in several simulation settings (scenarios 1, 4, 5, 8, 9), but the scatter plots of estimated vs true risk as well as the calibration plots (Figures S25‐S33) show that estimated risks were less strongly biased than when fitting CL‐PO models under MLR truth. ECI and rMSPE were best for CL‐PO and worst for AC‐PO (Tables 3 and S6). ECI and rMSPE results for MLR, AC‐PO and SLM were better than what was obtained when CL‐PO models were fitted under MLR truth. Results for small sample simulations were similar to those under MLR truth: again, MLR had the strongest decrease in performance and CL‐PO and AC‐PO the least (Tables 4, 5). Model coefficients for all large sample models are given in Table S6.
FIGURE 5.
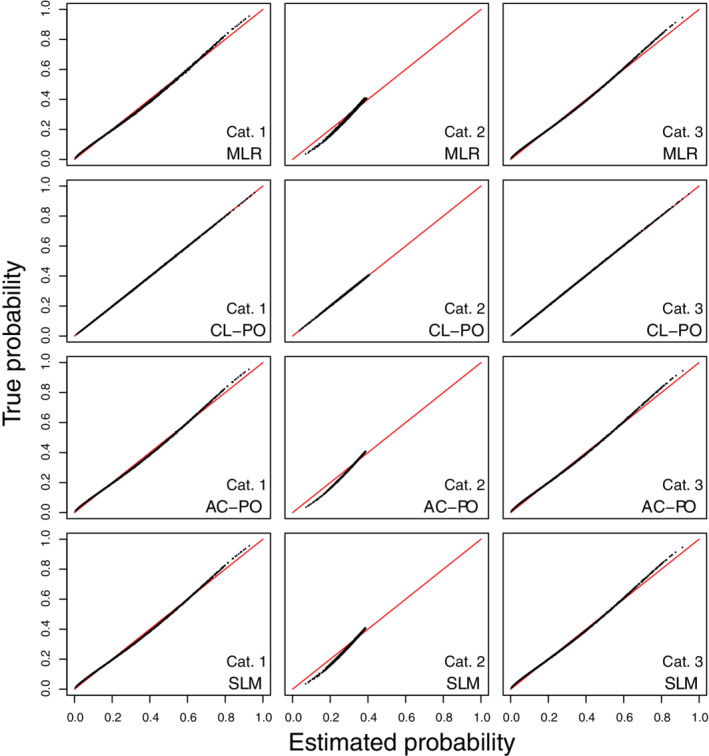
Scatter plots of true risks vs estimated risks for simulation scenario 1 when the true model has the form of a cumulative logit model with proportional odds. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 6.
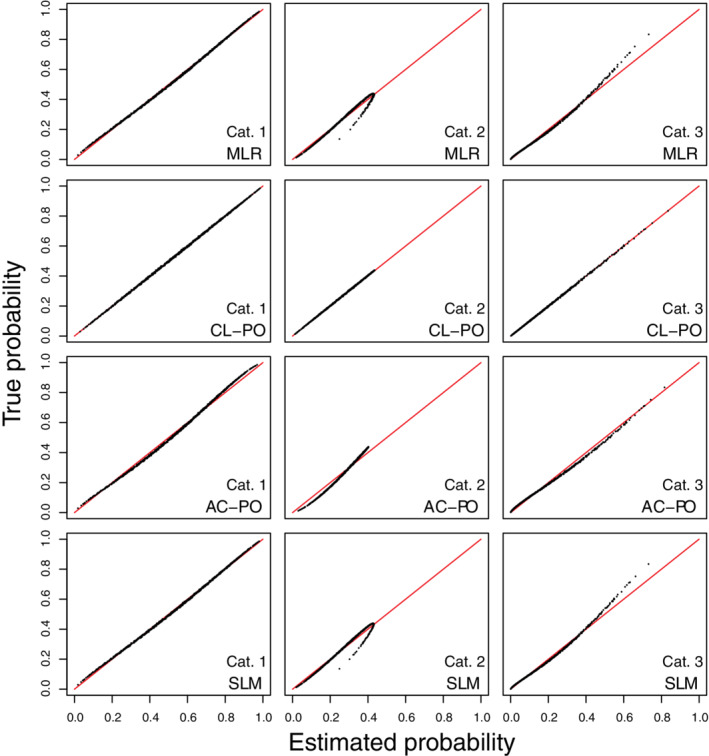
Scatter plots of true risks vs estimated risks for simulation scenario 2 when the true model has the form of a cumulative logit model with proportional odds. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 7.
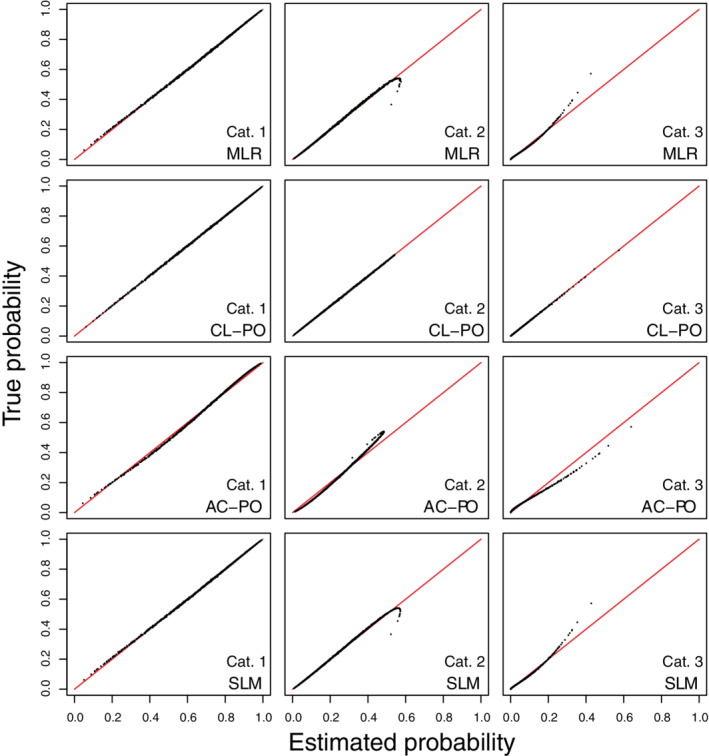
Scatter plots of true risks vs estimated risks for simulation scenario 3 when the true model has the form of a cumulative logit model with proportional odds. The plots are based on a random subset of 1000 cases from all 200 000 cases. AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
5. CASE STUDY: PREDICTION OF CORONARY ARTERY DISEASE
5.1. Methods
The coronary artery disease risk determination in innsbruck by diagnostic angiography (CARDIIGAN) cohort includes patients with suspected coronary artery disease that were recruited between 2004 and 2008 at the University Clinic of Cardiology in Innsbruck (Austria). 32 A prediction model based on the CL‐PO model was developed with the CARDIIGAN data, concerning the diagnosis of nonobstructive coronary artery and multivessel disease in five ordinal disease categories: no coronary artery disease, nonobstructive stenosis, one‐vessel disease, two‐vessel disease, and three‐vessel disease. 1 This outcome has clinical relevance because different categories require different treatment decisions. 32 The patient group involved 4888 individuals, presenting with symptoms at the hospital, who had not had a known previous coronary artery or other heart disease and without coronary revascularization in the past. For earlier studies, the missing values had already been multiply imputed 33 ; in the current illustration we used one of the imputed data sets for convenience.
We applied the following algorithms: MLR (identical to AC‐NP), CL‐PO, AC‐PO, CR‐PO, CR‐NP, and SLM. The proportional odds assumption in the CL‐PO framework was tested per variable using a likelihood ratio test. We used the enhanced bootstrap with 200 bootstrap samples to internally validate the models. 11 We used eleven predictors covering demographic information, symptoms, comorbidities and biomarkers (Table S7). This means that 15 coefficients (including intercepts) have to be estimated for the proportional odds models, 18 for SLM, and 48 for nonproportional odds models. If we focus on the smallest outcome category (three‐vessel disease, n = 429), this implies an EPP (events per parameter excluding intercepts) of 39 for proportional odds models, 31 for SLM, and 10 for nonproportional odds models. See Data S1 for example R code to fit models and evaluate performance. The complete R code is available on GitHub (https://github.com/benvancalster/OrdinalCalibration).
5.2. Results
The likelihood ratio tests suggested violations of the proportional odds assumption for the CL‐PO model, mainly for age and hypertension (Table S8). All models had an optimism‐corrected ORC of 0.693‐0.694 (Table 6, see Table S9 for model coefficients). The risk estimates varied strongly between methods, and this was most obvious for the outcome category “nonobstructive stenosis” (Figures 8 and S34‐S37). For proportional odds models, risk estimates for intermediate outcome categories were capped at some point (see also Table S10). Apparent calibration curves (per outcome category as well as per outcome dichotomy) deviated most from the ideal diagonal line for AC‐PO and CR‐PO, to a lesser extent for CL‐PO, and least for MLR, CR‐NP, and SLM (Figures 9, 10 show calibration scatter plots per outcome category and outcome dichotomy, Figures S38 to S43 also provide flexible calibration plots). The bootstrap‐corrected slopes per outcome category or per outcome dichotomy deviated from the target value of 1 most strongly for CR‐PO and AC‐PO, and least strongly for MLR, CR‐NP, and SLM (Table 6). The model‐specific calibration slopes largely reflect overfitting, because for proportional odds models this assessment assumes the model's proportional odds assumption holds. Hence, model‐specific calibration slopes were closer to 1 for the proportional odds models and SLM, which required fewer parameters than MLR and CR‐NP.
TABLE 6.
Results for the case study on coronary artery disease (CAD)
| Performance statistic | MLR | CL‐PO | AC‐PO | CR‐PO | CR‐NP | SLM |
|---|---|---|---|---|---|---|
| Apparent performance | ||||||
| Calibration intercepts and slopes per outcome category | ||||||
| 1 (No CAD) | 0.00/1.00 | −0.02/1.13 | 0.00/1.38 | 0.00/1.48 | 0.00/1.00 | 0.00/1.00 |
| 2 (Nonobstructive stenosis) | 0.00/1.06 | 0.00/0.82 | 0.00/0.63 | −0.04/0.65 | 0.00/1.09 | 0.00/1.16 |
| 3 (One‐vessel disease) | 0.00/0.97 | 0.02/0.82 | 0.00/1.11 | 0.03/1.08 | 0.00/0.93 | 0.00/0.96 |
| 4 (Two‐vessel disease) | 0.00/1.02 | 0.01/1.06 | 0.00/1.04 | 0.06/1.20 | 0.00/1.04 | 0.00/1.03 |
| 5 (Three‐vessel disease) | 0.00/0.98 | 0.00/0.89 | 0.00/0.70 | −0.02/0.61 | 0.00/0.98 | 0.00/0.98 |
| Calibration intercepts and slopes per outcome dichotomy | ||||||
| 2‐5 vs 1 | 0.00/1.00 | 0.02/1.13 | 0.00/1.38 | 0.00/1.48 | 0.00/1.00 | 0.00/1.00 |
| 3‐5 vs 1‐2 | 0.00/0.99 | 0.02/0.91 | 0.00/0.94 | 0.04/0.99 | 0.00/1.00 | 0.00/1.00 |
| 4‐5 vs 1‐3 | 0.00/1.00 | 0.00/0.95 | 0.00/0.83 | 0.03/0.83 | 0.00/1.01 | 0.00/1.00 |
| 5 vs 1‐4 | 0.00/0.98 | 0.00/0.89 | 0.00/0.70 | −0.02/0.61 | 0.00/0.98 | 0.00/0.98 |
| Calibration intercepts and slopes, model‐specific | ||||||
| Linear predictor 1 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 |
| Linear predictor 2 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 |
| Linear predictor 3 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 |
| Linear predictor 4 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 | 0.00/1.00 |
| ECI | 0.005 | 0.030 | 0.141 | 0.194 | 0.005 | 0.004 |
| ORC | 0.696 | 0.695 | 0.695 | 0.695 | 0.695 | 0.694 |
| Bootstrap‐corrected performance | ||||||
| Calibration intercepts and slopes per outcome category | ||||||
| 1 (No CAD) | 0.00/0.99 | −0.02/1.12 | 0.00/1.37 | 0.00/1.47 | 0.00/0.98 | 0.00/0.99 |
| 2 (Nonobstructive stenosis) | 0.00/0.99 | −0.01/0.81 | 0.00/0.62 | −0.04/0.64 | 0.00/1.02 | 0.00/1.13 |
| 3 (One‐vessel disease) | 0.00/0.89 | 0.02/0.80 | 0.00/1.09 | 0.03/1.06 | 0.00/0.86 | 0.00/0.95 |
| 4 (Two‐vessel disease) | 0.00/0.97 | 0.01/1.05 | 0.00/1.02 | 0.06/1.17 | 0.00/0.97 | 0.00/1.03 |
| 5 (Three‐vessel disease) | 0.00/0.94 | 0.01/0.87 | 0.01/0.68 | 0.00/0.60 | 0.01/0.93 | 0.00/0.98 |
| Calibration intercepts and slopes per outcome dichotomy | ||||||
| 2‐5 vs 1 | 0.00/0.99 | 0.02/1.12 | 0.00/1.37 | 0.00/1.47 | 0.00/0.98 | 0.00/0.99 |
| 3‐5 vs 1‐2 | 0.00/0.98 | 0.02/0.90 | 0.00/0.93 | 0.04/0.98 | 0.00/0.98 | 0.00/0.99 |
| 4‐5 vs 1‐3 | 0.00/0.97 | 0.01/0.93 | 0.01/0.81 | 0.03/0.81 | 0.01/0.98 | 0.00/1.00 |
| 5 vs 1‐4 | 0.00/0.94 | 0.01/0.87 | 0.01/0.68 | 0.00/0.60 | 0.01/0.93 | 0.00/0.98 |
| Calibration intercepts and slopes, model‐specific | ||||||
| Linear predictor 1 | 0.00/0.95 | 0.00/0.99 | 0.00/0.98 | 0.00/0.98 | 0.00/0.98 | −0.01/0.99 |
| Linear predictor 2 | 0.00/0.96 | 0.00/0.99 | 0.00/0.98 | 0.00/0.98 | 0.00/0.96 | 0.00/0.98 |
| Linear predictor 3 | 0.01/0.96 | −0.01/0.99 | 0.00/0.98 | 0.01/0.98 | 0.01/0.89 | 0.00/0.99 |
| Linear predictor 4 | 0.00/0.96 | −0.01/0.99 | 0.01/0.98 | 0.01/0.98 | 0.01/0.65 | 0.00/0.99 |
| ORC | 0.694 | 0.693 | 0.693 | 0.693 | 0.693 | 0.693 |
Abbreviations: AC‐PO, adjacent category logit model with proportional odds; CAD, coronary artery disease; CL‐PO, cumulative logit model with proportional odds; ECI, estimated calibration index; LP, linear predictor; MLR, multinomial logistic regression; ORC, ordinal C statistic; rMSPE, root mean squared prediction error; SLM, stereotype logit model.
FIGURE 8.
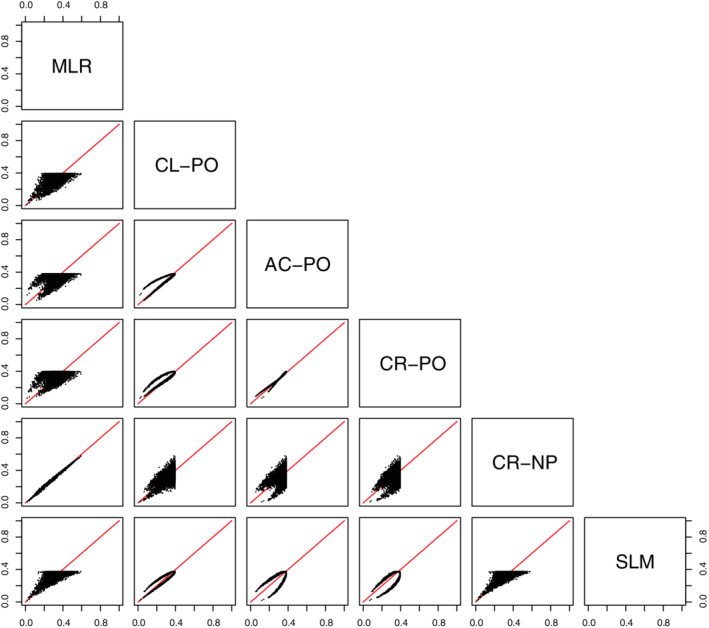
Scatter plot of estimated probabilities for having nonobstructive stenosis in the case study (n = 4888). AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; CR‐NP, continuation ratio logit model without proportional odds; CR‐PO, continuation ratio logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 9.
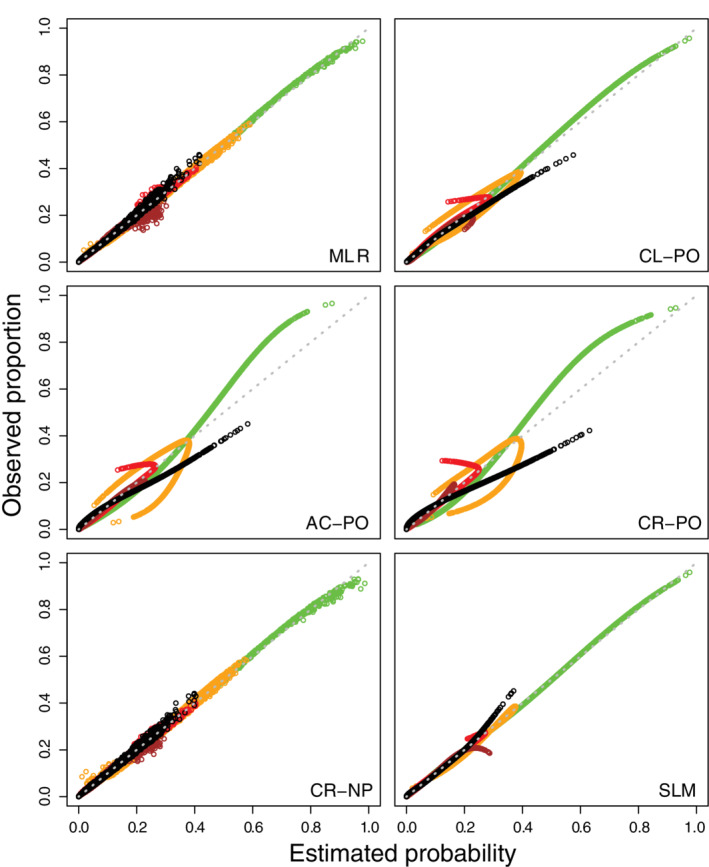
Calibration scatter plots per outcome category for the models in the case study (green for no coronary artery disease, orange for nonobstructive stenosis, red for one‐vessel disease, brown for two‐vessel disease, black for three‐vessel disease). These plots are generated for the model development data (ie, apparent validation, n = 4888). AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; CR‐NP, continuation ratio logit model without proportional odds; CR‐PO, continuation ratio logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
FIGURE 10.
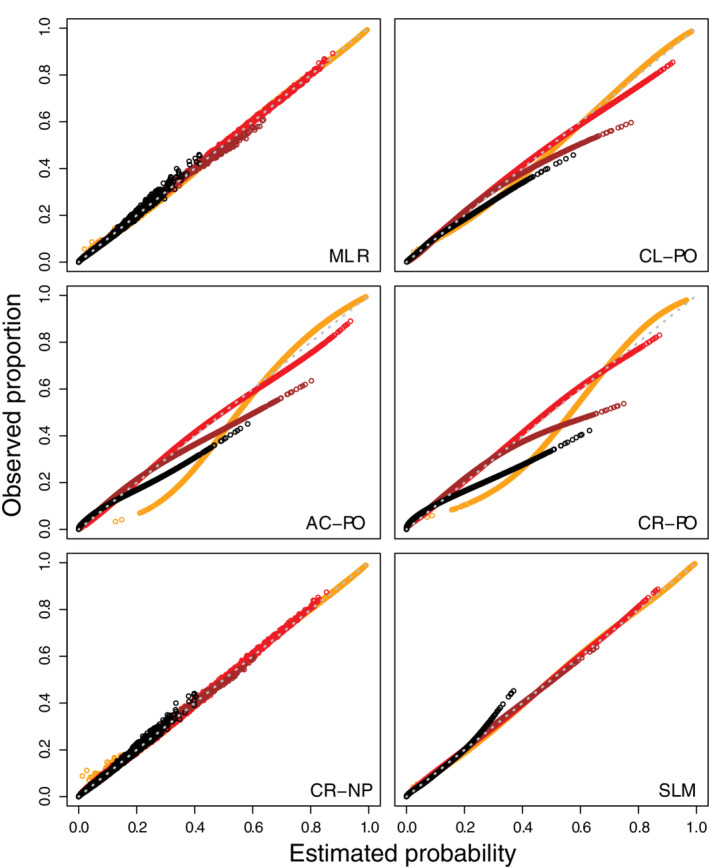
Calibration scatter plots per outcome dichotomy for the models in the case study (orange for nonobstructive stenosis or worse, red for one‐vessel disease or worse, brown for two‐vessel disease or worse, black for three‐vessel disease). These plots are generated for the model development data (ie, apparent validation, n = 4888). AC‐PO, adjacent category logit model with proportional odds; CL‐PO, cumulative logit model with proportional odds; CR‐NP, continuation ratio logit model without proportional odds; CR‐PO, continuation ratio logit model with proportional odds; MLR, multinomial logistic regression; SLM, stereotype logit model
6. DISCUSSION
In this study we focused on calibration of risk prediction models for discrete ordinal outcomes, and on the impact of assuming proportional odds on risk estimation and calibration performance. The results show that assuming proportional odds leads to (sometimes strongly) distorted risk estimates, calibration slopes, and calibration plots when the true model had MLR form and hence the proportional odds assumption was violated. Naturally, MLR models yielded appropriate risk estimates in these settings. In contrast, when the true model had the CL‐PO form, the MLR model had distorted risk estimates and calibration. The deviations for MLR under CL‐PO truth were less dramatic than the deviations of the CL‐PO model when the true model had the MLR form.
Perhaps surprisingly, when the true model had the CL‐PO form, other proportional odds models such as AC‐PO also had deviating risk estimates. This highlights the importance of the specific form of proportional odds that is assumed, which varies between the cumulative, adjacent category and continuation ratio logit models. The SLM model, which can be seen as a compromise between MLR and AC‐PO models, also showed distorted risk estimates when the true model had the MLR form. Due to its scaling factors, SLM did yield appropriate calibration intercepts and calibration slopes. When the true model had the CL‐PO form, however, SLM did not improve upon MLR. Our small sample size simulations showed that in smaller samples, the models that do not assume proportional odds suffer from more overfitting, due to the higher number of parameters that need to be estimated when proportional odds are not assumed.
For binary outcomes modeled with maximum likelihood logistic regression, the calibration intercept and slope are by definition 0 and 1 on the data on which the model is developed. This is a well‐known property of calibration intercepts and slopes, which was previously extended to models for nominal outcomes based on multinomial logistic regression. 18 In this article we further generalized in this work to models for ordinal outcomes under the label “model‐specific” calibration assessment. For proportional odds models, this approach assesses calibration under the assumption that proportional odds hold. Violations of the assumption are therefore not considered, which makes this approach inappropriate for quantifying calibration of ordinal prediction models. For other models, this approach performs satisfactorily, but a general drawback is that it is less intuitive than simple calibration assessment for each outcome category or dichotomy.
Based on our findings, we generally recommend nonproportional odds models such as MLR for developing risk prediction models for an ordinal outcome. We are inclined to believe that proportional odds assumptions will often not hold in the practice of medical risk prediction. But even when it does, we argue that the loss in efficiency and increased risk of overfitting associated with using MLR is less problematic than the opposite problem, that is, the risk of severe miscalibration when using proportional odds models (even under moderate deviation from the proportional odds assumption). However, MLR has more parameters and hence needs a larger sample size in order to obtain a reliable risk prediction model. 34 Sample size determination methods for prediction models based on MLR are currently underway. This will help to plan model development studies for ordinal outcomes by calculating the minimum sample size needed to use MLR. If this minimum sample size is too high given the resources for a given project, it can be discussed whether a proportional odds model would be defendable or whether no model should be developed until more resources become available. A compromise to assuming strict proportional odds may be the SLM model, which uses less parameters than MLR. This model can help to improve calibration slopes and flexible calibration curves, although risks on the individual level may still be distorted.
To assess calibration, we recommend to calculate the calibration intercepts and slopes per outcome category or per outcome dichotomy. Whether to focus on outcome categories or dichotomies depends on the specific (clinical) context, that is, on how risk estimates are used in clinical practice to decide upon patient management. If each outcome category is associated with a different management option, calibration per outcome category is preferred. When the management decision is binary, and depends on whether exceeds a given threshold, calibration per dichotomy may be preferred. For internal validation, these estimates can be based on bootstrapping. 11 When externally validating a model, flexible calibration plots (scatter plots as well as flexible calibration curves) are recommended because they provide a more general overview of calibration 29 : whereas calibration intercepts and slopes assess weak calibration, calibration curves assess moderate calibration. 26 Again, calibration plots can be constructed per outcome category or dichotomy. We based the flexible calibration plots on a flexible recalibration model with an MLR‐like setup (Equation (18)). In Data S1, we compared this approach to other approaches to assess whether non‐MLR prediction models are disadvantaged by this setup. Differences between the approaches were small. One may prefer to replace the in Equation (18) with to acknowledge the ordinal nature of the outcome (ie, the third approach in Data S1). Finally, when different models are compared at external validation, the ECI is an attractive single summary measure. Of course, summarizing performance into a single number always has limitations.
We did not address partial proportional odds models, in which the proportional odds assumption can be relaxed for some but not all predictors. 4 , 35 This usually requires the use of a test for proportional odds per variable, for example, likelihood ratio tests or the Brant test. 36 However, by evaluating the proportional odds assumption one considers the same number of parameters as in nonproportional odds models. Future studies could look into the power of these tests to detect deviations from proportional odds assumptions that would result in important miscalibration and distorted predictions. Further, the use of CL‐PO has been advocated in settings outside of prediction models. For instance, they can be used to model continuous outcomes, in particular when these outcomes have skewed or semi‐continuous distributions and in randomized controlled trials to improve statistical efficiency. 37 , 38 While our focus is in risk prediction modeling and hence our results do not directly generalize to these settings, our finding that the type of proportional odds assumption matters (eg, on the level of cumulative logits vs adjacent category logits) seems to warrant further investigation.
To conclude, when the proportional odds assumptions do not strictly hold, as we believe is often the case in practical application of risk prediction models, the use of proportional odds models to develop prediction models for discrete ordinal outcomes can result in poor risk estimates and poor calibration. For the development of risk prediction models, we therefore warn readers against using proportional odds models without careful argumentation, and to consider multinomial logistic regression to model ordered categorical outcomes.
ACKNOWLEDGEMENT
Michael Edlinger and Ben Van Calster were supported by Research Foundation ‐ Flanders (FWO) grant G0B4716N. BVC was supported by Internal Funds KU Leuven grant C24M/20/064. The funding bodies had no role in the design of the study, data collection, statistical analysis, interpretation of data, or in writing of the manuscript.
Supporting information
Data S1 Supporting Information
Calculating estimated probabilities for each type of model
MLR: , with set to 0.
CL‐PO: , and . Note that .
CL‐NP: analogous as for CL‐PO.
AC‐PO: , with set to 0.
AC‐NP: analogous as for AC‐PO.
CR‐PO: for , . Note that . Finally, .
CR‐NP: analogous as for CR‐PO.
SLM: , with .
Edlinger M, van Smeden M, Alber HF, Wanitschek M, Van Calster B. Risk prediction models for discrete ordinal outcomes: Calibration and the impact of the proportional odds assumption. Statistics in Medicine. 2022;41(8):1334–1360. doi: 10.1002/sim.9281
Funding information Fonds Wetenschappelijk Onderzoek, G0B4716N; Onderzoeksraad, KU Leuven, C24M/20/064
DATA AVAILABILITY STATEMENT
For the CAD data, collaboration is welcomed and data sharing can be agreed upon by contacting Michael Edlinger (michael.edlinger@i‐med.ac.at).
REFERENCES
- 1. Edlinger M, Dörler J, Ulmer H, et al. An ordinal prediction model of the diagnosis of non‐obstructive coronary artery and multi‐vessel disease in the CARDIIGAN cohort. Int J Cardiol. 2018;267:8‐12. [DOI] [PubMed] [Google Scholar]
- 2. Risselada R, Lingsma HF, Molyneux AJ, et al. Prediction of two month modified Rankin scale with an ordinal prediction model in patients with aneurysmal subarachnoid haemorrhage. BMC Med Res Methodol. 2010;10:86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Meisner A, Parikh CR, Kerr KF. Using ordinal outcomes to construct and select biomarker combinations for single‐level prediction. Diagn Progn Res. 2018;2:8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Fullerton AS, Xu J. Constrained and unconstrained partial adjacent category logit models for ordinal response variables. Sociol Methods Res. 2018;47(2):169‐206. [Google Scholar]
- 5. Scott SC, Goldberg MS, Mayo NE. Statistical assessment of ordinal outcomes in comparative studies. J Clin Epidemiol. 1997;50(1):45‐55. [DOI] [PubMed] [Google Scholar]
- 6. Ananth CV, Kleinbaum DG. Regression models for ordinal responses: a review of methods and applications. Int J Epidemiol. 1997;26(6):1323‐1333. [DOI] [PubMed] [Google Scholar]
- 7. Anderson JA. Regression and ordered categorical variables. J R Stat Soc Ser B Stat Methodol. 1984;46(1):1‐30. [Google Scholar]
- 8. Liu I, Agresti A. The analysis of ordered categorical data: an overview and a survey of recent developments. Test. 2005;14:1‐73. [Google Scholar]
- 9. Lunt M. Prediction of ordinal outcomes when the association between predictors and outcome differs between outcome levels. Stat Med. 2005;24(9):1357‐1369. [DOI] [PubMed] [Google Scholar]
- 10. Agresti A. Categorical Data Analysis. Hoboken, NJ: John Wiley & Sons; 2013. [Google Scholar]
- 11. Harrell FE Jr. Regression Modeling Strategies; with Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis. Cham, Switzerland: Springer; 2015. [Google Scholar]
- 12. Riley RD, van der Windt D, Moons KGM. Prognosis Research in Health Care; Concepts, Methods, and Impact. Oxford, UK: Oxford University Press; 2019. [Google Scholar]
- 13. Steyerberg EW. Clinical Prediction Models; a Practical Approach to Development, Validation, and Updating. Cham, Switzerland: Springer; 2019. [Google Scholar]
- 14. Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010;21(1):128‐138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Moons KG, Altman DG, Vergouwe Y, Royston P. Prognosis and prognostic research: application and impact of prognostic models in clinical practice. BMJ. 2009;338:b606. [DOI] [PubMed] [Google Scholar]
- 16. Wynants L, Collins GS, Van Calster B. Key steps and common pitfalls in developing and validating risk models. BJOG. 2017;124(3):423‐432. [DOI] [PubMed] [Google Scholar]
- 17. Altman DG, Royston P. What do we mean by validating a prognostic model? Stat Med. 2000;19(4):453‐473. [DOI] [PubMed] [Google Scholar]
- 18. Van Hoorde K, Vergouwe Y, Timmerman D, Van Huffel S, Steyerberg EW, Van Calster B. Assessing calibration of multinomial risk prediction models. Stat Med. 2014;33(15):2585‐2596. [DOI] [PubMed] [Google Scholar]
- 19. Van Calster B, Van Belle V, Vergouwe Y, Timmerman D, Van Huffel S, Steyerberg EW. Extending the c‐statistic to nominal polytomous outcomes: the polytomous discrimination index. Stat Med. 2012;31(23):2610‐2626. [DOI] [PubMed] [Google Scholar]
- 20. Van Calster B, Vergouwe Y, Looman CWN, Van Belle V, Timmerman D, Steyerberg EW. Assessing the discriminative ability of risk models for more than two outcome categories. Eur J Epidemiol. 2012;27(10):761‐770. [DOI] [PubMed] [Google Scholar]
- 21. Harrell FE, Margolis PA, Gove S, et al. Development of a clinical prediction model for an ordinal outcome: the world health organization multicentre study of clinical signs and etiological agents of pneumonia, sepsis and meningitis in young infants. WHO/ARI young infant multicentre study group. Stat Med. 1998;17(8):909‐944. [DOI] [PubMed] [Google Scholar]
- 22. Nakas CT, Yiannoutsos CT. Ordered multiple‐class ROC analysis with continuous measurements. Stat Med. 2004;23(22):3437‐3449. [DOI] [PubMed] [Google Scholar]
- 23. Obuchowski NA. Estimating and comparing diagnostic tests' accuracy when the gold standard is not binary. Acad Radiol. 2005;12(9):1198‐1204. [DOI] [PubMed] [Google Scholar]
- 24. Van Calster B, Van Belle V, Vergouwe Y, Steyerberg EW. Discrimination ability of prediction models for ordinal outcomes: relationships between existing measures and a new measure. Biom J. 2012;54(5):674‐685. [DOI] [PubMed] [Google Scholar]
- 25. Van Calster B, McLernon DJ, van Smeden M, Wynants L, Steyerberg EW. Calibration: the achilles heel of predictive analytics. BMC Med. 2019;17(1):230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Van Calster B, Nieboer D, Vergouwe Y, De Cock B, Pencina MJ, Steyerberg EW. A calibration hierarchy for risk models was defined: from utopia to empirical data. J Clin Epidemiol. 2016;74:167‐176. [DOI] [PubMed] [Google Scholar]
- 27. Yee TW, Wild CJ. Vector generalized additive models. J R Stat Soc B Stat Methodol. 1996;58(3):481‐493. [Google Scholar]
- 28. Yee TW. Vector Generalized Linear and Additive Models. New York, NY: Springer; 2015. [Google Scholar]
- 29. Van Hoorde K, Van Huffel S, Timmerman D, Bourne T, Van Calster B. A spline‐based tool to assess and visualize the calibration of multiclass risk predictions. J Biomed Inform. 2015;54:283‐293. [DOI] [PubMed] [Google Scholar]
- 30. Morris TP, White IR, Crowther MJ. Using simulation studies to evaluate statistical methods. Stat Med. 2019;38(11):2074‐2102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Yee TW. The VGAM package for categorical data analysis. J Stat Softw. 2010;32(10):1‐34. [Google Scholar]
- 32. Wanitschek M, Edlinger M, Dörler J, Alber HF. Cohort profile: the coronary artery disease risk determination in Innsbruck by diaGnostic ANgiography (CARDIIGAN) cohort. BMJ Open. 2018;8(6):e021808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Edlinger M, Wanitschek M, Dörler J, Ulmer H, Alber HF, Steyerberg EW. External validation and extension of a diagnostic model for obstructive coronary artery disease: a cross‐sectional predictive evaluation in 4888 patients of the Austrian coronary artery disease risk determination in Innsbruck by diaGnostic ANgiography (CARDIIGAN) cohort. BMJ Open. 2017;7(4):e014467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. De Jong VMT, Eijkemans MJC, Van Calster B, et al. Sample size considerations and predictive performance of multinomial logistic prediction models. Stat Med. 2019;38(9):1601‐1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Peterson B, Harrell FE Jr. Partial proportional odds models for ordinal response variables. Appl Stat. 1990;39(2):205‐217. [Google Scholar]
- 36. Brant R. Assessing proportionality in the proportional odds model for ordinal logistic regression. Biometrics. 1990;46(4):1171‐1178. [PubMed] [Google Scholar]
- 37. Liu Q, Shepherd BE, Li C, Harrell FE Jr. Modeling continuous response variables using ordinal regression. Stat Med. 2017;36(27):4316‐4335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. McHugh GS, Butcher I, Steyerberg EW, et al. A simulation study evaluating approaches to the analysis of ordinal outcome data in randomized controlled trials in traumatic brain injury: results from the IMPACT project. Clin Trials. 2010;7(1):44‐57. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1 Supporting Information
Data Availability Statement
For the CAD data, collaboration is welcomed and data sharing can be agreed upon by contacting Michael Edlinger (michael.edlinger@i‐med.ac.at).


