How Can We Resolve Lewontin’s Paradox?

Abstract

We discuss the genetic, demographic, and selective forces that are likely to be at play in restricting observed levels of DNA sequence variation in natural populations to a much smaller range of values than would be expected from the distribution of census population sizes alone—Lewontin’s Paradox. While several processes that have previously been strongly emphasized must be involved, including the effects of direct selection and genetic hitchhiking, it seems unlikely that they are sufficient to explain this observation without contributions from other factors. We highlight a potentially important role for the less-appreciated contribution of population size change; specifically, the likelihood that many species and populations may be quite far from reaching the relatively high equilibrium diversity values that would be expected given their current census sizes.

Significance.

The fact that levels of DNA sequence variability differ among species far less than would be expected from differences in their population sizes (Lewontin’s Paradox) has long presented a puzzle for evolutionary biologists. Here, we evaluate the relative importance of the main candidates for resolving this paradox: mutational biases, population subdivision and size changes, and direct and indirect effects of selection.

Introduction

If the polymorphism so widely observed is truly related to the evolutionary processes that have molded and will mold the history of various species, there ought to be some variation among species in the degree of their genetic variation. (Lewontin 1974, p.121).

It can be objected that species have not had time to reach their equilibrium values, but we know that H [heterozygosity] will be some function … of past numbers … it seems that the uniformity of H between species is powerful evidence against the view that the observed polymorphisms are in the main selectively neutral. The investigation in §§2-4 can therefore be regarded as a last ditch attempt to save the neutral mutation theory by showing that there is another process which can account for the uniformity of H between species. (Maynard Smith and Haigh 1974, p.34).

There has recently been much discussion of “Lewontin’s paradox” (LP)—the observation that the range of levels of genetic diversity in natural populations appears to be far smaller than the extent of variation among species in population size (e.g., Leffler et al. 2012; Romiguier et al. 2014; Corbett-Detig et al. 2015; Coop 2016; Filatov 2019; Mackintosh et al. 2019; Galtier and Rouselle 2020; Buffalo 2021). This seems to contradict the theoretical prediction that neutral diversity increases rapidly as the effective population size, N_e, increases (Kimura 1971). Even among multicellular animal taxa, there are many examples of species whose N_e values, as indicated by their levels of DNA sequence variability, are several orders of magnitude smaller than the estimated numbers of adult individuals, especially among invertebrates (see fig. 2 of Buffalo 2021). This discrepancy is even more striking for microbes—for example, the marine bacterium Prochloroccus marinus has an estimated N_e of 10⁸, whereas its census size is thought to be on the order of 10¹³ (Bobay and Ochman 2018).

Richard Lewontin originally posed this problem on the basis of data on electrophoretic variation, which is now known to show much less between-species variation than silent nucleotide site diversity for nuclear genes (Li and Sadler 1991; Bazin et al. 2006), probably reflecting the action of balancing selection in maintaining many common electrophoretic variants (Eanes 1999). Population genomic surveys have recently provided a mass of data on diversity levels based on silent nucleotide site diversity, denoted here by π. (Silent sites provide estimates of diversity that are the least likely to be influenced by selection, since they are defined as those where mutations fail to change the sequence of a protein.) The results show that the range of diversity levels across taxa is still quite limited: although some species have π values of 0.001 or less, very few have a mean silent site diversity across the genome greater than 0.15, despite differences in estimated census population sizes of many orders of magnitude (Leffler et al. 2012; Cutter et al. 2013; Buffalo 2021). Currently, the eukaryote species with the highest π appears to be the US population of the basidiomycete fungus Schizophyllum commune, with a mean silent site diversity of approximately 0.2 and no evidence of significant population subdivision (Baranova et al. 2015).

It is important to note, however, that estimates of census population sizes, such as those presented by Buffalo (2021), often use indirect methods that are likely to involve considerable uncertainties (Palstra and Fraser 2012), especially as different definitions of census size are used by different authors. In addition, LP concerns the long-term N_e relevant to nucleotide site diversity, not the short-term N_e estimated from temporal changes in allele frequencies, linkage disequilibrium or pedigrees (for an account of such estimates of N_e, see Palstra and Fraser 2012 and Waples 2022). Short- and long-term estimates of N_e may only be weakly related to each other, as we discuss later in relation to the effects of demographic factors on π. Despite these caveats, it can hardly be doubted that many species show huge discrepancies between estimates of census population sizes and the levels of nucleotide site diversity that would be expected if these sizes represented the long-term N_e of the species.

This fact challenges our current understanding of the processes controlling levels of natural variation, as has been pointed out many times before. Here, we discuss the major population genetic processes that could help to resolve LP (Box 1)—focusing specifically on why π has such a relatively narrow range, rather than reviewing the numerous ecological correlates of π, which have been discussed in depth by others (e.g., Romiguier et al. 2014; Mackintosh et al. 2019; Peart et al. 2019; Buffalo 2021). We do not pretend to have a complete answer to this problem, but hope that we have succeeded in giving pointers to the forces that are most likely to be involved. The asterisks in Box 1 indicate our tentative evaluations of the relative importance of each of the factors.

Box 1: Factors that potentially modulate the relation between census population size (N) and silent site diversity (π).

Selectively neutral genetic processes

1. Mutational bias **.

2. Biased gene conversion *.

3. A negative relation between mutation rate and population size *.

Effects of demography

1. Skewed distributions of offspring numbers **.

2. Metapopulation processes (extinction and recolonization of local populations) *.

3. Population size changes ***.

Effects of selection

1. Weak selection on silent sites *.

2. Background selection *.

3. Recurrent selective sweeps **.

The number of asterisks is proportional to the probable importance of the factor concerned.

In order to focus our discussion, we will frequently use Drosophila melanogaster as an example of a eukaryote species with a moderate level of silent site diversity despite its enormous population sizes in several continents, having expanded out of its ancestral range in East-Central Africa in the relatively recent past (Arguello et al. 2019; Sprengelmeyer et al. 2020). All the genetic, demographic and selective processes that we discuss as candidates for causing LP are likely to be operating in this species.

Effects of Selectively Neutral Genetic Processes

Mutational Bias

It is sometimes assumed that the standard infinite sites formula for the equilibrium neutral nucleotide site diversity, π = 4N_eu, where u is the neutral mutation rate per basepair (Kimura 1971), is always valid, implying that π increases indefinitely with increasing N_e. For example, Rajaei et al. (2021) introduced their study of mutational spectra in Caenorhabditis elegans with the remark that “It is a fundamental principle of population genetics that the DNA sequence diversity in a population (θ) represents the product of mutation (μ) and ‘everything else’, where ‘everything else’ subsumes the contributions of natural selection and random genetic drift in the composite parameter N_e, the genetic effective population size: θ = 4N_eμ ….” But a pairwise diversity measure like π must lie in the interval (0, 1), and the infinite sites formula becomes increasingly inaccurate as θ increases beyond 0.05, since it ignores the possibility of reverse mutations and multiple occurrences of the same class of mutation at polymorphic nucleotide sites (Tajima 1996; Cutter et al. 2013; Charlesworth and Jain 2014).

Here, we will use θ = 4N_eu to denoted the scaled neutral mutation rate, as opposed to the silent site diversity, π. For the purpose of interpreting observations on π, 2N_e can be defined for any genetic system as the mean coalescent time (T) for a pair of neutral alleles in a random sample from a population, such that 4N_e is the expected evolutionary time connecting the two alleles (Charlesworth 2009). The infinite sites assumption implies a linear relation between the probability that the pair of alleles differ at a given nucleotide site (π) and their mean coalescent time. But if the latter becomes sufficiently large, this probability will tend to an upper limit, just as sequence divergence along species phylogenies tends to saturation with increasing time (fig. 1A). LP should thus strictly be stated in term of estimates of T rather than π.

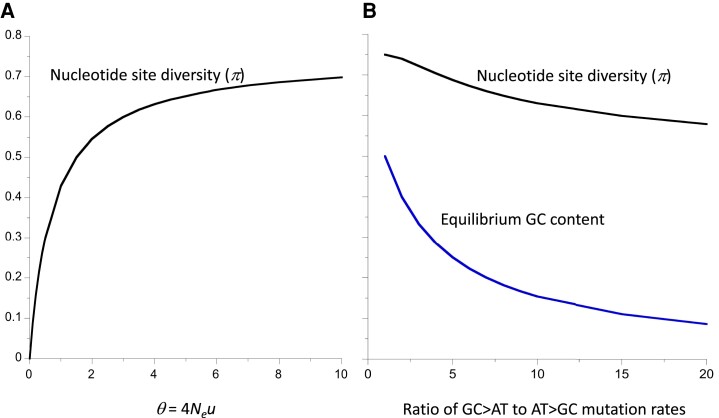
Fig. 1.

(A) Displays the nucleotide site diversity (π) as a function of the scaled mutation rate (θ = 4N_eu) for the Jukes–Cantor mutational model, with four alleles at a site and equal frequencies of mutation between each allele. (B) Shows the equilibrium GC content under neutrality and the corresponding infinite population equilibrium value of π, under a mutational model in which all mutation rates between possible basepairs are equal, except for an elevated rate of GC > AT transitions.

These considerations raise the question of whether a more realistic representation of the mutational process would place a relatively small upper limit on π, helping to resolve LP. The simplest model that takes into account mutations among all four possible bases at a nucleotide site assumes equal frequencies of mutations among A, G, T and C, which is equivalent to the Jukes–Cantor model of sequence evolution (Jukes and Cantor 1969). With a scaled mutation rate of θ = 4N_eu, this model gives equilibrium π = θ/(1 + 4θ/3) (Tajima 1996); the upper limit to π is 3/4, corresponding to the infinite population mutational equilibrium state with equal frequencies of each base. This is clearly far higher than the current eukaryote record of 0.2 mentioned above; figure 2 of Buffalo (2021) shows that this model predicts a much faster increase in π with N than is observed, assuming that the estimated value of N for a species is proportional to N_e.

It is also worth considering whether mutational models that include the well-known biases in favor of transitions over transversions, and GC to AT basepair mutations over AT to GC mutations (e.g., Assaf et al. 2017), could further reduce the upper limit to π. Exact finite population solutions for π are not available, so that numerical solutions such as those of Zeng (2010) must be used. However, it is straightforward to solve for the infinite population mutational equilibrium state by inverting the matrix of transition probabilities among the different bases (Charlesworth and Charlesworth 2010, pp. 45 and 610–611) (strand-specificity of mutation rates is ignored here; see the next section for a discussion of this phenomenon). This procedure can be applied to any given dataset on mutational spectra. For example, for D. melanogaster the data in supplementary table S9, Supplementary Material online of Assaf et al. (2017) give the following solution for the equilibrium frequencies of A, G, T, and C: 0.374, 0.148, 0.444, and 0.034, yielding π = 0.640.

It is known from the properties of mutational transition matrices that a bias in favor of transitions over transversions alone (as in Kimura’s two-parameter mutation model; Kimura 1980) does not produce a deviation from equal frequencies of the four bases; a GC to AT mutational bias is required for such a deviation (Ewens 2004, Chapter 12). In the Drosophila example, the main cause of such a deviation is the high rate of GC > AT transitions, which is approximately eight times larger than the rate for AT > CG transversions. If all other mutation rates are set equal to the AT > CG value, the equilibrium π is only decreased to 0.649 with this level of mutational bias. Figure 1B shows that, under this model, the equilibrium neutral GC content decreases much faster with the ratio of the GC > AT to AT > GC mutation rates than does the equilibrium π value, suggesting that a very high mutational bias in favor of GC versus AT (resulting in a very low GC content at neutral sites) is required to produce a value of π that is as low as 0.6. Given that a GC content less than 20% is exceptional, even in noncoding sequences, with Plasmodium falciparum having one of the lowest known noncoding GC contents of 13% (Gardner et al. 2002), the possibility that mutational biases alone can resolve LP can be excluded with high confidence, although such biases cause somewhat lower π values than are expected in its absence.

Biased Gene Conversion

The second factor that could potentially limit diversity at neutral sites is GC-biased gene conversion (gBGC), which causes the GC basepair at a site that is heterozygous for GC and AT to have a greater than 50% frequency among the products of meiosis. This process has been documented by direct genetic analyses in humans (e.g., Arbeithuber et al. 2015), and its operation has been inferred by population genetic analyses in many more species (Galtier and Duret 2007; Bergman and Schierup 2021). The frequency with which gene conversion events affect a given nucleotide site can be substantial at recombination hotspots (Arbeithuber et al. 2015) but is otherwise not likely to be much more than two or three orders of magnitude greater than the typical probability of initiation of a gene conversion tract at a given nucleotide site, given that mean conversion tract lengths are generally a few hundred to one thousand basepairs in taxa like D. melanogaster (Miller et al. 2016) and budding yeast (Borts and Haber 1989). The effect of gBGC on the relative frequencies of GC and AT basepairs in the population is similar to that of haploid or semi-dominant selection (Gutz and Leslie 1976). It can be quantified by the scaled intensity measure γ_gc = 2N_eω, where ω is the equivalent of a selection coefficient, given by the product of the frequency of a gene conversion event in a GC/AT heterozygote and the effect of such an event on the frequency of GC among the gametes (Charlesworth and Charlesworth 2010, p. 528).

While estimates of the mean value of γ_gc for putatively neutral sites are of the order of two at most in organisms such as Drosophila that lack recombination hotspots (Jackson and Charlesworth 2021), if N_e were to increase without limit, the population would become nearly fixed for GC basepairs. However, transversion mutations of the type GC to CG and vice-versa can still occur; these are likely to be selectively neutral in nonfunctional sequences, as is seen in population genomic studies (Jackson and Charlesworth 2021). Equation (12) of Charlesworth and Jain (2014) implies that the upper limit to π in a model of GC to CG and CG to GC mutations at a single site is 2λ/(1 + λ)², where λ is the ratio of the higher to the lower of the two mutation rates (λ ≥ 1); for λ = 2, π = 0.444, and with no strand-specificity of mutation rates (λ = 1) it is 0.5.

The possibility that gBGC plays a significant role in limiting diversity to much below 0.5 can therefore be ruled out, unless the extent of strand-specific mutational bias at GC basepairs is greater than is commonly thought to be the case (Polak and Arndt 2008; Bergman et al. 2015). In any case, the mean GC content of the genome would be close to 100% if there were a very large γ_gc; the highest known genome-wide value is approximately 75%, in some species of bacteria (Hildebrandt et al. 2010). Thus, while gBGC is probably a major factor in affecting the GC content of genomes, and is likely to reduce π below the expected neutral value in species with large N_e, it cannot in itself constrain π below a value of approximately 0.5.

A Negative Relation between Mutation Rate and Population Size

If the mutation rate of a species were a decreasing function of its population size, θ might reach an asymptote as N_e increases, providing an easy resolution of LP. There are two, nonmutually exclusive, possible reasons for expecting such a relation. First, if mutations occur mainly during cell divisions, large and long-lived multicellular organisms with many cell divisions between zygote and zygote (at least in the male germline) would be expected to have larger per-generation mutation rates than smaller, shorter lived multicellular organisms or single-celled organisms, unless selection against a higher mutation rate is able to reduce the mutation rate per cell division (Drake et al. 1998). Since species abundances tend to be inversely related to their body sizes (White et al. 2007), and body size is highly correlated with lifespan (Finch 1990), this effect would result in a negative relationship between mutation rate and N_e, assuming that N_e is correlated with N. Second, the mutation-drift barrier hypothesis (Lynch 2011; Sung et al. 2012) proposes that selection against higher mutation rates is likely to be less effective relative to drift in species with small N_e, leading to higher mutation rates in species with lower N_e values.

In broad-brush comparisons among taxa, there is indeed evidence for such a relationship—for example, figure 3 of Krasovec et al. (2020). A major source of this relationship is, however, the difference between unicellular and multicellular organisms. Within multicellular organisms, a relation between N_e and/or body size and mutation rate is less apparent, especially if phylogenetic corrections are applied—see Table 1 of Krasovec et al. (2018) and figure 3 of Yoder and Tiley (2021). For example, the mean per basepair mutation rates in D. melanogaster and H. sapiens are approximately 5 × 10^–9 and 7 × 10^–9, respectively (Assaf et al. 2017; Halldorsson et al. 2019), despite humans having a generation time of approximately 25 years (Amster et al. 2020) and D. melanogaster of 0.07 years (Lange et al. 2022), a 357-fold difference. The mean silent site diversities for these species are approximately 0.001 and 0.01 (fig. 2 of Buffalo 2021), giving only a 7-fold difference in their estimated N_e values. Within unicellular eukaryotes, the marine coccolithospore Emiliania huxleyi (now renamed Gephyrocapsa huxleyi: Filatov et al. 2021) has a mean silent site diversity of only 0.006, but its mutation rate per cell division of 5.6 × 10^–10 is within the typical range for such organisms (Krasovec et al. 2020). These data therefore suggest that LP cannot be fully explained on this basis alone.

Effects of Demography

Skewed Distributions of Offspring Numbers

Another possible contributor to LP is the effect on N_e of the variance in the distribution of progeny numbers per individual, such that nonrandom variation in offspring numbers can considerably reduce N_e compared with the value expected under a Poisson distribution of offspring number in a discrete-generation model (Wright 1938; Charlesworth and Charlesworth 2010, Chapter 5). A high variance that causes a reduction in N_e is often associated with organisms with extremely large census sizes (e.g., viruses), and a low variance with those with smaller census sizes (e.g., mammals). More specifically, the life history traits of long-lived/low-fecundity animal species compared to short-lived/high-fecundity species (i.e., those characterized by “sweepstakes reproduction”; Hedgecock 1994) are strong predictors of observed genetic diversity (Romiguier et al. 2014; Chen et al. 2017). Such sweepstakes reproductive behavior is thought to be common in many plants, marine organisms, and pathogens (Tellier and Lemaire 2014; Irwin et al. 2016); there are, however, relatively few reliable direct measurements (but see Vahey and Fletcher 2019).

There is a large body of mathematical theory describing coalescent models that depart from the standard Kingman coalescent, which assumes at most one coalescent event per generation between pairs of alleles ancestral to those in the initial sample (Charlesworth and Charlesworth 2010, Chapter 5). These models allow for varying degrees of the skew in the distribution of successful offspring per adult individual, which can cause the simultaneous coalescence of multiple lineages (reviewed in Wakeley 2013; Tellier and Lemaire 2014; Irwin et al. 2016; and see fig. 1 of Matuszewski et al. 2018 for an illustration). Such multiple merger processes mean that a few individuals may contribute an appreciable fraction of offspring to the next generation, so that N_e can be strongly constrained even when N becomes very large; indeed, N_e need not scale linearly with N (Huillet and Möhle 2011; Matuszewski et al. 2018). Accordingly, small values of N_e/N are often taken as potential evidence of a high variance and skewed distribution of offspring number, with the Pacific oyster and Atlantic cod both having estimated N_e/N values of approximately ∼10^–5 (Hedgecock 1994; Árnason 2004).

An important caveat is that multiple merger coalescent events can also result from selective sweeps (Durrett and Schweinsberg 2005). Accordingly, differentiating neutral progeny skew from skews caused by sweeps at multiple sites across the genome, or rapid population expansion (see below), presents a challenge (Sackman et al. 2019; Harris and Jensen 2020; Eldon 2020). Despite the fact that these processes are all expected to cause an excess of low frequency variants compared with the neutral equilibrium expectation under mutation and drift (Eldon and Wakeley 2006; Birkner et al. 2013; Blath et al. 2016), recent theoretical work and developments in statistical methods have suggested ways of differentiating between them using patterns of sequence variation (Eldon et al. 2015; Matuszewski et al. 2018; Sackman et al. 2019; Morales-Arce et al. 2020); for example, by first estimating the degree of progeny skew in putatively neutral genomic regions and utilizing that correction when evaluating functional regions for evidence of selection.

Although the large-scale data needed to fully assess this explanation of LP across the tree of life are currently lacking and are difficult to collect accurately, a finding that organisms with very large N values are often characterized by a large variance in, and a skewed distribution of, successful offspring number compared to small N species would suggest that these are significant factors contributing to LP. However, the relatively low diversities seen in highly abundant unicellular eukaryotes such as Gephyrocapsa species (Filatov et al. 2021), which reproduce by binary fission and occasional sexual matings, are unlikely to be explained by skewed offspring distributions.

Metapopulation Processes (Extinction and Recolonization of Local Populations)

At first sight, population structure seems an unlikely candidate for resolving LP. In the most familiar models of spatially separated local populations (demes) connected by gene flow, such as the island and stepping stone models, limited gene flow causes π measured by sampling from the metapopulation as a whole (π_T) to greatly exceed the value expected for a panmictic population with the same total number of breeding individuals (π_P), even though the mean π for alleles sampled within demes (π_S) is equal to π_P for the equivalent panmictic population (see Charlesworth and Charlesworth 2010, Chapter 7, for details). These differences reflect differences in the mean coalescent times for pairs of alleles sampled in different ways with respect to their population of origin. Indeed, one caveat concerning the interpretation of comparative studies of diversity estimates is that different sampling strategies across local populations have often been used for different species (e.g., Romiguier et al. 2014), so that differences in the extent of differentiation among populations are confounded with effects of total species abundance.

However, variance among the contributions from different demes can completely change the above conclusion about the effects of population structure, because it leads to a substantial reduction in both π_T and π_S below π_P (Whitlock and Barton 1997). Local extinction and recolonization of demes has an especially powerful effect of this kind; in the extreme case when a single ancestral population is the source of all extant populations, and there has been no gene flow among its descendants, the current diversity in the metapopulation simply reflects the diversity accumulated among the different lineages during the history of this single population. Analyses of equilibrium models of local deme extinction and recolonization show that both π_T and π_S are greatly reduced when the rates of extinction of local demes exceeds the rate of gene flow caused by migration; the level of differentiation between demes, as measured by F_ST = (π_T − π_S)/π_T, can either be increased or decreased by high rates of extinction and recolonization, depending on the number of individuals that found a new deme and on whether or not they come from single or multiple ancestral demes (the propagule pool model versus the migrant pool model; Slatkin 1977).

High values of F_ST with high rates of turnover are expected under the propagule pool model, or the migrant pool model with a small number of founders, contrasting with low values under the migrant pool model with a large number of founders (Slatkin 1977; Pannell and Charlesworth 1999). With sufficiently high rates of turnover of demes relative to the migration rate, the reduction in π_T and π_S (relative to the case with migration rather than turnover) can be of the order of 10³ or more, with π_S generally being more strongly affected than π_T, but without necessarily causing very high values of F_ST under the migrant-pool model with a large number of founders of a new deme (see figs. 1 and 2 of Pannell and Charlesworth 1999). The objection of Buffalo (2021) to population subdivision as a contributor to LP (that it requires a very high value of F_ST) appears to be based on models that ignore extinction and recolonization.

A high rate of population turnover can, therefore, sometimes cause much lower neutral diversity than when demes are connected purely by migration of individuals, especially for π_S. This raises the question of whether the signatures of such turnover are commonly observed. One potentially informative statistic in this regard is the site frequency spectrum (SFS) (Wakeley and Alicar 2001; Pannell 2003). With a high rate of extinction relative to migration, the case most favorable for a large reduction in diversity, the SFS will be distorted in favor of intermediate-frequency variants. With a migrant-pool model, this can be seen even in samples from a single deme (Wakeley and Alicar 2001; fig. 4), and with a propagule-pool model in samples from multiple demes (Pannell 2003, Table 3a). However, such a signature in genome-wide SNP data, reflecting long internal branches of gene trees produced by the coalescent process, is rarely reported. An exception is the case of Gephyrocapsa huxleyi discussed above (Filatov 2019), suggesting that populations of this species may undergo sudden local extinctions followed by recolonization from surviving populations.

At first sight, this suggests that population turnover can be rejected as a general explanation for relatively low diversity levels, but we should emphasize that it is rarely included in the demographic models used to make inferences about population history, which usually involve only population size changes and gene flow due to migration. In addition, the standard models of extinction and colonization are highly simplified, and it is possible that the development of more realistic models would result in better fits to empirical data.

Population Size Changes

While a role for changing/fluctuating population sizes is often mentioned in the context of LP (e.g., Romiguier et al. 2014; Coop 2016; Mackintosh et al. 2019; Buffalo 2021), it has received less attention than factors such as the effects of selection at linked sites, and is generally confined to a brief mention of “other possible contributors” rather than being given a quantitative treatment. Here we make the case that this process is probably underappreciated; in particular, we investigate the possibility that the very large population sizes of many contemporary species reflect expansions from much smaller ancestral population sizes, which were perhaps associated with speciation events.

There are three possible ways in which population size changes might help to explain LP. The first is seasonal variation in population size, seen in temperate zone species of insects with short generation times, such as many Drosophila species. It has long been known that N_e under such cyclical patterns of population size is approximately equal to the harmonic mean of the population size in each generation, and is thus closer to the smallest of the population sizes than to the largest (Wright 1938). For example, D. melanogaster in northern latitudes is known to overwinter as nonreproductive adults, and population numbers increase enormously during spring and summer, followed by a large reduction in numbers with the onset of winter (Ives and Band 1986). The genetic consequences of these changes are detected from reduced frequencies of allelism between recessive lethal mutations in samples from local populations; as the populations expand, gene flow between them reduces local inbreeding (Ives and Band 1986).

A coalescent model of the effects of this process on neutral diversity suggests that only a modest increase in mean π for a single deme (π_S) is likely to occur during the period of expansion, which occupies only a few generations, and that the mean π over demes (π_T) is almost constant over time (Shpak et al. 2010). The values of π_S and π_T can be approximated by those for an island model with a very large number of demes (d), with the effective population size N_e of a deme given by the harmonic mean of the population size over the annual cycle, and an effective migration rate m_e by the sum of the migration rates for each generation within the cycle: π_S ≈ 4N_edu and π_T ≈ π_S (1 + 1/[4N_em_e]) (Shpak et al. 2010). Thus, a seasonal cycle of population size that reduces N_e for individual demes to a very low level could help to reduce diversity well below that suggested by the peak census number of individuals. As an example, a recent study of SNP frequency changes in the Rhode Island population of D. melanogaster indicated a local N_e of approximately 10,000 (Lange et al. 2022). Similar estimates were obtained by Wright et al. (1942) for D. pseudoobscura in California, on the basis of the change in the lethal allelism rate with distance between samples, whereas up to 10-fold larger estimates were obtained for the Raleigh, North Carolina, population by Mukai and Yamaguchi (1974) using lethal allelism rates and estimates of the frequency of lethal mutations (for an explanation of these methods, see Charlesworth and Charlesworth 2010, pp.356–359). It is also likely that D. melanogaster experiences seasonal cycles in its ancestral habitat, the forests of south-east Africa (Sprengelmeyer et al. 2020), and this may apply to many other organisms in these habitats. The population genetic consequences of this process, and the extent to which they match observed population statistics, deserve more detailed investigation. However, it clearly cannot explain cases of unexpectedly low diversity in species that are not subject to seasonal cycles of numbers.

A second possibility is that contemporary populations with moderate levels of diversity have descended from much larger populations with high diversity levels and have lost diversity by genetic drift; the time-scale for such a loss is of the order of the post-reduction N_e and can therefore be relatively short in terms of evolutionary time if the new N_e is sufficiently small. A recent and large reduction in population size should leave traces in terms of a SFS skewed to intermediate and high frequency derived variants as well as increased LD (Charlesworth and Charlesworth 2010, Chapters 6 and 8). Several examples of such signals have been reported (e.g., for out-of-Africa human and D. melanogaster populations: Nielsen et al. 2017; Hutter et al. 2007). In these cases, however, samples from close to the presumed center of origin of the species show no such signatures and have much higher π values; if anything, they show evidence for recent population growth (Arguello et al. 2019). Recent reductions in population size cannot, therefore, provide a general resolution of LP, although they are consistent with low diversity in many individual instances, such as the unusually low π of the cabbage white butterfly Pieris brassicae pest species compared with other European butterfly species (Mackintosh et al. 2019).

The third possibility is that many contemporary populations have expanded from much smaller ancestral states, perhaps associated with small population sizes at the time of speciation, but that the timescale of expansion is such that π is often far from its (very high) equilibrium value, as has been suggested previously but without a quantitative analysis (e.g., Buffalo 2021). The time-scale for changes in neutral diversity has previously been studied within the framework of the infinite sites model (Kimura 1971). Under this model, it is well-known that the approach to a new equilibrium value of π after a step change in population size has a time-scale of the order of N_e1 generations, where N_e1 is the new effective population size (Malécot 1969, p.40). More formally, if diversity at time t after the size change is π(t), when looking forward in time we have π(t)/(4N_e1u) ≈ 1 − (1 – π(0)/[4N_e1u]) exp(–t/2N_e1), where t is the time since the change in population size, π(0) is the initial diversity, and 4N_e1u is the final diversity. An increase in π to its final value may therefore take a considerable time, of the order of 2N_e1 generations, so that the current π value may often not reflect the current population size. Perhaps counter-intuitively, the time-scale does not depend on the mutation rate.

This result is, however, of limited use when considering population sizes that are so large that 4N_e1u is >> 0.05, the threshold proposed for a “hyperdiverse” species (Cutter et al. 2013). In such cases, the assumptions of the infinite sites model break down, and π is no longer proportional to N_e, as was discussed above in the section on mutational bias. This raises the question of whether the dependence of the time to equilibration of diversity on population size extends to situations where the infinite sites model is invalid. As a simple alternative model, we use the case of four nucleotides at a given site, with equal mutation rates u per generation between each possible pair of nucleotides (the Jukes–Cantor model). This was described above in the section on mutational bias, where it was shown that it provides an upper bound to equilibrium diversity compared with more realistic models. It can therefore be regarded as a worst-case scenario for explaining LP in terms of demographic factors. We will consider the simple case of a population size change in a panmictic population, where the effective population size at the present-day is N_e1, with a step change from an initial value of N_e0 = RN_e1 at time T₀ in the past, measuring time in units of the present-day coalescent time, 2N_e1. This model also allows the fastest rate of approach to the new equilibrium, compared with more gradual alternatives. The algebraic details are given in the Appendix.

Equation (A3) shows that, under these conditions, π approaches its equilibrium value of ¾ at approximately the same rate as under the infinite sites model, allowing for the difference in equilibrium π values between the two models. As an example of the slow rate of approach to equilibrium, if the step change had involved a change in N_e to 10⁹ from a much lower value that is compatible with the modest π values seen in most species, the time for π to approach ¾ would be of the order of 10⁹ generations. Extremely long times are also needed to approach more realistic π values from much smaller initial values. For example, with T₀ = 0.05 (5 × 10⁸ generations with N_e1 = 10⁹, or 5 million years with ten generations a year), Equation (A3) gives π = 0.036, a value consistent with the mean silent site diversities for many invertebrate species (Leffler et al. 2012; Buffalo 2021). In contrast, sites subject to purifying selection, such as nonsynonymous sites, are expected to approach their equilibrium diversity values much faster than neutral sites, so that population expansions can result in higher ratios of nonsynonymous to silent diversities (Brandvain and Wright 2016).

These considerations show that current π values can be far lower than expected on the basis of the contemporary population size, if the population has undergone a large increase in numbers. The human population is an obvious example, where the current 7.9 billion individuals far exceeds the N_e value of approximately 25,000 suggested by the mean silent site diversity of African populations and the current estimate of the human mutation rate (Yu et al. 2002; Halldorsson et al. 2019). Evidence for an expansion of the human population size from a few thousand individuals living in Africa, starting around 45,000 to 60,000 years ago, is reviewed by Henn et al. (2012). With a generation time of 25 years (see the above discussion of mutation rates), an expansion time of 50,000 years ago corresponds to 2,000 generations. In this case, an exponential growth model is probably more appropriate than a step-change; this case was analyzed by Slatkin and Hudson (1991). With initial and final effective population sizes of N_e0 = 25,000 and N_e1 = 7.9 × 10⁹, respectively, the population growth rate is r = ln(7.9 × 10⁹/2.5 × 10⁴) = 6.33 × 10^–3. From Equation (5) of Slatkin and Hudson (1991), the probability of no coalescence over 2000 generations for a pair of alleles sampled at the present day is exp{–[exp(2000r)–1]/2N_e1r} ≈ 1. It follows that the net coalescent time is equal to 52,000 generations, only 4% longer than if the population size had remained unchanged.

For many other species, fits of population genomic data to demographic models often suggest population expansions, with evidence for population bottlenecks in some cases as well (e.g., Peart et al. 2019), so that expansions may well be the rule rather than the exception (but see the caveats discussed by Johri et al. 2020, 2021). The above calculations show that populations which have expanded from much smaller numbers in even the quite distant past may still be far from their very high equilibrium diversities. This scenario thus seems an excellent candidate for resolving LP.

Effects of Selection

Weak Selection on Silent Sites

We now consider ways in which departures from strict selective neutrality can help to resolve LP. A first potentially important contributor to this category is the Nearly Neutral Theory (Ohta 1973; Ohta and Gillespie 1996). The value of π when there is purifying selection against certain types of mutation at a site is affected by the product of N_e and the magnitude s of the selection coefficient against homozygotes for such mutations, as well as by the scaled mutation rate 4N_eu. While π at sites subject to purifying selection can increase with N_e if there is mutational bias towards deleterious mutations and N_es is < 0.5, it then declines to a value corresponding to the deterministic value under mutation-selection balance for N_es > 4, assuming semi-dominance of fitness effects (McVean and Charlesworth 1999, Equation 15). If weak selection is common, modest differences in mean π between species could correspond to differences in the extent to which silent sites experience the direct effects of purifying selection.

The best studied class of sites in this category are synonymous sites, especially 4-fold degenerate sites, for which there exists considerable evidence of weak selection effects in taxa with relatively large N_e, such as Drosophila, in part at least due to selection on codon usage (Choi and Aquadro 2016; Jackson et al. 2017; Canale et al. 2018; Machado et al. 2020). However, there are other classes of site, such as the 5´regions of short introns, which are presumed to be free from such selection and have substantially higher π values (Jackson et al. 2017, Machado et al. 2020; Jackson and Charlesworth 2021). These may be subject to biased gene conversion in favor of GC basepairs (gBGC), which shares the same relation with N_e as selection. As we discussed earlier, however, gBGC alone cannot impose a limit on the diversity achievable in a very large population; the same argument applies to selection on codon usage, which also tends to favor GC basepairs in many species (Charlesworth and Charlesworth 2010, p.532). To resolve LP in terms of the Nearly Neutral Theory alone, one would have to postulate that most nucleotide sites in large N_e species are subject to a strength of selection that is at least an order of magnitude larger than the mutation rate, causing variability to be controlled by the balance between mutation and selection rather than by the interplay of genetic drift and mutation.

Effects of Selection on Linked Sites (Hitchhiking): General Considerations

As the quotation from Maynard Smith and Haigh (1974) at the beginning of this paper shows, the earliest attempt to resolve LP invoked frequent effects of selective sweeps on neutral diversity at sites linked to the target of selection. This idea was revived by Kaplan et al. (1989) and Gillespie (2001, 2002) using a different mathematical framework, and has been advocated by several recent authors (e.g., Corbett-Detig et al. 2015; Roberts 2015). It has even led to recent suggestions that the effects of hitchhiking, involving selective sweeps of beneficial mutations and/or background selection (BGS) caused by deleterious mutations (Charlesworth et al. 1993), dominate over the effects of genetic drift to such an extent that π is determined by the rate of coalescent events caused by selection rather than by drift (Kern and Hahn 2018; but see the response by Jensen et al. 2019). If this hypothesis were correct, it would easily explain why π is not strongly correlated with N.

However, before discussing how the two different types of hitchhiking may influence the relation between π and N, it is important to emphasize that expectations are very different for species with very low natural levels of genetic recombination versus species where recombination occurs regularly each generation as a result of sexual reproduction involving unrelated individuals. Organisms that fall into the first category include bacteria, where genetic recombination usually involves only exchanges of small stretches of genetic material (Price and Arkin 2015), unicellular eukaryotes such as Chlamydomonas with extended periods of reproduction by mitotic divisions in between occasional meioses (Hasan and Ness 2020), and asexual or highly self-fertilizing multicellular species (Cutter and Payseur 2013). It can hardly be doubted that hitchhiking effects play a major role in shaping patterns of diversity in organisms where recombination events are rare across the whole genome or are genetically ineffective, as in the case of highly homozygous inbred populations (Cutter and Payseur 2013; Barrett et al. 2014), although there have been few detailed theoretical investigations—see Charlesworth et al. (1993) and Barrett et al. (2014) for self-fertilizing species, Agrawal and Hartfield (2016) for partially asexual diploid organisms, and Price and Arkin (2015) for bacteria. The latter study showed that N_e in bacteria can be reduced by several orders of magnitude by BGS caused by large numbers of weakly selected mutations, despite their relatively small genomes (Price and Arkin 2015). Much more could be done to quantify theoretical predictions about patterns and levels of diversity in such organisms, and to relate these predictions to observations, although this task is made difficult by the effects of life-styles that often involve local colonizations and extinctions, and rapid expansions of semi-clonal populations (Barrett et al. 2014; Price and Arkin 2015; Bobay and Ochman 2018).

Low recombination regions of the genomes of outbreeding, sexually reproducing species are also expected to exhibit severe effects of hitchhiking, and the contrast in their levels and patterns of genetic diversity with regions that experience ‘normal’ rates of recombination has long been known (Aguadé et al. 1989a, 1989b), with much supporting evidence having been collected subsequently (Charlesworth and Jensen 2021). For this reason, we will focus on the consequences of hitchhiking for coalescent times in genomic regions where recombination is reasonably frequent.

As we discuss below, this contrast between low and high recombination genomic regions, and the widespread observation of a correlation between π and the local rate of crossing over within a species (Begun and Aquadro 1992; Cutter and Payseur 2013; Corbett-Detig et al. 2015; Charlesworth and Jensen 2021), do not help to resolve LP for genomic regions with high rates of recombination, although they provide strong evidence that hitchhiking has major effects on π. Furthermore, nucleotide sites vary in the extent to which they are likely to be subjected to hitchhiking; even putatively neutral sites in coding sequences, and in functionally important regulatory sites, are surrounded by sites that are subject to selection. However, neutral sites that are far from such functionally important sequences in organisms with large genomes and long intergenic sequences (like mammals) are likely to be much less affected by hitchhiking than sites that are close to them. The tendency for π to increase with distance from functionally important sequences such as exons and conserved noncoding sequences in such species has been well-documented (Corbett-Detig et al. 2015; Booker and Keightley 2018). Different conclusions about the importance of hitchhiking are likely to be drawn from different sources of information about π, for example, synonymous sites (as in Romiguier et al. 2014) versus RAD sequences from more or less random parts of the genome (as in Peart et al. 2019).

Background Selection

Here we consider the possible contribution to LP from what is probably the most prevalent form of genetic hitchhiking, BGS. Much progress has been made in studying the effects of the recurrent elimination of deleterious mutations by purifying selection on levels and patterns of variation at linked neutral or nearly neutral sites (Comeron 2017; Charlesworth and Jensen 2021). The simplest BGS model that assumes mutation-selection balance at the underlying sites is likely to be valid for regions with sufficiently high recombination rates that Hill-Robertson interference among the sites subject to selection is absent (Charlesworth and Jensen 2021). Under a number of other assumptions (random mating, constant population size), this model predicts the mean pairwise coalescence time at a neutral site surrounded by m linked sites experiencing purifying selection (Hudson and Kaplan 1995; Nordborg et al. 1996). For autosomal inheritance, the quantity B, defined as the ratio of the mean coalescent time between a pair of alleles at a focal neutral site (T) to its value in the absence of selection (T_n), is given by:

$$B={\displaystyle \frac{T}{T_n}\approx \exp -{\displaystyle \sum _{i=1}^m}{\displaystyle \frac{u_i}{{[1+r_i(1-t_i)/t_i]}^2}}}$$ (1)

where u_i is the mutation rate to deleterious alleles at the ith selected nucleotide site, t_i is the selection coefficient against heterozygous carriers of mutations at this site, and r_i is its recombination frequency with the focal site.

When applying this equation, it is implicitly assumed that mutations are to be ignored if their selection coefficients are so small that the assumption of mutation-selection balance is violated, and genetic drift affects the frequencies of deleterious alleles. This is a somewhat arbitrary procedure, with some authors using N_ent ≤ 1 as the threshold (Comeron 2014) and others using N_ent ≤ 5 (Charlesworth 2012b), where N_en is the effective population size in the absence of the effects of selection at other sites. Under the infinite sites model, B is equal to the ratio of the corresponding expected π values. However, with θ = 2BT₀u > 0.05, π does not increase proportionally with BT₀, in line with the earlier discussion of the effects of the mutational process.

A very useful approximation when considering the effects of mutations distributed over a single chromosome is to approximate B for sites in the center of the chromosome by:

$$B_M\approx \exp -{\displaystyle \frac{U}{L}}$$ (2)

where U is the diploid deleterious mutation rate for the chromosome in question (ignoring mutations with selection coefficients that fall beneath the chosen threshold value), and L is the map length of the chromosome in Morgans (Hudson and Kaplan 1995; Nordborg et al. 1996; Charlesworth 2012b). There are, of course, qualifications about the accuracy of this approximation, as it ignores the effects of gene conversion (which are important over short distances: Campos and Charlesworth 2019) and assumes a linear relation between recombination frequency and map distance, that is, multiple crossovers are ignored, overestimating the effect of crossing over.

Equation (2) serves as a useful guide to what might be expected for the mean diversity levels across the recombining portions of chromosomes, and it seems to perform well against more exact models in predicting mean coalescence times (Charlesworth 2012b). It has the useful property of showing that the ratio of the density of deleterious mutations per unit map length is a major determinant of π, independently of the details of the distribution of fitness effects of mutations and their dominance coefficients, providing that they are not completely recessive. However, it neglects the contribution from deleterious variants on other chromosomes (Santiago and Caballero 1998; Charlesworth 2012a)—this could outweigh the within-chromosome effect in organisms with many chromosomes, such as most vertebrates, where U for an individual chromosome is << L. But it is not likely to cause a major reduction in coalescence time, since the relevant B value is approximately exp (– 4 [1–1/n] $U_T\overline{t}$), where $\overline{t}$ is the mean selection coefficient against heterozygotes, U_T is the total per genome deleterious mutation rate, and n is the number of chromosomes (Charlesworth 2012a, Equation 4). Unless U_T is much greater than one, this quantity is unlikely to exceed a few per cent, given current estimates of $\overline{t}$ for nonsynonymous mutations in Drosophila and humans that are substantially less than 0.01 (Charlesworth 2015; Kim et al. 2017).

The generally negative correlation between N and genome size implies larger fractions of functional sites in the genomes of large N species compared with those with small N (Lynch and Conery 2003; Charlesworth and Barton 2004), so that U/L is likely to be larger in large N species, especially as L and N are negatively correlated across metazoan species (Buffalo 2021), dampening any effect of larger N on neutral diversity. However, caution needs to be exercised in applying this result, since U in Equation (2) is inversely related to the number of chromosomes. Organisms like butterflies or mammals, with relatively large numbers of chromosomes, are thus likely to have much weaker effects of BGS than organisms like Drosophila species, with only five chromosomes at most, especially as the rate of crossing over per basepair tends to be higher on smaller chromosomes, due to the need to have one chiasma per bivalent in order to avoid nondisjunction at division I of meiosis (Hughes et al. 2018). Accordingly, π is found to be negatively correlated with chromosome size in organisms with large differences in chromosome size within the same genome, such as birds (e.g., Huynh et al. 2010; Manthey et al. 2015). Similarly, chromosome numbers in species of European butterflies are positively correlated with π, although the effect is too large to be explained by BGS alone, and is heavily influenced by just two species with unusually low chromosome numbers (Mackintosh et al. 2019).

But can BGS explain why even species with apparently very large N have modest diversity levels? Light is shed on this question by two analyses of the effects of BGS across the genome of D. melanogaster, which used different assumptions about the distribution of selection coefficients for mutations in coding and noncoding sequences but came to similar conclusions. These studies both found that BGS has a substantial influence on the level of diversity, with the mean π outside low recombination genomic regions having mean B values of approximately 0.5 for autosomes and 0.7 for the X chromosome (Charlesworth 2012b; Comeron 2014). Both relatively strongly selected sites, such as nonsynonymous sites and highly conserved noncoding sequences, as well as much more weakly selected noncoding sequences, were taken into account. As expected, the effect of BGS is modulated by recombination, with higher B values in higher recombination rate regions; accordingly, BGS appears to explain a considerable proportion of the variance in π across the genome (Comeron 2014, 2017). Overall, however, the results of the two studies imply that π in regions of the D. melanogaster genome with significant rates of crossing over would be increased by only a factor of two over the values observed in current populations, if BGS were to cease to operate at its current level of effectiveness.

It seems unlikely that this estimate would be greatly changed if the population size were increased to such an extent that all deleterious mutations behaved deterministically. Charlesworth (2012b, p.232) showed that the fraction of the strongly selected deleterious mutations that fell below the threshold of N_ent ≤ 5 was so small that B for such mutations was barely affected by ignoring them; on the other hand, 65% of the weakly selected mutations were ignored by this procedure. Including the contribution from these mutations would have the effect of increasing the contribution to U associated with such mutations by a factor of 1/0.35 ≈ 2.86. Using Equation (2) and applying this modification to the results in Table 2 of Charlesworth (2012b), the contributions of weakly selected noncoding sequence mutations to B then become 0.606 for autosomes and 0.730 for the X chromosome. Since B values are multiplicative, use of the corresponding strongly selected Bs in Table 2 of Charlesworth (2012b) (0.665 and 0.775 for autosome and X, respectively), gives final Bs of approximately 0.403 (autosomes) and 0.566 (X), as opposed to 0.558 and 0.695 after removing very weakly selected mutations. Thus, making the population size effectively infinite only slightly affects mean π in recombining regions of the D. melanogaster genome. It thus seems unlikely that BGS by itself provides a resolution of LP.

Effects of Recurrent Selective Sweeps

Results from a diversity of organisms have suggested that, although BGS often significantly influences observed levels of variation, it is unlikely to be the sole factor (Booker et al. 2017). For example, although 60% of the variance in π at noncoding sites in the D. melanogaster genome can be explained by BGS (Comeron 2017), BGS cannot explain the negative relationship between silent site diversity and nonsynonymous site divergence (Campos et al. 2017). This leaves hitchhiking caused by selective sweeps of beneficial mutations as the remaining candidate for resolving LP. Because the efficacy of selection increases with effective population size, the effects of selective sweeps are likely to become stronger with larger N, other things being equal. In addition, the effect of the relation between N and the fraction of genome subject to selection, which was discussed above in relation to BGS, is also likely to apply to sweeps, and to enhance their effects on diversity at linked sites. However, the increasing interference between beneficial mutations that occur with increasing N (Weissman and Barton 2012) may offset this effect by reducing their net rate of fixation (e.g., Johri et al. 2022a), at least as far as “hard” sweeps that rely on new/rare mutations are concerned.

The commonly used theory for analyzing these effects was developed by Kaplan et al. (1989) and Wiehe and Stephan (1993). Assume that the reduction in mean coalescence time (relative to the purely neutral value, 2N_en) caused by a single selective sweep is denoted by Δ. If these sweeps are occurring at rate ω_j per generation at a given site j, the rate of coalescence at a focal neutral site caused by sweeps is Σ_j ω_j Δ_j, in the absence of interference between selected sites. Together with a BGS effect of B on the focal site (see the previous section), the ratio of the expected value of the coalescent time at the focal site to the purely neutral value is:

$${\displaystyle \frac{T}{T_n}\approx {\displaystyle \frac{1}{B^{-1}+C^{-1}}}}$$ (3)

where C is the mean time to coalescence caused by sweeps, expressed relative to 2N_en: C = 1/(2N_enΣ_j ω_j Δ_j).

This formulation has been utilized in several analyses of the relationships between π and recombination rate, nonsynonymous substitutions, and/or sequence divergence, each using somewhat different formulae for Δ_j (e.g., Wiehe and Stephan 1993; Jensen et al. 2008; Corbett-Detig et al. 2015; Elyashiv et al. 2016; Campos et al. 2017; Buffalo 2021). Recent simulation and analytical results have shown that Equation (3) somewhat underestimates the effects of sweeps (Charlesworth 2020; Hartfield and Bataillon 2020), but it serves as a useful approximate guide as to what to expect.

The main difficulty in using Equation (3) in connection with LP is that, while there are several methods for estimating ω_j from population genomic data, such as the DFE-alpha approach of Eyre-Walker and Keightley (2009), it is more difficult to find ways of estimating Δ_j independently of the effects of sweeps on diversity, because it depends on both the strength of selection on favorable mutations and on their frequency of recombination with the focal site. This difficulty is brought out by the widely used formula for a hard selective sweep caused by the spread of a single new mutation, Δ_j ≈ $(2N_e{s}_{aj}{)}^{-4r_j/s_{aj}}$ (Barton 2000), where s_aj is the selection coefficient for homozygotes for a favorable mutation at site j (assuming semi-dominance) and r_j is the frequency of recombination between the focal site and selected site j. While r_j can be estimated with some confidence from genetic data, estimates of the selection coefficients for favorable mutations are far harder to obtain, and have given somewhat disparate results even when applied to datasets on African D. melanogaster populations, reflecting differences in the aspects of the data that are used for estimation (e.g., Jensen et al. 2008; Elyashiv et al. 2016; Campos et al. 2017).

Overall, these approaches suggest that the mean pairwise coalescent time at synonymous sites in normally recombining regions in organisms like Drosophila with compact genomes is indeed substantially reduced below its purely neutral value by the joint effects of selective sweeps and BGS, the maximum current estimate for autosomes being approximately 80% (Elyashiv et al. 2016), about 35% more than the above estimate for BGS alone. This estimate would imply that T_n, the purely neutral value of the coalescent time, is about 5-fold larger than the value indicated by current diversity levels; this is far smaller than the factor of 100 or more suggested by the probable current population size of D. melanogaster (Karasov et al. 2010; Buffalo 2021), and so is insufficient to resolve LP for this species.

However, our ability to accurately estimate the parameters of hypothesized recurrent selective sweeps, and to differentiate them from the effects generated by other evolutionary processes that act continuously, is still limited (Johri et al. 2022b, c), so that this conclusion should be treated with caution. For example, Johri et al. (2020) found that all the variation and divergence statistics that were examined in a set of approximately 100 autosomal single-exon genes from a Zambian population of D. melanogaster could be fitted by a model including only population size change, purifying selection, and BGS. Nevertheless, the inclusion of infrequent and weakly selected favorable mutations in the model also gave predictions consistent with the data, although this did not improve the fit, whereas the addition of frequent, strongly selected beneficial mutations resulted in patterns of variation unlike those empirically observed.

An alternative perspective on the possible contribution to LP from recurrent sweeps that avoids the problem posed by incomplete knowledge of the relevant parameters is provided by the idealized model of a single neutral site surrounded by a continuum of sites subject to recurrent sweeps at a rate ω per basepair, introduced by Kaplan et al. (1989). This probably provides an upper limit to the effects of sweeps on diversity. Using the above formula for Δ for semi-dominant autosomal mutations, integration of the effects of sweeps over the region surrounding the neutral site yields the following formula for C (Weissman and Barton 2012; Coop 2016; Mackintosh et al. 2019; Buffalo 2021):

$$C^{-1}\approx \omega {\gamma }_a/[\ln ({\gamma }_a)r_c]$$ (4)

where γ_a = 2N_ens_a and r_c is the rate of recombination per basepair for the genomic region in question. For a given value of ω and r_c, the effects of sweeps on diversity are heavily influenced by the scaled strength of selection. Estimates of ω and r_c for the D. melanogaster example can be obtained as described in the Appendix, which give ω/r_c ≈ 0.032 for genes with the typical recombination rate for D. melanogaster. With γ_a = 100,000, 10,000 and 1,000, C^–1 ≈ 278, 34.7, and 4.6, respectively.

LP for this example could thus be explained in principle by sufficiently strong selection on favorable sweeps, with an approximately 40-fold reduction in coalescent time when γ_a = 10,000. Of course, if N_en were really 10⁸ instead of the value of N_e of approximately 10⁶ suggested by current diversity and mutation rate data, γ_a = 10,000 would correspond to a selection coefficient of only 2.5 × 10^–5, which is extremely small in absolute terms. There are, however, difficulties in reconciling this γ_a value with all the available evidence, especially the fact that γ_a = 10,000 is substantially larger than estimates from previous studies (Jensen et al. 2008; Elyashiv et al. 2016; Campos et al. 2017).

In addition, strongly selected recurrent sweeps are known to have major effects on the shapes of gene trees at linked neutral sites, causing much longer external branches relative to the total size of the tree compared with the neutral expectation with a constant population size, leading to an excess of low frequency derived variants (Braverman et al. 1995; Kim 2006; Jensen et al. 2008; Campos and Charlesworth 2019). For example, a γ_a of 10,000 with ω/r_c = 0.032 would produce a much larger skew towards low frequency variants than is seen for autosomal loci in the Rwandan population of D. melanogaster (see the Appendix for details). Thus, at first sight it seems extremely hard to resolve LP in the case of D. melanogaster simply by appealing to sweeps caused by strongly selected mutations. It is worth noting here that, in agreement with Weissman and Barton (2012) and Campos and Charlesworth (2019), ω/r_c = 0.032 is inconsistent with a major effect of interference between sweeps on the rate of sweeps outside genomic regions with low crossing over rates. If the value of ω/r_c in the absence of interference is denoted by Λ, Equation (7) of Weissman and Barton (2012) implies that Λ = (ω/r_c)/[1–2 (ω/r_c)] = 0.034, suggesting only a small reduction in ω due to interference between favorable mutations in this case. This result suggests that the approach is at least self-consistent.

Coop (2016) and Buffalo (2021) have also used Equation (3) to argue that, contrary to Corbett-Detig et al. (2015), hitchhiking effects are inadequate to resolve LP. A particularly telling argument is that, if sweeps are sufficiently powerful to cause most coalescent events in Equation (3), the mean coalescent time relative to the neutral value, as given by C in Equation (4), is proportional to the local recombination rate per basepair, r_c. A reanalysis of the data in Corbett-Detig et al. (2015) showed that this expectation is falsified (fig. 2 of Coop 2016).

There are, of course, several caveats concerning this conclusion about the importance of selective sweeps. First, the effects of demographic changes have been ignored in this analysis. It could be postulated, for example, that the Rwandan population of D. melanogaster has suffered a recent population bottleneck, which reduced the skew towards low frequency variants; the Zambian population exhibits a much greater skew of this kind, despite having a similar diversity value (Johri et al. 2020). It is clear, therefore, that demographic factors strongly affect patterns of variability for D. melanogaster populations in East-Central Africa. Second, the model assumes recurrent hard sweeps. With a very large N_en value, the possibility of “soft” sweeps, where selection acts on standing variation or on multiple recurrences of the same favorable mutation (Hermisson and Pennings 2005), is more likely than with the N_e values suggested by the diversity data. The relevance of soft versus hard sweeps to the interpretation of patterns of natural diversity is still a matter for debate (Garud et al. 2015; Hermisson and Pennings 2017; Harris et al. 2018; Garud et al. 2021; Johri et al. 2022a). However, soft sweeps reduce diversity at linked sites much less than do hard sweeps (Pennings and Hermisson 2006). It is thus hard to understand how they could help to resolve LP. On the other hand, they have less effect on the SFS than hard sweeps, and so may be more consistent with datasets that show relatively little skew towards rare variants. Little attention has been given to predicting the effects of recurrent soft sweeps on patterns of diversity at linked sites.

A related issue is the effect of selection on highly polygenic traits, where changes in trait means can result from minor shifts in allele frequencies (Stephan 2016). The possible effects of polygenic selection on diversity at neutral sites are not well understood. Santiago and Caballero (1998) derived results for N_e at neutral sites linked to sites under selection, using the infinitesimal model of quantitative inheritance. However, their main result (their Equation 8) is based on the infinitesimal model of quantitative trait variability (Visscher and Goddard 2019), assuming that the population is at equilibrium under mutation, selection and drift. This assumption is open to question (Hill 2010), especially if the population is responding to directional selection caused by a change in the trait’s optimal value. Simulation studies suggest that signatures of selective sweeps can be detected at linked neutral loci when polygenic traits are subject to directional selection, but these signatures are caused by the loci with relatively major effects on the trait (Thornton 2019).

As in the case of BGS, the fitness variance contributed by loci on other chromosomes should also be considered, which is likely to be the major contributor for species with many chromosomes. In this case, the classical result of Robertson (1961) for unlinked loci can be used (Santiago and Caballero 1995, 1998), giving a coalescent time relative to neutrality of approximately 1/(1 + 4V_A), where V_A is the genome-wide additive genetic variance for fitness measured relative to the population mean fitness. A recent analysis of data measuring fitness in wild populations of birds and mammals yielded an estimate of 0.18 for the mean of V_A across studies, with a 95% confidence interval of 0.09 to 0.30 (Bonnet et al. 2022). This would reduce neutral diversity at unlinked sites by between 16% and 55%. Even larger estimates of V_A for net fitness were inferred from experiments on whole third chromosomes of D. melanogaster extracted from a long-term laboratory population (Gardner et al. 2005). These estimates are more than an order of magnitude larger than the variances predicted purely by mutation-selection balance (Charlesworth 2015), so that other forms of selection must be contributing; their nature is unclear.

Closing Thoughts

As with many questions in population genetics, the discussion is less about which factor constitutes a uniquely important explanation of LP and more about the relative contributions of each factor—all the genetic, demographic, and selective processes that we have discussed are likely to be important to varying degrees, depending on the species and population in question. Multiple decades after its first introduction, LP is rather less paradoxical than was initially thought, but its resolution is rendered difficult by the many factors that probably play a role. Nonetheless, we emphasize the possibility that many populations have expanded from historically smaller numbers, and may simply be far from their relatively high equilibrium diversity values. This factor appears to be potentially capable of explaining a significant proportion of cases of LP, together with more modest contributions from mutational biases, biased gene conversion, correlations between mutation rate and population size, skewed distributions of offspring numbers, extinction/recolonization events, genetic hitchhiking effects, and weak selection on silent sites.

The consequences of several of these processes are, however, hard to distinguish on the basis of the available data, making their contributions difficult to assess. Demographic histories incorporating extinction/recolonization events are much less frequently evaluated in population genomic inference procedures than are simple population size change models and may thus be more frequent than currently believed. Similarly, the contributions of recurrent selective sweeps are confounded with other processes, due to overlapping expectations for the resulting patterns of variation. On the other hand, if further studies were to reveal that species with very large values of N are reliably characterized by a large variance and skew in the number of successful offspring relative to small N species, we could infer that such demographic factors play a significant role. Future theoretical work, and the parallel development of improved methods of inference from population genomic data, is still needed to evaluate the relative importance of the possible contributors to LP.

Appendix

The Effects of Population Size Change under the Jukes–Cantor Model

The Jukes–Cantor model (Jukes and Cantor 1969) implies that the probability that a pair of sequences are different in state at a given site, assuming that they are descended from a common ancestral sequence at time T in the past (measured in units of 2N_e generations) and that this sequence was in mutational equilibrium (with equal probabilities of ¼ of each nucleotide at a site), is given by:

$$d(T)={\displaystyle \frac{3}{4}\left[1-\exp \left(-{\displaystyle \frac{4\theta T}{3}}\right)\right]}$$ (A1)

where θ = 4N_e1u.

The expected nucleotide site diversity, π(T₀), when there has been a population size change that started at time T₀ is given by the integral of the product of d(T) and the probability of coalescence ϕ(T) at time T in the past. The probability density of coalescence at time T for 0 ≤ T ≤ T₀ is given by the standard exponential distribution formula, ϕ(T) = exp (–T). For T > T₀, the probability of no coalescence by time T₀ is exp (–T₀) and the subsequent rate of coalescence is R^–1, so that ϕ(T) = R⁻¹exp [–(R⁻¹T + T₀)]. Applying these results to Equation 1, we have:

$$\pi (T_0)={\displaystyle \frac{3}{4}[1\text{–}{R}^{-1}{e}^{-T_0}{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}{e}^{-\left(\frac{4\theta +3R^{-1}}{3}\right)T}\mathrm{d}T-{\displaystyle \underset{0}{\overset{T_0}{\int }}}{e}^{-\left(\frac{4\theta +3}{3}\right)T}\mathrm{d}T]}$$ (A2a)

After evaluating the integrals and simplifying, the following expression is obtained:

$$\pi (T_0)={\displaystyle \frac{3}{4(4\theta +3)}\left[4\theta +3e^{-\left(\frac{3\theta +3}{3}\right)T_0}\right]-{\displaystyle \frac{9}{4(4R\theta +3)}{e}^{-T_0}}}$$ (A2b)

As T₀ tends to infinity, π(T₀) approaches the equilibrium value for this model, π = 3θ/(4θ + 3) (Tajima 1996). In contrast, if the effective population size had remained constant at N_e0 and Rθ << 1, we would have π ≈ Rθ, the infinite sites value.

For 4θ >> 3 and 4Rθ << 3, the exponential term in brackets can be neglected compared with the other terms, so Equation 2b reduces to:

$$\pi (T_0)\approx {\displaystyle \frac{3}{4}(1-e^{-T_0})}$$ (A3)

Estimating the Effects of Selective Sweeps in D. melanogaster

An approximate estimate of the mean value of ω for nonsynonymous mutations in D. melanogaster can be obtained from sequence divergence data between related species, if we assume that the proportion of such mutations that have been fixed by positive selection is approximately 50%, as indicated by a number of different studies (e.g., Eyre-Walker and Keightley 2009; Campos et al. 2017). Table 1 of Campos et al. (2014) yields a mean value of 0.0367 for divergence per nonsynonymous site (K_A) from D. yakuba, for autosomal genes outside the low recombining regions, after subtracting within-species nonsynonymous site diversity. Synonymous site divergence (K_S) is 0.248, suggesting a divergence time of 0.5 × 0.248/(5 × 10^–9) = 2.48 × 10⁷ generations, assuming neutrality and using the mutation rate estimate of Assaf et al. (2017). In reality, there is evidence that synonymous sites are subject to some degree of purifying selection and are evolving at about approximately 87% of the rate for putatively neutral sites (Halligan and Keightley 2006, Table 1), so this estimate should probably be increased to 2.85 × 10⁷ generations.

Combining this divergence time with an estimate of 0.25 × 0.0367 for the number of positively selected substitutions per nonsynonymous site, we obtain ω = 3.22 × 10^–10 per generation, which is comparable with estimates obtained by other means (e.g., Elyashiv et al. 2016). Genetic data suggest a mean crossing over rate per basepair (r_c) for the autosomes of D. melanogaster of 1 × 10^–8 (Comeron et al. 2012; Miller et al. 2016), after correcting for the absence of crossing over in males. This yields ω/ r_c ≈ 0.032.

The Effects of Sweeps on the Site Frequency Spectrum at Linked Neutral Sites

The results of Braverman et al. (1995) on the effects of recurrent sweeps on the SFS were expressed in terms of Tajima’s D statistic (Tajima 1989). As has been pointed out several times (Schaeffer 2002; Langley et al. 2014; Becher et al. 2020), this statistic is not ideal for comparisons across different studies, since its value is affected by the sample size (n) and the length of sequence used. A statistic that, at least partially, avoids this problem is Δθ_w, defined as 1 − π/θ_w, where θ_w is Watterson’s diversity estimator (Becher et al. 2020), obtained from the number of segregating sites divided by the product of the number of basepairs and the sum of the harmonic series up to n − 1 (the constant a₁ below). Fortunately, the study of Braverman et al. (1995) involved generating gene trees at the neutral locus in question, and then throwing down 17 segregating sites onto the trees, with n = 50, which enables Δθ_w to be determined from D, as shown by the following argument.

Tajima’s D statistic is defined as follows (Equation 38 of Tajima 1989):

$$D={\displaystyle \frac{d}{\sqrt{(e_1-e_2)S+e_2{S}^2}}}$$ (A4)

where S is the observed number of segregating sites for the sequence in a sample of n genomes, k is the mean pairwise differences between sequences, and d is defined as:

$$d=k-S/a_1$$ (A5)

The constants a₁, a₂, e₁ and e₂ are defined by Equations (3), (4), (36) and (37) of (Tajima 1989) and depend only on n. With n = 50, a₁ = 4.47, a₂ = 1.64, e₁ = 0.0275, and e₂ = 0.00353.

If the number of basepairs in the sequence in question is m, then k = mπ, and S/a₁ = mθ_w.

Using Equation (A5), Equation (A4) can be rearranged to give:

$$D={\displaystyle \frac{-\mathrm{\Delta }{\theta }_w}{a_1\sqrt{[(e_1-e_2)/S]+e_2}}}$$ (A6)

This expression thus allows Δθ_w to be obtained from a given value of D, provided S is known. In the present case, with n = 50 and S = 17 we have Δθ_w ≈ − 0.32D. Figure 4 of Braverman et al. (1995) shows that, with γ_a (their α) equal to 10⁴ or 10⁵, –D would be > 1 for the above value of ω/ r_c (their Λ). We would thus expect a Δθ_w of at least 0.32 from recurrent sweeps with this intensity of selection. For synonymous site diversity at autosomal loci outside regions with low crossing over rates in a Rwandan population of D. melanogaster, Table 1 of Campos et al. (2014) gives mean values of π and θ_w of 0.0141 and 0.0147, each with 95% confidence bands of 0.0005, so that Δθ_w = 0.041, with an approximate upper bound to its 95% CI of 0.018; the corresponding value of D is –0.173, with confidence interval (–0.190, –0.157).

Data availability

No new data were generated for this study.