Metabolism is a major driver of hydrogen isotope fractionation recorded in tree‐ring glucose of Pinus nigra

Summary

• Stable isotope abundances convey valuable information about plant physiological processes and underlying environmental controls. Central gaps in our mechanistic understanding of hydrogen isotope abundances impede their widespread application within the plant and biogeosciences.

• To address these gaps, we analysed intramolecular deuterium abundances in glucose of Pinus nigra extracted from an annually resolved tree‐ring series (1961–1995).

• We found fractionation signals (i.e. temporal variability in deuterium abundance) at glucose H¹ and H² introduced by closely related metabolic processes. Regression analysis indicates that these signals (and thus metabolism) respond to drought and atmospheric CO₂ concentration beyond a response change point. They explain ≈ 60% of the whole‐molecule deuterium variability. Altered metabolism is associated with below‐average yet not exceptionally low growth.

• We propose the signals are introduced at the leaf level by changes in sucrose‐to‐starch carbon partitioning and anaplerotic carbon flux into the Calvin–Benson cycle. In conclusion, metabolism can be the main driver of hydrogen isotope variation in plant glucose.

Introduction

Stable isotope measurements of the most abundant chemical elements in plants (H and C) convey valuable information about plant physiological and environmental processes. Plant archives, such as tree rings, preserve this information over millennia enabling elucidation of physiological and environmental dynamics that occur beyond the short time frames covered by manipulation or monitoring experiments (Loader et al., ²⁰¹¹; Peñuelas et al., ²⁰¹¹; Saurer et al., ²⁰¹⁴; Frank et al., ²⁰¹⁵; Köhler et al., ²⁰¹⁶).

Among all stable isotopes, the hydrogen isotopes protium (¹H) and deuterium (²H or D) exhibit the largest relative mass difference. As a result, hydrogen isotope effects are normally considerably larger than isotope effects of other elements (Melander & Saunders, 1980). Thus, from the physics point of view, hydrogen isotope compositions of plant compounds (commonly expressed in terms of δD) have a remarkable potential to further our knowledge about plant physiological and environmental processes. However, current plant δD models fail to predict the entire body of available empirical data (see later). Therefore, hydrogen isotopes, in contrast to carbon isotopes, have not yet evolved into standard tools within the plant and biogeosciences.

Current δD models of plant organic matter exhibit three main components: (1) the δD composition of plant water sources; (2) leaf water D enrichment; and (3) metabolic fractionations. (1) Plants take up soil water through roots. In most plants, this uptake and water transport through the xylem into leaves occur without detectable δD shifts (Cernusak et al., ²⁰¹⁶; Chen et al., ²⁰²⁰). Additionally, leaf water exchanges with atmospheric water vapour through stomata. Thus, leaf water inherits the δD compositions of both soil water and atmospheric water vapour (Cernusak et al., ²⁰¹⁶). (2) Stomatal evaporation causes D enrichment in leaf water. Adaptations of the Craig–Gordon model describe this process at the site of evaporation (Craig & Gordon, 1965; Flanagan et al., ¹⁹⁹¹; Farquhar et al., ²⁰⁰⁷). In a comprehensive series of gas exchange experiments over a range of isotopic and humidity conditions far exceeding natural conditions, Roden & Ehleringer (1999a) confirmed the robustness of a model that approximates leaf water D enrichment (Flanagan et al., ¹⁹⁹¹). Similarly, on an extensive δD data set of leaf waters from very dry to very wet field sites, Kahmen et al. (2013) confirmed the robustness of the precise δD enrichment model (Farquhar et al., ²⁰⁰⁷). Reanalysing this latter data set, Cernusak et al. (2016) reported a goodness of fit of R ² = 0.92 (n = 332) between modelled and measured δD data. These successful tests for robustness of leaf water δD models strongly suggest that inconsistencies between modelled and measured δD values of plant organic matter as reported by Waterhouse et al. (2002) derive from processes that occur downstream of leaf water D enrichment, that is from fractionating metabolic processes. (3) Yakir & DeNiro (1990) developed a δD model describing fractionation in cellulose of aquatic plants and estimated metabolic fractionation factors of autotrophic and heterotrophic growth. To predict δD values of tree‐ring cellulose, Roden et al. (2000) combined this model with a leaf water δD model (Flanagan et al., ¹⁹⁹¹) and added a term accounting for δD changes by partial reincorporation of hydrogen from xylem water during cellulose biosynthesis (=heterotrophic hydrogen exchange). Roden & Ehleringer (1999b, 2000) confirmed the robustness of their model for glasshouse‐ and field‐grown riparian trees with good access to water. A robustness test by Waterhouse et al. (2002) on tree rings of Quercus robur from a dry site failed. These latter authors suggested modelling metabolic fractionations as constants may be inadequate.

All hydrogen positions of leaf‐level metabolites inherit D fractionations present in leaf water, the hydrogen source of metabolism. By contrast, metabolic reactions cause D fractionations at specific intramolecular hydrogen positions that are directly or indirectly involved in the reaction mechanism (Schmidt et al., ²⁰¹⁵). Such fractionations are known to result in pronounced δD differences among hydrogen positions within a metabolite (Martin et al., ¹⁹⁸⁶; Schleucher, ¹⁹⁹⁸; Schmidt et al., ²⁰⁰³). Furthermore, it is now known that metabolic δD variability can occur at a given intramolecular hydrogen position (Schleucher, 1998). Specifically, δD variability at H⁶ of plant leaf glucose was explained by changes in the photorespiration‐to‐photosynthesis ratio (Schleucher, 1998; Ehlers et al., ²⁰¹⁵). Moreover, growing six C₃ species at ambient CO₂ concentrations of 280 and 150 ppm, Cormier et al. (2018) reported whole‐molecule δD differences of ≈ 20‰ (on average) in leaf α‐cellulose due to unknown fractionating metabolic processes. This shows the predictive abilities of plant δD models will improve by accounting for variability in metabolic fractionations. To this end, however, underlying mechanisms need to be elucidated.

Based on findings by Waterhouse et al. (2002), we hypothesise metabolic processes manifest significant fractionation signals (throughout the paper, the term ‘signal’ denotes temporal variability in deuterium abundance) at carbon‐bound hydrogens in tree‐ring glucose under dry conditions. Since metabolic fractionations occur at specific hydrogen positions within molecules, the interpretability of conventional whole‐molecule data is fundamentally limited. For instance, not knowing the intramolecular location of metabolic fractionation impedes attempts to elucidate its enzymatic origin. Additionally, if located at a single hydrogen position, a c. 20‰ whole‐molecule effect scales up to c. 140‰ because glucose has seven H‐C positions. Therefore, to test our hypothesis, we measured intramolecular D abundance in tree‐ring glucose of Pinus nigra from a dry site in the Vienna region. This region was chosen for its comprehensive environmental monitoring. We first screen for metabolic fractionation signals. Then, we analyse signal–environment and signal–growth relationships and estimate the contribution of metabolic to whole‐molecule fractionation. Lastly, we discuss mechanisms of signal introduction and implications of our findings for isotope studies in the plant and biogeosciences.

Materials and Methods

Site and samples

Pinus nigra Arnold was sampled at Bierhäuselberg, Vienna region, Austria (48.13°N, 16.23°E, 350 m amsl). The site exhibits shallow, very dry soil and an open canopy with apparently low competition among trees (Leal et al., ²⁰⁰⁸). Sampling targeted dominant trees with umbrella‐shaped crowns indicating regular water shortage. From each of 19 specimens (age range: c. 92–156 yr), two 5‐mm stem cores were taken at breast height. Individual tree rings were dated by standard dendrochronological methods (Speer, 2010) and separated using a binocular microscope and a scalpel. To preclude growth‐related isotope signals, we analysed tree rings formed from 1961 to 1995 when all trees had reached a comparably stable canopy position. Across trees, all tree‐ring material of a given year was combined into annual pools yielding one sample per year. Thus, analytical results represent properties of the tree species at the site rather than individual trees.

Intramolecular deuterium measurements

After sample randomisation, intramolecular D abundances of glucose were measured following a published protocol (Betson et al., ²⁰⁰⁶). Samples < 20 mg were excluded from analysis (1977, 1978, 1981 and 1982), because too much measurement time would have been required for sufficient precision. Quantitative D NMR spectra (n ≥ 3) were recorded using an AVANCE III 850 with a cryogenic probe optimised for D detection and ¹⁹F lock (Bruker BioSpin GmbH, Rheinstetten, Germany). Relative intramolecular D abundances were determined by signal deconvolution using Lorentzian line shape fits in TopSpin 4 (Bruker BioSpin GmbH, Rheinstetten, Germany). 3,6‐Anhydro‐1,2‐O‐isopropylidene‐α‐D‐glucofuranose has six methyl group hydrogens, which were introduced during derivatisation and were derived from a common batch of acetone. Their D abundance (arithmetic mean) was used as reference to compare glucose D abundances of tree‐ring samples from different years as follows:

$${\delta \mathrm{D}}_i=\frac{{\mathrm{D}}_i}{{\mathrm{\Sigma }\mathrm{D}}_{\mathrm{ME}}/6}‐1$$ (Eqn 1)

with D _i and D_ME denoting relative D abundance at glucose H‐C positions (Fig. 1) and the methyl group hydrogens, respectively.

Fig. 1.

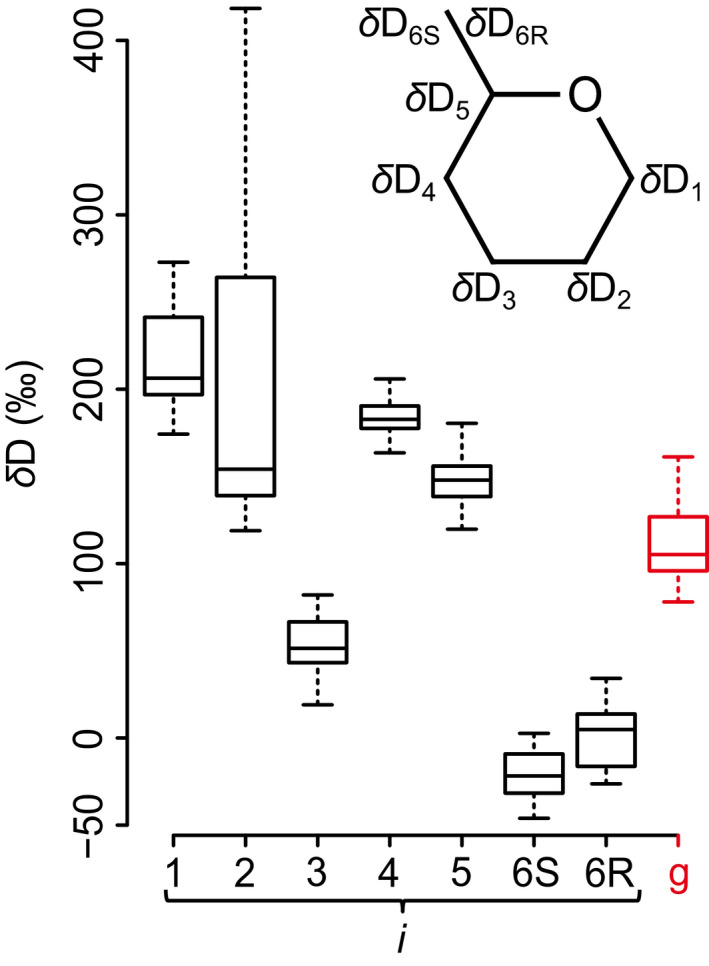
Variability in δD time series shown by boxplots. δD _i and δD_g denote time series of D abundance at intramolecular H‐C positions in tree‐ring glucose (black) and of the whole molecule (red), respectively. Data were acquired for tree‐ring glucose of Pinus nigra laid down from 1961 to 1995 at a site in the Vienna Basin (δD _i : ±SE = 5.4‰, n ≥ 3; δD_g: ±SE = 3.4‰, n ≥ 3). Outliers were removed before analysis (δD₁ to δD₃: n = 31; δD₄ and δD₅: n = 30; δD_6S: n = 26; δD_6R: n = 28; and δD_g: n = 25). Data reference: Average D abundance of the methyl group hydrogens of the glucose derivative used for NMR measurements. Insert: glucose carbon skeleton showing intramolecular locations of δD _i time series.

Environmental data

Monthly resolved data of precipitation, PRE, air temperature, TMP, sunshine duration, SD, global radiation, RAD and relative humidity were measured at the climate station Hohe Warte (WMO ID: 1103500). Air vapour pressure deficits, VPD, were calculated according to published procedures (Abtew & Melesse, 2013). We used monthly resolved data sets of the self‐calibrating Palmer drought severity index, PDSI, and the standardised precipitation–evapotranspiration index, SPEI, for 48.25N, 16.25E (Wells et al., ²⁰⁰⁴; Vicente‐Serrano et al., ²⁰¹⁰). Annual atmospheric CO₂ concentrations, C _a, were measured at the Mauna Loa Observatory, Hawaii, by Pieter Tans (NOAA/ESRL, Boulder, CO, USA) and Ralph Keeling (Scripps Institution of Oceanography, La Jolla, CA, USA). Both the selected grid point and climate station are no more than a horizontal distance of 15 km from the sampling site with a negligible vertical offset. CO₂ is well mixed in the atmosphere. Thus, all data should represent the site conditions well.

Statistical analyses

We calculated the variance contribution of each intramolecular D time series, δD _i , to the whole‐molecule D time series, δD_g, as follows:

$${\delta \mathrm{D}}_{\mathrm{g}}=\frac{{\mathrm{\Sigma }\delta \mathrm{D}}_i}{7}$$ (Eqn 2)

with the variance of δD_g equal to the covariance average between δD _i and δD_g as

$${\mathrm{Var}(\delta \mathrm{D}}_{\mathrm{g}})=\frac{{\mathrm{\Sigma }\mathrm{Cov}(\delta \mathrm{D}}_i,{\delta \mathrm{D}}_{\mathrm{g}})}{7}$$ (Eqn 3)

Thus, variance contributions of δD _i to δD_g are given as

$${\mathrm{VC}}_i=\frac{{\mathrm{Cov}(\delta \mathrm{D}}_i,{\delta \mathrm{D}}_{\mathrm{g}})}{7{\times \mathrm{Var}(\delta \mathrm{D}}_{\mathrm{g}})}$$ (Eqn 4)

See Supporting Information Notes S1 for information on other statistical analyses.

Results

To better understand metabolic fractionations, we measured intramolecular D abundances at all seven H‐C positions of glucose extracted across an annually resolved Pinus nigra tree‐ring series (Fig. 1). Our time series cover the period from 1961 to 1995 but lack data for 1977, 1978, 1981 and 1982. Hence, the data set consists of seven intramolecular δD _i time series each comprising 31 observations (n = 7 × 31 = 217). Additionally, we derived the molecular average time series, δD_g (n = 31).

Outlier analysis

Outliers can potentially impair statistical analyses because they may reflect either experimental errors or extreme states of the system. Since we were interested in the normal functioning of plant metabolism and metabolic fractionation, we removed outliers to ensure robust statistical results. We identified outliers in δD _i time series (n = 31) as values that were 1.5 times the interquartile range below the first or above the third quartile. We removed one data point each from δD₄ and δD₅ (n = 30), three data points from δD_6R (n = 28) and five data points from δD_6S (n = 26) resulting in six missing data points in δD_g (n = 25). The average standard errors of δD _i and δD_g measurements are 5.4‰ and 3.4‰, respectively.

δD₁ and δD₂ reflect highly variable and closely related metabolic processes

Intramolecular D abundances of Pinus nigra tree‐ring glucose differ among H‐C positions (Figs 1, 2b; Notes S2). Medial intramolecular differences exceed 225‰ (δD₁ vs δD_6S). This shows that metabolic fractionations, being position‐specific, have strong effects. Interestingly, in some years, intramolecular δD differences approach 450‰ (Notes S2). Thus, metabolic fractionations are highly variable on the interannual scale.

Fig. 2.

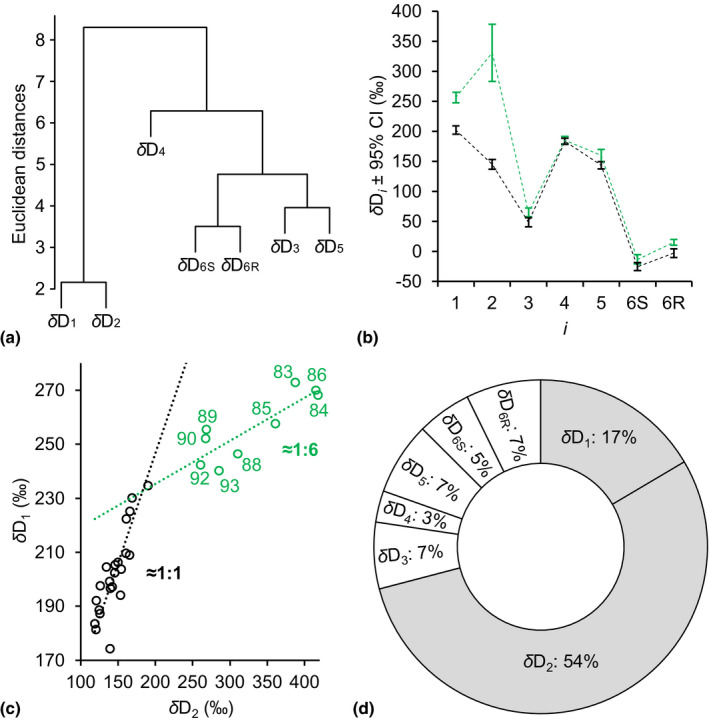
(a) Common variability in δD _i time series detected by hierarchical cluster analysis (HCA). (b) Intramolecular δD _i patterns of the low‐ and high‐value groups (black and green, respectively). (c) Relationship between δD₁ and δD₂ (overall R ² = 0.93, P < 10^–15, n = 31). Dotted lines: linear major axis regression models showing that δD₁ and δD₂ increase at a 1 : 1 ratio at low values (black) and at a 1 : 6 ratio at high values (green). (d) Per cent contributions of δD _i to the variance in δD_g. δD _i and δD_g denote time series of D abundance at intramolecular H‐C positions in tree‐ring glucose and of the whole molecule, respectively. Data were acquired for tree‐ring glucose of Pinus nigra laid down from 1961 to 1995 at a site in the Vienna Basin (δD _i : ±SE = 5.4‰, n ≥ 3; δD_g: ±SE = 3.4‰, n ≥ 3). Outliers were removed before analysis (δD₁ to δD₃: n = 31; δD₄ and δD₅: n = 30; δD_6S: n = 26; δD_6R: n = 28; and δD_g: n = 25). Low‐ and high‐value groups were identified by HCA (Supporting Information Notes S2). Fig. 2(b) shows discrete data. Dashed lines were added to guide the eye. The variance partitioning analysis (2d) is based on years without missing data after removing outliers (n = 8 × 25). Data reference: Average D abundance of the methyl group hydrogens of the glucose derivative used for NMR measurements.

Hierarchical cluster analysis (HCA) groups time series according to covariability. Time series carrying common signals, that is information about a common process or strongly related processes, form clusters. Performing HCA on our δD _i data set, we found a strong separation between a cluster comprising δD₁ and δD₂ and a cluster comprising δD₃ to δD_6R (Fig. 2a). Additionally, we found separations within the δD₃ to δD_6R cluster, with δD₄ showing the highest degree of independency. Thus, δD _i time series carry information about several fractionation processes.

While δD₃ to δD_6R exhibit similar degrees of variability (Fig. 1; SD = ±10.5‰ to ±16.8‰, range = 42‰ to 63‰, n = 26–31), δD₂ varies considerably (SD = ±91.8‰, range = 300‰, n = 31) and δD₁ is also relatively variable (SD = ±28.4‰, range = 99‰, n = 31). Increased D variability at two out of seven H‐C positions indicates highly variable metabolic fractionations at these positions, H¹ and H².

To further investigate this, we performed HCA on annual δD _i patterns and found two groups (Notes S2). Fig. 2(b) shows the arithmetic average patterns of both groups. While δD₃ to δD_6R values remain comparably constant under all conditions experienced by the trees, δD₁ and δD₂ separate annual δD _i patterns into a low‐value group (black, n = 22) and a high‐value group (green, n = 9). Average and median increases in δD₁ and δD₂ are statistically significant (one‐tailed Student’s t‐tests: δD₁, P < 10^–9; δD₂, p < 10^–4; one‐tailed Mood’s median tests: δD₁ and δD₂, P < 0.001). Since differences in δD _i patterns reflect differences in metabolism, this finding confirms that glucose H¹ and H² carry exceptionally variable metabolic fractionation signals. Underlying metabolic processes are closely related (Fig. 2a).

Nonmetabolic fractionation processes (e.g. leaf water D enrichment) have equal effects on all δD _i . In regression analysis investigating relationships among different δD _i , these processes can be expected to yield slopes = 1. By contrast, metabolic fractionation processes affect subsets of δD _i and may thus cause deviations from slope = 1. To investigate which kind of fractionation shapes the variation in the low‐ and high‐value groups, we performed major axis regression analysis on low and high δD₁ and δD₂ values (Fig. 2c, black and green circles, respectively). Compared with ordinary least squares regression analysis, major axis regression analysis yields truer parameter estimates when x‐variable data contain significant relative errors as is the case here for low‐value data. For low values, we found a slope of c. 0.81 with a 95% confidence interval of c. 0.60 to c. 1.07 (n = 22); that is, δD₁ and δD₂ increase at a c. 1 : 1 ratio. For high values, we found a slope of c. 0.16 with a 95% confidence interval of c. 0.07 to c. 0.25 (n = 9); that is, δD₁ and δD₂ increase at a c. 1 : 6 ratio. Thus, while δD₁ and δD₂ variability in the low‐value group is consistent with expectations related to nonmetabolic fractionation processes, high δD₁ and δD₂ values reflect additional effects by metabolic fractionation processes.

Metabolism changes in response to dry conditions after a change point is crossed

To investigate the controls of the metabolic fractionation processes, we estimated metabolic fractionation at glucose H¹ and H² as

$${\epsilon }_{\mathrm{met}}=\frac{1/2\mathrm{\Sigma }({\mathrm{D}}_1,{\mathrm{D}}_2)}{1/5\mathrm{\Sigma }({\mathrm{D}}_3,{\mathrm{D}}_4,{\mathrm{D}}_5,{\mathrm{D}}_{6\mathrm{S}},{\mathrm{D}}_{6\mathrm{R}})}‐1$$ (Eqn 5)

where D _i denotes relative D abundance at glucose H‐C positions (Fig. 1). This procedure maximises metabolic fractionation signals located at H¹ and H², removes fractionation signals equally present at all H‐C positions (leaf water D enrichment) and minimises signals of processes affecting all H‐C positions similarly (heterotrophic hydrogen exchange). Weaker metabolic fractionation signals present at glucose H³ to H⁶ (Figs 1, 2a) will be further explored in future analyses of the data set.

In general, the fractionating metabolic processes may be under developmental control (Gray & Song, 1984). However, the formation of tree rings analysed here occurred when the trees had reached a stable canopy position. On average, tree‐ring width measurements of the samples reach back to 1865 (range: 1840–1918) and δD _i time series start at 1961. Thus, the fractionating metabolic processes can be expected to be controlled by environmental parameters. In the following, these are elucidated in six steps, which motivate two integrated isotope–environment models presented subsequently.

Step 1

Increases in ε _met are temporally confined to the second part of the study period (Fig. 1, 2, 1983–1993). This may indicate the presence of a response change point. To test this, we performed a batch change point analysis based on the nonparametric Mann–Whitney–Wilcoxon test (Ross, 2015). We found a change point at 1980 (P < 0.001, n = 31), showing that the observed frequency distribution of ε _met (Notes S3) does not align with the properties of a single theoretical probability distribution. That is, ε _met data of 1961–1980 and 1983 to 1995 follow different probability distributions (1981 and 1982 are missing). Thus, the ε _met time series exhibits a change point beyond which the fractionating metabolic processes are activated or upregulated.

Step 2

Upregulation of the fractionating metabolic processes occurs beyond a change point. Before the change point, environmental variability exerts no significant control (Fig. 1, 2, 1 : 1 ratio). To investigate when the change point is crossed, we correlated ε _met with different climate parameters. Since ε _met does not follow a normal distribution (Notes S3), we calculated Spearman’s rank correlation coefficient, ρ. Our analysis included four time periods: January to December, year; March to May, spring; March to November, growing season (Wieloch et al., ²⁰¹⁸); and June to July, summer. For most periods, we found significant positive correlations of ε _met with VPD and significant negative correlations with PDSI and SPEI (Table 1). High VPD, low PDSI and low SPEI correspond to dry conditions. Thus, the results indicate that upregulation of the fractionating metabolic processes (high ε _met) occurs in response to dry conditions.

Table 1.

Spearman’s rank correlation coefficients and significance levels for relationships between ε _met and climate parameters within the period from 1961 to 1995 (n = 31).

	VPD	PRE	PDSI	TMP	SD	RAD	C a	SPEI 1	3	4	6	8	12	16	24	36	48
Year	0.40	0.01	−0.51	0.45	0.12	0.28	0.58	−0.21	−0.25	−0.27	−0.30	−0.37	−0.46	−0.47	−0.58	−0.60	−0.57
Spring	0.54	−0.13	−0.55	0.55	0.09	0.18	–	−0.24	−0.19	−0.15	−0.16	−0.29	−0.34	−0.43	−0.58	−0.54	−0.55
Growing season	0.39	−0.04	−0.50	0.33	0.01	0.24	–	−0.26	−0.21	−0.20	−0.29	−0.31	−0.43	−0.47	−0.59	−0.61	−0.56
Summer	0.28	−0.04	−0.49	0.02	−0.17	0.10	–	−0.09	−0.20	−0.21	−0.25	−0.31	−0.43	−0.41	−0.56	−0.65	−0.55

ε _met denotes the average deuterium fractionation by metabolic processes at glucose H¹ and H² (±SE = 3.5‰, n ≥ 3). Data for the calculation of ε _met were acquired for tree‐ring glucose of Pinus nigra laid down from 1961 to 1995 at a site in the Vienna Basin. Climate parameters: VPD, air vapour pressure deficit; PRE, precipitation; PDSI, the self‐calibrating Palmer drought severity index (Wells et al., ²⁰⁰⁴); TMP, air temperature; SD, sunshine duration; RAD, global radiation; C _a, atmospheric CO₂ concentrations; SPEI, the standardised precipitation–evapotranspiration index calculated for different timescales (1–48 months) (Vicente‐Serrano et al., ²⁰¹⁰). Integration periods for the calculation of climate parameters: January to December, year; March to May, spring; March to November, growing season (Wieloch et al., ²⁰¹⁸); and June to July, summer. Significance levels: < 0.05, light blue/light pink; < 0.01, blue/pink; and < 0.001, dark blue/dark pink.

Step 3

SPEI can be calculated for different timescales indicating different types of hydrological drought (Vicente‐Serrano et al., ²⁰¹⁰). While short timescales indicate variability in soil moisture, long timescales indicate variability in groundwater storage (Vicente‐Serrano et al., ²⁰¹⁰). To investigate the effects of different drought types on the fractionating metabolic processes, we correlated ε _met with SPEI calculated for timescales of 1, 3, 4, 6, 8, 12, 16, 24, 36 and 48 months. We found increasing correlation coefficients from short to long timescales (Table 1), indicating that long‐term drought promoted upregulations of the fractionating metabolic processes (possibly by groundwater depletion). Long‐term drought events have a low temporal frequency (Vicente‐Serrano et al., ²⁰¹⁰). This may explain why upregulations of the fractionating metabolic processes occur not scattered over the entire study period but over consecutive years during the second half of the study period (Fig. 2c).

Step 4

In addition to correlations indicative of drought control, we found a significant positive correlation between ε _met and C _a (Table 1), which may constitute a pseudocorrelation resulting from intercorrelation between C _a and long‐term drought (Pearson’s correlation between C _a and the growing‐season 48‐month SPEI: r = −0.83, P < 10^–7, n = 31). For the year and spring, we found significant positive correlations between ε _met and TMP (Table 1). Thus, air temperature may contribute to upregulations of the fractionating metabolic processes. Alternatively, the TMP correlation may be explained by intercorrelation with drought parameters. Overall, long‐term drought shows the highest correlation coefficients (Table 1), indicating that it is the most important environmental control. Furthermore, we considered pathogens as a cause for upregulations of the fractionating metabolic processes. The Research Centre for Forests (Vienna, Austria) closely monitors and reports on pathogen status. To our knowledge, there are no reports of major damage by pathogens for the studied Pinus nigra stand during the 1980s and the early 1990s. Thus, significant effects of pathogens on upregulations of the fractionating metabolic processes are unlikely. Similarly, effects by forest management interventions are unlikely since the stand is not used economically (Leal et al., ²⁰⁰⁸). Effects by air pollutants could not be assessed due to limited data availability.

Step 5

To assess the magnitude of the drought shift indicated by correlation, we plotted the growing‐season 48‐month SPEI as function of time (Fig. 3a). Trendline analysis shows a significant increase in drought severity with a long‐term shift from ‘nondrought’ from 1961 to 1978, to ‘mild drought’ from 1979 to 1988, to ‘moderate drought’ from 1989 to 1995 according to the classification of drought severity (R ² = 0.69, P < 10^–9, n = 35) (McKee et al., ¹⁹⁹³; Vicente‐Serrano et al., ²⁰¹⁰). Thus, upregulations of the fractionating metabolic processes in between 1983 and 1993 occurred when the study region experienced mild‐to‐moderate drought. Note that actual conditions at the site may have deviated from regional conditions plotted in Fig. 3(a).

Fig. 3.

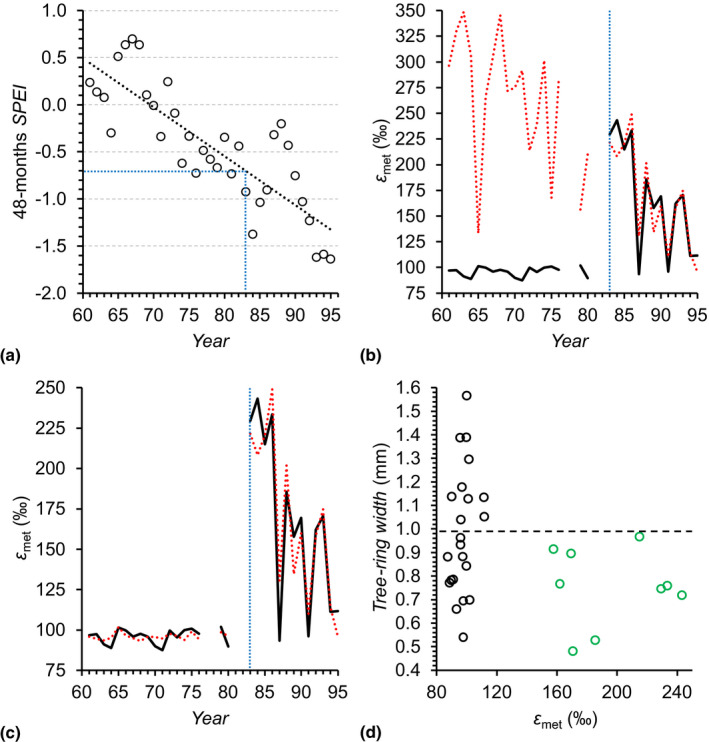
(a) Long‐term development of growing‐season drought in the study region. Trendline analysis shows a significant increase in drought severity with shifts from ‘nondrought’ from 1961 to 1978, to ‘mild drought’ from 1979 to 1988, to ‘moderate drought’ from 1989 to 1995 (dotted black line, R ² = 0.69, P < 10^–9, n = 35). SPEI denotes the standardised precipitation–evapotranspiration index (Vicente‐Serrano et al., ²⁰¹⁰). Here, it was calculated for the growing season (March to November (Wieloch et al., ²⁰¹⁸)) at 48.25°N, 16.25°E on a 48‐month timescale indicative of long‐term drought variability (black circles). Expressions of SPEI values indicate the drought severity as ≥−0.49, nondrought; −0.5 to −0.99, mild drought; −1 to −1.49, moderate drought; −1.5 to −1.99, severe drought; and <−2, extreme drought (McKee et al., ¹⁹⁹³; Vicente‐Serrano et al., ²⁰¹⁰). (b, c) Comparison of measured (solid black line) and modelled (dotted red line) metabolic fractionation at glucose H¹ and H², ε _met (n = 31). In (b) and (c), data were modelled by a multivariate linear model (Eqn 6) and a multivariate change point model (Eqn 7; Table 3) (Fong et al., ²⁰¹⁷), respectively. Dotted blue line: response change point as determined by the change point model. (d) Relationship between ε _met and tree‐ring width. Green and black circles: years in which the fractionating metabolic processes were upregulated and downregulated, respectively (Fig. 2). Dashed line: average tree‐ring width of years in which the fractionating metabolic processes were downregulated (black circles, 0.99 mm). Tree‐ring widths were measured for previous dendro‐ecological studies (Leal et al., ²⁰⁰⁸). Data for the calculation of ε _met were acquired for tree‐ring glucose of Pinus nigra laid down from 1961 to 1995 at a site in the Vienna Basin (±SE = 3.5‰, n ≥ 3).

Step 6

In 1994 and 1995, long‐term drought was exceptionally strong (Fig. 3a). However, this did not result in significant upregulations of the fractionating metabolic processes (Fig. 2c). Therefore, we hypothesise long‐term drought beyond a critical level is merely setting the stage for upregulation and secondary climate factors exert control on shorter timescales. To investigate this, we repeated the ε _met–climate correlation analysis with data of the second half of the study period, 1983 to 1995. We justify this data selection as follows. In 1983, the upregulation of the fractionating metabolic processes occurred for the first time (Fig. 2c). From 1983 to 1995, long‐term drought became more severe (Fig. 3a, dotted black line). Thus, the site conditions during this period may have been generally favourable for upregulation. Before 1983, long‐term drought was less severe and may have rendered upregulations impossible (Fig. 3a). In this scenario, control by secondary climate factors would have been impossible and considering their variability would impair correlation results. Since the selected subset of ε _met (1983–1995) follows a normal distribution (Notes S3), we calculated Pearson’s correlation coefficients, r. We found significant negative correlations between ε _met and PRE (Table 2). Under generally dry conditions, low precipitation may result in low soil moisture. Thus, the results indicate that upregulations of the fractionating metabolic processes (high ε _met) occurred in response to short‐term depletions in soil moisture when long‐term drought was beyond the critical level. In this respect, it is noteworthy that Pinus nigra reportedly has a well‐developed lateral root system in upper soil layers to access soil water but can additionally tap into deep water sources if available (Stokes et al., ²⁰⁰²; Peñuelas & Filella, ²⁰⁰³). Furthermore, we found a significant negative correlation between ε _met and annual C _a (Table 2). This correlation is not explained by intercorrelation between C _a and long‐term drought (Pearson’s correlation between C _a and the growing‐season 48‐month SPEI: r = −0.39, P > 0.1, n = 13). Thus, the result indicates that high atmospheric CO₂ concentrations counteracted upregulations of the fractionating metabolic processes (high ε _met) when long‐term drought was beyond the critical level.

Table 2.

Pearson’s correlation coefficients and significance levels for relationships between ε _met and climate parameters within the period from 1983 to 1995 (n = 13).

	VPD	PRE	PDSI	TMP	SD	RAD	C a	SPEI 1	3	4	6	8	12	16	24	36	48
Year	0.26	−0.69	−0.51	−0.17	−0.12	−0.34	−0.73	−0.18	−0.20	−0.24	−0.28	−0.28	−0.10	0.03	0.03	−0.04	0.04
Spring	0.52	−0.71	−0.29	0.23	−0.08	−0.19	–	−0.28	−0.01	0.02	−0.08	−0.13	0.20	0.27	0.10	0.07	0.22
Growing season	0.27	−0.67	−0.52	−0.14	0.01	−0.33	–	−0.27	−0.17	−0.20	−0.29	−0.29	−0.18	0.03	0.02	−0.04	0.03
Summer	0.17	−0.67	−0.54	−0.47	−0.30	−0.51	–	−0.39	−0.44	−0.46	−0.31	−0.35	−0.29	−0.05	−0.03	−0.10	0.05

ε _met denotes the average deuterium fractionation by metabolic processes at glucose H¹ and H² (±SE = 3.4‰, n ≥ 3). Data for the calculation of ε _met were acquired for tree‐ring glucose of Pinus nigra laid down from 1983 to 1995 at a site in the Vienna Basin. Climate parameters: VPD, air vapour pressure deficit; PRE, precipitation; PDSI, the self‐calibrating Palmer drought severity index (Wells et al., ²⁰⁰⁴); TMP, air temperature; SD, sunshine duration; RAD, global radiation; C _a, atmospheric CO₂ concentrations; SPEI, the standardised precipitation–evapotranspiration index calculated for different timescales (1–48 months) (Vicente‐Serrano et al., ²⁰¹⁰). Integration periods for the calculation of climate parameters: January to December, year; March to May, spring; March to November, growing season (Wieloch et al., ²⁰¹⁸); and June to July, summer. Significance levels: < 0.05, light blue; < 0.01, blue.

Model 1

To further corroborate the existence of a response change point (Step 1), and the requirement of long‐term drought (Steps 2 and 3) for the manifestation of effects by secondary climate factors (Step 6), we modelled two ε _met groups as functions of PRE and C _a as follows:

$${\epsilon }_{\mathrm{met}}={\alpha }_1+{\alpha }_2\mathit{PRE}+{\alpha }_3{C}_{\mathrm{a}}$$ (Eqn 6)

While the first group includes data from 1961 to 1982 corresponding to less severe long‐term drought, the second group includes data from 1983 to 1995 corresponding to more severe long‐term drought (Fig. 3a). For the latter group, we found adequate linear models including, as explanatory variables, spring PRE and annual C _a (R ² = 0.74, P < 0.01, n = 13), and summer PRE and annual C _a (R²  = 0.78, P < 0.001, n = 13). The most adequate model we found includes summed spring and summer PRE and annual C _a (R ² = 0.87, P < 10^–4, n = 13, α ₁ = 1801.97, α ₂ = −0.566, α ₃ = 4.1851; see Notes S4 for bivariate relationships of ε _met with PRE and C _a, respectively). Both PRE and C _a contributed significantly to all models (P < 0.05). For ε _met data of the first group, 1961 to 1982, the most adequate model has no explanatory power (P > 0.1, n = 18). Modelling ε _met by the most adequate model works well for the second group, 1983–1995, yet produces large offsets between all measured and modelled values of the first group (Fig. 3b). This corroborates that (1) a response change point exists and (2) the manifestation of effects by secondary climate factors requires long‐term drought. Furthermore, it should be noted that the most adequate model accounts well for low ε _met values in 1994 and 1995 (Fig. 3b). During these years, long‐term drought was exceptionally severe, yet PRE and C _a were high (Fig. 3a; Notes S4). Thus, long‐term drought alone may not necessarily lead to upregulation of the fractionating metabolic processes. High precipitation during spring and summer, as well as high atmospheric CO₂ concentrations, may exert counteracting effects.

Model 2

Above, we found indications for several properties of ε _met of Pinus nigra tree‐ring glucose. To test these properties in an integrated way and to estimate the change point value, we fitted a change point model to the entire dataset (Fong et al., ²⁰¹⁷). It takes the form

$${\epsilon }_{\mathrm{met}}={\beta }_1+{\beta }_2{z}_1+{\beta }_3{z}_2+{\beta }_{4}I\left(x>\mathrm{e}\right)+{\beta }_5{z}_{1}I\left(x>\mathrm{e}\right)+{\beta }_6{z}_{2}I\left(x>\mathrm{e}\right)$$ (Eqn 7)

where β ₁ to β ₆ are model coefficients, z ₁ is March‐to‐June PRE, z ₂ is annual C _a, x is the trend of the growing‐season 48‐month SPEI used as change point variable (Fig. 3a, dotted black line), and e is the change point value. If x > e, then I(x > e) equals 1, else I(x > e) equals 0. The fitted model explains 94% of the variability in ε _met and is highly significant (P < 10^–15, n = 31). All explanatory variables and the change point contribute significantly (Table 3). The estimated change point is at −0.7 ± 0.05SE corresponding to mild long‐term drought (P < 10^–15, Table 3; Fig. 3a). The presence/absence and directionality of modelled ε _met relationships with precipitation and atmospheric CO₂ concentration agree with findings given above (Tables 1, 2, 3). In contrast to the model without response change point (Fig. 3b), the change point model captures the variability in the entire ε _met data set (Fig. 3c). Thus, this integrated change point model corroborates the following findings. First, ε _met exhibits a response change point. Below this change point, ε _met is largely constant with values of c. 96‰. Above the change point, ε _met variability is high. Second, change point crossing may require long‐term drought beyond a critical level. Third, March‐to‐July precipitation and annual atmospheric CO₂ concentration may govern ε _met variability in short timescales when long‐term drought is beyond the critical level. Note, all relationships indicated by modelling require experimental confirmation in controlled settings.

Table 3.

Estimated coefficients of the ε _met change point model.

Coefficient	Estimate	SE*	Lower 95% CI	Upper 95% CI	P‐value*
β 1	1801.97	479.02	863.10	2740.85	<0.001
β 2	−0.56599	0.17577	−0.91051	−0.22147	<0.01
β 3	−4.1851	1.4164	−6.9613	−1.4090	<0.01
β 4	−1722.11	479.90	−2662.71	−781.51	<0.001
β 5	0.58782	0.17749	0.23993	0.93571	<0.001
β 6	4.2138	1.4574	1.3573	7.0703	<0.01
e	−0.70310	0.05296	−0.80690	−0.59930	<10–15

A change point model was fitted to measured ε _met data (R ² = 0.94, P < 10^–15, n = 31, Eqn 7) (Fong et al., ²⁰¹⁷). ε _met denotes the average deuterium fractionation by metabolic processes at glucose H¹ and H² (±SE = 3.5‰, n ≥ 3). Data for the calculation of ε _met were acquired for tree‐ring glucose of Pinus nigra laid down from 1961 to 1995 at a site in the Vienna Basin. β ₁ to β ₆, and e denote model coefficients (Eqn 7). SE and CI denote the standard error and confidence interval, respectively. Asterisks mark estimations, which assume that bootstrap sampling followed a normal distribution.

Variability in δD_g is predominantly controlled by fractionating metabolic processes

Metabolic fractionations in δD₁ and δD₂ have a strong weight on whole‐molecule D variability, δD_g. Variance partitioning shows that δD₁ and δD₂ together account for 71% of the variance in δD_g (Fig. 2d). By contrast, δD₃ to δD_6R each accounts for 5.8% on average. Assuming the variability in δD₃ to δD_6R reflects the combined influence of nonmetabolic fractionation processes affecting all δD _i , such as leaf water D enrichment, metabolic fractionations in δD₁ and δD₂ together account for 59.4% of the variance in δD_g (71%–2 × 5.8%). When years affected by metabolic fractionation are considered exclusively (green dots in Fig. 2c), metabolic fractionations in δD₁ and δD₂ together account for 74.2% of the variance in δD_g (Notes S5). After excluding the period affected by metabolic fractionation from the analysis (1983–1995), all δD _i exhibit similar degrees of variance and contribute similar to δD_g (Notes S6) consistent with expectations related to nonmetabolic fractionation processes. In conclusion, here, δD_g variability is predominantly controlled by fractionating metabolic processes unaccounted for in current models. Note, our estimations implicitly assume invariability of metabolic fractionations in δD₃ to δD_6R. This simplifies actual conditions and results in underestimation of the influence of metabolic fractionations on δD_g.

Altered metabolism is associated with below‐average yet not exceptionally low growth

Metabolic changes as reflected by changes in metabolic fractionation may impact on growth. To test this, we investigated the relationship between ε _met and tree‐ring width. We found that when the fractionating metabolic processes were upregulated, significantly more narrow tree rings were formed compared with those when they were downregulated (Fig. 3d, one‐tailed t‐test: green vs black circles, 0.75 vs 0.99 mm, P < 0.05, n = 9 and 22). Thus, altered metabolism is associated with below‐average growth. However, equally narrow tree rings were formed in > 50% of the years in which the fractionating metabolic processes were downregulated (Fig. 3d; tree‐ring widths < 0.99 mm, n = 12). Thus, upregulations of the fractionating metabolic processes are not associated with exceptional growth declines.

Discussion

ε _met: An isotope biomarker reports metabolic changes and drought

Here, we found highly variable metabolic fractionation signals at glucose H¹ and H² (Figs 1, 2). We approximated these signals by calculating ε _met (Eqn 5) and propose ε _met is a sensitive isotope biomarker reflecting changes in plant metabolism. Furthermore, we found a change point in ε _met (Step 1; Fig. 3a–c) suggesting ε _met features a two‐state property. This property promises unambiguous identification of alternate metabolic states: a stable state where the fractionating metabolic processes remain downregulated, and a state where these processes are upregulated (upon crossing a change point). By contrast, other biomarkers develop in a purely linear manner with indistinct transitions between states hindering attempts to ascertain plant functioning. While the mechanisms behind other biomarkers in plant archives often remain elusive, ε _met can be (1) linked to specific physiological processes and (2) incorporated into fractionation models (see later). Upon process elucidation, ε _met may help to find plants with the make‐up to support crucial ecosystem services such as food and resource security.

As indicated by modelling, atmospheric CO₂ concentrations and drought exert control over ε _met in Pinus nigra studied here (Tables 1, 2, 3; Fig. 3a–c). Values of ε _met > 105‰ indicate long‐term drought events affecting plant metabolism (Fig. 3a–c). Given careful sample selection (e.g. designed to avoid bias related to tree age), this may enable identification of historical occurrences. Fitting a model to ε _met values > 105‰ (Fig. 3b, ε _met = 1802–0.566PRE‐4.185C _a) may enable analyses of metabolic effects of short‐term drought and C _a during long‐term drought events (by interpretation of the respective model terms), and reconstructions of short‐term drought events during long‐term drought events (by solving for PRE with historical C _a data available).

Pinus nigra can access water from upper soil layers and from deep water sources (Stokes et al., ²⁰⁰²; Peñuelas & Filella, ²⁰⁰³). Accordingly, at our study site, metabolic responses apparently require long‐term drought (possibly involving groundwater depletion). In the absence of long‐term drought, ε _met is blind to variability in short‐term drought (possibly involving low soil moisture) and C _a (Fig. 3a–c). By contrast, species without groundwater access may provide this information. Lastly, ε _met may not always report drought, but it may always report source‐limited growth conditions (cf. Wieloch et al., ^2022a).

The role of leaf intercellular CO₂ concentrations

As indicated by modelling, upregulations of the fractionating metabolic processes occur in response to drought, yet high atmospheric CO₂ concentrations exert counteracting effects (Tables 1, 2, 3; Fig. 3a–c). Isohydric plant species such as Pinus nigra respond to drought by closing their stomata (Sade et al., ²⁰¹²). This impedes CO₂ uptake and promotes low intercellular CO₂ concentrations, C _i. By contrast, increasing C _a promotes increasing C _i. Thus, upregulations of the fractionating metabolic processes may be mediated by low C _i. In principle, whole‐molecule stable carbon isotope ratios of plant organic matter, δ ¹³C, enable C _i estimations because ¹³C fractionation during carbon uptake is related to C _i/C _a (Farquhar et al., ¹⁹⁸²; Evans et al., ¹⁹⁸⁶). However, in the samples studied here, processes that are independent of carbon uptake fractionation control δ ¹³C at three out of six glucose carbon positions (Wieloch et al., ^{2018, 2021b, 2022b}). Therefore, we decided against using δ ¹³C‐derived C _i estimates to test this hypothesis.

Stable isotope methodology

Variability in δD_g is predominantly controlled by metabolic fractionation at glucose H¹ and H² (Fig. 2d). Since δD_g can be measured by high‐throughput isotope ratio mass spectrometry, a technique accessible to numerous laboratories, we investigated possibilities to (1) detect δD_g data sets affected by metabolic fractionation; (2) separate δD_g data points affected by metabolic fractionation from other data points; and (3) retrieve information from δD_g about metabolic fractionation (Notes S7).

We found our δD_g data set holds clues to effects by metabolic fractionation at glucose H¹ and H² (Notes S7). Furthermore, the separation of δD_g data points affected by metabolic fractionation from other data points seems feasible yet not with high confidence. Discarding data sets/data points affected by metabolic fractionation at glucose H¹ and H² may improve δD_g analyses of nonmetabolic fractionation processes. However, analytical results will be impaired by other metabolic fractionations.

Modelling ε _met, we found both a response change point marking the onset of a period with conditions favourable for upregulation of metabolic fractionation processes and environmental dependences of upregulation (Table 3; Eqn 7; Fig. 3c). Applying this model to δD_g, we found the same change point, but the environmental dependences of upregulation were not sufficiently constrained for interpretation (Notes S7). Thus, by itself, δD_g analysis of glucose does not yield robust information about the environmental dependences of metabolic fractionation at H¹ and H². However, in combination with modelled or measured leaf water δD values, information on overall metabolic fractionation may be retrieved (cf. Cormier et al., ²⁰¹⁸). By contrast, resolving information about different metabolic fractionations requires the intramolecular approach.

Current δD_g models describe metabolic fractionations as being constant (Roden et al., ²⁰⁰⁰). As shown here, this is inadequate for plants grown under dry conditions where metabolic fractionations can exert predominant control over δD_g variability (Fig. 2d). Thus, to model plant D abundance over the whole range of environmental conditions, metabolic fractionations need to be incorporated as variables, which requires detailed knowledge about underlying processes.

Metabolic fractionation processes known to affect tree‐ring glucose H¹ and H² cannot explain our findings. Specifically, Picea abies reportedly exhibits similar heterotrophic hydrogen exchange rates at tree‐ring glucose H¹ and H² (c. 42%) (Augusti et al., ²⁰⁰⁶). Since Pinus nigra as a close relative can be expected to behave similarly, heterotrophic hydrogen exchange at these positions cannot cause pronounced deviations from slope = 1 as observed for the δD₁‐δD₂ regression (Fig. 2c). Therefore, we will now derive experimentally testable theories on the metabolic origins of the fractionation signals reported here.

Theory 1. Isotope fractionation related to sucrose‐to‐starch carbon partitioning

We found a highly variable metabolic fractionation signal at tree‐ring glucose H² (ε _met at H²: SD c. ±79‰, range c. 260‰, n = 31), which occurs upon the crossing of a response change point (Fig. 3a–c). At the leaf level, tree‐ring glucose has two precursors, starch and sucrose. Growing Phaseolus vulgaris and Spinacia oleracea under optimal conditions, Schleucher et al. (1999) reported D depletions at glucose H² of leaf starch relative to sucrose of 333‰ and 500‰, respectively. This difference may contribute to the signal at tree‐ring glucose H² when the relative flux of assimilated carbon into starch and sucrose changes (Fig. 4). Sucrose‐to‐starch carbon partitioning ratios are controlled primarily by the rate of carbon assimilation (Sharkey et al., ¹⁹⁸⁵) and were shown to increase with decreasing assimilation rates (Sharkey et al., ¹⁹⁸⁵), decreasing C _i (Sharkey et al., ¹⁹⁸⁵), decreasing light (Sharkey et al., ¹⁹⁸⁵; Quick et al., ¹⁹⁸⁹) and increasing drought (Quick et al., ^{1989, 1992}; Vassey & Sharkey, ¹⁹⁸⁹). Reported responses are functionally coherent and qualitatively consistent across all species studied. Furthermore, responses of sucrose‐to‐starch carbon partitioning to ecophysiological changes exhibit change points. For instance, in leaves of Phaseolus vulgaris, the sucrose‐to‐starch carbon partitioning ratio was found to be largely constant at C _i ≥ 150 ppm yet increases below this change point from c. 0.5 to c. 4 (Sharkey et al., ¹⁹⁸⁵). Thus, as C _i drops below the change point, the relative contribution of leaf sucrose to tree‐ring glucose biosynthesis may increase, and tree‐ring glucose H² may gradually approach the higher relative D abundance of leaf sucrose.

Fig. 4.

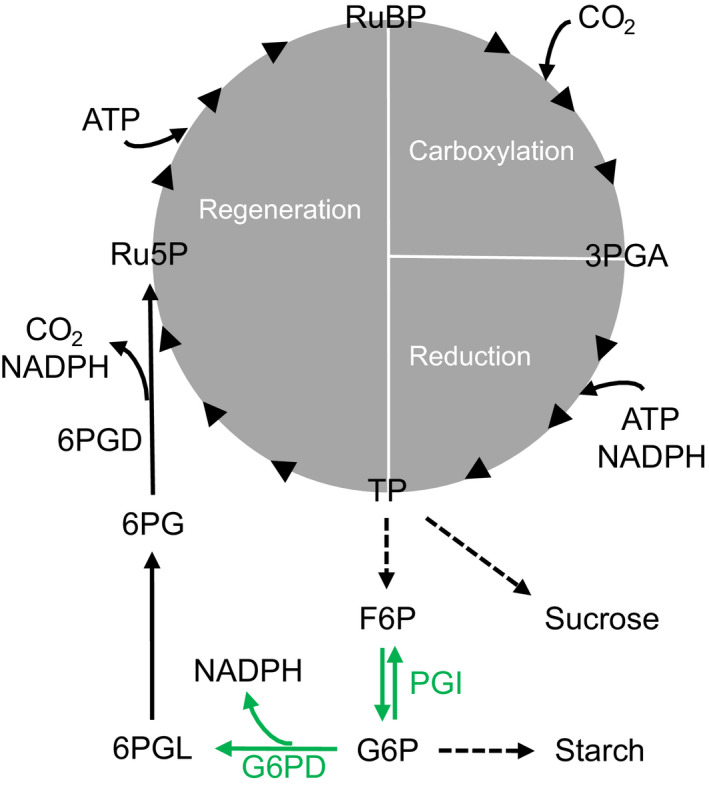
Sucrose‐to‐starch carbon partitioning and anaplerotic carbon flux into the Calvin–Benson cycle. Green: enzyme reactions proposedly introducing D isotope signals at glucose H¹ and H². G6PD has a kinetic isotope effect of α _D = k _H/k _D = 2.97 (Hermes et al., ¹⁹⁸²), while PGI has a kinetic isotope effect of 2.22 in the F6P to G6P direction and an equilibrium isotope effect of 1.11 in G6P (Rose & O’Connell, 1961; Wieloch et al., ^2022a). Dashed arrows: intermediate reactions not shown. Enzymes: 6PGD, 6‐phosphogluconate dehydrogenase; G6PD, glucose‐6‐phosphate dehydrogenase; and PGI, phosphoglucose isomerase. Metabolites: 3PGA, 3‐phosphoglycerate; 6PG, 6‐phosphogluconate; 6PGL, 6‐phosphogluconolactone; ATP, adenosine triphosphate; F6P, fructose 6‐phosphate; G6P, glucose 6‐phosphate; NADPH, nicotinamide adenine dinucleotide phosphate; Ru5P, ribulose 5‐phosphate; RuBP, ribulose 1,5‐bisphosphate; and TP, triose phosphates (glyceraldehyde 3‐phosphate, dihydroxyacetone phosphate).

Theory 2. Isotope fractionation related to anaplerotic carbon flux into the Calvin–Benson cycle

Metabolic fractionation signals at tree‐ring glucose H¹ and H² are closely related (Fig. 2a,c). We propose this is due to (1) isotope fractionation related to anaplerotic carbon flux into the Calvin–Benson cycle (CBC) affecting both positions; and (2) dependences of both anaplerotic carbon flux into the CBC and sucrose‐to‐starch carbon partitioning on the rate of carbon assimilation.

Sharkey & Weise (2016) proposed the CBC is anaplerotically refilled by injection of five‐carbon sugar phosphates from the stromal pentose phosphate pathway with glucose 6‐phosphate (G6P) as precursor (Fig. 4). Primary flux control is believed to be exerted at the level of stromal phosphoglucose isomerase (PGI), which catalyses interconversions between fructose 6‐phosphate (F6P) and G6P. Under optimal growth conditions, the PGI reaction is strongly removed from equilibrium on the side of F6P resulting in low stromal G6P concentrations (Dietz, 1985; Gerhardt et al., ¹⁹⁸⁷; Kruckeberg et al., ¹⁹⁸⁹; Schleucher et al., ¹⁹⁹⁹). Proposedly, low G6P concentrations restrict the anaplerotic flux (Sharkey & Weise, 2016). However, as the PGI reaction shifts towards equilibrium and G6P synthesis, anaplerotic flux into the CBC is believed to increase (Sharkey & Weise, 2016). This involves stromal glucose‐6‐phosphate dehydrogenase (G6PD), the first enzyme of the pentose phosphate pathway. In the light, G6PD is downregulated via redox regulation by thioredoxin (Née et al., ²⁰⁰⁹). However, downregulation can be allosterically reversed by increasing G6P concentrations (Cossar et al., ¹⁹⁸⁴; Preiser et al., ²⁰¹⁹).

Phaseolus vulgaris and Spinacia oleracea grown under optimal conditions exhibit pronounced D depletions at glucose H² of leaf starch relative to sucrose (as mentioned in the previous section) (Schleucher et al., ¹⁹⁹⁹). These depletions were attributed to the stromal PGI reaction being more strongly removed from equilibrium ([G6P]/[F6P] = 3.31) than the cytosolic PGI reaction (Dyson & Noltmann, 1968; Schleucher et al., ¹⁹⁹⁹). Thus, as the stromal PGI reaction shifts towards equilibrium, H² of stromal G6P and its derivatives including leaf starch and tree‐ring glucose may become less D‐depleted. Furthermore, G6PD catalyses the irreversible conversion of G6P to 6‐phosphogluconolactone and was shown to have a strong D isotope effect in vitro (α = 2.97) (Hermes et al., ¹⁹⁸²). Thus, upregulation of the anaplerotic flux may cause D enrichments at H¹ of stromal G6P and its derivatives.

As indicated by modelling, glucose H¹ and H² become D‐enriched as drought increases and C _a decreases beyond a change point (Tables 1, 2, 3; Fig. 3a–c). Increasing drought and decreasing C _a may cause decreasing C _i (as mentioned in a previous section), which may result in decreasing carbon assimilation. As carbon assimilation decreases below a change point, the stromal PGI reaction shifts towards equilibrium and G6P concentrations increase (Dietz, 1985). This may cause increasing G6PD activity and anaplerotic flux. Thus, expanding theory by Sharkey & Weise (2016), we propose anaplerotic flux into the CBC is upregulated in response to decreasing carbon assimilation, C _i and C _a, and increasing drought beyond a change point.

Analysis of intramolecular ¹³C/¹²C ratios of the samples studied here has already provided evidence consistent with anaplerotic flux into the CBC at high VPD (Wieloch et al., ²⁰¹⁸). These authors explained a strong common ¹³C signal at tree‐ring glucose C‐1 and C‐2 by anaplerotic flux changes. For shifts of the PGI reaction towards equilibrium, they predicted ¹³C/¹²C increases at C‐1 and C‐2 at a ratio of 2.25 and found a ratio of 2.74 (+1.35SE, −0.60SE) confirming their prediction. However, changes in sucrose‐to‐starch carbon partitioning would have the same effect. Furthermore, two recent studies report isotope and gas exchange evidence consistent with anaplerotic flux in Helianthus annuus at low C _i (Wieloch et al., ^{2021a, 2022a}). That said, other mechanisms than those discussed here may contribute to the signals at tree‐ring glucose H¹ and H². This includes carbon flux into the oxidative branch of the cytosolic pentose phosphate pathway, shifts of the cytosolic PGI reaction and secondary isotope effects both in leaf and in tree‐ring cells.

Metabolic fractionation signals at H¹ and H²: a general phenomenon in C₃ plants?

Cormier et al. (2018) grew six phylogenetically diverse angiosperms under varying C _a. For leaf α‐cellulose, these authors reported average whole‐molecule ε _met increases of c. 20‰ in response to C _a decreases from 280 to 150 ppm, yet no significant change above 280 ppm. Hence, their observations are qualitatively in line with ours (Tables 1, 2, 3; Fig. 3a–c). However, our data show an average ε _met increase at tree‐ring glucose H¹ and H² of up to 150‰ (Fig. 2b). Assuming c. 40% heterotrophic hydrogen exchanges as observed at these positions in Picea abies (Augusti et al., ²⁰⁰⁶), we calculate an undiluted leaf‐level increase of c. 250‰ (150‰/60 × 100), which corresponds to a whole‐molecule increase of c. 70‰ (2 × 250‰/7). Thus, ε _met increases in the gymnosperm Pinus nigra are considerably larger than the c. 20‰ angiosperm average effect reported by Cormier et al. (2018). Additionally, whole‐molecule data have a limited interpretability (cf. ‘Introduction’) and effects reported by Cormier et al. (2018) may be located at either of the seven H‐C positions within α‐cellulose glucose. Thus, it remains uncertain whether the fractionation signals reported here occur generally in C₃ plants.

Conclusion

Stable isotope analysis on plant archives such as tree rings may convey information (inter alia) about plant acclimation and adaptation (e.g. to CO₂ fertilisation), biosphere–atmosphere CO₂ exchange and palaeoclimate trends. This long‐term perspective is inaccessible to manipulation and monitoring experiments yet crucial for understanding plant and Earth system functioning. The better we understand plant isotope fractionation, the more information can be retrieved from archives (at higher quality). The present paper and recent studies on metabolic fractionation (Wieloch et al., 2018, 2021a,d,c; Ladd et al., ²⁰²¹) show there is much room for improvement. Thus, we recommend pushing the development of intramolecular isotope methodology.

Author contributions

TW and JS conceived the study. TW led the research. TW, MG, HS, JS and IE collected and prepared the samples and acquired data. TW and JY analysed the data. TW developed theories about the origin of reported isotope signals. TW wrote the paper with input from AA, HS, JS and JY.

Supporting information

Notes S1 Statistical analyses.

Notes S2 Grouping of annual δD _i patterns of tree‐ring glucose by HCA.

Notes S3 Histograms of ε _met.

Notes S4 Bivariate relationships of ε _met with precipitation and atmospheric CO₂ concentration.

Notes S5 Contributions of δD _i to the variance in δD_g after excluding data not affected by the fractionating metabolic processes.

Notes S6 Contributions of δD _i to the variance in δD_g after excluding data affected by the fractionating metabolic processes.

Notes S7 Metabolic fractionation at the whole‐molecule level.

Please note: Wiley‐Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.