Second-Sphere Lattice Effects in Copper and Iron Zeolite Catalysis

Abstract

Transition metal-exchanged zeolites perform remarkable chemical reactions from low temperature methane to methanol oxidation to selective reduction of NOx pollutants. As with metalloenzymes, metallozeolites have impressive reactivities that are controlled in part by interactions outside the immediate coordination sphere. These second-sphere effects include activating a metal site through enforcing an “entatic” state, controlling binding and access to the metal site with pockets and channels, and directing radical rebound vs cage escape. This review explores these effects with emphasis placed on but not limited to the selective oxidation of methane to methanol with a focus on copper and iron active sites, although other transition metal ion zeolite reactions are also explored. While the actual active site geometric and electronic structures are different in the copper and iron metallozeolites compared to the metalloenzymes, their second-sphere interactions with the lattice or the protein environments are found to have strong parallels that contribute to their high activity and selectivity.

Graphical Abstract

1. INTRODUCTION

The purpose of this review is to illuminate the strong parallels between the second-sphere effects in metalloenzyme and metallozeolite catalysis. We first present the more well-developed concepts of second-sphere effects in metalloenzymes to use as a reference for those we focus on in the metallozeolites in this review. These build on our earlier Chemical Review on metallozeolites (Chem. Rev. 2018, 118, 2718–2768) where the focus was on the first coordination sphere of the zeolite active site.¹ In bioinorganic chemistry, the metal ion cofactor plays the central role for enzymes to perform their functions. These functions encompass a remarkable number of applications including O₂ binding, transfer, and activation, proton pumping, metal regulation, substrate oxidation, oxygenation, reduction, and countless others. Although biology uses a wide range of transition metals from nickel to tungsten, copper and iron dominate the world of O₂ binding and activation.^2–5 This chemistry is particularly impressive given the inert triplet state of O₂ and the stability of the singlet substrates these sites are able to oxidize, e.g. methane by soluble and particulate methane monooxygenases (sMMO and pMMO).

Given the clear role the metal center plays in these reactions, a vast array of model complexes has been synthesized to better understand these enzymes as well as mimic their reactivity.^6–10 However, these homogenous models do not achieve the same level of reactivity and selectivity as their enzyme counterparts, even when the first sphere ligation is well reproduced. The protein serves much larger and more specific roles than simple ligation. These second-sphere effects, the perturbations to the active site from outside the immediate coordination sphere, are an indispensable part of metalloenzyme catalysis.

1.1. Second-Sphere Effects in Bioinorganic Chemistry

The effects of the protein scaffold in metalloenzymes have been well-documented, uncovering the fine evolutionary tuning of the protein to serve a variety of purposes. In polymetallic active sites, the metals are precisely positioned to interact with the substrate in a desired fashion. For example, in the coupled binuclear copper proteins hemocyanin (Hc) and tyrosinase (Tyr), the two Cu(I) sites reduce O₂ to form a side-on peroxo bridged complex capable of shuttling oxygen or oxidizing phenols and catechols.^11–15 There is a similar binuclear copper site in the multicopper oxidases (MCOs) called the type 3 (T3) center; however, without the additional type 2 (T2) Cu center to form a trinuclear copper cluster, it is unable to react with O₂, despite the similar histidine ligation in this binuclear site to those in Hc and Tyr.^16,17 This difference in reactivity is due mostly to the Cu···Cu distance in the two sites. In Hc and Tyr, the copper atoms are about 3.6 Å apart (Figure 1A) creating an electrostatic repulsion between the two metals that destabilizes the reactants and makes the transformation to the side-on peroxo overall exothermic.¹⁸ However, in the case of the T3 copper site in the MCOs, the Cu(I) atoms are ~6.5 Å apart, stabilizing the reactants and making O₂ binding endothermic, thus requiring the third (T2) copper for O₂ activation and generation of a different oxygen intermediate.¹⁸ The protein has tailored the histidine ligands to place the copper atoms at the appropriate distance necessary to react with O₂ for different functions (electrophilic activation versus reduction to H₂O).

Figure 1.

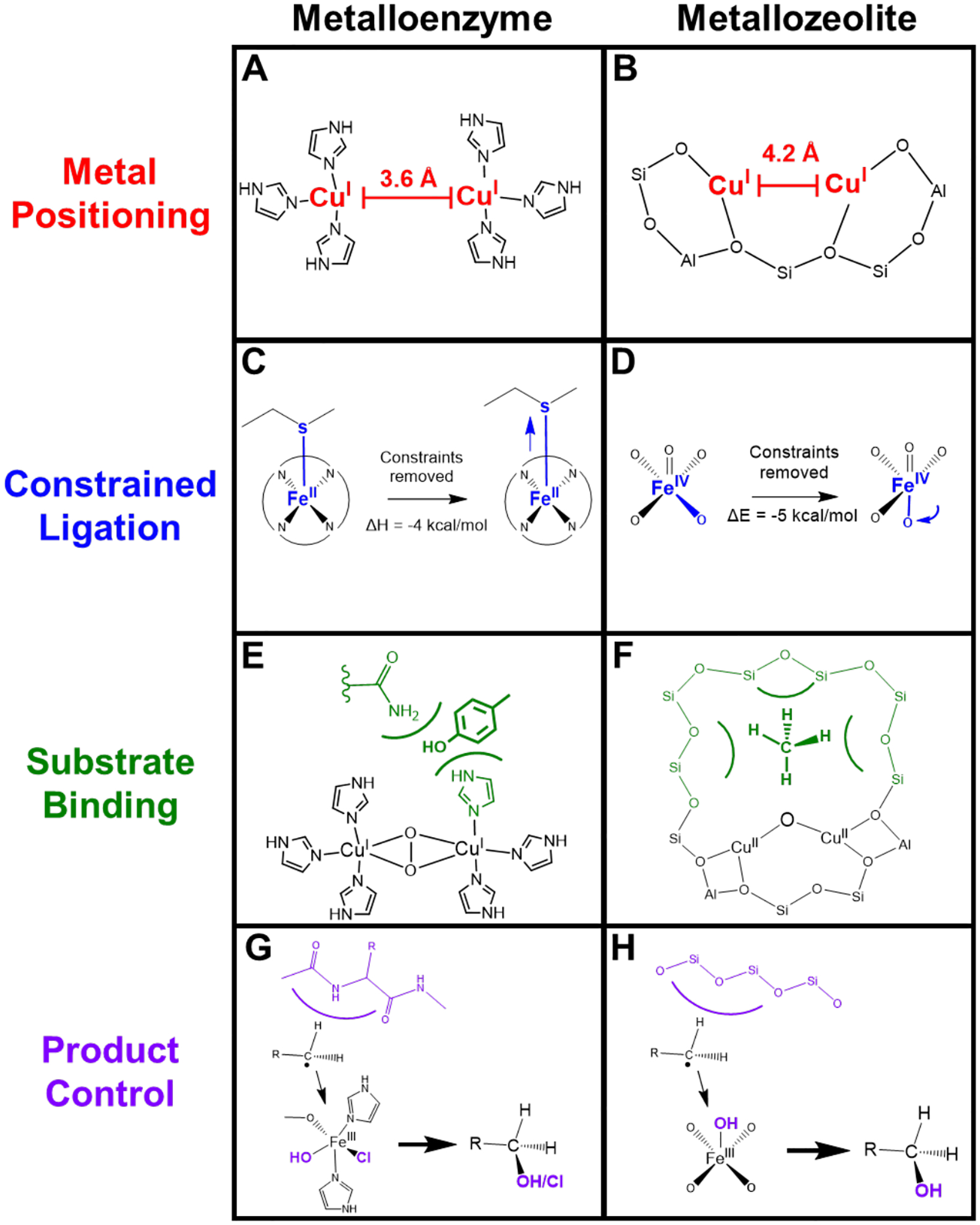
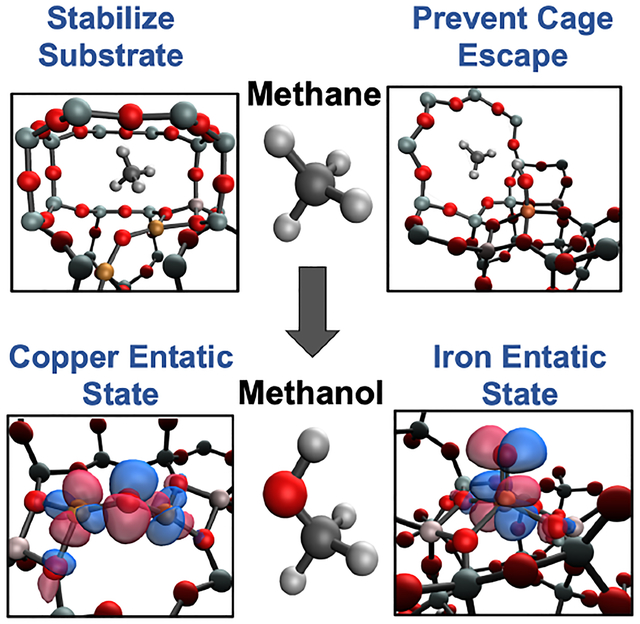
Comparison of second-sphere effects in metalloenzymes and metallozeolites. (A) Cu···Cu distance set by protein constraints. (B) Cu···Cu distance set by zeolite lattice. (C) Entatic state of Fe-Met bond in cytochrome c. (D) Entatic state of α-O in iron zeolites. (E) Stabilization of phenolic substrate in Tyr. (F) Stabilization of methane in copper zeolites. (G) Steric barrier in protein pocket (blue) leading to rebound of radical. (H) Steric barrier in zeolite cage (blue) leading to rebound of radical.

Proteins can also play a similar role in constraining amino acid ligand binding to the metal center. This is the case in the low-spin heme site in cytochrome c. The central Fe(II) atom is axially ligated by a histidine and a methionine, the latter having a surprising bond to the iron given the iron’s reduced state. Although this bond is weak, it plays an essential role, keeping the metal site low spin as it transfers between the 2+ and 3+ oxidation states, maintaining the correct reduction potential and a low inner-sphere reorganization energy to allow fast electron transfer.¹⁹ Using ultrafast photodissociation of the axial methionine ligand, and measuring its rebinding using X-Ray Absorption Spectroscopy (XAS) and X-Ray Emission Spectroscopy (XES), Mara et al. quantified the strength of the Fe-Met bond in cytochrome c to be 6.5 ± 1.2 kcal/mol.¹⁹ This is 4 kcal/mol stronger than what is found for Met binding to the heme Fe(II) without protein constraints (Figure 1C). This is substantial as it changes the association of the ligand from endergonic to exergonic at room temperature. This geometric constraint on the metal, commonly called an entatic state, allows cytochrome c to properly shuttle electrons quickly to cytochrome c oxidase at the correct redox potential to pump protons across the mitochondrial membrane for ATP synthesis.

In addition to the protein structure having direct effects on the central metal atom, the active site pocket is also critical in substrate binding. This is demonstrated well in the differential monooxygenase reactivity between Tyr and Hc. Despite their similar side-on peroxo copper dimer active site, Hc cannot monooxygenate phenolic substrates nor oxidize diphenols unlike Tyr (Figure 1E). This is a direct consequence of the difference in substrate access to the active site between the two enzymes. A similar reactivity differential is seen between Tyr and catechol oxidase where, although both have the same active site and can oxidize diphenols, catechol oxidase cannot oxygenate phenolic substrates. The Tyr protein scaffold has evolved to both oxygenate phenols and oxidize the resulting diphenol to quinone through protein pocket access, binding, and possibly via transition state control. This is unlike its evolutionary counterparts with similar active sites but different catalytic roles.²

Proteins also demonstrate control of generated intermediates that ultimately affect product formation. This control is essential in proteins that perform H-atom abstraction (HAA) like sMMO and cytochrome P450, where generation of a radical could potentially deactivate the metal center and create deleterious products if it escaped the protein pocket.^20,21 However, the surrounding amino acids create a steric barrier that guides the radical towards recombination with the metal hydroxide, allowing product formation and turnover. This kind of rebound can further be tuned by the active site to create different products, as in the difference in selectivity towards halogenation vs hydroxylation in SyrB2 (Figure 1G).²² Importantly, this allows functionalization of strong C-H bonds at room temperature, a difficult chemical feat.

Proteins utilize the constraints of their ligand scaffold and the influence of the surrounding amino acids in the active site pocket to perform difficult chemistry and dictate product formation. These well-tailored second-sphere effects are intrinsic to protein chemistry and explain the shortcomings of model complexes which often simply replicate the first coordination sphere. Although model complexes fail to mimic many of these second-sphere effects, transition metal doped zeolites can. These porous structures allow metals to bind to a rigid ligand scaffold and create protein pocket-like microenvironments that enable substrate activation and control, mimicking many of the second-sphere effects that are necessary for metalloenzyme chemistry.

1.2. Introduction to Zeolite Structure

Zeolites are microporous solids built from individual silica and aluminum tetrahedral units (T-sites) that connect to form various shapes and topologies. Over 250 topologies have been compiled by the International Zeolite Association, each designated by a three-letter code.²³ The size of the rings in zeolites are typically designated by the number of tetrahedra in the ring, e.g. a 10 membered ring (MR) channel would contain 10 silica/aluminum atoms and 10 oxygen atoms. Some topologies are composed of large open structures like the 12 MR pores in *BEA or the 10 MR pores in MFI, the latter are intersected by sinusoidal 10 MRs. There are also topologies that have more constricted environments like the cages seen in CHA and FER. Some topologies can have a mix of open and closed environments like MOR which contains both large 12 MR channels and constricted side pockets adjacent to these channels (Figure 2).²³ In addition to having various topological structures, zeolites contain isolated local negative charges at the aluminate sites in the lattice. These sites are charge balanced by cations such as protons, alkali earth metals, or transition metals. The topology that hosts these aluminate sites, the density of the sites, their locations in the lattice, and the charge balancing cations are all a function of the synthesis procedure, allowing fine tuning of a desired material, including tuning of second-sphere effects for catalysis. The purity of zeolites is often confirmed using powder X-ray diffraction with some zeolite syntheses utilizing the ability to incorporate defects into the zeolite through methods like dealumination. Some topologies are partially disordered like *BEA but have predictable patterns to the disorder.^24–26

Figure 2.

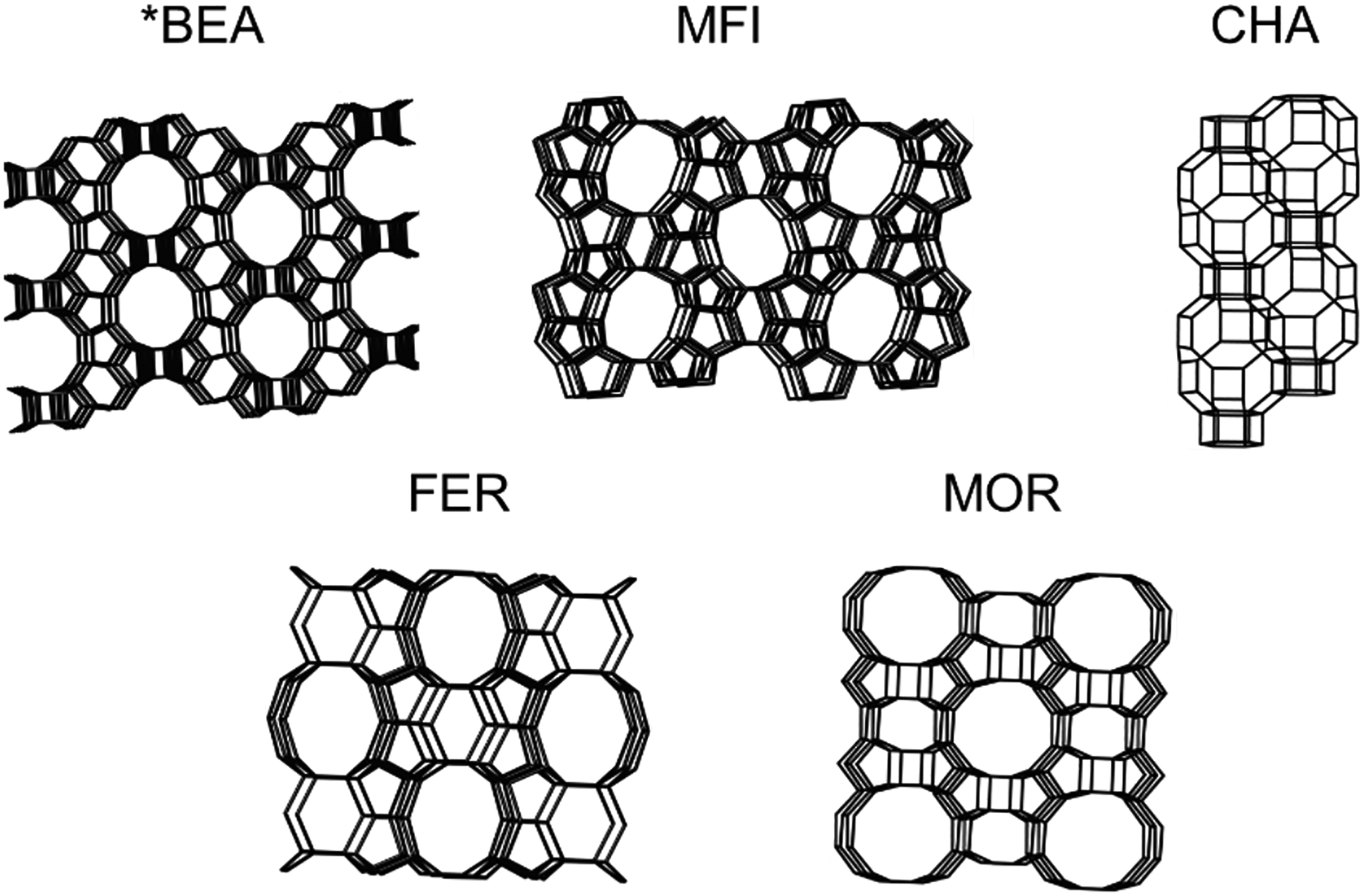
Framework structures of zeolites Beta (*BEA), mordenite framework, inverted (MFI), Chabazite (CHA), Ferrierite (FER), and Mordenite (MOR) zeolite topologies. Adapted with permission from ref 23. Copyright 2021 International Zeolite Association.

1.3. Second-Sphere Effects in Metallozeolites

While there are limitations in the comparison of second-sphere effects in metalloenzymes relative to metallozeolites, notably the ability for metalloenzymes to undergo significant structural and conformational changes upon substrate binding (eg. cooperativity effects) that are not possible in the more rigid zeolite lattice, there are strong parallels, The rigidity of the zeolite lattice allows it to bind transition metal complexes in a way that destabilizes and primes them for reactivity. Just as Hc and Tyr hold two Cu(I) sites at an ideal separation to react with O₂, metallozeolites can also place Cu(I) sites at appropriate distances to react with O₂ (and also with N₂O) as shown in Figure 1B.^27,28 The zeolite lattice can also bind individual metal sites in unstable conformations that prime them to react, like with the α-O active site in iron zeolites. This site is a high-spin square pyramidal Fe(IV)=O which reacts with CH₄ at room temperature; however, without zeolite constraints it would relax one of its equatorial ligands into the molecular z-axis, stabilizing the site and greatly decreasing its reactivity (Figure 1D).²⁹ This “entatic” state (nomenclature from bioinorganic chemistry)³⁰ imposed by the zeolite lattice is conceptually similar to the constrained Fe-Met bond in cytochrome c.¹⁹ The constrained binding by the zeolite lattice is expanded on in Section 3.

The zeolite can also affect substrate binding to the site through stabilizing van der Waals interactions. Just as the protein pocket lowers the barrier for oxidation of phenols in Tyr, a zeolite pocket can stabilize CH₄ through van der Waals interactions and lower the apparent barrier for CH₄ oxidation as discussed in Section 4 (Figure 1F).³¹ The lattice can also control the reactive outcome by creating barriers to prevent the loss of radical products. This directing of radical rebound is similar to that seen in enzymes that perform HAA and can be used to efficiently produce CH₃OH without deactivation of the catalyst, the focus of Section 5 (Figure 1H).³²

These second-sphere effects will be explored in-depth in this review; however, a complete understanding of these requires understanding the first coordination sphere of the metal sites of interest. Thus, we begin the review with an overview of how the relevant metallozeolites are synthesized, how metals bind to the lattice, and how active sites are formed and spectroscopically identified.

2. Copper and Iron Active Sites in Metallozeolites: Lattice Motifs that Stabilize Transition Metals

Spectroscopic definition of the first sphere ligation of copper and iron active sites in zeolites provides the foundational knowledge to understand and explore second-sphere effects. This section provides background on the active sites (and their precursors) used in this review to explore second-sphere lattice effects; however, it is not an exhaustive collection of the work on active site identification in copper and iron zeolites. For more information, we point readers to our previous review.¹

2.1. Copper and Iron Zeolite Preparation

Transition metal ions are often introduced into the zeolite lattice through solution ion-exchange of solubilized metal salts. For copper and iron, this exchange is most commonly done with Cu(II) and Fe(III) as Cu(I) and Fe(II) salts are readily oxidized in air. Although incorporation of Cu(II) through aqueous ion exchange is pretty standard, due to the insolubility of Fe(III) oxo/hydroxo polymers, iron is often incorporated through impregnation of the iron salt in an organic solvent like toluene. To remove residual organic anions, solvent, and water, exchanged zeolites are calcined in an O₂ atmosphere to combust any carbon containing compounds and desorb liquids. This leaves the bare metal ions bound to the zeolite lattice.

After calcination, the zeolite is – in some cases – heated in an inert atmosphere or in vacuum to undergo an autoreduction process where the metal is reduced concurrent with the production of O₂. For the autoreduction of Cu(II), two schemes have been suggested to explain this phenomenon that are yet to be experimentally validated:^33–35

$$\begin{gathered} 2{\left[\text{Cu-OH}\right]}^{+}\to {\left[\text{Cu-O-Cu}\right]}^{2+}+{\text{H}}_2{\text{O}}_{(\text{g})} \\ {\left[\text{Cu-O-Cu}\right]}^{2+}\to 2{\text{Cu}}^{+}+0.5{\text{O}}_{2(\text{g})} \end{gathered}$$ (1)

$$\begin{gathered} 2{\left[\text{Cu-OH}\right]}^{+}\to {\text{Cu}}^{+}+{\text{Cu}}^{2+}–{\text{O}}^{-}+{\text{H}}_2{\text{O}}_{(\text{g})} \\ {\text{Cu}}^{+}+{\text{Cu}}^{2+}{\text{-O}}^{-}\to 2{\text{Cu}}^{+}+0.5{\text{O}}_{2(\text{g})} \end{gathered}$$ (2)

Depending on the topology, Si/Al ratio, copper loading, and temperature of autoreduction, different percentages of copper can be reduced with the resultant Cu(I) ranging from 20–80%.^36,37 Some of the remaining non-reduced Cu(II) species can be observed via Electron Paramagnetic Resonance (EPR) with corresponding ligand field bands observed using Diffuse Reflectance UV-Vis (DR-UV-vis) spectroscopy. These sites are often referred to as “spectator ions” as they are unreactive in CH₄ oxidation chemistry. Density Functional Theory (DFT) models were generated for these spectator sites using large cation X-ray powder diffraction (XRD) studies, and spectroscopic handles (d-d transitions and EPR g-values) were calculated using complete active space perturbation theory (CASPT2). The models that best correlate to experiment suggest the Cu²⁺ ions preferentially bind to negatively charged aluminate sites with 4-fold coordination.^38–43 In zeolites with a high copper loading, autoreduction conditions can also lead to condensation of copper sites to EPR silent polynuclear species.⁴⁴ Given the presence of multiple different Cu species, further characterization of these spectators by techniques like Extended X-ray Absorption Fine Structure (EXAFS) is difficult.

To gain better understanding of spectator speciation, Paolucci et al. evaluated the stability of spectator sites bound to one vs. two aluminate sites (1 Al or 2 Al) in the CHA topology.⁴⁵ They calculated the energy of copper with various ligands and oxidation states for 1 Al and 2 Al as well as the exchange energy of copper moving between 1 Al and 2 Al. Over a variety of conditions, Cu(II) ions prefer to bind to 2 Al over 1 Al. In high temperature and ambient atmospheric conditions, they assume the 1 Al compound to be a Cu(II)OH based on a potential O-H stretch observed in infrared spectroscopy (IR) at 3660 cm⁻¹ and the 2 Al compound to be bound Cu(II) bridging two Al sites. Assuming random distribution of Al sites in the lattice, assuming Cu ions fill 2 Al sites first, and assuming only mononuclear copper sites, they constructed a phase diagram to predict the ratio of mononuclear [Cu(II)OH]¹⁺ to total copper present based on the Si/Al ratio and the copper loading (Cu/Al ratio) of an individual zeolite(Figure 3, color gradient). They tested their predictions by synthesizing a series of CuCHA materials with varying Si/Al and Cu/Al ratios (the white dots represent synthesized CuCHA material with a given Si/Al and Cu/Al ratio based on the dot’s location in the figure in Figure 3). For the test materials, they quantified residual H⁺ sites left on the aluminum T-sites that were not replaced by copper during ion exchange to gauge if copper replaced one or two Al T-sites and the former corresponds to [Cu(II)OH]¹⁺ formation. The quantification was performed by saturating the zeolite with NH₃ and quantifying Al-bound NH₄+ species through temperature programmed desorption. The amount of remaining H⁺ sites was tested across three different Si/Al ratios and various copper loadings and matched well with the predicted [Cu(II)OH]⁺¹/total copper ratio given by the color background at that point. This was validated through Co(II) exchange studies. Overall, spectator Cu(II) ions tend to fill all 2 Al sites prior to 1 Al sites and the proposed model in Figure 3 predicted well the relative abundance of 1 Al exchanged sites.⁴⁵

Figure 3.

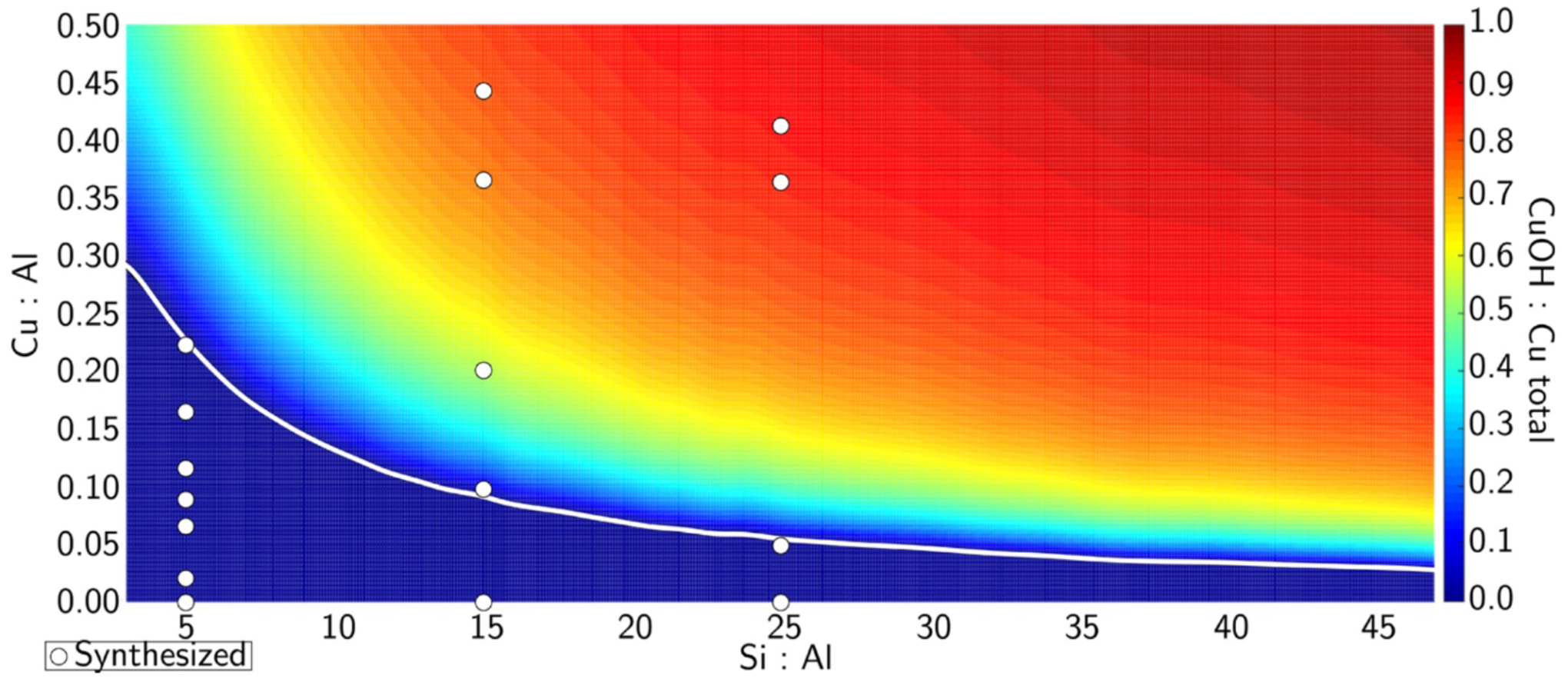
[Cu(II)OH]⁺¹/total copper ratio as a function of the Cu/Al and Si/Al ratios. Color scale indicates amount of [Cu(II)OH]⁺¹. White line is the border between a solely 2 Al region to a mixed 2Al and 1Al region. White circles represent materials synthesized in that study. Reproduced with permission from ref 45. Copyright 2016 American Chemical Society.

Like with copper, iron zeolites can also be autoreduced after calcination. The major proposed mechanism for the autoreduction of mononuclear Fe(III) to Fe(II) is:

$$2{\left[\text{Fe-OH}\right]}^{2+}\to {\left[\text{Fe-O-Fe}\right]}^{4+}+{\text{H}}_2{\text{O}}_{(\text{g})}$$

$${\left[\text{Fe-O-Fe}\right]}^{4+}\to 2{\text{Fe}}^{2+}+0.5{\text{O}}_{2(\text{g})}$$

and for oligomeric iron species found at high iron loading:

$$6{\text{Fe}}_2{\text{O}}_3\to 4{\text{Fe}}_3{\text{O}}_4+{\text{O}}_{2(\text{g})}$$

$$2{\text{Fe}}_3{\text{O}}_4\to 6\text{\hspace{0.17em}FeO}+{\text{O}}_{2(\text{g})}$$

Depending on the iron loading and autoreduction atmosphere, samples can have varying reduction ranging from 63% to close to 100% (using H₂ reduction at 700 °C following He autoreduction at 900 °C).^29,46–48 Non-reduced iron in these samples aggregates as iron oxide (Fe₂O₃) clusters with Mössbauer parameters similar to hematite.

2.2. Reduced Ion Binding Sites

The reduced copper and iron ions can be oxidized into active sites for CH₄ oxidation (O₂ and N₂O can be used as the oxidant for copper and only N₂O for iron). These ions bind to the negatively charged anionic aluminate T-sites. Al T-sites tend to form away from each other and do not form local pairs (Al-O-Al bonding motifs) an observation known as Loewenstein’s rule.⁴⁹ Al pairs also do not usually form in the same 5 member-ring (Takaishi-Kato rule).⁵⁰ The more general trend of aluminum ion repulsion is referred to as Dempsey’s rule.⁵¹ However, Al T-sites do not only organize based on this repulsion, and certain T-sites preferentially contain aluminum ions as revealed by solid state²⁹Si and²⁷Al Nuclear Magnetic Resonance (NMR), X-ray diffraction, XES, XAS, and cation sitting studies.^52–54 Dědeček et al. were able to significantly alter Al T-site occupation by varying synthetic conditions in the creation of zeolite Socony Mobil-5 (ZSM-5), concluding that the kinetics of zeolite synthesis determine the Al distribution.⁵⁵ There has also been work on varying synthetic conditions to change the proximity of aluminum T-sites to create “paired” and “unpaired” versions in the same topology. The CHA topology is an appropriate candidate for these studies given that it contains only a single crystallographically defined T-site, removing T-site bias as a variable. Crystallizing CHA in the presence of a large N,N,N-trimethyl-1-adamantyl ammonium cation predominantly creates isolated sites whereas crystallization with increasing amounts of Na⁺ leads to site pairing.^56,57 Using varying ratios of these two cations allows control of relative pairing in the zeolite. In addition, the exact aluminum sources employed⁵⁷ in the synthesis and whether amorphous or crystalline (e.g. zeolites themselves as starting materials in an interzeolite conversion) aluminum and silica sources are used also influence the final Al distribution.⁵⁸ These studies motivate further work on understanding the conditions that lead to a particular T-site Al occupation. This synthetic control is essential given that the location of aluminum sites in the lattice dictates possible binding modes for the reduced Cu(I) and Fe(II) species.⁵⁸

2.2.1. Copper Binding Sites

Because Cu(I) is a d¹⁰ ion, its characterization by techniques that have been useful for Cu zeolites like EPR and resonance Raman (rR) isn’t viable. However, using well-defined Cu(II) active sites formed from Cu(I), Cu(I) precursor structures can be predicted. These sites were explored in CuMFI by Tsai et al. using DFT calculations.²⁸ Cu(I) sites (generated from removing the O from a [Cu₂O]²⁺ active site) bind to aluminate sites with four major binding motifs: (I) two-coordinate with two O atoms binding from the same Al T-site with small bite angles (~80°), (II) three-coordinate with two O atoms binding from the same Al T-site and a third O atom from a Si T-site, (III) two-coordinate near linear (~149°) with one O atom binding from a Si T-site and the other from an Al T-site, and (IV) two-coordinate near linear with each O atom from a different Al T-site (Figure 4). Binding modes I and II are relatively close in energy and are 3–21 kcal/mol higher in energy than binding mode III. Linear binding mode IV is at least 24 kcal/mol more stable than binding modes I and II. Overall, the most stable Cu(I) sites bind with two major energetic preferences: 1) binding to the more basic Al T-sites 2) binding in a more linear fashion.

Figure 4.

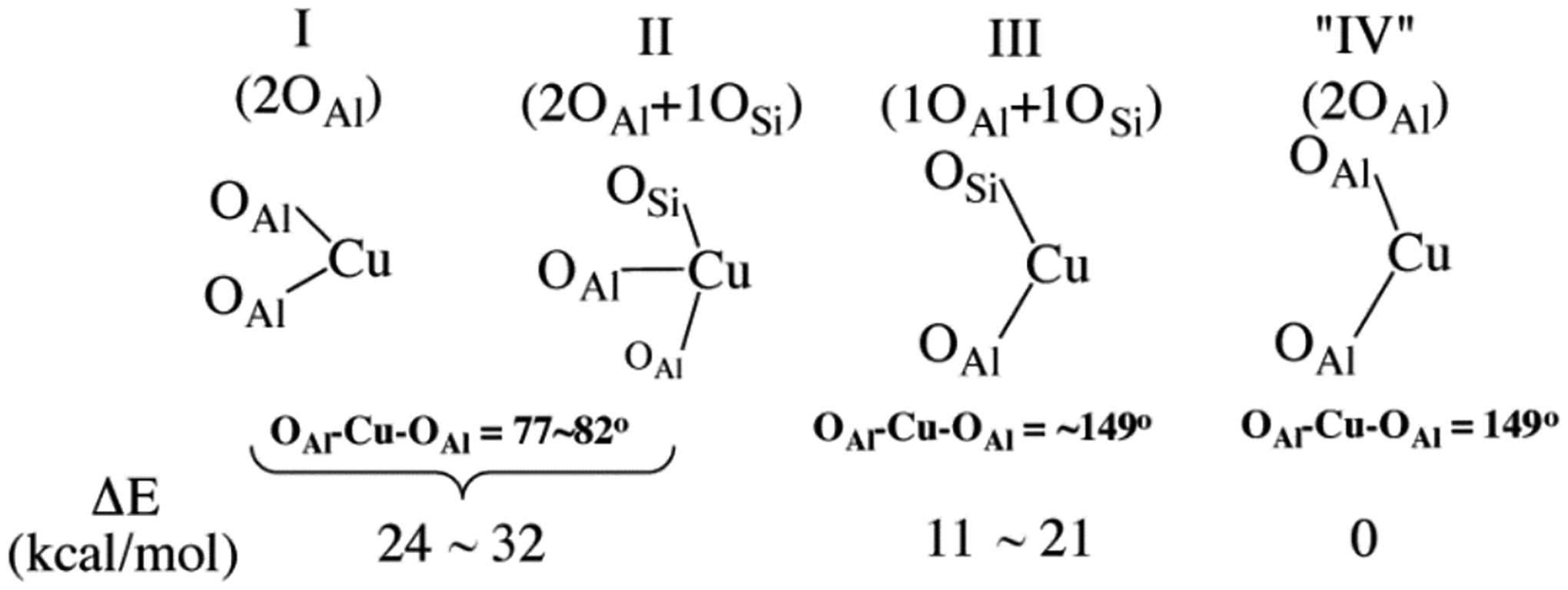
Structures, bond angles, and relative energies of four binding motifs for Cu(I) to the zeolite lattice. “IV” is hypothetical. Adapted with permission from ref 28. Copyright 2014 American Chemical Society.

2.2.2. Iron Binding Sites

The possible binding modes of Fe(II) in the lattice are distinctly different from Cu(I) given its higher oxidation state. These modes were evaluated spectroscopically through synchrotron techniques of the well-defined, > 70–80% abundant α-Fe(II) site in the *BEA topology.⁵⁹ Fe K-Edge EXAFS provides information on the first coordination shell of α-Fe(II) (Figure 5A), which is known to be mononuclear based on Mössbauer and VTVH-MCD vide infra. This site can be fit with a first coordination sphere of four oxygen atom ligands at 2.02 Å away from the Fe^II (r1 on Figure 5B), two T-site atoms can be fit at the second coordination shell at 2.81 Å away from the Fe^II (r2 in the diagram in 5B), and a third coordination shell with four T-site atoms can be fit at 3.29 Å (r3 in Figure 5B). The second and third coordination shells of T-sites are direct evidence of α-Fe(II) existing in 6 member-rings. The location of the negatively charged aluminate sites within the ring cannot be disambiguated from EXAFS (Figure 5B); however, Nuclear Resonance Vibrational Spectroscopy (NRVS) provided important complementary information, allowing the Al distribution in the 6MR to be resolved.

Figure 5.

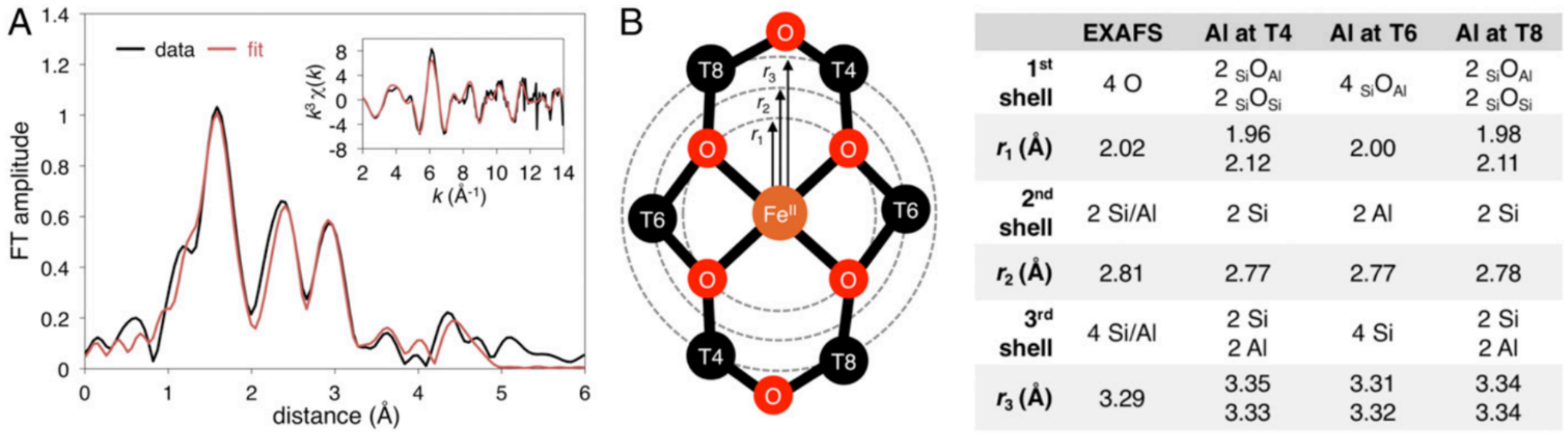
(A) Fourier transforms of the 2 ≤ k ≤ 14 Å⁻¹ EXAFS region (black) and fit (red) of α-Fe(II). Inset: k³-weighted EXAFS spectrum of α-Fe(II) in*BEA* (black) with fit (red). (B) EXAFS scattering interactions of square planar Fe(II) in a 6MR (left) and comparison of EXAFS fit to models with the Al located at different T-sites (right). Reproduced from ref 59. Copyright 2018 National Academy of Sciences.

The NRVS spectrum of α-Fe(II) in *BEA contains an intense plateau in the lower energy region that peaks around 200 cm⁻¹ before consistently descending until ~450 cm⁻¹. There is a broad feature centered at 530 cm⁻¹, and the spectrum is featureless from above 600 cm⁻¹ (Figure 6A). The potential aluminum distributions in the ring were probed with three DFT models: 2T6, 2T4, and 2T8 (Figure 6B). In NRVS, only vibrations with significant⁵⁷Fe motion are observed; for 4 coordinate planar α-Fe(II) this can be broken down into six principle vibrations shown in Figure 7. The out-of-plane (OOP) Fe translation mode (ν₁) has strong intensity between 50–150 cm⁻¹ in all three models. Given the lack of axial ligands in this square planar geometry, the Fe atom has more freedom to translate out of its ligand plane, giving these vibrations high intensity. The Fe - O₄ translation (ν₃) also contributes intensity in this region in all three models. The in-plane (IP) equatorial bending mode (ν₂) is also in this energy region but is a direct probe of the aluminum distribution within the ring. This bending mode is located in the 120–130 cm⁻¹ region for the 2T4 and 2T8 models while in the 2T6 model this vibration occurs higher at ~185 cm⁻¹, which is closer to the experimental feature ~200 cm⁻¹ (Figure 6). In the 2T6 model, the Fe(II) has 4 anionic oxo ligands with strong bonds that shift the frequency of the ν₂ vibration to higher energy compared to the other models. The α-Fe(II) site therefore binds in a square planar, four coordinate fashion to two opposite aluminate sites (Figure 6B, top) in a 6 MR.

Figure 6.

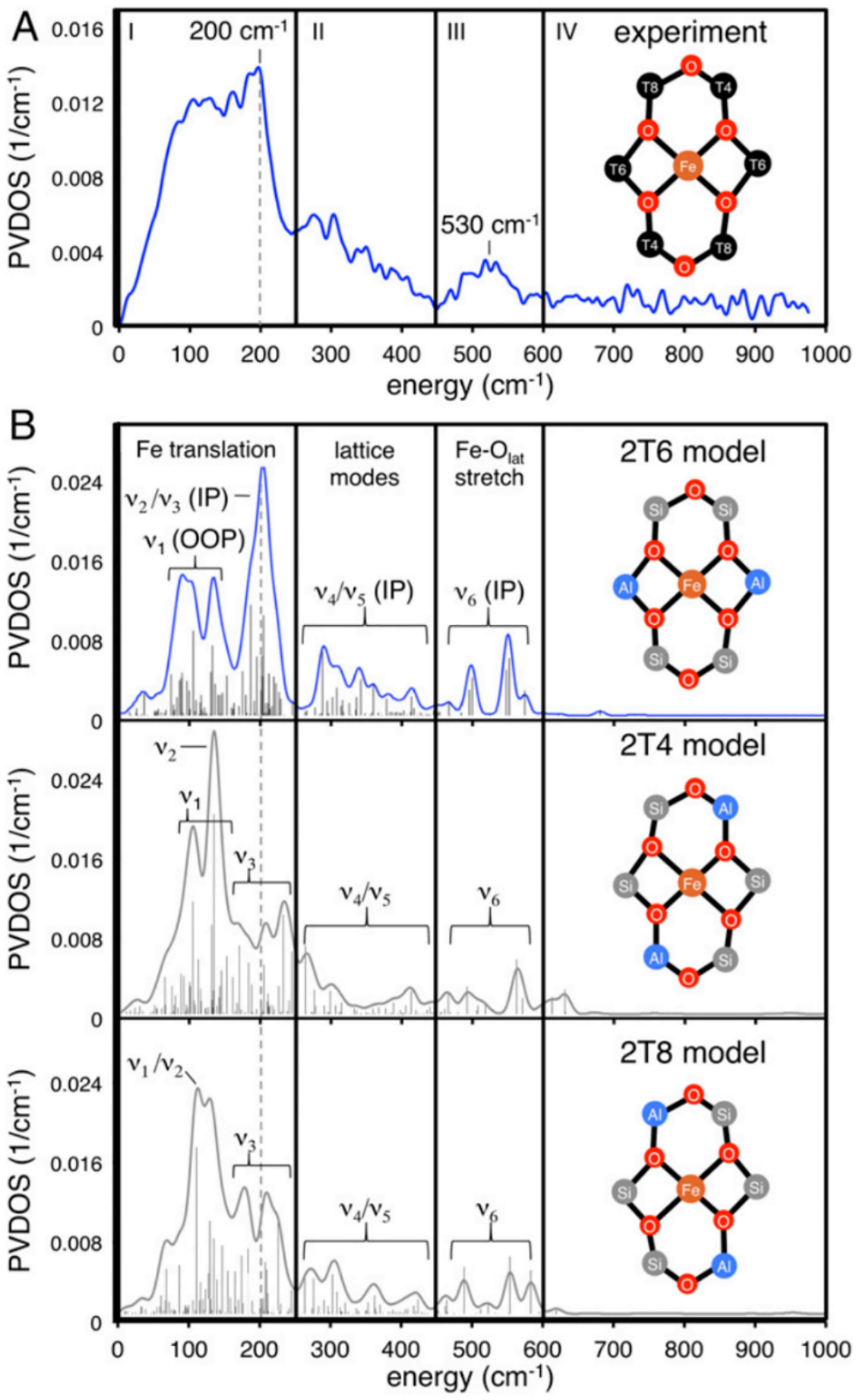
(A) NRVS spectrum of α-Fe(II). (B) DFT-simulated spectra for various aluminum configurations. Reproduced with permission from ref 59. Copyright 2018 National Academy of Sciences.

Figure 7.

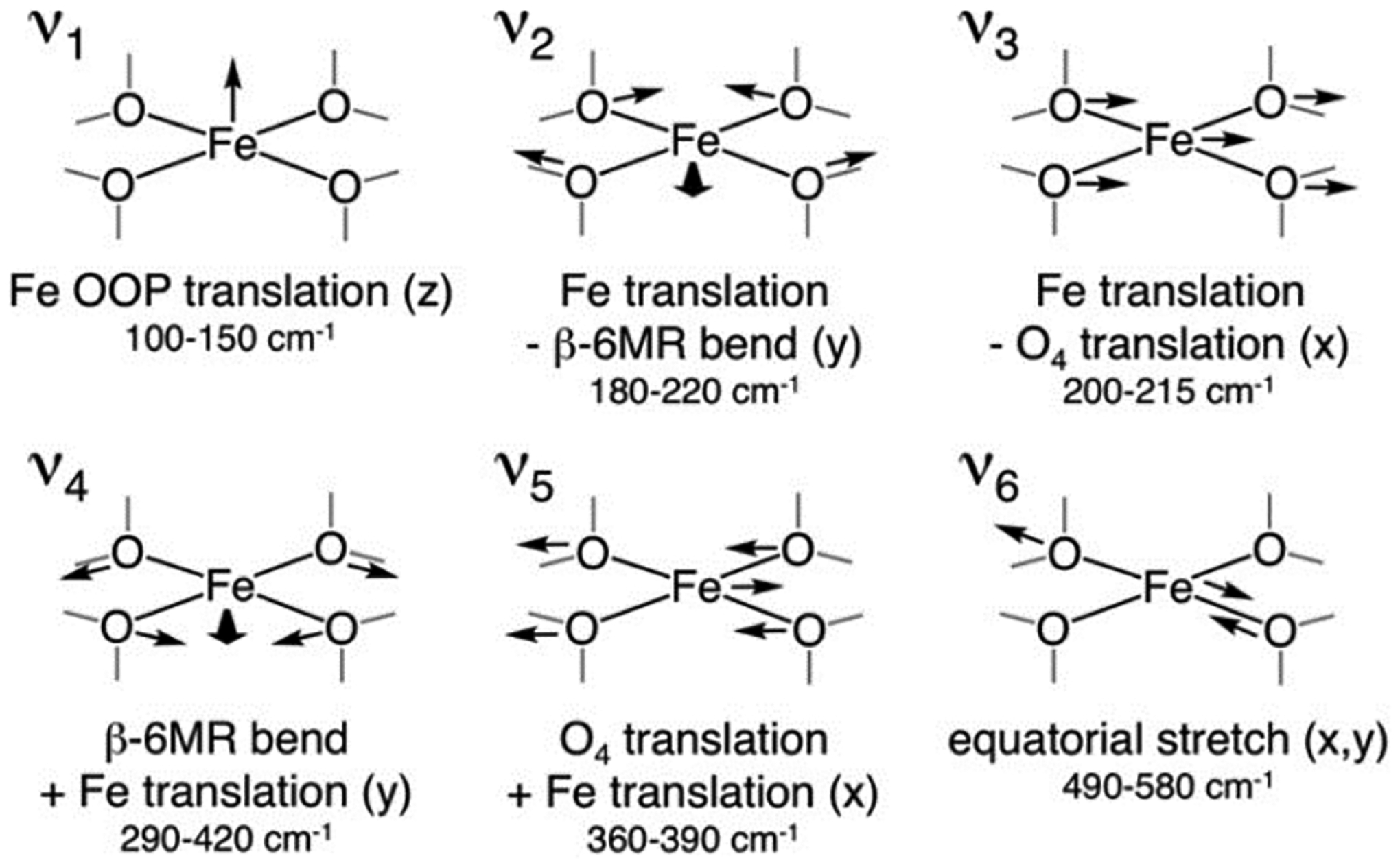
NRVS-active vibrations of α-Fe(II) and their DFT-predicted frequencies for the 2T6 model. Reproduced with permission from ref 59. Copyright 2018 National Academy of Sciences.

2.3. Spectroscopic Definition of Copper and Iron Active Sites

2.3.1. Copper Active Sites

Two Cu(I) sites separated by ~4.5 Å can be activated by O₂ or N₂O to form an active site capable of selectively converting CH₄ to CH₃OH. (note this activation with O₂ and N₂O is presented later in Section 3.1.). It has also been suggested in literature that water can oxidize Cu(I) sites but this remains a disputed topic in literature.⁶⁰ A strong absorption feature appears at ~22000 cm⁻¹ during O₂/N₂O activation that decays upon reaction with CH₄ (Figure 8, Inset A).⁶¹ Tuning into this feature with a 458 nm laser results in resonance enhancement of vibrations associated with the active site. Several vibrations show a distinct isotope shift upon activation with¹⁸O₂ (Figure 8). The vibration at 870 cm⁻¹ is in a region commonly associated with an O-O stretch. However, upon activation with the mixed isotope ^16/18O₂, the rR spectrum of this material is a sum of normalized¹⁶O₂ and¹⁸O₂ activation, eliminating the possibility of an O-O bond in this active site (this would display a new stretch at ~850 cm⁻¹) (Figure 8, Inset B). The observed stretches and isotope shifts were inconsistent with all previously defined Cu/O₂ species and correspond to a new species. In the case of MFI, the rR spectrum contains an intense 456 cm⁻¹ (Δ^16/18O = 8 cm⁻¹) vibration, a weak 870 cm⁻¹ (Δ^16/18O = 40 cm⁻¹) vibration, and a second quantum of the weak vibration at 1725 cm⁻¹ (Δ^16/18O = 83 cm⁻¹) that is 6 times more intense than the first quantum. The intense 456 cm⁻¹ vibration must be a symmetric vibration to be rR allowed and intense. Analogously, the 870 cm⁻¹ feature is a weak rR forbidden antisymmetric oxo stretch while its first overtone is symmetric and thus rR allowed. These isotope sensitive symmetric and antisymmetric stretches are indicative of a strong μ-oxo ligand and their energy splitting shows that the active site has a bent (140°) mono-μ-oxo bridged dicopper core [Cu₂O]²⁺. This same [Cu₂O]²⁺ motif has now also been defined using rR spectroscopy in the MOR and CHA topologies.^62,63 Other Cu/O active sites have been proposed in literature to hydroxylate CH₄ to CH₃OH in zeolites but lack rigorous assignments and insightful information regarding their second-sphere effects and therefore will not be a focus of this review.^64,65

Figure 8.

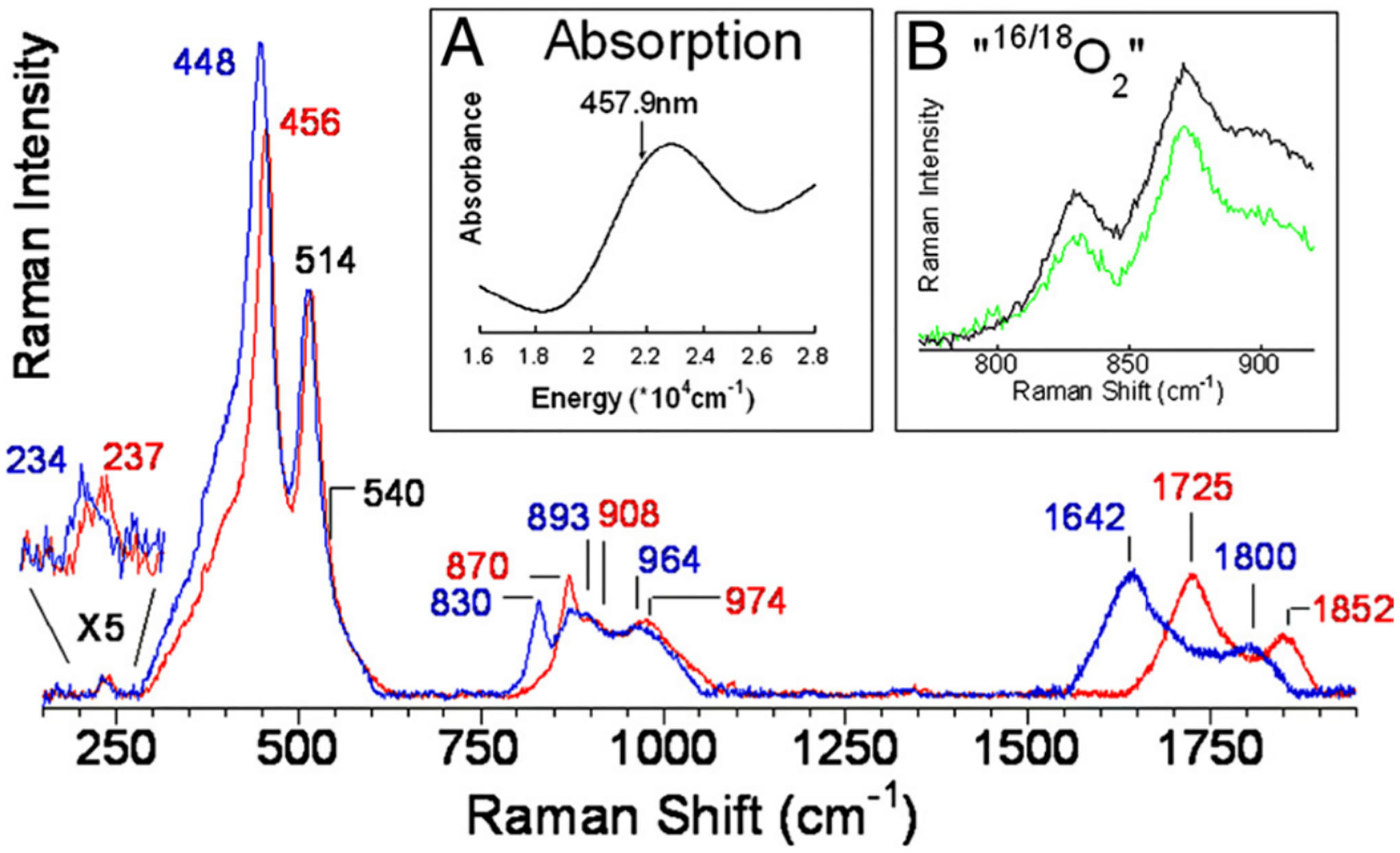
rR spectrum of CuMFI activated with¹⁶O₂ (red) and¹⁸O₂ (blue) (λ_ex = 458 nm). Inset A: DR-UV-vis spectrum of O₂ activated CuMFI. Inset B: “^16/18O₂” (green) and 1:1 normalized sum of¹⁶O₂ and¹⁸O₂ spectra (black). Reproduced with permission from ref 61. Copyright 2009 National Academy of Sciences.

In addition to CH₄ oxidation, Cu zeolites are also very effective in selective catalytic reduction (SCR) of nitrogen oxides (NO_x) compounds with NH₃ with the overall chemical transformation:

$$4\text{\hspace{0.17em}NO}+{\text{O}}_2+4{\text{NH}}_3\to 4{\text{N}}_2+6{\text{H}}_2\text{O}$$

This has been predominantly studied in CuCHA. To understand the compounds involved in this transformation, Giordanino et al.⁶⁶ looked at the interaction of NH₃ with CuCHA after O₂ activation via X-ray Absorption Near Edge Spectroscopy (XANES) and XES. Upon addition of NH₃, an intense rising edge feature grows in at 8983 eV along with decay of the Cu(II) 1s->3d pre-edge feature at 8977 eV (Figure 9A, Inset). An edge peak at around 8983 eV with high intensity is indicative of a linear Cu(I) compound, matching well with the loss of Cu(II) pre-edge intensity.¹⁶ To better understand the ligation, the material was studied by Kβ_2,5 XES. Upon reaction with NH₃, there is a clear blue shift in the Kβ” satellite (Figure 9B) indicating added N ligation, something also noted by other groups.⁶⁷

Figure 9.

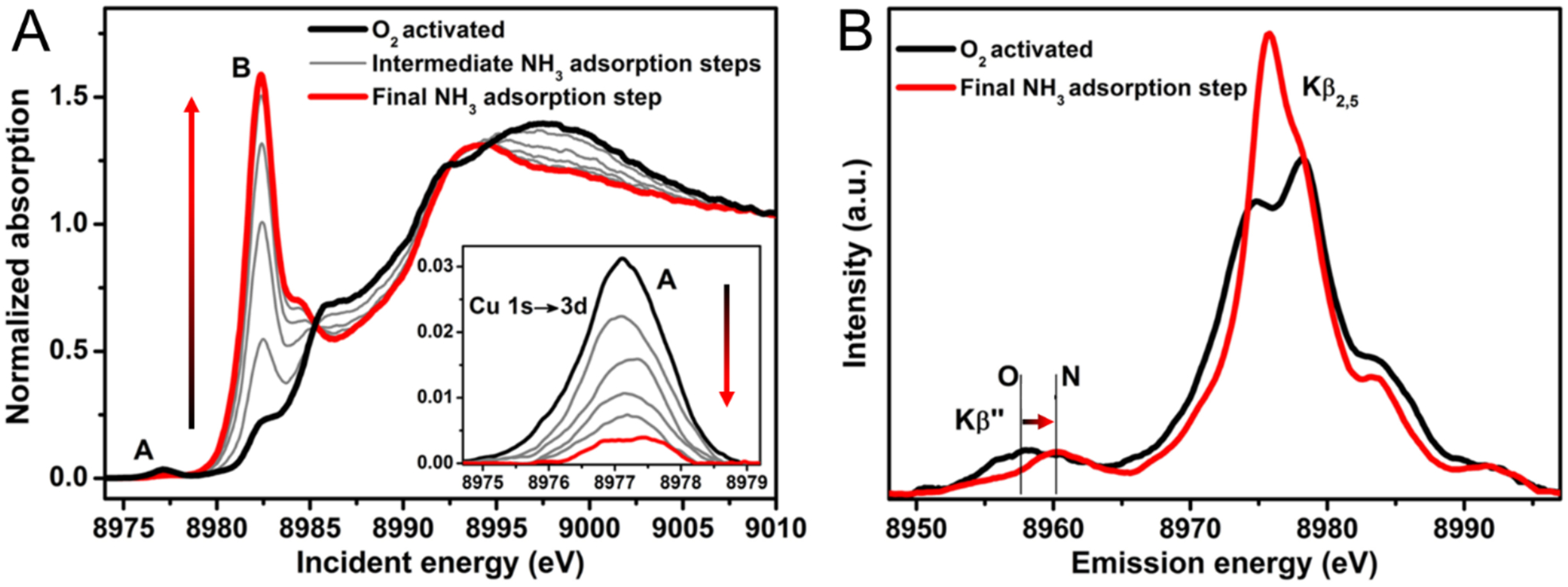
(A) In situ evolution of the Cu K-Edge XAS spectrum of O₂ activated CuCHA from interaction with NH₃ at 120°C. Inset: Background subtracted pre-edge region. (B) Background subtracted Cu Kβ_2,5 and Kβ” emission lines for O₂ activated (black) and NH₃ adsorbed (red) CuCHA. Adapted with permission from ref 66. Copyright 2014 American Chemical Society.

Paolucci et al. looked at NH₃ ligation in two different CuCHA materials: one with predominantly two aluminum bound Cu(II) and a second with one aluminum bound Cu(II) (these sites would be considered spectators in CH₃OH synthesis) to simplify the analysis.⁴⁵ Interestingly, under complete reducing conditions (NO + NH₃), both looked identical via XANES and EXAFS and had the characteristic intense 8983 eV feature of linear Cu(I) species. They assumed reduction of the Cu(II) sites to Cu(I) based on XANES, and in the 2 Al model, assumed charge compensation of the second aluminate site by an ammonium cation. To better understand the structures of these Cu(I) compounds, they computed sequential NH₃ binding energy to one aluminum and two aluminum Cu(I) sites via DFT. For both models, the first two NH₃ molecules bind strongly to the copper while additional NH₃ molecules bind weakly by hydrogen bonding with the first coordination sphere without direct coordination to the copper. Ab initio molecular dynamics (AIMD) simulations on the two NH₃ bound structures reveal liberation of the copper from the aluminate site so that it is simply electrostatically localized near the negative charge (example structures Figure 10B&D). These simulations match with the two coordinate N bound structure observed by XAS and XES and would be indistinguishable.

Figure 10.

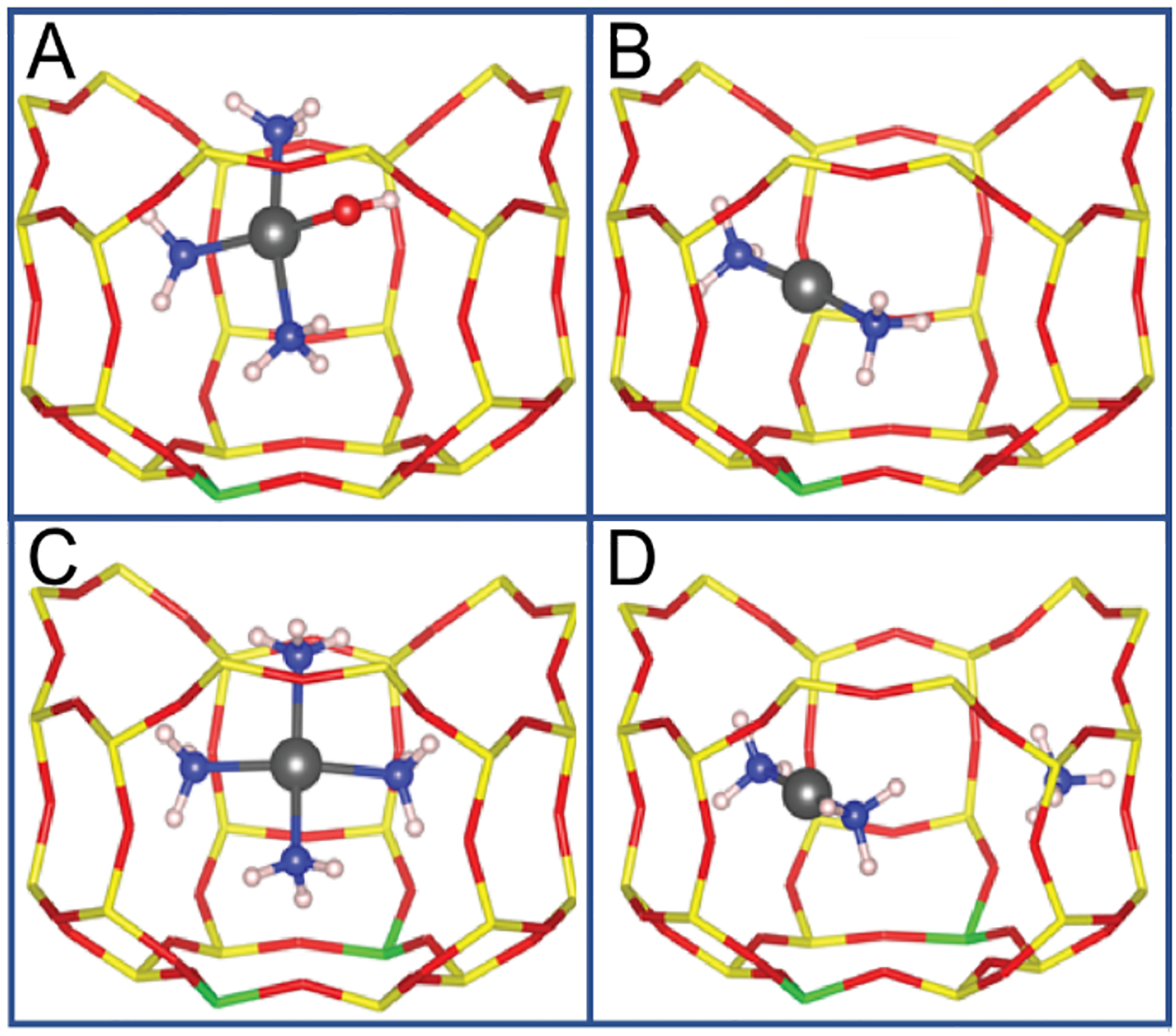
(A) 1 AlCu(II)OH(NH₃)₃. (B) 1 Al Cu(I)(NH₃)₂. (C) 2 AlCu(II)(NH₃)₄. (D) 2 Al Cu(I)(NH₃)₂. (Atom colors are as follows: Yellow is Si, red is O, green is Al, black is Cu(II), blue is N, and white is H). Adapted with permission from ref 45. Copyright 2016 American Chemical Society.

To explore the oxidized active site, Günter et al. looked at the XES spectrum of CuCHA in an NH₃ and O₂ atmosphere. The spectra show the blue shifted Kβ” satellite indicating there is still significant NH₃ ligation in this oxidized state.⁶⁷ Paolucci et al. looked at XANES and EXAFS on the one aluminum and two aluminum samples mentioned above but in an NH₃ and O₂ atmosphere.⁴⁵ The height of the 8983 eV peak dropped drastically in both samples with roughly 27% and 17% Cu(I) in the 1 Al and 2 Al samples respectively. They fit the EXAFS data to a first coordination shell of 3.2 and 3.5 O or N atoms at around 1.92 Å. To model the Cu(II) species appearing under these conditions, they created a 1 Al model (a [Cu(II)OH]⁺) and a 2 Al model (Cu(II) bound to the lattice). The sequential NH₃ binding energies were calculated, and for the 1 Al model, they found that three NH₃ molecules bind strongly to Cu(II) and a fourth binds weakly through H-bonding to the first sphere. In the 2 Al model, four NH₃ molecules bind strongly to the site. The Cu(II)(OH)(NH₃)₃ and Cu(II)(NH₃)₄ sites were modeled through AIMD and found to be four coordinate and liberated from the aluminate sites, although more electrostatically tethered than the NH₃ ligated Cu(I) models (example structures Figure 10A&C). Using the height of the 8983 eV XAS feature to calibrate relative ratios of the 2 coordinate and 4 coordinate species, they fit coordination shells within error of those observed experimentally. Through these XES, XAS, and AIMD simulations, two major intermediates were assigned in CuCHA SCR: a two coordinate NH₃ ligated Cu(I) species and a four coordinate NH₃ ligated Cu(II) species, the latter having either an OH or NH₃ as the fourth ligand depending on its interaction with one or two aluminum.

2.3.2. Iron Active Sites

Unlike copper zeolites which require elevated temperatures to oxidize CH₄, the active site in Fe-zeolites, α-O, can selectively oxidize CH₄ at room temperature and atmospheric pressure. This active site can also oxidize benzene to phenol, another industrially desirable reaction.^68,69 Fe-zeolites are typically activated with N₂O in order to form α-O, although a study has recently shown activation with O₂.⁷⁰ The α-Fe(II) and N₂O activated α-O sites were well defined using a combination of Variable Temperature Variable Field (VTVH) Magnetic Circular Dichroism (MCD) and Mössbauer spectroscopies.²⁹ The low-temperature MCD spectrum of Fe(II)-*BEA contains a strong feature at 15100 cm⁻¹ with temperature and magnetic field dependence (Figure 11A). VTVH MCD isofields for the 15100 cm⁻¹ ligand field band provide insight into the paramagnetic ground state of the site. The field dependence in the low-temperature saturation limit indicates field-induced mixing of Zeeman sublevels, altering the ground state wavefunction in a manner that is typical of non-Kramers (integer spin) sites. MCD intensity for a Non-Kramers Doublet (NKD) is influenced by temperature and field and parameterized by the effective g value (g_eff) and the rhombic Zero-Field Splitting (ZFS δ) of the NKD; both provide geometric and electronic information about the active site through their relation to molecular-spin Hamiltonian parameters. Fitting the VTVH MCD isotherms α-Fe(II) to a non-Kramers doublet model quantifies the g_eff at 8.6 and a δ of 9 cm⁻¹ (Figure 11B). A g_eff of ~8 would match either a monomeric or dimeric Fe high-spin (S = 2) site with opposite ZFS. Mössbauer spectroscopy of α-Fe(II) reveals a single quadrupole doublet (isomer shift (IS) = 0.89 mm/s; quadrupole splitting (|QS|) = 0.55 mm/s), ruling out the possibility of two different iron sites and definitively assigning the α-Fe(II) site as a square planar mononuclear high-spin Fe(II) site (Figure 12A). This is validated by the EXAFS experiments described in section 2.2.1. The low QS for high-spin Fe(II) is unusual and reflects the square planar nature of α-Fe(II) in a 6 MR (Figure 5B). The square planar ligation leads to a doubly occupied dz² orbital that has an electric field gradient with opposite sign to that of the ligands, resulting in the characteristically small QS. These unique parameters allowed α-Fe(II) to also be defined in the CHA topology with similar Mössbauer parameters (IS = 0.93 mm/s, |QS| = 0.63), providing a convenient handle for identification of this site.⁷¹

Figure 11.

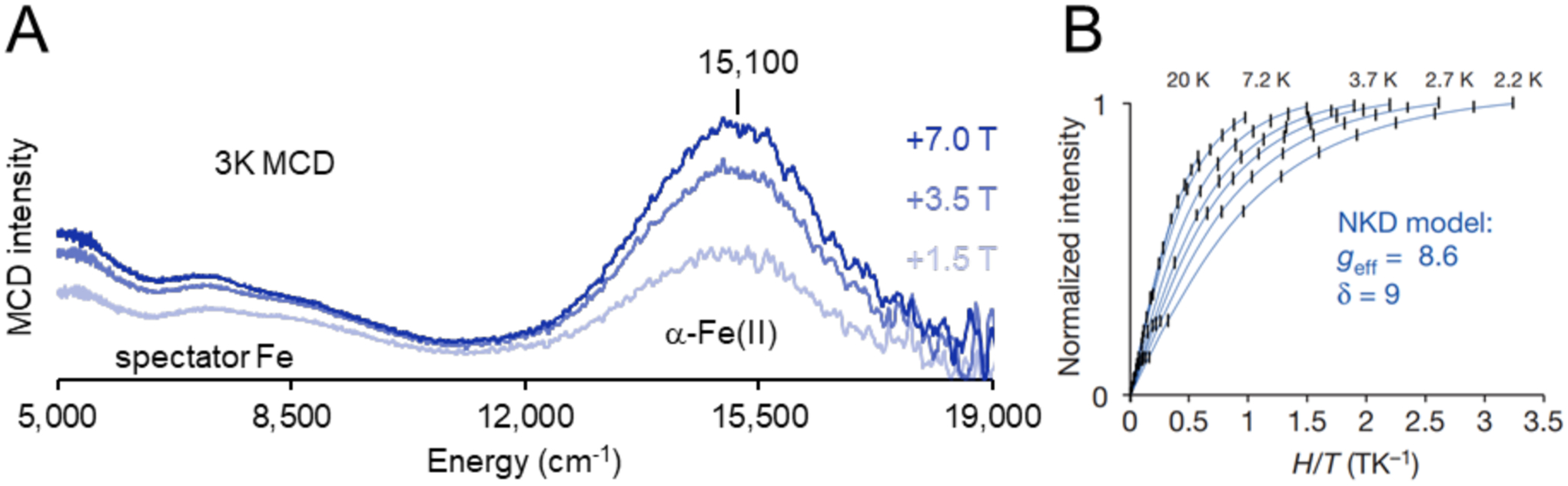
(A) Variable-field 3 K MCD data of Fe(II)-*BEA. (B) VTVH isotherms for α-Fe(II) (black) with Non-Kramers doublet fit (blue). Adapted with permission from ref 29. Copyright 2016 Nature Publishing Group.

Figure 12.

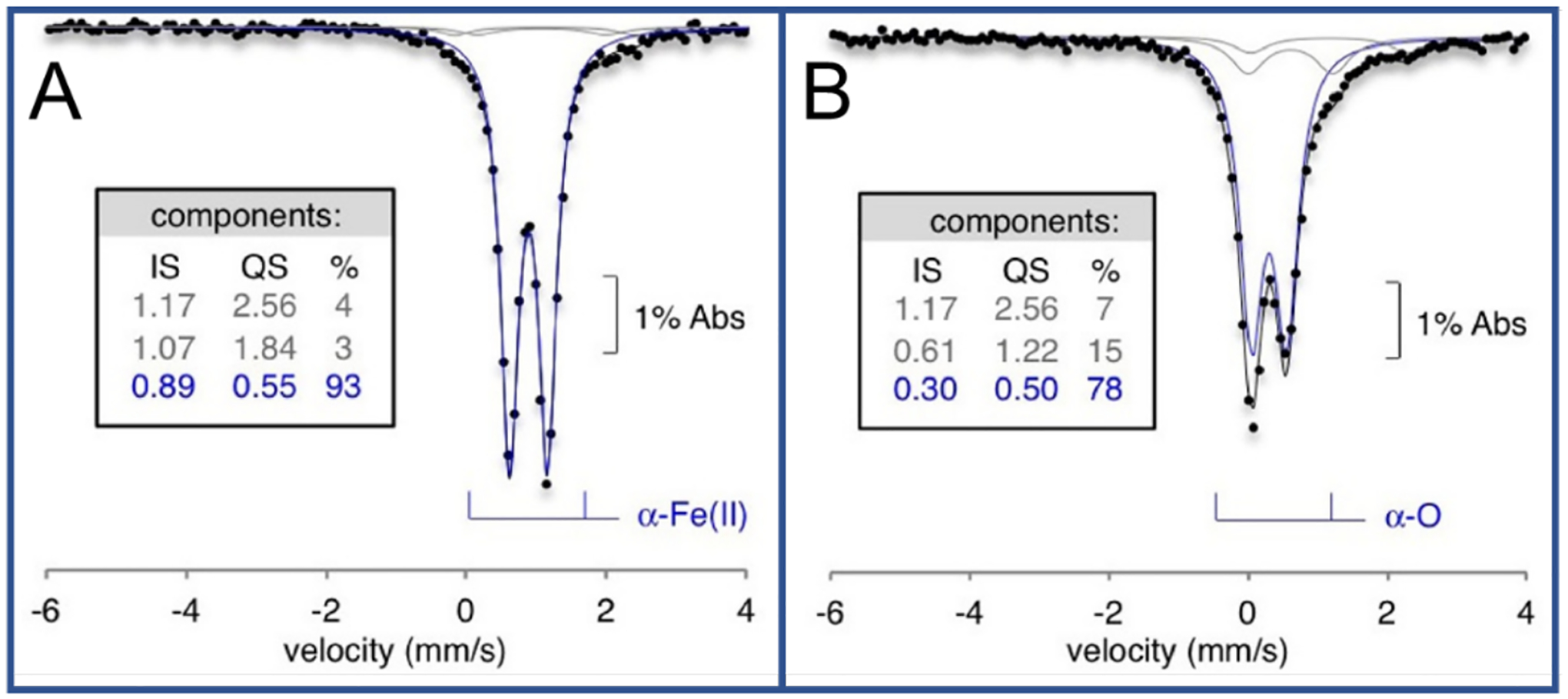
Room temperature Mössbauer data for (A) Fe(II)-*BEA and (B) N₂O Activated Fe*BEA. Overall fit (black), spectator Fe fit (gray), and principle species fit (blue). Tables include fit parameters. Adapted with permission from ref 29. Copyright 2016 Nature Publishing Group.

Upon N₂O activation of α-Fe(II), an O atom is transferred to the site, generating the new α-O site. In low temperature MCD, there is a predominant 20100 cm⁻¹ feature with a shoulder at 16900 cm⁻¹ (Figure 13A). There are also clear bands at 5500, 6700, and 7700 cm⁻¹. All five features decay upon reaction with CH₄. VTVH MCD data on the 20100 cm⁻¹ charge transfer feature show field dependence in the low-temperature saturation limit of the VTVH MCD isofields, indicating an integer-spin ground state in α-O. Fitting these data to a non-Kramers doublet model yields a g_eff of 8.0 and a δ of 7 cm⁻¹ (Figure 13B). This g_eff could correspond to either a mononuclear S = 2 site or a dimer of two S = 2 sites that are weakly coupled with opposite ZFS values. Like with α-Fe(II), Mössbauer spectroscopy of α-O revealed a single quadrupole doublet, with its own distinct parameters (IS = 0.3 mm/s, |QS| = 0.5 mm/s) (Figure 12B). This definitively assigns the site as a mononuclear S = 2 site, Fe(IV)=O. The δ of 7 cm⁻¹ is too large for a negative ZFS; fitting a positive ZFS S = 2 model to the VTVH MCD data elucidates a D = 8±1 cm⁻¹ and E = 0.5±0.5 cm⁻¹. The sign and magnitude of D are similar to known S = 2 Fe(IV)=O model complexes and not for an Fe(III)-O^.−. This site has also been defined in the CHA topology with similar α-O Mössbauer parameters (IS = 0.28 mm/s, |QS| = 0.72 mm/s).²⁹

Figure 13.

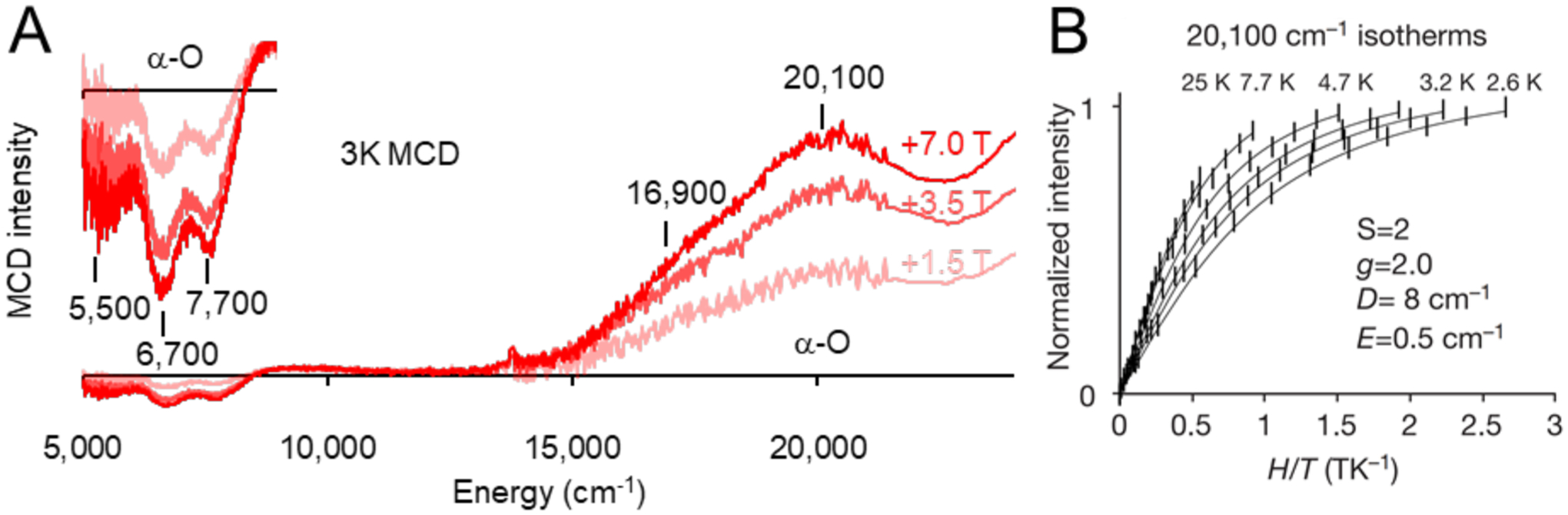
(A) Variable-field 3 K MCD data of N₂O Activated Fe*BEA. (B) VTVH isotherms for α-O with Non-Kramers doublet fit. Adapted with permission from ref 29. Copyright 2016 Nature Publishing Group.

The NRVS spectrum of α-O reveals an extremely strong Fe(IV)=O bind via an FeO stretch at 885 cm⁻¹ (Δ^16/18O = 40 cm⁻¹) (Figure 14).⁵⁹ From Badger’s rule, the 885 cm⁻¹ Fe(IV)=O stretch correlates to a 1.61 Å bond length, matching (within error) the observed distance in EXAFS of 1.63 Å. This 885 cm⁻¹ vibration is the highest frequency Fe(IV)=O stretch observed so far in literature. This is due to its vacant trans axial position which causes an extraordinarily covalent σ bond between the oxo and the iron dz² orbital. This highly covalent interaction leads to both low-lying Fe(IV)=O frontier molecular orbitals with high oxo 2p character to interact with CH₄ and results in a strong O-H bond strength for HAA. This primes the site for its exceptional reactivity with CH₄ at room temperature.

Figure 14.

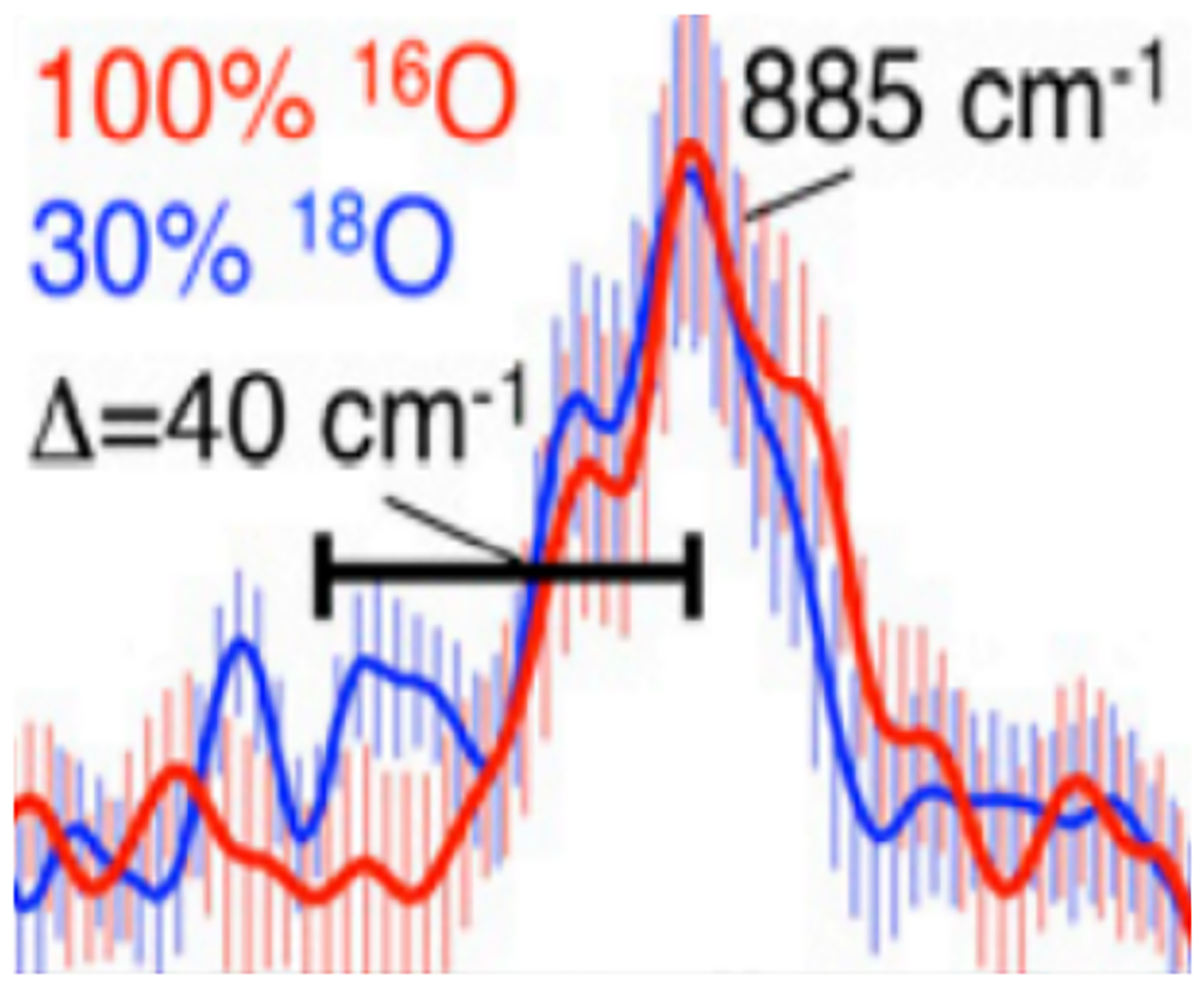
Fe(IV)=O stretch for α-O in NRVS. 100%¹⁶O (red) 70%¹⁶O 30% ¹⁸O (blue). Reproduced with permission from ref 59. Copyright 2018 National Academy of Sciences.

The spectroscopic techniques discussed above also provide essential information past the first coordination sphere. As these techniques generally cannot directly probe the second sphere, utilizing the appropriate technique(s) to evaluate the effects is essential. These can be combined with calculations to elucidate the location of active sites, identify how the lattice imposes specific geometries that activate metal sites for reactivity, and investigate how the zeolite pocket can stabilize substrate binding and control product formation.

3. Zeolite Lattice Imposed Entatic State

3.1. [Cu₂O]²⁺

As described in section 2.3.1., some Cu zeolites have been found to contain a [Cu₂O]²⁺ active site that can react with CH₄ to form CH₃OH. Here we consider the constraints that the rigid zeolite lattice can provide to enable the formation of this site and its reaction with CH₄. These constraints can be viewed as a second-sphere effect where the zeolite lattice enforces a coordination geometry, i.e., an “entatic” state as it is known in bioinorganic chemistry,³⁰ on the binuclear Cu active site.

3.1.1. Constrained Copper-Copper Distance

In copper zeolites, the [Cu₂O]²⁺ active site can be generated by reacting 2 Cu(I) centers with either O₂ or N₂O as oxidants.^27,28 Generation of a [Cu₂O]²⁺ active site with O₂ requires 4e⁻ (two of these originate from the 2 Cu(I) and two are proposed to originate from spectator Cu(II) in the lattice where the second O atom from O₂ is incorporated into the lattice. Alternatively, oxidation with N₂O requires only 2 e⁻ and only one O atom is transferred to the 2 Cu(I)s. The conversion of binuclear Cu(I) centers to the [Cu₂O]²⁺ core is enabled by two complementary contributions. When positioned close to each other due to the Al T-sites in the lattice, the bicuprous site is destabilized toward [Cu₂O]²⁺ formation. Additionally, one e⁻ reduction of O₂ or N₂O is not thermodynamically favorable thus the 2 Cu(I)s must be close enough to promote an efficient 2 e⁻ process.

With O₂, reaction of the reduced Cu(I) zeolite first results in the formation of a μ-(η²:η²) peroxo dicopper(II) intermediate that has been assigned by tuning a laser into its 29000 cm⁻¹ absorbance band (Figure 15A &C).²⁷ The rR spectrum in Figure 15C shows an O-O stretch vibration at 736 cm⁻¹ and a Cu···Cu vibration at 269 cm⁻¹ both characteristic of μ-(η²:η²) peroxo dicopper(II) site.^2,72 When heated, the O-O bond of this side-on peroxo intermediate cleaves removing one of the two O atoms and forming the [Cu₂O]²⁺ core (shown in Figure 15B, upon heating, the 29000 cm⁻¹ absorbance feature decreases while the 22500 cm⁻¹ feature associated with a [Cu₂O]²⁺ core grows in).^27,61 While there has been no systematic study on the properties of a zeolite lattice that enable this μ-(η²:η²) peroxo dicopper(II) intermediate to form, the formation of a μ-(η²:η²) peroxo dicopper(II) intermediate from the interaction of 2 Cu(I) centers and O₂ has been evaluated in metalloenzymes.

Figure 15.

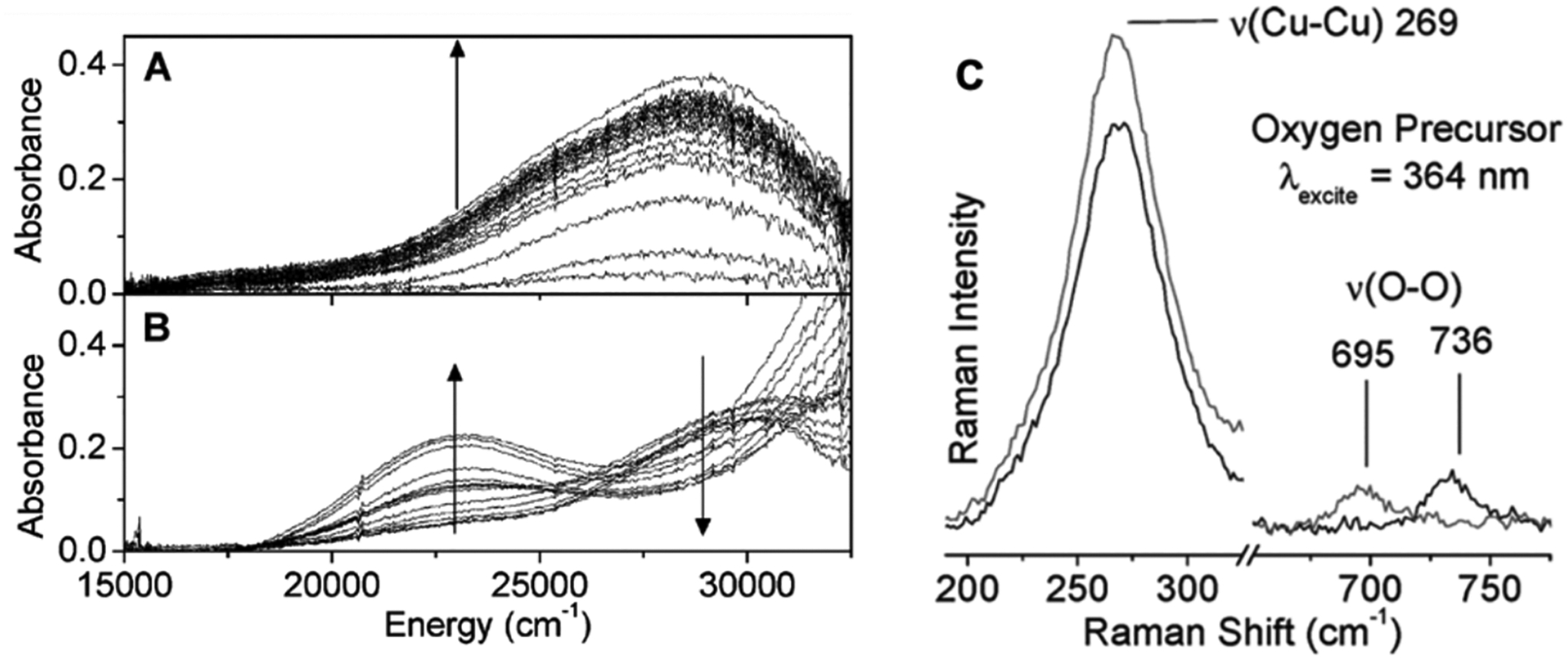
The DR-UV-vis spectra of A: the O₂ precursor that grows in (indicated by the arrow) upon exposure with O₂ at room temperature and B: the spectral changes that occur when the O₂ precursor is heated to form the [Cu₂O]²⁺ active site. The arrows in B show the band around 29000 cm⁻¹ decreases while the band around 22500 cm⁻¹ increase upon heating. The rR spectrum of the 363.8 nm excitation of the O₂ precursor is shown in C defining this site to be a μ-(η²:η²) peroxo dicopper(II) intermediate. Adapted with permission from ref 27. Copyright 2010 American Chemical Society.

The two Cu(I) centers that comprise the coupled binuclear Cu sites found in the metalloproteins Hc and Tyr (Figure 16A, top) bind O₂ reversibly to form a μ-(η²:η²) peroxo dicopper(II) site (Figure 16A, bottom). However, the binuclear Cu(I) T3 site in the MCOs does not bind O₂ in the absence of a third, T2 Cu center (Figure 16B). In the presence of the T2 Cu a different peroxo intermediate is formed where the O₂²- bridges all three Cu of the trinuclear copper cluster (Figure 16C).¹⁸ The ability to bind O₂ in the coupled binuclear Cu sites was found to be driven by electrostatic destabilization of the bicuprous sites where the Cu(I) - Cu(I) distances in the deoxy forms of Hc and Tyr are constrained to be short (~3.6 Å) by α-helices in the enzymes. This short distance increases the electrostatic destabilization of the deoxy site and promotes O₂ binding to form the μ-(η²:η²) peroxo dicopper(II) intermediate (favorable when the Cu···Cu distance is < 4.4Å). The Cu···Cu distance in the T3 site in MCOs is much larger (> 5.0 Å; Figure 16B) and it was determined from DFT calculations that this increase in Cu···Cu distance decreases the electrostatic repulsion in the deoxy form of the enzyme and stabilizes the reduced site precluding O₂ binding in the absence of the third type 2 Cu.

Figure 16.

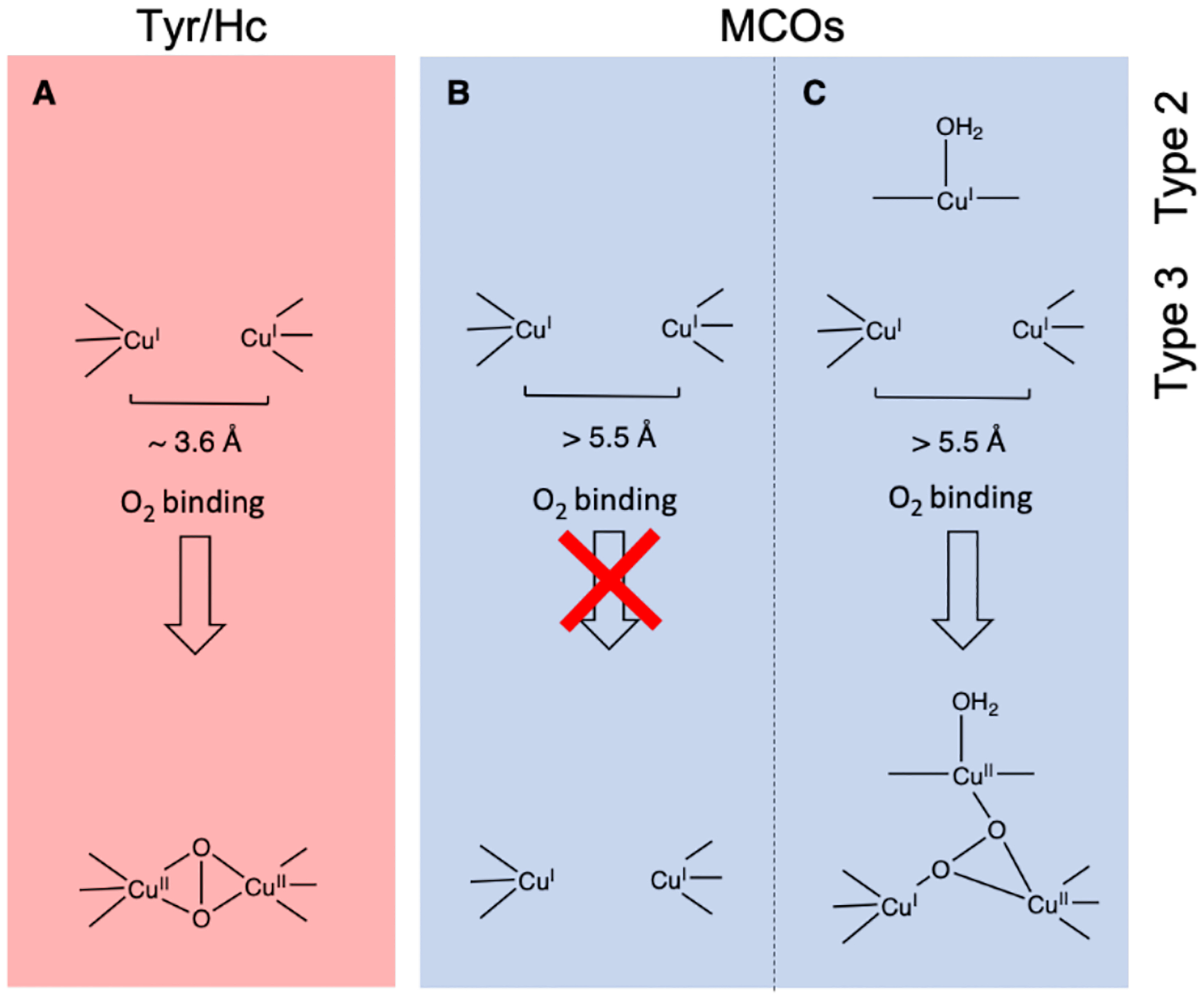
Comparison of the T3 sites in Tyr/Hc enzymes (A) and MCO enzymes (B&C). The O₂ binding to the T3 sites inTyr and Hc enzymes form a μ-(η²:η²) peroxo dicopper(II) intermediate while the T3 sites in MCOs bind O₂ only in the presence of an additional T2 Cu (C).

Depending on the coordination of the Cu(I)s, the zeolite lattice can also constrain the Cu···Cu distance to be short. This provides a potential explanation for the formation of this intermediate where the close Cu(I)···Cu(I) distance increases electrostatic repulsion in the zeolite thus activating this site to bind O₂ to form the side-on peroxo dicopper(II) intermediate (Figure 15). Formation of this side on peroxo also required the donation of 2 e⁻, where at long Cu(I)···Cu(I) distances, O₂ binds only weakly to a single Cu due to the low potential for O₂ reduction by 1 e⁻ to form a Cu(II)O₂⁻. This requirement of 2 Cu(I) centers to donate 2 e⁻ is also observed in the formation of the [Cu₂O]²⁺ using N₂O.

Like O₂ activation, N₂O must interact with the 2 Cu(I) sites in the zeolite to form the [Cu₂O]²⁺ active site and release N₂. N₂O can bind to a binuclear Cu(I) core in three different binding motifs: μ–1–1-O, μ−1–3-O,N, and η¹-N (Table 1). In CuMFI, these different binding modes were analyzed with DFT calculations to determine the requirements that enable formation of the [Cu₂O]²⁺ active site. Activation with N₂O has the advantage of not needing the second 2 e⁻ reduction to release the second O atom of O₂.

Table 1.

Binding motifs of N₂O with a binuclear Cu(I) center, the Cu···Cu distances of those motifs, and the activation energy for the formation of those motifs.

binding modes	Cu-Cu distance	activation energy
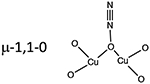
	3.45 Å	2 kcal/mol
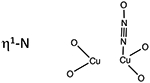
	4.62 Å	> 60 kcal/mol
	5.36 Å	5 kcal/mol

The formation of the [Cu₂O]²⁺ core by reaction of the reduced zeolite with N₂O has an apparent activation barrier of 2.5 ± 0.5 kcal/mol. It was determined through DFT analysis that only the μ–1–1-O binding motif has a low activation energy that is consistent with the low experimental value and enables an efficient 2 e⁻ reduction (Table 1).²⁸ Figure 17 shows the potential energy surfaces (PES) along the N-O cleavage for both a bridging N₂O (Figure 17A) and one that must first bind terminally (Figure 17B) to a single Cu(I) due to long Cu(I)···Cu(I) distance (> 5.0 Å). Along the PES for the bridging N₂O, the cleavage reaction occurs on the singlet surface, and, at the TS, one electron has transferred from one of the Cu(I) into the π* orbital of N₂O. Following the TS for the bridging N₂O (Figure 17A), a second electron is transferred from the remaining bound Cu(I) to cleave the O-N bond forming N₂ and the [Cu₂O]²⁺ site. In Figure 17B, when there is a long Cu···Cu distance, the N₂O molecule must terminally bind, and the second electron transfer is not efficient. This results in a much higher activation energy for this site.

Figure 17.

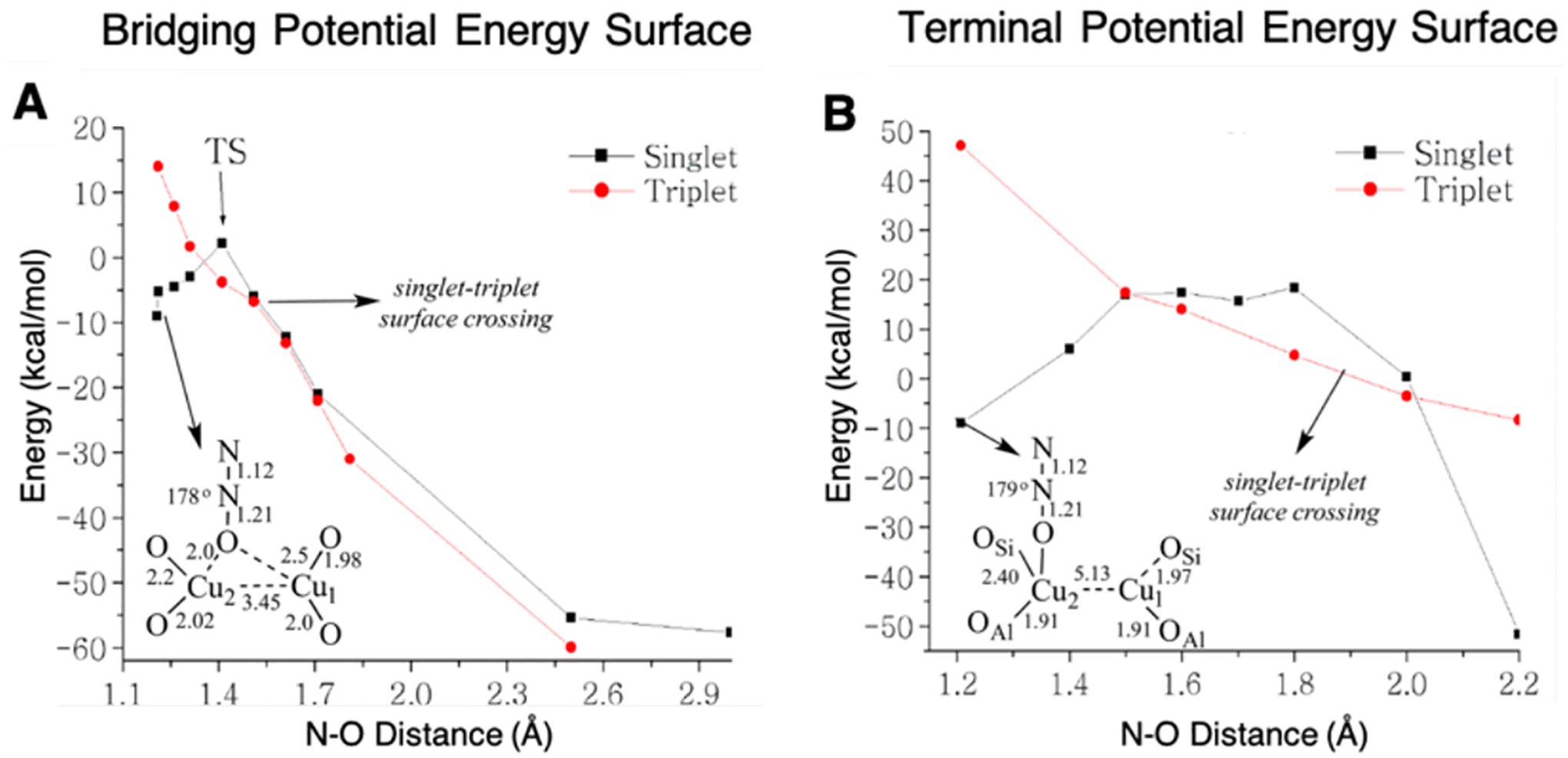
Potential energy surfaces for the singlet and triplet states of both the bridging N₂O (A) and the terminal bound N₂O (B) to 2 Cu(I) centers. Adapted with permission from ref 28. Copyright 2014 American Chemical Society.

Thus, DFT calculations indicate that relatively short Cu···Cu distances (< 4.0 Å) enable N₂O to bind in a μ–1–1-O model allowing its efficient 2 e⁻ reduction. Long Cu(I)···Cu(I) distances (> 5 Å) prohibit N₂O from bridging the Cu centers, eliminating [Cu₂O]²⁺ active site formation. The same [Cu₂O]²⁺ active site is generated with both O₂ and N₂O. In both cases, the zeolite lattice constrains the Cu(I)···Cu(I) distance to less than 5 Å enabling the 2 e⁻ transfer to form this intermediate and destabilizing the reduced site, increasing the thermodynamic driving force for its formation.

3.1.2. Constrained Chelation

As described in section 2.2, the Al T-site can act as a bidentate ligand set to the Cu core. The lattice topology controls the relative orientation of the bidentate chelation to the binuclear [Cu₂O]²⁺ site. Different [Cu₂O]²⁺ active sites have been observed in the CHA and MFI zeolite lattices through rR spectroscopy (Figure 18). Reactivity studies show that the active site formed in CHA is more reactive than the analogous site formed in the MFI lattice under the same reaction conditions.^61,63

Figure 18.

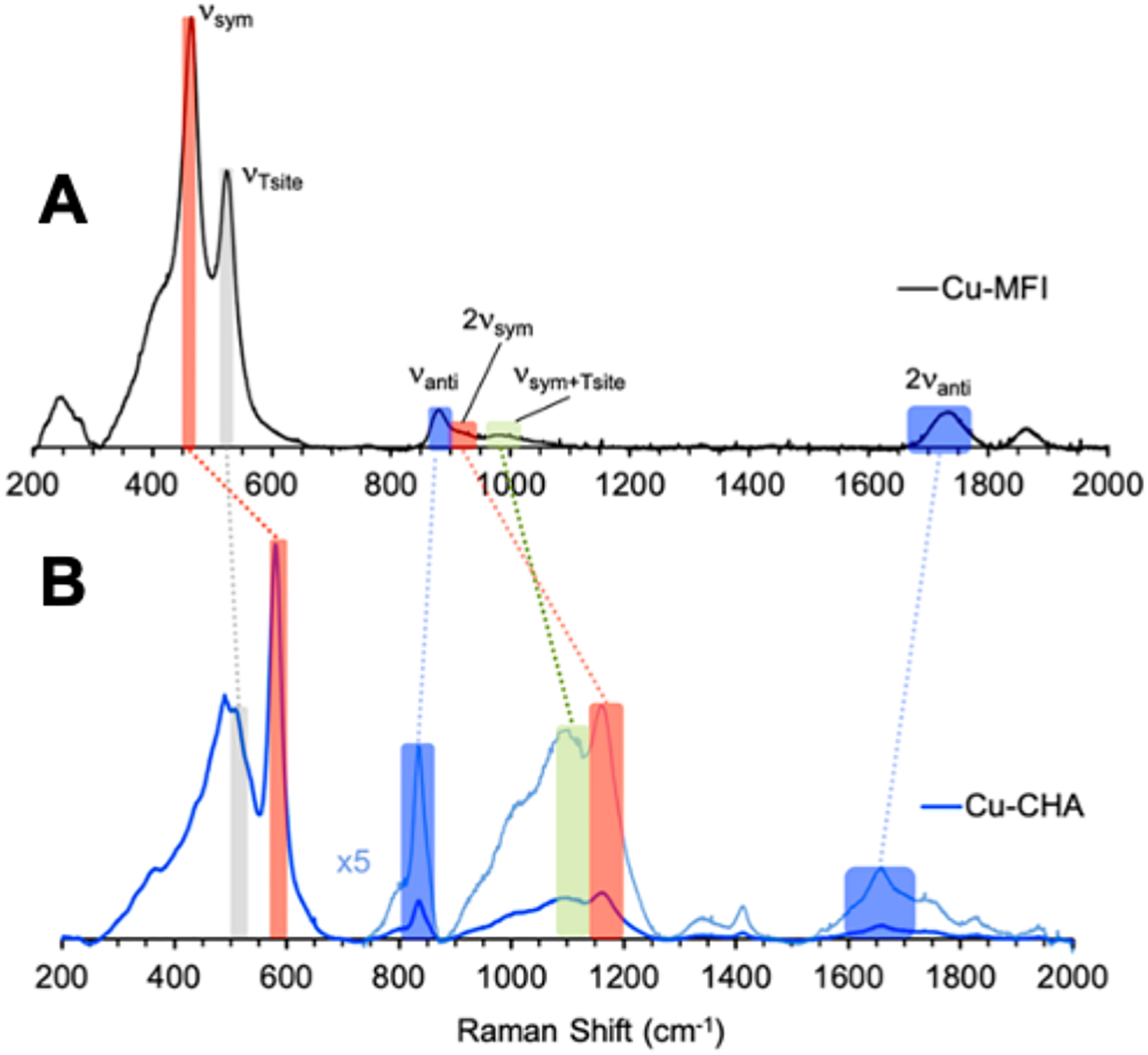
Comparison of the rR vibrations (457.9 nm excitation) of CuMFI (A) and CuCHA (B). Red highlights reflect the symmetric stretch, blue highlights reflect the antisymmetric stretches, gray highlight reflects the T-sites, and green reflects the symmetric + T-site vibrations. Adapted with permission from ref 63. Copyright 2021 American Chemical Society.

To determine the origin of this difference in reactivity, a combined spectroscopic and DFT computational comparison was pursued on these active sites. The rR spectra of the two active sites in CHA and MFI exhibit similar rR vibrations associated with a [Cu₂O]²⁺ site, however the energies of these vibrations are greatly shifted from each other (Figure 18). The symmetric (ν_sym) and 2 × symmetric (ν_2sym) stretches are shifted to higher energy in CuCHA (Figure 18, red and green highlights) whereas the antisymmetric and 2 × antisymmetric stretches are shifted to lower energy (Figure 18, blue highlight) in CuCHA compared to CuMFI. The T-site vibration (gray highlight) does not change in the CuCHA and CuMFI lattices.

Normal coordinate analysis of these spectral differences indicates that the Cu-O-Cu angle in these [Cu₂O]²⁺ active sites decrease from ~140° in MFI to ~120° in CHA. Experimentally calibrated DFT structures (Figure 19A & B) and HAA reaction coordinates (Figure 19E) were evaluated and show that the [Cu₂O]²⁺ active site of CHA has an apparent activation barrier 2.2 kcal/mol lower than in MFI, consistent with experiment. Unlike the results from other studies showing that physisorption of CH₄ into the zeolite lattice contributes to reactivity differences observed in some zeolites (vide infra), the physisorption values of CH₄ into the CHA and MFI lattices were calculated to be similar (Figure 19 E, left side of the diagram).

Figure 19.

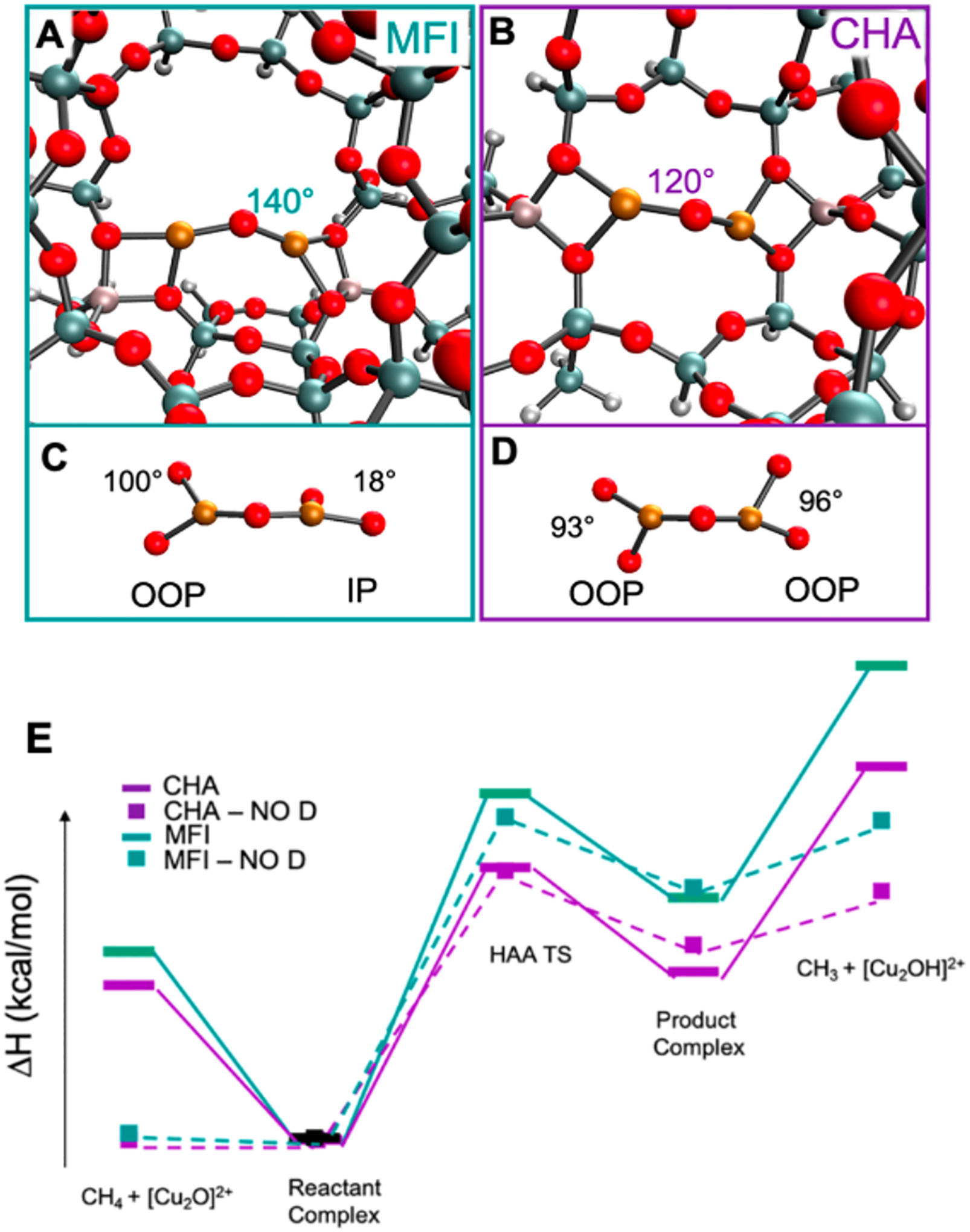
DFT optimized structures of MFI (A) and CHA (B). Orientation of the bidentate ligands around the Cu-O-Cu plane in MFI (C) and CHA (D). HAA reaction coordinate of MFI (E, green) and CHA (E, purple). Values for E can be found in Table 2. Adapted with permission from ref 63. Copyright 2021 American Chemical Society.

Starting at the reactant complex, the transition state energy was calculated to be 4.4 kcal/mol lower in CHA than in MFI (Table 2, with dispersion). To correct these TS energies for thermodynamic difference, Marcus Theory was used to calculate the intrinsic barriers. These were very similar (11.2 kcal/mol in CHA vs. 12.7 kcal/mol in MFI) indicating that the large 4.4 kcal/mol difference observed at the TS is due to the thermodynamic difference between the reactant and the HAA product. This reflects the strength of the O-H bond formed along the reaction coordinate in CHA is ~ 4 kcal/mol stronger than the one formed in MFI. This increase in the O-H bond strength in CHA compared to MFI (89.8 vs. 85.8 kcal/mol) can either be due to a stabilization of the product or a destabilization of the reactant.

Table 2.

Energy values (kcal/mol) for the HAA reaction coordinate in Figure 19E. Reproduced with permission from ref 63. Copyright 2021 American Chemical Society.

ΔH (kcal/mol)	no dispersion		dispersion
	CHA Cage	MFI Channel	CHA Cage	MFI Channel
CH4 + [Cu2O]2+	0.0	0.4	9.5	11.7
Reactant Complex	0.0	0.0	0.0	0.0
HAA Transition State	16.6	19.9	16.9	21.3
Product Complex	12.0	15.6	10.3	15.0
CH3 + [Cu2OH]2+	15.4	19.8	23.0	29.2

Removal of the reactant [Cu₂O]²⁺ and product [Cu₂OH]²⁺ cores from the larger models enables comparison of their energies. It was found that the [Cu₂OH]²⁺ products from the CHA and MFI lattices formed are comparable in energy, however the reactant site in CHA was found to be ~ 4 kcal/mol higher in energy than the reactant in MFI (Figure 20). Thus, the stronger O-H bond formed in the reaction coordinate for CHA in Figure 19E derives from a destabilization of the CHA [Cu₂O]²⁺ reactant site.

Figure 20.

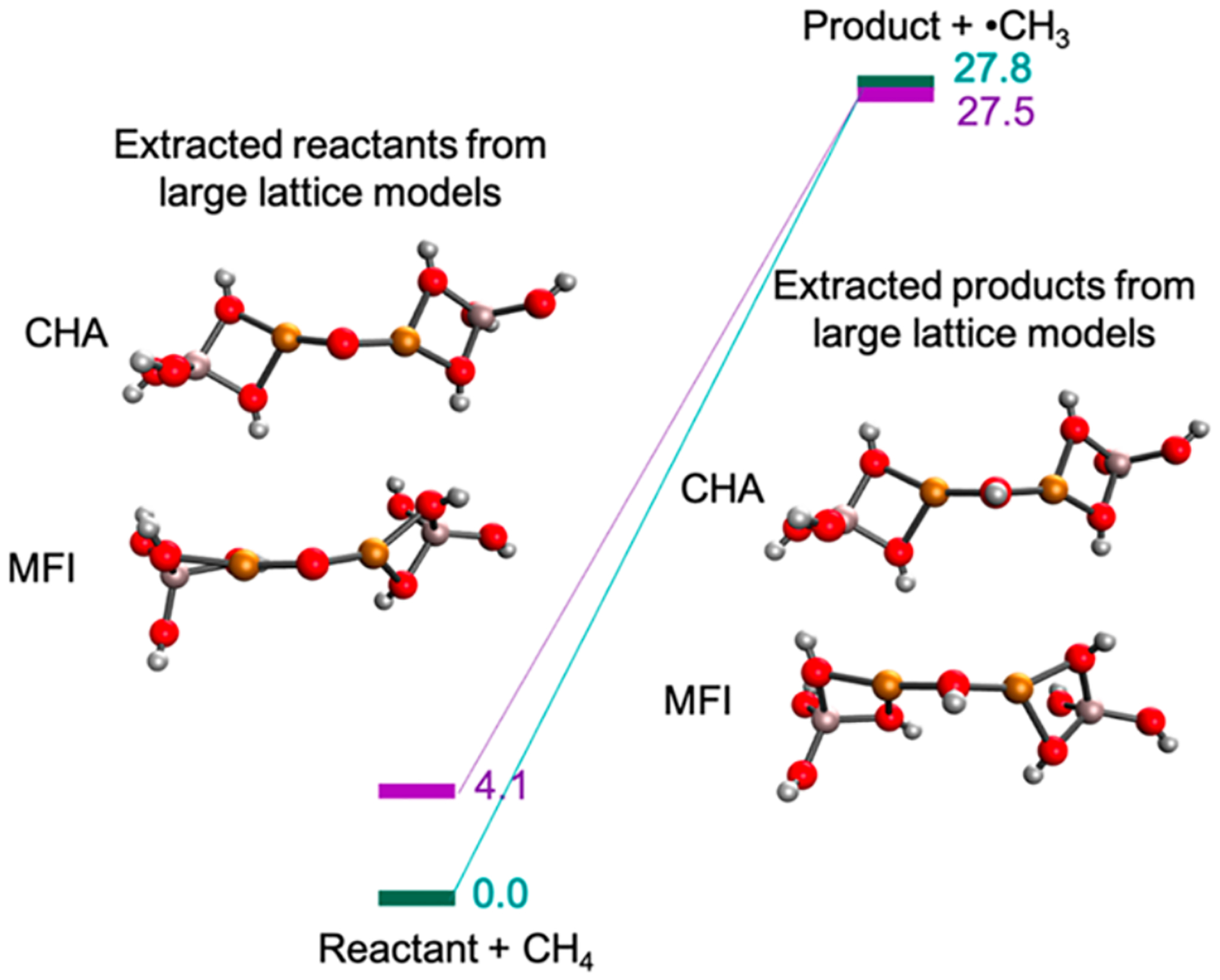
Comparison of the energies of small active site core models of the reactants (left) and products (right) in MFI and CHA (left). Reproduced with permission from ref 63. Copyright 2021 American Chemical Society.

Two main structural differences are present: the angle of the Cu-O-Cu core (120° in CHA vs. 140° in MFI) and the relative coordination of the O-Al-O bidentate T-sites that bind the Cu-O-Cu active site core to the lattice (Figure 19C & D). In CHA, the two bidentate T-sites are both out of plane (OOP) with respect to the Cu-O-Cu core but in the same plane as each other, whereas in MFI one of the O-Al-O bidentate T-sites is in the Cu-O-Cu plane and the other is OOP (the two bidentate T-sites are rotated 90° from each other). Note that the rR spectrum of the sites in the two zeolites (Figure 18) support these structural differences as these reproduce the constrained angle.

Effects of the Cu-O-Cu angle on reactivity with CH₄ for a variety of zeolites has been evaluated by Yoshizawa and coworkers. They found that within the same zeolite lattice, the reactivity of [Cu₂O]²⁺ cores could be different due to different Cu-O-Cu angles. In CHA, two [Cu₂O]²⁺ cores with angles of 93.6° and 112.3° were optimized and the core with the smaller Cu-O-Cu angle was calculated to be 3.7 kcal/mol more reactive. The bidentate Al T-site coordination to the Cu-O-Cu core was not analyzed.⁷³

To compare the [Cu₂O]²⁺ site in MFI to CHA, a series of small models was created to analyze the effects of both the angle of the Cu-O-Cu cores and the bidentate Al T-site rotations on the O-H bond energy.⁶³ The results are given in Table 3. It was found that within the same bidentate Al T-site configuration, the angle of the Cu-O-Cu core does not significantly affect the O-H bond energy. However, when the two bidentate Al T-Sites are oriented in the same plane as each other the energy is higher by about 6 kcal/mol relative to the orientation where the T-sites are rotated 90° from each other. This is due to the bonding interactions between the ½ occupied d x²-y² orbitals on each Cu(II) and the oxo π orbitals. When the bidentate Al T-sites are rotated 90° from each other (Figure 21, left), each of the Cu dx²-y² orbitals interact with a different oxo p orbital. In contrast, when the bidentate Al T-sites are in the same plane (Figure 21, right) these d orbitals interact with the same p orbital for bonding. This destabilizes the [Cu₂O]²⁺ reactant and results in a stronger O-H bond formed from HAA.

Table 3.

Energies (kcal/mol) for small models of a [Cu₂O]²⁺ cores with different Cu-O-Cu angles and different rotations of the bidentate oxygen ligands. Reproduced with permission from ref 63. Copyright 2021 American Chemical Society.

Energy (kcal/mol)		Cu–O–Cu angle
Bidentate Oxygen Ligand Rotations (with respect to the Cu–O–Cu plane)	161°	140°	120°
+45°/−45°	0.4	1.4	0.2
0°/0°	6.4	7.2	14.5a
90°/0°	0.0	2.5	0.3
90°/90°	6.7	5.5	5.9

^alarger energy difference due to steric interaction between two in plane Al T ligands at the acute 120° angle.

Figure 21.

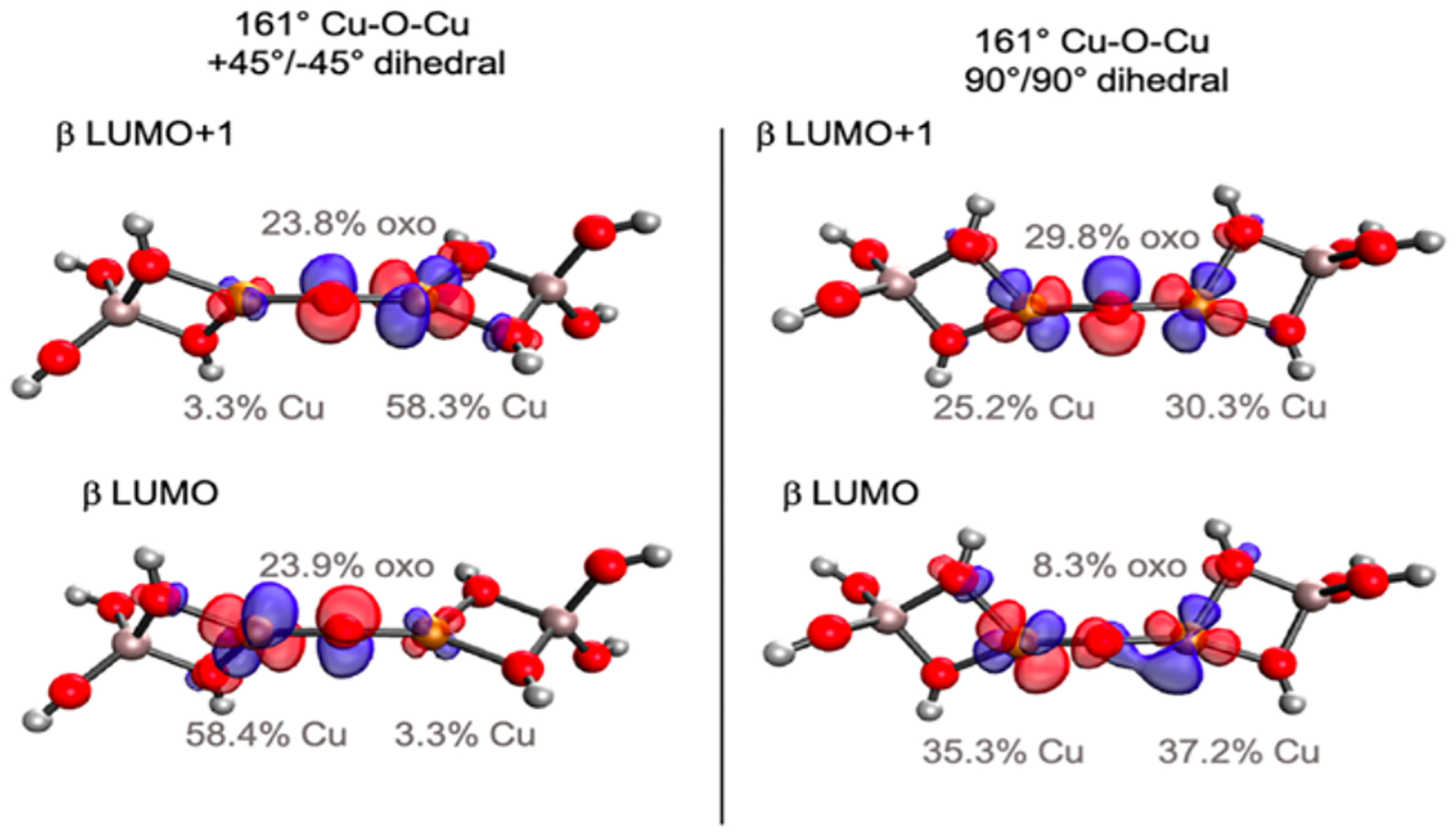
Comparison of the β LUMO and β LUMO+1 orbitals for bidentate Al T-sites rotated 90° from each other (left) and in the same plane (right). Reproduced with permission from ref 63. Copyright 2021 American Chemical Society.

In summary, the zeolite lattice plays several entatic “second-sphere” roles in Cu/O₂ catalysis. It constrains the Cu(I) – Cu(I) distance to < 4.5 Å enabling [Cu₂O]²⁺ formation, and it tunes this site for reactivity through the relative rotation of the bidentate Al T-site ligands, destabilizing the [Cu₂O]²⁺ reactant in CuCHA and driving [Cu₂OH]²⁺ formation.

3.1.3. Relevant Model Studies

Model studies have been published on complexes that contain a [Cu₂O]²⁺ core at different levels of characterization. Overall, the consensus on these models is that they are not particularly reactive. Here we will evaluate contributions to this low reactivity in the model complexes compared to that observed in the [Cu₂O]²⁺ zeolite.

Figure 22 compares the [Cu₂O]²⁺ core in a zeolite lattice (Figure 22A) with the structures of a model complex defined by Haack et al.⁷⁴, [FurNeu](Cu₂(μ-O))−(OTf)₂ model (Figure 22B), and a model characterized by Ali et al.¹⁰, {[(tmpa)Cu]₂−(O)}²⁺ (Figure 22C). Both model complexes have a +2 charge and bind the binuclear Cu core through nitrogen atoms (the [FurNeu](Cu₂(μ-O))−(OTf)₂ model has three nitrogen atoms bound to each Cu, and the {[(tmpa)Cu]₂−(O)}²⁺ model contains four nitrogen atoms bound to each Cu). In contrast, the [Cu₂O]²⁺ core is coordinated to the zeolite by two oxygen atoms to each copper and has charge balancing Al atoms close to the binuclear Cu core creating a neutral model. The {[(tmpa)Cu]₂−(O)}²⁺ model can be more quantitatively compared to the zeolite active site as quantitative kinetic reactivity data and bond dissociation free energy (BDFE) values were reported.

Figure 22.

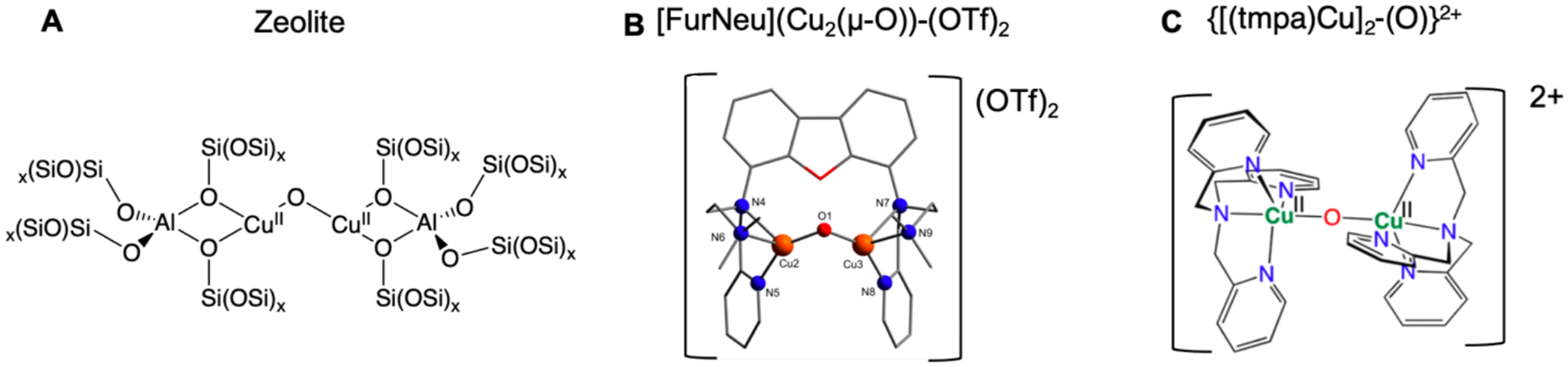
Comparison of zeolite and models with [Cu₂O]²⁺ cores: zeolite lattice (A), [FurNeu](Cu₂(μ-O))−(OTf)₂ (B), {[(tmpa)Cu]₂-(O)}²⁺ (C). Adapted with permission from references 74 and 10. Copyright from 2013 American Chemical Society and 2017 American Chemical Society, respectively.

Ali et al. reported that the {[(tmpa)Cu]2−(O)}²⁺ model complex reaction with TEMPOH in MeCN yielded a ΔS^‡ of −44 ± 11 cal/mol*K and a ΔH^‡ of 5.3 ± 2.8 kcal/mol (ΔG^‡ (298 K) of 18 ± 2.8 kcal/mol). They experimentally derived the BDFE(OH) of {[(tmpa)Cu]₂−(O)}²⁺ as 77.2 kcal/mol.¹⁰ This can be compared to the zeolite bond dissociation energy (BDE) estimated to be ~90 kcal/mol for the [Cu₂O]²⁺ CHA zeolite site. The kinetics of the zeolite’s reaction with CH₄ give a ΔS^‡ of −51.7 cal/mol*K and a ΔH^‡ of 6.2 kcal/mol (ΔG^‡ (298 K) of 21.6 kcal/mol). Changing the CH₄ to TEMPOH (BDE lower than CH₄ by ~ 35 kcal/mol) lowers the predicted free energy barrier by ~15 kcal/mol. Alternatively, lowering the O-H bond strength of the zeolite to that assigned to the {[(tmpa)Cu]₂−(O)}²⁺ model (weaker by ~ 13 kcal/mol) raises the barrier for the reaction with CH₄ by ~ 9 kcal/mol. This barrier increase can therefore be attributed to the weaker O-H bond formed in {[(tmpa)Cu]₂−(O)}²⁺.

The weaker O-H bond strength observed in the {[(tmpa)Cu]₂−(O)}²⁺ model complex could be due to a stabilization of the [Cu₂O]²⁺ reactant, or a destabilization of the [Cu₂OH]²⁺ product compared to the zeolite. In the {[(tmpa)Cu]₂−(O)}²⁺ reactant complex, the higher coordination number results in more donation from the ligand therefore stabilizing the more oxidized state. This increased chelate ligand donation is reflected in the weaker Cu-O bonds (~1.83 Å) predicted by DFT calculations for this model (compared to ~1.75 Å in zeolites).

Further, the [Cu₂OH]²⁺ product core of the {[(tmpa)Cu]₂−(O)}²⁺ model complex is destabilized relative to this product in the zeolite. Interestingly, the product Cu-OH-Cu angle in {[(tmpa)Cu]₂−(O)}²⁺ is calculated to be 142° (Figure 23, right). This does not alter much from the 143° Cu(II)-O-Cu(II) reactant angle predicted by DFT calculations. This contrasts with the zeolites where even though the reactant cores in CHA and MFI have different Cu-O-Cu angles, (120° and 140°, respectively) the product Cu-OH-Cu cores are all calculated to be close to 120° indicating a favorable structural change when forming the product complex (Figure 23, left). This suggests that the sterics of the TMPA ligands in the {[(tmpa)Cu]₂−(O)}²⁺ prevent the Cu-OH-Cu angle from becoming more acute. The positive charge of the {[(tmpa)Cu]₂−(O)}²⁺ model complex would also lower proton affinity and further destabilize the product. Therefore, the ligation of the {[(tmpa)Cu]₂−(O)}²⁺ model complex stabilizes the reactant and the sterics and charge destabilizes the product. Together this results in a weaker O-H bond in the model and its observed low reactivity. This emphasizes the importance of the Al T-site ligation of the zeolite in activating the active Cu site for reactivity.

Figure 23.

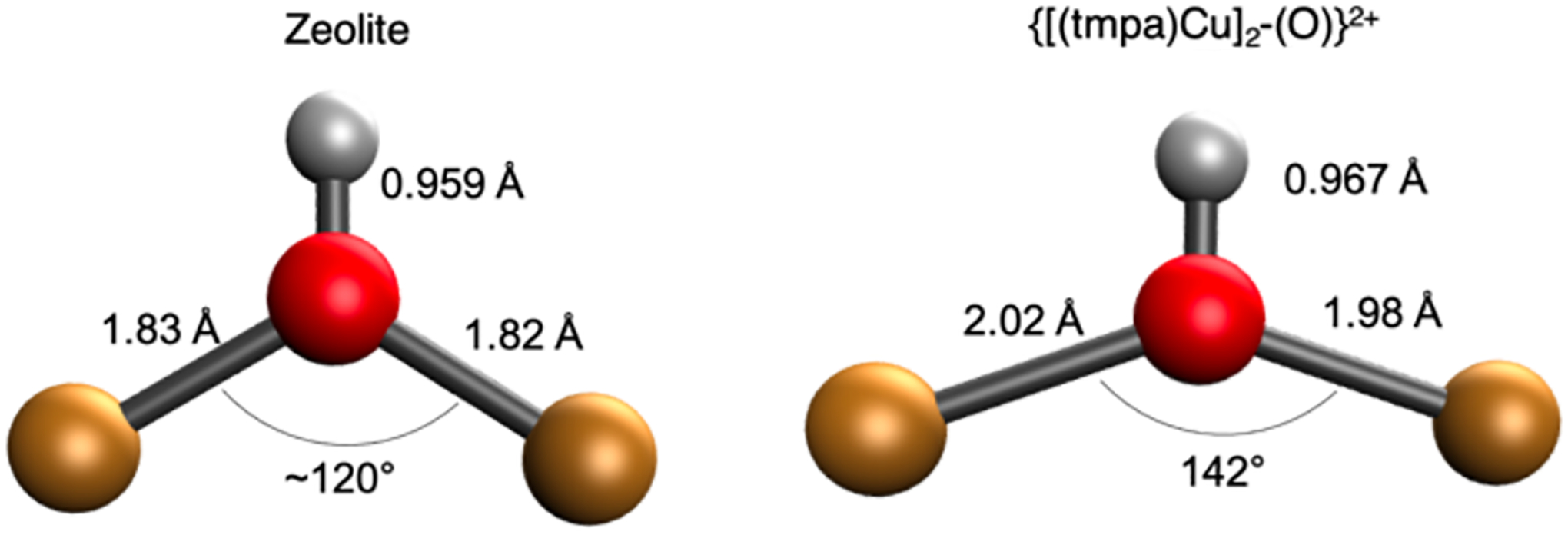
Schematic of Cu-OH-Cu product core in zeolite (left) and in the {[(tmpa)Cu]₂−(O)}²⁺ model complex (right).

3.2. α-Fe(II) and α-O

A number of zeolite lattices stabilize an oxidized iron active site known as α-O, which effects the selective conversion of CH₄ to CH₃OH and benzene to phenol under ambient conditions.^68,75,76 α-O forms from a reduced precursor known as α-Fe(II), which is activated through oxidation by N₂O (but not O₂). What follows is a discussion of how rigid ligation from a zeolite lattice activates these sites for N-O and C-H bond cleavage.

3.2.1. α-Fe(II)

α-Fe(II) is a mononuclear, square planar high spin (S = 2) Fe(II) site.²⁹ The geometric and electronic structure of this site are discussed in detail in section 2. α-Fe(II) binds and activates N₂O, via O atom transfer at moderate temperature (423–523 K), to form a highly reactive S = 2 Fe(IV)=O site known as α-O (see below).

Upon exposure to N₂O at room temperature, the 15900 cm⁻¹ ligand field band of α-Fe(II) in Fe-*BEA decays and a new band appears at 11500 cm⁻¹ (Figure 24A).⁷⁷ With subsequent heating, this band disappears, and the characteristic DR-UV-vis features of α-O are observed (Figure 24B). Combined data from Mössbauer spectroscopy, infrared spectroscopy, and density functional theory calculations indicate the 11500 cm⁻¹ band derives from an S = 2 Fe(II)-NNO species (η¹-N in Figure 24C). At elevated temperature, this interconverts to an Fe(II)-ONN species (η¹-O in Figure 24C), which then engages in O-atom transfer. The enthalpy of N₂O binding was quantified from variable-temperature DR-UV-vis data to be ΔH_ads = −4.8 kcal/mol. Subsequent kinetics studies quantified the activation barrier for O-atom transfer to be ΔH^‡ = 17.7 kcal/mol.⁷⁷

Figure 24.

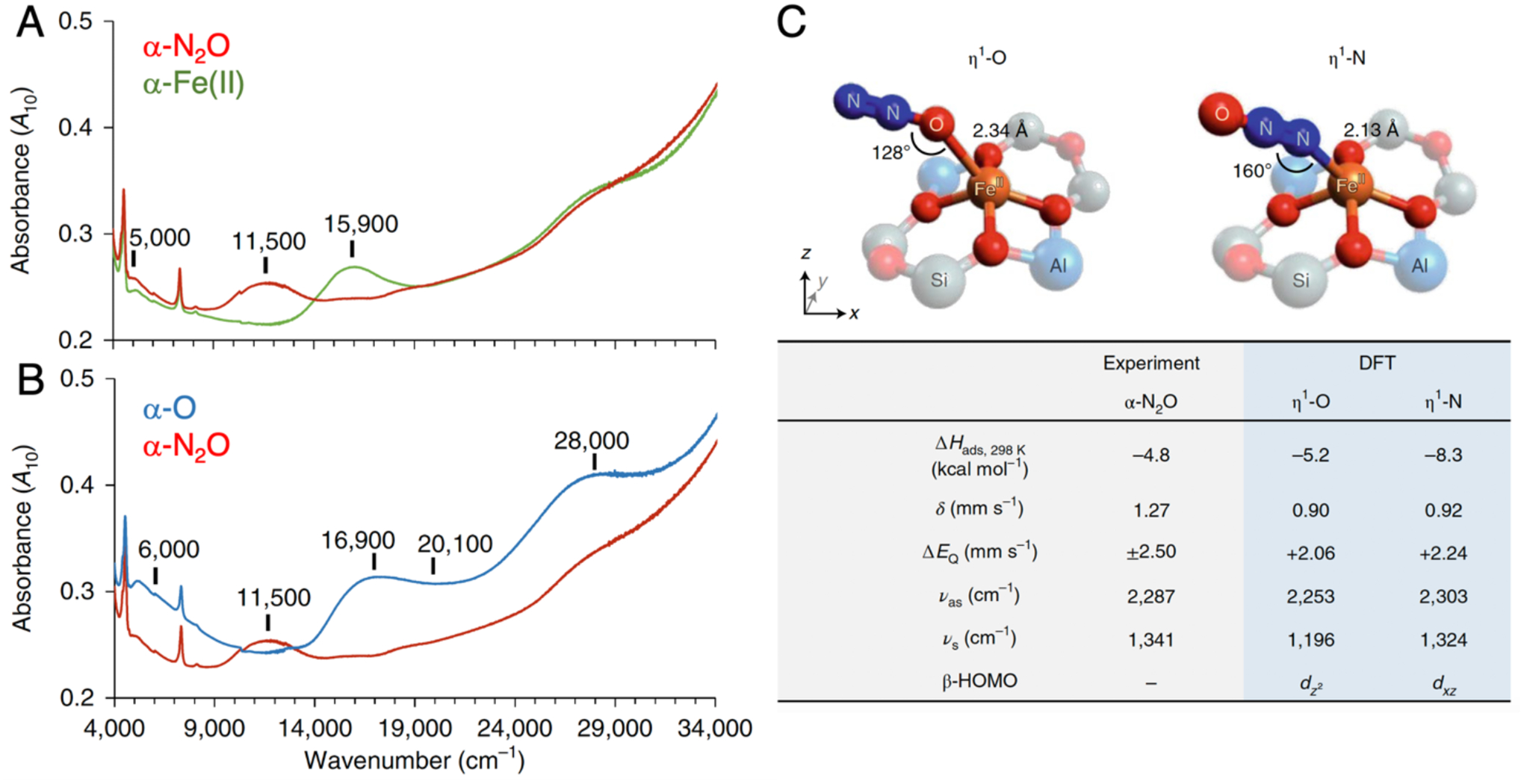
(A) DR-UV-vis data from Fe-*BEA tracking the conversion of α-Fe(II) in (green trace) into α-N₂O (red trace). (B) DR-UV-vis data tracking the subsequent conversion of α-N₂O (red trace) into α-O (blue trace). (C) Comparison of experimental data from α-N₂O to predicted values from DFT models of sites with N-versus O-bound N₂O ligands. Adapted from ref 77 with permission. Copyright 2020 Nature Publishing Group.

Many zeolite lattices stabilize α-Fe(II) sites that can interact with N₂O to form α-O. The α-Fe sites in the FeFER lattice, however, exhibit remarkable activity for the decomposition of N₂O compared to α-Fe(II) sites in other lattices.⁴⁸ This superior activity is proposed to occur due to the unique lattice of FER that stabilizes two α-Fe(II) sites across from each other in the 8MR channels (See Figure 2, FER). As N₂O binds to one of the α-Fe(II) sites to form an Fe(II)-NNO species, the α-Fe(II) site across the FER channel can interact with the O atom forming α-O.⁷⁸

Experimentally calibrated DFT calculations provide insight into geometric and electronic structure contributions to O-atom transfer. Studies of both small molecules and DFT models suggest a planar configuration with a slight tetrahedral distortion is the intrinsically stable geometry of the S = 2 FeO4 core.^79,80 This geometry was indeed found to be most stable for a DFT model of α-Fe(II) that was geometry optimized in the absence of constraints from a zeolite lattice (Figure 25, left).⁷⁷ However, comparing theory to experimental data, this unconstrained DFT model does not bind N₂O, and exhibits greatly diminished in silico reactivity in O-atom transfer (ΔH_ads = +2.7, ΔH^‡ = 29.1 kcal/mol). It is only after lattice constraints are properly accounted for – by using a larger model including a second shell of T-atoms fixed at their crystallographic positions in the *BEA lattice – that the predicted enthalpy for N₂O binding and the activation barrier for O-atom transfer (ΔH_ads = −4.4, ΔH^‡ = 21.4 kcal/mol) come in reasonable agreement with the experimental values. Correlating structure with function, lattice constraints enforce a 5–6 kcal/mol OOP distortion of the Fe(II) ion. This brings the geometry of the 4-coordinate α-Fe(II) site closer to the 5-coordinate products of N₂O binding (α-N₂O) and N-O cleavage (α-O). (Spectroscopically validated DFT models of both α-N₂O and α-O indicate a moderate displacement of the Fe atom from the basal O₄ plane.) DFT calculations suggest the imposed OOP distortion facilitates the binding and activation of N₂O by 5–8 kcal/mol, quantifying the role of lattice constraints in activating this site for reactivity.⁷⁷

Figure 25.

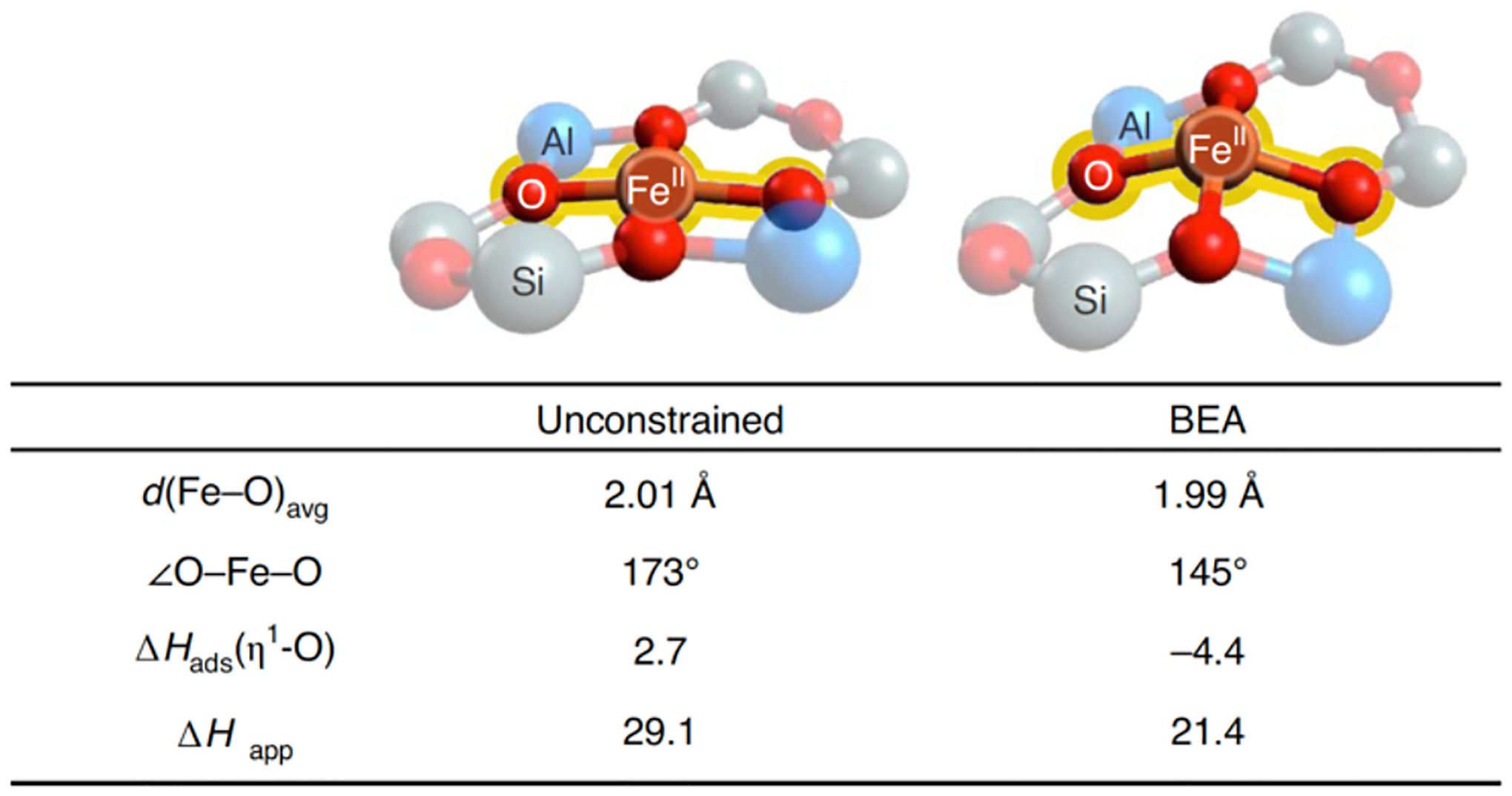
Comparison of the geometric structures of α-Fe(II) in the absence (left) and presence of geometric constraints from the zeolite lattice (right), with correlation to predicted enthalpies for binding and activation of N₂O. Reproduced from ref 77. Copyright 2020 Nature Publishing Group.

O₂ does not engage in O-atom transfer to α-Fe(II). This is in contrast to the 2 Cu(I) reduced active site of CH₄ hydroxylation in Cu-zeolites, which activates O₂ under mild conditions to form a [Cu₂O]²⁺ species.²⁷ The lack of reactivity between α-Fe(II) and O₂ likely reflects the calculated 45 kcal/mol reduction in driving force for O-atom transfer relative to the 2 Cu(I) site (Figure 26, right).⁷⁷ Indeed, the reaction α-Fe(II) + ½O₂→ α-O is predicted to be endothermic (ΔH = +5.6 kcal/mol at the 6–311G*/B3LYP level). A parallel thus emerges to biological mononuclear Fe(II) sites, where a similar thermodynamic barrier to O₂ activation is encountered.⁸¹ In mono-Fe enzymes, this is overcome by coupling the endergonic one-electron reduction of O₂ to the oxidation of a co-substrate. For example, in the α-ketoglutarate-dependent oxygenases, a thermodynamically unfavorable Fe-O₂ intermediate reacts with bidentate-bound α-ketoglutarate co-substrate. The resulting peroxide-bridged Fe(II)-succinate intermediate then generates a reactive Fe(IV)=O species. This behavior has also been demonstrated in pterin dependent non-heme Fe enzymes, where the ferrous peroxy-pterin precursor has been trapped and spectroscopically characterized.⁸² Recently, it was proposed that neighboring α-Fe(II) sites in Fe-FER can activate O₂ through a bridging interaction in which each Fe(II) center donates two electrons to cleave the O-O bond.⁷⁰ This is reported to form a pair of CH₄-reactive α-O sites. While this structural assignment requires further spectroscopic support, the idea that an oxygenated intermediate can form at paired α-Fe(II) sites is interesting and warrants further investigation.

Figure 26.

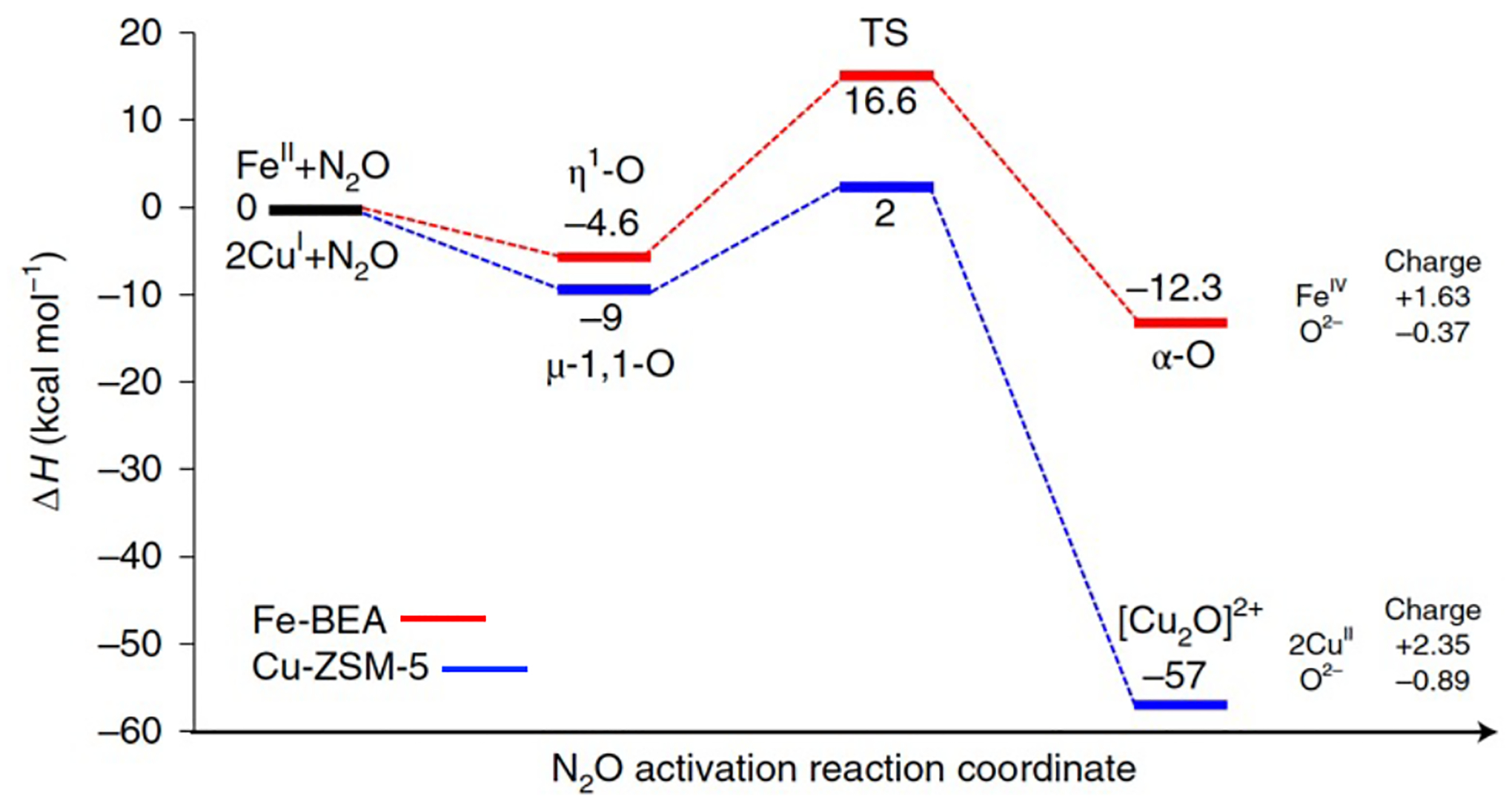
Comparison of DFT reaction coordinates for N₂O activation by α-Fe(II) in Fe-*BEA (red path) and the 2 Cu(I) active site of Cu-ZSM-5 (blue path), highlighting the much greater driving force for O-atom transfer for the Cu active site. Adapted from ref 77. Copyright 2020 Nature Publishing Group.

3.2.2. α-O

Spectroscopic data from NRVS and VTVH-MCD define α-O to be a high spin (S = 2) square pyramidal O=FeO₄ species formed by transferring an O-atom from N₂O to the open axial position of α-Fe(II).^29,59 EXAFS analysis indicates the equatorial ligand field of α-O is comparable to that of α-Fe(II), with four lattice O ligands at 2.02 Å (Figure 27A & B).⁵⁹ This equatorial ligand field is weak, but not remarkably so, serving to stabilize a high spin electronic structure. A unique feature of this site, relative to other less reactive S = 2 Fe(IV)=O intermediates, is the absence of a ligand trans to the Fe(IV)=O bond which is quite short as a result. (1.63 Å from EXAFS analysis in Figure 27B, 1.61 Å predicted from Badger’s rule applied to its 885 cm⁻¹ Fe(IV)=O stretching frequency in Figure 27C; Fe(IV)=O bond distances of 1.64–1.68 Å are more typical for non-heme Fe(IV)=O species.) The vacant trans axial position is also evident in Fe K-edge X-ray absorption spectroscopy, where it leads to an unusually intense pre-edge feature (Figure 28, bottom row). The combination of a high spin electronic structure and this particular five-coordinate geometry leads to a highly covalent Fe(IV)=O bond, and exceptional activation toward HAA: even at 150 K, α-O reacts in a diffusion-limited fashion with CH₄. DFT calculations suggest this high reactivity derives from efficient polarization toward an Fe(III)-oxyl-like electronic structure with minimal elongation of the Fe(IV)=O bond.^29,59

Figure 27.

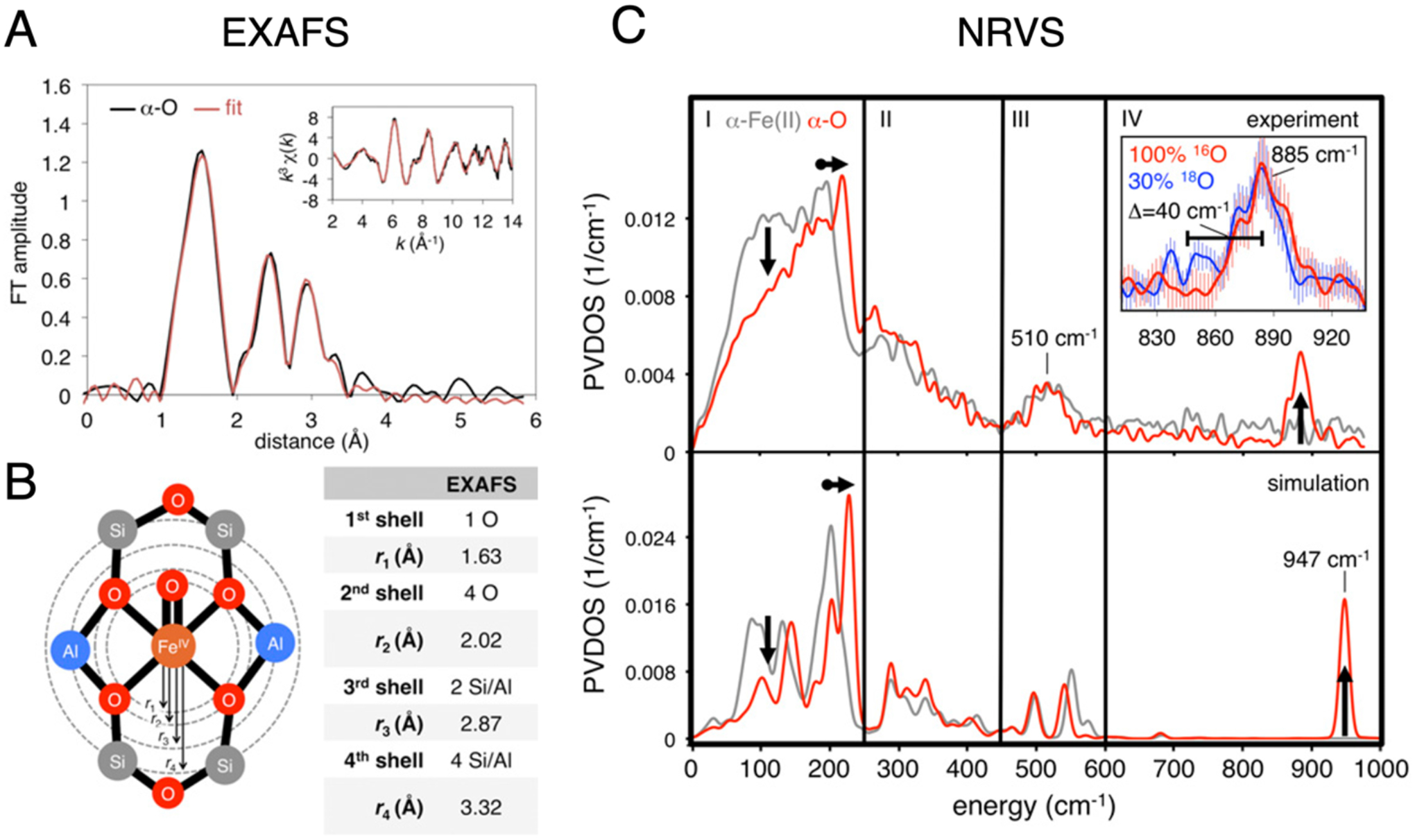
(A) FT-EXAFS spectrum of α-O (black), with fit in red. Parameters of the EXAFS fit are shown in (B). (C) Experimental NRVS spectra of α-Fe(II) (top, gray trace) and α-O (top, red trace). The 885 cm⁻¹ Fe(IV)=O stretching mode is shown in the inset in region IV, including data from¹⁸O isotopic perturbation. NRVS spectra simulated from DFT models of α-Fe(II) and α-O are shown in the bottom panel. Adapted from ref 59. Copyright 2018 National Academy of Sciences.

Figure 28.

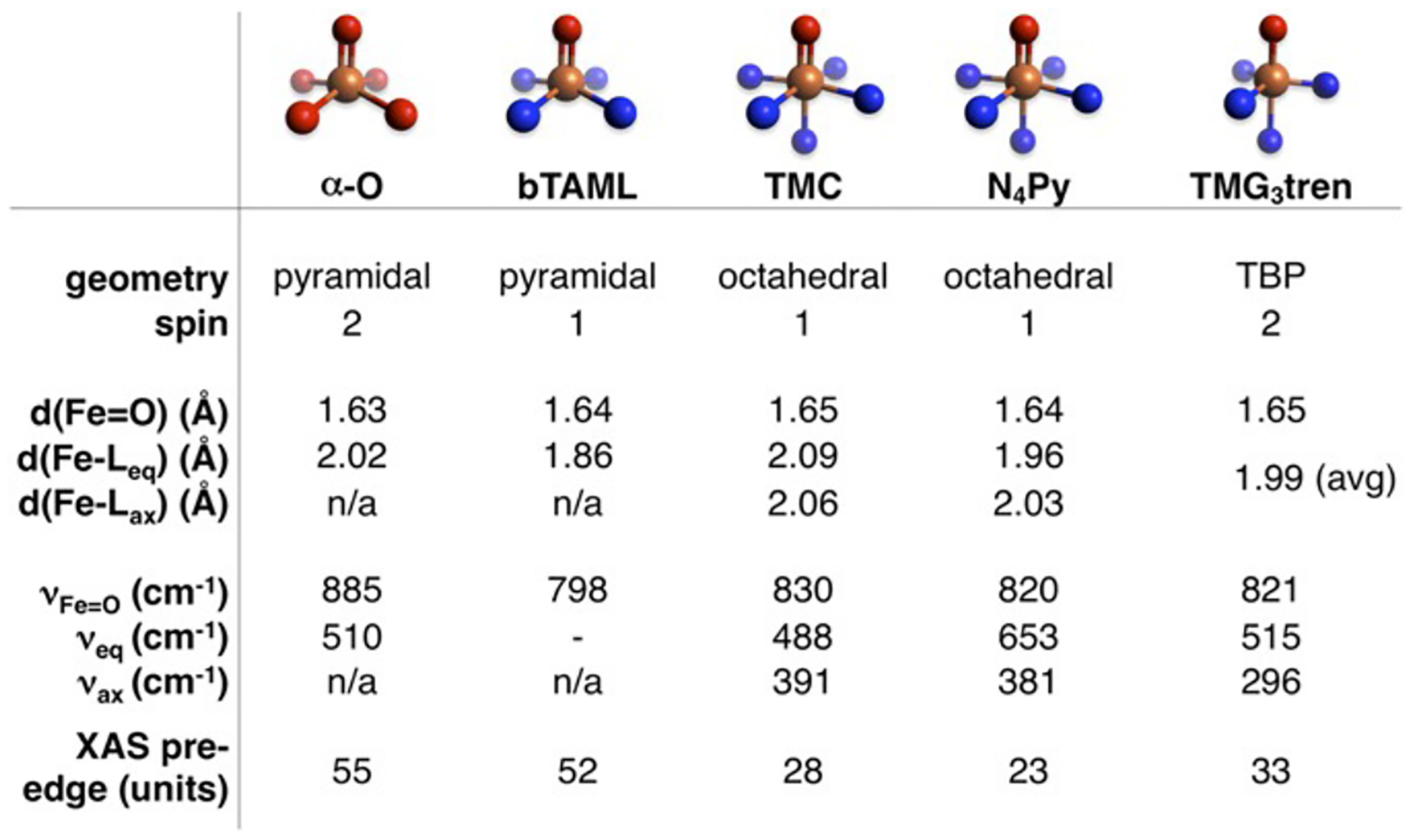
Tabulated spectroscopic and structural parameters of selected S = 1 and S = 2 non-heme Fe(IV)=O intermediates, whose first coordination spheres are illustrated at the top of the Figure. Reproduced from ref 59. Copyright 2018 National Academy of Sciences.

Studies of non-heme iron enzymes, small molecules, and DFT models suggest the intrinsically stable geometry of the S = 2 Fe(IV)=O core is one that places a ligand trans to the oxo (Figure 29, right).^1,29,83,84 This maximizes the overall strength of bonding to the non-oxo ligands but at the expense of a weakened Fe(IV)=O bond. Indeed, this geometry was found to be most stable for a DFT model of α-O optimized in the absence of constraints from a zeolite lattice.²⁹ However, this unconstrained model exhibits greatly diminished reactivity toward the C-H bonds of CH₄. Correlating structure to function, the inclusion of lattice constraints enforces an otherwise unfavorable five-coordinate geometry in which the oxo ligand occupies the axial position (Figure 29, left). On the other hand, this particular five-coordinate geometry is stable for the S = 5/2 Fe(III)-OH site produced during HAA. Thus, lattice constraints enforce a geometry that closely resembles that of the Fe(III)-OH product, destabilizing the Fe(IV)=O and increasing the driving force for HAA by ~ 5 kcal/mol.¹

Figure 29.

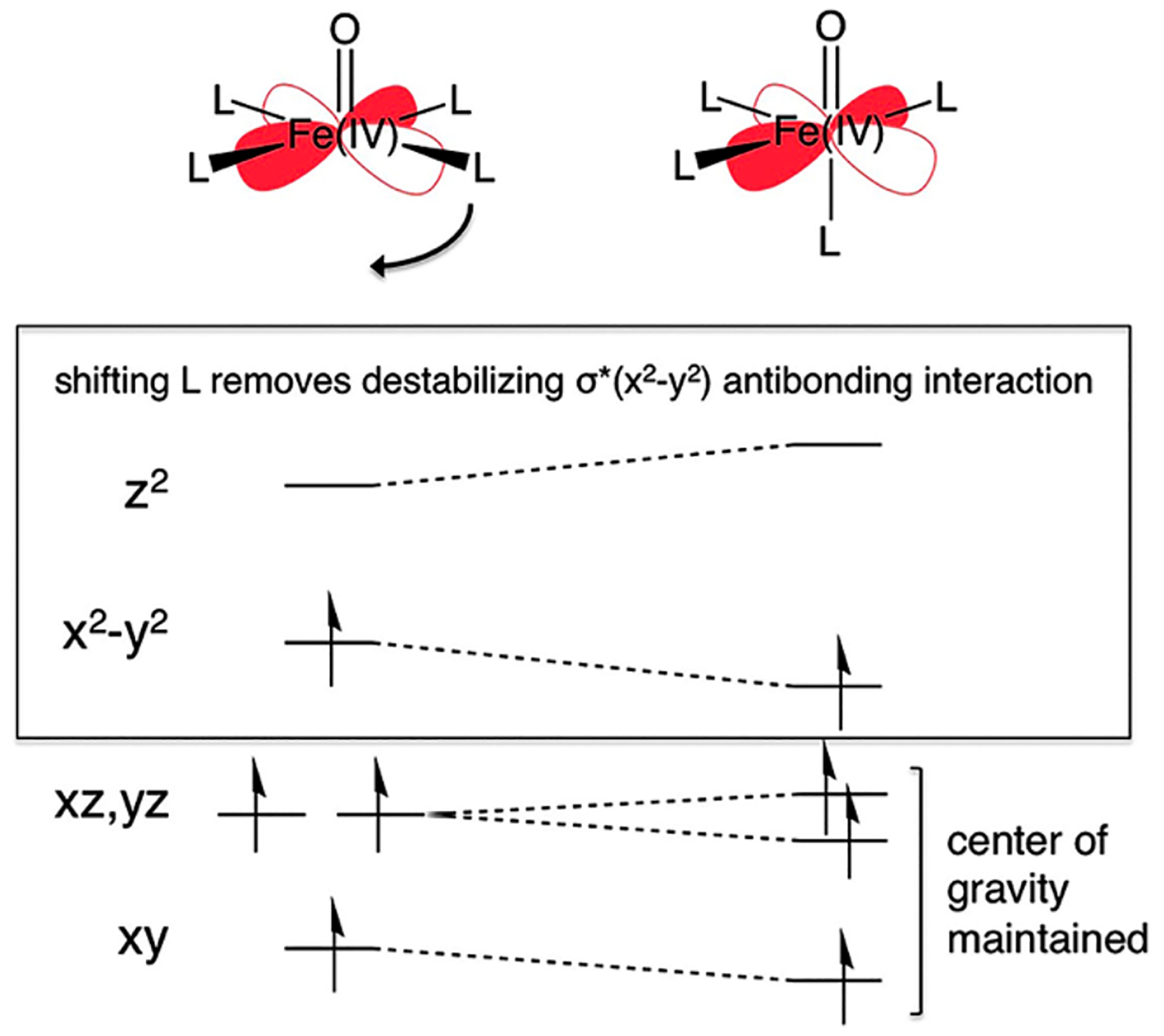
Walsh correlation diagram illustrating the ligand field origin of the instability of an axial square pyramidal S = 2 Fe(IV)=O site (left) with respect to shifting an equatorial ligand to fill the position trans to the oxo ligand (right). Reproduced from ref 1. Copyright 2016 American Chemical Society.

Factors contributing to the driving force for H-atom transfer were further elucidated with experimentally calibrated DFT calculations.⁵⁹ It was found that reactivity is driven by the extremely electrophilic nature of the α-O site. Its vacant trans axial position and enhanced exchange interactions on the S = 2 surface (relative to S = 1) both serve to stabilize the Fe(d_z2)/O(2p_z)-derived (dσ) redox-active molecular orbital (RAMO), substantially tuning up the site’s reduction potential. This also enhances the covalency of the Fe(IV)=O core, increasing the oxo 2p content of its RAMO, which reduces the activation barrier for H-atom transfer through enhanced orbital overlap with incoming C-H bonds.⁵⁹

3.2.3. Correlation of Structure with Function

The reactivity of high spin (S = 2) non-heme Fe(IV)=O species has been correlated extensively with their structural and spectroscopic features (see Figure 28), enabling quantitative comparisons that elucidate the extreme reactivity of α-O.⁵⁹ Here, we compare the five coordinate S = 2 species [(TMG₃tren)Fe(O)]²⁺ (Figure 30A) and the Fe(IV)=O reactive intermediate formed at the active site of the halogenase SyrB2 (Figure 30B) to α-O (Figure 30C).^59,85–87 These intermediates abstract H-atoms from their respective substrate C-H bonds (ligand C-H, threonine, and CH₄, respectively) to form a S = 5/2 Fe(III)-OH product and a substrate radical. In each case, the substrate takes a perpendicular approach to the Fe(IV)=O core, reacting through an excited state π channel. A detailed description of this orbital pathway mediating H-atom transfer is discussed elsewhere.^22,88 As tabulated in Figure 30 (right), [(TMG₃tren)Fe(O)]²⁺ and (Syrb2)Fe(O) abstract H-atoms from moderately strong C-H bonds (86–94 kcal/mol) with DFT-calculated activation barriers of ~20 kcal/mol.⁸⁷ On the other hand, using a similar DFT method to reference 87, α-O reacts with a very strong 104 kcal/mol C-H bond with a very low calculated activation barrier of 1.1 kcal/mol. The fact that all three reactions are predicted to be only modestly endo/exothermic indicates the O-H bonds of the S = 5/2 Fe(III)-OH products are similar in strength to the C-H bonds that are cleaved. Because the reaction of α-O with CH₄ is still exothermic even though the C-H bond in CH₄ is substantially stronger than the C-H bonds of the substrates in the TMG3tren and Syrb2 enzymes the driving force for O-H bond formation is uniquely large for α-O (see 3.2.1.).

Figure 30.

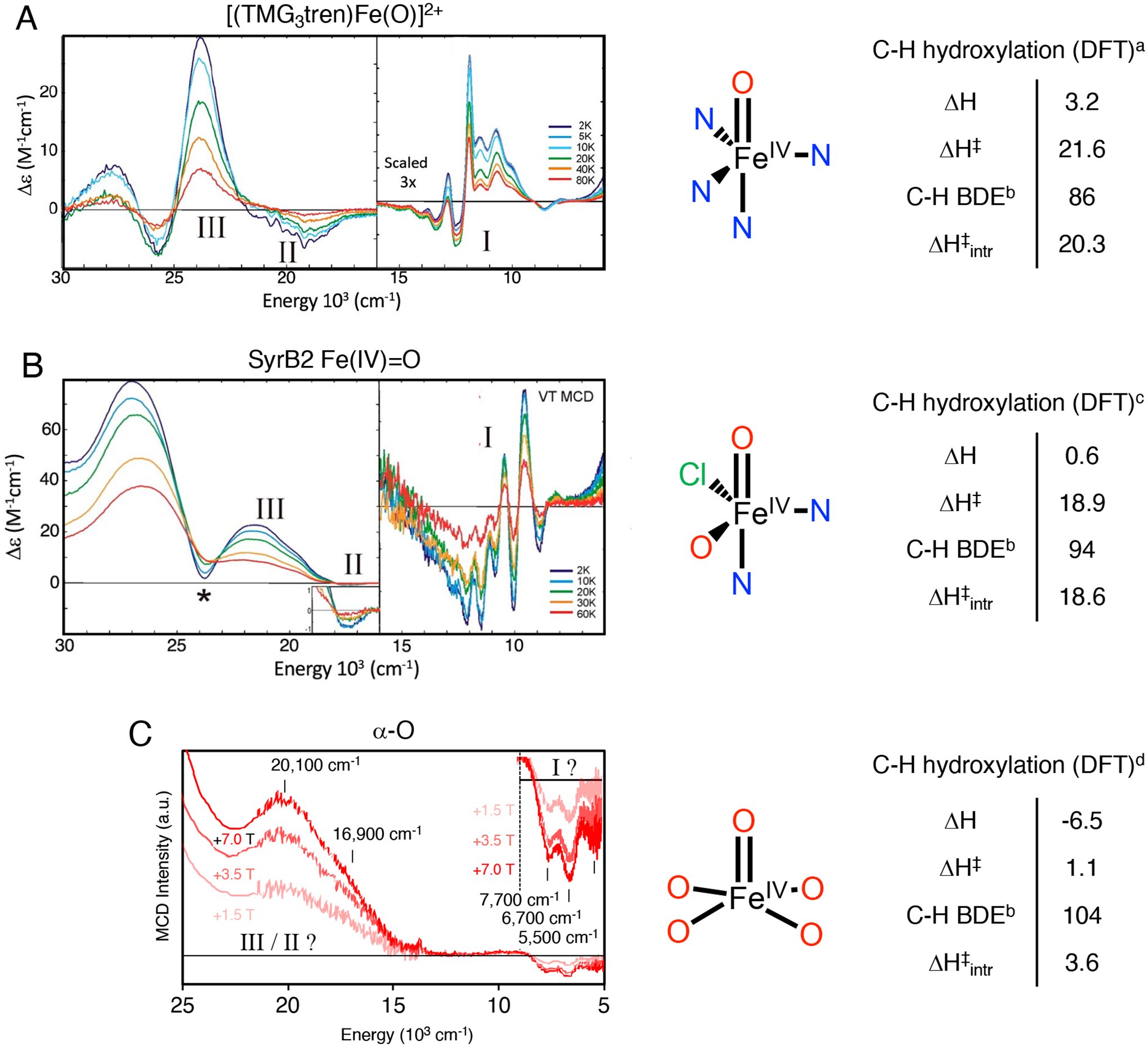
Left, low-temperature MCD spectra of [(TMG₃tren)Fe(O)]²⁺ (A), SyrB2 Fe(IV)=O (B), and α-O (C). Middle, geometric structures, including first shell atoms. All other atoms have been omitted for clarity. Right, corresponding DFT-calculated thermodynamics of HAA. Adapted from refs 87 and 29. Copyright 2016 American Chemical Society for ref 87 and Copyright 2016 Nature Publishing Group for ref 28. ^acalculated at the B3LYP+D2/def2-TZVP/COSMO(ε=4.0) level. ^bcalculated at the B3LYP+D2/def2-TZVP/COSMO(ε=4.0) level, in the absence of steric interference from a second-sphere Arg residue. ^cdetermined from experiment. ^dcalculated at the B3LYP+D3/6–311+G* level, using models reported in ref. 29.

Correcting for differences in thermodynamic driving force using Marcus theory,^89,90 the resulting intrinsic barrier for HAA by α-O (3.6 kcal/mol – see Figure 30, right) remains significantly lower than that calculated for the other S = 2 intermediates (18.6–20.3 kcal/mol). This suggests the electronic structure of α-O is uniquely activated for H-atom transfer. Low temperature magnetic circular dichroism spectroscopy can provide direct insight into the presence of low-lying acceptor orbitals that contribute to reactivity (Figure 30, left). For [(TMG₃tren)Fe(O)]²⁺ and (SyrB2)Fe(O), a dπ→dσ excitation is observed at ~9000–14000 cm⁻¹, with characteristic vibronic structure in Fe(IV)=O stretching modes (band I in Figures 30A and B).⁸⁷ This ligand field excited state, calculated to have considerable Fe(III)-oxyl character, correlates to the excited state π channel for H-atom transfer in S = 2 Fe(IV)=O intermediates.⁸⁸ For α-O, the high-energy shoulder of this band is likely observed in low temperature MCD as a negatively signed feature below ~8000 cm⁻¹ with potential vibronic structure (band I in Figure 30C).²⁹ The ~6000 cm⁻¹ redshift of this feature in α-O relative to the other two S = 2 intermediates correlates to a 17.2 kcal/mol reduction in the energy required to access the Fe(III)-oxyl-like dπ→dσ excited state. This correlates well with the 15–17 kcal/mol reduction in intrinsic barrier estimated from DFT calculations (see above), and suggests the extreme reactivity of α-O can be ascribed to facile polarization of this Fe(IV)=O core toward an Fe(III)-oxyl-like electronic structure.

Thus, the zeolite lattice enforces unstable geometries for both the α-Fe(II) and α-O sites. The unstable geometry of α-Fe(II) enables N₂O binding to the site which can then undergo an O-atom transfer mechanism to form the α-O active site. An unfavorable 5-coordinate geometry is also enforced on the α-O site due to the constraints of the lattice which increases the driving force for the HAA reaction with CH₄ and leads to the remarkable low temperature reactivity.

4. Active Site Pocket Contributions to Substrate Activation

Atoms in the vicinity of a transition metal center often contribute directly to the active site’s function. Enzymes have evolved precisely structured active site pockets to take advantage of these second-sphere effects. These include low dielectric environments with oriented dipoles, H-bond donors/acceptors, and steric constrictions that control the orientation and polarization of the substrate. An analogy can therefore be drawn between the active site pockets of enzymes and zeolite lattices. This similarity has been recognized for some time in the context of ‘classical’ zeolite catalysis, such as acid-catalyzed hydrocarbon cracking and isomerization reactions. Recent spectroscopic and computational studies have provided compelling examples of second-sphere effects in metallozeolite redox catalysis. What follows is an overview of gaseous small molecule substrate interactions with zeolite lattices, how these interactions affect catalytic rates and mechanisms, and a brief correlation to active site pocket effects in biology.

4.1. Interactions Between Substrates and Zeolite Lattices

When the zeolite pocket for substrate adsorption is positioned in close spatial proximity to the catalytic site, substrate adsorption can be directly coupled to catalysis. Adsorption can serve to localize the substrate in space (an entropy/enthalpy compensation effect), or polarize the substrate, both activating it for subsequent reactivity. Presented below are some of the physical (and chemical) contributions to substrate adsorption in zeolite lattices, as well as the experimental and computational methods used to probe these effects.

4.1.1. Interactions Contributing to Substrate Adsorption

Gaseous substrates engage in a range intermolecular interactions zeolite lattices. Van der Waals (vdW) forces are weak, short-range interactions (~1/r⁶) whose strength scales with the molecular surface area available for van der Waals contact (Figure 31, green). vdW interactions become increasingly important for larger substrates. The topology and local curvature of the zeolite lattice are also important considerations as vdW contact is maximized for snugly fitting substrates.⁹¹ This has important implications for catalytic rates and selectivity (see 4.2). Because vdW forces are weak, these interactions may not perturb the spectroscopic signatures of adsorbed substrates. Gas adsorption measurements and temperature programmed desorption provide convenient means to resolve weak substrate-zeolite interactions (see 4.1.2).

Figure 31.

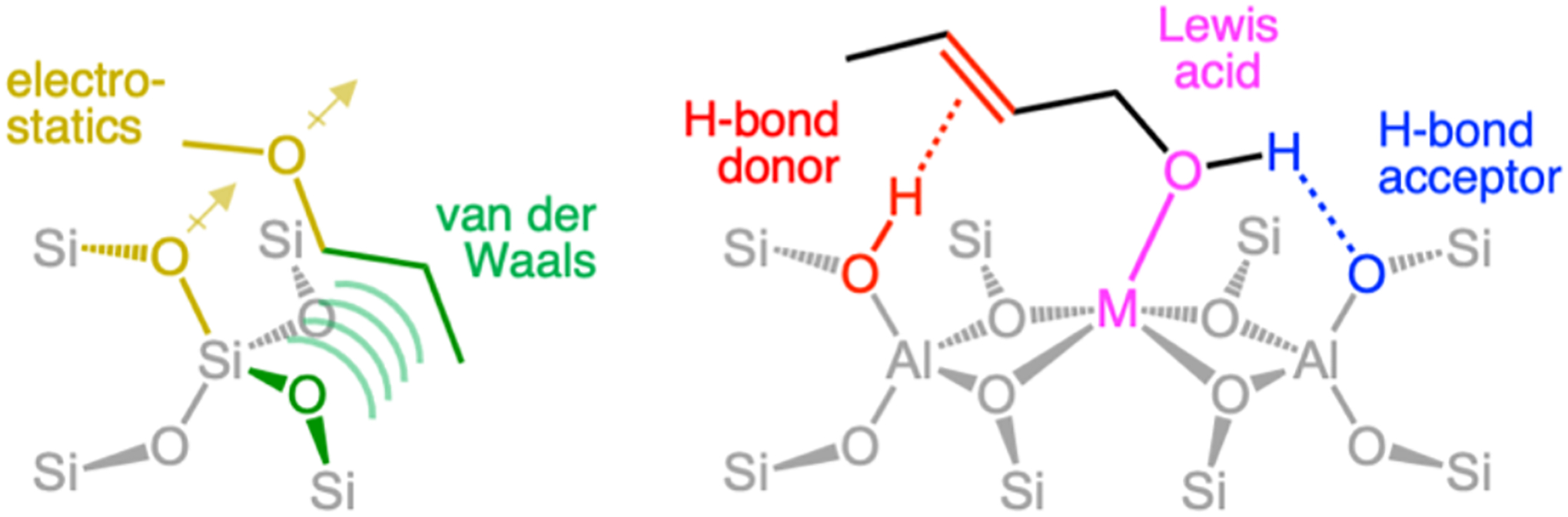
Illustrations of attractive intermolecular forces between zeolite lattices (gray) and organic substrates.

Substrates with permanent dipole and/or quadrupole moments can interact electrostatically with local polar regions of zeolite lattices (Figure 31, yellow). The strength of these effects depends on the lattice composition (i.e. presence of dipoles, extra-lattice cations, etc.). Hydrogen bonding is a particularly important subset of polar interactions. Lattice oxygen atoms can serve as weak hydrogen bond acceptors (Figure 31, blue), however purely siliceous zeolites are considered to be relatively nonpolar. Polarity increases with lattice Al content, as Al-OH-Si sites are strong hydrogen bond donors (Figure 31, red). Even weakly Lewis-basic adsorbates can deprotonate these Brønsted acid sites (BAS), forming tightly bound ion pairs. As a result, zeolites with high Al content bind substrates such as H₂O and NH₃ with high affinity. Interactions involving strong hydrogen bonding or proton transfer can often be studied using vibrational spectroscopy or¹H solid-state NMR (see 4.1.3). Local electrostatic interactions are also important in dynamic catalytic systems. In selective catalytic reduction of NO_x with NH₃ over CuCHA, electrostatic attraction between negatively-charged Al T-sites and positively-charged mobilized [Cu(NH₃)₂]⁺ ions affect the formation of active [Cu₂O₂(NH₃)₄]²⁺ species (see 4.3).⁹²

When acting as Lewis acids, Al-OH-Si sites (Figure 31, red) and extra-lattice cations (Figure 31, blue) can electronically polarize substrates, resulting in ion-induced dipole and dipole-induced dipole interactions. In some cases, bona fide covalent interactions arise between substrates and extra-lattice metal ions, including both forward- and back-donation. Covalent interactions activate bound substrates for reactivity and may be evident from e.g. vibrational spectroscopy (see 4.1.3). Extra-lattice cations also generate local electric field gradients, and this effect can be used to discriminate between substrates with different electric quadrupole moments. While electric quadrupole interactions are weak, they enable the discrimination of N₂ from O₂ in industrial air separation using Li-zeolites.⁹³

Long-range electrostatic effects arise from ordered (or partially ordered) arrays of oriented dipoles within zeolite lattices⁹⁴ (and other extended porous materials). The local electrostatic potentials of polar species (e.g. Brønsted acid groups, extra-lattice cations), when summed over an ‘infinite’ lattice, comprise a Madelung potential.⁹⁵ The presence of a Madelung potential is a unique facet of the chemical environment within zeolite pores that is distinct from solution or gas phases. Interactions of zeolite-confined substrates with a Madelung potential represent an important class of so-called ‘confinement effects’ – a hallmark of zeolite catalysis. These effects are more pronounced in dense structures with constricted pores and in lattices incorporating high concentrations of polar species. Long-range electrostatic effects can have important impacts on reactivity by stabilizing polar substrates and/or transition states (see 4.2.2).

4.1.2. Thermodynamic Probes

Gas adsorption measurements⁹⁶ and temperature programmed desorption (TPD)⁹⁷ have been used to quantify critical aspects of substrate adsorption in zeolite lattices, including overall uptake, enthalpies of adsorption/desorption, and the presence of multiple binding regions. In a gas adsorption measurement, known quantities of gas are dosed onto a zeolite sample held at a fixed temperature in a closed vessel. A portion of the gas is adsorbed within the micropores of the zeolite and does not contribute to raising the pressure within the vessel. The pressure in the headspace above the sample is then correlated to the amount of gas adsorbed, resulting in a gas adsorption isotherm. For weakly-interacting adsorbates, the shape of the gas adsorption isotherm is generally determined by the temperature, the number of different binding sites in the material, and their associated saturation uptakes and binding energies. As an example, in the acidic mordenite (H-MOR) zeolite, adsorption isotherms for several small molecule adsorbates are presented in Figure 32.⁹⁸ For strongly interacting adsorbates such as H₂O, condensation of a liquid phase within zeolite micropores can lead to more complicated adsorption profiles,⁹⁶ but under conditions that are not typically relevant to gas-phase catalysis.

Figure 32.

Adsorption isotherms for various small adsorbates on H-MOR collected at 210 K. (Xenon data were collected at 318 K; data are points, curves are multi-site Langmuir fits). Reproduced from ref 98. Copyright 1999 American Chemical Society.

Isosteric heats of substrate adsorption can be extrapolated from variable-temperature isothermal data⁹⁶ or microcalorimetry experiments.⁹⁹ For materials with a single type of isolated adsorption site, the variation of isosteric heat with substrate loading is expected to be minimal. If more than one adsorption site is present, the isosteric heat will vary with respect to loading – typically decreasing as successively weaker-binding sites become occupied. (Adsorbate-adsorbate interactions can result in the isosteric heat increasing once a threshold loading is achieved, however these situations are unlikely to be relevant to gas-phase catalysis.) As an example, isosteric heats for CH₄ adsorption in the H-MOR zeolite and the acidic Zeolite Socony Mobile–12 (H-ZSM-12) zeolite from microcalorimetry data are presented in Figure 33.¹⁰⁰ The structures of the two zeolites are difference and therefore have different isosteric heats of CH₄ adsorption. H-MOR is made up of large 12MR channels as well as constricted ‘side-pockets’. The isosteric heat of CH₄ adsorption therefore varies with loading, the side-pocket has a higher affinity for CH₄ and is filled preferentially, followed by the lower-affinity 12MR channel. This leads to the change in the isosteric heat of CH₄ for H-MOR (Figure 33, squares). In contrast, H-ZSM-12 has12MR channel environments but no small side-pockets, leading to an isosteric heat that is less sensitive to CH₄ loading and its isosteric heat of CH₄ adsorption is linear (shown in Figure 33, triangles).

Figure 33.

Isosteric heats of CH₄ adsorption in H-MOR (squares) and H-ZSM-12 (triangles) from microcalorimetry. Reproduced from ref 100. Copyright 2015 American Chemical Society.

Whereas gas adsorption measurements are well suited to studying weak-to-moderate binding (−ΔH_ads = 1–15 kcal/mol) at cryogenic to ambient temperatures, TPD experiments are regularly used to evaluate stronger binding interactions that are only interrupted at high temperature.⁹⁷ In a TPD experiment, a sample containing adsorbed substrate is subjected to a controlled temperature ramp. Each adsorption site within the material releases its adsorbed substrate to the gas phase at a characteristic temperature. Desorption is typically quantified using mass spectrometry or thermal conductivity detection, often with parallel use of IR (see 4.1.3). For conditions where desorption is under thermodynamic control, the adsorption enthalpy can be quantified by varying the temperature ramp rate. For conditions where desorption is kinetically limited, the activation barrier for substrate desorption is thus quantified. Different adsorption sites manifest as different MS peaks in TPD data, and the area under each peak quantifies the amount of substrate adsorbed at the corresponding site. TPD of Lewis-basic adsorbates (NH₃, pyridine) is one method commonly used to probe strong acid sites in zeolites.¹⁰¹ As shown in Figure 34, NH₃-loaded zeolites often show three distinct sets of TPD features. Desorption peaks below ~500 K have been ascribed to NH₃ hydrogen bonded to NH₄⁺ ions or to the zeolite lattice. TPD peaks between ~500–700 K are ascribed to desorption of NH₄⁺ ions as NH₃, with concurrent back proton transfer to the lattice. This is evident from the growth of O-H stretching modes in IR (e.g. features in the 3500–3800 cm⁻¹ regions of spectra in Figure 34B and 34 C). TPD peaks above 700 K correspond to loss of NH₃ bound to strong Lewis-acid sites (e.g extra-lattice Al), or to loss of lattice hydroxyl groups (as OH is observed at same M/Z as NH₃).¹⁰¹ Furthermore, the steric environment of acid sites can be probed using bulkier Lewis bases like pyridine. Active sites in constricted environments are not perturbed by bulky probe molecules. This provides a convenient method to discriminate between exposed versus buried active sites in zeolites lattices with complicated topologies (e.g. mordenite – see 4.2.1).

Figure 34.

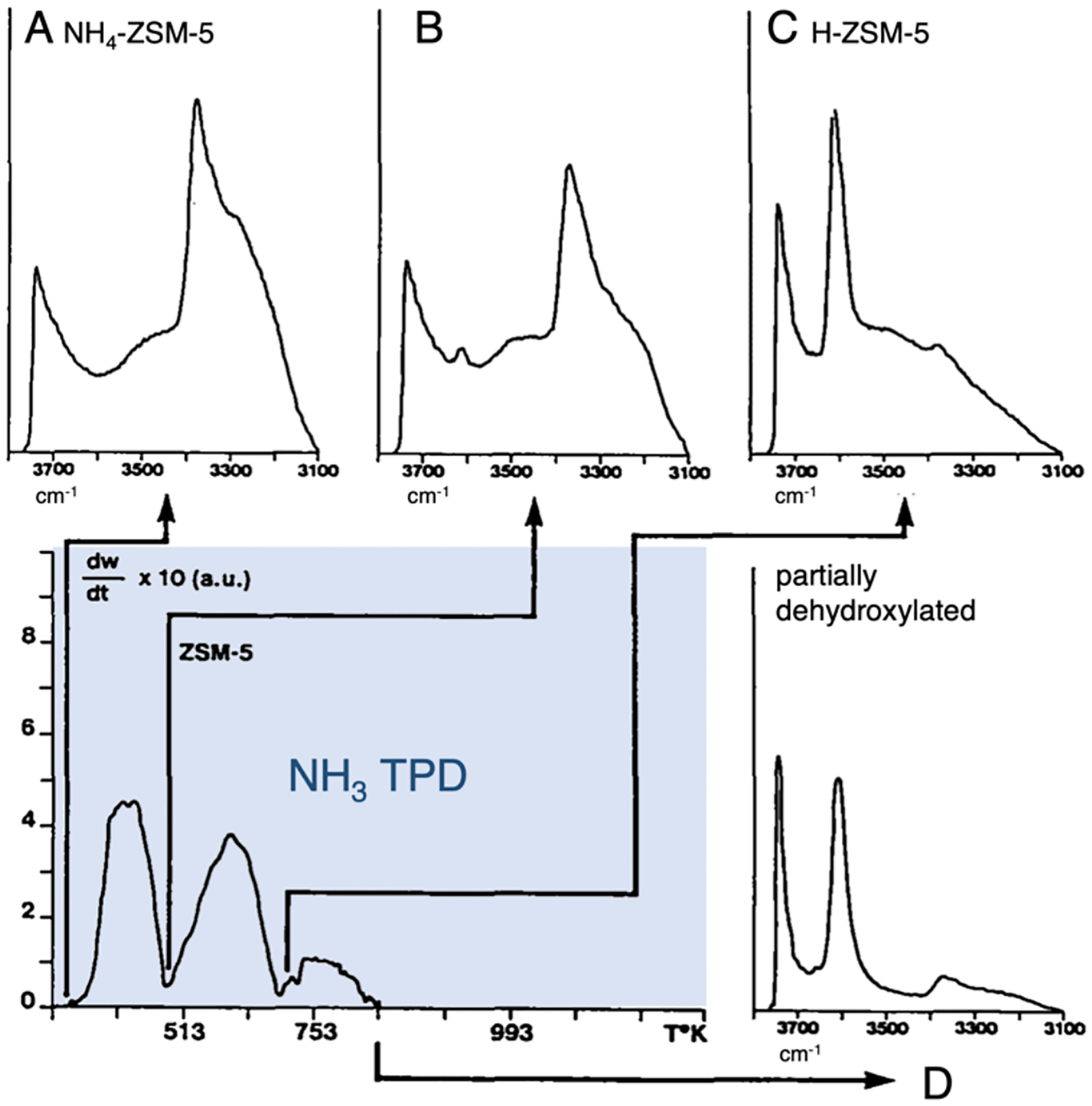
NH₃ TPD data from ammonia treated H-ZSM-5 (NH₄-ZSM-5), correlated with parallel IR data collected at room temperature (A), 478 K (B), 688 K (C), and 873 K (D). Adapted from ref 101. Copyright 1986 Elsevier.

4.1.3. Spectroscopic Probes

Spectroscopic methods can provide detailed, molecular-level insight into zeolite-adsorbate interactions.¹⁰² This information often complements thermodynamic data from gas adsorption or TPD experiments (see above, 4.1.2). Spectroscopic probes have been developed to focus on zeolite active sites, or their small molecule substrates. Active site spectroscopic probes are covered in detail elsewhere.¹ Here, the focus is on methods that elucidate second-sphere interactions of zeolite-confined substrates. Diffuse-reflectance IR plays a prominent role. Zeolite-substrate interactions may be evident from the perturbation of substrate vibrations upon adsorption. Weak interactions such as vdW are sufficient to partially (or entirely) eliminate rotational fine structure from the IR spectra of adsorbed small molecules. With sufficiently small IR linewidths, multiple chemical environments for substrate adsorption can be resolved. Weak intermolecular interactions do not significantly perturb vibrational frequencies, but they can substantially impact IR intensities. For example, for inversion-symmetric adsorbates such as N₂ or H₂, weak polarizing interactions from local electric fields give IR intensity to gerade modes that are otherwise symmetry forbidden.¹⁰³ Substrate vibrational frequencies are perturbed by stronger intermolecular interactions, such as hydrogen bonding to a Brønsted acid site. For example, the uptake of gaseous NH₃ in H-zeolites to form adsorbed NH₄⁺ ions is clearly evident from IR spectroscopy.¹⁰⁴ For symmetrical species like NH₄⁺, degenerate vibrational modes are split upon interaction with the lattice, providing some insight into the local symmetry of the adsorption site. Alongside IR,¹H and¹³C solid state NMR spectroscopy have found widespread use in zeolite catalysis. These experiments have been used to resolve different chemical environments and dynamics of substrates within zeolite pores, and to directly track Brønsted acid sites.^105–107

4.1.4. Structural Probes

In some cases, X-ray diffraction methods can be used to identify locations of substrate adsorption within zeolite lattices. These experiments can be routine for larger substrates that adsorb strongly (e.g. aromatics).¹⁰⁸ Structure solutions may be arrived at using either direct (single crystal) or indirect methods (Rietveld refinement). Gaseous small molecule adsorbates such as CH₄ present considerable additional challenges, however. Rietveld refinement of low temperature neutron powder diffraction data can provide critical structural insight,¹⁰⁹ but this may require deuterated substrates to resolve the positions of light atoms.¹⁰⁸

4.1.5. Computational Probes

Molecular dynamics (MD) simulations are routinely used to interrogate molecular-level details of substrate adsorption in zeolites.^110–112 Here, we will focus on DFT calculations, where over the past 10–15 years important advances have been made along two fronts: 1) the development of dispersion (vdW) corrected DFT functionals, and 2) the development of periodic DFT and mixed quantum-classical approaches to modeling extended materials. Using these methods, weak intermolecular interactions can now be modeled with high levels of chemical accuracy.

Intermolecular interactions occur at distances that are longer than bona fide chemical bonds. DFT basis sets and functionals must be chosen carefully to provide chemical accuracy at this length scale. Basis sets with diffuse functions are desirable, as these provide additional flexibility in describing the exponential ‘tail’ of wavefunctions. Polarization functions are desirable for describing ion-induced dipole and hydrogen bonding interactions. (This is in addition to their critical importance in accurately describing chemical bonds.) The challenges of describing intermolecular interactions with DFT extend beyond choosing an appropriately flexible basis set, however.⁹⁴ Dispersion has been an area of challenge, as it involves electron correlation over long distances. The DFT-D approach of Grimme has been used to circumvent this issue with almost no additional computational expense. Grimme’s original dispersion correction adds empirical, damped −1/r⁶ potentials between pairs of atoms.¹¹³ This correction can be added to both pure and hybrid DFT functionals. DFT-D3 – a more recent iteration that has found widespread use – has been refined to achieve higher accuracy, cover a larger range of atoms, and includes dispersion coefficients calculated from first principles.¹¹⁴ Dispersion-corrected DFT is now the standard approach to achieve high chemical accuracy for non-covalent interactions.

In addition to the choice of DFT method, the way in which an active site model is constructed can have a considerable impact on its calculated properties. Two approaches are commonly used for zeolites (and other extended porous materials). The first involves excising a portion of the active site and surrounding zeolite lattice from the extended crystal structure to create a ‘cluster’ model. Larger models that include more of the lattice environment surrounding the active site tend to offer greater chemical accuracy, but the benefit of including additional atoms drops off rapidly with model size.⁹⁴ For extra-lattice metal ions, models including an additional shell of T-atoms beyond the first coordination sphere are generally sufficient to model first-sphere properties (e.g. active site geometry, electronic structure). Much larger models may be required to accurately model second-sphere effects, however.

A potential deficit of cluster model analysis is its failure to properly account for long-range electrostatic effects that manifest in extended materials.^94,115 This is currently addressed using either mixed quantum-classical methods (e.g. QM/MM) or periodic DFT. Here, the end goal is the proper description of the interaction of the substrate and/or active site with the Madelung potential of the extended structure. Mixed quantum-classical methods for modeling zeolites are reviewed elsewhere.^94,116 While periodic DFT is considerably more computationally expensive than cluster analysis, this trade-off can be worthwhile when modeling the energetics of polar species in zeolite pores – particularly, polar transition states (see 4.2). A comparison of cluster and periodic models can provide valuable insight into the importance of long-range electrostatic effects in a system of interest. Indeed, there are many cases in the literature reporting the insufficiency of cluster analysis for certain reactions in zeolites.^94,115,117 However, there are also cases where periodic DFT offers limited benefit.⁷⁷ Long-range electrostatic effects are less likely to manifest for non-polar species and in zeolite lattices with large voids and open pore architectures. Periodic methods can become prohibitively expensive for certain basis sets and functionals required to accurately model transition metal active sites (notably, hybrid functionals). In some cases, the periodic models themselves can be problematic (i.e. independent of method). They invariably over-estimate the level of long-range order present in actual materials. Artificially ordered oriented dipoles (e.g. from Si-OH-Al groups) can lead to non-physical Madelung potentials, especially in dense structures. While this is not an issue for crystalline porous materials such as metal-organic frameworks, these issues should be considered when modeling compositionally heterogeneous structures like (metallo)zeolites.

4.2. Impact of Substrate Adsorption on Reactivity

Catalytic rates and selectivities can be substantially affected by non-covalent interactions between a substrate and second-sphere atoms within a zeolite active site pocket. This is a hallmark of ‘classical’ zeolite catalysis such as acid-catalyzed isomerization and cracking reactions. More recently, active site pocket stabilization effects have been identified in metallozeolite catalysis. A few examples are discussed below.

4.2.1. Substrate Recognition and Stabilization

For some time, interesting correlations have been documented between zeolite topology, substrate shape and size, and catalytic rates and selectivities. Early work identified the curvature of zeolite pores as a key determinant of reactivity.¹¹⁸ It was noted that catalytic rates are maximized in systems where the substrate makes a snug fit in the zeolite pore. This concept, known as the ‘nest effect’, grew out of studies of n-pentane cracking in acid zeolites.⁹¹ Recently, the ‘nest effect’ concept was found to be relevant in the selective oxidation of CH₄ to CH₃OH by Cu dimers in Cu-MOR.³¹ Two distinct CH₄-reactive [Cu₂O]²⁺ intermediates form in this lattice. These active sites have highly similar spectroscopic features in DR-UV-vis and rR, reflecting highly similar geometric and electronic structures.⁶² The first-sphere properties of these sites, labeled MOR-1 and MOR-2, also closely resemble the [Cu₂O]²⁺ core stabilized in Cu-ZSM-5,⁶¹ viz. a Cu-O-Cu angle of ~140° estimated from rR, and an oxo-Cu(II) LMCT band at 22,000–23000 cm⁻¹. However, in comparing the reactivity of MOR-1 and MOR-2, a distinct difference in CH₄ activation kinetics is observed. This was quantified in temperature-dependent reactivity studies, using the DR-UV-vis features of MOR-1 and MOR-2 as kinetic handles. It was found that MOR-1 has a larger activation enthalpy and smaller activation entropy (ΔH^‡ = 14.7 kcal/mol, ΔS^‡ = −36 cal/(mol*K)) than MOR-2 (ΔH^‡ = 11.1 kcal/mol, ΔS^‡ = −44 cal/(mol*K)). This difference in reactivity is too large to be ascribed to the subtle differences in active site geometric/electronic structure suggested by spectroscopy.⁶² The larger (more negative) ΔS^‡ for MOR-2 suggested a more constrained transition state, potentially reflecting a more sterically demanding second-sphere environment. However, this led to the somewhat counterintuitive idea that a constricted active site reacts with a lower ΔH^‡.⁶²

To evaluate this idea, MOR-1 and MOR-2 were distinguished based on their reactivity with bulky probe substrates such as tetrahydrofuran (THF).³¹ THF has weak C-H bonds relative to CH₄ (ca. 92 kcal/mol versus 104 kcal/mol). Figure 35 shows the overtones of the Cu-O-Cu antisymmetric stretching modes characteristic of MOR-1 and MOR-2. As shown in Figure 35A, both the MOR-1 and MOR-2 features decay in the presence of CH₄. On the other hand, as shown in Figure 35B, only the MOR-1 feature decays in the presence of THF, indicating MOR-2 does not react with this substrate. The ability of MOR-2 to activate CH₄ but not THF requires the presence of an additional large activation barrier for bulky substrates. This suggests MOR-2 is located in a sterically constricted region of the MOR lattice that is accessible to CH₄ but not THF – either the side pocket, or the 8 MR channels. In contrast, MOR-1 is located in the large 12MR channel that is accessible to both CH₄ and THF. This is in line with DFT calculations, which suggest THF is substantially destabilized in the constricted side pocket. The active site pocket of MOR-2 therefore engenders substrate specificity, accepting small alkane substrates while rejecting branched or cyclic species.³¹

Figure 35.

Loss of the 2ν_as rR features of MOR-1 and MOR-2 in the presence of CH₄ (top, with experimental activation barriers included) and THF (bottom). These data show MOR-2 reacts with CH₄, but not THF. Reproduced from ref 31. Copyright 2018 American Chemical Society.

These reactivity studies confirmed that MOR-2 is located in a sterically constricted region of the MOR lattice yet activates CH₄ with a lower enthalpic barrier than MOR-1. To understand this, DFT models of various candidate structures for MOR-1 and MOR-2 were constructed and then evaluated by comparing their predicted spectroscopic features against experimental spectroscopic data. Two candidate structures reproduced the spectroscopic features of MOR-1. These [Cu₂O]²⁺ cores are located in the 8MR windows lining the wall of the 12 MR channel. One is bound to an Al-(O-Si)₂-O-Al sequence, and the other to an Al-(O-Si)₃-O-Al sequence. Only one candidate structure reproduced the spectroscopy and THF inaccessibility of MOR-2. This [Cu₂O]²⁺ core is bound to an Al-(O-Si)₃-O-Al sequence at the intersection of the side pocket and the 8 MR channel.

As shown in Figure 36, the CH₄ HAA activation barrier of the MOR-2 model (ΔH^‡ = 11.8 kcal/mol) is indeed predicted to be lower than that of the MOR-1 model (ΔH^‡ = 18.0 kcal/mol).³¹ This is because CH₄ must enter the constricted side pocket to interact with MOR-2. In doing so, CH₄ forms close van der Waals contacts with the walls of the side pocket, resulting in a predicted stabilization of the substrate by ΔH = −6.2 kcal/mol. On the other hand, CH₄ loses van der Waals contact with the lattice as it approaches MOR-1, resulting in a small destabilizing effect (ΔH = +1.5 kcal/mol). The net difference in substrate stabilization of 7.7 kcal/mol correlates well with the experimentally determined isosteric heat of CH₄ adsorption into the side pocket (−7.2 kcal/mol).^119,120 This difference in substrate stabilization by the lattice is maintained throughout the HAA reaction coordinate. The HAA transition state and CH₃ first product formed at MOR-2 are both stabilized by ~7 kcal/mol relative to MOR-1. The larger (more negative) entropy of activation for MOR-2 (vide supra) is likely due to confinement of the substrate within the constricted side pocket. On the other hand, the predicted reaction energetics for MOR-1 and MOR-2 are comparable if the dispersion correction required to model van der Waals interactions is removed from the DFT functional. This difference in the reactivities of MOR-1 and MOR-2 therefore relates to differences in van der Waals stabilization of the substrate at these active sites, drawing an analogy to the ‘nest’ effect in classical zeolite catalysis.³¹

Figure 36.

DFT evaluation of the CH₄ HAA reaction coordinates for MOR-1 (top structures, blue path) and MOR-2 (bottom structures, red path), illustrating how van der Waals contact between the substrate and the zeolite lattice lowers the apparent activation barrier for MOR-2 (but not MOR-1). (Color legend: orange: Cu; red: O; green: Al; grey: C; and white: H.) Reproduced from ref 31. Copyright 2018 American Chemical Society

4.2.2. Modulation of Transition State Energies

The modulation of competing reaction pathways through active site pocket effects is a hallmark of ‘classical’ zeolite catalysis. For example, weak intermolecular interactions can stabilize a substrate conformation that favors a particular reaction channel. Notably, these ‘preorganization’ effects are observed in the competition between hydrocarbon cracking and desaturation over acid zeolite catalysts. In these reactions, physical confinement of the substrate in a zeolite pore can substantially tune both the enthalpies and entropies of activation.¹²¹

While our understanding of how zeolite pores tune reaction barriers in metallozeolite catalysis is less mature, this is an active and growing area of research. A computational study of CH4 oxidation by Fe(IV)=O centers in Fe-CHA provides an interesting illustration of how substrate confinement may tune activation barriers for hydrocarbon oxidation in metallozeolites.¹¹⁷ The in silico CH₄ reactivity of cluster and periodic models of the Fe(IV)=O intermediate were compared (see Figure 37). The predicted barrier for HAA from CH₄ is reduced by 35 kJ/mol for the periodic model (ΔH^‡ = 24 kJ/mol versus 59 kJ/mol). This difference is attributed to long-range electrostatic interactions that selectively stabilize polar species. Electrostatics have little impact on the stability of the non-polar CH₄ substrate, while the polar Fe(III)-OH···CH₃ first product is substantially stabilized. Furthermore, Bader charge analysis shows a difference in the extent of substrate polarization at the HAA transition state. However, this does not entirely account for the observed reduction to the barrier. Correcting for the increased driving force for HAA,⁹⁰ the intrinsic barrier is only 10 kJ/mol lower in the periodic model relative to the cluster model (35 kJ/mol versus 46 kJ/mol). The majority of the barrier reduction in the periodic calculation is therefore due to the stabilization of the Fe(III)-OH product.

Figure 37.

Comparison periodic (left) and cluster model analysis (right) of CH₄ hydroxylation by Fe(IV)=O centers in Fe-CHA, performed at the Adiabatic Connection Fluctuation−Dissipation Theorem in its Random Phase Approximation (blue) and PBE-D2 (red) levels of theory. Structures: A –reactant complex, B – H-atom transfer TS, C – CH₃ radical first product, D – C-O bond formation TS, E – Fe-methanol adduct. Color legend: blue: Al; yellow: Si; red: O; gold: Fe. Reproduced from ref 117. Copyright 2016 American Chemical Society.

This computational investigation provides a compelling example of how long-range electrostatics may affect metallozeolite catalysis. To further evaluate these ideas, a few potential issues are worthy of consideration. The inclusion of one active site per unit cell in the very dense CHA lattice could potentially lead to unphysical effects, especially considering the highly polar Fe(IV)=O units share the same orientation. A periodic calculation involving one active site per 2×2×2 supercell could be informative (but computationally expensive). Experimental quantification of the very low HAA barrier would be very useful, but this could prove to be challenging due to diffusion limitations. Nonetheless, more experimental data are required to evaluate the strengths and limitations of periodic DFT for this important reaction.

A similar approach – comparison of cluster and periodic calculations – was taken to understand the impact of long-range electrostatic effects on the activation of N₂O by α-Fe(II) in Fe-*BEA.⁷⁷ N₂O is a polar substrate, and its activation involves charge transfer from Fe(II) into the vacant π* orbitals of N₂O (see section 3.2.1). It was therefore important to evaluate the role of long-range electrostatic interactions in this reaction. In this case, the activation barrier for N-O cleavage has been measured experimentally, and this served as a benchmark for subsequent DFT analysis. It was found that cluster and periodic calculations both yield similar reaction profiles for N-O cleavage – both in reasonable agreement with the experimentally determined activation barrier. This suggests long-range electrostatic effects do not contribute significantly in this particular reaction, perhaps due to substantially diminished density of the *BEA lattice relative to CHA.

4.2.3. Correlation to Biology

There are many parallels to be drawn between active site pocket effects in metallozeolite and metalloenzyme catalysis. The substrate specificity and product selectivity of metalloenzymes derives from the structures of their active site pockets, raising an analogy to the ‘nest effect’ discussed above. For example, lipoxygenases (LOs) are mononuclear non-heme iron enzymes that catalyze the stereoselective hydroperoxidation of (Z,Z)-1,4-pentadiene containing fatty acid substrates like arachidonic acid (AA).^122,123 The reactive intermediate in LOs is a ferric hydroxide that abstracts an H atom from the weak C_sp3-H bond of the pentadiene unit, forming a delocalized organic radical and an Fe(II)-OH₂ center.¹²³ The organic radical is intercepted by O₂, forming an organic peroxy intermediate that abstracts a proton and electron from the Fe(II)-OH₂ center. This finishes the hydroperoxidated product and regenerates the active Fe(III)-OH intermediate. AA contains multiple (Z,Z)-1,4-pentadiene units, and different LOs have evolved to selectively hydroperoxidate different positions of this substrate. Site selectivity derives from the shape of the active site pocket – a hydrophobic tubular cavity with dimensions matching the substrate. This favors selective uptake of the linear non-polar substrate, in analogy to the nest effect.¹²³ As illustrated in Figure 38, different LOs enforce different conformations of the AA substrate, favoring head-first versus tail-first approach, and determining the depth of substrate penetration into the active site pocket. Furthermore, the sterics of the active site pocket determine how oxygen approaches the H-abstracted intermediate. Together, these effects determine the position of substrate hydroperoxidation. An example of this is shown in Figure 38 where the different positions of substrate hydroperoxidation are labeled by 8R, 12S, 8S, and 12R.¹²²

Figure 38.

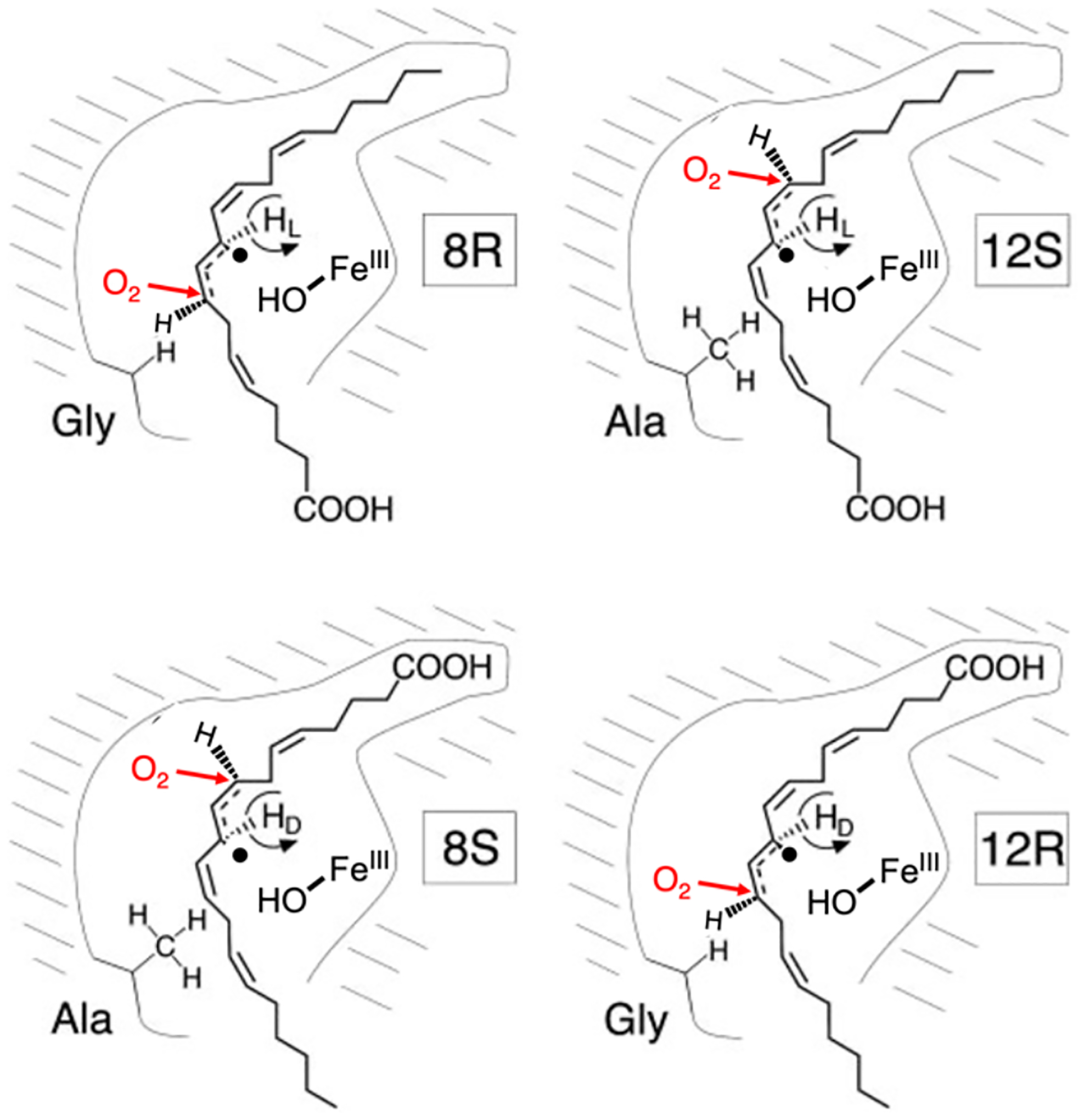
Cartoon of the LO active site pocket, illustrating the role of steric effects (Ala vs. Gly) and substrate orientation (CH₃ first – top, COOH first – bottom) on LO site selectivity for substrate C-H activation (see substrate radical) and subsequent peroxidation via sterically directed attack of O₂ (red). Adapted from ref 122. Copyright 2004 National Academy of Sciences.

The coupled binuclear copper enzymes provide another example of how metalloenzyme active site pockets control selectivity.² All contain a reduced 2 Cu(I)active site in which each Cu center is bound by a triad of histidine ligands. A short Cu···Cu separation is enforced by the protein environment, favoring reversible binding of O₂ to form a μ-η²:η² peroxodicupric intermediate with high intrinsic reactivity. The peroxo intermediates formed in the coupled binuclear copper enzymes have nearly identical geometric and electronic structures but markedly different reactivity with organic substrates. In the O₂ transporter Hc, the active site pocket is sterically congested, preventing potential substrates from accessing the reactive oxygenated core. Catechol oxidase (CO) has a larger active site pocket that can accommodate aromatic substrates and, in addition to reversibly binding O₂, CO selectively oxidizes catechols to o-benzoquinones. Tyr performs both aforementioned functions, as well as the selective hydroxylation of monophenols to diphenols. The structural origin of Tyr’s monophenolase activity remains the subject of active research. Finally, NspF is distinct member of the coupled binuclear family that is unique in its ability to mono-oxygenate o-amino phenols to o-nitroso phenols.¹²⁴ (In contrast, Tyr oxidizes o-amino phenols to o-imino quinones.) The N-oxygenation reaction requires a very different positioning of the substrate relative to o-hydroxylation (see overlay of calculated transition state structures in Figure 39). It has therefore been proposed that the differential reactivity of NspF and Tyr reflect differences in active site pocket structure, potentially involving the substitution of select aliphatic second-sphere residues in Tyr for hydrogen bonding residues in NspF.¹²⁴

Figure 39.

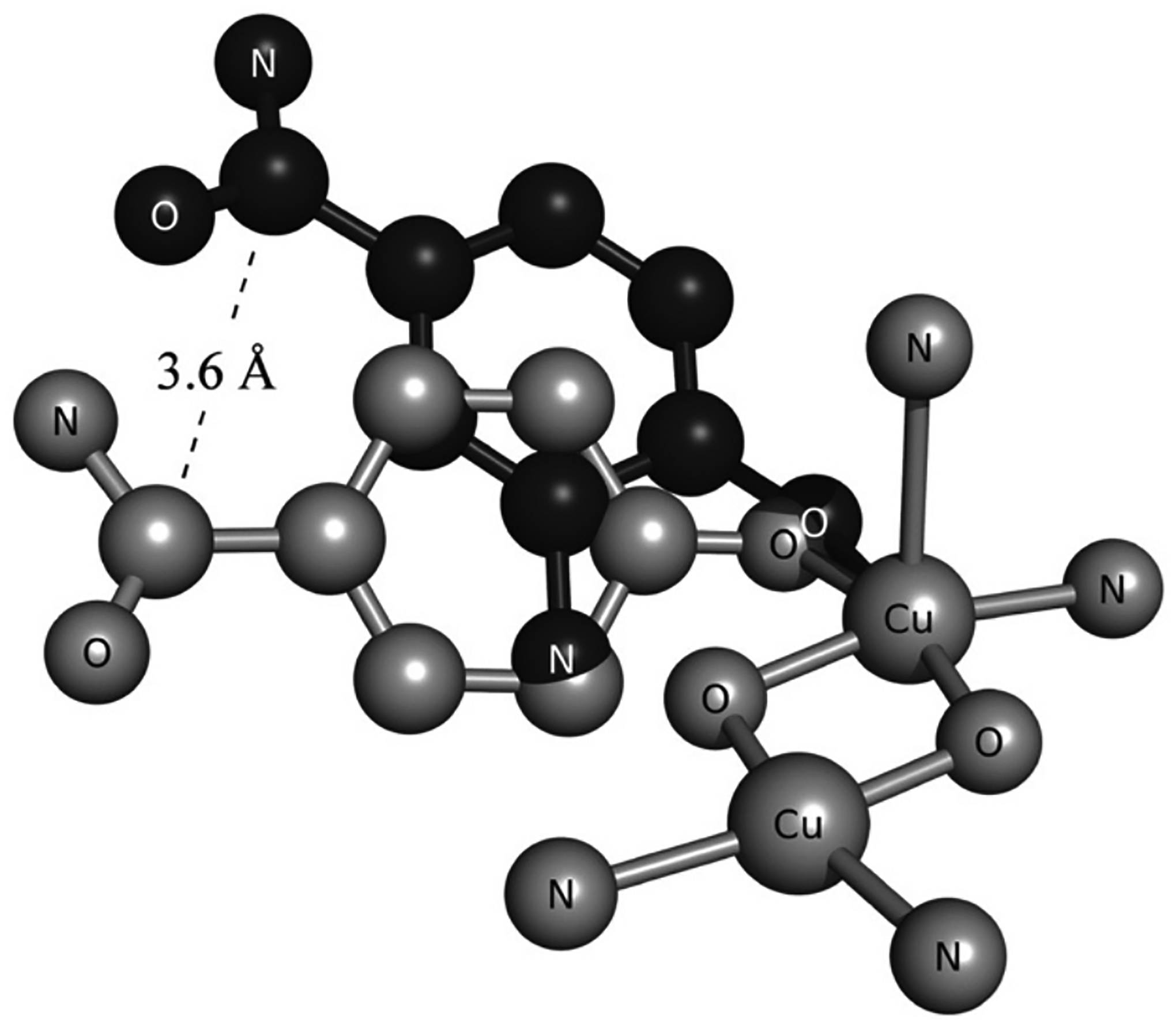
Comparison of DFT-calculated transition state structures for N-oxygenation of 2-amino-4-carboxamidophenolate (black) and ortho hydroxylation of 4-carboxamidophenolate (gray) by a simple [Cu₂(O₂)]²⁺ model. Reproduced from ref 124. Copyright 2012 National Academy of Sciences.

5. Cage Effects: Controlling Reactive Intermediates

Fe(IV)=O species can be highly reactive and undergo an HAA step with substrate converting the Fe(IV)=O to an Fe(III)-OH and creating a substrate radical. This radical can either rebound to the Fe(III)-OH forming an Fe(II) species and a hydroxylated product or this radical can dissociate from the Fe(III)-OH and perform unwanted chemistry, leaving oxidized Fe(III) sites. In metallobiochemistry a mechanism has evolved to control the fate of the radical and prevent this undesirable chemistry. To evaluate the reaction mechanisms of these enzymes, non-heme and heme iron models have been synthesized with Fe(IV)=O active sites.

5.1. Product Formation in Non-heme and Heme Models

Interestingly, in non-heme Fe(IV)=O model chemistry some of the Fe(IV) is converted into Fe(II) during this reaction but a large amount of Fe(III) product is formed.¹²⁵ In some cases it is observed that two Fe(III) are formed for every hydroxylated product produced indicating that the radical that forms after the first HAA step does not rebound to form an Fe(II) product but instead dissociates from the Fe(III)-OH and reacts with a second Fe(IV)=O site to create a second ferric species.¹²⁶ Additionally, in some cases when O₂ is also present, this can react with the dissociated radical resulting in O₂ labeled products.¹²⁷ Radical escape from the Fe(III)-OH site has also been observed in heme models.¹²⁸

Unlike these model complexes that lose the radical in solution chemistry, enzymes such as cytochrome P450, the αKG and pterin dependent enzymes, and sMMO control the rebound of the radical formed in this reaction to promote turnover. This is possible in these enzymes as the radical is formed in a constricted protein pocket that hinders diffusion away from the Fe(III)-OH. This prevents unwanted radical chemistry in the enzyme and promotes rebound to form the final product. Zeolites provide a mechanism like enzymes in controlling cage escape and enabling radical rebound.

5.2. Product Formation in Zeolites

As discussed above, the α-O active site in Fe zeolites is an Fe(IV)=O that forms in 6 MRs in the zeolite lattice.^29,71 6 MRs are located in many different topologies and α-O sites can be stabilized in these lattices with different second-sphere environments. Two α-O sites are compared in Figure 40 where the DFT calculated structure of the α-O site in the *BEA lattice (grey structure in Figure 40) is overlaid with the structure of the α-O site in the CHA lattice (colored structure in Figure 40). These sites are structurally very similar and have analogous room temperature Mössbauer parameters (*BEA (IS = 0.30 mm/s and |QS| = 0.50 mm/s), CHA = (IS = 0.28 mm/s and |QS| = 0.72 mm/s).^29,32,71

Figure 40.

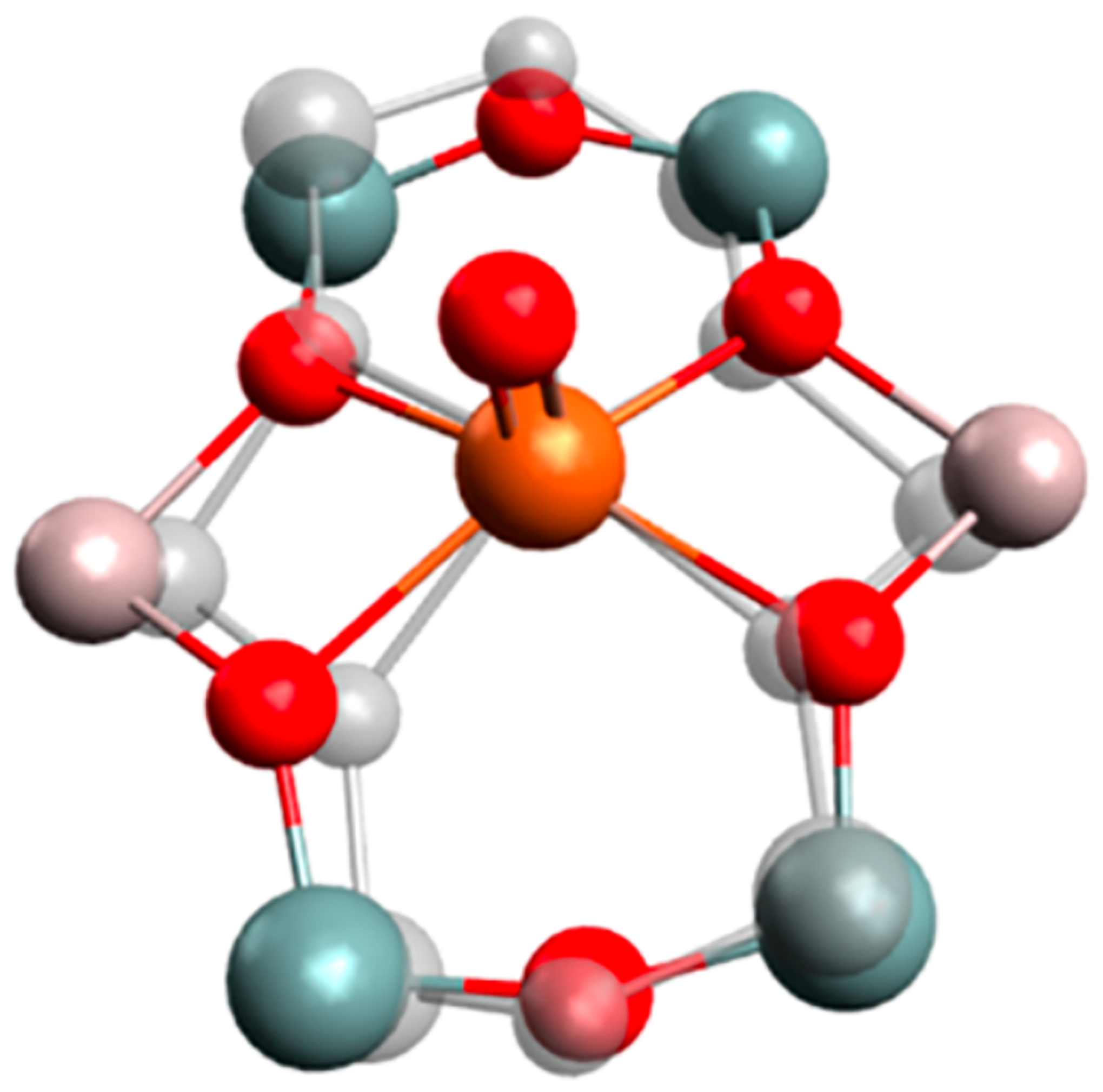
DFT optimized structural overlay of the α-O site that forms in the *BEA lattice (grey) and the CHA lattice (colored). (Color scale: red: O; pink: Al; grey: Si, and organe: Fe.) Reproduced from ref 71. Copyright 2018 American Chemical Society.

The 6 MRs in the *BEA lattice are in large 12 MR zeolite channels (Figure 41, left) whereas the 6 MRs in the CHA lattice are located at the top and bottom of the CHA cages which are connected to each other through 8MR windows (Figure 41, right). These windows that connect the different CHA cages together are small enough to restrict methyl radical diffusion out of the cage and away from the α-O sites. In contrast, the 12MR channels in the *BEA lattice do not limit this diffusion.

Figure 41:

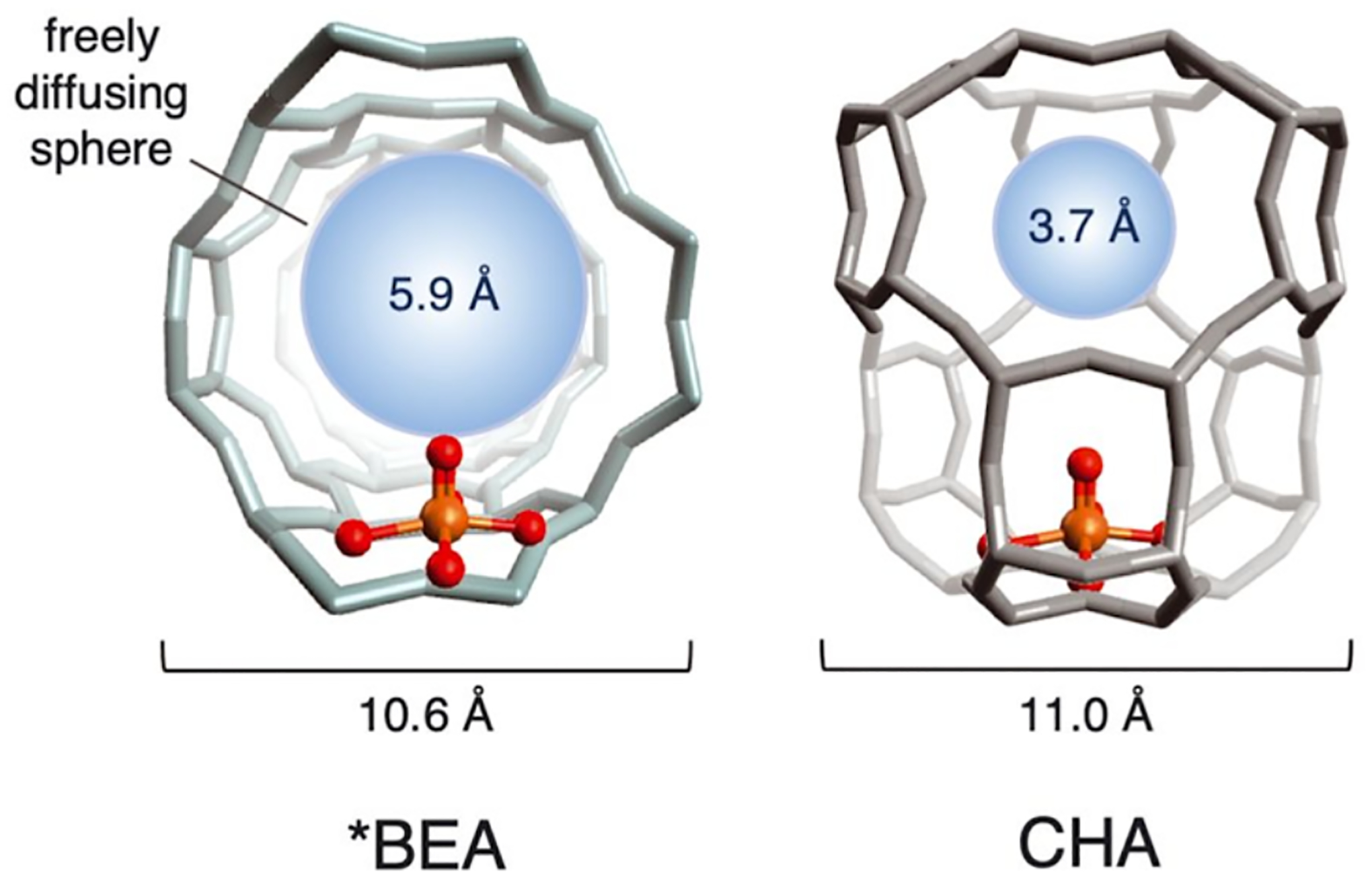
Different zeolite environments around the α-O sites in the *BEA lattice (left) and the CHA lattice (right). Adapted from ref 32. Copyright 2021 Science.

The effect of this change in the second-sphere environment on the α-O/CH₄ reaction in *BEA versus CHA was observed by Mössbauer spectroscopy. An overlay of the Mössbauer spectra of the α-O sites in *BEA (red) and CHA (grey) is shown in Figure 42A. The two α-O sites have very similar Mössbauer parameters but, upon reaction with CH₄, the iron products in the *BEA lattice (Figure 42B, red) are predominantly broad Fe(III) species but in CHA (Figure 42B, black), there is significant amount of a ferrous doublet that reflects regeneration of α-Fe.

Figure 42.

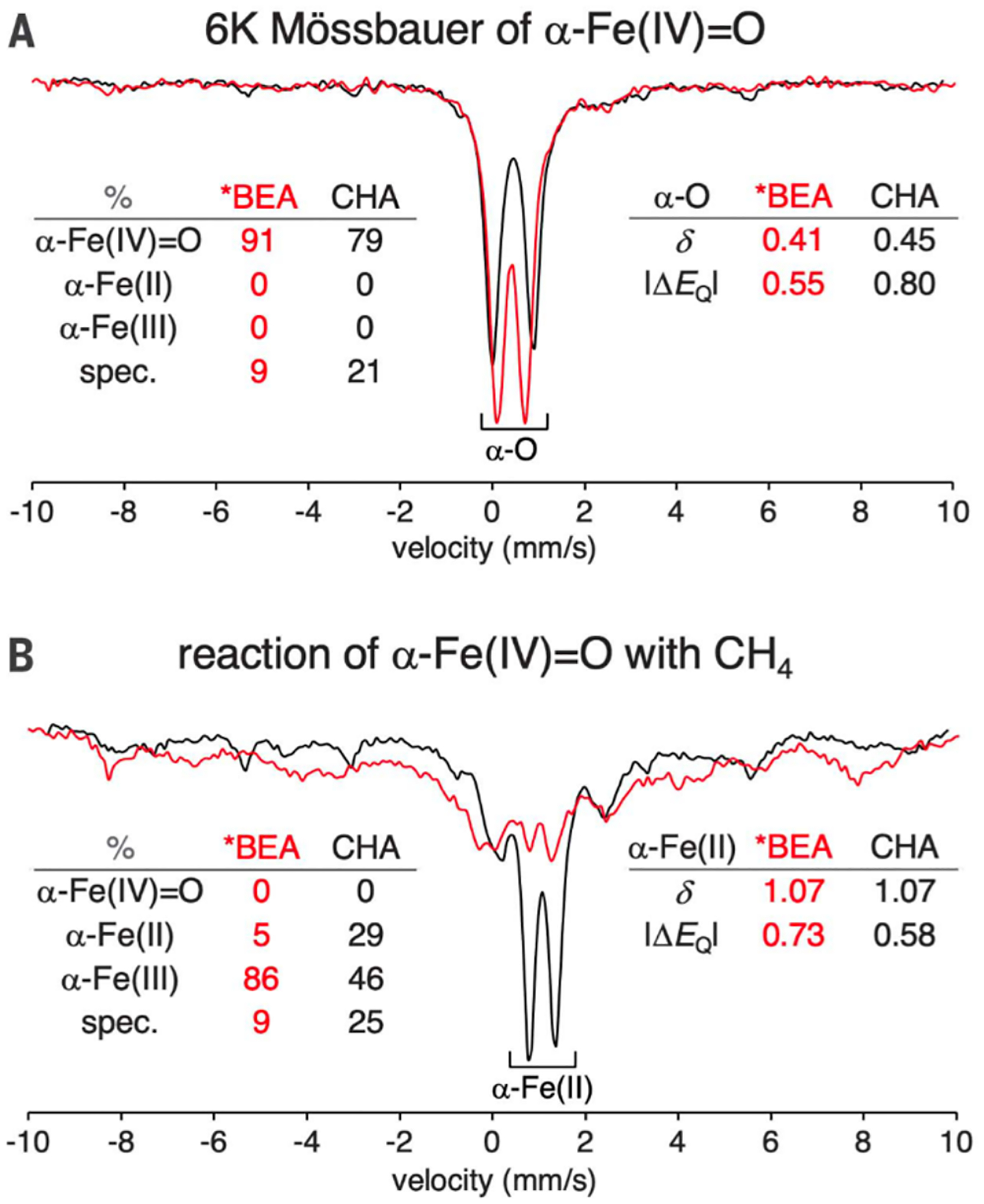
A) 6K Mössbauer spectra of α-Fe(IV)=O in *BEA (red) and CHA (black). B) 6K Mössbauer spectra after the reaction of α-Fe(IV)=O with CH₄ in *BEA (red) and CHA (black). Mössbauer parameters and speciation parameters are in the tables in the Figure. Reproduced from ref 32. Copyright 2021 Science.

A combination of rR and Mössbauer spectroscopies were utilized to define the ferric products formed in *BEA. The low temperature Mössbauer spectrum for the CH₄ reaction in *BEA is shown in Figure 43, top. The broad ferric signal can be fit with two similar Mössbauer contributions having different zero field splitting components. The rR spectrum (Figure 43, bottom) has two vibrations that grow in upon reaction of α-O in *BEA with CH₄: a vibration at 585 cm⁻¹ that is sensitive to¹²CH₄/¹³CH₄ isotope perturbation and one at 735 cm⁻¹ that is not sensitive to this perturbation. To evaluate the 735 cm⁻¹ feature, α-O was reacted with H₂ and the feature at 735 cm⁻¹ grew in along with one of the Mössbauer components. This 735 cm⁻¹ feature was found to be sensitive to deuterium isotope perturbation. Thus, the two ferric components were assigned as equal amounts of Fe(III)-OCH₃ and Fe(III)-OH. These same oxidized Fe sites were also observed in the reaction of α-O with CH₄ in CHA but were much more limited in number. Therefore in the *BEA lattice, all the α-O converts to Fe(III) products upon reaction with CH₄, whereas in CHA, while some of the α-O converts to the oxidized Fe products, most of the α-O is converted back to the α-Fe(II) precursor with the formation of CH₃OH. The origin of this difference in the reaction outcome was elucidated using DFT calculations as shown in Figure 44.

Figure 43.

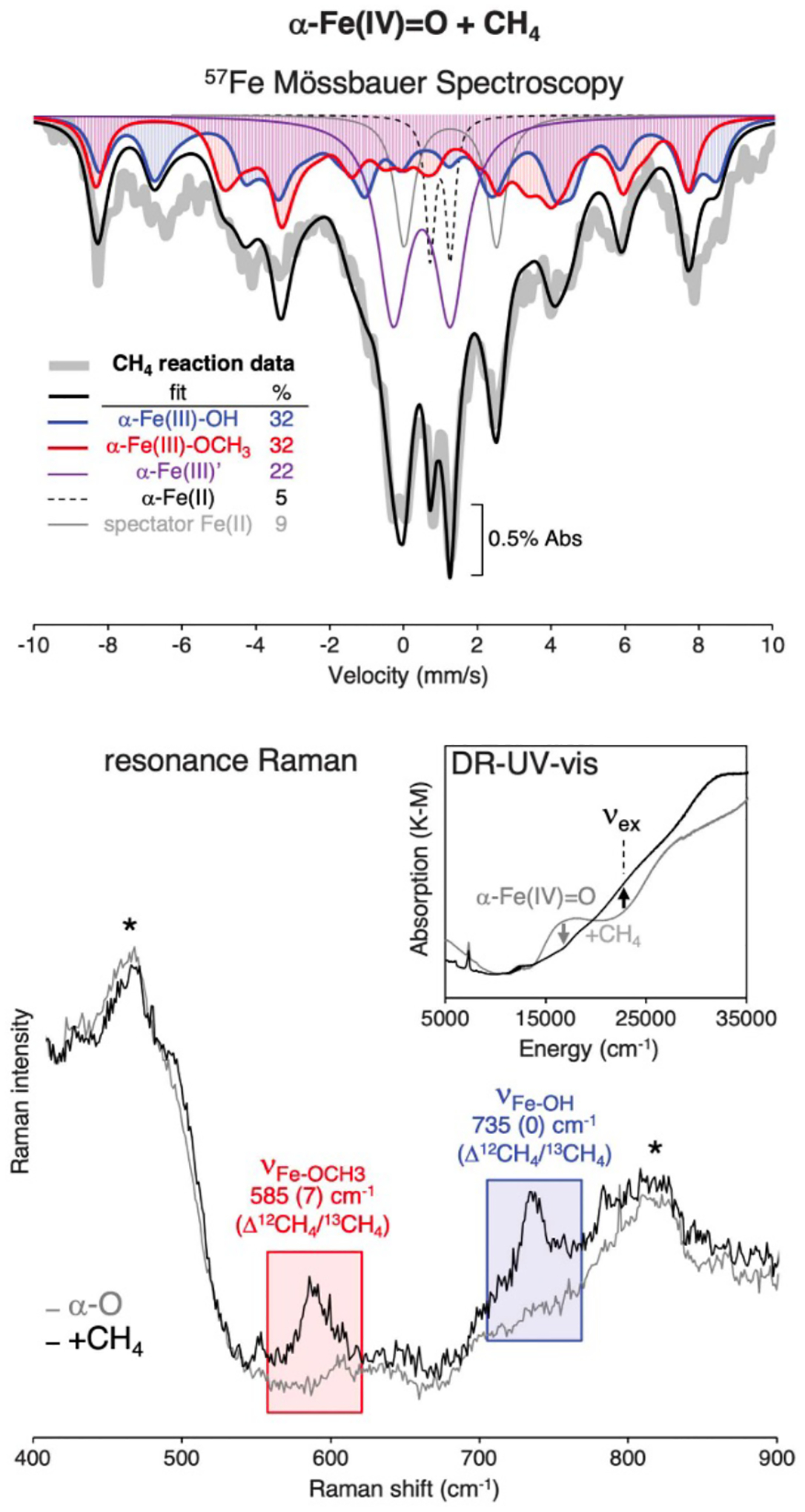
6K Mössbauer spectrum (top) and rR spectra (bottom) of the α-O Fe-*BEA sample (grey) and the CH₄ reacted α-O Fe-*BEA sample (black). Adapted from ref 32. Copyright 2021 Science.

Figure 44.

Reaction coordinate of the methyl radical rebound (middle to left of the diagram) and the methyl radical cage escape (middle to right of the diagram) after the first HAA step. Reproduced from ref 32. Copyright 2021 Science.

Methyl radical rebound and cage escape were calculated in both the *BEA (red) and CHA (black) zeolite lattices. The first product after HAA is given in the center of Figure 44, where the methyl radical is weakly adsorbed to the first Fe(III)-OH product after HAA. This methyl radical can either rebound with the Fe(III)-OH which forms the α-Fe precursor and CH₃OH (Figure 44, left side) or it can “cage escape” away from the Fe(III)-OH and interact with another α-O site to form Fe(III)-OCH₃ (Figure 44, right). The radical rebound reaction mechanisms were similar in both lattices with small barriers for rebound. However, in the cage escape mechanisms, while there is a barrier in the CHA lattice of ~5 kcal/mol for the methyl radical to diffuse away from the Fe(III)-OH through the small 8MR pore window, there is no barrier for the diffusion of the methyl radical through the 12MR channel in the *BEA lattice. This limitation of cage escape in the CHA lattice results in the production of CH₃OH and α-Fe (Figure 42B). The α-Fe is then capable of reaction with a second N₂O molecule reforming α-O. Indeed, multiple turnovers have been demonstrated in reference 32.

Thus, the cage effects of the zeolite mimic the protein pocket in enzymes, enabling control of the methyl radical that is formed during the HAA reaction. This second-sphere cage effect could be further tuned in zeolites to make a fully catalytic system for the conversion of CH₄ into CH₃OH. Additionally, this could be expanded to other reactive radical intermediates in other catalytic reactions.

6. Diffusion Through the Zeolite

Diffusion plays many important roles in zeolite catalysis. Diffusion of the transition metal ion (TMI) sites before and/or during the reaction can either hinder or allow the reaction to take place.^92,129,130 Selective diffusion of substrates and/or products through the zeolite during catalysis can affect product formation, rate, and the ability of the catalyst to continue turnover.^69,131

The micropore nature of zeolites sets them apart from nonporous or mesoporous heterogeneous support materials such as amorphous silica and aluminum. The size and shape of these micropores play a prominent role in the differentiation of the diffusion rate of different substrates. The size, shapes, and configurations of pores and channels in different zeolites are a unique advantage that can be used to tune TMI catalysis. By choosing a small pore zeolite, large bulky reagent molecules or poisons can be denied entry and large products can be trapped in the pores. This allows a customization of the second-sphere zeolite support which has been utilized in gas separation. A recent study elegantly showed the fine-tuning of the pore diameter in a MOR lattice by isomorphous Fe substitution into the framework’s twelve-membered rings improved CO₂ separation from N₂ and CH₄.¹³² Other microporous diffusion effects include inverse shape selectivity, molecular traffic, levitation effects, incommensurate diffusion, and single-file diffusion.¹³³ While microporosity can be a useful tool for catalyst design, it can also be a liability. In some applications, zeolites are used for reasons other than their micropore diffusion properties, and the micropore system may cause undesirable diffusion limitations. Here we briefly consider how the diffusion of transition metal ions or the substrate/products can affect catalysis.

6.1. Mobilized Active Sites

6.1.1. Active Site Mobility Hindering Catalysis

In some cases, the formation of the catalytic active site can be hindered by diffusion through the zeolite. SCR of NO_x species adsorbed on zeolites requires high temperature hydrostability for the catalyst to be used in industrial applications. These zeolites must be stable at medium temperatures (700–800 °C) over a long timescale and at high temperatures (~900 °C) for a short amount of time. While small pore zeolites can withstand this high temperature environment during SCR catalysis, large pore zeolites have been found to deactivate under these conditions.^129,134,135

In a study by Blakeman et al., the hydrothermal stability of a large pore zeolite (BEA) and a small pore zeolite (CHA) were compared using XRD.¹²⁹ Prior to copper addition, the two zeolites exhibit similar hydrothermal stability up to 900 °C. After introduction of the copper, the small pore CHA zeolite support maintains its hydrothermal stability, but the large pore*BEA begins to deactivate at 900 °C.

This decrease in hydrothermal stability observed in *BEA is likely due to dealumination which is generally accepted as the main reason for deactivation during this SCR process. During the high temperature dealumination, Al(OH)₃ detaches from the zeolite framework and diffuses through the lattice. Unlike in small pore zeolites where this Al(OH)₃ cluster (~0.5 nm) cannot fit through smaller windows (up to 8MR) that are similar in size, these Al(OH)₃ fragments can fit through the larger windows of *BEA and diffuse throughout the zeolite.¹³⁶ In the presence of copper sites in the zeolite, these Al(OH)₃ fragments interact with Cu ions to form stable Cu/Al clusters that can induce the collapse of the zeolite support above 800 °C.^129,136 This behavior has been observed in many zeolites^129,134,135 and emphasizes the idea that unwanted species can freely diffuse through zeolites with large pore windows. By changing the second-sphere, these unwanted diffusion effects can be controlled.

6.1.2. Active Site Mobility Aiding Catalysis

Diffusion through the zeolite can aid in the formation of TMI active sites for catalysis. A study by Dinh et al. found evidence for [Cu₂O]²⁺ formation at extremely low Cu loadings (0.4 Cu / CHA cage) in samples with high Al content. This is surprising as the likelihood of two Cu ions in one CHA cage to form the binuclear site at low Cu loading is low.¹³⁰

It is proposed that the formation of this binuclear active site at low Cu loading is facilitated by diffusion through the zeolite in which hydrated Cu ions can jump between nearby Brønsted acid [AlO₄]⁻ T-sites (Figure 45, blue).

Figure 45.

Schematic of proton aided diffusion of Cu⁺ diffusion through the zeolite (blue) and inhibition of Cu⁺ due to NH₃ interference (red). Reproduced from ref 130. Copyright 2019 American Chemical Society.

To support this proposed mechanism, a zeolite with comparable Cu loading but low Al loading was evaluated. This was hypothesized to restrict copper ions traveling through the zeolite at this low Al loading, and very little Cu dimer was detected based on limited Cu···Cu scattering in EXAFS.

To evaluate the involvement of protons in this diffusion, NH₃ was added to the zeolite to convert Cu⁺ ions to [NH₃-Cu-NH₃]⁺ species and replace the H⁺ with NH₄⁺at the [AlO₄]⁻ T-site. NH₃ could then be selectively removed from the copper ions whereas NH₄⁺ remained bound to the [AlO₄]⁻ T-site. This hinders the diffusion of the Cu ions through the zeolite lattice as these Cu ions cannot bind to the NH₄⁺ blocked [AlO₄]⁻ T-sites (Figure 45, red). Thus, by varying the aluminum density and charge compensating cations, diffusion can be leveraged to create active catalytic sites.

In a complementary study by Paolucci et al., SCR was evaluated in CHA zeolites with varying copper content. In samples with high copper density, the SCR rates increased linearly with Cu density consistent with reactions involving isolated Cu ions. However, in samples with low copper content, the SCR rates varied quadratically with Cu density. Therefore, there are different rate-controlling steps at the high and low copper density limits in steady state SCR.⁹²

The samples were evaluated using steady state XANES to monitor the oxidation states of the Cu ions during SCR. At steady state, the Cu(I)/Cu(II) ratio is significantly higher in samples with lower copper density implying that the Cu(I) to Cu(II) oxidation rate is the limiting step at lower copper density. This oxidation step was kinetically evaluated by looking at reduced samples with three different Cu densities. The oxidation with O₂ was measured via in-situ XANES and found to be second order in total Cu(I) density, matching the total SCR rate at low density and supporting the 2 Cu(I) oxidation with O₂ as the rate limiting step.

Molecular dynamics and DFT were utilized to show that diffusion of a Cu(I)(NH₃)₂ ion through an 8MR window to pair with another Cu(I)(NH₃)₂ ion in an adjacent cage enables SCR at the low copper density limit (Figure 46). The calculations suggest that these ions can diffuse but tethering to Al in the lattice limits their diffusion. It supports the second order rate in the reaction with O₂ (involving two Cu ions) and the isolated two coordinate Cu(I) assignment observed by XANES at steady state. At higher copper loading, the 2 Cu(I) oxidation step is fast and the rate limiting step changes to the reaction of the resulting isolated copper with NO_x and NH₃, a step that only requires a single Cu(II) site and is thus linear in copper density. This distinct reactivity is made possible by the TMI diffusion capabilities of the zeolite lattice.

Figure 46.

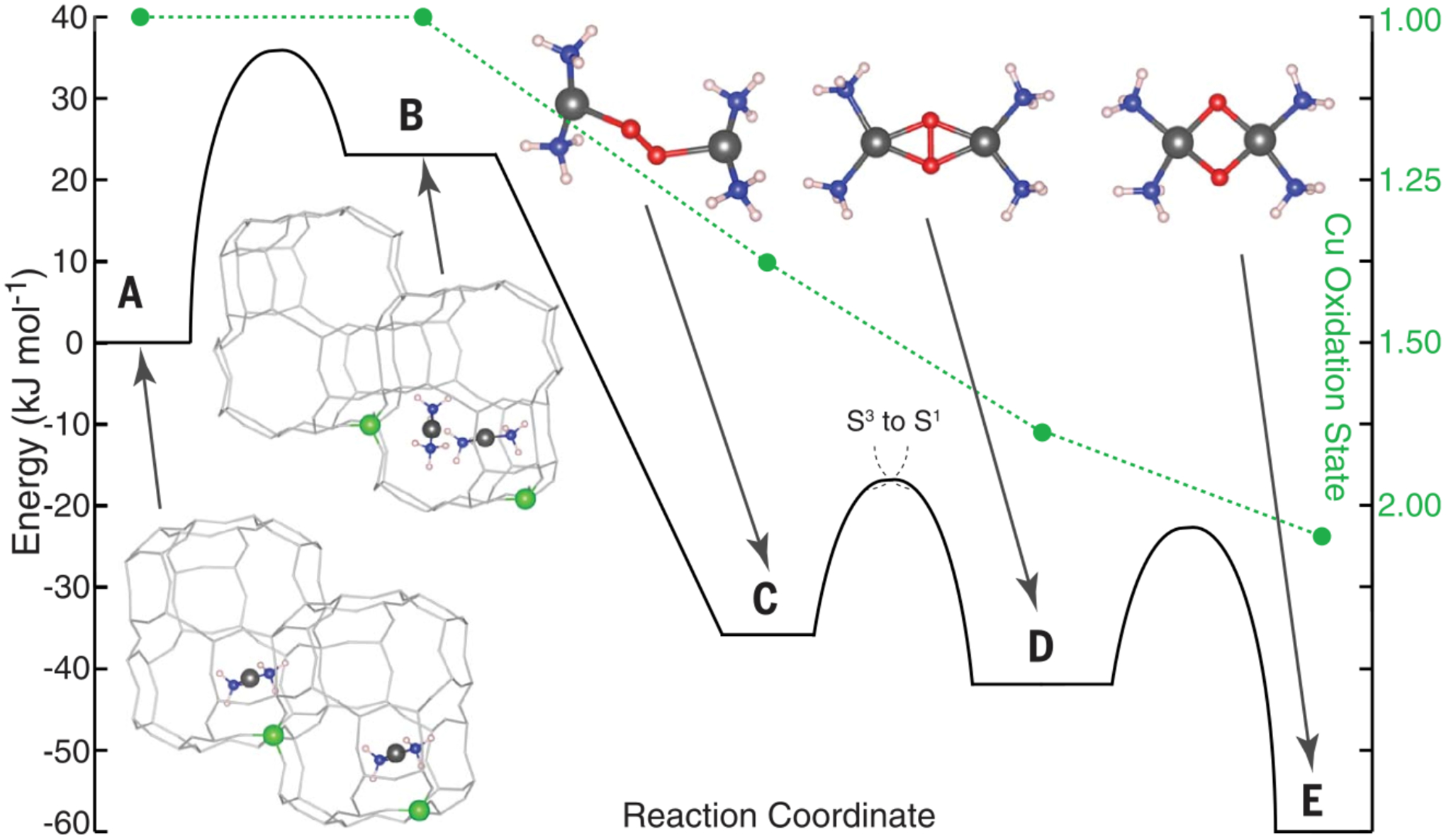
DFT-computed diffusion of Cu(I)(NH₃)₂ and subsequent oxidation with O₂. Cu: gray, Al: green, O: red, N: blue, and H: white. Reproduced from ref 92. Copyright 2017 Science.

6.1.3. Active Site Formation by Limiting Diffusion

While diffusion can aid in the formation and reaction of TMI active sites in zeolites, limiting diffusion can also hinder the formation of active sites. Postsynthetic impregnation of a transition metal ion into a zeolite lattice through ion exchange is a common way to add a transition metal into a lattice at an exchange site. However, in small pore zeolites, this process has been found to have limits.

The 6 MRs of small pore CHA zeolites have been observed to stabilize the α-Fe sites that react with N₂O to form the active α-O site that can convert CH₄ to CH₃OH. During the postsynthetic impregnation of Fe(acac)₃ only ~ 19% of the Fe ions from the Fe(acac)₃ source was retained in the lattice and only about 50% of Fe incorporated into the lattice was stabilized as α-Fe(II) (the remaining Fe formed Fe oxide clusters). By increasing the temperature of the postsynthetic impregnation from room temperature to 105°C, more Fe was retained (~ 42%) and less Fe oxide clusters were formed suggesting a kinetic diffusion barrier for Fe ions to migrate to the 6MRs of the zeolite.¹³⁷

To remove diffusion limitations from Fe formation, Fe was added into the zeolite through a one pot synthesis method where the Fe is added into the synthesis mixture. In this procedure, the Fe(III) is incorporated into the zeolite lattice. Heating then converts the framework Fe to α-Fe(II). This results in high Fe retentions (84–100% iron) with 72%–84% of the Fe forming α-Fe sites.

Thus, in cases where diffusion is limited and metal ion aggregates are formed, a one-pot approach to include the TMIs in the zeolite during synthesis, followed by activation, might lead to an improved active catalyst.¹³⁸

6.2. Substrate and Product Diffusion

In addition to the diffusion of TMIs, the diffusion of substrates and products can also affect catalysis. Diffusion control of substrates and products can be leveraged in redox catalysis to enhance selectivity and avoid poisoning.¹³⁹ The α-O active site defined in the *BEA lattice that can selectively convert CH₄ to CH₃OH is also able to selectively convert benzene to phenol. α-O oxidizes benzene to result in a desorbed phenol and the precursor α-Fe(II) site. Interestingly, overoxidation products that would result from a reaction of the remaining α-O sites with the more reactive phenol are not observed in this reaction.

The higher polarity of phenol limits its rate of diffusion through the zeolite lattice, whereas benzene diffuses faster and consumes all α-O sites. As a result, further oxidation of phenol is prevented due to diffusion limitations. Thus, differences in the interaction of the substrate and product with the zeolite can limit diffusion and enhance product selectivity.

Limiting overoxidation from product diffusion is also essential in CH₄ to CH₃OH synthesis in metallozeolites. In a MD study by Freitas et al., the free energy of diffusion of CH₄ vs CH₃OH was calculated in CuCHA.¹³¹ Given the strong interaction of CH₃OH with the Cu active site, there is a higher barrier for CH₃OH to diffuse through the lattice compared to CH₄. Similar to the benzene case, CH₄ reacts with Cu active sites before CH₃OH can reach them and overoxidize, creating the selectivity towards CH₃OH over overoxidation products in these Cu-zeolites.

7. Frustrated Lewis Pairs

As described in Section 3, the rigidity of the zeolite can be employed to bind transition metals in an unstable but reactive entatic state, it can also prevent bonding between two compounds with a strong propensity to interact, like a Lewis acid and base. This is the case with frustrated Lewis pairs (FLP), sites that consist of a Lewis acid and base that are prevented from forming a Lewis acid-base adduct by the zeolite lattice.¹⁴⁰ In solution chemistry, FLPs are typically generated by synthesizing Lewis acids and bases with bulky groups, e.g. bulky phosphines and bulky boranes, where steric clash prevents bonding (Figure 47).¹⁴¹ These FLPs can carry out unusual, novel chemistry by simultaneously performing acid and base reactions on a substrate. Interestingly, certain FLPs can cleave H₂ to H⁺ / H⁻ pairs that can perform hydrogenation without typical metal-containing catalysts.¹⁴¹ FLPs are also known to capture and activate a variety of small molecules, including olefins, alkynes, CO₂, SO₂, NO, CO, and N₂O.¹⁴⁰ This has led to metal-free pathways for CO₂ reduction to CH₃OH.¹⁴² For more on molecular FLPs and their applications, the reader is referred to the following references.^{140,141,143,144}

Figure 47.

Bulky phosphine and bulky borane forming a Frustrated Lewis Pair.

FLP research has been extended from solution phase organic catalysts to heterogeneous catalysts due to easier product and catalyst recovery as well as generally higher thermal and chemical stability.¹⁴⁵ In principle, only classic Lewis acid-base adducts can be formed on ideal solid surfaces. Surface engineering is required to introduce FLPs, for instance by creating defects/vacancies or using chemical dopants. Lattice constraints then impede mobility of the acid and base and thus prevent their Lewis acid-base adduct formation. This was observed in porous nanorods of CeO₂ where the highly defective structures showed higher activity towards hydrogenation of alkynes and alkenes due to the defect Ce³⁺ sites forming FLPs with anionic O sites in the lattice.¹⁴⁶

Unfortunately, these heterogeneous catalysts have little to no site selectivity as generating specific defects is difficult. They are also unstable given a range of conditions as many gases and solvent molecules can adsorb on the defects, preventing the desired FLP formation.¹⁴⁵ In contrast, zeolites have crystal structures with well-defined, separated cation exchange positions, offering an alternative route to FLPs that does not require defects.

This was demonstrated in Na⁺ containing Y zeolites (FAU topology) with Pt nanoparticles sputtered on the external surface.¹⁴⁷ After reaction with H₂ these Pt nanoparticles are active in the coupling of acetaldehyde to form the corresponding ethyl acetate ester via the Tishchenko reaction, a reaction that is performed by NaH powder as well.¹⁴⁷ Without H₂ treatment, Pt/NaY does not produce ethyl acetate. These results, coupled to Rietveld refinement and maximum entropy method analysis, indicate that hydride ions are binding to sodium cations in the zeolite (Figure 48). This conclusion was further supported by X-ray photoelectron spectroscopy where core-level spectra of the Na 1s peak redshift due to a greater electron density on Na⁺ after hydride binding. This hydride acts as the Lewis base member of the pair. The Lewis acid part was identified via IR experiments that showed an increase in O-H signals after the H₂ reaction. These peaks also shift appropriately when D₂ is used instead, demonstrating the origin of the peaks is from hydrogen gas. Importantly, the absence of an atomic hydrogen signal in EPR after H₂ treatment supports the heterolytic dissociation of H₂ in H⁺ and H⁻ as opposed to homolysis into hydrogen radicals.¹⁴⁷ This heterolytic dissociation into the FLP opens avenues to new chemistry. Neutron powder diffraction (NPD) of the H₂ reacted material demonstrates an increase in hydrogen in the material from the simultaneous rise of the Bragg peak intensity and the background signal.

Figure 48.

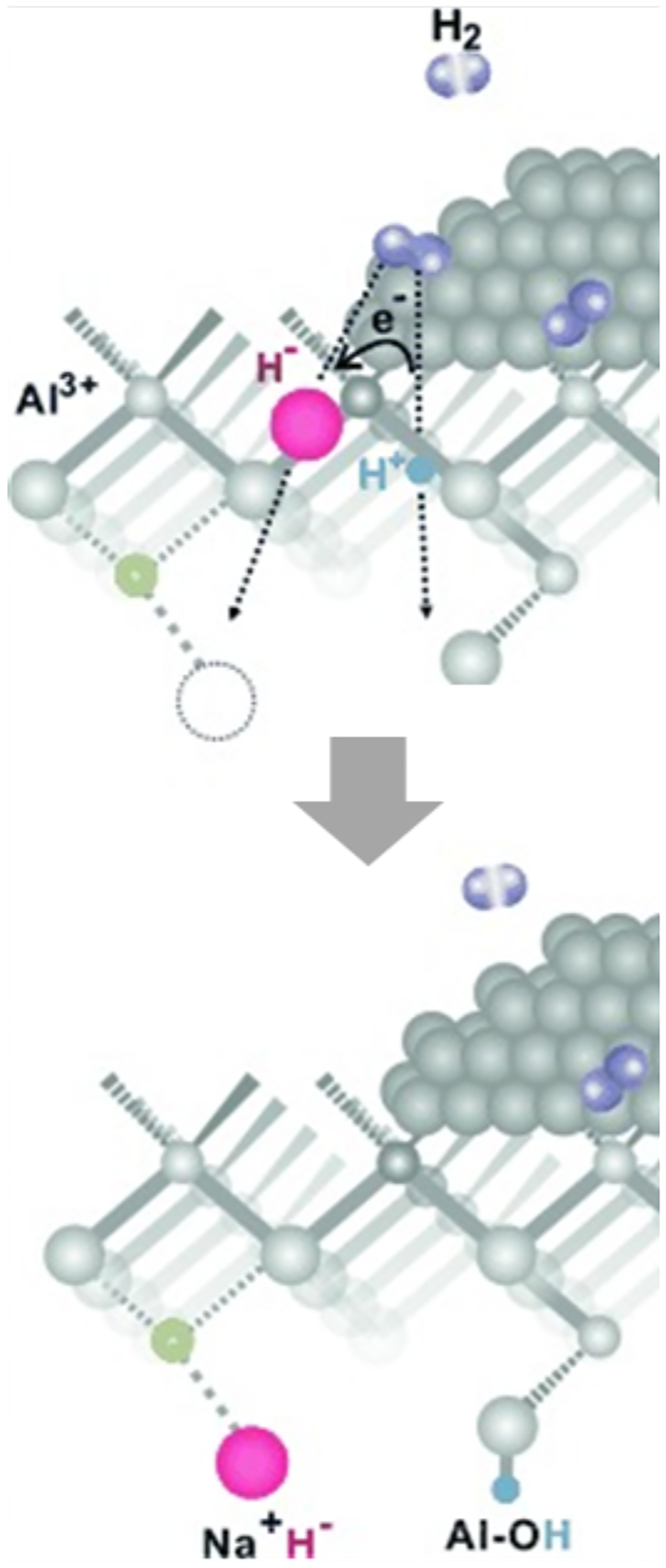
Schematic representation of the cleavage of H₂ over Pt_x nanoparticles on Pt/NaY zeolites, resulting in Na⁺H⁻ and O(H⁺) moieties. Adapted from ref 147. Copyright 2015 Wiley.

FLPs were also formed, defect-free, on transition metal ion (Fe, Zn and Ag) exchanged H-ZSM-5. In these materials, FLPs were used to activate small molecules such as CH₃OH and convert them to other commodity chemicals like aromatics and longer hydrocarbons.¹⁴⁸ Homogeneous dispersion of the metal ions was confirmed with EXAFS and high-angle annular dark-field scanning transmission electron microscopy. These experiments demonstrated that the chemistry is performed by a single metal ion acting as a Lewis acid. Synchrotron X-ray powder diffraction with Rietveld refinement was used to identify positions of the extra-framework transition metal, demonstrating the metal ion is bound near the deprotonated aluminate site which can bind the cationic metal and at the same time use another oxygen as a Lewis base. Further evidence was provided by Cross Polarization Magic-Angle Spinning¹³C NMR performed on Zn-ZSM-5 that was pre-adsorbed with isotope-enriched¹³CH₃OH. Upon adsorption, a peak appears around 54 ppm, distinct from the typical sharp peak of protonated CH₃OH on Brønsted acid site in zeolites without Zn (at 50.4 ppm). The 54 ppm peak is attributed to the methoxy group strongly interacting with the Zn cation (Lewis acid) after deprotonation by the aluminate oxo (Lewis base). This methoxy species can then react further with other carbon species (e.g. methyl cations after dehydration of protonated CH₃OH) to form dimethylether and subsequently aromatics or hydrocarbons.

Zeolites are promising carrier materials for FLPs (Figure 49). The rigid constraints of the lattice keep the acids and bases separated and they have varying pore sizes that can serve as sieves allowing only certain size substrates to react. The second-sphere around the FLPs could tune their apparent acid and base strength via van der Waals and electrostatic interactions, as was recently suggested for Brønsted acid sites in zeolites.¹⁴⁹ There are also a lot of design parameters in zeolites: topology, density of aluminum sites, location of aluminum sites, location of dealumination defects, and the types of metals doped into the material. The zeolite can be tuned to have specific Lewis acid-base pairs as well as particular distances between them. Despite their versatility, zeolites have been surprisingly underexplored as solid carriers of FLPs, likely due to the difficulty in confirming their presence and involvement in reactions. Techniques like synchrotron PXRD, NPD, IR, and XAS could help in identifying FLPs and their mechanistic importance in reactions where their relevance may have been overlooked.^148,150

Figure 49.

SXRD and Rietveld refinement for Fe-ZSM-5. Proposed Lewis acid Fe³⁺ site highlighted in blue. Proposed Lewis base oxygen atoms highlighted in green. Adapted from ref 148 with permission from the Royal Society of Chemistry.

8. Concluding Comments

In this review we have focused on the parallels between metallozeolites and metalloenzymes with respect to second-sphere effects that can enable and control catalysis. It is interesting that different Cu and Fe active sites are employed in the CH₄ to CH₃OH conversion in metallozeolites (as described in detail in this review a [Cu₂O]²⁺ binuclear site^61,63 and an Fe(IV)=O mononuclear site^29,59,71) versus metalloenzymes (a mononuclear Cu in pMMO¹⁵¹ and a binuclear Fe(IV)₂O₂ closed core in sMMO¹⁵²) but both use similar second-sphere effects to control their catalysis. These include entatic activation of the metal sites by their environments, control of substrate binding and access to active sites through pockets and channels, and the ability of the environment to control radical rebound and cage escape Similar concepts can likely be extended to other porous materials like metal-organic frameworks, which are highly synthetically flexible but considerably less stable than zeolites.^153,154 This review is mostly focused on these second-sphere effects in CH₄ conversion both for use in the generation of fuels and for the abatement of this potent greenhouse gas. Second-sphere contributions to copper and iron zeolite catalysis are at an early stage of understanding. Presently these require steam extraction and re-reduction at high temperature to activate: however, at least for the FeCHA zeolite, multiple turnovers have been demonstrated.³² For Cu Zeolites, some catalytic activity has been reported but further identification of active species is needed.^{130,155–158} As more TMI active sites are spectroscopically defined and a deeper understanding of how their second-sphere environments affect their mechanisms is developed, these metallozeolites will continue to be optimized for catalytic low temperature CH₄ conversion to CH₃OH as a fuel and synthon and for its abatement as a greenhouse gas potentially with further oxidation to CO₂ which is less potent.

Abbreviations

AA

arachidonic acid

AIMD

Ab initio molecular dynamics

*BEA

beta

BDE

bond dissociation energy

BDFE

bond dissociation free energy

CASPT

complete active space perturbation theory

CHA

chabazite

CO

catechol oxidase

DFT

density functional theory

DR

diffuse reflectance

EPR

electron paramagnetic resonance

EXAFS

extended X-ray absorption fine structure

FAU

faujasite

FER

ferrierite

FLP

frustrated Lewis pair

HAA

H-atom abstraction

Hc

hemocyanin

IP

in-plane

IR

infrared spectroscopy

IS

isomer shift

LO

lipoxygenases

MCD

magnetic circular dichroism

MCO

multicopper oxidase

MD

molecular dynamics

MFI

mordenite framework, inverted

MOR

mordenite

MR

membered ring

NKD

non-Kramers doublet

NMR

nuclear magnetic resonance

NOx

nitrogen oxide

NPD

neutron powder diffraction

NRVS

nuclear resonance vibrational spectroscopy

OOP

out-of-plane

PES

potential energy surfaces

pMMO

particulate methane monooxygenase

PXRD

powder X-ray diffraction

QS

quadrupole splitting

RAMO

redox-active molecular orbital

rR

resonance Raman

SCR

selective catalytic reduction

sMMO

soluble methane monooxygenase

T-site

tetrahedral units

THF

tetrahydrofuran

TMI

transition metal ion

TPD

temperature programmed desorption

Tyr

tyrosinase

UV

ultraviolet

vdW

van der Waals

vis

visible

VTVH

variable-temperature variable-field

XANES

X-ray absorption near edge spectroscopy

XAS

X-Ray absorption spectroscopy

XES

X-Ray emission spectroscopy

XRD

X-ray powder diffraction

ZFS

zero-field splitting

ZSM-5

zeolite Socony Mobil-5

Biographies

Hannah M. Rhoda received her B.S. in chemistry in 2014 and her M.S. in chemistry in 2016 from the University of Minnesota-Duluth, working with Professor Viktor Nemykin. She is currently pursuing her Ph.D. in physical inorganic chemistry at Stanford University under the supervision of Professor Edward I. Solomon. Her research focuses on the spectroscopic and computational elucidation of Cu and Fe active sites in zeolites and their mechanisms for selective hydrocarbon oxidation.

Alexander J. Heyer received his B.S. in chemistry at the University of Virginia where he researched proton coupled electron transfer in Mo and W scorpionate complexes with Professor Dean Harman. He is now a Ph.D. student in inorganic chemistry at Stanford University in Professor Edward Solomon’s research group. Using both spectroscopic and computational methods, he studies methane oxidation in Cu and Fe zeolites, and his research is supported by a Stanford Graduate Fellowship.

Benjamin E. R. Snyder received his B.S. in chemistry and B.A. in mathematics from the University of Rochester in 2012. He received his Ph.D. in inorganic chemistry from Stanford University in 2018, working with Professor Edward Solomon. Supported by fellowships from the NSF and Stanford University, his research focused on spectroscopic and computational elucidation of Cu and Fe active sites in zeolites, their activation for selective hydrocarbon oxidation, and their correspondence to Cu and Fe active sites in biology. Currently, Ben is an Arnold O. Beckman Postdoctoral Fellow at UC Berkeley, working with Professor Jeffrey Long to develop metal-organic frameworks for applications in gas storage and separation.

Dieter Plessers obtained his Master of Science in Bioscience Engineering focused on catalytic technology from KU Leuven in 2017, with a Master’s thesis on the identification of the active sites in copper- and iron-exchanged zeolites for the selective oxidation of methane to methanol. Supported by a grant of the Research Foundation - Flanders (FWO), he obtained a Ph.D. at the Center for Sustainable Catalysis and Engineering (CSCE) under the guidance of Prof. Bert Sels, where he used spectroscopy and kinetic analyses to identify the copper speciation on copper-exchanged zeolites and quantify their reactivity in methane activation. This topic continues to be his primary research interest as a postdoctoral researcher in the framework of an FWO research grant.

Max L. Bols received his B.S. and M.S. in bioscience engineering at the KU Leuven in 2015, doing his master’s thesis on the identification of the active site in iron zeolites for methane activation. Upon graduation, he started a Ph.D. with Prof. Bert Sels on the synthesis, kinetics, and spectroscopic characterization of transition metal active sites in zeolites, in the framework of an FWO research grant.

Robert A. Schoonheydt is emeritus professor of the KU Leuven, where he obtained his bioengineering degree in 1966 and his Ph.D. in 1970 under the guidance of Prof. Jan B. Uytterhoeven. He did a postdoc in the chemistry department of the Texas A&M University under the guidance of Jack H. Lunsford on adsorption of SO₂ on MgO. His research interests at the KU Leuven are the surface chemistry of clay minerals and zeolites with special emphasis on transition metal ions and spectroscopy. Presently he is a member of an international research collaboration of zeolite chemists, spectroscopists, and quantum chemists on active sites in Cu- and Fe-zeolites for selective oxidation, NO_x abatement, and electrophilic aromatic substitution reactions. He was dean of the Faculty of Bioscience Engineering from 1998 until 2004 and president of the International Association for the Study of Clays from 2001 until 2005.

Bert F. Sels (1972), full professor at KU Leuven (Belgium), obtained his Ph.D. in 2000 in the field of heterogeneous oxidation catalysis under the guidance of Prof. Pierre Jacobs. He was awarded the DSM Chemistry Award in 2000, the Incentive Award by the Belgian Chemical Society in 2005, and the international Green Chemistry Award in 2015. He is director of the Center for Sustainable Catalysis and Engineering (CSCE) and is active in designing heterogeneous catalysts for future challenges in industrial organic and environmental catalysis. His expertise includes heterogeneous catalysis in biorefineries, the design of catalysts for biomass conversion, and spectroscopy of and kinetics with active sites for small molecule activation such as methane and carbon dioxide. He is co-chair of the Catalysis Commission of the International Zeolite Association (IZA), cofounder of the European Research Institute of Catalysis (ERIC) and a spin-off company Zeopore. He is invited member of the European Academy of Sciences and Arts, elected member of Academia Europaea, member of the international advisory board of ChemSusChem (Wiley), and associate editor of ACS Sustainable Chemistry & Engineering.

Edward I. Solomon grew up in North Miami beach, FL, received his Ph.D. at Princeton (with D. S. McClure), and was a postdoctoral fellow at The Ørsted Institute (with C. J. Ballhausen) and then at Caltech (with H. B. Gray). He was a professor at the Massachusetts Institute of Technology until 1982, when he joined the faculty at Stanford University, where he is now the Monroe E. Spaght Professor of Humanities and Sciences and Professor of Photon Science at the SLAC National Accelerator Lab. He has been an invited professor in Argentina, Australia, Brazil, China, France, India, and Japan. Prof. Solomon’s research is in the fields of physical inorganic chemistry and bioinorganic chemistry with emphasis on the application of a wide range of spectroscopic methods combined with QM calculations to elucidate the electronic structure of transition metal sites and its contribution to physical properties and reactivity. He has received a wide range of medals and awards and is a member of the National Academy of Sciences and the American Academy of Arts and Sciences and a fellow in the American Association for the Advancement of Science and the American Chemical Society.