Abstract
Standard niche modelling is based on probabilistic inference from organismal occurrence data but does not benefit yet from genome‐scale descriptions of these organisms. This study overcomes this shortcoming by proposing a new conceptual niche that resumes the whole metabolic capabilities of an organism. The so‐called metabolic niche resumes well‐known traits such as nutrient needs and their dependencies for survival. Despite the computational challenge, its implementation allows the detection of traits and the formal comparison of niches of different organisms, emphasising that the presence–absence of functional genes is not enough to approximate the phenotype. Further statistical exploration of an organism's niche sheds light on genes essential for the metabolic niche and their role in understanding various biological experiments, such as transcriptomics, paving the way for incorporating better genome‐scale description in ecological studies.
Keywords: marine ecology, metabolic network, metabolic niche, microbial ecology, molecular ecology, niche modelling
Using metabolic modeling, we propose a metabolic formulation of the fundamental niche. Abstracting the phenotype of the organism with its Genome Scale Model, we compute its metabolic niche and extract well known metabolic traits. From the metabolic niche, one is able to compare organisms niche‐wise and also investigate metabolic pathways essentiality in the niche formulation.

INTRODUCTION
A hundred years ago, seminal studies introduced the general idea of a niche that still motivates current ecological investigations. In 1917, Joseph Grinnell proposed one of its first definitions by declaring the niche as the environmental conditions needed by a given species to survive (Grinnell, 1917). However, because such a description did not consider the impact of the species on its environment, Charles S. Elton (1927) proposed a complementary description examining the niche as the place of the species in its biotic environment. We have to wait 1957 for G. E. Hutchinson to publish his Concluding Remarks (Hutchinson, 1957) that formalises the n‐dimensional niche space, where each axis describes an environmental variable and excludes trophic interactions. The set of conditions allowing a species to survive defines its niche, forming an n‐dimensional volume in the niche space. This definition is referred to as the fundamental niche. It aims to reason on the biological system requirements and to highlight its impact on its environment. Nevertheless, modelling such n‐dimensional volume is challenging because of the nature of biological data. To overcome these limitations, many heuristics, leading to different definitions of the niche, are proposed. However, these numerous formalisations contribute to the complexification of the niche concept (McInerny & Etienne, 2012) and an oversimplification of the phenotype or organism's physiology.
Indeed, DNA sequencing techniques have changed the global perception of physiology and ecosystems (Coles et al., 2017; Green et al., 2008; Joyce & Palsson, 2006; Levering et al., 2017; Sunagawa et al., 2020). Nowadays, metabolic engineering targets understanding of internal machinery of organisms described originally via their gene content. This knowledge is then synthesised into the organism's metabolic network. It regroups all the metabolic reactions encoded in the genotype and their intertwining. By focusing only on biochemical properties, this metabolic modelling strives to investigate a phenotype linked to metabolic processes called the metabolic phenotype. These metabolic predictions from omics data have shown significant successes in biotechnology (Orth et al., 2010; Pál & Papp, 2017; Smith et al., 2019; Zelezniak et al., 2015). However, these predictions assume the biological system to adopt optimal behaviours such as growing at their maximal rate, which is not suited for the niche concept, where organisms show their plasticity to survive, not their ability to overgrow.
Here we proposed a novel computational framework where we extract the fundamental niche of an organism from its metabolic phenotype. Contrary to standard niche models, the metabolic niche does not consider a unique optimal solution. Still, it explores all metabolic exchange flux values with its environment that allow an organism to survive (i.e. nutrient uptakes) and impact the biotope (i.e. nutrient excretions). We first use the quantitative description of this metabolic niche to recover biological features of Escherichia coli such as conditions for aerobic or anaerobic growth. We then extend our computations to numerous prokaryotes, exhibiting metabolic niche inclusion and its putative link with ecotype. Finally, we investigate the metabolic niche of Phaeodactylum tricornutum showing the importance of particular reactions and pathways in the survival of the organism. Notably, we show that we can gather different kinds of omics data around our theoretical framework for improving our understanding of previous biological results in the light of the ecological success of diatoms.
METHODS
Genome‐scale metabolic modelling: a general definition
A metabolic reaction is a chemical transformation that occurs in living organisms allowing them to feed and grow. The substrates and products of metabolic reactions are called metabolites. When considering an organism, the products of one reaction are often the substrates of other reactions. A metabolic network of an organism is then a set of interconnected reactions that transforms step by step the nutriments imported from the environment to convert them into molecules needed by the organism. When modelling a metabolic network, we often distinguish between two categories of metabolites: external and internal. Those that are imported (resp. exported) from (resp. to) the environment are called external metabolites. They are not represented in our models and are responsible for uptake or secretion. Once they are in our model, they are called internal metabolites, as all the other metabolites involved in a reaction of the network. A metabolic reaction involving at least one external metabolite is called an exchange reaction.
Given a metabolic network containing reactions and internal metabolites, the corresponding Stoichiometric matrix, is an matrix , such that for each internal metabolite for and each reaction for :
By convention exchange reactions are written as:
where is the external metabolite . Hence, the forward reaction means that the system is producing into the environment, whereas a reverse reaction means that the system is consuming from the environment. According to kinetic theory, the change over time of the concentration of the metabolite is given by the mass balance equation:
where is the reaction rate or flux associated to reaction . Fluxes can be positive or negative, there is no constraint a priori. A positive flux means that the reaction is occurring in its forward direction, whereas a negative flux means that it is occurring in the reverse direction. In our formalism, fluxes are expressed in mole of product formed (resp. mole of reactant consumed) by gram of dry weight of the considered organism by hour, that is mol.gDW‐1.h‐1. Using a vector notation, the above equation can be written as:
where is the stoichiometric matrix, stands for the flux vector where each component is the flux through the reaction and is the metabolites concentration vector where component is the concentration .
When analysing metabolic networks using constraint‐based approaches, we often assume that most of metabolic reactions are much faster than the environmental changes (Varma & Palsson, 1994). One can thus assume the system at quasi‐steady‐states (Varma & Palsson, 1994), leading to:
| (1) |
In addition to this system of linear constraints, one also considers the bounds on fluxes that state that no reaction can have an infinite rate. All fluxes must satisfy an inequality like:
| (2) |
where represents the upper bound of the flux, meaning the highest rate of the direct reaction, and represents the lower bound of the flux, that is the highest rate of the reverse reaction. One can also encode thermodynamic information by tweaking those bounds. For instance, if the reaction is known to be direct and irreversible, it means that the flux cannot be negative. In that case, the inequality becomes:
For further reading on the mathematical framework in constraint based modelling the interested reader is referred to Price et al. (2004).
All solutions of that satisfy the steady state equation (1) and the thermodynamic constraints (2) are biochemically feasible. The set of solutions describes a steady‐state flux space defined by:
| (3) |
where and are lower and upper bounds of reaction fluxes. Those values may not be known. In that case, a very high value (or a very low value for reversible reactions) is generally used. The corresponding space is then an over‐approximation. Each solution of is a point satisfying all chemical and physical constraints in terms of fluxes. Thus, mathematically, points of are feasible, as they satisfy all the constraints. Biologically, we will call them functional, as they represent fluxes distribution that allow the organism to survive. We propose herein to investigate the whole set of solutions instead of focusing on one solution proposed by other mechanistic and ultra‐parameterised biological models.
General formulation of the metabolic niche
All solutions from are feasible but represent different phenotypes as the distributions of fluxes indicate different uses of metabolic pathways, or uptakes, or secretions. However, solutions belonging to do not form a proper functional niche space. Indeed, two additional constraints must be added to restrain that are described below.
The survival condition
State‐of‐the‐art metabolic modelling techniques consider a chimeric metabolic reaction, called the biomass reaction (Feist & Palsson, 2010). This reaction summarise all precursors required to create a new cell, including DNA, amino acids, lipids and polysaccharides (O’Brien et al., 2015). Usually, the determination of precursors coefficients is made experimentally or, when data are not available, by estimation from genome data. By ensuring that stoichiometric coefficients are normalised by mol.gDW‐1, biomass flux unit is in h‐1, matching a growth rate (Oberhardt et al., 2009). The survival of a species is ensured as long as the species grows at least as fast as it is dying, meaning that its growth rate should be above its death rate. As the flux through the biomass reaction is our surrogate of the growth rate, we can model this constraint by forcing the biomass reaction flux to be over a value representing the natural death of the organism:
We add this new inequality to the previous set of constraints on flux bounds . The corresponding solution flux space is noted (niche flux space).
| (4) |
The environmental space
The metabolic niche space is constrained by the environment, which implies decomposing the flux vector into two parts: one concerning the exchange reactions (), and the other concerning the internal reactions (). Hence, we seek for the set of acceptable such that there exists a so that is in . Thus, if among the reactions of the metabolic network, are exchange reactions, we define the metabolic niche by:
| (5) |
Noting the orthogonal projection of onto , the metabolic niche would be the image of by :.
Intuition of the projection
One property worth mentioning on is its topology. This space is convex by definition and also bounded as reactions cannot carry infinite fluxes. Moreover, all its constraints are linear, making it a convex polytope that can be described through the enumeration of its vertices. This representation is called the V‐representation (Ziegler, 1995). Let us call the set of vertices generating . We can write as a convex combination of the vertices in , that is, . From this description, the projection of can be done through the projection of each and we have:
This formulation is well suited for understanding the origin of the niche space in our formalism. However, vertex enumeration is a computationally challenging problem, and its complexity grows exponentially with the number of metabolic reactions involved in the system.
Metabolic niche computation
This projection of the niche flux space onto the niche space is general as it relies on the seminal definitions of Elton (1927) of the fundamental niche that considers all exchange reactions. However, exploring this space is a complicated numerical task. Therefore, we propose to reduce the complexity of the above projection by reformulating the original niche flux space , allowing its computation through the resolution of a linear programming problem.
Polytope formulation
As is a polyhedron, one can change its representation from the vertices description to the half‐spaces intersection, called the H‐representation:
with and . is the matrix composed by the vectors defining the half‐space constraints (as rows), such that for each row , the corresponding constraint is . The new formulation is similar as equation (4) if and vector are specific matrices defined as follows:
with the identity matrix of and the column vector of with all its components set to 0.
Projection through multi objective linear programming
Assuming exchange reactions of interest that represent axes for the metabolic niche space. Defining the metabolic niche following the formulation of Hutchinson consists in projecting onto the nutrient flux space defined by those exchange reactions. Formally, it is the polyhedron defined by:
| (6) |
with the two matrices and being submatrices of . is composed of the columns corresponding to the exchange reactions; corresponds to the remaining columns taking credit for interior reactions. Biologically speaking, is responsible for the interaction of the organism with its environment, and accounts for the inner mechanism of the organism.
In practice, computing this projection is similar to solve the following multi‐objective linear program (MOLP) (Löhne & Weißing, 2016) for which efficient solvers (Löhne & Weißing, 2017) are available:
| (7) |
with the column vector of with all its components set to 1. For passing from the MOLP solution to the solution of the projection problem, one only needs to get rid of the last component of the former to get the latter. Computing the niche following the formulation of Hutchinson is therefore equivalent to solve a multi‐objective problem in the context of genome‐scale metabolic modelling. The detailed pipeline and models used can be found in Supplementary Text S1.
RESULTS
Rationale of the metabolic niche and its application on a state‐of‐the‐art metabolic model
The metabolic niche is a new computational result estimated from the sole genomic composition of an organism. Contrary to other niche estimations (Guisan & Thuiller, 2005), our modelling does not consider statistical distributions over a range of parameters but rather a theoretical phenotype, synthesised in a metabolic network.
From genomic data (Figure 1a), metabolic network reconstruction techniques infer an organism's metabolic abilities. Reactions intertwine with products of reactions that are substrates of others, forming a metabolic network (Figure 1b). Some metabolites are constituents of the biomass reaction. This synthetic reaction models the growth rate of the organism. Exchange reactions are responsible for the organism's interaction with its environment, defining the limits of the biological system. The set of all biological constraints, such as (i) the interconnectivity of reactions, (ii) the stoichiometry, and (iii) a classical steady‐state approximation, describes a solution space (Figure 1c). From this solution space, state‐of‐the‐art systems biology approaches focus on distinct points of interest, generally minimising or maximising one particular flux (e.g. the red dot in Figure 1c which maximise the flux through the biomass reaction). The fundamental niche focuses on the species’ interaction with its environment and survival (Figure 1d). Projected in a metabolic modelling framework, considering the niche space implies abstracting the network's inner reactions and focusing on the exchange reactions while maintaining a minimal growth rate (Figure 1e). The former metabolic solution space is therefore further constrained by a death rate. Hence, the corresponding space describes all fluxes combinations that satisfy the fundamental niche constraints, so‐called the metabolic niche (Figure 1f).
FIGURE 1.
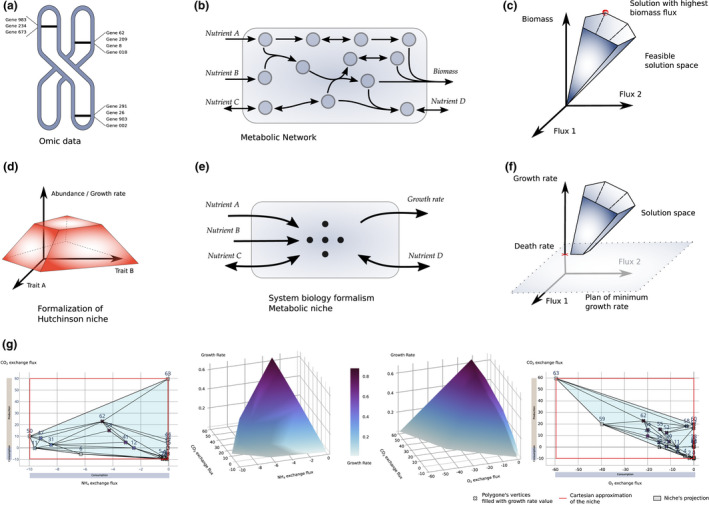
Formalising the metabolic niche from omic knowledge and application on E. coli. From the genomic content of an organism (a), we could infer the corresponding encoded catalytic proteins. These proteins support metabolic reactions that interplay (i.e. products are substrates for others). The resulting metabolic network (b) integrates all the physiological abilities of one species. Projected into a constraint‐based paradigm, solving the corresponding linear problem depicts a solution space (c) that describes all the fluxes in each metabolic reaction that satisfy all given constraints. Ecological traits define the axes of Hutchinson's niche space. The niche volume (d) guarantees that the species survives as long as its environmental conditions belong to this volume. If we apply this formalism to the metabolic network, we abstract the organism's inner mechanism and focus only on its exchange reactions (e). Using constraint‐based modelling on this new system, we have a new constraint, which is the survival of the species; that is, the flux through the growth rate reaction needs to be at least as high as the death rate of the species (f). Therefore, a formal description of the metabolic niche explores the solution space in which axes (or traits) are exchange reaction fluxes. When applied on E. coli, we reduced the number of axes of the niche space to allow visualisation of the volume of its niche (g)
For the sake of application, a metabolic niche was estimated for the core E coli metabolic network. An estimation of the maximum growth rate via flux balance analysis (Heirendt et al., 2019) is 0.874 h‐1. The metabolic niche was estimated for a death rate equals to 0.01 h‐1 and on six dimensions that correspond to exchange reactions for the following metabolites: CO2, O2, H2O, NH4, phosphate and glucose. The death rate value is herein strictly arbitrary, and results may vary for other values. For instance, a value of 0.7 h‐1 would shed light on high growth rate behaviour, whereas a lower value would add behaviours representing less than 2% of the growth rate range. A finer parameterisation of this rate is necessary to represent biotic interactions better, such as predation, but does not interfere in the fundamental niche definition.
The topology of a metabolic niche is complex. We could describe its volume with more than 210 vertices. In favour of representation, we clustered close vertices, dividing by three their number (64 vertices) while maintaining more than 95% of the niche volume for the represented axes. For the sake of simplicity, we represent the metabolic niche (a blue‐grey area) and its vertices in the CO2 versus ammonium and CO2 versus O2 exchange spaces (Figure 1g). As a companion illustration, we also represented the metabolic niche in the front of the growth rate as a 3D shape to picture each environmental condition's theoretical growth.
For approximating the state‐of‐the‐art niche space in the context of the metabolic network, we performed a flux variability analysis (FVA) (Heirendt et al., 2019) on the same exchange reactions with a minimum flux through the biomass reaction set to 0.01 mmol.gDW‐1.h‐1 to keep the same survival constraint as the one used for the metabolic niche. It defined the feasible range of fluxes for each exchange reactions (Figure 1g red lines). As a modelling validation, estimated ranges of fluxes embed the projection of the metabolic niche. The volume defined by the Cartesian product of each segment of the feasible range is called the Cartesian niche. The Cartesian niche volume is more than 86×106 units in the six dimensions, whereas the metabolic niche volume is less than 72×103. Thus, it occupies less than 1‰ of the approximate Cartesian niche, emphasising all the constraints that are not taken into account in the Cartesian niche approximation, in particular those that define phenotypic traits. This supports the previous results (Díaz et al., 2016) where models span trait space much bigger than the space occupied by in vivo observations.
The metabolic niche indicates an overall uptake of ammonia by E. coli (i.e. negative exchange fluxes), whereas CO2 could be produced (i.e. positive exchange fluxes) by respiration, or uptaken but in small amplitude for anaplerotic reactions and other carboxylation reactions. Flux distributions in this part of the metabolic niche are associated with lower uptake of oxygen (15 mmol.gDW‐1.h‐1), emphasising the anaerobic growth conditions. As a biological validation, the metabolic niche description correctly shows lower maximal growth rates in anaerobic than in aerobic conditions. Furthermore, the metabolic niche's overall shape exhibits a positive relationship between O2 consumption and CO2 production that defines respiration (i.e. a negative relationship between both fluxes), whereas the relationship between CO2 and ammonia is less obvious. This system's characteristic is a straightforward consequence of considering whole intracellular biochemical reactions, leading to mechanistic interdependencies between uptake reactions, that by construction, Cartesian niches could not consider. Furthermore, the metabolic niche extracts essential numerical descriptors of E. coli, mainly physiological switches of regime in function of available nutrients. These switches between regimes are traits, usually identified after extensive and tedious experimental efforts.
Comparing organisms via their metabolic niches
We arbitrarily defined traits for a systematic comparison of metabolic niches (i.e. exchange reactions for the following metabolites: NH4, SO4, H2S, glucose, NO3). We randomly selected 39 prokaryotic metabolic models (Machado et al., 2018) that share those reactions. When possible, we associated each model with its habitat (Davis et al., 2020). We then compared the metabolic niche distance (see Supplementary Text S2), a surrogate to the metabolic niche volume overlap, versus different state‐of‐the‐art distances between organisms (Figure 2a–c). Identical or included metabolic needs imply similar or included metabolic niches, and a metabolic niche‐based distance equals to 0. Conversely, a distance equals to 1 emphasises distinct niches and distinct metabolic needs. Each point describes a comparison between two bacteria. Coloured points indicate bacteria from similar habitats (respectively blue, brown and red for marine, soil and host‐associated). When removing inclusion cases, we show a strong positive correlation between Cartesian niche overlaps and metabolic niche overlaps (Figure 2a; R: 0.82, p‐value: 2.68×10‐181, slope: 0.98). This result was expected as the Cartesian niche embed the metabolic niche. Furthermore, most of the comparisons are above the scatter plot's diagonal. Several metabolic model comparisons are spread over vertical lines: showing the same Cartesian niche overlap but different metabolic niche overlaps, stressing an overall refinement in the distance brought by the use of the metabolic niche.
FIGURE 2.
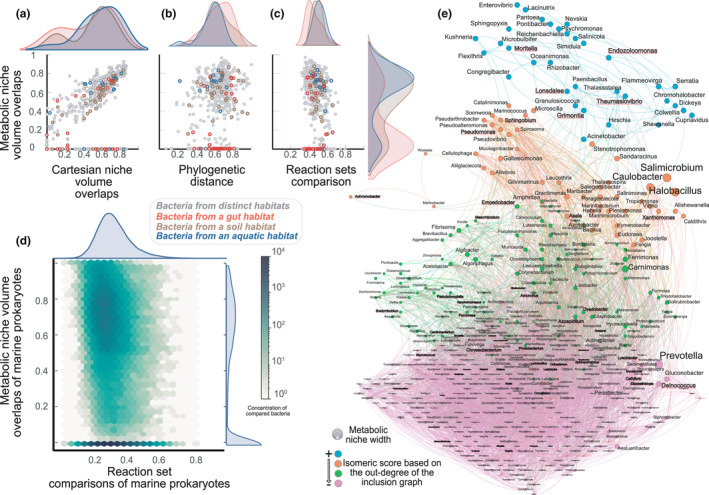
Comparison of the metabolic niche overlap with other pairwise distances and niche inclusion. (a) Comparison between metabolic niche overlaps and Cartesian niche overlaps estimated with a Jacquard distance. This comparison is performed for bacteria from different or common habitats. (b) Absence of a relationship between metabolic niche overlaps and pairwise phylogenetic distances based on 16S rRNA gene. (c) Absence of a relationship between metabolic niche overlaps and presence–absence of common reactions estimated via a Jaccard distance. (d) Absence of a relationship between metabolic niche overlaps and presence–absence of common reactions estimated for 502 marine bacteria metabolic models. Instead of a scatter plot, it shows concentrations for more than pairwise comparisons. For bacteria that show metabolic niche overlaps almost null, we investigate potential niche inclusion. (e) Metabolic niche inclusion graph of marine bacteria. The node size is proportional to metabolic niche volume, and an edge indicates a metabolic niche's inclusion into another. The graph layout follows an isomeric distribution driven by the out‐degree of the inclusion graph. Bacteria are divided into four categories based on the z‐score from most embedded metabolic niche (i.e. turquoise) to the least (i.e. purple). Labels of bacteria known for being associated with a host are in red/bold and underlined
Similarly, we compared the metabolic distance with the phylogenetic distance based on 16S rRNA sequence pairwise comparison (Figure 2b). The comparison exhibits a decoupling between the metabolic niche and taxonomy as already shown for marine prokaryotes (Louca et al., 2016). Because seminal genomic studies extrapolate organismal functionalities from their genomic content (Fahimipour & Gross, 2020; Louca et al., 2016), we further compared the metabolic niche overlap with a genomic composition distance by computing pairwise organismal reactions sets’ Jacquard distances (Figure 2c). In this context, high distance means low cardinality of the intersection of the sets. This straightforward metric stresses the topologies’ differences from a metabolic network perspective by emphasising similar reactions between organisms but not their use. Our computations reveal no significant relationship between the metabolic niche overlap and the presence‐absence of reactions, emphasising that the exclusive metabolic abilities do not approximate the organismal metabolic needs or phenotype.
To scale up this strong result in a more specific habitat, we applied the same protocol for 502 metabolic models of bacteria found in Tara Ocean Datasets (Vernette et al., 2021). Their pairwise comparison implies considering more than 105 points described by the logarithm of point densities (Figure 2d). This result confirms the lack of overall relationship between the metabolic niche overlap and the presence–absence of shared reactions for marine prokaryotes. Furthermore, the metabolic niche overlap computation showed several cases of distances near 0 (Figure 2a–d). This result implies that some metabolic niches were included in others. Due to numerical imprecisions, we stated that an intersection covering more than 999‰ of the smallest niche is an inclusion. We used this metric to depict a metabolic niche inclusion graph (Figure 2e), where nodes are marine bacteria with a node size proportional to the metabolic niche volume, and edges describe the inclusion of a bacteria niche into another. For the sake of clarity, the directed graph follows an isomeric layout driven by the out‐degree, and nodes are partitioned into four categories based on the z‐score that approximates the capacity to include other metabolic niches. Bacteria known for being associated with a host are depicted in red/bold. Mainly distributed at the bottom of the layout and coloured in purple (i.e. metabolic niche included in others), these bacteria show significantly smaller metabolic niche volume (Figure S1). These features indicate less phenotypic plasticity for the bacteria associated with host, potentially following more stable environmental conditions or gene loss (Mas et al., 2016).
In‐depth study of the metabolic niche flux space of a ubiquitous diatom
To assess the impact of primary metabolism on the metabolic niche and apply our approach beyond prokaryotes, we used one of the most comprehensive and ubiquitous eukaryotic models: the diatom P. tricornutum (Broddrick et al., 2019). Its metabolic model covers more than 2000 reactions and 1700 metabolites (Supplementary Text S3), which are suited to characterise the chimeric nature of diatom metabolism and incorporate compartmental targeting of biochemical reactions. We investigated the metabolic niche of P. tricornutum via a sampling procedure that estimates 105 samples of fluxes distribution that belong to the metabolic niche flux space. This numerical exploration is used to compute pairwise correlations between fluxes. This statistical score emphasises the relationship between flux variations of two reactions that results from mechanistic dependencies arising from metabolic constraints. Thus, a high absolute correlation value between two reaction fluxes indicates that a change in one of the reaction flux will induce a change in the other reaction flux, whereas not correlated (i.e. R 2 = 0) fluxes designate mechanistic independence of both reactions in the niche flux space, allowing independent variations of their fluxes. We resumed this exploration in a correlation graph where reactions are vertices and correlation between two reactions is an edge linking the corresponding vertices (Figure 3a). We assume that the reaction's importance to sustain the metabolic niche, that is organism survival, can be shown by the sum of all the correlation involving this particular reaction (as depicted in Figure 3a by the grey circular bar diagram). We showed that most Calvin–Benson–Bessham (CBB) cycle reactions are essential to the metabolic niche by pointing out reactions belonging to notable metabolic pathways, biologically reassuring for photosynthetic organisms. To be able to get the same kind of results on metabolic pathways, we look at the distribution of its correlation normalised by the number of reactions it is composed of (Figure 3b). All pathways show a modal distribution around 0, emphasising that no pathways are entirely dependent on the whole network. Proportionally to others, sulphur and iron show smaller correlations, whereas chlorophyll, carotenoid, amino‐acyl‐tRNA, glycerolipids, fatty acid biosynthesis and oxidative stress reactions exhibit higher correlations, as these pathways target energy storage or consumption. Interestingly, the photorespiration, carbon fixation, TCA and amino acid metabolism pathways have less high absolute correlation values but still show a normal distribution of the correlations. This result indicates a potential role in acclimating while still having a pivotal role in the organism's survival.
FIGURE 3.
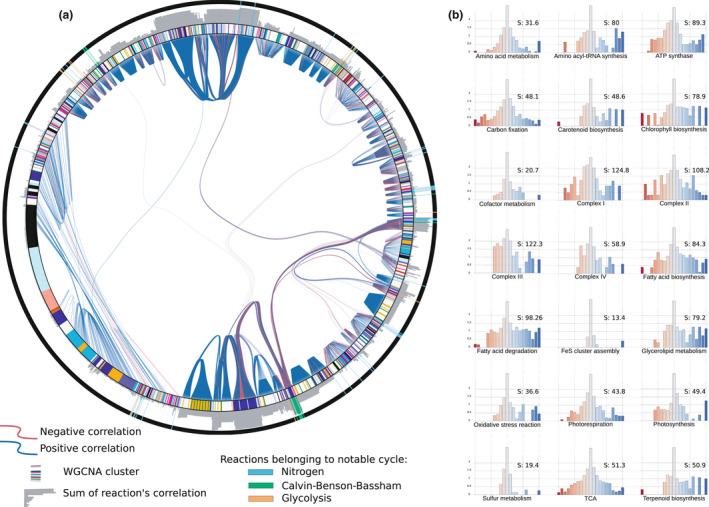
Correlation between Phaeodactylum reactions to support the metabolic niche. (a) Description of most significant dependencies between metabolic reactions. Metabolic reactions are ordered in an outer circle. Reactions associated with nitrogen, Calvin–Benson–Bassham and glycolysis cycles are emphasised. An edge between reactions corresponds to a correlation (positive or negative) between two fluxes’ reactions above 0.6. The inner‐circle describes WGCNA modules to which the gene associated with the reaction belongs. A grey circular bar plot shows the correlation sum of each reaction as a proxy of the reaction essentiality for the metabolic niche. (b) Shows essentiality of pathways for the metabolic niche. We represent the correlation histogram normalised by the number of genes present in the pathway for distinct pathways. Y‐axes are in log scale. The S score is the sum of the absolute correlation value of the histogram, which estimates pathway essentiality for the metabolic niche
We can benefit from previous extensive transcriptomic analysis of P. tricornutum, in which modules of co‐expressed genes over distinct experimental conditions are defined by weighted gene co‐expression network analysis (Ait‐Mohamed et al., 2020). Because most metabolic reactions are linked to genes that encode for their enzymes, we are able to integrate the information of membership to a module to our analysis (coloured ring of Figure 3a). For some modules, targeted reactions show high pairwise flux correlations, which indicates that the metabolic dependencies could explain the clustering of these genes. Nevertheless, we also see high correlations between modules, indicating metabolic dependencies between different modules (Figure S2a), insights that are not accessible from the standard transcriptomic analysis. Among others, the blue module is of particular interest. It is the most prevalent in the metabolic network. It has the highest intra‐module correlation sum and shares a high correlation with other modules, emphasising its importance in the metabolic niche. A previous study (Ait‐Mohamed et al., 2020) showed its implication in several metabolic pathways, mainly the CBB cycle, glycolysis and fatty acid pathways (for details, see Figure S6 of Ait‐Mohamed et al. (2020) that depicts the distribution of genes belonging to the pathways across all transcriptomic modules). The use of the metabolic niche allows fostering the previous interpretations of these modules. It shows that the module is correlated with reactions directly linked with the TCA pathway (this pathway was essentially associated with cyan module, explaining in part the connection between these two modules), amino acid metabolism and chlorophyll biosynthesis (explaining most of the connection with light steel module that encompasses genes associated with chlorophyll and isoprenoid synthesis). Notice that the connection with the dark grey module is primarily due to other pathways not labelled here (Figure S2b).
Finally, projecting the essentiality of genes for the metabolic niche at the chromosome level shows that all chromosomes contribute to the metabolic niche by considering the exact relationship between genes and essential reactions (Figure 4a). However, extraction of simple statistical parameters from the distribution suggests no particular pattern of gene essentiality for the niche among chromosomes (Figure 4b). Identifying these islands of essential genes for the metabolic niche versus segments less constrained paves the way to understand evolutionary processes further.
FIGURE 4.
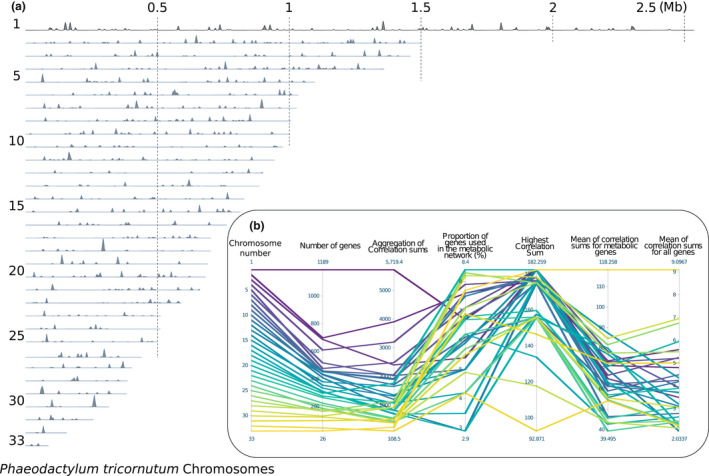
Description of the gene essentiality for the metabolic niche on Phaedactylum tricornutum's genome. (a) For each 33 diatom's chromosome, we emphasise genes that encode for a metabolic reaction catalyser. For each gene, we report the correlation sum of its associated reaction at its genomic position. In addition, (b) describes statistics for each chromosome (i.e. specific colour line), such as the total number of genes, the sum of all correlation sums, the proportion of genes from the chromosome involved in the metabolic network, the highest correlation sum found in the chromosome and mean values considering solely genes involved in the metabolic network or all genes
DISCUSSION
Our definition of the fundamental niche relies on the recent signs of progress of two recent complementary and productive fields. On the one hand, the genomic composition of organisms and ecosystems is now available via high throughput DNA sequencing fostering the identification of putative functions (Coles et al., 2017; Raes & Bork, 2008). Notably, a recent study formalises a metabolic niche space based on the presence–absence of microbe's metabolic traits, allowing well‐defined comparison and clustering of organisms upon metabolic abilities (Fahimipour & Gross, 2020). However, it does not investigate the dependency between metabolic capabilities and growth rate (Smith et al., 2019), putting aside one essential aspect of the niche: the survival of the considered organisms. By doing so, it steps away from Hutchinson's definition by throwing other niche specificities into the pool (McInerny & Etienne, 2012). On the other hand, systems biology takes advantage of using some of the most efficient computational solvers that enable new descriptions of biological systems phenotypes from networks. The complementarity between these fields allows analysing genome‐scale metabolic models identified from their environment and extrapolating their niche. However, it is worth noting that this models’ identification is a tedious and challenging task, (Lieven et al., 2020; Thiele & Palsson, 2010) and few metabolic models are available compared to the number of annotated genomes. In particular, this study (Figure 2d,e) considers a fraction of marine prokaryotes, for which metabolic models are available (Machado et al., 2018), compared to available marine microbial genomes (Louca et al., 2016). Nevertheless, preliminary metabolic niche exploration is insightful. The metabolic niche inclusion depicts the relative plasticity of bacteria compared to others (Figure 2e). In particular, it shows that bacteria associated with hosts rely on smaller niches and potentially more stable environmental conditions (Figure S1).
Our metabolic niche approach is a new formulation of Hutchinson's fundamental niche through the modelling of the metabolic phenotype of an organism. This mechanistic approach allows the identification of metabolic functional traits as it links exchange fluxes with the organism's growth rate. For instance, it identified the quantities of oxygen that lead E. coli to switch from anaerobic to aerobic growth by just considering its metabolic network (Figure 1g). This trait description is possible thanks to the theoretical phenotype modelled by the metabolic network when available.
From a computational viewpoint, the metabolic niche relies on a formal description of the metabolic solution space. Contrary to other metabolic modelling tools designed for metabolic engineering (used to maximise the growth rate of specific organisms or the production of given metabolites of societal interest), the metabolic niche investigates organismal behaviours considering all kinds of growth conditions, especially suboptimal. Previous studies advocate for these conditions as more realistic for studying ecological systems or organisms in biotic interactions (Budinich et al., 2017). This statement requires a more exhaustive and computationally challenging exploration of the solution space than extracting small sets of extreme points associated with the maximal growth rate. We proposed the metabolic niche abstraction and the original niche flux space sampling procedure for this purpose. However, the metabolic niche does not embed trophic interactions per se.
Interestingly, as shown for P. tricornutum, applying a fundamental ecological concept allows integrating a multi‐omics data set, which is a fundamental issue in systems biology that often eludes us. In particular, the use of the metabolic niche explains causal dependencies between groups of co‐expressed genes. In the case of P. tricornutum, it emphasises the role of the blue module for the diatom survival. Furthermore, when projected on its chromosomes, the metabolic niche concept shows that all chromosomes are necessary for the niche, but not all chromosomic regions are equivalent. This result has implications about the evolution of the organism and how chromosome regions must be more constrained than others for the sake of survival.
Despite biological validations, the metabolic niche remains conceptual and calls for further and extensive bioinformatics applications on large environmental genomic databases such as those provided by the Tara Oceans expedition (Sunagawa et al., 2020). This effort will be necessary to compare our formalism with in situ data about habitat. In addition, the metabolic niche formalisation allows precise estimation of the fundamental niche overlap between organisms. However, the work will be colossal as it needs to be performed on more than three thousand metabolic models built from the annotated genomes of reconstructed metagenome‐assembled genomes (MAGs) (Salazar et al., 2019).
The metabolic niche formalises the organismal function as a space in which an organism can survive. This new abstraction of the fundamental niche is an addition to other techniques that assess the niche from the presence‐absence of omics data (Fahimipour & Gross, 2020). In particular, this conceptual study illustrates the need for biological modelling to assess biological phenotype per se as it differs from the sole identification of functional genes. The metabolic niche is thus an essential step towards the design of new omics‐trait‐based models. It aims to be applied at the organismal and ecosystem levels where we could encompass the whole biological complexity as enclosed in the metagenomic knowledge associated with a superorganism hypothesis (Liautaud et al., 2019).
CODE AND DATA AVAILABILITY
The source code for the metabolic niche computation is available at https://gitlab.univ‐nantes.fr/aregimbeau/metabolic‐niche. Metabolic networks used in this study can be found on BiGG database (http://bigg.ucsd.edu/) and on Github (https://github.com/cdanielmachado/embl_gems). Data and codes can be found on Zenodo: https://doi.org/10.5281/zenodo.5780029.
AUTHORSHIP
AR designed the framework and the numerical experiments, ran the experiments, analysed the results and wrote the first draft of the manuscript. DE helped to design the framework, designed the numerical experiments, analysed the results and wrote the first draft of the manuscript. AL analysed the framework and helped to design the sampling experiments. JJPK and CB analysed the results and provided data on Phaeodactylum. OA and MB analysed the framework and the results. LM analysed the results. All co‐authors helped to write this manuscript with comments and insights.
PEER REVIEW
The peer review history for this article is available at https://publons.com/publon/10.1111/ele.13954.
Supporting information
Fig S1
ACKNOWLEDGEMENTS
We thank the commitment of the following sponsors: CNRS (80 PRIME), the H2020 project AtlantECO (award number 862923), BiRD bioinformatics facilities and the Roscoff Bioinformatics platform ABiMS for their computing resources. Damien Eveillard acknowledges CINNAMON (ANR‐17‐CE02‐0014). Chris Bowler acknowledges the Fonds Français pour l’Environnement Mondial (FFEM), French Government ‘Investissements d’Avenir’ programmes OCEANOMICS (ANR‐11‐BTBR‐0008), France GENOMIQUE (ANR‐10‐INBS‐09‐08), MEMO LIFE (ANR‐10‐LABX‐54), PSL Research University (ANR‐11‐IDEX‐0001‐02), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Diatomic; grant agreement No. 835067), and BrownCut (ANR‐19‐CE20‐0020) projects. Marko Budinich and Juan Jose Pierella Karlusich acknowledges postdoctoral funding from FFEM.
Régimbeau, A. , Budinich, M. , Larhlimi, A. , Pierella Karlusich, J.J. , Aumont, O. , Memery, L. , et al. (2022) Contribution of genome‐scale metabolic modelling to niche theory. Ecology Letters, 25, 1352–1364. Available from: 10.1111/ele.13954
Contributor Information
Antoine Régimbeau, Email: antoine.regimbeau@univ-nantes.fr.
Damien Eveillard, Email: damien.eveillard@univ-nantes.fr.
DATA AVAILABILITY STATEMENT
The code and data used in this article is on Zenodo (https://doi.org/10.5281/zenodo.5780029).
REFERENCES
- Ait‐Mohamed, O. , Novák Vanclová, A.M.G. , Joli, N. , Liang, Y. , Zhao, X. , Genovesio, A. et al. (2020) Phaeonet: a holistic RNAseq‐based portrait of transcriptional coordination in the model diatom Phaeodactylum tricornutum . Frontiers in Plant Science, 11, 1522. 10.3389/fpls.2020.590949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avis, D. (2000) A revised implementation of the reverse search vertex enumeration algorithm. In: Kalai, G. & Ziegleur, G.M. (Eds.), Polytopes—combinatorics and computation, Vol. c. DMV Seminar. 29, Basel: Birkhäuser Basel, pp. 177–198. 10.1007/978-3-0348-8438-9_9 [DOI] [Google Scholar]
- Broddrick, J.T. , Du, N. , Smith, S.R. , Tsuji, Y. , Jallet, D. , Ware, M.A. et al. (2019) Cross‐compartment metabolic coupling enables flexible photoprotective mechanisms in the diatom Phaeodactylum tricornutum . New Phytologist, 222, 1364–1379. 10.1111/nph.15685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budinich, M. , Bourdon, J. , Larhlimi, A. & Eveillard, D. (2017) A multi‐objective constraint‐based approach for modeling genome‐scale microbial ecosystems. PLoS One, 12, e0171744. 10.1371/journal.pone.0171744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulović, A. , Fisher, S. , Dinh, M. , Golib, F. , Liebermeister, W. , Poirier, C. et al. (2019) Automated generation of bacterial resource allocation models. Metabolic Engineering, 55, 12–22. 10.1016/j.ymben.2019.06.001 [DOI] [PubMed] [Google Scholar]
- Coles, V.J. , Stukel, M.R. , Brooks, M.T. , Burd, A. , Crump, B.C. , Moran, M.A. et al. (2017) Ocean biogeochemistry modeled with emergent trait‐based genomics. Science, 358, 1149–1154. 10.1126/science.aan5712 [DOI] [PubMed] [Google Scholar]
- Conci, A. & Kubrusly, C.S. (2017) Distance between sets – a survey. Advances in Mathematical Sciences and Applications, 26(1). [Google Scholar]
- Davis, J.J. , Wattam, A.R. , Aziz, R.K. , Brettin, T. , Butler, R. , Butler, R.M. et al. (2020) The PATRIC bioinformatics resource center: Expanding data and analysis capabilities. Nucleic Acids Research, 48, D606–D612. 10.1093/nar/gkz943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Díaz, S. , Kattge, J. , Cornelissen, J.H.C. , Wright, I.J. , Lavorel, S. , Dray, S. et al. (2016) The global spectrum of plant form and function. Nature, 529, 167–171. 10.1038/nature16489 [DOI] [PubMed] [Google Scholar]
- Elton, C.S. (1927) Animal ecology. New York: Macmillan Co. [Google Scholar]
- Fahimipour, A.K. & Gross, T. (2020) Mapping the bacterial metabolic niche space. Nature Communications, 11, 415–418. 10.1038/s41467-020-18695-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist, A.M. & Palsson, B.O. (2010) The biomass objective function. Current Opinion in Microbiology, 13(3), 344–349. 10.1016/j.mib.2010.03.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green, J.L. , Bohannan, B.J.M. & Whitaker, R.J. (2008) Microbial biogeography: from taxonomy to traits. Science, 320, 1039–1043. 10.1126/science.1153475 [DOI] [PubMed] [Google Scholar]
- Grinnell, J. (1917) The niche‐relationships of the California thrasher. The Auk, 34, 427–433. 10.2307/4072271 [DOI] [Google Scholar]
- Guisan, A. & Thuiller, W. (2005) Predicting species distribution: Offering more than simple habitat models. Ecology Letters, 8, 993–1009. 10.1111/j.1461-0248.2005.00792.x [DOI] [PubMed] [Google Scholar]
- Heirendt, L. , Arreckx, S. , Pfau, T. , Mendoza, S.N. , Richelle, A. , Heinken, A. et al. (2019) Creation and analysis of biochemical constraint‐based models using the COBRA Toolbox Vol 3.0. Nature Protocols, 14, 639–702. 10.1038/s41596-018-0098-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchinson, G.E. (1957) Concluding remarks. Cold Spring Harbor Symposia on Quantitative Biology, 22, 415–427. 10.1101/SQB.1957.022.01.039 [DOI] [Google Scholar]
- Joyce, A.R. & Palsson, B. (2006) The model organism as a system: integrating ’omics’ data sets. Nature Reviews Molecular Cell Biology, 7, 198–210. 10.1038/nrm1857 [DOI] [PubMed] [Google Scholar]
- King, Z.A. , Lu, J. , Dräger, A. , Miller, P. , Federowicz, S. , Lerman, J.A. et al. (2016) BiGG Models: a platform for integrating, standardizing and sharing genome‐scale models. Nucleic Acids Research, 44(D1), D515–D522. 10.1093/nar/gkv1049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levering, J. , Dupont, C.L. , Allen, A.E. , Palsson, B.O. & Zengler, K. (2017) Integrated regulatory and metabolic networks of the marine diatom Phaeodactylum tricornutum predict the response to rising CO2 levels. mSystems 2(1), e00142‐16. 10.1128/msystems.00142-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liautaud, K. , van Nes, E.H. , Barbier, M. , Scheffer, M. & Loreau, M. (2019) Superorganisms or loose collections of species? A unifying theory of community patterns along environmental gradients. Ecology Letters, 22, 1243–1252. 10.1111/ele.13289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieven, C. , Beber, M.E. , Olivier, B.G. , Bergmann, F.T. , Ataman, M. , Babaei, P. et al. (2020) MEMOTE for standardized genome‐scale metabolic model testing. Nature Biotechnology, 38, 272–276. 10.1038/s41587-020-0446-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löhne, A. & Weißing, B. (2016) Equivalence between polyhedral projection, multiple objective linear programming and vector linear programming. Mathematical Methods of Operations Research, 84, 411–426. 10.1007/s00186-016-0554-0 [DOI] [Google Scholar]
- Löhne, A. & Weißing, B. (2017) The vector linear program solver Bensolve – notes on theoretical background. European Journal of Operational Research, 260, 807–813. 10.1016/j.ejor.2016.02.039 [DOI] [Google Scholar]
- Louca, S. , Parfrey, L.W. & Doebeli, M. (2016) Decoupling function and taxonomy in the global ocean microbiome. Science, 353, 1272–1277. 10.1126/science.aaf4507 [DOI] [PubMed] [Google Scholar]
- Machado, D. , Andrejev, S. , Tramontano, M. & Patil, K.R. (2018) Fast automated reconstruction of genome‐scale metabolic models for microbial species and communities. Nucleic Acids Research, 46, 7542–7553. 10.1093/nar/gky537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mas, A. , Jamshidi, S. , Lagadeuc, Y. , Eveillard, D. & Vandenkoornhuyse, P. (2016) Beyond the black queen hypothesis. The ISME Journal, 10, 2085–2091. 10.1038/ismej.2016.22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGill, B.J. , Enquist, B.J. , Weiher, E. & Westoby, M. (2006) Rebuilding community ecology from functional traits. Trends in Ecology & Evolution, 21(4), 178–185. 10.1016/j.tree.2006.02.002 [DOI] [PubMed] [Google Scholar]
- McInerny, G.J. & Etienne, R.S. (2012) Ditch the niche – is the niche a useful concept in ecology or species distribution modelling? Journal of Biogeography, 39, 2096–2102. 10.1111/jbi.12033 [DOI] [Google Scholar]
- Megchelenbrink, W. , Huynen, M. & Marchiori, E. (2014) optGpSampler: an improved tool for uniformly sampling the solution‐space of genome‐scale metabolic networks. PLoS One, 9, e86587. 10.1371/journal.pone.0086587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagaraju, S.K. , Gudasalamani R., Barve N., Ghazoul J., Narayanagowda G.K., Ramanan U.S. et al. (2013) Do ecological niche model predictions reflect the adaptive landscape of species?: a test using Myristica malabarica Lam., an endemic tree in the Western Ghats, India. PLoS ONE, 8(11), e82066. 10.1371/journal.pone.0082066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien, E.J. , Monk, J.M. & Palsson, B.O. (2015) Using genome‐scale models to predict biological capabilities. Cell, 161, 971–987. 10.1016/j.cell.2015.05.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberhardt, M.A. , Chavali, A.K. & Papin, J.A. (2009) Flux balance analysis: interrogating genome‐scale metabolic networks. In: Maly, I.V. (Ed.) Systems biology, methods in molecular biology. Totowa, NJ: Humana Press, pp. 61–80. 10.1007/978-1-59745-525-1_3 [DOI] [PubMed] [Google Scholar]
- Orth, J.D. , Thiele I. & Palsson B.Ø. (2010) What is flux balance analysis? Nature Biotechnology, 28(3), 245–248. 10.1038/nbt.1614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pál, C. & Papp, B. (2017) Evolution of complex adaptations in molecular systems. Nature Ecology Evolution, 1, 1084–1092. 10.1038/s41559-017-0228-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peixoto, T.P. (2014. a) The graph‐tool python library. figshare. Dataser. 10.6084/m9.figshare.1164194.v14 [DOI]
- Peixoto, T.P. (2014. b) Hierarchical block structures and high‐resolution model selection in large networks. Physical Review X, 4(1). 10.1103/physrevx.4.011047 [DOI] [Google Scholar]
- Price, N.D. , Reed, J.L. & Palsson, B. (2004) Genome‐scale models of microbial cells: evaluating the consequences of constraints. Nature Reviews Microbiology, 2(11), 886–897. 10.1038/nrmicro1023 [DOI] [PubMed] [Google Scholar]
- Raes, J. & Bork, P. (2008) Molecular eco‐systems biology: towards an understanding of community function. Nature Reviews Microbiology, 6, 693–699. 10.1038/nrmicro1935 [DOI] [PubMed] [Google Scholar]
- Salazar, G. , Paoli L., Alberti A., Huerta‐Cepas J., Ruscheweyh H.‐J., Cuenca M. et al. (2019) Gene expression changes and community turnover differentially shape the global ocean metatranscriptome. Cell, 179(5), 1068–1083.e21. 10.1016/j.cell.2019.10.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, J.M. , Otokuni, H. , Akutsu, T. & Nacher, J.C. (2019) Probabilistic controllability approach to metabolic fluxes in normal and cancer tissues. Nature Communications, 10, 1–9. 10.1038/s41467-019-10616-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S.R. , Dupont C.L., McCarthy J.K., Broddrick J.T., Oborník M., Horák A. et al. (2019) Evolution and regulation of nitrogen flux through compartmentalized metabolic networks in a marine diatom. Nature Communications, 10(1), 4552. 10.1038/s41467-019-12407-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sunagawa, S. , Acinas S.G., Bork P., Bowler C., Eveillard D., Gorsky G., (2020) Tara Oceans: towards global ocean ecosystems biology. Nature Reviews Microbiology, 18(8), 428–445. 10.1038/s41579-020-0364-5 [DOI] [PubMed] [Google Scholar]
- Thiele, I. & Palsson, B.Ø. (2010) A protocol for generating a high‐quality genome‐scale metabolic reconstruction. Nature Protocols, 5, 93–121. 10.1038/nprot.2009.203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thuiller, W. , Albert, C.H. , Dubuis, A. , Randin, C. & Guisan, A. (2010) Variation in habitat suitability does not always relate to variation in species’ plant functional traits. Biology Letters, 6(1), 120–123. 10.1098/rsbl.2009.0669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varma, A. & Palsson, B.O. (1994) Metabolic flux balancing: basic concepts, scientific and practical use. Nature Biotechnology, 12, 994–998. 10.1038/nbt1094-994 [DOI] [Google Scholar]
- Vernette, C. , Henry N., Lecubin J., Vargas C., Hingamp P., Lescot M. et al. (2021) The Ocean barcode atlas: a web service to explore the biodiversity and biogeography of marine organisms. Molecular Ecology Resources, 21(4), 1347–1358. 10.1111/1755-0998.13322 [DOI] [PubMed] [Google Scholar]
- Zelezniak, A. , Andrejev S., Ponomarova O., Mende D.R., Bork P. & Patil K.R. (2015) Metabolic dependencies drive species co‐occurrence in diverse microbial communities. Proceedings of the National Academy of Sciences, 112(20), 6449–6454. 10.1073/pnas.1421834112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziegler, G.M. (1995) Faces of polytopes. In: Ziegler, G.M. (Ed.) Lectures on polytopes: updated seventh printing of the first edition, Graduate Texts in Mathematics. New York, NY: Springer, pp. 51–76. 10.1007/978-1-4613-8431-1_2 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1
Data Availability Statement
The source code for the metabolic niche computation is available at https://gitlab.univ‐nantes.fr/aregimbeau/metabolic‐niche. Metabolic networks used in this study can be found on BiGG database (http://bigg.ucsd.edu/) and on Github (https://github.com/cdanielmachado/embl_gems). Data and codes can be found on Zenodo: https://doi.org/10.5281/zenodo.5780029.
The code and data used in this article is on Zenodo (https://doi.org/10.5281/zenodo.5780029).


