Alignment and Integration of Spatial Transcriptomics Data

Abstract

Spatial transcriptomics (ST) measures mRNA expression across thousands of spots from a tissue slice while recording the 2D coordinates of each spot. We introduce Probabilistic Alignment of ST Experiments (PASTE), a method to align and integrate ST data from multiple adjacent tissue slices. PASTE computes pairwise alignments of slices using an optimal transport formulation that models both transcriptional similarity and physical distances between spots. PASTE further combines pairwise alignments to construct a stacked 3D alignment of a tissue. Alternatively, PASTE can integrate multiple ST slices into a single consensus slice. We show that PASTE accurately aligns spots across adjacent slices in both simulated and real ST data, demonstrating the advantages of using both transcriptional similarity and spatial information. We further show that the PASTE integrated slice improves the identification of cell types and differentially expressed genes, compared to existing approaches that either analyze single ST slices or ignore spatial information.

1. Introduction

Spatial transcriptomics (ST) measures mRNA expression in tissues while preserving spatial information [35]. ST involves placing a thin slice of tissue on an array covered by a grid of barcoded spots and sequencing the mRNAs of cells within the spots (Figure 1a). Early ST technologies [35] measured mRNA in up to 1000 spots, each spot containing 10 – 200 cells, while the latest technologies such as the Visium technology from 10X Genomics [1] measure up to 5000 spots, each spot containing approximately 1–30 cells [44]. ST has been used to study cancer tissue (e.g. breast [35], prostate [7], melanoma [39], pancreas [32], carcinoma [21]), diseased tissues (e.g. Alzheimer’s [11] and gingivitis [26]) and healthy tissues (e.g. mouse olfactory bulb [35], human heart [5], spinal cord [28], and brain [31]), as well as other applications. Multiple computational methods have been introduced to analyze ST data, including the identification of spatial patterns of gene expression [35, 25], spatially distributed differentially expressed genes [38, 7, 4] and spatial cell-cell communication patterns [4, 10]. In addition to the ST technology, other technologies that measure gene expression along with spatial locations in tissues include smFISH [22], seqFISH+ [15], STARmap [42], and Slide-Seq2 [36].

Figure 1: Alignment and integration of spatial transcriptomics slices with PASTE.

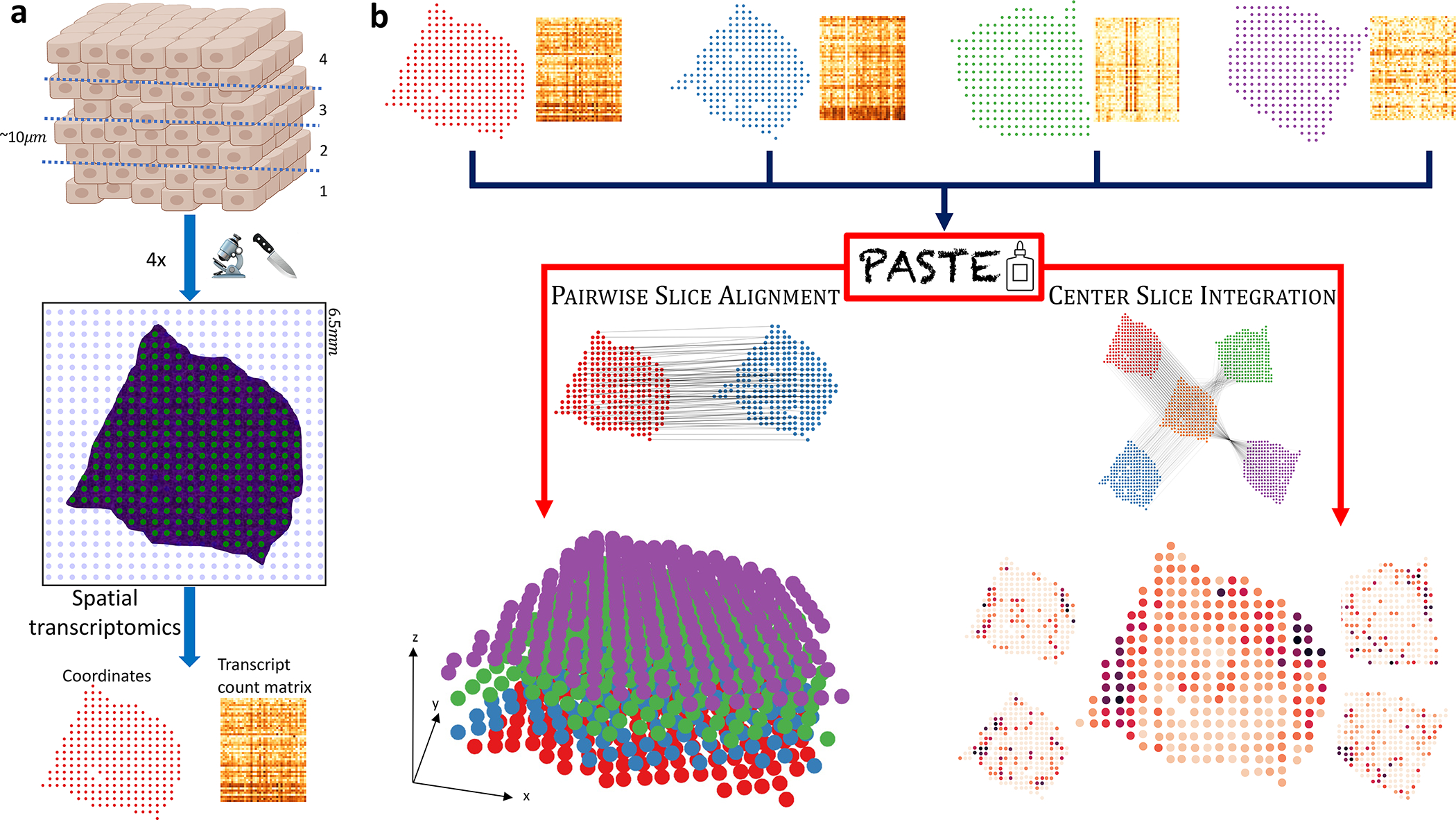
(a) Each slice generated for an ST experiment is placed on a 2D grid of barcoded spots, and mRNA expression of each spot is measured along with the spatial coordinates of each spot. Only a fraction of spots (green) contain tissue cells, with other spots (blue) not covered by a tissue. This results in a transcript count matrix for the tissue spots together with their spatial coordinates. (b) PASTE takes as input multiple ST slices consisting of spot expression matrices and spot spatial locations. In PAIRWISE SLICE ALIGNMENT mode, PASTE finds an optimal mapping between spots in one slice and spots in another slice while preserving the gene expression and the spatial distances of mapped spots. These mappings can then be used to reconstruct a stacked 3D alignment of the tissue by stacking slices on top of each other. In CENTER SLICE INTEGRATION mode, PASTE infers a “center” slice consisting of a low rank expression matrix and a collection of mappings from the spots of the center slice to the spots of each input slice. The inferred center slice generally has lower sparsity and lower variance than the individual ST slices.

While many ST studies generate data from multiple adjacent tissue slices, nearly all current ST analysis techniques either analyze single slices [32, 13] or pool gene expression data across slices without considering the spatial coordinates [7, 21]. However, since the number of unique molecular identifiers (UMIs) per spot is relatively small (≈ 5000), analysis of individual slices has lower power to detect lowly expressed transcripts that vary across space. One recently developed software package named STUtility [6] aligns histological images that sometimes accompany ST experiments by identifying transformations of the images that match the tissue edges. However, STUtility does not consider the gene expression data or locations of spots but relies on the availability of histological images, and depending on the topology of the tissue, STUtility may fail to automatically align images. More importantly, STUtility does not output a mapping between spots that can be used for downstream analysis. Another method named Splotch [2], aligns spatial transcriptomics data from multiple sections, but was designed for older ST platforms and requires prior manual annotation of spots based on their tissue context – information that is often not available.

The advantages of integrating data from multiple experiments has been demonstrated repeatedly for single-cell assays, and multiple methods have been introduced to integrate data from scRNA-seq, ATAC-seq, etc. [19, 37, 20, 27, 12, 41]. While these methods could be applied to ST data by ignoring the spatial coordinates of the spots, spatial information provides a rigid structure to ST data and cannot simply be treated as additional features. Moreover, due to differences in the dissection of the tissue slices and their placement on the array, spatial coordinates themselves cannot be easily compared across slices. Therefore, integration of ST data by incorporating both gene expression and spatial data is nontrivial.

We introduce PASTE (Probabilistic Alignment of ST Experiments), a method to align and integrate spatially resolved transcriptomics data from multiple tissue slices using information from both gene expression and spatial coordinates. PASTE computes probabilistic pairwise alignment of adjacent slices based on transcriptional and spatial similarity using Fused Gromov-Wasserstein Optimal Transport (FGW-OT) [40]. Thus, PASTE removes the need to physically align the tissue slices on the array and does not rely on additional histological images to perform the alignment. PASTE also combines these pairwise alignments from multiple adjacent slices into a stacked 3D alignment of a tissue. In a second mode, PASTE integrates multiple ST slices into a single “center”, or consensus, slice that preserves both expression and spatial information using a FGW-OT Barycenter formulation [40] and Non-negative Matrix Factorization (NMF) [24]. This center slice has the potential to increase the power of downstream analysis relative to independent analysis of individual slices.

We demonstrate the advantages of PASTE on both simulated ST datasets and recently published datasets of squamous cell carcinoma (SCC) [21] and human dorsolateral prefrontal cortex (DLPFC) [31]. We show on simulated data that PASTE accurately aligns spots across slices and recovers gene expression patterns of the tissue. On both the SCC dataset and the DLPFC dataset the pairwise alignments and stacked 3D alignment generated by PASTE preserve the spatial relationships between annotated regions, in comparison to methods that align slices based solely on similarity of expression or similarity of histological images. We demonstrate PASTE’s integrated slice enables the derivation of more spatially coherent gene expression clusters on the SCC data and more accurate clustering results on the DLPFC data. Finally, we show on the DLPFC data that the PASTE integrated slice recovers known marker genes in an unsupervised manner and outperforms scRNA-seq integration methods that do not utilize spatial information.

2. Results

2.1. PASTE Algorithm

The PASTE algorithm analyzes multiple slices of spatial transcriptomics (ST) data from the same tissue using two modes: Pairwise Slice Alignment and Center Slice Integration (Figure 1b). In Pairwise Slice Alignment mode, PASTE finds a mapping between spots in a pair of slices that preserves similarity of expression and physical distances between aligned spots. In CENTER SLICE INTEGRATION mode PASTE integrates multiple ST slices into a single center slice that is similar to the individual slices in both gene expression and spatial relationships between spots.

In Pairwise Slice Alignment, PASTE finds an optimal probabilistic (or fractional) mapping Π between spots in one slice and spots in another slice that minimizes both the transcriptional dissimilarity between aligned spots from different slices and the difference in spatial distance between pairs of aligned spots from the same slice (Supplementary Figure S1a and Methods Section M1.1.1). Importantly, the optimal mapping Π is not in general a one-to-one matching between spots in the two slices. Such a matching of the spots is neither always feasible nor desirable since the number of spots and their locations in the tissue may vary by slice, and the placement of the tissue with respect to the fixed position of the spots on the array usually varies across slices. Furthermore, a fractional mapping represents a spot in one slice as a combination of spots in the other slice, implicitly accounting for the situation where a spot is a mixture of different cell types.

Briefly, PASTE computes a probabilistic mapping Π = [π_ij] between spots in the two slices with the following properties:

1. If spot i in one slice is mapped to spot j in the other slice with a high weight π_ij, then the expression profile x_·i of spot i is similar to the expression profile $x_{\cdot j}^{\prime }$ of spot j.

2. If a pair (i, k) of spots in one slice is mapped to a pair (j, l) of spots in the other slice with high weights π_ij and π_kl, then the spatial distance d_ik between spots i and k in the first slice is close to the spatial distance $d_{jl}^{\prime }$ between spot j and l in the second slice.

PASTE computes Pairwise Slice Alignment using Fused Gromov-Wasserstein Optimal Transport [40], with a hyper-parameter α that controls the relative contributions of transcriptional dissimilarity and spatial distances among aligned spots (Equation 1). The value α = 0 computes an alignment using only transcriptional information and ignoring spatial locations, while the α = 1 corresponds to ignoring transcriptional information and using only the spatial coordinates. PASTE also combines pairwise alignments from multiple adjacent tissue slices into a stacked 3D alignment of a tissue (Figure 1b). We obtain this reconstructions by translating the spatial coordinates using a generalized Procrustes analysis (Methods Section M1.1.1 and Supplementary Section S1.1).

In Center Slice Integration, PASTE integrates multiple ST slices into a single center slice that has a low-rank transcript count matrix and high similarity to the individual slices in both gene expression and spatial relationships between spots. The motivation for CENTER SLICE INTEGRATION is to overcome variability in individual slices due to varying sequencing coverage, tissue dissection, or tissue placement on the array. Notably, in many current ST datasets the thickness of each tissue slice (10–20 microns) is smaller than the diameter of spots (100 microns in ST and 55 microns in Visium) and the spacing between spots (100–200 microns). With such datasets, the advantages of multi-slice integration – e.g. increasing power of downstream analysis by combining signal across slices – may outweigh the disadvantage of not obtaining a stacked 3D alignment.

PASTE computes the Center Slice Integration by combining a fused Gromov-Wasserstein barycenter [40] with Non-Negative Matrix Factorization (NMF) [24]. Similar to the fused Gromov-Wasserstein barycenter problem we seek to find a center ST slice that minimizes the weighted sum of distances to a given set of input ST slices, where the distance between slices is calculate by the minimum value of the Pairwise Slice Alignment objective across all mappings (Supplementary Figure S1b). We include an additional requirement that the consensus gene expression matrix is non-negative and low rank. We use NMF because the technique has been shown to be useful dimensionality reduction technique in single-cell RNAseq analysis, particularly using a Poisson likelihood model that accounts for missing values (“dropouts”) [34, 45, 14]. We compute the Center Slice Integration using a Block Coordinate Descent algorithm (Methods Section M1.1.2 and Supplementary Section S1.2).

2.2. Evaluation on Simulated Spatial Transcriptomics Data

We first evaluated PASTE on simulated ST data generated by resampling ST data from a slice of a breast tumor [35] (Extended Data Figure 1). Specifically, we generated simulated ST slices by rotating the locations of the spots and re-sampling the read counts after adding a pseudo-count of δ reads to each gene in each spot (Methods Section M1.2). We measured the accuracy of a mapping as the sum of probabilistic alignment weights π_ij over all pairs (i, j) of spots in the true alignment.

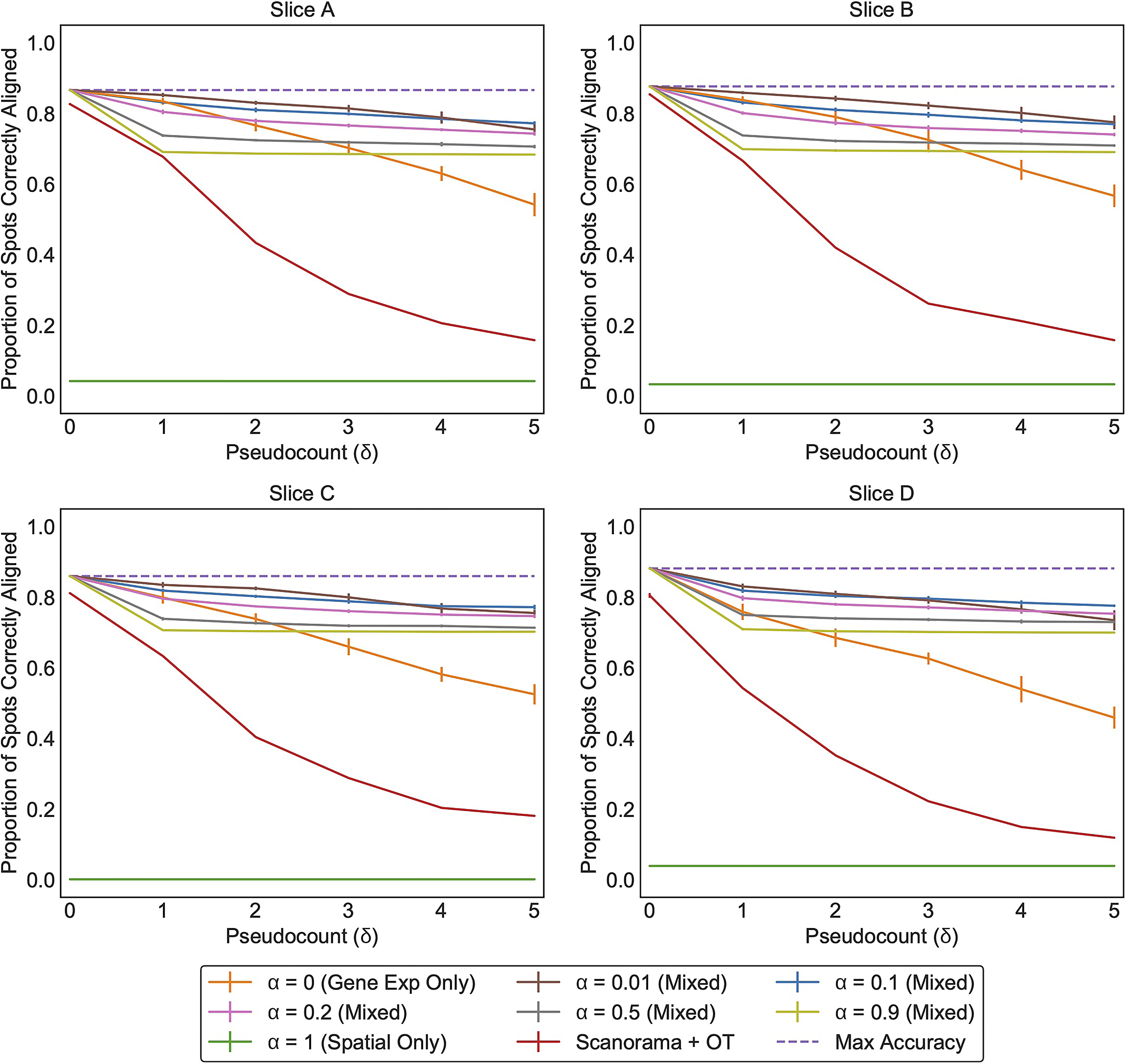
We observe that PASTE achieves highest accuracy in Pairwise Slice Alignment when using both gene expression and spatial information (α = 0.1), compared to the alignment computed using either expression information alone (α = 0) or spatial information alone (α = 1) (Figure 2a and Extended Data Figure 2). PASTE (α = 0.1) achieves the highest possible accuracy (a perfect alignment corresponds to ≈ 86% of spots aligned since the number of populated spots in each slice are not identical) for values of the pseudocount parameter δ ≈ 0.1–0.2 that corresponds to variability in read counts observed in real data (Supplementary Figure S2). Even for substantially larger values of δ > 4, PASTE correctly aligns > 73% of spots. Moreover, the performance of PASTE is robust across intermediate values of 0 < α < 1 (Extended Data Figure 2), and the mappings produced by PASTE are sparse, with a spot in the first slice mapped (π_ij > 0) to an average of 1.86 spots in the other slice (Supplementary Figure S3). In contrast, using only spatial data (α = 1), PASTE does not recover any matched pair of spots, demonstrating that the rotation used in generating the simulated slice provides a challenging spatial perturbation. On the other hand, using only gene expression (α = 0) to match spots, the accuracy of the alignment decays more quickly as the pseudocount δ increases. We also compared PASTE to a mapping obtained by applying optimal transport to integrated expression matrices obtained from the single-cell RNA-seq integration method Scanorama [20] (Supplementary Section S2.1.1). We found that PASTE had consistently higher accuracy (Extended Data Figure 2) demonstrating the advantages of PASTE’s use of both expression and spatial information when computing a pairwise alignment.

Figure 2: PASTE results on simulated ST slices from a breast cancer ST slice from [35].

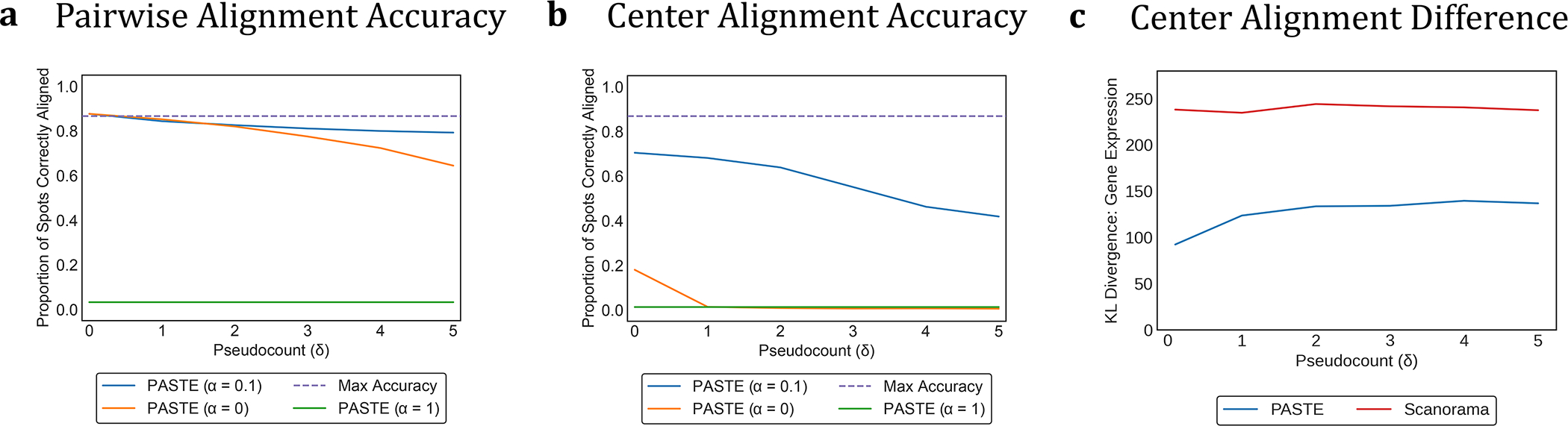
(a) Average percentage of spots correctly aligned by PASTE in PAIRWISE SLICE ALIGNMENT mode using α = 0 (gene expression data only), α = 1 (spatial information only), and α = 0.1 (both) as a function of the added pseudocount δ. The dotted line represents the maximum possible accuracy. (b) Average percentage of spots correctly aligned by PASTE in CENTER SLICE INTEGRATION mode between the original center slice and the simulated slices. (c) Difference between the gene expression matrix of the true center slice and the gene expression matrix inferred by PASTE and by Scanorama.

For Center Slice Integration, we find that PASTE has both high accuracy in mapping spots and low reconstruction error for the true expression matrix. PASTE (α = 0.1) correctly aligns 58 – 72 % of spots (compared to maximum possible accuracy of 86%) even with large values of pseudocount δ (Figure 2b and Supplementary Figure S5). In contrast, performing Center Slice Integration using only gene expression data (α = 0) or only spatial data (α = 1) performed poorly across all simulations with accuracy dropping below 3%.

Finally, we compared the integrated expression matrix computed by PASTE to integrated expression matrices computed by Scanorama [20], a single cell RNA-seq integration method (Supplementary Section S2.1.1). We find that PASTE infers a center slice expression matrix that is much closer to truth than the integrated gene expression matrices from Scanorama (Figure 2c and Supplementary Figure S6). We note that the Scanorama results are an upper bound on Scanorama’s performance since we compared the expression of spots using the true correspondence between slices. At the same time, Scanorama was not designed to utilize spatial data, and so the better performance of PASTE does not indicate a deficiency of Scanorama in solving the scRNA-seq integration problem for which it was designed.

2.3. Spatial transcriptomics of Squamous Cell Carcinoma

We applied PASTE to analyze ST datasets from four patients with cutaneous squamous cell carcinoma (SCC) [21]. For each patient there are three slices of ST data, with each slice containing ≈ 600 – 700 tissue spots. [21] applied independent component analysis to cluster the spots jointly across all three slices from each patient, an approach that utilizes only gene expression information and ignores the spatial locations of spots.

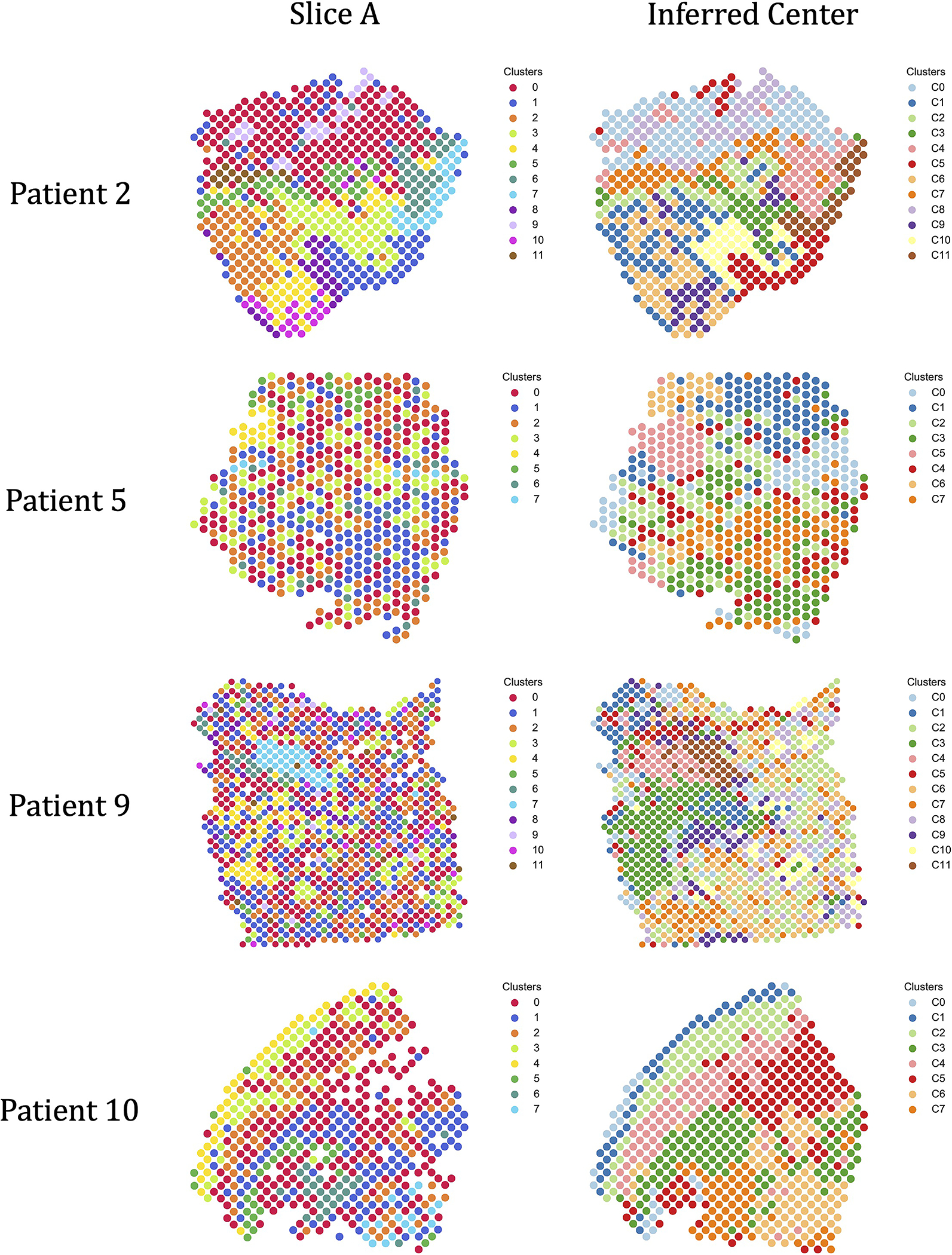
We first used PASTE to compute a Pairwise Slice Alignment of adjacent tissue slices. Although PASTE allows fractional mappings, we found that each spot in one slice mapped to an average of 1.7–2.1 spots in the adjacent slice (Supplementary Figure S3). We calculated the accuracy of the PASTE alignment as the fraction ${\sum }_{i,j;\ell (i)=\ell (j)}{\pi }_{ij}$ of pairs of aligned spots that have the same cluster labels in [21], relying on the hypothesis that aligned spots from adjacent slices are more likely to contain the same cell types and thus have similar expression (Methods Section M1.3.1). Interestingly, the four patients exhibited substantial variability in the agreement of cluster labels across PASTE aligned spots: for patient 2 approximately 70% of the spots in one slice aligned to spots in the adjacent slice having the same cluster label, but for patients 5, 9, 10 only 20%−50% of aligned spots had the same cluster labels (Figure 3a). This difference may be due to intrinsic differences in the spatial homogeneity of tumors, and indeed patient 2 does exhibit high spatial homogeneity of cluster labels within a single slice (Figure 3b) or across adjacent slices from the stacked 3D alignment derived by PASTE (Figure 3c). In contrast, the other three patients exhibit lower spatial homogeneity within a tissue slice or across stacked 3D alignments (Figure 3d and e, and Supplementary Figure S7).

Figure 3: PASTE Pairwise Slice Alignment of squamous cell carcinoma (SCC) [21].

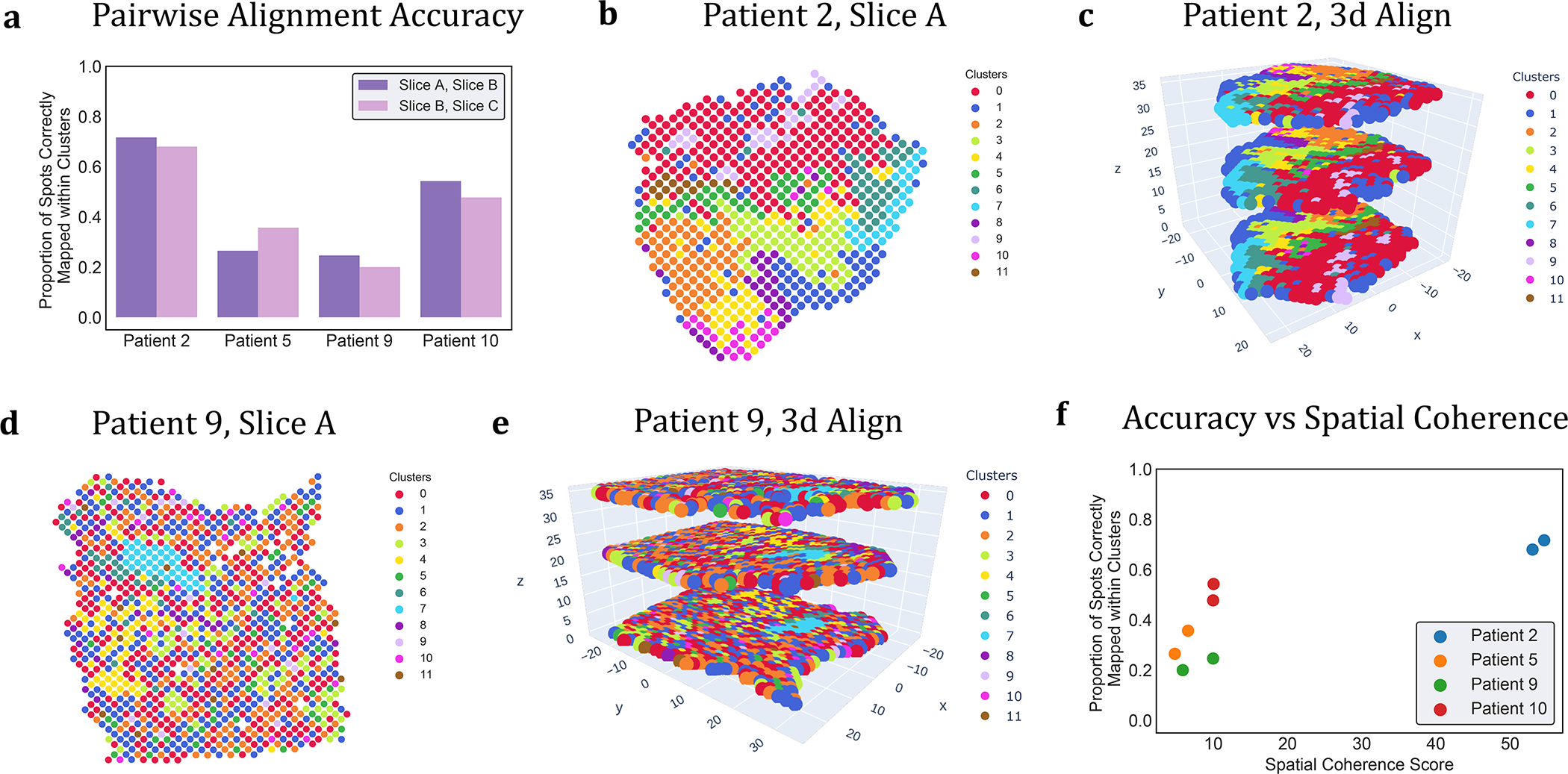
(a) Percentage of aligned spots from PASTE pairwise alignments of adjacent slices that have the same published cluster label from [21]. (b) Published cluster labels of spots in slice A of patient 2 have moderate spatial coherence. (c) Stacked 3D alignment of SCC tumor from patient 2 produced by PASTE using pairwise alignments of adjacent slices. Slices are colored according to published cluster labels. (d) Published cluster labels of spots in slice A of patient 9 have lower spatial coherence. (e) Stacked 3D alignment of SCC tumor from patient 9. (f) Percentage of aligned spots with same cluster label is larger for slices with higher spatial coherence score.

To quantify the observed differences in spatial coherence of clusters in different patients, we derived a spatial coherence score based O’Neill’s spatial entropy [33] (Method Section M1.3.2). This score measures the fraction of neighboring spots having the same cluster label compared to random assignments of cluster labels; higher spatial coherence scores indicate that neighboring spots tend to have the same cluster label. We find that patient 2 has substantially higher spatial coherence scores than the other 3 patients, quantifying the observation that the cluster labels in patient 2 are the most spatially coherent (Figure 3f).

While the observed heterogeneity and lower spatial coherence scores for patients 5, 9 and 10 suggest that these tumors have less spatially coherent tumors, there is an important confounding variable in this data. Namely, the slices from patient 2 were sequenced with more than two-fold higher sequence coverage than patients 5, 9, and 10. Thus, the observed difference in spatial heterogeneity could be an artifact of differences in sequence coverage. To further investigate the effect of the sequence coverage on the spatial coherence of gene expression clusters and the alignment accuracy, we downsampled UMIs from the ST slices of the highest coverage patient 2. We found that lower UMIs are associated with lower spatial coherence score and lower proportion of spots mapped to the same cluster (Supplementary Figure S9 and Supplementary Section S2.2.1). These results support the hypothesis that the lower spatial coherence scores observed in patients 5, 9, and 10 are likely due to lower sequence coverage.

To further evaluate the issue of low coverage in individual ST slices, we used the Center Slice Integration mode of PASTE to infer a single center slice that integrates data from the multiple ST slices for each SCC patient. We clustered the spots in the inferred center slice expression matrix using the low dimensional representation given by PASTE, using the same number of clusters as the the published analysis of each patient [21] (Methods Section M1.3.3). We find that for all patients the clusters obtained using the center slice computed by PASTE have higher spatial coherence scores than the spatial coherence scores of the published clusters (Figure 4a and Extended Data Figure 3). Moreover, we see that the improvement in spatial coherence score is greatest in patients 5, 9, and 10 that have lower coverage ST data. For example, we observe that the published cluster labels for slice A of patient 5 (spatial coherence score = 2.55) do not display much cluster coherence (Figure 4b), while the cluster labels obtained from PASTE (spatial coherence score = 33.45) are visually much more spatially coherent (Figure 4c). We obtain similar results of higher spatial coherence for the center slice inferred by PASTE using 10X Genomics Visium spatial transcriptomics data from an additional SCC patient from [21] (Supplementary Section S2.2.2 and Supplementary Figure S10). While it is not surprising that the integrated center slices from PASTE have higher spatial coherence scores than clusters derived using only expression data, we emphasize that PASTE uses the spatial information across slices, which is not as strong of a spatial prior as employed by methods that “smooth” expression across neighboring spots within one slice.

Figure 4: PASTE Center Slice Integration of SCC tumor [21] into a center slice.

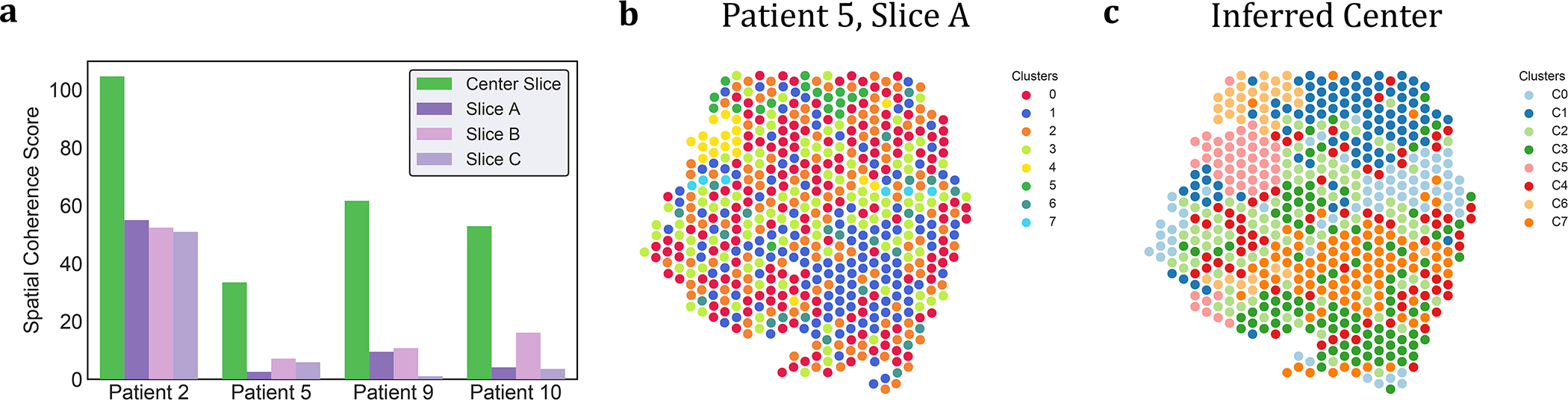
(a) Spatial coherence scores for the clusters obtained from the center slice inferred by PASTE (green) and for the published clusters from [21] on the individual slices from each patient (purple and pink). (b) Published cluster labels of spots in slice A of patient 5. (c) Cluster labels C₁, . . . , C₇ of spots obtained from PASTE’s inferred center slice for patient 5.

We also applied PASTE to two other ST datasets in order to evaluate the performance of PASTE on tissues with different spatial organization. We found that PASTE successfully aligned ST data from spinal cord [29], a tissue with a symmetric spatial organization (Supplementary Section S2.3). We also found that PASTE identified small spatial structures, including a small subset of four cancer spots in ST data from Her2 breast cancer [3] (Supplementary Section S2.4 and Extended Data Figure 4). These results demonstrate that PASTE is able to handle tissues with varying spatial organization and that integration of multiple ST slices can recover subtle gene expression patterns that are not apparent in coverage sequencing of individual slices.

2.4. Spatial Transcriptomics of Human Dorsolateral Prefrontal Cortex Data

We applied PASTE to analyze 10X Genomics Visium spatial transcriptomics data from the human dorsolateral prefrontal cortex (DLPFC) tissues from 3 individuals [31]. This dataset consists of 4 tissue slices (labeled A, B, C and D) for each individual (labeled I, II and III) (Figure 5a). In every individual, the first pair AB of slices and the last pair CD of slices are directly adjacent (10μm apart), while the middle pair BC of slices is located 300μm apart (Extended Data Figure 5). Maynard et al. [31] used a supervised approach to annotate the spots as white matter or one of six neocortical layers, and also used a supervised approach to identify differentially expressed genes between the annotated layers. In particular, they used known marker genes to cluster the spots and used a “pseudo-bulk” approach to identify differentially expressed genes by summing the UMI counts for a gene across all spots annotated with same layer in a tissue slice.

Figure 5: PASTE pairwise alignment and stacked 3D alignment of DLPFC sample III.

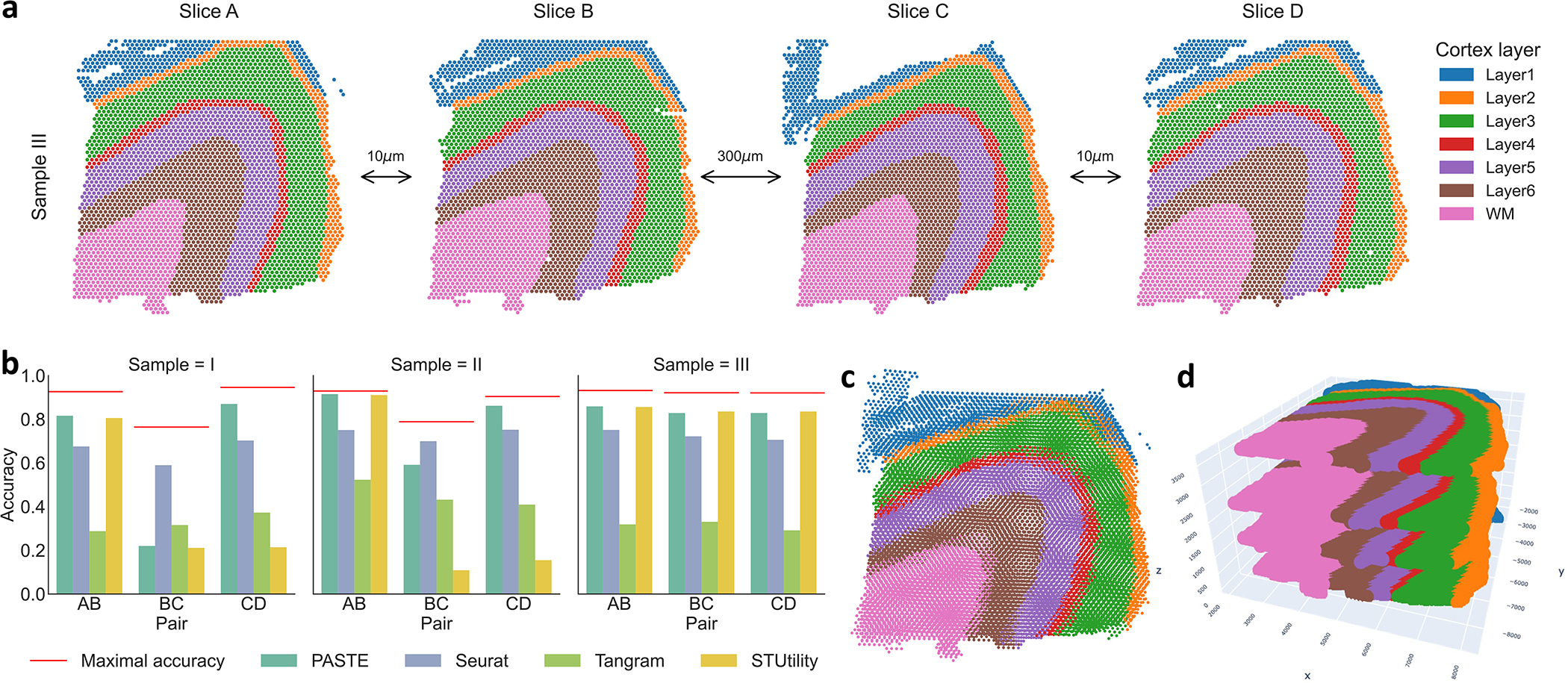
(a) One sample of DLPFC with four slices labeled A,B,C and D, with spots colored according to the manual annotations from [31]. The first pair (AB) and last pair (CD) of slices are adjacent (10μm) while the middle pair (BC) are further apart (300μm). Spots in each slice are colored according to the the annotation from [31] that classifies spots into six neocortical layers and white matter. (b) Accuracy of pairwise alignment of consecutive DLPFC slices (labeled AB, BC, and CD) for PASTE, Seurat, Tangram and STUtility. Accuracy is computed from the published annotation of each spot. Red line marks the maximal possible accuracy given the number of spots in each layer in the two slices. (c) Stacking four ST slices of DLPFC sample III using coordinates from PASTE pairwise alignments. (d) Stacked 3D alignment of the four tissue slices of DLPFC sample III after alignment with PASTE. The z-axis is not to scale.

We first used PASTE to compute a Pairwise Slice Alignment of each pair of consecutive slices from the same sample. We compared the pairwise alignments obtained by PASTE to three existing approaches: Seurat [37], a method that aligns scRNA-seq data by selecting “anchors” between datasets; Tangram [8], a method that aligns scRNA-seq data onto ST data; and STUtility [6], a method that aligns H&E stained images of ST tissue slices (Methods Section M1.4.1). We emphasize that none of these methods directly solve the pairwise alignment problem solved by PASTE as neither Tangram nor Seurat use spatial information when performing the alignment, while STUtility relies exclusively on the H&E stained images for alignment and does not consider the gene expression at each spot. We measured the quality of an alignment by calculating the accuracy ${\sum }_{i,j;\ell (i)=\ell (j)}{\pi }_{ij}$ as the fraction of spots belonging to the same annotated layer across slices (Methods Section M1.3.1).

We find that PASTE achieves the highest alignment accuracy in 5 of the 9 pairwise alignments, attaining high accuracy (> 81%) of the close pairs (AB and CD) of slices that are 10μm apart but lower accuracy (21%, 59% and 82%) for the middle pair BC of slices that are 300μm apart (Figure 5b). Seurat has the highest accuracy on two of the middle BC slice pairs that are far apart in space, but lower accuracy than PASTE on the other 7 pairs. Closer examination of the results for these two middle pairs shows that PASTE better preserves the spatial relationship between aligned spots in comparison to the expression-only integration methods (Extended Data Figure 6); however these widely separated slices have only modest consistency in layer structure as seen most clearly by the different size of layer 3 in the upper right corner of the two slices (Extended Data Figure 5). Tangram achieves a relatively low accuracy (0.28–0.53) on all slice pairs, slightly outperforming PASTE only on one middle BC slice pair. STUtility, which is based only on the spatial features of the H&E stained images, has marginally better accuracy (0.007 difference) than PASTE on 2 slice pairs but substantially worse accuracy (0.66 – 0.71 difference) on 2 slice pairs. Similar to PASTE, STUtilty also tends to preserve relationships between neighboring spots in its alignments. However, by not using the transcriptional information, STUtility is prone to subtle differences that are not apparent from the images. For instance, when aligning slices C and D of Sample I, STUtility actually mirrored the image and spot coordinates, resulting in low accuracy (Supplementary Figure S14). These results show that PASTE’s use of both transcriptional information and spatial information to align spatial transcriptomics data is often superior to using only transcriptional information or only spatial information.

To further demonstrate the advantages of PASTE we used the pairwise alignment between consecutive slices to reconstruct a stacked 3D alignment of each sample (Figure 5c and d). We found that translating the spatial coordinates using PASTE gives qualitatively better positioning of the neocortical layers on top of each other (Supplementary Figures S15, S16 and S17).

We leveraged the available annotations in the DLPFC dataset to evaluate the effect of parameter values on the alignment accuracy of PASTE. We found that PASTE’s performance varied slightly for intermediate values of 0 < α < 1 (Supplementary Section S2.5.1). Further, we found that running PASTE using all genes and with KL divergence as the expression dissimilarity gave better results than using log-transformed normalized expression and highly variable genes (Supplementary Section S2.5.2 and Extended Data Figure 7). Finally, we evaluated different weighting of spots and saw only minor differences in alignment when using weights derived from the estimated number of cells per spot compared to equal weights for all spots (Supplementary Section S2.5.3).

We next performed Center Slice Integration with PASTE on sample III – whose slices exhibited the greatest pairwise similarity – to examine the advantages of multi-slice integration for clustering of spots and identification of differentially expressed genes across neocortical layers. We compared gene expression clusters obtained from the center slice produced by PASTE to clusters from the semi-supervised analysis of Maynard et al. [31], to clusters obtained by analyzing each slice independently, and clusters inferred by the single cell RNA-seq integration methods Scanorama [20] and Seurat [37]. [31] report low Adjusted Rand Indices (ARIs) of 0.2–0.4 by clustering spots in individual slices using supervised sets of known and inferred marker genes. We obtain similarly low ARIs (0.21–0.24) when clustering spots from single slices according to gene expression (Figure 6a, Supplementary Figure S24, Supplementary Table S4 and Methods Section M1.4.2). These poor results are likely due to the low UMI counts in individual spots. Integrating the gene expression using Scanorama and Seurat achieved similarly low ARIs of 0.16–0.18 and 0.24–0.31, respectively (Supplementary Table S4 and Supplementary Figure S25). The problem of low UMI counts in individual slices is especially apparent when analyzing differential expression of individual marker genes. For example, marker genes MFGE8, MOBP and PCP4 show sparse expression patterns in individual slices (Figure 6b and Supplementary Figures S26a, S27a and S25) and weak difference in expression between neocortical layers (Figure 6c and Supplementary Figures S26b, S27b and S25).

Figure 6: PASTE center alignment of DLPFC sample III improves identification of layers and differentially expressed genes.

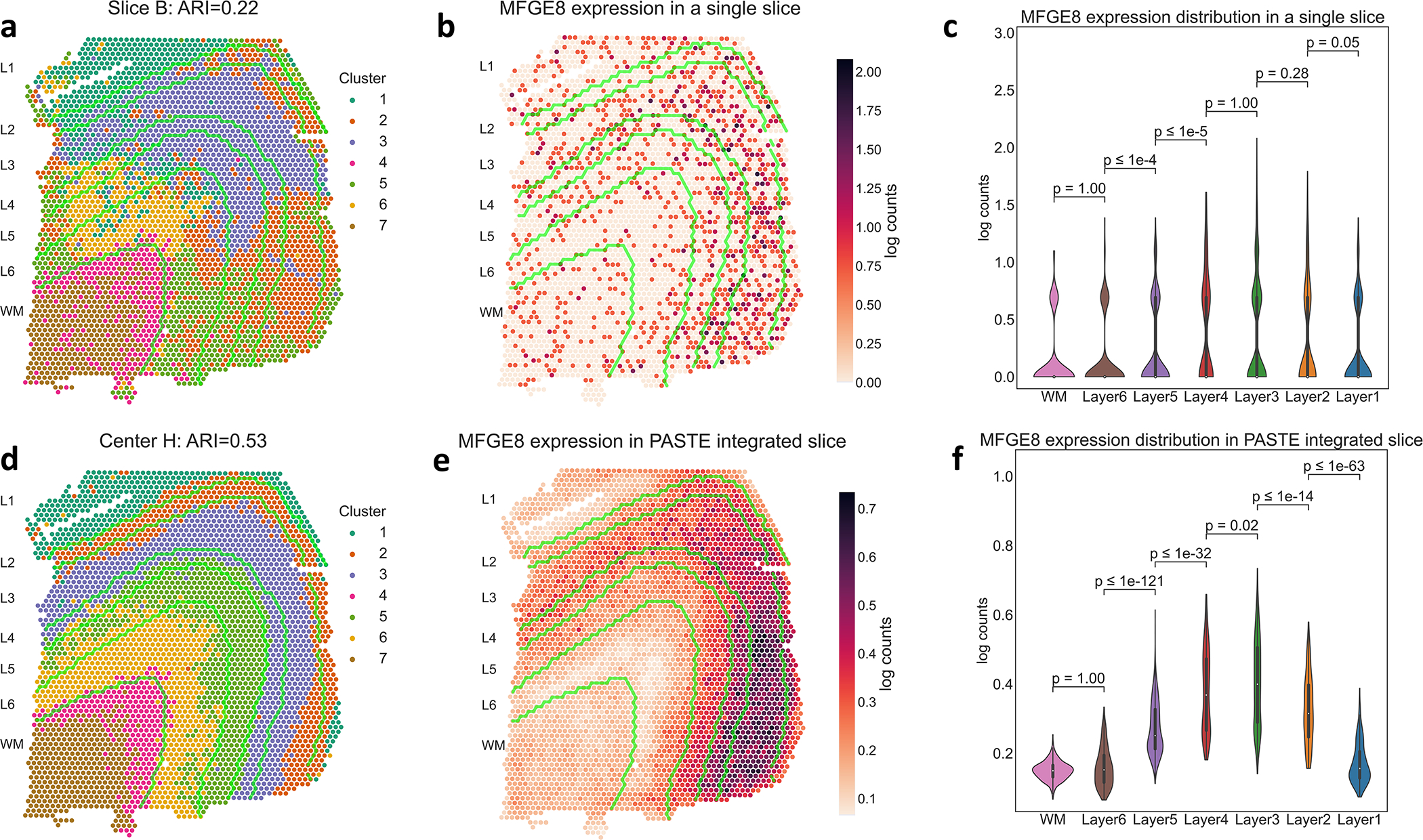
(a) Clustering of spots by gene expression in a single slice B shows low agreement (ARI = 0.22) with published layer labels, whose boundaries are marked by green curves. (b) Expression of the layer 3 marker gene MFGE8 in slice B. (c) Distribution of MFGE8 expression in annotated layers of slice B. WM and Layers 6 to 1 have 625, 614, 621, 247, 924, 224 and 380 spots respectively. Inner boxplots show the 25%, 50% and 75% quantiles of the distributions. p-values (rounded to the closest power of 10) for the difference in distribution (two-sided Mann-Whitney U test) between adjacent layers are indicated. (d) Clustering of spots using the low dimensional representation of the integrated center slice by PASTE shows better agreement (ARI = 0.53) with published layer labels. (e) Expression of the layer 3 marker gene MFGE8 in PASTE integrated center slice. (f) Distribution of MFGE8 expression in center slice, with p-values as described in (c).

In contrast, clustering of spots in the PASTE center slice obtained a substantially better agreement (ARI = 0.53) to manually annotated layers ( Figure 6d, Methods Section M1.4.2) and clearer patterns of marker gene expression with subtle gradients of expression across neocortical layers (Figure 6e and f and Supplementary Figures S26 and S27). This observation is even more striking in lowly expressed genes such as the TRABD2A gene that was expressed in less than 5% of spots and was validated as a layer 5 marker gene using smFISH by [31] (Extended Data Figure 8). Thus, the integrated center slice shows a great improvement in clustering spots and identifying spatial patterns of marker gene expression compared to analysis of individual slices.

Finally, we found that layer-specific marker genes show stronger patterns of differential expression in the PASTE integrated center slice than in a single ST slice or in expression data obtained using one of the scRNA-seq integration methods. Specifically, we evaluated the list of marker genes from [31] that were previously annotated to be differentially expressed in subsets of layers (Methods Section M1.4.4). Using the PASTE integrated transcript count matrix, we identify 80 of the 126 marker genes as significantly differentially expressed (adj. p-val<0.01 Wilcoxon rank-sum test) in the corresponding subset of layers compared to the 44–58 marker genes that were differentially expressed when using the raw count data from any single ST slice (Supplementary Table S4). Furthermore, the set of known marker genes that are significantly differentially expressed in PASTE analysis contains almost all of the known marker genes identified by analyzing each slice separately (Supplementary Table S4 and Supplementary Figure S28). Although the scRNA-seq integration methods Seurat and Scanorama report a similar number of significantly differentially expressed marker genes (79 and 84 respectively), they recover fewer marker genes found by analysis of individual slices.

Known marker genes also have higher ranks in the integrated spatial transcriptomics data produced by PASTE compared to the analysis of Maynard et al. [31] and the scRNA-seq integration methods Scanorama and Seurat (Supplementary Table S4). Specifically, the median rank of known marker genes in the PASTE center slice is 427 while the analysis of Maynard et al. results in a median rank of 1147 and the scRNA-seq integration methods Scanorama and Seurat have median ranks of 3380.5 and 1852 respectively (Extended Data Figure 9). At the same time, the PASTE integrated slice recovered some known marker genes that were not significant in the pseudo-bulk approach used by [31]. For example, the layer 3 marker gene MFGE8 is differentially expressed in the PASTE center slice (adj. p-val< 10⁻⁴⁰, ranked 117 for layer 3), but not in the analysis of [31] (adj. p-val< 0.15, rank 912 for layer 3) (Figure 6). Therefore, using the PASTE integrated slice for differential expression analysis yields superior results to single slice analysis and comparable results to the supervised pseudo-bulking approach from [31] at individual spot level, but has the advantage of being unsupervised and not requiring prior knowledge of marker genes or spatial organization.

3. Discussion

We introduce PASTE (Probabilistic Alignment of ST Experiments), a method to align and integrate multiple ST datasets from the same tissue by leveraging both transcriptional similarity and spatial distances between spots across datasets. PASTE computes a Pairwise Slice Alignment of spots across adjacent ST slices and performs Center Slice Integration of multiple ST slices by finding a center slice with a low rank expression matrix and mappings of its spots to all other slices. The two modes of PASTE provide a tradeoff between generating 3D spatial information but with the same read coverage per spot vs. increasing the read coverage per spot in 2D. The choice of which of the two modes to use depend on the biological questions of interest.

We demonstrate some advantages of PASTE on simulated ST data and ST data from normal and cancer tissues. On ST data from squamous cell carcinoma, we show that the center slice inferred by PASTE has higher spatial coherence than published clusters that were inferred using only transcriptomic similarity across replicates and ignoring spatial coordinates of spots. We show that the low spatial coherence of published transcriptomic clusters in 3 of the 4 patients is likely a result of lower sequence coverage in these samples, as transcriptomic clusters obtained from the PASTE integrated expression matrix have higher spatial coherence in all patients. This result demonstrates that drawing conclusions about spatial organization of tissues based only on transcriptomic similarity requires caution and that leveraging the available spatial information – both within or across tissue slices – yields more robust results. PASTE analysis of spatial transcriptomics data from the human dorsolateral prefrontal cortex provides further evidence of the advantages of integrating data from multiple tissue slices. We show that clustering of spots in the PASTE integrated slice recapitulates the known tissue layers more accurately than clustering of a single slice, without manual selection of genes as in [31] and without explicitly modeling spatial cluster correlation as in [44]. Moreover, we show that differential expression analysis in the PASTE integrated slice recovers known maker genes in an unsupervised manner. In both tasks, PASTE outperforms methods that integrate datasets based only on scRNA-seq data.

We anticipate that the aligned and integrated ST slices produced by PASTE will increase the statistical power in multiple downstream analyses including: the identification of cell types [7], derivation of spatial expression patterns [35, 25], deconvolution of spots into multiple cells [44], classification of tumor vs. non-tumor spots [43], inference of cell-cell communication [4, 10], identification of genomic copy number aberrations [14], integration of spatial transcriptomics data with other single cell modalities [8], and more. Further, we expect that the stacked 3D spatial reconstructions obtained by PASTE will facilitate the extension of current methods for these downstream analysis tasks to utilize 3D spatial information.

There are multiple opportunities to improve and extend PASTE. First, PASTE does not use the histological images that often accompany spatial transcriptomics data. In contrast, a recent software package, STUtility [6], aligns the histological images without using the accompanying gene expression data and spot locations. We anticipate that PASTE could be further improved by utilizing the histological images and using methods from the field of image registration [9]. Moreover, newer versions of the 10X Genomics Visium platform measure protein immunofluorescence in conjunction to gene expression, providing another signal to be included in PASTE alignment and integration. Second, the running time of PASTE could be further improved to support future generations of ST techoology that have a larger number of spots. In particular, one can use GPUs to accelerate the optimal transport mapping calculation [16] or approximate the optimal transport maps using minibatches, or subsets, of the data [17]. Third, PASTE could be applied to ST experiments from different patients in order to find conserved spatial patterns of gene expression across different patients. However, this requires adapting the objective function optimized by PASTE to account for slices with considerable differences in spatial structure and cell composition. Fourth, while we applied PASTE to data from ST technology from 10X Genomics, we note that PASTE can also be applied to other spatial technologies such as smFISH [22], seqFISH+ [15], STARmap [42], and Slide-Seq2 [36]. Finally, it would be helpful to develop improved simulators of spatial transcriptomics data that model additional complications of real data such as the squeezing/stretching of the tissue. With the increasing proliferation of spatial transcriptomics technologies [30, 23], we anticipate that alignment and integration of replicate experiments will be an increasingly important part of spatial transcriptomics analysis.

M1. Methods

M1.1. PASTE Algorithm

M1.1.1. Pairwise Alignment of ST slices

The result of an ST experiment is a pair (X, Z) of matrices, where $X=\left[x_{ij}\right]\in {\mathbb{N}}^{p\times n}$ is a p genes by n spots transcript count matrix and $Z\in {ℝ}^{2\times n}$ is the coordinate matrix of the spots. That is, $x_{ij}\in \mathbb{N}$ is the transcript count for gene i in spot j and the column vector $z_{\cdot j}\in {ℝ}^2$ is the 2D coordinate vector of spot j on the array. Since the placement and orientation of the tissue on the array are arbitrary, we find it more convenient to represent only the relative location of the spots. Therefore, instead of the actual spots locations Z, we use the spot distance matrix $D\in {ℝ}_{+}^{n\times n}$, where d_ij = ∥z_·i − z_·j∥ is the spatial distance between spot i and spot j. While this transformation is not reversible, it has an advantage of being invariant to the translation or rotation of the tissue on the array.

In addition to the transcript count matrix X and distance matrix D, we assume that each tissue spot i has a weight g_i > 0 representing its relative importance compared to the other spots¹. These weights encode prior information on the spots such as the relative number of cells in the spot, the presence of a cell surface marker in the spot or an importance score of the spot based on pathological examination of the tissue. We assume these weights are normalized so ${\sum }_i{g}_i=1$ and thus g = (g₁, . . . , g_n) is a distribution over the spots. If no prior information is given on the spots, we use a uniform distribution $g=\frac{1}{n}{\mathbf{1}}_n$ over the spots, where 1_n denotes a column vector of length n containing all ones.

A spatial transcriptomics slice of n spots over p genes is described by a triplet (X, D, g) where $X\in {\mathbb{N}}^{p\times n}$ is a gene by spot transcript count matrix, $D\in {ℝ}_{+}^{n\times n}$ is the spot pairwise distance matrix and g is a distribution over spots. We call the column vector x_·i the expression profile of spot i. An expression cost function $c:{ℝ}_{+}^p\times {ℝ}_{+}^p\to {ℝ}_{+}$ is a function that measures a non negative cost between the expression profiles of two spots over all genes.

Let (X, D, g) and (X′, D′, g′) be two slices of n and n′ spots respectively over the same p genes. We say that a matrix $\mathrm{\Pi }=\left[{\pi }_{ij}\right]\in {ℝ}_{+}^{n\times n^{\prime }}$ is a mapping/alignment between the two slices provided ${\sum }_j{\pi }_{ij}=g_i$ for all spots i in the first slice and ${\sum }_i{\pi }_{ij}=g_j^{\prime }$ for all spots j in the second slice. We denote by Γ(g, g′) the set of all mappings between the two slices. We formulate the problem of aligning a pair of slices as follows.

Pairwise Slice Alignment Problem.

Given slices (X, D, g) and (X′, D′, g′) containing n and n′ spots respectively over the same p genes, an expression cost function c and a parameter 0 ≤ α ≤ 1, find a mapping Π ∈ Γ(g, g′) minimizing the following transport cost:

$$F\left(\mathrm{\Pi };X,D,X^{\prime },D^{\prime },c,\alpha \right)=(1-\alpha )\sum _{i,j}c(x_{\cdot i},x_{.j}^{\prime }){\pi }_{ij}+\alpha \sum _{i,j,k,l}{(d_{ik}-d_{jl}^{\prime })}^2{\pi }_{ij}{\pi }_{kl}.$$ (1)

Notably, the Pairwise Slice Alignment Problem is invariant to translation or rotation of the coordinates of any slice since the transport cost F depends only on spatial distances D and D′ within a slice and not on the absolute spatial coordinates.

We solve the Pairwise Slice Alignment Problem using the iterative conditional gradient algorithm described in [40] for the fused Gromov-Wasserstein optimal transport problem. This algorithm takes O(n²n′ + nn′2) operations per iteration.

From the solution to the Pairwise Slice Alignment Problem between multiple pairs of adjacent slices we reconstruct a stacked 3D spatial representation of tissue. Namely, given a series (X⁽¹⁾, D⁽¹⁾, g⁽¹⁾), . . . , (X^(t), D^(t), g^(t)) of sequential slices we find the mapping Π^(k) between adjacent slices k and k + 1 for k = 1, . . . , t – 1. To project all slices to the same spatial coordinate system we use the mappings Π^(k) to solve a generalized weighted Procrustes problem [1, 8] (Supplementary Section S1.1). That is, we seek to project the spatial coordinates Z^(k+1) of slice k + 1 to the spatial coordinates Z^(k) of slice k by finding a translation vector $\widehat{v}$ and rotation matrix $\widehat{R}$ that minimize the weighted distances between mapped spots (Supplementary Section S1.1). Formally, we solve

$$\widehat{R},\widehat{v}=\underset{\begin{array}{c}R\in {ℝ}^{2\times 2},v\in {ℝ}^2\\ R^{T}R=I\end{array}}{\min }\sum _{i,j}{\pi }_{ij}^{(k)}{\Vert z_{\cdot i}^{(k)}-R{z}_{\cdot j}^{(k+1)}-v\Vert }^2.$$ (2)

The projected spatial coordinates of spot j in slice k + 1 are then given by $\widehat{R}{z}_{\cdot j}^{(k+1)}+\widehat{v}$. To solve the weighted Procrustes problem given by Equation 2 we use SVD (Supplementary Section S1.1).

M1.1.2. Integration of Multiple ST Slices

We define the Center Slice Integration Problem under a few reasonable biological and computational assumptions. First, we assume that the given ST slices are very similar to each other and thus can be summarized with a single slice. This assumption is again motivated by the fact that the thickness of an ST slice is small relative to the diameter of a spot and the spacing between spots. Therefore, ST slices from the same tissue are often referred to as technical replicates [7, 32, 21]. Second, we assume that spatial coordinates and the distribution over spots in our center slice are known in advance, up to rotation or translation. This is a reasonable assumption since the spatial coordinates on the array are fixed by the technology. Finally, we assume that the expression matrix of the center slice is low rank. This is a widely used assumption in both in single cell RNA-seq analysis and ST analysis and corresponds to the biological assumption that cells/spots often occupy a limited number of cell types or cell states [59, 63, 55]. In addition, in most ST experiments, the number of ST slices per tissue is small (2–4) and the gene expression matrices are sparse (≥75% zeros), and thus estimation of a full rank gene expression matrix is prone to overfitting.

Center Slice Integration Problem.

Given slices (X⁽¹⁾, D⁽¹⁾, g⁽¹⁾), . . . , (X^(t), D^(t), g^(t)) containing n₁, . . . , n_t spots, respectively over the same p genes, a spot distance matrix $D\in {ℝ}_{+}^{n\times n}$, a distribution g over n spots, an expression cost function c, a distribution $\lambda \in {ℝ}_{+}^t$, and parameters 0 ≤ α ≤ 1, $m\in \mathbb{N}$ and, find an expression matrix X = WH where $W\in {ℝ}_{+}^{p\times m}$ and $H\in {ℝ}_{+}^{m\times n}$, and mappings Π^(q) ∈ Γ(g, g^(q)) for each slice q = 1, . . . , t that minimize the following objective:

$$\begin{gathered} R(W,H,{\text{Π}}^{(1)},\dots {\text{Π}}^{(t)}\mathrm{)}=\sum _q{\lambda }_{q}F({\text{Π}}^{(q)};WH,D,X^{(q)},D^{(q)},c,\alpha ) \\ =\sum _q{\lambda }_q\left[(1-\alpha )\sum _{i,j}c(W{H}_{\cdot i},x_{\cdot j}^{(q)}){\pi }_{ij}^{(q)}+\alpha \sum _{i,j,k,l}{(d_{ik}-d_{jl}^{(q)})}^2{\pi }_{ij}^{(q)}{\pi }_{kl}^{(q)}\right]. \end{gathered}$$ (3)

We solve the Center Slice Integration Problem using a Block Coordinate Descent algorithm (Algorithm 1, Supplementary Section S1.2). This algorithm alternates between optimizing the mappings Π⁽¹⁾, . . . , Π^(t) given the current values of W, H and optimizing W, H given the current mappings Π⁽¹⁾, . . . Π^(t). The problem of finding the optimal mappings Π⁽¹⁾, . . . Π^(t) given W and H reduces to solving the Pairwise Slice Alignment Problem between the center slice (WH, D, g) and each slice (X^(q), D^(q), g^(q)) separately. Similarly, the problem of finding the optimal W and H given the current mappings Π⁽¹⁾, . . . , Π^(t) reduces to a new problem we call the Center Mapping NMF Problem. We show that the Center Mapping NMF Problem can be interpreted as a maximum likelihood optimization problem and prove this problem is equivalent to a weighted NMF problem (Theorem 1, Supplementary Section S1.2).

We analyze the Center Mapping NMF Problem for two commonly used expression cost functions [24]: (1) the Euclidean distance c(u, v) = ∥u − v∥² and (2) the KL divergence $c(u,v)=\text{KL}(v\Vert u)={\sum }_l{v}_l\log \frac{v_l}{u_l}$ and the generalized KL divergence $c(u,v)=\mathrm{gKL}(v\Vert u)=\sum _l{v}_l\log \frac{v_l}{u_l}-v_l+u_l$. While the generalized KL divergence is not symmetric and therefore not a distance measure, it has the advantage of having a probabilistic interpretation as the likelihood of a Poisson count model [18]. Thus, it has been used in the analysis of count data matrices such as sc-RNAseq [51, 69, 52].

Although the above problem formulation assumes that the low rank matrices W, H are non-negative, Theorem 1 does not use this assumption. Therefore, one can define and solve the Center Mapping NMF Problem using other factorization techniques such as PCA or generalized PCA [69].

M1.1.3. Software Implementation and Parameter Selection

We implemented the algorithms described above in a Python software package called PASTE. PASTE is built using AnnData, allowing it to be easily integrated with Scanpy [71] for visualization and further downstream analysis, including the simultaneous visualization of PASTE results and tissue images (Supplementary Figure S29). We use the Python Optimal Transport library [53] to solve the fused Gromov-Wasserstein optimal transport problem.

For the Pairwise Slice Alignment Problem we use a uniform distribution $g=\frac{1}{n}{\mathbf{1}}_n$ for the spots in a slice with n spots (unless otherwise specified). We normalize the UMI counts for each spot by the total UMIs and use the KL divergence to calculate the expression cost between spots in all our analyses. We set the parameter α = 0.1 (unless otherwise specified) based on our performance on simulated data (Extended Data Figure 2). Further details of the implementation and initialization procedure are in Supplementary Section S1.3.

For the CENTER SLICE INTEGRATION PROBLEM, we implemented the block coordinate descent algorithm (Algorithm 1, Supplementary Section S1.2). We give all slices an equal weight $\lambda =\frac{1}{t}{\mathbf{1}}_t$, and fixed m = 15 dimensions in the NMF to avoid overfitting [67]. These parameters can be set by the user in the PASTE software. In all our analyses, we use the slice with the highest number of spots as the template for the location of spots in the center slice.

On a personal computer with an Intel Core i7–10875H CPU @ 2.30GHz, pairwise slice alignment of slices with 260–270 spots and 8000 genes completed in ≈ 1.5 seconds, and center slice integration of four slices with similar number of spots and genes completed in ≈ 30 seconds. PASTE aligned pairs of Visium slices (containing 3431–4786 spots) in less than 7 minutes.

M1.2. Simulated Spatial Transcriptomics Data

We simulated ST data by resampling from real ST data from four slices of a breast tumor [35]. Each slice in this dataset consists of 251–264 spots and 7453–7998 genes (Extended Data Figure 1).

We simulate a new ST experiment (X′, Z′) with n′ tissue spots from a given ST experiment (X, Z) with n tissue spots by perturbing both the transcript counts and spatial data as follows. We assume that the locations $Y\in {ℝ}^{2\times N}$ of all spots on the array are known and that tissue spots will only be generated from these locations. This is a reasonable assumption since the spot locations on the array are fixed. For each spot i in the original ST experiment we generate new transcript counts according to a negative binomial distribution for the total counts per spot, and then a multinomial distribution for the counts of individual genes. This procedure is governed by a pseudocount parameter δ that perturbs the counts per transcript. Intuitively, with higher values of δ, the simulated counts become more uniform across the genes and thus are less informative. Finally, we derive the spatial coordinates for spots in the new slice by rotating coordinates and then dropping spots that do not align to the array coordinates Y following the rotation. This procedure is governed by a parameter θ controlling the spatial rotation of the tissue on the array. Dropping some of the spots mimics the case where some pieces of tissue get lost in the dissection. For instance, the original slice 1 contains a total of 254 spots while a simulated slice with $\theta =\frac{\pi }{3}$ (Supplementary Figure S4a and c) contains only 220 spots. Further details of the simulation procedure are provided in Supplementary Section S1.4.

We evaluated the performance of PASTE on the Pairwise Slice Alignment Problem by aligning a real breast cancer slice (X, Z) to simulated slices (X′, Z′) with a constant rotation of $\theta =\frac{\pi }{3}$ and increasing pseudocount δ (Supplementary Figure S4a and c). Since the exact alignment of spots is known, we measured performance by computing ${\sum }_{i~j}{\pi }_{ij}$, the percentage of spots correctly aligned between the original slice and simulated slice, where i ~ j a spot i in the original slice and a spot j in the simulated slice that are mapped to one another. We tested the performance of PASTE using only gene expression data (α = 0), using only spatial data (α = 1) and using both types of data (α = 0.1).

To evaluate the performance of PASTE on the Center Slice Integration Problem, we used the same simulation procedure described above to simulate three ST slices {(X^(q), Z^(q)); q = 1, 2, 3} from a real ST experiment (X, Z). We simulate the gene expression information of each slice independently and simulate the spatial information by a rotation of either $\frac{\pi }{6},\frac{\pi }{3},\frac{2\pi }{3}$ for each of the slices (Supplementary Figure S4). Since the exact alignment of spots from the center slice (X, Z) to each of the generated slices is known, we evaluated the performance of PASTE by computing $\frac{1}{3}{\sum }_q{\sum }_{i~j}{\pi }_{ij}^{(q)}$, the average percentage of spots correctly aligned between the center slice and each of the three simulated slices. In addition, we compared the KL divergence between the gene expression matrix X of the true center slice and the low rank gene expression matrix WH inferred by PASTE.

M1.3. Analysis of squamous cell carcinoma (SCC) ST Data

M1.3.1. Pairwise Alignment Accuracy

Given a label ℓ(i) (e.g. a cluster label) for each spot i, we compute the accuracy of a Pairwise Slice Alignment as follows. Let Π = [π_ij] be a pairwise alignment produced by PASTE. We define the accuracy as ${\sum }_{i,j;\ell (i)=\ell (j)}{\pi }_{ij}$, the weighted sum of pairs (i, j) of spots with the same label.

M1.3.2. Spatial Coherence Score

To quantify the observed differences in spatial coherence of clusters in different patients, we computed a spatial coherence score of the cluster labels based on O’Neill’s spatial entropy [33]. Specifically, let G = (V, E) be graph where V is the set of spots and where edges (i, j) ∈ E connect every pair (i, j) of adjacent spots on the array. Let K = {1, 2, . . . , k} be a set of k cluster labels and let L = [ℓ(i)] be a labeling of spots where ℓ(i) ∈ K is the cluster label of spot i. We define the spatial entropy as $H(G,L)=-{\sum }_{\{a,b\}:a,b\in K}\mathbb{P}(\{a,b\}\mid E)\log (\mathbb{P}(\{a,b\}\mid E))$, where $\mathbb{P}(\{a,b\}\mid E)=\frac{n_{\{a,b\}}}{|E|}$ and n_{a,b} is the number of edges {i, j} ∈ E such that ℓ(i) = a and ℓ(j) = b. A high value of spatial entropy indicates that the distribution of labels of neighboring spots is close to the uniform distribution, while a low value of spatial entropy indicates that neighboring spots frequently have the same label.

Spatial entropy values are not directly comparable across patients or slices having different number of clusters and spots. Thus, we define a normalized form of spatial entropy, the spatial coherence score, as the absolute value of the Z-score of spatial entropy over random permutations of the labels of spots in a slice (Supplementary Figure S8). A high spatial coherence score indicates that the cluster labels of adjacent spots are frequently identical while a low spatial coherence score indicates that cluster labels are closer to random distribution. For a pair of aligned slices we define the spatial coherence score as the average spatial coherence score of the two slices.

M1.3.3. Clustering center slice

We clustered the spots in the inferred center slice with the low rank expression matrix X = WH using k-means clustering. Specifically, we applied k-means clustering to cluster spots according to the log normalized coordinates in the lower-dimensional representation given by H. Because PASTE used KL divergence in the inference of the X, the entries of X are in count space. We log normalized each spot in H before running k-means. We set the number k of clusters equal to the published analysis of each patient [21].

M1.4. Analysis of DLPFC ST Data

M1.4.1. Pairwise Alignment using Other Methods

We compared PASTE to three other approaches to infer mapping scores between spots from pairs of slices. First, we used Seurat [37], a method based on finding mutual nearest neighbors for scRNA-seq integration. Using the FindIntegrationAnchors function in Seurat we obtained the list of anchor pairs between the datasets which were used for integration together with their confidence score. We integrated all slices for every sample using the IntegrateData function and used the anchor weights between consecutive slices to create an alignment. To scale these alignments to create a distribution similar to PASTE, we normalized the resulting alignment by the total sum of the weights. We note that the anchor mapping from Seurat only aligns high confidence pairs of spots between datasets whereas PASTE aligns all spot pairs.

Second, we used Tangram [8], a method that finds a probabilistic alignment of single cell expression data onto spatial transcriptomics data. To align a pair of ST slices to each other, we treated the first slice as an scRNA-seq dataset by dropping the spatial coordinates and mapped its spots onto the second second ST slice. To scale the alignments from Tangram to have uniform marginals similar to PASTE, we gave Tangram a uniform density prior over spots and normalized the resulting alignment by its sum. We ran Tangram with 300 iterations (instead of the default value of 1000 iterations) to reduce excessive run times, since we empirically observed that its objective function does not improve much after 300 iterations.

Lastly, we used STUtility [6], a method that aligns slices of ST data using only the H&E stained images. To align slices using STUtility we first masked the stained images using the MaskImages function with default parameters and subsequently used the AlignImages function also with default parameters to apply the iterative closest point algorithm. STUtility outputs only the new coordinates of the aligned spots, and does not provide mapping scores between pairs of spots. Thus, we computed mapping scores from the new spot coordinates using the following procedure. Given two slices with new spot coordinates Z and Z′, we find a mapping Π that minimizes the Wasserstein distance (also known as the earth mover distance) between the spots of the two slices, where the cost of transporting one spot into the other is given by the Euclidean distance between the new coordinates and the spots in each slice are weighted equally. Given the probabilistic mappings $\widehat{\mathrm{\Pi }}$ we compute the alignment accuracy exactly as in PASTE.

M1.4.2. Clustering Spot Expression

To cluster the raw counts of spots in each of the original ST slices, we used the standard Scanpy [71] pipeline to normalize counts in each spot by the total number of reads, perform log normalization, retain the top 2000 highly variable genes and run PCA with 50 dimensions. We then used the low dimensional representation to cluster the spots into 7 clusters with k-means (scipy implementation, 500 restarts) and calculated the Adjusted Rand Index (ARI) vs the manual spot annotations. We also tried using NMF for dimensionality reduction instead of PCA, but we observed lower ARIs on the DLPFC data (0.17, 0.24, 0.19 and 0.21 ARIs on slices A, B, C and D, respectively).

To cluster the spots in PASTE integrated slice, we used the low dimensional representation of the spots in the integrated center slice (H matrix). To avoid differences due to total transcripts per spot, we normalized the representation of each spot to sum to 1 (i.e., each column of H). We then used k-means (scipy implementation, 500 restarts) to cluster into 7 groups and calculated the ARI vs the manual spot annotations.

Finally, we compared PASTE to Scanorama [20] and Seurat [37], two methods that integrate multiple single cell RNA-seq datasets. We ran these methods with the default parameters for scRNA-seq integration using only the gene expression of all spots across all slices of a sample. The output of these methods is a new dataset with batch corrected expression of all spots across all slices of a sample. For Scanorama, we also retained the low dimensional representation of the spots in the shared space We clustered all spots from all slices together using k-means based on the low dimensional representation for Scanorama or based on the PCA embedding of the top variable genes for Seurat. We then calculated an ARI for each slice comparing the spots to their layer assignment.

M1.4.3. Differential Gene Expression Analysis on Full Rank Integrated Expression Matrix

We found that using the low rank expression matrix inferred by PASTE to find differentially expressed genes between the annotated neocortical layers in the DLPFC data results in most genes being significantly differentially expressed (Supplementary Table S5). This phenomena is attributed to the low rank of the expression matrix that reduces some of the variance and inflates the test statistic resulting in extremely low p-values and unreliable ranking (Supplementary Figure S30). Similar observations have been also made for other single cell RNAseq imputation methods [50]. Therefore, for differential gene expression analysis we use the full rank integrated expression matrix $\overline{X}=n{\sum }_q{\lambda }_q{X}^{{}^{(q)}}{{\mathrm{\Pi }}^{(q)}}^T$ induced by the mappings of PASTE rather than the low rank matrix.

M1.4.4. Validation on Known Layer Enriched Marker Genes

We evaluated differentially expressed genes by comparing to a list of previously published layer-enriched genes as gold standard marker genes for subsets of the neocortical layers [31]. Specifically, we obtained a list of 126 manually curated known marker genes from [31]. This list describes for each gene, a subset of the layers for which it was previously identified as a marker gene. For each subset of layers, we used the two-sided Wilcoxon rank-sum test to compare the expression of genes between spots in the subset of layers and spots outside the subset of layers. For each subset of layers tested, we ranked all the genes according to their adjusted p-value. We say that a gene is significantly differentially expressed for a subset of layers if its adjusted p-value is < 0.01.

M2. Data Availability

The ST datasets for the breast cancer [35], SCC [21], spinal cord [29], Her2 breast cancer [3] and DLPFC [31] were taken from the original publications. Preprocessed data sets to reproduced the results can be found at https://doi.org/10.5281/zenodo.6334774.

M3. Code Availability

The PASTE methods are implemented in an open-source, publicly available Python package that is available at: https://github.com/raphael-group/paste. All the code to reproduce the analysis can be found at: https://github.com/raphael-group/paste_reproducibility.

Extended Data

Extended Data Fig. 1. Spatial organization of breast cancer ST slices.

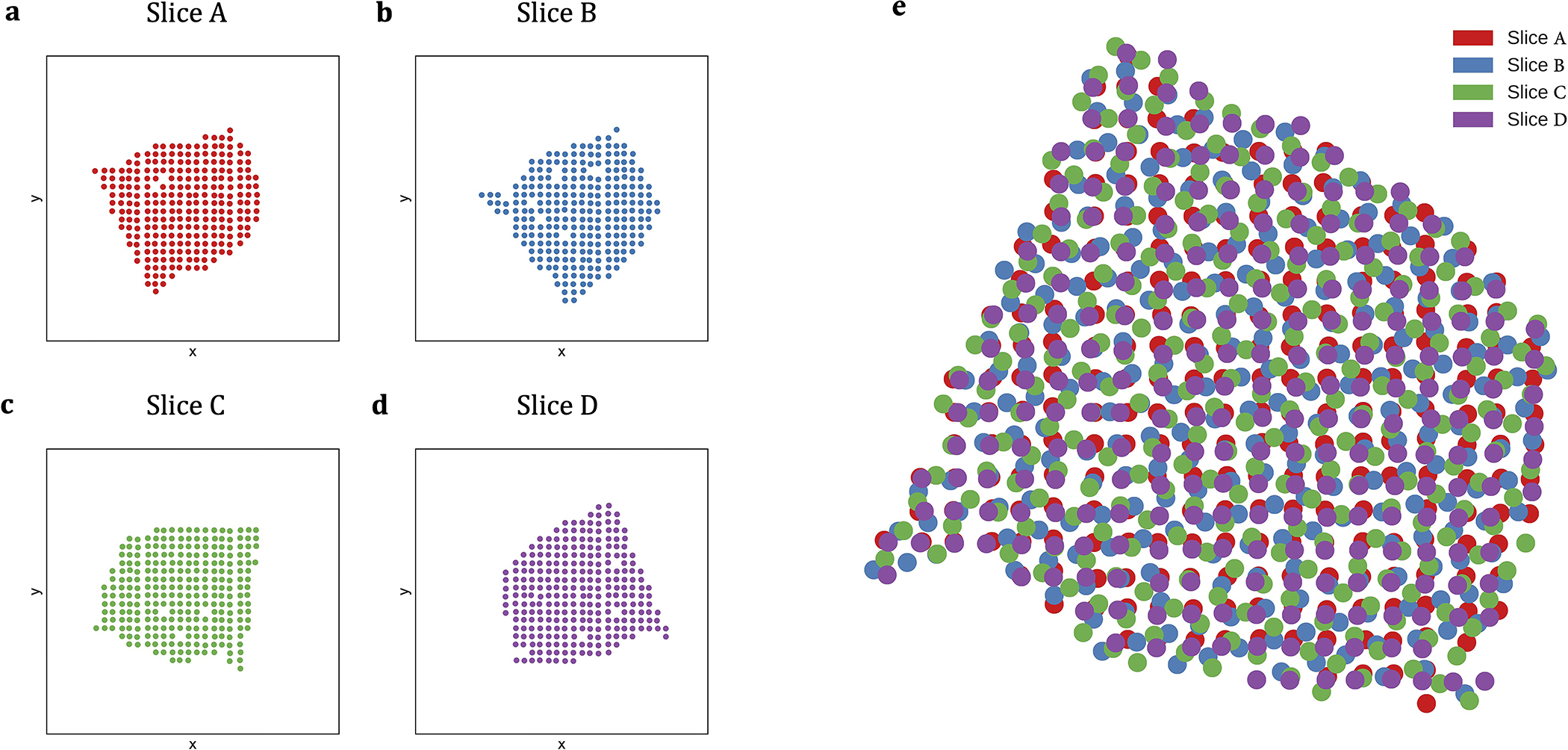
(a-d) Spatial organization of the four breast cancer ST slices from [35]. Each slice in this dataset consists of 251–264 spots and 7453–7998 genes. (e) Spatial coordinates of the four breast cancer ST slices from [35] after pairwise alignment via PASTE.

Extended Data Fig. 2. PASTE results on simulated data generated from each of the indicated breast cancer slices [35].

Each line (color) corresponds to running PASTE with a specific value for alpha. Error bars represent the standard deviation across 10 simulated instances.

Extended Data Fig. 3. Comparison of published clusters and clusters obtained by PASTE on ST data from SCC patients 2, 5, 9, and 10 in [21].

(Left) The published cluster labels from [21] of spots in slice A from each of the four patients. (Right) $k$-means clustering of inferred center slice from PASTE.

Extended Data Fig. 4. PASTE integration of Her2 breast cancer patient G from Andersson et al.

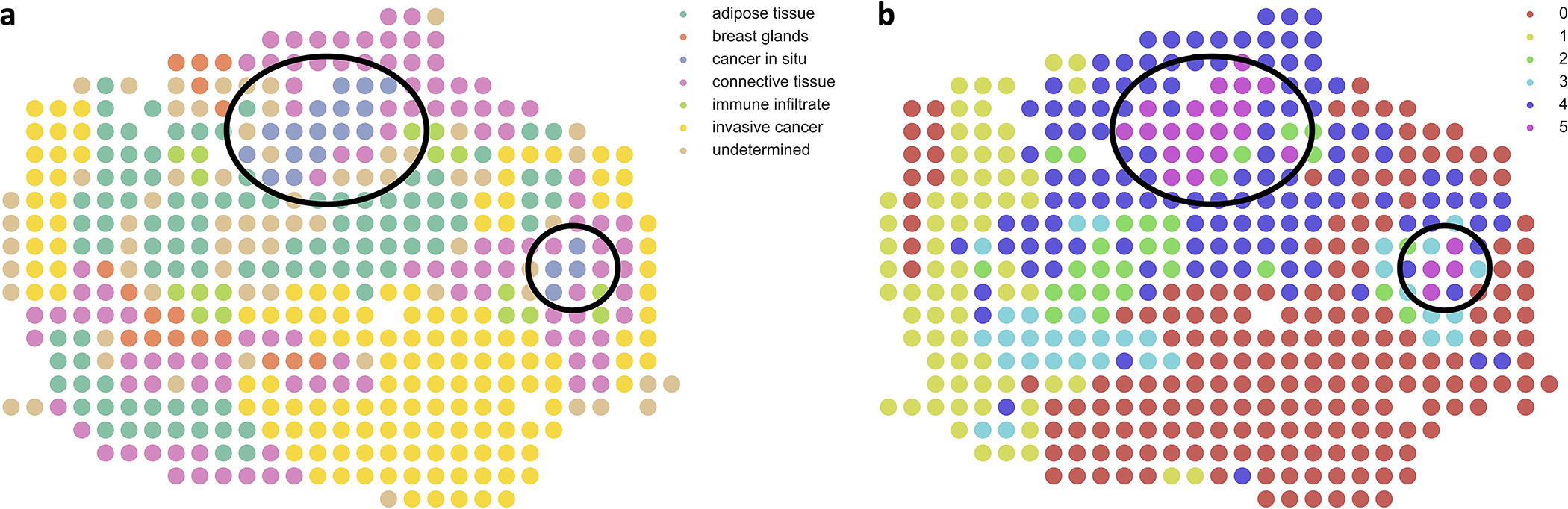
(a) Pathological annotations and (b) clustering results from PASTE integrated slice for a slice of breast cancer patient G from Andersson et al. Black circles indicate small region of spots of in situ cancer which are also clustered together in the PASTE integrated slice

Extended Data Fig. 5. Dorsolateral prefrontal cortex ST data from [31].

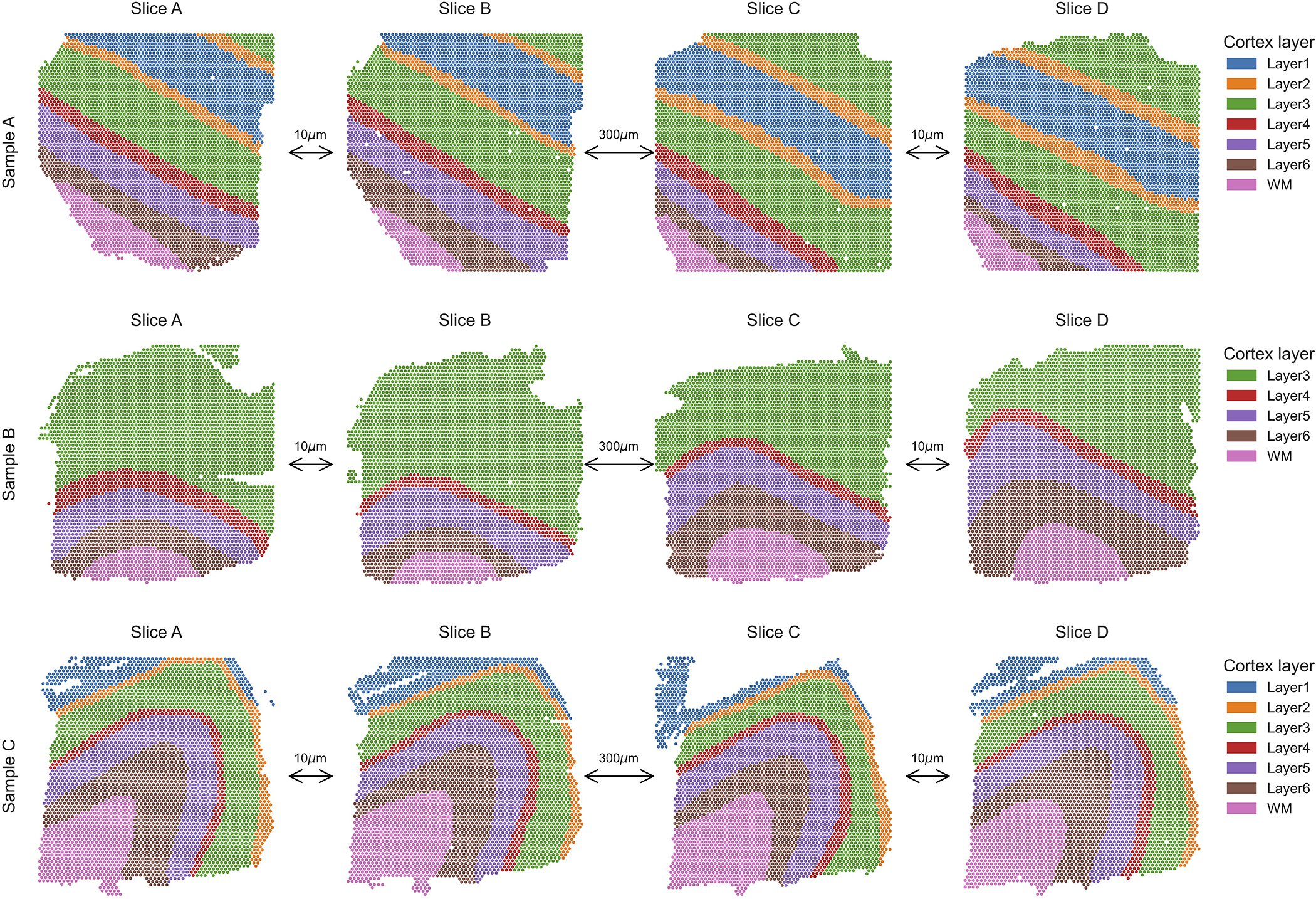
Each of the three samples is composed of four ST slices. The first two slices and last two slices are 10$\mu m$ apart while the middle pair of slices is taken 300$\mu m$ apart. Spots are colored by the six neocortical layers or the white matter according to the annotation of [31]

Extended Data Fig. 6. Pairwise alignment of slices B and C from DLPFC Sample I.

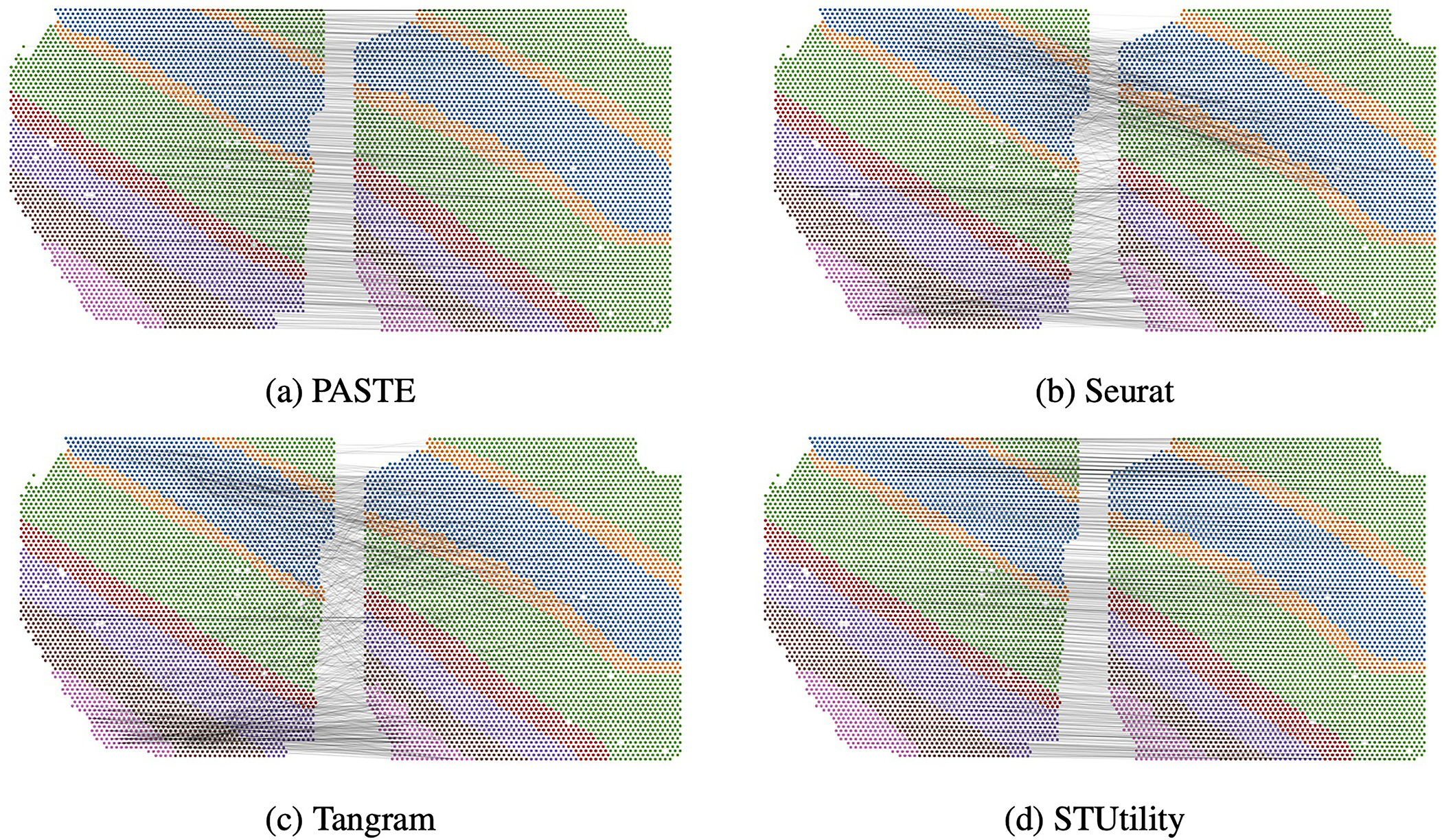
Pairwise alignment using (a) PASTE, (b) Seurat, (c) Tangram and (d) STUtility. Gray lines connect the 1000 spot pairs with highest alignment values from each method. PASTE and STUtility alignments are more consistent with spatial organization of slices than Seurat and Tangram alignments.

Extended Data Fig. 7. Alignment accuracy of adjacent DLPFC slices using PASTE with different expression costs.

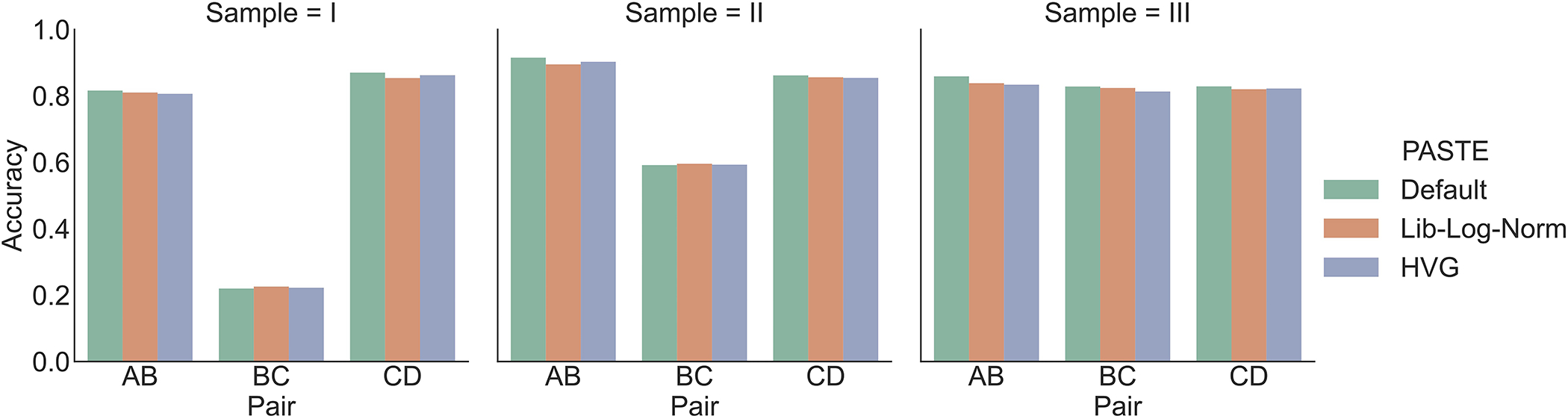
PASTE with: (Default) All genes and KL divergence, (Lib-Log-Norm) All genes with library size normalization and log transformation and Euclidean distance, (HVG) Same as Lib-Log-Norm but restricted to top 2000 highly variable genes.

Extended Data Fig. 8. TRABD2A expression in a single slice and PASTE integrated slice.

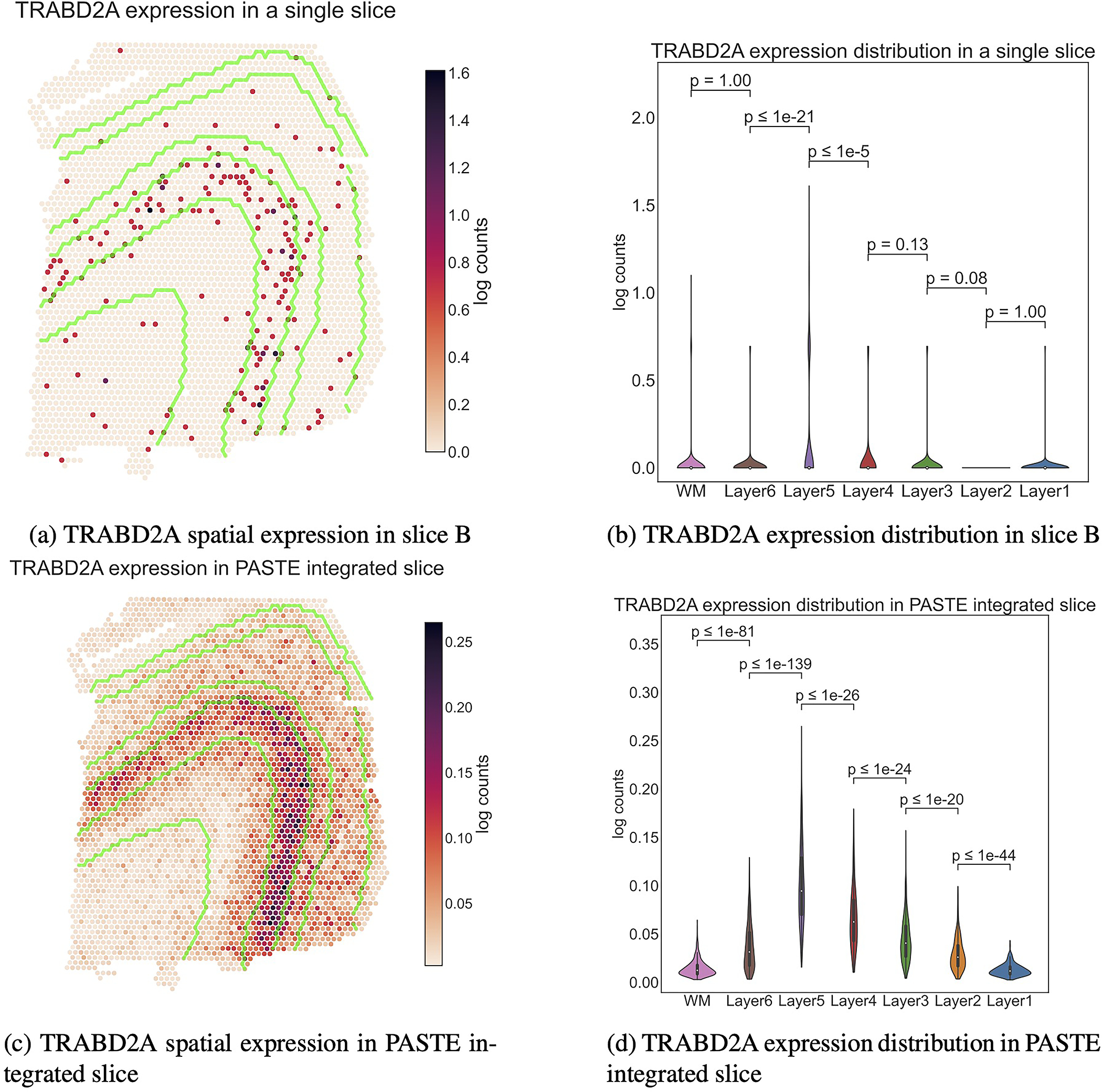
The boundaries between the layers are marked in green in a and c. WM and Layers 6 to 1 have 625, 614, 621, 247, 924, 224 and 380 spots respectively. Inner boxplots show the 25\%, 50\% and 75\% quantiles of the distributions. $p$-values (rounded to the closest power of $10$) for the difference in distribution (two-sided Mann-Whitney U test) between adjacent layers are indicated. TRABD2A was validated using smFISH in [31] as a layer 5 marker gene.

Extended Data Fig. 9. Ranking of known layer-specific marker genes by differential expression analysis.

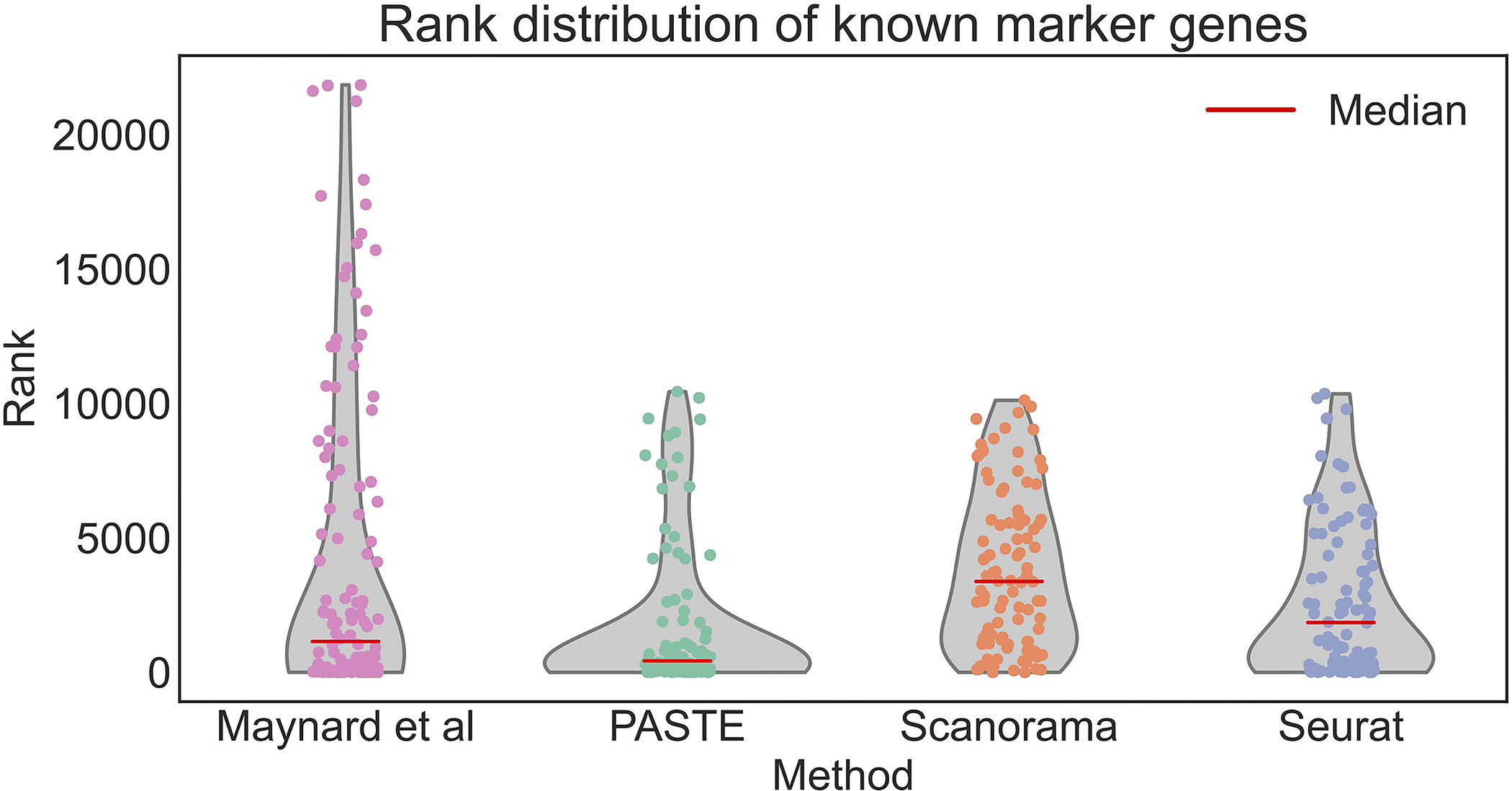
Gene ranking using: the pseudo-bulk approach of Maynard et al., PASTE center slice integration, Scanorama, and Seurat. Red lines indicate median rank of marker genes which are 1147 for Maynard et al, 427 for PASTE, 3380.5 for Scanorama, and 1852 for Seurat. Rank 1 is the highest rank.