Significance
One of the most fundamental physical constraints on living systems is temperature. Despite its importance, a simple, mechanistic, and general theory that fully predicts the response to temperature across all scales has not yet been derived. Here we develop such a theory based on the fundamental chemical kinetics and statistical physics governing the biochemical reactions that support life. Our mathematical framework includes an explanation for why temperature response curves have a maximum or minimum value and the derivation of a single universal curve onto which data for the temperature dependence of diverse biological quantities covering all levels of organization, collapse. The theory has multiple potential applications including predicting responses to global warming, yields of industrial processes, and epidemic outbreaks.
Keywords: temperature kinetics, scaling, metabolic theory
Abstract
At present, there is no simple, first principles–based, and general model for quantitatively describing the full range of observed biological temperature responses. Here we derive a general theory for temperature dependence in biology based on Eyring–Evans–Polanyi’s theory for chemical reaction rates. Assuming only that the conformational entropy of molecules changes with temperature, we derive a theory for the temperature dependence of enzyme reaction rates which takes the form of an exponential function modified by a power law and that describes the characteristic asymmetric curved temperature response. Based on a few additional principles, our model can be used to predict the temperature response above the enzyme level, thus spanning quantum to classical scales. Our theory provides an analytical description for the shape of temperature response curves and demonstrates its generality by showing the convergence of all temperature dependence responses onto universal relationships—a universal data collapse—under appropriate normalization and by identifying a general optimal temperature, around 25 ∘C, characterizing all temperature response curves. The model provides a good fit to empirical data for a wide variety of biological rates, times, and steady-state quantities, from molecular to ecological scales and across multiple taxonomic groups (from viruses to mammals). This theory provides a simple framework to understand and predict the impact of temperature on biological quantities based on the first principles of thermodynamics, bridging quantum to classical scales.
Temperature is a major determinant of reaction rates of enzymes, which regulate processes that manifest at all levels of biological organization. Empirical data show a high regularity in the temperature response across the entire range of biological phenomena from molecules to ecosystems and across multiple taxa and environments (1–8) (see also Fig. 1). These typically exhibit an asymmetric curve which increases exponentially followed by an even more rapid decrease. This remarkably regular behavior is indicative of a universal law, whose origins have, as yet, remained unexplained. Formulating a fundamental theory for the response of biological rates to changes in temperature, especially in ecological systems, has become a matter of some urgency with the intensification of the climate crisis, particularly since existing models are unable to account for such responses across the entire range of temperatures that support life. Despite its importance, a comprehensive theory that unifies several key properties simultaneously has not been as yet possible. Specifically, the key goals, which the framework we present here achieves, is a theory that 1) is based on first principles and fundamental physicochemical mechanisms; 2) is simple in terms of its assumptions and mathematical form, yet efficient in that it explains a plethora of data and generates many predictions with few free parameters; and 3) is general and applicable across multiple levels of biological organization and taxa, thereby manifesting a universal biophysical law.
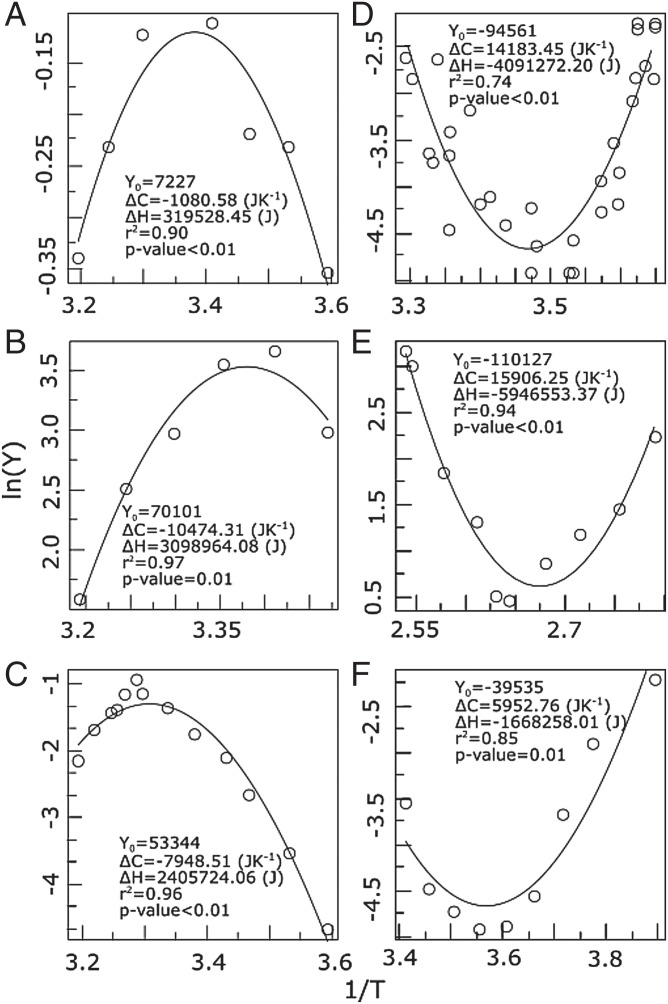
Fig. 1.
Temperature response curves compared to the predictions of Eqs. 5 and 7 for a wide diversity of biological examples. Plotted are vs. (in 1/K, where K is kelvin) showing (A–C) convex patterns and (D–F) concave patterns: (A) metabolic rate in the multicellular insect Blatella germanica, (B) maximum relative germination in alfalfa (for a conductivity of 32.1 dS/m), (C) growth rate in Saccharomyces cerevisiae, (D) mortality rate in the fruit fly (Drosophila suzukii), (E) generation time in the archaea Geogemma barossii, and (F) metabolic rate (during steady-state torpor) in the rodent Spermophilus parryii. Here the curve corresponds to the metabolic rate in response to environmental temperature and not body temperature. The x axis is in units of . Examples come from references 58–63.
Various models have been suggested for explaining temperature dependence in biology, among which the Arrhenius equation (8 and 9) has become the one most used by biologists and ecologists, as epitomized, for example, in the metabolic theory of ecology (MTE) (2). It can be expressed as
| [1] |
where k is some biological quantity (e.g., at the molecular level, enzyme reaction rate), kB is Boltzmann’s constant, T is absolute temperature, E is an effective activation energy for the process of interest, and a is an overall normalization constant characteristic of the process. Consequently, a plot of ln(k) vs. should yield a straight line, often referred to as an Arrhenius plot. This equation was originally an empirical formulation but was later motivated heuristically from chemical reaction theory (9) (SI Appendix, Text S1). Although it has been instrumental in explaining the approximately universal temperature dependence across many diverse biological rates (2, 4), it cannot account for the complete pattern of temperature response of different biological traits, including metabolism and growth rate, among others (3, 4, 10–13). Experiments and observations have long established that the form of the temperature response has an asymmetric concave upward or downward pattern relative to the canonical straight-line Arrhenius plot (e.g., ref. 10). Consequently, there are ranges of temperatures where the traditional Arrhenius expression, Eq. 1, even gives the wrong sign for the observed changes in biological rates: namely, they decrease with increasing temperature rather than increase, as predicted by Eq. 1.
The Eyring–Evans–Polanyi (EEP) transition state theory (TST) (14), which is the widely accepted theory of enzyme chemical kinetics, offers the possibility of developing a fundamental theory for the temperature dependence of biological processes that extends and generalizes the heuristic Arrhenius equation by grounding it in the first principles of thermodynamics, kinetic theory, and statistical physics (15, 16). The framework of the TST conceives a chemical reaction as a flux of molecules with a distribution of energies and a partition function given by the Planck distribution, flowing through a potential energy surface which effectively simulates molecular interactions. The configuration of molecules flowing through this surface proceeds from 1) a separate metabolite and enzyme to 2) an unstable metabolite–enzyme complex, which 3) after crossing a critical energy threshold barrier, or transition state, then forms the final product (the transformed metabolite). EEP thereby derived the following equation for the reaction rate (SI Appendix, Text S2):
| [2] |
where h is Planck’s constant, is the change in Gibbs free energy or free enthalpy, is the universal gas constant, and N is Avogadro’s number. An overall coefficient of transmission also is originally part of Eq. 2 but is usually taken to be 1. Since the change in Gibbs free energy, or the energy available to do chemical work, can be expressed in terms of enthalpy () and the temperature-dependent change in entropy, or dissipated energy (), as , Eq. 2 can then be written as (17)
| [3] |
Analogous to the Arrhenius expression, Eqs. 2 and 3 describe an exponential response of the rate k to temperature provided, however, that there is no temperature dependence of the thermodynamic parameters. Models have been developed for including this temperature dependence, but they typically invoke several additional assumptions and new parameters (18, 19) (SI Appendix, Text S1). Moreover, most models for temperature response have been conceived for a single level of biological organization (primarily at the enzymatic/molecular level) (6, 17) or for specific taxonomic groups, e.g., only for mesophilic ectotherms (18), endotherms (19), or thermophiles (20).
Here, starting with the EEP equation, Eq. 3, and assuming that all of the temperature dependence is in the entropy (see Derivation of the Theory below for details), we derive a simple mechanistic model that quantitatively explains the temperature dependence of biological attributes from microscopic to macroscopic scales.
To extend this model from the molecular level to larger scales we make three additional interrelated assumptions or considerations that can be summarized as follows: 1) the generic analytic form of temperature dependence does not change as one sums up to different levels of biological organization; 2) the classical limit of enzyme dynamics, in which , captures the temperature dependence across macroscopic scales (the conventional correspondence principle); and 3) all biological quantities can be connected with a rate that in turn depends on temperature. In the next section, we justify and elaborate on these ideas, using them to develop the theory and its mathematical details, which are then tested using a global database of biological quantities. Agreement with data and observations across all scales is very good, as detailed in the next section; indeed, our theory shows that the temperature dependence of almost all biological quantities can be encapsulated in a single equation. In addition, many predictions are derived. Having such a theory is critical for making accurate predictions of temperature dependence that are relevant in industrial processes, food production, disease spread, and responses to climate warming, among other potential applications.
Derivation of the Theory
Temperature changes the conformational entropy of proteins (21), which in turn determines the binding affinity of enzymes (22, 23) and affects the flexibility/rigidity and stability of the activated enzyme–substrate complex and hence the reaction rate (23). The resulting temperature dependence of the change in entropy, (with enthalpy and heat capacity remaining constant), is the simplest mechanism for giving rise to curvature in an Arrhenius plot and naturally leads, via Eq. 3, to power law deviations from the simple exponential form (24). Following ref. 20, the change of entropy for a given change in temperature can be expressed as , where is the heat capacity of proteins, assumed to be independent of temperature. Integrating over temperature gives , where is the entropy when T = T0, an arbitrary reference temperature, commonly taken to be 298.15 K (25 ∘C). Using this expression for in Eq. 3, and after simplifying, we straightforwardly obtain (SI Appendix, Text S3)
| [4] |
Eq. 4 has the form of a classic Arrhenius-like exponential term, modified by a power law, but with a different interpretation of the effective activation energy in terms of the change in enthalpy. The pattern described by Eq. 4 is a curved temperature response in an Arrhenius plot of vs. :
| [5] |
In Eq. 5 the terms in parentheses are estimable parameters, and the model takes the simple form .
Some important points should be noted about our result: based on three additional assumptions or principles this model can be applied from quantum to classical scales. These are as follows.
Averaging.
Following Gillooly et al. (24) and in the spirit of the MTE, we can extend our derivation from the microscopic up through multiple scales to multicellular organisms and ecosystems. Biological rates at a given level of organization represent the average rate over an ensemble of limiting reactions. For example, at the multicellular level a typical biological rate, K, is the weighted sum over all contributing intracellular enzymatic reaction rates, ki—some connected in series, some in parallel—appropriately averaged over all cells. Symbolically, , the bar indicating that an average is to be taken. If there is a single dominant rate limiting reaction, that is, a specific ai is significantly greater than the rest, then the temperature dependence of K can be well approximated by an equation of the form of Eq. 4. More generally, however, the variance in the distribution of the βi is small, reflecting the clustering of the various effective activation energies of the contributing reactions around a dominant common value, , typically in the range of 0.5 to 1.0 eV, thereby leading to . This statistical mechanics approach is an example of a general result (21) that if the variance in the parameters is small, then the average of a function describing a biological rate is approximately equal to the function of the average. Consequently, K can be approximated by an equation of the form of Eq. 4 but with the parameters being interpreted as corresponding averages. Metabolic rate, for example, can therefore be expressed as , where B0 is a normalization constant (see SI Appendix, Text S7, for details).
Correspondence Principle.
This principle specifies the connections between theories and the conditions by which one theory reduces to another. In the case of physics, it specifies the conditions under which quantum mechanics reduces to classical mechanics. In our theory, this principle suggests that care has to be taken with the normalization constants, such as B0 in the case of metabolic rate, since Eq. 4 would predict that these constants would naively be proportional to the ratio of the two fundamental constants, kB and h. The presence of Planck’s constant, h, for microscopic enzymatic reactions appropriately reflects the essential role of quantum mechanics in molecular dynamics. On the other hand, for macroscopic processes, such as whole-body metabolic rate, the averaging and summing over macroscopic spatiotemporal scales, which are much larger than microscopic molecular scales, must lead to a classical description decoupled from the underlying quantum mechanics and, therefore, must be independent of h. This is analogous to the way that the motion of macroscopic objects, such as animals or planets, are determined by Newton’s laws and not by quantum mechanics and therefore do not involve h. Formally, the macroscopic classical limit is, in fact, realized when . The situation here is resolved by recognizing that the partition function for the distribution of energies in the transition state of the reaction has not been explicitly included in Eq. 2. This is given by a Planck distribution which leads to an additional factor , where ν is the vibrational frequency of the bond, as first pointed out by Herzfeld (22). For purely enzymatic reactions discussed above this has no significant effect since , and thus , resulting in Eq. 2. Multicellular organisms, however, correspond to the classical limit where so and , thereby cancelling the h in the denominator of Eq. 4. Consequently, the resulting temperature dependences of macroscopic processes, such as metabolic rate, become independent of h, as they must, but lose a factor of T relative to the microscopic result, Eq. 4. So for multicellular metabolic rate, B, this becomes
| [6] |
with the normalization constant, , no longer depending on h. Note that the above correction can also be applied to the Eyring Eqs. 2 and 3, in which case they become mathematically identical to the Arrhenius relationship.
Extension Beyond Rates.
The third assumption, and a corollary of the first, is that all rates, whether transient, steady-state, or equilibrium, all follow the same temperature response relationship. It is also important to note here that most biological quantities, which are not obviously rates themselves, are fundamentally associated with rates. This is true because biological quantities are either the integral of past rates or maintained by current rates (e.g., ref. 23). For example, diversity and abundance are in general terms functions of mutation rate, generation times, mortality rate, and energy requirements, and all these rates and times do vary with temperature (2, 24–28) (see also Fig. 1D).
Accordingly, our model can be applied from the micro to the macro, leading to a single master expression for the temperature dependence of any variable, Y(T):
| [7] |
Here Y(T) represents either a rate, time, or transient/steady-state/equilibrium state (11), and for the molecular level and 0 otherwise. It should be noted that the thermodynamic parameters may have additional implicit parameters (e.g., embodied in Y0) that make the forms of Eqs. 6 and 7 more complicated under certain conditions (SI Appendix, Text S3) as, for instance, for reaction rates at the molecular level where Y0 is determined by Eq. 4.
In addition to quantitatively explaining the origin and systematic curvature of the Arrhenius plot, a mathematical analysis of our derived equation reveals important predictions regarding minima, maxima, and inflection points in the temperature landscape of the thermal niche, relevant to questions regarding range and safety margins. Among the many consequences of our analyses are the following:
-
1)
It provides an analytical equation for the minima and maxima, which was derived using the Lambert equation (SI Appendix, Eqs. S22 and S23 and Fig. S1).
-
2)
It derives an equation for the inflection point (SI Appendix, Eq. S20) where , leading to the extrema of occurring at (SI Appendix, Fig. S1 and Text S5). This is a minimum, i.e., the curve is concave upward, or a “happy mouth” (e.g., for most biological times or the reciprocal of rates), if , whereas it is a maximum, or a convex downward “sad mouth” (e.g., for most biological rates), if . Furthermore, for to be positive requires for a minimum or for a maximum. The expression for the inflection point implies linear relationship between heat capacity and enthalpy (SI Appendix, Eq. S21, which underlies the principle of optimization of the rate, i.e., when the rate of change of k respect to temperature is zero) and where the slope of the relationship is the optimum temperature of the temperature response curve (SI Appendix, Eq. S21 and Fig. S5).
-
3)
It provides analytical equations for the different measures of the width of the thermal niche, such as the range and thermal safety margin (difference between the optimum and maximum; SI Appendix, Eqs. S24–S26 and Fig. S1).
From considering consequences 1–3, is possible to deduce that thermal traits should vary among them, and the maximum value of a biological quantity should vary with thermal traits, as suggested in some previous hypotheses in thermal physiology (29, 30) that could be tested using this framework.
Universal Scaling and Data Collapse
A classic method for exhibiting and testing the generality of an equation is to express it in terms of rescaled dimensionless variables, which predict that a plot of all of the data collapses onto a single “universal” curve (e.g., ref. 23). To do so here, we introduce dimensionless rates, , and temperatures, , by rescaling them repectively by and Topt, where Y takes on either its minimum or maximum value, :
| [8] |
In terms of these rescaled variables, Eq. 7 reduces to the simple dimensionless form
| [9] |
where with α = 0 or 1, depending on whether the system is macroscopic or microscopic. Note that the optimum is given by and , where .
Our theory therefore predicts that when is plotted against , all of the various quantities, regardless of the specific processes, collapse onto a single parameterless curve whose simple functional form is given by Eq. 9. Notice that this optimizes at and encompasses in the same curve both the convex and concave behaviors predicted in the original Arrhenius plot as a function of T. In that regard, note also that the function
| [10] |
is predicted to be of a pure exponential Arrhenius form as a function of . Thus, an even more dramatic manifestation of the universality and collapse of the data is to plot vs. , which is predicted to yield a straight line with slope a (SI Appendix, Text S6).
Testing the Theory with Temperature Response Curve Data across Levels of Biological Organization and Taxa.
To assess the model performance, we compiled a database of 65 studies encompassing 128 temperature response curves including those which are explicitly predicted by biological theories such as the MTE. Our survey included data of different rates/times/properties in different environments ranging from psychrophilic to hyperthermophilic organisms and across all domains of life, including viruses, bacteria, archaea, and unicellular and multicellular eukaryotes covering both ectotherms and homeotherms (Materials and Methods).
We found that our theory provides an excellent fit to a wide variety of temperature response data, spanning individual to ecosystem-level traits across viruses, unicellular prokaryotes, and mammals (SI Appendix, Table S2). Fig. 1 shows some representative examples of fits to concave patterns with long tails at low and high temperatures (Fig. 1 A–C) as well as convex patterns, such as the effect of environmental temperature on endotherm metabolism (in torpor) and biological times (Fig. 1 D–F) also with tails at both ends. As shown in Eq. 10, our derived equation can alternatively be reexpressed in terms of rescaled rates and temperature differences, leading to a linear equation. As an example, we made a linear fit of enzyme activity vs. temperature, which fits the data significantly well, showing that curved temperature responses can be transformed into a linear relationship for discrete measures of both rates and temperatures (SI Appendix, Fig. S2).
The estimated thermodynamic parameters had a wide variation, reflecting the variation from molecular to ecosystem levels and from bacteria to mammals (SI Appendix, Fig. S3 and Table S2). Thermal traits also varied widely, showing optimum values for the minima and inflection points (SI Appendix, Fig. S4 and Table S2). For example, the distribution of optimum temperatures shows that the highest frequency of optima for all temperature response curves is around 25 ∘C. A way of visualizing this is by plotting the estimated thermodynamic parameters and (SI Appendix, Fig. S5) for all the 128 curves from our database where the slope of this relationship should be the average optimum temperature of all curves. Plotting the data in this way showed that the slope is roughly constant within a certain interval (0.003 to 0.004 K−1) with an optimum of 0.00335 K−1, which approximately corresponds to 25 ∘C. This is because the variation in optimum values is small compared to the range of variation of heat capacity and enthalpy.
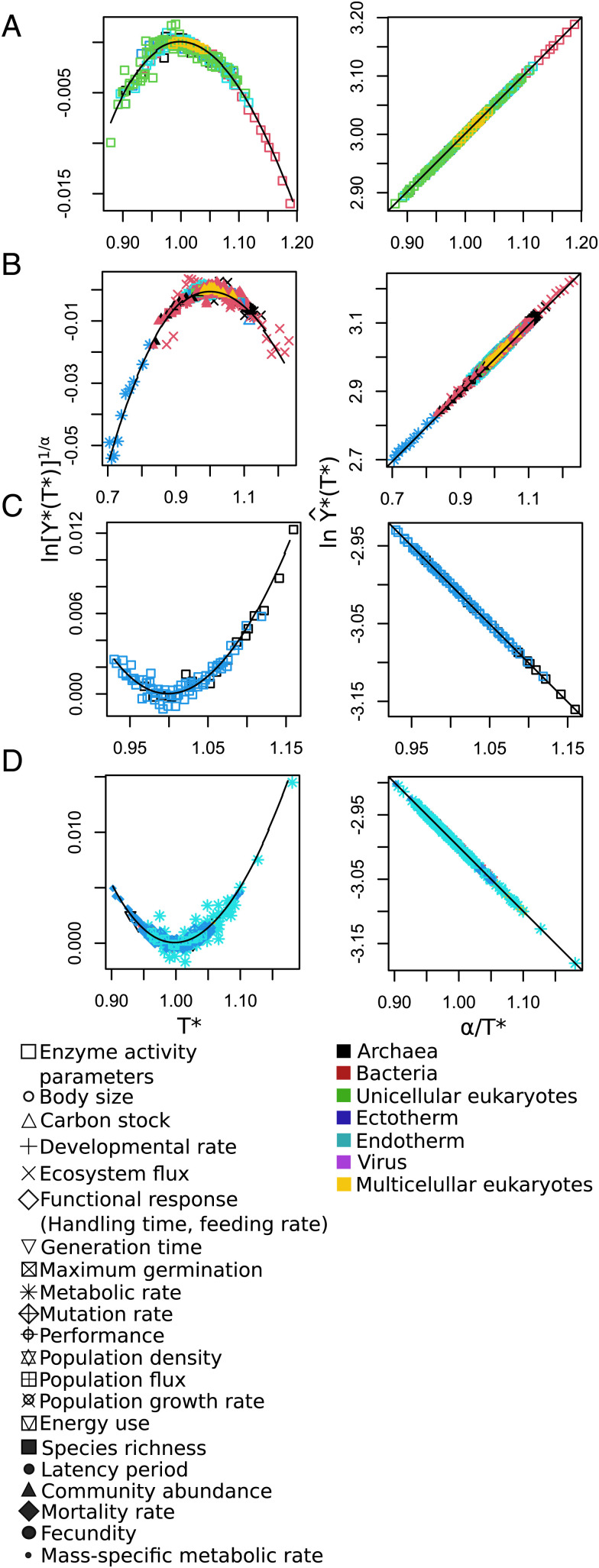
Our prediction of the universal curve is very well supported by data, as illustrated in Fig. 2, where the collapse of all the data from this study for both convex and concave patterns regardless of organizational level, temperature range, or taxa are shown. This result strongly supports the idea that our theory captures all of the meaningful dimensions of thermodynamic and temperature variation for diverse biological properties, which when appropriately rescaled, can ultimately be viewed as a single simple exponential relationship, Eq. 10. (See SI Appendix, Text S6 and Fig. S6, for an alternative formulation for data collapse.)
Fig. 2.
Universal patterns of temperature response predicted by Eqs. 9 and 10. (Left) The convex and concave nonlinear patterns predicted when is plotted vs. (Eq. 9) and (Right) the straight lines predicted when is plotted vs. (Eq. 10). In theory, if rescaled data collapse into a single relationship, it means that all respond to the same general law. As expected, all curves regardless of variable, environment, and taxa collapse onto a single curve when plotted in either of these ways. These rescalings explicitly show the universal temperature dependence of the data used in Fig. 1, as well as additional data from compiled studies. (A and B) Molecular (enzymatic) data exhibiting the predicted concave and convex patterns on the left, while (C and D) show corresponding concave and convex patterns for data above the molecular level. Note that there appears to be no variance in the fits to the linear predictions (Right), whereas there is significant variation in the nonlinear ones (Left). This is basically because . The value of is typically around 0.01 with a variance much smaller than 0.005. Since and is typically around 3, fluctuations in are very much smaller and consequently completely lost. The point is that the difference between what is plotted in Left vs. that in Right, namely, , is in absolute value very large [more than 10 times the value of ]; furthermore, it is almost a constant over the range of temperatures since it is logarithmic, whereas all of the temperature variation is in the much smaller term ).
Discussion
We developed a simple mechanistic theory based on a single general assumption for determining the temperature dependence of biological rates and quantities. The theory is able to capture the essential features of many different temperature responses and it is also capable of capturing what is general to all of them. Eyring was well aware of the potential of absolute reaction rates theory he formulated, which by combining thermodynamics with classical and quantum mechanics could account for the absolute rate of any chemical reaction, beyond the test tube. Indeed, he developed from it the steady-state theory of mutation rates based on observations of the effect of plutonium and radium in beagles, which led to the statistical analysis of survival and its generalization to understand cancer, aging, ontogenetic growth, nutrient uptake by plant and loss from soils, population growth, and species time relationships in islands (31–36). Interestingly, he did not analyze the contribution of temperature to the cellular and ecological processes he studied. By filling this gap, we have helped developing a general, first principles theory that could integrate disparate phenomena in biology, as was certainly Eyring’s aim.
An important consequence of our derivation is that it shows that a single assumption/principle (namely, that heat capacity is independent of temperature or, equivalently, that entropy depends linearly on temperature) is both necessary and sufficient for simultaneously explaining both the convex and concave curvatures commonly observed in temperature response curves. Under a thermodynamic interpretation, the decrease in enzymatic rate with increasing entropy due to increasing temperature beyond the optimal means that the number of the alternative configurational microstates of the protein increases, many of which have a decreased binding affinity to the ligands (1). In contrast, changes in enthalpy alone can only explain convex curvature but not concave curvature. To see this explicitly, we express in terms of heat capacity in Eq. 3, , to obtain , which leads to . Regardless of the sign of both and/or , this always results in a convex curve and so cannot explain, nor accommodate, concavity. Hobbs et al. (37) included temperature dependence in both enthalpy and entropy and derived a significantly more complicated expression than ours based also on TST, which highlights as we have done the role of in affecting optimum temperatures in enzyme performance.
Some empirical models can also explain curvature, but although mathematically simple, they are neither mechanistic nor general. For example, our mathematical form coincides with an empirical phenomenological equation suggested by Kooij in 1893 (38). Likewise, a heuristic derivation inspired by a Maxwell–Boltzmann distribution predicts a similar expression but with a power law modification of rather than (14, 39), which, apart from not having a mechanistic basis, is also unable to explain concave patterns.
More complex assumptions could lead to the inclusion of additional parameters that could increase the explained variance in temperature response curves. Among these possibilities, for example, one could assume a nonlinear temperature dependence of entropy or temperature dependence of other thermodynamic parameters such as heat capacity. Actually, the temperature dependence of heat capacity has been invoked in models based on the denaturation of proteins with temperature (40). We did not include temperature dependency in because there is no general theoretical expression for it and because assuming it to be invariant usually leads to little error (20). Other models have made even more complex assumptions to explain curved patterns (18), but they are limited in terms of making predictions and in their application to different levels of organization. The incorporation in our model of additional variables affecting biological rates and quantities, such as pH, salinity, and oxygen availability, however, may be important to consider as they usually interact in affecting temperature responses, especially in aquatic environments, and have become a priority for increased theoretical and empirical research in the context of current global changes (1, 41–43). It should be borne in mind, however, that our theory is based on equilibrium thermodynamics and as such is not designed to deal with fluctuations out of equilibrium, nor with temporal changes in state variables, such as, for example, those due to acute exposure or different exposure times to a given temperature (7, 44, 45), although it can in principle deal with slow changes, with respect to fast microscopic changes, assuming a quasi-equilibrium (quasistatic) condition or a slowly changing temporal sequence of equilibrium states (46). Future connections with nonequilibrium thermodynamics may prove valuable in this regard (47).
The additional considerations required to apply the model to levels above the enzymatic are well supported in the literature (e.g., refs. 21, 23). More importantly, our model applies to a large diversity of rates and quantities, including the temperature dependency of classical variables, such as metabolic rate and growth rate, as well as new ones not previously reported in the literature (e.g., DNA recombination rate and human population energy use rate), and across a wide spectrum of levels of organization and scales. This speaks to the robustness of our model as it holds even when potential deviations from assumptions are likely, as might be expected when a diverse array of biological rates and quantities are analyzed.
As is typical, as, for example, in the MTE and in scaling analysis, most of the data and theoretical predictions are for average trait values; variability and fluctuations (48, 49), which are an essential feature of all biological systems (50–52), have generally been ignored. The explicit consideration of stochasticity opens potentially important venues for extending the present theory to account for such variability. For example, some biological quantities, such as metabolic rate, population density, and body size, exhibit a characteristic scaling between the variance and the mean in trait value (48, 53, 54), which our theory predicts should change with temperature according to Eq. 4.
As already pointed out, due to its mathematical simplicity, this theory is easily extendable to explain other patterns such as relationships among attributes of the thermal response (e.g., ref. 55). These could be derived given that different thermal traits depend on the same parameters, such as the maximum value of the dependent biological quantity and its range. This could potentially shed light on several biological hypotheses such as “hotter is better” (30, 56) (i.e., a positive relationship between the maximum value of a dependent quantity and its optimum temperature) or “jack-of-all-temperatures” but “a master of none” (29, 56, 57) (i.e., a trade-off between the maximum value of a dependent quantity and the breath of performance).
It is common in different research traditions, such as cell biology, physiology, and ecology, usually enshrined as departments within universities, to work with a single process, organism, or species and emphasize the temperature dependence of that particular entity. Here we have developed an integrative theory that expresses temperature dependence as a universal law across all levels of biological organization, taxa, and the whole range of temperature within which life can operate (–25 to 125 C); our framework is applicable for predicting scenarios of global warming, disease spread, and industrial applications and provides a general equation to integrate in different theories in ecology and evolution, such as MTE. It allows us to better understand the diverse impacts of climate change upon processes at global scales, suggesting that processes such as mutation rates of viruses and mortality will likely increase, given their convex temperature response curves, but other such maximum germination and growth rates will likely decrease given their concave temperature response curves (Fig. 1). Here we show that simple thermodynamics principles and laws underlie all these complex biological processes, which we can now better understand, manage, and predict.
Materials and Methods
Data.
Data for temperature response curves were obtained directly from tables, or supplementary data of published articles, requested from the author or extracted from figures using the tool WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/) Response variables collected included biochemical reaction rate, individual metabolic rate, population abundance, population growth rate, richness, community abundance, biomass, and ecosystem flux, among others. Data are derived from experimental as well as field observations and cover different taxa from viruses to homeotherms and different environments/ecosystems. Some of these data correspond to recent global efforts such as the global ocean and Earth microbiome projects. We collected a total of 65 studies summing 128 curves. We show six examples in Fig. 1, corresponding to refs. 58–63.
Statistical Analysis.
Eq. 7 (in log scale) was fitted using nonlinear regression, using damped least-squares [Levenberg–Marquardt algorithm (64, 65); as implemented in the R package minpack.lm (66)]. Goodness of fit of models were assessed using r-squared and P value. We recorded the characteristics of the distribution of thermodynamic properties, r-square, and P value including minimum, maximum, median, interquartile range, mean, and variance. To compare the values of thermodynamic parameters between organizational levels and taxonomic groups we performed (one-sided) two-way ANOVA. For factor organizational level we grouped data in six levels (molecular, cellular, individual, population, community, and ecosystem), while for the factor taxonomic group, there were also six levels (viruses, bacteria, archaea, unicellular eukaryotes, ectotherms, and homeotherms). Previous to performing the ANOVA we tested for homoscedasticity using the LeveneTest function implemented in R, and since the groups were heteroscedastic, we used weighted least squares.
Supplementary Material
Acknowledgments
We thank the authors that contributed with raw data and Jim Brown for his comments on an early draft of this manuscript. J.I.A. was supported by a Beca de Doctorado Nacional Agencia Nacional de Investigación y Desarrollo (ANID) Grant 21130515. P.A.M. was supported by Grants AFB 17008 and ANID-Fondo de Desarrollo Científico y Tecnológico (FONDECYT) 1200925 entitled “The emergence of of ecologies through metabolic cooperation and recursive organization” and by Centro de Modelamiento Matemático (CMM), Grant FB210005, BASAL funds for centers of excellence from ANID-Chile, Grants ACE210006 and ACE210010 to the Instituto de Ecología y Biodiversidad and CMM, respectively and by Grant EcoDep PSI-AAP2020-0000000013. J.I.A. and G.B.W. were supported by NSF Grant 1838420, J.I.A. and C.P.K. were supported by NSF Grant 1840301, and G.B.W. and C.P.K. were supported by the Charities Aid Foundation of Canada for the grant entitled “Toward Universal Theories of Ecological Scaling.” B.D. acknowledges support from projects ANID-FONDECYT 1150171 and 1190998.
Footnotes
Reviewers: R.H., University of Washington; and A.R., Ecole Polytechnique Federale de Lausanne.
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2119872119/-/DCSupplemental.
Data Availability
All data and R codes used in the preparation of figures and in statistical analyses can be found in GitHub (67).
References
- 1.Hochachka P. W., Somero G. N., Biochemical Adaptation: Mechanism and Process in Physiological Evolution (Oxford University Press, 2002). [Google Scholar]
- 2.Brown J. H., Gillooly J. F., Allen A. P., Savage V. M., West G. B., Toward a metabolic theory of ecology. Ecology 85, 1771–1789 (2004). [Google Scholar]
- 3.Schulte P. M., Healy T. M., Fangue N. A., Thermal performance curves, phenotypic plasticity, and the time scales of temperature exposure. Integr. Comp. Biol. 51, 691–702 (2011). [DOI] [PubMed] [Google Scholar]
- 4.Dell A. I., Pawar S., Savage V. M., Systematic variation in the temperature dependence of physiological and ecological traits. Proc. Natl. Acad. Sci. U.S.A. 108, 10591–10596 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Grimaud G. M., Mairet F., Sciandra A., Bernard O., Modeling the temperature effect on the specific growth rate of phytoplankton: A review. Rev. Environ. Sci. Biotechnol. 16, 625–645 (2017). [Google Scholar]
- 6.Ritchie M.E., Reaction and diffusion thermodynamics explain optimal temperatures of biochemical reactions. Sci Rep 8, 11105 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rezende E. L., Bozinovic F., Szilágyi A., Santos M., Predicting temperature mortality and selection in natural Drosophila populations. Science 369, 1242–1245 (2020). [DOI] [PubMed] [Google Scholar]
- 8.Yap T. F., Liu Z., Shveda R. A., Preston D. J., A predictive model of the temperature-dependent inactivation of coronaviruses. Appl. Phys. Lett. 117, 060601 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Laidler K. J., King M. C., The development of transition-state theory. J. Phys. Chem. 87, 2657–2664 (1983). [Google Scholar]
- 10.Ratkowsky D. A., Olley J., Ross T., Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 233, 351–362 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Price C. A., et al., Testing the metabolic theory of ecology. Ecol. Lett. 15, 1465–1474 (2012). [DOI] [PubMed] [Google Scholar]
- 12.Knies J. L., Kingsolver J. G., Erroneous Arrhenius: Modified Arrhenius model best explains the temperature dependence of ectotherm fitness. Am. Nat. 176, 227–233 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Okie J. G., “Microorganisms” in Metabolic Ecology: A Scaling Approach, Sibly R. M., Brown J. H., Kodric-Brown A., Eds. (John Wiley & Sons, 2012), pp. 135–153. [Google Scholar]
- 14.Evans M. G., Polanyi M., Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 31, 875–894 (1935). [Google Scholar]
- 15.Hänggi P., Talkner P., Borkovec M., Reaction-rate theory: Fifty years after kramers. Rev. Mod. Phys. 62, 251 (1990). [Google Scholar]
- 16.Zhou H. X., Rate theories for biologists. Q. Rev. Biophys. 43, 219–293 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Eyring H., The activated complex and the absolute rate of chemical reactions. Chem. Rev. 17, 65–77 (1935). [Google Scholar]
- 18.Daniel R. M., Danson M. J., Eisenthal R., The temperature optima of enzymes: A new perspective on an old phenomenon. Trends Biochem. Sci. 26, 223–225 (2001). [DOI] [PubMed] [Google Scholar]
- 19.DeLong J. P., et al., The combined effects of reactant kinetics and enzyme stability explain the temperature dependence of metabolic rates. Ecol. Evol. 7, 3940–3950 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Prabhu N. V., Sharp K. A., Heat capacity in proteins. Annu. Rev. Phys. Chem. 56, 521–548 (2005). [DOI] [PubMed] [Google Scholar]
- 21.Savage V. M., Improved approximations to scaling relationships for species, populations, and ecosystems across latitudinal and elevational gradients. J. Theor. Biol. 227, 525–534 (2004). [DOI] [PubMed] [Google Scholar]
- 22.Herzfeld K. F., Zur theorie der reaktionsgeschwindigkeiten in gasen. Ann. Phys. 364, 635–667 (1919). [Google Scholar]
- 23.West G. B., Brown J. H., Enquist B. J., A general model for ontogenetic growth. Nature 413, 628–631 (2001). [DOI] [PubMed] [Google Scholar]
- 24.Gillooly J. F., Brown J. H., West G. B., Savage V. M., Charnov E. L., Effects of size and temperature on metabolic rate. Science 293, 2248–2251 (2001). [DOI] [PubMed] [Google Scholar]
- 25.Allen A. P., Brown J. H., Gillooly J. F., Global biodiversity, biochemical kinetics, and the energetic-equivalence rule. Science 297, 1545–1548 (2002). [DOI] [PubMed] [Google Scholar]
- 26.Allen A. P., Gillooly J. F., Savage V. M., Brown J. H., Kinetic effects of temperature on rates of genetic divergence and speciation. Proc. Natl. Acad. Sci. U.S.A. 103, 9130–9135 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Savage V. M., Gilloly J. F., Brown J. H., Charnov E. L., Charnov E. L., Effects of body size and temperature on population growth. Am. Nat. 163, 429–441 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Bernhardt J. R., Sunday J. M., O’Connor M. I., Metabolic theory and the temperature-size rule explain the temperature dependence of population carrying capacity. Am. Nat. 192, 687–697 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Huey R. B., Hertz P. E., Is a jack-of-all-temperatures a master of none? Evolution 38, 441–444 (1984). [DOI] [PubMed] [Google Scholar]
- 30.M. J. Angilletta, Jr, Huey R. B., Frazier M. R., Thermodynamic effects on organismal performance: Is hotter better? Physiol. Biochem. Zool. 83, 197–206 (2010). [DOI] [PubMed] [Google Scholar]
- 31.Stover B. J., Eyring H., The dynamics of life. I. Death from internal irradiation by 239Pu and 226Ra, aging, cancer, and other diseases. Proc. Natl. Acad. Sci. U.S.A. 66, 132–139 (1970). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Eyring H., Stover B. J., The dynamics of life. II. The steady-state theory of mutation rates. Proc. Natl. Acad. Sci. U.S.A. 66, 441–444 (1970). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stover B. J., Eyring H., The dynamics of life, 3. Mechanisms of nonsurvival and the relation of dose size. Proc. Natl. Acad. Sci. U.S.A. 66, 672–676 (1970). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Eyring H., Stover B. J., The dynamics of life: Aging. Proc. Natl. Acad. Sci. U.S.A. 69, 3512–3515 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Freeman D. C., Klikoff L. G., Eyring H., Applications of the survival theory to ecology. Proc. Natl. Acad. Sci. U.S.A. 71, 4332–4335 (1974). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wullstein L. H., Bjorklund R., Eyring H., Application of the Eyring-Stover survival theory to soil-related functions. Proc. Natl. Acad. Sci. U.S.A. 77, 3767–3768 (1980). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hobbs J. K., et al., Change in heat capacity for enzyme catalysis determines temperature dependence of enzyme catalyzed rates. ACS Chem. Biol. 8, 2388–2393 (2013). [DOI] [PubMed] [Google Scholar]
- 38.Kooij D., Über die zersetzung des gasförmigen phosphorwasserstoffs. Z. Phys. Chem. 12, 155–161 (1893). [Google Scholar]
- 39.Eyring H., The activated complex in chemical reactions. J. Chem. Phys. 3, 107–115 (1935). [Google Scholar]
- 40.Dzakula Z., Andjus R. K., Biophysical models of protein denaturation. I. An improvement of the model of two states. J. Theor. Biol. 153, 41–59 (1991). [DOI] [PubMed] [Google Scholar]
- 41.Pörtner H. O., Climate change and temperature-dependent biogeography: Oxygen limitation of thermal tolerance in animals. Naturwissenschaften 88, 137–146 (2001). [DOI] [PubMed] [Google Scholar]
- 42.Somero G. N., The physiology of global change: Linking patterns to mechanisms. Annu. Rev. Mar. Sci. 4, 39–61 (2012). [DOI] [PubMed] [Google Scholar]
- 43.Somero G. N., Lockwood B. L., Tomanek L., Biochemical Adaptation: Response to Environmental Challenges from Life’s Origins to the Anthropocene (Sinauer Associates, 2017). [Google Scholar]
- 44.Kingsolver J. G., Woods H. A., Beyond thermal performance curves: Modeling time-dependent effects of thermal stress on ectotherm growth rates. Am. Nat. 187, 283–294 (2016). [DOI] [PubMed] [Google Scholar]
- 45.Jørgensen L. B., Malte H., Overgaard J., How to assess drosophila heat tolerance: Unifying static and dynamic tolerance assays to predict heat distribution limits. Funct. Ecol. 33, 629–642 (2019). [Google Scholar]
- 46.Schroeder D. V., An Introduction to Thermal Physics (Oxford University Press, 2021). [Google Scholar]
- 47.Demirel Y., Gerbaud V., Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems (Elsevier, 2018). [Google Scholar]
- 48.Labra F. A., Marquet P. A., Bozinovic F., Scaling metabolic rate fluctuations. Proc. Natl. Acad. Sci. U.S.A. 104, 10900–10903 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Giometto A., Altermatt F., Carrara F., Maritan A., Rinaldo A., Scaling body size fluctuations. Proc. Natl. Acad. Sci. U.S.A. 110, 4646–4650 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rebolledo R., Navarrete S. A., Kéfi S., Rojas S., Marquet P. A., An open-system approach to complex biological networks. SIAM J. Appl. Math. 79, 619–640 (2019). [Google Scholar]
- 51.Tsimring L. S., Noise in biology. Rep. Prog. Phys. 77, 026601 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Marquet P. A., Espinoza G., Abades S. R., Ganz A., Rebolledo R., On the proportional abundance of species: Integrating population genetics and community ecology. Sci. Rep. 7, 16815 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Marquet P. A., et al., Scaling and power-laws in ecological systems. J. Exp. Biol. 208, 1749–1769 (2005). [DOI] [PubMed] [Google Scholar]
- 54.Cohen J. E., Xu M., Schuster W. S., Allometric scaling of population variance with mean body size is predicted from Taylor’s law and density-mass allometry. Proc. Natl. Acad. Sci. U.S.A. 109, 15829–15834 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dixon A. F., et al., Relationship between the minimum and maximum temperature thresholds for development in insects. Funct. Ecol. 23, 257–264 (2009). [Google Scholar]
- 56.Huey R. B., Kingsolver J. G., Evolution of thermal sensitivity of ectotherm performance. Trends Ecol. Evol. 4, 131–135 (1989). [DOI] [PubMed] [Google Scholar]
- 57.Gilchrist G. W., Specialists and generalists in changing environments. I. Fitness landscapes of thermal sensitivity. Am. Nat. 146, 252–270 (1995). [Google Scholar]
- 58.Dingha B., Appel A., Vogt J., Effects of temperature on the metabolic rates of insecticide resistant and susceptible German cockroaches, Blattella germanica (l.)(Dictyoptera: Blattellidae). Midsouth Entomol. 2, 17–27 (2009). [Google Scholar]
- 59.Esechie H., Interaction of salinity and temperature on the germination of alfalfa cv CUF 101. Agronomie 13, 301–306 (1993). [Google Scholar]
- 60.Zakhartsev M., Yang X., Reuss M., Pörtner H. O., Metabolic efficiency in yeast Saccharomyces cerevisiae in relation to temperature dependent growth and biomass yield. J. Therm. Biol. 52, 117–129 (2015). [DOI] [PubMed] [Google Scholar]
- 61.Gutierrez A. P., Ponti L., Dalton D. T., Analysis of the invasiveness of spotted wing Drosophila (Drosophila suzukii) in North America, Europe, and the Mediterranean basin. Biol. Invasions 18, 3647–3663 (2016). [Google Scholar]
- 62.Kashefi K., Lovley D. R., Extending the upper temperature limit for life. Science 301, 934–934 (2003). [DOI] [PubMed] [Google Scholar]
- 63.Buck C. L., Barnes B. M., Effects of ambient temperature on metabolic rate, respiratory quotient, and torpor in an arctic hibernator. Am. J. Physiol. Regul. Integr. Comp. Physiol. 279, R255–R262 (2000). [DOI] [PubMed] [Google Scholar]
- 64.Levenberg K., A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 2, 164–168 (1944). [Google Scholar]
- 65.Elzhov T. V., Mullen K. M., Spiess A., Bolker B., R interface to the Levenberg-Marquardt nonlinear least-squares algorithm found in minpack. Plus support for bounds. R package version 1.2-1 (2010). https://CRAN.R-project.org/package=minpack.lm.
- 66.R Core Team, R: A Language and Environment for Statistical Computing (Version 3.6.1, R Foundation for Statistical Computing, 2019).
- 67.Arroyo J. I., Data associated with “A general theory for temperature dependence in biology.” GitHub. https://github.com/jose-ignacio-arroyo/tem.mod. Deposited 11 May 2022. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data and R codes used in the preparation of figures and in statistical analyses can be found in GitHub (67).