Transition State Theory-Inspired Neural Network for Estimating the Viscosity of Deep Eutectic Solvents

Abstract

The lack of accurate methods for predicting the viscosity of solvent materials, especially those with complex interactions, remains unresolved. Deep eutectic solvents (DESs), an emerging class of green solvents, have a severe lack of viscosity data, resulting in their application still staying at the stage of random trial and error, and it is difficult for them to be implemented on an industrial scale. In this work, we demonstrate the successful prediction of the viscosity of DESs based on the transition state theory-inspired neural network (TSTiNet). The TSTiNet adopts multilayer perceptron (MLP) for the transition state theory-inspired equation (TSTiEq) parameters calculation and verification using the most comprehensive DESs viscosity data set to date. For the energy parameters of the TSTiEq, the constant assumption and the fast iteration with the help of MLP can allow TSTiNet to achieve the best performance (the average absolute relative deviation on the test set of 6.84% and R² of 0.9805). Compared with the traditional machine learning methods, the TSTiNet has better generalization ability and dramatically reduces the maximum relative deviation of prediction under the constraints of the thermodynamic formulation. It requires only the structural information on DESs and is the most accurate and reliable model available for DESs viscosity prediction.

Short abstract

A transition state theory-inspired neural network allows accurate determination of the viscosity of deep eutectic solvents.

Introduction

Solvent materials occupy a strategic position in the fields of biology, pharmacy, medical treatment, chemistry, and chemical engineering.¹⁻⁵ Green chemistry requires us to use green solvents that are nontoxic and harmless to the human body and the environment. Deep eutectic solvents (DESs) are expected to achieve the design of chemical processes without utilizing or generating harmful chemicals, due to their unique physical and chemical properties such as low vapor pressure, high thermal stability, low flammability, high solubility, wide liquid range, and designable structures.⁶ The synthesis of DESs is 100% atomically economical, requiring only simple mixing of the components, without waste generation and further purification steps.⁷ These attractive properties make it a potential substitute for conventional organic solvents and ionic liquids, and some breakthroughs have been made in the fields of gas absorption,^8,9 extraction and separation,^10,11 bioengineering,¹² nanotechnology,¹³ analytical chemistry,¹⁴ catalysis,^15,16 etc. Although DESs have received widespread attention, the serious lack of viscosity information has caused their application to remain in the stage of random trial and error, and it makes it difficult to apply them on an industrial scale.^17,18

Viscosity is internal friction or resistance to the flow caused by intermolecular interactions and is very important in all physical processes involving fluid movement or component dissolution. Viscosity information determines dimensions for a pipe system, specifications for pumps or heat exchangers, the operability of the mixing and separation process, and the application of the product. Understanding the viscosity of DESs is considered a top priority in investigating their applications in different fields and designing the application processes. To obtain viscosity information on the immeasurable number of DESs (the theoretical possible combinations of components that exhibit eutectic behavior are unlimited^19,20), accurate determination of their viscosity must be done. Most of the proposed viscosity models of DESs are based on a limited database and are applicable for only one kind of DES or for only a limited database of DESs. For example, the viscosity model for choline chloride-based DESs²¹ and the viscosity model that only applies to hydrophobic DESs²² belong to the former. The latter is common in applications based on some small modeling databases. For example, the models are proposed to predict the viscosity of 27 different DESs through cubic plus association (CPA) and perturbed chain-statistical associating fluid theory (PC-SAFT) equations of state (EOSs). Coupling with the friction theory²³ or free volume theory,²⁴ their models have deviations of 4.4% and 2.7%, respectively. It can be seen that such models can generally achieve small average absolute relative deviation (AARD), but, limited by their small scope of application, the practicability of this kind of model is low. There is only one viscosity model considering all types of DESs to date.²⁵ However, it is a regression model that requires some experimental viscosity data as inputs. Besides, the AARD of the model is as high as 10.4%, and maximum absolute relative deviation (MARD) achieves 83.9%. This result is still unsatisfactory. To predict the viscosity of DESs accurately and efficiently, it is necessary to develop a comprehensive prediction model with an extensive database covering every type of DESs and small prediction deviation.

The use of machine learning in physicochemical properties modeling has great potential to accelerate the discovery and application of emerging solvent materials. The neural network (NN) is currently one of the most commonly used machine learning methods.²⁶⁻²⁸ With powerful abilities of feature extraction and function learning, NN has arisen as a potential and very suitable approach in quantitative structure–property relationship (QSPR) models and quantitative structure–activity relationship (QSAR) models.²⁹⁻³³ However, the main weakness of the plain NN model is its poor portability. The prediction of the plain NN model is only driven by the stack of data, while the laws of physics are omitted. Hence, for an uneven data set (e.g., the viscosity data set has a large proportion of low viscosity data points), the plain NN models have difficulty capturing the correct input–output relationships in the region of the low proportion part in the data set.³⁴ Unfortunately, the data distribution is always biased. The data augmentation method is one possible way to alleviate this problem.³⁵ However, research on the data augmentation method for molecules is still in its early stages, especially in the field of molecule property prediction. In contrast to the most prominent fields of NN applications (e.g., computer vision, natural language processing), most physicochemical characteristics have theoretical or semiempirical equations that are represented by temperature and molecular information. A more efficient and feasible way is to combine the prior knowledge of humans with machine learning methods, and it has been proven to do well in various fields.³⁶⁻³⁸

Absolute rate theory³⁹ and free volume theory⁴⁰ based on transition state theory are currently the most commonly accepted theoretical models for calculating the viscosity of pure liquids. By introducing appropriate mixing rules, we establish a transition state theory-inspired neural network (TSTiNet) model, which needs only structural information on DESs. It is the most accurate and reliable model currently available for viscosity prediction of DESs. This work provides an initiative to develop reliable models to predict the viscosity of DESs and promote the application and inverse design of DESs.

Results and Discussion

Data Analysis

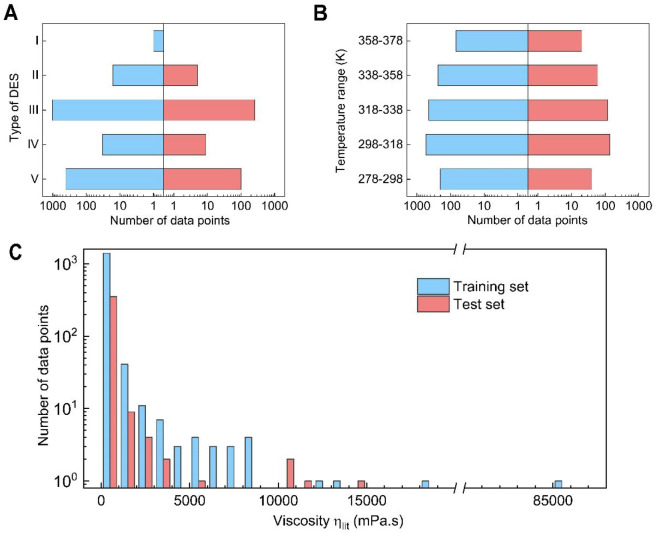
The database of the viscosity of DESs covers the viscosity values from 1.3 to 85 000 mPa·s, which confers higher chances of solvent manipulations to design task-specific solvents. As shown in Table 1, DESs are divided into five categories according to their compositions: (I) the combination of organic salt and metal salt, (II) the combination of organic salt and hydrated metal salt, (III) the combination of organic salt and nonionic hydrogen bond donor (HBD), (IV) the combination of hydrated metal salt and nonionic HBD, and (V) the combination of nonionic hydrogen bond acceptor (HBA) and nonionic HBD. The number of different types of DESs investigated in this work is shown in Figure 1A. Type I, II, and IV DESs have fewer examples in the database because of the limitation of hydrated and nonhydrated metal halides.⁴¹ Type III and V DESs have the most, as they are usually selected from a wide range of natural compounds and thus are less toxic and less expensive than other classes.⁴²

Table 1. General Formula for the Classification of DESs.

type	general formula	terms
Type I	Cat+X– + zMClx	M = Zn, Sn, Fe, Al, Ga, In
Type II	Cat+X– + zMClx·yH2O	M = Cr, Co, Cu, Ni, Fe
Type III	Cat+X– + zRZ	Z = CONH2, COOH, OH
Type IV	MClx + RZ	M = Al, Zn; Z = CONH2, OH
Type V	RZ1 + RZ2	Z1,2 = OH, COOH

Figure 1.

Number of DESs’ viscosity data on the training set and test set. (A) Number of DESs’ viscosity data in different types. (B) Number of DESs’ viscosity data in the different temperature ranges. (C) Number of DESs’ viscosity data in different viscosity value ranges.

The viscosity of DESs is a function of temperature.⁴³ In this work, the 2229 data points collected have a wide temperature range of 278.15–378.15 K, which is the operating temperature range of most solvents. As shown in Figure 1B, we divide the temperature range into 5 equal intervals, and each range includes at least 50 data points, which shows the temperature distribution in our data set is balanced. This feature is helpful for the viscosity model to learn the relationship between viscosity and temperature.

The histogram in Figure 1C shows a bimodal distribution of the viscosity values with 1000 mPa·s as an interval. Most data points are at a viscosity of less than 1000 mPa·s, and few data points are in the high viscosity region. That is because solvents with low viscosity are often of more interest due to energy consumption considerations. The imbalanced data distribution leads to poor performance of machine learning models in the region of high viscosity.⁴⁴⁻⁴⁹ Although limited information is available, the prediction of viscosity of DESs in the high-value region is very meaningful in the field of daily chemicals and petroleum chemicals. Taking the applications of DESs as lubricants as an example, the oil film with too low viscosity is unstable and easy to break, and a higher viscosity is preferred.

Viscosity Model from Transition State Theory

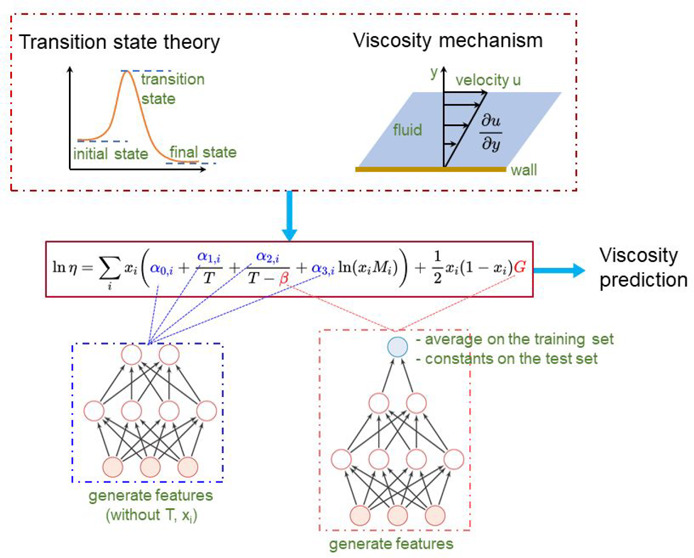
Transition state theory regards chemical reactions and other processes as continuous changes in the relative positions and potential energies of the constituent atoms and molecules. There is an intermediate configuration on the path between the initial and final arrangements of atoms or molecules, at which the potential energy has a maximum value. The configuration corresponding to this maximum is known as the activated complex, and its state is referred to as the transition state.⁵⁰ Both absolute rate and free volume theories of liquid viscosity based on the transition state theory are widely accepted for calculating the viscosity of pure liquids.⁵¹ Both theories are based on the assumption of a quasi-crystalline liquid structure.⁵² The flow process of Newtonian fluid can be expressed as

1

After the molecule at position X obtains the activation energy E, the activated molecule X′ will move to the new vacancy Y. That is, a molecule is considered to be vibrating near the equilibrium position; when it has enough energy and there is a free space, the molecule will jump to a new equilibrium position. The probability of this jump p_j can be expressed as

2

where p_E is the probability of attaining sufficient energy to cross the barrier, and p_v is the probability that there is sufficient local free volume for a jump to occur.

The absolute rate theory simplifies the processing of all pores in the fluid to have the same volume, so that the temperature dependence of viscosity is simplified to determine the number of possible jumps for molecules to cross the barrier at different temperatures. This simplification leads to inaccurate calculation of p_v. The free volume theory considers a liquid composed only of hard balls and repulsive force, and successfully deduced the distribution of pore sizes in the fluid. However, this theory ignores the role of attraction and is incomplete in calculating the probability p_E of molecular transitions. It was found that in a narrow temperature range, either the absolute rate theory or the free volume theory can fit the experimental data well. However, in a wide temperature range, neither equation can successfully depict the viscosity–temperature relationship. For this reason, the concept of combining absolute rate and free volume theories was proposed to depict the Newtonian viscosity of liquid under various temperatures.⁵³

According to the definition of Newtonian viscosity, considering two layers of molecules in a liquid, at a distance λ₁ apart, the force f applying on per square meter makes one layer slide past the other. The difference in the velocity of the two layers is Δu. Then the viscosity η is equal to

3

Absolute rate theory describes the process as molecules crossing the barrier from one equilibrium position to another.

4

where λ is the distance between the two equilibrium positions in the direction of movement; λ₂ and λ₃ are the average distances between two adjacent molecules in the moving layer perpendicular and the same to the direction of the movement, respectively. κ is the number of times a molecule passes over the barrier per second; k is Boltzmann’s constant, and T is the absolute temperature.

Substitution in eq 3 then gives

5

For normal viscous flow, f is relatively small, and since λ, λ₂, and λ₃ are all about molecular dimensions, it follows that 2kT ≫ fλ₂λ₃λ. It is thus possible, in expanding the exponentials included in eq 5, to neglect all terms beyond the first, and the result is

6

Although λ is not necessarily equal to λ₁, the two quantities are of the same order of magnitude and if, as a first approximation, they are taken to be identical (λ = λ₁). The product λ₂λ₃λ₁ is approximately the volume inhabited by a single molecule in the liquid state, and hence it may be put equal to V/N, where V is the molar volume and N is the Avogadro number; then eq 6 can be written as

7

If E is the standard free energy of activation per mole, κ is given by

8

where R is the gas constant; substitution in eq 7 then gives the classic absolute rate viscosity model⁵⁴

9

According to the free volume theory, the pore size distribution can be obtained as

10

then P(v) is the probability of finding the free volume v nearby. The average free volume per molecule is V_f. The constant r is a numerical factor needed to correct for the overlap of free volume. Assuming that a minimum local free volume V* is necessary for a jump to occur, one can calculate the probability of finding V* and thus the jump probability p_v.

11

So we can get the classic free volume viscosity model⁵⁵

12

Although these two viscosity models have shortcomings, the absolute rate model fully expresses p_E, while the free volume model expresses p_v better.

13

14

The quasi-crystalline theory of liquid viscosity assumes that the viscosity is inversely proportional to the jump probability. Combining the absolute rate and free volume theories, the viscosity of a liquid can be described as follows,

15

quantity V* should be close to V₀, the close-packed molecular volume per mole, and V_f is defined as

16

This hybrid equation has been applied to many types of liquid including polyatomic van der Waals as well as hydrogen-bonded liquids.⁵⁶

One method for obtaining V_f is to assume that the free volume is the total thermal expansion at constant pressure where V₀ is considered to be independent of temperature, and then, V_f can be obtained approximately by

17

where α is the thermal expansion coefficient, and T₀ is the temperature of completely ordered material.

For this case, eq 15 can be rearranged as,

18

where

19

As mentioned before, the composition of DES will affect its viscosity. It is found that⁵⁷ the DES system formed using glycerol as the HBD and different types of ammonium salts as the HBA has the viscosity decreasing along with the reduced molecular weight of the DES. Hence, in this work, we assumed that A_η varied with M^y, and eq 18 thus could be expressed as

20

A, E, α′, T₀, and y are adjustable parameters. Equation 20 can be used to correlate viscosity data of liquids, and these adjustable parameters can be obtained if viscosity-temperature data is available.

For temperatures ranging from the melting point to the normal boiling point, eq 20 can be expressed in a more general form as follows,

21

Assuming the temperature of completely ordered material (β) is ideal, the difference between different substances is slight. To simplify the model, in this work, we assume that β is a constant, and the adjustable parameters α₀, α₁, α₂, and α₃ are only molecules dependent.

Therefore, according to the Grunberg–Nissan method,⁵⁸ the viscosity of the binary nonideal mixture DES can be expressed as follows (which is called as TSTiEq):

22

where η_DES is the viscosity of DES, x is the mole fraction of the component, M is the molecular weight of the component, α₀, α₁, α₂, and α₃ are the structural parameters. G is the interaction factor of the component HBA and HBD. Both β and G are the energy parameters. To simplify the model, we supposed that the values of G, namely, G_I, G_II, G_III, G_IV, and G_V, are the same for the same type of DES, which has been proved to be reasonable in our previous work.^59,60

NN vs TSTiNet

Many metrics can be chosen to evaluate the performance of the models. Since our database has an extensive range of viscosity, the frequently used mean square error (MSE) and mean absolute error (MAE) are not suitable for evaluating the performance of the models. Therefore, we evaluate both models using AARD, MARD, and the coefficient of determination (R²). AARD can tell the average performance of the model on the data set. MARD and R² can tell the reliability of the model, which is essential for practical applications.

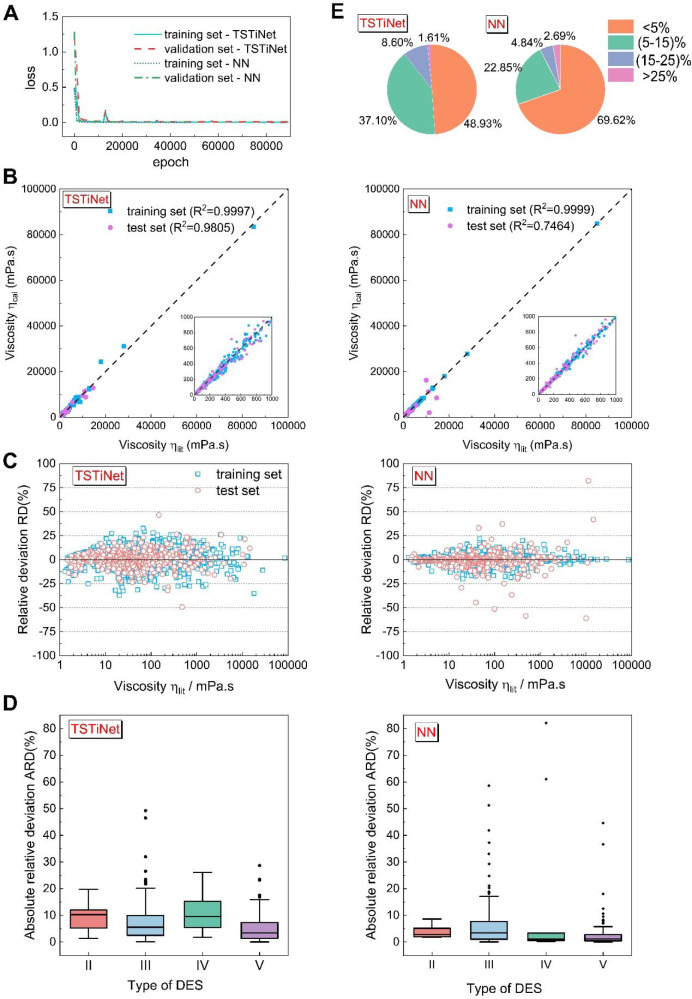
Figure 2 shows the network architecture of the TSTiNet model. As shown in Figure 2, we use three multilayer perceptrons (MLPs) to calculate the parameters in TSTiEq, and each MLP has different inputs. In addition to the TSTiNet model, we also implement a plain NN model to predict DESs’ viscosity as a comparison. The plain NN model takes all features as inputs to calculate logarithmic viscosity directly, and the architecture of the NN model is as same as the MLP in the TSTiNet.

Figure 2.

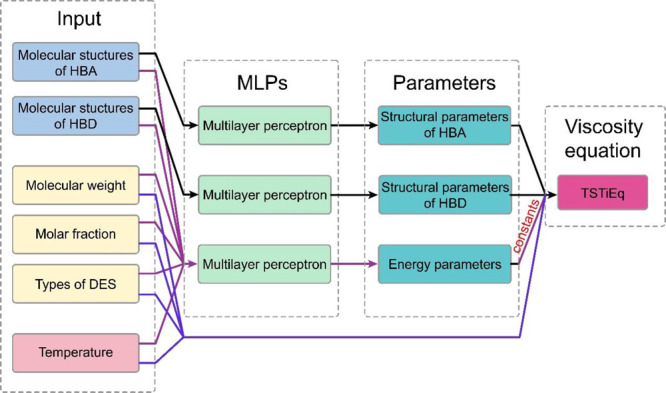
The network architecture of the TSTiNet model. The model takes the structure information, molecular weight, mole fraction, types of DESs with one-hot encoding, and temperature as input features. Then the model uses two MLPs to calculate structural parameters with molecular structures of HBA and HBD, respectively. Besides, the model uses one MLP to calculate energy parameters with all input features. It should be noted that the energy parameters are treated as constants. In other words, the final value of the energy parameters is the average of the values on the training set. The molecular weight, mole fraction, types of DESs, and temperature are directly driven into the TSTieq. Then TSTieq gives the final value of the logarithmic viscosity of DESs.

The training process and performances of both models are shown in Figure 3, and the metrics are provided in Table 2. As shown in Figure 3A, neither model falls into severe overfitting, which indicates both models achieve a trade-off between variance and bias. Figure 3B shows a scatter chart correlating the predicted and reported viscosity values of the training and test sets. The calculated viscosity of DESs using the TSTiNet model displays a better agreement with the corresponding experimental viscosity data than that of the plain NN model. It can be seen that most of the data points are close to the identity line on both models, but some noticeable deviation points appear in the plain NN model. Although the plain NN model has a higher R² on the training set (R² = 0.9999), it has an unacceptable R² on the test set (R² = 0.7464). In comparison, the TSTiNet model achieves high R² on both training and test sets (training set R² = 0.9997 and test set R² = 0.9805). Besides, to ensure a better understanding of the results, the distribution of relative deviations (RD) between the literature and the predicted viscosity on the training and test sets is shown in Figure 3C. Although most data points in the plain NN model are closer to the line with RD = 0, some data points are far from that line. As mentioned in the Data Analysis section, most models based on machine learning are not good at predicting the region of high viscosity. Thus, we can see that the points with the most significant deviation in the plain NN model are located in the right area of the figure. In contrast, the RD distribution in the TSTiNet model is more evenly on the line with RD = 0, and there are not many large deviation points appearing in the right region. The box plots of different types of DESs are plotted in Figure 3D. It can be seen that the plain NN model has very low median absolute relative deviation (ARD) (all less than 5%) for different types of DESs but has many outliers. Further, what is even more difficult to accept in the plain NN model is that some outliers have significantly large values, especially in the type IV DESs. This is further reflected in Figure 3E: the number of data points of ARD > 25% on the TSTiNet model (1.61%) is less than that of the plain NN model (2.69%). This result indicates that the TSTiNet model has a stronger generalization ability than that of the plain NN model. In other words, the TSTiNet model can predict the full range of data under the condition of an uneven distribution of data points.

Figure 3.

Training processes and performances of the plain NN model and the TSTiNet model. (A) Learning curve of the TSTiNet model and the plain NN model. An epoch is when all the training data pass through the network during the training phase. (B) Correlation between the predicted and reported viscosity values of data sets. The achieved R² on the training set and test set are given on the top. (C) Relative deviations between the literature and the predicted viscosity in both data sets. (D) Box plots of ARD on different types DESs. Each box shows the interquartile range (IQR between Q1 and Q3) for the corresponding set. The central mark (horizontal line) shows the median, and the whiskers show the rest of the distribution based on IQR (Q1 – 1.5 × IQR, Q3 + 1.5 × IQR). Data outside of this range are considered outliers and represented by dark dots. (E) Percentage of ARD on the test set in different ranges, which are <5%, 5–15%, 15–25%, and >25%.

Table 2. Metrics of Different Models on the Test Set.

metric	plain NN	TSTiNet-mixed	TSTiNet-variables	TSTiNet-constants
R2	0.7464	0.9805	0.8857	0.7320
AARD (%)	5.23	6.85	6.06	9.85
MARD (%)	82.15	49.28	69.47	99.03

More detailed information can be found in Table 2. Table 2 shows that the TSTiNet model has comparable AARD with the plain NN model but performs better on the metrics of R² and MARD. The plain NN model has a smaller AARD, which may be attributed to the fact that the plain NN model has learned a more complicated formula than the TSTiNet model. In the TSTiNet model, the relationships between viscosity and molecular weight, mole fraction, type of DES, and temperature are described by TSTieq whose formula is fixed. The constraints of the equation make the TSTiNet model perform slightly worse in AARD. However, from another perspective, the equation derived from viscosity theory can also limit the model from fitting incorrect relationships. In contrast, the plain NN model is completely driven by data, causing it tp not be well trained in some regions with few data points. Therefore, the plain NN model has worse performance on R² and MARD. In short, although the plain NN model with more flexibility can get good results in most data points, it is this flexibility that makes the plain NN model susceptible to the uneven data set in the training set, which makes the reliability of the model poor. In contrast to the plain NN model, the TSTiNet model can give a better prediction on all data sets with high R², which indicates that the TSTiNet model has better generalization ability. In industrial applications, the reliability of the model is of paramount importance. Since the TSTiNet model can accurately predict the viscosity of DESs in the full viscosity range and all types of DESs, it is a more appropriate model to be applied in the prediction of the viscosity of DESs.

As a comparison, we also test the performance of other traditional machine learning methods (random forest, gradient boosting, and LightGBM), after hyperparameter optimization, all the models cannot get comparable performance with TSTiNet (R² > 0.9, MARD < 50%). More detailed comparisons and discussions are shown in Supporting Information. To give a more comprehensive perspective of the proposed model, we also explore the relationships between viscosity with temperature, mole fraction, and types of HBA and HBD (as shown in Supporting Information), and the results show that the trends of model prediction value and experimental value matched very well.

Ways to Train the Energy Parameters

The energy parameters refer to β and G in TSTiEq. These two parameters are closely related to the intramolecular or intermolecular interaction energy.⁶¹ The parameter β affects the relationship between viscosity and temperature, and the parameter G affects the relationship between the viscosity of DESs and the type of HBA and HBD. Therefore, it is crucial to fit the energy parameters accurately. To achieve a more accurate viscosity prediction model, we examine three methods to fit the parameters.

Given that the energy parameters are theoretically related to the structure information of HBA and HBD, molecular weights, temperature, etc., we first take all features as input to train an MLP model, whose outputs are the energy parameters. The viscosity prediction model including this MLP is called TSTiNet-variables. As shown in Table 2, although the TSTiNet-variables model has a higher R², lower MARD, and comparable AARD compared with the NN model, its R² and MARD are still unacceptable. A possible explanation for this result is that all the features are involved in the training of the MLP for energy parameters in the TSTiNet-variables model; then the model will approximate the NN model to achieve a lower loss. For example, if the outputs of the MLPs for predicting structure parameters (α₀, α₁, α₂, α₃) get all zeros, the TSTiEq will degenerate to

23

This shows that the viscosity prediction is similar to the prediction of G. This similarity makes the TSTiNet-variables model and the NN model behave similarly (all have bad R² and MARD).

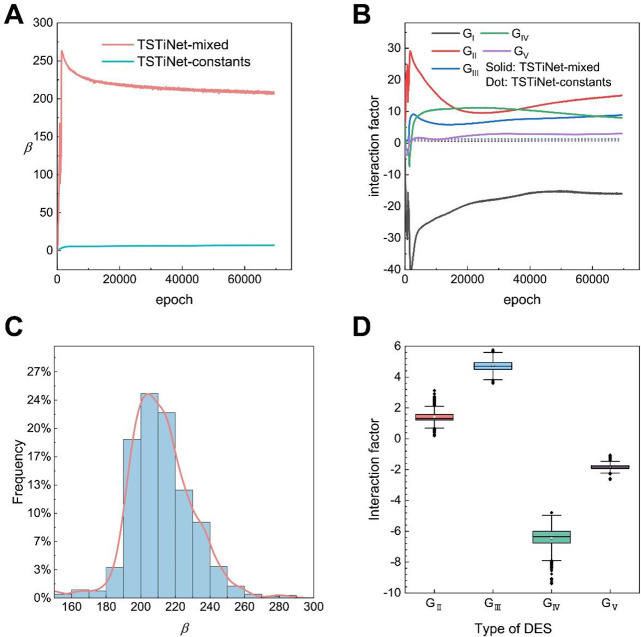
To prevent the TSTiNet model from degenerating to the NN model, we trained the energy parameters as constants. Consequently, the energy parameters can be embedded in the viscosity model as trainable model parameters. The viscosity prediction model, including this training method of the energy parameters, is called TSTiNet-constants. As Table 2 shows, the TSTiNet-constants model performs worse than both the NN and TSTiNet-variables models. This result suggests that the TSTiNet-constants model may have fallen into underfitting, and the higher training loss of the TSTiNet-constants model (Huber loss approaching 0.007) supports this explanation. As a comparison, the loss of the TSTiNet-variables model approaches 0.002. The reason for the underfitting of TSTiNet-constants model may be due to the model falling into the local minimum of the loss function. Furthermore, limited by a low learning rate, the iteration of the energy parameters is very slow, as shown in Figure 4A,B. Both Figure 4A and Figure 4B show that the value of the energy parameters change very little from the initial value, which means that the energy parameters are not well trained. The poor training of the energy parameters causes the TSTiNet-constants model to perform poorly.

Figure 4.

Energy parameters during the training process and final distribution on the training set. (A) The parameter β over training epochs on the TSTiNet-mixed model and the TSTiNet-constants model; (B) the interaction factors of different types of DESs over training epoch on the TSTiNet-mixed model and the TSTiNet-constants model. (C) The histogram describes the frequency of occurrence of different ranges of values of the parameter β on the training set. The orange curve is the kernel smooth of the histogram. (D) Box plot of interaction factors on different types of DES. Each box shows the interquartile range (IQR between Q1 and Q3) for the corresponding set. The central mark (horizontal line) shows the median, and the whiskers show the rest of the distribution based on IQR (Q1 – 1.5 × IQR, Q3 + 1.5 × IQR). Data outside of this range are considered outliers and represented by dark dots. Since type I DESs have only one data point in the training set, the interaction factor of type I DESs is not present in the box plot.

Since the TSTiNet-variables model has a degeneration problem and the TSTiNet-constants model has an underfitting problem, neither model can give good viscosity prediction performance. To solve these two problems, a novel method for training energy parameters is constructed. Since the TSTiNet-variables model can converge faster and converge to a lower training loss, we still use a two-layer MLP to calculate the energy parameters. Meanwhile, we still adopt the assumption that the energy parameters are constant to prevent model degeneration. Combining these two premises, we divide the calculation of energy parameters into two processes: the training and nontraining processes. In the training process, we use an MLP to calculate the energy parameters (β, G_I, G_II, G_III, G_IV, and G_V) of all the examples in the training set and take the average in the training set. In the nontraining process (validation process or test process), we ignore the MLP that calculates the energy parameters and directly use the average value of the energy parameters on the training set, which means all the energy parameters are considered as constants. The viscosity prediction model, including this training method of the energy parameters, is called TSTiNet-mixed. As shown in Table 2 and the results of the previous section, the TSTiNet-mixed model offers the best performance on R² and MARD and comparable performance on AARD with the NN model and the TSTiNet-variables model. The reason why the TSTiNet-mixed model performs better than the TSTiNet-constants model can be seen from Figure 4A,B. Because of the use of MLP for energy parameters in the training process, the model parameters are increased, which makes the energy parameters get more effective training. On the other hand, treating the energy parameters as constants during model evaluation avoids the degeneration of the model. Both Figure 4C and Figure 4D show that the assumption that the energy parameters are constants is reasonable. From the plotting of the frequency of β on the training set (Figure 4C), parameter β has 71% of the values between 180 and 220. Therefore, the assumption that the parameter β can be regarded as a constant is reasonable. The box plot of the interaction factor on the training set can be seen in Figure 4D. As shown in Figure 4D, the intervals between the upper and lower quartiles of the interaction factor of four types of DESs are small. It shows that the interaction factor is only related to the type of DESs, and the interaction factor of DESs under the same type can also be regarded as a constant. Consequently, the combination of MLP and assumption of constant energy parameters makes the TSTiNet-mixed model have the best performance.

Particularly, we wish to point out that our model is also illuminating for predicting other labels with a theoretical basis (e.g., density, thermal conductivity). When combining a theoretical equation with NN, the first thing to note is that certain features (e.g., temperature, composition) in the equation should have a fixed and reasonable relationship. Furthermore, these features should not be involved in the equation parameters. Otherwise, it will cause the degeneration of the model. Second, for the constant parameters in the equation, a feasible training method is to use an MLP to calculate the mean value of the parameters on the training set and discard this MLP during model evaluation. This method can avoid degeneration and underfitting problems according to the experiments. Finally, the theory-inspired neural network is especially suitable for occasions with few data points and uneven data distribution. For giant data sets and even data distribution, more complex deep neural networks may be more appropriate.

Conclusion

In this work, a model combining theoretical equations and NN is used to predict the viscosity of DESs. This model uses prior theoretical knowledge to solve the model generalization problem caused by the lack of data and uneven distribution. A novel viscosity equation that relates viscosity to molecular weight is derived based on the transition state theory. Then the energy parameters and structural parameters in the equation are calculated through three MLPs. The results show that our model (the TSTiNet model) exhibits better viscosity prediction performance compared to the plain NN model. The TSTiNet model overcomes the shortcoming of most viscosity models in predicting poorly for larger viscosities and dramatically improves the performance on R² and MARD. By now, the TSTiNet model is the most accurate and reliable model for predicting the viscosity of DESs.

Materials and Methods

Databank

The viscosity of DESs is one of the most challenging properties to predict as the difference in water content of DESs will dramatically change the viscosity.⁶² Furthermore, different measurement methods may also cause deviations in the measured viscosity values. In some cases, the experimental viscosity data show an undesirable variability; i.e., the viscosity presented in the literature shows apparent inconsistencies, and significant dispersions are present. For example, choline chloride–malonic acid (1:1) shows an apparent discrepancy at 293.15 K (2016 mPa·s⁶³ and 900 mPa·s⁶⁴). This variability in the experimental viscosities limits the application of these data in research activity and process development. Hence, experimental data on the viscosities of these solvents are not a reliable source without appropriate analysis and re-elaboration.

The data used in the current model development is screened as follows:⁶⁵

• (1)If there were several reported values of viscosity for a particular temperature and the difference between these viscosity values exceeds 50%, the value with the lowest uncertainty was incorporated into the data set utilized.
• (2)If the reported values had the same uncertainties, the latest published values were utilized.

A sufficiently large database is important for machine learning. Group values derived from a limited number of species may overfit and cannot be applied to new species with the same group. Therefore, a comprehensive literature review has been carried out in the first step to build an extensive set of liquid viscosity data for DESs. The data set used consists of 2229 experimental points, including all the experimental measurements reported in the published literature up to the date of writing this work to ensure that the developed models are highly reliable and robust. The collected data set includes 183 DESs that are prepared from 49 HBA and 70 HBD. The data set covers a wide range of viscosity (1.3–85000 mPa·s) measurements with a wide range of temperatures (278.15–378.15 K) and HBA/HBD mole ratios (1:19–49:1) measured at atmospheric pressure. The viscosity data set (η/mPa·s) provides a lot of important information, including both HBA and HBD names, CAS registry numbers, molecular formulas, molecular structures, mole masses, mole ratios, references, measurement methods of the viscosity, uncertainty, sample sources, purity, sample purification method, and experimental data of viscosity at different temperatures (Supporting Information). The complete data set of viscosity values, including the original reference sources of the experimental data, is presented in Supporting Information.

During the development of the model, the database for the viscosity is divided into three subsets: the training, validation, and test data sets. The training set is utilized to obtain parameters for the model. The validation set is used to tune the hyperparameters of the model, and the test set is implemented to evaluate the reliability and predictive ability of the model. In this study, we split the viscosity data of DESs into training, validation, and test set at a ratio of 4:1:1 randomly.

Generation of Chemical Features

The viscosity of a solvent is mainly determined by the molecular structure. Therefore, it is necessary to generate a series of chemical characteristics that can accurately describe the molecular structure of different solvents, which can be used as the input of the neural network. Here, the secondary division of groups has been utilized according to the practice of the group contribution method.⁶⁶

In the current method, the molecular structure of a DES is considered a combination of two types of groups: first-order groups and second-order groups. The first-order groups are used to describe the basic structure of DESs, whereas the role of the second-order groups is to provide supporting information for the molecular structure of DESs whose description is insufficient through the first-order groups.

First-Order Groups

The first level of estimation has a large set of simple groups that describe a wide variety of DESs. At present, most DESs with experimental data of viscosity can be described with only first-order groups.

The first-order groups are mainly determined based on the Joback and Reid method⁶⁷ and Valderrama method.⁶⁸ We selected 45 molecular groups as first-order groups to treat diverse types of DESs, as shown in Table 3.

Table 3. Chemical Features of the Molecules.

without rings				with rings
First-Order Groups
–CH3	–COOH	>NH/>NH+–	–S–	–CH2
–CH2	–COO–/–COO–	NH4+	–SO2–	>CH–
>CH-	-CHO	=NH	–F	=CH–
>C<	–OH	–NH2	–Cl/Cl–	>C=
=CH2	–OH(ph)	–NH2(C=O)	Br–	>C<
=CH-	–O–/–O–	>P<+	Mm	>C=O
>C=	–C≡N	P=O	H2O	–O–
>C=O	>N<+/>N–			>NH
				–N=
				>N–
Second-Order Groups
o-(ph)	m-(ph)	p-(ph)	R	S
Coefficients
Gl	Gll	Glll	GlV	GV

There are two points to be noted:

• (1).–NH₂ is defined in detail: with carbonyl- and with others. According to the initial fitting of viscosity data by the model, the viscosity fitting of DESs containing −NH₂ directly connected to the carbonyl group in the molecular structure is poor. We consider that this structure has a special effect on viscosity, so it is considered separately.
• (2).If metal ions are divided into different groups, many model input parameters will be introduced, which will easily lead to overfitting problems. Here, we assume that the difference in metal ions’ contribution is only related to the molecular weight and is equal to (n_m + 1)M_m, where n_m is the number of the metal ion, M_m is its molecular weight.

Second-Order Groups

The second-order groups listed in Table 3 provide more structural information about the molecular structure of DESs, which is not sufficiently described in the first-order groups, such as the differentiation among isomers for aromatics DESs and chiral DESs. Thus, three groups of ortho(o-(r)), meta(m-(r)), and para(p-(r)) among substituent groups in the benzene ring are considered. Using the primary functional group as the reference (determined following IUPAC nomenclature for organic compounds), the occurrence of these groups can be determined. Two configurations of chiral carbon (i.e., R_C and S_C) are introduced. For example, as shown in Figure 5, for thymol, based on the phenolic hydroxyl group, the second-order groups include one o-(r) and one m-(r); for d-glucose, the second-order groups include three R_C and one S_C.

Figure 5.

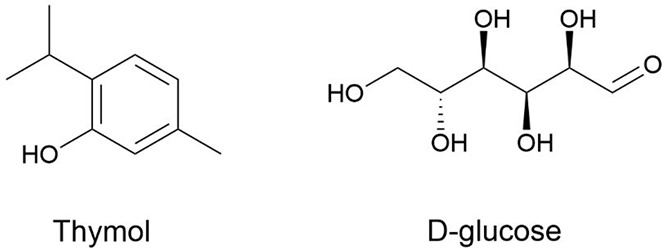
Structural formulas of thymol acid and d-glucose.

As mentioned earlier, we divided DESs into five categories and performed one-hot encoding on them. Therefore, the input features of the TSTiNet model include 45 × 2 structural features + G (1 × 5 one-hot vector) + temperature + composition ×2 + molecular weight ×2.

Model Details

According to the established chemical characteristics, two NNs are implemented based on Python and PyTorch libraries. One takes all features as input to calculate the viscosity of DESs directly. The other (TSTiNet) includes three MLPs, two of which take structural information on HBA or HBD as inputs to calculate the structural parameters, α₀, α₁, α₂, α₃, and the other takes all features as input to calculate the equation parameters of β and G. On the basis of the assumption that β, G_I, G_II, G_III, G_IV, and G_V are constants, the average value of all training sets is taken as the final value. With all parameters’ values obtained, viscosity can be calculated by the TSTieq.

We have examined a series of hyperparameter settings in MLPs according to the performance on the validation set, including network architecture and activation function. The search space can be found in Table S1. The results show that the same hyperparameter settings can get better performance in the two MLPs of calculating structural parameters.

The input features are normalized to make training faster and reduce the chances of getting stuck in local optima. All MLPs have two hidden blocks, and each block has a fully connected layer with 32 neurons, a GELU nonlinearity,⁶⁹ and a batch normalization⁷⁰ (BN) layer. Unlike the ReLU activation function, the GELU function output can be both negative and positive, so it can be used in predicting labels that have negative values. Besides, the GELU function has been widely used in natural language processing and recent state-of-art MLP related models. The experiments in this work show that the GELU function is more suitable for the TSTiNet than ReLU.

In the regression problem, MSE loss, MAE loss, and Huber loss are three main loss functions. After a series of experiments, it was found that Huber loss can obtain the best performance. This is because Huber loss can reduce the instability of MSE to outliers and enhance the convergence speed of MAE. The weights of neural networks are initialized with Xavier uniform.⁷¹ To avoid overfitting, L2 regularization and early stopping are applied in the models. The models are trained using AdamW algorithm⁷² with default parameters, learning rate = 0.001, weight decay = 0.0001, and patience of early stopping = 2000.^{43,57,81,73−80}

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.2c00157.

• Comparison with traditional machine learning methods. Further validation of the TSTiNet model. Comparison with models reported by different research groups. Chemical structure data set for DESs. Measurement methods data set for DESs. Figure S1. Dependence of mean cv score on the n_estimators in the random forest model. Figure S2. Correlation between the predicted and reported viscosity values of data sets in the random forest model. Figure S3. Relative deviations between the literature and the predicted viscosities in both data sets in the random forest model. Figure S4. Correlation between the predicted and reported viscosity values of data sets in the gradient boosting model. Figure S5. Relative deviations between the literature and the predicted viscosities in both data sets in the gradient boosting model. Figure S6. Correlation between the predicted and reported viscosity values of data sets in the LightGBM model. Figure S7. Relative deviations between the literature and the predicted viscosities in both data sets in the LightGBM model. Figure S8. Comparison between the trends of the experimental data and the proposed TSTiNet model for five randomly selected DESs in the high viscosity range. Figure S9. Comparison between the trends of experimental data and the proposed TSTiNet model for five randomly chosen DESs in the low viscosity range. Figure S10. Comparison of the viscosity behavior of choline chloride (HBA) with different ethylene glycol (HBD) ratios. Figure S11. Comparison of the viscosity behavior of choline chloride (HBA) with different HBDs. Figure S12. Comparison of the viscosity behavior of decanoic acid (HBD) with different HBAs. Table S1. The search space and results of parameters in the NN model. Table S2. The search space and results of parameters in the random forest model. Table S3. The search space and results of parameters in the gradient boosting model. Table S4. The search space and results of parameters in the LightGBM model. Table S5. The performance of different machine learning methods. Table S6. Comparison of the individual RD % values for DES by the TSTiNet model and the Bakhtyari et al. model. Table S7. Comparison of the individual AARD % values for DES by the TSTiNet model, the Bakhtyari et al. model, the Lewis and Squires model, the Haghbakhsh and Raeissi model, and the Dutt et al. model (PDF)

• Transparent Peer Review report available (PDF)

Author Contributions

^# L.Y. and G.R. contributed equally to this work. Y.H. contributed to conceptualization and study design, and supervised the data collection, analyses, and writing of this paper; K.W. contributed to study design and supervised the data collection, analyses, and writing of this paper; X.H. contributed to generate the chemical features; G.R. contributed to neural network computation, model parameters calculation, data analysis, and writing the paper; L.Y. contributed to establish the viscosity model, led the viscosity data collection, database establishment, data analysis, and writing the paper.

The authors are grateful for the financial support from National Natural Science Foundation of China (Grant No. 51874256) to this work.

The authors declare no competing financial interest.

Notes

To ensure reproducibility of the results, the source code of all the models used in this work can be acquired at https://github.com/fate1997/TSTiNet.