Navigable Space and Traversable Edges Differentially Influence Reorientation in Sighted and Blind Mice

Abstract

Reorientation enables navigators to regain their bearings after becoming lost. Disoriented individuals primarily reorient themselves using the geometry of a layout, even when other informative cues, such as landmarks, are present. Yet the specific strategies that animals use to determine geometry are unclear. Moreover, because vision allows subjects to rapidly form precise representations of objects and background, it is unknown whether it has a deterministic role in the use of geometry. In this study, we tested sighted and congenitally blind mice (Ns = 8–11) in various settings in which global shape parameters were manipulated. Results indicated that the navigational affordances of the context—the traversable space—promote sampling of boundaries, which determines the effective use of geometric strategies in both sighted and blind mice. However, blind animals can also effectively reorient themselves using 3D edges by extensively patrolling the borders, even when the traversable space is not limited by these boundaries.

Navigators use two types of cues to determine their location in space: idiothetic cues generated by internal proprioceptive, vestibular, and optic flow signals and allothetic cues reflecting external sensory information. Under oriented conditions, idiothetic and allothetic cues are complementary, signaling the same position in space. However, when navigators are lost, their internal sense of direction is unreliable, and they must reorient themselves using only allothetic information. In sighted animals, a large body of literature has shown that the shape of the layout—the geometry of the space—is critical for reorientation (Cheng et al., 2013; Vallortigara, 2017). This was first demonstrated by Cheng (1986), who showed that disoriented rats were unable to consistently find a reward placed in one of four cups located at the corners of a cue-rich rectangular environment. The animals searched equally often in the correct corner and the geometrically equivalent opposite corner, ignoring nongeometric cues even when they were informative. These observations led researchers to postulate that reorientation is driven by a mechanism that uses the shape parameters of the environment (e.g., an encapsulated geometric module) to realign the navigator’s cognitive map (Cheng, 1986; Gallistel, 1990), which requires the medial temporal lobe. A recent study provided support for this theory showing that the hippocampal map of disoriented mice aligns to the shape of the layout during reorientation, and this alignment serves to predict behavior (Keinath et al., 2017).

Despite the fact that the reliance on geometry for reorientation has been observed across species (Tommasi et al., 2012; Vallortigara, 2009), the modularity theory remains controversial because some studies have found that learning, saliency, and size of the environment also influence reorientation strategies under some conditions (Brown et al., 2007; Learmonth et al., 2001, 2002; Pearce et al., 2006; Sovrano & Vallortigara, 2006). Two alternative views have been postulated to account for these data. The image-matching theory proposes that navigators reorient themselves by matching a current panoramic view of the environment with a stored representation of a goal location (Cheng, 2008; Nardini et al., 2009; Sturzl et al., 2008; Wystrach & Beugnon, 2009), whereas the adaptive-combination theory suggests that environmental properties are weighted and selected according to their reliability and salience to guide reorientation (Ratliff & Newcombe, 2008). It is worth noting that both the view-matching and adaptive-combination theories do not rule out the possibility that geometric information can be used to reorient oneself. Indeed, experiments with chicks (Pecchia & Vallortigara, 2010) and ants (Wystrach & Beugnon, 2009) show that animals can reorient themselves using a view-matching strategy relying on geometry. In these cases, animals associate local geometric properties (e.g., angle and wall length) with a stored representation of the goal. However, there is evidence that view matching by itself does not support the use of geometry, at least in vertebrate animals (Lee et al., 2012). In sum, although there is substantial support for the geometric-module theory, the conditions under which animals can use geometry seem to vary.

At present, however, it remains uncertain how navigators determine the shape of task-relevant areas. Previous work showed that toddlers were able to extract geometric information when they were restricted to a small enclosure, suggesting that the traversable space of an environment could be a key feature for the perception of shape parameters (Learmonth et al., 2008). However, it is unclear how navigational affordances facilitate the extraction of geometry. Do animals patrol and/or spend more time at the borders when space is restricted to these boundaries? Moreover, because vision allows subjects to rapidly and accurately perceive objects and background, do blind animals require more extensive patrolling of borders to compensate for the absence of vision? Conversely, can sighted animals extract geometric properties even with poor sampling of borders? In the absence of vision, perceiving the geometry of a layout requires sequential exploration (i.e., haptic perception), which is more time consuming than visual perception. Because of this perceptual limitation, blind subjects have more difficulty using allocentric (environment centered) reference frames (Pasqualotto & Proulx, 2012). However, a human case study (Landau et al., 1981) and a study in blind cavefish (Sovrano et al., 2018) indicated that disoriented blind navigators can effectively use geometric information. Yet it remains to be determined whether blind subjects can reorient themselves as efficiently as sighted ones. In this study, we conducted a series of experiments to determine what aspects of an environment are important and what exploratory patterns are necessary to extract geometric information for reorientation in sighted and blind mice.

Statement of Relevance.

A fundamental aspect of spatial navigation is reorientation—the ability to regain one’s bearings after becoming lost. Although we know that geometry is a critical cue for reorientation, how navigators extract global shape parameters and what role vision plays in this process are unknown. In this study with mice, we manipulated the navigational affordances of their chamber (i.e., a traversable space) and used 3D edges to increase the salience of borders to determine how these variables influenced the use of geometry during reorientation. Restricting navigational affordances to the task-relevant area facilitated use of geometric strategies in both sighted and blind mice. However, increasing the saliency of borders improved geometry-based reorientation only in blind mice. Detailed analysis of the animals’ trajectories determined that patrolling of borders was necessary to detect global geometric parameters. These data provide important insights about how navigators extract geometric relationships and demonstrate that vision is not necessary for the effective use of geometry during reorientation, at least in mice.

Method

Subjects

The experiments were conducted using C57BL/6J male mice with normal vision and C57BL/6NJ male mice with congenital blindness due to retinal folds and pseudorosettes (Jackson Labs, Strain 005304). All mice were between 6 and 8 weeks old at the start of the experiment. Prior to training and testing, all mice were housed individually on a 12-hr light/dark cycle and food deprived until they reached 80% to 85% of the normal body weight observed following an ad libitum diet to increase motivation for the task. Food deprivation was continued throughout the experiment and ended on the last day of testing. Animal living conditions were consistent with the standard required by the Association for Assessment and Accreditation of Laboratory Animal Care. All experiments were approved by the Institution of Animal Care and Use Committee of The University of Texas at San Antonio and were carried out in accordance with National Institutes of Health guidelines.

Number of subjects

To determine sample size, we conducted a pilot study on the elevated-cliff task (see below) with five subjects per group, which allowed us to obtain an estimate of the size of the treatment effect associated with a mixed 2 (group) × 2 (day of testing) design. Cohen’s f values of 0.64, 0.75, and 0.79 were estimated for the size of the main effect of groups, days, and interaction, respectively. The significance level was set at a conventional value of .05, and the nonsphericity-correction coefficient was set at a neutral value of 1 because the design had only two levels of repeated measures. To arrive at a desired power of 80%, we estimated an optimal sample size of between 22 and 16 subjects in total, corresponding to 11 and eight subjects per group, for main effects and interaction, respectively (see Fig. S1a in the Supplemental Material available online). Despite the fact that on some occasions, data from some subjects were not usable (e.g., mice did not reach the digging criterion; see the Behavioral Training section), the sample sizes for all the designs remained at the optimal minimal size for the interaction (n = 8; see Fig. S1b in the Supplemental Material), except in the artificial-cliff condition, in which the size increased toward the most demanding optimal value (n = 11). Experiments were finished when the sample size predetermined in the power analysis was reached.

Visual acuity test

Vision was tested in two rectangular chambers (small: 33.02 cm × 22.86 cm; large: 78.74 cm × 54.61 cm) containing two cups embedded in opposite sides of the chambers. The chambers featured a different visual cue on each short wall—three black horizontal stripes on one side and three black vertical stripes on the other. The side of the reward was counterbalanced across animals. During training, the reward was visible during the first three trials to indicate which visual cue signaled its location, but it was buried on the five subsequent trials. During the intertrial interval, mice were placed in a cylinder and the environment was cleaned with a 70% ethanol solution. The chambers were surrounded by a black curtain to avoid distraction from external cues.

Navigation apparatuses

This study used four different navigational apparatuses. Each had in common a rectangular platform (33.02 cm × 22.86 cm), covered with a distinctive rubber texture, with four cups embedded in the corners. In the real-cliff condition, the rectangular rubber shape was elevated 20.96 cm above the floor, which limited the navigable space to only the rectangle. In the artificial-cliff condition, the rectangular platform was embedded in a circular (49.53 cm diameter), clear Plexiglas surface elevated 20.96 cm above a dark floor, which minimized depth perception. Because the rubber platform lay flat on the circular Plexiglas surface, the navigable space was the entirety of the area (i.e., circular surface and rectangular platform). In the artificial-cliff-with-3D-edge condition, this context was identical to the artificial cliff except that the rectangular area was raised 1.27 cm above the circular platform, creating a 3D edge. The navigable space was the entirety of the circular and rectangular platform. The real-cliff, artificial-cliff, and artificial-cliff-with-3D-edge platforms were surrounded by a large white cylinder (50.08 cm diameter and 40.64 cm tall). In the artificial-cliff-with-high-distal-rectangular-boundary condition, this context was identical to the artificial cliff, but it was surrounded by a white rectangle (54.61 cm × 78.74 cm) with high walls (66.04 cm) that did not touch the navigable circular surface. All apparatuses were surrounded by a black curtain to isolate the experimental chambers from external cues. Additionally, a white-noise generator was used to mask any external sound cue in all experiments.

Behavioral training

Each of the cups embedded near the corners of the rectangular rubber platform was filled with wood-chip bedding mixed with cumin (5 g of cumin per 500 g of bedding, 30 ml total volume). One cup contained a small cocoa puff (Cocoa Krispies; Kellogg’s, Battle Creek, MI) as a food reward. Each animal received eight consecutive trials per day for 4 days. Before each trial, the animal was placed inside a small black cylinder that had a removable bottom. The cylinder was mounted on a rotatable circular platform that was turned four times clockwise followed by four times counterclockwise. Following the disorientation, the animal and cylinder were transferred to the center of the apparatus (e.g., artificial cliff), and the removable bottom was slid sideways, placing the animal on the surface. The transportation cylinder was then removed and the trial commenced. Between each successive trial, the apparatus was rotated 90° clockwise to prevent the use of any distal cue that could confound the results. During the intertrial period (approximately 2 min), the cup bedding was replaced with fresh bedding, and the surface of the apparatus was thoroughly cleaned with a 70% ethanol solution.

On Day 1, the food was placed on top of the reward cup in the first two trials to teach the animal the reward location. On each subsequent trial, the reward was buried at increasingly deeper depths. On Days 2 to 4, all trials were conducted with the reward buried at the center of the cup. On Days 1 and 2 (training days), the animal remained in the apparatus until it found the reward. Testing was conducted on Days 3 and 4 with the introduction of alternating probe trials to ensure that the mouse was unable to smell the food reward. During probe trials, the mouse was removed after the first dig to avoid extinction, whereas on rewarded trials, the mouse was removed after it ate the food. Animals that did not dig in three or more trials during training were excluded (two sighted and two blind mice in the artificial-cliff condition did not meet this criterion).

Behavioral analysis of first dig and latency

Each trial was video recorded by a camera mounted above the apparatus using LimeLight software (Version 4.0; O’Leary & Brown, 2013; Yuan et al., 2021). The first dig location and associated latency to find the reward were subsequently scored by an experimenter who was blind to experimental condition. Performance on a given day was evaluated using the relative proportion of digs in the geometrically correct axis (i.e., rewarded correct cup location and geometrically congruent unrewarded cup location) relative to the total number of digs.

Sequential digging probability analysis

Digs recorded on Days 3 and 4 were used to form probability matrices. Given the four possible locations—correct corner (C), geometrically equivalent corner (G), near the location to the rewarded cup (N), and wrong location (W)—if the digging sequence of a mouse was C, C, N, G, W, G, C, and G, the seven combinations formed were (C, C), (C, N), (N, G), (G, W), (W, G), (G, C), and (C, G). Each of these transitions provided a count where the first element was the current dig (matrix row) and the second element was the next dig (matrix column), which resulted in a 4 × 4 matrix of counts. We repeated this procedure for all mice belonging to the same condition and then summed the matrices to form a total matrix for the group on each testing day. The matrix was then divided by the total counts resulting in a probability matrix—for example, a cell with a 0.10 value represents 10% of the transitions.

Path analyses

Each video (one per trial) was analyzed using DeepLabCut (Version 2.2rc3) to extract the path of the animal (Mathis et al., 2018; Nath et al., 2019). To convert the path from pixel coordinates to physical coordinates (in centimeters), we calculated a median frame for each video. An experimenter then marked the four corners of the rectangular surface in pixel coordinates. A coordinate transformation (homography) was then applied, which converted paths from pixels in video frame coordinates to physical units (centimeters) in a physical coordinate system (common origin and orientation), allowing for physical measurements and comparisons of paths from different trials. We successfully analyzed the paths of all animals, except four in which the algorithm failed because of reflections or poor quality of the video conversion (two sighted and one blind animal in the artificial-cliff condition and one sighted mouse in the artificial-cliff-with-3D-edge condition).

The distance-heading occupancy map was computed by calculating the heading direction using the difference of the animal’s spatial displacement and its minimum distance to the rectangular perimeter. If the animal’s position was interior to the rectangular perimeter, then a count of +1 was added to a 2D grid representing the binned distance and heading values; otherwise, no increment was added to the count. The average map was calculated as the average across all such maps associated with the same experimental group. To quantify the heading-distance spread relative to the peak occupancy of each map, we fitted a 2D Gaussian model to the data that composed the region surrounding the main peak (MATLAB built-in function Isqcurvefit; The MathWorks, Natick, MA) and reported the fitted model parameters to estimate the standard deviation for both angle and distance.

For each path, we computed the average speed (in centimeters per second) and total distance traveled (path length) by summing the Euclidean distances (centimeters) between successive points. We then constructed a uniform spatial grid (1-cm × 1-cm bins). For each bin, we counted how many times the animal’s path occupied that location. The end result was a spatial grid of values representing the times the mouse visited each bin of the grid. To analyze usage of the rectangle, we formed an imaginary border area around the inside perimeter of the rectangle containing the cups with a width of 5 cm. We computed a time ratio, defined as the amount of time that the mouse spent in the imaginary border area divided by the total trial time, and an occupation ratio, defined as the amount of border area visited divided by the total amount of border area. After obtaining the time ratios across all animals for a given experiment and group, we computed the time-ratio probability density function, obtained by fitting the time-ratio data parametrically using a smoothing kernel with a bandwidth of 0.1.

Statistics

All data were first tested for normality using the Shapiro-Wilk tests and equal variance using the Brown-Forsythe test. Following corroboration of normality and equal variance, two-way repeated measures analyses of variance (ANOVAs) with group (sighted or blind) as a between-subjects factor and testing time (Day 3 or Day 4) as a within-subjects factor were used to determine whether the proportion of geometrically correct responses was different between the groups across testing days in each condition. For variables with significant effects and more than two levels, a post hoc test with Rom’s sequentially rejective method to control Type I analysis was performed either on the simple effects or on the main effects. Because the latency to the first dig displayed asymmetric distributions, the generalized linear mixed model (GLMM) gamma family was used to analyze this variable across the different groups and sessions (results are reported as unstandardized regression coefficients and z statistics). To test whether animals smelled the reward, we used median, permutation, and Bayes factor (BF) analyses to compare the number of digs in the correct location on rewarded and probe trials. Finally, path variables were not normally distributed; therefore, we conducted robust 3 (navigational context) × 2 (group) ANOVAs and Rom’s post hoc tests applied on robust contrast, as previously described (Wilcox, 2012). For robust ANOVAs, we report F-distributed Welch-type tests (F_W) based on trimmed means (20% trimming level), and for Rom’s post hoc tests, we report Yuen tests for two-sample trimmed means (T_W; 20% trimming level). A standardized estimate of effect size was included in all analyses (with a 90% confidence interval [CI] around that estimate): generalized η² (η _G ²) for omnibus ANOVAs, Cohen’s d for pairwise contrasts (d_pair), and robust explanatory measures for robust analysis (ξ). We opted for generalized η to provide estimates of effect size that are comparable across variable research designs (for the statistical design, see Fig. S2 in the Supplemental Material). All statistical analyses were performed in the R programming environment (Version 4.0.3; R Core Team, 2020).

Hierarchical Bayesian analysis

Bernoulli models

The outcome of a single learning trial is denoted γ and takes the value 0 for an incorrect outcome and 1 for a correct outcome. The probability of a single outcome is given by the Bernoulli distribution, where θ represents the probability of a successful outcome:

$$p\left(\gamma |\theta \right)={\theta }^{\gamma }{\left(1-\theta \right)}^{1-\gamma }.$$

For the set of N outcomes, where N represents the total number of trials in one session, it was assumed that the outcomes were independent of each other. The likelihood function for the combined outcomes of all trials in one session was then defined as follows:

$$p\left(z,N|\theta \right)={\theta }^z{\left(1-\theta \right)}^{N-z},$$

where z is the number of trials with correct outcomes and N – z is the number of trials with incorrect outcomes.

Estimation approach

The characterization of the results could be done at the subject (mouse) level and/or at the group (experimental condition) level. At the subject level, the Bernoulli distribution was used as described above, whereas at the group level, the β and γ distributions were employed. The estimation of the parameters of the subject and group levels could be expressed by a chained hierarchy (see Fig. S3 in the Supplemental Material). The outlined process could obtain estimates of the parameters θ_S (subject parameter) and ω (group parameter) as well as their associated highest density intervals (HDI). The HDI is a way of summarizing a distribution by specifying an interval that comprises most of its values (commonly 95%), such that every point inside the interval has higher credibility than any point outside the interval. For example, if the digging probability is random, then 0.5 would fall within the 95% HDI. This means that a model that asserts that animals have not learned has higher credibility than one that asserts the opposite.

Model-comparison approach

The model comparison was used to determine which of two models best represented the performance of the animals. This was achieved through a comparative ratio between the models (called the BF; see Kruschke, 2015). This approach was based on the Bernoulli distribution described in the Bernoulli Models section.

The two models to be compared are defined as follows. The null model (M_null) represents the probability that the animal has not learned the task and the outcomes are the result of 50-50 chance (expressed as θ = 0.5):

$$p\left(z,N|M_{\mathrm{null}}\right)={0.0.5}^z{(1-0.5)}^{N-z}.$$

The alternative model (M_alt) represents the probability that the animal has learned the task, indicated as a probability between 0.5 and 0.9. To achieve a uniform distribution across the range of values, we calculated an integration over probability θ as follows:

$$p\left(z,N{|\mathrm{M}}_{\mathrm{alt}}\right)=\frac{1}{0.9-0.5}{\int }_{0.5}^{0.9}{\theta }^z{(1-\theta )}^{N-z}d\theta .$$

The BF for each animal (represented by i) was calculated as follows:

$${\mathrm{BF}}_i=\frac{p\left(z,N{\mathrm{|M}}_{\mathrm{alt}}\right)}{p\left(z,N{\mathrm{|M}}_{\mathrm{null}}\right)}=\frac{\frac{1}{0.9-0.5}{{\displaystyle \int }}_{0.5}^{0.9}{\theta }^z{(1-\theta )}^{N-z}d\theta }{{0.5}^z{(1-0.5)}^{N-z}}.$$

It was assumed that the two models were equally probable a priori, p(M_alt) = p(M_null). Then, the BF for a group of independent subjects could be estimated as follows:

$${\mathrm{BF}}_{\mathrm{group}}={\mathrm{BF}}_1.{\mathrm{BF}}_2\cdots {\mathrm{BF}}_i={\prod }_i{\mathrm{BF}}_i.$$

After the BF was calculated, the likelihood of the models was evaluated: Substantial credibility for Model 1 (included in the numerator; e.g., M_alt) occurred when the BF exceeded 3.0, and substantial evidence for Model 2 (placed in the denominator; e.g., M_null) happened when the BF was less than one third (Kruschke, 2015). We also report the BFs on a logarithmic scale, which has the advantage of quantifying the weight of the evidence that favors the null (H_null; chance) over the alternative (H_alt; learning) hypothesis (negative values) in comparison with H_alt over H_null (positive values) in a symmetrical manner. Credibility is substantial when logBF exceeds |0.48| and is strong when it exceeds |1|. The Bayesian information at the individual level of analysis is presented as the cumulative fraction of subjects as in Gallistel et al. (2014) but in terms of the weight of evidence.

Results

Experiment 1: visual acuity test

Mice from Strain C57BL/6NJ contain the Rd8 mutation of the crumbs cell polarity complex Component 1 gene, which causes substantial damage to the retina by the time the mice reach 4 weeks old (Mattapallil et al., 2012); however, there are no behavioral records substantiating loss of vision. To this end, we conducted a visual discrimination task in which mice had to discriminate between two visual cues to find a reward. Sighted C57BL/6J mice reliably dug in the correct cup, whereas C57BL6/NJ blind mice displayed random digging—percentage of correct responses: sighted (n = 6): 84.16 (SE = 5.07); blind (n = 6): 54.16 (SE = 10.67), t(10) = 2.54, p = .03. These results corroborate that the C57BL6/NJ strain exhibits profound visual impairment by 6 to 8 weeks of age.

Experiment 2: influence of navigational affordances during reorientation

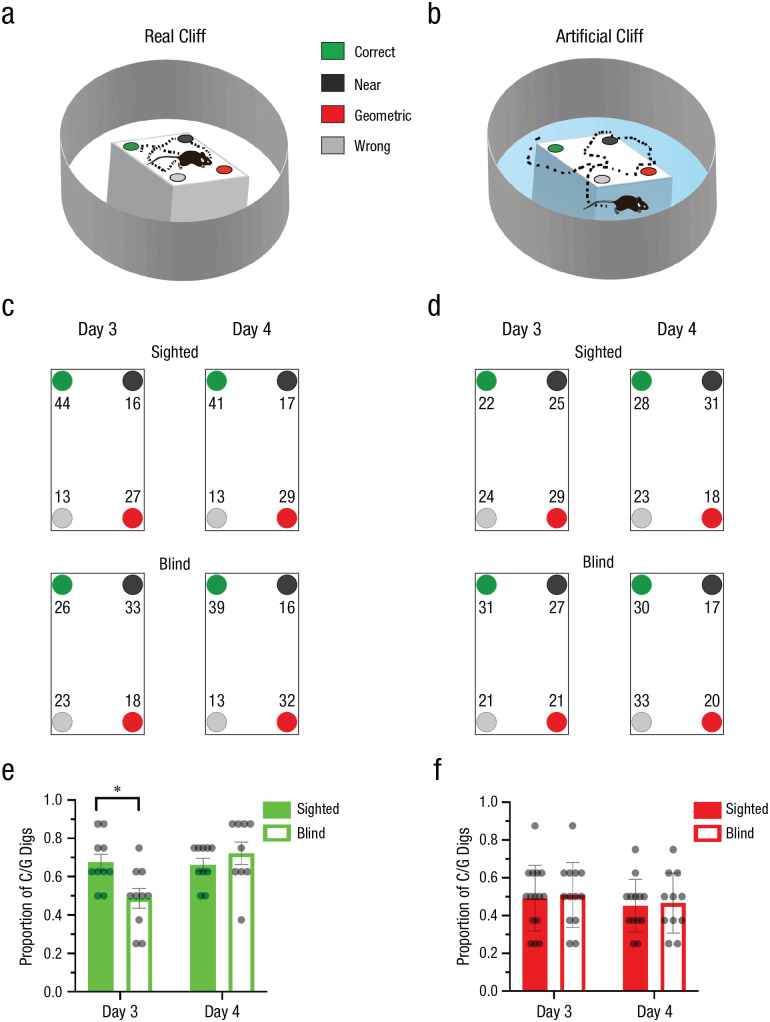
To test whether navigational affordances play a deterministic role in the use of geometric strategies, we trained different groups of sighted and blind animals in a real-cliff (Fig. 1a) or an artificial-cliff (Fig. 1b) environment for 2 days and tested on Days 3 and 4. The percentage of first digs in each cup location are shown in Figures 1c and 1d.

Fig. 1.

Experiment 2: reorientation in the real-cliff and artificial-cliff conditions. The schematics show the experimental setup in the real-cliff (a) and artificial-cliff (b) conditions. In the real-cliff condition, animals were forced to navigate a rectangular shape, whereas in the artificial cliff, a rectangular texture was placed on a circular platform that did not limit the traversable space to the task-relevant area (i.e., the rectangle containing the four cups). The task consisted in finding a reward hidden in one of the four cups at the edges of the rectangular shape that enclosed the cup locations. In the schematics, green indicates the correct rewarded location, black indicates the location nearest to the reward along the same short wall as the reward location, red indicates the geometrically opposite corner from the reward location, and gray indicates the location not associated with the correct geometric axis or the short wall near the reward. The percentage of digs in the four different cup locations is shown for the real-cliff (c) and artificial-cliff (d) conditions on Days 3 and 4; means are shown for sighted mice in the upper row and blind mice in the lower row. Results are shown separately for each cup location, using the color codes shown in (a) and (b). Digging preference (proportion of first digs in the geometrically correct axis relative to the total number of digs) is shown for sighted and blind mice in the real-cliff (e) and artificial-cliff (f) conditions on Days 3 and 4. Bars show means (error bars indicate standard errors of the mean), and dots represent individual data. The asterisk indicates a significant difference between means for sighted and blind mice (α = .05). Real-cliff condition: sighted mice: n = 10, blind mice: n = 9; artificial-cliff condition: sighted mice: n = 12, blind mice: n = 11.

Performance was assessed using the proportion of first digs in the geometrically correct axis (i.e., rewarded correct or unrewarded geometrically equivalent cup locations) relative to the total, hereafter called digging preference. The digging preference could vary between +1, indicating complete preference for the geometrically correct axis, and 0, indicating complete preference for the geometrically incorrect axis. We anticipated that if animals used the geometry of the layout to reorient themselves, their performance should show a digging-preference value above 0.5. Alternatively, if animals did not use a geometric strategy, digging-preference scores should be around 0.5 reflecting chance. In the real-cliff condition, where the traversable space was constrained by the task-relevant area, sighted mice used a geometric strategy on Days 3 and 4, whereas blind animals required more time to learn, showing evidence of using geometry only on Day 4 (Fig. 1e). To assess group differences, we ran a two-way repeated measures ANOVA with group (sighted or blind) and time of testing (Day 3 or Day 4) as independent variables and digging preference as a dependent variable. In the real-cliff condition, the group effect displayed a trend, F(1, 17) = 4.43, p = .050, η _G ² = .13 (medium effect), 90% CI = [0.00, 0.39], whereas the effect of time of testing and the interaction of the two variables were significant—time: F(1, 17) = 7.77, p = .013, η _G ² = .14 (large effect), 90% CI = [0.00, 0.40]; interaction: F(1, 17) = 11.39, p = .004, η _G ² = 0.22 (large effect), 90% CI = [0.00, 0.47]. Following Rom’s corrections for multiple comparisons, the data showed that sighted and blind mice were significantly different on Day 3, t(33.00) = 3.78, p < .001, d_pair = 1.91 (large effect), 95% CI = [0.77, 3.05], but not Day 4, t(33.00) = −0.56, p = .582, d_pair = −0.28 (small effect), 95% CI = [–1.31, 0.75].

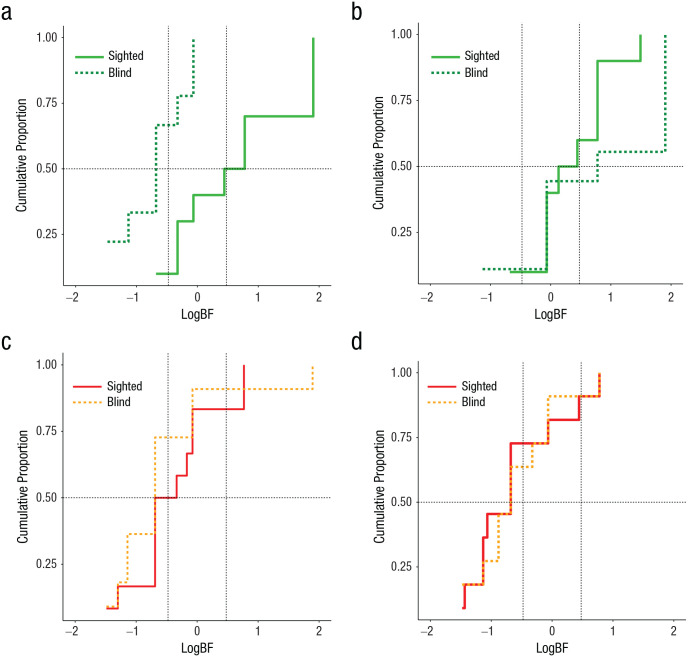
In the artificial-cliff condition in which the task-relevant area did not constrain the navigational affordances of the animals, both sighted and blind groups were unable to reorient themselves using geometry. This was evident in digging preference being around chance levels and the absence of statistical differences between groups, test days, or interactions, F(1, 21) < 1 (Fig. 1f). Bayesian analysis at the individual and group levels corroborated these results by testing the alternative hypothesis (H_alt) that animals preferentially dug in the geometrically correct axis against the null hypothesis (H_null) that animals had no preference in digging patterns. BFs greater than 3 or logBFs greater than 0.48 provide credibility for H_alt, whereas BFs less than one third or logBFs less than −0.48 support H_null. The cumulative function of subjects clearly differed between sighted and blind animals on Day 3 in the real-cliff condition, but not on Day 4 (Figs. 2a and 2b; for details on individual data, see Tables S1 and S2 in the Supplemental Material). No differences were observed between sighted and blind mice across days in the artificial-cliff condition, with both groups favoring H_null (chance performance; Figs. 2c and 2d; see Tables S1 and S2). Group BFs obtained by multiplying the individual BFs corroborated the individual data (Table 1).

Fig. 2.

Experiment 2: results of the hierarchical Bayesian analysis at the individual and group levels. The cumulative proportion of subjects in terms of the weight of evidence is shown for the real-cliff condition on Day 3 (a) and Day 4 (b) and the artificial-cliff condition on Day 3 (c) and Day 4 (d). Conventional values showing the border marking credibility for the null hypothesis (chance performance) and the alternative hypothesis (use of geometry) are indicated by vertical dashed lines, log(1/3) = −0.48 and log(3) = 0.48. The value of half (0.5) of the sample is marked by a horizontal dashed line. LogBFs > 0.48 indicate credibility for the alternative hypothesis (geometric learning), whereas logBFs < –0.48 indicate credibility for the null hypothesis (chance performance).

Table 1.

Experiment 2: Group Bayes Factors (BFs) Obtained by Multiplying Individual Scores

Condition and group	Day 3		Day 4
	BF	LogBF	BF	LogBF
Real cliff
Sighted	552.824	2.74	33.920	1.53
Blind	0.001	–2.86	1,172.344	3.07
Artificial cliff
Sighted	0.011	–1.97	0.014	–1.86
Blind	0.003	–2.59	0.001	–2.99

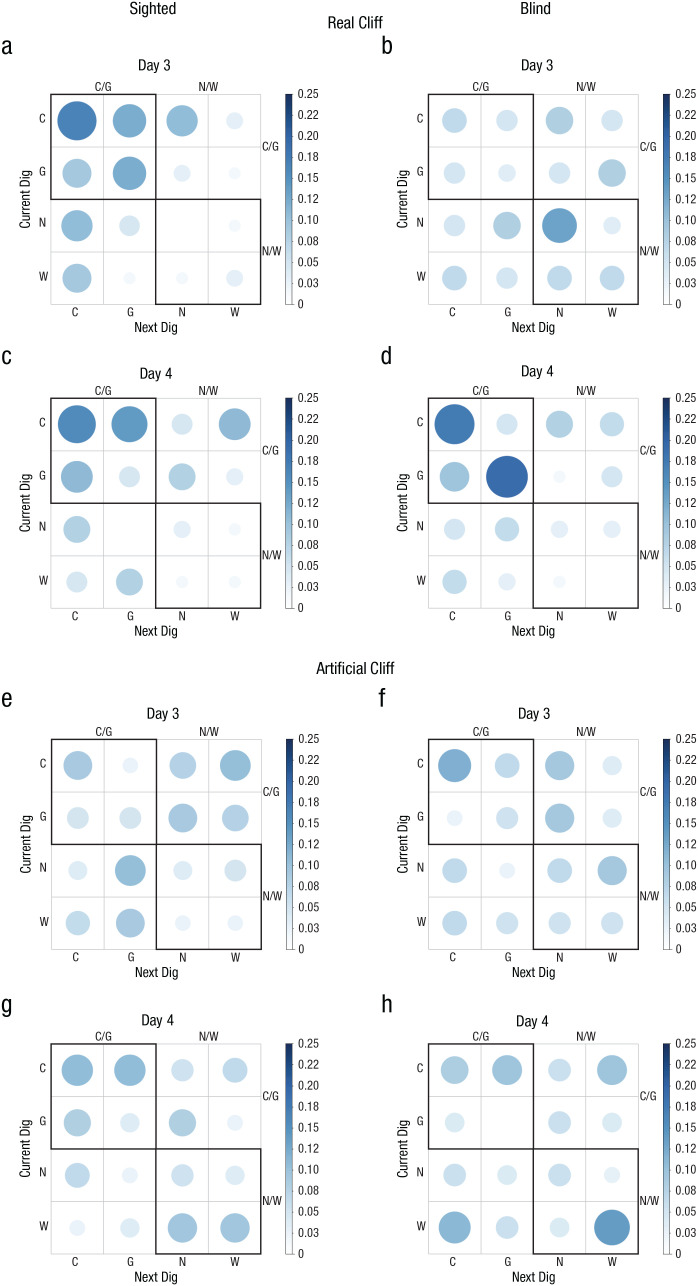
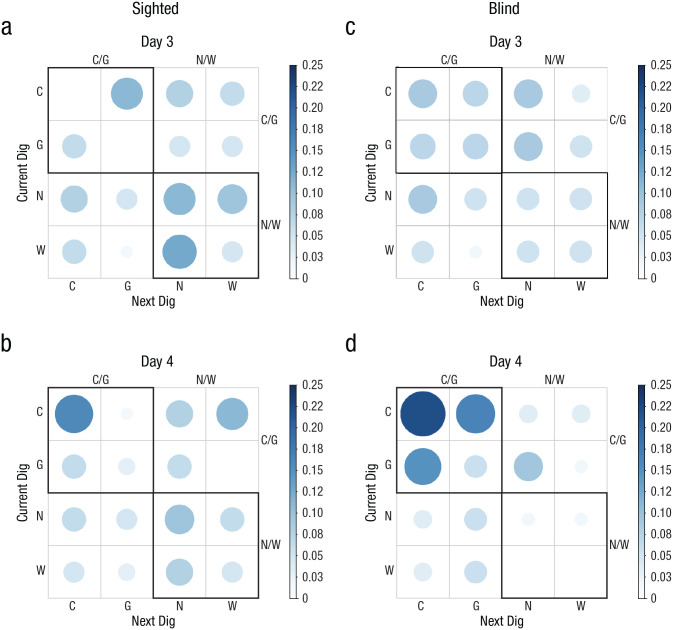
To further analyze the digging patterns of the groups, we generated probability matrices to determine whether a current dig location influenced the next choice. If animals were reorienting using geometry, it would be expected that sequences of digs in the geometrically correct axis would be prevalent (e.g., C/G, C/C, G/C, or G/G), whereas if animals did not reorient themselves, random sequences would be observed. The data showed that sighted animals were not random on Day 3 or 4, which was indicated by a higher probability of digging in the geometrically correct axis on consecutive trials (Figs. 3a–3c; upper quadrant shows maximal probability of responding), Day 3: χ²(15, N = 66) = 41.64, p < .05; Day 4: χ²(15, N = 64) = 34, p < .05. However, this effect was evident only on Day 4 in blind mice (Figs. 3b–3d), Day 3: χ²(15, N = 61) = 8.51, p > .05; Day 4: χ²(15, N = 63) = 42.40, p < .05. No pattern was observed in the artificial-cliff condition in either sighted or blind mice across testing days, indicating that the current digging location did not influence the next response. This was reflected in random probabilities in the four quadrants of the digging matrix (Figs. 3e–3h) for both sighted mice, Day 3: χ²(15, N = 78) = 14.31, p > .05; Day 4: χ²(15, N = 75) = 14.39, p > .05, and blind mice, Day 3: χ²(15, N = 76) = 12.00, Day 4: χ²(15, N = 72) = 20.89, p > .05.

Fig. 3.

Experiment 2: results of the probability analysis of digging sequence in the real-cliff (a–d) and artificial-cliff (e–h) conditions, separately for sighted mice (left column) and blind mice (right column) on Day 3 and Day 4 (upper and lower rows, respectively, for each group of subjects). The bar on the right of each graph indicates probability. Larger, darker circles indicate higher probability; smaller, lighter circles indicate lower probability. C = correct corner; G = geometrically equivalent corner; N = near location to rewarded cup; W = wrong location.

To rule out the possibility that animals were using the odor of the reward to guide performance, we conducted probe trials in which the reward was omitted every other trial. Nonparametric/Bayesian tests corroborated that there were no significant differences between the number of digs in the correct location during probe or rewarded trials in any condition, group, or testing day (p > .05 and BF < 3; see Table S4 in the Supplemental Material). Finally, in the real-cliff condition, there were no differences between the groups in latency to find the reward (b = 5.82, z = 0.35, p = .723), but the time of testing (b = −27.22, z = −4.19, p < .001) and interaction between group condition and time of testing (b = 24.23, z = 2.95, p = .003) were significant. Rom’s corrections for multiple comparisons showed that sighted mice were significantly faster in Session 4 than in Session 3 (b = 27.22, z = 4.19, p < .001). The rest of the comparisons were not significant (p > .05). There were no differences between groups across testing days or interactions in latency to find the reward in the artificial-cliff condition (effect of group: b = 13.51, z = 0.75, p = .450; effect of session: b = −6.62, z = −1.64, p = .102; interaction: b = 5.05, z = 0.88, p = .379). In sum, both sighted and blind animals could reorient themselves using geometry only in the real-cliff condition, suggesting that the navigational affordances of the context were critical to extract global parameters of geometry.

Experiment 3: artificial cliff with 3D edge

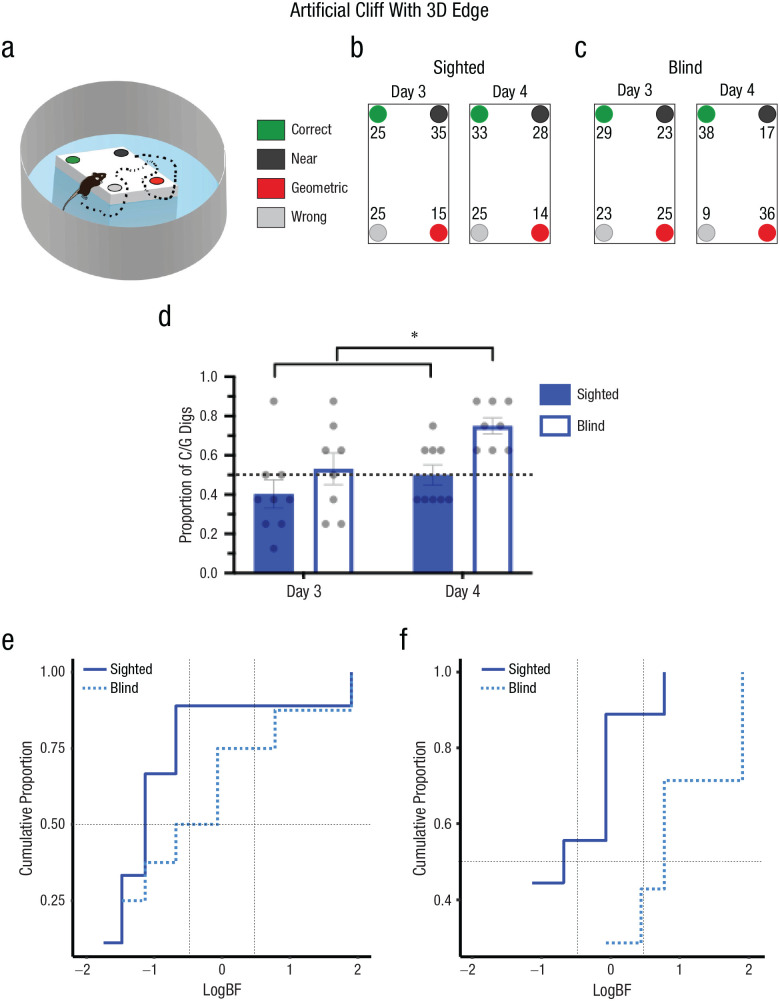
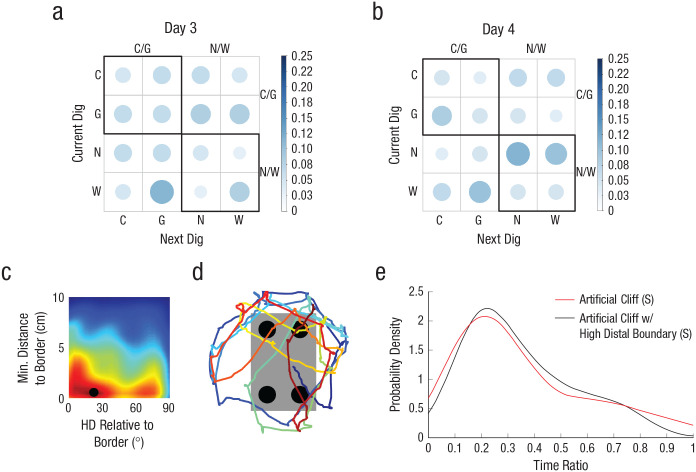
The observation that both sighted and blind mice failed to extract geometric information from the artificial-cliff apparatus when the task-relevant area was a 2D surface could be because the area did not constrain the traversable space or that perception of geometry requires the presence of 3D edges. To dissociate these possibilities, we trained and tested blind and sighted mice in an artificial cliff with a 3D edge that did not limit the navigable space to the task-relevant area (Fig. 4a). In this context, only blind animals could use the 3D edge to reorient themselves, and their performance improved with extensive training (Day 4). The percentage of digs in each cup location for sighted (right panel) and blind (left panel) animals are shown in Figures 4b and 4c. Two-way mixed ANOVAs comparing the performances of sighted and blind animals on Days 3 and 4 showed that there was a significant effect of group, F(1, 15) = 9.23, p = .008, η _G ² = .24 (large effect), 90% CI = [0.00, 0.51], and time of testing, F(1, 15) = 8.10, p = .012, η _G ² = .20 (large effect), 90% CI = [0.00, 0.47], but no interaction, F(1, 15) = 1.15, p = .300, η _G ² = .04 (small effect), 90% CI = [0.00, 0.28] (Fig. 4d). These results reflect that blind animals displayed better reorientation than sighted animals on both testing days. Bayesian analysis, weighting the model favoring H_alt (learning using geometry) over H_null (chance performance), confirmed that blind mice effectively reoriented themselves on Day 4, BF > 3.0 or log(3) = 0.43, but not on Day 3, BF < 1/3 or log(1/3) = −0.43. Conversely, the sighted group did not show an effect on either testing day, BF < 1/3 or log(1/3) = −0.43. This was evident in the group BFs (Table 2)—showing credibility for the model supporting use of geometry in blind animals on Day 4, BF > 3 or log(3) = 0.48—and cumulative function of subjects in terms of the weight of the evidence for H_alt and H_null (Figs. 4e and 4f; see Tables S1 and S3 in the Supplemental Material). The sequential digging probability analysis further corroborated these data, showing no preference in sighted animals on Days 3 and 4 (Figs. 5a and 5b), Day 3: χ²(15, N = 63) = 21.57, p > .05; Day 4: χ²(15, N = 63) = 22.08, p > .05, or blind animals on Day 3 (Fig. 5c), χ²(15, N = 56) = 5.71, p > .05. However, blind animals displayed persistent sequences of geometrically correct digging locations on Day 4 (Fig. 5d), χ²(15, N = 54) = 52.67, p < .05.

Fig. 4.

Experiment 3: reorientation in the artificial-cliff-with-3D-edge condition. A schematic of the arena is shown in (a). The environment was identical to the artificial cliff, but the rectangular shape in the center of the arena was elevated, creating a 3D edge that did not limit the traversable space. The task consisted in finding a reward hidden in one of four cups at the edges of the elevated rectangular shape that enclosed the cup locations. In the schematic, green indicates the correct rewarded location, black indicates the location nearest to the reward along the same short wall as the reward location, red indicates the geometrically opposite corner from the reward location, and gray indicates the location not associated with the correct geometric axis or the short wall near the reward. The percentage of digs in the four different cup locations is shown for sighted (b) and blind (c) mice on Days 3 and 4. Results are shown separately for each cup location, using the color codes shown in (a) and (b). Digging preference (proportion of first digs in the geometrically correct axis relative to the total number of digs) is shown (d) for sighted and blind mice on Day 4. Bars show means (error bars indicate standard errors of the mean), and dots represent individual data. The asterisks indicates significant differences between group performance on different days (α = .05). The cumulative proportion of subjects in terms of the weight of evidence supporting either the null hypothesis (H_null; chance performance) or the alternative hypothesis (H_alt; use of geometry) is shown for sighted and blind mice on Day 3 (e) and Day 4 (f). Conventional values showing the border marking credibility for H_null versus H_alt are indicated by vertical dashed lines, log(1/3) = −0.48 and log(3) = 0.48. The value of half (0.5) of the sample is marked by a horizontal dashed line. Sighted mice: n = 9, blind mice: n = 8.

Table 2.

Experiment 3: Group Bayes Factors (BFs) in the Artificial-Cliff-With-3D-Edge Condition

Group and day	BF	LogBF
Sighted
Day 3	0.001	–3.28
Day 4	0.010	–2.01
Blind
Day 3	0.109	0.96
Day 4	4,980.680	3.70

Fig. 5.

Experiment 3: results of the probability analysis of digging sequence in the artificial-cliff-with-3D-edge condition, separately for sighted mice (a, b) and blind mice (c, d) on Day 3 and Day 4 (upper and lower rows, respectively, for each group of subjects). The bar on the right of each graph indicates probability. Larger, darker circles indicate higher probability; smaller, lighter circles indicate lower probability. C = correct corner; G = geometrically equivalent corner; N = near location to rewarded cup; W = wrong location.

Analysis of the latency to the first dig showed a trend in the main effect of group (b = 50.90, z = 1.96, p = .051), which reflected that blind mice on average took longer to make the first dig than sighted mice (sighted: M = 78.86 s ± 17.95 s; blind: M = 149.63 s ± 28.49 s). However, there were no significant differences in main effect of testing day (b = 7.09, z = 1.75, p = .080) or interaction (b = 28.00, z = 1.54, p = .123). Nonparametric/Bayesian analyses showed that there were no differences between correct rewarded and correct probe trials on each testing day or visual condition (p > .05, and BF < 1; see Table S4), indicating that animals were not smelling the reward. In summary, these results show that with sufficient training, blind animals could use geometric strategies relying on 3D edges, but sighted animals were unable to reorient themselves under these conditions.

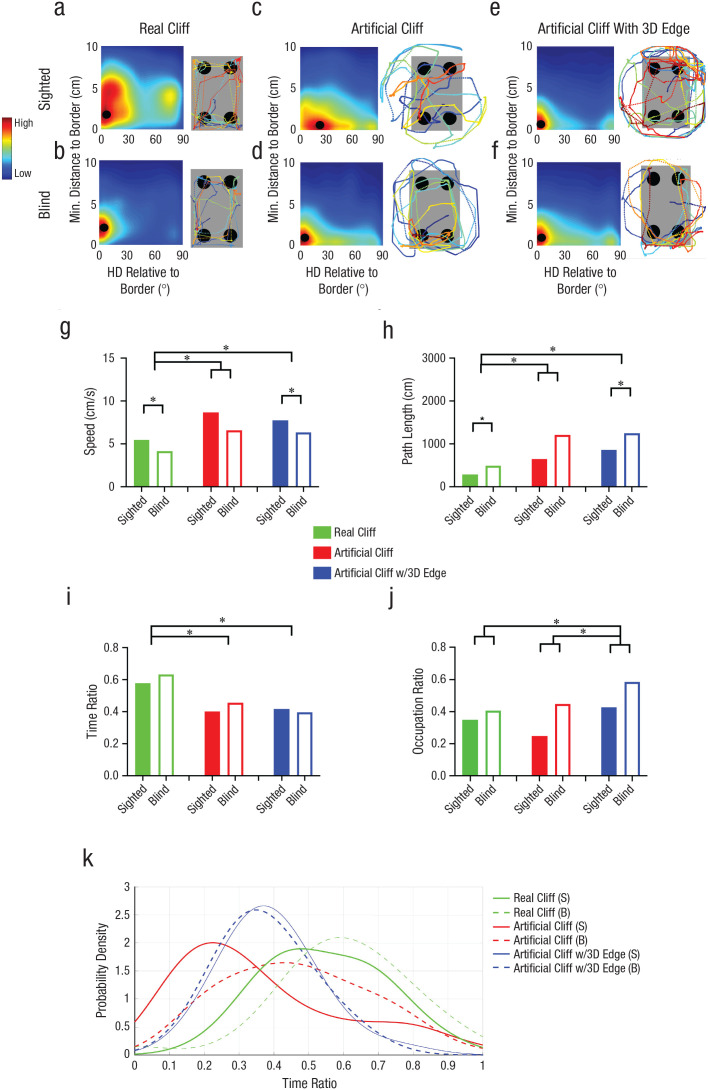
To further elucidate reorientation strategies across conditions, we analyzed the paths. We first calculated the heading of the animals to the closest border of the task-relevant area as a function of distance (Figs. 6a–6f). In the real-cliff condition (Fig. 6a), in which both sighted and blind animals effectively used geometry to reorient themselves, sighted mice patrolled the borders at a peak distance of 3 cm (SD = 4 cm) and a peak heading of 6° (SD = 26°). This indicated that animals patrolled the border and crossed along the diagonal connecting geometrically equivalent corners, as shown in the sample path (the angle between a straight line from the cup’s center and the diagonal connecting geometrically equivalent cups was 26°). Blind mice trained in this condition showed parallel sampling of the border—peak heading: 0° (SD = 16°), peak distance: 2 cm (SD = 1.5 cm), as depicted in the sample path shown in Figure 6b.

Fig. 6.

Experiment 3: results of the path analysis. Distance and heading orientation relative to border and sample paths from Day 4 in the real cliff (a, b), artificial cliff (c, d), and artificial-cliff-with-3D-edge (e, f) conditions is shown for sighted and blind mice (upper and lower row, respectively). The relative heading direction (HD) and distance to the task-relevant border (rectangle) were calculated for each path segment and added to the associated bin. Average color-coded maps show the heading orientation (x-axis) and distance from border (y-axis) distributions. Along the x-axis indicates, 0° indicates parallel and 90° indicates perpendicular heading to the border. The black dot indicates the location of the maximum orientation/distance. In all path diagrams, blue indicates the beginning of the path, and dark red indicates the first dig location. Speed and path length are shown in (g) and (h), respectively, for sighted and blind mice in each of the three conditions. Time and occupancy ratio are shown in (i) and (j), respectively, for sighted and blind mice in each of the three conditions. In (g–j), bars show means (error bars indicate standard errors of the mean), and dots represent individual data. The asterisks indicates significant differences between groups or between group performance on different days (α = .05). The density distribution of time ratios (k) shows the amount of time sighted and blind mice spent at the border in each condition. S = sighted; B = blind.

In the artificial-cliff condition, in which both sighted and blind animals failed to reorient themselves, sighted mice sampled the border with peak heading orientations of 24° (SD = 37°) at a peak distance of 0 cm (SD = 3.4 cm; Fig. 6c). This indicated that when sighted animals were close to the task-relevant borders, they crossed the edges rather than patrolling in parallel, which is illustrated in the sample path. Conversely, when blind animals were close to the task-relevant edges, they displayed parallel patrolling of borders—peak heading: 0° (SD = 31°), peak distance: 0.7 cm (SD = 2 cm), illustrated in the sample path (Fig. 6d). Finally, in the artificial-cliff-with-3D-edge condition, where only blind animals reoriented themselves, both sighted and blind animals patrolled the borders with parallel headings—sighted: peak heading: 0° (SD = 23°), peak distance: 0.8 cm (SD = 2 cm); blind: peak heading: 0° (SD = 22.5°), peak distance: 1 cm (SD = 2 cm); however, as shown in the sample path as well as the time and occupancy ratios discussed below, sighted mice occupied the circular edges more than the task-relevant area (Figs. 6e and 6f).

The observation that blind animals in the artificial-cliff condition and sighted animals in the artificial-cliff-with-3D-edge condition patrolled the borders with parallel headings was surprising and unexpected because these animals did not successfully reorient themselves in these conditions (Figs. 1f and 4d). This indicated that relative heading was not the only variable that influenced reorientation. Therefore, we also analyzed other parameters including speed (Fig. 6g), path length (Fig. 6h), time ratio (proportion of time at the border relative to other areas; Fig. 6i), occupation ratio (proportion of occupied border; Fig. 6j), and the probability distribution of the time ratio (Fig. 6k). Because the variability of these parameters across tasks was not homogeneous, the analysis was based on a robust ANOVA. The speed and path-length parameters showed effects of navigational condition—speed: F_W(2) = 29.86, p = .001, ξ = 0.57 (large effect); path length: F_W(2) = 22.18, p = .001, ξ = 0.65 (large effect)—and visual group—speed: F_W(1) = 14.00, p = .002, ξ = 0.52 (large effect); path: F_W(1) = 5.17, p = .034, ξ = 0.41 (medium effect)—but no interactions—speed: F_W(2) = 2.56, p = .322, ξ = 0.22 (medium effect); path length: F_W(2) = 1.26, p = .562, ξ = 0.29 (medium effect). Holm’s multiple comparisons revealed that in the artificial-cliff and artificial-cliff-with-3D-edge conditions, the animals’ speed was higher and the path length was longer than in the real-cliff condition—speed: real cliff versus artificial cliff: T_W(15.28) = −3.02, p = .009, ξ = 0.64 (large effect); real cliff versus artificial cliff with 3D edge: T_W(20.25) = −4.57, p < .001, ξ = 0.88 (large effect); artificial cliff versus artificial cliff with 3D edge: T_W(13.15) = 0.77 (large effect), p = .457, ξ = 0.19 (small effect; Fig. 6g); path length: real cliff versus artificial cliff: T_W(11.94) = −2.75, p = .018, ξ = 0.73 (large effect); real cliff versus artificial cliff with 3D edge: T_W(10.08) = −5.38, p < .001, ξ = 0.90 (large effect); artificial cliff versus artificial cliff with 3D edge: T_W(19.91) = −1.43, p = .169, ξ = 0.32 (medium effect; Fig. 6h). Importantly, blind animals moved more slowly and displayed longer paths than sighted animals across conditions, as shown in the main effects of groups.

Analysis of the time ratio showed a main effect of navigational condition, F_W(2) = 61.19, p = .001, ξ = 0.62 (large effect), but no effect of visual group, F_W(1) = 0.62, p = .443, ξ = 0.07 (small effect), or interaction, F_W(2) = 1.39, p = .527, ξ = 0.28 (medium effect). Holm’s multiple comparisons showed that animals trained in the real cliff spent more time at the border than in any other condition (Fig. 6i)—real cliff versus artificial cliff: T_W(14.8) = 3.47, p = .004, ξ = 0.75 (large effect); real cliff versus artificial cliff with 3D edge: T_W(19.71) = 6.80, p < .001, ξ = 0.95 (large effect); artificial cliff versus artificial cliff with 3D edge: T_W(15.46) = 0.47, p = .643, ξ = 0.15 (small effect)—despite the fact that the total path length in this environment was shorter that in other conditions, as mentioned above (Fig. 6h). These results suggest that in the real-cliff condition, animals sampled the border in one to two laps (reflected in short path lengths), which was sufficient to extract geometric information when the navigational affordances were constrained.

The occupation-ratio analysis revealed that blind animals occupied the border more than sighted animals across conditions, visual condition effect: F_W(1) = 13.29, p = .002, ξ = 0.53 (large effect). Additionally, there was an effect of navigational condition, F_W(2) = 12.16, p = .011, ξ = 0.47 (large effect), but no interaction, F_W(2) = 2.72, p = .296, ξ = 0.34 (medium effect). Holm’s multiple comparisons showed that the real-cliff and artificial-cliff conditions were statistically at the same level, T_W(22.59) = 0.93, p = .361, ξ = 0.17 (small effect), and both differed from artificial-cliff-with-3D-edge condition, where the occupation ratio was highest—real cliff versus artificial cliff with 3D edge: T_W(16.51) = −3.04, p = .008, ξ = 0.60 (large effect); artificial cliff versus artificial cliff with 3D edge: T_W(17.32) = −3.70, p = .002, ξ = 0.65 (large effect; Fig. 6j). Therefore, although both sighted and blind animals patrolled and occupied the borders in the artificial cliff with 3D edge, the blind mice might have been more successful they showed significantly higher occupation of the border area than sighted mice.

Finally, to further elucidate why blind animals in the artificial-cliff condition and sighted animals in the artificial-cliff-with-3D-edge condition did not reorient themselves even though they displayed parallel patrolling of the borders, we looked at the probability distribution of the time ratio (Fig. 6k). These distributions gave similar curves for sighted and blind animals in the real-cliff condition, where both groups spent substantial time at the border and reoriented themselves successfully. However, curves for the sighted and blind animals were very different in the artificial-cliff condition. Whereas the majority of sighted animals spent little time at the border, blind animals showed much more variability, with a few animals spending substantial time there. A positive correlation between performance and time ratio indicated that blind animals that spent substantial time at the task-relevant border used geometric strategies (p < .05; Table 3). In the artificial-cliff-with-3D-edge condition, sighted animals did not effectively reorient themselves (Fig. 4d) even though they patrolled the border (Fig. 6e) and displayed time ratios similar to those of blind mice (Fig. 6k); in this condition, the correlation between performance and time ratio was also significant (p < .05; Table 3), again corroborating that animals that spent more time at the border reoriented themselves effectively. Finally, successful performance of sighted and blind mice in the real-cliff condition and of blind mice in the artificial-cliff-with-3D-edge condition did not yield significant correlations (p > .05; Table 3), suggesting a ceiling effect due to less variability in performance.

Table 3.

Experiment 3: Correlations Between Reorientation Performance and Occupation or Time Ratio in Each Condition

Parameter and group	Real cliff	Artificial cliff	Artificial cliff with 3D edge
Occupation ratio
Sighted	.51 (p = .13)	.42 (p = .20)	.05 (p = .92)
Blind	–.03 (p = .93)	–.22 (p = .54)	–.01 (p = .98)
Time ratio
Sighted	–.23 (p = .53)	–.19 (p = .58)	.76 (p = .05)
Blind	.59 (p = .16)	.65 (p = .05)	.22 (p = .62)

In summary, our data indicate that when contexts limit the navigational affordances, patrolling the border is important for extraction of geometric parameters for animals to reorient themselves. However, the border exploration has to be much more extensive for effective use of geometry when borders are less salient, such as with a 3D edge. Furthermore, although blind animals require more exploration of the environments (e.g., display longer paths than sighted mice), they tend to patrol the borders with parallel headings regardless of the saliency of these edges and are very successful at reorienting themselves when they have sufficient experience with the borders.

Experiment 4: artificial cliff with high distal rectangular boundary

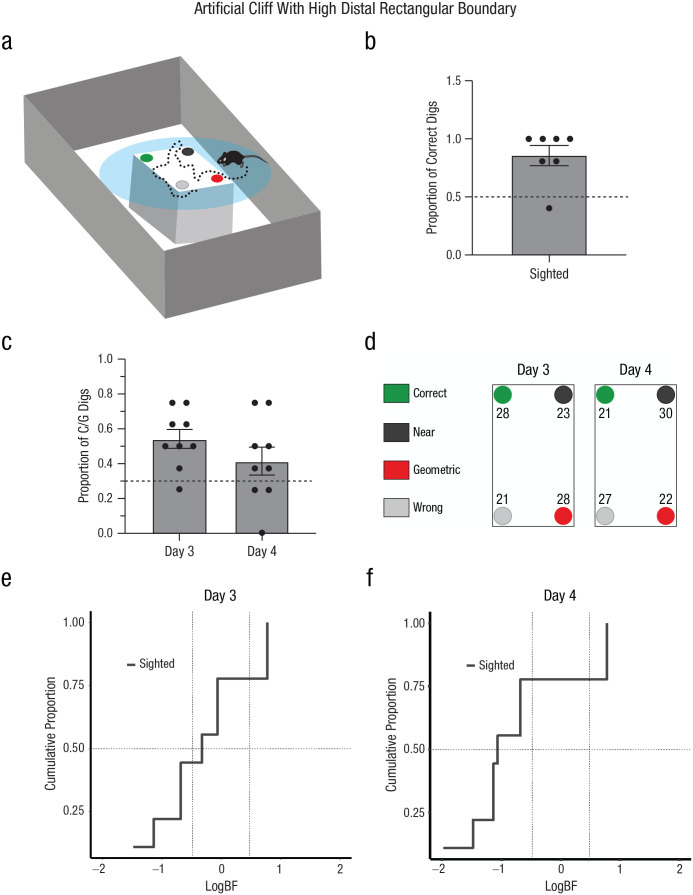
In the real-cliff condition, the navigational affordances of space promoted exploration of boundaries in sighted mice (e.g., time spent at the boundaries was maximal in this condition). However, another possibility could be that the visual saliency of the cliff encouraged more exploration in this condition. This could explain the inability of sighted mice to reorient themselves when the borders were less conspicuous (e.g., artificial-cliff or artificial-cliff-with-3D-edge condition). To disentangle whether sighted animals could reorient themselves using salient distal boundaries when the affordances of exploratory space did not correspond to that shape, we trained sighted mice in a circular artificial cliff surrounded by a high, distal rectangular boundary (Fig. 7a). Because animals could not touch the distal boundary, only sighted mice were used in this experiment.

Fig. 7.

Experiment 4: reorientation in the artificial-cliff-with-high-distal-rectangular-boundary condition. A schematic of the arena is shown in (a). The context was identical to the artificial cliff but was surrounded by a large rectangular shape. The task consisted in finding a reward hidden in one of four cups at the edges of the rectangular shape that enclosed the cup locations, which was placed on a circular platform. In the schematic, green indicates the correct rewarded location, black indicates the location nearest to the reward along the same short wall as the reward location, red indicates the geometrically opposite corner from the reward location, and gray indicates the location not associated with the correct geometric axis or the short wall near the reward. The proportion of correct digs (b) is shown for sighted mice. Digging preference (proportion of first digs in the geometrically correct axis relative to the total number of digs) is shown in (c) for Days 3 and 4. Bars show means (error bars indicate standard errors of the mean), and dots represent individual data. The dashed line indicates chance performance. The percentage of digs in the four different cup locations is shown (d) for Days 3 and 4. Results are shown separately for each cup location, using the color codes shown in (a) and (b). The cumulative proportion of subjects in terms of the weight of evidence supporting either the null hypothesis (H_null; chance performance) or the alternative hypothesis (H_alt; use of geometry) is shown for Day 3 (e) and Day 4 (f). Conventional values showing the border marking credibility for H_null versus H_alt are indicated by vertical dashed lines, log(1/3) = −0.48 and log(3) = 0.48. The value of half (0.5) of the sample is marked by a horizontal dashed line.

First, we tested whether sighted animals could see the distal rectangular boundaries by performing a visual discrimination test. Results showed that animals performed significantly above chance, F(7) = 4.62, p < .003, corroborating that sighted mice could see the distal rectangular walls (Fig. 7b). Then, we calculated the percentage of first dig locations during reorientation. Results indicated that animals performed at chance level across both testing days, F(1, 8) = 2.73, p = .137, η _G ² = .09 (small effect), 90% CI = [0.00, 0.45] (Fig. 7c). This result was corroborated by the percentage of cup digs (Fig. 7d) and the individual and group Bayesian analysis showing credibility for the model supporting the null hypothesis (chance) on Days 3 and 4, BF < 1/3 or log(1/3) = −0.48 (individual analysis: Figs. 7e and 7f and Tables S1 and S3; group analysis: Day 3: logBF = −1.25; Day 4: logBF = −2.86). Sequential digging probability analysis corroborated no support for the use of geometric strategies (Figs. 8a and 8b), Day 3: χ²(15, N = 62) = 6.13, p > .05; Day 4: χ²(15, N = 60) = 9.33, p < .05. Additionally, there were no differences between testing days in the latency to find the reward (b = 3.52, z = 0.48, p = .629) or between rewarded and probe trials (p > .05 and BF < 1/3; see Table S4).

Fig. 8.

Experiment 4: results of the sequential digging probability and path analysis in the artificial-cliff-with-high-distal-rectangular-boundary condition in sighted mice. Sequential digging probability is shown for Day 3 (a) and Day 4 (b). The bar on the right of each graph indicates probability. Larger, darker circles indicate higher probability; smaller, lighter circles indicate lower probability. C = correct corner; G = geometrically equivalent corner; N = near location to rewarded cup; W = wrong location. The average heading direction (HD) relative to the border is shown in (c). Along the x-axis indicates, 0° indicates parallel and 90° indicates perpendicular heading to the border. The black dot indicates the location of the highest value for head direction and distance to border. A sample path illustrating border crossings rather than parallel patrolling is shown in (d). The time-ratio density distribution (e) shows the amount of time sighted mice spent at the border in each condition. Sighted (S) mice: n = 9.

We then examined the paths of the animals in this condition. Heading relative to boundaries peaked at 16° (SD = 48°) when animals were close to the task-relevant area (0 cm, SD = 5 cm; Fig. 8c). This indicated crossings of the border rather than parallel patrolling, as illustrated in the sample path (Fig. 8d). Analysis of border parameters indicated low occupation and time ratios (see Fig. S4), resembling values observed in the artificial-cliff condition. The time-ratio probability density was almost identical to the artificial-cliff curve (Fig. 8e), showing that most mice did not spend time at the task-relevant edges. No significant correlations were observed between performance and time and occupation ratio (time ratio: r = .13, p = .760; occupation ratio: r = −.21, p = .612). The absence of significant correlations could have been due to the fact that the circular platform created a cliff that increased animals’ attention to areas that were not relevant for the task. These data indicated that animals were unable to reorient themselves using the high, distal boundaries, providing support for the idea that when local geometry is not salient, sighted animals fail to use geometric strategies.

Discussion

Our results indicate that the navigational affordances of space allow both sighted and blind mice to extract global parameters of the layout for reorientation. Furthermore, our data also show that geometry guides reorientation even in the absence of vision. Interestingly, whereas blind mice can use 3D edges to extract global parameters of shape, sighted animals fail to do so even when the 3D edges are distal and prominent.

Our findings provide support for the encapsulated geometric theory of reorientation in both sighted and blind mice. A cognitive map of allocentric space requires that the Euclidian distance between spatial features is preserved in the representation. Two views have been proposed to explain how this could be achieved. One account suggests that navigators extract the principal axes of the enclosure (Cheng & Gallistel, 2005), generating an orienting response (e.g., left or right) and the computation of a distance component. Another account proposes that geometry can be extracted associating local 2D features (e.g., long wall right, short wall left) with rewards (Dawson et al., 2010; Miller, 2009; Miller & Shettleworth, 2007; Ponticorvo & Miglino, 2010). Our path analysis provides support for the first view because animals required high occupation and time ratios as well as parallel patrolling of borders to extract geometry. View of corners (e.g., artificial cliff with high distal boundaries) or partial sampling (e.g., artificial cliff) did not facilitate reorientation. Some spatial brain regions contain egocentric boundary vector cells that code distance to borders and orientation (Alexander et al., 2020), making these cells ideal substrates to encode geometric relationships. Future studies manipulating the principal axis of an enclosure or local relationships while recording from brain regions containing egocentric boundary vector cells will provide further understanding of how geometric representations are built in the brain.

A recent study determined that visual areas, in particular, the dorsal occipitoparietal cortex, are critical for estimating traversable paths in sighted humans (Bonner & Epstein, 2017). Although less research has been devoted to studying how extravisual systems estimate spatial affordances, studies with blind cavefish indicate that senses other than vision can be extremely effective in delineating paths for navigation. Blind cavefish compensate for lack of vision with the lateral-line system, a sensory modality that allows detection of water motion and pressure gradients (Bleckmann & Zelick, 2009). The cavefish effectively use this system to reorient themselves using geometry (Sovrano et al., 2018). Our data further demonstrate that learning and experience strongly influence the effective use of global shape parameters in blind species. Blind mice can use 3D edges, whereas sighted animals fail to do so, which likely reflects that experience with haptic perception allows blind mice to be more sensitive and attentive to alterations of surface properties.

Studies testing spatial abilities in blind subjects have not revealed consistent findings (Proulx et al., 2014). As a result, three views have been proposed to account for blind navigation (Schinazi et al., 2016). The cumulative model proposes that the differences between sighted and blind subjects accumulate over time (von Senden, 1960). The persistent model states that blind and sighted subjects acquire spatial knowledge over time, but the differences in abilities remain constant (Worchel, 1951). Finally, the convergent model states that although blind subjects exhibit initial disadvantages, these differences disappear with experience (Landau et al., 1984; Tinti et al., 2006). Our findings support this latter view by demonstrating that blind mice can perform equally to or even better than sighted ones.

Our data show that both sighted and blind animals must patrol and spend time at the border to extract geometric parameters. Although this indirectly suggests that haptic perception plays a prominent role in not only blind but also sighted navigation (i.e., if vision were sufficient, even low occupation or time at borders should lead to the use of geometric strategies), we cannot exclude the possibility that sighted animals use a combination of both vision and haptic perception or that vision facilitates reorientation in some situations. Indeed, sighted animals learned to use geometry faster (Day 3) than blind animals (Day 4) in the real-cliff condition. Additionally, all of our environments were simple rectangular and/or cylindrical contexts; therefore, it is possible that in complex scenarios, vision provides a more significant advantage.

It is interesting to note that neither blind nor sighted animals could extract geometry from the artificial-cliff condition, in which a rectangular texture defined the task-relevant area. This is surprising because a recent study showed that a large percentage of hippocampal place cells, which fire in particular locations as animals navigate (O’Keefe & Dostrovsky, 1971), displayed distinctive activity close to the boundaries of surface textures (Wang et al., 2020). However, these neural responses do not necessarily imply that global relationships are being extracted from the texture cues. It is possible that place cells respond to texture edges in the same manner in which they respond to other cues in the environment, such as odors, sounds, or objects (Anderson & Jeffery, 2003; Aronov et al., 2017; Cohen et al., 2013; Wood et al., 1999). To demonstrate that place cells are responding to the global relationships defined by textures, we would need to manipulate the shape of the textures and determine whether neural activity changes (e.g., making one edge longer relative to another). Furthermore, the fact that blind animals in the artificial-cliff condition and sighted animals in the artificial-cliff-with-3D-edge condition were unable to reorient themselves but displayed significant positive correlations between performance and time spent at the border indicates that extraction of global parameters requires extensive sampling of borders, and perceiving edges is not enough.

Our results in the artificial-cliff-with-high-distal-boundaries condition differ from those found in the classic study by Margules and Gallistel (1988), in which some rats were able to use external room cues to find a correct goal location when local and global geometry were in conflict. However, it is important to note that in that study, the task was conducted in a rectangular geometric environment, allowing animals to associate external room cues with the local geometry. In our study, the local geometry did not constrain navigational affordances and lacked 3D salient features; therefore, sighted mice were unable to use distal geometric cues for reorientation, even when they perceived them, as demonstrated in the visual discrimination test.

In this study, we used reference memory tasks to assess how sighted and blind mice reorient themselves under different conditions. Because our focus was to determine how animals extract geometric parameters, we eliminated nongeometric landmarks. It has been shown that when geometric and nongeometric featural cues are present during working memory reorientation tasks, there are learning interactions between these cues, which are less obvious during reference memory tasks (Lee et al., 2015, 2020). It is thought that this is the case because reference tasks rely on cognitive systems and computations forming allocentric representations of space, which may bias or mask featural associations during reorientation. Our findings do not contradict these conclusions but strengthen the view that geometry is an important cue for navigation. In future studies using working memory tasks, it would be important to determine whether featural associations modulate geometric reorientation in the same way in sighted and blind animals.

In summary, our data show that geometry is critical for reorientation in sighted and blind animals, and the navigational affordances of space are important for promoting exploration of edges, a requirement for extracting global parameters of the layout.

Transparency

Action Editor: Daniela Schiller

Editor: Patricia J. Bauer

Author Contributions

M. E. Normandin and M. C. Garza contributed equally to this study and wrote the manuscript. I. A. Muzzio developed the study concept and designed the study along with M. E. Normandin and M. C. Garza. J. B. Julian, T. Eresanara, N. Punjaala, J. H. Vasquez, and M. R. Lopez collected and scored the data. M. E. Normandin conducted the statistical analysis and developed the code for the path and probability analyses. M. M. Ramos-Alvarez conducted the parametric and Bayesian statistical analyses. M. R. Lopez supervised undergraduates working on this project. I. A. Muzzio supervised all aspects of the data collection and analyses. All the authors approved the final manuscript for submission.