Abstract
Motivation
Phylogenetic tree optimization is necessary for precise analysis of evolutionary and transmission dynamics, but existing tools are inadequate for handling the scale and pace of data produced during the coronavirus disease 2019 (COVID-19) pandemic. One transformative approach, online phylogenetics, aims to incrementally add samples to an ever-growing phylogeny, but there are no previously existing approaches that can efficiently optimize this vast phylogeny under the time constraints of the pandemic.
Results
Here, we present matOptimize, a fast and memory-efficient phylogenetic tree optimization tool based on parsimony that can be parallelized across multiple CPU threads and nodes, and provides orders of magnitude improvement in runtime and peak memory usage compared to existing state-of-the-art methods. We have developed this method particularly to address the pressing need during the COVID-19 pandemic for daily maintenance and optimization of a comprehensive SARS-CoV-2 phylogeny. matOptimize is currently helping refine on a daily basis possibly the largest-ever phylogenetic tree, containing millions of SARS-CoV-2 sequences.
Availability and implementation
The matOptimize code is freely available as part of the UShER package (https://github.com/yatisht/usher) and can also be installed via bioconda (https://bioconda.github.io/recipes/usher/README.html). All scripts we used to perform the experiments in this manuscript are available at https://github.com/yceh/matOptimize-experiments.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
With over 10 million genome sequences now available on online databases, SARS-CoV-2 is the most sequenced pathogen in history by far (Shu and McCauley, 2017). Phylogenetics has been a foundational tool in analyzing this vast volume of genomic data for a public health response during the coronavirus disease 2019 (COVID-19) pandemic (Hodcroft et al., 2021). For example, phylogenetics has been instrumental in genomic surveillance, i.e. for identifying and naming its new variants (Rambaut et al., 2020) and for tracking the different SARS-CoV-2 variants circulating in a given geographic region (da Silva Filipe et al., 2021; Deng et al., 2020). Phylogenetic trees have also helped in establishing transmission links between infections (Lam-Hine, 2021), in disambiguating community transmission from outside introductions (Komissarov et al., 2021; McBroome et al., 2022), in identifying the mutations that might have conferred increased transmissibility to the virus (Korber et al., 2020; Richard et al., 2021), and for estimating the reproduction number (R0) of the virus and its variants (Lai et al., 2020; Volz et al., 2021).
Many of these far-reaching applications benefit from having a comprehensive phylogenetic tree—one produced without subsampling the available sequences. For example, when all available SARS-CoV-2 sequences are not represented in a single phylogenetic tree, transmission links between isolates may be lost. Likewise, subsampled phylogenetic trees could omit important lineages or sublineages corresponding to different variants of the virus. This can have adverse consequences on the downstream evolutionary and epidemiological studies. A comprehensive and up-to-date phylogenetic tree is therefore an essential goal for the global health response to the SARS-CoV-2 pandemic.
Online phylogenetics is a potentially transformative solution for the massive computational challenges imposed by continual genome sequence collection during the pandemic (Gill et al., 2020; Thornlow et al., 2021). It involves incorporating new sequences as they become available onto an existing phylogeny and periodically refining the updated phylogeny. The recent development of UShER (Turakhia et al., 2021b), which uses stepwise addition of new sequences onto an existing phylogenetic tree, helped overcome an important computational barrier for the maintenance of a comprehensive SARS-CoV-2 phylogenetic tree (McBroome et al., 2021). For large SARS-CoV-2 phylogenies, UShER’s maximum parsimony (MP) approach has been demonstrated to perform well, even when compared to the far more computationally expensive maximum likelihood approaches available currently (Thornlow et al., 2021). However, since UShER is based on the greedy approach of stepwise addition of new sequences, it sometimes places new sequences suboptimally in the tree (Turakhia et al., 2021b; Takahashi and Nei, 2000). Tree optimization tools, which use tree rearrangement to find more optimal tree configurations, can help ameliorate this issue. However, in the recent 6 months (December 2021 to May 2022), the UShER-derived comprehensive SARS-CoV-2 phylogenetic tree size grew by 1.6-fold, with an average of approximately 21 000 additional sequences being incorporated each day. Approaches capable of daily tree optimization of the massive SARS-CoV-2 phylogeny are therefore an urgent necessity for emerging online phylogenetic toolkits.
Phylogenetic tree optimization has been extensively studied in the context of MP, and tools such as TNT (Goloboff and Catalano, 2016), PAUP* (Swofford, 2003), MPBoot (Hoang et al., 2018), PHYLIP (Felsenstein, 2005) and MEGA (Kumar et al., 2018) are already available. Typically, tree optimization tools take as input an existing phylogenetic tree in the Newick format and the multiple sequence alignment (MSA) of the phylogenetic tips in FASTA format, then compute the parsimonious state assignments for every node of the tree for each alignment site, and then use tree rearrangement to find a more parsimonious tree. They also maintain multiple equally parsimonious candidate trees and sometimes use tree drifting (Goloboff and Catalano, 2016) during the optimization to avoid getting stuck in local optima. TNT also provides additional heuristics, such as sectorial search (Goloboff, 1999), to speed up tree search. Though these tools are remarkably efficient for the typical applications that they were developed for (such as for one-time species tree inference), they are inadequate for handling the scale and pace of the rapidly expanding SARS-CoV-2 data due to their prohibitive runtime and memory requirements.
Here, we developed matOptimize, a novel MP-based tree optimization tool that uses several domain-specific optimization techniques to greatly speed up, and reduce the cost of, optimizing the comprehensive SARS-CoV-2 phylogeny. Compared to previous approaches, matOptimize uses novel memory-efficient data structures and algorithmic techniques to handle the vast scale of SARS-CoV-2 data, and it is more efficiently parallelized for multicore CPUs as well as high-performance computing (HPC) clusters. As a result, the resources allocated to matOptimize can be scaled to meet the computational requirements of the ever-expanding comprehensive SARS-CoV-2 phylogeny. matOptimize also effectively uses preprocessing and algorithmic strategies better suited for ‘online phylogenetics’, which for example enable it to achieve rapid improvements in parsimony score in early stages of the optimization. Our analysis on real data suggests that matOptimize indeed qualitatively improves the comprehensive SARS-CoV-2 phylogeny. Starting from an UShER-derived SARS-CoV-2 phylogeny, matOptimize provides roughly the same parsimony score improvement (used as a measure of tree quality) as the previous state-of-the-art for a moderately sized phylogeny, and is the only tool that meets the constraints of daily-optimization for the current scale of comprehensive SARS-CoV-2 phylogeny.
2 Materials and methods
2.1 matOptimize: algorithm description
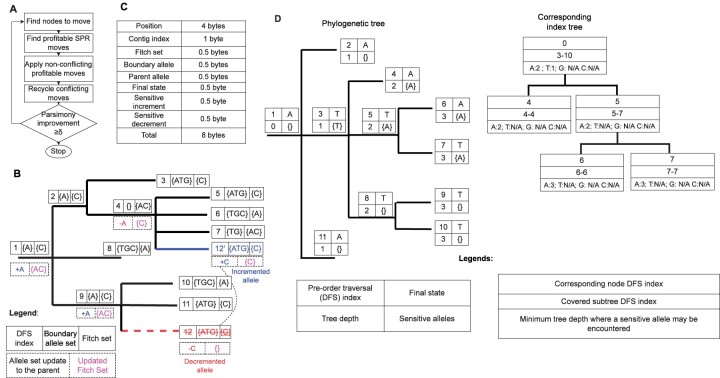
matOptimize is a parallel algorithm (Fig. 1) for parsimony-based optimization of large SARS-CoV-2 phylogenies, where the parsimony score is derived based on characters in nucleotide space. matOptimize takes as input a starting phylogeny, such as the UShER-derived mutation-annotated tree [MAT; which is a file format that stores a phylogenetic tree in which the branches are annotated with the mutations that are inferred to have occurred on them (Turakhia et al., 2021b)] or a Newick file, and an optional VCF file specifying the genotypes at the tips of the phylogeny. When a VCF input is provided, matOptimize uses a parallel implementation of the Fitch–Sankoff algorithm (Fitch, 1971; Sankoff, 1975) to infer the most parsimonious state for every VCF site at every branch of the tree. Otherwise, the algorithm accepts the states annotated in the MAT and skips to the next step. matOptimize allows the VCF file to specify ambiguous bases using the International Union of Pure and Applied Chemistry (IUPAC) format (https://www.bioinformatics.org/sms/iupac.html). matOptimize uses an MAT format that has been modified to maintain ambiguous bases at tree leaves, entire Fitch sets at internal nodes and a few additional data fields to aid the optimization process (Fig. 1C).
Fig. 1.
An illustration of the matOptimize algorithm. (A) A flowchart of the different algorithmic stages in matOptimize. (B) An example of how matOptimize estimates the parsimony score improvement achievable from a single SPR move using a small number of steps without redoing the entire Fitch algorithm (Fitch, 1971). Each node of this tree has an integer label (1–12) and is annotated with its Fitch and boundary allele sets (Section 2). This example evaluates a move in which the subtree rooted at node 12 is pruned from node 9 and regrafted at node 4. For this move, the alleles in the Fitch set of node 12 (i.e. the single allele C) must be decremented at node 9 (during pruning) and incremented at node 4 (during regrafting). Since C is the only allele in the Fitch set of node 9, the alleles from the boundary allele set of node 9 get added to its Fitch set, resulting in an updated Fitch set {A, C}, with a lower major allele count. The change in Fitch set of node 9 is propagated upwards to its parent, i.e. to root node 1. During the pruning step, the decrement of the major allele count at node 9 has no effect on the parsimony score since it is offset by the decrement in the children count. During regrafting, since allele C, which is already present in the Fitch set of node 4, is incremented, its major allele count is now higher than the remaining alleles in the Fitch set, i.e. allele A, which is decremented. This change is propagated upwards, i.e. to parent node 2, but has no effect on it since allele A is not present in its Fitch set. Since the regrafting step also does not change the parsimony, the net parsimony score change of this move is 0. (C) Storage requirements for a mutation in the MAT data structure of matOptimize. This is a modified version of the original MAT proposed in UShER (Turakhia et al., 2021b) in order to maintain auxiliary information (such as Fitch and boundary allele sets) for performing optimization. Each mutation in matOptimize is stored compactly using only 8 bytes, which helps it maintain a small memory footprint overall. (D) An example phylogenetic tree (left) and its corresponding index tree (right). The index tree is used to speed up the search for promising destination nodes for SPR moves from a single source node via search space pruning (Section 2). Each node in the phylogenetic tree is annotated with (i) a pre-order traversal index, (ii) the depth of the node, (iii) the final allele assignment and (iv) the sensitive allele (Section 2). The index tree uses a B-Tree (Cormen, 2009; Knuth, 2011) to store the nodes at which the sensitive alleles are found (Section 2). Each node in the index tree corresponds to one node in the phylogenetic tree and stores the DFS index range of the subtree that the node covers and the minimum depth within the subtree at which a sensitive allele may be encountered. ‘N/A’ implies that the allele is not present in the subtree
The matOptimize algorithm (Fig. 1) performs several iterations of optimization consisting of two phases: (i) the parallel search phase, which searches for parsimony-reducing subtree pruning and regrafting (SPR) moves from multiple starting nodes in parallel while holding the starting tree constant and (ii) the non-conflicting moves application phase, in which a subset of the profitable moves that were discovered during the parallel search are applied to the starting tree. These phases are described in more detail below. The iterations continue until the percent parsimony score improvement in the last iteration is less than the user-specified threshold (δ in Fig. 1A, default: 0.5%), or the wall-clock time limit specified by the user (default: unlimited) is exceeded (Fig. 1A). Only one tree is maintained throughout the optimization in matOptimize. We use the following terminologies for the remaining description of the algorithm:
Child node: A direct descendant of a node in the tree.
Tree depth: The distance from root to a node.
Allele: The nucleotide found or inferred at a particular genomic position.
Fitch set: The most common allele(s) among the Fitch sets of the children of the current node. On leaf nodes, Fitch sets are observed alleles.
Least common ancestor (LCA) nodes: The node furthest from the root that is the ancestor of both source node and destination node.
DFS: Pre-order depth first search.
Allele frequency: The number of children of the node that contains the allele in its Fitch set. On leaf nodes, zero for alleles not observed, 1 for observed alleles.
Major allele frequency: Allele frequency of an allele in the Fitch set (the same for all alleles in the Fitch set).
Boundary allele set: Alleles whose frequency is exactly one less than the major allele frequency. This set is updated once before every parallel search phase in every iteration.
Final state: A single allele inside the major allele set obtained by arbitrary tie-breaking strategy among multiple equally parsimonious alleles.
An allele is incremented: An allele is added to the Fitch set.
An allele is decremented: An allele is removed from the Fitch set.
Sensitive allele: An allele that will improve the parsimony score of the tree when incremented alone, excluding parent alleles. Parent alleles are excluded because they do not contribute to parsimony scores.
2.1.1 Parallel search phase
In this phase, multiple nodes are searched in parallel for SPR moves within a fixed radius that may reduce the parsimony score. In the first iteration, all nodes in the tree are considered for SPR moves. In subsequent iterations, SPR moves starting from only those nodes that are within a fixed radius of nodes that were modified through pruning or regrafting of an SPR move in the previous iteration are considered. The SPR radius in the first iteration is limited to 2, and this limit doubles at the end of every iteration. To calculate the parsimony score change of a single move, matOptimize uses a modified version of Gladstein’s incremental update method (Gladstein, 1997) that can also handle polytomies. When sample genotypes are specified through an input VCF file, matOptimize first pre-processes the tree to calculate the Fitch set, boundary allele set and final state for every site at every node of the tree using a reverse breadth-first traversal.matOptimize calculates the change in parsimony score from a single move by tracking the change in major allele frequency as the effect of the move propagates toward the root (i.e. in a reverse pre-order traversal order). Figure 1B illustrates this with an example SPR move. An allele can be incremented (i.e. added to the Fitch set from the boundary allele set) at a node if: (i) it is incremented in any of its children nodes (e.g. in Fig. 1B, allele A is incremented at node 1 after an increment of A at its child node 9) or (ii) all alleles in the Fitch set are decremented in any of its children nodes (e.g. in Fig. 1B, allele A is decremented at node 9 after a decrement of the single allele C in the Fitch set of its child node 12). Similarly, an allele is decremented when it has been decremented in any of its children nodes, or if some other alleles in the Fitch set have been incremented in any of its children nodes (e.g. in Fig. 1B, allele A at node 4 is decremented from an increment of C at 12). Finally, the parsimony score is calculated as the sum of change in children count minus change in major allele count at each node on the path from source or destination node to root. The starting tree remains immutable and shared among all threads throughout the parallel search phase, so the memory consumption only increases negligibly with the number of threads.
2.1.2 Parallelization of the parallel search phase
In matOptimize, different source nodes are evaluated in parallel to find profitable SPR moves during the parallel search phase. Parallelism across different instances of a CPU cluster is achieved through multiprocessing that is implemented using the message passing interface (Gropp et al., 1999). At the start of a new iteration, the main process broadcasts the intermediate MAT to all worker processes, assigns unique source nodes to each process to evaluate and collects the profitable moves found by worker processes. For load balancing, each worker process maintains its own running estimate of the throughput of the number of source nodes processed per minute and requests source nodes corresponding to a maximum of 1 min of workload from the main process at a time. matOptimize also parallelizes source node evaluation on multiple threads of a single instance using Intel’s TBB library (https://github.com/oneapi-src/oneTBB). Here, source nodes assigned to a process are uniformly partitioned on each available thread, which then evaluates all the SPR moves originating within the specified radius from its corresponding source node. By default, matOptimize not only creates CPU threads to utilize all available cores on a CPU instance but also allows the number of threads to be specified by the user as a command-line argument.
2.1.3 Search space pruning
To minimize the number of non-profitable moves explored from a source node in the parallel search phase, matOptimize quickly calculates a lower bound of parsimony score change of moving the pruned subtree to other nodes within a specified radius. It does this by first pre-computing the sensitive alleles for each site at each node using a dynamic programming algorithm. The sensitive allele sets are then organized into a B-Tree (Cormen, 2009; Knuth, 2011), called index tree (Fig. 1D), using the DFS index of the nodes. The internal nodes of the index tree are also annotated with the minimum depth at which each allele will be encountered and corresponding the DFS indices of phylogenetic tree nodes it covers (Fig. 1D). The parsimony score change lower bound is initialized with the parsimony score change that would result from removing the source node alone. Then, matOptimize queries the index tree for the minimum depth at which the allele that source node carries may be encountered. If it is larger than the maximum radius minus the distance between the source node and the node being examined, the lower bound of parsimony score change is incremented. In this step, the DFS index range in the index tree is queried to find the minimum depth of the node in the subtree of the currently examined node at which the sensitive allele may be encountered. All destination nodes in a subtree rooted at the node being examined are skipped if the parsimony score change lower bound at this node is higher than that of the most profitable move from the source node found so far (Fig. 1D).
2.1.4 Non-conflicting moves application phase
Moves that share nodes on the paths from source nodes to destination nodes are defined to be conflicting as they cannot be simultaneously applied. Empirically, most profitable moves found in the parallel search phase have one or more conflicts. Among conflicting moves, matOptimize accepts the most profitable move and defers the remaining to the next iteration. Then, all non-conflicting moves are applied in a batch. matOptimize recomputes the Fitch and boundary allele sets of the altered nodes and their ancestors serially in post-order traversal order. If the parsimony score is found to increase during the application of a non-conflicting move, matOptimize terminates the current iteration and begins a new one. Sensitive alleles are recomputed from scratch at the beginning of every new iteration. Profitable source nodes in the last iteration are searched again, until there is no parsimony improvement, after which a new round of iterations is started with doubled SPR radius and all possible source nodes.
2.2 Tree evaluation
To calculate the likelihood scores of our trees, we used IQ-TREE2 (Minh et al., 2020) COVID-19 release 2.1.3, with Jukes-Cantor (JC) model and a minimum branch length of 1e-11. Trees were visualized with Taxonium (https://cov2tree.org/). Pango lineages for sequences were assigned using the Pangolin software (O’Toole et al., 2021) and parsimony scores for the lineage assignments were computed using TNT (Goloboff and Catalano, 2016), taking clade assignment as binary characters.
2.3 Datasets
We collected SARS-CoV-2 genome sequence data from major online databases: GISAID (Shu and McCauley, 2017), COG-UK (Nicholls et al., 2020), GenBank (Clark et al., 2016) and CNCB (https://bigd.big.ac.cn/ncov/release_genome) until August 25, 2021 and used it to build a comprehensive SARS-CoV-2 phylogeny based on the methodology described in McBroome et al. (2021). We used the GenBank MN908947.3 (RefSeq NC_045512.2) sequence as the reference for rooting the tree and used the sampling date metadata to derive from our comprehensive tree three subtrees containing the earliest 100K, 1M and 3M samples, referred to as 100K-sample tree, 1M-sample tree and 3M-sample tree, respectively. The GISAID Data Access Agreement prohibits the sharing of these datasets, but allows us to communicate it to GISAID members on request.
To test generalizability of matOptimize, we also collected a Mycobacterium tuberculosis dataset consisting of 10 248 M.tuberculosis samples from the NCBI Sequence Read Archive (Leinonen et al., 2011) and generated a multisample VCF with a GATK-based pipeline (https://github.com/cademirch/ccgp_workflow). The multisample VCF was then compressed with GENOZIP (Lan et al., 2021) and is made available at https://doi.org/10.6084/m9.figshare.19799374. We then removed all samples for which fewer than 95% of polymorphic sites contained a genotype. The resulting multisample VCF was then used to infer a de novo phylogenetic tree using UShER (Turakhia et al., 2021b). To do this, we seeded UShER with a “tree” that contained just the reference sequence and then we added each sample sequentially until each had been added and we saved the final mutation-annotated tree file.
2.4 Baseline comparison
2.4.1 Performance benchmarking
Among the available tree optimization programs, we found TNT (Goloboff and Catalano, 2016) (June 2021 version) to be the only suitable baseline for comparison with matOptimize on large SARS-CoV-2 datasets. We could not compare with PAUP* (Swofford, 2003), as it limits the tree size to only 16K taxa. Similarly, we found that MPBoot (Hoang et al., 2018) fails due to the prevalence of identical sequences in SARS-CoV-2 datasets. Other tools, such as PHYLIP (Felsenstein, 2005) and MEGA (Kumar et al., 2018), infer a de novo tree from the input alignment on every run, and therefore cannot be used in the online phylogenetics framework.
Given its high peak memory requirements, we used a single m1-ultramem-40 instance (40 vCPUs, 961 GB, $6.30/h) for TNT. For matOptimize, we used seven e2-highcpu-32 instances for matOptimize that cumulatively have an hourly cost ($5.54/h) comparable to the m1-ultramem-40 instance. The peak memory requirements were estimated by reading the resident set size of each process every 2 min. The parsimony scores were computed after rerooting the trees to GenBank MN908947.3 (RefSeq NC_045512.2).
2.4.2 Parallelization of TNT
TNT does not natively include a multithreaded optimization mode, so in order to parallelize it, we used multiple processes performing exclusive sectorial search (XSS), which had better performance compared to parsimony ratchet, tree drifting or direct branch swapping modes in TNT (Goloboff and Catalano, 2016). In the XSS mode, TNT splits the tree into non-overlapping sectors of roughly equal size and optimizes each sector separately using tree bisection and reconnection (TBR) moves. If the parsimony score improves within the sector, TNT uses it to replace the corresponding sector in the starting tree. We parallelized XSS by splitting the starting tree into 10 non-overlapping sectors, which offered the best runtime and parsimony score tradeoff. During global TBR moves, we let each TNT process optimize the entire tree independently and broadcast the tree to other processes. We parallelized TNT with the highest number of processes possible within the available memory of the instances. This corresponded to 40, 8 and 1 processes for 100K-sample, 1M-sample and 3M-sample SARS-CoV-2 trees, respectively.
3 Results
3.1 matOptimize rapidly and efficiently optimizes massive SARS-CoV-2 phylogenies
We used the database of UShER-based SARS-CoV-2 trees (McBroome et al., 2021) to pick phylogenies at three different time points, containing 100K, 1M and 3M samples, respectively. We used these as starting phylogenies to compare the performance of matOptimize with TNT (Goloboff and Catalano, 2016), the fastest and most efficient MP-based tree optimization tool currently available (Fig. 2). Since TNT is not multithreaded, it had to be manually parallelized across multiple processes (Section 2). We also limited the optimization to 24 h to meet the constraints for enabling daily tree optimization which is required for comprehensive phylogenetics during the pandemic. Of the three trees we evaluated, TNT (Goloboff, 1999) completed its optimization for only one, i.e. the smallest 100K-sample tree, achieving a parsimony score improvement of 0.63% in 1.13 h. matOptimize completed this tree optimization 19× faster and with 37× lower peak memory (Fig. 2A), achieving a comparable but slightly smaller parsimony improvement of 0.59%. The smaller parsimony score improvement of matOptimize could be explained by the fact that it searches from one starting tree and uses SPR moves only, which have a smaller search space than the TBR moves and the independent search of multiple trees used in TNT (Goloboff, 1996). matOptimize achieved 5× improvement over TNT on the 100K-sample tree even when executed on the same CPU instance as TNT with an identical number of threads (Supplementary Fig. S1).
Fig. 2.
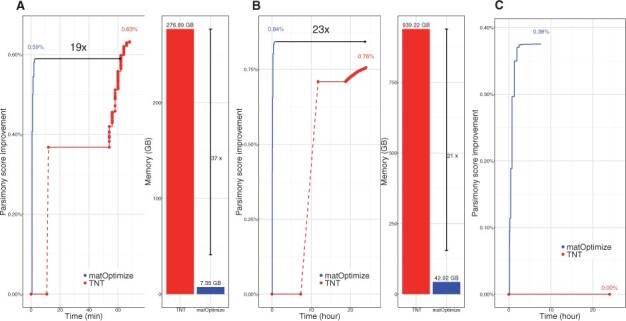
Comparison of parsimony score improvement and peak memory requirement of matOptimize and TNT starting from an SARS-CoV-2-based UShER-derived (A) 100K-sample tree, (B) 1M-sample tree and (C) 3M-sample tree. For (C), the peak memory requirement is not shown since TNT did not begin the optimization phase by the time it was terminated after 24 h of execution
The benefits of matOptimize become apparent when the tree size gets larger—it completed optimization for the 3M-sample tree in only 7.7 h (Fig. 2C). On this tree, TNT did not even start applying profitable moves within the 24-h time limit. This is because, for the scale of this tree, TNT was still loading the input files and initializing its internal data structures when the 24-h cutoff was reached. Since matOptimize also uses SPR radius doubling at each iteration, and since smaller radii iterations are quick to complete, the largest improvements in parsimony score are achieved very quickly during optimization (Fig. 2, Supplementary Fig. S1). Due to its memory-efficient internal data structures and parallel implementation of the Fitch–Sankoff algorithm during initialization (Sections 2 and 4), matOptimize starts optimizing the tree after a small delay, which is desirable for time-constrained optimization scenarios imposed by the COVID-19 pandemic. In contrast, TNT incurs a long startup delay followed by a slow improvement of parsimony. matOptimize is therefore especially well-suited for SARS-CoV-2 online phylogenetics (Thornlow et al., 2021).
Detailed analysis of the resulting tree revealed that matOptimize indeed improves the tree quality. For example, on the 100K-sample tree, the 0.59% parsimony score improvement also translated into a 0.48% improvement in the log-likelihood score—from -919354.028 to -914925.186. For the TNT-optimized tree, the log-likelihood is even higher, -914592.653, i.e. 0.51% higher than the starting tree. This is consistent with our previous analyses (Thornlow et al., 2021) in which we observed that parsimony and likelihood scores are strongly correlated for SARS-CoV-2 phylogenies. We also observed that in some cases, the PangoLEARN lineage assignments (O’Toole et al., 2021) appeared a little less dispersed through the tree (Supplementary Fig. S2), with the Pango lineage parsimony score decreasing from 17043 to 17014 post-optimization with matOpimize. Here, the small improvement through optimization reaffirms the observation that even the stepwise addition of samples through UShER has high accuracy for lineage assignments (Dudas et al., 2021; McBroome et al., 2021).
3.2 matOptimize scales well in runtime and memory requirement with the number of available processors
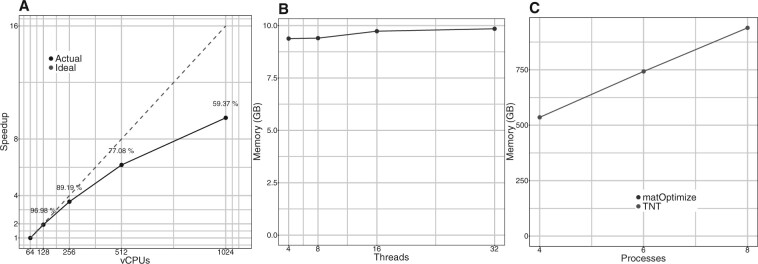
Efficient parallelism ensures that matOptimize can keep up with the increasing computational demands for optimizing SARS-CoV-2 phylogenies. We designed it to parallelize over all available virtual cores on a CPU (vCPUs), as well as a large number of CPUs available in an HPC cluster, which includes cloud platforms. Figure 3A shows that matOptimize shows a high strong scaling efficiency. matOptimize requires 109 min to complete one round of optimization on the 1M-sample tree with 64 vCPUs over two CPU instances, which reduces to 11.5 min with 1024 vCPUs over 32 CPU instances (scaling efficiency of 59%, Fig. 3A). In the latter, the parallel search for profitable moves required 7.5 min and the sequential step of applying the moves took 4 min. We therefore expect strong scaling efficiency to improve as the SARS-CoV-2 tree gets bigger, and the parallel search phase consumes a larger fraction of the total runtime.
Fig. 3.
Performance and memory scaling efficiency of matOptimize using the 1M-sample tree. (A) Strong multi-node scaling efficiency of matOptimize. Each node is a GCP instance e2-highcpu-32 consisting of 32 vCPUs and 32 GB memory. The number above each data point corresponds to the actual runtime in minutes: seconds format. (B) The peak memory requirement of matOptimize is small (below 10 GB) and remains roughly constant with the number of CPU threads. This allows matOptimize to exploit all available parallelism on a multicore CPU instance without being limited by the available memory. (C) In comparison, the peak memory requirement of TNT is large (>500 GB) and increases linearly as the parallelism is increased. This limits the amount of parallelism that TNT can exploit—in the example shown, TNT could exploit only up to 8 available vCPUs out of the 40 available on the memory-optimized GCP instance m1-ultramem-40 before running out of memory
A key reason why matOptimize scales efficiently is its low memory requirement. This is enabled through its compact MAT data structure derived from UShER, which we use in lieu of the traditional matrix representation of the MSA in existing frameworks (Figs. 1C and 3B, Section 2). When the number of CPU threads used by matOptimize is increased from 4 to 32, the memory requirement for the 1M-sample SARS-CoV-2 tree increases only marginally, from 9.38 to 9.84 GB (Fig. 3B). In contrast, the large and linear memory requirement of TNT limits the amount of parallelism it can exploit (Fig. 3C). For example, with the 1M-sample SARS-CoV-2 tree, we could only parallelize TNT to utilize 8 of the 40 available vCPUs on the m1-ultramem-40 instance that we used on the Google Cloud Platform (GCP), since eight TNT processes consumed nearly all of 961 GB available memory on this instance. It is therefore unlikely that TNT would scale to the much larger SARS-CoV-2 phylogenies anticipated in the future due to its prohibitive memory requirement.
3.3 Larger SPR radii provide smaller, but measurable improvements in parsimony score
We explored the contribution of different SPR radii to the improvement in parsimony score on the 100K-sample tree, 1M-sample tree and the 3M-sample tree (Supplementary Fig. S3). On the 100K-sample tree, a small SPR radius of 2 alone could achieve 70% of the total parsimony score improvement. For the 3M-sample tree, SPR moves of radius 2 could achieve only 20% of the total possible parsimony score improvement. However, even for larger trees, the parsimony score still improves most rapidly with small radii (Fig. 2)—90% of parsimony improvement is achieved with less than 25% of the total runtime for both the 1M-sample and 3M-sample trees. Therefore, matOptimize doubles the search radius after each round in order to provide the largest parsimony improvement at the early stages of optimization. The difference between radius doubling and fixed large radius strategy is negligible (Supplementary Table S1). Combined with the small preprocessing time, this radius doubling strategy makes matOptimize particularly suitable for ‘online’ optimization of large SARS-CoV-2 phylogenies. The reason is that it may be necessary to halt optimization if the runtime exceeds the time allowed until additional sample additions are necessary.
3.4 matOptimize also performs well on a M.tuberculosis dataset
To investigate whether matOptimize generalizes well to other datasets for which online phylogenetics may be useful, we used matOptimize to optimize an UShER-derived starting tree of approximately 10K M.tuberculosis genomes and compared it to TNT (Section 2). We found matOptimize to provide over an order of magnitude improvement in runtime (15×) and peak memory (51×) relative to TNT on this dataset as well (Supplementary Fig. S4). Notably, matOptimize completed the entire optimization in only 6 min, whereas it took TNT 1 h 22 min to even begin the optimization process and an additional 8 min to complete it. Though the parsimony improvement in the TNT tree was noticeably higher than matOptimize (0.61% versus 0.48%), the log-likelihood score of the two trees differed only by 0.012%. Our results seem to indicate that matOptimize may generalize well to large datasets beyond SARS-CoV-2.
4 Discussion
Several evolutionary studies, such as inferring SARS-CoV-2 recombination (Turakhia et al., 2021a) or characterizing the transmissibility of different mutations (Richard et al., 2021), rely on, or can benefit from, the knowledge of a comprehensive SARS-CoV-2 phylogenetic tree. Currently, the UCSC Genome Browser uses a comprehensive SARS-CoV-2 phylogenetic tree which is updated daily through phylogenetic placements of new sequences performed by UShER (Lee et al., 2022). This tree is being used widely by health officials and researchers worldwide through UShER’s command line (https://github.com/yatisht/usher) and web interface (https://genome.ucsc.edu/cgi-bin/hgPhyloPlace) to perform genomic surveillance (Abe and Arita, 2021; Dudas et al., 2021; Foster et al., 2022; Garushyants et al., 2021) and contact tracing (Lam-Hine, 2021) of the COVID-19 pathogen. This tree has also been applied for SARS-CoV-2 lineage assignment in the optional mode of Pangolin (https://github.com/cov-lineages/pangolin/), the most widely used scientific nomenclature system for SARS-CoV-2 lineages (Rambaut et al., 2020), as well as in several recently developed phylogenetic toolkits (Chen et al., 2021; McBroome et al., 2022; Sanderson, 2021). GISAID’s Audacity tree (Shu and McCauley, 2017) is also based on the UShER package. Maintaining a high-quality comprehensive SARS-CoV-2 phylogeny consisting of all available SARS-CoV-2 sequences has emerged as a problem of utmost importance during the COVID-19 pandemic.
Currently, matOptimize appears to be the only viable tree optimization tool for SARS-CoV-2 online phylogenetics. matOptimize’s performance is the result of several optimization and parallelization techniques that it incorporates. For example, matOptimize benefits from the recently developed, space-efficient data structure of an MAT—an uncompressed MAT file of 3 million SARS-CoV-2 sequence requires only 136 MB to encode basically the same information that is contained in an 88 GB MSA FASTA file. By using a modified MAT, matOptimize can compactly store all the information necessary for optimization and avoid the high cost of maintaining the entire alignment in memory. Widely used phylogenetic programs, such as TNT (Goloboff and Catalano, 2016), MPBoot (Hoang et al., 2018) and MEGA (Kumar et al., 2018), use strategies for parsimony score optimization that are far too expensive at SARS-CoV-2-scale. As a result of its scale up (more vCPUs per node) and scale out (more CPU nodes) capability, matOptimize is the only parsimony-based tree optimization software that is currently able to meet the computational demands for optimizing the ever-increasing SARS-CoV-2 phylogeny. Overall, matOptimize is 1–2 orders of magnitude more cost and memory efficient than the state-of-the-art, and we expect that matOptimize would help maintain a high-quality comprehensive SARS-CoV-2 phylogeny for several months to come. It also appears to generalize well to large datasets beyond SARS-CoV-2 (Supplementary Fig. S4) and could be applicable to other densely sampled pathogens in the future.
Supplementary Material
Acknowledgements
We thank the Willi Hennig Society for the TNT software. We thank Bui Quang Minh and Diep Thi Hoang for helpful discussions about MPBoot.
Funding
C.Y., A.K. and Y.T. were supported by the Centers for Disease Control and Prevention BAA 200-2021-11554. B.T. was supported by the National Institutes of Health grants T32HG008345 and F31HG010584. R.L. is supported by an Australian National University Futures Grant, an Australian Research Council Discovery Grant [DP200103151] and a Chan-Zuckerberg Initiative Grant for Essential Open Source Software for Science. R.C.-D was supported by the National Institutes of Health grant R35GM128932. This work was also supported by the generous donations by the Eric and Wendy Schmidt Foundation.
Conflict of Interest: none declared.
Data availability
The 100K and 1M-sample SARS-CoV-2 trees used in this study are made available at https://github.com/yceh/matOptimize-experiments. The larger 3M-sample SARS-CoV-2 dataset relies on GISAID data and its access agreement prohibits sharing it publicly but it will be shared with GISAID members on request to the corresponding author. The multisample VCF used for the Mycobacterium tuberculosis dataset is made available at https://doi.org/10.6084/m9.figshare.19799374.
Contributor Information
Cheng Ye, Department of Electrical and Computer Engineering, University of California, San Diego, San Diego, CA 92093, USA.
Bryan Thornlow, Department of Biomolecular Engineering, University of California, Santa Cruz, Santa Cruz, CA 95064, USA; Genomics Institute, University of California, Santa Cruz, Santa Cruz, CA 95064, USA.
Angie Hinrichs, Genomics Institute, University of California, Santa Cruz, Santa Cruz, CA 95064, USA.
Alexander Kramer, Department of Biomolecular Engineering, University of California, Santa Cruz, Santa Cruz, CA 95064, USA; Genomics Institute, University of California, Santa Cruz, Santa Cruz, CA 95064, USA.
Cade Mirchandani, Department of Biomolecular Engineering, University of California, Santa Cruz, Santa Cruz, CA 95064, USA; Genomics Institute, University of California, Santa Cruz, Santa Cruz, CA 95064, USA.
Devika Torvi, Department of Bioengineering, University of California, San Diego, San Diego, CA 92093, USA.
Robert Lanfear, Department of Ecology and Evolution, Research School of Biology, Australian National University, Canberra, ACT 2601, Australia.
Russell Corbett-Detig, Department of Biomolecular Engineering, University of California, Santa Cruz, Santa Cruz, CA 95064, USA; Genomics Institute, University of California, Santa Cruz, Santa Cruz, CA 95064, USA.
Yatish Turakhia, Department of Electrical and Computer Engineering, University of California, San Diego, San Diego, CA 92093, USA.
References
- Abe T., Arita M. (2021) Genomic surveillance in Japan of AY.29—a new sub-lineage of SARS-CoV-2 delta variant with C5239T and T5514C mutations. medRxiv, 10.1101/2021.09.20.21263869. [DOI]
- Chen C. et al. (2021) CoV-spectrum: analysis of globally shared SARS-CoV-2 data to identify and characterize new variants. Bioinformatics, 38, 1735–1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark K. et al. (2016) GenBank. Nucleic Acids Res., 44, D67–D72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cormen T.H., ed. (2009) Introduction to Algorithms. 3rd edn. MIT Press, Cambridge, MA. [Google Scholar]
- da Silva Filipe A. et al. ; COVID-19 Genomics UK (COG-UK) Consortium. (2021) Genomic epidemiology reveals multiple introductions of SARS-CoV-2 from mainland Europe into Scotland. Nat. Microbiol., 6, 112–122. [DOI] [PubMed] [Google Scholar]
- Deng X. et al. (2020) Genomic surveillance reveals multiple introductions of SARS-CoV-2 into Northern California. Science, 369, 582–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudas G. et al. (2021) Emergence and spread of SARS-CoV-2 lineage B.1.620 with variant of concern-like mutations and deletions. Nat. Commun., 12, 5769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. (2005) PHYLIP (Phylogeny Inference Package) Department of Genome Sciences. University of Washington, Seattle, WA. [Google Scholar]
- Fitch W.M. (1971) Toward defining the course of evolution: minimum change for a specific tree topology. Syst. Biol., 20, 406–416. [Google Scholar]
- Foster C.S.P. et al. (2022) Assessment of inter-laboratory differences in SARS-CoV-2 consensus genome assemblies between public health laboratories in Australia. Viruses, 14, 185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garushyants S.K. et al. (2021) Insertions in SARS-CoV-2 genome caused by template switch and duplications give rise to new variants that merit monitoring. 10.1101/2021.04.23.441209. [DOI] [PMC free article] [PubMed]
- Gill M.S. et al. (2020) Online Bayesian phylodynamic inference in BEAST with application to epidemic reconstruction. Mol. Biol. Evol., 37, 1832–1842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gladstein D.S. (1997) Efficient incremental character optimization. Cladistics, 13, 21–26. [DOI] [PubMed] [Google Scholar]
- Goloboff P.A. (1996) Methods for faster parsimony analysis. Cladistics, 12, 199–220. [DOI] [PubMed] [Google Scholar]
- Goloboff P.A. (1999) Analyzing large data sets in reasonable times: solutions for composite optima. Cladistics, 15, 415–428. [DOI] [PubMed] [Google Scholar]
- Goloboff P.A., Catalano S.A. (2016) TNT version 1.5, including a full implementation of phylogenetic morphometrics. Cladistics, 32, 221–238. [DOI] [PubMed] [Google Scholar]
- Gropp W. et al. (1999) Using MPI: Portable Parallel Programming with the Message-Passing Interface. 2nd edn. MIT Press, Cambridge, MA. [Google Scholar]
- Hoang D.T. et al. (2018) MPBoot: fast phylogenetic maximum parsimony tree inference and bootstrap approximation. BMC Evol. Biol., 18, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodcroft E.B. et al. (2021) Want to track pandemic variants faster? Fix the bioinformatics bottleneck. Nature, 591, 30–33. [DOI] [PubMed] [Google Scholar]
- Knuth D.E. (2011) The Art of Computer Programming. 3rd edn. Addison-Wesley, Amsterdam. [Google Scholar]
- Komissarov A.B. et al. (2021) Genomic epidemiology of the early stages of the SARS-CoV-2 outbreak in Russia. Nat. Commun., 12, 649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korber B. et al. ; Sheffield COVID-19 Genomics Group. (2020) Tracking changes in SARS-CoV-2 spike: evidence that D614G increases infectivity of the COVID-19 virus. Cell, 182, 812–827.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S. et al. (2018) MEGA X: molecular evolutionary genetics analysis across computing platforms. Mol. Biol. Evol., 35, 1547–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai A. et al. (2020) Early phylogenetic estimate of the effective reproduction number of SARS-CoV-2. J. Med. Virol., 92, 675–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam-Hine T. (2021) Outbreak associated with SARS-CoV-2 B.1.617.2 (delta) variant in an elementary school—Marin County, California, May–June 2021. MMWR Morb. Mortal Wkly. Rep., 70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan D. et al. (2021) Genozip: a universal extensible genomic data compressor. Bioinformatics, 37, 2225–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee B.T. et al. (2022) The UCSC genome browser database: 2022 update. Nucleic Acids Res., 50, D1115–D1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leinonen R. et al. ; International Nucleotide Sequence Database Collaboration. (2011) The sequence read archive. Nucleic Acids Res., 39, D19–D21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McBroome J. et al. (2021) A daily-updated database and tools for comprehensive SARS-CoV-2 mutation-annotated trees. Mol. Biol. Evol., 38, 5819–5824. [DOI] [PMC free article] [PubMed]
- McBroome J. et al. (2022) Identifying SARS-CoV-2 regional introductions and transmission clusters in real time. Virus Evol., veac048. [DOI] [PMC free article] [PubMed]
- Minh B.Q. et al. (2020) IQ-TREE 2: new models and efficient methods for phylogenetic inference in the genomic era. Mol. Biol. Evol., 37, 1530–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholls S.M. et al. (2020) MAJORA: continuous integration supporting decentralised sequencing for SARS-CoV-2 genomic surveillance. bioRxiv, 10.1101/2020.10.06.328328. [DOI] [PMC free article] [PubMed]
- O’Toole Á. et al. (2021) Assignment of epidemiological lineages in an emerging pandemic using the pangolin tool. Virus Evol., 7, veab064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A. et al. (2020) A dynamic nomenclature proposal for SARS-CoV-2 lineages to assist genomic epidemiology. Nat. Microbiol., 5, 1403–1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard D. et al. (2021) A phylogeny-based metric for estimating changes in transmissibility from recurrent mutations in SARS-CoV-2 genomics, bioRxiv, 2021.05.06.442903.
- Sanderson T. (2021) Chronumental: time tree estimation from very large phylogenies. https://doi.org/10.1101/2021.10.27.465994.
- Sankoff D. (1975) Minimal mutation trees of sequences. SIAM J. Appl. Math., 28, 35–42. [Google Scholar]
- Shu Y., McCauley J. (2017) GISAID: global initiative on sharing all influenza data—from vision to reality. Eurosurveillance, 22, 30494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K., Nei M. (2000) Efficiencies of fast algorithms of phylogenetic inference under the criteria of maximum parsimony, minimum evolution, and maximum likelihood when a large number of sequences are used. Mol. Biol. Evol., 17, 1251–1258. [DOI] [PubMed] [Google Scholar]
- Thornlow B. et al. (2021) Online phylogenetics using parsimony produces slightly better trees and is dramatically more efficient for large SARS-CoV-2 phylogenies than de novo and maximum-likelihood approaches. [DOI] [PMC free article] [PubMed]
- Turakhia Y. et al. (2021a) Pandemic-scale phylogenomics reveals elevated recombination rates in the SARS-CoV-2 spike region. https://doi.org/10.1101/2021.08.04.455157.
- Turakhia Y. et al. (2021b) Ultrafast sample placement on existing tRees (UShER) enables real-time phylogenetics for the SARS-CoV-2 pandemic. Nat. Genet., 53, 809–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E. et al. (2021) Transmission of SARS-CoV-2 lineage B.1.1.7 in England: insights from linking epidemiological and genetic data infectious diseases (except HIV/AIDS). 10.1101/2020.12.30.20249034. [DOI]
- Swofford D.L. (2003) PAUP. Phylogenetic Analysis Using Parsimony (and Other Methods).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The 100K and 1M-sample SARS-CoV-2 trees used in this study are made available at https://github.com/yceh/matOptimize-experiments. The larger 3M-sample SARS-CoV-2 dataset relies on GISAID data and its access agreement prohibits sharing it publicly but it will be shared with GISAID members on request to the corresponding author. The multisample VCF used for the Mycobacterium tuberculosis dataset is made available at https://doi.org/10.6084/m9.figshare.19799374.