Abstract
Metallic Mimosa pudica, a three-dimensional (3D) biomimetic structure made of metallic glass, is formed via laser patterning: Blooming, closing, and reversing of the metallic M. pudica can be controlled by an applied magnetic field or by manual reshaping. An array of laser-crystallized lines is written in a metallic glass ribbon. Changes in density and/or elastic modulus due to laser patterning result in an appropriate size mismatch between the shrunken crystalline regions and the glassy matrix. The residual stress and elastic distortion energy make the composite material to buckle within the elastic limit and to obey the minimum elastic energy criterion. This work not only provides a programming route for constructing buckling structures of metallic glasses but also provides clues for the study of materials with automatic functions desired in robotics, electronic devices, and, especially, medical devices in the field of medicine, such as vessel scaffolds and vascular filters, which require contactless expansion and contraction functions.
A 3D structure of metallic glass–crystal composite, formed by laser patterning, blooms and closes by magnetic force.
INTRODUCTION
The Mimosa pudica (also known as shameplant) closes its leaves as a defense mechanism against insects in response to touch, vibration, and wind (1), and when external stimuli stop, it reopens. This is due to its ability to redistribute water inside the leaves, inducing cell contraction on one side of the leaves and enlargement on the other. The shrinkage and expansion of cells on different sides of leaves result in size mismatch between upper and lower sides of leaves (1), and the size mismatch on different sides plays a key role in the opening and closing of leaves. Moreover, leaves and petals of many plants have curved shapes originating from size mismatch between different parts of plants such as veins and nonvein parts, forming during their growth process (2–4), and the curvature of leaves and petals can be reversible because of buckling ability. If the structure of seismonastic plants is imitated by structural materials, such as metals, then the plants’ functionality could be obtained by the three-dimensional (3D) biomimetic manufacturing (5–11).
Many researchers are interested in 3D shape changing on specific materials. Under external stimuli, hydrogels (11–14), shape-memory polymers (5, 11, 12), liquid crystal elastomers (5, 11, 12, 15), and shape-memory alloys (7, 16) have been selected for shape change applications. The shape changes of materials have great potentials in specific applications such as actuators (11, 15, 17–19), sensors (11, 15, 17, 18), inductors (18, 20, 21), microelectromechanical systems (5, 22), soft robots (18, 23–25), and electronic (25), medical (11, 18, 26), and spacecraft devices (18, 20, 27). For example, 3D shape-change materials coupled with magnetic properties are promising for microgrippers, vessel scaffolds, and vascular filters in the blood vessels, which need contactless expansion and contraction or closing and reopening functionality with untouched manner (26). In the field of spacecraft, a flat plate is very attractive as an input geometry for 3D structures because of its efficient storage, transportation, and scalability (18), which automatically transforms into 3D structures when eventually required.
Metallic glasses (MGs) represent one of the good candidates for forming 3D biomimetic structures. The MGs have excellent mechanical performance (28–30), such as a high elastic strain limit of ~2% and high mechanical strength, and, upon crystallization, their density and/or elastic modulus between glassy and crystalline parts can change (31, 32), which can result in an appropriate size mismatch between glass and crystal parts. Previous studies of MGs focused on 3D structures (33–40), similar to 3D printing complex structures, wave springs and honeycomb structures, etc. However, the 3D structure with buckling functionality of metallic composites has rarely been reported so far. Therefore, achieving the shape change function of buckling-induced 3D structure in MGs remains challenging, and it is scientifically and technologically important for functional applications of MGs.
In this work, we designed a buckling-induced 3D structure with an MG ribbon by laser patterning and realized its 3D shape change to imitate biomimetic functionality by a magnet bar. 3D biomimetic structures were fabricated using an MG-crystal (MGC) composite material consisting of a glassy matrix and an array of crystallized parts. In the MG ribbon, crystallization of parallel stripes was induced by nanosecond-pulsed (ns-pulsed) laser patterning, which induced size mismatch between glassy matrix and shrunken crystallized stripes with an increase in density and/or moduli. The curvature radii (R) of buckled structures were controlled by the linewidth ratio of crystallized and glassy stripes. Here, Fe78Si9B13 MG ribbon was chosen because of its soft magnetic properties. In the elastic limit, the shape change of MGC is controlled by an external magnetic field (movie S1) or even manually reshaped and reversed (movie S2). A one-step, fast, and scalable fabrication method using laser patterning demonstrates the suitability to achieve buckling functionality with any metallic materials that can provide appropriate size mismatch in the elasticity limit through the changes of density and/or modulus of their different parts.
RESULTS
MGC composite structure
Figure 1A shows the folding and drooping of M. pudica leaves on touch. Inspired by nature, a reversible shape-changing and configuration-controllable biomimetic metallic M. pudica was designed and fabricated via ns-pulsed laser patterning of Fe78Si9B13 MG (Fig. 1B). To start, the 2D leaf-like geometry of the Fe78Si9B13 MG ribbon (30 mm in width and 24 μm in thickness) was cut by a picosecond-pulsed (ps-pulsed) laser source and then patterned by an ns-pulsed laser source, transforming the 2D cuts into 3D buckling structures. Figure S1 provides details of the parallel line processing mode of the ns-pulsed laser source.
Fig. 1. Seismonastic M. pudica plant and the inspired buckled metallic M. pudica.
(A) M. pudica leaves close upon touching. (B) Fabrication of MGC composite leaves via ps-pulsed laser cutting and ns-pulsed laser patterning. (C) Snapshots of the closing and opening of the leaves in the magnetic field (images are snapshots taken from movie S1). (D) Multiconfigurational shapes are made by manual alteration of the concave or convex curvatures of the leaves. (E) Helixes with various rolling angles and (F) rolls with the controlled radius of curvature can be made.
Closing and opening of the metallic leaves were stimulated by a magnet bar giving controllable shape changes as demonstrated in Fig. 1C, which shows snapshots taken from movie S1. The closing and opening (movie S1) were continuously tested up to about 20,000 cycles, and no damage or property deterioration was found, suggesting an excellent fatigue resistance performance. The response of the 3D structure (after laser parallel line processing; Fig. 1B) to the magnet bar is compared with that of the 2D structure (before laser parallel line processing; Fig. 1B) in movie S3, where it can be seen that the 3D structure is essential to achieve closing and opening performance. The buckling allows the leaf curvature reversible, i.e., alterations between convex and concave curvatures of the leaves, and therefore, five configurations were made by modifying the curvature sign (Fig. 1D and movie S2). The response to the applied magnetic field, the possibility of manual reshaping, and the various available biomimetic structures demonstrate the nature-inspired functionality of the composite material. By modifying the processing parameters, laser line directions, line spacing (s), and scanning speed (v), helixes with various angles (Fig. 1E) and rolls with a wide range of the curvature radius (Fig. 1F) could be easily produced. The concave and convex directions can also be easily achieved by manual reshaping (see fig. S2, A and B). Immediately after the laser line patterning, there always exists a preferential direction of the curvature for all buckled ribbons (see fig. S2C): The top surface (facing the laser source) is convex, and the bottom surface remains concave.
Buckling mechanism of MGC composite structure
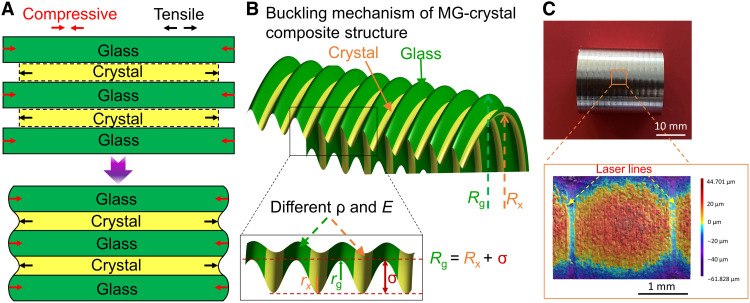
The basic mechanisms of buckling are appropriate size mismatch between the laser-patterned stripes and matrix regions and the sufficient elastic deformability of the composite materials. For an MG ribbon, when local stripes of the ribbon are crystallized by laser patterning, the density and modulus of crystallized stripes become relatively larger [density increases by about 2 to 5% (31) and modulus by 20 to 30% (32)]. Accompanying the shrinkage of crystallized regions, the size mismatch between crystallized stripes and glassy matrix occurs, introducing a size mismatch distortion energy and the inner stress, and these allow the buckling performance within the elastic limit. As shown in Fig. 2A, residual stress was generated after laser processing because of the shrinkage of the crystallized regions (yellow area). There are tensile internal stresses (black arrows) in the crystals, and the compressive internal stresses (red arrows) act on the glass matrix (green area) in the parallel stripe direction. In Fig. 2B, the green stripes represent the glass parts and the yellow stripes represent the crystallized regions. Rg and Rx (the subscripts “g” and “x” stand for glass and crystal, respectively) are the radii of curvature responsible for the shape change in the laser line length direction. σ is the difference between Rg and Rx. rg and rx are the radii of curvature responsible for the shape change in the vertical laser line direction. Because the crystal parts are shrunk, Rx < Rg maintains in the curved sheet. When the glass and crystal stripes with different ρ and E are parallelly integrated, such a composite thin sheet can buckle either in the convex or concave directions (14, 41). The ribbon perpendicular to the length of the stripes exhibits periodical modulation structure, and the ribbon parallel to the length of the stripes generates a large curvature (see Fig. 2B). Modulation of buckling that appears on the width direction of the ribbon (transverse to laser line direction) and large curvature of buckling in the length direction of the ribbon (along the laser line direction) are demonstrated in Fig. 2. A confocal laser scanning microscope was used to visualize the height change on the buckled surface (see Fig. 2C).
Fig. 2. The schematic of buckling mechanism of a glass (green)/crystal (yellow) composite.
Crystallization occurred in the laser-scanned regions. (A) The periodic structure of the glass matrix and crystallized regions. Along the laser line direction, the glass regions suffer compressive stress (red arrows) and the crystal regions suffer tensile stress (black arrows). (B) Buckling occurs in both transverse and parallel to stripe directions due to the energy minimum requirement (ρ, density; E, elastic modulus; Rg or Rx, radius of curvature of the glass or crystal along laser lines direction; rg or rx, radius of curvature of the glass or crystal transverse to laser lines direction; σ, the difference between Rg and Rx). (C) Top view and the enlarged height change of the surface of buckled ribbon.
The MGC composite structure with buckling function within the elastic limit obeys the minimum elastic energy criterion. To quantitatively determine R of the MGC composite structure, a 2D model (14) has been applied. The R is determined by the energy minimum of the total energy QT, the sum of the stretching energy QS, and bending energy QB for glass and crystal, respectively (14). Considering the influences of R, rx, and rg, we have
| (1) |
| (2) |
| (3) |
where R is the half sum of Rg and Rx; Eg and Ex are the elastic moduli; wg and wx are the widths of the glass and crystal stripes; dg and dx are the thicknesses; and fg and fx are the relative length change of the glass and crystal stripes, respectively. By determining Eg, Ex, wg, wx, dg, dx, fg, and fx from experiments or estimation, QT is now a function of R, rx, and rg. The analytical calculation could be performed to search for the QT minimum, from which the corresponding R is derived. In particular, fx/fg can be estimated by the density ratio between the two stripes, i.e., fx/fg = (ρx/ρg)1/3, and wx = w, wg = s − w, s is the distance between centers of two laser lines. Hence, from the Eqs. 1 to 3, R versus ρx/ρg, Ex/Eg, and w/s of the two kinds of the stripes are determined (see fig. S3).
Residual stress distribution in MGC composite structure
The Fe78Si9B13 MGs have nonzero magnetostriction and no magnetocrystalline anisotropy, and their magnetic easy axis direction is governed by mechanical stress. In Fe78Si9B13 MG, the induced mechanical stresses are essentially inhomogeneous because of fast melt-spinning process, and, thus, magnetic easy axis varies locally without specific direction. Therefore, observation of the magnetic domain structure of the ribbon surface in demagnetized state can be used to evaluate the change of local distribution of mechanical stress distribution caused by laser patterning (42–44).
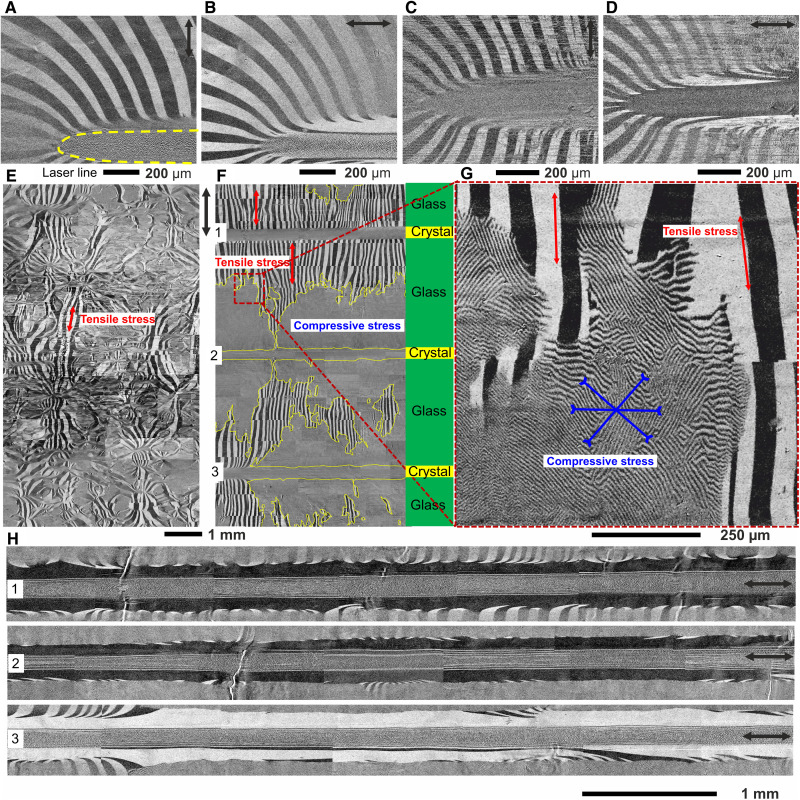
The residual stress distribution at the surface of metallic leaves was studied by Kerr microscopy. Because the positive magnetostriction constant of Fe78Si9B13 MG [fig. S4; in agreement with (45)], the observed wide domains are strictly magnetized in plane across the ribbon thickness, indicating that the areas are dominated either by uniaxial tensile stress along the 180° domain wall direction or by compressive stress in transverse to the direction of domains. The magnetic domains at the surface of the same Fe78Si9B13 sample area in the as-spun state (fig. S5A) and after one-line laser scanning (fig. S5B) are captured. In the as-spun state (fig. S5A), the ribbon has two types of domains: One has wide black-and-white stripes, and one has narrow closure domains, which appear as gray areas at low magnification. In the ribbon after laser patterning, the internal tensile stresses in specific directions spread up to several millimeters away from the laser lines because of the crystallization-induced shrinkage (Fig. 3A and fig. S5B). The magnetic domains shown in Fig. 3 (A to D) are identical for the top (A and B) and the bottom (C and D) surfaces of the Fe78Si9B13 ribbon after laser pattering, suggesting uniform tensile stress distribution across the ribbon thickness caused by shrinkage of MG crystallization under one-line laser scanning. The domain structure is observed on the surface of the same Fe78Si9B13 sample in the as-spun state (Fig. 3E) and the processed state (Fig. 3F) with a glass matrix and an array of crystallized material. In Fig. 3F, the gray areas contain narrow closure domains with in-plane magnetization at the surface and perpendicular-to-the-surface magnetization in the volume of the ribbon, representing the dominating presence of compressive stress. A high-resolution domain image of the region indicated by the red frame in Fig. 3F can be found in Fig. 3G. A local effective tensile stress results in an in-plane magnetic easy axis and wide 180° domains oriented along the stress axis, while planar compressive stress results in an orientation of the easy axis perpendicular to the ribbon surface and, thus, narrow stripe closure domains on the surface oriented in the direction transverse to the compressive stress as indicated by arrows (Fig. 3G). The glass areas containing wide domains that run transverse to the laser lines (Fig. 3F) show predominating tensile stress along the same direction. The glassy areas also include gray zones with narrow closure domains showing planar compressive stress. Thus, the glassy areas mainly suffer from compressive stress in the buckling structure along the laser line direction (Fig. 3F). The residual tensile stress in glassy areas perpendicular to the laser lines direction, responsible for periodical modulation buckling structure (Fig. 2, B and C), is revealed in Fig. 3 (F and H). In general, the glassy parts suffer from compressive stress, and the crystalline parts are subjected to tensile stress along the laser lines.
Fig. 3. Influence of the laser patterning on the magnetic domains in the Fe78Si9B13 ribbon.
The magnetic domains on the top (A and B) and on the bottom (C and D) surfaces of the Fe78Si9B13 ribbon with a single laser line (v = 100 mm s−1). (E) Disordered domains in as-spun ribbon. (F) Laser-patterned ribbon with stripes of the glass and crystal aligned in periods (laser line spacing is 3 mm and laser scanning speed is 100 mm s−1). (G) A high-resolution image of the magnetic domains on the surface of as-spun Fe78Si9B13 ribbon for a region indicated by the red rectangle in (F). The directions of tensile and compressive stress are indicated by red and blue arrows, respectively. (H) Close-up view of the domains in the proximity of the laser lines shown in (F). The Kerr sensitivity for (A), (C), and (E) to (G) is along the vertical direction (transverse to laser patterning) and for (B), (D), and (H) is along the horizontal direction (along with the laser patterning) concerning the image plane.
Patterning conditions of successful buckling
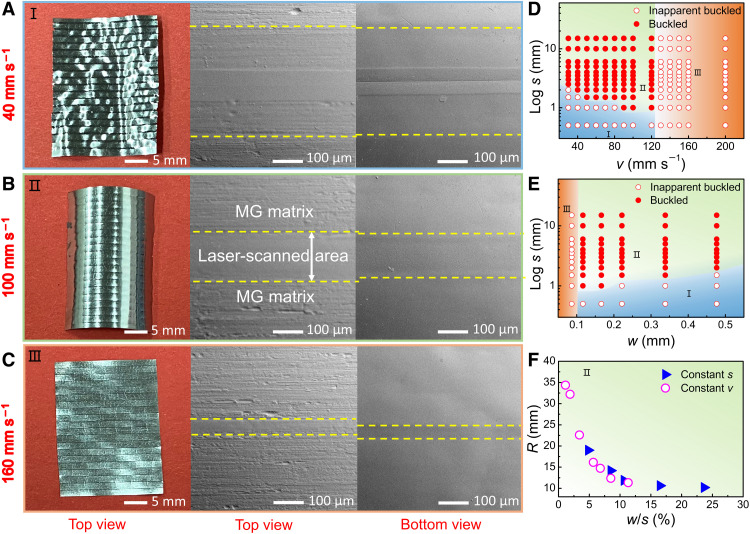
The laser patterning procedure is shown in movie S4. The scanning electron microscopy (SEM) images show the appearance of laser lines on both top and bottom surfaces of the Fe78Si9B13 ribbon at the three laser scanning speeds v of 40, 100, and 160 mm s−1, demonstrating that the buckling structures penetrate through the ribbon thickness by laser patterning (Fig. 4, A to C). A seriously wavy structure was formed with the largest w = 355 ± 10 μm at the lowest v of 40 mm s−1 (Fig. 4A). The successfully buckled ribbon has an appropriate w = 178 ± 10 μm at an intermediate v of 100 mm s−1 (Fig. 4B). Meanwhile, Fig. 4C shows that the ribbon buckled slightly at a relatively high laser scanning speed (v) of 160 mm s−1, where narrow stripes could be written on the top and bottom surfaces as revealed by SEM. Thus, appropriate laser line width (w) and laser line spacing (s) are critical to obtain successful buckling. The patterning structures in regimes I, II, and III correspond to the photographs in Fig. 4 (A to C), respectively. Figure 4D maps the patterning conditions, expressed as laser line spacing (s) versus scanning speed (v) for buckling in Fe78Si9B13 MG. The three different regimes can be identified, representing: excessive regime I, moderate regime II, and insufficient regime III of patterning conditions. In regime I, the ribbon exhibits a seriously wavy structure, making it hard to have an effective R. In regime II, R is smaller than 40 mm, representing successful buckling. In regime III, R is larger than 40 mm, which can be understood in terms of insufficient laser penetration, a result considered as less efficient for buckling. The low v causes larger w, inducing excessive laser penetration beyond the elasticity limit, even resulting in damage of the ribbon. The conditions of the three regimes demonstrate that appropriate w and sufficient elasticity of the composite material are important. Figure 4D is a processing map designed for the practical use of laser manufacturing, but from a fundamental point of view, one can link v to w. Figure S6 shows w increases with decreasing v, so a similar contour based on s and w was constructed in Fig. 4E. Furthermore, the R is a function of w and s (fig. S7). The appropriate w/s for successful buckling with different R is revealed in Fig. 4F, corresponding with regime II (Fig. 4, B, D, and E). Note that there is a minimum for R around w/s ~ 0.4 to 0.5 (see fig. S3C).
Fig. 4. The conditions of buckling of the Fe78Si9B13 MG ribbon.
Optical and SEM micrographs of the Fe78Si9B13 MG ribbons laser-processed at (A) v = 40 mm s−1, (B) v = 100 mm s−1, and (C) v = 160 mm s−1. SEM micrographs of the laser-patterned lines (the line width is highlighted by the white arrows and the lines are enclosed by the yellow dashed lines) viewed from the top surface (the second column) and from the bottom surface (the third column). (D) The processing map of buckling for which large line spacing (s) and low scanning speed (v) conditions are favored. (E) Processing map based on s and w. (F) R decreasing with ratio w/s. Blue triangles represent the condition at constant s, and pink circles represent the condition at constant v.
DISCUSSION
In this work, a kind of glass and crystal stripe composite with buckling performance is designed. The fundamental mechanisms of buckling are that there are appropriate size mismatch between laser-patterned and matrix stripe regions and sufficient elastic deformability of the composite material. More generally, an ideal composite structure is that different parts of the material have appropriate size mismatch and sufficient elasticity. The size mismatch in the patterned Fe78Si9B13 ribbon is induced by the change of density and/or elastic modulus, which originated from shrinkage of crystallization of laser-patterned stripes. The residual stress and corresponding elastic distortion energy enable the composite to have buckling function within the elastic limit and obey the minimum elastic energy criterion. The MGC structure made by the laser-patterned Fe78Si9B13 ribbon not only has a buckling function but also can be controlled by a magnet bar to open and close repeatedly because of ferromagnetic attraction between the leaves and the magnetic bar. The curvature radius of R of the buckled ribbon is decided by a variety of factors, such as changes of density, elastic modulus, linewidth ratio of laser-patterned and glass parts and thickness of the ribbon. Essentially, R is determined by the degree of size mismatch between different parts, the elastic deformability of composite and energy minimum principle. The elasticity required for buckling depends on the radius of curvature R; larger elasticity is required for smaller R and vice versa. The degree of elasticity required can be evaluated. For example, the bending strain (εB) is d/2R, where d is the thickness of the ribbon. When R is 10 mm and d is 24 μm, εB is only 0.12%. This εB is much smaller than the elastic strain limit of MGs (2%) and even smaller than that of the crystalline metals in general. While large elasticity would be requested for smaller R, such as for R = 1 to 2 mm, elastic strain εB = 0.6 to 1.2%. Therefore, within the elastic limit of composite materials, buckling behavior is allowed.
Residual stress is often a natural consequence of laser treatments on MGs (46, 47) and induces buckling shape change. The shrunken crystal stripes are subjected to tensile stress from the glass stripes, which, in turn, the glass is subjected to compressive stress from the crystal stripes. When the buckled ribbon is annealed below its glass transition temperature, the curved shape is largely flattened as Δρ between the annealed glass and the laser-patterned crystallized stripes decreased (fig. S8), implying that the extent of the size mismatch of the composite structure is an important factor that affects its buckling. The good buckling performance is limited to certain MG compositions only. As demonstrated in fig. S9A, a single line was scanned along the center of three MG ribbons with different compositions and one Fe80Cr20 polycrystalline ribbon. Only Fe78Si9B13 and Zr46Cu46Al8 MGs buckled, while La55Ni20Al25 MG and Fe80Cr20 polycrystal buckled slightly (fig. S9A) because the size mismatch is not large enough in the latter two. X-ray diffraction (XRD) patterns (fig. S9B) show that the three MG ribbons are crystalized after laser-scanned, but the Fe80Cr20 polycrystalline ribbon does not show obvious change. Table S1 shows a density and elastic modulus change of Fe78Si9B13 and Zr46Cu46Al8 MGs before and after laser processing. The extent of the density change (Δρ) during the glass-to-crystal transformation (31) depends on the MG composition (table S1). For Fe78Si9B13 MG, its ρ at the fully crystallized state is 7.375 ± 0.003 g cm−3, which is 3.1% larger than that of glass (7.154 ± 0.003 g cm−3). The Cu46Zr46Al8 MG also shows good buckling performance after laser processing (fig. S9A), and its relative ρ increased by 0.9% after crystallization. The laser-scanned La55Ni20Al25 ribbon was crystallized, but only slightly buckled (see fig. S9A). For the Fe80Cr20 polycrystalline ribbon, melting and recrystallization could happen during the laser-patterning process. Figure S9A shows that Fe80Cr20 flexes only slightly after laser patterning, i.e., the patterned ribbon is not as flat as it was before patterning. A slight size mismatch occurred and small inner stress remained in Fe80Cr20 after laser patterning, and the radius R is larger. From the strict definition of buckling, the Fe80Cr20 polycrystalline ribbon also buckled, but it cannot be used to make a MGC composite structure successfully. Therefore, an appropriate size mismatch or an appropriate density difference is necessary for successful (or evident) buckling behavior. Note that a too large size mismatch, correspondingly a too large density difference, which is beyond the elasticity limit of the composite material, also does not favor for buckling behavior. Plastic deformation or fracture would occur when the elastic limit is exceeded. In addition, the crystalline ribbons of the Fe78Si9B13 and Cu46Zr46Al8 alloys also cannot buckle (fig. S10A) compared with their glass ribbons because of small density change. The results emphasize that the laser-induced 3D buckling structure needs glasses, because they have excellent elastic deformability and appropriate density changes by crystallization; therefore, appropriate size mismatch of different parts of composites can be achieved.
To conclude, we constructed a 3D biomimetic buckling structure by ns-pulsed laser patterning of the MG ribbon. A 3D biomimetic metallic flower can open and close repeatedly by applying an external magnetic field and can be reshaped manually. The fundamental mechanisms of buckling are appropriate size mismatch between laser-patterned and matrix stripe regions and sufficient elastic deformability of the composite materials. The different densities and/or elastic moduli between the glassy and the shrunken crystallized regions, inducing appropriate size mismatch, are responsible for the internal stress distribution in the MGC composite structure. The residual stress originates from the size mismatch of the different parts. The buckling behavior obeys the minimum elastic energy criterion. The elasticity of the composite enables the metallic flower to bloom, close, or reverse its curvature under applied forces freely and repeatedly. This work provides hints for materials needed for noncontact expansion and contraction functions in medical devices and soft robotic devices, etc.
MATERIALS AND METHODS
Commercial Fe78Si9B13 [atomic % (at %)] MG and Fe80Cr20 polycrystalline ribbons (containing traces of Mn, Ni, Cu, Mo, and C in total of ≤1.5 at %) were purchased from the Advanced Technology and Materials Co. Ltd. of the Central Iron and Steel Research Institute (China) and from Ding-Yuan Metallic Materials (China), respectively. The typical thickness of the commercial ribbons was 24 μm and has a width of 30 mm. Cu46Zr46Al8 and La55Ni20Al25 MG ribbons were obtained by melt spinning, where the master ingots were prepared by arc-melting of high-purity elements, Cu (99.99%), Zr (99.9%), La (99.5%), Ni (99.9%), and Al (99.99%), under a Ti-gettered argon atmosphere. Master ingots were molten at 1100 K and spun on a copper wheel at a rotation speed of 80 rpm in argon atmosphere. The products were MG ribbons with a typical thickness of 30 μm and a width of 1.5 mm.
For laser cutting, to keep the Fe78Si9B13 ribbon amorphous, a ps-pulsed laser (Photonics Industries International Inc.) was used with the parameters of a laser wavelength of 355 nm, an output power of 20 W, a pulse duration of 7 ps, a repetition frequency of 2000 kHz, and a scanning speed of 2000 mm s−1. The ribbon was cut by repeating the cutting path 300 times with a cutting interval time of 1 s and a focused beam diameter of 20 μm.
Laser patterning was carried out in the air. Before the writing, MG ribbons were first cleaned by ethanol and then taped on a platform beneath the laser source. An ns-pulsed optical fiber laser source (Shenzhen JPT OPTO Electronics Co. Ltd.) was used, operating at a wavelength of 1064 nm, a maximum output power of 20 W, a beam diameter of 100 μm, a power factor of 100%, a pulse duration of 2 ns, a repetition frequency of 400 kHz, and a focus distance of 3.5 mm. A positive defocus condition was maintained, where the laser focus was set above the sample position and maintained throughout the patterning. During laser scanning, a line spacing of 1 to 15 mm and a scanning speed of 40 to 200 mm s−1 were used. The processing geometry is schematically illustrated in fig. S1.
The ribbons’ amorphicity and crystallinity were checked by XRD (Bruker D8 Advance) using Cu-Kα radiation (wavelength of 1.5418 Å). The surface morphology of the laser-processed samples was examined by Phenom XL SEM and using confocal laser scanning microscopes (Keyence VK-X1000). The composition was checked by energy disperse spectroscopy (using a silicon drift detector) inside the Phenom XL SEM. Elastic modulus E was measured using the TriboIndenter, Bruker TI 980 nanoindentation system. A Berkovich tip, made of diamond with a tip radius of about 200 nm, was used, and the elastic part of the unloading curve was taken to calculate E. The density was measured using a helium gas pycnometer (Micromeritics 1345), with all the measurements repeated 10 times.
The residual stress distribution around the laser-scanned lines and the domain structure of Fe78Si9B13 MG were recorded by using a Kerr microscope as reported in (42) and (48). Magnetic domains were imaged in a wide-field Kerr microscope with selective sensitivity to pure in-plane magnetization using the longitudinal Kerr effect (48). Domain maps of the enlarged sample areas were obtained by merging independent high-resolution domain images, which were acquired with a 10× objective lens. Before imaging, an external alternating magnetic field was applied in the sample plane along the in-plane sensitivity direction of the Kerr microscope to demagnetize the sample. To determine the sign of the magnetostriction constant, tensile stress along the ribbon axis of an increasing amplitude was applied, and domains were observed using overview Kerr microscopy (49).
Acknowledgments
We thank B. S. Dong and S. X. Zhou in the Advanced Technology and Materials Co. Ltd. of Central Iron and Steel Research Institute for supplying commercial samples. We thank F.-C. Li for help in nanoindentation. We thank C. Wang for the discussion of this work.
Funding: This research was supported by the National Key Research and Development Plan (2018YFA0703603), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB30000000), the National Natural Science Foundation of China (52192600, 11790291, 61999102, 61888102, and 51971239), Beijing Municipal Science and Technology Commission (Z191100007219006), and the Natural Science Foundation of Guangdong Province (2019B030302010). J.O. acknowledges the assistance provided by the Research Infrastructure NanoEnviCz, which is supported by the Ministry of Education, Youth and Sports of the Czech Republic (LM2018124). J.O. and Y.-H.S. acknowledge the financial support of the promising Young Scientist Award from the Center for International Collaboration (IOPCIC), Institute of Physics, Chinese Academy of Sciences. This work is supported by the Center for Materials Genome.
Author contributions: H.-Y.B. directed the project, conceived the idea, and interpreted all the mechanisms. J.-F.L. performed the sample treatments and conducted the experiments. I.-V.S., R.S., and J.O. performed the Kerr microscopy measurements and data interpretation. X.-C.T. attended discussion. B.-Y.S. provided the assistance with nanoindentation, and S.-L.L. made 3D drawings. Y.-Q.Y. and H.-B.K. provided the help with the laser cutting and patterning. H.-Y.B. wrote the manuscript and responses to reviewers. H.-Y.B., J.-F.L., and Y.-H.S. wrote the Supplementary Materials.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S11
Table S1
References
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S4
REFERENCES AND NOTES
- 1.Volkov A. G., Foster J. C., Ashby T. A., Walker R. K., Johnson J. A., Markin V. S., Mimosa pudica: Electrical and mechanical stimulation of plant movements. Plant Cell Environ. 33, 163–173 (2010). [DOI] [PubMed] [Google Scholar]
- 2.Dervaux J., Amar M. B., Morphogenesis of growing soft tissues. Phys. Rev. Lett. 101, 068101 (2008). [DOI] [PubMed] [Google Scholar]
- 3.Sharon E., Roman B., Marder M., Shin G. S., Swinney H. L., Buckling cascades in free sheets. Nature 419, 579 (2002). [DOI] [PubMed] [Google Scholar]
- 4.Sharon E., Marder M., Swinney H. L., Leaves, flowers and garbage bags: Making waves. Am. Sci. 92, 254–261 (2004). [Google Scholar]
- 5.Cheng X., Zhang Y., Micro/nanoscale 3D assembly by rolling, folding, curving, and buckling approaches. Adv. Mater. 31, 1901895 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Leong T. G., Zarafshar A. M., Gracias D. H., Three-dimensional fabrication at small size scales. Small 6, 792–806 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu N., Burgueño R., Buckling-induced smart applications: Recent advances and trends. Smart Mater. and Struct. 24, 063001 (2015). [Google Scholar]
- 8.Jamal M., Zarafshar A. M., Gracias D. H., Differentially photo-crosslinked polymers enable self-assembling microfluidics. Nat. Commun. 2, 527 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chung J. Y., Nolte A. J., Stafford C. M., Surface wrinkling: A versatile platform for measuring thin-film properties. Adv. Mater. 23, 349–368 (2011). [DOI] [PubMed] [Google Scholar]
- 10.Liu Z., Cui A., Li J., Gu C., Folding 2D structures into 3D configurations at the micro/nanoscale: Principles, techniques, and applications. Adv. Mater. 31, 1802211 (2019). [DOI] [PubMed] [Google Scholar]
- 11.van Manen T., Janbaz S., Zadpoor A. A., Programming the shape-shifting of flat soft matter. Mater. Today 21, 144–163 (2018). [Google Scholar]
- 12.Gladman A. S., Matsumoto E. A., Nuzzo R. G., Mahadevan L., Lewis J. A., Biomimetic 4D printing. Nat. Mater. 15, 413–418 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Erb R. M., Sander J. S., Grisch R., Studart A. R., Self-shaping composites with programmable bioinspired microstructures. Nat. Commun. 4, 1712 (2013). [DOI] [PubMed] [Google Scholar]
- 14.Wu Z. L., Moshe M., Greener J., Therien-Aubin H., Nie Z., Sharon E., Kumacheva E., Three-dimensional shape transformations of hydrogel sheets induced by small-scale modulation of internal stresses. Nat. Commun. 4, 1586 (2013). [DOI] [PubMed] [Google Scholar]
- 15.Ohm C., Brehmer M., Zentel R., Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 22, 3366–3387 (2010). [DOI] [PubMed] [Google Scholar]
- 16.Peraza-Hernandez E. A., Hartl D. J., Malak R. J. Jr., Lagoudas D. C., Origami-inspired active structures: A synthesis and review. Smart Mater. Struct. 23, 094001 (2014). [Google Scholar]
- 17.Stoychev G., Turcaud S., Dunlop J. W. C., Ionov L., Hierarchical multi-step folding of polymer bilayers. Adv. Funct. Mater. 23, 2295–2300 (2013). [Google Scholar]
- 18.Lazarus N., Smith G. L., Dickey M. D., Self-folding metal origami. Adv. Intell. Syst. 1, 1900059 (2019). [Google Scholar]
- 19.Lazarus N., Wilson A. A., Smith G. L., Contactless laser fabrication and propulsion of freely moving structures. Extreme Mech. Lett. 20, 46–50 (2018). [Google Scholar]
- 20.Lazarus N., Smith G. L., Laser folding in a roll-to-roll manufacturing process. Lasers Manuf. Mater. Process. 5, 237–247 (2018). [Google Scholar]
- 21.Lazarus N., Bedair S. S., Smith G. L., Origami inductors: Rapid folding of 3D coils on a laser cutter. IEEE Electron Device Lett. 39, 1046–1049 (2018). [Google Scholar]
- 22.Ning X., Yu X., Wang H., Sun R., Corman R. E., Li H., Lee C. M., Xue Y., Chempakasseril A., Yao Y., Zhang Z., Luan H., Wang Z., Xia W., Feng X., Ewoldt R. H., Huang Y., Zhang Y., Rogers J. A., Mechanically active materials in three-dimensional mesostructures. Sci. Adv. 4, eaat8313 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.16. Rus D., Tolley M. T., Design, fabrication and control of origami robots. Nat. Rev. Mater. 3, 101–112 (2018). [Google Scholar]
- 24.Wang X., Mao G., Ge J., Drack M., Bermúdez G. S. C., Wirthl D., Illing R., Kosub T., Bischoff L., Wang C., Fassbender J., Kaltenbrunner M., Makarov D., Untethered and ultrafast soft-bodied robots. Commun. Mater. 1, 67 (2020). [Google Scholar]
- 25.Kim Y., Yuk H., Zhao R., Chester S. A., Zhao X., Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 558, 274–279 (2018). [DOI] [PubMed] [Google Scholar]
- 26.Randall C. L., Gultepe E., Gracias D. H., Self-folding devices and materials for biomedical applications. Trends Biotechnol. 30, 138–146 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pohl D., Wolpert W. D., Engineered spacecraft deployables influenced by nature. Proc. SPIE 7424, 742408 (2009). [Google Scholar]
- 28.Greer A. L., Metallic glasses. Science 267, 1947–1953 (1995). [DOI] [PubMed] [Google Scholar]
- 29.Löffler J. F., Bulk metallic glasses. Intermetallics 11, 529–540 (2003). [Google Scholar]
- 30.Wang W. H., Dong C., Shek C. H., Bulk metallic glasses. Mater. Sci. Eng. R 44, 45–89 (2004). [Google Scholar]
- 31.Li Y., Guo Q., Kalb J. A., Thompson C. V., Matching glass-forming ability with the density of the amorphous phase. Science 322, 1816–1819 (2008). [DOI] [PubMed] [Google Scholar]
- 32.Wang W. H., The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 57, 487–656 (2012). [Google Scholar]
- 33.Zhang C., Li X.-M., Liu S.-Q., Liu H., Yu L.-J., Liu L., 3D printing of Zr-based bulk metallic glasses and components for potential biomedical applications. J. Non Cryst. Solids 790, 963–973 (2019). [Google Scholar]
- 34.Aljerf M., Georgarakis K., Yavari A. R., Shaping of metallic glasses by stress-annealing without thermal embrittlement. Acta Mater. 59, 3817–3824 (2011). [Google Scholar]
- 35.Xian H., Liu M., Wang X., Ye F., Wen P., Bai H., Liu Y., Wang W., Flexible and stretchable metallic glass micro- and nano-structures of tunable properties. Nanotechnology 30, 085705 (2019). [DOI] [PubMed] [Google Scholar]
- 36.Panagiotopoulos N. T., Georgarakis K., Jorge A. M. Jr., Aljerf M., Botta W. J., Yavari A. R., Advanced ultra-light multifunctional metallic-glass wave springs. Mater. Des. 192, 108770 (2020). [Google Scholar]
- 37.Liu Z., Chen W., Carstensen J., Ketkaew J., Ojeda Mota R. M., Guest J. K., Schroers J., 3D metallic glass cellular structures. Acta Mater. 105, 35–43 (2016). [Google Scholar]
- 38.Carstensen J. V., Lotfi R., Chen W., Szyniszewski S., Gaitanaros S., Schroers J., Guest J. K., Topology-optimized bulk metallic glass cellular materials for energy absorption. Scr. Mater. 208, 114361 (2022). [Google Scholar]
- 39.Panagiotopoulos N. T., Yousfi M. A., Georgarakis K., Yavari A. R., Mechanically induced waves in metallic glass foils. Mater. and Des. 90, 1110–1114 (2016). [Google Scholar]
- 40.Kaltenboeck G., Demetriou M. D., Roberts S., Johnson W. L., Shaping metallic glasses by electromagnetic pulsing. Nat. Commun. 7, 10576 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sharon E., Efrati E., The mechanics of non-Euclidean plates. Soft Matter 6, 5693–5704 (2010). [Google Scholar]
- 42.Soldatov I. V., Zehner J., Leistner K., Kang T., Karnaushenko D., Schafer R., Advanced, Kerr-microscopy-based MOKE magnetometry for the anisotropy characterisation of magnetic films. J. Magn. Magn. Mater. 529, 167889 (2021). [Google Scholar]
- 43.A. Hubert, R. Schäfer, Magnetic Domains: The Analysis of Magnetic Microstructures (Springer Berlin Heidelberg, 1998). [Google Scholar]
- 44.Lopatina E., Soldatov I., Budinsky V., Marsilius M., Schultz L., Herzer G., Schäfer R., Surface crystallization and magnetic properties of Fe84.3Cu0.7Si4B8P3 soft magnetic ribbons. Acta Mater. 96, 10–17 (2015). [Google Scholar]
- 45.R. Hilzinger, W. Rodewald, Magnetic Materials: Fundamentals, Products, Properties, Applications (Wiley, 2013). [Google Scholar]
- 46.Zhang C., Dong Y., Ye C., Recent developments and novel applications of laser shock peening: A review. Adv. Eng. Mater. 23, 2001216 (2021). [Google Scholar]
- 47.Chen B., Li Y., Yi M., Li R., Pang S., Wang H., Zhang T., Optimization of mechanical properties of bulk metallic glasses by residual stress adjustment using laser surface melting. Scr. Mater. 66, 1057–1060 (2012). [Google Scholar]
- 48.Soldatov I. V., Schäfer R., Selective sensitivity in Kerr microscopy. Rev. Sci. Instrum. 88, 073701 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Schäfer R., Soldatov I. V., Arai S., Power frequency domain imaging on Goss-textured electrical steel. J. Magn. Magn. Mater. 474, 221–235 (2019). [Google Scholar]
- 50.J. M. Dowden, The Mathematics of Thermal Modeling: An Introduction to the Theory of Laser Material Processing (Chapman & Hall/CRC USA, 2001). [Google Scholar]
- 51.Harms U., Shen T. D., Schwarz R. B., Thermal conductivity of Pd40Ni40-xCuxP20 metallic glass. Scripta Mater. 41, 411–414 (2002). [Google Scholar]
- 52.Li J. F., Sun Y. H., Ding W. D., Wang W. H., Bai H. Y., Nanosecond-pulsed laser welding of metallic glass. J. Non Cryst. Solids 537, 120016 (2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S11
Table S1
References
Movies S1 to S4