Improving GWAS discovery and genomic prediction accuracy in biobank data

Significance

Biobanks linking genomic data to individual electronic health records are increasing in number and in size around the world and are important both for the discovery of associations between DNA variation and health outcomes and in the context of precision medicine. There is a need to analyze individual-level data from such biobanks using the most powerful and efficient software applications. Using two large biobank studies, we show that both for detecting associations and for making predictors of health outcomes from the DNA, we can greatly improve current approaches by using statistical models that allow the strength of association to differ according to the properties of the genetic markers.

Abstract

Genetically informed, deep-phenotyped biobanks are an important research resource and it is imperative that the most powerful, versatile, and efficient analysis approaches are used. Here, we apply our recently developed Bayesian grouped mixture of regressions model (GMRM) in the UK and Estonian Biobanks and obtain the highest genomic prediction accuracy reported to date across 21 heritable traits. When compared to other approaches, GMRM accuracy was greater than annotation prediction models run in the LDAK or LDPred-funct software by 15% (SE 7%) and 14% (SE 2%), respectively, and was 18% (SE 3%) greater than a baseline BayesR model without single-nucleotide polymorphism (SNP) markers grouped into minor allele frequency–linkage disequilibrium (MAF-LD) annotation categories. For height, the prediction accuracy R² was 47% in a UK Biobank holdout sample, which was 76% of the estimated $h_{\mathit{SNP}}^2$. We then extend our GMRM prediction model to provide mixed-linear model association (MLMA) SNP marker estimates for genome-wide association (GWAS) discovery, which increased the independent loci detected to 16,162 in unrelated UK Biobank individuals, compared to 10,550 from BoltLMM and 10,095 from Regenie, a 62 and 65% increase, respectively. The average ${\chi }^2$ value of the leading markers increased by 15.24 (SE 0.41) for every 1% increase in prediction accuracy gained over a baseline BayesR model across the traits. Thus, we show that modeling genetic associations accounting for MAF and LD differences among SNP markers, and incorporating prior knowledge of genomic function, is important for both genomic prediction and discovery in large-scale individual-level studies.

As biobank datasets increase in size, it is important to understand the factors limiting the prediction of phenotype from genotype. Alongside others, we have recently shown that genomic prediction accuracy can be improved through the use of random-effects models that incorporate prior knowledge of genomic annotations and allow for differences in the variance explained by single-nucleotide polymorphism (SNP) markers, depending upon their linkage disequilibrium (LD) and their minor allele frequency (MAF) (1–8). These improvements in prediction accuracy should also translate into greater genome-wide association study (GWAS) discovery power. Mixed-linear models of association (MLMA) are commonly applied in GWASs in a two-step approach, where a random-effects model is first used to estimate leave-one-chromosome-out (LOCO) genetic values, and these are then used in a second marginal regression coefficient estimation step. Theory suggests that the test statistics obtained in the MLMA second step depend upon the accuracy of the LOCO genomic predictors produced from the first step. Current MLMA implementations use a blocked ridge regression model (9), a Restricted Maximum Likelihood (REML) genomic relationship model (10), or a Bayesian spike-and-slab model (11) within the first step.

Here, we improve the computational implementation of our recently developed Bayesian grouped mixture of regressions model (GMRM), which estimates genetic marker effects jointly, but with independent marker inclusion probabilities and independent $h_{\text{SNP}}^2$ parameters across LD, MAF, and functional annotation groups (Materials and Methods). This allows us to apply the model to 21 traits in the UK Biobank to test for prediction accuracy improvements over existing approaches. We then extend the model to provide MLMA SNP marker association estimates to test whether improved prediction accuracy translates to improved GWAS discovery compared to existing MLMA approaches.

Results

Genomic Prediction.

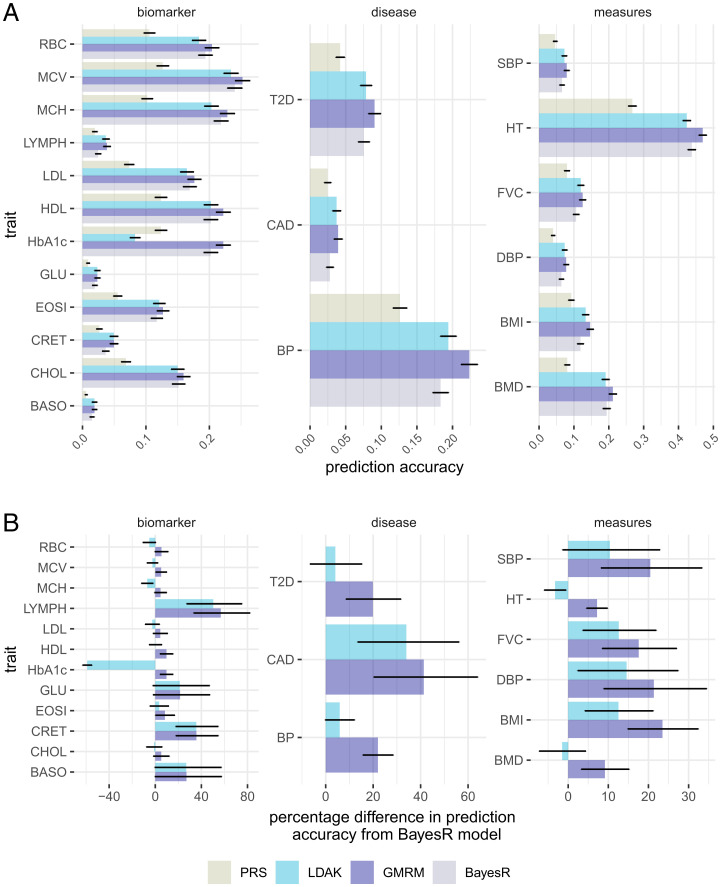
We begin with an analysis of 428,747 UK Biobank individuals genotyped at 8,430,446 markers with MAF > 0.0002 that overlap with markers imputed in the Estonian Genome Centre data. For computational convenience we then removed markers in very high LD using the “clumping” approach of plink, where we ranked SNPs by minor allele frequency and then selected the highest MAF SNPs from any set of markers with LD $R^2\ge 0.8$ within a 1-Mb window. This results in the selection of a tagging set of 2,174,071 variants, with only variants in very high LD with the tag SNPs removed (Materials and Methods). We show that our GMRM yields higher prediction accuracy than previously published estimates that we are aware of for all 21 traits in a UK Biobank holdout sample of 30,000 individuals (Fig. 1). A GMRM improves over a baseline BayesR model implemented in our software that assumes that markers come from five mixtures, of four normal distributions and a Dirac spike at zero, by an average of 18% (SE 3%, Fig. 1). Our prior is composed of 78 marker sets, each with five mixtures, with marker sets selected based on genomic annotations, LD, and MAF (Materials and Methods), and for a subset of five of the traits we also explore different prior formulations (SI Appendix, Fig. S1). We find that our prediction accuracy gains generally stem from addition of a large number of mixture distributions with independent variance parameters and from MAF and LD groupings, with only small gains in prediction accuracy achieved through annotation grouping (SI Appendix, Fig. S1). We find similar patterns of phenotypic variance attributable to our 13 annotation groups across traits, with ubiquitous enrichment at intronic regions, few examples of transcription factor binding site and enhancer enrichment, and much less variance attributed to SNP markers that are distal to genes than expected given the number of markers in this group (SI Appendix, Fig. S2). Additionally, we also modeled height and body mass index (BMI) without the LD clumping, using the full set of 8,430,446 markers, and found the same prediction accuracy of 0.468 for height and 0.146 for BMI.

Fig. 1.

Prediction accuracy of a GMRM. (A) Prediction accuracy obtained by GMRM for the 21 traits compared to the best individual-level LDAK prediction model (LDAK), a BayesR model with five mixture groups (BayesR), or polygenic risk scores calculated using BoltLMM mixed-linear model association SNP marker effects (PRS). (B) The prediction accuracy of LDAK and GMRM models as a percentage difference from the accuracy obtained from the BayesR model. Error bars in give 95% CIs. Full trait code descriptions are given in SI Appendix, Table S1.

We then compared our approach to a variety of other methods at different sets of SNP markers. At the same set of 2,174,071 SNP markers, we determined the best possible prediction accuracy obtained from the LDAK software (5), using either the BLD -LDAK annotations or the same annotation groups used by the GMRM and the models LDAK-Bolt-Predict and LDAK-BayesR-Predict. We find that LDAK improves prediction accuracy over an individual-level baseline BayesR model (Fig. 1), but that prediction accuracy was generally lower than that obtained by a GMRM (Fig. 1), with a GMRM improving prediction accuracy over the best LDAK model by an average of 15% (SE 7%). Both LDAK and the recently presented LDPred -funct model use an LD score framework to determine the variance attributable to the SNPs, and thus we removed markers of MAF < 0.01, giving a set of 6,991,095 markers, and from this we also conducted LD clumping to give a set of 1,410,525 markers (Materials and Methods). This tests whether the prediction accuracy improvements of a GMRM are attributable to the fact that our software can accommodate rare variants. For common SNPs, we find that a GMRM outperforms LDPred-funct by 14% (SE 2%) and an LDAK-BayesR-Predict model by 6% (SE 0.7%), but an LDAK-Bolt-Predict model by only 2% (SE 0.7%). Compared to the GMRM results presented in Fig. 1 at 2,174,071 SNP markers, changes in prediction accuracy resulting from the exclusion of rare variants differed among traits, but generally including rare variants improved prediction accuracy (SI Appendix, Fig. S3). Thus, we highlight that there is no “best” model for all human phenotypes, but a flexible prior formulation that can accommodate differences in phenotypic variance attributable to the MAF, LD, and annotation properties of the markers across traits generally provides improved genomic prediction.

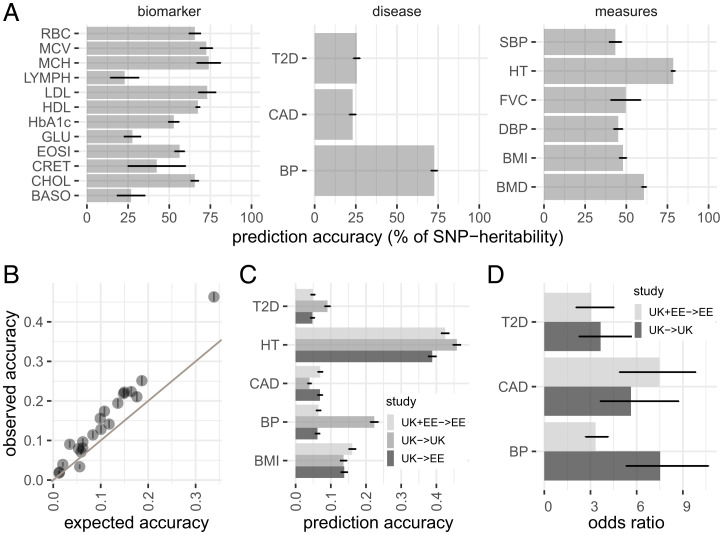
The $h_{\mathit{SNP}}^2$ estimate obtained from GMRM sets the upper bound for prediction accuracy in an independent sample and we achieve over 76% of the $h_{\mathit{SNP}}^2$ for height and over 50% for 12 of the traits in the UK Biobank holdout sample (Fig. 2). The expected prediction accuracy in an independent sample under ridge regression assumptions is given by ref. 12 and we use this equation, with the number of markers in the model as a proxy for M and the estimates of SNP heritability obtained from GMRM, to compare to the prediction accuracy we obtain. We find that the accuracy obtained by GMRM is higher than that expected from theory by up to 12.5% (mean 4.1%, SD 3.4%; Fig. 2). We meta-analyzed the posterior mean effect sizes obtained from the UK Biobank, with those obtained from a GMRM analysis of 105,000 Estonian Genome Centre participants, and then predicted into an Estonian holdout sample of 20,000 individuals, improving prediction of BMI (prediction accuracy of 16.1%) and cardiovascular disease (CAD) (prediction accuracy of 7%) over the accuracy obtained in the UK Biobank holdout sample (Fig. 1). Previous results have highlighted the lack of transfer of genomic predictors across populations, and here we achieved reduced prediction accuracy for high blood pressure (BP) and type-2 diabetes (T2D) diagnoses in Estonia compared to the UK Biobank. Thus, while these results highlight the potential of running individual-level analyses in each biobank and then meta-analyzing the results to improve genetic predictors, they also highlight the likely trait dependency of applicability of predictors across different health systems. Nevertheless, we show high stratification across both populations of early-onset risk groups with individuals in the top 1% of predicted genetic values having seven times (95% CI 4 to 9) higher risk of CAD, eight times (95% CI 6 to 11) higher risk of high BP in the UK Biobank holdout sample, and four times (95% CI 3 to 8) higher risk of T2D prior to 60 y of age, compared to the rest of the population (Fig. 2). Thus, we show how Bayesian posterior SNP effects size estimates can be meta-analyzed across studies to improve identification of individuals at high risk of early common disease onset.

Fig. 2.

Prediction accuracy of GMRM in UK and Estonian Biobanks. (A) Prediction accuracy of the GMRM effects sizes as a percentage of their upper bound (the SNP heritability) for 21 traits. (B) Prediction accuracy obtained by GMRM for the 21 traits compared to that expected from ridge-regression theory. (C) Prediction accuracy obtained using GMRM UK Biobank estimates in UK Biobank holdout data (UK →UK), GMRM UK Biobank estimates in Estonian data (UK →EE), and UK Biobank and Estonian meta-analysis GMRM estimates in Estonian holdout data (UK+EE →EE) for five focal traits. (D) Odds ratio for top 1% of the GMRM genetic predictor compared to all others, within UK →UK and UK+EE →EE for T2D, CAD, and high BP. Error bars in give 95% CIs. Full trait code descriptions are given in SI Appendix, Table S1.

Mixed-Linear Model Association.

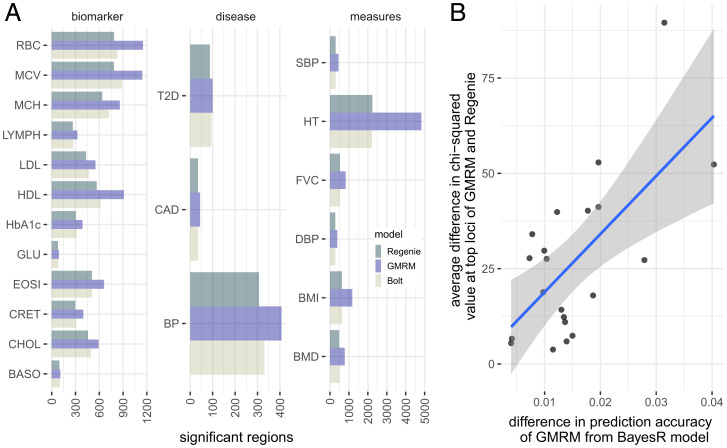
We now change focus from genomic prediction to GWAS discovery, in particular, the commonly applied MLMA approach. We modified our GMRM approach to provide MLMA SNP estimation within a leave-one-genomic-region-out or leave-one-chromosome-out framework. We validate this approach in simulation study, showing that our GMRM MLMA approach yields higher power at associated variants, while controlling for pervasive population stratification, but not strong common environment effects (SI Appendix, Fig. S4). In simulation, GMRM MLMA shows higher true positive rates, but at the cost of slightly higher and still well-controlled false discovery rate compared to BoltLMM (11), being < 5% with relatives and strong common environment confounding and < 1% with close relatives excluded. Thus, we applied this approach to the UK Biobank data, with first-degree relatives removed to minimize the potential for common environment confounding. We find that GMRM MLMA yields greater association testing power than comparable MLMA methods of BoltLMM or Regenie (9) for all traits (Fig. 3). The number of independent GWAS loci detected at P value $5\times {10}^{-8}$ was 16,162 for GMRM MLMA, compared to 10,550 from BoltLMM and 10,095 from Regenie, a 65 and 62% increase, respectively. At regions identified by all approaches at P value $5\times {10}^{-8}$, we find that the difference in the ${\chi }^2$ values obtained by GMRM MLMA compared to Regenie scales with the difference in prediction accuracy obtained in independent samples (Fig. 3), a relationship expected by theory (Materials and Methods). The average ${\chi }^2$ value of the leading markers was higher for GMRM MLMA compared to Regenie by 26.94 (SE 4.59) and increased by 15.24 (SE 0.41) for every 1% increase in prediction accuracy gained over a baseline BayesR model across the traits, consistent with an increase in power. We reanalyzed the data removing rare variants and compared our results to those obtained by Findor (13), BoltLMM, and Regenie at 6,991,095 common variants and at the 2,174,071 LD-pruned tagging variant set, finding the same improved performance for GMRM MLMA (SI Appendix, Fig. S5).

Fig. 3.

GWAS discovery of a GMRM in the UK Biobank. (A) Number of LD-independent genomic regions identified at $5\times {10}^{-8}$ by GMRM, compared to in BoltLMM (Bolt) and Regenie (Regenie) across 21 traits. (B) For SNP markers identified at $5\times {10}^{-8}$ by Bolt, Regenie, and GMRM, we estimated the difference in ${\chi }^2$ value between GMRM and Regenie and plotted this against the difference in prediction accuracy of GMRM compared to a BayesR model, to test whether discovery power scales with improved prediction accuracy of using MAF-LD annotation groups. Shaded area gives the 95% CIs of the regression line. Full trait code descriptions are given in SI Appendix, Table S1.

A GMRM approach also provides fine mapping of the associations (window posterior probability of association [WPPA] approach) (Materials and Methods) and we fine map 170 associations to single markers with posterior inclusion probability $\mathit{PIP}\ge 0.95$, 307 associations to SNP sets of 2 to 5 markers with $\mathit{PIP}\ge 0.95$, and 497 to groups of 6 to 20 markers with $\mathit{PIP}\ge 0.95$ (SI Appendix, Fig. S6). A total of 60% of the total GMRM MLMA associations fine mapped regions that contained $\ge 100$ SNPs in LD. Thus, while we show that modeling genetic associations accounting for marker properties is important for discovery in large-scale individual-level biobank-scale studies, we highlight how LD in the genome creates difficulty for pinpointing the mechanistic basis of the associations.

Discussion

Here, we show that association discovery and genomic prediction can be improved simply by better utilizing current data with flexible prior formulations. However, there remain important limitations. All of the above analyses were conducted using imputed genetic markers of minor allele frequency >0.0002 in a sample of UK Biobank European-ancestry individuals (Materials and Methods and SI Appendix, Table S1) as a demonstration of the utility of our approach. The portability of polygenic scores across human populations needs to be addressed to avoid polygenic risk stratification that is discriminatory toward groups little represented in currently available genomic data. This is an active research area, and our future work will involve accessing performance in analyses of diverse samples and examining how transfer learning can improve model estimation across worldwide biobank data. Second, summary statistic approaches have been developed, some of which also account for genomic annotations, MAF, and LD when creating genetic predictors (4, 5, 14, 15), and these methods are essential for utilizing currently available summary data and for situations when individual-level data are not accessible. However, summary statistics approaches have yet to yield the prediction accuracy obtained in this study (4, 5, 14, 15). Here, we have shown how using empirical data from two biobanks can facilitate gains in discovery and polygenic prediction, through a focus on creating powerful and efficient software applications to maximize individual-level data analysis and then meta-analyzing the results across biobanks. Thus, we hope that previous consortia analyses can be revisited with a range of improved methodology to facilitate further gains in discovery and polygenic prediction. Achieving similar prediction accuracy while minimizing computer resources is a focus of future work, but currently our approach is coded in highly optimized C++ code, with run times comparable to existing approaches, albeit with greater central processing unit (CPU) use (SI Appendix, Figs. S7 and S8). For example, our main analyses (2 million SNPs and 400,000 individuals) took on average 30 h using 24 CPUs.

Materials and Methods

UK Biobank Data.

UK Biobank has approval from the North-West Multicenter Research Ethics Committee (MREC) to obtain and disseminate data and samples from the participants (https://www.ukbiobank.ac.uk/ethics/), and these ethical regulations cover the work in this study. Written informed consent was obtained from all participants. From the measurements, tests, and electronic health record data available in the UK Biobank data (16), we selected 12 blood-based biomarkers, 3 of the most common heritable complex diseases, and 6 quantitative measures. The full list of the 21 traits, the UK Biobank coding of the data used, and the covariates adjusted for are given in SI Appendix, Table S1. For the quantitative measures and blood-based biomarkers we adjusted the values by the covariates, removed any individuals with a phenotype greater or less than 7 SD from the mean (assuming these are measurement errors), and standardized the values to have mean 0 and variance 1.

For the common complex diseases, we determined disease status using a combination of information available. For high BP, we used self-report information of whether high blood pressure was diagnosed by a doctor (UK Biobank code 6150-0.0), the age high blood pressure was diagnosed (2966-0.0), and whether the individual reported taking blood pressure medication (6153-0.0, 6177-0.0). For T2D, we used self-report information of whether diabetes was diagnosed by a doctor (2443-0.0), the age diabetes was diagnosed (2976-0.0), and whether the individual reported taking diabetes medication (6153-0.0, 6177-0.0). For CAD, we used self-report information of whether a heart attack was diagnosed by a doctor (3894-0.0), the age angina was diagnosed (3627-0.0), whether the individual reported a heart problem diagnosed by a doctor (6150-0.0), and the date of myocardial infarction (42000-0.0). For each disease, we then combined this with primary death ICD-10 (International Classification of Diseases 10th Revision) codes (40001-0.0); causes of operative procedures (41201-0.0); and the main (41202-0.0), secondary (41204-0.0), and inpatient ICD10 codes (41270-0.0). For BP we selected ICD10 codes I10, for T2D we selected ICD10 codes E11 to E14 and excluded from the analysis individuals with E10 (type-1 diabetes), and for CAD we selected ICD10 codes I20 to I29. Thus, for the purposes of this analysis, we define these diseases broadly simply to maximize the number of cases available for analysis. For each disease, individuals with neither a self-report indication nor a relevant ICD10 diagnosis were then assigned a zero value as a control.

We restricted our discovery analysis of the UK Biobank to a sample of European individuals. To infer ancestry, we used both self-reported ethnic background (21000-0) selecting coding 1 and genetic ethnicity (22006-0) selecting coding 1. We also took the 488,377 genotyped participants and projected them onto the first two genotypic principal components (PC) calculated from 2,504 individuals of the 1,000 Genomes project with known ancestries. Using the obtained PC loadings, we then assigned each participant to the closest population in the 1,000 Genomes data: European, African, East Asian, South Asian, or Admixed, selecting individuals with PC1 projection < absolute value 4 and PC 2 projection < absolute value 3. Samples were excluded if in the UK Biobank quality-control procedures they 1) were identified as extreme heterozygosity or missing genotype outliers, 2) had a genetically inferred gender that did not match the self-reported gender, 3) were identified to have putative sex chromosome aneuploidy, 4) were excluded from kinship inference, or 5) had withdrawn their consent for their data to be used. We used the imputed autosomal genotype data of the UK Biobank provided as part of the data release. We used the genotype probabilities to hard call the genotypes for variants with an imputation quality score above 0.3. The hard-call threshold was 0.1, setting the genotypes with probability $\le 0.9$ as missing. From the good-quality markers (with missingness less than 5% and P value for Hardy–Weinberg test larger than ${10}^{-6}$, as determined in the set of unrelated Europeans) we selected those with MAF > 0.0002 and rs identifier, in the set of European-ancestry participants, providing a dataset 9,144,511 SNPs. From this we took the overlap with the Estonian Genome Centre data described below to give a final set of 8,430,446 markers. For computational convenience we then removed markers in very high LD using the clumping approach of plink, where we ranked SNPs by minor allele frequency and then selected the highest-MAF SNPs from any set of markers with LD $R^2\ge 0.8$ within a 1-Mb window. This results in the selection of a tagging set of variants, with only variants in very high LD with the tag SNPs removed. These filters resulted in a dataset with 458,747 individuals and 2,174,071 markers.

We split the sample into training and testing sets for each phenotype, selecting 30,000 individuals that were unrelated (SNP marker relatedness <0.05) to the training individuals to use as a testing set. This provides an independent sample of data with which to access prediction accuracy. For the complex diseases, we randomly select 1,000 cases and match to 29,000 controls, again ensuring that these individuals were unrelated to those in the training sample.

Estonian Biobank Data.

All Estonian Biobank participants have signed a broad informed consent form and the study was carried out under ethical approval 1.1-12/2856 from the Estonian Committee on Bioethics and Human Research (Estonian Ministry of Social Affairs) and released under data release P03. The Estonian Biobank (EstBB) is a population-based cohort encompassing 20% of Estonia’s adult population (200,000 individuals, 66% females; https://genomics.ut.ee/en/content/estonian-biobank). Individuals underwent microarray-based genotyping at the Core Genotyping Lab of the Institute of Genomics, University of Tartu. A total of 136,421 individuals were genotyped on Illumina Global Screening Arrays (GSAs) and we imputed the dataset to an Estonian reference, created from the whole-genome sequence data of 2,244 participants (17). From 11,130,313 markers with imputation quality score >0.3, we selected SNPs that overlapped with those selected in the UK Biobank, resulting in a set of 8,430,446 markers.

General data, including basic body measurements, were collected at recruitment. Project-based questionnaires were sent later and filled out on a voluntary basis. Health records are regularly updated through linkage with the national Health Insurance Fund and other relevant databases, providing sporadic access to blood biomarker measurements and medical diagnoses (18). For the genotyped individuals, we had data available for height and body mass index and we removed individuals plus or minus 7 SD from the mean and adjusted both phenotypes by the age at enrollment, sex, and the first 20 PCs of the SNP marker data. Prevalent cases of BP, CAD, and T2D in the Estonian Biobank cohort were first identified on the basis of the baseline data collected at recruitment, where the information on prevalent diseases was either retrieved from medical records or self-reported by the participant. The cohort was subsequently linked to the Estonian Health Insurance database that provided additional information on prevalent cases (diagnoses confirmed before the date of recruitment) as well as on incident cases during the follow-up. For BP we selected ICD10 code I10, for CAD we selected codes of I20 to I29, and for T2D we selected codes E11 to E14 and excluded E10. We also split the sample into training and testing sets for each phenotype, selecting 20,000 individuals that were unrelated (SNP marker relatedness <0.05) to the training individuals to use as a testing set. This provides an independent sample of data with which to access prediction accuracy. For the complex diseases, we randomly select 1,000 cases and match to 19,000 controls, again ensuring that these individuals were unrelated to those in the training sample.

Bayesian GMRM.

We extend the software implementation of our recently developed Bayesian grouped mixture of regression model (1):

$$\mathbf{y}=\mathbf{1}\mu +{\displaystyle \sum _{\phi =1}^{\mathrm{\Phi }}{\mathbf{X}}_{\phi }}{\mathit{\beta }}_{\phi }+\mathit{ϵ},$$ [1]

where there is a single intercept term $\mathbf{1}\mu$ and a single error term $\mathit{ϵ}$ but SNPs are allocated into groups $({\phi }_1,\dots ,{\phi }_{\mathrm{\Phi }})$, each of which has its own set of model parameters ${\mathrm{\Theta }}_{\phi }=\left\{{\beta }_{\phi },{\pi }_{{\beta }_{\phi }},{\sigma }_{{\beta }_{\phi }}^2\right\}$. As such, each ${\beta }_{{\phi }_j}$ is distributed according to

$${\beta }_{{\phi }_j}\sim {\pi }_{0_{\phi }}{\delta }_0+{\pi }_{1_{\phi }}\mathcal{N}\left(0,{\sigma }_{1_{\phi }}^2\right)+\dots +{\pi }_{5_{\phi }}\mathcal{N}\left(0,{\sigma }_{5_{\phi }}^2\right)\text{},$$ [2]

where for each SNP marker group $\left\{{\pi }_{0_{\phi }},{\pi }_{1_{\phi }},\dots ,{\pi }_{5_{\phi }}\right\}$ are the mixture proportions and $\left\{{\sigma }_{1_{\phi }}^2,{\sigma }_{2_{\phi }}^2,\dots ,{\sigma }_{5_{\phi }}^2\right\}$ are the mixture-specific variances proportional to ${\sigma }_{{\beta }_{\phi }}^2\times 0.0001,{\sigma }_{{\beta }_{\phi }}^2\times 0.001,{\sigma }_{{\beta }_{\phi }}^2\times 0.01,{\sigma }_{{\beta }_{\phi }}^2\times 0.1$. Note that our software facilitates different choices of groups, mixture number, and mixture scaling constants.

The mixture proportions and variance explained by the SNP markers are all unique and independent across SNP marker groups. Following our previous work (1), we partition SNP markers into seven location annotations using the knownGene table from the University of California Santa Clara browser data, preferentially assigning SNPs to coding (exonic) regions first; then in the remaining SNPs we preferentially assign them to intronic regions, then to 1-kb upstream regions, then to 1- to 10-kb regions, then to 10- to 500-kb regions, and then to 500-kb to 1-Mb regions. Remaining SNPs were grouped in a category labeled “others” and also included in the model so that variance is partitioned relative to these also. Thus, we assigned SNPs to their closest upstream region; for example, if a SNP is 1 kb upstream of gene X, but also 10 to 500 kb upstream of gene Y and 5 kb downstream of gene Z, then it was assigned to be a 1-kb region SNP. This means that SNPs 10 to 500 kb and 500 kb to 1 Mb upstream are distal from any known nearby genes. We further partition upstream regions to experimentally validated promoters, transcription factor binding sites (tfbs), and enhancers (enh) using the HACER, snp2tfbs databases. All SNP markers assigned to 1-kb regions map to promoters; 1- to 10-kb SNPs, 10- to 500-kb SNPs, and 500-kb to 1-Mb SNPs are split into enh, tfbs, and others (unmapped SNPs), extending the model to 13 annotation groups. Within each of these annotations, we have three minor allele frequency groups (MAF < 0.01, 0.01 > MAF > 0.05, and MAF > 0.05), and then each MAF group is further split into two based on median LD score. This gives 78 nonoverlapping groups for which our model jointly estimates the phenotypic variation attributable to, and the SNP marker effects within, each group. For each of the 78 groups, SNPs were modeled using five mixture groups with variance equal to the phenotypic variance attributable to the group multiplied by constants (mixture 0 $=$ 0, mixture 1 $=$ 0.00001, mixture 2 $=$ 0.0001, 3 $=$ 0.001, 4 $=$ 0.01, 5 $=$ 0.1). The probabilities that markers enter each of the five mixtures (the mixture components) and the variance attributable to the marker group (${\sigma }_{{\beta }_{\phi }}^2$) are all estimated independently, linked only by a residual updating scheme and thus a regression problem where the number of covariates greatly exceeds the number of measured individuals is broken down into a series of interdependent regressions where the number of covariates within a group is always far less than the total sample size.

We first extend our prediction software to accommodate the analysis of multiple traits simultaneously. While this approach does not yet utilize estimates of the genetic or residual covariance among different outcomes when estimating the SNP effects, a number of coding developments were made to improve speed of the baseline calculations and facilitate the random number generation, vectorization of the effect size estimation, and missing data handling for multiple outcomes. We benchmarked the timing of our software increasing the sample size, marker number, number of traits analyzed, and the number of Message Passing Interface (MPI) processes, to demonstrate the scalability of our approach as the dimensionality of the data increases. We present these results in SI Appendix, Figs. S7 and S8.

Assessment of Prediction Accuracy and Method Comparisons.

We apply the model to the 21 UK Biobank traits described above and use the posterior mean SNP marker effects to predict into the holdout sample. We repeat the analysis without the MAF-LD annotation groups, fitting five mixture components, which is equivalent to a BayesR model. SEs are calculated by the method proposed by Fisher (19). Additionally, we explore other prior options for five UK Biobank traits, presenting these results in SI Appendix, Fig. S1.

We then repeat the analysis using the individual-level prediction models implemented in LDAK (LDAK-Bolt-Predict and LDAK-BayesR-Predict) described in a recent paper (5), with both the BLD-LDAK annotations and the same annotations used for the GMRM model as described above. We then present the highest prediction accuracy obtained as measured by the correlation between the predictor and the phenotype within the holdout UK Biobank sample. With the aim of providing a simple benchmark, we also repeated the analysis using BoltLMM, selecting an LD-clumped ($R^2\le 0.01$ within a 1-Mb window) subset of markers for the random-effect term, and we then used the mixed-linear model association marker effects at the same set of 2,174,071 SNPs to create a predictor. We present these comparisons in Fig. 1.

We then select 1,410,525 common variants with MAF $\ge 0.01$ from the 2,174,071 marker sets and repeat the GMRM and LDAK prediction analysis to compare the model prediction accuracy obtained from a set of common SNPs. Additionally, we used BoltLMM to generate mixed-linear model association summary statistics for 6,991,095 SNPs of minor allele frequency $\ge 0.01$, again using an LD-clumped ($R^2\le 0.01$ within a 1-Mb window) subset of markers for the random-effect term. We used these summary statistics and compared to the LDPred-funct method (4) using UK Biobank LD score annotations (baselineLF v2.2.UKB) (20). We present these comparisons in SI Appendix, Fig. S3.

We then predict into the Estonian Biobank data, run the GMRM in the Estonian data, and predict into the Estonian holdout sample using both UK Biobank model estimates and UK and Estonian Biobank combined estimates. We present these in Fig. 2.

Mixed-Linear Association Modeling.

We extended our software to return the typical fixed-effect SNP regression coefficients estimated by other MLMA approaches. In the first step of running GMRM, the SNP marker effects that we obtain are jointly estimated and thus within each iteration, estimation is made accounting for the effects of other markers in both short- and long-range LD. From these estimates, we can obtain partitioned predictors for each focal block k of the genome ${\tilde{\mathbf{g}}}_{{\text{block}}_k}={\displaystyle {\sum }_{j=1}^j{\mathbf{x}}_{j,-k}}{\beta }_{j,-k}$, where ${\mathbf{x}}_{j,-k}$ are the values of SNP markers that are not part of block k and ${\beta }_{j,-k}$ are their jointly estimated posterior mean effects. These can then be used when testing for association in a second step to yield standard frequentist mixed-model summary statistics, following other approaches. When testing for association of the phenotype with a marker ${\mathbf{x}}_j$ from focal block k, we consider a simple linear model

$${\tilde{\mathbf{y}}}_{{\text{block}}_k}={\mathbf{x}}_{j,k}{\beta }_{j,k}+{\mathit{ϵ}}_k,$$ [3]

where ${\tilde{\mathbf{y}}}_{{\text{block}}_k}=\tilde{\mathbf{y}}-{\tilde{\mathbf{g}}}_{{\text{block}}_k}$ gives the phenotypic residuals where the polygenic effects estimated across the genome other than the focal testing block are adjusted for, ${\mathbf{x}}_j$ is the jth marker in the focal block, β_j is the ordinary least-squares estimate for the jth marker in block k, and ${\mathit{ϵ}}_k$ is the residual error, with $\mathit{ϵ}\sim N\left(0,{\mathbf{I}}_N{\sigma }_{ϵ}^2\right)$ with M_k the number of markers within block k.

A t-test statistic is then straightforward to obtain as

$$T_{j,k}=\frac{{\mathbf{x}}_{j,k}^T{\tilde{\mathbf{y}}}_{{\text{block}}_k}}{{[{\sigma }_{{\tilde{\mathbf{y}}}_{{\text{block}}_k}}^2{\mathbf{x}}_{j,k}^T{\mathbf{x}}_{j,k}]}^{0.5}},$$ [4]

where ${\sigma }_{{\tilde{\mathbf{y}}}_{{\text{block}}_k}}^2$ is calculated as $\frac{1}{N}\left|\right|{\tilde{\mathbf{y}}}_{{\text{block}}_k}^T|{|}_2^2$, where N is the number of individuals. A normal approximation of $T_{j,k}^2\approx {\chi }_1^2$ is used to give the P value. A step-by-step algorithm for this GMRM MLMA approach is given in Algorithm 1 in SI Appendix.

The test statistic values obtained are an approximation of the mixed-model ${\chi }^2$ statistic if one were to model the SNP as a fixed effect with a full mixed-model equation. This approach follows recent studies (ref. 9 and equations 23 and 24 of supplementary online material of ref. 11), in particular as the ${\chi }^2$ statistic obtained from BoltLMM is equivalent to computing the squared correlations between SNPs being tested and a best linear unbiased predictor, which is the approach taken here. The power of mixed-model association is driven by the fact that focal test SNPs are tested against a “denoised” residual phenotype, from which other SNP effects estimated by the mixed model have been conditioned out. Here, we expect the SNP marker-effect estimation to be improved as the genetic predictor used to residualize the phenotype should have a higher prediction accuracy within an independent sample if the true underlying SNP marker effects differ across MAF-LD annotation groups. While further work is required to optimize this approach for rare diseases using saddle-point approximations and to account for the covariance of multiple outcomes, here we wished to simply demonstrate that modeling SNP effects in MAF-LD annotation groups in the first step yields improved MLMA fixed-effect marker estimates in the second step. We verify this approach in a simulation study as described below.

Guided by the simulation study results, we subset the UK Biobank data to individuals that were related to less than first-degree relatives (n = 414, 055). We then obtained MLMA estimates using GMRM MLMA in a leave-one-chromosome-out approach and we also verified these by placing the LOCO predictors that we obtain from GMRM into the second step of the Regenie software. This enabled a direct comparison with Regenie and we also compared to the results obtained by BoltLMM. We present these MLMA results in Fig. 3 for the full 8,430,446 SNPs set, where the LOCO predictors of GMRM were obtained from the 2,174,071 LD-clumped SNPs set and MLMA SNP estimates were made for the full 8,430,446 SNPs set. For BoltLMM and Regenie we selected an LD-clumped ($R^2\le 0.01$ within a 1-Mb window) ∼1 million subset of markers for the variance component/LOCO predictions as the authors suggest this is optimal, and then we obtained MLMA SNP estimates for the full 8,430,446 SNPs set. In SI Appendix, Fig. S5, we present the MLMA results for the 2,174,071 LD-clumped SNPs set, again using all 2,174,071 variants for the GMRM LOCO predictor and LD-clumped ($R^2\le 0.01$ within a 1-Mb window) 1 million subset of markers for the variance component/LOCO predictions of BoltLMM/Regenie. We also present MLMA results for 6,991,095 SNPs of minor allele frequency $\ge 0.01$, where the 1,410,525 common variants with MAF $\ge 0.01$ from the 2,174,071 markers set were used for the variance component/LOCO predictions of all approaches. Additionally, for the 6,991,095 SNPs of minor allele frequency $\ge 0.01$ we compare our results to Findor (13), a P-value weighting approach using the expected variance attributable to SNPs through an LD score UK Biobank annotation model based on BoltLMM summary statistics. For all approaches, we clump the results with the following Plink commands: –clump-kb 5000 –clump-r2 0.01 –clump-p1 0.00000005, which represents a conservative definition of independent loci within a 5-Mb window and an R² threshold of 0.01.

Simulation Study.

We follow a similar simulation study design to that presented in a number of recent studies (10). From our quality-controlled UK Biobank data, we first randomly selected 100,000 individuals with relatedness estimated from SNP markers of $\le 0.05$ and used marker data from chromosomes 1 through 10 with MAF $\ge 0.001$ to give 1.36 million SNPs. For the odd chromosomes, we randomly selected 10,000 LD-independent SNP markers as causal variants. We simulated effect sizes for the causal variants, b, by drawing from a normal distribution with zero mean and variance 0.5/10,000. We then scaled the 10,000 causal variant SNP markers to have mean 0 and variance 1 and multiplied them by the simulated marker-effect sizes to give genetic values with mean 0 variance 0.5. In previous work (1), we have extensively explored the ability of our GMRM approach to recover SNP effects sizes and accurately estimate SNP-heritability parameters independently of the relationship of effect sizes, MAF, and LD, and so here we simply assume a simple underlying genetic model of randomly selected causal variants and no relationship between effect size and MAF or LD. We then simulate population stratification effects by scaling the loadings of the 100,000 individuals on the first principal component calculated from the genetic data and multiplying the values by $\sqrt{0.05}$; this gives a vector of values, ps with variance 0.05. Finally, individual environment values are drawn from a normal distribution with zero mean and variance $1-\text{Var}(\mathbf{X}\mathbf{b})-\text{Var}(ps)$, so that the sum of the genetic, ps, and environmental values gives a phenotype with zero mean and variance 1. We replicate this simulation 10 times, referring to it in the main text and the figures as “random unrelated” causal variant allocation.

Using the same randomly selected individuals, we repeat the simulation but we separate the genetic markers into four groups, randomly selecting 1,000 LD-independent exonic markers, 1,000 LD-independent intronic markers, 1,000 LD-independent transcription factor binding site markers, and 7,000 LD-independent markers from other annotation groups. We then sample the marker effects for each of the four groups, drawing from independent normal distributions with zero mean and variance 0.1/1,000, 0.25/1,000, 0.1/1,000, and 0.05/7,000, respectively. This gives three annotation groups with larger effect size variance but the same number of causal variants and a total variance explained by the SNP markers $\text{var}(\mathbf{X}\mathbf{b})=0.5$ as the previous simulation setting. We then simulated population stratification effects in the same way and individual environment values by drawing from a normal distribution with zero mean and variance $1-\text{Var}(\mathbf{X}\mathbf{b})-\text{Var}(ps)$, so that the sum of the genetic, ps, and environmental values gives a phenotype with zero mean and variance 1. We also replicate this simulation setting 10 times, referring to it in the main text and the figures as “enrichment unrelated” causal variant allocation.

We then repeat the “random” and the “enrichment” simulation settings, but we change the selection of the individuals used for the simulation. We randomly select 10,000 unique sibling pairs from the UK Biobank data and combine these with 80,000 randomly selected unrelated individuals to give a mixture of relatedness similar to the proportions of related and unrelated individuals in the UK Biobank data. We simulate the same genetic and ps values, but we also add a common environmental variance by drawing a value for each sibling pair from a normal distribution with mean 0 and variance 1 and allocating a value of 0 to each of the unrelated individuals. We scale these values by $\sqrt{0.12}$ to give a vector of among-family differences, pe, with variance 0.12. Finally, individual environment values are drawn from a normal distribution with zero mean and variance $1-\text{Var}(\mathbf{X}\mathbf{b})-\text{Var}(ps)-\text{Var}(pe)$, so that the sum of the genetic, ps, pe, and environmental values gives a phenotype with zero mean and variance 1. We replicate this simulation 10 times, referring to it in the main text and the figures as “random related” and “enrichment related” causal variant allocation.

We then analyze these data using BoltLMM, fastGWA (10), and GMRM-MLMA and calculate the average ${\chi }^2$ values (using an approximation that $T^2\approx {\chi }^2$) for the causal variants, which gives a comparative measure of the power of each approach. We also calculate the average ${\chi }^2$ values (again using an approximation that $T^2\approx {\chi }^2$) obtained from markers on the even chromosomes that contain no causal variants, comparing to the null expectation of 1. These results are presented in SI Appendix, Fig. S4. We find improved power of GMRM-MLMA over other approaches in all settings, with control of the pervasive population stratification. We find only moderate ${\chi }^2$ inflation when relatives share strong common environment effects that is the same as that obtained by BoltLMM. This inflation never increased the false discovery rate (FDR) above 3.5% in any of the simulations, but was best controlled by a fastGWA approach.

Utilizing the Posterior Distribution Obtained.

We apply our model to each UK Biobank and Estonian Genome Centre data trait, running two short chains for 5,000 iterations and combining the last 2,000 posterior samples together. We show in SI Appendix, Fig. S9 that the prediction accuracy obtained from our model and the hyperparameter estimates of $h_{\mathit{SNP}}^2$ converge within the first 2,000 iterations. While obtaining a full posterior distribution with many hundreds of independent samples would require running longer chains, we show that the posterior mean effect size for each SNP that we use for prediction (and thus also in the estimation of the MLMA effect sizes) is well approximated within this run time (SI Appendix, Fig. S9), which is sufficient in this work to assess the prediction accuracy of our approach and to estimate the variance attributable to different genomic regions.

We estimate the proportion of total $h_{\mathit{SNP}}^2$ attributable to each genomic annotation and we divide this proportion by the proportion of SNP markers in the model for this annotation given the total number of SNP markers in the model. This gives an estimate of the enrichment of the marker effects, whereby if the average effect sizes of markers within a given annotation are larger than expected given the number of markers entering the model for that annotation, then the value obtained should be greater than 1. Conversely, smaller than expected marker effects will yield values less than 1. We present these results in SI Appendix, Fig. S2, where we find substantial enrichment of SNP heritability in intronic regions across traits and weak evidence that enrichment differs across traits, with exonic enrichment for height, forced vital capacity, mean corpuscular hemoglobin, low- and high-density lipoprotein, and blood cholesterol levels (SI Appendix, Fig. S2). Generally, blood-based biomarkers show enrichment at proximal promotors, transcription factor binding sites, and enhancers, with variation in complex diseases and quantitative traits attributable to distal transcription factor binding sites and enhancers in proportion to that expected given the number of markers in the model (SI Appendix, Fig. S2). SNP markers located greater than 500 kb from a gene explained a far smaller proportion of variance explained then expected given the number of markers that map to the region (SI Appendix, Fig. S2).

We previously presented a WPPA approach (1). The WPPA is estimated by counting the proportion of Markov chain Monte Carlo samples in which the regression coefficient β_j is greater than a given threshold for at least one SNP j in a given genomic window, which can be used as a proxy for the posterior probability that the genomic region contains a causal variant. Because WPPA for a given window is a partial association conditional on all other SNPs in the model, including those flanking the region, the influence of flanking markers on the WPPA signal for any given window will be inversely related to the distance k of the flanking markers. Thus, as the number of markers between a causal variant and the focal window increases, the influence of the causal variant on the WPPA signal will decrease and so WPPA computed for a given window can be used to locate associations for that given window, while also controlling the false discovery rate. Thus, it represents an approach to fine-mapping association results to groups of SNP markers. Here, we group markers by LD into 341,380 LD-independent groups using plink’s clumping procedure, which selects groups of markers (from single SNPs to groups of 100 or more) with LD $R^2\ge 0.1$ within a 1-Mb window. For each of these 341,380 SNP groups we calculate the WPPA, defined as the posterior probability that a group explains at least 0.0001% of the phenotypic variance. The number of groups with WPPA $\ge 0.95$ is shown in SI Appendix, Fig. S6.

Comparisons to Theory.

We note the important distinction between prediction SNP effect sizes that are obtained from mixed-models/penalized regression models, in which a single model is fitted where all SNPs are included as random effects, and those obtained from an MLMA model where individual SNP association estimates are typically sought. Here, we sought to make this distinction clear by comparing the prediction accuracy obtained by GMRM and its baseline BayesR model to that obtained from using other random-effect models implemented in LDAK and to predictors created from MLMA estimates to demonstrate that it is inappropriate to create polygenic risk scores from MLMA estimates compared to random-effect models. The expected prediction accuracy in an independent sample under ridge regression assumptions is given by ref. 12 as

$$R^2=\frac{h_{\mathit{SNP}}^2}{1+\frac{M}{N{h}_{\mathit{SNP}}^2}(1-R^2)}$$ [5]

and we use this equation, with the number of markers in the model as a proxy for M and the estimates of $h_{\mathit{SNP}}^2$ obtained from GMRM, to compare to the prediction accuracy we obtain.

For the common complex disease traits, we place the estimates of the proportion of variance explained by the SNP markers on the liability scale to facilitate comparison with the quantitative measures. The linear transformation of heritability from the observed 0 to 1 scale, $h_o^2$, to that of liability scale $h_l^2$ is

$$h_l^2\sim \frac{h_o^{2}K(1-K)}{z^2}$$ [6]

with K the population lifetime prevalence and z the height of the normal curve at the truncation point pertaining to K (21). We did not observe the population lifetime prevalence of any disease within either population and so we make the assumption that the prevalence in the UK Biobank and Estonian Biobank samples provides a very distant approximation. We scale the estimates of the prediction accuracy to also place these on the liability scale, $R_l^2$, as

$$R_l^2\sim \frac{R_o^2{K}^2(1-K^2)}{z^{2}P(1-P)}$$ [7]

with P the proportion of cases in the testing sample. Note that this expression is also an approximation and can result in bias when ascertainment is extreme and heritability on the liability scale is high, although this is expected to be small in practice and negligible for the three disease traits considered here (22).

Previous work (23) has shown that the expectation of the mean ${\chi }^2$ value at causal SNPs is given by

$$E[{\chi }_{\text{causal} \text{SNPs}}^2]=1+\frac{N{h}_{\mathit{SNP}}^2}{M_{\mathit{causal}}·\frac{1}{1-R^2}}$$ [8]

with N the sample size. Thus, under the assumptions of no confounding, no case–control ascertainment-induced confounding, and no pervasive familial relatedness, increased prediction accuracy should yield increased power (${\chi }^2$ statistics) at SNPs that are associated with underlying causal variants.

Data Availability

Data from this project were held under UK Biobank project ID 35520. The individual-level genotype and phenotype data are available through formal application to the UK Biobank (www.ukbiobank.ac.uk). The Estonian Biobank data are available upon request from the cohort author R.M. according to data access protocols to researchers with approval from the Estonian Committee on Bioethics and Human Research (Estonian Ministry of Social Affairs). Summaries of all posterior distributions obtained and the MLMA-associated results are deposited in Dryad (24). GMRM software is fully open source and available at https://github.com/medical-genomics-group/gmrm (25). Anonymized data have been deposited in Dryad (24). Some study data are available (the individual-level genotype and phenotype data are available through formal application to the UK Biobank (https://www.ukbiobank.ac.uk/).