Multi-scale spatial heterogeneity enhances particle clearance in airway ciliary arrays

Abstract

Mucus clearance constitutes the primary defence of the respiratory system against viruses, bacteria and environmental insults [1]. This transport across the entire airway emerges from the integrated activity of thousands of multiciliated cells, each containing hundreds of cilia, which together must coordinate their spatial arrangement, alignment and motility [2, 3]. The mechanisms of fluid transport have been studied extensively at the level of an individual cilium [4, 5], collectively moving metachronal waves [6–10], and more generally the hydrodynamics of active matter [11, 12]. However, the connection between local cilia architecture and the topology of the flows they generate remains largely unexplored. Here, we image the mouse airway from the sub-cellular (nm) to the organ scales (mm), characterising quantitatively its ciliary arrangement and the generated flows. Locally we measure heterogeneity in both cilia organisation and flow structure, but across the trachea fluid transport is coherent. To examine this result, a hydrodynamic model was developed for a systematic exploration of different tissue architectures. Surprisingly, we find that disorder enhances particle clearance, whether it originates from fluctuations, heterogeneity in multiciliated cell arrangement or ciliary misalignment. This resembles elements of ‘stochastic resonance’ [13–15], in the sense that noise can improve the function of the system. Taken together, our results shed light on how the microstructure of an active carpet [16, 17] determines its emergent dynamics. Furthermore, this work is also directly applicable to human airway pathologies [1], which are the third leading cause of deaths worldwide [18].

PATTERNING AND ALIGNMENT OF AIRWAY CILIA ACROSS THE SCALES

The many functions of the airway are reflected by the variety of specialised cell types it contains, including multiciliated, secretory, nerve, immune and basal cells [19]. This inevitably leads to constraints in the organisation of the airway cilia, which is compounded over several orders of magnitude [20, 21] (Fig. 1A). Previous studies have noted the heterogeneity in airway cilia arrangement [22, 23], but they lack quantitative descriptions of disorder across all relevant spatial scales (nm to mm).

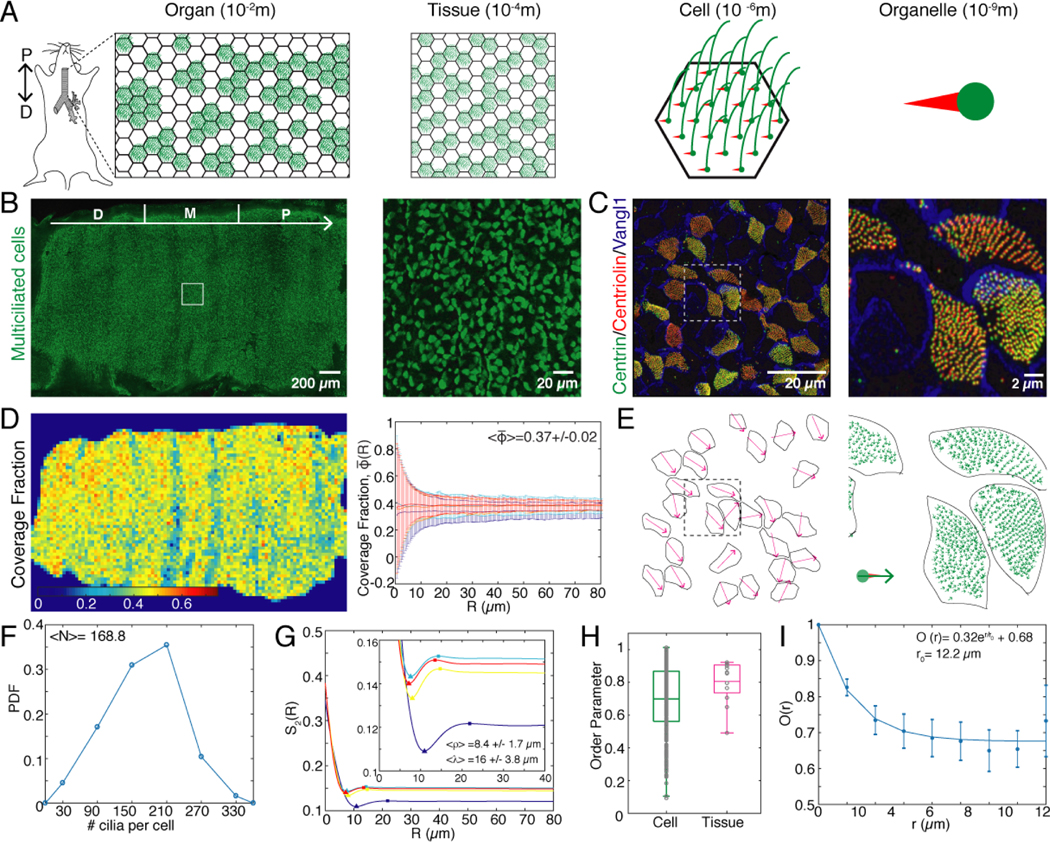
FIG. 1. Heterogeneity in spatial patterning of cilia in the mouse airway epithelium.

A. Schematic of the organisation of multiciliated cells across spatial scales. Thousands of multiciliated cells line the trachea, forming a “patchwork” pattern at the tissue scale. Each multiciliated cell contains hundreds of cilia anchored to the cell by the basal body. B. Fluorescence image of an entire trachea where multiciliated cells are labelled by Centrin-GFP. The distal, medial and proximal (D|M|P) segments of the organ, each one third, are indicated by white separation marks. The direction of fluid transport is D→P (lung→oral). Right: Magnification of region outlined by the white square. C. Fluorescence image of a section of the multiciliated epithelium. Vangl1 localizes to cell membranes. Fluorescently labelled Centrin and Centriolin mark individual basal bodies. The vector that connects Centriolin→Centrin defines the orientation of an individual cilium. Right: Magnification of region outlined by the white square. D. Heat map of the coverage fraction of multiciliated cells ($\overline{\phi }$). Right: Coverage fraction measured in circular non-overlapping windows of radius R, uniformly distributed along the trachea. $\langle \overline{\phi }\rangle$ is the average over all R and all tracheas imaged. E. Tissue scale orientation field obtained by averaging the orientation of cilia within each multiciliated cell shown in C. Right: Orientation of individual cilia shown in panel C. F. Probability density function of the number of cilia measured in 375 multiciliated cells. G. Plot of the spatial correlation function, S₂, of the pattern of multiciliated cells. Inset: Magnified region where the minima and maxima of S₂(R) occur. Triangles mark the minimum, which corresponds to the typical diameter of a cell ρ, while squares mark the maximum which corresponds to the wavelength of the patchwork pattern λ. H. Orientational order parameter m calculated for multiciliated cells (green) and tissue-scale orientational order parameter M (magenta). I. Spatial correlation function of the cellular scale orientation $O(r)=\langle P_j\cdot P_{j+r}\rangle$. The orientation of cilia in the jth cell is compared to the orientation in the cells that are at a distance less than or equal to r. Points show the measured values while solid line is the exponential fit.

To quantitatively map the airway architecture across these scales, we imaged transgenic mice expressing a fluorescently tagged version of Centrin (multiciliated cell, basal body specific marker). Along the distal-proximal (D-P, lung-oral) axis of the trachea, multiciliated cells cover only a fraction of the surface, corresponding to $\overline{\phi }=0.37\pm 0.02$, giving rise to a ‘patchwork’ pattern of regions with beating cilia and areas devoid of cilia (Fig. 1B; Fig.S1A). Multiciliated cells are distributed uniformly along the D-P axis, except at the cartilage rings where their coverage fraction decreases (Fig. 1D; Fig. S1A).

To characterise the structure of the multiciliated cell pattern, we calculated its spatial correlation function S₂(R) (Methods §2a). We extract two relevant length scales of the multiciliated cell pattern from this function: The characteristic diameter of a cell, $\rho =8.4\pm 1.7\mu \text{m}$ (the first local minimum of S₂), and the wavelength of the pattern, $\lambda =16\pm 3.8\mu \text{m}$ (the first local maximum), which corresponds to approximately two cell diameters (Figure 1G). Furthermore, by analysing time-lapse videos of living tissue (Suppl. Video 1) we confirm that the area fraction where cilia beat actively is indeed $\overline{\phi }=0.43\pm 0.05$. Similarly, the wavelength measured from live trachea imaging $\lambda =22.8\pm 3.9\mu \text{m}$, agrees with values obtained from fixed tissues (Fig. S1D, E; Methods §2b).

Each multiciliated cell is decorated with tens to hundreds of cilia (Fig. 1F) [21, 24]. Quantification of the number of basal bodies from images of fixed trachea segments (Fig. 1C; Methods §2c) showed that each multiciliated cell has on average $\langle N\rangle =169\pm 61$ cilia. We note that this number fluctuates between 20–350 cilia per cell (Fig. 1F).

Individual cilia beat with an asymmetric wave form that is confined to a plane [25, 26]. The direction of the active stoke of a cilium is determined by the relative orientation of the structures that anchor the cilium to the cell membrane. Thus, the beating plane of a cilium is defined uniquely by the relative orientation of the basal body [21], which in our experiments we marked by Centrin, and its basal foot, which we marked with Centriolin [27]. This polarity is established during organismal development through cytoskeletal rearrangements and hydrodynamic interactions, and becomes fixed at adulthood [20, 21, 28].

Therefore, to quantify the orientation of each cilium i, we establish its polarity unit vector p_i by connecting the relative positions of its Centrin and Centriolin puncta (Fig. 1E; right panel, green arrows; Fig. S1C; Methods §2c). Subsequently, to define the average orientation of cilia within a given cell, for each multiciliated cell j we average its cilia vectors an denote the cellular-scale polarity by the unit vector P_j (Fig. 1E; left panel, magenta arrows). From these vectors we observe that cilia exhibit significant fluctuations in their relative orientation, both across the tissue and within individual cells. These fluctuations are quantified by the order parameter, $m=\left|\langle p_i\rangle \right|$, analogous to magnetisation. We find an average order parameter of $\langle m\rangle =0.67\pm 0.2$, representing the orientational heterogeneity at the subcellular scale. At the tissue scale the order parameter is $M=\left|\langle P_j\rangle \right|$, where the average is taken over all cells in a field of view. Here, we find that $\langle M\rangle =0.80\pm 0.13$, with small variations across different tissue sections (Fig. 1H). To determine how the orientation of cilia varies across neighboring cells in the tissue, we compute the spatial correlation function, $O(r)=\langle P_j\cdot P_{j+r}\rangle$, where P_j is orientation vector of the jth cell and $P_{j+r}$ are the orientation vectors of all the cells found a distance less than or equal to r from the jth cell. (Fig. 1I; Methods §2c). Interestingly, this function decays to its minimum value with a characteristic length scale of r₀ = 12.2μm, which corresponds approximately to one cell diameter, showing that cells are only aligned with their immediate neighbors. However, since the correlation function does not decay to zero, all cells in the tissue are still correlated globally. Altogether, these results show that heterogeneity is a feature of the spatial organisation of airway cilia from the subcellular to the organ scale.

CILIARY FLOWS ARE GLOBALLY COHERENT BUT LOCALLY HETEROGENEOUS

Perfectly aligned and densely covered ciliary arrays will generate directed flows [29], but our results show that the trachea inherently features patchiness and misalignment (Fig. 1). In particular, this patchy architecture raises the key question of how particle transport is connected over regions devoid of cilia. Thus, we next investigated the flows generated by multiciliated cells in the trachea.

To monitor flow structure, fluorescent beads were added to the media as tracer particles. We find that flows across entire tracheas are coherent and globally directed along the D-P axis (Fig. 2A,C left panel; Fig. S2 A; Suppl. Video 2) with an average speed of (8.4±2.6)μm/s (Fig. 2E). However, at a scale comparable to the wavelength of the multiciliated cell “patchwork” pattern, λ = 16±3.8μm, we observe variations in the local flow direction and magnitude (Figure 2A,C right panel; Fig. S2B; Suppl. Video 3). Specifically, we see connected regions with stronger flow, separated by regions of weaker flows. To quantify the structure of these currents we calculate the spatial, $\delta C_{vv}(R)$, and temporal $\delta C_{vv}(\tau )$ correlations (see Methods §2d). For each of our measurements, $\delta C_{vv}(R)$ decays exponentially over 30μm and can be fitted well in this range by an exponential with an oscillatory component, $\delta C_{vv}(R)=A{e}^{\left(-R/R_0\right)}\cos (wR)+\kappa$ (Fig. S2F), which defines the correlation length R₀. Thus, the domain size of correlated flow is R₀ = (14.6 ± 6.4)μm (Fig. 2H), which is comparable to the wavelength λ of the multiciliate cell pattern. Moreover, the timescale of temporal decorrelation, τ = (0.019±0.01)s (see Methods §2d) is on the same order of magnitude as the timescale of the cilia beat frequency, CBF = (11.8 ± 2.3)Hz (Fig. S2C, D; Suppl. Video 4). Therefore, the spatiotemporal flow structure coincides with the spatiotemporal organisation of the heterogeneous ciliary carpet.

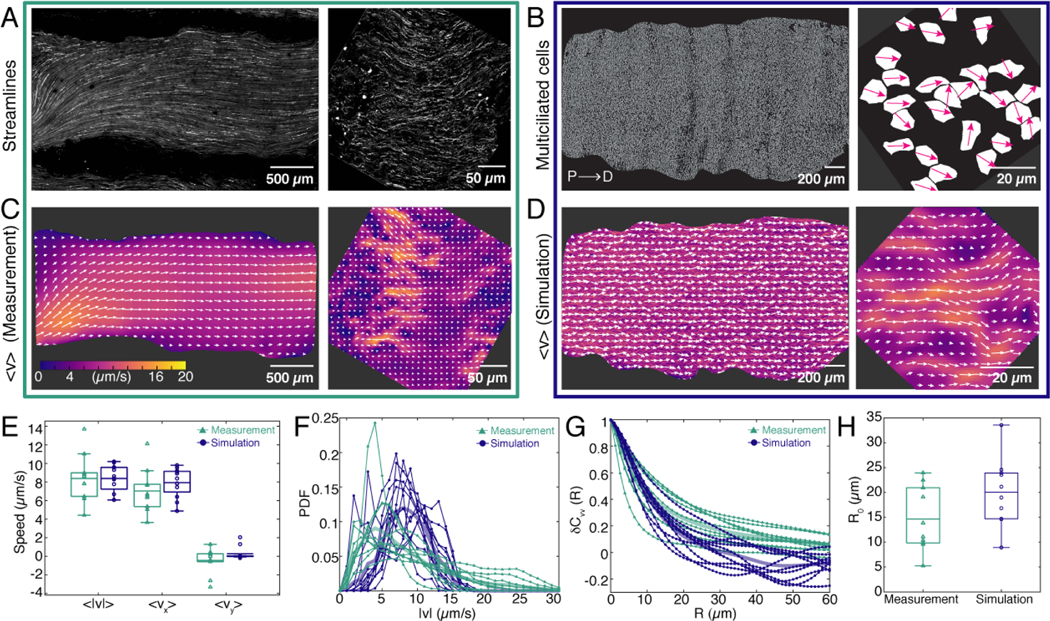
FIG. 2. Measurements of ciliary flows at the tissue and cellular scales.

A. Pathlines of the flow generated by multiciliated cells across the entire trachea (left). Right: Pathlines of the flow visualized at a scale comparable to the wavelength of the cilia patchwork pattern. B. Binary images obtained from thresholding the images of multiciliated cell localization shown in Fig. 1B,C (left panels). White regions represent multiciliated cells. Right: Magenta arrows show the average orientation of cilia within each multiciliated cell measured from Fig. 1C. These coverage and orientation fields are used as input for the model, shown in panel D. C. Representative experimental flow fields measured at the scale of the entire trachea (left) and with micrometer resolution (right). Colours show the flow velocity magnitude and white arrows indicate the streamlines. D. Simulated flow fields, using the experimental data of panel B as an input.Colours show the flow velocity magnitude and white arrows indicate the streamlines. E. Comparison of flow speeds between experiment (green) and model (blue). The majority comes from the x component. Boxplot central mark indicates the mean, and the bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. F. Comparison of the flow magnitude distribution, PDF $(\langle |v|\rangle )$, between experiment and model. Thin lines show the PDF from a field of view of the size shown in C,D (right). Thick lines are the average of all flow fields analyzed. G. Comparison of the spatial autocorrelation function between experiment and model. Thin lines show measurements from a field of view of the size shown in C,D (right). H. Comparison of correlation length R₀ from the experiment, $\langle R_0\rangle =(14.6\pm 6.4)\mu \text{m}$, and from the simulation, $\langle R_0\rangle =(20\pm 6.8)\mu \text{m}$.

To understand how globally directed flows emerge from micron-scale fluctuations, we develop a hydrodynamic model inspired by the ‘envelope approach’ introduced by Lighthill and Blake (see Methods §3). Using a computational fluid dynamics (CFD) solver, we simulate the ciliary flows of the liquid film covering the epithelium (Fig. 3A). As boundary condition input, we use the experimentally measured global and local tissue configurations (Fig. 2B). Specifically, the multiciliated cells are represented by a slip velocity U imposed at the tissue surface, while a no-slip condition is set in the absence of cilia. Hence, we compute the 3D flow structure at different scales.

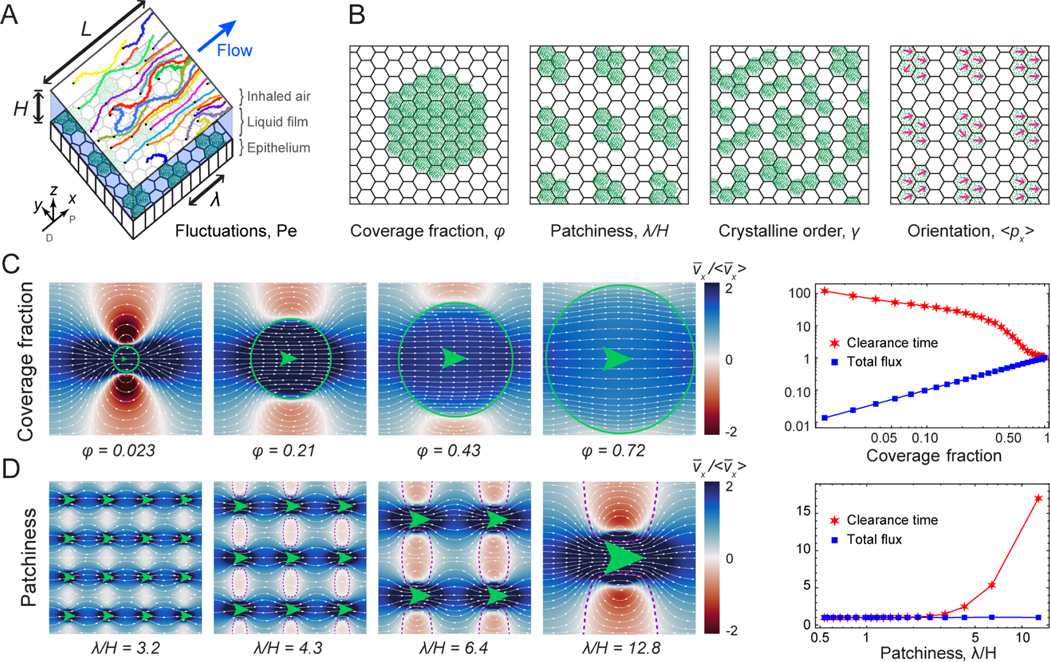
FIG. 3. Hydrodynamic model for particle flux and clearance.

A. Diagram of simulation geometry. A pattern of multiciliated cells (green) drives a liquid film flow (blue) in a 3D computational fluid dynamics (CFD) simulation with periodic boundary conditions in x and y. Particle trajectories with random initial positions are subject to this flow and fluctuations. B. Total flux and clearance times are examined as a function of ciliary organisation, characterised by the coverage fraction φ, wavelength λ, crystallinity γ, and orientation order $\langle p_x\rangle$. C. Higher coverage fractions improve clearance. Left: Shown are streamlines (white) and the longitudinal flow strength (red-blue) as a function of coverage fraction $\phi$. Green circles indicate the area covered by cilia and green arrows their orientation. Right: Corresponding plot of clearance time and total flux, normalised with respect to full coverage, showing the mean of an ensemble of N_p = 10⁴ particle trajectories. D. Patchiness induces recirculation and slows clearance. Left: Flows as a function of wavelength λ. Dashed purple lines are separatrix streamlines that isolate recirculation zones (red) from the main currents (blue). Right: Corresponding clearance time and flux, normalised with respect to uniform coverage, again averaged over N_p = 10⁴ particle trajectories.

In agreement with our experiments, the simulated flows also show globally coherent currents directed across the trachea, but at the micrometer scale we see heterogeneity in the magnitude and direction of the flows (Fig. 2D). Comparison of the statistical properties of simulated and measured flows shows that the flow velocity distributions and their correlation lengths also agree, establishing the validity of our model (Fig. 2E-H).

FLOW STRUCTURE IS DETERMINED BY MULTICILIATED CELL ARCHITECTURE

Importantly, our measurements of the flow generated by multiciliated cells in the trachea show that complete orientational order and coverage are not a requirement for a ciliary carpet to generate directed fluid flows. However, it is unclear how much variability in multiciliated cell configuration can be tolerated before fluid transport is impaired. Therefore, we next use our model to uncover how controlled changes in the spatial distribution of multiciliated cells impact the properties of the flow they generate (Fig. 3A,B).

We explore systematically how total flux and particle clearance time change as a function of variations in multiciliated cell coverage fraction, wavelength, and orientational and geometrical order. The total flux $J=\int v_{x}dydz$ measures the strength of the flow υ(r) globally. To account for the local flow microstructure, we compute the mean first passage time $\langle T\rangle$ taken to travel a distance L along x for an ensemble of particles advected by the flow (See Methods §3d). These particles could represent viruses, bacteria or other pathogens that are cleared by the ciliary carpet. This first passage time is a measure of streamline connectivity, thus flow topology, rather than only flow strength.

First, we test the role of coverage fraction on flow architecture. We observe that the total flux generated by the ciliary carpet increases linearly with coverage fraction (Fig. 3C, right panel). In the limit of low coverage ($\phi \to 0$) the flow structure features recirculating eddies, approaching the Stokeslet flow due to a point force confined in a liquid film (see Methods §3a). As the coverage fraction grows, regions of negative flux disappear and in the limit $\phi \to 1$ a uniform flow is recovered. Consequently, the clearance time (red stars) increases at low $\phi$, as expected, but not linearly. A reduction of coverage therefore strongly impacts flow strength.

We then vary the periodicity of the multiciliated cell pattern. We define the “patchiness” as the dimensionless number λ/H, where λ is the wavelength of the multiciliated cell pattern and H is the height of the fluid film. We keep the coverage fraction and film height constant, distributing the same amount of multiciliated cells in clusters of different sizes (green arrows), varying only the wavelength λ (Fig. 3D). The total flux J is constant for all configurations, because the total force exerted on the liquid is the same. However, the streamline structure changes as a function of multiciliated cell arrangement. For large patchiness, recirculating eddies emerge that create zones where particles are trapped in closed streamline orbits (dashed purple separatrices). However, when cells are distributed more homogeneously, these zones disappear and consequently clearance times are reduced (Fig. 3D). We note that the emergence of recirculation zones can be tuned independently by reducing the film height. Therefore, higher patchiness caused either by dehydration of the liquid film or long wavelengths leads to impaired clearance.

DISORDER CAN ENHANCE PARTICLE TRANSPORT

Having examined how deterministic parameters of multiciliated cell organisation influence flow structure, we now analyse the impact of introducing disorder in these ciliary arrays. Surprisingly, we find that different types of disorder can improve clearance.

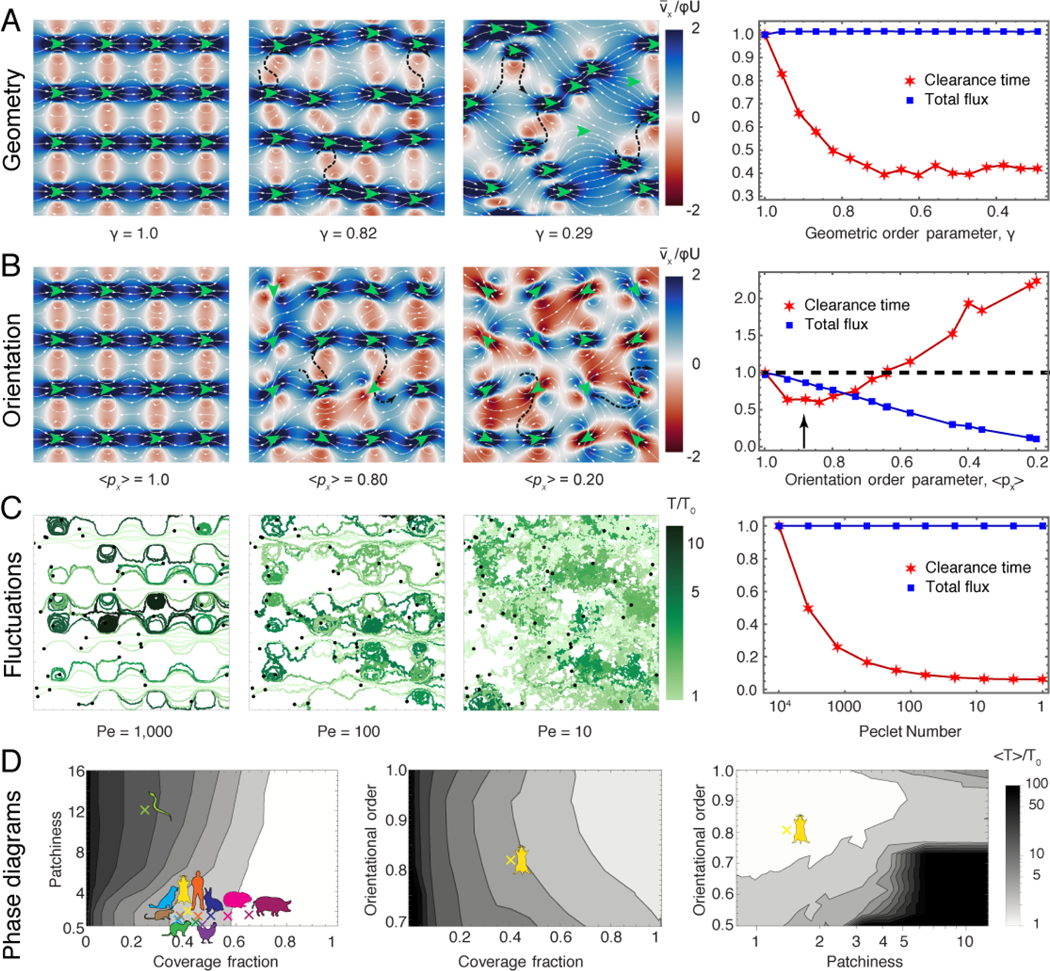
In the trachea, patches of multiciliated cells lack crystalline order (Fig. 1B,D). We introduce this geometric heterogeneity by shifting the positions of ciliated patches along x and y with standard deviation σ. Thus, geometric heterogeneity is described by the order parameter $\gamma =1-\frac{\sigma \sqrt{2}}{\lambda }$, the crystallinity. The resulting flows (Fig. 4A) again feature a constant total flux but, importantly, the geometric disorder breaks open the closed orbits, causing streamlines to cut through the recirculation zones (black dashed streamlines), and strongly reducing clearance time 〈T〉.

FIG. 4. Disorder improves clearance in heterogeneous epithelia.

A. Left: Flow strength along the D-P axis (red-blue) and streamlines (white) as a function of crystallinity γ. Green arrows indicate the position and orientation of the cilia patches. A few typical (black dashed) streamlines are shown to cross through recirculation areas. Right: Corresponding total flux and clearance time, normalised with respect to crystalline order. N_p = 10³ particle trajectories. B. Flow and clearance as a function of cilia orientational order $\langle p_x\rangle$. Same as (A) otherwise. C. Left: Particle trajectories subject to flow and diffusion for a range of Péclet numbers, $\text{Pé}=\lambda \phi U/D$. Right: Corresponding total flux and clearance time, normalised with respect to weak fluctuations. N_p = 10⁴ particle trajectories. D. Phase diagrams showing clearance time (grey scale, defined in legend) for the combinations of $(\phi ,\lambda /H,M)$, with constant M = 1, λ/H = 8 and $\phi =0.4$, respectively. The mouse cartoon indicates the measurements for the mouse epithelium. Other coloured cartoons on the first panel show values of patchiness and coverage fraction measured for several different animals, from data available in the literature (See Methods §2g and Figure S7).

Next, we examine disorder in the cilia orientations (Fig. 1H), by varying the orientational order parameter $\langle p_x\rangle =M$ (Fig. 4B). The total flux is no longer conserved and decreases with orientational noise. Interestingly, we observe a biphasic behaviour in clearance time: for weakly misaligned cilia the recirculation zones are broken up and the clearance time is reduced, yet, the clearance time increases for strong misalignment. We predict an optimum around M = 0.89 ± 0.06 (black arrow). Looking back at measured values, M = 0.81±0.12 (Fig. 1H), we see that the mouse tracheas occupy the same region in this parameter space.

Finally, we study the effect of diffusion, D, which can be due to thermal or ciliary beating noise (Suppl. Video 5). To understand how diffusion impacts particle clearance, we compare the advection time ${\tau }_a=\lambda /(\phi U)$ with the diffusion time ${\tau }_d={\lambda }^2/D$ required for particles to escape eddies of size $\epsilon \sim \lambda$. The ratio of these times defines the Péclet number, $\text{Pé}={\tau }_d/{\tau }_a=\phi \lambda U/D$, and their sum gives the mean clearance time, $\langle T\rangle \sim {\tau }_d+{\tau }_a$. Therefore, with weak fluctuations ($\text{Pé}\gg 1$) the particles remain stuck in closed orbits (Fig. 4C, left), but strong diffusion (${\tau }_d\to 0$) reduces clearance times by helping particles escape, and connecting regions of closed streamlines (Fig. 4C, right). We note that diffusion only reduces clearance time in carpets with closed eddies, e.g. at high patchiness, since τ_d = 0 for all values of Pé in the absence of recirculation zones.

To verify the robustness of these results, we extended our simulations to a non-Newtonian fluid with a shear-dependent viscosity (see Methods §3g and Fig. S5), and we also control for different ciliary array cell structures (see Methods §3h and Fig. S6). Closed streamline areas still appear at high patchiness, both in shear-thinning and shear-thickening fluids, leading to long clearance times due to particle recirculation. We find that for these flow structures clearance can still be reduced by disorder.

To cast our results in a broader context, we map the phase space of clearance times in terms of ciliary organisation (Fig. 4D). First, we observe that for a large range of coverage fractions ($\phi \gtrsim 0.58$) the clearance time is minimal. Surprisingly, the mouse airway operates below this ideal regime, but its low patchiness and moderate disorder in cilia orientation still allow for clearance times to be relatively small. This observation raises the question whether airway tissues from other animals have similar, sub-optimal, coverage fractions. A brief literature survey showed that different species have similar coverage fractions and patchiness (Figure S7), clustering in the same region of phase diagram as the mouse (Figure 4). Snakes form an exception, potentially because of their unique trachea morphology. Given that patchiness is conserved among organisms with drastically different trachea length, we conjecture that maintaining this number fixed among different species provides an effective mechanism for clearance. However, further studies comparing the morphology of tracheas in large sets of images for every species will be required to understand whether this design principle is universal.

DISCUSSION

Our work establishes a quantitative link between the topology of the flow generated by a ciliary array and its underlying spatial organisation. We investigate the arrangement of cilia and their associated flow generation, from the molecular to the organ scale, in the mouse conductive airway. Using a hydrodynamic model, we explore the effect of varying ciliary arrangements on flow structure. We find that while patchiness due to spatial constraints generally reduces streamline connectivity, a moderate amount of disorder can enhance particle clearance. This beneficial disorder can arise from heterogeneity in ciliary arrangement, ranging from the patterning and alignment of individual cilia, up to the arrangement of multiciliated cells in the entire trachea. Similarly, thermal noise and fluctuations in cilia activity including enhanced diffusion due to flows near beating cilia [30] could decrease the effective Péclet number and hence reduce clearance times. Therefore, particle clearance in the airway is not necessarily proportional to the overall liquid flux, but rather set by streamline connectivity.

Even if surprising, it is not uncommon in physical and biological systems that ‘noise’ can prove advantageous, a concept sometimes referred to as stochastic resonance (SR) [13–15]. In these systems noise levels are initially beneficial but often only up to a point, the resonance peak, after which more fluctuations become unfavourable [13]. The organisation of cilia should be understood in this context of trade-offs in self-assembled systems. Indeed, across diverse physiological contexts, disorder in the spatio-temporal organisation of cilia can be harnessed to optimise their biological function. For example, dynamic switches in beating patterns modulate the transport of cerebrospinal fluid [31], length differences can create hydrodynamic microhabitats [32], and topological defects can enhance feeding in starfish larvae [16] and attract nutrients to active carpets [17].

However, disorder can also be detrimental to physiology, as reduced ciliary coverage and alignment are a hallmark of airway pathologies [33, 34]. Our phase diagrams (Fig. 4D) provide a framework to understand how much heterogeneity can be tolerated before clearance times increase beyond a critical value. Understanding the link between ciliary organisation and flow structure could open up new avenues for diagnostics and therapies for airway pathologies.

Beyond understanding airway physiology, our phase diagrams (Fig. 4D) prescribe the design principles for synthetic active carpets. This could open new doors to fabricate active surfaces that drive fluid flows with programmable and adaptive topologies, with diverse engineering applications including microseparation and cellular rheometry.

MATERIALS AND METHODS

1. Tissue imaging

a. Mouse husbandry

Arl13b-mCherry; Centrin2-GFP (JAX 027967,[35]) were maintained in FVB/N background. This mouse strain was used for all imaging performed, unless otherwise stated. Mice imaged were of a stage>p15, to ensure ciliary development was complete and patterning of multiciliated cells and cilia was fixed [22]. Mice were housed in an animal facility and maintained in a temperature-controlled and light-controlled environment with an alternating 12-h light/dark cycle. A maximum of five mice were housed per cage. Mice were euthanized by cervical dislocation. All protocols were approved by the University of California San Francisco Institutional Animal Care and Use Committee.

b. Tissue staining

After euthanasia, tracheas (segments C1-C10 or C1-C12) were dissected from mice and placed in ice cold Dulbecco’s Modified Eagle Medium: Nutrient Mixture F-12 (DMEM/F12, Invitrogen). Tracheas processed for basal body staining were cut into segments of 2–3 rings, while tracheas processed for multiciliated cell imaging were left intact lengthwise. Tissues were sliced open along the proximal-distal axis and fixed and stained as follows.

Dissected tissue was fixed with ice cold methanol for 10 minutes. After fixation samples were washed 3 times (5–10 minutes each) and blocked (30–60 minutes) with IF buffer (1x PBS with 1% heat-inactivated goat/donkey serum and 0.3% Triton X-100). Primary antibodies were added and incubated for 1 hour at room temperature or overnight at 4 °C. Primary antibodies used for trachea segments were: mouse monoclonal anti-Centriolin (Santa Cruz: sc-365521; 1:500 dilution) and rabbit anti-Vangl1 (Sigma: HPA025235; 1:1000 dilution). After incubation with primary antibody samples were washed 3 times (5–30 minutes each) and incubated in secondary antibody for 1 hour. Secondary antibodies used were: Alexa Fluor conjugated 594-goat anti-rabbit and 633-donkey anti-mouse (Invitrogen; 1:1000 dilution). Samples were washed with 1x PBS and mounted with Fluoromount-G (SouthernBiotech).

c. Microscopy and live-tissue imaging

Multiciliated cell imaging:

Whole-mount fixed trachea samples stained with E-Cadherin, were imaged using a Zeiss LSM 780 laser scanning confocal microscope and a 20X Plan Apo NA 0.8 air objective (Stanford Cell Sciences Imaging Facility). Tracheas were imaged using the tile scan and z-stack image acquisition functions in the Zeiss zen software (Zen 2.3 SP1, Carl Zeiss Microscopy). Individual tiles acquired had dimensions of 1024×1024 pixels (425.1μmx421.1μm). For each tile a z-stack with 50–70 μm (20–40 slices) in thickness was acquired. Overlap between tiles acquired was 10% of their area.

Basal body imaging:

Fixed trachea segments stained with Centriolin and Vangl1 antibodies were imaged using a Zeiss LSM 880 laser scanning confocal equipped with Airyscan and 40X Plan Neo NA 1.3 oil immersion objective (Gladstone Institutes Histology and Microscopy Core). Images were acquired using the superresolution mode and had dimensions of 1584×1584 pixels (67.48μmx67.48μm). For each image a z-stack with 5–10 μm (5–12 slices) in thickness was acquired.

Flow imaging:

After euthanasia, tracheas (segments C1-C12) were dissected from mice and placed in ice cold DMEM/F12 media. Tracheas used for local flow imaging were cut into segments of 2–3 rings, while tracheas used for global flow imaging were left intact lengthwise. In all cases tissues were sliced open along the proximal-distal axis. Prior to imaging samples were kept on ice (30–60 minutes) and mounted for imaging as follows.

Tracheas were mounted on a 35mm glass bottom dish (MatTek, Part No:P35G-0.170–14-C). Two strips of parafilm were attached to the bottom of the dish to serve as spacers. A single trachea was placed between the parafilm strips in a ∼ 500μl drop of live imaging media. The trachea was mounted with its multiciliated surface facing the glass bottom. An 18mm round coverslip was placed on top of the trachea to bring its multiciliated surface closer to the glass and enable imaging. The live imaging media consisted of DMEM/F-12 with fluorescent beads (2 or 0.5 μm diameter; FluoSpheres Invitrogen, Carboxylate-modified Microspheres; 1:250 to 1:500 dilution). The imaging plane was chosen as close to the tips of the cilia as possible.

Imaging was performed in an environmental chamber with temperature control (5% CO₂ at 36 °C; Okolab) with an inverted microscope (Ti-E;Nikon). Samples were allowed to equilibrate 5 minutes before imaging. The microscope was equipped with a confocal scan head (Andor Borealis CSU-W1), laser merge module containing 405-,488-, 561-, and 640-nm laser lines (Andor 4-line laser launch) and Zyla 4.2 sCMOS camera (Andor, Oxford Instruments; Active pixels: 2048 × 2048; Pixel size: 6.5×6.5 μm). Global flows were imaged using a 4X Plan Apo NA 0.2 dry objective, while local flows were imaged with a 40X Plan Apo LWD NA 1.5 water immersion objective.

Images acquired had dimensions of 2048×2048 pixels. Global flow images were captured at 1 frame per second, while local flow images were recorded at 18–30 frames per second.

Cilia live imaging:

After euthanasia, tracheas (segments C1-C12) were dissected from mice and placed in ice cold DMEM/F12 media. Tracheas were kept on ice 30–60 minutes before imaging. Right before imaging tracheas were cut into segments of 2–3 rings and sliced open along the proximal-distal axis.

For live imaging tissue pieces were mounted on a 35mm glass bottom dish (MatTek, Part No:P35G-0.170–14-C). Two strips of parafilm were attached to the bottom of the dish to serve as spacers. Two-three tissue pieces were placed between the parafilm strips in a ∼ 500μl drop of DMEM/F12 media. Trachea fragments were mounted with their multiciliated surface facing the glass bottom. An 18mm round coverslip was placed on top of the trachea fragments to bring the multiciliated cell surface closer to the glass and enable imaging.

Imaging was performed in an environmental chamber (5% CO₂ at 36 °C; Okolab) with an inverted microscope (Ti-E; Nikon). Samples were allowed to equilibrate 5 minutes before imaging. The microscope was equipped with a light source (Sutter XL lamp), DIC optics and ORCA-Flash4.0 V2 camera (Hamamatsu; Active pixels: 2048×2048; Pixel size: 6.5×6.5 μm). Cilia were imaged using DIC optics with a 40X DIC Plan Apo LWD NA 1.5 water immersion and 60X DIC Plan Apo VC NA 1.4 Oil immersion objectives. Images acquired had dimensions of 2048×2048 pixels and were captured at a frequency>100 frames per second.

2. Image analysis

Calculations were performed in MATLAB using custom built code unless otherwise stated.

a. Measurement of cilia coverage fraction and wavelength from fixed samples

Coverage fraction and wavelength were measured from 2D binarized images of the entire trachea surface as the one shown in Figure S1B. The raw data from which these images were obtained was collected as described in §1c (Multiciliated cell imaging). Binarized images were assembled from the raw data as follows.

First, the maximum intensity projection of the z-stack collected for each tile was calculated. Maximum intensity projections of all the tiles from a trachea were stitched together using the ImageJ [36] “Stitching” plugin [37], yielding an image as the one shown in S1A.

Next, a bandpass filter was applied to stitched image to reduce noise. The filtered image was then binarized using the “imbinarize” function in matlab. “Imbinarize” computes a threshold for each pixel using the local mean intensity around the neighborhood of each pixel (Bradley’s method). The sensitivity factor for the adaptive threshold can have values in the range [0,1]. A high sensitivity value leads to thresholding more pixels as foreground at the risk of including some background pixels. We chose a value of 0.99 since the spatial filtering was effective in discriminating the background from the signal. Visual inspection showed that the threshold was accurate at identifying multiciliated cells. However, the high value of sensitivity used introduced isolated white pixels that did not correspond to multiciliated cells. To remove these artifacts, objects with areas smaller than 30 pixels were excluded from the final binarized image (for reference a typical multiciliated cell is composed of ∼90 pixels). All binarized images were further inspected manually to validate the thresholding. Figure S1B shows the binarized image obtained by applying this procedure to the image shown in figure 1B.

Finally, we note that a mask was used to exclude from the coverage fraction and wavelength calculations the pixels at the edge of each stitched trachea image. These edge pixels are not part of the trachea. All masks were drawn manually.

Coverage fraction measurement:

Each binarized trachea image is described by the function:

$$I(r)=\left\{\begin{array}{ll}1,& \text{if}r\in \text{Multiciliated cell}\\ 0,& \text{otherwise}\end{array}\right.$$ (M1)

where $r_i=\left(x_i,y_i\right)$ is the position of the i-th pixel of the 2D image.

To measure the coverage fraction we compute $\langle I(r)\rangle$ in N circular non-overlapping regions of the image. These regions are distributed uniformly over the entire image. Therefore, the average coverage fraction for a given trachea image is defined as:

$$\overline{\phi }(R)=\frac{1}{N}\sum _{i=1}^N\langle I\left(r_i\right)\rangle$$ (M2)

where the average is taken over all the points in the circle of radius R centered at r_i. The coverage fraction $\langle I\left(r_i\right)\rangle$ depends on the center, r_i and the radius, R, of the region considered. The window centers are fixed for all R and are chosen such that for the maximum value of R (200 pixels), the entire circle is contained inside the image.

Wavelength measurement:

To measure the wavelength of the pattern, λ, we compute the spatial correlation function of I.

The spatial correlation function of a rectangular image, I, with size mxn is defined as:

$${\widehat{S}}_2(R)=\langle I(\text{r})I(\text{r}+R)\rangle$$ (M3)

A discretized version of this equation is:

$${\widehat{S}}_2(x,y)=\frac{1}{N_2}\sum _{i=1}^{i_{\max }}\sum _{j=1}^{j_{\max }}I(i,j)I(i+x,j+y)$$ (M4)

where $i_{max}=m-i$, $j_{max}=n-j$ and $N_2=i_{max}\times j_{max}$.

Given this two-dimensional function ${\widehat{S}}_2(x,y)$ we obtain the one dimensional isotropic correlation function $S_2(R)$ by averaging over the ${\widehat{S}}_2(x,y)$ values at a fixed radius R.

We extract two relevant length scales of the multiciliated cell pattern from this function. The first local minimum of S₂ occurs at the characteristic size of a cell, ρ. While, the first local maximum of S₂ corresponds to the wavelength of the pattern, λ. Figure 1G shows a plot of S₂ for all tracheas analysed. The triangles mark first local minima of S₂, which correspond to ρ, while the square symbols mark the first local maxima, corresponding to λ.

b. Measurement of cilia coverage fraction and wavelength from live samples

Coverage fraction and wavelength were measured from 2D binarized images where regions with white pixels correspond to regions of cilia activity (See figure S1D). The raw data from which these images were obtained was collected as described in §1c (Cilia live imaging). Binarized images were obtained from the raw data as follows. The median intensity projection of each image stack was calculated. Subsequently, the median image was substracted from each frame of the original stack. From this resulting stack a maximum intensity projection was obtained. The maximum intensity projection was binarized in ImageJ using the default threshold. This method allowed for identification of regions where pixel values fluctuate due to ciliary beating, rendering a binarized image where the white pixels correspond to regions of cilia activity. Images were inspected manually to verify that only regions where cilia activity was observed were included.

The coverage fraction, $\overline{\phi }$, was calculated from binarized images according to equation M2. To obtain the wavelength, λ, we computed the correlation function defined in equation M3. From this function we extracted the wavelength, λ, by determining its first local maximum. Figure S1E shows a plot of S₂ for all the fields of view analysed. The squares mark the first local maximum of S₂, which corresponds to λ.

c. Analysis of number and orientation of cilia

The number and orientation of cilia was measured from maximum intensity projections of Centrin and Centriolin image z-stacks. Figure S1C shows an example of such images. The raw data from which the maximum intensity projection was obtained was collected as described in §1c (Basal body imaging).

Cilia quantification: The boundary of each cell was traced manually from Vangl1 staining. Each cilium extends from a single basal body, therefore the number of cilia in a cell corresponds to the number of basal bodies in a cell. Centrin-GFP images were analysed to identify individual basal bodies as follows. First, images were filtered using a bandpass filter. The center of bright puncta that corresponded to basal bodies was identified with subpixel resolution based on local maximum intensity and size. Basal bodies were binned by cell and counted to obtain the number of cilia in each cell. Figure 1F shows a histogram of the number of cilia per cell counted from 375 cells.

Cilia orientation measurement: The orientation of a cilium is defined by the unit vector, p_i that connects each basal body (marked by Centrin) with its corresponding basal foot (marked by Centriolin). For a pair of Centrin and Centriolin images, the orientation of each cilium was obtained as follows.

First, the center of each basal body was identified from the Centrin-GFP image as described in the previous section. The image was then binned in windows of 80×80 pixels centered around every identified basal body. The same windows were identified in the Centriolin image. For each pair of Centrin-Centriolin windows, the 2D crosscorrelation function of the images was calculated for all possible directions. The orientation of a cilium, p_i was defined as the direction where the crosscorrelation between Centrin and Centriolin windows was maximum (For an illustration of this see Figure S1C). Prior to computing the crosscorrelation, each image window was processed by substracting its mean and multiplying it by a gaussian kernel of size 80×80 pixels and standard deviation 20.

In some cases Centriolin staining was weak, and the analysis yielded a spurious direction. To correct for this, orientation vectors were filtered by calculating the maximum to mean ratio of each window. Vectors obtained from windows with a maximum to mean ratio less than 40 were excluded from further calculations. Once the orientations of all cilia, p_i, in an image were obtained, their organisation was measured as follows.

To measure the cellular-scale organisation, we define the order parameter, m:

$$m=\left|\langle p_i\rangle \right|$$ (M5)

where p_i is the unit vector that describes the orientation of the i-th cilium in a cell. The average is taken over all cilia in a cell. Values of m for all cells analysed are shown in Figure 1H (cell).

To measure tissue-scale cilia organisation we assign an orientation to each cell defined by:

$$P=\langle p_i\rangle$$ (M6)

Thus P is a unit vector obtained by averaging the unit orientation vectors of all cilia within a cell. The tissue-scale organisation of cilia is then measured by calculating the order parameter, M, according to:

$$M=\left|\langle P_j\rangle \right|,$$ (M7)

where the average is calculated over all the cells in a field of view. All fields of view analysed have dimensions of 1584×1584 pixels and contain ∼ 35 multiciliated cells. All values obtained are shown in Figure 1H (Tissue).

To determine how the orientation of cilia varies across neighboring cells in the tissue, we compute the spatial correlation function of P defined as:

$$O(r)=\langle P_j\cdot P_{j+r}\rangle$$ (M8)

where P_j is the average orientation of cilia in the jth cell as defined by M6 and $P_{j+r}$ is the average orientation of cilia in the cells at a distance less than or equal to r. The average is taken over the polarity vectors that correspond to all multiciliated cells in an image. This function is well approximated by an exponential decay of the form $O=0.32e^{-n/r_0}+0.68$ where $r_0=12.2\mu \text{m}$. While the orientation of cilia decays with a characteristic length scale of $r_0=1.13$ cells, we note that O decays to a constant value of 0.68, showing that orientation of cilia in cells remains highly correlated over the entire field of view.

d. Analysis of flows

Flow fields were measured from time-lapse imaging of tissues with tracer particles. The raw data was collected as described in §1c (Flow imaging). Particle Image Velocimetry (PIV) fields were generated using “mpiv” [38]. Field parameters were optimized based on bead dilution used in flow field visualization experiments, and then held constant across all analyses to reduce systematic errors due to inconsistent discretization. Parameters used are given in table I.

TABLE I.

Parameters used for PIV analysis

PIV type	‘MQD’
Window size	128
Window overlap	0.5
Iterations	4

Using these parameters a velocity vector is obtained every 8 pixels (in the x and y directions). Therefore, the typical number of velocity vectors per field of view was ∼ 50,000. Velocity fields were filtered using a standard filter and interpolated spatially using Kriging interpolation. Filtering and interpolation were done with “mpiv_filter” [38].

To calculate the speed of the flow, velocity fields were averaged temporally. For images captured with a 4X objective temporal averaging= 5 minutes and time step=1 second. For images captured at 40X magnification, temporal averaging= 1 second and time step=0.3–0.13 seconds. Probability density functions (PDFs) of the the velocity vectors of the time averaged fields were obtained (Figure 2F). From these PDFs the average speed, and the average values of the x (υ_x) and y (υ_y) components of the velocity were calculated (Figure 2E). To assign units to the simulated data, the average speed for all simulated flows was matched to the average speed in ten flow fields measured (Figure 2F).

To characterise the temporal and spatial structure of the flow we calculated the spatial and temporal autocorrelations of the velocity.

To calculate the spatial autocorrelation we first average temporally the velocity fields for a time interval of 1 second (16–18 frames) and use this time averaged field, $\overline{v}$. Since we are interested in understanding flow fluctuations, we subtract the spatial average from the velocity field, $\langle \overline{v}\rangle$, and autocorrelate the velocity fluctuation field, defined as $\delta \overline{v}=\overline{v}-\langle \overline{v}\rangle$. Given that we substract the mean velocity vector of the field, we expected that an isotropic autocorrelation function, defined as:

$$\delta C_{vv}(R)=\frac{\langle \sum _i\delta \overline{v}\left(r_i\right)\cdot \delta \overline{v}\left(r_i+R\right)\rangle }{\langle \sum _i\delta {\overline{v}}_i\left(r_i\right)\cdot \delta \overline{v}\left(r_i\right)\rangle }$$ (M9)

will be appropriate to describe the structure of the flow. Here, $\delta \overline{v}\left(r_i\right)$ is the velocity fluctuation vector at position r_i and $\delta \overline{v}\left(r_i+R\right)$ is the velocity fluctuation vector at the point $r_i+R$. The sum is taken over all velocity fluctuation vectors in the field of view and the angle brackets indicate averaging over all directions. We first calculate the autocorrelation, as defined by equation M9, but without performing the spatial averaging, i.e. $\delta C_{vv}(R)$, where $R=x{\widehat{e}}_x+y{\widehat{e}}_y$. This two dimensional function is isotropic (Fig. S2E, left panel), thus we confirm that the isotropic autocorrelation function, $\delta C_{vv}(R)$, defined by equation M9 is appropriate to describe the spatial structure of the flow.

To obtain the correlation length R₀, we fit an exponential function of the form: $\delta C_{vv}(R)=A{e}^{-R/R_0}cos(wR)+\kappa$, to δC_vv(R), where w, A and κ are fit constants with the constraint $\text{A}+\kappa =1$, due to the normalization of the autocorrelation function.

To calculate the temporal correlation length we compute the temporal autocorrelation function of the velocity fluctuation field $\delta v_i=v\left(r_i\right)-\langle v\rangle$ where $\langle v\rangle$ is the spatial average velocity vector at each time point t. The temporal autocorrelation function is defined as:

$$\delta C_{vv}(\tau )=\frac{\langle \sum _i\delta v_i(t)\cdot \delta v_i(t+\tau )\rangle }{\langle \sum _i\delta v_i(t)\cdot \delta v_i(t)\rangle }$$ (M10)

In this case the angle brackets indicate averaging over different starting time points t. This function is well fitted by a decaying exponential function with an oscillatory component of the form:

$$\delta C_{vv}(\tau )=A{e}^{-\tau /{\tau }_0}cos(\omega \tau )+\kappa$$ (M11)

where the temporal correlation length is given by τ₀ and A, κ and ω are fit constants bluewith the constraint $\text{A}+\kappa =1$, due to the normalization of the autocorrelation function.

e. Analysis of ciliary beating

The cilia beat frequency and wave velocity were measured from time-lapse imaging of ciliary beating with a temporal resolution of 250–350 frames per second. This data was obtained as described in §1c (Cilia live imaging).

Kymographs were obtained for lines drawn parallel or perpendicular to cilia in an image (Figure S2E). Lines were drawn along traces in the kymograph that correspond to cilia beat cycles. The slope of these lines was averaged over all lines in a kymograph, yielding a measurement of cilia beat frequency (parallel to cilium, blue line) or group wave velocity (perpendicular to cilium, green line).

f. Size of all images analysed in this paper

The maximum size of the field of view for every camera used is given in section §1c. Table II lists the size of all regions of interest analyzed in this paper. For basal body imaging twelve fields of view of the size specified in the table were analysed. For cilia live imaging 60X, seven fields of view of the size specified in the table were analysed. All sizes are given in pixels.

TABLE II.

Size of all images analyzed. All sizes are given in pixels.

Multiciliated cells	Basal Body	Flow		Cilia Live
12983×5312		4X	40X	40X	60X
7788×6864 6688×4080 8000×7088	1584×1584	1215×936 2048×1302 2048×1431 2048×1674 2048×1404	2048×1022 2048×1022 2048×2048 2048×2048 2048×2048 2048×2048 1024×1024 1482×1405 2048×2048 2048×2048	1095×2044 1088×406 994×1022 2048×2044 2048×2044 2048×2044 926×2042 1354×2042 1245×1088 2048×2048	1494×286

g. Literature survey of patchiness and coverage fraction

We conducted a literature survey to find images of the airway tissue where the pattern formed by multiciliated cells could be identified. Scanning electron microscopy images were found in the literature for airway tissue from the animals shown in table III.

TABLE III.

Measurements of φ and λ for different species.

Animal	Reference	φ	λ
chicken	[39]	0.37 0.40 0.64	- - 6
dog	[40]	0.36	12.47
ferret	[41]	0.44	10.5
hamster	[42]	0.58	14.8
human	[43]	0.44 0.48	14.1 16.5
pig	[44] [45]	0.69 0.57	21.4 11.3
rabbit	[46]	0.49	15.2
rat	[47]	0.38	14.6
snake	[48]	0.19	121.3

Images were cropped from figures, to include only the region where the multiciliated tissue was present. Regions of the image containing multiciliated cells were identified and drawn manually. This generated a binary image where the white pixels corresponded to areas where multiciliated cells are present. Since image frame had a limited number of pixels, instead of binning we calculated coverage fraction over the entire image as:

$$\phi =\frac{1}{N}\sum _{i=1}^{N}I\left(r_i\right)$$ (M12)

where $I\left(r_i\right)$ are the values of all the pixels in the binary image as defined in equation M1 and N is the number of pixels in the image. Wavelength was calculated by computing S₂ according to equation M3. The wavelength λ corresponds to the local maximum of S₂. In the case of chicken, two images found were too small to measure λ, we indicate this by a dash in table III. Our measurements from this brief literature survey provide an estimation of $\phi$ and λ, however, large data sets for each species will be required to measure these parameters conclusively.

3. Simulation

a. Fundamental solution

The fundamental solution of Stokes flow (also known as the Stokeslet or Green’s function) in a liquid film was derived recently by Mathijssen et al. [49]. The confinement drastically changes the flow structure in these geometries, and therefore it is helpful to revise this briefly.

The hydrodynamics of an incompressible Newtonian fluid at low Reynolds number are described by the Stokes equations,

$$0=-\nabla p+\mu {\nabla }^{2}v+F(r,t),0=\nabla \cdot v.$$ (M13)

where $v(r,t)$ is the flow velocity field at position r and time t, $p(r,t)$ is the pressure field, μ is the dynamic viscosity and $F(r,t)$ is a force acting on the liquid. In the absence of boundaries, the flow due to a point force, $F_s={\delta }^3\left(r-r_s\right)f_s$, with magnitude $f_s(t)$ and position r_s, with boundary conditions $v=0$ as $|r|\to \infty$, is

$$v_s(r,t)=\mathcal{J}\left(r-r_s\right)\cdot f_s,$$ (M14)

where the Oseen tensor ${\mathcal{J}}_{ij}(r)$ in Cartesian components is

$${\mathcal{J}}_{ij}(r)=\frac{1}{8\pi \mu }\left\{\frac{{\delta }_{ij}}{r}+\frac{r_i{r}_j}{r^3}\right\},$$ (M15)

with i, $j\in \{x,y,z\}$ and $r=|r|$. In a thin film, this flow is modified by the boundaries. At the bottom surface we enforce the no-slip condition, $v=0$ at $z=0$, and at the liquid-air interface we enforce the no-shear condition, $\frac{\partial v}{\partial z}=0$ at $z=H$. These conditions can be satisfied exactly using a Fourier-transform method (page 56 in [49]) or approximated by truncating an infinite series of images (ibid. p. 37). The resulting expressions are rather complex, but analytically tractable. In the thin-film limit the solution simplifies to

$${\mathcal{F}}_{\alpha \beta }=-\frac{3z}{\pi \mu }\left(1-\frac{z}{2H}\right)\frac{z_s}{H}\left(1-\frac{z_s}{2H}\right)\frac{1}{{\rho }^2}\left\{\frac{{\delta }_{\alpha \beta }}{2}-\frac{r_{\alpha }{r}_{\beta }}{{\rho }^2}\right\},$$ (M16)

with horizontal components α, $\beta \in \{x,y\}$ and relative distance ${\rho }^2={\left(x-x_s\right)}^2+{\left(y-y_s\right)}^2$, but vertical flows are suppressed exponentially (ibid. p. 63). Here the thin-film limit is defined as $H\ll \rho$, which is equivalent to the far-field limit. The prefactors describe a half-parabolic flow profile in z, and the last part gives the horizontal flow structure (in curly brackets). A first difference with the Oseen tensor (Eq. M15) is that the flows decay faster, as 1/ρ² rather than 1/ρ, since the surfaces impart viscous dissipation. Secondly, the streamline structure is very different.

This is demonstrated in Fig. S3, where we show the exact solution as a function of confinement, H, with the Stokeslet in the middle of the film, $z_s=H/2$. For weak confinement, we recover the bulk Stokeslet flow (Eq. M15), where the streamlines are open and oriented along the force direction. For strong confinement we recover the thin-film limit (Eq. M16), the forward flows are weaker because of surface dissipation. Moreover, a recirculation emerges with liquid moving backwards (red colours), and the streamlines all completely close onto one another. For intermediate confinement, a more complex flow structure arises with two vortexes that are separated a distance δ ∼ H (green circles). Locally (ρ < H) the Stokeslet limit still holds, but globally (ρ > H) the far-field limit applies and all liquid recirculates.

Once the Green’s function ${\mathcal{F}}_{\alpha \beta }$ is known, it is possible to calculate the flow generated by an active carpet by integrating the Green’s function over the carpet architecture [17]. Puzzlingly however, because the liquid recirculates in the far-field in a film geometry, the flux due to a Stokeslet through any cross-section of the film is actually zero, for any finite film height H. Specifically, the flux through any yz plane due to a Stokeslet oriented along x is $J={\int }_0^H{\int }_{-\infty }^{\infty }{\mathcal{F}}_{xx}dydz=0$. As pointed out by Liron, this is also true for channels with two parallel no-slip surfaces, or cylindrical pipes of finite radius R, or any double-sided confinement [29]. In an infinite or semi-infinite (single surface) geometry, however, the flux does not vanish. This apparent dilemma is resolved by realising that one may add a constant Poiseuille flow $v_P(z)=-\frac{2H^2}{\mu }\frac{\partial p}{\partial x}\frac{z}{2H}\left(1-\frac{z}{2H}\right){\widehat{e}}_x$ to the solution without violating the boundary conditions on the film surfaces, at z = 0, H. The flux is then specified by the pressure gradient generated by the cilia. Therefore, if each cilium on average exerts a force F_c along x and if cilia are distributed with a density n_c per unit area, then the flux per unit length in y is $J=n_c{F}_c{H}^2/3\mu$. Note that other forces can also generate pressure gradients, such as gravity, $\nabla p=-\rho g$, which must be added to (or subtracted from) the total flux and flow profile.

b. Envelope approach

Here, we follow an alternative method inspired by the ‘envelope approach’ introduced by Lighthill and Blake [50, 51] to study ciliary propulsion. Instead of modelling the cilia with point forces, one can consider an envelope that covers the tips of numerous beating cilia that together form a continuous moving sheet. The no-slip condition on the bottom surface is then replaced by the motion of this envelope, $v_e=Up$, a tangential slip velocity that follows the orientation field p of the underlying cilia with an average local flow velocity U. This approximation is justified in the case when the cilia are close together, which is true for multiciliated cells with $N_{cilia}\sim 200$ cilia.

On the one hand, this approach coarse-grains the length scales smaller than the cell, so it cannot resolve the interesting flows around the individual cilia that can give rise to mixing and nutrient exchange [8, 30]. On the other hand, it is very tractable analytically (as seen in the study of micro-swimmers and active colloids [11]) and it is straightforward to implement numerically, as is discussed next, being suitable even for very large systems.

c. CFD solver

The flow velocity υ(r) is simulated using a 3D computational fluid dynamics (CFD) solver for the incompressible Navier-Stokes equations. Throughout this paper we focus on Newtonian fluids, but in §3g we also consider viscoelastic fluids with a shear-dependent viscosity. The CFD solver is implemented in a custombuilt MATLAB code, optimised for low Reynolds numbers by using an implicit Crank-Nicolson method for the viscous terms and an Adams-Bashforth method for the advection terms [52]. This algorithm is implemented on a staggered grid of size $N_x^g\times N_y^g\times N_z^g$ corresponding to a liquid film of size $L_x\times L_y\times H$ [μm] and with periodic boundary conditions in the x and y directions, where x is defined as the distal-to-proximal direction of the trachea. At the fluid-air interface we enforce the no-shear condition, $\frac{\partial v}{\partial z}=0$ at z = H. On the tissue surface we apply the no-slip condition in the absence of cilia (c = 0), and in the presence of cilia (c = 1) we impose a slip velocity set by the envelope model, which gives the boundary condition

$$v(r)=cUp\text{on}z=0.$$ (M17)

Here the cilia distribution c(r) and orientations p(r) are either taken directly from experiments (§3e), or systematically generated in silico for different coverage fractions, wavelengths, and disorder (§3f). We simulate this system until the (unique) solution is reached at steady state, after which we save the three-dimensional velocity field and the pressure field of the ciliary flow.

d. Total flux & clearance time

Once the flow is solved we compute the total flux in the distalto-proximal direction,

$$J={\int }_0^H{\int }_0^{L_y}{v}_{x}dydz,$$ (M18)

which due to incompressibility is the same for all planes perpendicular to x. Because of this condition, the flux is equivalent to the volume-averaged flow along x, since $\iiint v_{x}dxdydz=J{\int }_0^{L_x}dx=J{L}_x$. Using the linearity of the Stokes equations, the flux can also be rewritten as

$$J=\phi H{L}_{y}U\langle p_x\rangle ,$$ (M19)

where the coverage fraction $\phi ={\int }_0^{L_x}{\int }_0^{L_y}c(r)dxdy/\left(L_x{L}_y\right)$, which is equivalent to Eq. M2. We also define the z-averaged flow velocity, $\overline{v}={\int }_0^H\left\{v_x,v_y\right\}dz/H$, the mean longitudinal flow $\langle {\overline{v}}_x\rangle =\phi U\langle p_x\rangle$, and the largest back-flow, $\beta ={\min }_x{\min }_y{\overline{v}}_x$.

Subsequently, the clearance time is obtained by simulating particle trajectories that represent non-motile viruses, bacteria or other harmful pathogens. These particles are subject to the computed flow and also Gaussian fluctuations with diffusivity D. The Stokes-Einstein diffusivity due to thermal noise is D ∼ 10⁻¹μm²/s for micron-sized particles in water of viscosity μ = 10⁻³ Pa.s. However, in mucus the diffusivity is generally smaller than water, D ∼ 10⁻¹ −10⁻⁴ μm²/s for micron-sized particles, because the mucus is much thicker than water with viscosities μ ∼ 10⁻³ −1 Pa.s [53].

We run a Brownian dynamics (BD) simulation to find the trajectories for an ensemble of $N_1\ge {10}^3$ particles. Initially the particle positions r_p are uniformly distributed across the simulation box, and follow the Langevin equation,

$$\frac{\partial r_p}{\partial t}=\overline{v}\left(r_p\right)+\sqrt{2D}\eta (t),$$ (M20)

where the noise is defined by the correlation functions $\langle {\eta }_i(t)\rangle =0$ and $\langle {\eta }_i(t){\eta }_j\left(t^{\prime }\right)\rangle =\delta \left(t-t^{\prime }\right){\delta }_{ij}$. The Péclet number is defined as

$$\text{Pé}=\frac{\lambda \phi U}{D},$$ (M21)

which is large if the effects of advection outcompete diffusion.

These equations are integrated with a fourth order Runge-Kutta scheme, again with periodic boundary conditions in the x and y directions. For each pathogen i we then record the time T_i taken to travel a distance L_x in the x direction, along the D-P axis. Hence, we define the clearance time $T_c=\langle T\rangle$ as the first-passage time averaged over an ensemble of N₁ independent particles. We verified that this quantity does not depend on individual initial positions or the simulation geometry. Rather than absolute values, we report a non-dimensional ratio in all figures, such as $\frac{\langle T\rangle (\phi )}{\langle T\rangle (\phi =1)}$ to analyse the effect of each parameter.

Importantly, this clearance time is not only a measure of the total flux, but also of the flow structure. In particular, it is a measure of the connectivity between streamlines. If the streamlines are open and connected with the trachea outlet, the larynx, then pathogens will follow the river and rapidly be cleared. If the streamlines are closed, however, the particles are trapped in recirculation zones for a long time. Therefore, even small fluctuations (i.e. a large Péclet) can have a significant effect on the clearance times.

To the best of our knowledge, evaluating streamline connectivity using the first-passage time is a new concept. Having said that, streamline topology is important for transport and percolation in plasma physics [54] and affects particle diffusion in turbulence [55]. Recent results also show that changes in streamline topology can greatly enhance the rate of heat and mass transfer from neutrally buoyant particles in a shear flow [56, 57].

e. Experimental input

Large scale flows:

The entire trachea is imaged with a resolution of 7176 × 4496 pixels, corresponding to 3013.9 × 1888.3 microns, with the D-P axis aligned along x. Here the multiciliated cells are marked with Centrin [Fig. 1B], so from this fluorescence signal we identify the positions and shapes of approximately 3 · 10⁴ multiciliated cells using the Mathematica built-in segmentation function MorphologicalComponents[]. This measurement is course-grained by a factor of 5 to generate a grid of 1476 × 940 points, which subsequently is binarised to determine the coverage field c(r) = 0, 1. The orientation of the cilia cannot be measured in this assay, so for each cell we assign a stochastic direction p such that $\langle p_x\rangle =0.8$, in accordance with Fig. 1H. The ciliary envelope velocity $v_e=cUp$ is then computed on each grid point of the bottom boundary in the CFD simulation. The resulting flows are shown in Fig. 2D, left panel. Note, this is not the same mouse as the one shown for the flow measurement in Fig. 2C, because that tissue is alive with beating cilia whereas the former tissue is fixed to identify the basal bodies from fluorescence.

Small scale flows:

The tissue scale is imaged with fields of view of size 68 × 68μm. Here we identify the boundary of multiciliated cells by segmenting the membrane stain Vangl1 [see §1b], which determines the coverage field c(r). Next, we identify each cilium and its orientation by linking the relative positions of its ciliary rootlet and basal foot [see §2c]. For each cell, we then interpolate between its N_cilia ∼ 200 cilia to extract the orientation field p(r). The ciliary envelope velocity υ_e = cUp is then computed on each of the bottom boundary grid points of the CFD solver, with box size L_x = L_y = 68μm. The resulting flow from one field of view is shown in Fig. 2D, right panel. Again, this should not be compared directly with Fig. 2C because it shows a different organism.

Nonetheless, even if it is not possible to compare the experimental and simulated flow fields directly, we compare the correlation functions and flow distributions across an ensemble of different tissues, as shown in Fig. 2E-H, using the same definitions as in the experiments, as described in Methods §2d.

f. Controlled variations

Next, we systematically explore how the total flux and clearance time depend on the physical properties of the mucus flow [Fig. 3A,B]. One by one, we address (1) the ciliary coverage fraction, (2) the patchiness, (3) Brownian fluctuations, (4) the spatial heterogeneity, and (5) the orientational disorder.

1. The coverage fraction $\phi$ is varied while keeping the wavelength constant, with a square periodic box of size λ = L = 128μm and film height H = 10μm. The envelope model is enforced by discretising Eq. M17 on a grid (i, j) of 128×128 cells. A patch of cilia sits at the centre of this grid, with radius $R(n)=64\frac{n-1}{24-1}$ where $n=1,2,3,\dots ,34$. The discretised coverage field is then generated with the function $c_{ij}=\text{Θ}\left[R^2-{(i-65)}^2-{(j-65)}^2\right]$, where $\text{Θ}(x)$ is the unit step function. Consequently, the coverage fraction is $\phi ={\sum }_{i,j}{c}_{ij}/{128}^2$. All cilia are aligned along the trachea axis, $p_x=1$, so we find the velocities $v_{ij}^x=c_{ij}U$ and $v_{ij}^y=0$ at the tissue surface. The Stokes equations are solved with these boundary conditions (§3c) and the resulting flows are shown in the left panels of Fig. 3C. We then simulate an ensemble of N₁ = 10⁴ particle trajectories, initially distributed randomly, and subject to this flow and Brownian diffusion. We non-dimensionalise our system to λ∗ = 1, U∗ = 1, D∗ = 10⁻⁴, so the Péclet number $\text{Pé}=\phi {10}^4$, which is equivalent to a diffusivity D = 0.128μm²/s, L = 128μm and envelope velocity U = 10μm/s. In the right panel of Fig. 3C we show the resulting mean clearance times, $\frac{\langle T\rangle (\phi )}{\langle T\rangle (\phi =1)}$, as well as the total flux, $\frac{J(\phi )}{J(\phi =1)}$, both normalised with respect to the case of full coverage (φ= 1).

2. The patchiness λ/H is explored by varying the wavelength λ while keeping the film height H = 10μm constant, and also a constant periodic box size L = 128μm, coverage fraction $\phi =0.1$ and cilia alignment p_x = 1. We again use a grid (i, j) of 128×128 cells, on which we implement a square array of n_p × n_p ciliary patches, with wavelength $\lambda =L/n_p$ and radius $R\left(n_p\right)=L\sqrt{\phi /n_p\pi }$, where $n_p=1,2,3,\dots ,24$. In other words, the same number of cilia are spread out in more and smaller patches. Using these boundary conditions the flows are simulated, which are shown in the left panels of Fig. 3D. For large patchiness a back flow emerges. We again simulate N₁ = 10⁴ particle trajectories with constant diffusivity D = 0.128μm²/s, L = 128μm and mean flow velocity $\langle {\overline{v}}_x\rangle =\phi U\langle p_x\rangle =10\mu \text{m}/\text{s}$. In the right panel of Fig. 3D we show the resulting mean clearance times, $\frac{\langle T\rangle (\lambda /H)}{\langle T\rangle (0)}$, as well as the total flux, $\frac{J(\lambda /H)}{J(0)}$, and the back flow, $\frac{\beta (\lambda /H)}{\beta (0)}$, all normalised with respect to the case of uniform coverage (λ = 0). In Fig. S4 the 3D structure of the resulting flow for a square ciliary array is shown for patchiness λ/H = 12.8, with a top view and cross sections at and between the ciliated cells. As predicted by the Stokeslet flow solution (Eq. M16), the flows above a no-slip surface tend to follow a half-parabolic profile. However, the flows above an active surface have an inverted profile to satisfy the conservation of mass and momentum. There is also a vertical component to the flow, especially near the edges of the multiciliated cells, but this component along z is smaller than the components along x and y.

3. The geometric order is varied by considering the crystallinityγ, while keeping the coverage fraction $\phi =0.1$, the mean patchiness $\langle \lambda \rangle /H=8$ and the cilia alignment p_x = 1 constant. We begin with a crystalline array of 4 × 4 cilia patches, as in §3f2 above with n_p = 4. These patches are displaced spatially by a random vector (X, Y), where both components are drawn from a Gaussian distribution with standard deviation σ. The geometric order parameter is then defined as $\gamma =1-\frac{\sigma \sqrt{2}}{\lambda }$, the crystallinity. As before we implement these patches on a periodic 128 × 128 grid, but we also consider periodic image systems so that if (X, Y) leaves the grid, it appears on the other side. Moreover, we allow patches to overlap randomly, so the relation $\langle {\overline{v}}_x\rangle =\phi U$ remains satisfied. We generate these initial conditions for an ensemble of N₂ = 50 epithelia, and for N₃ = 16 different values of the order parameter, so N₂N₃ = 800 flows are simulated. A few examples of these flow patterns are shown in Fig. 4A. For each configuration we then simulate N₁ = 1000 particle trajectories, with a Péclet number of Pé = 10³, so 800,000 trajectories total. In the right panel we show the resulting clearance times, now averaged over the ensembles N₁ and $\frac{\langle T\rangle (\gamma )}{\langle T\rangle (1)}$, and the total flux, $\frac{J(\gamma )}{J(1)}$, both normalised with respect to the case of crystalline order.

4. The effect of cilia alignment is examined by varying the orientational order parameter, $M=\langle p_x\rangle$, while keeping the coverage fraction $\phi =0.1$, the patchiness $\lambda /H=8$ and the crystallinity γ = 1 constant. Again we begin with a crystalline array of 4 × 4 cilia patches, c_ij, as in §3f2 with n_p = 4. Now each cilia patch k is given a random orientation P_k, which is drawn from a circular Gaussian, the Von Mises distribution,

   $$f(\theta \mid \alpha )=\frac{e^{\alpha \cos (\theta )}}{2\pi I_0(\alpha )},\alpha >0,$$ (M22)

   where α is the distribution width and the Bessel function of the first kind $I_0(\alpha )$ is just a normalisation factor such that $\int f(\theta )d\theta =1$. Random numbers θ are drawn from this distribution using the Smirnov transform, i.e. solving the inverse of the cumulative distribution, such that $\langle \cos (\theta )\rangle =M\in [0,1]$. Hence we compile a grid for the longitudinal and perpendicular surface velocities, $v_{ij}^x=c_{ij}Ucos\left({\theta }_{ij}\right)$ and $v_{ij}^y=c_{ij}U\sin \left({\theta }_{ij}\right)$, where ${\theta }_{ij}={\theta }_k$ for each patch. These initial conditions are generated for an ensemble of N₂ = 50 epithelia, and for N₃ = 16 different values of the order parameter, $M(n)=1-\frac{n-1}{16}$. We again simulate N₁ = 1000 particle trajectories for each configuration, with Pé = 10³. In the right panel of Fig. 4B we show the resulting clearance times averaged over N₁ and N₂, $\frac{\langle T\rangle (M)}{\langle T\rangle (1)}$, and the total flux, $\frac{J(M)}{J(1)}$, both normalised with respect to the case of aligned cilia.

5. The effect of Brownian fluctuations is tested by varying the Péclet number, while keeping constant the wavelength λ = L = 128μm, the film height H = 10μm, the coverage fraction $\phi =0.1$, crystallinity γ = 1, and cilia alignment p_x = 1. We use the same ciliary arrangement $v_{ij}^x$ as before, (§3f2 above with n_p = 1), for which the flow is shown in the fourth panel of Fig. 3D. Using this flow, in Fig. 4C the trajectories of 50 particles are presented for each value of the Péclet number, Pé = 100, 100, 10, by varying the diffusivity D. We then gather statistics of N₁ = 10⁴ trajectories for the Péclet number $\text{Pé}={10}^{4\frac{n-1}{10-1}}$, where $n=1,2,3,\dots ,10$. In the right panel we show the resulting mean clearance times, $\frac{\langle T\rangle (\text{Pé})}{\langle T\rangle \left({10}^4\right)}$, and the total flux, $\frac{J\left({\text{Pe}}^{\prime }\right)}{J\left({10}^4\right)}$, both normalised with respect to the case of weak fluctuations.

g. Shear-dependent viscosity

We verify the robustness of our results with respect to viscoelastic effects [58] by considering a power-law fluid with a shear-dependent viscosity [59]. Instead of simulating a Newtonian liquid, we generalise the Stokes equations of Eq. M13 to

$$0=\nabla \cdot \underset{\_}{\underset{\_}{S}},0=\nabla \cdot v,$$ (M23)

where the stress tensor is given by a constitutive equation,

$$\underset{\_}{\underset{\_}{S}}=-p\underset{\_}{\underset{\_}{I}}+2\mu (\dot{\gamma })\underset{\_}{\underset{\_}{E}},$$ (M24)

where $\underset{\_}{\underset{\_}{I}}$ is the identity matrix, and the shear rate is defined as $\dot{\gamma }=\sqrt{2\underset{\_}{\underset{\_}{E}}:\underset{\_}{\underset{\_}{E}}}$ in terms of the deformation tensor,

$$\underset{\_}{\underset{\_}{E}}=\frac{(\nabla v)+{(\nabla v)}^T}{2}.$$ (M25)

The power-law for the shear-dependent viscosity is

$$\mu (\dot{\gamma })=k{\dot{\gamma }}^{n-1},$$ (M26)

where k is a constant relative to the properties of the fluid and the exponent n indicates whether the liquid is shear-thinning (n < 1) or shear-thickening (n > 1). The Newtonian flow is recovered in the case of n = 1. The resulting shear-dependent viscosities are shown in Fig. S5A.

We implement this constitutive equation in our CFD solver following Neofytou [60]. First, we simulate the Newtonian flow solution as before, using the Newtonian viscosity μ_N, from which we determine the shear rate averaged across the volume of the liquid film, $\langle {\dot{\gamma }}_N\rangle$. Then, we simulate the viscoelastic flow for various values of the exponent n, where we non-dimensionalise the shear rate with respect to the Newtonian limit and set $k={\mu }_N/{\langle {\dot{\gamma }}_N\rangle }^{n-1}$.

To validate this solver, we first simulate the Poiseuille flow between two parallel plates due a pressure gradient. The analytical solution is known [59, 61] exactly for this viscoelastic flow,

$$v_P(z)=v_{\max }\left(1-{\left(\frac{\left|z\right|}{H}\right)}^{\frac{n+1}{n}}\right)\widehat{x},$$ (M27)

where υ_max is the maximum flow speed at the centre line. Figure S5B compares the power-law CFD simulations (points) with this theoretical flow profile (lines). For the Newtonian case (n = 1, green) we recover the usual parabolic Poiseuille profile, for the shear-thickening fluid (n = 2, red) we recover the sharper ‘cusp’ flow and for the shear-thinning fluid (n = 0.5, blue) we recover the flatter ‘plug’ flow.

We then apply the power-law CFD solver to simulate the ciliary flows, using the boundary conditions set by the envelope approach as before, following the same methods as in §3f. Hence, we compare the flow structure due to an array of multiciliated cells for different values of the power-law exponent, n, with a constant coverage fraction $\phi =0.1$, patchiness $\lambda /H=12.8$, crystallinity γ = 1 and the cilia are all aligned $\langle p_x\rangle =1$. Perhaps surprisingly, both the shear-thinning and the shear-thickening fluids have very similar flow structures compared to the Newtonian flow [Fig. S5C]. For the shear-thinning flow, the flow strength is slightly weaker compared to the shear-thickening flow, but the recirculation zones (red areas) are also slightly smaller. Still, in both cases, particles stuck in these eddies feature a large clearance time. We test this quantitatively in Fig. S5D, where we show the total flux and the clearance time as a function of patchiness, repeating the analysis described in §3f2, for both a shear thinning (n = 0.5) and a shear-thickening fluid (n = 2). As in the Newtonian case, the clearance time is small for a homogeneous carpet (low λ) but large for patchy epithelia because of the emergence of recirculation. In Fig. S5E we also vary the Péclet number, repeating the analysis described in §3f5. Again as in the Newtonian case, the noise reduces the clearance time.

In summary, we conclude that if multiciliated cells drive a film of a generalised Newtonian fluid with a shear-dependent viscosity, recirculation still emerges with patchiness, but the particle clearance can still be reduced by disorder. It would be interesting to generalise this further to other viscoelastic constitutive equations that include normal stress differences, a yield stress or memory effects. Then, the deformation of streamlines and recirculation zones could be larger, which may enhance particle clearance. Indeed, these complex fluids can be implemented using the CFD framework described here, which provides an interesting avenue for future research.

h. Hexagonal arrays

We also test for robustness with respect to ciliary lattice structure by simulating hexagonal arrays of multiciliated cells, in a Newtonian fluid, with three different orientations [Fig. S6A-C]. Compared to the rectangular arrays, we still see back-flow (red areas) and streamline recirculation when the patchiness λ/H is large, which for large Péclet numbers still leads to increased clearance times: In Fig. S6D we vary the wavelength λ, as in §3f2, and simulate N₁ = 10⁴ particle trajectories with constant diffusivity D = 0.128μm²/s, box size L_x = 128μm, film height H = 10μm, and mean flow velocity $\langle {\overline{v}}_x\rangle =\phi U\langle p_x\rangle =10\mu \text{m}/\text{s}$. In Fig. S6E we also vary the Brownian fluctuations, as in §3f5, by varying the diffusivity D with constant patchiness, $\lambda /H=12.8$. Compared to the square lattice, the clearance times are smaller because the recirculating areas are smaller, but qualitatively the results are identical.

i. Phase diagrams

Finally, we cross-compare these parameters in three phase diagrams that combine the coverage fraction, the patchiness, and the ciliary orientation. For all diagrams, we generate an ensemble of ciliary carpet structures starting from a crystalline array of n_p × n_p cilia patches, as in §3f2 with γ = 1. As before the coverage fraction is varied by changing the patch size R so that $n_p^2\pi R^2=\phi L^2$, the patchiness is varied by the number of patches n_p and the patches are given a ciliary orientation with order parameter $M=\langle p_x\rangle$ using the Von Mises distribution.

1. For the $\phi -\lambda$ diagram we simulate N₂N₃ epithelia for N₂ = 14 values of coverage and N₃ = 10 values of patchiness. In the resulting flow profiles we simulate N₁ = 10³ tracer trajectories with $\text{Pé}/\phi ={10}^3$ and constant p_x = 1, which together yield the mean clearance time. The clearance time is normalised with respect to an ideal carpet, $\phi =1$ and λ = 0.

2. For the $\phi -M$ diagram we simulate N₂N₃N₄ flows for N₂ = 14 different values of coverage, N₃ = 16 different values of orientational order, and for each an ensemble of N₄ = 20 epithelia. In all the resulting flow profiles we simulate N₁ = 10² tracer trajectories with ${\text{Pe}}^{\prime }/\phi ={10}^3$ and constant $\lambda /H=8$. The clearance time is normalised with respect to $\phi =1$ and M = 1.

3. For the λ−M diagram we simulate N₂N₃N₄ flows for N₂ = 16 different values of patchiness, N₃ = 14 different values of orientational order, and for each an ensemble of N₄ = 20 epithelia. In all the resulting flow profiles we simulate N₁ = 10² tracer trajectories with Pé = 10⁴ and constant $\phi =0.4$. The clearance time is normalised with respect to λ = 0 and M = 1.

Supplementary Material

video1. Video 1. Activity of a field of multiciliated cells in the trachea.

Time-lapse ex-vivo DIC imaging of a section of the mouse trachea multiciliated tissue.

video2. Video 2. Ciliary driven flows are globally coherent.

Flow generated by multiciliated cells across the entire trachea. Flow is imaged by time-lapse confocal microscopy. Fluorescent beads serve as tracer particles.

video3. Video 3. Ciliary driven flows are locally heterogeneous.

Microstructure of the flow generated by a subsection of the trachea multiciliated tissue. Flow is imaged by time-lapse confocal microscopy. Fluorescent beads serve as tracer particles.

video4. Video 4. Activity of multiciliated cells in the trachea.

Time-lapse ex-vivo DIC imaging of a cross-section of the mouse trachea multiciliated tissue.

video5. Video 5. Fluctuations improve particle clearance in patchy arrangements of multiciliated cells.

Particle trajectories (N_p = 1000) are simulated for a range of noise strengths. Initially, the particles are distributed evenly and identically in all three panels, emulating a uniform deposition from breathed-in air. Over time, they are subject to flow (same as in Fig. 4C) and fluctuations with different diffusion constants, such that the Péclet number is Pé = 10⁴,10³,10², respectively. Colours indicate particle index and black trails show their pathlines. For weak noise the particles accumulate in recirculation zones, but strong fluctuations facilitate a faster clearance.