A Fast and Interpretable Deep Learning Approach for Accurate Electrostatics-Driven pK_a Predictions in Proteins

Abstract

Existing computational methods for estimating pK_a values in proteins rely on theoretical approximations and lengthy computations. In this work, we use a data set of 6 million theoretically determined pK_a shifts to train deep learning models, which are shown to rival the physics-based predictors. These neural networks managed to infer the electrostatic contributions of different chemical groups and learned the importance of solvent exposure and close interactions, including hydrogen bonds. Although trained only using theoretical data, our pKAI+ model displayed the best accuracy in a test set of ∼750 experimental values. Inference times allow speedups of more than 1000× compared to physics-based methods. By combining speed, accuracy, and a reasonable understanding of the underlying physics, our models provide a game-changing solution for fast estimations of macroscopic pK_a values from ensembles of microscopic values as well as for many downstream applications such as molecular docking and constant-pH molecular dynamics simulations.

Introduction

Many biological processes are triggered by changes in the ionization states of key amino acid side-chains.^1,2 Experimentally, the titration behavior of a molecule can be measured using potentiometry or by tracking free-energy changes across a pH range. For individual sites, titration curves can be derived from infrared or NMR spectra. Detailed microscopic information can be quickly and inexpensively obtained with computational methods, and several in silico pK_a calculations are widely used to provide insights about structural and functional properties of proteins.³⁻⁵

In Poisson–Boltzmann (PB) based methods, the solvent is implicitly described while proteins are represented by point charges in a low-dielectric medium.^3,4,6,7 These continuum electrostatics (CE) methods assume that pK_a^single (the proton binding affinity for a chemical group in a given conformation, often called pK_half in theoretical calculations) is a good estimate for the macroscopic pK_a value. This assumption holds when the protein structure is sufficiently representative of the conformational ensembles corresponding to both protonation states. Experimentally determined structures exhibit conformations at a the minimum energy state, which in turn is related to a specific protonation state. However, biomolecular systems can explore different energy basins, which may exhibit alternative protonation states. Energy minima can be affected by experimental conditions, such as temperature, ionic strength, and pH. Inaccuracies in pK_a predictions due to limited conformational rearrangements can be reduced by increasing the protein dielectric constant from its default value (2–4), which only accounts for electronic polarization. The dielectric constant can be used as an empirical parameter to mimic the effect of mechanisms responding to a local electric field that is not explicitly taken into account in the model.⁸⁻¹² A more computationally expensive approach is to explicitly include protein motion by sampling conformers via Monte Carlo (MC) or molecular dynamics (MD) simulations and applying conformational averaging.^4,13−15 Finally, by coupling the sampling of protonation states at given pH levels and conformations, constant-pH MD methods¹⁶⁻²⁰ provide greater insights into pH-dependent processes.²¹⁻²⁵

As larger data sets of experimental pK_a values have become available, a new class of purely empirical methods has been developed. These models rely on statistical fits of empirical parameters, weighting the different energetic contributions into simplified functions. PROPKA,⁵ arguably the most popular of such methods,²⁶ has been shown to perform competitively even when compared to higher-level theory methods.^6,27 The empirical methods are much faster than the physics-based ones, although at the cost of providing fewer microscopic insights. Additionally, their predictive power is unknown on mutations or proteins dissimilar to those that compose the training set.

The accuracy of most predictors is bound to the estimation of the same quantity, the so-called ΔpK_a. This is the free energy of transferring the ionizable residue from the solvent to the protein compared to that of its neutral counterpart. Since pK_a values for all amino acids in water have been experimentally determined, the pK_a^solvent term can be fixed and, in practice, can also be adjusted to incorporate systematic errors. The ΔpK_a can be regarded as a sum of mostly electrostatic contributions stemming from the residue microenvironment. Therefore, the accurate prediction of pK_a values for a given conformation requires a correct description of the residue’s interactions with both the surrounding protein charges and the solvent.

At their core, deep learning (DL) models are complex nonlinear empirical functions fitted to best map input variables to output properties. Considering chemical properties such as pK_a values, which are dictated by molecular configurations, it is possible to train a model to map this relationship without the need to solve nonlinear equations in 3D or to sort through the massive space of possible states, provided that enough examples are presented.

In this paper, we have developed two DL-based pK_a predictors, namely, pKAI and pKAI+, for pK_a^single and experimental pK_a values, respectively. These models were trained on a database with ∼6 million pK_a values estimated from ∼50,000 structures using the continuum electrostatics method PypKa.⁶ pKAI+ displays an unrivaled performance by predicting experimental pK_a values on a data set with ∼750 members. Also, pKAI exhibits an accuracy comparable to that of the PB-based predictor used to generate the training set while being approximately 10–1000× faster. By applying explainable artificial intelligence (XAI) analysis, we show that these simple models are able to implicitly model most of the required energetic contributions, such as Coulomb interactions, desolvation, and hydrogen bonding. Therefore, the presented models feature the best characteristics of CE-based methods—accuracy and interpretability—with the speed of empirical approaches.

Methods

Data Set

To train our DL models, we used a large publicly available data set of estimated pK values, namely, the pKPDB database.²⁸ This data set of ∼3 million pK_a values was created by running the PypKa tool with default parameters⁶ over all the protein structures deposited on the Protein Data Bank. The PB solver DelPhi¹¹ was used with a dielectric constant equal to 15 and an ionic strength of 0.1 M. A two-step focusing procedure was employed with a coarser grid spacing of 1 Å, and the subsequent calculation was employed using a finer grid with 0.25 Å between the nodes. Monte Carlo sampling was used to sample protonation microstates and tautomers.

The target values to be fitted by our model are theoretical pK_a^single values estimated with a PB-based method. This implies that pKAI will inherit the assumptions and limitations of this class of predictors. Our approach contrasts with the one usually adopted for training empirical predictors, which entails the use of experimental values to fit the model’s parameters. The main advantage of this novel approach is that we can train models with significantly more parameters, such as deep learning ones, since there is now a much larger abundance of training data. As a comparison, in PROPKA3, only 85 experimental values of aspartate and glutamate residues were used to fit 6 parameters.⁵ Recently, traditional ML models have been trained on ∼1500 experimental pK_a values.^29,30 However, testing the real-world performances of such methods is difficult, as there is a high degree of similarity among available experimental data. Our larger data set translates into more diversity in terms of protein and residue types and, more importantly, a wider variety of residue environments. It also helps our models avoid the undesired overfitting. Furthermore, the relationship between a structure and our target property is deterministic contrary to that of experimental pK_a values, which suffers from the lack of entropic information.

The ultimate goal of these methods is to accurately predict experimental pK_a values; thus, we have assessed the model’s performance with ∼750 experimental pK_a values taken from the largest compilation of experimentally determined pK_a values of protein residues reported in the literature, namely, the PKAD database.³¹ The 97 proteins in the experimental test set are reported in the Supplementary Table S1. We compare our experimental results with a Null model (attributing to each titratable group the corresponding pK_a value in water), PypKa (the method used to generate the training set), and PROPKA with default settings (the empirical method of reference).

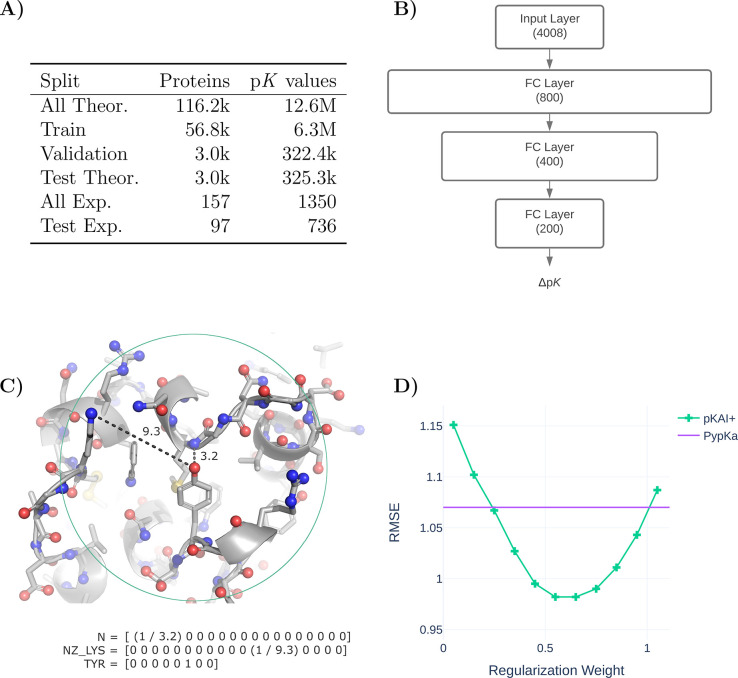
Before training our models on our data set, we applied a curated data split (Table 1A) to ensure that the training, validation, and test sets did not contain proteins with a high degree of similarity and to prevent overfitting. First, we randomly selected 3000 proteins from the full data set of ∼120,000 proteins as our holdout test set of theoretical pK_a values. The program mmseqs³² was then used to exclude all proteins that contained at least one chain similar to any of the chains found in either the experimental or theoretical test sets. Chains were considered to be similar if they presented a sequence identity over 90%. From the remaining set of proteins, 3000 more were randomly assigned to the validation set, while the rest became the training set. Finally, we excluded proteins similar to those of the validation set from the training set. In the experimental data set, we excluded all duplicated proteins, nonexact pK_a values (e.g., >12.0), and residues for which PypKa or PROPKA failed to produce an estimate.

Figure 1.

(A) Overview of the data split and the similarity exclusion performed on the pKPDB and PKAD databases.^28,31 (B) pKAI model architecture. (C) Illustration of the encoding of the titratable amino acid environment. Only nitrogen, oxygen, and sulfur atoms (shown as spheres) within a 15 Å cutoff (green circle) are included, while all carbon (shown as sticks) and hydrogen atoms (omitted) are ignored. The included atoms are represented by the inverse of their distance to the titratable residue in an OHE vector featuring 16 categories of atom classes (Supplementary Table S6). The titratable residue is represented by an OHE vector comprised of eight classes. (D) Performance of pKAI+ with different regularization weights in the experimental test set.

Model Architecture and Implementation

pKAI was implemented and trained using PyTorch ver. 1.9.0³³ and PyTorch Lightning ver. 1.2.10.³⁴ The model has a simple architecture comprised of three fully connected hidden layers in a pyramidal configuration fitted to the pK_a shifts of titratable amino acids (Figure 1B). The simplicity of the architecture is intentional; it has a simple architecture proof-of-concept so that deep learning models can capture the effect of electrostatic interactions in the pK_a of titrable residues. Recent work has shown that it is possible to have an ML model that accurately predicts electrostatic solvation energies of proteins.³⁵ However, pK_a estimations are even more complex, requiring at least 2 PB calculations per residue state for the physics-based counterpart (e.g., in PypKa, each carboxylic acid has 5 states, hence 10 PB calculations are required for each Asp/Glu residue).

The encoding of the environment of each titratable residue has been simplified to retain only the most important electrostatic descriptors (Figure 1C). Considering the decay rate of the electrostatic potential, we decided to truncate the contributions to the environment of a residue by applying a cutoff of 15 Å around the labile atom(s) of the titratable residue. In practice, this cutoff is slightly smaller for some residue environments, as the necessary input layer size normalization resulted in the truncation of the closest 250 atoms. It is expected that larger proteins will have a higher occurrence of residues with a cutoff less than 15 Å. Nevertheless, the truncation only excludes quite distant atoms, and 14.85 Å was the minimum cutoff value observed in the test set. A further approximation was made by considering only highly charged atoms, as they have the strongest electrostatic interactions with the titrable site, and assuming that solvent exposure can be inferred from the distances from the titrable residues to nearby atoms (similar to the half-sphere exposure³⁶). This simplification can be slightly compensated by using atom classes instead of charges or element names, as they implicitly provide information about adjacent atoms. The atoms were one-hot encoded (OHE) and, to reduce the input layer size, chemically similar atoms were assigned to the same category (Supplementary Table S6). While carboxylic oxygen atoms (C-termini OXT, aspartates OD1 and OD2, and glutamates OE1 and OE2) and primary amine atoms (arginines NH1 and NH2) atoms were merged, others with similar names but different chemical properties were separated (glutamines OE1 and NE2 from glutamates OE1 and histidines NE2, asparagines OD1 from aspartates OD1, and main-chain N from N-termini N).

The final 4008-sized input layer consisted of 250 atoms represented by 16 OHE classes concatenated to an 8-dimension OHE vector that corresponded to the titrating amino acid. Each atom’s OHE was multiplied by its reciprocal distance to the titrating residues to include this valuable information without increasing the size of the input layer.

pKAI is freely available as a python module that can be installed via pip. The source code can be found at https://github.com/bayer-science-for-a-better-life/pKAI.

Training

Training was performed with mini-batches of 256 examples and the Adam optimizer³⁷ with a learning rate of 1 × 10^–6 and a weight decay of 1 × 10^–4. Dropout regularization was applied to all fully connected layers with the exception of the last one. Hyper-parameter optimization was performed with Optuna³⁸ using the performance in the validation set. Training these models takes approximately 10 min on an NVIDIA Tesla M40 24 GB system using 16-bit precision and an early stopping strategy on the minimization of the cost function with a Δ of 1× 10^–3 and a patience of five steps.

The pKAI model was trained on an MSE cost function, while for pKAI+ we added a regularization parameter α to penalize ΔpK_a predictions (y). Thus, the loss function of pKAI+ becomes

1

where y_i is the true value and ŷ_i is the estimation. Different regularization weights were tested to check for overfitting (Figure 1D). While we selected an α of 50%, any value in the 40–70% range would lead to a similar improvement. Moreover, the same trend was observed when the experimental test was divided into five folds (Supplementary Figure S1).

XAI Methods

For each input atom feature â = (a, r_a), where a indicates the atom class and r_a indicates the corresponding distance to the liable atom(s) of the titrating residue, we computed the corresponding attribution I(â) with the Integrated Gradients (IG) algorithm³⁹ as implemented in the shap package.⁴⁰I(â) measures the sensitivity of the network output with respect to changes in the input â. A large absolute value of I(â) indicates that the network assigns a high importance to this feature, while the sign of I(â) indicates whether the feature contributes positively or negatively to the output. Given that the most important contributions to ΔpK_a are of an electrostatic nature, one can try to explain the model-inferred charges for each atom class a by computing the distant-independent score C as follows:

2

where I_– and I₊ are negative and positive I values, respectively. The C score of an atom class is thus the difference between the distance-weighted average of examples with negative and positive I values over a large subset (10 000 samples) of the test set. The sign of C(a) in eq 2 resembles the charge that the network, on average, assigns to a given atom type. For example, if an atom class is perceived by the model as contributing negatively to the ΔpK_a (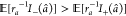, hence C(a) > 0), this would mean that the network learned that this particular atom stabilizes the deprotonated state, which is characteristic of positively charged groups.

The solvent-accessible surface area (SASA) values shown in Supplementary Table S2, and in the XAI subsections were taken from pKPDB.²⁸

Results

The main goal of pKAI is to mimic the pK_a-predictive ability of PB-based methods with a significant improvement in the computational performance. Our training set was comprised of pK_a values calculated using PypKa on a large number of proteins taken from the Protein Data Bank.²⁸ An elaborate data split was performed to minimize data leakage from the training set to the validation and test sets (see Methods). pKAI was designed to be a simple and interpretable model, as it uses the minimum structural features that still capture the electrostatic environment surrounding every titratable residue. The model has been trained on ΔpK_a values rather than on absolute values. The pK_a shift is, in fact, a more appropriate quantity to learn, less dependent on the chemical peculiarities of individual amino acids, and more sensitive to the local electrostatic environment. For example, residues that share a common side-chain chemical group (such as glutamate and aspartate, which share a carboxylic acid) are influenced by the same environment in a similar way.

We wanted our model to capture the electrostatic dependence between the environment of a residue and its consequent pK_a shift while keeping the input layer as small as possible (see Methods). By ignoring all carbon and hydrogen atoms, we greatly reduced the dimensionality of our input layer while retaining most of the information regarding charged particles. There is, of course, a significant loss of topological information, although much can be inferred from the positions of the included atoms. In fact, there is no performance gain when solvent exposure measurements (e.g., SASA and residue depth) are added to the environment embedding. Considering that solvent exposure entails topological information and that the model is not able to extract additional information from it, we conclude that the model was already estimating, to some degree, these molecular properties (see Model Explainability).

pKAI: Predicting Theoretical pK_a

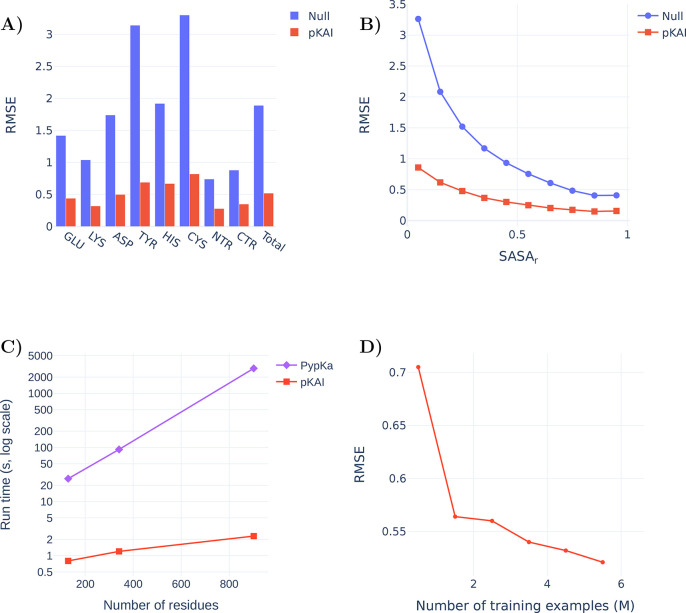
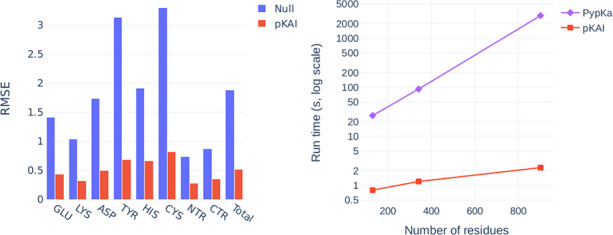
The performance of the model on the test set is reported in Supplementary Table S2 and Figure 2A. The null model used for comparison consists of the reference pK_a value in water for each residue type, corresponding to 0 in the ΔpK_a scale. Overall, pKAI reproduces the PB-based ΔpK_a values with an MAE value of 0.31, an RMSE of 0.52, and an R² of 0.93. However, in this case, we are only predicting theoretical values with a well-defined relationship between structure and pK_a^single (pK value of a single conformation). Estimating experimental pK_a values is a much more complex task, since the pK_a values that correspond to the different conformations spanned by the protein should be weighted according to their occurrence probability at equilibrium. The performance of pKAI is impressive considering the high complexity of the dependence between pK_a and the electrostatic environment of the site, as illustrated by the high RMSE value of the Null model (1.89). Some residues are easier to predict (e.g., LYS and termini residues), while others are more challenging (e.g., CYS and TYR). This can be explained by their solvent exposure distribution (Figure 2B): well-solvated residues exhibit small ΔpK_a values, while more buried ones are more affected by the desolvation effect and establish more interactions with other residues, causing their pK_a values to shift. There is a clear dependency between the solvent exposure of a residue, its ΔpK_a value, and the prediction difficulty (Supplementary Figure S2). The excellent performance of pKAI is also demonstrated by the fact that most predictions (81.2%) exhibit an error below 0.5 pK units, which is sufficient for most use cases.

Figure 2.

(A) Comparison of the RMSE values between from the Null model and pKAI (values are shown in Supplementary Table S2). The Null model is defined as the pK_a values of the residues in water taken from ref (41). (B) Performance at predicting the dependency of the pK_a^single values on the magnitude of solvent exposure (SASA). The calculations were performed for the pKAI and Null models using the PypKa predictions as a reference. (C) Execution time comparison between PypKa and pKAI (values are shown in Supplementary Table S3). This benchmark was executed on a machine with a single Intel Xeon E5–2620 processor. (D) Effect of the size of the training set on the model performance for the validation set.

The main advantage of DL models is the potential speedup they can provide. Since continuum electrostatics (CE) pK_a estimations need to sample thermodynamic equilibrium microstates, several iterative simulations have to be performed on each protonation state and the environment of every residue. On the other hand, pKAI merely needs to apply its learned function over each residue; as such, it is remarkably faster (Figure 2C). Moreover, the convergence of the CE simulations becomes harder to achieve as the protein size increases. Consequently, in PypKa, as the protein size increases, so does the time required to estimate each pK_a value. In contrast, the run time of pKAI’s DL model has a different dependence on the protein size. Since the larger the protein is, the larger is the amount of calculations that can be performed simultaneously, the model loading cost becomes less significant and the average per-residue execution time becomes faster. This results in a sublinear scaling performance and a pKAI speedup that can exceed over a 1000× compared to its CE counterpart. As such, pKAI is a particularly valuable tool for dealing with very large systems with thousands of residues, where the only added computational cost stems from the prepossessing of the structure.

Another important factor contributing to the high accuracy obtained is the considerable size of the training set. Despite using the largest repository of experimental protein structures and the largest pK_a database available,²⁸ we show that there is still a correlation between the number of examples in the training set and the accuracy of the model (Figure 2D). This indicates that our model can still be improved by providing further examples of pK_a values.

pKAI+: Predicting Experimental pK_aValues

The main goal of pK_a predictors, such as PypKa, is to estimate the macroscopic pK_a values for titratable residues using structures (usually experimental ones). Since pKAI aims to reproduce the pK_a^single value calculated with PypKa at a fraction of the computational cost, it is not expected to outperform the PB-based method in predicting experimental values. When using PB to predict experimental pK_as, a higher dielectric constant for the solute is often adopted to compensate for the lack of conformational flexibility in the method and the lack of representation in the experimental input structure. A similar approach can be implemented in pKAI by introducing a regularization weight to the cost function (pKAI+). This regularization penalizes the magnitude of the ΔpK_a prediction. In practice, this procedure biases our estimates toward the pK_a values in water, similarly to what is done by the increased solute dielectric constant in PB-based approaches. However, the analogous effect is applied evenly to all residues independent of the solvent exposure. Thus, adding the regularization penalty is different from training pKAI with a data set generated with a higher protein dielectric constant. Furthermore, we previously benchmarked PypKa on a range of dielectric constants (4–20) and showed that there was no benefit to increasing the dielectric constant to values greater than 15.⁶ It should be noted that pKAI+ was not trained on experimental pK_a values but rather on the same training set as pKAI.

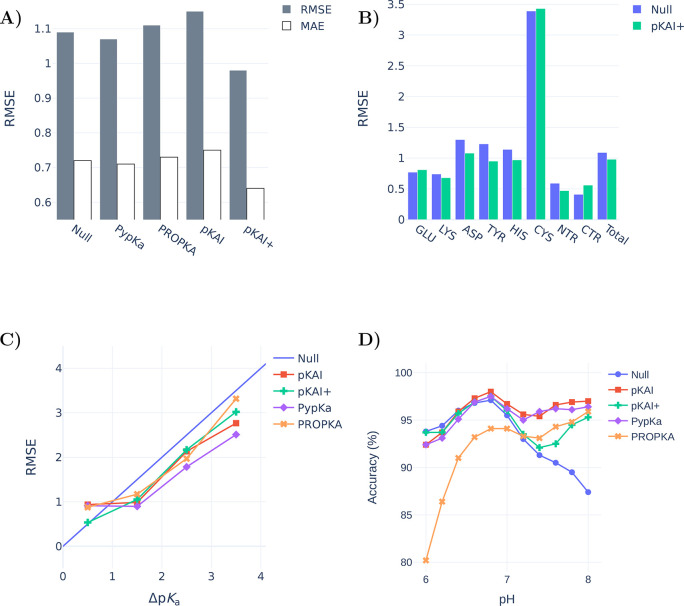
To evaluate the performance of our model, we benchmarked it using a data set of 736 titratable residues in 97 proteins with experimentally determined pK_a values (Figure 3A). Remarkably, pKAI+ (RMSE of 0.98) is able to outperform both PypKa (RMSE of 1.07) and PROPKA (state-of-the-art empirical pK_a predictor, RMSE of 1.11). Furthermore, the improvement over the other methods is significant for most residue types (Figure 3B) and can be quantified using metrics that are more (RMSE, 0.9 quantile) or less (MAE, error percentage under 0.5) sensitive to the presence of outliers (Supplementary Table S4). Cysteine residues are particularly difficult to predict because they naturally occur less frequently and are more buried than all other titratable residues. This leads to an under-representation of these residues in the training set, while they exhibit the largest pK_a shifts. To illustrate the difficulty of this data set, note that some methodologies are not able to improve on the Null model (RMSE of 1.09). The reported deviations are specific to this data set. Even though our benchmark is one of the largest ever used to validate a pK_a predictor, it is likely still insufficient to quantify the true accuracy of these methods. Furthermore, besides being limited, the test sets used to validate new pK_a predictors tend to always be different. This makes it very hard to compare methods without rerunning them. In this benchmark, PypKa represents the PB-based methods like DelPhiPKa⁷ and H++.³ More computationally expensive methods such as MCCE⁴³ and constant-pH MD are not represented here. These methods are expected to outperform PB-based methods that rely on a single structure, although the exact improvement on this test set is hard to predict. DeepKa is a recently published convolutional neural network trained on theoretical pK_a values from constant-pH MD (CpHMD) simulations.⁴⁴ As expected, CpHMD implemented in the Amber suite⁴⁵ (RMSE of 1.02) outperformed PROPKA (RMSE of 1.12) in the test set, which only includes the four residues (Asp, Glu, His, and Lys) predicted by DeepKa (RMSE of 1.05).

Figure 3.

(A) Experimental pK_a benchmarks of several methods for a data set of 736 residues from 97 proteins (values are shown in Supplementary Table S5). The Null model values are the pK_a values of each amino acid substituted in an alanine pentapeptide (Ace–AA–X–AA–NH₂).^41,42 (B) Comparison between the Null model and the pKAI+ performance by residue type. (C) Prediction errors of the different models given the experimental pK_a shift (ΔpK_a). (D) Accuracies of several methods for predicting representative protonation states derived from experimental pK_a values. Residues at a pH within 1.5 units of the experimental pK_a are considered not to have a representative protonation state.

The difficulty of estimating pK_a values is not the same for all residues. pK_a predictors are usually valuable tools for predicting residues in which the shift is significant. For example, if a residue is completely exposed to the solvent and performs no other interactions, its pK_a will be equal to its known value in water. To assess our model’s performance while avoiding cherry-picking, no particular cases were analyzed. Instead, we classified the residues according to their solvent exposure level (Supplementary Figure S3) and the magnitude of the experimental pK_a shifts. pKAI+ shows RMSE values comparable to those of PypKa for both the most solvent-exposed and buried residues. Interestingly, it is also able to surpass the PB-based model for partially exposed residues. Notably, pKAI+ only improves the PypKa predictions for pK_a shifts smaller than 1 pK unit (Figure 3C). This indicates that pKAI+ corrects the pK_a values of partially exposed residues, which establish nonrepresentative interactions in the experimental structure. Since there is a large number of residues with these characteristics in the test set,²⁸ the overall performance improvement is significant (Supplementary Table S5).

From the pK_a value of a residue, it is possible to derive the residue’s most likely protonation state at a given pH. To perform this conversion, one must assume that the Henderson–Hasselbalch (HH) equation can describe the residue’s protonation behavior, implying that no other titrable residues influence its titration. According to the HH equation, at a pH equal to the pK_a value, the protonated and deprotonated species exist in the same proportion. Hence, at this pH value, there is no most probable protonation state. At a pH value that is 1.0 unit away from the pK_a value, the least likely protonation state still occurs 30% of the time. To account for this fact and alleviate the aforementioned approximation, when calculating the most representative protonation state of a residue from pH 0 to 12, only residues with an experimental pK_a at a minimum distance of 1.5 units were considered at each pH value. The 1.5 pH cutoff is arbitrary, but the same trend was observed when slightly different values (0.5–2) were used. The most abundant protonation states obtained from pKAI predictions are in good agreement with those derived from experiments and outperform those of PROPKA in a wide range of pH values (Supplementary Figure S4). Moreover, pKAI is the best model for assigning a fixed protonation state to a protein at biologically relevant pH values (Figure 3D), arguably the most common task pK_a predictors are used for. In contrast to the poor performance of the Null model and PROPKA in the physiological pH range, both models outperform pKAI and PypKa at pH levels lower than 4.0. In the acidic region, most Glu and Asp residues, which make up around 60% of the experimental test set, are titrated. PROPKA was trained on some of these Glu and Asp residues,⁵ which may have resulted in an overoptimistic evaluation of its performance at lower pH values. pKAI+ is biased to predict pK_a values between those of pKAI and the Null model. This bias has granted the model an edge in experimental pK_a estimations. However, in tasks in which the Null model does not perform well, pKAI+’s ability is also affected. This can be seen in the biological range at the more basic pH values.

Model Explainability

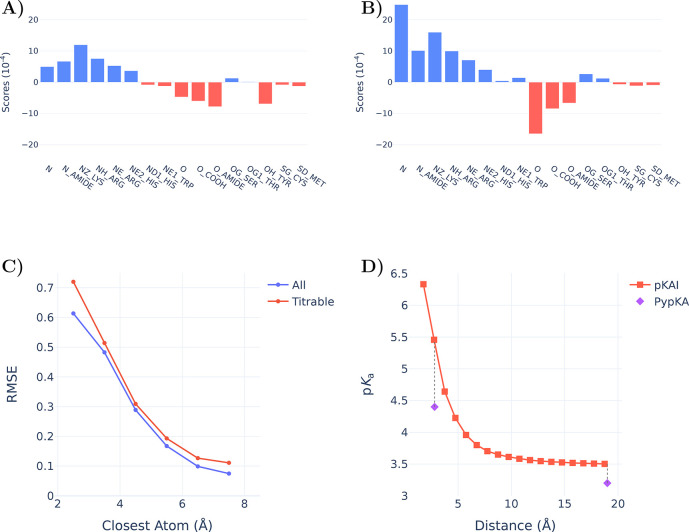
The main driving force for pK_a shifts in proteins is electrostatic in nature. In our model, each atom of the environment represents the contribution of a chemical group or part of a residue. This individual contribution toward the final ΔpK_a prediction can be estimated (see XAI in the Methods section for further details) and is shown in Figure 4A. Remarkably, although our model is given no information about atomic charges, it assigns contributions that are in agreement with the expected overall charge of the atom class. Cationic amine groups (NZ_LYS, NH_ARG, NE_ARG, and NE2_HIS) are clearly assigned positive scores (i.e., destabilize the protonation of the titratable residue) and are easily distinguishable from the anionic carbonyl groups (O_COOH from Glu, Asp, and C-termini residues). These scores provide a general insight into the network’s interpretation of each atom and should not be used for more quantitative analysis. Since the atom score is an averaged measure across the test set, an imbalance of closely interacting atoms of a specific class can dramatically skew its median contribution.

Figure 4.

Charge scores attributed by pKAI to all considered input atoms classes (Supplementary Table S6) of (A) all atoms and (B) atoms closer than 6 Å. C) Influence of the closest atom on the pKAI performance. (D) Impact of changing the distance of the closest atom on pKAI predictions of residue TYR-315 from structure 2BJU. For reference, we have included PypKa predictions of the same residue in the state presented in the experimental structure (closest distance of 2.8 Å) and in a modified structure in which the closest atom is absent.

Hydrogen bonds are some of the strongest interactions found in proteins; as such, their proper description is crucial to obtain accurate pK_a predictions. By comparing Figures 4 A and B, we can observe marked differences between the atom scores at close proximity and those farther away from the titrating residue. For example, the average scores of the very abundant classes of primary amines (N and N_AMIDE) and carbonyl groups (O and O_AMIDE) are much lower compared to their short-range contributions, where these become hydrogen donors and acceptors, respectively. The anionic Tyr residue is perceived to have an overall negative contribution except when it is close to another titratable residue; in this case, there seems to be no preferred state, as like any titratable residue it can act both as a donor and as an acceptor. On the other hand, the contribution of neutral nontitrating alcohol groups (OG_SER and OG1_THR) is almost exclusively attributed to their potential to form hydrogen bonds at short range.

Beyond the general understanding shown before, hydrogen bond contributions are hard to account for compared to other interactions. As shown in Figure 4C, the closer another residue (blue curve) is to the titrating one, the harder its is for the model is to correctly describe their interaction. The difficulty of the prediction increases dramatically at the typical distance of hydrogen bonds (2.5–3.2 Å). This is even more marked if one considers interactions established between two titratable residues (red curve). In this case, the network has to solve for the pK_a values of both residues simultaneously and in many instances is unable to do so. Hence, predicting the contribution of the remaining environment is easier than predicting that of a single hydrogen bond. This is illustrated in Figure 4D, where the agreement with the physics-based method is much higher when the closest atom is removed from the structure than when it is kept in its original position. Although many other profiles can be observed (Supplementary Figure S6), this trend is generally conserved. Considering that the model did not receive explicit information about hydrogen bonds, it is quite remarkable that it was able to correlate this type of interaction with larger pK_a shifts.

Solvent exposure is another property that is usually a key contributor to pK_a shifts. The models are trained without explicit knowledge of the 3D structure of the protein and are deprived of information regarding carbon atoms. Nevertheless, they seem to learn about the solvent exposure contribution. We compared the correlations (the Pearson correlation coefficient r and Spearman’s rank correlation coefficient ρ) between the calculated SASA and the pK_a shifts over the entire test data set. Using the known ΔpK_a, we obtained r_ΔpKa = −0.68 and −0.60, while using the predicted ΔpK_a, we got r_pred = −0.66 and −0.62, respectively. The similarity between these values indicates that the model learned the correct correlation between the SASA and the pK_a shift. Additionally, we tested different solvent exposure metrics as an additional input and observed virtually no performance improvement (Supplementary Table S7).

Finally, it is worth mentioning that the XAI analysis was a driving factor in the development of pKAI. In fact, the importance that the model assigns to each atom class (similar to Figure 4) was pivotal in the selection of the final set of atom classes aimed at describing the surrounding environment residues.

4. Discussion

We have introduced pKAI and pKAI+, two deep DL models, to predict theoretical and experimental ΔpK_a values, respectively. pKAI offers unprecedented efficiency, exhibiting a remarkable trade-off between accuracy and computational speed, and performance rivals those of CE-based methods, such as PypKa. pKAI could be used as a replacement for such methods, especially when dealing with large proteins or applications requiring multiple CE calculations, such as constant-pH MD simulations.¹⁶⁻²⁰ Considering the latest advances in sequence-to-structure predictions,⁴⁶ faster methods, such as pKAI, will likely be of use as exponentially more structures become available. Furthermore, when optimizing new structures for binding to specific targets (e.g., in the design of enzymes or antibodies), it is vital to have an accurate prediction of the protonation states.

While we strive for optimal accuracy, we are aware that many applications will only require a binary decision (hence, a qualitative prediction of pK_a shifts would be sufficient). For example, when selecting the most likely protonation state of a protein to run MD simulations, one only needs to predict whether each pK_a is larger or smaller than the pH value of interest. As intended, pKAI shows a performance similar to that of a PB-based model. Furthermore, it significantly surpasses PROPKA and the Null model in the physiological pH range.

Several other applications only require an estimation of the proton binding affinity using a fixed conformation. This quantity, termed pK_a^single, renders a good prediction of the macroscopic pK_a when averaged over a representative ensemble of conformations. From pK_a values, the most abundant or representative protonation states for a particular conformation can be calculated, improving the realism of methods such as molecular dynamics¹⁶⁻²⁰ and molecular docking.⁴⁷ pKAI is nearly perfect at mimicking representative protonation states given by PypKa, and it is particularly effective at physiological pH, achieving an astounding accuracy of 99.4% (Supplementary Figure S5). In a conformational ensemble, there are always many representative protonation states that differ significantly from the one calculated using the macroscopic pK_a values. Therefore, coupling pK_a^single calculations with conformational sampling techniques is very appealing in theory but difficult in practice due to the computational cost. By using pKAI instead of PypKa (or any other PB-based method), one would drastically decrease the computational overhead (up to 1000×).

pKAI does not handle all residues with the same performance. Difficult cases are caused by low representation in the training set, low solvent exposure, or close residues providing hydrogen bond interactions. These peculiar environments usually present high ΔpK_a values, which are not handled very well by the method. One clear way to improve our models would therefore be to introduce more training examples. Furthermore, the inclusion of more training data with rare environments would definitely enhance the performance. To avoid limiting the scaling rate by the availability of new experimental protein structures, we plan to generate new uncorrelated protein structures using conformational sampling methods, such as MD and MC. Another advantage of using computational methodologies is the ability to guide the protein conformational sampling to achieve electrostatic environments that are underrepresented in the training set. To better handle interactions with neighboring titratable groups, a change of environment encoding would be needed. One approach to be explored in future work would be to represent the whole protein as a graph and use graph neural network algorithms to learn the ΔpK_a values.

Although pKAI excels at predicting pK_a^single values, its performance is modest when estimating experimental pK_a values. Inspired by the observation that increasing the dielectric constant in PB-based methods improves the agreement with experimental results, we introduced a regularization parameter into the cost function. Similar to the dielectric constant, this regularization weight biases all predictions toward the residue’s pK_a values in water. The new model, pKAI+, outperformed all methods tested in this work, including PypKa, which was used to create the training set. However, this improvement, while significant for partially exposed residues that would otherwise exhibit overestimated pK_a shifts, penalizes the accuracies of more shifted residues.

In this work, we made the conscious decision to train our models solely on theoretical pK_a values and to use all the available experimental data as a test set. The reason for this choice is twofold. First, there are not enough experimental data points to successfully train large models such as DL ones. This issue could be circumvented with pretrained embeddings, assuming these representations hold the necessary information for the new task. Gokcan et al. used molecular representations encoding quantum mechanical information to obtain a neural network model with an RMSE of 0.5–0.75 for most titrable residues.²⁹ The second problem with this approach is that the available data is quite limited in variability. Since a model trained on experimental data will not be exposed to a wide variety of environments, in real-world applications it will likely need to extrapolate in many cases. Both these issues contribute to the risk of model overfitting and poor generalizability. Chen et al. trained tree-based machine learning models, such as XGBoost or LightGBM, on experimental data, and their best model exhibited an RMSE of 0.69.³⁰ To compare pKAI with these models and illustrate the data leakage problem at hand, we have refined our pKAI model by training it on same data split reported in ref (30). This new model seems to have an unparalleled performance (RMSE of 0.32 and MAE of 0.21). However, this level of accuracy likely cannot be expected for a rigid body calculation due to the missing entropic information. Furthermore, at the moment there are only 18 and 23 experimental pK_a values reported for Cys and Tyr residues, respectively. Even considering some degree of information transfer from other residue types, it is extremely unlikely that a few dozen residues are able to convey enough information to create a model with a robust predictive ability at inference. Contrarily, pKAI was trained on millions of environments, and as such we believe that the reported performance estimates are much better reflections of its predictive ability. Finally, it must be noted that experimental data (both structures and pK_a values) should not be taken as absolute truths with no associated errors. In fact, old measurements of a popular benchmark protein (hen egg-white lysozyme) were evaluated with modern NMR spectroscopy, and discrepancies of more than one pH unit were found.⁴⁸ It is reasonable to assume that at least some of the ≈1500 available experimental values have comparable errors, which only reinforces the importance of blind prediction exercises such as the pK_a Cooperative.⁴⁹

With pKAI and pKAI+, we are introducing the first DL-based predictors of pK_a shifts in proteins trained on continuum electrostatics data. The unique combination of speed and accuracy afforded by our models represents a paradigm shift in pK_a predictions. pKAI paves the way for accurate estimations of macroscopic pK_a values from ensemble calculations of pK_a^single values, overcoming previous computational limits. By design, the models were trained using a very simplified view of the surroundings of the titratable group, accounting only for residues within a 15 Å cutoff and ignoring all carbon and hydrogen atoms. This informed design choice allowed the models to stay small and fast. Explainability methods confirmed that this input information was enough for the model to capture crucial features such as electrostatics, solvent exposure, and environment contributions. The initial success of these models introduces several opportunities for further research, including problem encoding, accounting for conformational flexibility, interactions with other molecule types (i.e., small molecules, nucleic acids, and lipids), and adding further target properties that could be of interest for other applications.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00308.

• Performance of pKAI+ in various tests, accuracy of pKAI+, RMSE variation versus the magnitude of the pKa shift, and impact of changing the distance of the closest atom (PDF)

The authors declare no competing financial interest.