Trend estimation and short-term forecasting of COVID-19 cases and deaths worldwide

Significance

We present a globally applicable trend estimation method and a simple short-term forecasting strategy based on it for more than 200 countries and territories. Our trend estimation scheme relies on minimal information about the evolution of the pandemic, and is based on robust seasonal trend decomposition techniques. We demonstrate the performance of the proposed method in comparison with 1) a range of forecasting methods in prediction of cases in European countries and 2) a naive, but hard to beat, baseline. Based on the estimated trends, we estimate the effective reproduction number and propose global risk maps. The methodology has been integrated in our public dashboard since September 2020. Our forecasts have been used for providing recommendations to governmental organizations.

Abstract

Since the beginning of the COVID-19 pandemic, many dashboards have emerged as useful tools to monitor its evolution, inform the public, and assist governments in decision-making. Here, we present a globally applicable method, integrated in a daily updated dashboard that provides an estimate of the trend in the evolution of the number of cases and deaths from reported data of more than 200 countries and territories, as well as 7-d forecasts. One of the significant difficulties in managing a quickly propagating epidemic is that the details of the dynamic needed to forecast its evolution are obscured by the delays in the identification of cases and deaths and by irregular reporting. Our forecasting methodology substantially relies on estimating the underlying trend in the observed time series using robust seasonal trend decomposition techniques. This allows us to obtain forecasts with simple yet effective extrapolation methods in linear or log scale. We present the results of an assessment of our forecasting methodology and discuss its application to the production of global and regional risk maps.

It is of utmost importance for governments and decision makers in charge of the healthcare system response to anticipate the evolution of the current COVID-19 pandemic (1). When accurate and reliable, predictions can be very informative in defining appropriate policy measures and interventions, such as lockdown and containment measures, border closures, quarantines, school openings, and physical distancing. They are also useful for predicting hospital surge capacity, in order to manage hospital resources (2). Given that the pandemic is affected by these measures, testing policies, the appearance of new variants, the diffusions across borders, etc., long-term forecasts are difficult, and their usefulness remains unclear (3), whereas accurate short-term forecasts provide useful actionable information. Nevertheless, even short-term forecasts are far from trivial, as recently evidenced by (4), where a simple baseline appears to be not so easy to beat on a 1-wk horizon.

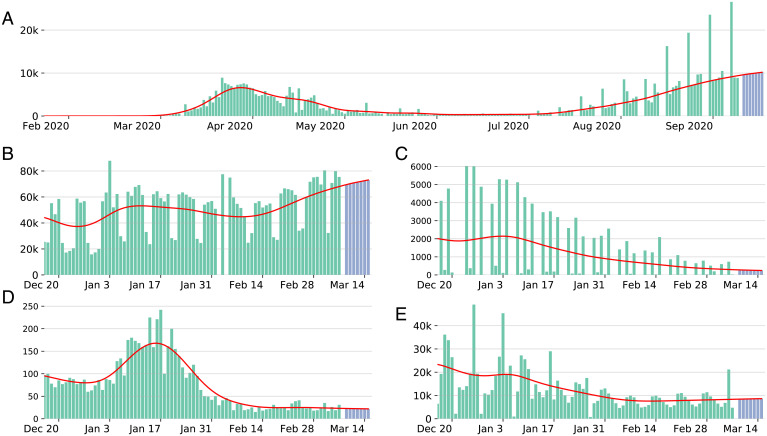
In this work, we propose a general methodology to produce forecasts on a 1-wk horizon, which is applicable to close to 200 countries, and as many states/regions or provinces. An additional challenge to achieve this goal is that the quality of the reported data varies significantly from country to country. This translates into different fluctuations and irregularities that can be observed in the reported time series (5). Many countries do not report on a daily basis or delay their reports to particular days of the week. In particular, seasonal patterns with a weekly cycle are observed for many countries. In several countries, for example, in Switzerland, the number of reported cases shows a significant decline during or immediately after the weekend, which is probably due to the fact that, on those days, fewer patients get tested and/or that the reporting is less active and thus delayed. Also, it is important to note that, as illustrated in the data from Spain in Fig. 1A, seasonal patterns are nonstationary and can actually change in time, in particular, if the reporting policies change. Furthermore, delays in reporting, changes in death cause attribution protocols, and changes in testing policies lead to abrupt corrections that introduce backlogs on some days, such that a number of daily cases or deaths which are anomalously high or even negative are reported. To take into account these peculiarities, we propose a forecasting methodology that relies on estimating the underlying trend with a robust seasonal trend decomposition method and on using simple extrapolation techniques to make a forecast over a week.

Fig. 1.

Green bars correspond to daily cases. Blue bars show the forecast for the next 7 d. The red line shows the estimated trend smoothed together with the forecast. (A) JHU daily cases for Spain with forecasts starting from September 10, 2020, with a negative observation in June 2020 (not shown in the plot), visible outliers, and seasonality patterns in reporting starting from July. Daily cases in the last 3 mo preceding December 3, 2021, for (B) Brazil, (C) Kansas, (D) China, and (E) Germany. Shown are the observed number of cases (green), estimated trend (red), and trend forecast for the following week (blue).

We apply the proposed algorithms to produce daily updated forecasts available on our public dashboard at https://renkulab.shinyapps.io/COVID-19-Epidemic-Forecasting/ (6). Since the early phases of the pandemic, we delivered trend estimates and forecasts of the evolution of the number of cases and deaths over a horizon of 1 wk for 192 countries at the national level. We subsequently added regional trends and forecasts for several countries, namely, Switzerland (cantonal), Canada (province level), the United States (state level), and France (departmental level). These forecasts were produced daily, including on Sunday and on holidays. Our dashboard provides, as well, today, calibrated probabilistic forecasts in the form of prediction intervals and the effective reproduction number based on our trend estimate via the method of (7), together with risk maps that assign to each country a color corresponding to its current epidemiological status (see Discussion).

The forecasting methodology presented in this paper was put into production already in September 2020 and has therefore been producing results on the dashboard since then. Our forecasts were available during the whole period of the pandemic and reported on the platforms of the European and US COVID-19 Forecast Hubs. Besides that, based on our estimated effective reproduction number (R-eff) and our forecasts, epidemiologists and global health experts from the Institute of Global Health have been providing recommendations to the European governments via the High-Level European Expert Group for the stabilization of COVID-19 of the World Health Organization and, additionally, to the Swiss National Science Taskforce for COVID-19 since its inception.

Related Work

The problem of forecasting the evolution of the COVID-19 pandemic has attracted the attention of many researchers, institutions, and individuals across the globe. As a result, a significant number of dashboards have appeared that monitor and/or make predictions about the evolution of the pandemic based on past observations. All these efforts are also being leveraged to build ensemble predictive models for different regions in the world. For instance, the United States Center for Disease Control and Prevention provides ensemble predictions for the United States at the state level in the US COVID-19 Forecast Hub (8). Similarly, the German and Polish COVID-19 Forecast Hub (9) provides ensemble predictions at the regional level for Germany and Poland. In March 2021, the European Centre for Disease Prevention and Control (ECDC) launched a European COVID-19 Forecast Hub (10) to provide short- and long-term ensemble forecasts for Europe. The considered modeling approaches rely on different data sources used (cases or/and death data, tests data, hospital data, mobility data, etc.) and aim at forecasting horizons ranging from 1 wk to several months. Epidemiological compartmental models or models inspired by them are among the most popular ones for the forecasting task, for example, the model by Institute for Health Metrics and Evaluation (11), YYG-ParamSearch (12), UMass-MechBayes (13), IEM_Health-CovidProject (14), and USC-SIkJalpha (15). Such models [e.g., structured SEIR (16)] split the population into different groups (age, demographics) and states (susceptible, infected, etc.) and model the transition dynamics of the population between the different states over time. The different parameters of the models can be deterministic or random, or be allowed to vary in time. Other approaches use statistical regression [e.g., UMich-RidgeTfReg (17) and LANL (18)], curve fitting [e.g., RobertWalraven-ESG (19)], and deep learning [e.g., GT-DeepCOVID (20)] to learn a predictor from past observations, or time series (e.g., ARIMA; e.g., MUNI-ARIMA) (21) to learn a representation describing the evolution of the dynamics of the observed measurements, for example, CMU TimeSeries (22, 23). Some models make strong assumptions on the transmission dynamics (24) or specific assumptions on the effect of different policies, for example, (25-27). These are just a few selected references, and the list is by no means exhaustive. For a more complete list of recent related literature, we refer the reader to (4, 28–31).

Our approach differs from most of the other existing approaches, in two ways. First of all, given that the usefulness of long-term (e.g., several weeks or months) forecasts has been subject to debate, because of the complexity of the phenomenon and the impossibility of taking into account a number of important factors, we consider, like (32), “that short-term projections are the most that can be expected with reasonable accuracy.” We thus focus on the prediction of short-term (1 wk to 2 wk ahead) forecasts of daily numbers for deaths and cases. Second, instead of building, directly, a forecasting model, our approach implements, first, a trend estimation model from daily cases/deaths observations that makes few or no assumptions about the underlying dynamics, doesn’t require estimating a large number of parameters (as opposed to, e.g., SEIR-type), and is therefore more robust and easier to apply at a more global scale. Our forecast is then obtained from the trend estimated via a simple extrapolation scheme. Our trend estimates are of independent interest, and we further use them to provide an independent estimate of the R-eff, which is an important measure for decision-making.

Results

Trend Estimation.

To model a potentially quickly varying seasonal pattern on a weekly horizon and suppress the influence of outliers, we implemented a piecewise trend estimation method based on a robust Seasonal Trend decomposition procedure using LOESS (locally estimated scatterplot smoothing) (33), which is further referred to as STL. It is a filtering procedure for decomposing time series into trend, seasonal, and residual components, which is furthermore robust to outliers. Specifically, the raw daily observations are modeled as

$$x_t={\tau }_t+{\delta }_t+r_t,$$

where τ_t is a slowly changing trend, δ_t is a possibly slowly changing seasonal component, and r_t is a residual. Since the magnitude of the seasonal term can reasonably be expected to be proportional to the trend, allowing for the seasonal component to change with time is relevant here, especially since, as discussed, reporting patterns change in time in several time series. To obtain a more quickly adaptive algorithm, we use STL to produce separate trend estimates on overlapping windows of 6 wk and recombine them using weighted averaging. Outliers identified as a by-product of the STL procedure are removed, the corresponding counts are redistributed in recent history, and the trend estimation procedure is run one more time on the cleaned data (see Materials and Methods for more details).

Fig. 1 illustrates the behavior of our trend estimation procedure for different countries that represent a certain diversity. In the cases of Germany and Brazil (Fig. 1B and E), the weekly seasonal effect is quite significant and clearly nonstationary, in particular between December 22, 2020 and January 3, 2021. For China (Fig. 1D), no particular seasonal effect can be identified, and several outliers seem to cooccur with the peak of the wave. The state of Kansas (Fig. 1C) illustrates an example of a fairly irregular seasonal effect. In all these cases, the trend estimation proposed appears to be robust to outliers and to changes in seasonality or lack thereof, and adapts to the regularity of the underlying trend. Beyond a qualitative evaluation of the trend estimation, a quantitative evaluation is difficult because of the lack of any ground truth, especially since the underlying dynamics of the trend in various countries and provinces are quite different. To some extent, the trend estimation proposed can be validated quantitatively via the forecasting algorithm which relies on it, since the quality of the forecast depends on the quality of the estimation of the trend.

Forecasting.

To predict cases and deaths 1 wk ahead, we propose to simply extrapolate, linearly, the daily trend, which was obtained with the above trend estimation algorithm (Fig. 1) either on the original or on the log scale, by preserving the most recent slope of the estimated trend. In the case of a decreasing trend slope, the extrapolation is carried out in log scale to prevent undershooting. For the case of an increasing trend, the extrapolation is performed in linear scale to prevent overshooting. To forecast the number of deaths, some models have been using lagged cases as input. Given the diversity of situations in different territories, and the fact that the relation between deaths and cases was sometimes quite unclear or changing in a short amount of time, we used the same simple forecasting approach as for cases. See SI Appendix for a discussion and references.

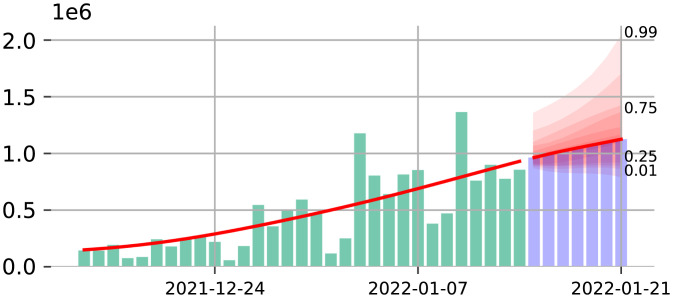
Following the recommendations of (4) and the requests of different forecast hubs, we also produced probabilistic forecasts for the weekly counts, in the form of a collection of 23 quantiles corresponding to the levels $0.05k$ for $k=1,\dots ,19$ and the extreme levels $\alpha =(0.001,0.025,0.975,0.99)$. These quantiles are estimated from quantile estimates of appropriately normalized errors of our forecast on a recent history, that are extrapolated for extreme levels using a tail model. See Fig. 2 and SI Appendix, Figs. S12–S14 for illustrations, and see Materials and Methods for more detail.

Fig. 2.

Illustration of the probabilistic forecast as a collection of nested intervals (red shaded regions) for the forecast of the number of cases in the United States.

Evaluations.

We evaluate our forecasts of the number of new cases in two ways, first, by comparing them with the forecasts obtained by several methods submitted to the European COVID-19 Forecast Hub (10) and, second, by comparing our forecast with a baseline on a larger set of countries, namely, the naive forecast (used on several hubs) that assumes that the weekly number of cases remains constant over the following week. To obtain interval forecasts, quantiles of the baseline predictive distribution are estimated from symmetrized observed errors of the baseline as in the US and European COVID-19 Forecast Hubs (4, 34).

The comparison is made in terms of mean absolute error (MAE) and average weighted interval score (WIS) (35) (see Materials and Methods). We also provide some details on the performance of our deaths forecasts in SI Appendix, section A.

To compare our method to the baseline, we compute the relative improvement in MAE (RMAE), the relative improvement in median absolute error (RmedianAE), and the relative improvement in average WIS (RWIS). The relative improvement is positive when the proposed forecasting method has a smaller error than the baseline. It can be thought of as a rate of decrease in error with respect to the baseline.

European Countries, European Hub.

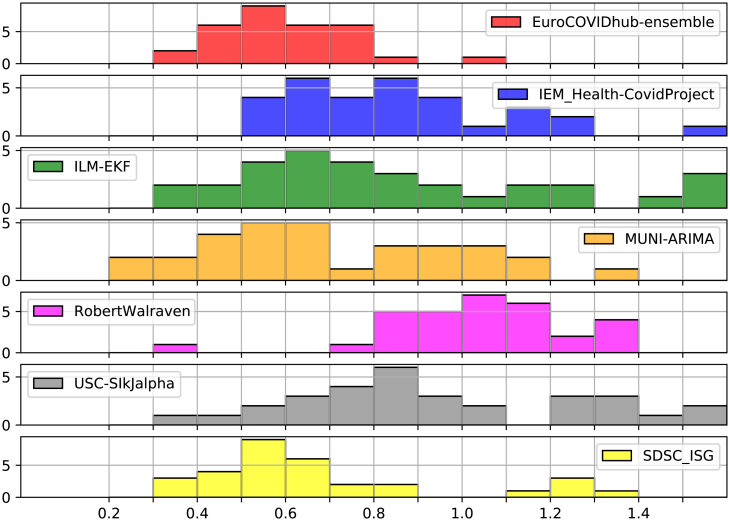
In order to compare the performance of our method with other methods, we used the data available at the European COVID-19 Forecast Hub. The methods submitted to the Hub are aggregated in order to obtain a EuroCOVIDhub-ensemble method, and a baseline (EuroCOVIDhub-baseline) is available. The weekly forecasts can be submitted once a week. Between April 1 and December 15, 2021, 43 submissions are available for both the EuroCOVIDhub-ensemble and the EuroCOVIDhub-baseline. We included, in our comparison, five other methods whose forecasts were all available for all 31 countries included in the hub, on a common large subset of 32 wk (i.e., 75% of all weeks). These methods are MUNI-ARIMA, IEM_Health-CovidProject, USC-SIkJalpha, RobertWalraven-ESG, ILM-EKF (36). In order to obtain results comparable across different countries, we report the ratio of the MAE (or average WIS) of each method to the MAE (or average WIS) of the EuroCOVIDhub-baseline, following the reporting standards (37) of the hub (SI Appendix, section A).

The results show that the proposed method (SDSC_ISG) performs well for most of the countries; for example, see the histogram of average WIS in Fig. 3 (for MAE, see SI Appendix, Fig. S1). It is clear that, in terms of average WIS, the performance of our method is one of the best ones and is close to the performance of the ensemble method and MUNI-ARIMA.

Fig. 3.

Histograms for the average WIS (in x axis) of 1-wk-ahead forecasts for the 31 European countries.

Additionally, we ranked the methods, according to their performance, from one to seven, where one corresponds to the method with the smallest value of MAE or average WIS. The results can be summarized as follows: For average WIS, our method outperforms all other methods (including the ensemble) for 8 countries, it ranks second or best for 16 of them, and it is among the top three for 25 countries; for MAE, it ranks first for 9 countries, second or best for 18, and within the top three for 25. More details can be found in SI Appendix, section A and Tables S1 and S2. Additionally, we used our methodology to perform 2-wk-ahead forecasts and obtained similar results (SI Appendix, Tables S3 and S4 and Figs. S2 and S3). Given that our forecast is based on a simple extrapolation of our trend estimate, this suggests that the trend estimate is accurate even on the boundary of the period where data are available.

Global Comparison with a Baseline.

For countries that report new cases with irregular delays, it is difficult to know whether the discrepancy between the forecast and reported weekly numbers is due to errors of the forecast or the fact that the reported numbers actually do not reflect accurately the current number of new cases.

We, therefore, present the main evaluation of our forecasting strategy on a restricted set of 80 countries, which report sufficiently frequently with a relatively low number of outliers. These countries were selected based on a set of criteria that are independent from our trend estimation and forecast methodology (see Materials and Methods). Nevertheless, we present the evaluation on the full list of countries in SI Appendix, section A. We use the data provided by Johns Hopkins University (38) after April 1, 2020, which corresponds approximately to the date after which all countries started reporting regularly.

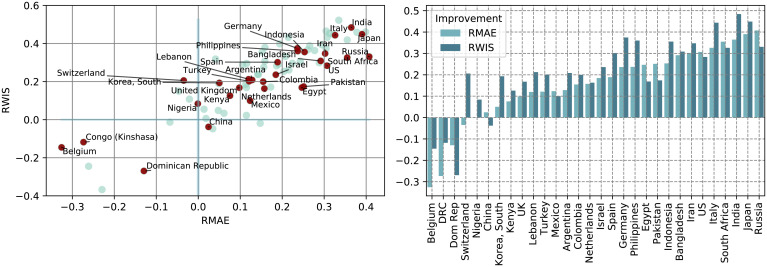
For the 80 selected countries, we performed a retrospective analysis from April 1, 2020 until December 15, 2021. For each day in this period, we forecast the total number of cases over the week following that day, using our methodology, and forecast the baseline using the data that were available at that date (and thus without corrections made a posteriori). As ground truth, we used the weekly data available on January 10, 2022. We evaluate our forecast by reporting, for each country, the RMAE, the RmedianAE, the relative improvement in coverage, and RWIS. The detailed evaluation results for the full list of considered countries can be found in SI Appendix, section A. In Fig. 4, Left, we display a scatter plot of the relative improvement in terms of RMAE and RWIS of our proposed forecast methodology over the baseline for the subset of 80 regularly reporting countries and for the 1-wk-ahead forecast. As can be seen, our method outperforms the baseline in both metrics for most of the selected countries. The same RMAE and RWIS values are displayed in Fig. 4, Right for 30 countries with either large populations or large population density, where the impact of the pandemic is potentially more important in terms of scale.

Fig. 4.

(Left) Scatter plot of RMAE and RWIS on 1-wk-ahead forecast for the selected subset of 80 countries, with points in red corresponding to the 30 countries with either larger populations or larger population density included in (Right) the bar plot.

Out of the 80 countries, 72 (i.e., 90%) show an improvement in MAE, 66 (82.5%) show an improvement in median AE, 71 (88.75%) show an improvement in WIS, and 68 countries show an improvement in both MAE and WIS. Only five countries do not show an improvement in either of these criteria. We also measure the coverage of the estimated prediction intervals, where our forecast is more accurate than the baseline for 66 countries. There are 53 out of 80 countries for which our method shows an improvement in all four metrics (MAE, median AE, average WIS, and coverage). This is the case, for example, for the United States, where the improvement in MAE and WIS over the baseline is 25%. We note that, in the work of (4), which compares forecasting algorithms focusing on US data, only 6 algorithms out of 23 achieve an improvement of more than 20% in MAE over the baseline [for forecasts on horizons of 1 wk to 4 wk; see table 2 in (4)].

The countries for which our method did not perform better than the baseline typically have long plateaus that the baseline benefits from, or/and have quickly changing seasonality patterns and direction of the trend, where the simple and robust baseline makes smaller errors. We analyzed how the AE varies as a function of the growth rate of the trend and evaluated to what extent, as soon as the trend is not flat, our method produces improved forecasts compared to the baseline (SI Appendix, section F and Fig. S4). Our method outperforms the baseline predictor when the growth rate is larger than 3% in absolute value, which shows that the proposed forecast is informative as soon as the trend is not flat.

Discussion

The comparisons with the forecasts submitted to the European COVID-19 Forecast Hub and the baseline demonstrate that the proposed forecasting methodology performs well. It should be noted that, as a forecasting method, the considered baseline is uninformative in the sense that it does not attempt to characterize the evolution of the curve. Despite this, as reported in (4), it is not easy to outperform this type of baseline in terms of pure predictive accuracy. Thus, any forecasting method characterizing the evolution of the curves which improves over this baseline can be useful. Our forecasts are available in the US COVID-19 Forecast Hub, European COVID-19 Forecast Hub, and German and Polish COVID-19 Forecast Hub.

Apart from producing forecasts and estimates of prediction intervals, the trend estimates that we obtain are of independent interest. We use them, in particular, to produce a stable estimate of the R-eff. The R-eff measures the expected number of people that can be infected by an individual at any given time (39) and has been used as a key indicator in this pandemic. Since its estimation requires, essentially, solving a deconvolution problem (7), it is quite sensitive to the irregularities in the data. In the original paper (7), the authors use LOESS smoothing in order to decrease the influence of the irregularities. In our case, we propose to apply the deconvolution based on our piecewise robust STL trend estimate.

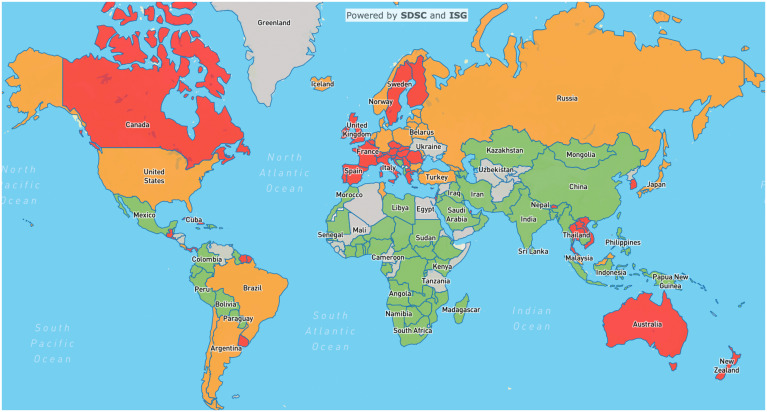
Finally, we use our estimates of the R-eff together with our forecasts to produce global daily risk maps according to the following scheme: If the number of tests as reported in Our World in Data is available and is above 10,000 per 1 million individuals, we compare the prediction for the number of weekly cases per 100,000 and R-eff with corresponding thresholds to color code the map. Green is assigned if the number of weekly cases per 100,000 inhabitants is below 30, orange is assigned if it is above 30 and the epidemic curve is descending (R-eff < 0.9), and red is assigned if it is above 30 and the epidemic curve is ascending or plateauing (R-eff > 0.9). Other organizations use similar thresholds for the cumulative rate per 100,000. For instance, our choice of a threshold coincides with the upper value of the third level (out of seven) in the ECDC map of the geographic distribution of COVID cases. The value of the R-eff is not taken into account in the risk assessment (color code) of a country when the incidence numbers are low, since its estimation becomes less reliable. Besides, it theoretically converges to one at the end of an epidemic, and, in such a regime, it is no longer an indicator of the severity of the pandemic. As a consequence, if no test data are available, or the number of tests is below 10,000 per 1 million population, the region is colored in gray, meaning that the data are missing/unreliable, and no risk assessment can be made. An example of a risk map is given in Fig. 5. These maps are useful for comparing the levels of epidemic activity between countries based on a discrete color code. These comparisons can be insightful, especially if the R-eff and different nonpharmaceutical interventions of countries are taken into account.

Fig. 5.

Snapshot of world risk map from March 25, 2022.

The fact that our model makes minimal assumptions about the data is an advantage in making it applicable to a large number of countries and regions. But there are, of course, downsides. In particular, our models only take into account a fairly limited amount of information, and, in particular, no indicators of mobility, prophylactic measures, or lockdowns are taken into account. Our models can, however, detect the effect of changes of behavior, which can be quite informative for decision makers. For example, when Ireland faced a second wave and the decision of lockdown was made on the October 21, 2020, our models predicted exponential growth for the seven following days. However, almost the day after, the curve broke, and, on October 25, the R-eff was clearly below one, with a descending epidemic trend. That could not be attributed to the lockdown measures only 4 d after they were taken.

Conclusion

We have proposed a methodology for trend estimation and short-term forecasts of the evolution of the number of COVID-19 cases and deaths, which is broadly applicable to a large number of different countries, states, and regions. Beyond its use to produce forecasts, our trend estimation method is of independent value, as it aims at providing a clear view of the current local evolution of the trend. Estimating the recent behavior of the trend is important as a tool to assess the current epidemic situation and to be able, subsequently, to analyze the effect of various measures. We use, in particular, our trend estimate to produce our own estimates of the R-eff curves, which are, in turn, used to produce risk maps. For the forecast, our evaluation shows that 1) the methodology performs well compared to several methods submitted to the European COVID-19 Forecast Hub and 2), for the 80 selected countries in which we can reliably use weekly data as ground truth, we outperform the baseline in a large fraction of countries.

Materials and Methods

Preprocessing.

Before applying the trend estimation model to the data, we remove negative values corresponding to reassessment of the counts, while making sure that the cumulative counts are preserved by appropriately scaling our estimates. We infer which zero counts on a given day correspond to missing reports, and we eventually impute the counts corresponding to these missing reports. The corresponding procedures are detailed in SI Appendix, section B.

STL.

Our trend estimation algorithm leverages the STL proposed in (33). STL consists of an iterative procedure that alternates between the estimation of the seasonal and trend components, each of them being estimated using a LOESS model, as well as the reestimation of importance weights associated with each observation for robust estimation. More precisely, the algorithm consists of two nested loops: The inner loop comprises several steps involving moving average and LOESS nonparametric regressions (40) in order to estimate the seasonal and trend components for the current set of robustness weights. The importance weights are then updated in the outer loop, based on the residuals after the update of the seasonal and trend components. The procedure is repeated for a number of iterations.

Trend Estimator.

First, we smooth with STL separately all intervals of 6 wk that are starting every 3 wk from the end of the time series (so that each interval is half overlapping with the previous one). In the absence of outliers (which should be detected by the robust STL procedure), each trend estimate computed on a 6-wk interval is rescaled to account for the same total number of counts as the observed data, and, to obtain the final trend estimate, on each disjoint 3-wk interval defined from the end of the time series, we compute a pointwise weighted combination of the two overlapping trend estimates computed on this interval. In the presence of outliers, these are first identified by our method and redistributed in the past. After that, the same procedure as explained before is applied to the corrected data. For further details, we refer to SI Appendix, section C.

Probabilistic Forecast.

We produce probabilistic forecasts under the form of a collection of 23 quantiles for the predicted average daily counts, which produce, as well, a collection of nested prediction intervals of the form $[q_{\alpha },q_{1-\alpha }]$. These quantiles are estimated based on empirical quantiles of the retrospective deviations of the daily forecast $f_{h,t}$ from the actual weekly rolling mean ${\overline{x}}_{t+h}=(1/7){\displaystyle {\sum }_{k=-3}^3{x}_{t+h+k}}$ for horizons $h=1,\dots ,H$ and 19 levels $\alpha =0.05,0.10,\dots ,0.95$, normalized by $\sqrt{f_{t,h}}$, namely, the scaled errors

$$({\overline{x}}_{t+h}-f_{t,h})/\sqrt{f_{t,h}}.$$

The length of the history for estimation of the 19 quantiles was set to $40+H$ days. The normalization by $\sqrt{f_{t,h}},$ which performed better than $f_{t,h}$ or one, is motivated by a Poisson error distribution model. For the lowest/highest levels ($\alpha =0.01,0.025,0.975,0.99$), we extrapolated the quantiles based on an exponential tail model whose scaling parameter is estimated from the other estimated 19 quantiles. Finally, we shift all quantiles ${\tilde{q}}_{{\alpha }_i,h}$ on the scaled errors by a constant to enforce that ${\tilde{q}}_{0.5,h}=0.$ This is motivated by the fact that we expect our forecast to be close to the conditional best median forecast. The prediction quantiles are finally of the form $q_{{\alpha }_i,h}=f_{t,h}+{\tilde{q}}_{{\alpha }_i,h}\sqrt{f_{t,h}},$ where $f_{t,h}$ is the current forecast. See Fig. 2 and SI Appendix, Figs. S12–S14 for an illustration.

Similarly, for the weekly total number of cases/deaths k weeks ahead, $k=\{1,2\},$ the ground truth can be computed as $X_{t+4+7(k-1)}={\displaystyle {\sum }_{h=1}^7{x}_{t+h+7(k-1)}}$, and the point forecast is just $F_{t,4+7(k-1)}={\displaystyle {\sum }_{h=1}^7{f}_{h,t+7(k-1)}}$. The probabilistic forecast can be computed using the same approach as above by replacing ${\overline{x}}_{t+h}$ with $X_{t+4+7(k-1)}$ and replacing $f_{t,h}$ with $F_{t,4+7(k-1)}.$ In that case, the horizon is in weeks instead of days.

Evaluation Metrics for Point Forecasts.

If ${\overline{x}}_t=(1/7){\displaystyle {\sum }_{k=-3}^3{x}_{t+h+k}}$ is, as before, the rolling mean of the number of daily new cases over a week and f_t is the corresponding point forecast (which we identify with the median forecast), the absolute error of f_t is $\text{AE}(f_t)=|f_t-{\overline{x}}_t|$. We consider, as evaluation metrics, the MAE and the median absolute error over the evaluation period. Given a baseline $b_t={\overline{x}}_{t-7}$, the RMAE is defined as

$$\text{RMAE}=(\text{MAE}(b)-\text{MAE}(f))/\text{MAE}(b).$$

Similarly, one can define RmedianAE.

Evaluation Metrics for Probabilistic Forecasts.

Following the methodology presented in (4), we evaluate our probabilistic forecasts using proper scoring rules defined for forecasts taking the form of a collection of quantiles or equivalently of nested intervals, namely, the WIS.

The interval score (24) at level $\alpha \in (0,1)$ for the interval $[\ell ,u]$ and observation ξ is defined as

$$I{S}_{\alpha }([\ell ,u],\xi )=u-\ell +\frac{2}{\alpha }[(\ell -\xi )\mathbb{1}\{\xi <\ell \}+(\xi -u)\mathbb{1}\{\xi >u\}],$$

where $\mathbb{1}\{·\}$ is one if the condition is satisfied and is zero otherwise. The WIS (24) is a proper scoring rule for probabilistic forecast, which is defined as follows: for a number of levels $A=\{{\alpha }_1,\dots ,{\alpha }_K\},\hspace{0.17em}{\alpha }_i\in [0,0.5)$ and the corresponding estimated quantiles of the predictive distribution P, defined as $q_{\alpha }=\inf \left\{q\right|P(\mathrm{\Xi }\le q)\ge \alpha )$ for the level ${\alpha }_i\in \{{\alpha }_1,\dots ,{\alpha }_K,0.5,1-{\alpha }_K,\dots ,1-{\alpha }_1\}$, where Ξ is the random variable associated with the observation $\xi ,$ as follows:

$$\text{WIS}(P,A,\xi )=|\xi -q_{0.5}|+{\displaystyle \sum _{k=1}^K{\alpha }_k}I{S}_{2{\alpha }_k}([q_k,q_{2K+2-k}],\xi ).$$

The average WIS is defined as the mean of the WIS for the predictive quantiles of distributions P_t constructed to predict ${\overline{x}}_t$ over the times t in the estimation interval; that is, $\text{MWIS}=(1/T){\displaystyle {\sum }_{t=1}^T\text{WIS}}(P_t,A,{\overline{x}}_t).$ Relative improvement in MWIS (RWIS) is defined in similarly as RMAE.

Selection of Countries with More Reliable Data.

For our main results, we kept 80 countries whose reports of cases are sufficiently frequent and have only a few missing values and a limited number of outliers. We proceeded as follows. First, we excluded 52 countries that reported cases on less than 70% of the days, since these countries have either a very small number of cases or are reporting very irregularly, and, among the remaining countries, the 39 countries for which more than five consecutive days were missing. Then, we performed robust outlier detection (described in SI Appendix, section D) to estimate the number of outliers in each time series, and we excluded the 20 countries with the largest number of outliers among the remaining ones. It is important to note that the selection criteria proposed here are independent of our trend estimation and forecast methodology.

Data Availability

Code and evaluations are accessible at (41). We use the data, which is publicly available in COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (38, 42). The forecasts of models submitted to European Covid-19 Forecast hub (10) used in comparisons for horizons 1 and 2 wk are stored in (43).