Number neurons in the nidopallium of young domestic chicks

Significance

Numerosity, that is, the number of items in a set, is a significant aspect in the perception of the environment. Behavioral and in silico experiments suggest that number sense belongs to a core knowledge system and can be present already at birth. However, neurons sensitive to the number of visual items have been so far described only in the brain of adult animals. Therefore, it remained unknown to what extent their selectivity would depend on visual learning and experience. We found number neurons in the caudal nidopallium (a higher associative area functionally similar to the mammalian prefrontal cortex) of very young, numerically naïve domestic chicks. This result suggests that numerosity perception is possibly an inborn feature of the vertebrate brain.

Abstract

Numerical cognition is ubiquitous in the animal kingdom. Domestic chicks are a widely used developmental model for studying numerical cognition. Soon after hatching, chicks can perform sophisticated numerical tasks. Nevertheless, the neural basis of their numerical abilities has remained unknown. Here, we describe number neurons in the caudal nidopallium (functionally equivalent to the mammalian prefrontal cortex) of young domestic chicks. Number neurons that we found in young chicks showed remarkable similarities to those in the prefrontal cortex and caudal nidopallium of adult animals. Thus, our results suggest that numerosity perception based on number neurons might be an inborn feature of the vertebrate brain.

Be it a number of conspecifics in a group (1), a number of food items (2), or a number of motifs in a song (3), correct estimation of quantities is of vital importance for animals. Several behavioral studies have confirmed that numerical competence is not a prerogative of human beings but is a widespread phenomenon in the animal kingdom (reviewed by refs. 4 and 5). Mammals (6–8), birds (3, 9, 10), reptilians (11), amphibians (12), fishes (13), and invertebrates (14), although evolutionarily distant, all can spontaneously assess quantities using an approximate number system (15).

For the approximate number system, which is based on Weber’s law (16), the perception of cardinal numbers resembles the perception of continuous physical stimuli, and the just noticeable difference is proportionate to the quantity being estimated. As a consequence, discrimination of quantities is imprecise and depends on the numerical distance between stimuli. In other words, it is easier to tell apart 5 and 10 than 9 and 10. Moreover, discrimination of quantities becomes increasingly difficult with the numerical size. For a given numerical distance (e.g., one), it is easier to discriminate between numbers with low magnitudes (1 vs. 2) than with high magnitudes (9 vs. 10).

Recent research has uncovered that the approximate number system relies on the activity of a specific neuronal population. Neurons that respond to abstract numerosity irrespective of objects’ physical appearance (shape, color, size) have been found in the forebrain of human and nonhuman primates (17, 18) and in crows (19). In mammals, numerical responses were recorded in the parietal and the prefrontal cortices (PFCs) (17). In birds, similar neurons have been described in the caudolateral nidopallium (NCL) (19). The NCL is believed to be an analog of the PFC in the avian brain (20) and is involved in a variety of cognitive processes, including memory formation (21, 22), abstract rule learning (23), and action planning (24).

Both monkeys and crows are among the most evolutionarily advanced species of their phylogenetic groups. They independently developed sophisticated intellectual capacities (25), and both possess enlarged forebrains (26). The neural representations of numerosities described in these species also share remarkable similarities (19, 27–29). In both species, the number neurons show the strongest response to a preferred numerosity, which gradually decreases along with the numerical distance (numerical distance effect, but see ref. 30). Their tuning curves are skewed toward larger numerosities and become progressively broader (less selective) with increasing numerosities (numerical size effect). However, it is unclear whether the presence of similar number neurons in these two species emerges as a consequence of their elaborate cognitive skills and enlarged forebrains. To understand the evolution of the number sense, we need to explore its neural correlates in distant bird species with more ancestral traits.

Moreover, until now, number neurons have been described only in adult animals (e.g., refs. 19, 27–29, and 31). At the same time, behavioral data from human infants (32) and young domestic chicks (10, 33) indicate that some core numerical abilities might be an inborn or spontaneously emerging (34, 35) property of the vertebrate brain. Testing the presence of number neurons in young and untrained organisms is crucial to verify this hypothesis.

In our study, we aimed to describe the neural correlates of the number sense in domestic chicks (Gallus gallus), which belong to a sister group of modern Neoaves (36). The domestic chick is a well-established developmental model for studying numerical cognition. Soon after hatching, these birds are already capable of discriminating quantities (33, 37) and even performing basic arithmetic operations (10). It has also been shown that young chicks represent numbers across the mental number line (38), a cognitive ability that had been previously attributed only to humans.

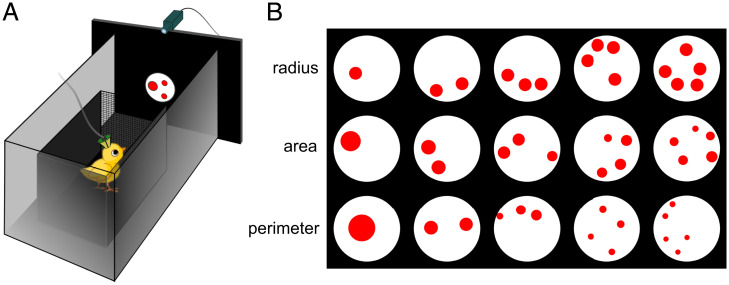
We hypothesized that neural processing of numerical information in young untrained chicks might be similar to that in crows, despite them having evolved independently over the last ∼70 million years (36). In a domestic chicken, the NCL is morphologically different from that of corvids (39), but it is unclear whether this reflects any functional difference. Therefore, we decided to search for neural responses to numerical stimuli in the NCL of domestic chicks. For this purpose, we habituated young chicks to a computer monitor, where numerical stimuli were presented (Fig. 1A). We explored neural responses to numerosities from one to five. To control for nonnumerical parameters, we presented three different categories of stimuli: “radius-fixed,” “area-fixed,” and “perimeter-fixed” (Fig. 1B).

Fig. 1.

Experimental design. (A) Schematic drawing of the experimental setup. Young chicks were placed in a small wooden box in front of the screen, where numerical stimuli appeared. They were trained to pay attention to the stimuli without any further discrimination between different numerosities. (B) Examples of different types of numerosity stimuli that we presented in every neural recording: “radius-fixed,” “area-fixed,” and “perimeter-fixed.”

Results

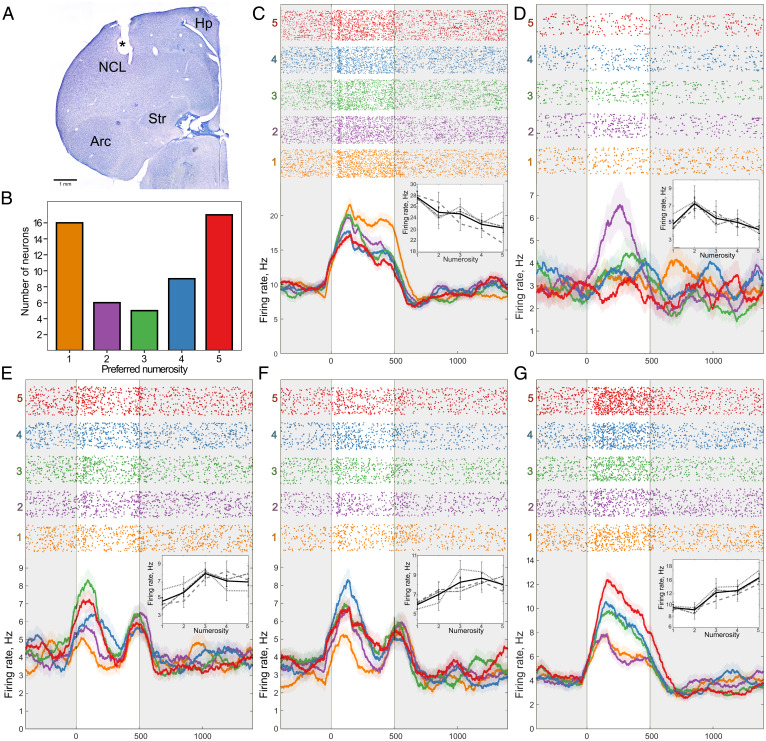
To test the neural responses to numerical stimuli in young domestic chicks, we recorded the activity of 471 units in the NCL and examined the mean firing rate of each unit during stimulus presentation (Fig. 2 A and B). To identify how many of these neurons would convey numerical information, we performed a two-way ANOVA with the factors “numerosity” (five levels: one to five) and “stimulus type” (three levels: “radius-fixed,” “area-fixed,” and “perimeter-fixed”). A unit was considered as a number neuron only if the main effect of the factor “numerosity” was highly significant (P < 0.01), but not the effect of the “stimulus type” nor the interaction between the two factors (19). Among these 471 units that we recorded, 53 (11%) responded to numerosity irrespective of the stimulus type.

Fig. 2.

Neurons in the NCL of chicks responding to numerosity. (A) An exemplary coronal section of the chicken forebrain showing the recording site in the NCL (electrolytic lesion is marked by an asterisk). Arc, arcopallium; Hp, hippocampus; Str, striatum. (B) Distribution of neurons that preferred each numerosity stimulus. Examples of neurons that were tuned to numerosity one (C), two (D), three (E), four (F), or five (G). (Top) Raster plots representing neural activity, where each line corresponds to one trial, and each dot corresponds to a spike. Trials are grouped by numerosity. The 500-ms duration of the stimulus is marked by a transparent window. (Bottom) Averaged spike density functions (smoothed by a 100-ms Gaussian kernel; SEM is plotted as a shaded area along the lines). (Insert) Average firing rate in response to numerosities of each stimulus type. Gray dotted line corresponds to “radius-fixed,” dashed line corresponds to “perimeter-fixed,” dot-dashed line corresponds to “area-fixed” stimuli, and black solid line corresponds to an average. Error bars correspond to SEM.

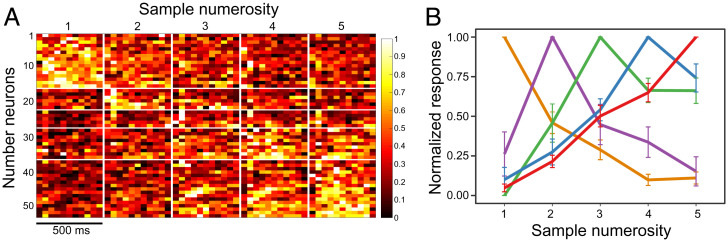
We then wanted to compare the tuning curves of neurons that preferred different numerosities. The preferred numerosity for every number neuron was defined as the numerosity that elicited the strongest neural response (after ref. 19). Five examples of number neurons tuned to different numerosities are shown in Fig. 2 C–G. The corresponding statistics of these five neurons are summarized in Table 1. The responses of all 53 number neurons are summarized in Fig. 3A (for statistical results, see SI Appendix, Table S1; for an example of trials with numerical responses, see Movie S1). Most of the number neurons were tuned to the numerosities one (30%, n = 16) and five (32%, n = 17). However, we found neurons responsive to other numerosities as well (two: 11%, n = 6; three: 9%, n = 5; four: 17%, n = 9), covering the whole range of tested numerosities (Fig. 2B).

Table 1.

Results of the two-way ANOVA for five example number neurons shown in Fig. 2 C–G

Preferred numerosity	ANOVA (Firing rate ≈ stimulus type * numerosity)
	Numerosity	Stimulus type	Interaction
num1	F(4,251) = 5.7273, P < 0.001	F(2,251) = 0.9275, P = 0.396	F(8,251) = 1.2411, P = 0.273
num2	F(4,253) = 3.5881, P = 0.007	F(2,253) = 0.2355, P = 0.79	F(8,253) = 0.454, P = 0.887
num3	F(4,496) = 5.8789, P < 0.001	F(2,496) = 0.1179, P = 0.889	F(8,496) = 1.4538, P = 0.173
num4	F(4,308) = 4.2385, P = 0.002	F(2,308) = 0.1141, P = 0.892	F(8,308) = 0.9124, P = 0.506
num5	F(4,355) = 13.4938, P < 0.001	F(2,355) = 1.832, P = 0.162	F(8,355) = 0.3219, P = 0.958

Preferred numerosity: numerosity eliciting the strongest response. ANOVA results (F statistics and P value) for the factor “stimulus type” (“radius-fixed,” “area-fixed,” or “perimeter-fixed”), “numerosity” (numerosity one to five), or interaction between them.

Fig. 3.

Neural responses and tuning curves of number neurons. (A) Neural response of all recorded number neurons to numerosity stimuli. Heatmap values represent the mean firing rate during the stimulus presentation (binned by 50 ms), normalized [0, 1] for the corresponding neuron in each row. Values are further grouped by the numerosity stimuli from one to five (vertical white lines), and by the numerical preference of recorded neurons (horizontal white lines) from neurons that preferred numerosity one (Top) to neurons that preferred numerosity five (Bottom). (B) Average tuning curves of numerosity selective neurons. The neural activity of neurons is first normalized (0 = response to the least preferred numerosity, 1 = response to the most preferred numerosity) and then grouped by their most preferred numerosity. Error bars correspond to SEM.

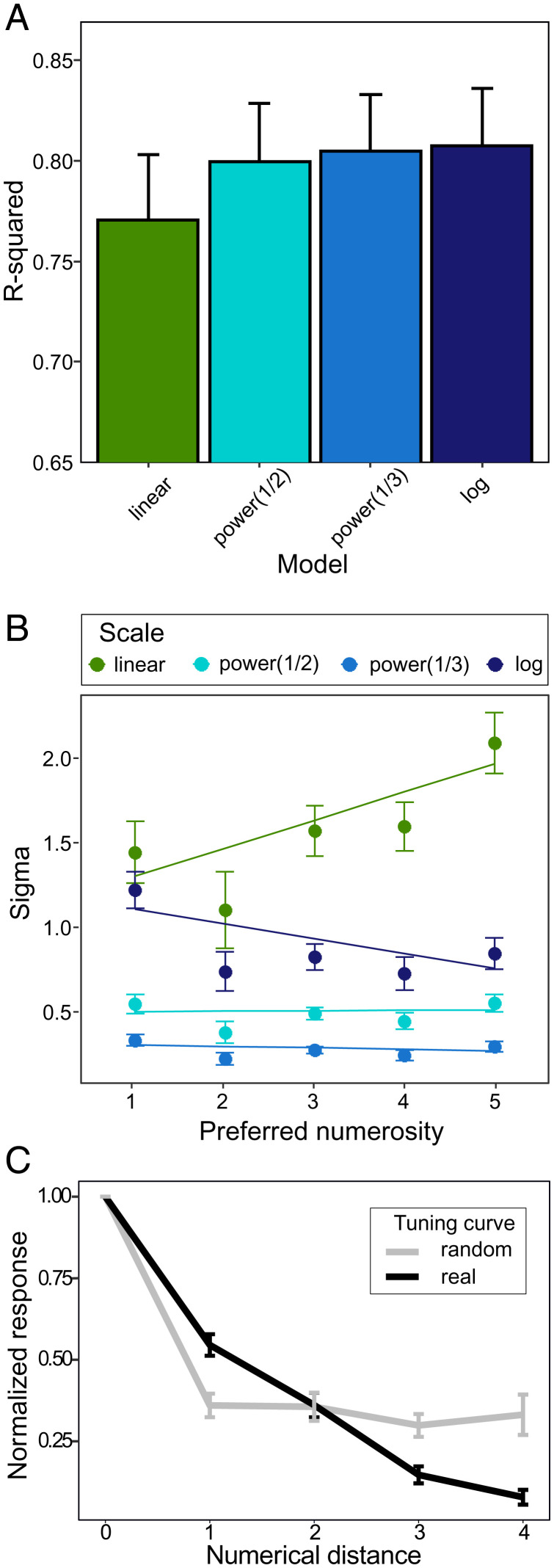
To verify whether our number neurons would behave as expected from the numerical magnitude effect, we grouped neurons by their preferred numerosity. In accordance with the magnitude effect, the tuning curves of number neurons were asymmetric and increasingly wider toward larger numerosities (Fig. 3B). To quantify this numerical magnitude effect, we plotted neural filter functions of single neurons on four different scales: a linear scale, a power function with an exponent of 0.5, a power function with an exponent of 0.33, and a logarithmic (log2) scale. The neural filter functions became significantly more symmetric on a nonlinear scale (Friedman test: X²(3) = 10.653; P = 0.014; Fig. 4A), with the linear scale significantly different from the power 0.33 and logarithmic scales (Nemenyi test: P = 0.022 and P = 0.028, respectively), but not from the power 0.5 scale (Nemenyi test: P = 0.176). The sigma of the Gaussian fit increased with numerosity only when plotted on a linear scale (Fig. 4B, slope of the linear fit = 0.17) but not with other nonlinear scales (Fig. 4B, power 0.5: slope = −0.003; power 0.33: slope = −0.01; log2: slope = −0.03), as expected based on traditional models of number coding.

Fig. 4.

Response properties of number neurons. (A and B) Comparison of different scaling schemes for the tuning curves. (A) R-squared, a measure of goodness of fit reflects symmetry of the tuning curves plotted on the four different scales. The tuning curves of number neurons become more symmetric when plotted on the nonlinear scale. (B) Sigma of the Gaussian fit for neurons preferring different numerosities. When plotted on the linear scale, the tuning curves become wider with increased numerosity. Error bars correspond to SEM. (C) Averaged normalized activity of all numerosity selective neurons compared to the random tuning curve (see Materials and Methods for details). The neural activity was normalized (0 = response to the least preferred numerosity, 1 = response to the most preferred numerosity) and then plotted as a function of absolute numerical distance from the most preferred numerosity. Neural response of numerosity selective neurons (black line) gradually decreased with the numerical distance. The slope of this tuning curve is notably different from the random tuning curve (gray line) of false-positive neurons obtained by random shuffling of trials. Error bars correspond to SEM.

We verified that the apparent numerosity responses that we observed could not have emerged just by chance, and they represent a true feature of the networks from which we recorded. Therefore, to evaluate the probability of finding false-positive numerical responses in our dataset, we used the trial-shuffle method. We shuffled trials of every recorded unit (n = 471) 1,000 times. After each shuffling, we selected false-positive number neurons by the same statistical criteria described above. The proportion of real number neurons (11%; 53 out of 471) was significantly higher than the proportion of false-positive units (0.95%; 4,488 out of 471,000) obtained by the analysis of randomly shuffled trials (proportion test: X²(1) = 512,56, P < 0.001). This result makes it extremely unlikely that described numerical responses represent a statistical artifact.

We further compared the tuning curves between the false-positive number neurons and the real number neurons. This allowed us to show that these false positives created by shuffling behave remarkably differently from the real number neurons that we recorded. First, for each numerical category, we randomly selected the same number of corresponding false-positive neurons as the actually recorded number neurons in that category, that is, 16, 6, 5, 9, and 17 false-positive neurons that were “tuned” to numerosities one to five, respectively (Fig. 2B). Then, we compared the tuning curves of the real and false-positive neurons (Fig. 4C), computing a two-way ANOVA with the factors “absolute numerical distance” (five levels: zero to four) and “data type” (two levels: real and false positive). The response of real neurons decreased gradually with numerical distance, meaning that the closest numerosities were more likely to trigger the number neurons. In contrast, the tuning curve of the false-positive neurons, which, by chance, happened to have higher firing rates for a random numerical stimulus, was markedly different from real number neurons (interaction for the factor “numerical distance * data type”: F_(1,526) = 6.275; P = 0.01).

We further wanted to quantify the degree of selectivity of each number neuron for its preferred numerosity. This allowed us also to test whether the neurons would behave according to the expected numerical size effect, by which neurons tuned to lower numerosities are generally more selective than neurons coding for larger numerosities. This was done by performing a post hoc analysis and comparing the response between the most preferred numerosity and the other numerosities (Table 2). Nine out of 53 number neurons showed statistically different firing rates between the most-preferred and closest neighboring numerosities. In line with the numerical size effect, neurons tuned to lower numerosities were generally more selective than neurons coding for larger numerosities. For instance, 6 out of 16 neurons with the preferred numerosity one significantly decreased their firing rate in response to the numerosity two. At the same time, out of 17 neurons that preferentially responded to the numerosity five, only 1 neuron showed significantly lower response to the numerosity four.

Table 2.

The summary of the post hoc analysis

Summary		Number of neurons
Sum	Group	num1	num2	num3	num4	num5
16	num1		6	9	12	14
6	num2	4		2	1	3
5	num3	5	1		0	0
9	num4	6	2	1		1
17	num5	15	12	6	1

For each group, based on their preferred numerosity, we calculated the number of neurons that showed significant difference between the most preferred and the given numerosity.

As the next step, we wanted to verify whether our number neurons would behave according to the expected numerical distance effect. The number neurons generally better differentiated between numerosities with increasing numerical distance (Generalized Linear Model (GLM) for absolute numerical distance: X²(18) = 3.935, P = 0.047; GLM for the log of the numerical distance: X²(18) = 6.544, P = 0.011). This effect was more prominent when the numerical distance was calculated on the logarithmic scale: The GLM for the log of the numerical distance had a better fit than the GLM for absolute numerical distance (difference in the Bayesian information criterion [ΔBIC] = 6.36). For a summary of all post hoc results, see SI Appendix, Table S2.

Discussion

We recorded number neurons in 8- to 12-d-old chicks, the youngest animals in which number neurons have been described so far. In the NCL of young domestic chicks, 11% of neurons showed a strong selective response to numerical stimuli, confirming the role of this structure in avian numerical cognition. Moreover, our chicks were not trained in any numerical discrimination task. Instead, they were simply paying attention to the screen, where the numerical stimuli were presented [passive fixation (40)]. Thus, our young chicks can be considered numerically naïve (see ref. 28).

This result is in line with previous studies on numerically naïve adult animals of distant lineages: 14% of neurons in the PFC of adult monkeys (28) and 12% of neurons in the NCL of adult crows (29) have shown numerical response. It is important to note that, in any of these studies, including our own, we cannot completely exclude a potential unsupervised learning effect due to repeated exposure to numerical stimuli. Indeed, recent studies have found that, in a deep neural network designed to analyze images, a similar amount of number detectors can emerge spontaneously (35), even without pretraining (34, 41). However, the hypothesis that number neurons can spontaneously emerge in the biological visual system has not been directly tested so far.

Our data, together with behavioral evidence from newly hatched domestic chicks (10, 33) and newborn infants (32), suggest that numerosity detection might be an inborn or spontaneously emerging feature of the brain. Our results certainly should not be automatically extrapolated to other newborn organisms, since the domestic chicken is a precocial species with a very rapid development after hatching. Nevertheless, even in 2-wk-old chicks, the functional organization of the brain still remains immature and flexible (42). Thus, the presence of number neurons in young chicks, which were not trained to discriminate any specific numerosity, supports the idea of an inborn number sense. Moreover, since behavioral studies (10, 37) show that newly hatched chicks perceive numerical information, we might expect to find number neurons already at the first day after hatching.

The number neurons in domestic chicks showed very similar features to those observed in primates and crows (19, 28, 43). First, the number neurons we observed were tuned to specific numerosities, in accordance with the labeled-line code shown for the number neurons in the NCL of crows (19, 43). Second, chicks’ number neurons showed a specific decay in response to nonpreferred numerosities, which was similar to number neurons in other species and could not have been obtained by chance (see false-positive neurons in Fig. 4C). Third, we observed the numerical magnitude effect: The tuning curves of number neurons became wider with increased numerosity and became more symmetrical when plotted on the nonlinear scale (Fig. 3B), although this feature might be not exclusive for labeled-line coding (41, 44). Also, the selectivity of the neural response to nonpreferred numerosities increased with the logarithm of the numerical distance, rather than with the absolute numerical distance (for similar results in monkeys, see, e.g., ref. 45).

Here we have followed the approach that is most commonly used in the literature to identify the presence of number neurons and to describe their response properties in accordance with the labeled-line hypothesis (e.g., refs. 18, 19, 45, and 46). One should, however, mention an alternative hypothesis for coding of numerical information, that is, a summation coding scheme (30, 47). Summation coding predicts that a neuron, instead of being tuned to a specific cardinal numerosity, monotonically increases/decreases its firing rate with the numerical magnitude (SI Appendix, Fig. S2). Cardinal numerosity might then be decoded from the pooled activity of this cell. To distinguish between labeled-line and summation coding, one can test whether tuning curves of neurons preferring the numerosities in the middle of the tested range (in our case, numerosities two and three) are better described with the linear or with the Gaussian fit. We tackled this problem and performed additional analyses reported in SI Appendix, Fig. S2. The majority of our neurons did not show the linear increase/decrease of their firing rate with numerosity, and their tuning curves were bell shaped rather than linear. This, however, does not account for all of our number neurons. Therefore, to unequivocally tell apart summation vs. labeled-line coding schemes, future studies would need to test a wider range of numerosities. However, regardless of the underlying coding mechanism, our data still represent direct evidence of neural representation of numerical information in the brains of young naïve chicks.

The overall low selectivity to specific numerosity at a single-cell level, as revealed by the post hoc analysis (Table 2), appears to be similar to what was observed in other species (19, 28, 43). How brains can depict precise numerosities with such a noisy system may be explained by a population rate code (16). Single cells respond to every trial in a probabilistic way and only, on average, show increased firing rates to a given numerosity. Smooth tuning curves only emerge after the neural filter functions of many single cells tuned to the same numerosity are pooled together (Fig. 3B). For an animal to immediately assess numerosity, independent responses of several number neurons should be averaged simultaneously over a large population. Thus, at the neural population level, stimulation by a specific numerosity would result in a distinct activation pattern. Alternatively, the response to specific numerosities might be a result of summation coding (30, 47). These two hypotheses can be further tested only by implementing methods that allow recording of single-cell activity over a large neural population.

Given these striking similarities between number neurons in the NCL of crows and chicks, it seems a reasonable guess that they share the same evolutionary origin. This, in turn, would mean that the neural mechanism of the number sense is not an advanced evolutionary adaptation of a few highly intelligent species. Number neurons in the NCL are likely an ancestral feature in avian species, since domestic chicks belong to the sister group of modern Neoaves (36). Cladogenesis in Galloanseres and Neoaves occurred just before the Cretaceous–Paleogene transition (48). The last common ancestor of modern domestic chicks and crows lived ca. 70 million to 85 million years ago (36, 48) in the jungle of West Gondwana (48), where radiation of all modern avian groups started.

While it is very tempting to go one step further and discuss the idea of the common evolutionary origin of number neurons for all vertebrates, this would be too speculative. The NCL in birds and the PFC in mammals do share similar functions, but they are not homologous structures (49, 50). Birds independently developed cortical brain regions, including the NCL, that enabled their high cognitive functions (20, 51). The same is likely true also for the Dc (dorsal central) region in the telencephalon of zebrafish, which has been recently shown to process numerical information (52). The possibility of a direct homology between the Dc and either the PFC or the NCL can only be addressed at a macroscopic level. These three regions likely belong to larger neocortex homologs in the respective species (53) (but see ref. 54). However, given the developmental and morphological differences between these areas, new cortical subregions with similar functions must have appeared multiple times during independent evolution of these structures.

Two hypotheses can be put forward on the evolution of number sense in vertebrates. The first one is that number perception evolved independently several times in different phylogenetic groups (55), although our data strongly suggest that number neurons in the nidopallium are an ancestral trait of birds. This mechanism, however, still can be an adaptation that evolved in parallel to mammalian number neurons. In this case, the identical labeled-line coding scheme for numerosities adopted by birds and mammals might be computationally advantageous and, therefore, evolved independently in both groups (19). The second hypothesis is that numerosity processing can be based upon an ancient core neural circuit shared among all vertebrates. In this case, we would expect to find numerosity responses in other, evolutionarily conserved brain regions homologically shared among vertebrates (5). Indeed, some indirect evidence suggests that at least a coarse estimation of quantity, that is, more vs. less, might be present already at the subcortical level in humans (56) and in the midbrain of birds (57) and zebrafish (58).

These hypotheses are, however, not mutually exclusive. The putative ancestral neural circuit might be dedicated to assess continuous physical parameters normally associated with numerosity, like total area of the stimulus. Conversely, higher-order brain processing leading to estimation of cardinal numerosities at a more abstract level may have developed several times, together with the independent evolution of new cortex homolog brain areas in distant phylogenetic groups (59).

Summing up, our study provides a step in addressing a complex evolutionary and developmental aspect of numerical cognition. We demonstrate the existence of number neurons in young numerically naïve domestic chicks. In the future, this method might be easily adopted for studying the neural correlates of numerical cognition in other brain regions, as well as in other species.

Materials and Methods

Subjects.

Twelve domestic chicks (G. gallus domesticus) of both sexes from the Aviagen ROSS 308 strain were used. Fertilized eggs were obtained from a local commercial hatchery (CRESCENTI Società Agricola S.r.l.–AllevamentoTrepola–cod. Allevamento 127BS105/2). Eggs were incubated and hatched within incubators (Marans P140TU-P210TU) at a temperature of 37.7 °C, with 60% humidity in a dark room. After hatching in dark incubators, chicks were isolated and housed individually in metal cages (28 cm wide × 32 cm high × 40 cm deep) with food and water available ad libitum, at a constant room temperature of 30 °C to 32 °C and a constant light–dark regime of 14 h light and 10 h dark. All experimental protocols were approved by the research ethics committee of the University of Trento and by the Italian Ministry of Health (Permit 745/2021-PR).

Experimental Setup.

The setup consisted of a rectangular shaped arena (28 × 40 × 32 cm; width [W] × length [L] × height [H]) with metal walls that were grounded. In the center of one of the shorter walls, there was a circular opening (diameter 12 cm). A computer screen (AOC AGON AG271QG4, 144 Hz) used for stimuli presentation was positioned directly behind the circular opening. Within the rectangular arena, was a small wooden box 14 × 13 × 22 cm (W × L × H) whose frontal wall was made of a metal grid. The box was placed 25 cm in front of the circular opening with the screen (Fig. 1A). During the experiments, chicks remained inside the box, from where they could observe the stimuli. Stimulus presentation was controlled by the PsychoPy toolbox (60).

Habituation Procedure.

The habituation occurred between the third and the sixth day after hatching. On the third day post hatching, chicks learned to peck on mealworms. During day 4 after hatching, chicks were, first, habituated to the experimental setup and then to the number stimuli appearing on the screen. The birds received mealworms every time after the stimulus appeared on the screen, which motivated them to pay attention to the moment when any stimulus would appear. The stimuli were presented and rewarded randomly, so that chicks would not associate any particular numerosity with the reward. During days 5 and 6 post hatching, we gradually decreased the reward rate, so that birds would still pay attention to the screen even without getting a mealworm. This procedure allowed us to minimize rewarding during actual recording sessions.

Surgery and Recordings.

On the seventh day after hatching, chicks were fully anesthetized using Isoflurane inhalation (1.5 to 2.0% gas volume, Vetflurane, 1,000 mg/g, Virbac) and placed in the stereotaxic apparatus with a bar fixed at the beaks’ base and tilted 45° to ear bars. Local anesthesia (Emla cream, 2.5% lidocaine + 2.5% prilocaine, AstraZeneka, S.p.A.) was applied to the ears and skull skin before and after the surgery. Metal screws were placed into the skull for grounding and stabilization of the implant. A small craniotomy was made in the skull on the right hemisphere above the NCL (1.0 mm anterior to the bregma, 4.5 mm lateral to the midline). For extracellular recordings, we used self-wired tetrodes made out of formvar-insulated Nichrome wires (17.78 µm diameter, A-M Systems), which were gold plated to reduce the impedance to 300 kOm to 400 kOm (controlled by nanoZ, Plexon Inc.). Then, a commercially available Halo-5 microdrive (Neuralynx) was assembled according to the producer instructions, where four single tetrodes were put into polymicro tubes (inner diameter 0.1 mm) and glued to the plastic shuttles. The microdrive was implanted and fixed first with quick adhesive silicone (Kwik-Sil, World Precision Instruments) and then with dental cement (Henry Schein Krugg Srl). To increase the probability of finding number-responsive units, we did not glue the electrode tips within the tetrodes We, thus, considered each tetrode as a brush-like arrangement of four single electrodes. Since, in this brush arrangement, the positions of the electrode tips can vary, some of the electrodes may have recorded signals from the same neurons. Hence, for sorting and subsequent analyses, we chose only the best electrode from each tetrode at every recording position to avoid double counting of the same neurons.

After the surgery, the chicks were left to recover until the next day in their home cages. Between the eighth and the twelfth day after hatching, we recorded neural responses to numerical stimuli in the NCL of chicks. Before every recording session, the microdrive was connected to the Plexon system (Plexon Inc.) via a QuickClip connector and an omnetics headstage (Neuralynx). After every recording session, the tetrodes were manually advanced by 60 µm to 100 µm.

Signals were preamplified with a 16-channel head-stage (20×, Plexon Model PX.HST/16V-G20-LN) subsequently amplified 1,000×, digitalized and filtered (300-Hz high-pass filter, 3-kHz low-pass filter, and 50-Hz noise removal). The common average referencing method (the averaged signal across channels) of the PlexControl system was used for referencing. Spikes were detected with the PlexControl software with an automatic 4-sigma threshold from the average noise level. Subsequently, spike sorting was performed manually in the Plexon Offline Sorter (see SI Appendix, Fig. S1 for examples of the raw signal and spike sorting).

Stimuli.

As numerical stimuli, we used red dots outlined with a thin black line that appeared in the center of the screen in a white background circle 6 cm in diameter. The size of stimuli ranged from 0.25 cm to 1.4 cm [0.6° to 3.2° (61)]. We explored neural responses to numerosities from one to five. To control for visual parameters that might interfere with numerosity perception, during every recording session, we presented three different types of stimuli (Fig. 1B). “Radius-fixed” type of stimuli consisted of dots with a fixed radius, meaning that area and perimeter increase with numerosity. “Area-fixed” stimuli have constant total area over all numerosities, while the total perimeter of the dots increases with numerosity. “Perimeter-fixed” stimuli have constant total perimeter over all numerosities, while total area of these stimuli decreases with numerosity. To further control that neurons do not respond to other visual parameters except for quantity, the interdistance interval between dots varied randomly. Moreover, for every day of recording, we created a new batch of stimuli consisting of 30 unique images for each numerosity/stimulus type combination. Numerosity stimuli were created using GeNEsIS software (62).

During recording sessions, we randomly presented stimuli for 500 ms with 2,000 ms of interstimulus interval. Experiments were video recorded using CineLAB system (Plexon Inc.). To enhance the motivation of birds to pay attention to the screen, random trials were occasionally rewarded. These trials were subsequently discarded from the analysis.

Histological Analysis.

After the last neural recording, birds were overdosed with the ketamine/xylazine solution (1:1 ketamine 10 mg/mL + xylazine 2 mg/mL). Electrolytic lesions were made at the recording sites by applying a high-voltage current to the tetrodes for 10 s to 15 s. Then, the birds were perfused intracardially with the phosphate buffer (phosphate-buffered saline; 0.1 mol, pH = 7.4, 0.9% sodium chloride, 5 °C) followed by 4% paraformaldehyde (PFA). Brains were incubated for at least 2 d in PFA and a further 2 d in 30% sucrose solution in PFA. Coronal 60-μm brain sections were cut at −20 °C using a cryostat (Leica CM1850 UV), mounted on glass slides, stained with the Giemsa dye (MG500, Sigma-Aldrich), and coverslipped with Eukitt (FLUKA). Brain sections were examined under the stereomicroscope (Stemi 508, Carl Zeiss) to estimate the anatomical position of recording sites.

Data Analysis.

Based on the analysis of video recordings, we selected only those trials when birds were not rewarded. Since, in birds, there is an almost complete decussation of the optic fibers, we recorded from the right hemisphere, and we selected only trials when birds looked at the stimulus with both eyes or with the contralateral (left) eye. For each recorded unit, we excluded trials with a firing rate of less than 1 Hz. For the final analysis, we considered only those units that were recorded for at least seven trials for each numerosity and stimulus type (on average, 23 trials per numerosity/stimulus type).

The neural activity of recorded units was analyzed as the mean firing rate over 500 ms of stimulus presentation. To find numerosity-responsive neurons, we performed two-way ANOVA with the numerosity (one to five) and the stimulus type (“radius-fixed,” “area-fixed,” or “perimeter-fixed”) as factors. We considered the recorded neuron as numerosity responsive if only the effect of the “numerosity” factor was highly significant (P < 0.01), but not of the stimulus type or the interaction between the two factors. The numerosity that elicited the strongest neural response was defined as a preferred numerosity for this neuron.

For every number neuron, we performed a post hoc analysis (Tukey’s test) to compare the neural response between the most preferred and other numerosities. To test for the numerical distance effect, we applied a GLM for binomial data with the logit-link function. In the model, the proportion of neurons that significantly differentiate between given numerosities was taken as the response variable, and either the absolute numerical distance or the logarithm of the numerical distance was taken as a factor. We then compared the goodness of fit of these two models based on the ΔBIC, where the lower the BIC value, the better the model’s fit.

To validate the stability of our recordings, we performed a cross-validation analysis. For each numerosity-responsive unit, we calculated the preferred numerosity for the first and the second half of all trials separately. If the neural response to number stimuli was stable across the recording, we expected the Pearson’s correlation between the first and the second half of the trials to be close to one for the whole population of number neurons. The cross-validation analysis showed a strong correlation of 0.82 (P < 0.001) between the preferred numerosity in the first and the second half of the trials, confirming the stability of our recordings.

For every number neuron, we normalized neural activity by setting the firing rate in response to the preferred numerosity at 100% and in response to the least preferred numerosity at 0%. The resulting neural filter functions were averaged by group based on the preferred numerosity, thus creating numerosity tuning curves for, for example, neurons preferring numerosity one, numerosity two, etc.

To evaluate the chance level of finding false-positive numerical responses in our dataset, for every recorded neuron, we shuffled all the trials 1,000 times and performed an ANOVA each time to select false-positive number neurons. We compared the proportion of false-positive and real number neurons with the proportion test. We further compared the tuning curves between the false-positive number neurons and the real number neurons. For this, we randomly sampled, from the false-positive neurons, the same number of neurons as of actually recorded number neurons. We compared the tuning curves of real and false-positive neurons performing a two-factor ANOVA with the interaction of “numerical distance” and “data type” (real/false positive).

According to Weber’s law, the perception of sensory stimuli (including quantities) is proportional to the quantity being estimated. The just noticeable difference was hypothesized to be constant on a logarithmic (63) or power (64) scale of stimulus magnitude. Therefore, when plotted on a linear scale, one might expect tuning curves to become increasingly asymmetric and wide with increasing numerosity. These properties are usually referred to as a numerical distance effect and a numerical magnitude effect, respectively. To evaluate the symmetry and the width of the neural filter functions, we fitted the Gaussian function to the curves (MATLAB Curve Fitting Toolbox) plotted on four different scales: linear, a power function with an exponent of 0.5, a power function with an exponent of 0.33, and a logarithmic (log2) scale (43). The symmetry of the Gaussian fit was estimated based on R-squared (r²) values; that is, the higher the r², the better and more symmetric the fit. The width of the Gaussian fit was reflected by its sigma (σ). The four scaling methods were compared based on the r² values by the Friedman’s test for nonparametric data with repeated measures with the post hoc pairwise comparison with the Nemenyi test. The relationship between the numerosity and the sigma of the Gaussian was tested by an ANOVA for different scaling methods separately.

All statistical analyses and visualization of the data were performed in R (65) with packages “tidyverse,” “ggplot2,” and “PMCMRplus” and in MATLAB using custom-made scripts and the Curve Fitting Toolbox.

Availability of Data and Material

A summary table including the mean firing rates for all numerosity-responsive neurons for all trials is included as Dataset S1. The raw spike train data and the custom code that was used for data analysis and visualization are available at the GitHub repository https://github.com/dmkobylkov/number_neurons.

All other study data are included in the article and/or supporting information.