A hierarchy of linguistic predictions during natural language comprehension

Significance

Theorists propose that the brain constantly generates implicit predictions that guide information processing. During language comprehension, such predictions have indeed been observed, but it remains disputed under which conditions and at which processing level these predictions occur. Here, we address both questions by analyzing brain recordings of participants listening to audiobooks, and using a deep neural network to quantify the predictions evoked by the story. We find that brain responses are continuously modulated by linguistic predictions. We observe predictions at the level of meaning, grammar, words, and speech sounds, and find that high-level predictions can inform low-level ones. These results establish the predictive nature of language processing, demonstrating that the brain spontaneously predicts upcoming language at multiple levels of abstraction.

Abstract

Understanding spoken language requires transforming ambiguous acoustic streams into a hierarchy of representations, from phonemes to meaning. It has been suggested that the brain uses prediction to guide the interpretation of incoming input. However, the role of prediction in language processing remains disputed, with disagreement about both the ubiquity and representational nature of predictions. Here, we address both issues by analyzing brain recordings of participants listening to audiobooks, and using a deep neural network (GPT-2) to precisely quantify contextual predictions. First, we establish that brain responses to words are modulated by ubiquitous predictions. Next, we disentangle model-based predictions into distinct dimensions, revealing dissociable neural signatures of predictions about syntactic category (parts of speech), phonemes, and semantics. Finally, we show that high-level (word) predictions inform low-level (phoneme) predictions, supporting hierarchical predictive processing. Together, these results underscore the ubiquity of prediction in language processing, showing that the brain spontaneously predicts upcoming language at multiple levels of abstraction.

Understanding spoken language requires transforming ambiguous stimulus streams into a hierarchy of increasingly abstract representations, ranging from speech sounds to meaning. It is often argued that during this process, the brain relies on prediction to guide the interpretation of incoming information (1, 2). Such a “predictive processing” strategy has not only proven effective for artificial systems processing language (3, 4) but has also been found to occur in neural systems in related domains such as perception and motor control, and might constitute a canonical neural computation (5, 6).

There is a considerable amount of evidence that appears in line with predictive language processing. For instance, behavioral and brain responses are highly sensitive to violations of linguistic regularities (7, 8) and to deviations from linguistic expectations more broadly (9–13). While such effects are well documented, two important questions about the role of prediction in language processing remain unresolved (14).

The first question concerns the ubiquity of prediction. While some models cast prediction as a routine, integral part of language processing (1, 15, 16), others view it as relatively rare, pointing out that apparent widespread prediction effects might, instead, reflect other processes like semantic integration difficulty (17, 18), or that such prediction effects might be exaggerated by the use of artificial, prediction-encouraging experiments focusing on highly predictable “target” words (17, 19). The second question concerns the representational nature of predictions: Does linguistic prediction occur primarily at the level of syntax (15, 20–22) or rather at the lexical (16, 23), semantic (24, 25), or the phonological level (13, 26–29)? And is prediction limited to incremental, anticipatory processing within a given level, or does it extend to top-down prediction across levels (30)?

Event-related potential (ERP) studies have described brain responses to violations of, and deviations from, both high- and low-level expectations, suggesting prediction might occur at all levels simultaneously (1, 31) (but see refs. 19 and 32). However, it has been disputed whether these findings would generalize to natural language, where violations are rare or absent and with few highly predictable words. In these cases, prediction may be less relevant or might, perhaps, be limited to the most abstract levels (17, 19, 32). Studies on naturalistic comprehension, on the other hand, have found neural sensitivity to various metrics of linguistic unexpectedness, suggesting prediction does, in fact, generalize to natural language (10, 11, 13, 22, 27, 28, 33, 34). However, these studies often focused on just one [or two (35)] levels of analysis—for example, speech sounds, words, or grammar. This leaves open whether metrics at different levels provide different vantage points onto a single underlying process or whether prediction happens at multiple levels simultaneously—and, if so, whether predictions at different levels may interact. Moreover, it is unclear whether such overall predictability effects actually reflect continuous prediction, or might be driven by a subset of (highly predictable) events in naturalistic stimuli.

Here, we address both issues, probing the ubiquity and nature of linguistic prediction during natural language understanding. Specifically, we analyzed brain recordings from two independent experiments of participants listening to audiobooks, and used a powerful deep neural network (GPT-2) to quantify linguistic predictions in a fine-grained, contextual fashion. First, we obtained evidence for predictive processing, confirming that brain responses to words are modulated by linguistic predictions. Critically, the effects of predictability could not be reduced to nonpredictive factors such as integration difficulty, were logarithmically related to word probability, and were not confined to a subset of constraining words, but were widespread—supporting the notion of continuous, probabilistic prediction. Next, we investigated at which level prediction occurs. To this end, we disentangled the model-based predictions into distinct dimensions, revealing dissociable neural signatures of predictions about syntactic category (parts of speech), phonemes, and semantics. Finally, we found that higher-level (word) predictions constrain lower-level (phoneme) predictions, supporting hierarchical prediction. Together, these results underscore the ubiquity of prediction in language processing, and demonstrate that prediction is not confined to a single level of abstraction but occurs throughout the language network, forming a hierarchy of predictions across many levels of analysis, from phonemes to meaning.

Results

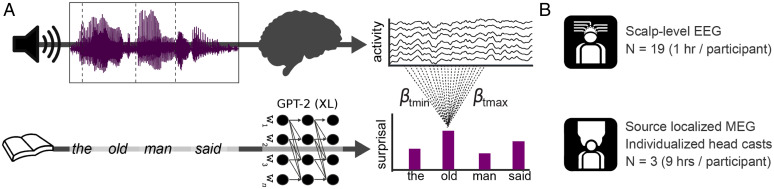
We consider data from two independent experiments, in which brain activity was recorded while participants listened to natural speech from audiobooks. The first experiment is part of a publicly available dataset (36), and contains 1 h of electroencephalographic (EEG) recordings in 19 participants. The second experiment collected 9 h of magnetoencephalographic (MEG) data in three individuals, using individualized head casts that allowed us to localize the neural activity with high precision. While both experiments had a similar setup (Fig. 1), they yield complementary insights, both at the group level and in three individuals.

Fig. 1.

Schematic of experimental and analytical framework. (A) (Top) In both experiments, participants listened to continuous recordings from audiobooks while brain activity was recorded. (Bottom) The texts participants listened to were analyzed by a deep neural network (GPT-2) to quantify the contextual probability of each word. A regression-based technique was used to estimate the effects of (different levels of) linguistic unexpectedness on the evoked responses within the continuous recordings. (B) Datasets analyzed: one group-level EEG dataset, and one individual subject source-localized MEG dataset.

Neural Responses to Speech Are Modulated by Continuous Linguistic Predictions.

We first tested for evidence for linguistic prediction in general. We reasoned that, if the brain is constantly predicting upcoming language, neural responses to words should be sensitive to violations of contextual predictions, yielding “prediction error” signals which are considered a hallmark of predictive processing (5). To this end, we used a deconvolution technique (regression ERP; see Materials and Methods) to estimate the effects of prediction error on evoked responses within the continuous recordings. We focus on the low-frequency evoked response because it connects most directly to earlier work on neural signatures of prediction in language (7, 32, 37, 38).

To quantify linguistic predictions, we analyzed the books participants listened to with a deep neural language model: GPT-2 (39). GPT-2 is a large transformer-based model that predicts the next word given the previous words, and is currently among the best publicly available models of its kind. Note that we do not use GPT-2 as a model of human language processing but purely as a tool to quantify how expected each word is in context.

To test whether neural responses to words are modulated by contextual predictions, we compared three regression models (SI Appendix, Fig. S2). The baseline model formalized the hypothesis that natural, passive language comprehension does not invoke prediction. This model did not include regressors related to contextual predictions, but did include potentially confounding variables (such as frequency, semantic integration difficulty, and acoustics). The constrained guessing model formalized the hypothesis that, during comprehension, 1) predictions are not generated constantly but only for a subset of words, in constraining contexts; and 2) these predictions are all or none. These assumptions capture how prediction was traditionally conceived of by many in psycholinguistics (38). We implemented them as a regression model using all regressors from the baseline model, plus an unexpectedness regressor. This unexpectedness regressor was 1) only included for a subset of words in the most constraining contexts; and 2) used a linear metric of word improbability, since all-or-none prediction results (on average) in a linear relationship between word probability and brain response. This is because the probability of an all-or-none prediction error scales linearly with a word’s improbability. Therefore, while the regression model was itself not categorical, it provides the best approximation to an all-or-none prediction error, given that we do not know participants’ moment-by-moment all-or-none predictions (see Materials and Methods).

Finally, we considered a continuous prediction model. This model included all regressors from the baseline model, plus a logarithmic metric of word improbability (surprisal) for every word in the audiobook. This formalized the hypothesis that the brain continuously generates probabilistic predictions, and that the response to a stimulus is proportional to its negative log probability, as postulated by predictive processing accounts of language (1, 9, 37) and neural processing more broadly (5, 6).

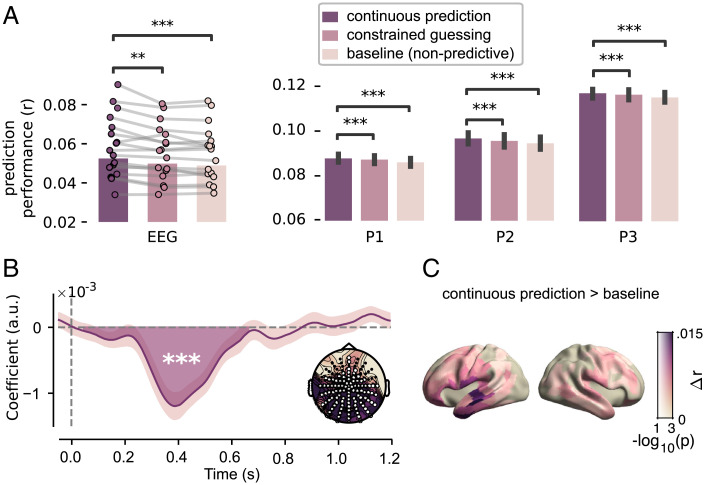
When we compared the ability of these models to predict brain activity using cross-validation, we found that the continuous prediction model performed better than both of the other models (Fig. 2A). The effect was highly consistent, both in the EEG participants (continuous prediction vs. constrained guessing, $t_{18}=3.18,\hspace{0.17em}p=5.20\times {10}^{-3}$; prediction vs. baseline, $t_{18}=5.01,\hspace{0.17em}p=9.04\times {10}^{-5}$) and within each MEG participant (continuous prediction vs. constrained guessing, all $p<1.78\times {10}^{-4}$; probabilistic vs. baseline, all $p<1.58\times {10}^{-11}$).

Fig. 2.

Neural responses are modulated by probabilistic predictions. (A) Model comparison. Cross-validated correlation coefficients for EEG (Left) and each MEG participant (Right). EEG: dots with connecting lines represent individual participants (averaged over all channels). MEG: bars represent median across runs, error bars represent bootstrapped absolute deviance (averaged over language network sources). (B) EEG: coefficients describing the significant effect of lexical surprise (see SI Appendix, Fig. S3 for the full topography over time). Highlighted area indicates extent of the cluster, and shaded error bar indicates bootstrapped SE. Inset shows distribution of absolute t values and of channels in the cluster. (C) Difference in prediction performance across cortex (transparency indicates family-wise-error (FWE)-corrected P values). Significance levels correspond to P < 0.01 (**), P < 0.001 (***) in a two-tailed paired Student’s t or Wilcoxon sign rank test.

The constrained guessing model differed from the continuous prediction model in two ways—by assuming 1) a linear relationship between probability and brain response and 2) that predictions are limited to constraining contexts. To understand which of these explains the continuous prediction model’s superiority, we also compared control models to probe the issues separately. This confirmed that both contributed: Effects of word predictability are both logarithmic (SI Appendix, Fig. S5) and not limited to words in constraining context, but are found much more broadly, and not just for content words but also for function words (SI Appendix, Figs. S5 and S6). These results are in line with earlier work on surprisal effects, and support the notion that predictions are ubiquitous and automatic (see Discussion).

Having established that word unexpectedness modulates neural responses, we characterized this effect in space and time. In the MEG dataset, we asked for which neural sources lexical surprise was most important in explaining neural data, by comparing the prediction performance of the baseline model to the predictive model in a spatially resolved manner. This revealed that overall word unexpectedness modulated neural responses throughout the language network (Fig. 2C). To investigate the temporal dynamics of this effect, we inspected the regression coefficients, which describe how fluctuations in lexical surprise modulate the neural response at different time lags—together forming a modulation function also known as the regression evoked response (40). When we compared these across participants in the EEG experiment, cluster-based permutation tests revealed a significant effect ($p=2\times {10}^{-4}$) based on a posteriocentral cluster with a negative polarity peaking at 400 ms post word onset (Fig. 2B and SI Appendix, Fig. S3). This indicates that surprising words lead to a stronger negative deflection of evoked responses, an effect tightly matching the classic N400 (7, 24, 32). Coefficients for MEG subjects revealed a similar, slow effect at approximately the same latencies (SI Appendix, Fig. S4).

Together, these results constitute clear evidence for predictive processing, by confirming that brain responses to words are modulated by predictions. These modulations are not confined to constraining contexts, occur throughout the language network, evoke an effect reminiscent of the N400, and are best explained by probabilistic predictive processing accounts.

Linguistic Predictions Are Feature Specific.

The results, so far, revealed modulations of neural responses by overall word unexpectedness. What type of prediction might be driving these effects? Earlier research suggests a range of possibilities, with some proposing that the effect of overall word surprisal primarily reflects syntax (15, 20), while others propose that prediction unfolds at the semantic (24, 25) or the phonemic level (13, 26, 27)—or at all levels simultaneously (1).

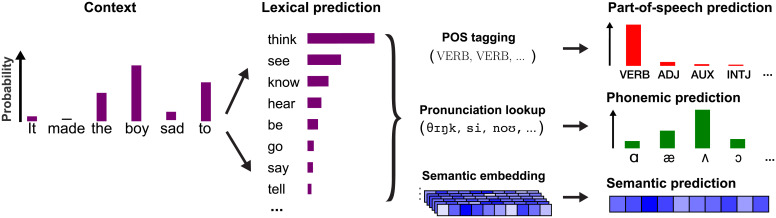
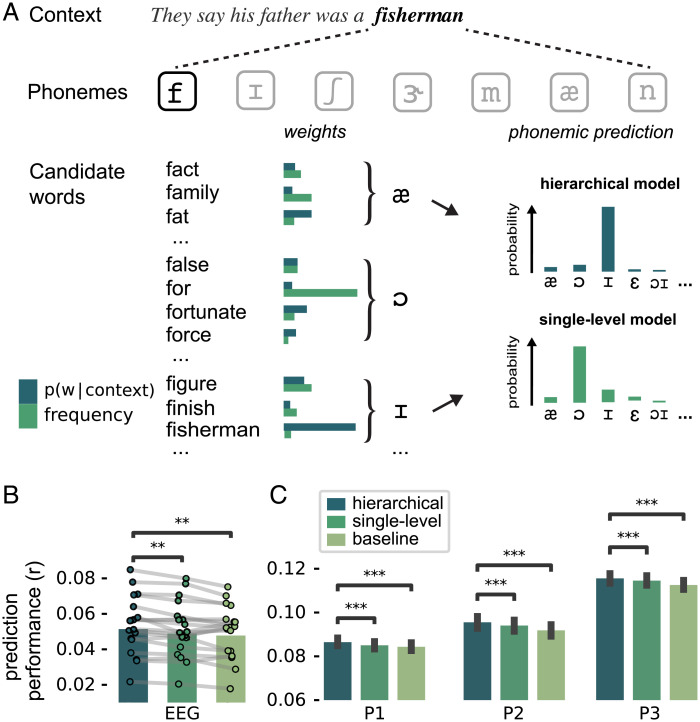
To evaluate these possibilities, we disentangled the aggregate, word-level linguistic predictions from the artificial neural network into distinct linguistic dimensions (Fig. 3). This allows us to derive estimates of three feature-specific predictions: the part of speech (POS) prediction (defined as the probability distribution over syntactic categories), semantic prediction (defined as the predicted semantic embedding), and phonemic prediction (the distribution over phonemes, given the phonemes in the word so far and the prior context). Note that, since each of these predictions is based on the same aggregate prediction from GPT-2, the features refer to the prediction content, and not its source. For instance, the POS prediction is a prediction about the part of speech, but not necessarily based on the part of speech or syntactic category alone. By comparing these predictions to the presented words, we derived feature-specific prediction error regressors which quantified not just the extent to which a word is surprising but also in what way: semantically, (morpho)syntactically, or phonemically.

Fig. 3.

To disentangle the model-derived predictions into distinct linguistic dimensions, the lexical predictions were analyzed. For the prediction about syntactic category, POS tagging was performed over all potential sentences (e.g., “It made the boy sad to think,” “It made the boy sad to see,” etc.). To compute the phonemic prediction, each predicted word was decomposed into its constituent phonemes, and the predicted probabilities were used as a contextual prior in a phoneme model (Fig. 6). For the semantic prediction, a weighted average was computed over the GLoVe embeddings of all predicted words to retrieve the expected semantic vector, based on GPT-2.

We reasoned that, if the brain is generating predictions at a given level (e.g., syntax or grammar), then the neural responses should be sensitive to prediction errors specific to this level. Moreover, because these different features are processed by partly different brain areas over different timescales, the prediction errors should be at least partially dissociable. To test this, we formulated a new regression model (SI Appendix, Fig. S7). This included all variables from the lexical prediction model as nuisance regressors, and added three regressors of interest: POS surprisal (defined for each word), semantic prediction error (defined for each content word), and phoneme surprisal (defined for each phoneme).

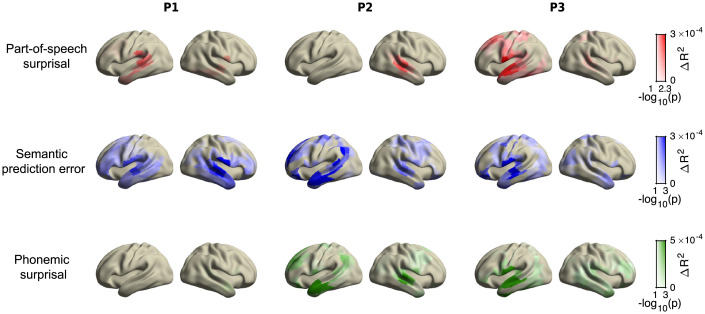
Because these regressors were, to some degree, correlated, we first asked whether, and in which brain area, each of the prediction error regressors explained any unique variance not explained by the other regressors. In this analysis, we turn to the MEG data because of their spatial specificity. As a control, we first performed the analysis for a set of regressors with a known source: the acoustics. This revealed a peak around the auditory cortex (SI Appendix, Fig. S9), in line with earlier work (41) and confirming that the approach can localize areas sensitive to a given regressor. We then tested the three prediction error regressors, finding that each explained significant additional variance in each individual (Fig. 4), although, in one participant, the variance explained by phonemic surprisal was only marginally significant after multiple comparisons correction.

Fig. 4.

Dissociable patterns of explained variance by syntactic category (POS) and semantic and phonemic predictions. Unique variance is explained by different types of unexpectedness (quantified via surprise or prediction error) across cortical sources in each MEG participant. In all plots, color indicates amount of additional variance explained; opacity indicates FWE-corrected statistical significance. Note that p < 0.05 is equivalent to $-{\log }_{10}(p)>1.3$. For the maps of additional control variables (lexical surprisal and acoustics), see SI Appendix, Fig. S9.

The statistically thresholded patterns of explained variance appear spatially distinct (Fig. 4). To test whether this spatial dissociation was statistically reliable, we performed a dissociability analysis (see Materials and Methods). This revealed that the patterns of variance explained by each unexpectedness regressor were dissociable, both overall, in a four-way classification (all p $<2\times {10}^{-5}$), and for all pair-wise comparisons (SI Appendix, Table S1). To validate that this dissociation was not an artifact of our analysis (of subdividing linguistic unexpectedness into multiple regressors), we also performed control analyses with simplified regressions, which confirmed that the spatial patterns were not an artifact of our analysis (SI Appendix, Fig. S16), and that phoneme-level regressors were indeed temporally aligned to phonemes (SI Appendix, Fig. S8).

Although there was variation in lateralization and exact spatial locations between individuals, the overall pattern of sources aligned well with prior research on the neural circuits for each level. We observed a wide set of areas responsive to semantic prediction errors—consistent with the observation that the semantic system is widely distributed (42, 43), whereas, for the phonemic and POS surprisal, we found more focal, temporal areas, that are known to be key areas for syntactic processing (21, 44, 45), and for speech perception and auditory word recognition, respectively (see Discussion).

Together, this shows that the brain responds differently to different types of linguistic unexpectedness, implying that linguistic predictions are feature specific and occur at multiple levels of processing.

Dissociable Spatiotemporal Signatures of Predictions at Different Levels.

Having established that the three different types of prediction errors independently modulated neural responses in different brain areas, we further investigated the nature of these effects. This was done by inspecting the coefficients, which describe how fluctuations in a given regressor modulate the response over time. We first turn to the EEG data because, there, the sample size allows for population-level statistical inference on the coefficients. We fitted the same integrated model (SI Appendix, Fig. S7) and performed spatiotemporal cluster-based permutation tests. This revealed significant effects for each type of prediction error (Fig. 5).

Fig. 5.

Spatiotemporal signatures of syntactic, semantic, and phonemic prediction errors. EEG (Left): coefficients averaged across the channels participating for at least one sample in the three main significant clusters (one per predictor). Highlighted area indicates temporal extent of the cluster. Shaded area around waveform indicates bootstrapped SEs. Stars indicate cluster-level significance; p < 0.05 (*), p < 0.01 (**). Insets represent selected channels and distribution of absolute t values. Note that these plots only visualize the effects; for the full topographies of the coefficients and respective statistics, see SI Appendix, Fig. S10. MEG (Right): polarity aligned coefficients averaged across the sources with significant explained variance (Fig. 4) across participants. Shaded area represents absolute deviation. Insets represent topography of absolute value of coefficients averaged across the highlighted period. Note that, due to polarity alignment, sign information is to be ignored for the MEG plots. For average coefficients for each source, see SI Appendix, Figs. S13–S15 for coefficients of source in each individual.

First, POS surprisal evoked an early, positive deflection ($p=8.7\times {10}^{-3}$) based on a frontal cluster between 200 and 500 ms. This early frontal positivity converges with two recent studies that investigated specifically syntactic prediction using models trained explicitly on syntax (22, 33), suggesting the effect is not specific to the POS formulation used here but reflects predictions about syntax more broadly (see Discussion). We also observed a late negative deflection for POS surprisal ($p=0.02$;SI Appendix, Fig. S11), but this was neither in line with earlier findings nor replicated in the MEG data. The semantic prediction error also evoked a positive effect ($p=0.013$), but this was based on a much later, spatially distributed cluster between 600 and 1,100 ms—an effect reminiscent of late “post-N400 positivities (PNP)” observed for purely semantic anomalies (38, 46). Notably, although semantic prediction error was also associated with a cluster for an N400-like modulation, this effect was not significant ($p=0.075$), presumably because the negative deflection was already explained by the overall lexical surprisal, which was included as a nuisance regressor (SI Appendix, Fig. S12). Finally, the phoneme surprisal evoked a negative effect ($p=5.1\times {10}^{-3}$) based on an early, distributed cluster between 100 and 500 ms. This effect was similar to the word-level surprise effect (Fig. 2C and SI Appendix, Fig. S12) but occurred earlier, peaking at about 250 ms to 300 ms (jackknife-based latency t test: $t_{18}=6.96,p=1.69\times {10}^{-6}$). This effect strongly resembles N250 or phonological mismatch negativity (PMN) components from ERP studies on phonological mismatch (47) and effects from recent model-based studies of predictive phonological processing of natural speech (13, 28, 48).

When we performed the same analysis on the MEG data, we observed striking variability in the exact shape and timing of the modulation functions between individuals (SI Appendix, Figs. S13–S15). Overall, however, we could recover a temporal pattern of effects similar to the EEG results: phonemic and POS surprisal modulating early responses, and semantic prediction error modulating later responses—although not as late in the EEG data. This temporal order holds on average (Fig. 5 and SI Appendix, Fig. S12), and is especially clear within individuals (SI Appendix, Figs. S13–S15).

Finally, to confirm that these dissociable signatures were not an artifact of subdividing linguistic unexpectedness into multiple regressors, we again performed simplified regressions as a control. The observed effects were preserved in simplified regressions, suggesting they are, indeed, independent effects (SI Appendix, section B and Fig. S17).

Overall, our results (Figs. 4 and 5) demonstrate that the distinct classes of prediction errors evoke brain responses that are both temporally and spatially dissociable. Specifically, while phonemic and POS predictions modulate relatively early neural responses (100 ms to 400 ms) in a set of focal temporal (and frontal) areas that are key for syntactic and phonetic/phonemic processing, semantic predictions modulate later responses (>400 ms) across a widely distributed set of areas across the distributed semantic system. These results reveal that linguistic prediction is not implemented by a single system but occurs throughout the speech and language network, forming a hierarchy of linguistic predictions across all levels of analysis.

Phoneme Predictions Reveal Hierarchical Inference.

Having established that the brain generates linguistic predictions across multiple levels of analysis, we finally asked whether predictions at different levels might interact. One option is that they are encapsulated: Predictions in separate systems might use different information, for instance, unfolding over different timescales, rendering them independent. Alternatively, predictions at different levels might inform and constrain each other, effectively converging into a single multilevel prediction—as suggested by hierarchical predictive processing (5, 6, 49).

One way to adjudicate between these hypotheses is by evaluating different schemes for deriving phonemic predictions. One possibility is that such predictions are only based on information unfolding over short timescales. In this scheme, the predicted probability of the next phoneme is derived from the cohort of words compatible with the phonemes so far, with each candidate word weighted by its frequency of occurrence (Fig. 6A). As such, this scheme entails a single-level model: Predictions are based only on a single level of information—short sequences of within-word sequences of phonemes, plus a fixed prior (of word frequencies in a language).

Fig. 6.

Evidence for hierarchical inference during phoneme prediction. (A) Two models of phoneme prediction during incremental word recognition. Phonemic predictions were computed by grouping candidate words by their identifying next phoneme, and weighting each candidate word by its prior probability. This weight (or prior) could be either based on a word’s overall probability of occurrence (i.e., frequency) or on its conditional probability in that context (from GPT-2). Critically, in the frequency-based model, phoneme predictions are based on a single level: short sequences of within-words phonemes (hundreds of milliseconds long) plus a fixed prior. By contrast, in the contextual model, predictions are based not just on short sequences of phonemes but also on a contextual prior which is, itself, based on long sequences of prior words (up to minutes long), rendering the model hierarchical (see Materials and Methods). (B and C) Model comparison results in EEG (B) and all MEG participants (C). EEG: dots with connecting lines represent individual participants (averaged over all channels). MEG: bars represent median across runs; error bars represent bootstrapped absolute deviance (averaged over language network sources). Significance levels correspond to P < 0.01 (**) or P < 0.001 (***) in a two-tailed paired t or Wilcoxon sign rank test.

Alternatively, phoneme predictions might not only be based on sequences of phonemes within a word but also on the longer prior linguistic context. In this case, the probability of the next phoneme would still be derived from the cohort of words compatible with the phonemes presented so far, but, now, each candidate word is weighted by its contextual probability (Fig. 6A). Such a model would be hierarchical, in the sense that predictions are based both—at the first level—on short sequences of phonemes (i.e., of hundreds of milliseconds long) and on a contextual prior which itself is based—at the higher level—on long sequences of words (i.e., of tens of seconds to minutes long).

Here, the first model is more in line with the classic cohort model of incremental (predictive) word recognition, which suggests that context is only integrated after the selection and activation of lexical candidates (50). By contrast, the second model is more in line with contemporary theories of hierarchical predictive processing which propose that high-level cortical predictions (spanning larger spatial or temporal scales) inform and shape low-level predictions (spanning finer spatial or temporal scales) (49, 51). Interestingly, recent studies of phoneme predictions during natural listening have used both the frequency-based single-level model (27, 29) and a context-based (hierarchical) model (13). However, these studies did not compare which of these best accounts for prediction-related fluctuations in neural responses to phonemes.

To compare these possibilities, we constructed three phoneme-level regression models (SI Appendix, Fig. S19), which all only included regressors at the level of phonemes. First, the baseline model only included nonpredictive control variables: phoneme onsets, acoustics, word boundaries, and uniqueness points. This can be seen as the phoneme-level equivalent of the baseline model in Fig. 2 and SI Appendix, Fig. S5. The baseline model was compared with two regression models which additionally included phoneme-level predictability regressors. In one regression model, these regressors were calculated using a single-level model (with a fixed, frequency-based prior); in the other, the predictability regressors were derived from a hierarchical model (with a dynamic, contextual prior derived from GPT-2). To improve our ability to discriminate between the hierarchical and single-level model, we used not only phoneme surprisal but also phoneme entropy as a regressor (13).

When we compared the cross-validated predictive performance, we first found that, in both datasets, the predictive model performed significantly better than the nonpredictive baseline (Fig. 6 B and C; hierarchical vs. baseline, EEG: $t_{18}=3.15,\hspace{0.17em}p=5.50\times {10}^{-3}$; MEG: all $p<7.99\times {10}^{-12}$). This replicates the basic evidence for predictive processing but now at the phoneme rather than word level. Critically, when we compared the two predictive models, we found that the hierarchical model performed significantly better, both in EEG ($t_{18}=3.61,\hspace{0.17em}p=7.28\times {10}^{-3}$) and MEG (all $p<3.34\times {10}^{-4}$). This suggests that neural predictions of phonemes (based on short sequences of within-word speech sounds) are informed by lexical predictions, effectively incorporating long sequences of prior words as contexts. This is a signature of hierarchical prediction, supporting theories of hierarchical predictive processing.

Discussion

Across two independent datasets, we combined deep neural language modeling with regression-based deconvolution of human electrophysiological (EEG and MEG) recordings to ask whether and how evoked responses to speech are modulated by linguistic expectations that arise naturally while listening to a story. The results demonstrated that evoked responses are modulated by continuous predictions. We then introduced a technique that allowed us to quantify not just how much a linguistic stimulus is surprising but also at what level—phonemically, morphosyntactically, and/or semantically. This revealed dissociable effects, in space and time, of different types of predictions: Predictions about syntactic category (part of speech) and phonemes modulated early responses in a set of focal, mostly temporal areas, while semantic predictions modulated later responses across a widely distributed set of cortical areas. Finally, we found that responses to phonemic surprisal and entropy were best modeled by a hierarchical model incorporating two levels of context: short sequences of within-word phonemes (up to hundreds of milliseconds long) and long sequences of prior words (up to minutes long). This suggests predictive processing is not limited to anticipatory incremental processing within levels, but includes top-down prediction across levels (30). Together, the results demonstrate that, during natural listening, the brain is engaged in prediction across multiple levels of linguistic representation, from speech sounds to meaning. The findings underscore the ubiquity of prediction during language processing, and fit naturally in predictive processing accounts of language (1, 2) and neural computation more broadly (5, 6, 51, 52).

A first result of this paper is that evoked responses to words are modulated by a logarithmic metric of unexpectedness (surprisal). This replicates earlier work on surprisal effects on reading times (9, 53–55) and brain responses (10, 37, 56–58) (but see ref. 59 for contrasting results using cloze probabilities). Regression models including word unexpectedness performed better than a strong nonpredictive baseline, indicating that predictability effects cannot be reduced to confounding factors like semantic integration difficulty. This aligns with recent ERP studies aimed at distinguishing prediction from semantic integration (60, 61) and extends those by analyzing not just specific “target” words but all words in a story.

The fact that predictability effects were ubiquitous and logarithmic supports a view of prediction as continuous and probabilistic. One possibility is that the logarithmic effect at the word level reflects explicit log-probabilistic prediction (or logarithmic error calculation)—as suggested by some predictive processing models (e.g., ref. 6). Alternatively, it may reflect probabilistic prediction at a much lower level. In this scenario, prediction (or error) is not necessarily logarithmic at the level of the predicted fragments, but becomes logarithmic at the word level, as long as the predicted fragments are much smaller, such that many fragments combine into one word (see ref. 9 for derivation). Interestingly, such a “highly incremental” account also implies that prediction is hierarchical in linguistic structure, which is exactly what we find (Fig. 6). Importantly, both possibilities cast prediction as continuous and probabilistic, and hence both contrast with the classic view of prediction as the occasional all-or-none preactivation of specific words (38). However, we acknowledge that these views are not strictly incompatible: Occasional all-or-none commitment could occur in addition to continuous probabilistic prediction, and predictability may have combined linear and logarithmic effects, as suggested recently (62).

Because our regression ERP analysis focused on evoked responses, the results can be linked to the rich literature on linguistic violations using traditional ERP methods. This is powerfully illustrated by the regression ERP of lexical surprisal (Fig. 2B) tightly following the N400 modulation effect, one of the first proposed, most robust, and most debated ERP signatures of linguistic prediction (7, 24, 32). Similarly, the early negativity we found for phoneme surprisal and later positivity for semantic prediction error (Fig. 5) align well with N250 or PMN and the semantic P600 or PNP effects of phonological mismatch and semantic anomaly, respectively (31, 38). Unlike most ERP studies, we observed these effects in participants listening to natural stimuli—without any anomalies or violations—not engaged in a task. This critically supports that these responses reflect deviations from predictions inherent to the comprehension process—rather than reflecting either detection of linguistic anomalies or expectancy effects introduced by the experiment (17, 19).

A notable discrepancy between our results and the traditional ERP literature was the early effect of POS surprisal. In traditional ERP studies, syntactic violations are primarily associated with a much later positivity [P600 (8)]. The early frontal positivity we observed does, however, replicate recent regression-based analyses of syntactic surprisal (22, 33). One explanation for this discrepancy is that syntactic surprisal might not fully capture syntactic violations as used in ERP studies. Indeed, a recent paper on syntactic prediction using a related regression-based approach, found a similar early positive effect for word-level syntactic surprisal, and a later P600-like effect not for syntactic surprisal but for the number of syntactic reinterpretation attempts a word induced (22). In this view, the early effect we observe may reflect the prediction error or update incurred by registering local (morpho)syntactic attributes of a word, while the later P600 effect reflects updates in the global structural interpretation—which are possibly not well captured by word-by-word POS surprisal.

Beyond the ERP literature, our results also build on prior electrophysiological studies that used model-based approaches to probe prediction during naturalistic comprehension. Those studies mostly focused on lexical unexpectedness (12, 37, 56–58) or on a single level of linguistic analysis such as syntax (22, 33) or phonemes (13, 27, 28). We extend these works by showing 1) distinct effects of predictions at four levels (phonemes, words, syntactic categories, and semantics), 2) interactions between levels. and 3) a method for extracting multilevel predictions from a single (large, pretrained) model. Probing predictions at different levels simultaneously is important, because unexpectedness metrics at different levels are correlated. Therefore, when metrics at different levels are used in isolation, they could capture a single underlying process.

An advantage of our disentangling method (Fig. 3) is that one can derive predictions at multiple levels from a pretrained large language model (LLM). Such LLMs have a deeper grasp of linguistic regularities than domain-specific models used by previous studies, that have to be independently trained and typically only take limited amounts of context into account (e.g., refs. 33, 35, 37, and 45). However, a disadvantage of our method is that the source of the disentangled predictions is unknown, since an LLM will use any statistical cue available to it to generate predictions. Both approaches are thus complementary, as testing hypotheses about which information is used to generate predictions cannot be done with disentangled predictions alone. One avenue to combine the two is to test whether the interaction between levels we find for phonemes applies to all linguistic levels—or whether predictions at some levels (e.g., syntax) might be independent.

We combined group-level analysis (of the EEG data) and individual-level analysis (of the MEG data). These approaches are complementary. By combining both, we found that the effects of prediction and the comparison of hypotheses about its computational nature were identical on the group level and within individuals (Figs. 2 and 6). However, the spatiotemporal signatures showed substantial variability (Figs. 4 and 5 and SI Appendix, Figs. S4 and S13–S15)—even for the strongest and least correlated regressors, suggesting the variability reflects real individual differences and not just uncertainty in the regression estimate (SI Appendix, Fig. S18). This suggests that, while the overall effects are likely present in each individual, the spatiotemporal signatures are best understood as an average, not necessarily representative of underlying individuals.

Two recent functional MRI (fMRI) studies on linguistic prediction also report evidence for prediction hierarchies (63, 64). Like the current study, those fMRI studies align well with the notion of hierarchical predictive processing. However, a key difference is that they probe predictions based on a hierarchy of timescales into the past (63) or into the future (64), and formalize different levels in a data-driven fashion, using different layers of a deep network. By contrast, we study distinct, linguistically interpretable levels of analysis using well-established formalizations (words, phonemes, parts of speech, lexical semantics), that more directly connect to the traditional psycholinguistic literature. Understanding how these predefined, linguistically motivated levels relate to data-driven, model-based levels is an interesting challenge for future work.

Why would the brain constantly predict upcoming language? Three (nonexclusive) functions have been proposed. First, predictions can be used for compression: If predictable stimuli are represented succinctly, this yields an efficient code (6, 51). A second function is that predictions can guide inference, in line with findings that linguistic context can enhance neural representations in a top-down fashion (refs. 65 and 66; but see refs. 67 and 68). Finally, predictions may guide learning: Prediction errors can be used to perform error-driven learning without supervision. While learning is the least-studied function of linguistic prediction in cognitive neuroscience (but see ref. 16), it is its primary application in artificial intelligence (69, 70). In fact, the model we used (GPT-2) was created to study such predictive learning. These models are trained simply to predict lexical items (words or word-part tokens), but learn about language more broadly, and can then be applied to practically any linguistic task (39, 70–72). Interestingly, models trained with this predictive objective also develop representations that are “brain-like,” in the sense that they are currently the best encoders of linguistic stimuli to predict brain responses (73–77). And yet, these predictive models are also brain-unlike in an interesting way—they predict upcoming language only at a single (typically lexical) level.

Why would the brain predict at multiple levels? For compression or inference, this seems useful, since redundancies and ambiguities also occur at multiple levels. But, if predictions drive learning, this is less obvious, since effective learning can be achieved using simple, single-level prediction. One fascinating possibility is that it might reflect the brain’s way of performing credit assignment. In artificial networks, credit assignment is done by first externally computing a single, global error term, and then “backpropagating” this through all levels of the network—but both steps are biologically implausible (78). Interestingly, it has been shown that hierarchical predictive coding can approximate classical backpropagation while using only Hebbian plasticity and local error computation (6, 78, 79). Therefore, if the brain uses predictive error-driven learning, one might expect such prediction to be hierarchical, so error terms can be locally computed throughout the hierarchy—which is in line with what we find.

Beyond the domain of language, there have been other reports of hierarchies of neural prediction, but these have been limited to artificial, predictive tasks or to restricted representational spans, such as successive stages in the visual system (80–82). Our results demonstrate that, even during passive listening to natural stimuli, the brain is engaged in prediction across disparate levels of abstraction (from speech sounds to meaning), based on timescales separated by three orders of magnitude (hundreds of milliseconds to minutes). These findings provide important evidence for hierarchical predictive processing in the cortex. As such, they highlight how language processing in the brain is shaped by a domain-general neurocomputational principle: the prediction of perceptual inputs across multiple levels of abstraction.

Materials and Methods

We analyzed EEG and source localized MEG data from two experiments. The EEG data are part of a public dataset that has been published about before (36, 83).

Participants.

All participants were native English speakers and gave informed consent before participating in the study. In the EEG experiment, 19 subjects (13 male) between 19 and 38 y old participated; in the MEG experiment, 3 subjects participated (2 male), aged 35, 30, and 28 y. Both experiments were approved by local ethics committees (EEG: ethics committee of the School of Psychology at Trinity College Dublin; MEG: CMO region Arnhem-Nijmegen).

Stimuli and Procedure.

In both experiments, participants were presented with continuous segments of narrative speech extracted from audiobooks. The EEG experiment used a recording of Hemingway’s The Old Man and the Sea. The MEG experiment used 10 stories from The Adventures of Sherlock Holmes by Arthur Conan Doyle. Excluding breaks, EEG subjects listened to 1 h of speech (∼11,000 words and 35,000 phonemes); MEG subjects listened to 9 h (excluding breaks) of speech (containing ∼85,000 words and ∼290,000 phonemes).

In the EEG experiment, each participant performed only a single session, which consisted of 20 runs 180 s long, amounting to the first hour of the book. Participants were instructed to maintain fixation and minimize movements but were otherwise not engaged in any task.

In the MEG experiment, each participant performed a total of 10 sessions, each 1 h long. Each session was subdivided into six or seven runs of roughly 10 min, although the duration varied, as breaks only occurred at meaningful moments (making sure, for example, that prominent narrative events were not split across runs). Unlike in the EEG experiment, participants in the MEG dataset were asked to listen attentively and had to answer questions in between runs: one multiple choice comprehension question, a question about story appreciation (scale 1 to 7), and a question about informativeness.

Stimulus Annotation.

To retrieve onset times for each word and phoneme, the original texts were matched to the audio recordings in a forced alignment procedure. For the EEG dataset, this was performed by the authors who originally collected the data, and who provided the onset times for phonemes and function words (36, 83). For the MEG dataset, the forced alignment was performed using the Penn Forced Aligner (P2FA). Here, we used ARPABET for transcription; phonetic transcriptions missing from the phonetic dictionary were manually added. For the phoneme-by-phoneme analysis, the phonemes from the stimulus annotation had to be aligned and recognized by our pronunciation tree–based phoneme model. To this end, phonemic annotation mismatching those from our phoneme dictionary (e.g., alternative pronunciations) were manually checked, and added to the dictionary or corrected.

MRI Acquisition and Headcast Construction.

To produce the headcast, we needed to obtain accurate images of the participants’ scalp surface, which were obtained using structural MRI scans with a 3T MAGNETOM Skyra MR scanner (Siemens AG). We used a fast low-angle shot sequence with the following image acquisition parameters: slice thickness of 1 mm; field of view of 256 × 256 × 208 mm along the phase, read, and partition directions, respectively; TE/TR = 1.59/4.5 ms.

Data Acquisition and Preprocessing.

The EEG data were originally acquired using a 128-channel (plus two mastoid channels) ActiveTwo system (BioSemi) at a rate of 512 Hz, and down-sampled to 128 Hz before being distributed as a public dataset. We visually inspected the raw data to identify bad channels, and performed independent component analysis (ICA) to identify and remove blinks; rejected channels were linearly interpolated with nearest-neighbor interpolation using MNE-python.

The MEG data were acquired using a 275 axial gradiometer system at 1,200 Hz. For the MEG data, preprocessing and source modeling was performed in MATLAB 2018b using fieldtrip (84). We applied notch filtering (Butterworh IIR) at the bandwidth of 49 Hz to 51 Hz, 99 Hz to 101 Hz, and 149 Hz to 151 Hz to remove line noise. Artifacts related to muscle contraction and SQUID jumps were identified and removed using fieldtrip’s semiautomatic rejection procedure. The data were down-sampled to 150 Hz. To identify and remove eye blink artifacts, ICA was performed using the FastICA algorithm.

For both MEG and EEG analyses, we focus on the slow, evoked response, and hence restricted our analysis to low-frequency components. To this end, we filtered the data between 0.5 and 8 Hz using a bidirectional finite impulse response (FIR) band-pass filter. Restricting the analysis to such a limited range of low frequencies (which are known to best follow the stimulus) is common when using regression ERP or temporal response function (TRF) analysis, especially when the regressors are sparse impulses (28, 36, 85). The particular upper bound of 8 Hz is arbitrary but was based on earlier papers using the same EEG dataset to study how EEG tracks acoustic and linguistic content of speech (36, 56, 66).

Head and Source Models.

The MEG sensors were coregistered to the subjects’ anatomical MRIs using position information from three localization coils attached to the headcasts. To create source models, FSL’s Brain Extraction Tool was used to strip nonbrain tissue. Subject-specific cortical surfaces were reconstructed using Freesurfer, and postprocessing (down-sampling and surface-based alignment) of the reconstructed cortical surfaces was performed using the Connectome Workbench command-line tools (v 1.1.1). This resulted in cortically constrained source models with 7,842 source locations per hemisphere. We created single-shell volume conduction models based on the inner surface of the skull to compute the forward projection matrices (leadfields).

Beamformer and Parcellation.

To estimate the source time series from the MEG data, we used linearly constrained minimum variance beam forming, performed separately for each session, using Fieldtrip’s $\mathtt{ft}\_\mathtt{sourceanalysis}$ routine. To reduce the dimensionality, sources were parcellated, based on a refined version of the Conte69 atlas, which is based on Brodmann’s areas. We computed, for each session, parcel-based time series by taking the first principal component of the aggregated time series of the dipoles belonging to the same cortical parcel.

Lexical Predictions.

Lexical predictions were computed using GPT-2—a large, pretrained language model (39). We passed the raw texts through GPT-2 (see SI Appendix, section A for details) for each run independently (assuming that listeners’ expectations would, to some extent, “reset” during the break). This resulted in a sequence of conditional (log-)probability distributions over the lexicon for each token. From the token-level probabilities, we derived word-level probabilities, $p(w_i|\text{context})$, for each word w_i. We used the XL version of GPT-2, and used a windowed approach to process texts longer than the maximum context window of 1,024 tokens. For details on the model and procedure, see SI Appendix, section A.

Feature-Specific Predictions.

Feature-specific predictions were derived by analyzing the lexical prediction, illustrated in Fig. 3. For the part-of-speech prediction, we did POS tagging on every potential sentence to derive the probability distribution over POS. From this distribution, unexpectedness was quantified via surprisal: the negative log probability of the POS of the presented word (SI Appendix).

For the semantic prediction, the predicted lexicosemantic vector was computed as the average of the GloVe embedding of each predicted word, weighted by its predicted probability. From this vector, semantic unexpectedness was computed as a prediction error: the cosine distance between the vector of the actually presented word and the predicted vector.

For phoneme predictions, we used a phoneme model to compute the probability of the next phoneme, given the phonemes so far, and given a prior probability assigned to each lexical candidate (see Fig. 6for an illustration). We compared two formulations of the phoneme model, that either used a fixed (frequency-based) prior over lexical candidates (single-level model) or used a GPT2-derived contextual prior (hierarchical model). Both models compute a probability distribution over phonemes, from which unexpectedness was defined via surprisal.

Note that the difference between prediction error and surprisal is not important, since surprisal is simply a probabilistic metric of prediction error. For technical details, see SI Appendix, section A.

Non-Prediction-Related Control Variables.

To ensure we were probing effects of predictions, we had to control for various nonpredictive variables: onsets, acoustics, frequency, and semantic distance or integration difficulty. We will briefly outline our definitions of each.

Each model contained onset regressors for each word and phoneme; content words onsets were included separately, to allow the model to capture different average responses to content words and function words. Second, a range of acoustic confound regressors were included, all on a phoneme-by-phoneme basis (SI Appendix, Figs. S2 and S7). To capture spectral differences between different speech sounds, we computed a log mel spectrogram with eight bands spaced on a log-mel scale. For each band, average spectrogram amplitude was computed for each phoneme, to compute a spectrally resolved amplitude pattern for speech sound. For speech, it is known that the cortical responses are also highly sensitive to fluctuations in the broadband envelope—a response specifically driven by rapid increases of the envelope amplitude, or “acoustic edges” (86). To capture these acoustic edges, we quantified variance of the broadband envelope over each phoneme, following ref. 66. Finally, we analyzed all speech materials using Praat (87), via parselmouth (88), to compute the average pitch of each phoneme. For voiceless phonemes or other segments in which the pitch could not be identified, pitch values were zeroed out.

In addition to acoustic regressors, we included word-level lexical confound regressors. First, we accounted for frequency via unigram surprisal $-\log P(\text{word})$ based on its frequency of occurrence in subtlex. Second, we accounted for word class (content or function word). Finally, we controlled for the semantic distance or semantic integration difficulty. This speaks to the “prediction vs. integration” question: Are unpredictable words more difficult to process because they violate a prediction, or because they are more difficult to semantically integrate for a different reason? This can be illustrated by considering a constraining context (“coffee with milk and …”). When we contrast a highly expected word (“sugar”) and an unexpected word (e.g., “dog”), the unexpected word is not just less likely but also semantically incongruous. As such, the increased processing cost reflected by effects like N400 increases might not (only) be due to a violated prediction but due to difficulty integrating the target word (“dog”) in the semantic context (“coffee with milk”) (7, 18, 60, 61). The primary explanation for differences in semantic integration difficulty is intralexical priming (18, 38, 89). Bottom-up priming between words facilitates processing of related words (coffee, milk, sugar) without requiring linguistic prediction. Such bottom-up semantic priming can occur through multiple mechanisms (18), but all imply that the degree of priming depends on the semantic proximity or association between words. To control for this effect, we computed the semantic distance (inverse of proximity) between each content word and the preceding context. This was defined as the cosine distance between the average semantic vector of the prior context words and the target content word, following ref. 36. This metric is known to predict N400-like modulations and can hence capture the extent to which such effects can be explained by semantic distance alone (36).

Word-Level Regression Models.

The word-level models (see SI Appendix, Fig. S2 for graphical representation) captured neural responses to words as a function of word-level processing. The baseline model formalized the hypothesis that responses to words were not affected by word unexpectedness but only by the following nonpredictive confounds: word onsets, word class, semantic distance (semantic integration difficulty), word frequency, phoneme onsets, and acoustics covariates for each phoneme, that is, spectrogram amplitudes (eight bands), broadband envelope variance (acoustic edges), and pitch.

The continuous prediction model formalized the hypothesis that predictions were continuous and probabilistic. This model was identical to the baseline model plus the lexical surprisal (or negative log probability of a word), for every word. This was based on normative theories of predictive processing which state that the brain response to a stimulus should be proportional to the negative log probability of that stimulus (6).

The constrained guessing model formalized the classical notion of prediction as the all-or-none preactivation of specific words in specific (highly constraining) contexts (38). This was formalized as a regression model using the insight by Smith and Levy (9) that all-or-none predictions result in a linear relationship between word probability and brain responses. The argument follows from two assumptions: 1) All predictions are all or none; and 2) incorrect predictions incur a cost, expressed as a prediction error brain response (fixed in size because of assumption 1). So, while, for any individual word, the size of the prediction error is categorical (either zero or $y_{\text{error}}$), on average, the expected error response for a given word is a linear function of the size of the error (which is a constant), and the probability of mispredicting the word: $(1-p)$. In other words, it scales linearly with word improbability. Note that this linear improbability is a continuous approximation that will never fully match the (hypothesized) categorical prediction error for individual words. However, it provides the best possible approximation of categorical prediction error effects, given that we know the statistics participants are tracking, but not the exact all-or-none predictions any participant may sample from moment to moment.

To capture the notion that predictions are only generated in specific contexts, the improbability regressor is only defined for constraining contexts, and we add a constant to those events to capture the effects of correct predictions (SI Appendix, Fig. S2). To identify “constraining contexts,” we simply took the 10% of words with the lowest prior lexical entropy. The choice of 10% was arbitrary—however, using a slightly more selective definition would not have changed the conclusion because the naive guessing model (which included linear predictability for every word) performed consistently better (SI Appendix, Fig. S5).

Integrated Regression Model.

For all analyses on feature-specific predictions, we formulated an integrated regression model with lexical predictions, and feature-specific predictions, at both the word and phoneme level (SI Appendix, Fig. S7). As regressors of interest, this model included phoneme surprisal, POS surprisal, and semantic prediction error. In principle, we could have also included phoneme and POS entropy rather than just surprisal (e.g., ref. 13)—however, these are highly correlated with the respective surprisal. Since this was already a complex regression model, including more correlated regressors would have made the coefficients estimates less reliable and hence more difficult to interpret. As such, we did not include both but focused on surprisal because it has the most direct relation to stimulus evoked effect.

Phoneme-Level Regression Models.

To compare different accounts of phoneme prediction, we formulated three regression models with only regressors at the individual phoneme level (SI Appendix, Fig. S19). In all models, following ref. 27, we used separate regressors onset and information-theoretic regressors for word-initial and word-noninitial phonemes, to account for juncture phonemes being processed differently. This was not done for the acoustic regressors, since we do not expect such an effect for the prelinguistic acoustic level. The baseline model only included nonpredictive factors of word boundaries, phoneme onsets, and uniqueness points. The two additional models also included phoneme surprise and phoneme entropy from either the hierarchical model or nonhierarchical model. To maximize our ability to dissociate the hierarchical prediction and nonhierarchical prediction, we included both entropy and surprise. Although these metrics are correlated, adding both should add more information to the model comparison, assuming that there is some effect of entropy (13). (Note that, here, we were only interested in model comparison, and not in comparing the coefficients, which may become more difficult when including both.)

Time-Resolved Regression.

As we were interested in the evoked responses, variables were regressed against EEG data using time-resolved regression, within a regression ERP/ERF framework (40). The regression ERP technique is similar to TRF modeling (90), except that the predictors are event-based (impulses) rather than continuous stimuli. We use regression ERP because it is formally equivalent to ERP analysis (used by majority of prior literature), and because the use of sparse impulses allows to model all 10 MEG sessions jointly. Briefly, we use impulse regressors for both constants and covariates defined at event onsets, and then temporally expand the design matrix such that each predictor column C becomes a series of columns over a range of temporal lags $C_{t_{\mathit{min}}}^{t_{\mathit{max}}}=(C_{t_{\mathit{min}}},\dots ,C_{t_{\mathit{max}}})$. For each predictor, one thus estimates a series of weights ${\beta }_{t_{\mathit{min}}}^{t_{\mathit{max}}}$ (Fig. 1) which can be understood as the modulation function describing how a given regressor modulates the neural response over time, and which corresponds to the effective evoked response that would have been obtained in a time-locked ERP/ERF design. Here, we used a range between –0.2 and 1.2 s. All data and regressors were standardized, and coefficients were estimated with ${\mathcal{l}}_2$-norm regularized (Ridge) regression, using the scikit learn sparse matrix implementation (91). In both datasets, models were estimated by concatenating the (time-expanded) design matrix across all runs and sessions. Regularization was set based on leave-one-run-out R² comparison; for inference on the weights in the EEG data, this was done across subjects to avoid doing statistics over coefficients with different amounts of shrinkage.

Model Comparison.

In both datasets, model comparison was based on comparing cross-validated correlation coefficients. Cross-validation was performed in a leave-one-run-out cross-validation scheme, amounting to 19-fold cross-validation in the EEG data and between 63- and 65-fold cross-validation for the MEG data (in some subjects, some runs were discarded due to technical problems).

For the EEG data, models’ cross-validated prediction performance was compared across subjects to perform population-level inference. To this end, we reduced the scores into a single n_subs dimensional vector by taking the median across folds and taking the mean across channels. Critically, we did not select channels but used the average across the scalp. For the MEG data, models were primarily compared on a within-subject basis, except in some isolated cases (see below). Because the MEG data were source localized, we could discard sources of no interest (e.g., visual cortex). To this end, we focused on the language network, using a rather unconstrained definition encompassing all Brodmann areas in the temporal lobe, plus the temporoparietal junction, and inferior frontal gyrus and dorsolateral prefrontal cortex, bilaterally (SI Appendix, Fig. S20).

Statistical Testing.

All statistical tests were two-tailed and used an alpha of 0.05. For all simple univariate tests performed to compare model performance within and between subjects, we first verified that the distribution of the data did not violate normality and was outlier-free. If both criteria were met, we used a parametric test (e.g., paired t test); otherwise, we resorted to a nonparametric alternative (Wilcoxon sign rank). For the MEG data, most statistical tests were performed on a within-subject basis only. However, in some isolated cases, we aggregated across participants for simplicity or additional statistical power. For this, we used a multilevel nonparametric test (hierarchical bootstrap t test), using hierarchical bootstrapping (92). P values were obtained using 10,000 resamples, and a fixed random seed was used across the project. To statistically compare the rERP latencies (between phoneme and lexical surprisal), we performed the jackknife-based latency t test, using the relative amplitude criterion (set at 0.5), following recommendations in ref. 93.

In EEG, we performed mass univariate tests on the coefficients across participants between 0 and 1.2 s. This was, firstly, done using cluster-based permutation tests (94, 95) to identify clustered significant effects as in Fig. 5 (10,000 permutations per test). Because the clustered effects as in Fig. 5only provide a partial view, we also reported more comprehensive picture of the coefficients across all channels (SI Appendix, Figs. S3 and S10); there, we also provide multiple-comparison-corrected P values to indicate statistical consistency of the effects; these were computed using threshold-free cluster enhancement (TFCE). In the MEG, multiple comparison correction for comparison of explained variance across cortical areas was done using TFCE. In both datasets, mass univariate testing was performed based on one-sample t tests plus the “hat” variance adjustment method with $\sigma ={10}^{-3}$.

Spatial Dissociability Test.

To test whether the distinct signatures of spatial patterns of explained variance (Fig. 4 and SI Appendix, Fig. S9) were not just statistically significant (compared to a null distribution) but also significantly dissociable (compared to each other), we performed a classification-based test. In this test, we evaluated whether a linear classifier could robustly distinguish spatial patterns of additional variance explained by different unexpectedness regressors, on held-out cross-validation folds. For this test, we compared the map of four unexpectedness regressors: lexical surprisal, phoneme surprisal, POS surprisal, and semantic prediction error (SI Appendix, Fig. S9). To avoid the classifier picking up overall differences in the amount of variance explained, all patterns were mean normalized. To assess the separability, we trained a linear logistic regression model, implemented in scikit learn (91), using all default parameters. The model was evaluated both in a multinomial classification and in all pairwise comparisons, by computing accuracy in a stratified sixfold cross-validation scheme, across the independent patterns of additional explained variance for each regressor, for each run.

Polarity Alignment.

In the source localized MEG data, the coefficients in individuals (e.g., SI Appendix, Figs. S13–S18) are symmetric in polarity, with the different sources in a single response having an arbitrary sign, due to ambiguity of the source polarity. To harmonize the polarities, and avoid cancellation when visualizing the average coefficient, we performed a polarity alignment procedure. This was based on first performing singular value decomposition (SVD), $\mathbf{A}=\mathbf{A}\mathrm{\Sigma }{\mathbf{V}}^{\top }$, where A is the m × n coefficient matrix, with m being the number of sources and n being the number of regressors, and then multiplying each row of A by the sign of the first right singular vector. Because the right singular vectors (columns of U) can be interpreted as the eigen vectors of the source-by-source correlation matrix, this can be thought of as flipping the sign of each source as a function of its polarity with respect to the dominant correlation. This procedure was used for visualization purposes only (SI Appendix, Figs. S4 and S13–S18).

Data Availability

EEG data was previously published and is openly available (see ref. 36, and https://doi.org/10.5061/dryad.070jc). The full raw MEG dataset is availlable and described in detail in ref. 96 and at https://doi.org/10.34973/5rpw-rn92. Data and code required to reproduce the results in this paper are found at https://doi.org/10.34973/dfkm-h813 (97).