The grid code for ordered experience

Abstract

Entorhinal cortical grid cells fire in a periodic pattern tiling space, suggestive of a spatial coordinate system. However, irregularities in the grid pattern as well as responses outside the spatial domain have presented a challenge to existing models of entorhinal function. In this perspective, we propose that hippocampal input provides a key drive to the grid network in both spatial and non-spatial circumstances, particularly around salient events. We build upon previous models in which neural activity propagates through the entorhinal-hippocampal network in time. This temporal contiguity in network activity points to temporal order as a necessary characteristic of representations generated by the hippocampal formation. We advocate that interactions in the entorhinal-hippocampal loop build a topological representation rooted in the temporal order of experience. In this way, the structure of grid cell firing supports a learned topology rather than a rigid coordinate frame bound to measurements of the physical world.

Introduction

The discovery of grid cells in the medial entorhinal cortex (MEC) inspired theories for an elegant spatial code in the brain^1,2. Grid cells exhibit spatially periodic fields that tile the environment^2,3, suggestive of a spatial coordinate system. Together with hippocampal place cells that fire in individual locations⁴, grid cells are thought to construct an internal spatial map of the external world^5,6. Because grid cell firing corresponds to reliable coordinates in open-field environments and is maintained across environments, grid cells are often interpreted to reflect a universal positional code capturing veridical measurements of external space. However, both grid cells and place cells fire selectively in circumstances outside of spatial navigation, and research in humans has long implicated both the entorhinal cortex and hippocampus in structuring newly learned information into episodic memories^7,8. In this perspective, we seek to resolve this tension between spatial and non-spatial functionality by revising existing network models thought to support MEC processing, proposing that the MEC-hippocampus loop builds topological representations^7,9–14 that reflect temporal contiguity between events within experience (Fig. 1A).

Figure 1. Representations argued to be supported by grid cells.

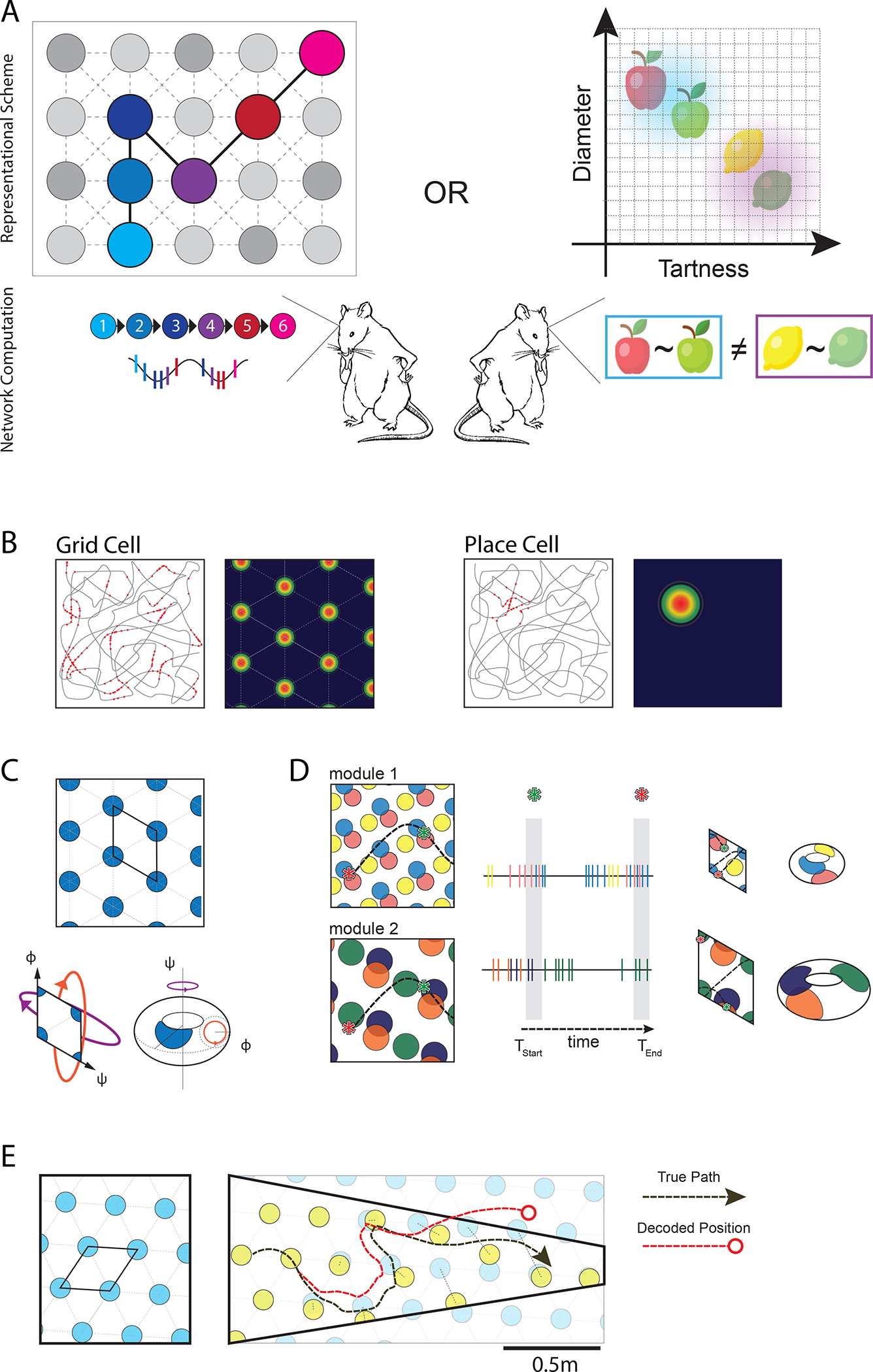
A) Comparison of conceptual models that may be supported by grid cells. The ‘Representational Scheme’ illustrates how the entorhinal-hippocampal network represents relationships (top), and the ‘Network Computation’ illustrates the nature of the information supplied to readers of the entorhinal-hippocampal network (bottom). Left: Topology based in temporal order. Structure across nodes is rooted in the order of events in experience; relationships reflect temporal adjacency. This structure formulates sequences that can link disparate items, which may be manifest in the fine timing of spikes within each theta cycle (see Fig. 2). Right: Feature space defined by axes that quantify featural attributes of items. Relationships between items are defined by the qualities measured within the feature space, which can be used to derive categories (e.g. types of apples or citrus fruits; see Box 2).

B) Firing patterns of an archetypical grid cell in MEC (left) and place cell in hippocampus (right) in a square open arena. Grey line depicts the trajectory of the animal; red dots are spikes. The spatially averaged firing rates of the cells are shown with warmer colors indicating higher firing rates.

C) Grid cell fields are organized in a rhombus-shaped tile that spans the environment. Relative position within the tile is given by coordinates (phi, psi) defined by the rhombus axes. In one proposed implementation of connectivity within the tile, connecting the rhombus edges forms a twisted torus^19,20,50,51, creating a continuous surface capable of generating periodic fields.

D) Grid cells with similar field spacing and orientation are organized in modules. Spatial offset between grid cells indexes relative position within a module tile. Combining activity across modules disambiguates individual positions in the environment (trajectory: dotted line). Spike rasters demonstrate the activity of each module over time as the trajectory progresses. The population rate code across modules creates a unique identifier for each position in space (green and red stars).

E) Inaccurate decoded positions resulting from distortion in grid field spacing (adapted from ⁶⁴).

In several prominent network models proposed to support spatial navigation, the recurrent connectivity within the entorhinal-hippocampal circuit allows the network to continuously track position in allocentric space. Precision of spatial measurement is an emergent feature of these models, and some recent works propose that the ‘metric’ ability of the grid cell network to make veridical measurements in physical space also allows it to encode measurements in abstract feature spaces^15–17 (Fig. 1A). We challenge the notion of metric rigidity in these models, but we highlight the utility of the physiological mechanisms they invoke to explain experimental observations across both spatial and non-spatial tasks. In light of mounting evidence that recurrent connectivity and continuous attractor dynamics are critical to processing across the entorhinal-hippocampal circuit, we advocate that temporal contiguity is an essential characteristic of coding in the MEC and hippocampus. We propose that network activity progresses sequentially over time through reciprocal interactions between the MEC and hippocampus to create topological representations of experience. Under this hypothesis, a topology is defined as a structural representation of relationships between elements in an experience, preserving their arrangement independent of the exact time or metric distance between them. We suggest that the topology supported by the entorhinal-hippocampal network is specifically derived from the temporally ordered relationships between experiential elements, or ‘events’. This proposed function builds on existing models to explain how the grid system can both map spatial positions under certain navigational circumstances as well as learn the temporally structured relationships between events in non-spatial episodic experiences. Under this framework, both spatial and mnemonic processing are aspects of a more general function of the hippocampal formation in learning topological structure from experience rather than coding for measurable features.

Continuous attractor networks

To lay a foundation for our updated model of hippocampal-entorhinal function, we first discuss the MEC as a continuous attractor network (CAN). We then review the influential proposal that a CAN specialized for estimating allocentric position governs activity in the MEC.

Recent studies describing the anatomy and physiology of cells within the MEC have converged with computational work to describe the grid network using continuous attractor models^18–26. In a continuous attractor network (CAN), local “bumps” of excitation flow through an interconnected matrix of neurons through recurrent synaptic connections and surrounding feedforward inhibition. Excitatory drive to the network can propel activity through this neural sheet, stabilizing in local subsets of neurons via the intrinsic connectivity. Grid cell firing is thus thought to be a readout of the excitatory bumps of activity “passing through” individual neurons in the sheet and eliciting spikes^18,19. The possibility that the MEC operates as a CAN is strongly supported by the intrinsic microcircuitry between MEC neurons (Box 1)^22–26.

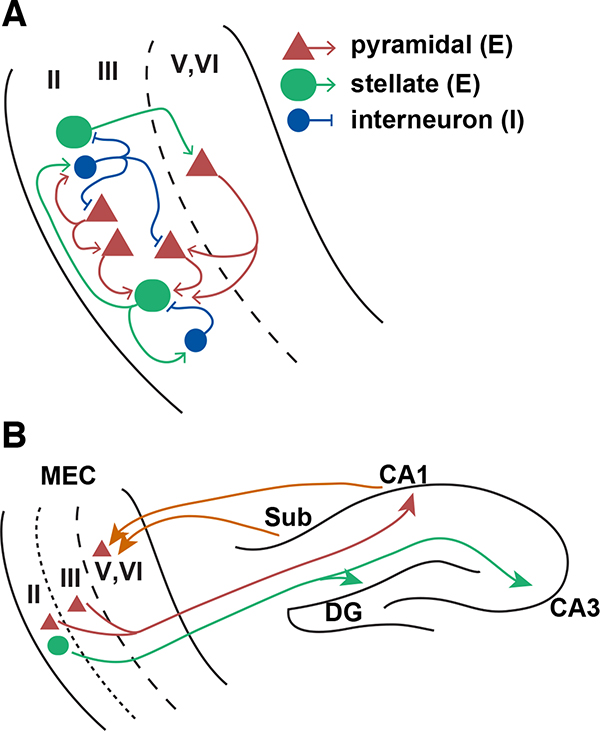
BOX 1. Connectivity of the MEC and HPC supporting continuous attractor dynamics.

Principal cells in layers II and III of the MEC comprise a multitude of functionally-defined cell types, including grid cells, head direction cells, border cells, and non-grid spatial cells^{27,35,212–214}. Within the MEC, grid cells are embedded within a network that has elaborate intrinsic connectivity, with recurrent excitation between subsets of nearby excitatory neurons and strong feedforward inhibition via local interneurons^{22,23,26,215–218}. This connectivity is poised to support recurrent activity patterns and supplies an anatomical substrate for intrinsic propagation of activity through the tissue.

Grid firing patterns have been observed in both excitatory principal cell types of the MEC^219,220, stellate cells and pyramidal cells^221,222. Layer II (L2) pyramidal cells make lateral excitatory synapses onto stellate cells, interneurons, and other pyramidal cells within L2^217,218, whereas L2 stellate cells are thought to communicate with each other primarily via feedforward inhibition through interneurons^22,216 (Box 1, A). Inhibition to the principal cell in layers II and III diminishes in strength as a function of distance^{22,23,26,143,215,216}, suggesting that activity propagates through the network by successive recruitment of anatomically restricted microcircuits. Communication across layers is facilitated by ascending excitatory synapses from L5b pyramidal cells to L5a, L3, and L2^142,143,223, as well as from L3 pyramidal cells to L2 stellate cells²¹⁸. Descending excitation flows primarily from L2 stellate cells to L5b pyramidal cells, the primary recipients of hippocampal input²²⁴. The dendritic field of excitation ascending from deep to superficial layers of MEC is asymmetrically offset from the receiving neuron¹⁴³, which suggests that deep layers may direct an asymmetric flow of activity within the CAN comprising the superficial layers^39,52,225.

MEC stellate cells (green circle) in layer II project primarily to the dentate gyrus (DG) and CA3, while pyramidal cells (red triangles) in layers II and III project to CA1^226–228 (Box 1, B). Reciprocally, hippocampal CA1 and subiculum (Sub) project primarily back to layers V and VI of the MEC^226,229, where grid cells are present but less numerous than in the superficial layers²⁷. A direct projection from CA1/subiculum to layer III²³⁰ and from CA2 to layer II has also been observed²³¹, as have minor projections from layer V back to the hippocampus²³². Ascending excitatory connections from the deep to superficial layers of MEC close the MEC-hippocampal loop^{142,143,218,223}.

Box 1 illustration.

The path integration continuous attractor network (PI-CAN)

During spatial navigation, grid cells fire in a repeating pattern of equilateral triangles (Fig. 1B). This pattern persists across environments irrespective of running speed or the route taken, suggesting that the grid cell circuitry may continuously track idiothetic, or self-movement, information to estimate allocentric position^2,27. This process is known as path integration and is thought to be a central function of the grid network^21,28,29.

To derive the allocentric specificity of grid cells from self-movement information, the path integration continuous attractor network (PI-CAN) model posits that neural activity is driven through the attractor manifold by an afferent velocity signal^18,19,21. This signal has two critical elements: direction and speed. The direction component is hypothesized to be supplied by head direction cells within the MEC, which respond maximally at a particular head orientation relative to the external environment^27,30–32. Head direction cells rotate their preferred directions coherently with grid cell orientations to remap new environments^33–35, suggesting that these cell types are integrated into a single attractor network. Though theories differ on the source of the speed component of the velocity signal, the principal candidates are MEC speed cells^36–38 or the amplitude and frequency modulation of the theta rhythm driven by inputs from the medial septum^39–43. The velocity-driven activity of the PI-CAN is anchored to allocentric space via interactions with landmarks, the most salient of which are often environmental borders^44–46. By linking each element of a path integration circuit to concrete physiological mechanisms, the PI-CAN model has elicited enduring support for the theory that spatial navigation is central to the function of the MEC.

The combined idiothetic and sensory inputs to the PI-CAN are theorized to generate a direct mapping between translocation through space and advancement of neural activity through the neural sheet (i.e. the attractor state)^21,29. The attractor state yields a positional code through the collective activity of grid cell modules, sub-networks of grid cells with shared field size, spacing, and orientation of the grid axis⁴⁷. Each grid cell module maps a tile that repeats throughout the environment (Fig. 1C), and the fields of grid cells within the module are offset from each other, collectively mapping the relative space within a tile^47–49. Periodicity is posited to arise from connectivity within the module that allows the activity to repeatedly cycle through the attractor whenever the animal reaches the edge of the module tile^{18–20,50,51}. Due to this connectivity, the grid network is thought to provide a geometrically consistent code irrespective of the shape or size of the environment. Because the pattern of activity within each module repeats, unique locations across the entire environment are disambiguated by combining information across different modules with different orientation and spacing^{18,48,49,52,53} (Fig. 1D). If the grid field spacing of each module is consistent across the environment, the combined activity across modules can map a one-to-one relationship between the attractor state and the animal’s coordinates in space. With these elements, the PI-CAN model of the grid cell system is thought to create an efficient and boundless code, allowing a downstream structure to calculate the distance and vectoral bearing between two points^48,53,54.

Evaluating the PI-CAN framework

Data consistent with the PI-CAN model

Experimental findings support the idea that a local attractor network underlies MEC processing. Grid cell spiking is accompanied by sustained membrane depolarization as animals pass through the firing fields of a grid cell^55,56, consistent with a link between translocation and excitatory bumps of activity moving through the neural sheet. As predicted by CAN models, anatomically neighboring grid cells are roughly clustered into modules with similar grid spacing and orientation^24,47,57 that maintain their spatial relationships across different environments^25,58. Spike correlations between cells within a module are preserved during sleep^59–61, demonstrating that structured activity during waking is supported by intrinsic connections rather than solely reliant on external inputs. In addition, manipulations of both MEC layer II pyramidal cells²⁶ and parvalbumin interneurons⁶² (see Box 1) disrupt the spatial specificity of grid fields, indicating that grid cell firing is critically shaped by intrinsic MEC connectivity consistent with a CAN.

Spatial data requiring an update of the PI-CAN model

While there is strong evidence of CAN dynamics, accumulating experimental evidence presents two main challenges to the PI-CAN framework. First, the PI-CAN model posits that symmetric field spacing of grid cells allows a metric measurement of space. To provide this metric measurement, symmetric spacing should be static across experience and independent of environmental features. However, several lines of evidence have shown that grid spacing is instead dynamic with experience and malleable with changing environmental features. Displacing the walls of 2D environments causes grid fields to elongate their spacing in proportion to the environmental change^37,47,63, and open fields that lack symmetry cause distortions in the geometry of the grid pattern near the asymmetric wall^64,65 (Fig. 1E). These shifts in grid field spacing may depend on the recent experience of the animal in encountering borders⁶⁶, driving history-dependent updates to the relationship between the attractor state and the external environment^44,45,66. Consistent with a role for experience in shaping the grid pattern, environmental novelty increases grid field spacing, while gaining familiarity reverses this effect⁶⁷ and shifts grid spacing in accordance with the learned layout of the environment^68,69. During goal-directed behaviors, grid fields can migrate towards learned reward locations, locally distorting grid spacing and overrepresenting goals⁷⁰. The symmetric spatial periodicity implied by the PI-CAN model is therefore not an immutable feature of grid cells. Rather, environmental features anchor grid fields, which sometimes results in irregular spacing. This limits the interpretability of grid patterns as a metric code⁷¹. Instead, the grid network is well suited to represent the spatial relationships between environmental borders and other types of landmarks learned over the course of experience.

Second, the locomotor velocity input in the PI-CAN model, provided putatively by speed and head direction cells, is often assumed to be uniform across behavioral conditions to supply the consistent driving force for a universal and boundless grid pattern. Contrary to this assumption, changes to environmental boundaries cause speed cells to rescale their firing responses and head direction cells to reorient³⁷. While the rescaling of speed signals can account for changes in grid spacing in the PI-CAN model¹⁹, it is unclear what drives speed cells to rescale or why these changes would occur asymmetrically. In addition to a dynamic speed signal, head direction cells can transiently reorient when local salient cues are moved relative to the allocentric reference frame⁷². These observations suggest that like grid spacing, speed and head direction cells are anchored to salient environmental characteristics rather than absolute metrics of locomotion³⁷. Moreover, speed and head direction signals do not seem sufficient to drive grid cell firing. Locomotion exerts a variable influence on the positional specificity of MEC cells⁷³ and competes with the influence of optic flow information to drive grid cell periodicity⁷⁴. In addition, head direction cells can decouple from the grid network in linearized environments, maintaining allocentric orientation to room cues while grid cells reorient^58,75–78. This finding is contrary to the expectation of the PI-CAN model since static coupling between head direction and grid cells is posited to support path integration calculations irrespective of environment. Finally, head direction fails to accurately capture true movement direction⁷⁹, further calling into question the role of head direction coding in generating grid fields according to path integration. Together, the irregularity of grid fields and the inconstancy of the velocity signals demonstrate that activity in the MEC network is not dedicated to making precise spatial measurements. As the PI-CAN model is insufficient to explain MEC firing, a revision of the model is required to accommodate these new experimental observations.

Spatial data unanticipated by the PI-CAN model

Recent data have exposed additional sources of variability in grid cell firing that may elucidate a more complex drive to the MEC. The PI-CAN model predicts that each field of the grid pattern will have a consistent firing rate due to uniform drive from velocity inputs irrespective of position. Empirically, however, individual grid fields can exhibit different directional sensitivity⁸⁰ and often have consistently different firing rates^35,81–83 or fail to fire altogether⁸⁴. Variable firing rates may also signal motivationally salient information, as grid cells selectively increase field firing rates based on route⁶¹ and near hidden reward locations³³. The variable firing within grid cells suggests that input to the MEC varies by position throughout the environment -- a feature that cannot be derived from a location-independent velocity vector.

In addition, reliable location-specific activity is exhibited by two-thirds of the neurons in the MEC outside of the grid cell population^35,85. These ‘non-grid spatial cells’ remap the locations of their firing fields under the same conditions that produce rate remapping in individual fields of grid cells^33,35. These coherent changes suggest that non-grid spatial cells are integrated within the grid network and may even provide an input to grid cells. Together, the location-specificity of both grid and non-grid cell firing indicates that position-specific input may be a strong determinant of MEC activity, which is not anticipated by the PI-CAN model.

Non-spatial data unanticipated by the PI-CAN model

Despite the historic focus on spatial navigation, there is increasing evidence that neurons within the hippocampal formation exhibit selective responses in domains beyond physical space. In the MEC of rats, both grid cells and head direction cells recorded in open arenas fire at specific points within a sequence of tones during a stationary auditory task⁸⁶. MEC neurons also fire sequentially in time during delay periods^87,88, indicating that the grid and head direction networks can be engaged outside of physical navigation. In both humans and non-human primates, grid-like firing patterns have been observed in entorhinal neurons during virtual spatial navigation⁸⁹ and during visual exploration of a scene^90,91, in absence of physical translocation and even eye movement⁹¹. Finally, studies in humans using functional imaging and electroencephalography have observed mesoscopic signals suggestive of grid-like activity, not only in response to virtual spatial navigation^92–95 but also in response to the progression of ordered visual stimuli^93,96–100.

In the hippocampus, non-spatial response properties are even more well established across multiple modalities^101–103 and across species^7,104,105. Neurons in CA1 respond in tasks with continuously changing stimuli, showing place-like activity when presented with a series of tones⁸⁶ or concentration gradients from one odor to another¹⁰⁶. In tasks entailing a sequence of discrete odors or tones, hippocampal neurons respond depending on the order of the stimuli presented^107–110. As in the MEC, hippocampal sequential tuning has also been shown for the temporal structure of a task¹¹¹, corresponding to elapsed time during forced delay periods^{110,112–117} and to a specific number of laps around a track¹¹⁸. Together, these findings demonstrate that both continuous and discrete sequences of events can evoke hippocampal and entorhinal firing even in the absence of translocation through space.

The collection of multisensory responses in the hippocampal formation has led some to the hypothesis that these regions map non-spatial featural dimensions^{15,16,94,96,99,119,120}. Several of these theories leverage aspects of the PI-CAN model to propose that the grid cell system can encode feature metrics^15,16. One example of this proposal is the suggestion of a ‘car space’, with MEC grid cells coding a 2D space of car weight versus engine power and hippocampal place cells coding for individual categories of cars¹⁵. Under this framework, grid cells serve as a measurement system for regularly spaced intervals within continuous feature axes, while place cells specify unique feature identities¹⁵. However, this framework requires mechanisms that deviate from the physiological CAN dynamics that underlie the PI-CAN model (Box 2). Specifically, relationships within this type of feature space are not defined by experiencing transitions within the space through time. Instead, the feature space maps similarity of elements based on featural identifiers, akin to the process of categorization. A structural relationship (e.g. an orange is bigger than a lime but of similar size as an apple) in the feature space framework is an attribute built on the relative similarity of the neuronal representation (e.g. population firing rate). By contrast, mechanisms of path integration necessitate that neural activity moves through the network in time in concert with ongoing experience (Box 2). This temporal contiguity is preserved in certain abstract spaces tested experimentally, such as the “bird space” explored by Constantinescu and colleagues⁹⁶. In this study, the subjects learned about relationships between features in the space by viewing bird necks and legs change continuously, thus linking features sequentially in time. In the following section, we propose a revised CAN model to explain why temporal contiguity is a critical aspect of spaces learned and represented in the hippocampal formation.

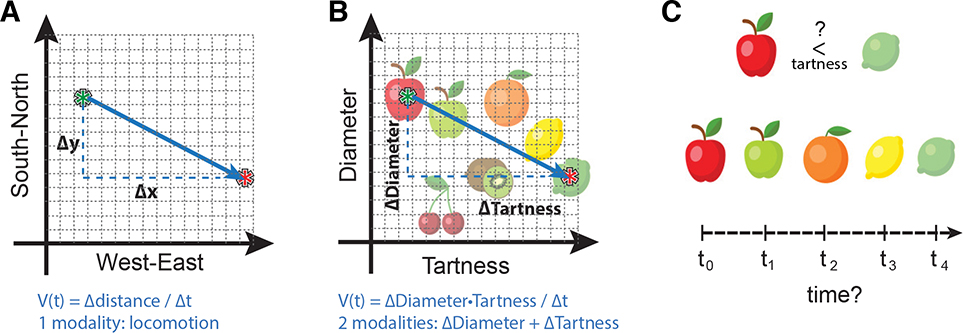
BOX 2. Incongruity of abstract feature spaces with CAN dynamics.

To assess whether abstract features spaces could be supported by the mechanisms proposed to underlie the MEC CAN, let us imagine a two-dimensional conceptual space of fruit. In this space, fruit diameter lies on one dimension and tartness on the other dimension. For the hippocampal formation to code this ‘fruit space’, the fields of each grid cell would span the measurement range of each fruit dimension (e.g. smaller to large diameter), and hippocampal neurons would be selectively active for a subclass of fruit, such as lemons and limes. Generalizing the PI-CAN model to this space utilizes the model’s assumed metric relationship between features of the physical world and the firing patterns of grid cells and place cells. However, to adapt the mechanistic framework from the PI-CAN model to fruit space, two key model constructs must be reconciled, each creating unique challenges in featural domains.

First, measurements of change along the feature axes (i.e. delta-x and delta-y) (Box 2, A) must be conveyed to the grid network through afferents specifying information about each feature, analogous to a velocity signal containing direction and speed. These inputs must either bypass the velocity input to advance the attractor state through the CAN independently, or somehow convert the relationship between abstract features, such as perceived differences in tartness between fruits, to a velocity signal (Box 2, B). The possible mechanisms for converting sensory inputs specific to each feature to a velocity-like input are unclear. To drive the CAN independently of this conversion would require a combinatorial explosion of extrinsic inputs to drive MEC representations of all possible abstract spaces. Moreover, in order to decode measurements of fruit diameter and tartness from the firing of a grid field, the network must generate regular field spacing that reflects metric intervals in the feature space. Such fixed regularity is often absent even in physical space outside of symmetric open-field environments.

Second, to measure displacements in the feature space using PI-CAN mechanisms, activity must move through successive states of the CAN. Because activity states evolve continuously over time, rather than shifting in large jumps across the manifold, updates require a “path” through the space that can be “path-integrated” through time from the velocity analog. To construct such a path, elements in the space must be ordered in time. It is unclear how feature spaces that lack temporal contiguity between their elements would correspond to updates in the CAN -- for example, does defining the tartness relationship between limes and apples traverse a path through oranges and lemons? (Box 2, C) While landmark inputs alone (i.e. inputs specific to limes) can shift the network activity toward the landmark⁴⁴, these inputs must be used in concert with a continuously evolving input like velocity in the PI-CAN model to drive the activity through intervening states. Together, these constraints imposed by the mechanisms in the PI-CAN model limit the scope of abstract spaces that can be plausibly mapped according to our current understanding of network dynamics in the MEC.

Box 2 illustration.

A revised CAN model of the MEC-hippocampal loop

To address the gaps left by the PI-CAN model in explaining experimental data, we propose that the dynamics of the MEC attractor network are substantially shaped over time by sequential hippocampal cell input. Hippocampal neurons can track sequences of task-relevant stimuli, just as the activity of place cells continuously changes during movement on a maze, thereby bridging events within spatial and non-spatial experiences. With its prominent anatomical projections to the MEC and flexible responses across modalities, the hippocampus is a strong candidate to provide informative drive to the MEC CAN. Because the location-specific variability of grid cells and the prevalence of non-grid spatial cells are not explained by the PI-CAN model, a velocity signal may provide only a component of the drive to the MEC even in the context of navigation^26,121.

Supporting a critical role for hippocampal input, grid patterns appear only after place cells achieve spatial tuning during development^50,122–125. Moreover, inactivation of the hippocampus decimates the two-dimensional periodicity of grid firing¹²⁶, although spike correlations remain intact between grid cells^126,127. These findings suggest that local intrinsic connections help determine the order of spiking between grid cells, but hippocampal input is required for periodic spatial patterns during behavior. Some authors advocating for the PI-CAN model interpret this to mean that the hippocampus is providing uniform excitatory drive to the entire grid network¹²⁶. However, we advocate that the hippocampus provides non-uniform, event-specific input that can shape the flow of activity through the MEC CAN. For example, the unique ensembles of hippocampal place cells active at each location in an environment may drive location-specific variability in grid cell firing^33,81,83,128, as well as the specificity of non-grid spatial patterns³⁵. This hypothesis aligns with computational models which show that location-based inputs can generate grid patterns^{50,51,128–137}, even in the absence of an explicit velocity input^{51,128,131,134–137}. Thus, the ability of ordered hippocampal activity to generate periodic grid cell firing could be particularly critical in non-spatial circumstances without locomotion.

The MEC-hippocampal loop progresses network activity in time

We hypothesize that interactions between the hippocampus and MEC reciprocally drive updates to the attractor state within each region (Fig. 2A). In this model, the bidirectional communication is temporally coordinated by the theta rhythm¹³⁸, which reflects windows of disinhibition that create discrete epochs of activity within each local network¹³⁹. Hippocampal and MEC theta oscillations are offset from each other, such that spiking in MEC occurs out of phase with spiking in the hippocampus⁷⁷ (Fig. 2B). Hippocampal input is thus well-timed to prime the flow of MEC CAN activity within each theta epoch, because the bulk of CA1 spiking occurs just before the rhythmic disinhibition of MEC neurons. Since each CA1 neuron has anatomically restricted axon terminals in the deep layers of the MEC^140–142 which in turn generate non-uniform drive to the superficial layers¹⁴³ (Box 1), the population of CA1 neurons active on each theta cycle is poised to bias the directional flow of activity through the grid attractor network. This possibility is supported by the loss of grid cell periodicity when either hippocampal inputs^126,144 or medial septal inputs supporting theta^42,43 are removed, as well as computational work demonstrating that theta-time scale hippocampal inputs can generate MEC grid patterns¹³⁴.

Figure 2. Topological representations in the spike order of theta sequences.

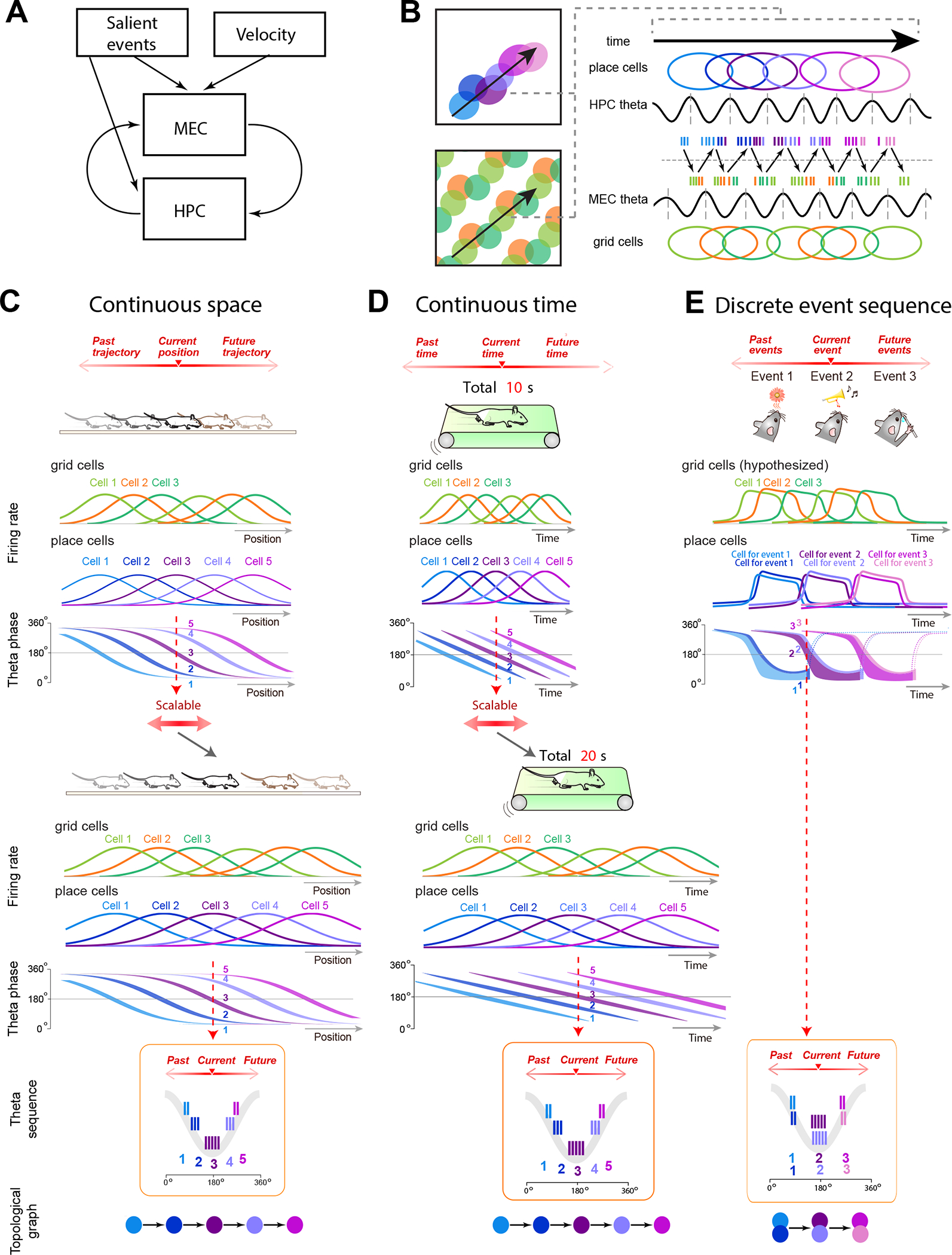
A) The MEC-hippocampus loop model for updates to network activity in each region. Information about velocity and salient events are proposed to influence the MEC CAN, which reciprocally interacts with the hippocampus -- though this does not preclude a direct effect of these inputs on the hippocampus as well.

B) Theta sequences in hippocampus and hypothesized theta sequences in MEC. Left: A trajectory through an open arena (black arrow) passes through a sequence of place cells (top) and grid cells from a single module (bottom). Right: Place cells and grid cells both exhibit ordered spiking at the theta timescale that progresses in concert with movement through the maze. Vertical dotted lines mark theta cycle boundaries. Theta disinhibition is out of phase between hippocampus and MEC, allowing communication to alternate across regions.

C-E) MEC grid cells and hippocampal place cells fire as a rodent moves along a linear track (C), runs continuously on a treadmill (D), or progresses through a sequence of discrete sensory events involving odors and tones ¹⁰⁹ (E) (grid cell firing patterns in E are hypothetical). As the animal progresses in position or time, neurons exhibit theta phase precession, shown for hippocampal cells as the transition of spikes from later to earlier theta phases. In each of these experiences, neuronal spikes are ordered within a single theta cycle (red dashed arrow) according to the animal’s past, present, and future. This spike ordering generates a topological graph of the experience, with each node of the topology corresponding to an ordered instance in the experience (bottom panels). When a linear track is stretched ¹⁹³ (C) or when the time of a treadmill run is increased ^87,195 (D), both grid cells and place cells demonstrate the capacity to rescale to span the entire experience. Despite this field stretching, spike ordering is preserved within a theta cycle (bottom panels), preserving the topological representation from the original to the stretched experience by maintaining temporal relationships between neurons. Future work remains to determine the scalability of topological representations for discrete sequences of events. Adapted from ^109,195.

The reciprocal projections from the MEC back to the hippocampus complete a loop, allowing the MEC to mutually shape the activity within the hippocampus. Under the synchronizing guidance of the theta oscillation, these two regions alternate between speaker and listener. As each region responds to its input, it primes the subsequent state in its counterpart, inextricably binding the activity across regions as a progression of handshakes across time. This reciprocal communication may even explain sequential activity in the loop in absence of changing sensory input to the hippocampal-entorhinal system during delay periods^{87,113,114,145,146}. Because the flow of states across time is inherent to the physiology of the network¹⁴⁷, the activity of neurons throughout the MEC-hippocampal loop reflects a continuous link of events through time.

The proposed handshake between the hippocampus and MEC may manifest at the fine time scale as the propagation of ‘theta sequences’ in each region. Hippocampal neurons display finely ordered spiking nested within a theta cycle^148–150 mirroring the sequence of place cells that fire over the course of seconds as an animal traverses the environment (Fig. 2B–D). These theta sequences similarly track the progression of discrete events during non-spatial tasks¹⁰⁹ (Fig. 2E). Each hippocampal theta sequence thereby constitutes a time-compressed representation of a momentary trajectory through the experience^150,151 (Fig. 2B). Because theta sequences project ahead of the animal’s current position, this activity is poised to guide the flow of activity within the MEC network¹⁵². While theta sequences have not yet been thoroughly characterized in the MEC (but see ⁶¹), computational models suggest that MEC theta sequences would arise naturally from theta-paced inhibition mediating CAN dynamics¹⁵³. Moreover, individual MEC cells show spiking temporally organized by the theta rhythm (i.e. theta phase precession)¹⁵⁴, consistent with the existence of theta sequences. We hypothesize that as hippocampal input helps direct the entorhinal attractor through successive states, the MEC returns information to the hippocampus influencing the progression of the next theta sequence¹⁵⁵ (Fig. 2B). Since theta sequences develop over the course of experience¹⁵⁶ and have been linked to the retention of learned spatial information^157–160, theta sequences in the MEC-hippocampal loop are well suited to support the representation of ordered events in episodic memory. Though some non-rodent species lack a continuous theta rhythm, temporally structured activity can nonetheless be observed relative to the underlying oscillation^161–163. These observations point to compressed spike sequences, organized relative to a periodic or aperiodic carrier oscillation, as a general mechanism for updating attractor states across regions.

The MEC-hippocampal loop builds the topology of experience

We advocate that hippocampal input to the grid cell CAN shapes the progression of MEC activity in accordance with structured hippocampal firing around salient events. For example, place cells tend to shift their fields toward learned reward sites^164,165, which could yield the changes in grid field spacing⁷⁰ and firing rate³³ observed near recalled reward locations¹⁶⁶. The shared variability in field density and firing rates across the MEC-hippocampal loop reflect mnemonic properties as well. MEC field rates are modulated by route destination or origin during goal-directed movement in linear environments^61,167,168 in concert with similar firing rate changes in hippocampal neurons^{167,169–171}. Collectively, evidence of parallel flexibility in hippocampal and MEC firing patterns suggests that the hippocampus supplies structured drive to the grid network particularly around behaviorally relevant locations and events.

The MEC grid network is situated to provide a key input to the hippocampus, allowing it to bridge the gaps between salient stimuli with reliable sequences of activity¹⁷². It was once thought that hippocampal place cells read the MEC grid code to index specific locations, but an accumulation of studies using lesions^{155,173–176}, optogenetics^146,177,178, and pharmacology^83,179–181 has now demonstrated that hippocampal neurons retain the capacity for place fields irrespective of grid cell input. Instead, altering grid cell activity degrades hippocampal cell tuning in the middle of large arenas^157,182,183 and during long delay periods^146,157 when the animal is spatially or temporally far from salient landmarks. These studies suggest that grid cell input to the hippocampus is key to structuring hippocampal activity in absence of salient stimuli. This role of the MEC may be particularly vital in novel settings, before the structure of the environment has been learned. By supplying a regularly structured input from the beginning of learning, the periodicity of the grid CAN may help generate new sequences of hippocampal activity that bridge disparate landmarks^172,184,185. In this way, the grid CAN could provide a temporal scaffolding onto which situation-specific activity can be linked across time, preserving the ordinal structure that supports a topology.

Bridging salient stimuli through the MEC-hippocampus loop

In order for grid network activity to link events into a topological representation of a given experience, the periodic scaffolding provided by the grid network must be anchored to salient landmarks that demarcate that experience. Salient landmarks may therefore influence grid CAN dynamics similar to the manner in which boundaries have been proposed to anchor the location of MEC attractor states to the external environment^45,66,186. During spatial exploration, it is thought that velocity inputs drive the flow of activity within the grid CAN during locomotion, but encounters with walls, signaled by MEC border cells or hippocampal place cells, pull the flow of activity toward the state associated with the landmark^44,66. In this way, the MEC attractor state becomes anchored to the physical environment, ensuring reliable spatial activity^45,186. However, landmarks do not need to be physical walls to provide an anchoring stimulus. The hippocampal population over-represents the start and end points of virtual linear tracks^106,187,188 and non-spatial task sequences^86,109, and thus could entrain the grid CAN to event boundaries by virtue of focal increases in excitation from the hippocampus. Reward would act as a particularly salient feature to alter the structure of the topology, anchoring the MEC grid pattern^33,70 and the hippocampal population activity^164,165 to salient goal locations. Updating by the hippocampus about salient landmarks can thus help provide waypoints that regulate the flow of activity through the grid cell CAN. In turn, the MEC facilitates the ability of both regions to form stable patterns of activity especially in novel settings. Together, these interactions in the MEC-hippocampus loop generate a topological representation of experience foundationally defined by the link between the progression of neural activity and the temporal order of events in the world.

Experimental results are consistent with the hypothesis that the MEC-hippocampal loop constructs a topological representation. Importantly, topological structure is preserved despite changes in spacing between salient events defining the topology¹⁸⁹. In agreement with this, the grid pattern dynamically stretches in proportion to the displacement of a moveable wall^{63–65,68,69,190} -- a finding that has been mirrored in hippocampal place cells in the open field¹⁹¹. Experiments using expandable^192–194 and reconfigurable¹⁰ linear tracks have further demonstrated that hippocampal cell firing corresponds to relative order in the environment as opposed to precise distances (Fig. 2C). The flexibility of this topological code is evident in MEC and hippocampal neurons that rescale their responses to span the duration of a forced delay period^88,195 (Fig. 2D). These findings suggest that the topology can be rescaled relative to the progression between salient events rather than providing veridical measurements of space or clock time. Indeed, neither elapsed time nor distance traveled definitively captures the specificity of grid cells and hippocampal neurons during treadmill runs in forced delays^87,114. By adapting to changing intervals between salient events^{37,44,63–66,68,69}, the grid CAN would aid in guiding the flow of activity in the hippocampus despite variability across individual experiences.

Though representations are malleable with manipulations to time or space, the fine spike timing between neurons remains intact within theta cycles^193,195, indicating that the topological structure is maintained at the theta time scale despite the stretching that occurs at the behavioral time scale. This preservation of spike order between cells suggests that theta packets reflect an ordinal structure stored in the hippocampal formation, raising the possibility that the rescaling seen in time or space is an emergent property of pacing the progression of theta sequences^11,196. This pacing is likely determined by the combination of inputs to the MEC-hippocampal system. As described in the PI-CAN model, inputs to the MEC conveying information about speed and allocentric orientation contribute to the flow of activity in the grid CAN^31,42,43. These velocity inputs may even help to “label” each attractor state with metric information^12,13,197, resulting in activity that can reflect a spatial code. Complementing inputs that reflect self-movement information, recent research has elucidated the additional importance of visual perception on attractor network activity¹⁹⁸. Just as landmarks have been proposed to drag the flow of the attractor^44,66, the MEC-hippocampus loop may be updated by perceptual information reflecting the approach or expectation of a salient event. Since salient features of a task are known to influence the extent of theta sequences^199,200, perceptual updates to the network may shape the rate of sequence progression. If the approach to an upcoming salient event can be predicted by continuously evolving input, then we would expect to see a continuously changing set of theta sequences, as is the case with running on a linear track (Fig. 2C). However, if a task is solely defined by discrete events that progress in a punctuated manner, then we would expect the attractor to be drawn to these salient features and likewise demonstrate piecewise advancement through theta sequences¹⁰⁹ (Fig. 2E). In either case, the progression of activity is always linked across time as a topology that binds experiences of the world within an ordinal structure.

Temporal contiguity defines the ordered topology

The reciprocity between the hippocampus and MEC illuminates the function of the hippocampal formation as building topological representations of experience^7,9–14. As events unfold in time, the states of the MEC attractor continuously update in concert with the ongoing activity of the hippocampus. Because each state flows from a progression of previous states, the information supported by this network inherently incorporates temporal adjacency. Continuous attractor models that support path integration similarly track movement through physical space according to temporal adjacency²⁸, and only differ by rigidly mapping the neural activity to measurements of physical distance. In casting the circuitry of the hippocampal formation as a sequence generator¹¹, the need for a priori dimensionality or metric relationships is avoided. Instead, the topology is built through synaptic plasticity between neurons repeatedly activated in a particular order during learning, similar to existing theories highlighting the importance of ordered spiking^11,151,196. In this topological framework, the grid network supports ordered relationships between elements of experience without needing to measure exact feature quantities. Our proposal thus synergizes the activity exhibited by MEC and hippocampus during spatial navigation with the roles of these structures in forming episodic memories.

Once this topological representation is built, it can be used to facilitate decision-making. States within the topology span the sequence of events from task initiation to the outcome, similar to the progression of states described in reinforcement learning models^136,166. With decision points in the topological graph anchored to salient features, the network would be able to propagate a series of states from the decision point to the goal to aid in choice^{61,167–169,171,172}. Consistent with a role in decision-making, representations across the MEC-hippocampal network reflecting future choices^{61,167–169,201} manifest on the theta time scale in both spatial^202,203 and non-spatial tasks¹⁰⁹. Leading up to a choice, the representations of possible futures can even alternate on successive theta cycles²⁰², suggesting that neuronal sequences mediate cognitive access to multiple possible outcomes via the task topology.

The topological interpretation also suggests that tuning in non-spatial tasks does not rely on particular stimulus features (e.g. auditory frequency). Instead, hippocampal and entorhinal neurons encode the position of the stimulus in a sequence. Such a sequential topology can be constructed from stimuli which are either continuously changing in time^28,86,106 or discretized^94,105,109, since punctuated multimodal events are likewise represented by hippocampal tuning and compressed into theta sequences¹⁰⁹ (Fig. 2E). While individual neurons may show specificity for particular odors or sounds during these tasks^108–110, we advocate that tuning arises from the association of individual stimuli with specific transition probabilities in the sequence¹³⁶ rather than detection of the sensory features of the stimulus. Our topological model therefore stands contrary to feature space proposals (Box 2) which cast the hippocampal formation more as a semantic organizer, determining relationships between objects based on measurable feature qualities^15,16. Instead, given the accumulating evidence that the MEC-hippocampal network operates as a CAN, we highlight its defining attribute as the sequential progression of network activity through adjacent states over time. In sum, abstract feature spaces (Box 2) lacking temporal contiguity between neighboring elements would not be supported by the model mechanisms we propose here.

Critical aspects of our proposal are consistent with recent works that have formalized the coding of non-spatial domains without relying on feature measurements. One of these approaches is a model known as the Tolman-Eichenbaum Machine (TEM), which dissociates the representation of structural relationships in the MEC from their binding to sensory features in the hippocampus²⁰⁴. Similar to experimental training paradigms, TEM must be trained through ordered presentation of task stimuli to generate grid firing patterns consistent with structural relationships after learning. In this way, our emphasis on temporal contiguity aligns well with this model, although temporal progression is not an explicit focus of TEM. However, we suggest that the MEC and HPC work together to learn structure, while the TEM advocates that the MEC has a special role in abstracting and storing relational structure. Despite this difference, both TEM and our model are also parsimonious with work proposing that hippocampal place cells represent predicted future states¹³⁶, or successor representations^{135,136,205,206}. In simplified terms, the successor representation (SR) model posits that hippocampal firing signals how much a current state predicts that the agent will occupy future possible states¹³⁶. A topological representation storing the connectivity between states in an experience is highly compatible with both this predictability and the requirement for learning inherent in SR. Further, SR highlights the ability of a topology to facilitate decision-making at any step, because the agent learns the transition probabilities from each state to the outcome. The commonalities between TEM and SR are likewise compatible with multiple past works advocating for hippocampal topological representations^{9,12–14,207–209} as well as the foundational notion of relational memory^7,210.

Our proposal raises several testable predictions (Box 3) and complements previous works in three important ways. First, we suggest a biological implementation of the MEC-hippocampal network’s ability to construct a topology via reciprocal communication organized by the theta rhythm. Second, we emphasize temporal contiguity in the information represented topologically, aligning this function more closely with learning sequences than learning featural relationships and differing from theories of conceptual organization^15,94,211. Third, we unite a topological framework with continuous attractor networks, updating the hypothesized role of the grid network beyond allocentric spatial navigation.

BOX 3. Open Questions.

We have proposed that the MEC-hippocampal loop supports topological representations based in temporal contiguity. Here we suggest experiments to test several key predictions of the model:

1. Robust communication across the MEC-hippocampal loop manifests at the theta timescale. If large ensembles of neurons are simultaneously recorded in MEC and CA1, this model predicts several findings: 1) Theta sequences exist within the MEC. 2) Distortions in grid field patterns near reward sites should correspond to a concentration of fields in hippocampal neurons. 3) Trajectories decoded from the population activity on each theta cycle would be similar across regions, including cases where theta sequences sweep ahead toward goals^201,202. 4) Disruption of firing order within hippocampal theta sequences via localized manipulation (e.g. ¹⁵⁸) should also disrupt the structure of activity within the MEC, even though the aggregate hippocampal input will remain similar (see ¹²⁶).

2. Order of stimulus presentation shapes the responses to individual stimuli, even if the featural qualities are the same. We predict that if an animal were trained to advance a continuously changing series of tones⁸⁶ involving repeats of a tone within the sequence (for example), the MEC-hippocampal network would exhibit unique responses to each presentation of the tone. This result would strongly suggest that spiking is driven by sequential order informed by the history of experience, whereas similar responses to each presentation of the tone would suggest that spiking is driven by featural measurements. The results would inform the interpretation of similar phenomena observed in the spatial domain^167,169 and with discrete sequences¹⁰⁸.

3. Links in the topology depend on temporal contiguity. Virtual mazes offer the possibility of teleporting across space, allowing the animal to travel continuously through time while experiencing a discontinuity in space. We would expect the topology to smoothly link the two points of teleportation¹⁹⁷, much like adjacent locations are represented by place cells. We would also expect theta sequences to extend across the points of teleportation but not through the intervening positions, since traversing the intervening space is not necessary to connect the two nodes in the topology. These expectations contrast with the predictions of a path integration framework, which would allow for interpolation of shortcuts via Euclidean geometry.

Remaining open questions:

1. Are navigational inputs privileged in driving the MEC attractor? Does the relative strength of navigational inputs vary across species with increases in cognitive flexibility?

2. Is the intrinsic circuitry of the grid CAN static, or can novel sequences of grid cells be formed through plasticity?

3. How do extrinsic cortical afferents, such as those from the prefrontal cortex, influence activity in the MEC CAN? Which inputs inform MEC activity around goals and salient features according to task demands?

4. How do subpopulations and subcircuits of the hippocampus and MEC (e.g. CA1 sublayers; trisynaptic pathway; CA1 versus subiculum input to MEC) contribute to the computations in the MEC-hippocampus loop?

5. What happens to attractor dynamics in absence of a continuous theta rhythm, either during waking immobility or in primate species in which theta occurs in bouts?

Conclusion

We propose that the interplay between hippocampus and MEC works synergistically to build ordinal topologies based on experience. While the velocity inputs in the PI-CAN model may be sufficient to drive the MEC attractor network during navigation with few salient features, the hippocampus is ideally suited to bind the MEC representation to important elements of experience in the order they occur. We advocate that the function of grid cells is best interpreted through the lens of activity across the MEC network, rather than the patterning of spikes from individual cells in relation to an experimenter-chosen predictor. Under this broadened scope of entorhinal-hippocampal function, moving through physical space is just one example of progressing through a topology. Importantly, correspondence to measurements of physical or abstract spaces would be incidental to the necessary relationship between the temporal structure of experiences while moving through space. Recasting the hippocampal formation as a builder of topologies comports well with the role of this region in linking a series of events to construct new memories, and potentially resolves the tension between the navigation and memory literature.