Interpreting Neural Networks for Biological Sequences by Learning Stochastic Masks

Abstract

Sequence-based neural networks can learn to make accurate predictions from large biological datasets, but model interpretation remains challenging. Many existing feature attribution methods are optimized for continuous rather than discrete input patterns and assess individual feature importance in isolation, making them ill-suited for interpreting non-linear interactions in molecular sequences. Building on work in computer vision and natural language processing, we developed an approach based on deep learning - Scrambler networks - wherein the most salient sequence positions are identified with learned input masks. Scramblers learn to predict Position-Specific Scoring Matrices (PSSMs) where unimportant nucleotides or residues are scrambled by raising their entropy. We apply Scramblers to interpret the effects of genetic variants, uncover non-linear interactions between cis-regulatory elements, explain binding specificity for protein-protein interactions, and identify structural determinants of de novo designed proteins. We show that Scramblers enable efficient attribution across large datasets and result in high-quality explanations, often outperforming state-of-the-art methods.

Deep Neural Networks have successfully been applied to a diverse set of biological sequence prediction problems, including predicting transcription factor binding [1, 2, 3, 4], chromatin modification and accessibility [5], RNA processing [6, 7, 8, 9], translation regulation [10] and protein structure [11, 12]. Neural networks excel at learning complex relationships from large datasets without requiring much tuning, but interpreting their predictions is challenging because the learned regulatory logic is embedded deep within the network layers. Nevertheless, interpretability is necessary to connect network predictions to established biology, learn new regulatory rules or validate sequence designs [13, 14, 15, 16, 17, 18, 19, 20, 21].

Nonlinear interactions are abundant between biological sequence features. Such dependencies make it necessary to consider groups of features and their surrounding context when interpreting a model prediction instead of independently evaluating each feature in isolation. However, many current neural network attribution methods rely on local perturbations, limiting their ability to identify such relationships. For example, 5’ UTRs can contain multiple upstream start codons (uAUGs) [22, 23, 24] preceding the primary start. Which AUG is chosen as the start of translation depends on the extent to which the surrounding context – e.g., competing AUGs – represses its usage. Two nearby uAUGs may even “hide” each other, as each AUG is capable of repressing translation initiation at the primary start independently. In-silico saturation mutagenesis – which systematically exchanges one nucleotide and approximates its importance by predicted functional change – would incorrectly conclude both uAUGs are irrelevant: Neither uAUG would be identified as repressive, as knocking down only one would not change the prediction. Other local approximation methods face similar problems, such as those basing their estimation on gradients [25, 26, 27, 28, 29, 30] or local linear models [31].

In this paper, we introduce a feature attribution approach tailored for biological sequence predictors and based on previous work in learning interpretable input masks [32, 33, 34, 35, 36, 37, 38, 39, 40, 41]. We train a deep neural network, referred to as the Scrambler, to learn masks that include only the smallest set of features in an input sequence necessary to reconstruct the original prediction. A mask that fulfills the inclusion objective overcomes the issues with local approximation mentioned above. For example, such a mask would learn to include one of the uAUGs from the 5’ UTR example to preserve the repressive prediction. In a complementary formulation, we optimize masks to occlude the smallest set of features that destroy the prediction. These features may overlap with those identified by inclusion masks but are not necessarily identical; for the 5’ UTR example, the occlusion mask would need to occlude both of the uAUGS to destroy the repressive prediction. In general, for features involved in an OR-relationship, inclusion would identify one feature while occlusion would identify all. Conversely, for AND-like features, inclusion would identify all features and occlusion just one.

The earliest mask-based attribution methods masked inputs by either fading or blurring [32, 34], which is ill-suited for one-hot encoded sequence patterns. More recent methods replace masked input features with random samples or counterfactual values to keep masked inputs in the distribution of valid predictor patterns [37, 39]. However, these recent methods are based on individually optimizing each mask rather than learning a parametric model. Here, we combine ideas from deep learning with probabilistic masking to interpret biological sequences. Specifically, Scramblers learn to output Position-Specific Scoring Matrices (PSSMs) with minimal (inclusion) or maximal (occlusion) conservation such that discrete samples either reconstruct or destroy the prediction. A sequence position is ‘masked’ by raising the entropy, or temperature, of the underlying feature distribution such that samples sent to the predictor become less informative, and the Scrambler is trained by backpropagation using a gradient estimator.

We show that Scramblers avoid overfitting to spurious per-example signals, which can be problematic for model-free methods. Furthermore, using a parametric masking model allows us to interpret new patterns more efficiently than per-example masking methods. Scramblers are also conceptually different from methods such as L2X [35] and INVASE [36], which mask input patterns by replacing features with zeros while simultaneously training a new ad-hoc predictor model that attempts to reconstruct the original predictions. Re-training the predictor is required since the zero-based masks push the patterns out-of-distribution. In contrast, Scramblers directly reconstruct the original predictor model without re-training, and keep patterns in distribution with a sample-based mask. This allows us to efficiently train the Scrambler on a smaller, or more narrowly defined, dataset than the original predictor and still obtain high-quality interpretations. We show in our benchmarks that L2X and INVASE produce lower-quality interpretations than Scramblers when trained on reduced datasets ranging in size from 10, 000-40, 000 sequences, and they converge poorly when trained on the full data. See Supp. Table 1 for a summary comparison of all masking methods.

In addition to introducing probabilistic masks to biological sequences, we develop several improvements for mask-based interpretation. For example, Scramblers can discover multiple salient feature sets within a single input pattern using mask dropout- and bias layers, enabling users to specify features to include or exclude in the solution at inference time. In addition to finding reconstructive features, we alternatively optimize the Scrambler to find enhancing or repressive features that either maximize or minimize the prediction. We also explore different architectures for interpreting pairwise predictors in the context of protein-protein interaction. Finally, to reduce interpretation artifacts for predictors where input patterns contain a highly variable number of features, we apply per-example optimization as a fine-tuning step to the initial Scrambler outputs. Throughout the paper, we show that Scramblers learn meaningful feature attributions for several visual- and sequence-predictive tasks, including RNA regulation, protein-protein interaction, and protein tertiary structure, often outperforming other interpretation methods.

Results

Scrambling Networks

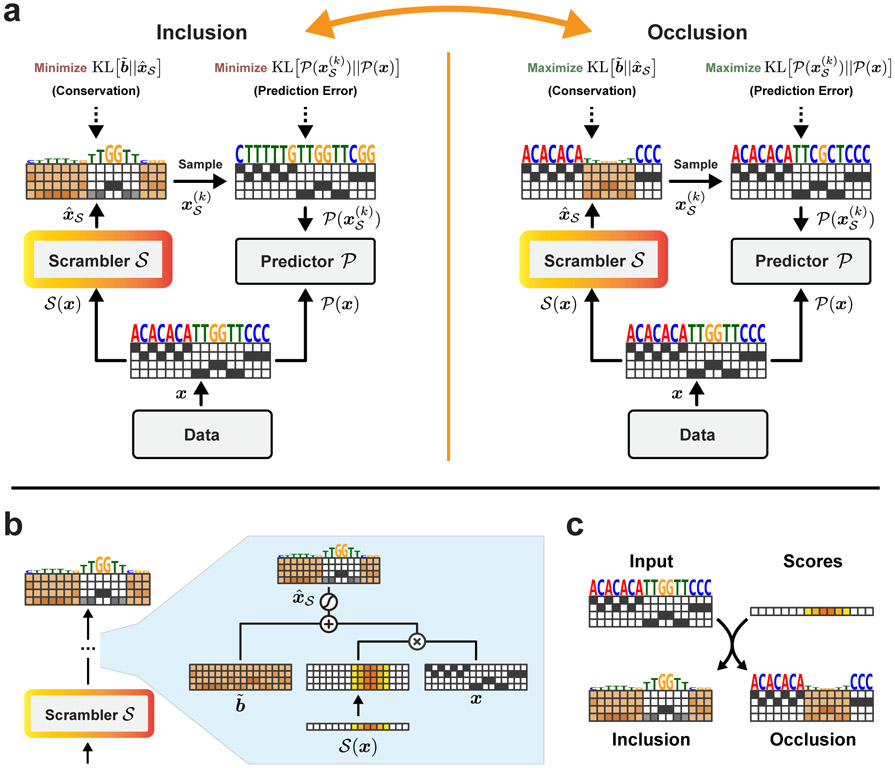
The Scrambler architecture is illustrated in Fig. 1a (left). Given a differentiable pre-trained predictor $\mathcal{P}$ and a one-hot encoded input pattern x ∈ {0, 1}^N×M (representing an N-length sequence), we let a trainable network $\mathcal{S}$ called the Scrambler predict a set of real-valued importance scores $\mathcal{S}(\mathit{x})\in (0,\infty {]}^N$. These scores are used in Eq. 1 below to produce a probability distribution which interpolates between the input pattern x and a non-informative background distribution $\tilde{\mathit{b}}\in {\mathbb{R}}^{N\times M}$ (Fig. 1b-c).

Figure 1:

Scrambler Architecture and Masking Operator (a) High-level architecture. Inclusion: Maximize the entropy of the PSSM predicted by the Scrambler and minimize the prediction error of samples drawn from it. Occlusion: Minimize PSSM entropy and maximize sample prediction error. (b) The temperature-based masking operation. The Scrambler predicts sampling temperatures (‘importance scores’) for the PSSM. (c) The Inclusion and Occlusion scrambling operations. Individual nucleotides (or amino acid residues) are perturbed by raising the sampling temperature of its corresponding categorical feature distribution.

$${\widehat{\mathit{x}}}_{\mathcal{S}}=\sigma \left(\log \tilde{\mathit{b}}+\mathit{x}\times \stackrel{.}{\mathcal{S}}(\mathit{x})\right)$$ (1)

Here, σ denotes the softmax $\sigma (\mathit{l}{)}_{ij}=\frac{e^{{\mathit{l}}_{ij}}}{{\sum }_{k=1}^M{e}^{{\mathit{l}}_{ik}}}$ and $\stackrel{.}{\mathcal{S}}(\mathit{x})\in (0,\infty {]}^{N\times M}$ represent the importance scores $\mathcal{S}(\mathit{x})$ which have been broadcasted at position i to all channels j. In all experiments, the Scrambler $\mathcal{S}$ is a residual network of dilated convolutions (Extended Data Fig. 1a-c) [42]. The output ${\widehat{\mathit{x}}}_{\mathcal{S}}$ becomes a parameterization of a probability distribution of the input. Specifically, ${\widehat{\mathit{x}}}_{\mathcal{S}}$ is a set of N categorical softmax-nodes, or a PSSM. The role of $\tilde{\mathit{b}}$ is to keep samples from this PSSM in distribution and along the manifold of valid patterns, and is here taken as the mean input pattern across the training set (Eq. 10). When $\mathcal{S}(\mathit{x}{)}_i$ is close to 0, ${\widehat{\mathit{x}}}_{\mathcal{S},i}$ becomes ${\tilde{\mathit{b}}}_i$ (the background distribution) and when $\mathcal{S}(\mathit{x}{)}_i$ is close to ∞, ${\widehat{\mathit{x}}}_{\mathcal{S},i}$ becomes x_i (the original input). $\mathcal{S}(\mathit{x}{)}_i$ thus defines the inverse feature sampling temperature at position i in the PSSM.

K discrete samples ${\mathit{x}}_{\mathcal{S}}^{(k)}$ drawn from ${\widehat{\mathit{x}}}_{\mathcal{S}}$ are passed to the predictor $\mathcal{P}$ and gradients are backpropagated to $\mathcal{S}$ using either Softmax Straight-Through estimation [43] or the Gumbel distribution [44]. By comparing the predictions $\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})$ of the scrambled input samples to the original prediction $\mathcal{P}(\mathit{x})$, we train the Scrambler $\mathcal{S}$ to minimize a predictive reconstruction error subject to a conservation penalty which enforces high entropy. We refer to this formulation as the Inclusion-Scrambler, as it must learn to include features to reconstruct the original prediction while maintaining high entropy of ${\widehat{\mathit{x}}}_{\mathcal{S}}$. Alternatively, we can train $\mathcal{S}$ to find the smallest set of features in x to randomize (i.e., maximizing the conservation of ${\widehat{\mathit{x}}}_{\mathcal{S}}$) to maximally perturb $\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})$ from $\mathcal{P}(\mathit{x})$ (Fig. 1a, right). We refer to this inverse formulation as the Occlusion-Scrambler. For both formulations, we define the reconstruction error as the KL-divergence $\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})\Vert \mathcal{P}(\mathit{x})]$ between scrambled and original predictions. To minimize the conservation of ${\widehat{\mathit{x}}}_{\mathcal{S}}$ while still keeping samples in distribution, we optimize the KL-divergence $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]$ between ${\widehat{\mathit{x}}}_{\mathcal{S}}$ and the background distribution $\tilde{\mathit{b}}$. We control the expected entropy by fitting $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]$ to a target conservation value t_bits rather than minimizing or maximizing it unbounded. The full training objective for the Inclusion-Scrambler is given in Eq. 2.

$$\underset{\mathcal{S}}{\text{min}}\left(\frac{1}{K}\sum _{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})\Vert \mathcal{P}(\mathit{x})]\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (2)

We compare several different attribution methods in our experiments. The baseline method used for comparison, Perturb, exchanges the categorical value of one letter or pixel at a time and estimates the absolute value in predicted change as the importance score. Comparisons are made against Perturb (baseline), Gradient Saliency [25], Guided Backprop [27], Integrated Gradients [28], DeepLIFT [29] (using RevealCancel for MNIST and Rescale from DeepExplain [45] for the remaining tasks), SHAP DeepExplainer [30], the preservation/perturbation methods of Fong et al. (TorchRay) [33], Dabkowski et al. (Saliency Model) [34] and Carter et al. (‘SIS’) [39] and, finally, the feature selection methods L2X [35] and INVASE [36]. For comparison, we also test a version of the Scrambler with a zero-based masking operator (referred to as Zero Scrambler). See Methods for a detailed description of how each method was used and which task(s) were tested. Note that for methods that learn ad-hoc interpreter models (e.g., Scramblers, L2X, INVASE), we train the ad-hoc models on a reduced data set of ~ 10, 000-40, 000 examples (depending on the task), in contrast to the 100, 000s to millions of examples the original predictor models were trained on. However, in supplemental analyses we also attempted to train L2X and INVASE on the full data.

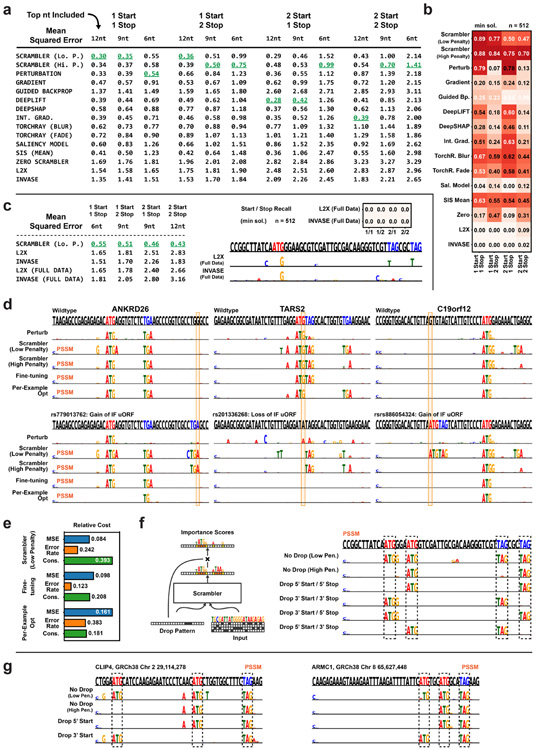
Finding Salient Pixels in MNIST Images

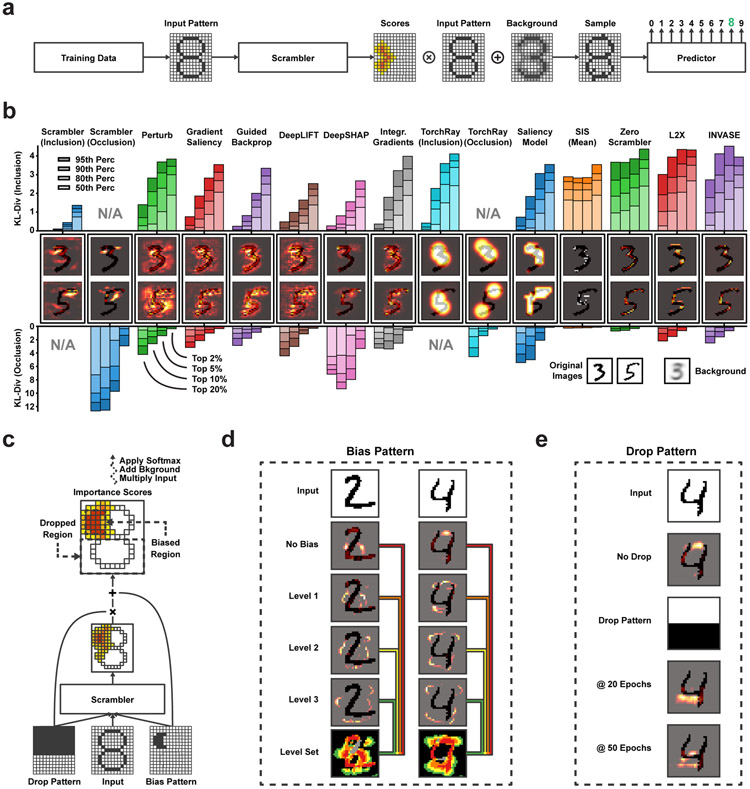
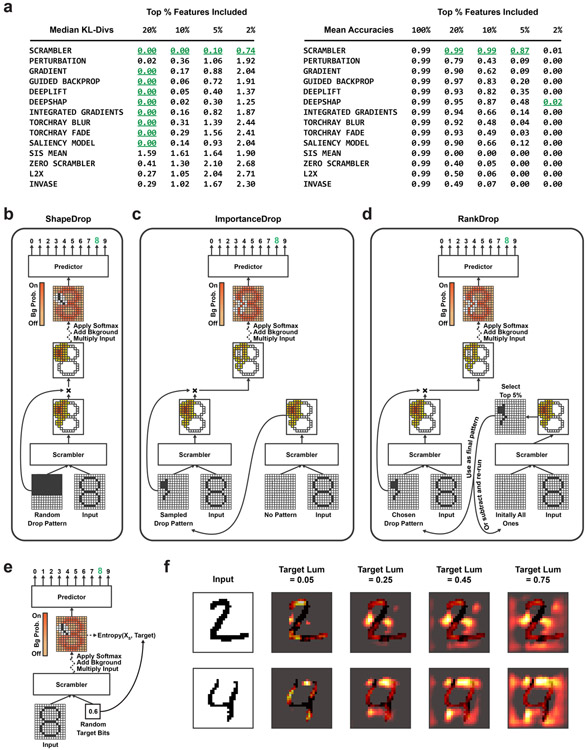
We first used the Scrambler to visualize important regions in binarized images of the two MNIST digits ‘3’ and ‘5’ (Fig. 2a). The predictor was a convolutional neural network (CNN) [46] trained to discriminate between all ten digits. We trained one Inclusion-Scrambler (t_bits = 0.005, λ = 500) and one Occlusion Scrambler (t_bits = 0.3, λ = 500). We performed two benchmark comparisons to other attribution methods (Fig. 2b, Extended Data Fig. 2a): first, based on the importance scores of each method, we replaced all but the top X% most important pixels with random samples from the background and measured the KL-divergence between the predictions of the original and randomized test set images. Next, we inversely tested how well these top-ranked features perturbed the prediction by replacing only the top X% pixels with random samples. The Scramblers were superior in each benchmark, as the median KL-divergence was the lowest and highest, respectively. In addition to the upper portions of the digits themselves, the Scramblers identified open regions adjacent to the digits as important, indicating that the classifier relies on both foreground and background pixels when making its prediction. For example, the open background region in the top left quadrant of digit ‘3’ is a unique distinguishing feature shared among all examples of ‘3’. These salient ‘background’ features are identified by methods such as DeepLIFT and DeepSHAP, but not by other methods that only identify foreground pixels.

Figure 2:

MNIST Feature Attribution (a) Workflow for finding salient pixel regions within MNIST digits. The Scrambler learns to predict the salient feature set of the input image, which is superimposed on an uninformative background distribution. (b) Attributing feature importance for binarized MNIST digits ‘3’ and ‘5’. (Upper bar chart) Keeping the top X% pixels according to importance scores and replacing all other pixels with random values. (Lower bar chart) Replacing the top X% pixels with random values. n = 1, 888. (c) Importance score dropout and bias layers for finding alternate interpretations. (d) Example of dynamically sized feature sets using progressive bias patterns for differentiating digits ‘2’ vs. ‘4’. The pixels found at each level are added to the next level of bias pattern to discover the next set of features. (e) Example of finding alternate salient features when dropping the upper half of the image importance scores.

Identifying Alternate Feature Sets with Dropout and Bias Layers

There are often multiple feature sets a classifier can use within a single input pattern to make its prediction. Scramblers can be trained to select these alternate salient feature sets dynamically using a dropout pattern D which is used to mask some positions in the predicted scores $\mathcal{S}(\mathit{x})$. Similarly, bias patterns T are used to encode specific positions to be included in the solution. Importantly, the Scrambler $\mathcal{S}$ also receives D and T as additional input, allowing the network to learn to output alternate (or additional) scores conditioned on which positions were dropped or enforced (Fig. 2c, Extended Data Fig. 2b-d; see Methods for details). During training, we sample random dropout- and bias patterns. At attribution time, we supply specifically crafted patterns to exclude or enforce in the predicted solution to enable targeted feature attributions.

For the MNIST classifier, bias patterns allow us to explore features beyond the initial salient pixels found by default (Fig. 2d). Conversely, we can use dropout patterns to focus attribution to pixels in a subsection of an image to discover new salient features (Fig. 2e). In Extended Data Fig. 2e-f, we trained a Scrambler with tunable divergence against the background $\tilde{\mathit{b}}$, demonstrating how the entropy of the solution can be set dynamically at attribution time, thus providing solutions at multiple scales of t_bits with a single network.

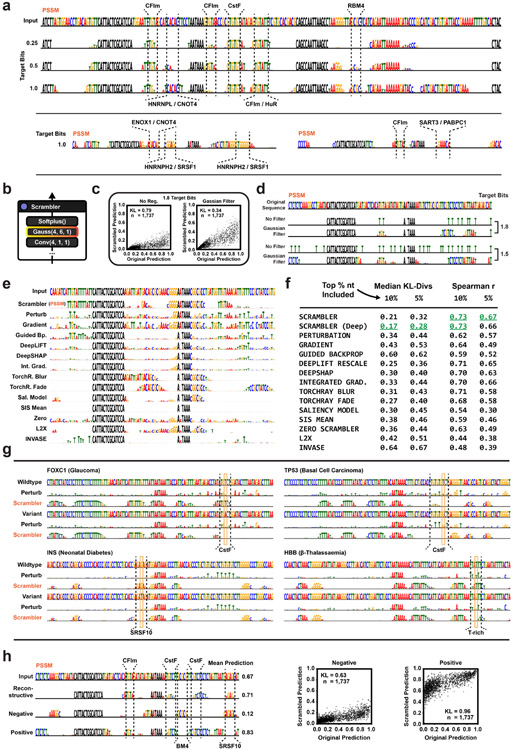
The cis-Regulatory Code of Alternative Polyadenylation

Next, we used Scramblers to interpret regulatory sequence elements in the 3’ untranslated region (UTR) of pre-mRNA (Fig. 3a). Specifically, using APARENT [7] – a CNN capable of predicting cleavage and polyadenylation from primary sequence – we trained an Inclusion-Scrambler to reconstruct isoform predictions for a subset of the original APARENT training data (t_bits = 0.25, λ = 1). Since we anticipated important polyadenylation features like RNA binding protein (RBP) motifs to consist of short subsequences, we regularized the Scrambler by fixing the final layer of the network to a Gaussian filter to encourage the selection of contiguous nucleotides for masking (reminiscent of a technique proposed by Fong et al. [33]). We found that the Inclusion-Scrambler learned to recognize known regulatory binding factors associated with alternative polyadenylation (Extended Data Fig. 3a), such as CFIm, CstF, HNRNPL, ENOX1, PABPN1, HuR, and RBM4 [47, 48, 49, 50]. When re-training the Scrambler under the Occlusion objective, the network learned patterns that resulted in more extreme perturbations without the fixed Gaussian filter than with it (Extended Data Fig. 3b-c). However, when inspecting these patterns, they clearly exploited the importance of scattered T’s in favor of knocking out biologically relevant motifs (Extended Data Fig. 3d).

Figure 3:

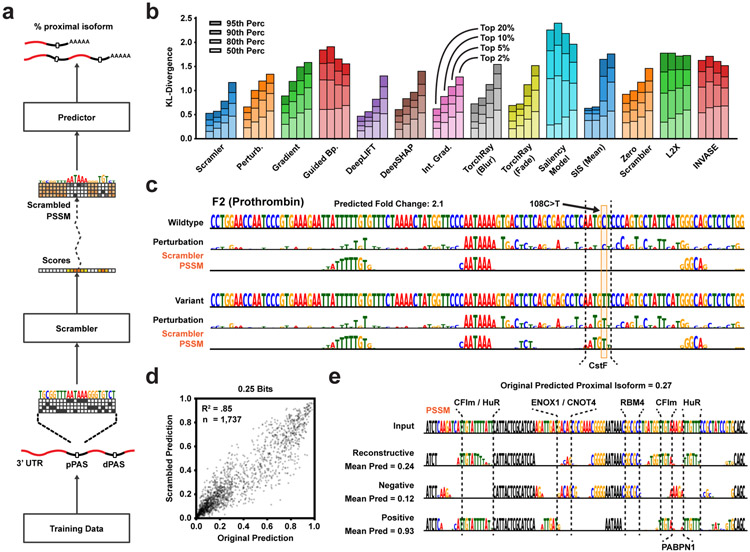
APA Feature Attribution (a) Scrambler architecture for APA isoform attribution using the pre-trained model APARENT as the predictor. (b) Perturbing sequences by keeping the top X% nucleotides according to importance scores and replacing all other positions with random letters. The bar chart measures KL-divergence of APARENT-predictions between original- and perturbed test sequences (n = 1, 737). (c) Example attributions of a deleterious variant (108C>T) in the 3’ UTR of the Prothrombin (F2) gene, comparing the Perturbation method to an Inclusion-Scrambler trained on the APARENT data. (d) APARENT predictions of original test set sequences compared to predictions made on sequence samples produced by the Scrambler PSSMs. (e) Example of Inclusion-Scramblers trained to reconstruct, maximise or minimize predictions, thus finding overall important, enhancing, or repressing motifs, respectively.

The Scrambler outperformed other attribution methods when reconstructing the isoform predictions of the APARENT model using only the top-ranked nucleotides and replacing the remaining positions with random letters (Fig. 3b, Extended Data Fig. 3e-f; Median KL = 0.32 when keeping the 5% most important features). We next tested how well the discovered features generalized to other APA-predictive models. To this end, we again perturbed the sequences by keeping only the 5% most important nucleotides when interpreting APARENT, but we now tested how well these features reconstructed predictions made by DeeReCT-APA, a model trained on Mouse 3’-end sequencing data [51] (Extended Data Fig. 3f). The Scrambler reconstructed the DeeReCT-APA predictions the most (Spearman r = 0.67 when keeping the 5% most important features, n = 1, 737), but was closely followed by DeepLIFT (r = 0.65) and Integrated Gradients (r = 0.66). Finally, we trained a deeper version of the Scrambler with 20 residual blocks instead of 4 blocks. While the deeper Scrambler reconstructed APARENT predictions even better (Median KL = 0.28), the performance marginally decreased on DeeReCT-APA (r = 0.65) (Extended Data Fig. 3f).

Interpreting Genetic Variants of APA

We can interpret the functional impact of mutations by running the Scrambler on wild-type and variant human polyadenylation signals. For example, the Scrambler correctly detects the creation of a cryptic CstF binding site caused by a deleterious variant (108C>T) in the F2 (Prothrombin) gene, which is known to cause or contribute to Thrombophilia due to increased polyadenylation efficiency (Fig. 3c) [52, 53, 54]. The detected CstF motif is qualitatively better separated from the Scrambler sequence logo’s background compared to Perturbation. Furthermore, the Scrambler appears highly sensitive in detecting loss of RBP binding motifs due to single nucleotide variants for several disease-associated human polyadenylation signals [55, 56, 57, 58] (Extended Data Fig. 3g).

Reconstructive, Enhancing and Repressive Motifs

Interestingly, with as little as 0.25 out of 2.0 target bits of mean conservation in the scrambled sequences, there was a very high correlation between scrambled and original sequence predictions from the APARENT test set (R² = 0.85; Fig. 3d). In other words, a small set of regulatory features in each polyadenylation signal explained most of the variation. Next, we altered the Scrambler training objective to find the smallest set of features that maximize or minimize a prediction rather than reconstructing it (see Methods for details). We found that the Scrambler could partition cis-regulatory elements within polyadenylation signals into enhancing (e.g., CFIm, HuR, Cstf) and repressive motifs (e.g., ENOX1, RBM4, PABPN1), in agreement with the known function for these motifs and associated RBPs (Fig. 3e, Extended Data Fig. 3h).

The Rules of Translation Efficiency in the 5’ UTR

The translation efficiency of mRNA is controlled by complex regulatory logic in its 5’ UTR. For example, an in-frame (IF) start and stop codon create an IF upstream open reading frame (uORF), which typically represses translation, while neither an IF upstream start or upstream stop codon individually represses translation (NAND logic). Sequences with multiple IF starts and stops can further complicate translational logic by creating NAND-OR hybrid functions with overlapping IF uORFs.

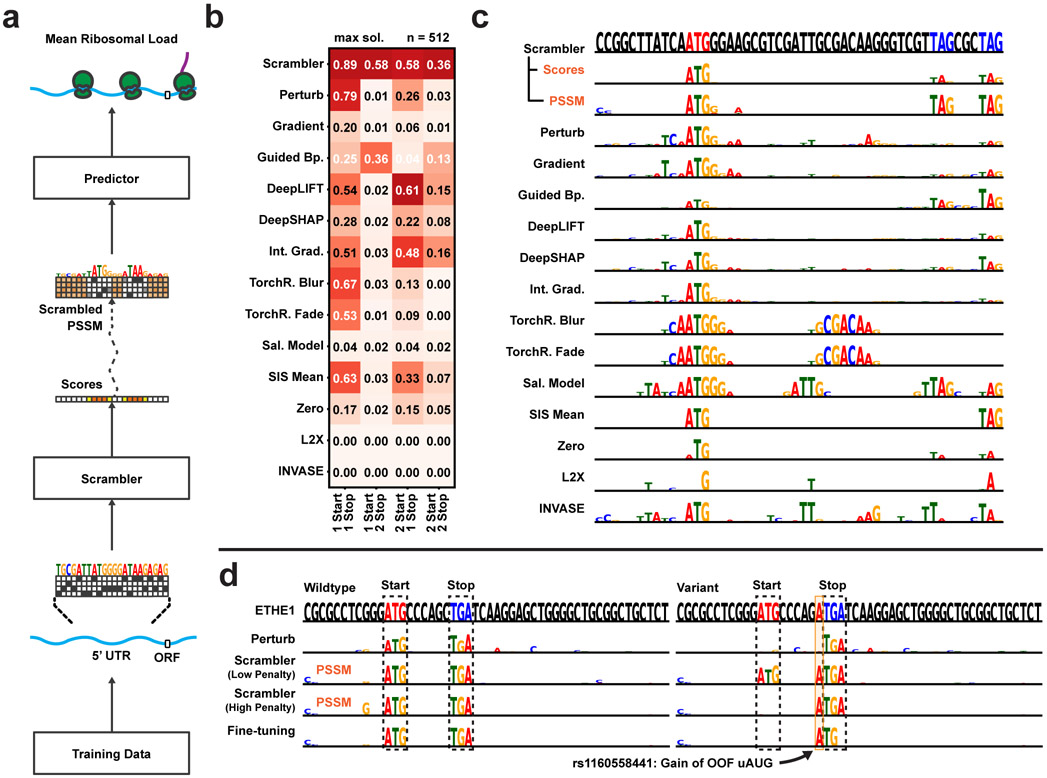
We trained an Inclusion-Scrambler to reconstruct the mean ribosome load (MRL – a proxy for translation efficiency) of 10, 000 5’ UTRs as predicted by the CNN Optimus 5-Prime (Fig. 4a) [10]. To test how well attribution methods detect multiple regulatory elements, we generated synthetic 5’ UTR test sets with one (1 IF start, 1 IF stop), two (1 IF start/2 IF stops or 2 IF starts/1 IF stop), or four (2 IF starts/2 IF stops) overlapping IF uORFs. We then measured to what extent the most important nucleotides of each method corresponded to the IF start and stop positions (Fig. 4b, Extended Data Fig. 4a-b). In the simplest case of a single start and stop, nearly all methods had high accuracy for recovering these elements. However, as the number of IF uORFs increased, the Scrambler often outperformed other methods considerably. An example 5’ UTR with multiple IF uORFs is shown in Fig. 4c; here, the multiple stops effectively hide one another from many local attribution methods. Furthermore, L2X, which trains a new predictor model simultaneously as the interpreter is learned, overfits by only selecting one of the nucleotides in each of the ‘ATG’ and ‘TAG’ motifs (hence the low accuracy). The results did not improve for L2X even when trained on the full 5’ UTR dataset (Extended Data Fig. 4c).

Figure 4:

5’ UTR Feature Attribution (a) Scrambler architecture for 5’ UTR ribosome load attributions using the pre-trained model Optimus 5’ as the predictor. (b) Average recall of in-frame (IF) start and stop positions in a test set of synthetic IF uORF 5’ UTRs. In this test, all start and stop codons must be among the highest scored nucleotides of a sequence to count as successfully recalled for a given method. n = 512. (c) Example attribution in a 5’ UTR with multiple IF stop codons. (Top sequence) Red letters = IF start codon, Blue letters = IF stop codon. (d) Interpreting a rare, functionally silent mutation (rs1160558441) in the 5’ UTR of the ETHE1 gene, where an out-of-frame (OOF) upstream start codon (uAUG) is created within an in-frame (IF) upstream open reading frame (uORF). The ‘Fine-tuning’ optimization was performed on the importance scores predicted by the ‘Low Penalty’-Scrambler.

Interpreting Genetic Variants in the 5’ UTR

The combinatorial nature of out-of-frame start codons (OOF uAUGs) and IF uORFs makes variant interpretation in human 5’ UTRs complicated [22, 23, 24]. In Fig. 4d, we interpret a variant, rs1160558441, which creates an OOF uAUG that Optimus 5-Prime predicts to be functionally silent. The OOF uAUG is created within an IF uORF, which hides its effect, as either element alone is sufficient to repress translation. Therefore, the variant sequence is not interpretable by Perturbation as the uAUGs are not found. A Scrambler trained with a low entropy penalty (t_bits = 0.125, λ = 1) detects both possible interpretations. With a higher penalty (λ = 10), the Scrambler must find a smaller set of salient features and marks only the OOF uAUG as important, which is sufficient to explain the repression. However, rather than just identifying ‘ATG’, the Scrambler identifies the subsequence ‘ATGA’, even though the trailing adenine is not important for the explanation. This occurs because the number of salient features is highly variable in any given 5’ UTR, and so a Scrambler trained for a target entropy t_bits may ‘over-interpret’ some examples.

Per-example Fine-tuning Removes Interpreter Artifacts

To overcome issues with over-interpretation for datasets with a highly variable number of important features, we apply a per-example fine-tuning step: starting with $\mathcal{S}(\mathit{x})$, we optimize new scores s by gradient descent which are specific to x and remove excessive features of $\mathcal{S}(\mathit{x})$ by maximizing the entropy of the PSSM unbounded. Specifically, s is optimized to subtract scores from $\mathcal{S}(\mathit{x})$ in order to maximize the PSSM entropy $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathit{s}}]$ unbounded, while still minimizing the predictive reconstruction error $\text{KL}[\mathcal{P}({\mathit{x}}_{\mathit{s}}^{(k)})\Vert \mathcal{P}(\mathit{x})]$. As seen with the variant example (Fig. 4d), fine-tuning of the Low entropy-penalty Scrambler removes the trailing ‘A’. We also compared the Scrambler with and without fine-tuning to interpret silent uORF-altering and gain-of-function mutations (Extended Data Fig. 4d). Importantly, when compared on one of the benchmarks of Fig. 4b, we find that applying per-example fine-tuning to the pre-trained Scrambler scores produces more robust attribution results than individual per-example optimization of importance scores (Extended Data Fig. 4e). This is likely because the latter approach can become stuck in local minima or produce poorly generalizable interpretations, essentially ‘overfitting’ to spurious predictor signals.

Dropout for Alternate Open Reading Frame Discovery

Sequences with multiple IF uORFs are examples of patterns with redundant salient feature sets. By adding an importance score dropout layer to the Inclusion-Scrambler and training it on random dropout patterns, we obtain a model capable of dynamically proposing different IF uORFs as attributions (Extended Data Fig. 4f-g). Without dropout and a low entropy penalty (t_bits = 0.125, λ = 1), the Scrambler marks all IF starts and stops (i.e. all IF uORFs) as important in the example shown in Extended Data Fig. 4f. However, with a higher penalty (λ = 10), the Scrambler finds a smaller interpretation with only one IF uORF. When using dropout patterns to exclude either of the IF starts and stops, the Scrambler dynamically finds the alternate operands.

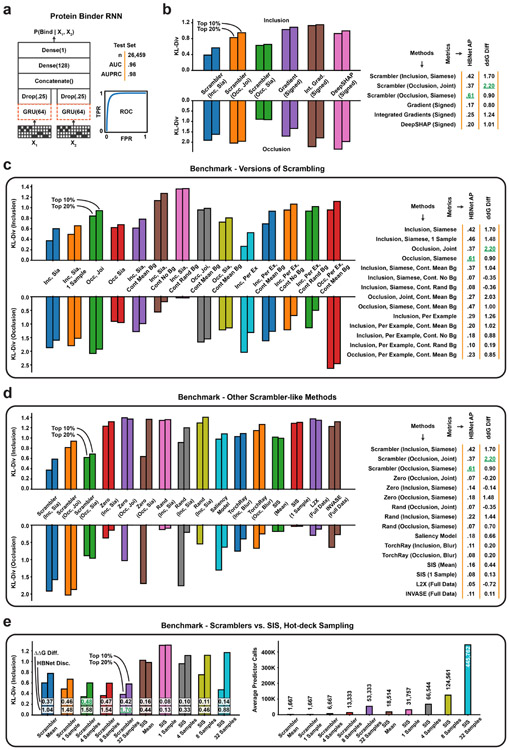
The Determinants of Protein-Protein Interactions

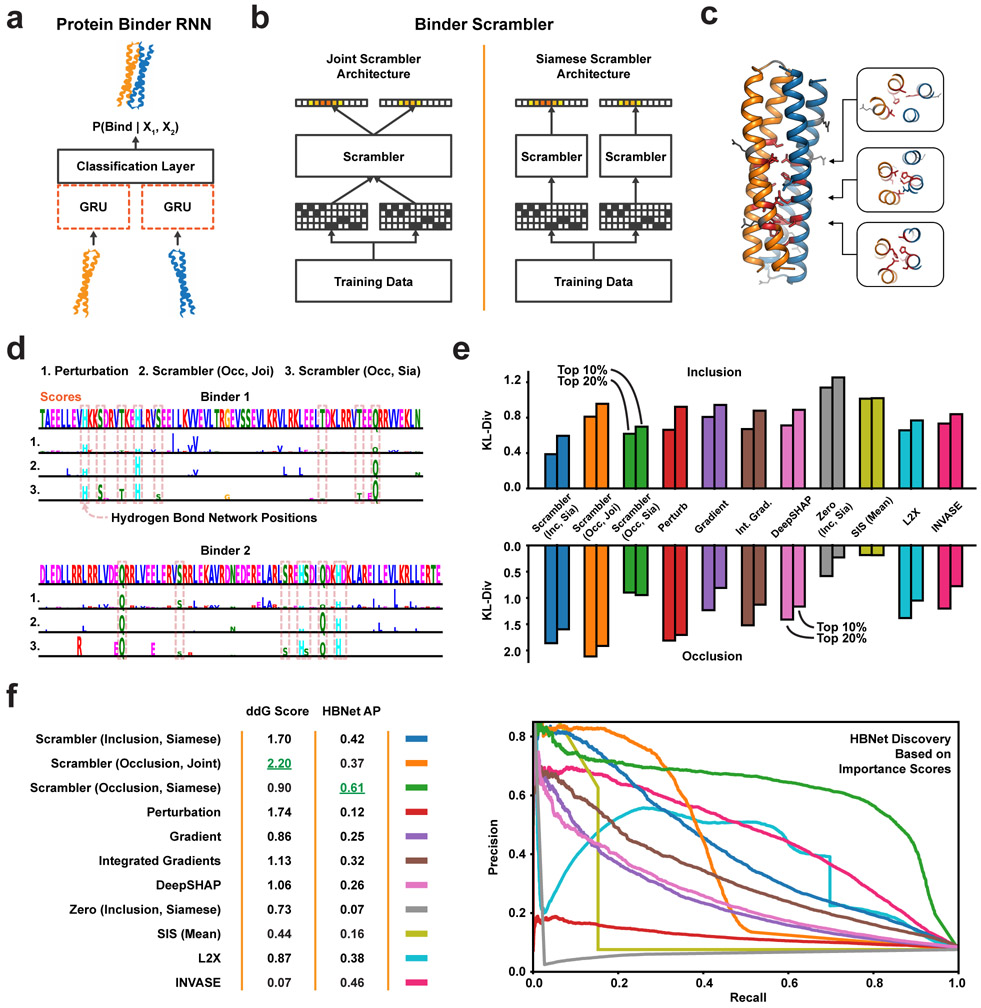
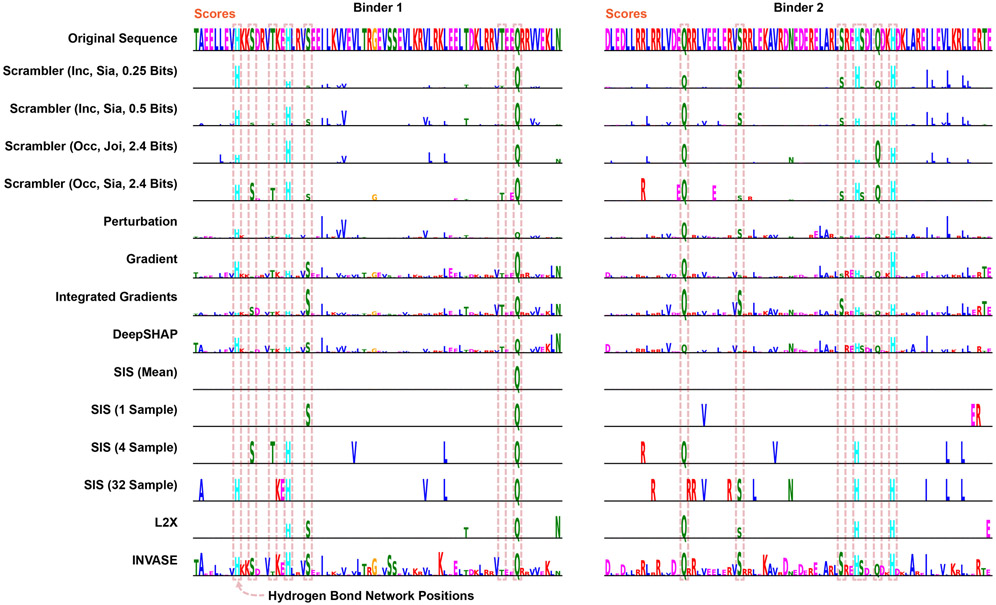
Here we apply Scramblers to interpret predicted interactions for pairs of proteins. This can be challenging, as proteins are defined along a narrow manifold of stably folded sequences. Any interpretation method must ensure that masked or perturbed sequences stay in distribution for predictions to remain accurate. We focused on a set of rationally designed coiled-coil heterodimers, where binding specificity is induced by hydrogen bond networks (HBNets) at the dimer interface [59, 60]. Using approximately 180, 000 designed heterodimers as positive training data and randomly paired monomers as a negative set, we trained a recurrent neural network (RNN) to predict dimer binding (Fig. 5a, Extended Data Fig. 5a; AUC = 0.96 on held-out test data, n = 26, 459). These coiled-coil proteins follow a conserved heptad repeat structure, but binder sequences of different lengths have their heptad motifs shifted by different offsets. Consequently, when training Scrambler networks on this data, we used a separate background distribution for each sequence length. A test set of 478 designed heterodimers was used to investigate how well different attribution methods could capture HBNet positions and residues important for complex stability.

Figure 5:

Protein Heterodimer Feature Attribution (a) The protein binding predictor is a RNN based on a siamese GRU layer (orange dashed lines). (b) The joint and siamese Scrambler architectures for protein binder attribution. (c) 3D-visualization of an example binder pair structure. Discovered HBNet residues (by a siamese Occlusion-Scrambler) are shown in red licorice, important residues not part of the HB-net are shown as gray sticks. A cross-section of each of the three buried hydrogen bond networks is shown on the right. (d) Example attribution. Hydrogen bonds at the designed binding interface are marked with dashed red boxes. (e) Keeping the top X% residues according to the importance scores of each method and replacing the rest with random amino acids (top), or replacing the top X% with random amino acids (bottom), measuring prediction KL-divergence. Zero refers to a Scrambler with a zero-based masking operator. (f) Left: In silico Alanine scanning benchmark. The 8 most important residues of each method were replaced with Alanines, measuring ΔΔG in Rosetta Energy Units (REU). Shown are the mean ΔΔG differences in a permutation test of 10,000 re-labelings. Right: Precision-recall curves and Average Precision (AP) for discovering the HBNet positions, based on the importance scores of each benchmarked method.

Unlike the DNA attribution tasks above, each dimerization prediction involves two input sequences. Consequently, there are multiple ways in which to define the Scrambler architecture. We first tested a joint Occlusion-Scrambler (Fig. 5b; left), which receives both sequences as input and can learn to recognize partner-specific binding features. After training, this architecture identified a subset of HBNet positions and hydrophobic residues at the interface necessary for binding specifically to the cognate partner (Fig. 5d). We also tested a siamese architecture, which saw only one input sequence at a time and was therefore constrained to learn global, partner-independent features (Fig. 5b; right). This architecture learned to identify nearly all HBNets, as these are the best determinants of binding specificity to any possible partner (Fig. 5c-d). We compared these Scrambler architectures to other attribution methods based on how much the positions with largest absolute-valued score either preserved or perturbed the RNN predictions (Fig. 5e; t_bits = 0.25, Inclusion; t_bits = 2.4, Occlusion). The siamese Inclusion-Scrambler and joint Occlusion-Scrambler had the best (lowest and highest) median KL-divergence for these tasks.

Importance Scores Reflect Dimer Stability and Hydrogen Bonds

Next, using in-silico Alanine scanning, we estimated the mean difference in ΔΔG between the original and mutated dimers for the eight most important residues per binder and attribution method [61]. We also compared the methods by their ability to discover HBNet positions based on their importance scores. We found that the joint Occlusion-Scrambler identified residues that destabilized the complex the most (mean difference ΔΔG = 2.20, Fig. 5f), while the siamese model discovered significantly more HBNet positions (AUPRC = 0.61). These results support the idea that the siamese architecture learned discriminative features for both interacting and non-interacting pairs – HBNet residues – while the joint model learned features important for positive interaction, such as hydrophobic residues at the interface. While Integrated Gradients and DeepSHAP perturbed the RNN predictions more when considering only their positive-valued scores, the Scramblers had better ΔΔG scores and HBNet discovery rates (Extended Data Fig. 5b). This suggests that using a parametric masking model results in more generalizable features by overcoming spurious RNN signals. We performed additional comparisons to other attribution methods in Extended Data Fig. 5c-d and 6. We found that the temperature-based masking operator of Eq. 1 consistently outperforms other masks, that model-based interpretations were better than per-example masking approaches, and that methods such as L2X and INVASE failed to converge when trained on the full set of binders.

Finally, we tested the Scrambler against different versions of the ‘hot-deck’ SIS method (Extended Data Fig. 5e) [39, 40]: For each iteration of SIS, we sampled a number of background sequences and used these to mask de-selected features. The mean sample prediction was used as the function value. Similarly, we varied the number of Gumbel patterns sampled from the Scrambler PSSM during training (K in Eq. 2). The Scrambler operated well with few (≥ 4) samples and consistently outperformed SIS with 32 samples, both in predictive reconstruction and ground-truth comparisons. Additionally, the total number of predictor queries required to interpret the entire dataset with comparable quality was ~ 70 times lower than SIS. Interestingly, using a simple masking scheme such as mean features resulted in poor interpretations for the dimer RNN predictor.

Interpreting Protein Structure Predictions

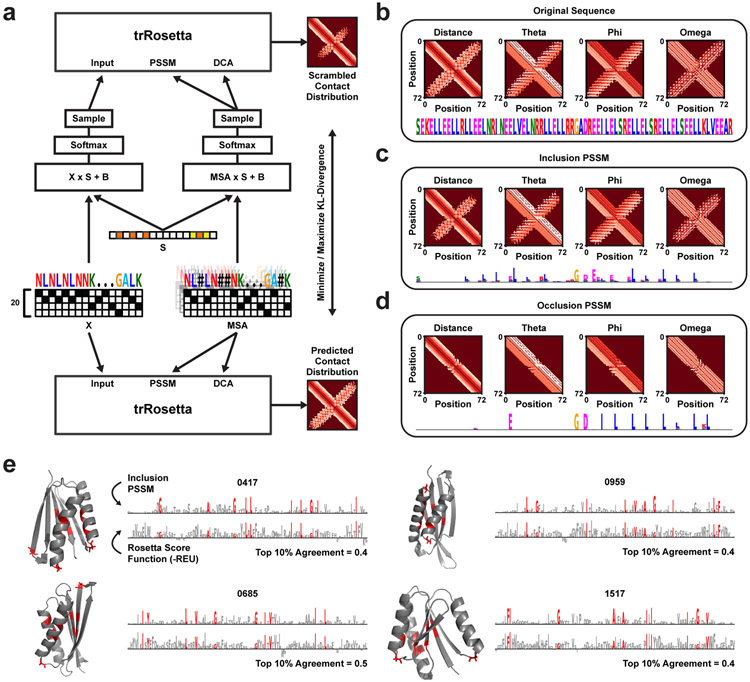
Recent advances in deep learning have made homology-free protein structure prediction possible. Such neural networks use the primary sequence and corresponding multiple sequence alignment (MSA) as input to predict three-dimensional atom-atom distances and backbone torsion angles [11]. Here, we apply Scramblers to the predictor trRosetta [12] to detect important sequence features for predicted structures. Since it is computationally heavy to query the predictor – and would likely require many iterations to train a Scrambler network – we demonstrate the approach for a single protein at a time (Fig. 6a). A trainable vector of scrambler scores (PSSM temperatures) is used to perturb the input sequence and MSA to minimize or maximize the total KL-divergence between predicted contact distributions (see Methods for details). We tested our approach on one of the alpha-helical hairpin binders from the previous dimer data set (Fig. 6b). PSSMs for the hairpin binder were optimized for the Inclusion (Fig. 6c) and Occlusion objectives (Fig. 6d). Both PSSMs used hydrophobic leucines and a symmetry-breaking glycine in the hairpin region to reconstruct or distort the original hairpin structure prediction, which aligns well with previous results [60]. We further tested the method on naturally occurring proteins with more complex 3D structures (Extended Data Fig. 7a-b).

Figure 6:

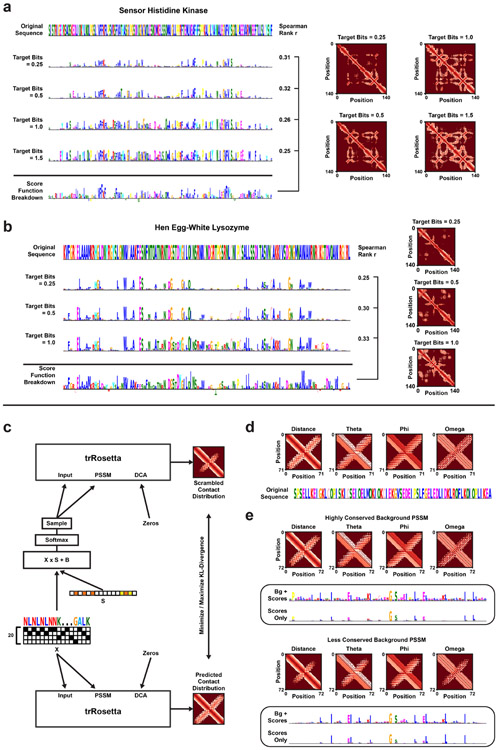
Protein Structure Feature Attribution (a) The single-sequence Scrambling architecture for tr-Rosetta. Both the primary sequence (‘X’) and the multiple sequence alignment (‘MSA’) are scrambled with the same trainable mask (‘S’). (b) Alpha-helical hairpin protein sequence and original structure prediction. (c) Inclusion-Scrambled PSSM of the hairpin protein, with the average predicted distance- and angle distributions for 512 samples drawn from the PSSM. (d) Occlusion-Scrambled PSSM of the hairpin protein and average structure prediction for 512 samples. (e) Inclusion-Scrambled PSSMs of four de novo proteins which have been designed by deep network hallucination. Each PSSM was optimized for t_bits = 1.0 target bits of conservation, using the amino acid frequency of naturally occurring sequences from the Protein Data Bank as background distribution. The bottom sequence logos represent the Rosetta score function breakdown per residue (−REU). The 10 most important residues according to the Scrambler scores are colored red.

Next, we altered the Scrambling architecture to enable MSA-free interpretation of de novo engineered proteins lacking natural sequence homology (Extended Data Fig. 7c). We optimized Inclusion-PSSMs to reconstruct the structure prediction of four proteins designed by deep network hallucination [62] (Fig. 6e). Important features found by the Scrambler included hydrophobic residues in the core for all four proteins. For validation, each protein’s structure prediction was relaxed, and the per-residue breakdown of the Rosetta score function was computed [63]. We found that the per-residue energy values agreed reasonably well with the Scrambler importance scores (mean top 10 residue agreement = 0.425). However, note that some features marked by the Scrambler as important for the structure prediction are missed by the Rosetta energy breakdown. For example, as can be seen in Fig. 6e, the Scrambler marked loop glycines between alpha-helices as important for the structure prediction, even though they do not have a large energetic contribution to overall stability. Glycines frequently occur in loops and turns and are thought to be important for maintaining protein loop structure due to their size and flexibility compared to other residues [64, 65]. The MSA-free approach was also tested on a hairpin-like protein engineered by Activation Maximization (Extended Data Fig. 7d-e) [66].

Discussion

Here we introduced a new attribution method – Scrambler Networks – that builds on and extends earlier work in input masking approaches. The goal is to explain an input pattern for a machine learning model by finding the smallest set of features which either reconstruct or destroy its prediction [32, 33, 34, 35, 36, 37, 38, 39, 40, 41]. Scrambler networks are based on learning a parametric model that predicts a set of real-valued importance scores given an input pattern. These predicted scores are used as sampling temperatures within a PSSM that interpolates between the current input and a non-informative background distribution. We demonstrated the performance of Scramblers on several attribution tasks, ranging from identifying cis-regulatory elements in RNA sequences to protein-protein interactions and protein tertiary structure. Furthermore, Scramblers can be trained to find not only reconstructive, but also enhancing and repressive features, and can be used to dynamically find multiple salient feature sets within a single input pattern. For prediction problems where the salient feature sets vary widely in size, per-example fine-tuning can be employed to correct positions that were misidentified as important.

At the core of mask-based interpretation is the masking operator, which must be carefully chosen according to the problem domain. Earlier work in computer vision masked input patterns by fading or blurring [32, 33, 34], and other methods for discrete variable selection masked features with zeros [35, 36]. Neither of these operators are suitable for predictors trained on biological sequences, which expect discrete one-hot encoded patterns as input and predict poorly on patterns outside of the training data manifold. The Scrambler masking operator is conceptually similar to ‘hot-deck’ masking proposed in the SIS method by Carter et al. [39] and in the interpretation method of Zintgraf et al. [38], where deactivated features are replaced with random samples from the marginal distribution of that input. Scramblers generalize this concept by maintaining a categorical feature sampling distribution at each position in the sequence, where the predicted temperature (inverse importance score) defines how random a sample from that position will be on a continuous scale. An immediate benefit is that, in contrast to SIS, Scramblers output real-valued importance scores that reflect an internal ranking of feature importance. This masking operator also shares similarities with the counterfactual masking introduced by Chang et al. [37], but the temperature-based operator is simpler as it does not require training a generative fill-in model.

We showed in extensive benchmarks that temperature-based masking outperforms the hot-deck masking done with SIS and any of the fade-, blur- or mean-masking schemes used in [32, 33, 34]. By training a parametric model, we end up with a more sample-efficient method at interpreting patterns than per-example methods [32, 39]. We also showed that Scramblers produced better interpretations than L2X [35] and INVASE [36], which either overfit their interpretations when trained on the reduced datasets or did not converge well when trained on the full data. This highlights the difficulty in jointly training a sparse feature selector and a predictor on very heterogeneous data and showcases the potential in applying post-hoc interpretation to rich, pre-trained predictors. By optimizing over a sufficiently large training set, Scramblers avoid overfitting to spurious per-example signals and learn to generalize feature importance. Generalizable attributions are highly desirable in genomics and proteomics as they allow us to infer higher-quality biological discoveries from trained predictors, thereby offering richer insights into molecular processes that were previously considered black boxes. We envision that Scramblers will be particularly useful for rational sequence design, where they can be employed to either validate known design rules (as demonstrated on the protein-protein interaction task) or – as demonstrated on the protein structure task – to discover determinants which data-driven design methods have produced.

Methods

Scrambling Neural Network Definition

Masking Operator

Let x ∈ {0, 1}^N×M be a one-hot-encoded sequence and let $\mathcal{S}(\mathit{x})\in (0,\infty {]}^N$ be the corresponding real-valued importance scores predicted by Scrambler network $\mathcal{S}$. The channel-broadcasted importance scores $\stackrel{.}{\mathcal{S}}(\mathit{x})\in (0,\infty {]}^{N\times M}$ are defined as $\stackrel{.}{\mathcal{S}}(\mathit{x}{)}_{ij}=\stackrel{.}{\mathcal{S}}(\mathit{x}{)}_i,$ ∀i, j. $\stackrel{.}{\mathcal{S}}(\mathit{x})$ are used as (differentiable) interpolation coefficients in log-space between background distribution $\tilde{\mathit{b}}$ and the current input pattern x according to Eq. 1 for the Inclusion objective. Conversely, the scrambling operation for the Occlusion-model is defined in Eq. 3 below. Here, the expression $\mathit{x}\times \stackrel{.}{\mathcal{S}}(\mathit{x})$ has been replaced with $\mathit{x}∕\stackrel{.}{\mathit{S}}(\mathit{x})$. Either of these formulas return a softmax-relaxed distribution (a Position-Specific Scoring Matrix; PSSM) ${\widehat{\mathit{x}}}_{\mathcal{S}}\in [0,1{]}^{N\times M}$, which can be interpreted as a representation of the input sequence where the information content at position i has been perturbed according to the sampling temperature $\mathcal{S}(\mathit{x}{)}_i$ predicted by the Scrambler.

$${\widehat{\mathit{x}}}_{\mathcal{S}}=\sigma \left(\log \tilde{\mathit{b}}+\mathit{x}∕\stackrel{.}{\mathcal{S}}(\mathit{x})\right)$$ (3)

Given the scrambled PSSM ${\widehat{\mathit{x}}}_{\mathcal{S}}$, we sample approximate discrete one-hot-coded patterns ${\mathit{x}}_{\mathcal{S}}^{(k)}$ using the Concrete distribution (or Gumbel-distribution) [44], enabling differentiation:

$${\mathit{x}}_{\mathcal{S}}^{(k)}=\{{\mathbb{C}}_i{\}}_{i=1}^N,{\mathbb{C}}_i\sim \text{Concrete}({\widehat{\mathit{x}}}_{\mathcal{S}i1},\dots ,{\widehat{\mathit{x}}}_{\mathcal{S}iM})$$ (4)

Alternatively, we sample exact discrete patterns ${\mathit{x}}_{\mathcal{S}}^{(k)}$ from ${\widehat{\mathit{x}}}_{\mathcal{S}}$ and use the Softmax Straight-Through Estimator (ST-sampling) [43] to approximate the gradient ${\nabla }_{W_{\mathcal{S}}}{\mathit{x}}_{\mathcal{S}}^{(k)}$ of the input pattern with respect to the Scrambler network weights. To reduce variance during training, we draw K samples $\{{\mathit{x}}_{\mathcal{S}}^{(k)}{\}}_{k=1}^K$ at each iteration of gradient descent and walk down the average gradient (by default, K = 32).

Objective Functions

Given the scrambled PSSM ${\widehat{\mathit{x}}}_{\mathcal{S}}$, a collection of differentiable sequence samples $\{{\mathit{x}}_{\mathcal{S}}^{(k)}{\}}_{k=1}^K$ and the background distribution $\tilde{\mathit{b}}$, the Scrambler is trained by backpropagation to either minimize Eq. 2 (Inclusion) or Eq. 5 below (Occlusion). For predictor models $\mathcal{P}$ with a sigmoid or softmax output (classification), the prediction reconstruction error between $\mathcal{P}(\mathit{x})$ and $\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})$ is the standard cross-entropy error. For regression tasks, the cost is defined as the mean squared error. The cost parameter t_bits defines the target per-position PSSM conservation and λ defines the conservation penalty weight. With a smaller value of λ, the Scrambler is allowed to output PSSMs with a larger spread of conservation around the target t_bits (example: for one input pattern, the scrambled PSSM may have a mean conservation of 0.05, for another pattern, it may be 0.25). With a larger λ, the conservation values are forced closer to t_bits.

$$\underset{\mathcal{S}}{\text{min}}-\left(\frac{1}{K}\sum _{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})\Vert \mathcal{P}(\mathit{x})]\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (5)

Rather than optimizing the Scrambler to reconstruct predictions using a small feature set, we can train the model to find feature sets that either positively or negatively influence the prediction. For classification tasks, we either maximize or minimize the log-probability log $\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})$ (Eq. 6-7). For regression tasks, we either maximize or minimize the regressor $\mathcal{P}({\mathit{x}}_{\mathcal{S}}^{(k)})$ (Eq. 8-9).

$$\underset{\mathcal{S}}{\text{min}}-\left(\frac{1}{K}\sum _{k=1}^K\log \mathcal{P}({\widehat{\mathit{x}}}_{\mathcal{S}}^{(k)})\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (6)

$$\underset{\mathcal{S}}{\text{min}}-\left(\frac{1}{K}\sum _{k=1}^K\log (1-\mathcal{P}({\widehat{\mathit{x}}}_{\mathcal{S}}^{(k)}))\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (7)

$$\underset{\mathcal{S}}{\text{min}}-\left(\frac{1}{K}\sum _{k=1}^K\mathcal{P}({\widehat{\mathit{x}}}_{\mathcal{S}}^{(k)})\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (8)

$$\underset{\mathcal{S}}{\text{min}}\left(\frac{1}{K}\sum _{k=1}^K\mathcal{P}({\widehat{\mathit{x}}}_{\mathcal{S}}^{(k)})\right)+\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]\right)}^2$$ (9)

Note that we could have defined the conservation penalty of Eq. 2-5 and 6-9 in many other ways. The KL-divergence $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]$ corresponds to the generalized entropy of ${\widehat{\mathit{x}}}_{\mathcal{S}}$ and is particularly suitable for the Inclusion-Scrambler: the expression reaches 0 when ${\widehat{\mathit{x}}}_{\mathcal{S}}$ is maximally entropic (with respect to $\tilde{\mathit{b}}$). For the Occlusion-Scrambler where entropy should be minimized, it may seem more appropriate to minimize the KL-divergence $\text{KL}[{\widehat{\mathit{x}}}_{\mathcal{S}}\Vert \mathit{x}]$ to the original input pattern rather than maximizing $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]$, as this cost corresponds to the cross-entropy of ${\widehat{\mathit{x}}}_{\mathcal{S}}$ with respect to x and is 0 at minimum entropy. Alternatively, for both Scramblers, we could simply minimize the area scrambled by the importance scores, $\sigma (\mathcal{S}(\mathit{x}))\times 2-1$ (we refer to these as lum values). Overall, $\text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathcal{S}}]$ resulted in better performance, which we hypothesize has to do with the information content of $\tilde{\mathit{b}}$ otherwise being lost.

Background Distribution

The background distribution $\tilde{\mathit{b}}$ is intended to keep the scrambled sequence samples in distribution and along the manifold of valid patterns, no matter where on the interpolation line between $\tilde{\mathit{b}}$ and x the scrambled distribution ${\widehat{\mathit{x}}}_{\mathcal{S}}$ is. There are several possible choices of $\tilde{\mathit{b}}$, with varying degrees of complexity:

$$(0\text{-BG}){\tilde{\mathit{b}}}_{ij}=P(x_i=j)=\frac{{\sum }_{k=1}^N{1}_{x_i^{(k)}=j}}{N}$$ (10)

$$(\text{H-BG}){\tilde{\mathit{b}}}_{ij}(\mathit{x})=P(x_i=j\mid x_{i-H},\dots ,x_{i+H})=\frac{{\sum }_{k=1}^N{1}_{x_i^{(k)}=j\cap x_{i-H}^{(k)}=\dots }}{{\sum }_{k=1}^N{1}_{x_{i-H}^{(k)}=\dots }}$$ (11)

$$(\text{DATA}){\tilde{\mathit{b}}}_{ij}=x_{ij}^{(\mathbb{K})},\mathbb{K}\sim \{1,\dots ,N\}$$ (12)

$$(\text{GEN}){\tilde{\mathit{b}}}_{ij}(\mathit{x})=\mathcal{G}(\mathit{z},\mathit{x},\mathcal{S}(\mathit{x}){)}_{ij},\mathit{z}\sim \mathcal{N}(0,1{)}^d$$ (13)

The simplest background distribution, 0-BG, corresponds to the mean input pattern across the training set (i.e. marginal feature probabilities). A more complex background, H-BG, is the distribution of a particular feature conditioned on its neighboring features [38]. Finally, the DATA- and GEN distributions consist of input patterns randomly chosen from the dataset (DATA), or patterns generated by a distribution-capturing model such as a conditional GAN or Variational Autoencoder (GEN) [37]. In all of our experiments, we relied on the simplest background distribution, 0-BG, since all tested sequence-predictive models behaved well on such samples. Still, for more narrowly defined manifolds, H-BG or DATA/GEN may be more appropriate to stay in distribution.

Network Architecture

The Scrambler is based on a Residual Neural Network architecture with dilated convolutions (Extended Data Fig. 1) [42]. For the MNIST, 5’ UTR, and protein binder attribution tasks, the network consisted of 5 groups of 4 dilated residual blocks (20 blocks in total), with filter width 3. For the alternative polyadenylation task, the network had just one group of 4 residual blocks, with filter width 8.

Mask Dropout and Biasing

Scramblers can find multiple salient feature set solutions for an input pattern using input-masking layers such as dropout- or biasing layers, which either disallow or enforce specific sequence positions in the retained feature set. Specifically, we let D, T ∈ {0, 1}^N be the dropout- and biasing masks and apply them to the importance scores by element-wise multiplication and addition respectively:

$${\widehat{\mathit{x}}}_{\mathcal{S}}=\sigma (\log \tilde{\mathit{b}}+\mathit{x}\times (\stackrel{.}{\mathcal{S}}(\mathit{x},\mathit{D},\mathit{T})\times \stackrel{.}{\mathit{D}}+\stackrel{.}{\mathit{T}}\cdot c))$$ (14)

Here c is the temperature of the biasing mask T (smaller c allows more randomness in selecting the letter at a biased position, a larger c makes it more likely to select the current input letter at the biased position). The Scrambler network $\mathcal{S}$ also receives D and T as additional input, allowing the network to learn to output alternate scores conditioned on which positions were dropped or enforced. During training, we use random samples of D and T (various training schemes are illustrated in Extended Data Fig. 2; for the MNIST task, we used all three schemes; for the 5’ UTR task we used only the first scheme, i.e. uniform random training patterns consisting of squares). After training on randomized dropout and biasing patterns, we can provide hand-crafted patterns at inference time to detect alternate feature sets of new input examples.

Fine-tuning and Per-example Optimization

For heterogeneous datasets where the number of important features per example is highly variable, we apply a per-example fine-tuning step to the importance scores predicted by the (pre-trained) Scrambler network $\mathcal{S}$ to remove any excessive (or redundant) features. Specifically, for each input pattern x, we predict Scrambler scores $\mathcal{S}(\mathit{x})$ and optimize the subtraction scores s according to Eq. 15-16 (for Inclusion) or Eq. 17-18 (for Occlusion) below. The scrambling Eq. is reformulated with the expression max$[\stackrel{.}{\mathcal{S}}(\mathit{x})-\mathit{s},0]$; this forces the resulting fine-tuned importance scores to select a subset of the features identified by the original scores $\mathcal{S}(\mathit{x})$, i.e., the new scores cannot find a new alternate explanation for example x. This restriction prevents ‘overfitting’ to the predictor, which is otherwise a problem with per-example optimization. Architecturally, we do not optimize s directly; we optimize parameters w, which are instance-normalized and softplus-transformed (s = Softplus(IN(w))). In our experiments, we optimize w for 300 iterations of gradient descent (Adam, learning rate = 0:01).

$$\underset{\mathit{s}}{\text{min}}\left(\frac{1}{K}\sum _{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathit{s}}^{(k)})\Vert \mathcal{P}(\mathit{x})]\right)+\lambda \cdot \frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathit{s}}]$$ (15)

$${\widehat{\mathit{x}}}_{\mathit{s}}=\sigma \left(\log \tilde{\mathit{b}}+\mathit{x}\times \max [\stackrel{.}{\mathcal{S}}(\mathit{x})-\mathit{s},0]\right)$$ (16)

$$\underset{\mathit{s}}{\text{min}}-\left(\frac{1}{K}\sum _{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathit{s}}^{(k)})\Vert \mathcal{P}(\mathit{x})]\right)-\lambda \cdot \frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathit{s}}]$$ (17)

$${\widehat{\mathit{x}}}_{\mathit{s}}=\sigma \left(\log \tilde{\mathit{b}}+\mathit{x}∕\max [\stackrel{.}{\mathcal{S}}(\mathit{x})-\mathit{s},ϵ]\right),\underset{ϵ\to +0}{\text{lim}}$$ (18)

For comparison, we also perform per-example optimization from scratch (i.e., we start with randomly initialized values rather than pre-trained Scrambler scores). To this end, we optimize Eq. 15 (for Inclusion) or Eq. 17 (for Occlusion). The perturbation operators are identical to Eq. 1 and 3, but with individual scores s per pattern $\mathit{x}:{\widehat{\mathit{x}}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathit{x}\times \stackrel{.}{\mathit{s}})$ (Inclusion), ${\widehat{\mathit{x}}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathit{x}∕\stackrel{.}{\mathit{s}})$ (Occlusion).

Attribution Tasks and Predictors

MNIST: The predictor was a CNN with 2 convolutional layers, 1 max-pool layer and a single fully connected hidden layer. The network was trained for this study. Predicts a 10-way classification score $\mathcal{P}(\mathit{x})\in {\mathbb{R}}^{10}$ (softmax) given a binarized MNIST image x ∈ {0, 1}^28×28 as input.

APA (3’ UTR): [7] The predictor was a pre-trained CNN (APARENT) which predicts relative alternative polyadenylation isoform abundance $\mathcal{P}(\mathit{x})\in [0,1]$ given a 206 nt one-hot DNA sequence x ∈ {0, 1}^206×4 as input. The trained model was downloaded from: https://github.com/johli/aparent/tree/master/saved_models.

Translation (5’ UTR): [10] The predictor was a CNN (Optimus 5-Prime) which predicts mean ribosome load $\mathcal{P}(\mathit{x})\in \mathbb{R}$ given a 50 nt one-hot DNA sequence x ∈ {0, 1}^50×4 as input. The model was re-trained for this study but the training procedure was based on the code from: https://github.com/pjsample/human_5utr_modeling.

Protein heterodimer binders: The predictor was a RNN with siamese recurrent GRU layers, a dropout layer and a single fully connected hidden layer. The network was trained for this study. Predicts protein dimer binding probability $\mathcal{P}(\mathit{x})\in [0,1]$ (sigmoid activation) given two right-padded, 81 residues long protein binder sequences x₁, x₂ ∈ {0, 1}^81×20 as input. Note: When training Scrambler networks on these data, we used a separate background distribution $\tilde{\mathit{b}}$ for each unique protein sequence length.

Protein structure: [12] Predicts distance and angle distributions of backbone atoms in 3D given an input primary sequence. The trained model was downloaded from: https://files.ipd.uw.edu/pub/trRosetta/model2019_07.tar.bz2.

Given a one-hot-encoded sequence pattern x ∈ {0, 1}^N×20 and Multiple Sequence Alignment MSA ∈ {0, 1}^K×N×21, trRosetta predicts the atom-atom distance distribution D(x, MSA) ∈ [0, 1]^N×N×37 and backbone torsion angle distributions θ(x, MSA), ω(x, MSA) ∈ [0, 1]^N×N×24, ϕ(x, MSA) ∈ [0, 1]^N×N×12. In the paper, we performed per-example scrambling to interpret example protein structures, i.e. we did not train a discriminative Scrambler model to predict importance scores. Instead, this method optimizes a set of importance scores s for each pattern x that we wish to interpret. In the context of inclusion-scrambling, we find the smallest set of residues that minimizes the total KL-divergence of the target structure:

$$\begin{gathered} \underset{\mathit{s}}{\text{min}}\frac{1}{K}(\sum _{k=1}^K\text{KL}[\mathit{D}({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \mathit{D}(\mathit{x},\mathbf{MSA})]\phantom{)} \\ +\text{KL}[\theta ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \theta (\mathit{x},\mathbf{MSA})] \\ +\text{KL}[\omega ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \omega (\mathit{x},\mathbf{MSA})] \\ \phantom{(}+\text{KL}[\varphi ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \varphi (\mathit{x},\mathbf{MSA})]) \\ +\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathit{s}}]\right)}^2 \end{gathered}$$

For occlusion-scrambling, we optimize the inverse objective:

$$\begin{gathered} \underset{\mathit{s}}{\text{min}}\frac{1}{K}(-\sum _{k=1}^K\text{KL}[\mathit{D}({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \mathit{D}(\mathit{x},\mathbf{MSA})]\phantom{)} \\ -\text{KL}[\theta ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \theta (\mathit{x},\mathbf{MSA})] \\ -\text{KL}[\omega ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \omega (\mathit{x},\mathbf{MSA})] \\ \phantom{(}-\text{KL}[\varphi ({\mathit{x}}_{\mathit{s}}^{(k)},{\mathbf{MSA}}_{\mathit{s}}^{(k)})\Vert \varphi (\mathit{x},\mathbf{MSA})]) \\ +\lambda \cdot {\left(t_{\text{bits}}-\frac{1}{N}\cdot \text{KL}[\tilde{\mathit{b}}\Vert {\widehat{\mathit{x}}}_{\mathit{s}}]\right)}^2 \end{gathered}$$

In the above formulations, we define ${\mathit{x}}_{\mathit{s}}^{(k)}$, ${\mathbf{MSA}}_{\mathit{s}}^{(k)}\sim {\widehat{\mathit{x}}}_{\mathit{s}}$, $\mathbf{M}\widehat{\mathbf{S}}{\mathbf{A}}_{\mathit{s}}$ (letter-by-letter Gumbel-sampling). For inclusion-scrambling, we define:

$$\begin{gathered} {\widehat{\mathit{x}}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathit{x}\times \stackrel{.}{\mathit{s}}) \\ \mathbf{M}\widehat{\mathbf{S}}{\mathbf{A}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathbf{MSA}\times \ddot{\mathit{s}}) \end{gathered}$$

For occlusion-scrambling, we define:

$$\begin{gathered} {\widehat{\mathit{x}}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathit{x}∕\stackrel{.}{\mathit{s}}) \\ \mathbf{M}\widehat{\mathbf{S}}{\mathbf{A}}_{\mathit{s}}=\sigma (\log \tilde{\mathit{b}}+\mathbf{MSA}∕\ddot{\mathit{s}}) \end{gathered}$$

Here $\stackrel{.}{\mathit{s}}\in {\mathbb{R}}^{N\times M}$ is a channel-broadcasted copy of the importance scores $\mathit{s}\in {\mathbb{R}}^N$ and $\ddot{\mathit{s}}\in {\mathbb{R}}^{K\times N\times M}$ is a MSA-broadcasted copy. We obtain s from a vector of real-valued (trainable) numbers that we instance-normalize and apply the softplus activation on. We train s until convergence using the Adam optimizer with learning rate = 0.01, β₁ = 0.5 and β₂ = 0.9.

Attribution Methods

The attribution methods listed below were included in all the benchmark comparisons. However, DeepLIFT- and Guided Backprop were excluded from the PPI task (Fig. 5) since they were incompatible with the heterodimer RNN predictor model. See the Supplemental Information for a list of additional attribution methods that were tested only for the PPI task.

Scrambler (Inclusion): Scrambler network trained to minimize Eq. 2 using the temperature-based perturbator of Eq. 1, with background $\tilde{\mathit{b}}$ set to the mean input pattern across the training set. The network was trained between 20-50 epochs depending on task (when the validation error started to saturate).

Scrambler (Occlusion): Scrambler network trained to minimize Eq. 5 using the temperature-based perturbator of Eq. 3, with background $\tilde{\mathit{b}}$ set to the mean input pattern across the training set.

Perturbation: Baseline attribution method where each nucleotide or residue in the input pattern x is systematically exchanged for every other possible letter, measuring the change in prediction as a proxy for the importance score. Let ${\tilde{\mathit{x}}}^{(ij)}$ be the sequence pattern corresponding to exchanging the current nucleotide/residue at position i for letter j. We then calculate the importance score s_i at position i as the absolute mean change in prediction across all letters $j:s_i=\mid 1∕M\cdot {\sum }_{j=1}^M\mathcal{P}({\tilde{\mathit{x}}}^{(ij)})-\mathcal{P}(\mathit{x})\mid$. For classification tasks, we compare the log-scores of the predicted probabilities: $s_i=\mid 1∕M\cdot {\sum }_{j=1}^M\log \mathcal{P}({\tilde{\mathit{x}}}^{(ij)})-\log \mathcal{P}(\mathit{x})\mid$.

Gradient Saliency [25]: The Gradient Saliency method was executed using the implementation from Ancona et al. [45]. We used either the absolute value of the saliency scores (‘Gradient Saliency’) or the signed scores (‘Gradient Saliency (Signed)’).

Code: https://github.com/marcoancona/DeepExplain.

Guided Backprop [27]: The Guided Backprop method was executed using the implementation from Shrikumar et al. [29]. We used either the absolute value of the saliency scores (‘Guided Backprop’) or the signed scores (‘Guided Backprop (Signed)’).

Code: https://github.com/kundajelab/deeplift.

DeepLIFT [29]: For the MNIST task, the RevealCancel method was used. For all other tasks (due to predictor compatibility issues), the Rescale implementation from Ancona et al. [45] was used instead. The reference was set to the mean sequence pattern (PSSM) of the data set. We used either the absolute value of the saliency scores (‘DeepLIFT’) or the signed scores (‘DeepLIFT (Signed)’).

Code: (RevealCancel) [29] https://github.com/kundajelab/deeplift.

(Rescale) [45] https://github.com/marcoancona/DeepExplain.

DeepSHAP [30]: SHAP DeepExplainer (‘DeepSHAP’) was executed for each input pattern with 100 reference patterns sampled uniformly from the data set. We used either the absolute value of the saliency scores (‘DeepSHAP’) or the signed scores (‘DeepSHAP (Signed)’).

Code: https://github.com/slundberg/shap.

Integrated Gradients [28]: Integrated Gradients was executed using the implementation from Ancona et al. [45]. 10 integration steps were used per pattern. The reference was set to the mean sequence pattern (PSSM) of the data set. We used either the absolute value of the saliency scores (‘Integrated Gradient’) or the signed scores (‘Integrated Gradients (Signed)’).

Code: https://github.com/marcoancona/DeepExplain.

TorchRay [33]: The extremal preservation/perturbation method from the TorchRay package was executed using either the perturbation operator where masked pixels/letters are zeroed (‘TorchRay Fade’) or blurred by a gaussian (‘TorchRay Blur’). For the sequence-predictive tasks, we changed the code base to support 1-dimensional patterns. In all tasks, we set the blur operator σ to 3, the mask operator σ was set to 5 or 3 and the ‘step’ argument was set to 2. The ‘area’ was set to either 0.1 or 0.2.

Code: https://github.com/facebookresearch/TorchRay.

Saliency Model [34]: The Saliency Model-method was trained using a ResNet-50 network architecture. For the sequence-predictive tasks, we changed the code base to support 1-dimensional input patterns. The ‘encoder’-part of the network was not pre-trained and the ‘selector’-component was not used. In all tasks, the blur kernel size was set to either 9 or 5 and σ was set to 3. For every training iteration, blur was used 50% of the time as the perturbation operator and fade (zeroing features) otherwise.

Code: https://github.com/PiotrDabkowski/pytorch-saliency.

Sufficient Input Subsets [39]: Sufficient Input Subsets (SIS) was executed with the threshold set to the 50th percentile of the predicted scores $(\mathcal{P}(\mathit{x}))$ across the data set. For input patterns with non-masked predictions below this threshold, we used a dynamic threshold of 0.8 times the non-masked predicted score.

We tested multiple masking schemes: (1) Replacing masked residue positions with the mean letter value (‘SIS (Mean)’) and (2) Replacing masked residue positions with letters sampled from the marginal letter distribution, repeating the sampling process X times, and calculating the mean prediction across all X samples (‘SIS (X Sample)’).

Code: https://github.com/google-research/google-research/tree/master/sufficient_input_subsets.

Zero Scrambler: Optimizes the same high-level objective as the Scrambler, but this model uses a perturbation operator similar to that of L2X [35] and INVASE [36] where de-selected features are zeroed. Specifically, ‘Zero Scrambler’ optimizes ${\text{min}}_{\mathcal{M}}\text{KL}[\mathcal{P}(\mathit{x}\times {\mathcal{M}}^{(\mathrm{G})}(\mathit{x}))\Vert \mathcal{P}(\mathit{x})]+\lambda \cdot {\left(t_{\text{area}}-1∕N\cdot {\sum }_{i=1}^N{\mathcal{M}}^{(\mathrm{S})}(\mathit{x}{)}_i\right)}^2$, where $\mathcal{M}$ is a binary 0/1 masking model. The continuous-valued mask ${\mathcal{M}}^{(\mathrm{S})}(\mathit{x})$ and binarized mask ${\mathcal{M}}^{(\mathrm{G})}(\mathit{x})$ are obtained by applying sigmoid activations and Gumbel sampling on the output vector of $\mathcal{M}$ respectively. Internally, the network $\mathcal{M}$ is identical to the Scrambler.

L2X [35]: The ‘approximator’-model used in the L2X procedure always had the same architecture as the original predictor of each task. The ‘explainer’-model was the default network found in the example code, consisting of multiple layers of convolutions with global pooling to capture high-level features. The size parameter k was set to 0.1 · N or 0.2 · N depending on the task, where N is the length of the sequence. The L2X models were trained until convergence (early stopping on validation data).

Code: https://github.com/Jianbo-Lab/L2X/.

INVASE [36]: The ‘critic’- and ‘baseline’-models used in the INVASE procedure were standard convolutional neural networks with 3-5 convolutional layers, interlaced with instance-normalization layers, and one fully-connected hidden layer. The ‘actor’-model was a convolutional neural network with 3-5 instance-normalized convolutional layers. The λ parameter varied between 0.05 and 50 depending on the task. The INVASE models were trained until convergence.

Code: https://github.com/jsyoon0823/INVASE.

Scrambler (Inclusion, Siamese): The ‘siamese’ Inclusion-Scrambler architecture used in the PPI task (Fig. 5). Given pairs of input patterns x₁ and x₂, we optimize ${\text{min}}_{\mathcal{S}}\left(1∕K\cdot {\sum }_{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S},1}^{(k)},{\mathit{x}}_{\mathcal{S},2}^{(k)})\Vert \mathcal{P}({\mathit{x}}_1,{\mathit{x}}_2)]\right)+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_1\Vert {\widehat{\mathit{x}}}_{\mathcal{S},1}]\right)}^2+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_2\Vert {\widehat{\mathit{x}}}_{\mathit{S},2}]\right)}^2$, where ${\mathit{x}}_{\mathcal{S},1}^{(k)}$, ${\mathit{x}}_{\mathcal{S},2}^{(k)}\sim {\widehat{\mathit{x}}}_{\mathcal{S},1}$, ${\widehat{\mathit{x}}}_{\mathcal{S},2}$ (letter-by-letter Gumbel-sampling) and ${\widehat{\mathit{x}}}_{\mathcal{S},\#}=\sigma (\log {\tilde{\mathit{b}}}_{\#}+{\mathit{x}}_{\#}\times \stackrel{.}{\mathcal{S}}({\mathit{x}}_{\#}))(\#=1\text{or}2)$. $\mathcal{S}$ is a (siamese) Scrambler network.

Scrambler (Occlusion, Joint): The ‘joint’ Occlusion-Scrambler architecture used in the PPI task (Fig. 5). Given pairs of input patterns x₁ and x₂, we optimize ${\text{min}}_{\mathcal{S}}-(1∕K\cdot {\sum }_{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S},1}^{(k)},{\mathit{x}}_{\mathcal{S},2}^{(k)})\Vert \mathcal{P}({\mathit{x}}_1,{\mathit{x}}_2)])+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_1\Vert {\widehat{\mathit{x}}}_{\mathcal{S},1}]\right)}^2+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_2\Vert {\widehat{\mathit{x}}}_{\mathcal{S},2}]\right)}^2$, where ${\mathit{x}}_{\mathcal{S},1}^{(k)}$, ${\mathit{x}}_{\mathcal{S},2}^{(k)}\sim {\widehat{\mathit{x}}}_{\mathcal{S},1}$, ${\widehat{\mathit{x}}}_{\mathcal{S},2}$ (letter-by-letter Gumbel-sampling) and ${\widehat{\mathit{x}}}_{\mathcal{S},\#}=\sigma \left(\log {\tilde{\mathit{b}}}_{\#}+{\mathit{x}}_{\#}∕\stackrel{.}{\mathcal{S}}({\mathit{x}}_1,{\mathit{x}}_2)\right)(\#=1\text{or}2)$. $\mathcal{S}$ is a two-input Scrambler network.

Scrambler (Occlusion, Siamese): The ‘siamese’ Occlusion-Scrambler architecture used in the PPI task (Fig. 5). Given pairs of input patterns x₁ and x₂, we optimize ${\text{min}}_{\mathcal{S}}-(1∕K\cdot {\sum }_{k=1}^K\text{KL}[\mathcal{P}({\mathit{x}}_{\mathcal{S},1}^{(k)},{\mathit{x}}_{\mathcal{S},2}^{(k)})\Vert \mathcal{P}({\mathit{x}}_1,{\mathit{x}}_2)])+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_1\Vert {\widehat{\mathit{x}}}_{\mathcal{S},1}]\right)}^2+\lambda \cdot {\left(t_{\text{bits}}-1∕N\cdot \text{KL}[{\tilde{\mathit{b}}}_2\Vert {\widehat{\mathit{x}}}_{\mathcal{S},2}]\right)}^2$, where ${\mathit{x}}_{\mathcal{S},1}^{(k)}$, ${\mathit{x}}_{\mathcal{S},2}^{(k)}\sim {\widehat{\mathit{x}}}_{\mathcal{S},1}$, ${\widehat{\mathit{x}}}_{\mathcal{S},2}$ (letter-by-letter Gumbel-sampling) and ${\widehat{\mathit{x}}}_{\mathcal{S},\#}=\sigma \left(\log {\tilde{\mathit{b}}}_{\#}+{\mathit{x}}_{\#}∕\stackrel{.}{\mathcal{S}}({\mathit{x}}_{\#})\right)(\#=1\text{or}2)$. $\mathcal{S}$ is a (siamese) Scrambler network.

Benchmarking Details

Synthetic IF uORF 5’ UTR Datasets

Synthetic IF uORF 5’ UTR sequences were generated for feature attribution with varying numbers of IF uORFS by selecting sequences from the Optimus 5-Prime egfp_unmod_1 dataset [10], which contained no upstream starts or stops and had MRL values that fell between the 5th and 10th percentile of the dataset. This set of sequences (n = 537) had the original sequence nucleotides replaced by “ATG” and “TAG” uniformly at random at possible IF positions as needed to create the number of IF uORFs for the dataset, keeping the rest of the UTR fixed. Four synthetic 5’ UTR datasets of n = 512 sequences were generated: one IF uORF by inserting an “ATG” and followed by a “TAG”, two IF uORFs by inserting an “ATG” followed by two “TAG”, two IF uORFs by inserting two “ATG” followed by “TAG,” and four IF uORFs by inserting two “ATG” followed by two “TAG”.

Hydrogen Bond Network Detection

The Chen et al. [60] dimers were designed to have a minimum of 4 residues involved, contacting all four helices, with all heavy-atom donors and acceptors in the network satisfied. However, in later design steps for the hetero-dimers, these networks were slightly disrupted making complete recovery difficult using the original parameters. As such, slightly relaxed criteria from the original design specifications were used to recover as many HBNet residues as possible from the test set designed structures. HBNet residues were recovered from test coiled-coil dimers using PyRosetta [67] and the HBNetStapleInterface protocol, with the settings min_network_size=3, min_helices_contacted_by_network=3, hb_threshold=−0.3, and find_only_native_networks=True. The ref2015 score function was used during HBNet mover setup [63].

Mean AAG Difference Calculation and Alanine Scanning

Computational Alanine scanning was carried out for all residues in a hetero-dimer pair using PyRosetta [67]. Each position was mutated to Alanine and repacked with the neighboring residues prevented from design and repacking. The InterfaceAnalyzerMover was used with set_pack_input as False and set_pack_separated as True to calculate the mean mutation ΔΔG in Rosetta Energy Units (REU) at each position. For each attribution method, the eight most important residues per dimer were selected, and the difference of the mean ΔΔG of the top residues and the mean ΔΔG of all other residues was computed.

Per-Residue Score Function Breakdown and Substitution Scoring Matrix

Lysozyme and Sensor Histidine Kinase structures were predicted with trRosetta [12]. Each de novo structure was provided by [62]. All structures were relaxed using fast relax with PyRosetta [67], scored using the beta_nov16 score function [63], and broken down into individual residue contributions. This was done ten times per structure, and the average residue contributions were calculated.

Extended Data

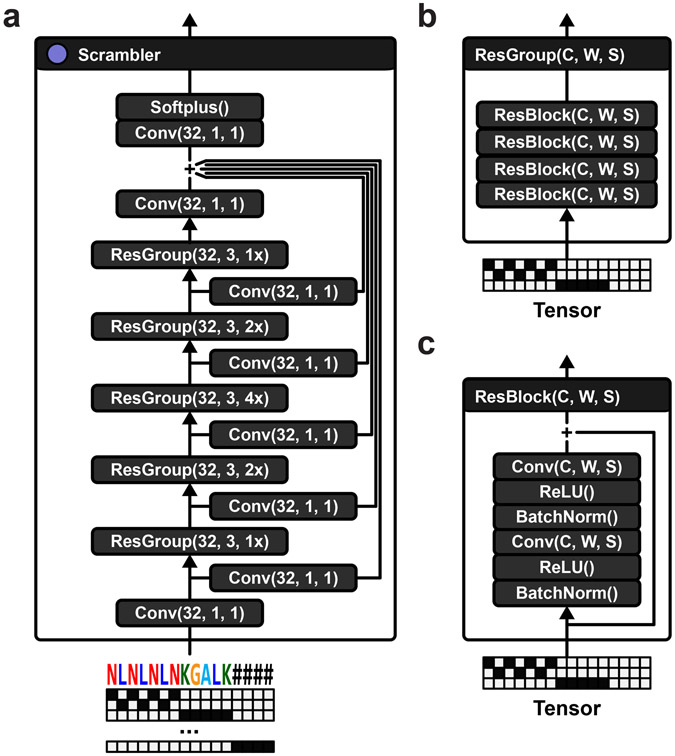
Extended Data Fig. 1.

(a) Scrambler network architecture. The network is based on groups of residual blocks. This particular network configuration has 5 groups of residual blocks, with 32 channels, filter width 3 and varying dilation factor (1x, 2x, 4x, 2x, 1x). There is a skip connection (single convolutional layer with 32 channels and filter width 1) before each residual group. All skip connections are added together with the output of the final residual group. A softplus activation is applied to the final tensor in order to get importance scores that are strictly larger than 0. (b) Each residual group consists of 4 identical residual blocks connected in series. (c) Each residual block consists of 2 dilated convolutions, each preceded by batch normalization and ReLU activations. A skip connection adds the input tensor to the output of the final convolution.

Extended Data Fig. 2.

(a) Comparison of attribution methods on the 'Inclusion'-benchmark of Figure 2B (Perturbing the input patterns by keeping the top X% most important features according to each method and replacing all other features with random samples from a background distribution, n=1,888). Left table: Median KL-divergence between original predictions and predictions made on perturbed input patterns (lower is better). Right table: Classification accuracy of the predictor using the perturbed input patterns (higher is better). The '100%'-case refers to the original (non-perturbed) input pattern. The best method(s) are highlighted in green. (b) Uniformly random mask dropout training procedure, which teaches the Scrambler to find alternate salient feature sets. For each input pattern, we sample a random dropout pattern containing squares of varying width. The pattern is multiplied with the predicted importance scores, effectively zeroing out certain regions (forcing the background distribution to be used). The dropout pattern is also passed as additional input to the Scrambler (it is concatenated along the channel dimension), allowing the network to learn which other feature set to choose. (c) Biased dropout training procedure. Instead of randomly sampling dropout patterns, we first let the Scrambler predict importance scores with an all-ones dropout pattern (no dropout), which we use to form an importance sampling distribution. We then sample a dropout pattern and use it for training the same way we trained on uniformly random patterns. (d) Another biased dropout training approach. We first use the Scrambler to predict the importance scores given the all-ones dropout pattern as input (no dropout). The top 5% most important features are subtracted from the all-ones pattern. Then, with a certain probability, we either re-run the Scrambler on this updated pattern (repeating the previous steps), or we end the loop and choose this as our final dropout pattern to train on. (e) Procedure for training the Scrambler to dynamically change the entropy of its solutions. Instead of fitting the network to a constant KL-divergence of its scrambled input distribution, we here randomly sample KL-divergence values and use them both as input to the network and as the target for the conservation penalty. The bit value is broadcasted and concatenated along the input channel dimension. (f) Example attributions of MNIST digit '2' and '4' with dynamically resized feature sets, by passing increasingly large target 'lum' values as input to the Scrambler ('lum' values are normalized KL-divergence bits, see Methods).

Extended Data Fig. 3.

(a) Top: Example attribution of a polyadenylation signal sequence from the APARENT test set, using Inclusion-Scramblers trained with increasingly large t_bits of conservation. Known regulatory motifs annotated. Bottom: Two additional example attributions, showing only the results for the t_bits = 1.0 case. (b) Non-trainable convolutional filter with a 1D gaussian kernel (filter width 6) is prepended to the final softplus activation function of the Scrambler. (c) APARENT isoform predictions of original sequences and of corresponding sampled sequences from the PSSMs predicted by an Occlusion-Scrambler trained with t_bits = 1.8, with and without the Gaussian filter. (d) Example attributions of t_bits = 1.8 - and 1.5 Occlusion-Scramblers, with and without the Gaussian filter. (e) Example attributions of a polyadenylation signal sequence, comparing different methods. (f) Comparison of attribution methods on the 'Inclusion'-benchmark of Figure 3B (Perturbing the input patterns by keeping the top X% most important features according to each method and replacing all other features with random samples from a background distribution, n=1,737). Median KL-divergences are computed between original predictions and predictions made on perturbed input patterns (lower is better). These predictions were made using the APARENT model. Shown are also the Spearman r correlation coefficients between original and perturbed predictions using the DeeReCT-APA model (higher is better). The default Scrambler network for the APA task uses 4 residual blocks, while the 'Deep' architecture uses a total of 20 residual blocks. The best method(s) are highlighted in green. (g) Attributions of four human polyadenylation signals which are associated with known deleterious variants, comparing the Perturbation method to the reconstructive Inclusion-Scrambler (t_bits = 0.25 target bits) on hypothetical variants which have not been found in the population. Gene names and clinical condition associated with the PAS annotated above each sequence. In each of the four examples, the Scrambler correctly detects the loss of the presumed RBP binding site or otherwise important motif due to each respective variant (loss of the CstF binding motif in FOXC1, TP53; loss of the SRSF10 binding motif in INS; loss of the T-rich DSE motif in HBB). (h) Left: Example attributions of a medium-strength polyadenylation signal sequence, using three Scramblers which have been optimized for different objectives: (Reconstructive features) reconstructing the original prediction, (Negative features) minimizing the prediction, and (Positive features) maximizing the prediction. Right: APARENT isoform predictions of original sequences and of corresponding sampled sequences from the PSSMs predicted by the Negative-feature and Positive-feature Scrambler respectively.

Extended Data Fig. 4.

(a) Benchmark comparison on the synthetic Start / Stop test sets, where input patterns are perturbed by keeping the most important features according to each method (6, 9 or 12 nt) and replacing all other features with random samples from a background distribution, n=512). Mean squared errors are computed between original predictions and predictions made on perturbed input patterns using the Optimus 5-Prime model (lower is better). We trained two Scramblers, one with a low entropy penalty (t_bits = 0.125, λ= 1) and one with a higher penalty (λ = 10). The best method(s) are highlighted in green. (b) Average recall for finding one of the start codons and one of the stop codons in the 6 most important nucleotides, as identified by each method, measured across the synthetic test sets. (c) Additional benchmark comparison for L2X and INVASE, when using the full 260,000 5' UTR dataset for training the interpreter model. Shown are the mean squared errors between predictions of original and perturbed input patterns, average recall for finding start and stop codons, and example visualizations on the synthetic start / stop test sets. (d) Left: Attribution of a ClinVar variant, rs779013762, in the ANKRD26 5' UTR, which is predicted by Optimus 5-Prime to be a functionally silent mutation. The variant creates an IF uORF overlapping an existing IF uORF. The per-example fine-tuning step (which starts from the Low entropy penalty-Scrambler scores) finds a minimal salient feature set in the variant sequence (one IF uORF), while the per-example optimization (which starts from randomly initialized scores) gets stuck in a local minimum. Middle: Attribution of a ClinVar variant, rs201336268, in the TARS2 5' UTR, which destroys two overlapping IF uORFs and is predicted to lead to upregulation. Both the fine-tuning step and the independent per-example optimization finds that no features are important in the variant sequence (both IF uORFs were removed by the variant and a fully random sequence has on average the same predicted MRL as the variant sequence). The Perturbation method has trouble explaining either of these variants due to saturation effects of the multiple IF stop codons. Right: Attribution of a rare variant, rs886054324, in the C19orf12 5' UTR, which creates two IF uORFs overlapping a strong OOF uAUG (hence a silent mutation). All attribution methods identify the OOF uAUG as the major determinant, however the Low entropy penalty-Scrambler incorrectly marks an (unmatched) stop codon in the wildtype sequence as important. Both the High entropy penalty-Scrambler and the fine-tuning step based off the Low penalty-Scrambler correctly filters the stop codon. (e) Benchmarking results on the 1 Start / 2 Stop dataset, comparing the Low entropy penalty-Scrambler network to running per-example fine-tuning of those scores and to the baseline method of optimizing each example from randomly initialized scores. Reported are the mean squared error between predictions on original and scrambled sequences ('MSE'), the error rate (1 - Accuracy) of not finding one Start codon and one Stop codon in the top 6 nt ('Error Rate'), and the mean per-nucleotide KL-divergence between the scrambled PSSM and the background PSSM ('Conservation'). (f) Example attributions using a Scrambler network trained with the mask dropout procedure (see Methods for details). By dropping different parts of the importance score mask, the Scrambler learns to discover alternate salient feature sets. In the example on the right: Finding alternate IF uORF regions by separately dropping each of the Start and Stop codons. (g) Example Scrambler attributions with the mask dropout mechanism on two native human 5' UTRs.

Extended Data Fig. 5.

(a) Protein heterodimer binder RNN predictor, which was trained on computationally designed (dimerizing) pairs for positive data and randomly paired binders as negative data (see Methods for details). The RNN consists of a shared GRU layer, a dropout layer, and two fully-connected layers applied to the concatenated GRU output vectors. The final output (sigmoid activation) is treated as the Bind / No Bind classification probability. (b) Supplemental benchmark of Gradient Saliency, Integrated Gradients and DeepSHAP, using only the positive-valued importance scores. Left: Prediction KL-divergence of scrambled sequences compared to original test set sequences when either replacing all but the top X% most important amino acid residues with random samples (inclusion) or, conversely, when replacing the top X% nucleotides with random samples and keeping the remaining sequence fixed (occlusion). Right: Mean ddG Difference for the top 8 most important residues according to each method, measured across the test set, and HBNet Average Precision based on each method's importance scores. (c) Supplemental comparison of different versions of the Scrambling Neural Network (see Methods for a full description of each version). Left: KL-divergence benchmark based on the predictor RNN. Right: Mean ddG Differences and HBNet Discovery Precisions. (d) Supplemental comparison of other methods that optimize similar objectives as the Scrambler (see Methods for a full description of each method). Left: KL-divergence benchmark based on the predictor RNN. Right: Mean ddG Differences and HBNet Discovery Precisions. (e) Supplemental comparison between Scrambling Neural Networks and Sufficient Input Subsets (SIS) with 'hot-deck' sampled masking (the number of samples used at each iteration is varied from 1 to 32; see Methods for details). Left: KL-divergence benchmark based on the predictor RNN, Mean ddG Differences and HBNet Discovery Precisions annotated on top of the bar chart. Right: Average number of predictor queries used to interpret a single input pattern (for the Scrambler, this is the amortized cost of training divided by the number of test patterns interpreted).

Extended Data Fig. 6.

Example attributions of a designed heterodimer binder pair, for a selection of benchmarked methods.

Extended Data Fig. 7.

(a) Four different Inclusion-PSSMs optimized to reconstruct the structural trRosetta prediction of a Sensor Histidine Kinase. Each PSSM is optimized for increasingly larger t_bits. The bottom sequence logo represents the Rosetta score function breakdown per residue (−REU). Spearman r ranged between 0.25 and 0.32 when comparing the absolute numbers of Rosetta energy values to the optimized importance scores. Shown is also the average structure prediction for 512 samples. (b) Inclusion-Scrambled PSSMs of the Hen Egg-white Lysozyme. The PSSM was re-optimized for three different target conservation bits. Spearman r ranged between 0.25 and 0.33 compared to the Rosetta score function. (c) Architecture for per-example scrambling of a single protein sequence according to the contact distributions predicted by trRosetta. Here, we do not use a Multiple Sequence Alignment (MSA), but instead pass the Gumbel-sampled sequence to the PSSM input and an all-zeros matrix to the DCA input. Total KL-divergence between trRosetta-predicted distributions (distance and angle-grams) of the original sequence and samples drawn from the scrambled PSSM is either minimized or maximized (inclusion or occlusion respectively). (d) Reference sequence and predicted contact distribution for a hairpin protein engineered by Activation Maximization. (e) Top: Inclusion-PSSM of the engineered hairpin protein, obtained after optimization with a highly conserved background distribution based on the MSA. Bottom: Inclusion-PSSM of the engineered hairpin protein with a less conserved background distribution (smoothed with pseudo counts).

Data Availability

The data analyzed in this study originated from several previous publications and data repositories:

For the MNIST prediction task (Fig. 2), the data is available at (https://keras.io/api/datasets/mnist/). For the polyadenylation prediction task (Fig. 3), the data from Bogard et al. (2019) [7] is available on Gene Expression Omnibus (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE113849). For the 5’ UTR prediction task (Fig. 4), the data from Sample et al. (2019) [10] is available on Gene Expression Omnibus (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE114002). For the protein-protein interaction prediction task (Fig. 5), the full data from Chen et al. (2019) [60] is available from the authors, upon request. The subset of sequences used in the benchmark comparisons are included in the Github repository (http://www.github.com/johli/scrambler). For the protein structure prediction task (Fig. 6), the de novo designed sequences from Anishchenko et al. (2020) [62] are available from the authors upon request.