Toward a clearer definition of selection bias when estimating causal effects

Abstract

Selection bias remains a subject of controversy. Existing definitions of selection bias are ambiguous. To improve communication and the conduct of epidemiologic research focused on estimating causal effects, we propose to unify the various existing definitions of selection bias in the literature by considering any bias away from the true causal effect in the referent population (the population prior to the selection process), due to selecting the sample from the referent population, as selection bias. Given this unified definition, selection bias can be further categorized into two broad types: type 1 selection bias due to restricting to one or more level(s) of a collider (or a descendant of a collider), and type 2 selection bias due to restricting to one or more level(s) of an effect measure modifier. To aid in explaining these two types – which can co-occur – we start by reviewing the concepts of the target population, the study sample, and the analytic sample. Then we illustrate both types of selection bias using causal diagrams. In addition, we explore the differences between these two types of selection bias, and describe methods to minimize selection bias. Finally, we use an example of “M-bias” to demonstrate the advantage of classifying selection bias into these two types.

Background

When estimating causal effects, selection bias remains a subject of controversy in epidemiology.¹ The definition of selection bias is not as clear as that of confounding or information bias. This controversy and ambiguity may stem from the fact that in the literature selection bias has sometimes been considered a threat to internal validity, while at other times it has been considered a threat to external validity.^2-4 To improve communication and the conduct of epidemiologic research focused on estimating causal effects, we propose a definition of selection bias with two types.

This paper is organized as follows. First, we review the concepts of the target population, the study sample and the analytic sample and provide a refined definition of selection bias. Next, we describe two types of selection bias: type 1 selection bias due to restricting to one or more level(s) of a collider (or a descendant of a collider), and type 2 selection bias due to restricting to one or more level(s) of an effect measure modifier. Then, we use an example to demonstrate the importance of classifying selection bias into these two types. Last, we describe the utility of defining selection bias as having two types and conclude with a brief discussion.

Before proceeding, it will be useful to state the following assumptions. First, we assume that causal consistency is satisfied.^5,6 That is, here we will not consider interference⁷ or multiple treatment versions⁶. For clarity and simplicity, hereafter we also assume no confounding of the exposure-outcome relationship, no measurement bias, and no random variability. For causal diagrams, we consider only four types of variables: binary exposure E, binary outcome D, selection S, and covariates L (e.g., L1, L2). Throughout, S=1 means selection into the sample. It should also be noted that, in terms of treatment effect heterogeneity related to type 2 selection bias, two terms are involved – effect measure modification and interaction. While there are differences between the meanings of these two terms⁸, hereafter we use effect measure modification to describe the scenario of effect heterogeneity. Finally, in this article, we focus on the risk difference and risk ratio to avoid issues of noncollapsibility.^9,10

Target Population, Study Sample and Analytic Sample

Unlike confounding and information bias, selection bias results from a change in the sample under study. Thus we need to define the populations that are involved in terms of selection bias: in our setting, the target population is the population that inference is to be made about; the study sample (sometimes called study population) is the complete population that is included in the study, and it is used to make inference about the target population and may or may not be representative of the target population; and the analytic sample is the observed portion of the study sample that is used for analysis. The relationships between the target population, the study sample, and the analytic sample are visualized in Figure 1. It should be noted that in the absence of confounding and measurement bias, the observed association (i.e., associational risk difference or risk ratio) between the exposure and the outcome in the analytic sample is typically used as the effect estimate. Further, it is conceptually straightforward to imagine an epidemiologic study involving several steps: first, identify a target population, then select the study sample from that target population, and then select the analytic sample from the study sample. Following Westreich et al.³, we define internal validity as the case when the effect estimated from the analytic sample is equal to the true causal effect in the study sample; and external validity as the case when the true causal effect in the study sample is equal to the true causal effect in the target population. Based on these definitions, external validity will be threatened by the degree to which the distribution of effect measure modifiers differs between the study sample and the target population.² Of note, here we focus on the target population from which the study sample was selected, and thus generalizability is of interest. However, broader definitions of the target population have been proposed.^11,12 For example, sometimes researchers want to transport the study results to a target population that is partially or completely non-overlapping with the study sample.¹¹ Transportability of study results is beyond the scope of this paper, we refer the reader to Westreich et al.¹¹ and Bareinboim and Pearl¹³. It is also worth noting that here we focus on the scenarios where membership in the target population is not dependent on exposure or other variables. We avoid complexities that may arise when target population membership does have determinants, since addressing these complexities is beyond the scope of the present work.^14-16

Figure 1:

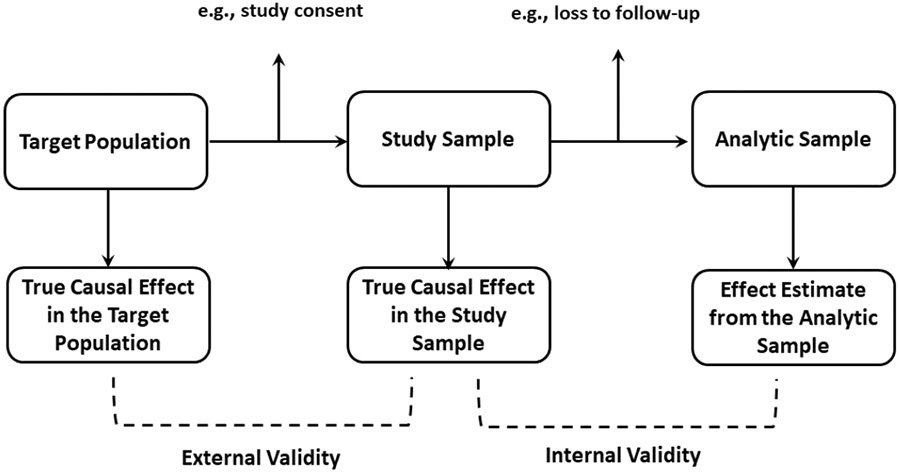
Relationships between target population, study sample, and analytic sample. Note that, in addition to selection bias, threats to internal validity also includes confounding and measurement bias.

To facilitate discussion, we further define the referent population as a population prior to the selection process, in contrast to the selected sample. Hence when selecting the study sample from the target population, the referent population is the target population; when selecting the analytic sample (as a whole or to be within specific stratum) from the study sample, then the referent population is the study sample.

Broadly, we propose to unify the various existing definitions of selection bias in the literature by considering any bias away from the true causal effect in the referent population, due to selecting the sample from the referent population, as selection bias. That is, selection bias is defined as the difference between the true causal effect in the referent population and the effect estimate in the selected sample. For example, consider the risk difference scale, and assume the true causal risk difference in the referent population is P(D^e=1 = 1) − P(D^e=0 = 1) and the true causal risk difference in the selected sample is P(D^e=1 = 1∣S = 1) − P(D^e=0 = 1∣S = 1). In the absence of confounding and measurement bias, the (observed) associational risk difference P(D = 1∣E = 1, S = 1) − P(D = 1∣E = 0, S = 1) in the selected sample is typically used as the effect estimate. Then selection bias can be expressed in notation as follows (see eAppendix I for detail):

$$[P(D^{e=1}=1)-P(D^{e=0}=1)]-[P(D=1\mid E=1,S=1)-P(D=1\mid E=0,S=1)]$$

Given this unified definition, selection bias can be further categorized into two broad types: type 1 selection bias, which is due to restricting to one or more level(s) of a collider (or a descendant of a collider), and type 2 selection bias, which is due to restricting to one or more level(s) of an effect measure modifier. That is to say, if the selection (S in the causal diagrams) is a collider or an effect measure modifier, restricting to one or more level(s) of the selection S (e.g., S=1) can lead to selection bias. Type 1 selection bias will result in a difference between the true causal effect in the selected sample and the effect estimate in the selected sample; type 2 selection bias will result in a difference between the true causal effect in the referent population and the true causal effect in the selected sample. Therefore, we can rewrite our above definition of selection bias in two parts:

$$\begin{gathered} [P(D^{e=1}=1)-P(D^{e=0}=1)]-[P(D=1\mid E=1,S=1)-P(D=1\mid E=0,S=1)] \\ =\underset{Type2selectionbias}{\underbrace{\{[P(D^{e=1}=1)-P(D^{e=0}=1)]-[P(D^{e=1}=1\mid S=1)-P(D^{e=0}=1\mid S=1)]\}}} \\ +\underset{Type1selectionbias}{\underbrace{\{[P(D^{e=1}=1\mid S=1)-P(D^{e=0}=1\mid S=1)]-[P(D=1\mid E=1,S=1)-P(D=1\mid E=0,S=1)]\}}} \end{gathered}$$

TYPE 1 SELECTION BIAS

Type 1 selection bias is selection bias due to restricting to one or more level(s) of a collider (or a descendant of a collider). Hernán et al¹⁷ and Cole et al¹⁸ have explained type 1 selection bias in detail. Type 1 selection bias is sometimes called collider stratification bias^17,19, and sometimes, more specifically, called collider restriction bias when restricting to one level of a collider.^20,21 Selection bias due to restricting to one level of a collider is a special case of collider stratification bias; here, we distinguish the two and chiefly address restriction. Briefly, type 1 selection bias arises if we restrict to one (or more) level(s) of a common effect of two causes, of which one is the exposure or a cause of the exposure, and the other is the outcome or a cause of the outcome.

The mechanism of type 1 selection bias is that restricting to one (or more) level(s) of a collider (or a descendant of a collider) opens a non-causal backdoor path between the exposure and the outcome. Here we provide some common examples of type 1 selection bias using causal diagrams (Figure 2).²² For instance, Figure 2 (a) is the typical example for Berkson’s bias.²³ In this example, restricting to one level of selection S induces a non-causal association between exposure E and outcome D through two paths. First, it creates a non-causal association between exposure E and outcome D by opening the path E→[S=1]←D.¹⁷ Second, given that there may exist another cause of outcome D (i.e., L1) that is not shown in the causal diagram explicitly (because L1 is not a confounder for E-D relationship; we can consider it a hidden variable or error term not shown in the causal diagram²⁴), then outcome D becomes a collider for exposure E and covariate L1 as in Figure 2 (a). Restricting to one level of a descendant of the collider D, which is S, induces another non-causal association between E and D by opening the backdoor path E-L1-D. Similarly, Figure 2 (b) shows an example of a case–control study. It suffers from type 1 selection bias by restricting to one level of a descendant of the collider D, leading to a biased effect estimate on both risk difference and risk ratio scales.^25,26 For the rules to identify sources of non-causal paths in the presence of hidden variables (i.e., error terms), we refer the reader to Daniel et al.²⁶ Figure 2 (c) is a typical example of type 1 selection bias by restricting to one level of a descendant of the collider L1. Figure 2 (d) is a common example of selection bias due to differential loss to follow-up.²⁷ It occurs when loss to follow-up is differential among exposure groups, and is also connected with the outcome by a common cause (i.e., L1). Figure 2 (e) is the M-bias example where S is a collider in relation to the covariates L1 and L2 that affects the exposure and the outcome, respectively.

Figure 2:

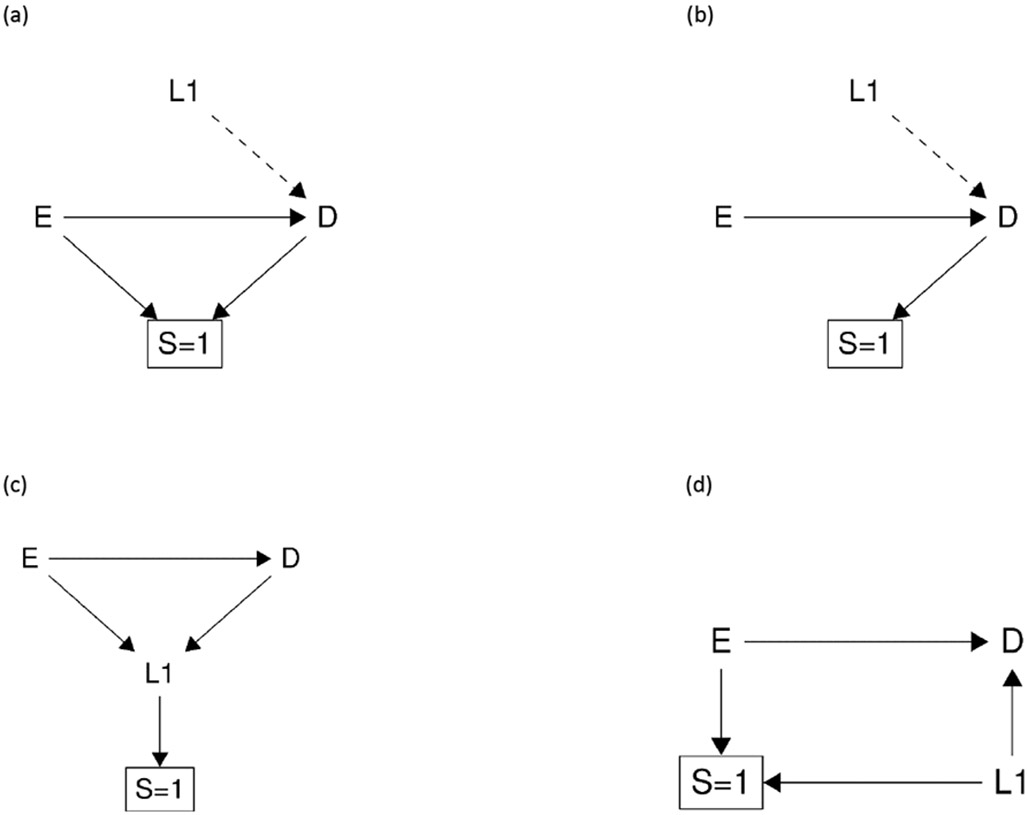
examples of type 1 selection bias. E is exposure, D is outcome, S is selection, L (i.e., L1, L2) are covariates. The dashed line indicates the potential hidden cause.

Type 1 selection bias can occur under the null hypothesis of no average causal effect or under the alternative (off-null) hypothesis, and even under the sharp null hypothesis of no causal effect for any individual. Importantly, restricting to one (or more) level(s) of a collider (or a descendant of a collider) as in type 1 selection bias can produce an association measure that is biased not only for the referent population, but also for the selected sample. That is, type 1 selection bias will result in a difference between the true causal effect in the selected sample and the effect estimated from the selected sample. However, if only type 1 selection bias occurs (in the absence of other biases such as type 2 selection bias), the true causal effect in the selected sample will be equal to the true causal effect in the referent population. Therefore, when type 1 selection bias occurs during the selection of the study sample from the target population, the true causal effect in the study sample will be equal to the true causal effect in the target population, and thus external validity is not affected. However, the effect estimated from the study sample (which is also the analytic sample if no further selection processes occur) will not be equal to the true causal effect in the study sample, or in the target population. When type 1 selection bias occurs during the selection of the analytic sample from the study sample, the effect estimated from the analytic sample will not be equal to the true causal effect in the study sample. Therefore, we say type 1 selection bias only affects internal validity. Details are provided in eAppendix I.

Type 1 selection bias can be further classified into two subtypes based on whether the causal effect in the referent population is identifiable or not. Type 1A selection bias can be addressed, and the true causal effect recovered by measuring and adjusting for covariates that lie on the non-causal path that is opened by restricting to one (or more) level(s) of a collider via inverse probability weighting, g-computation, and sometimes stratification.²⁸ For example, one can adjust for L1 in Figure 2 (d) and adjust for either L1 or L2 in Figure 2 (e) to correct type 1 selection bias.

In contrast, type 1B selection bias occurs when there are no measured covariates that lie on the non-causal path opened by restricting to one (or more) level(s) of a collider or a descendant of a collider (e.g., shown in Figure 2 (a) and (c)). Unlike type 1A selection bias, type 1B selection bias can generally not be addressed, and the causal effect in both the selected sample and the referent population is not identifiable unless the selection probability of each combination of exposure, covariates (if any) and outcome is known, which is typically unattainable in practice.²⁹ One important note is if the selection is outcome-dependent (that is, the selection is a descendant of the outcome, as for instance in case–control studies as shown in Figure 2 (b)) and the selection probability is unknown, the causal effect in the referent population is not generally identifiable on risk difference or risk ratio scales, but is identifiable for the odds ratio measure once the covariates that affect the exposure E and the selection S, if any, are adjusted for.^24,30,31 For those interested in the conditions and theorems to recover a causal effect under type 1 selection bias, we refer the reader to Bareinboim and colleagues.^24,32

TYPE 2 SELECTION BIAS

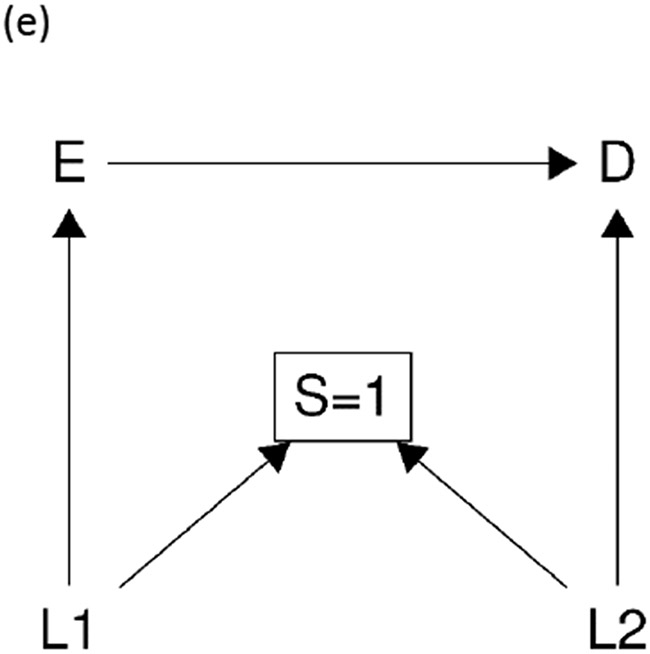
In 1977, Greenland gave an example of selection bias that was distinct from type 1 selection bias, which recently received attention.³³ First, we briefly review Greenland’s example: in the context of no confounding, the relative risk of disease comparing the exposed with the unexposed among those who were uncensored and remained over follow-up period (i.e., the analytic sample in this example) was a biased estimate for the causal risk ratio in the entire population of interest including both the censored and the uncensored (i.e., the study sample). But interestingly, the exposed and unexposed groups were equally likely to be lost to follow-up. How can this bias occur in the situation of the nondifferential loss to follow-up with regards to exposure status? Greenland explained that it is because the association between selection (i.e., censoring in this context) and the outcome varies across levels of the exposure.^10,33 In another way, it means that the association between the exposure and the outcome varies across levels of the selection (i.e., the censored and the uncensored in this context). More recently Hernán used causal diagrams, as shown in Figure 3 (a), to explain Greenland’s example graphically.³⁴ As in Figure 3 (a), even though there is no arrow from exposure E to selection S (in contrast to Figure 2 (d)), which indicates the absence of restricting to one (or more) level(s) of a collider, selection bias can still arise. The presence of selection bias is due to effect measure modification of selection, S, for the relationship between exposure E and outcome D. By restricting to only one level of the effect measure modifier (S=1) in this example, the observed effect of exposure E on outcome D in the analytic sample is not guaranteed to be equal to the causal effect in the study sample.

Figure 3:

two basic causal diagrams for type 2 selection bias. E is exposure, D is outcome, S is selection, L (i.e., L1, L2) is covariates.

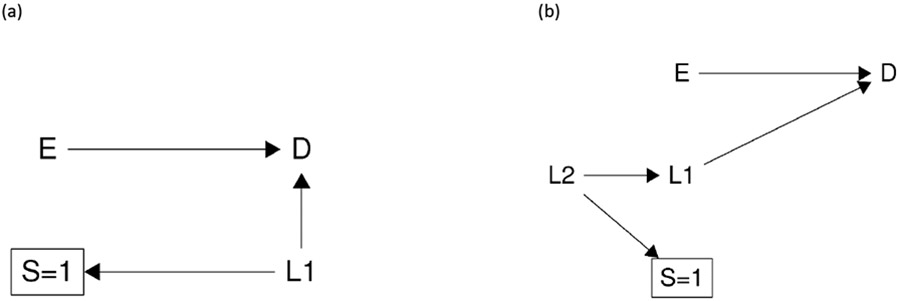
Greenland’s and Hernán’s explanations of selection bias without colliders^33,34 indeed leads us to another type of selection bias: type 2 selection bias due to restricting to one or more level(s) of an effect measure modifier. That is, when the selection S is an effect measure modifier, restricting to one or more level(s) of the selection S (e.g., S=1) can result in type 2 selection bias. To better understand type 2 selection bias, we need to review the structure of effect measure modification. VanderWeele and Robins³⁵ proposed four types of effect measure modification in causal diagrams (see eAppendix II Figure 1): direct effect measure modification, indirect effect measure modification, effect measure modification by proxy, and effect measure modification by common cause. Briefly, a direct cause of the outcome is potentially a direct effect measure modifier (i.e., X in eAppendix II Figure 1 (a)); a variable that causes a direct effect measure modifier is an indirect effect measure modifier (i.e., C in eAppendix II Figure 1 (b)); a downstream surrogate of a direct effect measure modifier is an effect measure modifier by proxy (i.e., R in eAppendix II Figure 1 (c)); and a variable that is connected with the direct effect measure modifier by a common cause is an effect measure modifier by common cause (i.e., M in eAppendix II Figure 1 (d)). If we assume that the effect measure modifier is the selection S, and that selection S can only be affected by other variables (rather than affect other variables), we obtain two subtypes of type 2 selection bias, as shown in Figure 3 (a) and (b). In Figure 3 (a), the selection S is an effect measure modifier by proxy when L1 is a direct effect measure modifier, and type 2 selection bias can occur by restricting to one or more level(s) of the effect measure modifier by proxy; in Figure 3 (b), the selection S is an effect measure modifier by common cause when L1 is a direct effect measure modifier, and type 2 selection bias occurs by restricting to one or more level(s) of the effect measure modifier by common cause. In Greenland’s example and elsewhere, the structural relationship between selection S and outcome D cannot usually be determined from the observed data, and thus either Figure 3 (a) or (b) or even a more complex diagram can be the source of the type 2 selection bias (see eAppendix III Figure 2 (a)).

Type 2 selection bias has several properties. First, as Hernán explained³⁴, type 2 selection bias cannot occur under the sharp null hypothesis, because no effect measure modification can exist if there is no causal effect of exposure E on outcome D for any individual. Second, type 2 selection bias is scale dependent (multiplicative vs. additive) since type 2 selection bias is dealing with restricting to one or more level(s) of an effect measure modifier.³⁶ Even if there is type 2 selection bias for the causal risk ratio in the referent population, there is no guarantee that type 2 selection bias for the causal risk difference occurs. But it is worth noting the certainty that, when the sharp causal null does not hold, there always exists a type 2 selection bias for either the additive (e.g., risk difference) or multiplicative (e.g., risk ratio) scale if the selection is not conditionally independent of the outcome D within levels of the exposure E.^3,37 Third, type 2 selection bias can produce an association measure that is biased only for the referent population, but not for the selected sample. That is, type 2 selection bias will result in a difference between the true causal effect in the referent population and the true causal effect in the selected sample, while the effect estimated from the selected sample will be equal to the true causal effect in the selected sample in the absence of other biases including type 1 selection bias. When selecting the study sample from the target population, type 2 selection bias is considered to affect external validity as the true causal effect in the study sample may not be equal to the true causal effect in the target population, and thus is often called generalizability bias.² When selecting the analytic sample from the study sample (e.g., loss to follow-up, withdrawal due to adverse effects, protocol deviation in per-protocol analyses^38,39, or other missing data scenarios), type 2 selection bias is considered to affect internal validity as the effect estimated from the analytic sample may not be equal to the true causal effect in the study sample. Details are provided in eAppendix I. Last, it should be noted that, if there is no type 2 selection bias that occurs during selection, the true causal effect in the selected sample should be equal to the true causal effect in the referent population, even in the presence of type 1 selection bias.

Type 2 selection bias can be minimized or even eliminated either during the design or analytic stage. Addressing type 2 selection bias during the analytic stage is possible if one can accurately measure and properly adjust for a sufficient set of covariates (e.g., L) that affect selection S and outcome D in order to achieve d-separation between the selection and the outcome.⁴⁰ Such adjustment is analogous to the classic scenario of adjusting for a sufficient set of confounders to achieve conditional exchangeability and obtain an unbiased causal effect estimate of exposure on the outcome.² For example, one could adjust for L1 in Figure 3 (a) and adjust for either L1 or L2 in Figure 3 (b) to address type 2 selection bias and recover the causal effect in the referent population. Technically, once the full distribution of covariates that affect the selection and the outcome are known, g-computation⁴¹, inverse probability (or odds) weighting (IPW)^38,42 or augmented IPW^43,44 can be employed to adjust for the covariates, and thus account for type 2 selection bias and recover the unconditional causal effect in the referent population under certain assumptions^2,41 (i.e., causal consistency^5,6 [no interference⁷ and treatment version irrelevance⁶], positivity^45,46, no measurement error, and correct model specification). For those interested in details of identification and estimation of causal effects in the referent population in the presence of type 2 selection bias, we refer the reader to Lesko et al² and Dahabreh et al⁴⁴.

AN ILLUSTRATIVE EXAMPLE: M-BIAS

Sometimes both type 1 selection bias and type 2 selection bias occur together in an epidemiologic study. That is, the selection node can act as both a collider and an effect measure modifier simultaneously. We use the “M-bias” diagram to further illustrate this point.¹⁹ M-bias is a bias caused by conditioning on a common effect of two causes, of which one is a cause of the exposure, and the other is a cause of the outcome, resulting in a so-called M-structure in its causal diagram. An example of M-bias is volunteer bias where the individuals’ characteristics affect their exposures and outcomes, and influence their decisions to participate in the study. As shown in Figure 4 (same as Figure 2 (e)) as a standard M-bias diagram, the selection S is driven only by the covariates L1 and L2 which are causes of exposure E and outcome D, respectively, but neither of which is a confounder for the exposure-outcome relationship. Hence the selection S is a collider, and restricting to one level of S (S=1) induces a non-causal association between exposure E and outcome D. This implies that we must adjust for either L1 or L2 to explain away the non-causal association induced by type 1 selection bias and recover the causal effect in the referent population. One might think that adjusting for either one will work because either adjustment will block the non-causal path E←L1→[S=1]←L2→D that is opened by restricting to one level of a collider due to selection. However, this perception is incorrect. In fact, it is critical to measure and adjust for covariate L2 rather than L1²⁶, because oftentimes selection S is not only a collider but also an effect measure modifier by proxy as it is connected with a potential direct effect measure modifier L2. Measurement and adjustment of L1 instead of L2 may not remove type 2 selection bias. As previously mentioned, when the sharp null does not hold, if risk of the outcome changes across strata of L2, L2 must be an effect measure modifier of the relationship between E and D on either the risk difference or risk ratio scale, and therefore, there must exist type 2 selection bias for one scale (or both). Even though adjusting for either L1 or L2 enables us to address type 1 selection bias and recover the causal effect in the selected sample, we must accurately measure and properly adjust for L2 to account for type 2 selection bias to recover the causal effect in the referent population using one of the previously described approaches to addressing selection bias in the analytic stage. Specifically, the average potential outcome in the referent population can be identified from the observed data because

$$E(D^e)=\sum _{L2}E(D\mid E=e,L2=l2,S=1)P(L2=l2)$$

Figure 4:

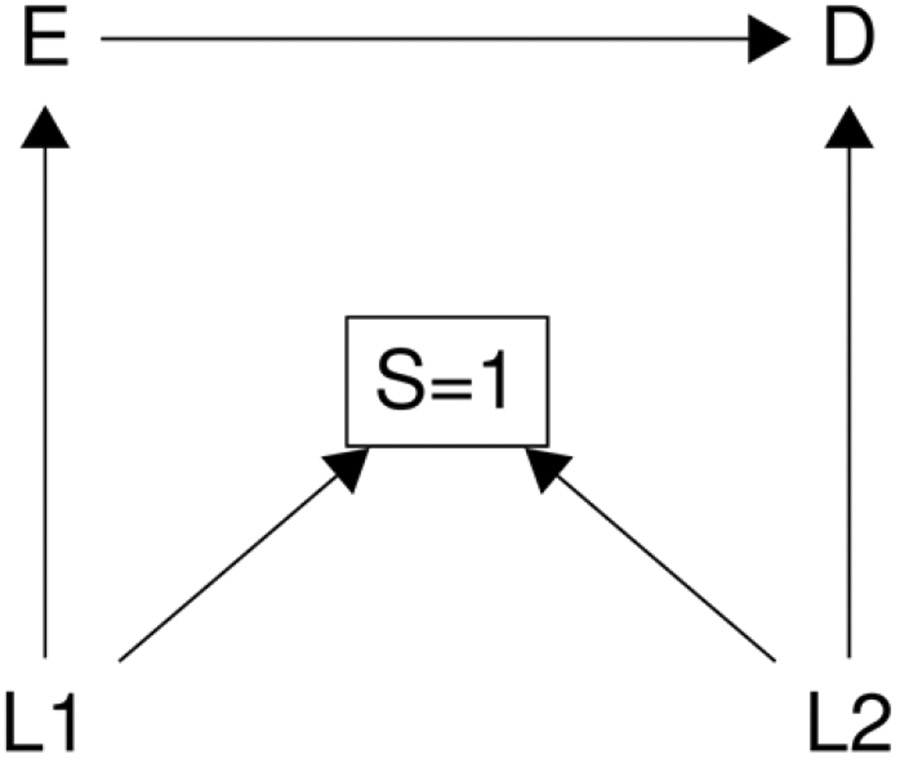
A typical example of “M-bias”. E is exposure, D is outcome, S is selection, L (i.e., L1, L2) is covariates.

A proof of this equivalence as well as code for a simulation of 1,000,000 individuals is given in eAppendix IV.

Similarly, in Figure 2 (d), the selection S acts as both a collider and an effect measure modifier when the covariate L1 is a direct effect measure modifier. In such cases, both type 1 and type 2 selection bias can arise. Fortunately, one can eliminate both biases if the distribution of L1 in the referent population is measured and accounted for.

DISCUSSION

The term “selection bias” is widely used in epidemiologic studies, but the distinction between different types of selection bias is usually not articulated. Varying use of the term by epidemiologists and others generates further confusion and impedes communication among medical researchers.⁴⁷ Here, using causal diagrams, we illustrate the two types of selection bias that can hinder accurate estimation of causal effects: type 1 selection bias due to restricting to one or more level(s) of a collider (or a descendant of a collider), and type 2 selection bias due to restricting to one or more level(s) of an effect measure modifier. That is, when the selection (S in the causal diagrams) is a collider or an effect measure modifier, restricting to one or more level(s) of the selection (e.g., S=1) can result in selection bias. This taxonomy may help improve the understanding, communication, and teaching of selection bias among epidemiologists and other health researchers.

A summary and comparisons of type 1 and type 2 selection bias are described in the Table. When estimating causal effects, type 1 selection bias, which is due to restricting to one or more level(s) of a collider (or a descendant of a collider), is the classic selection bias we often encounter in epidemiologic literature.^17,18,28,47 It is often called collider stratification bias or collider restriction bias,^17,19,20 and can produce bias under the sharp null. Type 1 selection bias can be difficult to minimize analytically, especially when selection is the direct common effect of both the exposure and the outcome, or selection is dependent on the outcome and causal effects on risk difference or risk ratio scale are desired (i.e., type 1B selection bias).²⁴ But when selection is affected by a measured cause of the exposure or by a measured cause of an outcome and selection is not a descendant of the outcome (i.e., type 1A selection bias), analytically adjusting for type 1 selection bias is possible.

Table:

Summary of type 1 and type 2 selection bias

Selection bias	Type 1	Type 2
Definition	Restricting to one or more level(s) of a collider (or a descendant of a collider)	Restricting to one or more level(s) of an effect measure modifier
Other names	Collider stratification bias; collider restriction bias	generalizability bias
Can occur on sharp null?	Yes	No
Bias in the referent population?	Yes	Yes
Bias in the selected sample?	Yes	No
Can affect internal validity?	Yes	Yes
Can affect external validity?	No	Yes
Effect measure scale dependent?	No	Yes

Here we make a distinction between collider restriction bias and collider stratification bias. While collider restriction bias is the bias introduced by restricting to one level of a collider, collider stratification bias is broadly defined as the bias introduced by conditioning on the collider.¹⁷ This includes not only bias due to restricting on a collider, but also bias introduced through (for example) the unnecessary inclusion of a collider in a regression model (analogous to restricting to more than one level of a collider¹⁷). Some consider collider stratification bias as a form of selection bias even in the absence of one-level restriction^17,28,29; others consider only collider restriction bias to be a selection bias and collider stratification bias by restricting to more levels of a collider as a form of overadjustment bias,²¹ in the sense that the inclusion of a collider in a regression does not change the overall sample under study or analysis despite the fact that including a collider in a regression does restrict estimation to be within strata of the collider.

Type 2 selection bias, which results from restricting to one or more level(s) of an effect measure modifier, is likely ubiquitous and underappreciated in epidemiologic studies.⁴⁸ More attention should be paid to type 2 selection bias and effect heterogeneity for several reasons. First, let us consider the scenario in which type 2 selection bias affects external validity when selecting the study sample from the target population. In both randomized trials and observational studies, it is rarely the case that the study sample is randomly selected from the target population, due in part to informed consent. Thus, we cannot assume that the effect in the study sample is the same as the effect in the target population in epidemiologic studies. Further, the conventional hierarchy in which internal validity, as previously defined, is given priority and external validity is considered secondary in clinical research is also problematic and misleading. Both internal and external validity are essential ingredients for achieving target validity (i.e., “a joint measure of the validity of an effect estimate with respect to a specific-population of interest (target population)”).³ A lack of either internal or external validity leads to bias with regards to the target population. Work by Breskin et al. demonstrates that the relative strength of the exchangeability assumptions for internal and external validity generally depend on the proportion of the target population that is selected into the study.⁴⁹ Establishing external validity does not necessarily require stronger assumptions than does internal validity. Last, as aforementioned, type 2 selection bias can affect internal validity as well, when selecting the analytical sample from the study sample (e.g., loss to follow-up or other missing data). Thus, one still needs to take type 2 selection bias into account when addressing the threats to internal validity. Fortunately, type 2 selection bias might be minimized if all effect measure modifiers that affect selection are measured.

Some caveats should be noted. First, the examples we illustrated are simple. Throughout the paper, we assume no confounding. However, the examples can be extended to include confounding bias as shown in eAppendix III Figure 2 (b) and (c). For instance, eAppendix III Figure 2 (b) provides an example of a special type 2 selection bias through exposure when the confounder L also acts as an effect measure modifier.⁵⁰ Further, caution should be taken when confounding is present, since simultaneously adjusting for confounding and adjusting for type 1 and type 2 selection bias may induce new collider bias. Second, here we only focus on causal effects measured on the risk difference and risk ratio scales. Some of our conclusions may not apply to other commonly used effect measures, for example the odds ratio due to its unique invariance property.⁵¹ Third, while we describe the two types of selection bias, we do not quantitively compare (on different scales) the relative magnitude of type 1 and type 2 selection bias . Future work is needed to explore this issue in different scenarios. Last, here we only considered the case where membership in the target population is not dependent on the exposure or other variables. Sometimes when membership in the target population depends on the exposure or other variables, complexities arise, which are beyond the scope of the present work.^14-16

To conclude, in this work, we present a refined definition for selection bias with two types: type 1 selection bias is due to restricting to one or more level(s) of a collider (or a descendant of a collider), and type 2 selection bias is due to restricting to one or more level(s) of an effect measure modifier. This classification aims to facilitate understanding and communication, and thereby improve epidemiologic research.