Abstract
The origin of major volatiles nitrogen, carbon, hydrogen, and sulfur in planets is critical for understanding planetary accretion, differentiation, and habitability. However, the detailed process for the origin of Earth’s major volatiles remains unresolved. Nitrogen shows large isotopic fractionations among geochemical and cosmochemical reservoirs, which could be used to place tight constraints on Earth’s volatile accretion process. Here we experimentally determine N-partitioning and -isotopic fractionation between planetary cores and silicate mantles. We show that the core/mantle N-isotopic fractionation factors, ranging from −4‰ to +10‰, are strongly controlled by oxygen fugacity, and the core/mantle N-partitioning is a multi-function of oxygen fugacity, temperature, pressure, and compositions of the core and mantle. After applying N-partitioning and -isotopic fractionation in a planetary accretion and core–mantle differentiation model, we find that the N-budget and -isotopic composition of Earth’s crust plus atmosphere, silicate mantle, and the mantle source of oceanic island basalts are best explained by Earth’s early accretion of enstatite chondrite-like impactors, followed by accretion of increasingly oxidized impactors and minimal CI chondrite-like materials before and during the Moon-forming giant impact. Such a heterogeneous accretion process can also explain the carbon–hydrogen–sulfur budget in the bulk silicate Earth. The Earth may thus have acquired its major volatile inventory heterogeneously during the main accretion phase.
Subject terms: Geochemistry, Core processes
How and when Earth acquired its major volatiles N-C-H-S remains unclear. Here the authors show that Earth may have acquired its major volatiles from both reduced and oxidized impactors before and during the Moon-forming giant impact.
Introduction
Both dynamic models1,2 and observational evidence3,4 indicate delivery of volatiles by volatile-rich asteroids to the inner solar system; however, the mechanism for the accretion of Earth’s major volatiles (N–C–H–S) remains unresolved5–8. Some argued that Earth accreted its volatiles from carbonaceous chondrite (CI type)-like materials in the form of undifferentiated “late veneer” after core-formation ceased9,10, as evidenced by the CI chondrite-like S, Se, and Te ratios, and Se isotopes, in the bulk silicate Earth (BSE)11,12. However, some argued that Earth accreted its volatiles from oxidized chondritic materials at its full or late accretion stages, in which volatiles participated in Earth’s core-formation in the magma ocean2,13–16. Some models also proposed that Earth acquired its volatiles from a single giant impactor, such as the Moon-forming impactor17–19. Although some7,16–18 of these previous models have attempted to explain the major volatile budget and ratios in the BSE, it remains unknown whether such models are consistent with the observed isotopes of major volatiles in the BSE.
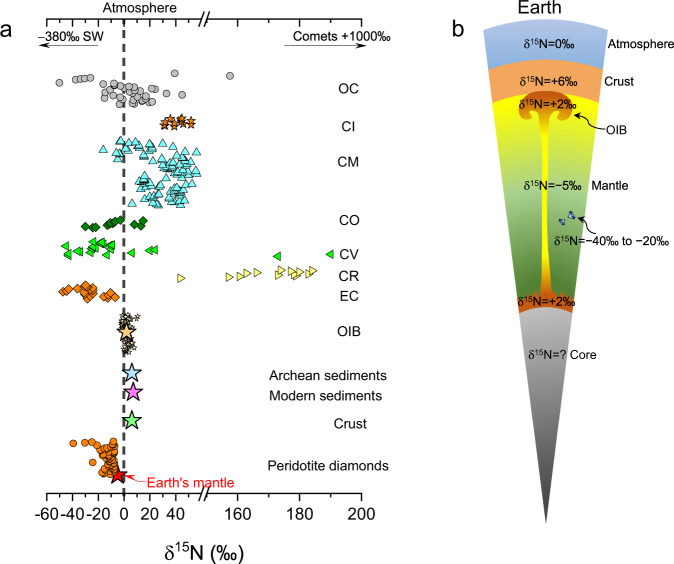
The N-isotopes (14N and 15N) are excellent proxies in tracing the sources of volatiles accreted to the terrestrial planets4,5,20,21 due to their large fractionations among geochemical and cosmochemical reservoirs as summarized in Fig. 1. The δ15N values of Earth’s mantle (δ15N = [(15N/14N)sample/(15N/14N)standard – 1)] × 1000, where the standard is the atmospheric N2), inferred from fibrous diamonds and mid-ocean ridge basalts, are mainly between −10‰ and 0‰ and converge towards a globally uniform value of −5‰ (ref. 22). More negative δ15N values down to −20‰ and −40‰ were observed in diamonds from Earth’s deep mantle, which were interpreted to be relict primordial N and used to argue for an enstatite chondrite (EC)-origin of Earth’s N23–25, because the EC δ15N are −45‰ to −15‰ (ref. 26). The average δ15N of Earth’s surface (crust + atmosphere) is approximately +3‰ (refs. 22,27), and the δ15N imbalance between Earth’s mantle and surface forms a long-standing unresolved puzzle22. The δ15N of oceanic island basalts (OIB) are overall positive (−2‰ to +6‰), which was usually interpreted as resulting from recycled sediments in the OIB mantle source28,29. However, such positive δ15N are more likely primordial features because of the inefficiency of deep N-subduction30. Most diamond populations of Archean ages also define a mantle δ15N of −5‰ (ref. 31); accordingly, the N-isotopic signature of Earth’s different reservoirs may have been established before Archean.
Fig. 1. The N-isotopic composition (δ15N) of cosmochemical and geochemical reservoirs.
a, b Earth’s mantle δ15N, inferred from fibrous diamonds and mid-ocean ridge basalts, converges towards a globally uniform value of −5‰; however, in some mantle peridotite diamonds, the δ15N are as low as −40‰, which are comparable to EC δ15N. The positive OIB δ15N are regarded to be primordial features of Earth’s deep mantle30. Earth’s sediments and crust also show positive δ15N. Solar wind (SW) and comets show extremely negative and positive δ15N, respectively. Note that Earth’s atmosphere δ15N is zero. All δ15N data were taken from references compiled in Supplementary Note 1.
The protosolar nebula (PSN) has δ15N as low as −380‰, while comets have δ15N up to +1000‰ (Fig. 1). Both cannot be a substantial source of Earth’s volatiles4,5, in light of Earth’s mantle δ15N of −5‰. The CI and CM chondrite-like materials, which are likely partial sources of Earth’s water4,5, have average δ15N of +42 to +175‰ (ref. 4). These δ15N also exclude CI and CM chondrite-like materials as Earth’s solo N-source. An EC-origin of Earth’s N is essentially consistent with the observation that the BSE and ECs have largely identical isotopic compositions for O, Ca, Ti, Cr, Ni, Mo, and Ru32,33. However, if EC-like materials are Earth’s main N-source, it remains unclear how Earth’s N-isotopes have evolved from initial EC δ15N to the present-day observations (Fig. 1). The addition of CI chondritic late veneer to the proto-Earth has long been proposed34 to cause an increment of Earth’s mantle δ15N to −5‰, but Earth’s mantle Ru-isotopes rule out an outer solar system origin of the late veneer32,33. The non-chondritic relative volatile abundance in the BSE5,6 is also against the late veneer as an important source of Earth’s major volatiles. Two recent studies emphasized that Earth’s mantle δ15N could have been achieved from EC-like materials through Earth’s core–mantle segregation and preferential partitioning of 14N into Earth’s core35,36. If correct, the Earth must have acquired its N and other major volatiles from EC-like materials, rather than from volatile-rich CI or CM chondrite-like materials.
Here we report experimental determinations of N-partitioning and -isotopic fractionation between Fe-rich metallic and silicate melts. Using the newly measured N-partitioning and -isotopic fractionation, we demonstrate that core-formation cannot cause significant core/mantle N-isotopic fractionation, but Earth’s heterogeneous accretion of volatiles before the cessation of core-formation can explain the N-budget and -isotopic composition of Earth’s different reservoirs, which places tight constraints on the accretion process of Earth’s major volatiles.
Results and discussion
Metal/silicate N-partitioning
The experiments were performed at 1700–2200 °C, 1–8 GPa, and oxygen fugacity (fO2) of 0.3–4.7 log units below the iron-wüstite (IW) buffer to determine N-partitioning and -isotopic fractionation between Fe-rich metallic and silicate melts ( and ∆15 Nmetal-silicate), using piston cylinder and multi-anvil devices (Supplementary Data 1, 2 and Methods). The silicate melt NBO/T (the ratio of non-bridging oxygens to tetrahedral cations) was 0.2–3.1. The Fe-rich metallic melts contained 87.0–98.8 wt.% Fe and up to 6.8 wt.% Si, 1.8 wt.% S, and 11.5 wt.% C. The N-content and δ15N of quenched samples (Supplementary Fig. 1) were quantified by using a modified noble gas mass spectrometry (Methods). The metallic and silicate melts contained 43–6390 ppm and 44–1590 ppm N (by weight), respectively (Supplementary Data 3, 4). In two N2-saturated experiments (LY24 and LY25; Supplementary Data 2), the metallic melts contained ~1.1 and 1.4 wt.% N, respectively, which are comparable to previously determined N-solubility values37. Raman spectroscopy measured N–C–H–O species in the quenched silicate melts at fO2 of ~IW−0.5 included OH−, CH4/CH, N2, NH3/NH, and/or H2 (Supplementary Fig. 2), consistent with the previous measurements36,38,39.
The calculated varied from 0.03 to 78 (Fig. 2), which are mainly controlled by fO2 as recognized previously35,36,40,41. Note that the present were determined by using ppm level N in the samples, differing from previous studies (Fig. 2) that added wt.% level N in the samples to measure N by using electron microprobe. The change of N-species in silicate melt as a function of fO2 has been proposed to explain the –fO2 correlation35,36,40. In oxidized silicate melt (fO2 > IW), N dissolves physically and mainly as N2; however, the other N-species such as CN-, NH3 and/or N3- dissolve chemically in reduced silicate melt and become dominant at fO2 <IW–2 (refs. 38,39). Therefore, decrease with decreasing fO2 under otherwise equivalent conditions. In addition to fO2, other parameters such as P–T and the compositions of metallic and silicate melts also affect (refs. 40–43). Using the present and previous (Fig. 2) and the multiple linear regression approach, we derived a comprehensive equation to describe :
| 1 |
where T is temperature in K, P is pressure in GPa, ΔIW denotes fO2 relative to the IW buffer, and is the mole fraction of element i in the metallic melt. The experimental data cover pressures from 0.85 to 26 GPa, temperatures from 1523 to 3400 K, silicate melt NBO/T from 0.02 to 3.12, and fO2 from IW–0.1 to IW–5.9 (n = 241). The agreement within 0.5 log units between the experimentally determined and the predicted values using Eq. (1) indicates the consistence of our new and previous data, including those obtained under C-undersaturated conditions (Supplementary Fig. 3). Equation (1) indicates that increasing pressure or NBO/T would increase , but increasing temperature or the light element content in metallic melt would decrease .
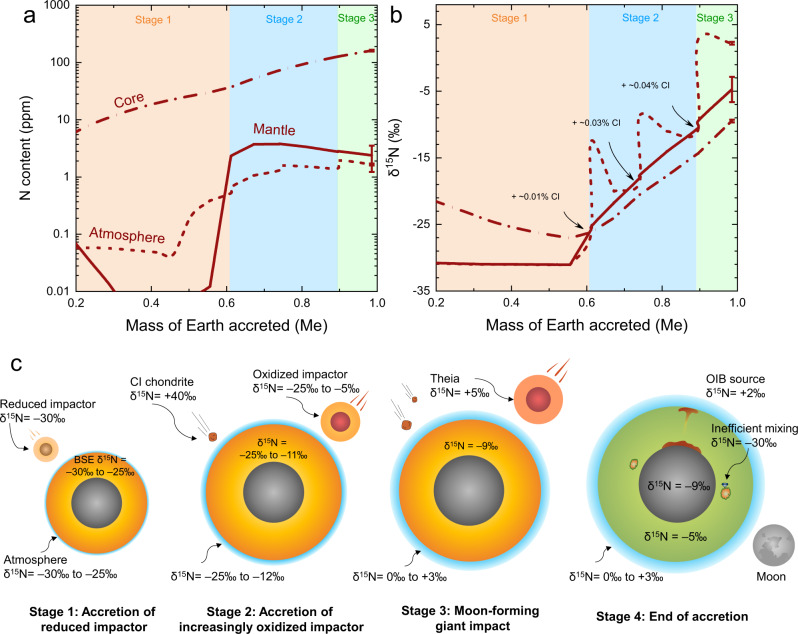
Fig. 2. Metal/silicate N partition coefficients (DNmetal/silicate) as a function of oxygen fugacity.
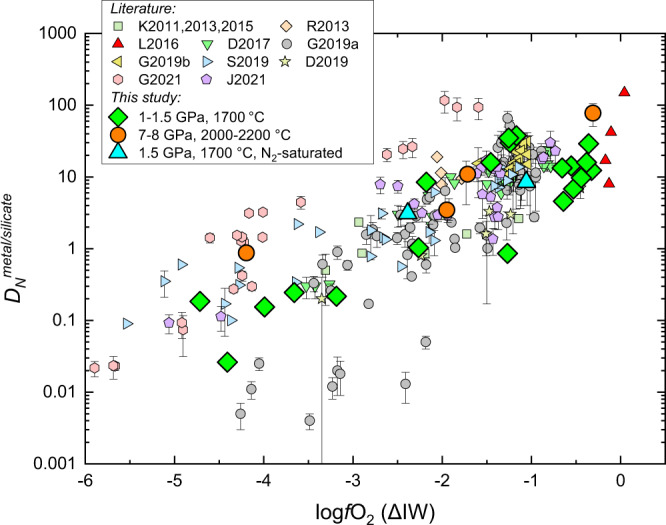
All data were obtained under largely variable conditions (P = 0.85–26 GPa; T = 1523–3400 K; NBO/T = 0.02–3.1; and fO2 = IW–0.1 to IW–5.5) and were taken from K2011, 2013, 2015 (refs. 64,92,93), R2013 (ref. 94), L2016 (ref. 35), D2017 (ref. 95), G2019a (ref. 40), G2019b (ref. 18), S2019 (ref. 41), D2019 (ref. 36), G2021 (ref. 42), and J2021 (ref. 43). The are dominantly controlled by fO2, and the scatter of at a given fO2 is caused by the variation of other parameters, such as P–T and the compositions of metallic and silicate melts as summarized in Eq. (1). Note that all literature fO2 values were recalculated by using the approach described in Methods. Source data are provided in Supplementary Data 2.
Metal/silicate N-isotopic fractionation
The metallic melt δ15N (δ15Nmetal) increase from −7.0‰ to +7.6‰ with decreasing fO2, while the silicate melt δ15N (δ15Nsilicate) decrease from +0.42‰ to −7.0‰ with decreasing fO2 (Fig. 3a, b). The calculated metal/silicate N-isotopic fractionation factor ∆15 Nmetal-silicate, which equals δ15Nmetal − δ15Nsilicate, increases from −4‰ to +10.4‰ with decreasing fO2 (Fig. 3c). The fO2 is the primary factor responsible for the ∆15 Nmetal-silicate variation. However, the fO2 is weakly correlated with the content of Ni, Si, and S in metallic melt, which also shows a weak correlation with the metallic melt δ15N (Supplementary Fig. 4). Therefore, light elements and Ni in metallic melt might play a non-negligible role in affecting ∆15 Nmetal-silicate. Figure 3d shows that ∆15 Nmetal-silicate and are also correlated. The negative correlations between ∆15 Nmetal-silicate and fO2 (Fig. 3c), and between ∆15 Nmetal-silicate and (Fig. 3d), indicate that the ∆15 Nmetal-silicate variation can also be explained by the change of N-species in silicate melt as a function of fO2. The negative ∆15 Nmetal-silicate at fO2 > IW−2 could be caused by the much stronger triple bond of N2 in silicate melt than the Fe–N bond in metallic melt, because heavy isotopes tend to be concentrated in species with strong bonds44. In contrast, the positive ∆15 Nmetal-silicate at fO2 <IW−2 could reflect a stiffer Fe–N and/or Si–N bond in metallic melt than the N–H or N3-–cation bond in silicate melt. Available data45,46 show that in gasses and solids at 0–25 °C, the relative bond energy is N≡N (945 kJ/mol) >Si–N (470 kJ/mol) >Fe–N (398 kJ/mol) >N–H (390 kJ/mol), which supports our explanations for the ∆15 Nmetal-silicate variation. However, the relative bond energy of Fe–N and Si–N in metallic melt and N–H and N3-–cation in silicate melt at the present experimental P–T conditions cannot be evaluated because of the lack of relevant data.
Fig. 3. The N-isotopic composition (δ15N) of the metallic and silicate melts and metal/silicate N-isotopic fractionation (∆15Nmetal-silicate).
a The δ15N of metallic melt increase with decreasing fO2. b The δ15N of silicate melt generally decrease with decreasing fO2. c The ∆15 Nmetal-silicate of this study and Li et al.35 are consistent and mainly controlled by fO2. In the study of Dalou et al.36, ∆15 Nmetal-silicate vary from −49‰ to −257‰ (the gray-filled blue stars and right-hand blue Y axis). The large N-isotopic fractionations observed in Dalou et al.36 could be caused by significant N-loss in their experiments as shown in Supplementary Fig. 5. d The ∆15 Nmetal-silicate and obtained in this study and Li et al.35 are negatively correlated. More explanations for these data are given in “Methods”. Source data are provided in Supplementary Data 2–4.
The present ∆15 Nmetal-silicate are consistent with the data of Li et al.35 at fO2 near the IW buffer, but in striking contrast to the results of Dalou et al.36, which show that ∆15 Nmetal-silicate decreases from −49‰ to −257‰ with fO2 decreasing from IW–0.5 to IW–3.1 at 1400 °C (Fig. 3c). The large contrast in ∆15 Nmetal-silicate between these two studies cannot be explained by the difference in experimental temperature or N-species in silicate melt. We note that in the experiments of Dalou et al.36, a large fraction of sample N was lost during the experiment, which may have caused kinetic N-isotopic fractionation, rather than equilibrium fractionation. The negative correlation between ∆15 Nmetal-silicate and the N-loss fraction, as observed for the experiments in Dalou et al.36 (Supplementary Fig. 5), supports this inference. Kinetic processes can cause significant light element isotopic fractionations even at high temperatures, for example, H-isotopic fractionations with δD variation up to 550‰ having been observed during hydration or dehydration of silicate glasses, melts, and nominally anhydrous minerals at 1000 °C (ref. 47).
The equilibrium mass-dependent isotopic fractionation between two phases is a function of 1/T2 (ref. 44). We tentatively fit our ∆15 Nmetal-silicate along with the data of ref. 35 as a multi-function of fO2, temperature (K), and all other parameters that potentially affect ∆15 Nmetal-silicate. We then obtained the following equation to best describe ∆15 Nmetal-silicate:
| 2 |
In Eq. (2), the light element and Ni content in metallic melt, pressure, and NBO/T are not included as variables, because our trial-and-error fitting yielded that their effects on ∆15 Nmetal-silicate are statistically negligible. The negligible effect of pressure on ∆15 Nmetal-silicate is consistent with theoretical calculations for carbon, which show that the pressure-dependence of C-isotopic fractionation between Fe-carbide and mantle phases at mantle temperatures is insignificant48. Equation (2) allows for calculating ∆15 Nmetal-silicate under T–fO2 conditions relevant for planetary core formation, and thus can be used to constrain N-isotopic fractionations between planetary cores and mantles.
N-partitioning and -isotopic fractionation during Earth’s accretion and core-formation
A multistage core-formation model49, which involves the Earth accreting through a series of violent collisions with differentiated impactors, has successfully reproduced Earth’s mantle major and some trace element compositions. The model was further refined by combining it with Grand Tack N-body accretion simulations15. In order to investigate N-partitioning and -isotopic fractionation between Earth’s core and mantle, we applied Eqs. (1) and (2) into the multistage model with inputs of the Grand Tack N-body simulation results (Methods). We first tested whether the Earth’s mantle could have obtained its present-day δ15N of −5‰ through core-formation alone, if the Earth accreted its 100% mass through the collisions of reduced, EC-like impactors with δ15N = −30‰. Supplementary Fig. 7 shows that core-formation alone cannot lead to Earth’s present-day mantle δ15N from an initial δ15N of −30‰, which contradicts previous arguments based on limited ∆15 Nmetal-silicate data35,36.
Following the success of the multistage model with inputs of the Grand Tack N-body simulation results, we modeled the N-behavior by considering that the Earth accreted its first 60% mass through the collisions of reduced, EC-like impactors, and its last 40% mass through the collisions of increasingly oxidized impactors. Reduced, EC-like impactors formed at heliocentric distances of <0.9–1.2 AU with δ15N = −30‰, while increasingly oxidized impactors originated from great heliocentric distances (1.2–3 AU). Since the solar system δ15N increases with the heliocentric distance4,20, the increasingly oxidized impactor δ15N should increase from −30‰ (EC’s value) to a slightly positive value at 3 AU. We used a δ15N value of +5‰ for the last impactor, which added Earth’s last 10% mass through the Moon-forming giant impact, and a δ15N of +5‰ represents the mixing of ECs (δ15N = −30‰) and CCs (δ15N = +40‰) with a same N content and mass ratio of ~1:1 as constrained by Mo isotopes for the Moon-forming giant impactor19. In the N-body simulations, after Earth accreted its 60% mass, a small mass of completely oxidized or CI chondrite-like materials, which contains ~1000 ppm N with δ15N = +40‰ and formed from beyond 6–7 AU, was delivered to Earth’s magma ocean50. No metal–silicate segregation occurred when CI chondrite-like materials added in the magma ocean, but the N in the silicate magma ocean participated in the subsequent core-formation events when metal-bearing impactors were accreted15. Large and oxidized impactors may hold more N than small and reduced ones, and the N is mainly stored in the cores42. In our model, we varied the bulk N-content from 50 ppm for small and reduced impactors to 150 ppm for large and oxidized impactors. We also considered the other factors that potentially affect the N-content and -isotopic composition of Earth’s different reservoirs, which include the formation of a proto-atmosphere, the equilibrium degree between the silicate magma ocean and the proto-atmosphere, catastrophic loss of the proto-atmosphere during each collisional accretion, and the light element composition of Earth’s core. Details for the setup of our model are given in “Methods”.
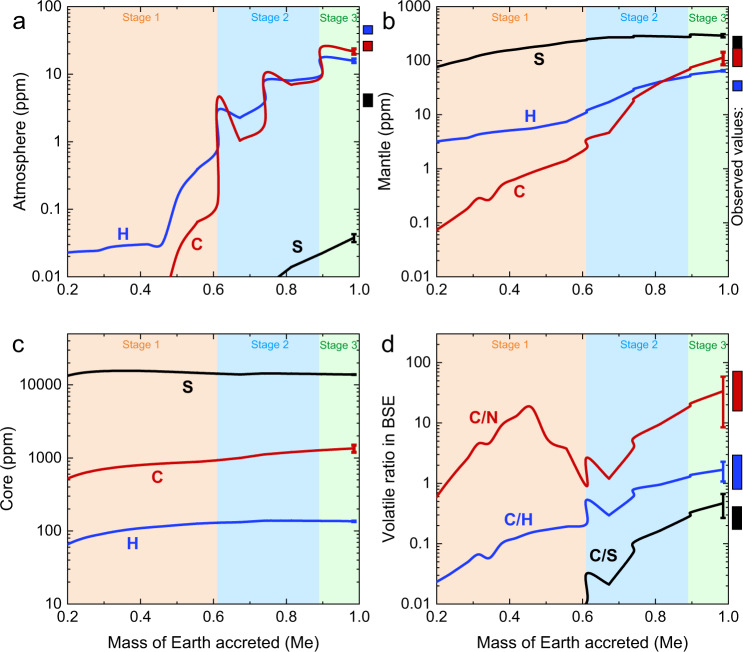
The model results are shown as a function of accretion mass fraction in Fig. 4a, b. At the end of Earth’s accretion, the N-content and δ15N of the proto-Earth’s mantle are ~2.4 ppm and about −4.7‰, respectively, both of which are consistent with the present-day mantle estimates of ~1–3 ppm5,6,8,51 and −5 ± 2‰ (ref. 22). The N-content of the proto-atmosphere is ~1.7 ppm (normalized to Earth’s mantle mass), i.e., ~1.7 times present-day atmospheric N-mass, which well matches the N-mass estimated for Earth’s early atmosphere52. In addition, the proto-atmosphere δ15N are 0‰ to +3‰, which are consistent with Earth’s surface reservoir δ15N (crust + atmosphere; Fig. 1). Although the totally added CI chondrite-like materials were only ~0.1% of Earth’s mass, they play a significant role in enhancing the proto-atmosphere δ15N to the values of 0‰ to +3‰ (Fig. 4b). This is because most N in the shallow magma ocean, sourced from CI chondrite-like materials, were released into the proto-atmosphere due to the rather low N-solubility in silicate melt under relatively oxidized conditions53.
Fig. 4. Earth’s heterogeneous accretion of nitrogen during its main accretion phase.
a, b The N-content and -isotopic composition of the proto-Earth’s core, mantle, and atmosphere as a function of mass fraction accreted. At the end of Earth’s accretion, the N-content and δ15N of the proto-Earth’s mantle are ~2.4 ppm and −4.7‰, respectively, consistent with previous estimates for the present-day mantle5,6,8. The N-content of the proto-Earth’s atmosphere is ~1.7 ppm, consistent with previous estimates for Earth’s early atmosphere52 (note that the ppm N in the atmosphere is based on the atmosphere N-mass normalized to the silicate Earth mass). The delivery of oxidized, CI chondrite-like materials plays an important role in enhancing the proto-atmosphere δ15N from −30‰ to 0‰–+3‰, which are close to Earth’s surface δ15N (atmosphere + crust; Fig. 1). Earth’s core contains more than 90% of Earth’s bulk N. The error bars at ~99% accretion were based on ±2σ for and ∆15 Nmetal-silicate. c Illustration showing the delivery of N to the proto-Earth by first reduced, EC-like impactors and then increasingly oxidized impactors. The Earth accreted its first 60% mass from EC-like planetesimals/embryos with δ15N of −30‰ (Stage-1). After acquiring its 60% mass, the Earth started to accrete from increasingly oxidized impactors which have δ15N varying from −30‰ to +5‰, and from minimal CI chondrite-like materials which have an average δ15N of +40‰ (Stages-2 and −3). As shown in Stage-4, inefficient mantle mixing of EC-like impactor materials may explain the negative δ15N of some deep mantle diamonds25, while a long-term preservation of oxidized impactor materials at Earth’s core–mantle boundary may explain the positive δ15N of OIB30.
We noticed that the largely negative δ15N features of some deep mantle diamonds (Fig. 1) could be primordial, representing the relicts of inhomogeneous mantle mixing of EC-like impactors, as suggested previously25. The positive δ15N features of OIB mantle source could also be primordial, representing a long-term preservation of materials from oxidized impactors, such as those from the Moon-forming giant impactor (Fig. 4c). Accordingly, our model can explain the observed N-content and δ15N of Earth’s different reservoirs (Fig. 4c). It is also worth noting that Earth’s core may contain ~160 ppm N (Fig. 4a), which accounts for more than 90% of Earth’s bulk N, and that Earth’s core may have δ15N close to −9‰ (Fig. 4b), more negative than those of Earth’s silicate reservoirs.
Our model demonstrates that the N-content and δ15N of Earth’s different reservoirs were determined by complex processes but happening naturally during Earth’s main accretion phase. We recognized that during Earth’s multistage accretion, the processes such as collision-induced catastrophic atmosphere loss and the degree of silicate magma ocean–atmosphere equilibrium remain loosely constrained; however, the target N-content and δ15N of Earth’s different reservoirs can still be obtained if the used parameters in our model were varied simultaneously (Supplementary Figs. 8–14 and “Methods”). We thus suggest that Earth established its N-inventories and -isotopic signatures through heterogeneous accretions of impactors formed at different heliocentric distances in the solar system.
Implications for the distribution and origin of Earth’s major volatiles
Figure 4 illustrates that Earth first acquired its N from EC-like impactors, and then acquired additional N from increasingly oxidized impactors and minimal CI chondrite-like materials before and during the Moon-forming giant impact. Similarly, the Earth could have also accreted its other major volatiles from these objects. Both ECs and CI chondrites contain significant amounts of H, C, and S4,54,55; therefore, H, C, and S may have also been delivered and participated in Earth’s core-formation during Earth’s main accretion phase. We applied our above “N-accretion model” (Fig. 4) to C–H–S to constrain the distribution and origin of C–H–S in Earth’s different reservoirs (“Methods” and Supplementary Data 5). Figure 5 shows that at the end of Earth’s accretion, the proto-atmosphere contains ~16 ppm H, ~22 ppm C, and negligible S; the proto-mantle contains ~65 ppm H, ~112 ppm C, and ~290 ppm S. After Earth’s accretion, the H2O in the proto-atmosphere would condensate to forming primitive oceans56 and the CO2 in the proto-atmosphere would deposit as carbonates in Earth’s surface (atmosphere + crust)57. Our model yields C-contents in the proto-atmosphere and proto-mantle consistent with the observed values in Earth’s present-day surface and mantle51. Nevertheless, our model yields lower H- and S-contents in the proto-atmosphere but higher H- and S-contents in the proto-mantle (Fig. 5a, b), compared to the estimates for Earth’s present-day surface and mantle51,58,59. However, the obtained C–S–H–N contents and C/H, C/S, and C/N ratios in the BSE are in good agreement with the estimates for the present-day BSE (Figs. 5d, 6). This implies a contribution of Earth’s mantle to surface in H and S through degassing after Earth’s accretion. In addition, our model results show that Earth’s core is a major reservoir for C–H–S (Fig. 5c), as in the case for N (Fig. 4a), which includes ~1300 ppm C, ~160 ppm H, and ~1.4 wt.% S, consistent with the estimates for Earth’s core60.
Fig. 5. Earth’s heterogeneous accretion of C–H–S during its main accretion phase.
a–c The C–H–S contents in proto-Earth’s atmosphere, mantle, and core as a function of mass fraction accreted. Note that the C–H–S contents in the proto-atmosphere is based on the proto-atmospheric C–H–S-mass normalized to the silicate Earth mass. d The C/N, C/H, and C/S ratios in the BSE (atmosphere + mantle) change as the mass of Earth accreted. The observed C and H contents in Earth’s present-day reservoirs were taken from ref. 51, and the S content in Earth’s present-day atmosphere and mantle were taken from ref. 59 and ref. 58, respectively. The error bars at ~99% accretion were based on ±2σ for the used metal/silicate partition coefficients. Note that the atmosphere in panel (a) represents Earth’s surface reservoir including atmosphere and crust, due to the condensation of water and deposit of CO2 from atmosphere to crust. Source data are provided in Supplementary Data 5.
Fig. 6. Comparison between our modeled volatile contents and the observed values in the bulk silicate Earth (BSE).
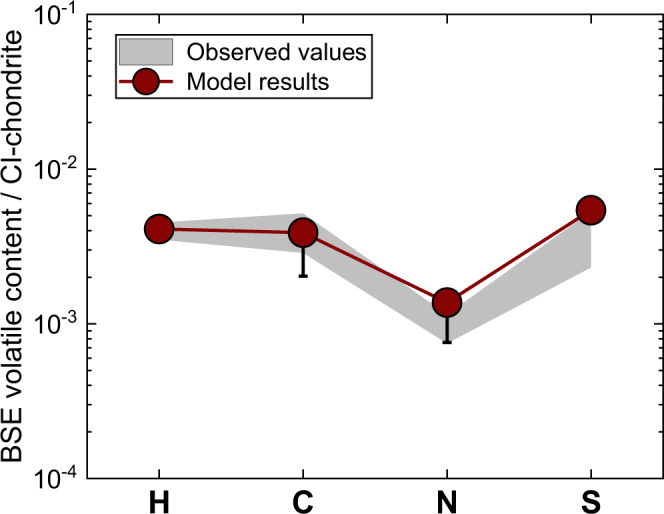
The observed C, N, and H contents in Earth’s present-day BSE were taken from ref. 51, and the S content in BSE were calculated based on refs. 58,59. Note that our modeled H–C–N–S contents are in good agreement with the observed values in the BSE, indicating that the Earth acquired its major volatile inventory through its heterogeneous accretion. Source data are provided in Supplementary Data 5.
We performed mass-balance calculations to constrain the contributions of different types of impactors to Earth’s major volatile budget. Our results (Supplementary Data 6) show that the firstly accreted EC-like impactors supply ~45%, ~72%, ~38%, and ~12% of Earth’s H, S, C, and N, respectively; the lately accreted increasingly oxidized impactors supply ~46%, ~28%, ~60%, and ~87%, respectively; whereas, the oxidized CI chondrite-like materials supply less than 10% of Earth’s major volatiles. The fraction of H (~45%) supplied by EC-like impactors in our model is lower than that (~70%) in a previous model54, which used a simple EC–CC mixing to explain the H-isotopic composition in the BSE. However, the disparity could be resolved by the lately accreted increasingly oxidized impactors, because they are composed of mixed EC and CC, as suggested by Mo isotopes19,61.
Conclusively, our results (Figs. 4–6) demonstrate that the Earth acquired its major volatiles from different cosmochemical reservoirs during its main accretion phase, rather than from a single giant impactor or at its late accretion stages. Combined contributions of reduced and oxidized impactors and minimal CI chondrite-like materials, formed at different heliocentric distances in the solar system, to Earth’s major volatile inventory agree with the observed geochemical and cosmochemical constraints5,19,21,32,54 and dynamic models of planetary formation2,15.
Methods
Starting materials
Starting materials included synthetic silicates and mixtures of metal Fe + Fe7N3 ± FeS ± Si powder. The first three silicates (refer to as G-1, G-2, and G-3) had major element compositions similar to those of mid-ocean ridge basalts (MORB), but the FeO in G-3 silicate was replaced by MgO and CaO (i.e., FeO-free). A fourth silicate (G-4) also had a basaltic composition but a large fraction of its MgO was replaced by FeO. A fifth silicate (G-5) had major element compositions similar to those of Earth’s mantle pyrolite. All silicates were prepared from analytical grade oxides and carbonates. To minimize absorbed water, SiO2, TiO2, Al2O3, and MgO powder were each fired over night at 1000 °C, MnO2 at 400 °C, CaCO3 at 200 °C, and Na2CO3 and K2CO3 at 110 °C. After drying, all these oxides and carbonates were first mixed and ground in ethanol in an agate mortar and dried at room temperature overnight. Well mixed powders were decarbonated at 1000 °C. Then the FeO powder, stored in a vacuumed oven at 100 °C, was added to the mixture and further ground in ethanol in an agate mortar, and then dried at room temperature overnight. G-1 to G-3 silicates were synthesized as glasses at 1600 °C and powdered before use. In addition, G-1 and G-2 silicate powders were reduced at 1000 °C and fO2 of FMQ–2 for 24 h using a CO–CO2 gas mixing furnace. G-4 and G-5 silicates were not synthesized as glass. The major element compositions of G-1 to G-5 silicates are provided in Supplementary Data 1. The Fe+Fe7N3±FeS±Si powder was prepared from high-purity Fe, Fe7N3, Si, and FeS powder, homogenized by grinding under ethanol in an agate mortar, and dried at room temperature. Nominally, Fe7N3 was the only N source in the sample. The bulk sample N-contents were prepared to be at 1000–2000 ppm, far below the N-solubility in Fe-rich metallic melt under P–T conditions adopted in this study37. For comparison, in two experiments LY24 and LY25, ~50 wt.% silicate and ~50 wt.% Fe7N3 were used to produce a large amount of N2 gas in the graphite capsules. In addition, different amounts of Mg(OH)2 were added in a few experiments to obtain hydrous conditions. All of the dried starting materials were stored in a vacuumed oven at 100 °C for >24 h before loading into graphite capsules, zirconia-lined Pt95Rh05 capsules, or graphite-lined Pt95Rh05 capsules for high-pressure experiments.
High-pressure experiments
All experiments at 1–1.5 GPa and 1700 °C were conducted in an end-loaded, solid media piston cylinder apparatus, using 0.5-inch diameter talc–Pyrex assemblies with stepped graphite heaters (Supplementary Data 2). For these experiments, starting materials of 30–50 wt.% metallic mixture and 50–70 wt.% silicate powder were loaded into zirconia-lined or graphite-lined Pt95Rh05 capsules. The use of zirconia-lined Pt95Rh05 capsules was to avoid the presence of C in the sample. The hot piston-in method was used to pressurize the assembly. Pressure was calibrated against the quartz–coesite and kyanite–sillimanite transitions, and a friction correction of 18% was applied to the nominal pressure. The pressure uncertainty is estimated to be better than 5% relative. We used W97Re03–W75Re25 thermocouples and temperature was controlled to ±2 °C and is accurate to ±10 °C. The experimental durations ranged from 1 to 3 h. All experiments were quenched to below 100 °C within 10–20 s by turning off electric power to the graphite heaters.
The experiments at 2000–2200 °C and 5–8 GPa were conducted in a 1000-ton DIA-type multi-anvil apparatus. The starting material was loaded into graphite capsules. Tungsten carbide (WC) anvils with 8-mm truncated edge lengths, together with a Cr2O3-doped MgO octahedron (14 mm edge length) as the pressure medium, were used to generate high pressures. The furnace is composed of a stepped cylindrical graphite or LaCrO3 heater and a ZrO2 thermal insulator. Sample pressures were estimated from the hydraulic pressure using calibrations based on the phase transitions of Bi, ZnS, and Mg2SiO4 polymorphs. Temperatures were measured using a W95Re05–W74Re26 thermocouple whose junction was located near the end of the graphite capsule. The cell assemblies were first pressurized to target pressures at room temperatures in 4 h and then heated to target temperatures at a rate of 100 °C/min. The temperature fluctuation during the experiments was approximately ±10 °C, and the experimental durations ranged from 20 to 40 mins. All experiments were quenched by switching off the electric power, and then decompressed to ambient pressure for more than 16 h.
All recovered sample capsules were sectioned longitudinally into two halves. One half was mounted in epoxy and polished for electron microprobe and Raman spectroscopy analysis, and the other half prepared for noble gas mass spectrometry analysis.
Electron microprobe analysis
Major element compositions of the quenched metallic and silicate melts were measured with a JEOL JXA–8200 microprobe. The analyses were performed in wavelength-dispersive mode, and a PAP matrix correction was applied to the raw data. The metallic melts were analyzed with 20 kV acceleration voltage and 20 nA beam current, whereas the silicate melts were analyzed with 15 kV/10 nA. Natural and synthetic standards were used to calibrate the instrument. For the metallic melt analysis, Fe, Si, Ni, and Cu were calibrated on pure metals, S was calibrated on a synthetic pyrrhotite with well-known Fe: S ratio, and O was calibrated on magnetite. For the analysis of C in metallic melt, the samples and standards were uncoated but surrounded with silver-bearing conductive varnish to avoid charging, and Fe3C was the standard. For the silicate melt analysis, Na was calibrated on albite, Ca on wollastonite, K on orthoclase, Ti and Mn on ilmenite, Si on enstatite, Mg on forsterite, Al on spinel, P on GaP, and Fe on metallic Fe. Sulfur in the quenched silicate melts was analyzed with 50 nA beam current and 60 s peak counting time using a pyrrhotite standard. A defocused beam of 10 or 20 µm diameter was used for all standardizations and sample measurements.
Noble gas mass spectrometry analysis
The coexisting metallic melt and silicate melt in one half of all samples were physically separated and measured for N-content and -isotopic composition, using a modified noble gas mass spectrometry at the Atmosphere and Ocean Research Institute, the University of Tokyo, which has a capacity to precisely measure N-content and -isotopes at the sub-Nanomole levels62. Big metal blobs and clean silicates were separated readily under binocular microscope, except for run PYH01 synthesized at 5 GPa and 2200 °C (Supplementary Data 2), which only contained small metal grains (10–30 µm) being heterogeneously distributed in the quenched silicate melt. For this sample, we did not measure its N-content and -isotopic composition.
Silicate chips with a mass of ~1 mg and metal chips with a mass of ~0.1 mg were prepared for each sample. Each silicate or metal was loaded into a small quartz glass tube, which was then loaded into a large quartz glass container. The large quartz glass sample container was then placed in a furnace equipped with a tungsten wire. The sample container was baked out at 150 °C overnight under vacuum to remove any atmospheric N. A high-vacuum line was used for N gas extraction and purification. The vacuum line is basically composed of four parts: a gas-extraction part connected to the sample container, a gas-purification line (AQ-line) including cold trap-1, cold trap-2, a copper oxide finger (CuO) and a Pt finger, a vacuum line (AC-line), and a vacuum line directly connected to the mass spectrometer VG3600 (CE-line) for N-measurements. The AQ vacuum line is connected to a quadrupole mass spectrometer for checking whether N-intensity is appropriate for measurements. The vacuum lines are evacuated by a turbo molecular pump and an ionic pump. About 0.2 torr and 1 torr O2 was produced for silicate sample and metal sample, respectively, by heating a copper oxide finger (CuO) to 850–900 °C. The produced O2 was sealed in the quartz glass sample container and used for oxidizing the sample. All samples were firstly heated to 200 °C to remove any potential surficial contamination and to check the leakage of the system. During heating, the excess O2 in the AQ line was absorbed by the Cu finger through decreasing temperature of the finger to 600 °C. After the excess O2 was absorbed, the AQ line was evacuated, and the copper oxide finger (CuO) was reheated to 850 °C to produce O2. After oxidizing the samples at 200 °C for 30 min, the gases in the system produced at 200 °C were then directed to the purification vacuum line (AQ) by opening the valve of the sample container for 2 min. Condensable gases such as carbon dioxide and water were trapped using liquid N at cold trap-1. The non-condensable gases such as carbon monoxide, hydrocarbons, and hydrogen in the AQ line were then reacted for 5 min with pure O2, catalyzed by a platinum foil at 1000 °C. Carbon monoxide, hydrocarbons, and hydrogen were oxidized to CO2 and H2O by the pure O2. After reaction for 5 min, excess O2 was again resorbed by copper by decreasing the furnace temperature to 600 °C for 20 min and eventually to 450 °C for another 20 min. During this time, the produced gases such as CO2 and H2O were trapped using liquid N at cold trap-2. The pressure in the purification line, which is measured by a capacitance manometer, is no more than 0.0001 torr higher than the baseline pressure. A quadrupole mass spectrometer (QMS; HAL201, Hiden Analytical) was used to check whether the sample volume is proper for analysis through determining the sample size. If the N2 intensity in QMS is in the appropriate range, then the purified gases would be measured using the high-sensitivity static vacuum mass spectrometer (a modified VG3600, VG Micromass Ltd.). The determined concentration of N released at 200 °C was negligible (less than 1 ppm). After the measurements of gases released at 200 °C, following the same procedure, the samples were then heated to 1200 °C and kept for 30 min for glasses and 60 min for metals to ensure that the samples were completely oxidized for releasing N. The purification and measurement procedure for gases released at 1200 °C was the same as the procedure at 200 °C. After each measurement finished, the VG3600 mass spectrometer was evacuated for at least 20 min.
The running standard gas for N-isotopes was reserved in a large metal container attached to CE-line. The N-isotopic ratio of the standard gas was measured before and after the sample analysis, and the N-isotopic ratio of the standard gas was checked periodically by comparison with that of the local air. After the standard/sample gas was introduced into the VG3600 mass spectrometer, the intensities of 28 and 29 were measured for 15 times, and the 28/29 ratio was extrapolated by the mass spectrometer, with a system error of ~0.3‰. Repeated analysis of the standard in a day showed that the overall reproducibility was better than 0.5‰ for N-isotopes, and repeated analysis of a same sample yielded consistent results with uncertainties of <5% relative. The N-isotopic ratio of the air was analyzed for a number of times during the course of analysis, which gave an average δ15N value of −0.03‰. The concentration and isotopic composition of N in each sample, released at 1200 °C, was corrected by subtracting the hot blank (i.e., background), and the hot blank was analyzed with glass tube that contained no sample but using the same heating duration, same amounts of oxygen, and same purification procedure as in the case for measuring the samples. An average N-isotopic composition of +2.99‰ ± 0.70‰ is obtained for the hot blank.
The error (σ) of the measured N-concentration was calculated based on the error of the N-concentration measured by the VG3600 mass spectrometer, the error of the hot blank, and the error of weighing the sample mass, which can be defined as:
| 3 |
In Eq. (3), N (ppm) is the blank-corrected N-concentration in the sample; and the error of sample weighing (σweighing) is usually 1% relative; N2original (mol) is the uncorrected N-concentration measured by the VG3600 mass spectrometer; σN2 (mole) is the error of background-corrected N-concentration in the sample, which can be defined as:
| 4 |
| 5 |
where the is about 9.9%. The error of N-isotopic composition of the sample was calculated based on the error of sample gas δ15N (‰) measured by the VG3600 mass spectrometer, the error of reproducibility of standard N2 (0.5‰), and error of δ15N of the air (0.43‰), which can be defined as:
| 6 |
| 7 |
where is the error of δ15N (‰) of sample gas measured by the VG3600 mass spectrometer; is the error of the reproducibility of the standard gas; repeated analysis of the standard in a day showed that the overall reproducibility was better than 0.5‰; is the error of the δ15N (‰) value of the air, which is 0.43‰; is the standard deviation of 15 times measurements of 28/29 ratio of sample gas extrapolated by the mass spectrometer, which is approximately 0.3‰; and are the standard deviation of 15 times measurements of 28/29 ratio of the standard gas before and after each sample analysis.
Raman spectroscopy analysis
To obtain information on the speciation of N–C–H–O in the silicate melt, Raman spectra of some silicate glasses were collected. Micro-Raman spectra were recorded in back-scattering geometry using a Horiba LabRAM HR UV spectrometer with CCD detector, 1800 mm−1 grating, 50× objective, and confocal mode. A confocal pinhole of 100 μm was used, which limits spectral resolution to 3.5 cm−1. The 514.5 nm line of an Ar+ ion laser with an output power 0.1 W was used for excitation. Spectra were collected from 200 to 4500 cm−1 with an acquisition time of 2 × 300 s for each range, in order to detect N–C–H–O species with very low concentrations. Typical Raman spectra of some silicate glasses at fO2 of ~IW−0.5 are shown in Supplementary Fig. 2. We encountered significant fluorescence when measuring the reduced silicate melts. Such fluorescence could significantly mask the weak peaks of N–C–H–O species; we therefore only reported the Raman spectra that were not affected by fluorescence (Supplementary Fig. 2). Actually, the variation of N–C–H–O species in silicate melt as a function of fO2 has been extensively measured and discussed in the literature36,38,39,53,63,64, and their results are consistent with one another. Here we only cited these previous studies to discuss the effect of the variation of N-species in silicate melt on the N-isotopic fractionation (see the main text).
Major element compositions of experimental products and calculation of sample fO2
In all experiments, the basaltic melts were quenched into glasses, while the mantle pyrolitic melts had a dendritic texture (Supplementary Fig. 1). Major element compositions of the quenched metallic and silicates are given in Supplementary Data 3, 4. The ratio of non-bridging oxygens to tetrahedral cations (NBO/T) of the quenched silicate melt was 0.2–3.1, and the Fe-rich metallic melts contained 87.0–98.8 wt.% Fe, 0–6.8 wt.% Si, 0–1.8 wt.% S, and 0–11.5 wt.% C.
The fO2 prevailing in our experiments was calculated from the coexistence of Fe-rich metallic melt and silicate melt with finite FeO content using the following equilibrium:
| 8 |
from which the fO2 relative to the Fe-FeO buffer at any given P–T can be defined as:
| 9 |
aFeO represents the activity of FeO in the silicate melt; aFe represents the activity of Fe in the metallic melt; XFeO and XFe are molar fractions of FeO in the silicate melt and Fe in the metallic melt, respectively; γFeO and γFe are activity coefficients of FeO in the silicate melt and Fe in the metallic melt, respectively. Calculations of fO2 using both ideal (γFeO = 1 and γFe = 1; ideal fO2) and non-ideal solution models (non-ideal fO2) were performed. The fO2 calculation using the non-ideal solution model was performed assuming γFeO = 1.5 (refs. 17,65). γFe was calculated using the ε-approach and the online “Metal Activity Calculator” (http://www.earth.ox.ac.uk/~expet/metalact/) provided by the University of Oxford, which take into account the non-ideal interaction between all components in the Fe-rich metallic melt66. The calculated non-ideal fO2 values are between IW and IW–5. The calculated ideal fO2 values are between IW–0.7 and IW–6, which are 0.7–1 log units lower than the non-ideal fO2 values. The calculated fO2 values decrease with decreasing the FeO content of the silicate melt or increasing the Si content of the metallic melt, consistent with previous results17.
Sample N-content and δ15N
The δ15N of the starting Fe7N3 was −7.9 ± 1‰. The N-contents of the metallic and silicate melts are 43–14293 ppm and 44–4620 ppm (by wt.), respectively (Supplementary Data 3, 4). In two experiments (LY24 and LY25; Supplementary Data 2), where ~50 wt.% Fe7N3 was added in the starting material, the metallic melts contained ~1.1 and 1.4 wt.% N, respectively. These values are comparable to the N-solubility in Fe-rich metallic melts determined under similar conditions37, implying that these two experiments must have been N2-saturated. The δ15N of metallic melts ranged from −7.0‰ to +7.6‰, and the δ15N of silicate melts ranged from −7‰ to +0.42‰ (Supplementary Data 3, 4). Except for the two N2-saturated experiments, mass-balance calculations of bulk sample N content and δ15N were performed for all other experiments (Supplementary Data 2). The results show that the bulk sample N-contents vary from 650 to 3000 ppm, with most values (780–2200 ppm) generally consistent with the N-mass added in the starting materials. Most of the bulk sample δ15N values vary between −3‰ and −7‰, with the δ15N values of three multi-anvil experiments above +0.2‰ (N-18, N-19, and N-20; Supplementary Data 2). The deviation of the bulk sample δ15N from that of the starting Fe7N3 could be explained by air N2 contamination when loading silicate powder into the graphite capsule, the presence of N in the starting metallic Fe, and/or δ15N inhomogeneity of the starting Fe7N3. Nevertheless, the positive δ15N values of the three multi-anvil experiments are difficult to explain. However, as shown in the main text, the calculated and of these three experiments are fully consistent with those of the other experiments.
N-loss during experiments?
Previous studies showed that N-loss occurred during the run in some of the high P–T experiments36,37,40,41. The N-loss could be either related to the storage of some N in the porosity of the graphite capsules or to N diffusive loss through the graphite (-Pt) capsule walls41. We note that in previous experiments, ~0.5–2 wt.% N was put in the starting materials, so that the samples were usually saturated with a N2 vapor phase. However, in our experiments, we added only ~1000–2000 ppm N in the starting materials, which are far below the solubility limit37. Our experiments were therefore not saturated with a N2 vapor phase, except for two experiments (LY24 and LY25; Supplementary Data 2). As mentioned above, the reconstructed bulk N content in our samples ranged from 650 to 3000 ppm, with most values between 780 and 2200 ppm and consistent with the N-mass added in the starting materials (Supplementary Data 2). We therefore believe that N-loss in our experiments was limited. Some experiments, as shown in Supplementary Data 2, even gained N, which could be caused by air N2 contamination during loading sample materials into the capsules, and the presence of N in the starting metallic iron. And our experiments LY24 and LY25 were still saturated with a N2 vapor after running 90 mins. The factors that control the N-loss or the N-loss rates are elusive, but at least, the absence of a N2 vapor phase should effectively suppress the N-loss rates or the storage of N2 gas in the porosity of the graphite capsule walls.
Attainment of equilibrium partitioning
The experimental durations ranged from 60 to 180 mins at 1700 °C, and from 10 to 20 mins at 2000–2200 °C. The observation that ∆15 Nmetal-silicate are time-independent over a small fO2 range (Supplementary Fig. 6) demonstrates 60 mins being sufficient for approaching metal/silicate N-isotopic equilibrium at 1700 °C. A time series of experiments are usually not performed at temperatures of 2000–2200 °C, because the diffusion of elements at such high temperatures are thought to be very fast. If metal/silicate N-isotopic equilibrium at 1700 °C was approached within 60–180 min, there is no doubt that N-isotopic equilibrium at 2000–2200 °C must have also been approached within 10–20 min, because the diffusion coefficient of an element in a given system increases by orders of magnitude with temperature increasing from 1700 to 2000–2200 °C. In addition, as shown in Fig. 2 and summarized in Eq. (1), our are consistent with previous data, also indicating equilibrium partitioning of N in our experiments.
Model N-partitioning and -isotopic fractionation during Earth’s accretion and core-formation
Using the multistage core-formation model with inputs of the Grand Tack N-body simulation results15,49, and using our Eqs. (1) and (2), we modeled the N-partitioning and -isotopic fractionation between Earth’s core and mantle. We first considered Earth accreted its first 60% mass through the collisions of reduced, EC-like impactors, and then its last 40% mass through the collisions of increasingly oxidized impactors. Reduced, EC-like impactors formed at heliocentric distances of <0.9–1.2 AU with δ15N = −30‰, while increasingly oxidized impactors originated from great heliocentric distances (1.2–3 AU). Since the solar system δ15N increases with the heliocentric distance4,20, the increasingly oxidized impactor δ15N should increase from −30‰ (EC’s value) to a slightly positive value at 3 AU. We used a δ15N value of +5‰ for the last impactor, which added Earth’s last 10% mass through the Moon-forming giant impact, and a δ15N value of +5‰ represents the mixing of EC (δ15N = −30‰) and CC (δ15N = +40‰) with a same N content and mass ratio of ~1 : 1 as constrained by Mo isotopes for the Moon-forming giant impactor19. The N content in the impactors depends a number of conditions. For example, large and oxidized impactors may hold more N than small and reduced ones, and N is mainly stored in impactor cores42. For an internally differentiated planetesimal67, i.e., no surface magma ocean, more volatiles could be retained in the planetesimal, no matter the planetesimal is oxidized or reduced. However, even oxidized planetesimals may have undergone severe evaporative volatile loss, if the surface magma ocean lasted sufficiently long. Iron meteorites contain a few ppm to 200 ppm N21, whereas basalts in asteroids may contain up to 10 ppm N68. However, both iron meteorites and asteroid basalts may have experienced extensive volatile loss, considering the pressure-dependence of N solubility in both metallic and silicate melts37,69. In our model, we varied the bulk N-content from 50 ppm for small and reduced impactors to 150 ppm for large and oxidized impactors.
We also considered the other factors that potentially affect the N-content and -isotopic composition of Earth’s different reservoirs. Since N is a strong volatile element, we have to consider the degassing of the silicate magma ocean. Degassing of the silicate magma ocean may have inevitably formed a proto-atmosphere7. However, for Earth-sized planets, it is unlikely that the entire silicate magma ocean is in equilibrium with the proto-atmosphere in volatile partitioning70. We defined a factor Φ, which represents the mass percentage of silicate magma ocean that is in equilibrium with the proto-atmosphere. We fix Φ at 100% at Earth’s first ~50% accretion, but varied it from 50% to 5% at Earth’s ~50–100% accretion. In addition, the N-isotopic fractionations during degassing of the hot magma ocean are thought to be inconsiderable, as even the degassing of mid-ocean ridge basalts may have not caused N-isotopic fractionations71. A kinetic process during degassing of a hot silicate may cause significant N-isotope fractionation;72 however, it remains unfeasible to quantify such effect during the degassing of a hot magma ocean. We therefore did not consider kinetic process-induced N-isotope fractionation in our model. Hydrodynamic escape of light gases in the early atmosphere to space may have resulted in preferential loss of 14N in space; however, such effect on Earth’s δ15N is difficult to quantify and the hydrodynamic escape model is inconsistent with the abundance and isotopic composition of Earth’s atmospheric xenon22. We therefore did not consider hydrodynamic escape of Earth’s proto-atmosphere in our model. However, it is important to consider catastrophic loss of the Earth’s proto-atmosphere during impacting73, because it surely affects Earth’s total N budget. Depending on a number of parameters, such as impact velocity and angle and the impactor to target mass ratio, the loss fraction of N in the proto-atmosphere during each impacting is difficult to quantify but could vary from <5% to 100% (refs. 73,74). In the Moon-forming giant impact, ~10–50% of the growing Earth’s atmosphere could have been lost from the immediate effects of the collision73. We fix a N-loss fraction of 100% during Earth’s first ~50% mass accretion, and from 80% to 10% during the last ~50% accretion, because small planets more readily lose their atmosphere during impacting74. Finally, we considered the delivery of completely oxidized or CI chondrite-like materials from beyond 6–7 AU, which contain 1000 ppm N with δ15N = +40‰ (refs. 50,75), to Earth’s magma ocean after Earth accreted its 60% mass. No metal–silicate segregation occurred when CI chondrite-like material added in the magma ocean, but the N in the silicate magma ocean participated in the subsequent core-formation events when metal-bearing impactors were accreted15. Inefficient emulsification of impactor cores may have occurred during Earth’s accretion of large and oxidized impactors. We used the degree of core–mantle disequilibrium during accretion as that in ref. 49. We also considered the light element content of the metallic melt that segregated into Earth’s core; we used a C-content of 0.2 wt.% and S-content of 1.5 wt.% (see below), and Si- and O-contents following the model in refs. 15,49.
The P–T–fO2 conditions of metal–silicate equilibration are critical for the resulting mantle and core compositions because of the dependence of and ∆15 Nmetal-silicate on P–T–fO2. We used the approach used by refs. 15,49 for modeling multistage core formation. For each impact-induced core formation event, the metal–silicate equilibration pressure Pe is a constant fraction of the target’s evolving core–mantle boundary pressure:
| 10 |
where fP is a constant proportionality factor; PCMB, the core–mantle boundary (CMB) pressure at the time of impact. The metal–silicate equilibration temperature, Te, lies between the peridotite liquidus and solidus at the equilibration pressure Pe. The equilibration fO2 varied from ~IW-5 to IW-2 with the accreted impactors changing from reduced to oxidized composition.
In an ith stage of collisional accretion, the distribution of N among the reservoirs of Earth’s core, silicate magma ocean, and atmosphere must follow a mass balance:
| 11 |
where , , and are the N mass in the atmosphere, silicate melt, and metallic melt, respectively; is the total N mass that participates in the equilibrium partitioning. Equation (11) can be further written as:
| 12 |
| 13 |
In Eqs. (12) and (13), denotes the mass of N lost during impacting; denotes the N concentration in the silicate melt at the (i-1)th stage of accretion; denotes the mass of silicate melt at the (i-1)th stage of accretion; denotes the N concentration in the impactor; is the mass of the impactor; and denote the N concentration in the metallic and silicate melts, respectively. are a function of pressure, temperature, fO2, and compositions of the metallic and silicate melts, as summarized in Eq. (1) in the main text. In order to model the N partitioning between the atmosphere and the silicate, the N solubility in silicate melt is needed. If the mantle is in full equilibrium with the atmosphere, its N concentration should be equal to the N solubility corresponding to the partial pressure of N2 in the atmosphere. Following the model of Libourel et al.53, the N solubility in silicate melt () can be written as:
| 14 |
where PN is the partial pressure of N in the atmosphere. Generally, the partial pressure of a volatile element E (PE) on the surface of magma ocean can be expressed as:
| 15 |
where gi is the gravitational acceleration, is surface area of the planet, and r is the mass number ratio of the volatile species and the element of interest (for N2, r = 1). It is worth noting that in Eq. (14), the fO2 denotes to the fO2 of the surface magma ocean. Following the method of ref. 76, we calculated the surface magma ocean fO2, which varies from IW−3.6 to IW+3.0 during Earth’s early to late accretions in our model. The fO2 variation could significantly affect the composition of the proto-atmosphere77. The combination of Eqs. (12)–(15) can be used to constrain the N distribution in the atmosphere, silicate magma ocean, and core in the framework of a multistage core-formation model.
For N-isotopic fractionations among the atmosphere, silicate melt, and metallic melt at the ith stage of accretion, δ15N also follows the mass balance rule:
| 16 |
where , , and are the N fractions in the silicate melt, metallic melt, and atmosphere, respectively; is the bulk N isotope composition of the silicate melt, metallic melt, and atmosphere. At the ith stage of accretion, can be expressed as:
| 17 |
where is the N-isotopic composition of the accreting impactor. The N-isotopic fractionation between metallic melt and silicate melt is:
| 18 |
is a multi-function of temperature and fO2, as summarized in Eq. (2) in the main text. The equilibrium N-isotopic fractionation between the atmosphere and silicate melt at high temperatures is negligible71, so the following equation was used:
| 19 |
The combination of Eqs. (16)–(19) can be used to constrain the N-isotopic composition in the atmosphere, silicate magma ocean, and core in the framework of a multistage core formation model.
Test the sensitivity of varying the parameters used in the above N-accretion model
We recognized that during Earth’s multistage accretion, the processes such as collision-induced catastrophic atmosphere loss and the degree of silicate magma ocean–atmosphere equilibrium remain poorly constrained. We therefore performed additional modeling to test the effect of varying the parameters used in our model on the final N-content and δ15N of the proto-Earth’s atmosphere and mantle (Supplementary Figs. 8−14). Supplementary Fig. 8 shows that fixing Φ at 20–60% would result in N-content and δ15N of ~1.1 to 1.7 ppm and ~ −1.8‰ to −0.3‰ for the proto-atmosphere, and ~0.7 to 2.2 ppm and ~ −6.8‰ to −0.1‰ for the proto-mantle. These values cover the observed ones for Earth’s mantle and surface. Supplementary Fig. 9 shows that varying the degree of impact-induced atmospheric loss from 40% to 60% would vary the proto-atmospheric N-content from 0.7 to 1.5 ppm and δ15N from −3‰ to +4.2‰, but does not change the mantle values. These proto-atmospheric values also cover those observed values for Earth’s surface reservoir. In addition, Supplementary Fig. 10 shows that slightly increasing the degree of equilibrium between silicate magma ocean and overlying atmosphere or decreasing the added mass of CI chondrites would decrease the proto-atmosphere δ15N to ~0‰ and meanwhile increase the atmosphere N-content at ~1 ppm. Supplementary Fig. 11 shows that changing the relative timing of the delivery of CI chondrite-like materials would either not change the main conclusions, as long as the CI chondrite-like materials were delivered after Earth accreting its ~60% mass but before complete core–mantle segregation. Supplementary Fig. 12 shows that varying the C-content in the impactor core from 0.5 to 2 wt.% would either not change the conclusions. Supplementary Fig. 13 shows that varying the relative contributions of EC and CC to the Moon-forming giant impactor in δ15N would nearly not affect the δ15N of the proto-Earth’s atmosphere, mantle, and core. This is because most of the N in the last impactor was in the impactor core, and limited emulsification (5%) of the impactor core resulted in most of the N in the impactor delivered to Earth’s core. The N-content in the impactors must affect Earth’s bulk N-content. We compare the modeling results using impactors containing 80–200 ppm N (N-rich) and 20–100 ppm N (N-poor) in Supplementary Fig. 14. It shows that the final N-contents in the proto-atmosphere (1.8 vs. 1.4 ppm) and proto-mantle (2.9 vs. 2.1 ppm, respectively) are well comparable, while the N-content in the core is more different in these two cases (234 vs. 118 ppm), because N is siderophile during the whole accretion phase. Supplementary Fig. 14 also shows that the δ15N of the proto-atmosphere, proto-mantle, and core is nearly not changed in these two cases, and any slight change in δ15N can be counterbalanced by slightly increasing the mass of CI chondrites added.
Constrain the distribution and origin of other major volatiles (C–H–S) during Earth’s heterogeneous accretion
The other major volatiles (C–H–S) would undergo similar accretion process as modeled above for N. Since these volatile elements have very different geochemical behaviors relative to N, we had to consider the C–H–S contents in the accreted materials, their solubilities in silicate melts at the atmosphere–mantle equilibrium conditions, and their metal/silicate partition coefficients at the core-formation conditions, before we applied our above N-accretion model to constrain the distribution and origin of C–H–S in Earth’s different reservoirs.
For the C–H–S contents in the accreted materials, we assumed that the completely oxidized materials have CI chondrite-like C–H–S contents, and the C–H–S contents in other impactors were inferred from the asteroid meteorites. Hydrogen is mainly concentrated in the silicate part of the impactors due to the lithophile nature of H under asteroid conditions where the interior pressure is <20 GPa. Since the H contents in the achondrites are in the range of 50–170 ppm78,79, in our model the bulk H contents were changed from ~50 ppm in the reduced impactors to ~150 ppm in the oxidized impactors. Carbon and S are more concentrated in the metal core of the impactors because of their siderophile nature under asteroids conditions80,81. The C contents in iron meteorites are no more than 1500 ppm82, and the C contents in achondrites are in the range of 10–140 ppm83,84. We hence set the C contents in the impactors at ~150–1000 ppm. The S contents vary greatly in iron meteorites (0.4–19 wt.%)82 and achondrites (110–5000 ppm)85,86. However, the log(C/S) of iron meteorites are well correlated with the log(C) (ref. 82). Hence, we set the S contents in the bulk impactors in the range of ~2000–11000 ppm.
The surface magma ocean fO2 changes from IW−3.6 to IW+3 during Earth’s accretion in our model, as stated above, which would significantly influence the species and hence the solubilities of C–H–S in silicate melts77. In silicate melt, the relative fraction of H existing as H2 or H2O follows a relationship as:87
| 20 |
In our model, the H contents in the impactors are no more than 150 ppm (see above), Eq. (20) indicates that the fraction of H as H2 is less than 30% at fO2 of IW−3.6 and would be negligible if the fO2 is higher than IW−2.5. This means that the main H species in the surface magma ocean is H2O during the whole accretion process. We hence used the H2O solubility model from ref. 88 in our model:
| 21 |
where and are the mole fraction of water in the silicate melt and the fugacity of water in the fluid, respectively. Pgas is the total pressure of the gas, bj and Xj are the constant factor and oxide mole fraction of component j in silicate melt (bAl2O3 = −1.997, bFeO(T) = −0.9275, bNa2O = 2.376)56. Assuming that the fugacity coefficient of H2O is equal to 1, the is equal to its partial pressure and could be calculated by using Eq. (15) with r(H2O) = 9. The Pgas could be obtained by summing the partial pressure of all volatiles in the atmosphere.
The species of C in H-bearing silicate melts are also controlled by fO2. At reduced conditions (fO2 < IW−1), the main C species is methane, while at oxidized conditions (fO2 >IW−1), the main C species is carbonate89. For C solubility in silicate melt (SC-silicate) at fO2 < IW−1, we used the model from ref. 89 as:
| 22 |
At fO2 >IW−1, we used the model from ref. 90, which is more valid for peridotitic melt. For S solubility in silicate melt (SS-silicate), we used a recent model of ref. 77:
| 23 |
where the CFeO is the FeO content in the silicate melt (in wt.%), fS2 is sulfur fugacity, which could be approximately regarded as partial pressure of S2 in the atmosphere, and then could be expressed in a form like Eq. (15).
As for the metal/silicate partition coefficients, we used the parameterized from ref. 91, from ref. 80, and from ref. 43.
With the above parameters for C–H–S, we applied our N-accretion model to C–H–S to constrain the distribution of C–H–S in Earth’s different reservoirs during Earth’s heterogeneous accretion. Our results presented in Figs. 5, 6 in the main text show that our modeled C–H–S contents in Earth’s different reservoirs are consistent with the present-day observations. Our study suggests that Earth acquired its volatiles through very complicated processes, but these complicate processes happened naturally during Earth’s main accretion phase. Therefore, the establishment of Earth’s volatile inventory was a natural outcome of Earth’s heterogeneous accretion processes.
Supplementary information
Description of Additional Supplementary Files
Acknowledgements
We appreciate encouraging comments of Hans Keppler and Pierre Cartigny on this paper. This project received support from Key Research Program of Frontier Sciences, CAS (grant No. DBS-LY-DQC013) and NFSC (grant No. 41673064) to Y. Li.
Author contributions
Y.Li. conceived and designed the project. Y.Li., Z.G., and L.S. performed the experiments. L.S., T.K., Y. Li., and Y.S. performed the analyses. W.L. and L.S. performed model calculations under the guidance of Y. Li. Y. Li interpreted the data and wrote the paper with comments and improvements from W.L., Y.S., Z.D., Y. Liu, and Y.F.
Peer review
Peer review information
Nature Communications thanks Celia Dalou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Data availability
All data supporting the findings of this study are available within the paper and supplementary information and source data files (Supplementary Data 1–6). Additional data related to this paper may be requested from the authors.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Lanlan Shi, Wenhua Lu.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-32516-5.
References
- 1.Walsh KJ, Morbidelli A, Raymond SN, O’Brien DP, Mandell AM. A low mass for Mars from Jupiter’s early gas-driven migration. Nature. 2011;475:206. doi: 10.1038/nature10201. [DOI] [PubMed] [Google Scholar]
- 2.Morbidelli A, et al. Source regions and timescales for the delivery of water to the Earth. Meteorit. Planet Sci. 2000;35:1309–1320. doi: 10.1111/j.1945-5100.2000.tb01518.x. [DOI] [Google Scholar]
- 3.Fujiya, W. et al. Migration of D-type asteroids from the outer Solar System inferred from carbonate in meteorites. Nat. Astronomy10.1038/s41550-019-0801-4 (2019).
- 4.Alexander, C. M. O. The origin of inner Solar System water. Philos. Trans. A Math. Phys. Eng. Sci.375, 10.1098/rsta.2015.0384 (2017). [DOI] [PMC free article] [PubMed]
- 5.Marty B. The origins and concentrations of water, carbon, nitrogen and noble gases on Earth. Earth Planet. Sci. Lett. 2012;313-314:56–66. doi: 10.1016/j.epsl.2011.10.040. [DOI] [Google Scholar]
- 6.Halliday AN. The origins of volatiles in the terrestrial planets. Geochim. Cosmochim. Acta. 2013;105:146–171. doi: 10.1016/j.gca.2012.11.015. [DOI] [Google Scholar]
- 7.Hirschmann MM. Constraints on the early delivery and fractionation of Earth’s major volatiles from C/H, C/N, and C/S ratios. Am. Mineralogist. 2016;101:540–553. doi: 10.2138/am-2016-5452. [DOI] [Google Scholar]
- 8.Bergin EA, Blake GA, Ciesla F, Hirschmann MM, Li J. Tracing the ingredients for a habitable earth from interstellar space through planet formation. Proc. Natl Acad. Sci. USA. 2015;112:8965–8970. doi: 10.1073/pnas.1500954112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Albarede F. Volatile accretion history of the terrestrial planets and dynamic implications. Nature. 2009;461:1227–1233. doi: 10.1038/nature08477. [DOI] [PubMed] [Google Scholar]
- 10.Braukmüller, N., Wombacher, F., Funk, C. & Münker, C. Earth’s volatile element depletion pattern inherited from a carbonaceous chondrite-like source. Nat. Geosci.10.1038/s41561-019-0375-x (2019). [DOI] [PMC free article] [PubMed]
- 11.Varas-Reus, M. I., König, S., Yierpan, A., Lorand, J.-P. & Schoenberg, R. Selenium isotopes as tracers of a late volatile contribution to Earth from the outer Solar System. Nat. Geosci.10.1038/s41561-019-0414-7 (2019). [DOI] [PMC free article] [PubMed]
- 12.Wang Z, Becker H. Ratios of S, Se and Te in the silicate Earth require a volatile-rich late veneer. Nature. 2013;499:328–331. doi: 10.1038/nature12285. [DOI] [PubMed] [Google Scholar]
- 13.Fischer RA, Cottrell E, Hauri E, Lee KKM, Le Voyer M. The carbon content of Earth and its core. Proc. Natl Acad. Sci. USA. 2020;117:8743–8749. doi: 10.1073/pnas.1919930117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schönbächler M, Carlson R, Horan M, Mock T, Hauri E. Heterogeneous accretion and the moderately volatile element budget of Earth. Science. 2010;328:884–887. doi: 10.1126/science.1186239. [DOI] [PubMed] [Google Scholar]
- 15.Rubie DC, et al. Accretion and differentiation of the terrestrial planets with implications for the compositions of early-formed Solar System bodies and accretion of water. Icarus. 2015;248:89–108. doi: 10.1016/j.icarus.2014.10.015. [DOI] [Google Scholar]
- 16.Sakuraba H, Kurokawa H, Genda H, Ohta K. Numerous chondritic impactors and oxidized magma ocean set Earth’s volatile depletion. Sci. Rep. 2021;11:20894. doi: 10.1038/s41598-021-99240-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Y, Dasgupta R, Tsuno K, Monteleone B, Shimizu N. Carbon and sulfur budget of the silicate Earth explained by accretion of differentiated planetary embryos. Nat. Geosci. 2016;9:781–785. doi: 10.1038/ngeo2801. [DOI] [Google Scholar]
- 18.Grewal DS, Dasgupta R, Sun C, Tsuno K, Costin G. Delivery of carbon, nitrogen, and sulfur to the silicate Earth by a giant impact. Sci. Adv. 2019;5:eaau3669. doi: 10.1126/sciadv.aau3669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Budde G, Burkhardt C, Kleine T. Molybdenum isotopic evidence for the late accretion of outer Solar System material to Earth. Nat. Astron. 2019;3:736–741. doi: 10.1038/s41550-019-0779-y. [DOI] [Google Scholar]
- 20.Füri E, Marty B. Nitrogen isotope variations in the Solar System. Nat. Geosci. 2015;8:515–522. doi: 10.1038/ngeo2451. [DOI] [Google Scholar]
- 21.Grewal, D. S., Dasgupta, R. & Marty, B. A very early origin of isotopically distinct nitrogen in inner Solar System protoplanets. Nat. Astronomy, 10.1038/s41550-020-01283-y (2021).
- 22.Cartigny P, Marty B. Nitrogen isotopes and mantle geodynamics: the emergence of life and the atmosphere-crust-mantle connection. Elements. 2013;9:359–366. doi: 10.2113/gselements.9.5.359. [DOI] [Google Scholar]
- 23.Javoy M. The major volatile elements of the earth: Their origin, behavior, and fate. Geophys. Res. Lett. 1997;24:177–180. doi: 10.1029/96GL03931. [DOI] [Google Scholar]
- 24.Cartigny, P., Boyed, S. R., Harris, J. W. & Javoy, M. Nitrogen isotopes in peridotitic diamonds from Fuxian, China: the mantle signature. Terra Nova, 175–179 (1997).
- 25.Palot M, Cartigny P, Harris JW, Kaminsky FV, Stachel T. Evidence for deep mantle convection and primordial heterogeneity from nitrogen and carbon stable isotopes in diamond. Earth Planet. Sci. Lett. 2012;357-358:179–193. doi: 10.1016/j.epsl.2012.09.015. [DOI] [Google Scholar]
- 26.Grady MM, Wright I, Carr L, Pillinger C. Compositional differences in enstatite chondrites based on carbon and nitrogen stable isotope measurements. Geochim. Cosmochim. Acta. 1986;50:2799–2813. doi: 10.1016/0016-7037(86)90228-0. [DOI] [Google Scholar]
- 27.Thomazo C, Papineau DJE. Biogeochemical cycling of nitrogen on the early Earth. Elements. 2013;9:345–351. doi: 10.2113/gselements.9.5.345. [DOI] [Google Scholar]
- 28.Dauphas N, Marty B. Heavy nitrogen in carbonatites of the Kola Peninsula: a possible signature of the deep mantle. Science. 1999;286:2488–2490. doi: 10.1126/science.286.5449.2488. [DOI] [PubMed] [Google Scholar]
- 29.Marty B, Dauphas N. The nitrogen record of crust–mantle interaction and mantle convection from Archean to Present. Earth Planet. Sci. Lett. 2003;206:397–410. doi: 10.1016/S0012-821X(02)01108-1. [DOI] [Google Scholar]
- 30.Labidi J, et al. Hydrothermal (15)N(15)N abundances constrain the origins of mantle nitrogen. Nature. 2020;580:367–371. doi: 10.1038/s41586-020-2173-4. [DOI] [PubMed] [Google Scholar]
- 31.Cartigny P, et al. A mantle origin for Paleoarchean peridotitic diamonds from the Panda kimberlite, Slave Craton: Evidence from 13C-, 15N- and 33,34S-stable isotope systematics. Lithos. 2009;112:852–864. doi: 10.1016/j.lithos.2009.06.007. [DOI] [Google Scholar]
- 32.Dauphas N. The isotopic nature of the Earth’s accreting material through time. Nature. 2017;541:521–524. doi: 10.1038/nature20830. [DOI] [PubMed] [Google Scholar]
- 33.Fischer-Godde M, Kleine T. Ruthenium isotopic evidence for an inner Solar System origin of the late veneer. Nature. 2017;541:525–527. doi: 10.1038/nature21045. [DOI] [PubMed] [Google Scholar]
- 34.Javoy M. The major volatile elements of the Earth: Their origin, behavior, and fate. Geophys. Res. Lett. 1997;24:177–180. doi: 10.1029/96GL03931. [DOI] [Google Scholar]
- 35.Li, Y., Marty, B., Shcheka, S., Zimmermann, L. & Keppler, H. Nitrogen isotope fractionation during terrestrial core-mantle separation. Geochem. Perspect. Lett. 138–147, 10.7185/geochemlet.1614 (2016).
- 36.Dalou C, et al. Redox control on nitrogen isotope fractionation during planetary core formation. Proc. Natl Acad. Sci. USA. 2019;116:14485–14494. doi: 10.1073/pnas.1820719116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Speelmanns, I. M., schmidt, M. W. & Liebske, C. Nitrogen solubility in core materials. Geophys. Res. Lett. 45, 10.1029/2018GL079130 (2018).
- 38.Grewal DS, Dasgupta R, Farnell A. The speciation of carbon, nitrogen, and water in magma oceans and its effect on volatile partitioning between major reservoirs of the Solar System rocky bodies. Geochim. Cosmochim. Acta. 2020;280:281–301. doi: 10.1016/j.gca.2020.04.023. [DOI] [Google Scholar]
- 39.Dalou C, Hirschmann MM, Jacobsen SD, Le Losq C. Raman spectroscopy study of C-O-H-N speciation in reduced basaltic glasses: implications for reduced planetary mantles. Geochim. Cosmochim. Acta. 2019;265:32–47. doi: 10.1016/j.gca.2019.08.029. [DOI] [Google Scholar]
- 40.Grewal DS, et al. The fate of nitrogen during core-mantle separation on Earth. Geochim. Cosmochim. Acta. 2019;251:87–115. doi: 10.1016/j.gca.2019.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Speelmanns IM, Schmidt MW, Liebske C. The almost lithophile character of nitrogen during core formation. Earth Planet. Sci. Lett. 2019;510:186–197. doi: 10.1016/j.epsl.2019.01.004. [DOI] [Google Scholar]
- 42.Grewal DS, Dasgupta R, Hough T, Farnell A. Rates of protoplanetary accretion and differentiation set nitrogen budget of rocky planets. Nat. Geosci. 2021;14:369–376. doi: 10.1038/s41561-021-00733-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jackson CRM, Cottrell E, Du Z, Bennett NR, Fei Y. High pressure redistribution of nitrogen and sulfur during planetary stratification. Geochem. Perspect. Lett. 2021;18:37–42. doi: 10.7185/geochemlet.2122. [DOI] [Google Scholar]
- 44.Schauble EA. Applying stable isotope fractionation theory to new systems. Rev. Mineral. Geochem. 2004;55:65–111. doi: 10.2138/gsrmg.55.1.65. [DOI] [Google Scholar]
- 45.Luo, Y. R. Comprehensive Handbook of Chemical Bond Energies (CRC Press, Boca Raton, 2007).
- 46.Glibin VP, Dodelet J-P. Thermodynamic stability in acid media of FeN4-based catalytic sites used for the reaction of oxygen reduction in PEM fuel cells. J. Electrochem. Soc. 2017;164:F948–F957. doi: 10.1149/2.1041709jes. [DOI] [Google Scholar]
- 47.Roskosz M, et al. Kinetic D/H fractionation during hydration and dehydration of silicate glasses, melts and nominally anhydrous minerals. Geochim. Cosmochim. Acta. 2018;233:14–32. doi: 10.1016/j.gca.2018.04.027. [DOI] [Google Scholar]
- 48.Horita J, Polyakov VB. Carbon-bearing iron phases and the carbon isotope composition of the deep Earth. Proc. Natl Acad. Sci. USA. 2015;112:31–36. doi: 10.1073/pnas.1401782112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rubie DC, et al. Heterogeneous accretion, composition and core–mantle differentiation of the Earth. Earth Planet. Sci. Lett. 2011;301:31–42. doi: 10.1016/j.epsl.2010.11.030. [DOI] [Google Scholar]
- 50.Pearson V, Sephton M, Franchi I, Gibson J, Gilmour I. Carbon and nitrogen in carbonaceous chondrites: elemental abundances and stable isotopic compositions. Meteorit. Planet Sci. 2006;41:1899–1918. doi: 10.1111/j.1945-5100.2006.tb00459.x. [DOI] [Google Scholar]
- 51.Hirschmann MM. Comparative deep Earth volatile cycles: The case for C recycling from exosphere/mantle fractionation of major (H2O, C, N) volatiles and from H2O/Ce, CO2/Ba, and CO2/Nb exosphere ratios. Earth Planet. Sci. Lett. 2018;502:262–273. doi: 10.1016/j.epsl.2018.08.023. [DOI] [Google Scholar]
- 52.Mallik A, Li Y, Wiedenbeck M. Nitrogen evolution within the Earth’s atmosphere–mantle system assessed by recycling in subduction zones. Earth Planet. Sci. Lett. 2018;482:556–566. doi: 10.1016/j.epsl.2017.11.045. [DOI] [Google Scholar]
- 53.Libourel G, Marty B, Humbert F. Nitrogen solubility in basaltic melt. Part I. Effect of oxygen fugacity. Geochim. Cosmochim. Acta. 2003;67:4123–4135. doi: 10.1016/S0016-7037(03)00259-X. [DOI] [Google Scholar]
- 54.Piani L, et al. Earth’s water may have been inherited from material similar to enstatite chondrite meteorites. Science. 2020;369:1110–1113. doi: 10.1126/science.aba1948. [DOI] [PubMed] [Google Scholar]
- 55.Kerridge JF. Carbon, hydrogen and nitrogen in carbonaceous chondrites: abundances and isotopic compositions in bulk samples. Geochim. Cosmochim. Acta. 1985;49:1707–1714. doi: 10.1016/0016-7037(85)90141-3. [DOI] [PubMed] [Google Scholar]
- 56.Sossi, P. A. et al. Redox state of Earth’s magma ocean and its Venus-like early atmosphere. Sci Adv6, 10.1126/sciadv.abd1387 (2020). [DOI] [PMC free article] [PubMed]
- 57.Krissansen-Totton, J. Constraining the climate and ocean pH of the early Earth with a geological carbon cycle model. Proc. Natl Acad. Sci. USA 201721296 (2018). [DOI] [PMC free article] [PubMed]
- 58.Palme, H. & O’Neill, H. S. C. in Treatise on Geochemistry (Second Edition) (eds Holland, H. D. & Turekian, K. K.) 1–39 (Elsevier, 2014).
- 59.Canfield, D. E. The evolution of the Earth surface sulfur reservoir. Am. J. Sci. 304, 839–861 (2004).
- 60.McDonough, W. F. in Treatise on Geochemistry (Second Edition) (eds Holland, H. D. & Turekian, K. K.) 559-577 (Elsevier, 2014).
- 61.Hopp, T., Budde, G. & Kleine, T. Heterogeneous accretion of Earth inferred from Mo-Ru isotope systematics. Earth and Planetary Science Letters534, 10.1016/j.epsl.2020.116065 (2020).
- 62.Takahata, N., Nishio, Y., Yoshida, N. & Sano, Y. J. A. S. Precise isotopic measurements of nitrogen at the sub-nanomole level. 14, 485-491 (1998).
- 63.Boulliung J, et al. Oxygen fugacity and melt composition controls on nitrogen solubility in silicate melts. Geochim. Cosmochim. Acta. 2020;284:120–133. doi: 10.1016/j.gca.2020.06.020. [DOI] [Google Scholar]
- 64.Kadik AA, et al. Influence of oxygen fugacity on the solubility of nitrogen, carbon, and hydrogen in FeO-Na2O-SiO2-Al2O3 melts in equilibrium with metallic iron at 1.5 GPa and 1400 °C. Geochem. Int. 2011;49:429–438. doi: 10.1134/S001670291105003X. [DOI] [Google Scholar]
- 65.O’Neill HSC, Eggins SM. The effect of melt composition on trace element partitioning: an experimental investigation of the activity coefficients of FeO, NiO, CoO, MoO2 and MoO3 in silicate melts. Chem. Geol. 2002;186:151–181. doi: 10.1016/S0009-2541(01)00414-4. [DOI] [Google Scholar]
- 66.Wood BJ, Li J, Shahar A. Carbon in the core: its influence on the properties of core and mantle. Rev. Mineral. Geochem. 2013;75:231–250. doi: 10.2138/rmg.2013.75.8. [DOI] [Google Scholar]
- 67.Elkins-Tanton LT, Weiss BP, Zuber MT. Chondrites as samples of differentiated planetesimals. Earth Planet. Sci. Lett. 2011;305:1–10. doi: 10.1016/j.epsl.2011.03.010. [DOI] [Google Scholar]
- 68.Abernethy FAJ, Verchovsky AB, Franchi IA, Grady MM. Basaltic volcanism on the angrite parent body: comparison with 4 Vesta. Meteorit. Planet Sci. 2018;53:375–393. doi: 10.1111/maps.13016. [DOI] [Google Scholar]
- 69.Bernadou, F., Gaillard, F., Füri, E., Marrocchi, Y. & Slodczyk, A. Nitrogen solubility in basaltic silicate melt - Implications for degassing processes. Chem. Geol.573, 10.1016/j.chemgeo.2021.120192 (2021).
- 70.Bower, D. J. et al. Linking the evolution of terrestrial interiors and an early outgassed atmosphere to astrophysical observations. Astron. Astrophys.631, 10.1051/0004-6361/201935710 (2019).
- 71.Marty B, Dauphas N. “Nitrogen isotopic compositions of the present mantle and the Archean biosphere”: Reply to comment by Pierre Cartigny and Magali Ader. Earth Planet. Sci. Lett. 2003;216:433–439. doi: 10.1016/S0012-821X(03)00506-5. [DOI] [Google Scholar]
- 72.Dalou, C., Deligny, C. & Füri, E. Nitrogen isotope fractionation during magma ocean degassing: tracing the composition of early Earth’s atmosphere. Geochem. Perspect. Lett. 27–31, 10.7185/geochemlet.2204 (2022).
- 73.Kegerreis, J. A., Eke, V. R., Massey, R. J. & Teodoro, L. F. A. Atmospheric erosion by giant impacts onto terrestrial planets. Astrophys. J.897, 10.3847/1538-4357/ab9810 (2020).
- 74.Schlichting HE, Sari RE, Yalinewich A. Atmospheric mass loss during planet formation: The importance of planetesimal impacts. Icarus. 2015;247:81–94. doi: 10.1016/j.icarus.2014.09.053. [DOI] [Google Scholar]
- 75.Grady MM, Wright IP. Elemental and isotopic abundances of carbon and nitrogen in meteorites. Space Sci. Rev. 2003;106:231–248. doi: 10.1023/A:1024645906350. [DOI] [Google Scholar]
- 76.Deng J, Du Z, Karki BB, Ghosh DB, Lee KKM. A magma ocean origin to divergent redox evolutions of rocky planetary bodies and early atmospheres. Nat. Commun. 2020;11:2007. doi: 10.1038/s41467-020-15757-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Gaillard, F. et al. Redox controls during magma ocean degassing. Earth Planet. Sci. Lett.577, 10.1016/j.epsl.2021.117255 (2022).
- 78.Sarafian AR, et al. Angrite meteorites record the onset and flux of water to the inner solar system. Geochim. Cosmochim. Acta. 2017;212:156–166. doi: 10.1016/j.gca.2017.06.001. [DOI] [Google Scholar]
- 79.Sarafian AR, John T, Roszjar J, Whitehouse MJ. Chlorine and hydrogen degassing in Vesta’s magma ocean. Earth Planet. Sci. Lett. 2017;459:311–319. doi: 10.1016/j.epsl.2016.10.029. [DOI] [Google Scholar]
- 80.Blanchard, I. et al. The metal–silicate partitioning of carbon during Earth’s accretion and its distribution in the early solar system. Earth Planet. Sci. Lett.580, 10.1016/j.epsl.2022.117374 (2022).
- 81.Suer T-A, Siebert J, Remusat L, Menguy N, Fiquet G. A sulfur-poor terrestrial core inferred from metal–silicate partitioning experiments. Earth Planet. Sci. Lett. 2017;469:84–97. doi: 10.1016/j.epsl.2017.04.016. [DOI] [Google Scholar]
- 82.Hirschmann, M. M., Bergin, E. A., Blake, G. A., Ciesla, F. J. & Li, J. Early volatile depletion on planetesimals inferred from C-S systematics of iron meteorite parent bodies. Proc. Natl Acad. Sci. USA118, 10.1073/pnas.2026779118 (2021). [DOI] [PMC free article] [PubMed]
- 83.Abernethy, F. A. J. et al. Stable isotope analysis of carbon and nitrogen in angrites. 48, 1590–1606, 10.1111/maps.12184 (2013).
- 84.Grady, M. M., Wright, I. P. & Pillinger, C. T. Carbon in howardite, eucrite and diogenite basaltic achondrites. 32, 863–868, 10.1111/j.1945-5100.1997.tb01576.x (1997).
- 85.Keil K. Angrites, a small but diverse suite of ancient, silica-undersaturated volcanic-plutonic mafic meteorites, and the history of their parent asteroid. Geochemistry. 2012;72:191–218. doi: 10.1016/j.chemer.2012.06.002. [DOI] [Google Scholar]
- 86.Wu N, Farquhar J, Dottin JW, Magalhães N. Sulfur isotope signatures of eucrites and diogenites. Geochim. Cosmochim. Acta. 2018;233:1–13. doi: 10.1016/j.gca.2018.05.002. [DOI] [Google Scholar]
- 87.Li Y, Dasgupta R, Tsuno K. The effects of sulfur, silicon, water, and oxygen fugacity on carbon solubility and partitioning in Fe-rich alloy and silicate melt systems at 3 GPa and 1600 °C: Implications for core–mantle differentiation and degassing of magma oceans and reduced planetary mantles. Earth Planet. Sci. Lett. 2015;415:54–66. doi: 10.1016/j.epsl.2015.01.017. [DOI] [Google Scholar]
- 88.Moore G, Vennemann T, Carmichael I. An empirical model for the solubility of H2O in magmas to 3 kilobars. Am. Mineralogist. 1998;83:36–42. doi: 10.2138/am-1998-1-203. [DOI] [Google Scholar]
- 89.Li, Y., Dasgupta, R. & Tsuno, K. Carbon contents in reduced basalts at graphite saturation: Implications for the degassing of Mars, Mercury, and the Moon. J. Geophys. Res. Planets, 10.1002/2017je005289 (2017).
- 90.Duncan MS, Dasgupta R, Tsuno K. Experimental determination of CO2 content at graphite saturation along a natural basalt-peridotite melt join: Implications for the fate of carbon in terrestrial magma oceans. Earth Planet. Sci. Lett. 2017;466:115–128. doi: 10.1016/j.epsl.2017.03.008. [DOI] [Google Scholar]
- 91.Tagawa S, et al. Experimental evidence for hydrogen incorporation into Earth’s core. Nat. Commun. 2021;12:2588. doi: 10.1038/s41467-021-22035-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kadik AA, et al. Solution behavior of reduced N–H–O volatiles in FeO–Na2O–SiO2–Al2O3 melt equilibrated with molten Fe alloy at high pressure and temperature. Phys. Earth Planet. 2013;214:14–24. doi: 10.1016/j.pepi.2012.10.013. [DOI] [Google Scholar]
- 93.Kadik AA, et al. Solubility of nitrogen, carbon, and hydrogen in FeO–Na2O–Al2O3–SiO2 melt and liquid iron alloy: Influence of oxygen fugacity. Geochem. Int. 2015;53:849–868. doi: 10.1134/S001670291510002X. [DOI] [Google Scholar]
- 94.Roskosz M, Bouhifd MA, Jephcoat AP, Marty B, Mysen BO. Nitrogen solubility in molten metal and silicate at high pressure and temperature. Geochim. Cosmochim. Acta. 2013;121:15–28. doi: 10.1016/j.gca.2013.07.007. [DOI] [Google Scholar]
- 95.Dalou C, Hirschmann MM, von der Handt A, Mosenfelder J, Armstrong LS. Nitrogen and carbon fractionation during core–mantle differentiation at shallow depth. Earth Planet. Sci. Lett. 2017;458:141–151. doi: 10.1016/j.epsl.2016.10.026. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
All data supporting the findings of this study are available within the paper and supplementary information and source data files (Supplementary Data 1–6). Additional data related to this paper may be requested from the authors.