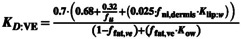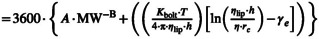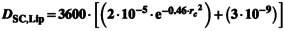Abstract
Physiologically‐based pharmacokinetic models combine knowledge about physiology, drug product properties, such as physicochemical parameters, absorption, distribution, metabolism, excretion characteristics, formulation attributes, and trial design or dosing regimen to mechanistically simulate drug pharmacokinetics (PK). The current work describes the development of a multiphase, multilayer mechanistic dermal absorption (MPML MechDermA) model within the Simcyp Simulator capable of simulating uptake and permeation of drugs through human skin following application of drug products to the skin. The model was designed to account for formulation characteristics as well as body site‐ and sex‐ population variability to predict local and systemic bioavailability. The present report outlines the structure and assumptions of the MPML MechDermA model and includes results from simulations comparing absorption at multiple body sites for two compounds, caffeine and benzoic acid, formulated as solutions. Finally, a model of the Feldene (piroxicam) topical gel, 0.5% was developed and assessed for its ability to predict both plasma and local skin concentrations when compared to in vivo PK data.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
Previous models range from simple quantitative structure activity relationship models to depth resolved mechanistic models, such as the one presented here. However, many of the previous models face challenges related to their implementation and parameterization.
WHAT QUESTION DID THIS STUDY ADDRESS?
The current model aims at using physiologically‐based pharmacokinetic modeling and simulation methodologies to reliably predict local bioavailability of active pharmaceutical ingredients formulated in drug products applied on the skin.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
The model accounts for differing physiology between various anatomic regions. Formulation properties are accounted for to improve predictions of systemic and local bioavailability and the impact of formulation attributes on bioavailability.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
The multiphase, multilayer mechanistic dermal absorption model provides a mechanistic understanding of the impact of drug product characteristics, as such, it may be used to support decision making on formulation design and drug product development for reference and generic drugs.
INTRODUCTION
Physiologically‐based pharmacokinetic models (PBPK) 1 , 2 have a unique advantage compared with other in silico approaches in that they consider physicochemical properties, pharmacokinetic (PK) characteristics, and drug product quality attributes, as well as physiology of individual subject(s) within a mechanistic framework. This allows for inter‐ and intra‐individual differences to be accounted for within the model structure resulting in more accurate predictions of absorption, distribution, metabolism, excretion in the population of interest. 3 This is of particular importance when the aim of the modeling and simulation exercise is to assess bioequivalence between the reference product and its generic. 4 , 5 Another advantage of the PBPK modeling approach is its capability for extrapolation to special populations (i.e., pediatrics, pregnancy, or diseased populations). Once the model performance is verified for a particular drug/drug product in one population, it can be assessed with reasonable confidence in another verified population. 6 For instance, it is possible to leverage the information about product performance in young healthy volunteers to predict a drug's disposition in elderly patients, provided that the physiological differences between these populations including barrier properties of the skin are well‐characterized. This unique feature of PBPK is of particular interest from an industrial and regulatory perspective as conducting clinical studies in a particular population may not be feasible or ethical.
PBPK models along with appropriate human physiology data have already been shown to reduce and refine clinical trials in other areas, such as drug–drug interactions, dose selection in first in human clinical studies, formulation optimization, oral dissolution, dose optimization in special populations, and assessment of oral drug absorption under fed conditions. 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
Estimating the rate and extent of drug exposure both locally and in the systemic circulation is crucial for assessing the bioavailability and/or safety of drug products applied to the skin, cosmetics, and environmental chemicals. To that end, animal models have been developed and used to support drug development programs. However, due to the fact that animal data are sometimes poorly correlated with human data when comparing bioavailability following application to the skin, 16 combined with the high cost and time‐consuming attributes of animal experiments, many academic and industrial researchers have been prompted to develop economically viable and scientifically informative in silico and in vitro methods to describe dermal drug absorption.
There are a number of in silico models that have been developed to describe the skin absorption of xenobiotics applied to the skin surface available in the literature. These models range from quantitative structure–activity relationship (QSAR) to mechanistic physiologically based models. 17 , 18 , 19 , 20 , 21 , 22 , 23 However, in certain instances, these models fail to account for the complexity associated with formulation attributes of the applied drug products and often consider just the case of absorption from aqueous solutions in an average individual. A critical aspect of utilizing PBPK modeling and simulation toward predicting the local and systemic absorption of drugs applied to the skin with a therapeutic intent is accounting for drug product (formulation) attributes, physicochemical and structural characteristics, and dynamic changes, such as evaporation of volatiles. 24 These parameters may impact local bioavailability and, thereby, the clinical response. 25 , 26 , 27 Knowledge gaps related to the presence and role of excipients, their relative amounts in a drug product, the microstructure of drug products applied to the skin, and the changes the product undergoes following application (metamorphosis) are continuously getting narrower. As such, appropriately parameterized dermal PBPK models may be able to predict the in vivo performance of various drug products applied to the skin, and thereby support their development. To that end, the development of enhanced quantitative tools that implement PBPK modeling and simulation approaches for such products and account for drug product attributes are considered promising. 27 , 28 , 29 , 30
Here, we introduce the multiphase and multilayer mechanistic dermal absorption (MPML MechDermA) model implemented within the Simcyp Simulator, which is an enhanced version of an in silico model previously reported by Polak et al. 31 The MPML MechDermA model allows for a quantitative description of drug uptake and permeation through human skin following application of drug products to the skin by accounting for formulation characteristics as well as body site‐ and sex‐specific population variability. The objective of this work is to introduce the MPML MechDermA model and provide potential users with a detailed description of the structure of the model at its current state and the relevant assumptions and limitations. Example simulations for caffeine and benzoic acid are provided to demonstrate the effect of sex and body‐site specific physiology parameters incorporated in the model. A detailed overview of the development and verification of a dermal PBPK model for Feldene (piroxicam) topical gel 0.5%, for which data on drug product attributes is available, is also provided here to demonstrate model functionality. The model functionality is constantly expanding, and new features are added with the goal of more reliable predictions. The predictive performance of the model in terms of local tissue and systemic exposure has been assessed using limited case studies available in the literature and is ongoing. 5 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44
Throughout this paper, the term “uptake” is used to describe the process of drug partitioning from the vehicle into the skin. The term “permeation” is used to describe the process of drug movement through the skin, including partitioning, diffusion, and binding processes within the skin. The term “absorption” encompasses both processes and describes the entire process of drug transport from the vehicle to its end point, whether that be the systemic circulation or a local site.
METHODS
Description of the MPML MechDermA model
The MPML MechDermA model, accounts for one‐dimensional partitioning and diffusion processes within a three‐dimensional physiologically based compartmental framework. The model was built using a “bottom‐up” approach based on a database of physiological parameters describing the spatial geometry and composition of skin physiology (see Tables S1 and S2). Some parameters, such as viable epidermis thickness, were found to be relatively constant between sexes and body sites; however, other parameters, such as pH (which is expressed on a log scale), varied considerably.
There are eight anatomic locations available in the current model: face (cheek), forehead, volar forearm, dorsal forearm, upper arm, back (torso), upper leg (thigh), and lower leg. In addition, sex‐specific differences are accounted for where the data allow. The richest amount of information was available for the volar forearm, therefore, if a region‐specific parameter was not available, the value of the same parameter for the volar forearm was assumed to fill the data gap.
Each physiological parameter is expressed as a mean with an associated percentage coefficient of variation (%CV) describing either a normal or log‐normal distribution. When constructing each simulation, each individual is assigned a unique parameter value from the distribution. This results in the construction of a series of unique individuals; the simulation is executed once for each individual. 2
The model is implemented within the Simcyp Simulator, and is therefore integrated into a full body PBPK distribution model 45 , 46 which allows prediction of systemic exposure following application of products to the skin. Therefore, the further distribution of drug to other tissues following dosing, pharmacodynamic effects, 47 and finally metabolism, elimination, and systemic drug–drug interactions can be modeled mechanistically. 2 , 48
As such, to simulate the in vivo scenario, information describing the broader PK of the compound is also required. This includes fraction unbound in plasma (f u ), blood:plasma partition ratio (B:P), and volume of distribution at steady‐state; all of which can be predicted from physicochemical properties of the drug within the Simulator. However, prediction of key parameters based on the physicochemical properties alone increase the parameter uncertainty and therefore measured parameters should be sought where possible. Information is also required describing the systemic clearance of the compound. As a minimum, this could be a single parameter describing total plasma clearance obtained from data following intravenous administration. However, depending on the compound and the simulation objective, more information relating to metabolizing enzyme kinetics and transporter affinity may be required for accurate simulation outputs.
A vast array of options for clinical trial simulation is available. These include single or multiple dosing regimens, and the application area at several body sites where different product doses/volumes may be applied. Figure 1 shows details of formulation models, the MPML MechDermA model structure, and the different populations that can be simulated.
FIGURE 1.
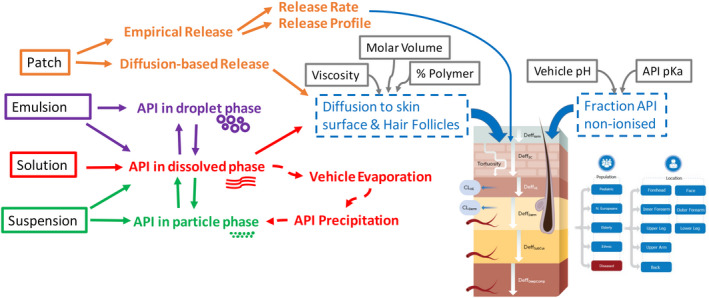
Schematic representation of the multiphase, multilayer mechanistic dermal absorption (MPML MechDermA) Model Structure within the Simcyp Simulator. API, active pharmaceutical ingredient.
Model structure
The model is constructed based on three types of parameters: system (physiology), compound, and formulation. These parameters are then combined using a system of ordinary differential equations (ODEs) that describe their interactions mechanistically.
The model framework is composed of a series of physiologically based compartments; each has an ODE which accounts for movement of drug in and out based on concentration gradient, diffusion coefficients, and relative affinities.
The below generalized diffusion equation is an ODE‐based approximation of Fick's law, which forms the basis of mass transport between all compartments in the MPML MechDermA model. 31 , 49 , 50 The rate of mass change in compartment i is described in Equation 1.
| (1) |
where, D refers to a diffusion coefficient, K is a partition coefficient, H is a compartment thickness, M is a compartment mass, and V is a compartment volume.
The diffusional aspect of the equation was based on a model designed by Shatkin and Brown. 50 In the Shatkin and Brown model, a scalar of 0.5 was applied to the i + 1 compartment volume when moving between compartments, as an attempt to address the boundary condition challenges in a simpler compartmental model. A similar approach has been used in other works 51 , 52 to handle the boundary conditions. This approach was originally introduced in the Polak et al., 2012 model 31 and extended to the MPML MechDermA model described here. For a more detailed derivation of the differential equations, see Appendix S1.
System parameters (physiology)
Stratum corneum
The stratum corneum (SC) is modeled as a “brick‐and‐mortar” structure, where “bricks” (corneocytes) are embedded within the “mortar” of an intercellular lipid matrix. 53 , 54 The inter‐cellular lipids form an isotropic phase through which the drug diffuses via a tortuous path. Within each SC layer, the drug can pass into corneocytes, where it can bind to keratin or become entrapped by ionization. 55 , 56
The SC, in terms of parameterization, is split into four “bins” which are increasingly hydrated with depth. Each simulated individual is assigned a total number of SC layers from the defined distribution for the relevant body site, and these are split evenly among the four bins, and any excess layers are assigned to the bottom bin. Input parameters, such as hydration, change from bin to bin but remain constant within the bin. Calculated parameters, such as height of the corneocytes (H corn) are assigned per layer of SC. A detailed outline of how the SC is constructed in the model can be found in the Appendix S1.
Given the corneocyte dimensions assigned to each individual, it is possible to calculate the effective diffusion path length L eff of the inter‐cellular lipid pathway in each layer.
| (2) |
where Tort is the tortuosity of the lipid filled inter‐cellular pathway (i.e., ratio between the effective distance that the drug molecule must cover by diffusion and the thickness of one cell layer []).
The default value for Tort is assumed to be as 12.7 (unitless) based on path‐length (calculated by Talreja et al. 57 ) obtained from analysis of the stained images of SC samples from multiple donors. An alternative theoretical approach has been presented by Johnson and colleagues where tortuosity was calculated based on the dimensions of corneocytes and the number of cell layers assuming corneocytes are impermeable (impediments) making the estimated effective tortuosity very large. 58 This value is considerably higher than the value suggested by Talreja et al., 57 which is used as the default value within the model. However, if combined with the SC diffusion coefficient presented by Johnson in the same publication, 58 the permeation rates are more comparable.
Viable skin and subdermal tissues
The viable tissue is composed of four layers–viable epidermis (VE), dermis, subcutis, and muscle. Each of these layers are modeled as a single well‐stirred compartment but can be further discretized if required. The volume of the VE (V VE) and dermis (V D ) are calculated from the effective area At accounting for the volume exclusion of the traversing hair follicles, and their relative thickness, H VE and H D . The follicles are assumed to terminate in the dermis, therefore, the area of application (A app) is used to calculate the volume of deeper layers.
Hair follicles
Hair follicles are simulated as a vertical cylinder, with a hair shaft in the middle and the remaining volume consisting of sebum. Only vellus hair follicles are accounted for in the model. The hair follicle extends from the surface of the skin to the dermis, no exchange of diffusing drug mass with the epidermis is assumed. Therefore, the hair follicle acts as a shunt that can take the drug from the surface of the skin and exchanges with the dermis; depending on the drug's relative affinity to, and diffusivity in, sebum. The surface area occupied by hair follicles (A HF) is calculated from the application area, number of hair follicles per unit area (N HF), and the radius of the follicle r HF.
| (3) |
The area and volume occupied by sebum can similarly be calculated (Equations 4 and 5) assuming that the hair follicle spans to the top of the dermis: N HF refers to the hair follicle density (hair follicles per cm2), and r HF and r HS refer to the hair follicle and hair shaft radius, respectively.
| (4) |
| (5) |
Compound parameters
Parameters that describe the physicochemical properties of the drug of interest are essential user input parameters. The absolute minimum set of parameters required to run a simulation in the MPML MechDermA is molecular weight (MW), LogP (octanol: water), and ionizability (pKa) and information on systemic clearance. This would be sufficient to simulate uptake and permeation of a drug through the skin layers, from an aqueous vehicle using all QSAR‐predicted parameters, such as skin partition coefficients describing drug partitioning between the different skin layers and diffusion coefficients describing drug diffusion within a skin layer. However, it is advisable to provide the model with measured parameters as much as possible to reduce the uncertainty caused by QSAR‐predicted parameters. If a formulation other than an aqueous solution is to be simulated, then further information is required for parametrization of the formulation models, the extent of which would depend upon the complexity of the formulation in question.
Following release from the formulation (discussed below), permeation of the drug is determined by an interplay between physiology and the various drug parameters. Partitioning into the first layer of the SC is controlled by the partition coefficient K SClip:v and is often rate limiting. Diffusion of the drug through the SC is then controlled by the diffusion coefficient D SC,lip, as the intercellular pathway is assumed to be the major route for most drugs. The progress of the drug across the SC can be prolonged in each layer due to partitioning into the corneocyte, where it can bind to keratin based on fraction unbound in SC (f u,sc) or become entrapped by ionization. However, the drug must partition back into the extracellular lipid in order to diffuse to the next layer, therefore, it is assumed transcellular transport does not occur. Once the drug has diffused through all of the SC layers, it then partitions to the viable epidermis based on the relevant partition coefficient (K ve:sclip), diffuses through the VE, as described by the viable epidermis diffusion coefficient (D VE), and goes to the dermis based on the partition coefficient K D:VE. Once in the dermis, the drug can partition to the blood (systemic circulation), but can also continue to diffuse to deeper layers, which is dictated by the diffusion and partition coefficients of the relative layers. Table 1 lists the QSAR models embedded into the MPML MechDermA model used to predict drug parameters. Where multiple options (multiple QSAR models) are available, the current default method is highlighted in bold. The non‐ionized drug fraction, “f ni,” term below is calculated using the Henderson–Hasselbalch equation at the relevant pH.
TABLE 1.
Available QSAR models for predicting various parameters in the MPML MechDermA (default methods in bold)
| Parameter | QSAR name and equation | Reference | Description | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Drug partition parameters | ||||||||||||
| Stratum corneum lipid to water partition coefficient (K SClip:w) |
Equation 42 ‐ Nitsche 2006 Equation 43 ‐ Raykar 1988 Equation 44 ‐ Hansen 2013 |
108, 109, 110 | K SClip:w describes the relative affinities of water and the stratum corneum lipid phase | |||||||||
| Sebum: water partition coefficient (K sb:w) |
Equation 45 ‐ Valiveti 2008 Equation 46 ‐ Yang 2018
where: f ni – fraction of the drug which is in non‐ionized form for current pH f CAT – fraction of the drug which is cation form for the current pH |
111 | K sb:w describes the relative affinities of water and sebum | |||||||||
| Stratum corneum to viable epidermis partition coefficient (K SC:VE) |
Equation 47 ‐ Shatkin and Brown 1991 Equation 48 ‐ Modified Chen 2015 |
20, 50 |
K
SClip:VE describes the relative affinities of viable epidermis and stratum corneum
|
|||||||||
| Dermis to viable epidermis partition coefficient (K D:VE) |
Equation 49
|
20, 50 | Calculated based on estimated affinities from Chen and Shatkin and Brown methods | |||||||||
| Dermis to blood partition coefficient (K D:b ) |
Equation 50 ‐ Shatkin and Brown |
50 | ||||||||||
| Dermis to Sebum partition coefficient (K D:sb) |
Equation 51 |
|||||||||||
| Subcutis to dermis; muscle to subcutis; blood to subcutis; blood to muscle partition coefficients | User defined (No QSARs available) Default value = 1 | These subdermal tissue partition coefficients should be obtained from experimental methods or other theoretical calculations or QSARs. These tissues can be modified to mimic other deep tissues such as synovial fluid | ||||||||||
| Drug Diffusion Parameters | ||||||||||||
| Diffusion coefficient for SC and sebum lipid (D sc,lip/D sb) (cm2/h) |
Equation 52 ‐ Johnson Method
A = 0.000145 B = 1.32 K bolt = 1.38E‐16 J/K T [°K] = Skin[°C] + 273.15 Equation 53 ‐ Mitragotri Method
Where
Equation 54 ‐ Wang 2006 |
112 |
Johnson model is an adaptation of Stokes‐Einstein equation for diffusivity of the molecule where the parameters A, B, and gammas were estimated using the dermal diffusion data through lipid bilayer systems. The MPML MechDermA model allows modification of viscosity of SC over depth as well as that of sebum Mitragotri derived a relationship with molecular weight based on first principles and parameterization from experimental data Wang equation is similar to Mitragotri where the coefficients were estimated with a different set of experimental data |
|||||||||
| Diffusion Coefficient in VE and Dermis (D D or D VE) (cm2/h) |
Equation 55 ‐ Modified Chen 2015 Where: fu–unbound fraction of the drug; f ni,D–fraction of the drug which is in non‐ionized form for current pH; D D,free–free (unbound) drug diffusion in the dermis |
20, 68 | This is an adaptation of original Kretsos 2008 model by Chen et al. 2015 by using lipid fraction of 2.5% and using K sc,lip:w rather than LogP | |||||||||
| Diffusion coefficients in muscle and subcutis compartments | User defined (No QSARs available) Default = 1 · 10−5 | ‐ | These subdermal tissue partition coefficients should be obtained from experimental methods or other theoretical calculations or QSARs | |||||||||
| Binding in various tissues and Corneocyte permeability | ||||||||||||
| Cornecoyte permeability (P cell) (cm/h) | User defined (No QSARs available). Default = 1 · 10−5 | ‐ | The default value of this parameter is 10−5. However, this likely varies by compound. Currently no methods are available to predict this parameter | |||||||||
| Steady state binding in SC (f u,sc) |
Equation 56 ‐ Polak et al. 2018 (requires HBA, and LogP) f u,sc = 1 – (EXP(logK Nernst )/(1 + EXP(logK Nernst )) where: logK Nernst = (ln[HBA + 4.824]) (ln(abs[LogP])) Equation 57 ‐ Nitsche 2006 f u,sc = 1 / (1 + PCpro) where PCpro = 5.4·(K o:w 0.27) PCpro is the SC protein to water partition coefficient |
108, 113 | This model assumes the keratin binding is non‐saturable and equilibrium is established instantaneously. Binding is reversible | |||||||||
| Dynamic Binding in SC (K on/K off model) |
Equation 58 ‐ Seif et al. 2012 |
114 | This model accounts for difference in “on and off” rate for drug adsorption onto skin protein accounting for time‐dependent nonlinearity in binding. Binding/adsorption is reversible | |||||||||
| Binding in muscle (f u,muscle) |
Equation 59 Minimum predicted value truncated to 0.001 |
In‐house empirical model | ||||||||||
| Binding in dermis and VE |
Equation 60 where: f u –unbound fraction of the drug; f ni,t –fraction of the drug which is in non‐ionized form for current pH; Cut is the unbound concentration in tissue (dermis or VE) |
20, 68 | ||||||||||
Abbreviations: MPML MechDermA, multiphase, multilayer mechanistic dermal absorption; QSAR, quantitative structure activity relationship; SC, stratum corneum; VE, viable epidermis.
Formulation and drug product parameters
When predicting dermal absorption using in silico methodologies, accounting for the specific quality attributes of the drug product is often overlooked. Most published models describe uptake from aqueous solutions, which is generally not representative of the dosage forms in clinical use. Marketed products are frequently semi‐solid dosage forms (often multiphase systems) and typically contain multiple inactive ingredients that are formulated to modulate the drug delivery into the skin and to optimize the therapeutic effectiveness of the product. Therefore, accounting for the physical properties of a specific drug product formulation is crucial for accurate simulation of drug uptake into the skin.
The MPML MechDermA model incorporates four distinct formulation types, which allow mechanistic simulation of the majority of available semisolid dosage forms that are applied to the skin. These are solution (monophasic), emulsion (biphasic), emulsion with particles (triphasic), and suspension (biphasic).
Solution
The solution formulation type is used to simulate solutions and single‐phase gel‐based systems where the drug is fully dissolved. Viscosity (as an apparent viscosity) and molar volume of the vehicle are the input parameters used to predict drug diffusion within the vehicle. Dose refers to the amount of drug applied on the skin surface. is the volume of applied formulation.
Thickness of applied formulation is calculated as:
| (6) |
The applied dose is distributed to the tissue (Dose T ) and hair follicle (DoseHF) accessible area relative to the surface area available for each as shown in equations below.
| (7) |
| (8) |
It is assumed that only a drug positioned directly above the hair follicles can be absorbed via that route.
Similarly, the applied formulation volume is also distributed between tissue and hair follicles based on their relative surface area, as shown below.
| (9) |
| (10) |
In order to model diffusion of drug within the formulation, and the effect of parameters such as viscosity on diffusion, in the current model, the formulation compartment is subdivided into three compartments. At the start of the simulation, the tissue accessible dose (Dose T ) is split evenly between these discretized tissue accessible formulation compartments. The hair follicle accessible dose ( is placed in a single hair follicle accessible formulation compartment. All other skin tissue compartments initial states are zero. The method utilized by the MPML MechDermA model to describe drug diffusion within the formulation involves the implementation of the Scheibel 1954 method and is in Table S3. Another important parameter is solubility in the vehicle continuous phase as relative to water. If the continuous phase consists mainly of water, then the QSAR predicted value of K sclip:w may be appropriate for use in the model. However, if the continuous phase contains solubility modifiers that can influence the thermodynamic activity of the drug in the formulation, such effects can potentially be captured by multiplying by the solubility ratio (see Equation 41).
Emulsion and suspension
The emulsion formulation type can be used to simulate biphasic systems, such as oil in water emulsions (e.g., creams and lotions). An emulsion with solid particles can also be simulated to account for more complex triphasic systems. A triphasic system is described below which encompasses both solid particles and dispersed phase globules. The MPML MechDermA is capable of simulating poly‐dispersed populations 59 of solid particles and globules; for simplicity, a monodispersed system is described here.
The percentage volume fraction of the dispersed phase and solid particles with reference to volume of the developed formulation are user‐defined parameters. This is used to calculate volume of solid particles (TVpart Equation 11), dispersed phase (TVdisp, Equation 12), and continuous phase (TVcont, Equation 13) in the formulation as mentioned below:
| (11) |
| (12) |
| (13) |
Amount of drug present as solid particles (mg) is calculated by:
| (14) |
where ρ is the density of the solid particles.
In addition, the ratio of amount of drug in the dispersed phase/continuous phase, is required for defining initial conditions (Equation 15):
| (15) |
This means the amount of the drug (mg) in continuous phase can be calculated from Equation 16.
| (16) |
The radii of the solid particles and dispersed phase globules are used to calculate total number of solid particles, and globules present in the formulation, assuming a spherical shape.
| (17) |
where N part is the number of solid particles, Dosepart is the mass of the drug, r part is the radius of the solid particles, and ρ is the particle density. TNpart is the total number of particles.
| (18) |
where N drop is the number of dispersed phase globules, DispVolume is the volume of the dispersed phase, is the radius of the globules, and ρ is the particle density.
The total surface area of the globules in the emulsion is calculated by Equation 19:
| (19) |
Similar to the solution formulation, formulation components of the emulsion are divided to the tissue and hair follicular accessible regions. In addition, the tissue accessible formulation region is subdivided into three compartments with the dose split equally. The relevant doses for each phase, as described above, are assigned as initial conditions. The continuous phase is modeled as described for the solution above, taking viscosity, molar volume, and solubility as input parameters.
Dynamic changes
Parameterizing the model to describe the formulation of interest requires information on the formulation composition that can be obtained using in vitro drug product characterization studies. This information may include the qualitative composition of ingredients in the formulation (Q1), the quantitative composition of their relative amounts of each ingredient in the formulation (Q2), and the physical and structural properties of the drug product (Q3). The latter may be characterized by rheological tests and by measuring particle and globule size distributions, pH, and the relative affinities of the drug to be in one phase compared to another, among others. These static properties can be used as initial input to the model, describing the formulation at the beginning of its application upon the skin. However, for accurate simulation, dynamic properties of the formulation, such as drug particle dissolution, vehicle evaporation, and drug precipitation, should also be accounted for when adequate data for model parameterization is available.
Drug dissolution
For a suspension or emulsion with drug particles present in the formulation, some drug will be present in solid form, and will therefore not be available for uptake initially. This is usually because the continuous phase is assumed to be saturated. However, as the drug is absorbed from the continuous phase into the skin, the drug can dissolve from the solid phase to take its place. If the rate of dissolution is faster than the rate of uptake, then the drug concentration in the continuous phase may be expected to increase and then remain at the saturation solubility of the formulation at each point in time, and the dissolution rate would not impact the flux of drug into the skin. However, if the rate of dissolution is slower than the rate of uptake, then the drug concentration in the continuous phase can drop, and uptake can become limited by the dissolution rate.
In the MPML MechDermA model, dissolution of solid particles is modeled via the diffusion layer model, which has been described previously. 2 , 60 , 61 The dissolution rate into the continuous phase compartment for layer i can be described by Equation 20:
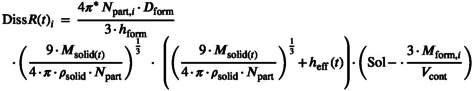 |
(20) |
where:
| (21) |
This equation assumes the relevant diffusion coefficient for dissolution is the bulk formulation diffusion coefficient. This means that dissolution of the drug in a highly viscous formulation will be slower than in a less viscous one. It is unclear whether this representation is accurate, or if it would be more suitable to use a microscopic localized diffusion coefficient closer to that in aqueous media. The is the thickness of the diffusion layer, it is limited to a maximum of 30 μm.
Vehicle evaporation
For most semisolid drug products applied to the skin, some of the excipients will be volatile, the most common candidate being water. As these products are often applied in thin layers, these volatile components often evaporate rapidly. Evaporation of formulation components results in a reduction in vehicle volume, which can cause the concentration of drug in the formulation to increase. If, during this process, the saturation solubility of the drug in the formulation is reached at any given point in time, then supersaturation or precipitation can occur. As the rate of uptake into the skin can be influenced by the concentration of the drug in the formulation vehicle, evaporation can have a large effect on the rate and extent of drug uptake. Within the MPML MechDermA model, a method is available to predict a zero‐order evaporation rate originally published by the US Environmental Protection Agency. 62 , 63
The original equation was in lbs/s, but has been converted to ml/h in Equation 22.
| (22) |
where ER is the evaporation rate in ml/h; u is the air velocity in m/s; MW is the molecular weight of vehicle in g/mole; A is the surface area in cm2; Vp is the vapor pressure of vehicle at temperature T (°C) in mmHg.
However, this model is only expected to be accurate for single solvent systems, which, in most cases, is not the case for drug products applied to the skin. Therefore, it is possible to input measured evaporation rates into the model either by use of a zero or first‐order rate constant or by interpolating a discretized evaporation time profile.
Evaporation is assumed to occur only from the continuous phase of the formulation. Therefore, TVcont at time t can be described by Equation 23 and a condition is added that sets ER to 0 once a defined maximum volume has evaporated.
| (23) |
Drug precipitation
As evaporation proceeds, once the concentration of drug reaches the saturation solubility (plus a defined “Critical Supersaturation Ratio,” default = 1) in the continuous phase at any given point in time, if the precipitation model is active, the drug will begin to precipitate. This can be predicted using a growth model, which is the reverse of Equation 20. Alternatively, an empirical precipitation rate can be defined, which can also include a secondary rate constant. This is a dynamic process; therefore, it is possible for precipitated drug to redissolve, as defined in Equation 20, should the concentration drop below saturation at a later timepoint. More detail on the precipitation models available in the Simcyp Simulator has been published previously in the context of oral absorption. 64 , 65 , 66
Drug release from the drug product, uptake and permeation through the skin layers
Equation 24 shows a generalizable form of the formulation tissue‐accessible compartment closest to the surface of the skin. The formulation can be discretized, the MPML MechDermA is discretized into three such compartments with only the compartment closest to the skin able to exchange with the SC. Therefore, the parameter (number of discretized formulation layers) would have a value of three. The P drop parameter represents the rate of transfer between dispersed and continuous phase and K disp:cont represents the drugs relative affinity between the two phases.
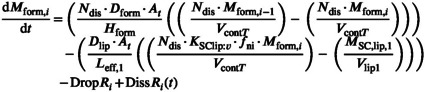 |
(24) |
where DropR i is calculated by Equation 25 and DissR i in Equation 20 above.
| (25) |
Partitioning between formulation and SC lipid is determined by Ksclip:v. This parameter is distinct from the partition coefficient between the SC lipid and water (Ksclip:w) for which it is assumed that the drug is presented to the skin in an aqueous solution. Ksclip:w should be corrected by accounting for the solubility of drug in the continuous phase of the vehicle to inform the K SClip:v parameter. The MPML MechDermA model assumes that only unionized drug (f ni) can partition from the vehicle into the lipid phase and that partitioning only occurs from the continuous phase of the vehicle. It is unclear whether the skin surface pH or the formulation pH are responsible for the f ni at the skin surface, therefore the simulator allows the user to select which of these values is used for the calculation. Currently, the interplay between these two and their buffering capacities is not modeled.
Formulation directly overlying a hair follicle is assumed to be in the hair follicle accessible formulation compartment, the rate of mass exchange in this compartment is described by Equation 26. No exchange is assumed to occur between this compartment and the tissue accessible compartment.
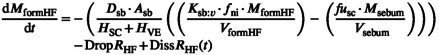 |
(26) |
The rate of mass exchange in the first SC layer lipid phase is shown in the equation below:
 |
(27) |
Drug movement between lipid and corneocyte phases depends on the corneocyte permeability (P cell). Once drug is inside the corneocyte, it can ionize (f ni,corn) and become entrapped as only non‐ionized drug may cross the cell membrane. The drug can also bind to keratin assuming static binding, dictated by f u,sc, or dynamic binding, which is dictated by a K on/off parameter. K on and K off are on and off rate for reversible drug adsorption onto skin protein accounting for time‐dependent nonlinearity in binding, respectively (see Table 1 for calculation methods). The drug must diffuse distance (Equation 2) in each lipid layer before it can be exchanged with the next layer.
All subsequent SC lipid layers two to n‐one follow the generalized form shown in Equation 28. The number of layers and therefore iterations of this compartment type are dictated by the application body site and sex of each simulated individual.
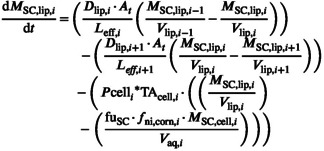 |
(28) |
For each SC lipid layer, an additional term is required to describe the rate of drug transfer to its respective corneocyte phase.
Therefore, the rate of mass change in SC layer corneocyte phase i can be described by Equation 29.
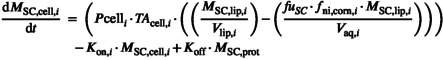 |
(29) |
In addition, the rate of mass change in the SC layer protein adsorption phase i (Equation 30):
| (30) |
The protein adsorption phase is only relevant if K on/K off method is activated, in which case f u,SC is assumed equal to one. If the fuSC model is activated, then K on = K off = 0.
The last lipid layer, for each simulated individual, exchanges with the viable epidermis at a rate determined by K SC:VE (Equation 31):
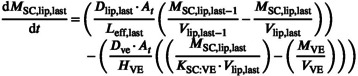 |
(31) |
Parallel to the SC layers, the drug is able to take the alternative shunt route via the sebum, the rate of mass change in the sebum compartment can be seen in Equation 32.
| (32) |
The viable epidermis can be described by simply substituting the relevant parameters into Equation 33 as there is no blood flow in this layer.
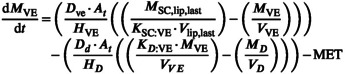 |
(33) |
where metabolism (MET) can be defined as a drug linear clearance (Equation 34) or a saturable process described by kinetic metabolite (K m) and maximum value (Vmax; Equation 35):
| (34) |
| (35) |
MET is provided by the user from the in vitro studies or can be optimized with the use of clinical data.
The remaining layers of the skin, dermis, subcutis and muscle can be discretized into as many or few compartments as deemed necessary using the generalized equation (Equation 36):
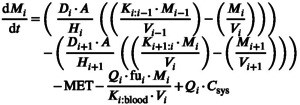 |
(36) |
where Q represents blood flow, f u fraction unbound in plasma, the partition coefficient between the layer and blood, and C sys the concentration in the systemic circulation. The term in the equation above illustrates the capability of the MPML MechDermA model to account for drug recirculating back to the skin from the systemic circulation. This feature is discussed in more detail below.
The blood flow Q i is calculated based on the application area as a proportion of the total body surface area (BSA) and the total body blood flow (Q i,total).
The total body blood flow for compartment i is calculated from the cardiac output of each simulated individual and the fraction of total blood flow assigned to that layer (f bf,i ) as presented in Equation 37:
| (37) |
This is then multiplied by a scalar (BFscalar), derived from literature analysis, which accounts for the relevant site and sex differences (Equation 38):
| (38) |
Removal of drug to the systemic circulation is largely perfusion limited as the values for K D:B predicted by the Shatkin and Brown (Equation 50 in Table 1) method only varies between around one and four between the two extremes of lipophilicity.
The dermis also requires an additional term to account for drug permeating via sebum (Equation 39):
| (39) |
Finally, the amount of drug that has permeated to the systemic circulation can be described by Equation 40:
| (40) |
Drug redistribution from the systemic circulation to the skin (recirculation)
The MPML MechDermA model considers two‐way exchange between the skin and blood circulation, as opposed to many previous models which assume a sink. 67 , 68 Recirculation of the drug and the constant exchange between the systemic circulation and local tissue at the site of application is modeled to mimic the reality as closely as possible. The drug can diffuse from the dermis, subcutis, and muscle to blood and back; however, any direct shunt in the microcirculation passing between deeper layers is not currently considered. This may be important to simulate local exposure for highly protein bound drugs, for which it has been proposed that convection or local perfusion may play a role. 69 , 70
APPLICATION OF THE MPML MECHDERMA MODEL: CASE STUDIES
Dermal PBPK models for caffeine and benzoic acid topical solutions
One of the main advantages of PBPK models is that they separate the physiological parameters and associated variability from those of the drug or drug product. Within the MPML MechDermA model, this feature is used to allow simulation of multiple body sites from the same individual. The physiology data collected to describe the eight body sites was compiled from disparate sources, which results in many permutations between body sites that compete with each other to affect the rate and extent of dermal absorption. Therefore, the aim of this example was to examine the net effect of the compiled physiological differences for sex and body site on local and systemic drug absorption. Dermal PBPK models for caffeine and benzoic acid were developed, the physicochemical properties and relevant PK parameters of the two compounds can be found in the Tables S4–S6. All model parameters were predicted using the default QSAR models, as defined in Table 1. All model workspaces and output files can be found in the Appendix S1. A series of simulations were run where 1 ml of a 10 mg/ml solution was applied to 10 cm2 of each body site. The simulation was run in a population of 100 all‐male or all‐female virtual healthy volunteers, for each body site. All simulations were run in the Simcyp Simulator version 19.
Dermal PBPK model for Feldene (piroxicam) gel 0.5%
Feldene (piroxicam) topical gel 0.5% was chosen as there is in vivo data available in the literature and some information on the formulation composition. Therefore, it was included as an example here to demonstrate the capabilities of the MPML MechDermA model in integrating information on drug product attributes, a product of added complexity compared to the simple caffeine and benzoic acid solutions. The MPML MechDermA model was parameterized based on this available formulation information, as detailed below.
Piroxicam is a non‐steroidal anti‐inflammatory drug. Relevant physicochemical and PK parameters for piroxicam, along with their references are shown in Table S7. Piroxicam is a relatively lipophilic compound with a LogP (octanol: water) of 3.06, it is an ampholyte which results in high ionization at physiological pH.
The B:P partition ratio was calculated based on rat data, 71 corrected for hematocrit and plasma binding. Volume of distribution values from 72 , 73 , 74 , 75 were 0.31, 0.15, 0.12, and 0.14 L/kg, respectively. As these values agree with the value predicted by Method two in the Simcyp Simulator, 45 the full PBPK model was used. No intravenous data were available for piroxicam, therefore oral clearance from the oral data 75 was used to estimate the plasma clearance.
In order to parameterize the MPML MechDermA, information on the Feldene (piroxicam) gel 0.5% was required. Available data in the public domain provided approximate knowledge related to the Q2 of Feldene (piroxicam) topical gel 0.5%. 76 Based on this data, it was assumed that the minor nonvolatile components make up 10% of the formulation, with the remainder comprised of 30% ethanol and 70% water (i.e., 27% and 63% of the total formulation respectively).
Evaporation rate of the volatile components of the formulation (90% v/v) was predicted using the US EPA method (Equation 22), parameterized for a 30:70 ethanol: water mixture.
The value predicted for partitioning K sclip:water, describes partitioning between water and the SC lipids. However, the enhanced intrinsic solubility of piroxicam in the vehicle caused by the addition of 30% ethanol must be accounted for. This assumed Q2 was also used to calculate the density and molar volume of the vehicle.
Calculation of the relative solubility between water and 30:70 ethanol:water was predicted using Abraham solvation parameters. 77 Solvent parameters are available for binary mixtures of ethanol and water. 78 Solvent parameters for piroxicam were taken from the LSER database. 79 The solubility ratio for the unionized form of piroxicam (the form relevant for partitioning to skin) between the binary mixture and water was found to be 9.32 (i.e., unionized piroxicam has an affinity 9.32 times higher for the binary mixture than water alone), this value was used to correct the partition coefficient between the SC lipid and the vehicle as in Equation 41, and resulted in a K sclip:vehicle parameter of 15.9.
| (41) |
A summary of the formulation inputs in the simulator is provided in Appendix S1. All of the simulations used the same compound/formulation parameters as described above, the only modifications made between simulations was to the trial design in order to replicate the relevant experimental conditions as described in the respective papers. To assess model predictability, the predefined acceptance criteria 7 , 80 , 81 of simulated PK metrics (maximum plasma concentration [Cmax] and area under the curve [AUC]) being within two fold of the observed data were used.
RESULTS
Thickness of the stratum corneum
Figure 2 shows a comparison between simulated SC thickness for 100 individuals using the theoretical calculations and measured values for each body site. The simulated thickness appears to be an accurate reflection of measured values for all body sites except the upper leg and back for which there is an overprediction, which may be attributed to the limited information available for corneocyte thickness and/or number of cell layers for these sites. However, because of the disparate sources from which they were obtained, the exact source of error cannot be determined.
FIGURE 2.
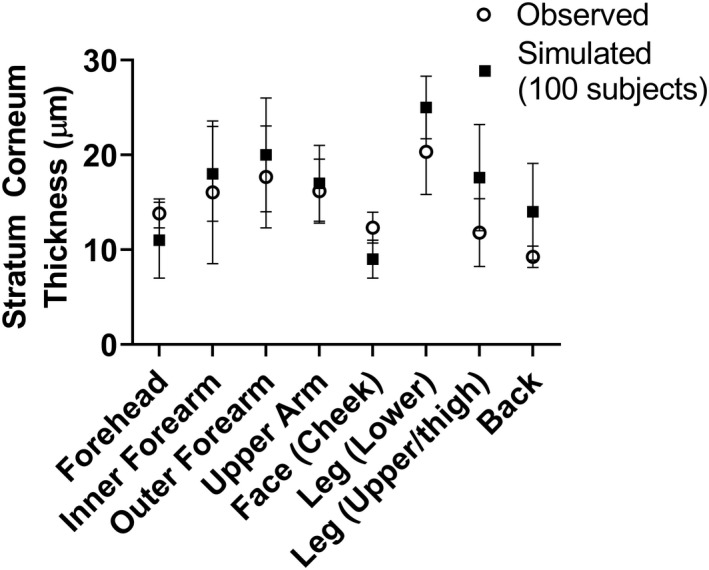
Simulated and observed (mean + SD) SC thickness for different anatomic skin sites provided by the multiphase, multilayer mechanistic dermal absorption (MPML MechDermA) model. Observed data were extracted from relevant literature sources. SC, stratum corneum.
Dermal PBPK models for caffeine and benzoic acid topical solutions
Simulations were generated leveraging the MPML‐MechDermA model to assess the impact of sex and body site on systemic (plasma) and local (SC and dermis) bioavailability, as shown in Figure 3.
FIGURE 3.
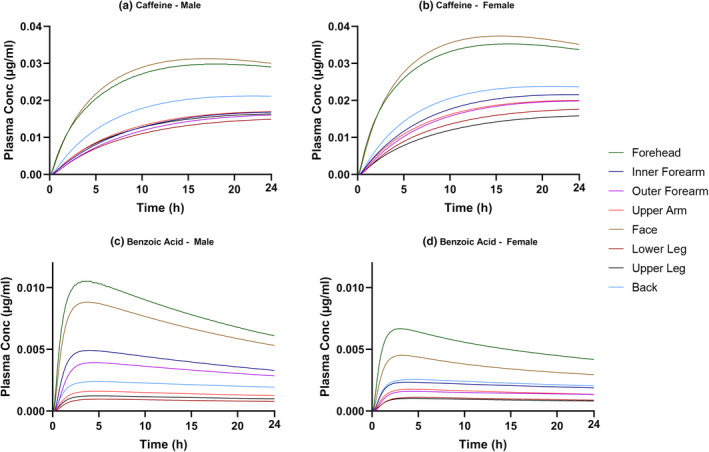
Predicted plasma concentration versus time profiles describing the absorption of caffeine (a, b) and benzoic acid (c, d) for male and female skin for eight application sites (forehead, inner forearm, outer forearm, upper arm, face, lower leg, upper leg, and back).
Although theoretical, the results presented here (Figure 3) agree with observations of Rougier et al. 82 who found total caffeine and benzoic acid absorption to be greater through forehead skin as compared to the upper arm following a 30‐min application. There was not sufficient information given in the Rougier study to replicate the trial design exactly in the simulations and because the study reported urinary recovery of radioactivity, a direct quantitative comparison was not possible.
Effect of body site
Considerable variability was observed between body sites for both compounds; however, the rank order of body sites was different between compounds and location of measurement. For both compounds, the highest plasma concentrations were observed when the drug was applied to the face or forehead (Figure 3). This outcome is expected because these two sites having the lowest number of SC layers among all body sites, on average, 13 and 12, respectively, and SC is the rate‐limiting step for permeation of most compounds across the skin. The face body site also has the thinnest corneocytes, which combined with the low number of layers results in the thinnest stratum corneum and therefore, for caffeine, the highest systemic exposure (AUC; Figure 3a,b). For benzoic acid, however, application to the forehead site, rather than the face resulted in the higher plasma concentration (Figure 3c,d). This may be attributed to the surface pH of the forehead site being lower than the face surface pH, which results in a higher fraction non‐ionized (f ni) at the skin surface for an acidic molecule and therefore higher uptake of benzoic acid. This was not a factor for caffeine as it is mainly unionized in this pH range (base, pKa 1.05).
Despite having the highest plasma concentrations, the face and forehead sites were not predicted to show the highest dermis concentrations (Figure 4). This may be because the dermis blood flow for these two sites is the highest among all body sites and therefore the drug is cleared rapidly from the dermis to the systemic circulation. This can be seen most clearly for caffeine when applied to these sites; an initial spike in dermis concentration can be seen, followed by a rapid decline as the flux is gradually decreasing while systemic uptake is continuing. Conversely, AUC in the dermis was the highest when the drug was applied to the outer forearm for both compounds. This may be attributed to the low dermis blood flow at this body site.
FIGURE 4.
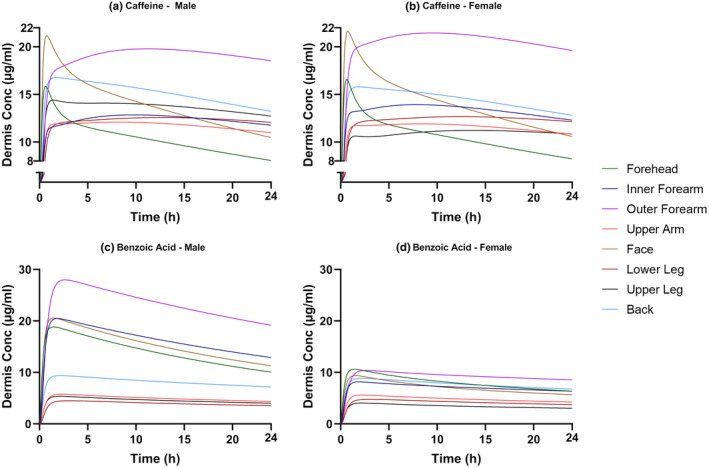
Predicted dermis concentration versus time profiles describing the absorption of caffeine (a, b) and benzoic acid (c, d) for male and female skin for eight application sites (forehead, inner forearm, outer forearm, upper arm, face, lower leg, upper leg, and back).
The concentration of drug in the SC over time (Figure 5) showed a further difference in rank order between body sites. The inner forearm had this highest local SC AUC for benzoic acid and for caffeine when applied to females. However, when applied to males, the local AUC concentration was lower than in females. However, this appears to be caused by the lower %CV for “number of SC layers” assigned to males, which results, by virtue of random sampling, in a population with a higher SC volume.
FIGURE 5.
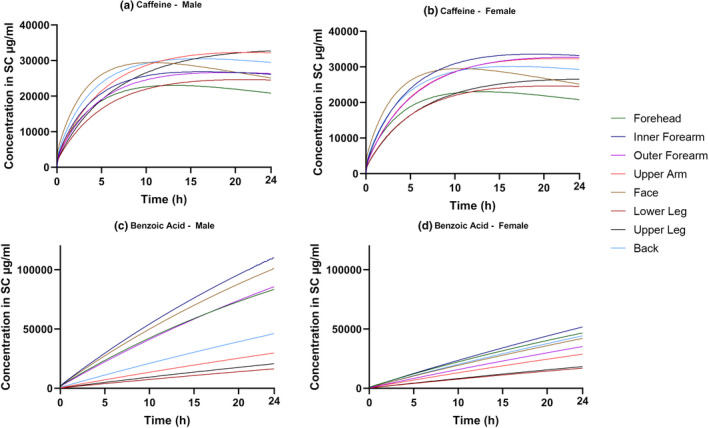
Predicted stratum corneum concentration versus time profiles describing the absorption of caffeine (a, b) and benzoic acid (c, d) for male and female skin for eight application sites (forehead, inner forearm, outer forearm, upper arm, face, lower leg, upper leg, and back).
Effect of sex
For all body sites, caffeine plasma concentrations were higher in females than males (Figure 3a). This, however, does not appear to be related to any parameters of the MPML MechDermA model. As within the Simcyp Simulator, many important parameters are calculated from BSA based on correlations defined in the literature, 2 lower exposure in females may be attributed to the lower average BSA of simulated female individuals. In this case, a lower average BSA is associated with lower average liver weight and therefore a lower absolute abundance of CYP1A2, the major metabolizing enzyme of caffeine. 83 If caffeine is dosed mg/m2 (i.e., dose normalized to BSA), no significant difference is observed in the simulated plasma concentrations between sexes (data not shown). This effect is seen in the simulation for caffeine because clearance of caffeine was described mechanistically based on known metabolism pathways. However, the benzoic acid clearance was defined using a total plasma clearance parameter (see Table S6) which does not include such an effect on metabolism in the model. The sex differences observed in benzoic acid permeation (Figure 3b,d) may be explained by the values for skin surface pH, which are different between males and females for certain body sites. For those sites, namely forehead, inner forearm, outer forearm, and face, the pH in males are lower than in females resulting in higher plasma and dermis concentration in males compared to females. For example, the average surface pH of the forehead in males is 4.5 as compared to five in females, this results in ~2.5‐fold difference in f ni (0.329 and 0.134, respectively).
Dermal PBPK model for Feldene (piroxicam) topical gel 0.5%
The PBPK model describing the gel formulation of piroxicam was verified against in vivo data from the literature. 84 , 85 , 86
A study by Fourtillan and Girault, 1992 84 reported the plasma concentration time profile after application of 2 g of the 0.5% topical gel to 20 healthy volunteers (6 female and 14 male, age range 18–30 years) twice daily for 14 days. The application area was 113 cm2 on each upper arm (226 cm2 total). The simulations were run according to the clinical study design and replicated 10 times (total 200 subjects, 30% female, age range 18–30 years). The simulated results overlaid with observed data is shown in Figure 6.
FIGURE 6.
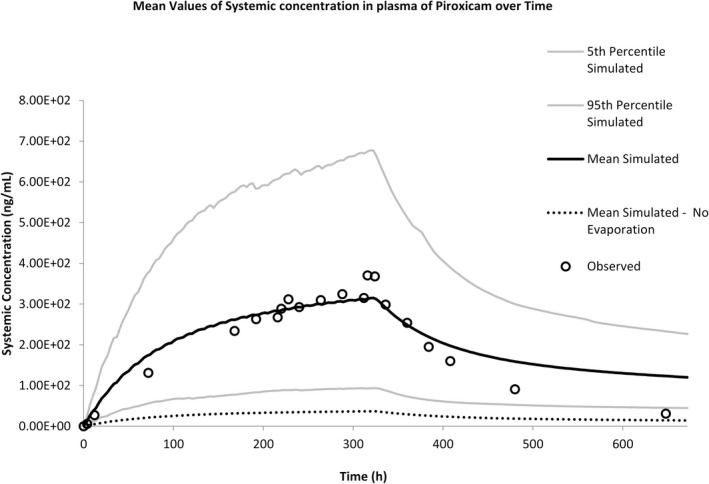
Predicted plasma concentration versus time profile describing absorption of piroxicam from Feldene Gel.
The simulation accurately captured the rate and extent of systemic absorption and met the predefined acceptance criteria. The clearance of piroxicam following removal of the formulation was slightly underpredicted, this could be due to the use of oral clearance as an estimate of clearance rather than intravenous clearance. To demonstrate the importance of accounting for evaporation in the simulation, results from a simulation where evaporation was turned off are also plotted (dashed line). This results in a large underprediction of systemic concentrations.
Another study by Kanazawa et al. 86 reported plasma concentration time profiles after topical application of a single 3 g dose of gel (15 mg of piroxicam) to a 289 cm2 area. The application site was the back, and the Japanese population within Simcyp 87 was used for the simulation, due to the origin of the study. Figure 7a shows a simulation where formulation was removed at 8 h, as stated in the study; time to Cmax (Tmax) and Cmax are both underpredicted. The study states that “residue was wiped off after 8 hours” therefore, in this simulation, the entire formulation was removed at 8 h, meaning uptake of piroxicam stops in the simulation and therefore the systemic concentration slowly decreases.
FIGURE 7.
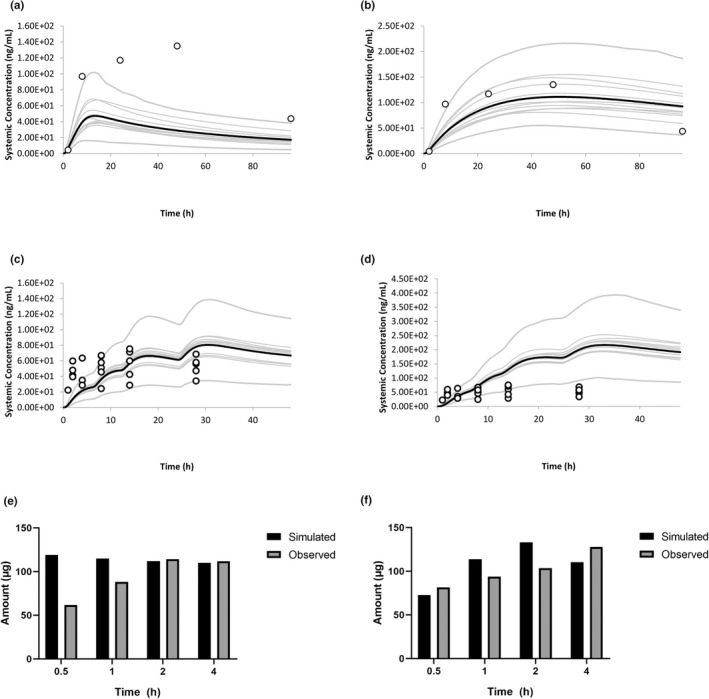
Results from Kanazawa 1987. (a) Washed at 8 h. (b) No wash performed results from Marks 1994, (c) upper leg, (d) lower leg results from Marks 1994, (e) stratum corneum skin surface biopsy, (f) viable tissue punch biopsy.
If a “what if?” simulation is run assuming that the formulation was not removed (Figure 7b), but left on the skin for the entire duration of the study, then the results are more accurately recovered for Tmax, Cmax, and AUC.
A study by Marks et al. 85 reported the plasma concentration time profile after application of 1 g of Feldene (piroxicam) topical gel 0.5% (5 mg piroxicam) to 1200 cm2 of the knee. Doses were applied at 0, 6, 12, and 24 h to 12 healthy subjects. Plasma samples were taken for 48 h.
The study was simulated 10 times (total 120 subjects) and the profiles overlaid with observed data. As the site “knee” is not available in the current model, simulations were run on the two closest anatomic sites available, the upper and lower leg. Figure 7c shows the upper leg simulation, and Figure 7d shows the lower leg.
When the drug was applied to the upper leg, predictions met the predefined acceptance criteria, however, when applied to the lower leg, the predefined acceptance criteria was not met. This may be due to the physiology of the knee being more similar to that of the upper leg in the model and demonstrates the importance of simulating the correct body site.
It should also be noted that more than 75% of the data points in this study were below the limit of detection, therefore, the observed mean PK data points plotted represent only the higher range (above the limit of quantification) of the plasma concentrations.
The same study also investigated the local concentrations of piroxicam in the skin following application of 0.1 g of piroxicam gel to 40 cm2 of the inner forearm in 24 patients. Following application, the study was terminated at 0.5, 1, 2, or 4 h and five “skin surface biopsies” were taken (i.e., tape strips). Due to the uncertainty on how much SC is removed with each biopsy, and if the size of these is even, all five biopsies were added together to obtain the “total drug in stratum corneum.” The data were corrected for the biopsy area and 74% recovery of the biopsy extraction procedure as stated in the study. The skin was not washed before taking the first biopsy, therefore any residual drug on the surface of the skin is included in these biopsies. For the simulated results, the remaining drug in the formulation was added to the total. These observed results alongside simulated results can be seen in Figure 7e. Amount in the SC + residue was well‐predicted in general, except a twofold overprediction at the first timepoint.
Following the tape stripping, a punch biopsy of the remaining skin was taken for each patient, per Marks et al. For simulation results, this was calculated as the amount in the viable epidermis + dermis. This was then corrected for the volume of the biopsy, calculated based on the 4 mm diameter, and recovery. The amount of piroxicam in the viable skin was well‐predicted for all timepoints (Figure 7f).
DISCUSSION
The MPML MechDermA model has been developed to describe the absorption of drugs applied to the skin that act either locally or systemically. This is achieved by describing partition and diffusion processes across multiple skin layers and deeper tissues, which allows local concentration predictions following the application of drugs and drug products on the skin. More realistic model predictions are made possible by accounting for sex and body site‐specific population variability in skin as well as multiple other organs affecting the PK of the drug. The latter is being made possible by the integration of the MPML MechDermA model in the Simcyp Simulator.
To demonstrate the capabilities of the MPML MechDermA model, the skin absorption and systemic disposition of caffeine and benzoic acid applied as solutions on all the available body sites were modeled (Figures 3 and 4). The performed simulations illustrated the interplay between skin physiology and drug physicochemical properties and underline the interplay is compound‐specific and varies among application sites (body sites). The simulations also demonstrated differences in the effect of body site and sex depending on which layer concentration was examined, highlighting the importance of measuring or simulating concentration at the site of action. Therefore, a simple “rank order” of permeability by body site may not be appropriate. The interaction between skin physiology and drug physicochemical properties can be further complicated by factors relating to the formulation and environmental conditions in which the drug is applied. Additional verification of the model's ability to simulate transdermal absorption at different body sites has been published elsewhere. 88
A number of considerations have guided development of the MPML MechDermA model and several limitations should be acknowledged. 89 When collecting data for each body site, data gaps were filled by applying the parameter from the inner forearm, as this site had the most data. In some cases, it may have been more appropriate to apply data from the “nearest” or “most similar” site instead; however, this would involve subjective judgment on these criteria. The dependence of dermis concentration on dermis blood flow simulated here may not be accurate for all compounds. It may be necessary to account for processes, such as binding to interstitial albumin, which could reduce uptake of drug to the systemic circulation creating a permeability‐limited blood uptake scenario and thereby reduce the impact of blood flow. 67 , 70 The validity of the assumption that the pH of the body site determines the non‐ionized fraction of the compound of interest at the skin surface has not been formally tested. If a reasonable amount of buffered formulation is applied to the skin, it may be more appropriate to assume that formulation pH will dictate f ni. In addition, the ability of the drug to ionize within the corneocyte, as in the model, is unknown and should be treated with caution for highly ionizable drugs. The interplay between buffering capacities of the skin and formulations is still largely unknown. 89
Here, dermal PBPK models for caffeine and benzoic acid topical solutions were developed to demonstrate the interplay between physicochemical properties and physiology within the model. A case study was detailed for the Feldene piroxicam topical gel 0.05% formulation of piroxicam that demonstrated the model's ability to simulate complex formulations. For the development of a credible model, it was important to account for the effect of ethanol in the formulation, which involved simulating an increased evaporation rate and accounting for the increased affinity of piroxicam for the ethanol as compared to water. The model was able to accurately capture both systemic and local concentrations across multiple studies, with no changes in parameters, with the exception of the study by Kanazawa et al. It is possible that this result is due to a large reservoir having formed in the SC, which is not accurately simulated by the model. However, the accurate simulation results from the other studies, which used the same formulation, would suggest this is unlikely. An alternative explanation may be that the wash procedure in the Kanazawa study was less than thorough, and some piroxicam remained on the skin after 8 h available for uptake into the skin. It has been observed that even theoretically thorough wash procedures may leave large amounts of drug on the skin surface. 90 , 91
Figure 7b shows a theoretical simulation where the formulation was left on the skin for the duration of the study. The results of this simulation match quite closely to the observed data. This ability to simulate “what if?” scenarios is a major advantage of PBPK modeling and allows the user to explore alternative trial design scenarios and potentially inform the design of clinical trials.
Dermal PBPK models used in development, optimization, and assessment of locally acting drug products should be sufficiently verified before leveraged for their intended purpose. Zhao et al., in 2019, have discussed at length challenges and approaches for verification of such PBPK models. Systemic plasma exposure is routinely used as a surrogate for exposure at the site of action for assessing the bioavailability of drug products that are administered orally. However, following topical application of locally acting drug products, systemic concentrations may be negligible. As demonstrated by the example dermal PBPK models developed for caffeine and benzoic acid in this paper, with the skin being one of the most robust barriers to drug absorption, local tissue and systemic circulation may not be in constant equilibrium due to a prolonged transient phase of absorption. On the other hand, measurement of local exposure can be challenging. 92 Performance assessment and verification for the MPML MechDermA model has been described in limited cases that are currently available in the public domain. 93 , 94 , 95 , 96 , 97 Additional verification of the MPML MechDermA model is ongoing to assess the predictive power of its various components.
PBPK models, such as the MPML MechDermA model, provide a mathematical representation of current knowledge and scientific understanding for the processes involved in dermal drug absorption. As these models factor in the impact of drug properties, drug product characteristics, and physiological variability, they can help understand local and systemic drug absorption under physiology considerations, such as application on various body sites, sex, age, disease, and study design considerations, such as duration of single or repeated applications of different doses and drug product removal. In the case when the MPML MechDermA model accounts for formulation parameters, such as particle size, apparent viscosity, pH, and the evaporation rate of the vehicle, the impact of drug product characteristics on drug skin permeation may be assessed. These capabilities render the MPML MechDermA model a useful tool in dermal drug product development. A case study describing successful application of the MPML MechDermA model to assess virtual bioequivalence of a diclofenac gel formulation at a local site of action has been published recently. 5
In spite of the mechanistic nature of the MPML MechDermA model, there are processes involved in drug permeation through the skin which cannot be captured by a one‐dimensional diffusion model, such as the one described here. For example, in the MPML MechDermA model, it is assumed that the lateral surface area of corneocytes in the SC is constant, although this may not be entirely accurate in reality; variable lateral dimensions are challenging to simulate using a one‐dimensional model structure. This assumption may result in an overprediction of the path length for deeper layers (Equation 2) because the values for corneocyte dimensions were assigned based on measurement of the outermost layer. 98 , 99 Even though detailed, the MPML MechDermA model is still macroscopic in nature, the SC lipid is assumed a homogeneous continuous matrix for drug diffusion, the corneocytes are composed of “protein” and water only. As such, factors, such as lipid bilayer structure, and corneocyte packing and adhesion, proposed to alter the barrier function of the skin 100 , 101 , 102 cannot be accounted for currently. In addition, in reality, the shape of a corneocyte is more complex and deviates from the ideal cuboid shape assumed in this model. 103 Maturation of keratinocytes and upward transition, including desquamation, is not considered in the model. However, given the desquamation process is considerably slower (in days) 102 compared to drug permeation kinetics (minutes and hours), its impact on drug permeation through the skin may be limited. Modeling dermal drug absorption in certain inflammatory skin diseases, such as psoriasis, may warrant consideration of such processes in the model, as the desquamation rate may be increased. 104 To model permeation through skin appendages, the model assumes the hair follicle as an insulated shunt that spans from skin surface to dermis with no drug exchange between SC and VE. In addition, the hair follicle accessible compartment does not exchange with the rest of the formulation, and therefore could become depleted for drugs with high follicular uptake. These assumptions may affect prediction of drugs for which hair follicles play a significant role.
Additional assumptions in the MPML MechDermA model are that drug partitioning can only occur from the continuous phase of emulsions and drug diffusion through the formulation is predicted using an apparent viscosity value instead of leveraging a battery of rheology data that is typically available as part of the in vitro characterization of a drug product. Further enhancements on the implementation of drug product quality attributes within the model are ongoing and aim at more reliable model predictions in the future, for example, simulating dynamic modification of formulation parameters, such as solubility as the vehicle composition is modified by metamorphosis over time and impact of inactive ingredients on active pharmaceutical ingredient permeation.
Following uptake into the SC, the drug reaches the viable epidermis and dermis, which are considered well‐mixed homogeneous layers in this model, a significant simplification of the physiological reality for these layers. If the intention is to predict the spatial distribution of drug in these layers for locally acting drugs, then more mechanistic models of these layers may be required. 70 The metabolic activity of the skin has been reported to directly impact the local bioavailability of drugs applied to the skin. 105 , 106 , 107 The model allows empirical descriptions of metabolism in the viable epidermis and dermis; however, this is not currently possible in a mechanistic manner due to a lack of quantitative data on enzyme abundances in skin layers and established in vitro–in vivo extrapolation techniques.
CONCLUSION
The MPML MechDermA model developed in this work integrates information from various published QSAR models and investigative physiology studies in a mechanistic PBPK framework. A major constituent of this work was developing a database describing the physiology and variability of multiple body sites, for both sexes in humans. This allows the model to simulate dermal absorption in virtual populations providing more realistic predictions than using a population average approach and allows extrapolation to other body sites. The case studies examined here exemplified the PBPK modeling approach in exploring the complex interplay between the physicochemical properties of the compound and skin physiological factors, as these are defined independently in the mechanistic framework. The case study for Feldene (piroxicam) topical gel 0.05% demonstrated the model's ability to simulate “real‐world” scenarios by accounting for formulation attributes and generating population predictions that were verified with clinical PK data.
AUTHOR CONTRIBUTIONS
J.F.C., N.P., and E.T. wrote the manuscript. N.P., J.F.C., F.S., T.A., F.M., E.T., S.C., P.G., K.A., S.G.R., and S.P. designed the research. N.P., J.F.C., F.S., T.A., F.M., S.A., S.C., and S.P. performed the research. A.H., O.A.T., N.P., J.F.C., F.S., T.A., F.M., S.A., S.C., M.J., and S.P. analyzed the data.
CONFLICT OF INTEREST
N.P., J.F.C., F.S., T.A., F.M., S.A., A.H., O.A.T., S.C., M.J., and S.P. are employees of Certara UK (Simcyp Division). All other authors declared no competing interests for this work.
DISCLAIMER
This article reflects the views of the individual authors and should not be construed to represent the views, policies or nomenclature of their organizations, including the FDA.
Supporting information
Appendix S1
ACKNOWLEDGEMENTS
The authors would like to thank Drs. Xinyuan Zhang and Zhanglin Ni from the US Food and Drug Administration for their support and encouragement in this work. The authors would also like to thank Dr. Yuri Dancik for his help in manuscript preparation.
Patel N, Clarke JF, Salem F, et al. Multi‐phase multi‐layer mechanistic dermal absorption (MPML MechDermA) model to predict local and systemic exposure of drug products applied on skin. CPT Pharmacometrics Syst Pharmacol. 2022;11:1060‐1084. doi: 10.1002/psp4.12814
Funding information
This research was supported by the US Food and Drug Administration (FDA) of the US Department of Health and Human Services (HHS) as part of a financial assistance award 1U01FD006521 totaling $381,876 with 100 percent funded by the FDA/HHS. The contents are those of the author(s) and do not necessarily represent the official views of, nor an endorsement, by the FDA/HHS, or the US Government
REFERENCES
- 1. Jones H, Rowland‐Yeo K. Basic concepts in physiologically based pharmacokinetic modeling in drug discovery and development. CPT Pharmacomet Syst Pharmacol. 2013;2:e63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Jamei M, Dickinson GL, Rostami‐Hodjegan A. A framework for assessing inter‐individual variability in pharmacokinetics using virtual human populations and integrating general knowledge of physical chemistry, biology, anatomy, physiology and genetics: a tale of 'bottom‐up' vs 'top‐down' recognition of covariates. Drug Metab Pharmacokinet. 2009;24:53‐75. [DOI] [PubMed] [Google Scholar]
- 3. Loisios‐Konstantinidis I, Cristofoletti R, Fotaki N, Turner DB, Dressman J. Establishing virtual bioequivalence and clinically relevant specifications using in vitro biorelevant dissolution testing and physiologically‐based population pharmacokinetic modeling. case example: naproxen. Eur J Pharm Sci. 2020;143:105170. [DOI] [PubMed] [Google Scholar]
- 4. Cristofoletti R, Rowland M, Lesko LJ, Blume H, Rostami‐Hodjegan A, Dressman JB. Past, present, and future of bioequivalence: improving assessment and extrapolation of therapeutic equivalence for oral drug products. J Pharm Sci. 2018;107:2519‐2530. [DOI] [PubMed] [Google Scholar]
- 5. Tsakalozou E, Babiskin A, Zhao L. Physiologically‐based pharmacokinetic modeling to support bioequivalence and approval of generic products: a case for diclofenac sodium topical gel,1. CPT Pharmacomet Syst Pharmacol. 2021;10:399‐411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Doki K, Darwich AS, Patel N, Rostami‐Hodjegan A. Virtual bioequivalence for achlorhydric subjects: the use of PBPK modelling to assess the formulation‐dependent effect of achlorhydria. Eur J Pharm Sci. 2017;109:111‐120. [DOI] [PubMed] [Google Scholar]
- 7. Shebley M, Sandhu P, Emami Riedmaier A, et al. Physiologically based pharmacokinetic model qualification and reporting procedures for regulatory submissions: a consortium perspective. Clin Pharmacol Ther. 2018;104:88‐110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Grimstein M, Yang Y, Zhang X, et al. Physiologically based pharmacokinetic modeling in regulatory science: an update from the U.S. Food and Drug Administration's office of clinical pharmacology. J Pharm Sci. 2019;108:21‐25. [DOI] [PubMed] [Google Scholar]
- 9. Heimbach T, Suarez‐Sharp S, Kakhi M, et al. Dissolution and translational modeling strategies toward establishing an in vitro–in vivo link—a workshop summary report. AAPS J. 2019;21:29. [DOI] [PubMed] [Google Scholar]
- 10. Jamei M. Recent advances in development and application of physiologically‐based pharmacokinetic (PBPK) models: a transition from academic curiosity to regulatory acceptance. Curr Pharmacol Rep. 2016;2:161‐169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Zhao P, Zhang L, Grillo JA, et al. Applications of physiologically based pharmacokinetic (PBPK) modeling and simulation during regulatory review. Clin Pharmacol Ther. 2011;89:259‐267. [DOI] [PubMed] [Google Scholar]
- 12. Huang SM, Abernethy DR, Wang Y, Zhao P, Zineh I. The utility of modeling and simulation in drug development and regulatory review. J Pharm Sci. 2013;102:2912‐2923. [DOI] [PubMed] [Google Scholar]
- 13. Sager JE, Yu J, Ragueneau‐Majlessi I, Isoherranen N. Physiologically based pharmacokinetic (PBPK) modeling and simulation approaches: a systematic review of published models, applications, and model verification. Drug Metab Dispos. 2015;43:1823‐1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Zhang X, Duan J, Kesisoglou F, et al. Mechanistic oral absorption modeling and simulation for formulation development and bioequivalence evaluation: report of an FDA public workshop. CPT: Pharmacomet Syst Pharmacol. 2017;6:492‐495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. McAllister M, Flanagan T, Boon K, et al. Developing clinically relevant dissolution specifications for oral drug products‐industrial and regulatory perspectives. Pharmaceutics. 2019;12:19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jung EC, Maibach HI. Animal models for percutaneous absorption. J Appl Toxicol. 2015;35:1‐10. [DOI] [PubMed] [Google Scholar]
- 17. Potts RO, Guy RH. Predicting skin permeability. Pharm Res. 1992;9:663‐669. [DOI] [PubMed] [Google Scholar]
- 18. Wang TF, Kasting GB, Nitsche JM. A multiphase microscopic diffusion model for stratum corneum permeability. I. Formulation, solution, and illustrative results for representative compounds. J Pharm Sci. 2006;95:620‐648. [DOI] [PubMed] [Google Scholar]
- 19. Wang TF, Kasting GB, Nitsche JM. A multiphase microscopic diffusion model for stratum corneum permeability. II. Estimation of physicochemical parameters, and application to a large permeability database. J Pharm Sci. 2007;96:3024‐3051. [DOI] [PubMed] [Google Scholar]
- 20. Chen L, Han L, Saib O, Lian G. In silico prediction of percutaneous absorption and disposition kinetics of chemicals. Pharm Res. 2015;32:1779‐1793. [DOI] [PubMed] [Google Scholar]
- 21. Amarah AA, Petlin DG, Grice JE, Hadgraft J, Roberts MS, Anissimov YG. Compartmental modeling of skin transport. Eur J Pharm Biopharm. 2018;130:336‐344. [DOI] [PubMed] [Google Scholar]
- 22. Anissimov YG, Jepps OG, Dancik Y, Roberts MS. Mathematical and pharmacokinetic modelling of epidermal and dermal transport processes. Adv Drug Deliv Rev. 2013;65:169‐190. [DOI] [PubMed] [Google Scholar]
- 23. Cleek RL, Bunge AL. A new method for estimating dermal absorption from chemical exposure. 1. General approach. Pharm Res. 1993;10:497‐506. [DOI] [PubMed] [Google Scholar]
- 24. FDA . Draft Guidance on Acyclovir Topical Cream, 5%, Recommended Dec 2014. Office of Generic Drugs; 2016. Revised December 2016. [Google Scholar]
- 25. Raney SG, Franz TJ, Lehman PA, Lionberger R, Chen ML. Pharmacokinetics‐based approaches for bioequivalence evaluation of topical dermatological drug products. Clin Pharmacokinet. 2015;54:1095‐1106. [DOI] [PubMed] [Google Scholar]
- 26. Raney SG, Luke MC. A new paradigm for topical generic drug products: impact on therapeutic access. J Am Acad Dermatol. 2020;82:1570‐1571. [DOI] [PubMed] [Google Scholar]
- 27. Lionberger RA. Innovation for generic drugs: science and research under the generic drug user fee amendments of 2012. Clin Pharmacol Ther. 2019;105:878‐885. [DOI] [PubMed] [Google Scholar]
- 28. Lionberger RA. FDA critical path initiatives: opportunities for generic drug development. AAPS J. 2008;10:103‐109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Zhao L, Kim MJ, Zhang L, Lionberger R. Generating model integrated evidence for generic drug development and assessment. Clin Pharmacol Ther. 2019;105:338‐349. [DOI] [PubMed] [Google Scholar]
- 30. GDUFA . Locally Acting Physiologically‐Based Pharmacokinetic Modeling: Summary of FY2019 Activities. FY2019 GDUFA Research Report; 2019. [Google Scholar]
- 31. Polak S, Ghobadi C, Mishra H, et al. Prediction of concentration–time profile and its inter‐individual variability following the dermal drug absorption. J Pharm Sci. 2012;101:2584‐2595. [DOI] [PubMed] [Google Scholar]
- 32. Puttrevu SK, Arora S, Polak S, Patel NK. Physiologically based pharmacokinetic modeling of transdermal selegiline and its metabolites for the evaluation of disposition differences between healthy and special populations. Pharmaceutics. 2020;12:942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Ngampanya A, Udomnilobol U, Sermsappasuk P, et al. Development and qualification of a physiologically based pharmacokinetic model of finasteride and minoxidil following scalp application. J Pharm Sci. 2021;110:2301‐2310. [DOI] [PubMed] [Google Scholar]
- 34. Salem F, Patel N, Polak S. Development of a PBPK model for topical lidocaine in order to predict systemic absorption in healthy volunteers, geriatrics and paediatrics. ASCPT; 2019 March 13–16; Washington, DC; 2019.
- 35. Polak S, Patel N. Development of the dermal absorption model for the ketoprofen local and systemic exposure prediction. Skin Forum Annual Meeting; 2018 June 20–21; Tallin, Estonia; 2018.
- 36. Polak S, Patel N, Rowland Yeo K, Jamei M. Assessing formulation attributes' impact on local and systemic exposure of clindamycin after topical application of pro‐drug clindamycin phosphate using PBPK modelling. Controlled Release Society Annual Meeting and Exposition; 2018 July 22–24; New York, NY; 2018.
- 37. Patel N, Cristea S., Rose R., et al. Mechanistic modelling of dermal drug absorption using the Simcyp Multi‐phase Multi‐layer MechDermA model: Case study of a transdermal patch formulation of weak base drug timolol. Gordon Research Conference; 2015.
- 38. Martins F, Patel N, Clarke JF, Polak S. Multi‐phase multi‐layer mechanistic physiologically based pharmacokinetic dermal absorption model verification including inter and intra individual variability assessment using nicotine as a model drug. AAPS PharmSci. 2018;360. Accessed May 01, 2022. https://www.certara.com/app/uploads/Resources/Posters/Multi‐Phase‐Multi‐Layer‐Mechanistic‐Physiologically‐based‐Pharmacokinetic‐Dermal‐Patel.pdf [Google Scholar]
- 39. Arora S, Patel N, Polak S. Performance verification of mechanistic dermal physiological based pharmacokinetic (PBPK) model for enhanced understanding of dermal absorption: prediction of local tissue exposure after topical application of acitretin. Ninth American Conference on Pharmacometrics (ACoP9); 2018 October 6‐11; San Diego; 2018.
- 40. Martins F, Patel N, Jamei M, Polak S. Development and validation of a dermal PBPK model for prediction of the hair follicular absorption of caffeine: application of the Simcyp MPML MechDermA model. 14th ISSX; 2017 June 26‐29; Cologne, Germany; 2017.
- 41. Martins F, Patel N, Salem F, Jamei M, Polak S. Multi‐phase multi‐layer MechDermA model: development, verification and application of a PBPK‐PD model of dermal absorption for transdermal product assessment. Perspective in Percutaneous Penetration; 2018 April 4; La Grande Motte, France; 2018.
- 42. Patel N, Benkali K, Osman‐Ponchet H, Neuhoff S, Polak S, Wagner N. Development and verification of PBPK model for a topical ceram formulation of trifarotene to simulate local and systemic exposure and model application to simulate potential CYP‐mediated drug–drug interactions. AAPS Annual Meeting and Exposition; 2018 April 4; La Grande Motte, France; 2017.
- 43. Martins F, Patel N, Salem F, Jamei M, Polak S. Multi‐phase Multi‐layer MechDermA model: development, verification and application of pbpk‐pd model of dermal absorption for topical product assessment. Gordon Research Conference; Paris; 2016.
- 44. Martins F, Patel N, Cristea S, Polak S. Development and validation of dermal PBPK model towards virtual bioequivalence assessment: prediction of dermal drug absorption of various ibuprofen formulations using Simcyp MechDermA model. DMDG; 2016 October 19–21; 2016.
- 45. Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95:1238‐1257. [DOI] [PubMed] [Google Scholar]
- 46. Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate‐to‐strong bases. J Pharm Sci. 2005;94:1259‐1276. [DOI] [PubMed] [Google Scholar]
- 47. Abduljalil K, Edwards D, Barnett A, Rose RH, Cain T, Jamei M. A tutorial on pharmacodynamic scripting facility in Simcyp. CPT Pharmacomet Syst Pharmacol. 2016;5:455‐465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Rowland Yeo K, Jamei M, Yang J, Tucker GT, Rostami‐Hodjegan A. Physiologically based mechanistic modelling to predict complex drug–drug interactions involving simultaneous competitive and time‐dependent enzyme inhibition by parent compound and its metabolite in both liver and gut–the effect of diltiazem on the time‐course of exposure to triazolam. Eur J Pharm Sci. 2010;39:298‐309. [DOI] [PubMed] [Google Scholar]
- 49. Hickson RI, Barry SI, Mercer GN, Sidhu HS. Finite difference schemes for multilayer diffusion. Math Comput Model. 2011;54:210‐220. [Google Scholar]
- 50. Shatkin JA, Brown HS. Pharmacokinetics of the dermal route of exposure to volatile organic chemicals in water: a computer simulation model. Environ Res. 1991;56:90‐108. [DOI] [PubMed] [Google Scholar]
- 51. Suzuki A, Higuchi WI, Ho NFH. theoretical model studies of drug absorption and transport in the gastrointestinal tract i. J Pharm Sci. 1970;59:644‐651. [DOI] [PubMed] [Google Scholar]
- 52. Yotsuyanagi T, Higuchi WI, Ghanem A‐H. Theoretical treatment of diffusional transport into and through an oil–water emulsion with an interfacial barrier at the oil‐water interface. J Pharm Sci. 1973;62:40‐43. [DOI] [PubMed] [Google Scholar]
- 53. Elias PM. Structure and function of the stratum corneum permeability barrier. Drug Dev Res. 1988;13:97‐105. [Google Scholar]
- 54. Marks R, Plewig G. Stratum Corneum. Springer‐Verlag; 1983. [Google Scholar]
- 55. Egawa M, Tagami H. Comparison of the depth profiles of water and water‐binding substances in the stratum corneum determined in vivo by Raman spectroscopy between the cheek and volar forearm skin: effects of age, seasonal changes and artificial forced hydration. Br J Dermatol. 2008;158:251‐260. [DOI] [PubMed] [Google Scholar]
- 56. Querleux B, Richard S, Bittoun J, et al. In vivo hydration profile in skin layers by high‐resolution magnetic resonance imaging. Skin Pharmacol. 1994;7:210‐216. [DOI] [PubMed] [Google Scholar]
- 57. Talreja P, Kleene NK, Pickens WL, Wang TF, Kasting GB. Visualization of the lipid barrier and measurement of lipid pathlength in human stratum corneum. AAPS PharmSci. 2001;3:E13‐E56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Johnson ME, Blankschtein D, Langer R. Evaluation of solute permeation through the stratum corneum: lateral bilayer diffusion as the primary transport mechanism. J Pharm Sci. 1997;86:1162‐1172. [DOI] [PubMed] [Google Scholar]
- 59. Lu AT, Frisella ME, Johnson KC. Dissolution modeling: factors affecting the dissolution rates of polydisperse powders. Pharm Res. 1993;10:1308‐1314. [DOI] [PubMed] [Google Scholar]
- 60. Wang J, Flanagan DR. General solution for diffusion‐controlled dissolution of spherical particles. 1. Theory. J Pharm Sci. 1999;88:731‐738. [DOI] [PubMed] [Google Scholar]
- 61. Hintz RJ, Johnson KC. The effect of particle size distribution on dissolution rate and oral absorption. Int J Pharm. 1989;51:9‐17. [Google Scholar]
- 62. Gajjar RM. Absorption and Evaporation of Volatile Organic Solvents from Human Skin In Vitro . PhD thesis, University of Cincinnati; 2010.
- 63. US EPA . Technical Guidance for Hazards Analysis. U.S. Department of Transportation; 1987. [Google Scholar]
- 64. Pathak SM, Ruff A, Kostewicz ES, Patel N, Turner DB, Jamei M. Model‐based analysis of biopharmaceutic experiments to improve mechanistic oral absorption modeling: an integrated in vitro in vivo extrapolation perspective using ketoconazole as a model drug. Mol Pharm. 2017;14:4305‐4320. [DOI] [PubMed] [Google Scholar]
- 65. Pathak SM, Schaefer KJ, Jamei M, Turner DB. Biopharmaceutic IVIVE‐mechanistic modeling of single‐ and two‐phase in vitro experiments to obtain drug‐specific parameters for incorporation into PBPK models. J Pharm Sci. 2019;108:1604‐1618. [DOI] [PubMed] [Google Scholar]
- 66. Arora S, Pansari A, Kilford P, Jamei M, Gardner I, Turner DB. Biopharmaceutic in vitro in vivo extrapolation (IVIV_E) informed physiologically‐based pharmacokinetic model of ritonavir norvir tablet absorption in humans under fasted and fed state conditions. Mol Pharm. 2020;17:2329‐2344. [DOI] [PubMed] [Google Scholar]
- 67. Ibrahim R, Nitsche JM, Kasting GB. Dermal clearance model for epidermal bioavailability calculations. J Pharm Sci. 2012;101:2094‐2108. [DOI] [PubMed] [Google Scholar]
- 68. Kretsos K, Miller MA, Zamora‐Estrada G, Kasting GB. Partitioning, diffusivity and clearance of skin permeants in mammalian dermis. Int J Pharm. 2008;346:64‐79. [DOI] [PubMed] [Google Scholar]
- 69. Dancik Y, Anissimov YG, Jepps OG, Roberts MS. Convective transport of highly plasma protein bound drugs facilitates direct penetration into deep tissues after topical application. Br J Clin Pharmacol. 2012;73:564‐578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Clarke JF, Patel N, Polak S. Predicting depth resolved concentrations in the dermis using PBPK modelling: design, development and verification of the model with five drugs. AAPS PharmSci. 2018;360. Accessed May 01, 2022. https://www.certara.com/app/uploads/Resources/Posters/Predicting‐Depth‐Resolved‐Concentrations‐in‐the‐dermis‐Clarke‐Patelk‐Polak.pdf [Google Scholar]
- 71. Troconiz JIF, Lopez‐Bustamante LG, Fos D. Effect of induced hypoalbuminemia on distribution, total clearance and unbound clearance of Piroxicam in vivo in the rat. Eur J Drug Metab Pharmacokinet. 1993;18:165‐171. [DOI] [PubMed] [Google Scholar]
- 72. Woolf AD, Rogers HJ, Bradbrook ID, Corless D. Pharmacokinetic observations on piroxicam in young adult, middle‐aged and elderly patients. Br J Clin Pharmacol. 1983;16:433‐437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Rogers HJ, Spector RG, Morrison PJ, Bradbrook ID. Comparative steady state pharmacokinetic study of piroxicam and flurbiprofen in normal subjects. Eur J Rheumatol Inflamm. 1981;4:303‐308. [PubMed] [Google Scholar]
- 74. Tilstone WJ, Lawson DH, Omara F, Cunningham F. The steady‐state pharmacokinetics of piroxicam: effect of food and iron. Eur J Rheumatol Inflamm. 1981;4:309‐313. [PubMed] [Google Scholar]
- 75. Ishizaki T, Nomura T, Abe T. Pharmacokinetics of piroxicam, a new nonsteroidal anti‐inflammatory agent, under fasting and postprandial states in man. J Pharmacokinet Biopharm. 1979;7:369‐381. [DOI] [PubMed] [Google Scholar]
- 76. Pfizer . Safety Data Sheet–Feldene Gel. 2014. Accessed March 30, 2021 Available from: https://safetydatasheets.pfizer.com/MyDocuments/DownloadSingleFile?content=2EC721FD‐4352‐403D‐B2E3‐EB415AD6BFDC_PDF
- 77. Abraham MH, Chadha HS, Martins F, Mitchell RC, Bradbury MW, Gratton JA. Hydrogen bonding part 46: a review of the correlation and prediction of transport properties by an LFER method: physicochemical properties, brain penetration and skin permeability. Pestic Sci. 1999;55:78‐88. [Google Scholar]
- 78. Bradley J‐C, Abraham MH, Acree WE, Lang ASID. Predicting Abraham model solvent coefficients. Chem Cent J. 2015;9:12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Ulrich N, Endo S, Brown TN, et al. UFZ‐LSER database v 3.2.1 [Internet]. Helmholtz Centre for Environmental Research‐UFZ; 2017. Accessed June 07, 2022. http://www.ufz.de/lserd [Google Scholar]
- 80. Abduljalil K, Cain T, Humphries H, Rostami‐Hodjegan A. Deciding on success criteria for predictability of pharmacokinetic parameters from in vitro studies: an analysis based on in vivo observations. Drug Metab Dispos. 2014;42:1478‐1484. [DOI] [PubMed] [Google Scholar]
- 81. Rostami‐Hodjegan A. Reverse translation in PBPK and QSP: going backwards in order to go forward with confidence. Clin Pharmacol Ther. 2018;103:224‐232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Rougier A, Lotte C, Maibach HI. In vivo percutaneous penetration of some organic compounds related to anatomic site in humans: predictive assessment by the stripping method. J Pharm Sci. 1987;76:451‐454. [DOI] [PubMed] [Google Scholar]
- 83. Ha HR, Chen J, Krahenbuhl S, Follath F. Biotransformation of caffeine by cDNA‐expressed human cytochromes P‐450. Eur J Clin Pharmacol. 1996;49:309‐315. [DOI] [PubMed] [Google Scholar]
- 84. Fourtillan JB, Girault J. Piroxicam plasma concentrations following repeated topical application of a piroxicam 0.5% gel. Drug Investig. 1992;4:435‐440. [Google Scholar]
- 85. Marks R, Dykes P. Plasma and cutaneous drug levels after topical application of piroxicam gel: a study in healthy volunteers. Skin Pharmacol. 1994;7:340‐344. [DOI] [PubMed] [Google Scholar]
- 86. Kanazawa M, Ito M, Shimooka K, Mase K. The pharmacokinetics of 0.5% piroxicam gel in humans. Eur J Rheumatol Inflamm. 1987;8:117. [Google Scholar]
- 87. Matsumoto Y, Cabalu T, Sandhu P, et al. Application of physiologically based pharmacokinetic modeling to predict pharmacokinetics in healthy Japanese subjects. Clin Pharmacol Ther. 2019;105:1018‐1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Abdulla T, Patel N, Polak S, Martins F, Rostami‐Hodjegan A, Jamei M. Quantitative prediction of dermal drug absorption using MPML MechDermA model: relative effects of applications site on rivastigmine pharmacokinetics from a transdermal delivery system. AAPS Annual Meeting & Exposition; 2017 November 12–15; San Diego, USA; 2017.
- 89. Proksch E. Buffering capacity. Curr Probl Dermatol. 2018;54:11‐18. [DOI] [PubMed] [Google Scholar]
- 90. Moore CA, Wilkinson SC, Blain PG, Dunn M, Aust GA, Williams FM. Percutaneous absorption and distribution of organophosphates (chlorpyrifos and dichlorvos) following dermal exposure and decontamination scenarios using in vitro human skin model. Toxicol Lett. 2014;229:66‐72. [DOI] [PubMed] [Google Scholar]
- 91. Nielsen JB. Efficacy of skin wash on dermal absorption: an in vitro study on four model compounds of varying solubility. Int Arch Occup Environ Health. 2010;83:683‐690. [DOI] [PubMed] [Google Scholar]
- 92. Ortiz PG, Hansen SH, Shah VP, Menné T, Benfeldt E. The effect of irritant dermatitis on cutaneous bioavailability of a metronidazole formulation, investigated by microdialysis and dermatopharmacokinetic method. Contact Derm. 2008;59:23‐30. [DOI] [PubMed] [Google Scholar]
- 93. Puttrevu SK, Arora S, Polak S, Patel N. Evaluation of methamphetamine and amphetamine disposition discrepancy upon selegiline transdermal patch administration in healthy volunteers versus special populations using PBPK modelling. AAPS PharmSci. 2019;360. [Google Scholar]
- 94. Polak S. PBPK model development and evaluation for the topically applied nimesulide gel–assessment of the local tissue penetration and systemic absorption. Controlled Release Society Annual Meeting; Valencia, Spain; 2019.
- 95. Martins F, Patel N, Salem F, Jamei M, Polak S. Multi‐phase multi‐layer MechDermA model: development, verification and application of a PBPK‐PD model of dermal absorption for transdermal product assessment. Gordon Research Seminar on Barrier Function of Mammalian Skin; Waterville Valley, NH, USA; 2017.
- 96. Polak S, Patel N, Rowland Yeo K, Jamei M. Towards virtual exposure assesment of dermally applied drugs–PBPK model of buprenorphine transdermal patches. American Conference on Pharmacometrics; Fort Lauderdale, FL; 2017.
- 97. Polak S, Patel N, Rowland Yeo K, Jamei M. Assessing formulation attributes' impact on local and systemic exposure of clindamycin after topical applciation of pro‐drug clindamycin phosphate using PBPK modelling. Controlled Release Society Annual Meeting; New York, USA; 2018.
- 98. Plewig G, Marples RR. Regional differences of cell sizes in the human stratum corneum. J Invest Dermatol. 1970;54:13‐18. [DOI] [PubMed] [Google Scholar]
- 99. Plewig G. Regional differences of cell sizes in the human stratum corneum. II. Effects of sex and age. J Invest Dermatol. 1970;54:19‐23. [DOI] [PubMed] [Google Scholar]
- 100. Yamamoto A, Serizawa S, Ito M, Sato Y. Stratum corneum lipid abnormalities in atopic dermatitis. Arch Dermatol Res. 1991;283:219‐223. [DOI] [PubMed] [Google Scholar]
- 101. Janssens M, van Smeden J, Gooris GS, et al. Lamellar lipid organization and ceramide composition in the stratum corneum of patients with atopic eczema. J Invest Dermatol. 2011;131:2136‐2138. [DOI] [PubMed] [Google Scholar]
- 102. Brysk MM, Rajaraman S. Cohesion and desquamation of epidermal stratum corneum. Prog Histochem Cytochem. 1992;25:1‐53. [DOI] [PubMed] [Google Scholar]
- 103. Yokouchi M, Atsugi T, Logtestijn M, et al. Epidermal cell turnover across tight junctions based on Kelvin's tetrakaidecahedron cell shape. Elife 5 e19593. (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Leigh IM, Navsaria H, Purkis PE, IA MK, Bowden PE, Riddle PN. Keratins (K16 and K17) as markers of keratinocyte hyperproliferation in psoriasis in vivo and in vitro. Br J Dermatol. 1995;133:501‐511. [DOI] [PubMed] [Google Scholar]
- 105. Kazem S, Linssen EC, Gibbs S. Skin metabolism phase I and phase II enzymes in native and reconstructed human skin: a short review. Drug Discov Today. 2019;24:1899‐1910. [DOI] [PubMed] [Google Scholar]
- 106. Pyo SM, Maibach HI. Skin metabolism: relevance of skin enzymes for rational drug design. Skin Pharmacol Physiol. 2019;32:283‐294. [DOI] [PubMed] [Google Scholar]
- 107. Steinsträsser I, Merkle HP. Dermal metabolism of topically applied drugs: pathways and models reconsidered. Pharm Acta Helv. 1995;70:3‐24. [DOI] [PubMed] [Google Scholar]
- 108. Nitsche JM, Wang TF, Kasting GB. A two‐phase analysis of solute partitioning into the stratum corneum. J Pharm Sci. 2006;95:649‐666. [DOI] [PubMed] [Google Scholar]
- 109. Raykar PV, Fung M‐C, Anderson BD. The role of protein and lipid domains in the uptake of solutes by human stratum corneum. Pharm Res. 1988;5:140‐150. [DOI] [PubMed] [Google Scholar]
- 110. Hansen S, Lehr CM, Schaefer UF. Improved input parameters for diffusion models of skin absorption. Adv Drug Deliv Rev. 2013;65:251‐264. [DOI] [PubMed] [Google Scholar]
- 111. Valiveti S, Wesley J, Lu GW. Investigation of drug partition property in artificial sebum. Int J Pharm. 2008;346:10‐16. [DOI] [PubMed] [Google Scholar]
- 112. Mitragotri S. Modeling skin permeability to hydrophilic and hydrophobic solutes based on four permeation pathways. J Control Release. 2003;86:69‐92. [DOI] [PubMed] [Google Scholar]
- 113. Polak S, Mendyk A, Patel N. Combining machine learning and mechanistic modeling approaches to solve real life problems ‐ assessment of the local tissue binding and its influence on the systemic exposure after topical application of drugs. American Conference on Pharmacometrics; Fort Lauderdale, FL, USA; 2018.
- 114. Seif S, Hansen S. Measuring the stratum corneum reservoir: desorption kinetics from keratin. J Pharm Sci. 2012;101:3718‐3728. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1