Item-Fit Statistic Based on Posterior Probabilities of Membership in Ability Groups

Abstract

A novel approach to item-fit analysis based on an asymptotic test is proposed. The new test statistic, ${\chi }_w^2$ , compares pseudo-observed and expected item mean scores over a set of ability bins. The item mean scores are computed as weighted means with weights based on test-takers’ a posteriori density of ability within the bin. This article explores the properties of ${\chi }_w^2$ in case of dichotomously scored items for unidimensional IRT models. Monte Carlo experiments were conducted to analyze the performance of ${\chi }_w^2$ . Type I error of ${\chi }_w^2$ was acceptably close to the nominal level and it had greater power than Orlando and Thissen’s $S-{\mathrm{x}}^2$ . Under some conditions, power of ${\chi }_w^2$ also exceeded the one reported for the computationally more demanding Stone’s ${\chi }^{2\ast }$ .

Introduction

Item response theory (IRT) models are a potent tool for explaining test behavior. However, the validity of analyses that involve IRT is critically related to the extent to which an IRT model fits the data. Several authors pointed to consequences of lack of fit of the IRT model for subsequent analyses (e.g., Wainer & Thissen, 1987; Woods, 2008; Bolt et al., 2014). The Standards for Educational and Psychological Testing (AERA, APA, and NCME, 2014) recommend that provision of evidence of model fit should be a prerequisite for making any inferences based on IRT.

Analysis of fit at a level of single item plays an especially important role in the assessment of IRT model validity, since IRT models are designed for the very purpose of explaining observable data by separating item properties from the properties of the test-takers. In unidimensional IRT models for dichotomous items, the probability of the response pattern $\mathit{y}=(y_1,\dots , y_n )$ conditional on ability of the test-taker, $\theta ,$ is assumed to follow

$$p\left(\mathit{y}|\mathit{\theta }\right)={\displaystyle \prod }_{j=1}^n{\left(f_j\left(\mathit{\theta }\right)\right)}^{y_j}{\left(1-f_j\left(\mathit{\theta }\right)\right)}^{1-y_j},$$ (1)

where $f_j$ is a monotonically increasing function that describes the conditional probability of a correct response to item $j\in \left\{1,\dots ,n\right\}$ . The marginal likelihood of response vector $y$ is given by

$$p\left(\mathit{y}\right)={{\displaystyle \int }}^{\text{}}p\left(\mathit{y}|\mathit{\theta }\right)g\left(\mathit{\theta }\right)d\mathit{\theta },$$ (2)

where $g$ is the a priori ability distribution. Finally, a posteriori density of $\theta$ given response vector $\mathbf{y}$ is

$$g\left(\theta |\mathit{y}\right)=\frac{p\left(\mathit{y}|\mathit{\theta }\right)g(\mathit{\theta })}{p\left(\mathit{y}\right)}.$$ (3)

These equations illustrate how item response functions $f_j$ mirror the structure of observable data. They serve as building blocks of the whole IRT model, and their form impacts any inferences regarding test-taker position on the $\mathit{\theta }$ continuum. Therefore, item-fit analysis is crucial in IRT. The item-level misfit information allows one to improve the overall model fit by discarding the misfitting items from analyses or by replacing the IRT model with one defined over a richer parameter space.

Many different approaches to item-fit testing have been developed. Despite ample research on the topic, the available solutions either are restricted to special cases of models and testing designs or require resampling. This article describes a universal and computationally feasible method for testing item-fit that aims at filling the gap in what is currently proposed.

Existing Item-Fit Statistics

Item-fit statistics are measures of discrepancy between the expected item performance, based on $f_j$ , and the observed item performance. Usually, the difference between the observed and expected item-score is calculated over groups of test-takers with similar ability and aggregated into a single number. The pursuit of an item-fit measure that would allow for statistical testing started with the first applications of IRT. A selective account of previous research is presented to provide the context for the development of the approach proposed in the article. An in-depth review of research on item-fit is available, for example, in Swaminathan et al. (2007).

Grouping on Point Estimates of $\theta$

First advancements in this field of research were inspired by the solutions available for models that did not deal with latent variables. These early approaches grouped test-takers on their point estimates of $\theta$ and computed Pearson’s $X^2$ (Bock, 1972; Yen, 1981) or likelihood-ratio test statistic $G^2$ (McKinley & Mills, 1985). Uncertainty in measurement of $\mathrm{\theta }$ is not accounted for under such grouping and the observed counts within groups are treated as independent from each other. Consequently, these fit statistics produce inflated Type I error rates, especially when tests are short (Orlando & Thissen, 2000; Stone & Hansen, 2000). Only in the case of Rasch-family of models, where the number-correct score is a sufficient statistic for $\widehat{\mathrm{\theta }}$ , such approaches yield item-fit statistics that are in accordance with the postulated asymptotic distribution (Andersen, 1973; Glas & Verhelst, 1989).

Grouping on Observed Sum-Scores

Orlando and Thissen (2000) approached the problem from a different angle. Instead of relying on the partition of latent trait, they grouped test-takers on their number-correct scores. This allowed to compute the observed frequency of correct responses directly from observable data. In order to compute the expected frequency of correct responses at a given score group, Orlando and Thissen ingeniously employed the algorithm of Lord and Wingersky (1984). Their version of Pearson’s statistic, $\mathrm{S}-{\mathrm{X}}^2$ , has become a standard point of reference in studies on item-fit because $\mathrm{S}-{\mathrm{X}}^2$ is fast to compute and has Type I error rates very close to the nominal level.

A likelihood-based approach to item-fit with aggregation over sum-scores was developed by Glas (1999) and further expanded by Glas and Suarez-Falcon (2003). This approach stands out from other item-fit measures, not only by accounting for the stochastic nature of item parameters, but also because it does not directly bank on the observed versus expected difference. Item misfit is modeled by additional group-specific parameters, modification indices, introduced in order to capture systematic deviance of data from the item response function. To test for significance, the modification indices are compared to zero and the Lagrange multiplier test is employed. However, as pointed by Sinharay (2006), results of simulations run by Glas and Suarez-Falcon (2003) show that Type I error of their statistic can be elevated under some score groupings.

Resampling Methods

Partitioning of ability on observed scores, rather than latent $\theta$ , limits practical applications of statistics such as $\mathrm{S}-{\mathrm{X}}^2$ or LM proposed by Glas. When test-takers respond to different sets of items their raw sum-scores become incomparable. However, a lot of appeal of IRT arises exactly from the fact that it can be applied in analysis of incomplete testing designs. So, the pursuit for a solution that relies on residuals computed over $\theta$ scale has never stopped.

Stone (2000) developed a simulation-based approach. He proposed a ${\chi }^{2\ast }$ statistic calculated over quadrature points of $\theta$ , with a resampling algorithm for determining the distribution of ${\chi }^{2\ast }$ under the null hypothesis. Stone’s ${\chi }^{2\ast }$ repeatedly proved to provide acceptable Type I error rate and it exceeded $\mathrm{S}-{\mathrm{X}}^2$ in power (Stone & Zhang, 2003; Chon et al., 2010; Chalmers & Ng, 2017). However, this came at a significant computational cost.

Other computationally intensive approaches were also developed. Sinharay (2006) and Toribio and Albert (2011) applied the posterior predictive model checking (PPMC) method, that is, available within Bayesian framework (Rubin, 1984). Theoretical advantage of PPMC method over Stone’s ${\chi }^{2\ast }$ or Orlando and Thissen’s $\mathrm{S}-{\mathrm{X}}^2$ lies in the fact that the uncertainty of item parameter estimation is taken into account in PPMC. However, simulational studies performed by the authors showed that PPMC tests were too conservative in terms of Type I error, albeit still being practically useful in terms of statistical power. Chalmers & Ng (2017) proposed a fit statistic averaged over a set of plausible values (draws from (3)) that required additional resampling to obtain the $p$ -value. Their statistic had deflated Type I error rates, similarly to PPMC.

Problem With Existing Item-Fit Statistics

From a practical stance, the existing research on item-fit is disappointing. The researcher assessing item-fit faces a choice either to use Orlando and Thissen’s $\mathrm{S}-{\mathrm{X}}^2$ , which has low power and is not always applicable, or must refer to methods that require considerable CPU time. In consequence, they may decide not to give any consideration to statistical significance and assess item-fit merely on the value of some discrepancy measure. An example of such an approach is found in PISA 2015 technical report (OECD, 2017, p. 143), where mean deviation (MD) and root mean square deviation (RMSD) are used with disregard for their sampling properties.

The statistic proposed in this article aims at filling the gap by providing a method of testing item fit that is suitable in contexts when raw-score grouping is not applicable and is computationally feasible for practical use.

The Proposed Item-Fit Test

Let ${\mathrm{\Delta }}_1,\dots , {\mathrm{\Delta }}_r$ be non-intersecting grouping intervals of ability $\text{θ}$ , such that

$${\mathrm{\Delta }}_1{{\displaystyle \cup }}^{\text{}}\dots {{\displaystyle \cup }}^{\text{}} {\mathrm{\Delta }}_r=ℝ, {\mathrm{\Delta }}_k {{\displaystyle \cap }}^{\text{}} {\mathrm{\Delta }}_h=ø \text{for}k\ne h.$$ (4)

The proposed approach to item-fit analysis compares two types of estimates of the expected item score over intervals ${\mathrm{\Delta }}_k$ : ${\widehat{\mathit{O}}}_j$ and ${\widehat{\mathit{E}}}_j$ . Row vector ${\widehat{\mathit{O}}}_j$ is computed from the observed item responses, $y_j$ , with a covariance estimate ${\widehat{\mathit{V}}}_j$ . Row vector ${\widehat{\mathit{E}}}_j$ consists of model-based expectations that are obtained from ${\widehat{f}}_j$ .

To test for model fit, the following Wald-type statistic is employed

$${\chi }_{w j}^2=\left({\widehat{\mathit{O}}}_j-{\widehat{\mathit{E}}}_j\right) {\widehat{\mathit{V}}}_j^{-1}{\left({\widehat{\mathit{O}}}_j-{\widehat{\mathit{E}}}_j\right)}^T,$$ (5)

which is assumed to be asymptotically chi square distributed with $r-q$ degrees of freedom, where $q$ is the number of estimated model parameters used in computation of ${\widehat{\mathit{E}}}_j$ .

The following sections will define quantities used in equation (5) and lay out the rationale behind the asymptotic claim about ${\chi }_w^2$ . The presentation will be restricted to unidimensional IRT models for dichotomous items because most of the research in the field was done under these restrictions and it also allows to keep things simple. Therefore, ${\mathit{O}}_j$ and ${\mathit{E}}_j$ will be henceforth referred to as vectors of the pseudo-observed and expected proportions of correct responses. It should be kept in mind, however, that equation (5) is defined in terms that apply to polytomous items and equation (4) could also be defined over multidimensional ability space.

A possibility of developing a Wald-type item-fit statistic such as equation (5) was mentioned by Stone (2000), at the very end of his paper. Stone discussed ${\widehat{\mathit{O}}}_j$ and ${\widehat{\mathit{E}}}_j$ computed at quadrature points, rather than over ability intervals, and did not indicate any way of obtaining ${\widehat{\mathit{V}}}_j$ . To give due credit for the general idea to Stone, the symbol ${\chi }_w^2$ is adopted for equation (5), as in the original article.

Case When Item Parameters are Known

Assume that the IRT model holds, and the parameters of $f_j$ are known. A posterior probability that ability of test-taker $i$ with a response vector ${\mathit{y}}_i$ falls into interval ${\mathrm{\Delta }}_k$ is a definite integral of (3) over ${\mathrm{\Delta }}_k$

$${\tau }_{ki}=g\left(\mathit{\theta }|{\mathit{y}}_i, {\mathrm{\Delta }}_k\right)={{\displaystyle \mathrm{\int }}}_{{\mathrm{\Delta }}_k}g\left(\mathit{\theta }|{\mathit{y}}_{\mathit{i}}\right)d\mathit{\theta }=\frac{{{\displaystyle \int }}_{{\mathrm{\Delta }}_k}p\left({\mathit{y}}_{\mathit{i}}|\mathit{\theta }\right)g\left(\mathit{\theta }\right)d\mathrm{\theta }}{p\left({\mathit{y}}_{\mathit{i}}\right)}.$$ (6)

After observing $m$ response vectors, an estimate of $O_{jk}$ , that is, of the pseudo-observed proportion of correct responses to item $j$ in interval ${\mathrm{\Delta }}_k$ , is given by

$${\overline{O}}_{jk}=\frac{{{\displaystyle \sum }}_{i=1}^m{y}_{ij}{\tau }_{ki}}{{{\displaystyle \sum }}_{i=1}^m{\tau }_{ki}}.$$ (7)

${\overline{O}}_{jk}$ is a weighted mean of item responses with weights being the posterior probabilities of test-taker membership in grouping interval ${\mathrm{\Delta }}_k$ . This estimate closely resembles the ML estimate of component mean in Bernoulli mixture model (McLachlan & Peel, 2000). A mixture model analogy can be further seen by noting that for each response vector ${\mathit{y}}_{\mathit{i}}$ : ${\tau }_{ki}\ge 0$ , ${\displaystyle \sum }_{k=1}^r{\tau }_{ki}=1$ and $p\left(y_j\right|{\mathit{y}}_{\mathit{i}})={\displaystyle \sum }_{k=1}^r{\tau }_{ki}p\left(y_j| {\mathit{y}}_{\mathit{i}},{\mathrm{\Delta }}_k\right)$ . The difference with mixture model is that a posteriori group membership, ${\tau }_{ki}$ , used in (7) is obtained “externally” from the IRT model likelihood and not estimated via the likelihood of a mixture model.

The proposed item-fit test statistic assumes that the vector of estimates of pseudo-observed proportions (7) over all ability intervals (4), ${\overline{\mathit{O}}}_{\mathit{j}}$ , is asymptotically multivariate normal with mean ${\mathit{O}}_j$ and covariance matrix ${\mathit{V}}_{\mathit{j}}$ . That is, as $m\to \infty$

$$\left({\overline{\mathit{O}}}_{\mathit{j}}-{\mathit{O}}_{\mathit{j}}\right) {\mathit{V}}_j^{-\frac{1}{2}} \stackrel{d}{\mathbf{\to }} N_r\left(\mathbf{0},{\mathit{I}}_{\mathit{r}}\right).$$ (8)

A test regarding ${\mathit{O}}_{\mathit{j}}$ can be derived from (8). To verify $H_0: {\mathit{O}}_j={\mathit{O}}_{0j}$ versus $H_1: {\mathit{O}}_j\ne {\mathit{O}}_{0j}$ the following quadratic form with an asymptotic ${\text{χ}}_r^2$ distribution is employed

$$\left({\overline{\mathit{O}}}_{\mathit{j}}-{\mathit{O}}_{\mathrm{0}j}\right) {\mathit{V}}_j^{-1}{\left({\overline{\mathit{O}}}_{\mathit{j}}-{\mathit{O}}_{\mathrm{0}j}\right)}^T \stackrel{d}{\to }\mathbf{ }{\chi }_r^2.$$ (9)

The covariance matrix ${\mathit{V}}_{\mathit{j}}$ in (9) is replaced by an estimator ${\overline{\mathit{V}}}_{\mathit{j}}=\left[{\overline{v}}_{jkh}\right]{ }_{r\times r}$ , where the $(k,h)$ th element, a covariance between ${\overline{O}}_{jk}$ and ${\overline{O}}_{jh}$ , is given by

$${\overline{v}}_{jkh}=\frac{{{\displaystyle \sum }}_{i=1}^m{\tau }_{ki}{\tau }_{hi}\left(y_{ij}-{\overline{O}}_{jk}\right)\left(y_{ij}-{\overline{O}}_{jh}\right)}{\left({{\displaystyle \sum }}_{i=1}^m{\tau }_{ki}\right)\left({{\displaystyle \sum }}_{i=1}^m{\tau }_{hi}\right)}.$$ (10)

As pointed out in Shao (1999, p. 404), (9) is also true if ${\mathit{V}}_{\mathit{j}}$ is replaced by a consistent estimator.

Let ${\mathit{y}}_{\mathit{i}\backslash j}$ denote a response vector of test-taker $i$ to all items but the item $j$ . Model-based probability of a correct response to item $j$ in interval ${\mathrm{\Delta }}_k$ upon observing $y_{i\backslash j}$ is given by

$$e_{jki}=p\left({\mathbf{y}}_j=1|{\mathit{y}}_{i\backslash j},{\mathrm{\Delta }}_k\right)=\frac{p\left(y_j=1,{\mathit{y}}_{\mathit{i}\backslash j}|{\mathrm{\Delta }}_k\right)}{p\left({\mathit{y}}_{i\backslash j}|{\mathrm{\Delta }}_k\right)}=\frac{{{\displaystyle \int }}_{{\mathrm{\Delta }}_k}{f}_j\left(\theta \right)p\left({\mathit{y}}_{\mathit{i}\backslash j}|\theta \right)g\left(\theta \right)d\theta }{{{\displaystyle \int }}_{{\mathrm{\Delta }}_k}p\left({\mathit{y}}_{\mathit{i}\backslash j}|\theta \right)g\left(\theta \right)d\theta }.$$ (11)

After observing $m$ response vectors, a model-based expected proportion of correct responses to item $j$ in interval ${\mathrm{\Delta }}_k$ to par with (7) can be computed as

$${\overline{E}}_{jk}=\frac{{{\displaystyle \sum }}_{i=1}^m{e}_{jki}{\tau }_{ki}}{{{\displaystyle \sum }}_{i=1}^m{\tau }_{ki}}.$$ (12)

Finally, the item-fit is tested by stating $H_0: {\mathit{O}}_j={\overline{\mathit{E}}}_{\mathit{j}}$ against $H_1: {\mathit{O}}_j\ne {\overline{\mathit{E}}}_{\mathit{j}}$ with a test statistic

$${\chi }_{w j}^2=\left( {\overline{\mathit{O}}}_{\mathit{j}}-{\overline{\mathit{E}}}_{\mathit{j}}\right) {\overline{\mathit{V}}}_{\mathit{j}}^{-1}{\left({\overline{\mathit{O}}}_{\mathit{j}}-{\overline{\mathit{E}}}_{\mathit{j}}\right)}^T,$$ (13)

that is asymptotically chi squared with $r$ degrees of freedom.

Case When Item Parameters are Estimated

When IRT model parameters are estimated from data, item response functions $f_j$ are replaced with ${\widehat{f}}_j$ ; a posteriori group membership ${\tau }_{ki}$ (6) is replaced with an estimate ${\widehat{\tau }}_{ki}$ ; and pseudo-observed proportion (7), model-expected proportion (12), and covariance element (10) are replaced, respectively, by estimates

$${\widehat{O}}_{jk}=\frac{{{\displaystyle \sum }}_{i=1}^m{y}_{ij}{\widehat{\tau }}_{ki}}{{{\displaystyle \sum }}_{i=1}^m{\widehat{\tau }}_{ki}},$$ (14)

$${\widehat{E}}_{jk}=\frac{{{\displaystyle \sum }}_{i=1}^m{\widehat{e}}_{jki}{\widehat{\tau }}_{ki}}{{{\displaystyle \sum }}_{i=1}^m{\widehat{\tau }}_{ki}},$$ (15)

$${\widehat{v}}_{jkh}=\frac{{{\displaystyle \sum }}_{i=1}^m{\widehat{\tau }}_{ki}{\widehat{\tau }}_{hi}\left(y_{ij}-{\widehat{O}}_{jk}\right)\left(y_{ij}-{\widehat{O}}_{jh}\right)}{\left({{\displaystyle \sum }}_{i=1}^m{\widehat{\tau }}_{ki}\right)\left({{\displaystyle \sum }}_{i=1}^m{\widehat{\tau }}_{hi}\right)}.$$ (16)

The item-fit statistic (13) for an IRT model with parameters estimated from data becomes ${\chi }_{w j}^2=\left({\widehat{\mathit{O}}}_{\mathit{j}}-{\widehat{\mathit{E}}}_{\mathit{j}}\right) {\widehat{\mathit{V}}}_{\mathit{j}}^{-1}{\left({\widehat{\mathit{O}}}_{\mathit{j}}-{\widehat{\mathit{E}}}_{\mathit{j}}\right)}^T$ as previously stated in (5). Number of degrees of freedom of ${\chi }_{w j}^2$ needs to be adjusted to account for the number of estimated model parameters used in computation of ${\widehat{\mathit{E}}}_j$ .

Monte Carlo Experiments

This section describes results of three simulation studies conducted to examine properties of ${\chi }_w^2$ . First simulations dealt with implementation issues and their main purpose was to verify how well the asymptotic claims about ${\chi }_w^2$ hold upon varying approaches to construction of grouping intervals. Second simulations replicated a Monte Carlo experiment designed by Stone and Zhang (2003) that was augmented to include additional condition of incomplete response vectors. This experiment allowed to analyze Type I error rates and power of ${\chi }_w^2$ against a benchmark of Orlando and Thissen’s $\mathrm{S}-{\mathrm{X}}^2$ and Stone’s ${\chi }^{2\ast }$ , and to verify performance of ${\chi }_w^2$ in an incomplete-data design setting. Final study was based on the “bad items” design by Orlando and Thissen (2003) and aimed at providing further information about power of ${\chi }_w^2$ .

Ability parameters in all three simulation studies were sampled from normal distribution $g\left(\theta \right)=N\left(\mathrm{0,1}\right)$ . Item response functions belonged to the logistic family of IRT models: the three-parameter logistic model (3PLM)

$$f_j\left(\theta \right)=P\left(y_j|\theta \right)=c_j+\frac{1-c_j}{1+e^{-a_j\left(\theta -b_j\right)}} ,$$ (17)

the two-parameter logistic model (2PLM, (17) with $c_j=0$ ) and the one-parameter logistic model (1PLM, (17) with $c_j=0$ and $a_j=a$ ).

All analyses were performed in Stata. Item responses under (17) were generated using uirt_sim (Kondratek, 2020). Parameters of IRT models were estimated by uirt (version 2.1; Kondratek, 2016) with its default settings—EM algorithm, Gauss–Hermite quadrature with 51 integration points, and 0.0001 stopping rule for maximum absolute change in parameter values between EM iterations. The uirt software was also used to compute $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }_w^2$ . Indefinite integrals over $g\left(\theta \right)$ , needed for expected proportions used in $\mathrm{S}-{\mathrm{X}}^2$ and to obtain $p\left({\mathit{y}}_{\mathit{i}}\right)$ seen in denominator of (6), were computed by Gauss–Hermite quadrature with 151 integration points. Definite integrals over $g\left(\theta \right)$ , seen in the numerator of (6), employed Gauss–Legendre quadrature with 30 integration points at each bin of ability, ${\mathrm{\Delta }}_k$ .

Each of the Monte Carlo experiments involved 10,000 replications of the simulated conditions. Type I error and power were computed as percentage of rejected $H_0$ at significance level $\alpha =0.05$ , averaged over replications.

Simulation Study 1 – Number and Range of Grouping Intervals

Implementation of ${\chi }_w^2$ has required decisions on the number of grouping intervals (4) and their range. Postulated distribution of ${\chi }_w^2$ is derived from asymptotic normality of the vector of the pseudo-observed proportions (8); therefore, the conventional rule for appropriateness of normal approximation to sample proportion was adopted to govern range of ability intervals. This resulted in item-specific intervals ${\mathrm{\Delta }}_k$ that were constructed so that

$$m_{jk}{\widehat{\pi }}_{jk}\left(1-{\widehat{\pi }}_{jk}\right)\approx const,$$ (18)

where ${\widehat{\pi }}_{jk}$ is a simple model-based estimate of proportion of correct responses in interval ${\mathrm{\Delta }}_{jk}$

$${\widehat{\pi }}_{jk}=\widehat{p}\left(y_j=1\text{|}{\mathrm{\Delta }}_{jk}\right)=\frac{{{\displaystyle \int }}_{{\mathrm{\Delta }}_{jk}}{\widehat{f}}_j\left(\theta \right)g\left(\theta \right)d\theta }{{{\displaystyle \int }}_{{\mathrm{\Delta }}_{jk}}g\left(\theta \right)d\theta }.$$ (19)

and $m_{jk}$ is the expected number of observations in interval ${\mathrm{\Delta }}_{jk}$ , $m_{jk}=m{{\displaystyle \int }}_{{\mathrm{\Delta }}_{jk}}g\left(\theta \right)d\theta$ .

Ranges of ${\mathrm{\Delta }}_{jk}$ that would meet the condition (18) were determined by first splitting the ability distribution into smaller ${\mathrm{\Delta }}_{jv}$ intervals that were equiprobable with respect to $g\left(\theta \right)$ , $m_{jv}=0.001m$ , and $v\in \left\{1,\dots ,1000\right\}$ . The finer intervals were then aggregated into ${\mathrm{\Delta }}_{jk}$ = $\underset{v=a}{\overset{v=b}{{\displaystyle \mathrm{U}}}}{\mathrm{\Delta }}_{jv}$ so that ${\displaystyle \sum }_{v=a}^{v=b}{\widehat{\pi }}_{jv}\left(1-{\widehat{\pi }}_{jv}\right)\approx \frac{1}{r}{\displaystyle \sum }_{v=1}^{v=1000}{\widehat{\pi }}_{jv}\left(1-{\widehat{\pi }}_{jv}\right),$ where $r$ was the desired number of ${\mathrm{\Delta }}_{jk}$ (4). Computation of ${\widehat{\pi }}_{jv}$ in this step was performed with Gauss–Legendre quadrature with 11 integration points.

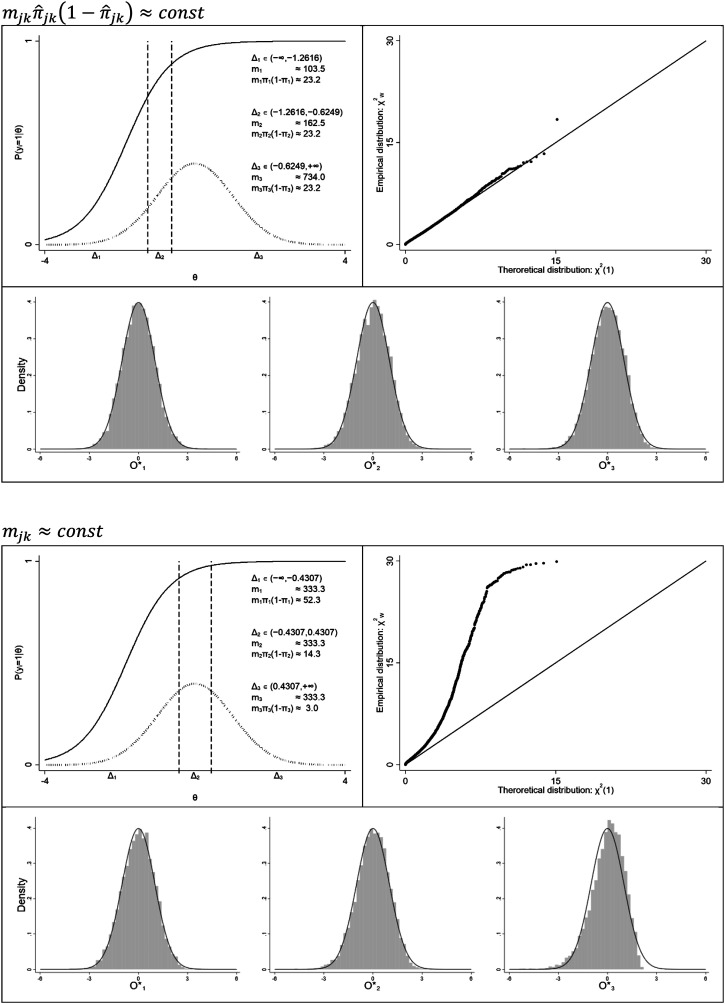
Behavior of ${\chi }_w^2$ upon adopting criterion (18) with three ability bins when testing fit of an easy 2PLM item ( $a_j=1.7$ and $b_j=-1.84$ ) under true $H_0$ is illustrated in Figure 1 (upper panel) and compared to an alternative equiprobable division of ability (lower panel). Graphs presented in Figure 1 were obtained in a simple Monte Carlo experiment in which the item tested for fit was embedded in a 30-item 2PLM test. The remaining 29-item parameters were sampled from $\ln a_{v\ne j}\sim N(\ln 1.7, 0.4)$ and $b_{v\ne j}\sim N\left(\mathrm{0,1}\right)$ , and the sample size was $m=1000$ . In each replication, ${\chi }_{w j}^2$ was computed and the pseudo-observed proportions of correct responses ${\widehat{O}}_{jk}$ ( $14$ ) were stored. Upon completing 10,000 replications, the resulting empirical distribution of ${\chi }_{w j}^2$ was compared against theoretical ${\chi }^2\left(1\right)$ in a Q–Q plot, and the pseudo-observed proportions were transformed according to (8) so that standardized variables were obtained and compared against theoretical $N\left(\mathrm{0,1}\right)$ on histograms.

Figure 1.

Distribution of ${\chi }_w^2$ under different choices of interval range.

The equiprobable division would be a tempting alternative to (18) as it results in equal expected number of observations in each interval, $m_{jk}\approx const$ . By being independent from item parameters, it would decrease the computational cost of ${\chi }_w^2$ because the group membership probabilities, ${\widehat{\tau }}_{ki}$ , would need to be obtained only once. However, simulation results presented in Figure 1 indicate that ${\chi }_{w j}^2$ grossly deviated from theoretical ${\chi }^2\left(1\right)$ upon such division. The expected number of observations in each bin exceeds 333, but because of the extreme easiness of the item, the rightmost bin is associated with a very small value on the $m_{jk}{\widehat{\pi }}_{jk}\left(1-{\widehat{\pi }}_{jk}\right)$ criterion. The transformed proportion of correct responses in this bin experiences a visible ceiling effect, and thus the ${\chi }^2\left(1\right)$ assumption does not hold. Yet, when ${\chi }_{w j}^2$ was computed with intervals constructed using criterion (18), it resulted in a good approximation to ${\chi }^2\left(1\right)$ , even at these rather difficult conditions in terms of sample size and item difficulty.

A second problem of implementation of ${\chi }_w^2$ required deciding on the number of ability bins, $r$ . It was expected that increasing $r$ would be detrimental to the normal approximation of pseudo-observed proportions. So, from the standpoint of Type I error, the safest approach would be to use the smallest possible number of intervals, $r=q+1$ , leading to ${\chi }_w^2$ with a single degree of freedom. However, the relation between $r$ and power of ${\chi }_w^2$ was not obvious. On the one hand, increasing $r$ would allow to detect a locally finer grade of deviances between (14) and (15). On the other hand, it would increase the entries of the covariance matrix (16) because of smaller effective sample size per interval.

Number of Ability Bins – Simulation Design

To investigate properties of ${\chi }_w^2$ under varying number of bins, a Monte Carlo experiment was conducted under similar scheme that was used to obtain results reported in Figure 1. The conditions of experiment were extended to cover different IRT models (1PLM, 2PLM, and 3PLM), items of varying marginal difficulty, ${\pi }_j={{\displaystyle \int }}^{\text{}}{f}_j\left(\theta \right)g\left(\theta \right)d\theta$ ( ${\pi }_j=0.5$ and ${\pi }_j=0.9$ for all models and additionally ${\pi }_j=0.3$ for 3PLM), two sample sizes ( $m\in \left\{400, 4000\right\}$ ), and two test lengths ( $n\in \left\{10, 40\right\}$ ). Under each of these conditions Type I error was obtained in both fixed and estimated parameters case, and Q–Q plots were plotted for certain number of ability bins for closer assessment of the distribution of ${\chi }_w^2$ . Additionally, power to detect misfit was analyzed with varying number of ability bins by fitting a 1PLM or 2PLM model to an item estimated under 3PLM. This article presents only main conclusions from the experiment; detailed results under all tested conditions are provided in the online supplement.

Number of Ability Bins – Simulation Results

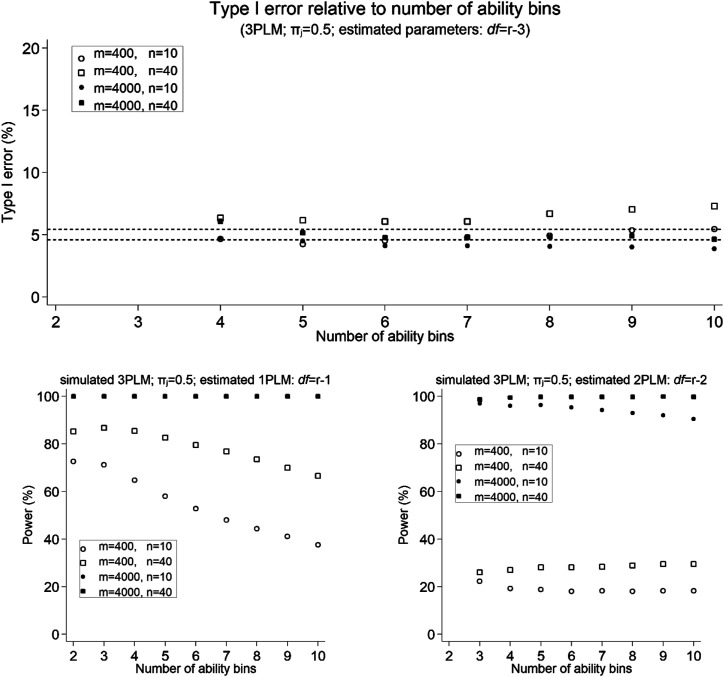
Figure 2 depicts relationship between the number of ability intervals and resulting detection rates for an item of medium difficulty ( ${\pi }_j=0.5$ ) that was simulated as 3PLM and then estimated as 3PLM (Type I error) or as either 2PLM or 1PLM (statistical power). It illustrates that increasing the number of ability bins results in decrease of statistical power of ${\chi }_w^2$ . Additionally, increase of $r$ eventually leads to elevated Type I error rates. These patterns were also seen in other conditions considered in the experiment, with the detrimental effect of increased $r$ on the Type I error being especially prominent for difficult items in small samples (online supplement).

Figure 2.

Type I error and power of ${\chi }_w^2$ in relation to the number of ability bins.

Based on these results, it was decided to implement ${\chi }_w^2$ with $r=q+1$ intervals for 3PLM and 2PLM. For 1PLM: either $r=3$ if criterion (18) exceeds 20, or $r=2$ otherwise. Number 20 precautiously doubles the conventional rule for when a normal approximation to sample proportion is appropriate. These settings were used in all the simulation studies covered in the rest of the article.

Q–Q plots were obtained according to the adopted rule for the number of intervals for a more detailed verification of the postulated asymptotic distribution of ${\chi }_w^2$ (online supplement). For $m=4000$ , the empirical distribution of ${\chi }_w^2$ was well aligned with theoretical ${\chi }^2$ under all tested conditions, both in the known and the estimated parameters case. Approximation was also well-behaved for $m=400$ and moderate item difficulty. However, combined conditions of small sample size and extreme item difficulties resulted in deviation of ${\chi }_w^2$ from its theoretical asymptotic distribution. We should notice that under such conditions, the criterion for appropriateness of normal approximation of sample proportion (18) is small in value, even when the lowest possible number of ability intervals is used. This alerts us that ${\chi }_w^2$ should be used with caution whenever fit of extremely easy or difficult item is to be assessed in small samples. A condition $m_{jk}{\widehat{\pi }}_{jk}\left(1-{\widehat{\pi }}_{jk}\right)>20$ seems to be a good guideline on deciding if results of ${\chi }_w^2$ are trustworthy (see Figure 1).

Simulation Study 2 – Type I Error and Power

Simulation Design

This study replicated Monte Carlo experiment designed by Stone and Zhang (2003). Three test lengths, $n\in \left\{10, 20, 40\right\}$ , were crossed with three sample sizes, $m\in \left\{500, 1000, 2000\right\}$ , and data was generated under two IRT models: 2PLM and 3PLM. Under the 2PLM generating scenario, a set of 10 pairs of item parameters was constructed by crossing two values of item discrimination parameter, $a_j\in \left\{1.2, 2.2\right\}$ , with five values of item difficulty parameter, $b_j\in \left\{-2, -1, 0, 1, 2\right\}$ . 20-item and 40-item tests were built by adding another 10 or 3x10 items defined by repetition of the same parameter set. The 3PLM scenario used the same discriminations and difficulties as the 2PLM. All items, except the easiest one with $b_j=-2$ , were added a pseudo-guessing parameter $c_j=0.25$ in the 3PLM scenario.

This design was extended to create additional incomplete-data conditions. It was accomplished by taking the complete data generated under the original design for $n\in \left\{20, 40\right\}$ and $m\in \left\{1000, 2000\right\}$ , and treating random 50% of responses for each item as missing. In result, additional four generating conditions were introduced in which number of observations per item and expected number of items per observation halved the size of the original complete data.

In each replication, all item parameters were estimated from the simulated data under two IRT models: 1PLM and 2PLM. In complete data conditions, Orlando and Thissen’s $\mathrm{S}-{\mathrm{X}}^2$ and the ${\chi }_w^2$ statistics were computed from the estimates of the IRT model. In the missing responses scenario, only ${\chi }_w^2$ was obtained because $\mathrm{S}-{\mathrm{X}}^2$ is not applicable to data with incomparable sum-scores. The case when generating model was the same as estimating model (2PLM) served to analyze Type I error. Other three combinations, when generating model had more parameters than estimating model, were used to assess statistical power of $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }_w^2$ .

Simulation Results

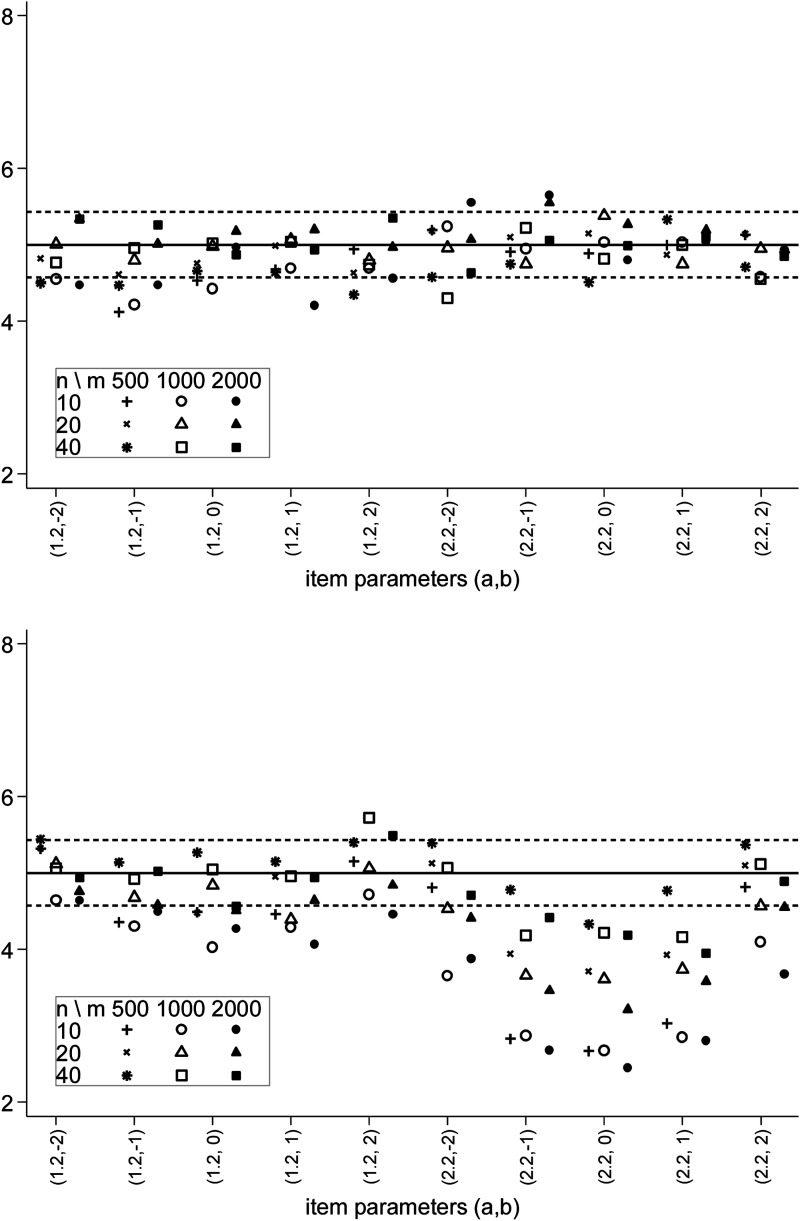
Table 1 summarizes performance of $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }_w^2$ when both the generating and the estimating model were 2PLM. Entries in the table are percentages of rejected $H_0$ at significance level $\alpha =0.05$ averaged over all items and all replications. Results for $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }^{2\ast }$ reported in Stone & Zhang (2003) are also included for reference. It should be kept in mind that Stone and Zhang results were obtained with two orders of magnitude fewer replications. Figure 3 expands the analysis of Type I errors of $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }_w^2$ , by presenting rejection rates of true $H_0$ at an item level. Results for the first 10 items are plotted against a 95% confidence bound around the nominal significance level $\alpha =0.05$ , assuming standard error of $\sqrt{\alpha (1-\alpha )/{10}^4}$ .

Table 1.

Type I error rates for different item-fit statistics (%).

Test length	Sample size	Results of current study			Results of Stone and Zhang
		$S-X^2$	${\chi }_w^2$	${\chi }_w^2$	$S-X^2$	${\chi }^{2\ast }$
		Complete data	Complete data	50% missing
$n=10$	$m=500$	4.8	4.2		4	5
	$m=1000$	4.7	3.8		4	4
	$m=2000$	4.9	3.7		5	3
$n=20$	$m=500$	4.9	4.7		5	5
	$m=1000$	4.9	4.3	4.3	5	3
	$m=2000$	5.0	4.2	4.1	5	3
$n=40$	$m=500$	4.7	5.1		6	6
	$m=1000$	4.8	4.8	4.8	4	4
	$m=2000$	5.0	4.7	4.5	3	4

Note. Stone and Zhang (2003, Table 1).

Figure 3.

Type I error rates for $S-X^2$ (top) and ${\chi }_w^2$ (bottom) conditional on item parameters.

Type I error of $\mathrm{S}-{\mathrm{X}}^2$ , as seen in Table 1 and Figure 3, was almost flawlessly nominal for all items, test-lengths, and sample sizes that were considered in the study. This result confirms what was previously observed by Orlando and Thissen (2000) or Stone and Zhang (2003).

The averaged Type I error of ${\chi }_w^2$ was in 0.037–0.045 range (Table 1) which is acceptable. These values do not exceed ranges reported for both $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }^{2\ast }$ by Stone and Zhang (2003) under the same experimental conditions. However, the item-level information in Figure 3 reveals that for higher discriminating items ( $a_j=2.2$ ) with moderate difficulty ( $b_j\in \left\{-1, 0, 1\right\}$ ) Type I error of ${\chi }_w^2$ is deflated. This effect diminishes with increase in test length. From practical standpoint deflated false rejection rates would not be a problem as long as ${\chi }_w^2$ has sufficient power to detect misfit.

Power of $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }_w^2$ was examined by averaging rejection rates in three scenarios when the model used for simulating responses had more item parameters than the model used in estimation: 2PLM-1PLM, 3PLM-1PLM, and 3PLM-2PLM. The results are presented in Table 2, together with power of $\mathrm{S}-{\mathrm{X}}^2$ and ${\chi }^{2\ast }$ from simulation by Stone and Zhang (2003). The ${\chi }_w^2$ statistic outperformed $\mathrm{S}-{\mathrm{X}}^2$ with regard to power under all experimental conditions. When compared to results for ${\chi }^{2\ast }$ reported in Stone and Zhang (2003), ${\chi }_w^2$ was more sensitive in detecting misfit under the 3PLM-2PLM. In other misfit scenarios ${\chi }^{2\ast }$ and ${\chi }_w^2$ achieved similar power under long tests ( $n=40$ ) and the reported power of ${\chi }^{2\ast }$ exceeded that of ${\chi }_w^2$ for shorter tests. Power of Stone’s ${\chi }^{2\ast }$ seems to be unaffected by the test length. This puts Stone’s ${\chi }^{2\ast }$ in a position of an especially useful item-fit measure for short tests.

Table 2.

Power rates for different item-fit statistics (%).

Test length	Sample size	Results of current study			Results of Stone and Zhang
		$S-X^2$	${\chi }_w^2$	${\chi }_w^2$	$S-X^2$	${\chi }^{2\ast }$
		Complete data	Complete data	50% missing
Simulated 2PLM – Estimated 1PLM
$n=10$	$m=500$	23.8	35.1		26	51
	$m=1000$	49.5	59.9		53	75
	$m=2000$	80.7	86.5		81	94
$n=20$	$m=500$	23.2	47.5		23	56
	$m=1000$	46.2	73.1	36.4	45	78
	$m=2000$	78.7	93.7	60.8	80	96
$n=40$	$m=500$	20.3	52.3		22	52
	$m=1000$	38.4	77.2	46.6	40	78
	$m=2000$	71.9	95.5	71.9	75	94
Simulated 3PLM – Estimated 1PLM
$n=10$	$m=500$	36.5	47.8		35	69
	$m=1000$	58.6	64.3		59	82
	$m=2000$	75.0	77.8		75	88
$n=20$	$m=500$	41.4	61.9		42	67
	$m=1000$	63.7	74.9	49.7	65	80
	$m=2000$	75.9	86.2	66.0	77	87
$n=40$	$m=500$	41.5	66.2		42	68
	$m=1000$	63.4	78.0	61.5	64	80
	$m=2000$	74.6	88.2	74.6	75	90
Simulated 3PLM – Estimated 2PLM
$n=10$	$m=500$	7.1	23.7		7	13
	$m=1000$	9.3	40.2		10	30
	$m=2000$	13.3	62.4		14	46
$n=20$	$m=500$	8.3	25.9		9	13
	$m=1000$	11.5	41.0	23.9	10	25
	$m=2000$	16.8	58.6	40.2	17	44
$n=40$	$m=500$	8.0	20.6		6	15
	$m=1000$	11.4	32.1	25.1	7	28
	$m=2000$	17.4	46.1	40.3	12	44

Note. Stone and Zhang (2003, Table 2).

To conclude remarks on this Monte Carlo experiment, it is worth noticing that ${\chi }_w^2$ performed well when random 50% of item responses were missing both in terms of its averaged Type I error rates (Table 1) and power (Table 2). Results for ${\chi }_w^2$ under the missing responses condition closely resemble the ones that are observed for complete data but with twice less items and observations, which is exactly the expected outcome. This result puts ${\chi }_w^2$ at advantage of over methods that rely on observed sum-score portioning of ability, like $\mathrm{S}-{\mathrm{X}}^2$ .

Simulation Study 3 – Power

Simulation Design

Last experiment adapted a design proposed by Orlando and Thissen (2003) to analyze power in misfit scenarios that go beyond fitting of a restricted IRT model to data generated from an unrestricted model. It involved three “bad” items that are described by response functions

$\mathrm{B}\mathrm{A}\mathrm{D}\mathrm{1}: P\left(y_j|\theta \right)=\frac{c_j}{1+e^{a_j(\theta -(b_j-d_j))}}+\frac{1}{1+e^{-a_j\left(\theta -b_j\right)}},$

where $a_j=1.7,2.5$ , $b_j=1$ , $c_j=0.25$ , and $d_j=1.5$ ;

$\mathrm{B}\mathrm{A}\mathrm{D}\mathrm{2}: P\left(y_j|\theta \right)=\frac{d_j}{1+e^{-a_j\left(\theta -b_j\right)}},$

where $a_j=1.7,2$ , $b_j=0.5$ , $d_j=0.7$ ; and $\mathrm{B}\mathrm{A}\mathrm{D}\mathrm{3}: P\left(y_j|\theta \right)=\frac{x_j}{1+e^{-a_j\left(\theta -b_j\right)}}+\frac{y_j}{1+e^{a_j(\theta -(b_j-d_j))}},$

where $a_j=1.7,3.5$ , $b_j=-1$ , $d_j=3$ , $x_j=0.55$ , and $y_j=\mathrm{0.45.}$

These bad items were, one at a time, embedded in tests consisting of $n\in \left\{10, 20, 40, 80\right\}$ total items. The remaining $v\ne j$ items were drawn from 2PLM with $\ln a_{v\ne j}\sim N(0, 0.5)$ and $b_{v\ne j}\sim N\left(\mathrm{0,1}\right)$ . For each test length $m\in \left\{500, 1000, 2000\right\}$ , item responses were generated and IRT model was fit to data. Items BAD2, BAD3, and all $v\ne j$ items were modeled with 2PLM without imposing priors on item parameters, and item BAD1 was modeled with 3PLM using noninformative priors: $N\left(\mathrm{0,3}\right)$ for $b_j$ , $N(1.1,3)$ for $a_j$ , and $\beta (1.01,1.03)$ for $c_j$ . Estimated item parameters were used to compute ${\chi }_w^2$ and $\mathrm{S}-{\mathrm{X}}^2$ for the three bad items.

This design deviated from the original conditions used by Orlando and Thissen (2003) by adopting 3PLM only for the item BAD1, instead of using it for all items. It was motivated by observation that the $c_j$ parameter for items BAD2 and BAD3 approached 0 with increase of $m$ . The 3PLM would be an unnecessarily over-parametrized choice for items BAD2 and BAD3.

Simulation Results

Resulting power rates (Table 3) support previous evidence (Table 2) that ${\chi }_w^2$ is more sensitive in detecting misfit than $\mathrm{S}-{\mathrm{X}}^2$ . Power of both statistics rose with increase of test length and sample size, but under all tested conditions ${\chi }_w^2$ exceeded $\mathrm{S}-{\mathrm{X}}^2$ .

Table 3.

Power rates for three types of misfitting items.

Item	Test length	n = 500		n = 1000		n = 2000
		$S-X^2$	${\chi }_w^2$	$S-X^2$	${\chi }_w^2$	$S-X^2$	${\chi }_w^2$
BAD1	m = 10	0.379	0.634	0.551	0.845	0.790	0.969
	m = 20	0.539	0.868	0.753	0.982	0.955	0.999
	m = 40	0.598	0.964	0.861	0.999	0.992	1.000
	m = 80	0.533	0.987	0.865	1.000	0.998	1.000
BAD2	m = 10	0.130	0.228	0.209	0.413	0.378	0.680
	m = 20	0.221	0.450	0.406	0.749	0.731	0.953
	m = 40	0.315	0.607	0.586	0.875	0.912	0.993
	m = 80	0.351	0.641	0.659	0.905	0.957	0.996
BAD3	m = 10	0.221	0.520	0.444	0.802	0.783	0.969
	m = 20	0.359	0.764	0.756	0.967	0.982	1.000
	m = 40	0.443	0.842	0.873	0.990	1.000	1.000
	m = 80	0.444	0.851	0.878	0.992	1.000	1.000

Summary

Multiple Monte Carlo experiments were conducted to examine properties of the new ${\chi }_w^2$ item-fit statistic. Type I error of ${\chi }_w^2$ was close to nominal level. It outperformed Orlando and Thissen’s $\mathrm{S}-{\mathrm{X}}^2$ on power under all tested conditions. In the 3PLM-2PLM, misfit scenario ${\chi }_w^2$ was also more sensitive in comparison with Stone’s ${\chi }^{2\ast }$ . The results are promising and ${\chi }_w^2$ poses as a viable candidate to test for item fit. It is especially attractive because it can be applied to incomplete testing designs, unlike alternatives that use observed scores for partitioning, and is far less computationally demanding than available statistics that involve residuals over the latent trait.

It is worth pointing to the possibility of other applications of the item-fit approach that was proposed in the article. First, ${\chi }_w^2$ is straightforwardly generalizable to polytomous items and to multivariate abilities. Also, the quadrature used in implementation of ${\chi }_w^2$ can be replaced with other solutions to cover cases when ability is not normally distributed. Second, estimates of observed proportions and of the covariance matrix in (5) can be utilized to construct confidence bounds around observed proportions. Such confidence intervals can be plotted against ${\widehat{f}}_j$ to aid graphical analysis of item-fit. And finally, approach outlined in the article can also be applied to perform differential item functioning (DIF) analysis.

It should be noted that mathematical underpinnings of ${\chi }_w^2$ laid out in the article are incomplete. Asymptotic multivariate normality of vector of pseudo-observed proportions, (8), is assumed without proof. Consistency of the proposed estimator of the covariance, (10), is likewise just assumed. Careful consideration should also be exercised on how replacing item response functions in the known parameter case of ${\chi }_w^2$ by their ML estimates impacts the asymptotic claims about ${\chi }_w^2$ – especially when item parameters are estimated with priors. Results of simulational studies support asymptotic claims made about ${\chi }_w^2$ . However, they cannot be automatically generalized to cover conditions that would deviate from the specific ones that were considered here. This opens ground for future research on ${\chi }_w^2$ .

ORCID iD

Bartosz Kondratek https://orcid.org/0000-0002-4779-0471