Towards clustered carbonyl cations [M₃(CO)₁₄]²⁺ (M = Ru, Os): the need for innocent deelectronation

Abstract

To access the hitherto almost unknown class of clustered transition metal carbonyl cations, the trimetal dodecacarbonyls M₃(CO)₁₂ (M = Ru, Os) were reacted with the oxidant Ag⁺[WCA]⁻, but yielded the silver complexes [Ag{M₃(CO)₁₂}₂]⁺[WCA]⁻ (WCA = [Al(OR^F)₄]⁻, [F{Al(OR^F)₃}₂]⁻; R^F = –OC(CF₃)₃). Addition of further diiodine I₂ to increase the redox potential led for M = Ru non-specifically to divalent mixed iodo-Ru^II-carbonyl cations. With [NO]⁺, even the N–O bond was cleaved and led to the butterfly carbonyl complex cation [Ru₄N(CO)₁₃]⁺ in low yield. Obviously, ionization of M₃(CO)₁₂ with retention of its pseudo-binary composition including only M and CO is difficult and the inorganic reagents did react non-innocently. Yet, the radical cation of the commercially available perhalogenated anthracene derivative 9,10-dichlorooctafluoroanthracene (anthracene^Hal) is a straightforward accessible innocent deelectronator with a half-wave potential E_1/2 of 1.42 V vs. Fc^0/+. It deelectronates M₃(CO)₁₂ under a CO atmosphere and leads to the structurally characterized cluster salts [M₃(CO)₁₄]²⁺([WCA]⁻)₂ including a linear M₃ chain. The structural characterization as well as vibrational and NMR spectroscopies indicate the presence of three electronically independent sets of carbonyl ligands, which almost mimic M(CO)₅, free CO and even [M(CO)₆]²⁺ in one and the same cation.

Trimeric M₃(CO)₁₂ (M = Ru, Os) reacts with typical inorganic oxidants to unwanted side products. Yet, the 9,10-dichlorooctafluoroanthracene radical cation deelectronates these under CO pressure to give the first homotrimetallic [M₃(CO)₁₄]²⁺ salts.

Introduction

The carbon monoxide ligand is omnipresent in organometallic chemistry and of high interest for both fundamental chemistry as well as industrial applications.^1,2 The combination of the σ-bonding and π-backbonding interactions with transition metals enables the stabilization of transition metal carbonyls (TMCs) in formal oxidation states between −IV and +III.³ There is no other neutral ligand class, with the exception of the closely related alkylisocyanides (−II to +V),⁴ which allows the stabilization of homoleptic transition metal complexes over such a huge range of eight formal oxidation states.

Closer analysis of the bonding within the transition metal carbonyls has led to the classification of two different kinds of carbonyl complexes by S. H. Strauss et al. in 1994:⁵ the first class is addressed as being “classical”, in which the π-backdonation from the d-electrons of the metal centre towards the π*-orbital of the ligand is the primary interaction, leading to a weakening of the carbon–oxygen bond and a red shift of the _CO stretching vibrations compared to free carbon monoxide. The second class is addressed as “nonclassical” carbonyl complexes, where the σ-donation of the carbonyl ligand towards the metal centre is the dominant interaction, apparently leading to a strengthening of the carbon–oxygen bond and a blueshift of the _CO stretch relative to free carbon monoxide.⁶ Alternatively, Aubke and Willner addressed them as predominantly σ-bonded carbonyl cations or σ-carbonyls.⁷

The prediction of the nature of the carbonyl ligand within homoleptic transition metal carbonyl cations (TMCCs) is not intuitive: while [Ag(CO)_1–2]⁺ complexes are nonclassical, other monocationic homoleptic TMCCs like [Mn(CO)₆]⁺ are classical.⁸ The prediction is even less straightforward for heteroleptic TMCCs: an illustrative example is [(Cp*)₂Fe–CO]²⁺, which bears iron in the formal oxidation state +IV, but is a classical carbonyl complex.^9,10 Hence, the investigation of novel homoleptic TMCCs remains an interesting field with potential for new discoveries, despite the fact that meanwhile the monometallic TMCCs of many transitions metals were already isolated in condensed phases.^2,7,11

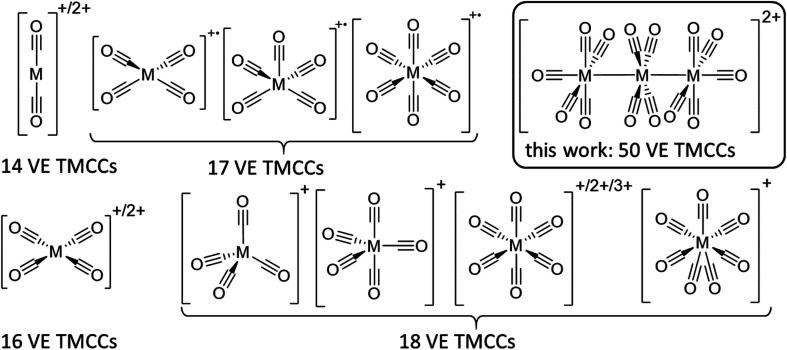
Still, the weak interaction of carbon monoxide with metal cations requires the strict absence of other nucleophiles, which implies the use of both weakly coordinating anions (WCAs) and weakly coordinating solvents/media. Hence, super acids are a common medium to stabilize transition metal complexes in unusually high oxidation states in general.¹² Likewise, reductive carbonylation in super acidic mixtures like fluoroantimonic acid (HF/SbF₅) or “magic acid” (HSO₃F/SbF₅) was utilized by Willner and Aubke to yield several diamagnetic 14, 16 & 18 valence electron (VE) TMCCs containing mono-to trivalent metals.⁷ Yet, this system is limited by the coordination ability of the [SbF₆]⁻ anion, which is incompatible with the strong fluorophilicity of early transition metals^13,14 as well as the strong acidity, which obstructs Brønsted basic TMCs as starting materials.¹⁵ While perfluorinated alkoxyaluminate based WCAs have a higher affinity to protons than hexafluoroantimonate,¹⁶ transition metal complexes are much more weakly coordinated with this class of anions due to the poor polarizability of the C–F bonds and the delocalization of the negative charge over a much larger volume.¹⁷ The combination of this type of WCA, paired with inorganic oxidative cations in fluorinated benzene derivatives by our group has enabled the access to paramagnetic 17 VE TMCCs like [M(CO)₆]⁺˙ (M = Cr, Mo, W),^18,19, [Fe(CO)₅]⁺˙²⁰ and [Ni(CO)₄]⁺˙²¹ from their respective neutral TMCs as well as the isolation of the first metal heptacarbonyls [M(CO)₇]⁺ (M = Nb, Ta) (Fig. 1).²²

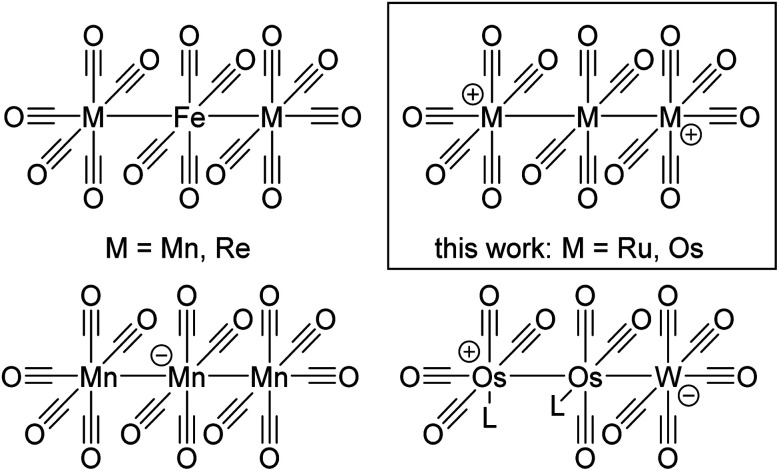
Fig. 1. Known structurally characterized homoleptic TMCCs without strong contacts to counterions. 14 VE: [M(CO)₂]^+/2+ Ag⁺, Hg²⁺; 16 VE: [M(CO)₄]^+/2+ Rh⁺, Pd²⁺, Pt²⁺; 17 VE: [M(CO)₄]⁺˙ Ni⁺; [M(CO)₅]⁺˙ Fe⁺ [M(CO)₆]⁺˙ Cr⁺, Mo⁺, W⁺; 18 VE: [M(CO)₄]⁺ Cu⁺; [M(CO)₅]⁺ Co⁺; [M(CO)₆]^{+/2+/3 +} Mn⁺, Tc⁺, Re⁺, Fe²⁺, Ru²⁺, Os²⁺, Ir³⁺; [M(CO)₇]⁺ Nb⁺, Ta⁺; 50 VE: [M₃(CO)₁₄]²⁺ {Ru₃}²⁺, {Os₃}²⁺.

By contrast, clustered TMCCs are still very scarce and in their infancy: apart from mass spectrometric investigations,²³ there are only two reports of homodinuclear transition metal carbonyl cations available in the condensed phase: [Hg₂(CO)₂]²⁺ and [Pt₂(CO)₆]²⁺. Yet, the instability of these complexes has not allowed full characterisation including single crystal X-ray diffraction (scXRD).²⁴ Therefore, we turned our attention to the preparation of clustered TMCCs. With the thermodynamic instability of their respective monometallic pentacarbonyl complexes M(CO)₅ ref. 25,26 (M = Ru, Os) and their manifold of known cluster chemistry,²⁷ triruthenium and triosmium dodecacarbonyl M₃(CO)₁₂ seemed to be good candidates for the deelectronation to the first homotrimetallic TMCCs.

Results and discussion

To convert the trimetal dodecacarbonyls to their respective TMCCs, an oxidation agent is needed which retains the pseudo-binary composition of the complexes. Previously we showed, e.g. for the group 6 hexacarbonyls,^19,28 that the typical inorganic oxidants Ag⁺, Ag⁺/0.5 X₂ and NO⁺ act in several unwanted non-innocent side reactions (eqn (1b), (2b) and (3b)) instead of the desired deelectronation (eqn (1a), (2a) and (3a)). Note, that we use electronation and deelectronation in their strict sense, i.e. removal/addition of electrons in innocent reactions, hence without non-innocent complications. For reasoning see^29,30 and the literature included with.^29,31 In this work we even observed the cleavage of the N–O bond in [NO]⁺ in eqn (3c). Hence, the strongest bond known to condensed phase chemistry.³²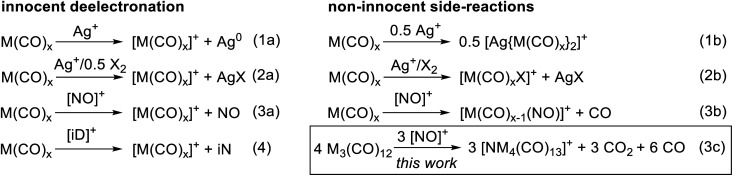

Accordingly, we learned that the use of innocent deelectronators ([iD]⁺), that do not perform side reactions with Lewis basic transition metal complexes, are superior for an innocent deelectronation towards homoleptic TMCCs as in eqn (4). In the following, we first introduce the reactions of M₃(CO)₁₂ with the non-innocent inorganic oxidants before turning to a novel [iD]⁺ deelectronator salt accessible from a commercial innocent neutral (iN) and describing its structural demands and reactions according to eqn (4) in separate sections.

Syntheses with inorganic oxidant cations

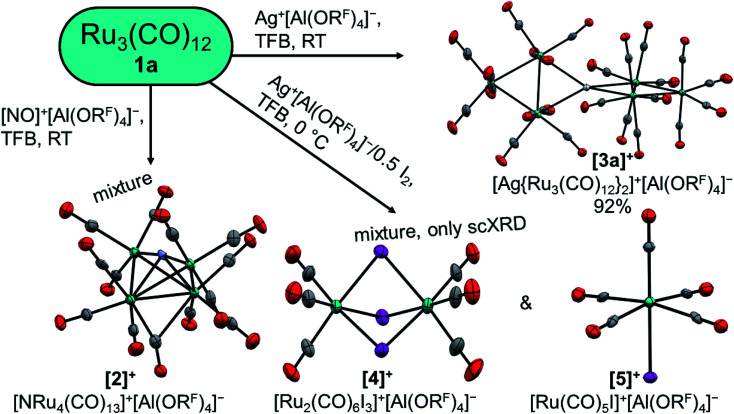
At first, we reacted the commercially available carbonyl complexes Ru₃(CO)₁₂ and Os₃(CO)₁₂ with the inorganic oxidant cations [ox]⁺ ([NO]⁺, Ag⁺, Ag⁺/0.5 I₂) partnered with the weakly coordinating perfluorinated alkoxyaluminate anion [Al(OR^F)₄]⁻ (R^F = OC(CF₃)₃). All reactions were performed in 1,2,3,4-tetrafluorobenzene (TFB) as a polar, but very weakly coordinating and non-basic solvent. Fig. 2 includes an overview of the outcome of the reactions with triruthenium dodecacarbonyl (1a).

Fig. 2. Reactions of 1a with typical inorganic oxidant cations. Molecular structures of the cations are drawn with thermal ellipsoids set at 50% probability; WCAs and co-crystallized solvent molecules were omitted for clarity. Colour code: carbon – grey, nitrogen – light blue, oxygen – red, ruthenium – turquoise, silver – white, iodine – purple.

[NO]⁺ as oxidant: formation of a cationic butterfly complex

Due to the facile and clean removal of nitrogen monoxide as the gaseous by-product of a deelectronation, the use of nitrosyl cations was our first attempt towards a clustered TMCC. The reaction of triruthenium dodecacarbonyl with [NO]⁺[Al(OR^F)₄]⁻ in TFB led to a red solution. Upon diffusion with n-pentane a small crop of red crystals forms besides an undefined viscous oil. This red material, isolated in low crystalline yield, was shown to be [Ru₄N(CO)₁₃]⁺[Al(OR^F)₄]⁻via scXRD. The homotetranuclear cluster cation [2]⁺ is coordinated by one μ₄-nitride ligand, one semi bridging carbonyl ligand and twelve terminal carbonyl ligands. It is formally a twofold deelectronated and carbonyl-rich form of [Ru₄N(CO)₁₂]⁻.³³ The reaction probably begins with a [NO]⁺-insertion to an [Ru₃(CO)₁₂(NO)]⁺ intermediate, followed by the hypothetic reduction of the nitrosyl ligand by carbon monoxide leading to a nitride ligand, carbon dioxide and ruthenium(ii), followed by a Ru(CO)₄ addition and the loss of two CO ligands. A related reaction sequence is known for Ru₃(CO)₁₀(μ₂-NO)₂, which decomposes at 110 °C under a carbon monoxide atmosphere to [Ru₄N(CO)₁₂(μ₂-NO)].³⁴ While ligand substitution reactions were often reported for TMCs with nitrosyl cations, cleavage of the N–O bond was not detected so far.^18,19,21,35 The presence of terminal nitrosyl-ligands could be excluded by IR spectroscopy of the mixture and by DFT calculations, where the semi-bridging mode of the ligand was exclusively observed in the butterfly complex with carbonyl ligands only (see (ESI†): Chapter ‘Absence of Nitrosyl Ligands in [2]⁺’). Unfortunately, the reaction of [NO]⁺[Al(OR^F)₄]⁻ with Os₃(CO)₁₂ only led to an undefined oil.

Ag⁺ as oxidant: formation of MOLPs including M₃(CO)₁₂ moieties

With the degradation of the nitrosyl cation, we changed to the even simpler monoatomic oxidant, the silver(i) cation. This already led to the successful synthesis of TMCCs, e.g. [Co(CO)₅]⁺ and [M(CO)₇]⁺ (M = Nb, Ta).^22,36 In our case, the reaction of Ag⁺[Al(OR^F)₄]⁻ with two equivalents of 1a or 1b has led to the respective silver complexes with two trimetal dodecacarbonyl ligands in almost quantitative yield (eqn (5)).

5

While the structure of [3a]⁺[Al(OR^F)₄]⁻·C₆F₄H₂ is well resolved, the structure of the osmium analogue has severe disorders within the structure of the cluster cation. Therefore, the reaction was performed analogously with Ag⁺[F{Al(OR^F)₃}₂]⁻, which yielded the salt [3b]⁺[F{Al(OR^F)₃}₂]⁻˙C₆F₄H₂, in which the cluster cation is well ordered. In both structures, the silver cation is coordinated by the M–M bonds of two trimetal dodecarbarbonyls in a D_2d coordination geometry (τ = 73°). In addition to the strong interactions of the metal atoms with the silver cation, the proximal carbonyl ligands coordinate weakly to the silver(i) cation, which results in reduced M–C–O angles of ca. 171° and weakly bonding Ag–C distances between 2.69 and 2.77 Å (cf. sum of vdW radii Ag + C = 3.42 Å).³⁷ All aspects of the structures are well in line with the DFT calculated optimized structures (B3LYP(D3BJ)/def2-TZVPP).

The formation of adducts of TMCs with silver(i) cations has already been observed by our group^28,38 with recent additions from the Dias group.^39,40 These complexes can be seen as metal-only Lewis pairs (MOLPs).⁴¹ While zero valent and pentacoordinated group 8 complexes are known for having Lewis-basic behaviour and silver cations are known to be Lewis acidic, their heterodinuclear complexes are scarce.^41,42 In contrast to the previously known cationic group 8 → group 11 MOLPs, the primary interaction in [3a]⁺ and [3b]⁺ is the donation of electron density from a metal–metal σ-bond instead of a single metal donor orbital. This donation leads to an elongation of the tangential metal–metal bond by 0.13 Å,⁴³ while the other metal does not experience significant shifts.

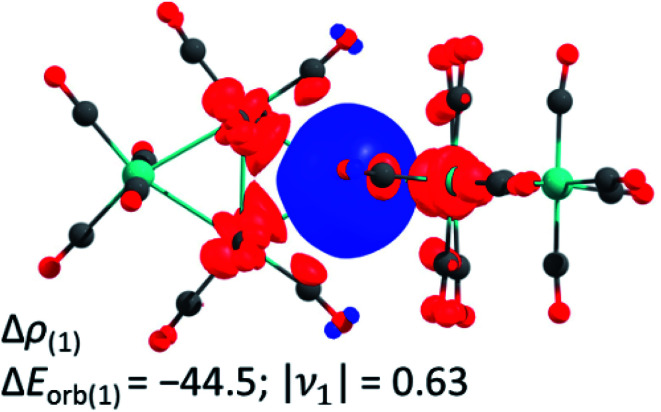
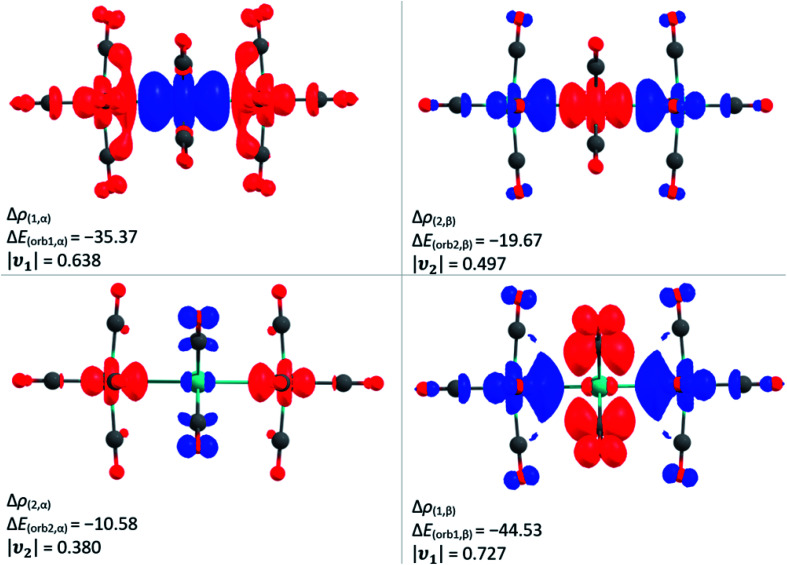
In addition, we investigated the bonding situation between the {M₃(CO)₁₂}₂ (M = Ru, Os) and the Ag⁺ fragments with the EDA-NOCV method.⁴⁴ The assignments of the orbital interactions are closely related to those observed in [Ag{M(CO)₆}₂]⁺ (M = Cr, Mo, W).²⁸ Therefore they are omitted here and shown in the ESI.† The interaction energies of the silver cation with {M₃(CO)₁₂}₂ are relatively strong (−118.5/−123.7 kcal mol⁻¹ Ru/Os) and even exceed the values of Ag⁺ with the group 6 hexacarbonyls {M(CO)₆}₂ −79.8/−86.1/−86.7 (Cr/Mo/W) kcal mol^{−1 28} and iron pentacarbonyl {Fe(CO)₅}₂ (−97.6 kcal mol⁻¹).³⁹ The deformation density plot of the [(OC)₁₂M₃]→Ag⁺←[M₃(CO)₁₂] σ-donation explains the elongation of the tangential metal–metal bond and the bending of the carbonyl ligands proximal to the silver(i) cation very well (Fig. 3).

Fig. 3. The shape of the deformation density of Δρ₍₁₎, which is associated with ΔE_orb(1) in kcal mol⁻¹ calculated at the BP86(D3BJ)/TZ2P level; relativistic effects were considered with ZORA. It presents mainly the donation of electron density from the M–M σ-bond to the empty 5s orbital of Ag⁺. The eigenvalue ν₁ gives the value of the charge migration. The direction of the charge flow is from red to blue. Colour code: carbon – grey, oxygen – red, ruthenium – turquoise.

The synergistic Ag⁺/0.5 I₂ system: competing iodonium additions

The oxidation power of the silver(i) cation can be increased by the addition of elemental dihalogens.^45,46 This additional driving force has led to the successful synthesis of multiple TMCCs.^19,21 However, the trimetal dodecacarbonyls react already at low temperatures with dihalogens over [M₃(CO)₁₂(μ₂-X)]⁺ to M₃(CO)₁₂X₂ (X = Cl, Br, I).⁴⁷ Therefore, the salt Ag⁺[Al(OR^F)₄]⁻ was reacted with half an equivalent of diiodine to generate the molecular [Ag₂I₂]²⁺([Al(OR^F)₄]⁻)₂in situ,⁴⁵ before Ru₃(CO)₁₂ was added. Despite these efforts, only a mixture containing inter alia single crystals of [Ru₂(CO)₆I₃]⁺[Al(OR^F)₄]⁻, [Ru(CO)₅I]⁺[Al(OR^F)₄]⁻ and other undefined products was observed. Due to the non-specific reactions giving Ru(ii) compounds we refrained from optimizing these reactions.

Development of a perhalogenated arene radical cation salt as a new innocent deelectronator

The challenging syntheses with the classical reagents delineate the need for alternative means of deelectronation. Therefore, our group has recently developed an [iD]⁺ salt: perfluoro-5,10-bis(perfluorophenyl)-5,10-dihydrophenazinium [“phenazine^F”]⁺˙[Al(OR^F)₄]⁻ with a formal potential of 1.29 V vs. Fc^0/+ in 1,2-difluorobenzene (oDFB). Yet, the synthesis of its perfluorinated amine as innocent neutral (iN) is laborious and very time consuming. Therefore, we looked for an alternative, for which the corresponding innocent neutral is commercially available and which has a similar redox potential in its deelectronated [iD]⁺ state. However, this potential should not be overly high, to ensure the compatibility with both the perfluorinated alkoxyaluminate WCAs and the partially fluorinated benzene derivatives as non-basic and weakly coordinating, but polar solvents. Additionally, the innocent character should be retained. The comparison of [“phenazine^F”]⁺˙ to the archetypical organic oxidant tris(4-bromophenyl)aminium (“magic blue”) [N(C₆H₄-4-Br)₃]⁺˙ shows, that perhalogenation is needed additionally to avoid unwanted side reactions of generated cations with aromatic C–H bonds.¹⁰

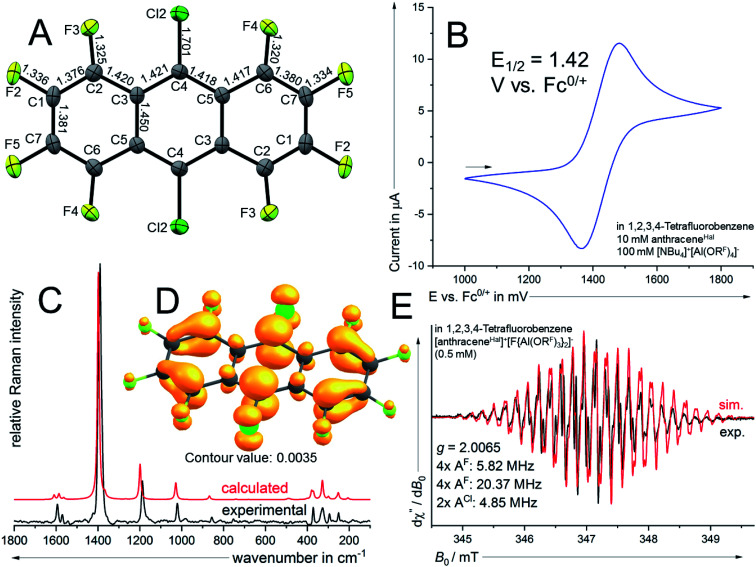
As a potential candidate, the simplest perfluorinated arene, perfluorobenzene (benzene^F), needs extreme reagents like iridium hexafluoride for the deelectronation to its radical cation.⁴⁸ Additionally, the benzene^F radical cation is highly Lewis acidic and causes the slow decomposition of the hexafluorometalate WCAs [MF₆]⁻ (M = Ir, Sb) at room temperature. Fortunately, the ionization energies of the fluorinated arenes decrease with the number of linearly fused rings. Seppelt et al. investigated the deelectronation of larger fluorinated arenes like perfluoronaphthalene (naphthalene^F) and 9,10-dichlorooctafluoroantracene (anthracene^Hal).⁴⁹ While the first was deelectronated and crystallographically characterized as [naphthalene^F]⁺˙[As₂F₁₁]⁻ naphthalene^F, the latter, under reaction conditions, undergoes a halogen exchange to perfluoroanthracene (anthracene^F), which was deelectronated twice to give [anthracene^F]²⁺ ([Sb₂F₁₁]⁻)₂. By contrast, the larger fluorinated arenes like perfluorotetracene (tetracene^F) and perfluoropentacene (pentacene^F) have surprisingly low half-wave potentials of just 1.02 V and 0.79 V vs. Fc^0/+ in 1,2-dichlorobenzene.⁵⁰ Yet, tetracene^F and pentacene^F can be only accessed by multi-step syntheses, while anthracene^Hal is commercially available. Cyclovoltammetry of anthracene^Hal (6) shows an electrochemically reversible half-wave potential E_1/2 at 1.42 V vs. Fc^0/+ in both oDFB and TFB, which is 130 mV higher than that of the previously used “phenazine^F” (Fig. 4B).¹⁰ When 6 is reacted with [NO]⁺[F{Al(OR^F)₃}₂]⁻ in TFB (but not in oDFB), a dark green solution and evolution of gas is observed, indicating the generation of [6]⁺˙ and nitrogen monoxide (eqn (6)).

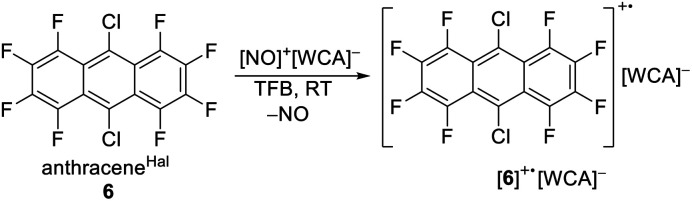6

Fig. 4. (A) Molecular structure of the radical cation in [6]⁺˙[F{Al(OR^F)₃}₂]⁻ (ellipsoids set at 50% probability, distances in Å and standard deviations of the C–C bonds in the range of 0.003 Å). Colour code: carbon – grey, fluorine – light green, chlorine – dark green. (B) Cyclovoltammetry (2^nd cycle; 100 mV s⁻¹) of 6. (C) calculated (B3LYP(D3BJ)/def2-TZVPP) Raman spectrum of [6]⁺˙ and experimental Raman spectrum of crystalline [6]⁺˙[F{Al(OR^F)₃}₂]⁻. (D) Spin density plot (B3LYP(D3BJ)/def2-TZVPP) of [6a]⁺˙. (E) EPR spectrum of a 0.5 mM solution of [6]⁺˙[F{Al(OR^F)₃}₂]⁻ in TFB and simulated EPR spectrum using the hyperfine coupling constants indicated in the figure.

Dark green crystalline blocks suitable for scXRD could be obtained by layering the solution with n-pentane in 80% yield. The product was further analysed with pXRD, as well as IR, Raman, NMR and EPR spectroscopy (Fig. 4). The comparison of the solid state structure of [6]⁺˙[F{Al(OR^F)₃}₂]⁻ with its innocent neutral (6)⁵¹ shows a shortening of all the carbon halogen bonds and an alternation of shortening and elongation of the carbon carbon bond lengths of the aromatic core, this fits the DFT calculated (B3LYP(D3BJ)/def2-TZVPP) SOMO of [6]⁺˙ (see ESI Chapter 3†). The EPR spectrum shows a delocalization of the spin density across all the substituents (Fig. 4E). The hyperfine coupling constants of the fluorine atoms on the α-position are bigger than those for the fluorine atoms in the β-position, which is in line with the smaller spin density at the β-fluorine atoms (Fig. 4D). The spin in [6]⁺˙ is therefore similarly delocalised as in the [iD]⁺ [“phenazine^F”]⁺˙. Favourably, 6 has a higher availability, a smaller molecular weight and a higher deelectronation potential as phenazine^F.

Synthesis and characterisation of the trimetal tetradecarbonyl dications

To test the novel [iD]⁺ reagent, we reacted two equivalents of the in situ generated [6]⁺˙[Al(OR^F)₄]⁻ with the trimetal dodecacarbonyls 1a and 1b under CO pressure according to eqn (3). The intense green colour vanishes after a few minutes leading to brownish solutions, which were layered with n-pentane yielding clear colourless crystals of [7a]²⁺([Al(OR^F)₄]⁻)₂·2C₆F₄H₂ and [7b]²⁺([Al(OR^F)₄]⁻)₂·2C₆F₄H₂ suitable for scXRD and in 88% (Ru)/72% (Os) yield.

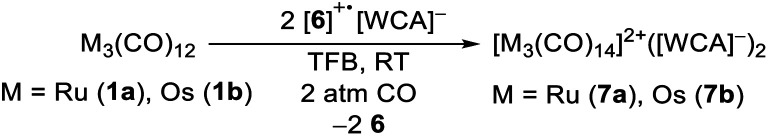3

The products were additionally analysed in the bulk by pXRD and by NMR, IR and Raman spectroscopy. The reaction works analogously with [6]⁺˙[F{Al(OR^F)₃}₂]⁻, which yields [7a]²⁺([F{Al(OR^F)₃}₂]⁻)₂·C₆F₄H₂ and [7b]²⁺([F{Al(OR^F)₃}₂]⁻)₂·C₆F₄H₂.

Metal–metal bonding-situation

The dications [7a]²⁺ and [7b]²⁺ are the first structurally characterized homomultimetallic TMCCs. However, some examples of neutral and anionic trimetal tetradecacarbonyls and derivatives isoelectronic to [7a]²⁺ and [7b]²⁺ are known, including [Mn₃(CO)₁₄]⁻,⁵² M₂Fe(CO)₁₄ (M = Mn, Re)⁵³ and the tandem MOLPs WOs₂(CO)₁₂(L)₂ (L = CN^tBu, P(OCH₂)₃CMe) (Fig. 5).⁵⁴

Fig. 5. Overview of known and new trimetal tetradecacarbonyls and their relatives.

Trimetal tetradecacarbonyls with 50 valence electrons (VE) and their heteroleptic derivatives can be seen as a combination of two terminal -M(CO)₅ fragments (17 VE → pseudohalogen)⁵⁵ and an inserted -M(CO)₄- fragment (16 VE → pseudochalcogen), which are connected by metal metal single bonds. The Lewis-structure shows a positive formal-charge on each terminal metal atom at [7a]²⁺ and [7b]²⁺. A quantum theory of atoms in molecules (QTAIM) analysis of [7a]²⁺ (B3LYP(D3BJ)/def2-TZVPP) is well in line with this Lewis structure and assigns a +0.875 charge on each terminal -Ru(CO)₅ fragment and only a charge of +0.25 on the central -Ru(CO)₄- fragment. The charge-distribution in [7b]²⁺ is even more unequal with a +0.17 charge on the central -Os(CO)₄- fragment.

Molecular structures

[7a]²⁺([Al(OR^F)₄]⁻)₂·2C₆F₄H₂ and [7b]²⁺([Al(OR^F)₄]⁻)₂·2C₆F₄H₂ crystallize both in the space group P1̄ and are isomorphous. The linear homotrimetallic core is coordinated by fourteen carbonyl ligands resulting in a square pyramidal coordination geometry for the terminal metal atoms and a square planar coordination geometry for the middle metal atom always referring to the carbonyl ligands. The torsion angles between the equatorial carbonyl ligands of two neighbouring metals are close to 45° leading to an ecliptic arrangement of the terminal -M(CO)₅ fragments in an overall D_4h symmetry. Through minor interactions of the complex dication with the WCA and solvent, the ideal D_4h geometry is slightly distorted in [M₃(CO)₁₄]²⁺ to the crystallographic C_i symmetry. The co-crystallized solvent molecules have weak interactions with the complex salt leading to the degradation of the crystalline phase upon drying of the crystals in vacuo (see ESI†). It is noticeable, that, in all the four crystal structures of [7a]²⁺ and [7b]²⁺, the metal carbon bond lengths elongate from M–CO_cen,eq over M–CO_out,eq to M–CO_out,ax, while the opposite trend is observed for the carbon–oxygen bond lengths. This can be explained by a more pronounced π-backbonding in the central fragment. The span of the bond lengths is remarkable, because the bond lengths of M–C O_cen,eq are similar to those observed in the respective neutral metal pentacarbonyls M(CO)₅ (M = Ru, Os),⁵⁶ while the bond lengths of M–C O_out,ax are close to those observed in the superelectrophilic [M(CO)₆]²⁺ dications.⁵⁷

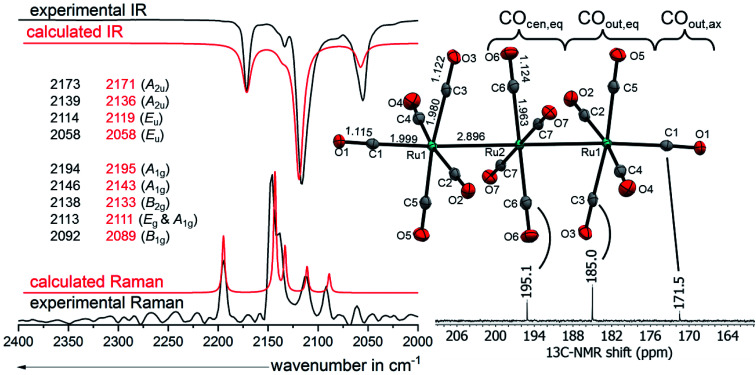
Vibrational spectroscopy

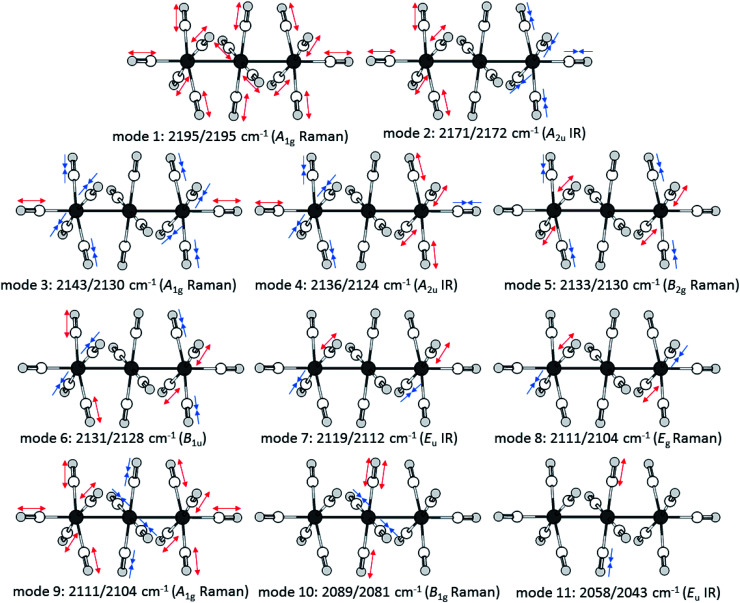
While the scXRD has relatively high errors relative to the subliminal shifts of the CO bond length, the vibrational spectroscopy at hand gives a high precision of the experimental results. The vibrational modes of [7a]²⁺ and [7b]²⁺ are the result of the linear combination of all the carbonyl ligands. In order to assign the bands in the experimental IR and Raman spectra to the right vibrational modes, the respective spectra of the complexes were simulated with DFT methods (B3LYP(D3BJ)/def2-TZVPP). By utilizing the published specific scaling factor of 0.968 for metal carbonyls at this level of theory,⁵⁸ the simulated spectra fit to the observed bands to within 1-6 cm⁻¹ for [7a]²⁺ and 1-7 cm⁻¹ for [7b]²⁺. Eleven vibrational modes are expected for the trimetal tetradecacarbonyls, four of them are IR active, six are Raman active and one is neither IR, nor Raman active. The ten experimentally observable vibrational (CO) modes spread over 136 cm⁻¹ in [7a]²⁺([Al(OR^F)₄]⁻)₂ (Fig. 6) and 158 cm⁻¹ in [7b]²⁺([Al(OR^F)₄]⁻)₂. The average carbonyl stretching vibrational frequencies weighed over the degeneracies⁵⁹ of (CO)_av = 2120/2117 (Ru/Os) cm⁻¹ are slightly below that of free CO_(g) at 2143 cm⁻¹ and lay between that of the respective metal pentacarbonyls M(CO)₅ (2038/2032 cm⁻¹) and the known metal hexacarbonyl dications [M(CO)₆]²⁺ (2220/2216 cm⁻¹).^25,57 This shows the presence of some π-interactions between the carbonyl ligands and the metal centres, classifying the complexes as still being “classical carbonyl complexes”.

Fig. 6. Molecular structure of the dication [7a]²⁺ in [7a]²⁺([Al(OR^F)₄]⁻)₂·2C₆F₄H₂ (ellipsoids set at 50% probability, average distances in Å and standard deviations of the C–O bonds in the range of 0.002 Å) colour code: carbon – grey, oxygen – red, ruthenium – turquoise with the experimental and calculated IR and Raman spectra calculated at B3LYP(D3BJ)/def2-TZVPP level and scaled by 0.968 according to M. A. Duncan et al.⁵⁸ and ¹³C-NMR from [7a]²⁺([Al(OR^F)₄]⁻)₂ in TFB.

Upon closer look to the vibrational modes, however, not all different carbonyl ligands are active in all vibrational modes (Fig. 7). Therefore, we calculated the respective (CO)_av for the symmetry inequivalent carbonyl ligands. While this method does not “unmix” the vibrational modes, the trend from the scXRD can be reproduced, showing a more prominent π-interaction in the M–CO_cen,eq modes (CO_cen,eq)_av = 2103/2095 cm⁻¹ in comparison to a “nonclassical” interaction in the M–CO_out,ax modes (CO_out,ax)_av = 2153/2150 cm⁻¹.

Fig. 7. Visualisation of the movements of the vibrational modes of the dications [7a]²⁺ and [7b]²⁺ according to calculations at the B3LYP(D3BJ)/def2-TZVPP level and scaled by 0.968 as suggested by M. A. Duncan et al.⁵⁸.

The force constants of the carbon–oxygen bonds can be estimated with the Cotton–Kraihanzel approximation (see ESI chapter 9 for detailed formulae†).⁶⁰ Through this approximation, the force constants of all the symmetrical inequivalent carbonyl ligands can be compared separately with free CO_(g), which has a force constant of 1856 N m⁻¹.⁶¹ The B_1g symmetric mode 10 gives the force constant of the carbonyl ligands in the central –M(CO)₄– fragment k_cen,eq = 1767/1753 N m⁻¹, which is just a little stronger than those for Ru(CO)₅ (k_eq = 1653 N m⁻¹ and k_ax = 1728 N m⁻¹).⁶² The same procedure could be used to determine k_out,eq from B_1u mode 6. However, this mode is neither IR nor Raman active, but it has a close relative: the Raman active B_2g mode 5, in which the two –M(CO)₅ fragments vibrate in a symmetric instead of an antisymmetric fashion. The vibrational coupling between the two fragments is expected to be negligible and the DFT calculations just show a subliminal spit of 2 cm⁻¹ between the modes. Therefore, the experimentally observed mode 5 was used as an approximation for mode 6, which yields k_out,eq = 1846/1842 N m⁻¹. This force constant of the interaction between the cis-standing carbonyl ligands in the –M(CO)₅ fragment is determined from the previously calculated k_out,eq and mode 8, which yields k_out-out = 21/23 N m⁻¹. The A_2u symmetric mode 2 yields finally with the previously calculated k_out,eq and k_out-out the force constant for the axial carbonyl ligands as k_out,ax = 1981/2039 N m⁻¹, which are near the force constants of the respective [M(CO)₆]²⁺ dications of k = 2048/2059 N m⁻¹.⁵⁷

The large difference of k_out,ax between [7a]²⁺ and [7b]²⁺ (1981/2039 N m⁻¹) is surprising at the first glance, especially given the relatively similar k_out,eq and k_cen,eq values between the ruthenium and osmium analogues. This can be also directly read out of the experimental vibrational spectra: the complex [7b]²⁺ has generally slightly lower frequencies than [7a]²⁺ except for the two most blue shifted experimental bands, which are located at higher frequencies. These two modes, 1 and 2, deviate the most from the DFT calculated values in [7b]²⁺ with 7 cm⁻¹, while these modes are well predicted for [7a]²⁺ with a deviation of lower than 2 cm⁻¹. The strengthening of k_out,ax relative to k_out,eq is known for group 7 dimetal decacarbonyls. While the axial carbonyl ligands have weaker C–O bonds than the equatorial carbonyl ligands in Mn₂(CO)₁₀, the relative bond strengths are inverse in Re₂(CO)₁₀.⁶³ A possible explanation could be the increasing trans effect on the axial CO-ligand from the –M(CO)₅ or the –M(CO)₄–(CO)₅ fragments, which increases with the metal metal bond strength from 3d over 4d to 5d metals.

EDA-NOCV analysis

The interaction between the central –M(CO)₄– fragment with the two -M(CO)₅ fragments of [7a]²⁺ and [7b]²⁺ was further analysed with the EDA-NOCV method (Fig. 8). In analogy to the Lewis structure and the results of the QTAIM analysis, the [M₃(CO)₁₄]²⁺ complexes were split in the triplet state fragments M(CO)₄ and [{M(CO)₅}₂]²⁺. As expected, the strong interactions are coming from the covalent bonds between the metals at 55.0/62.6 kcal mol⁻¹. However, the interactions of the metal atoms with the equatorial carbonyl ligands of the neighbouring metal contribute an additional 55.1/56.1 kcal mol⁻¹. This type of interaction has been discussed already for Mn₂(CO)₁₀, but experimental proof is to the best of our knowledge missing so far.⁶⁴

Fig. 8. The shape of the deformation densities Δρ of [7a]²⁺, which are associated with ΔE_orb calculated at the BP86(D3BJ)/TZ2P level; relativistic effects were considered with ZORA. The eigenvalue ν gives the value of the charge migration. The direction of the charge flow is from red to blue. Colour code: carbon – grey, oxygen – red, ruthenium – turquoise.

NMR spectroscopy

Additionally, we analysed the salts [7a]²⁺([Al(OR^F)₄]⁻)₂ and [7b]²⁺([Al(OR^F)₄]⁻)₂ in TFB solution with NMR spectroscopy (Fig. 6). In contrast to vibrational spectroscopy, it is not possible to determine the primary interaction of the carbonyl ligand with the transition metal by just comparing the ¹³C NMR shift relative to free carbon monoxide. However, TMCs bearing the same transition metal can be compared to one another. Hence, in this case an upfield shift indicates a higher oxidation state of the metal.^13,65 The ¹³C NMR spectrum of [7a]²⁺([Al(OR^F)₄]⁻)₂ shows the expected three peaks with an intensity distribution of 2 : 4 : 1. The ¹³C NMR peak of the central –Ru(CO)₄– fragment CO_cen,eq (195.1 ppm) is little upfield shifted relative to binary ruthenium carbonyl complexes e.g. Ru(CO)₅ (200.4 ppm)²⁵ and Ru₃(CO)₁₂ (199.7 ppm).⁶⁶ This indicates, that the central ruthenium atom is indeed only slightly influenced by the dicationic charge of the cluster. The ¹³C NMR peaks of the equatorial ligands of the –Ru(CO)₅ fragment CO_out,eq on the other hand are more high-field shifted towards 185.0 ppm. The shielding of the ¹³CO_out,ax at 171.5 ppm is even more pronounced, being only a few ppm upfield from the superelectrophilic [Ru(CO)₆]²⁺ (168.8 ppm).⁵⁷ The ¹³C NMR spectrum of [7b]²⁺([Al(OR^F)₄]⁻)₂ is very similar, except for a 15–20 ppm upfield shift, which is also observed for the (pseudo)binary osmium carbonyls compared to their respective ruthenium analogues.^57,66 The peak of ¹³CO_out,ax in [7b]²⁺ is unfortunately not visible, probably because it overlaps with the large TFB solvent signal expected to occur in the same spectral range.

QTAIM analysis

The different interactions of the carbonyl ligands with the metal centre can be simulated with the QTAIM analysis: a predominant π-interaction between the carbonyl ligand and the metal centre is leading to a negative partial charge on the carbonyl ligand, which is the case for the neutral metal pentacarbonyls M(CO)₅q(CO) = −0.157/−0.180 (Ru/Os). In the nonclassical [M(CO)₆]²⁺ dications, the opposite charge QTAIM charge is observed with q(CO) = +0.150/+0.128, which is the result of the predominant σ-bonding. In line with our previous experimental results, the carbonyl ligands with a predominant π-interaction like CO_cen,eq are bearing a negative partial charge, while the σ-carbonyls CO_out,ax are bearing a positive partial charge (Table 1).

Comparison of the carbonyl ligands of [7a]²⁺/[7b]²⁺ with M(CO)₅ and [M(CO)₆]²⁺ (M = Ru, Os) using the hitherto applied methods. The CO-bond lengths d_C–O are the averages of the respective carbonyl ligands in the solid state structures [7a]²⁺[Al(OR^F)₄]₂·2C₆F₄H₂ and [7b]²⁺[F{Al(OR^F)₃}₂]⁻₂·C₆F₄H₂.

	Ru(CO)5/Os(CO)5	[7a]2+/[7b]2+				[Ru(CO)6]2+/[Os(CO)6]2+
		COcen,eq	COaverage	COout,eq	COout,ax
d C–O/Å	1.126(2)/1.130(4)	1.126(2)/1.126(6)	1.122(2)/1.121(6)	1.121(2)/1.123(6)	1.115(2)/1.105(5)	1.100(8)/1.109(11)
d M–C/Å	1.941(13)ax& 1.961(9)eq/1.982(20)ax & 1.937(19)eq	1.964(1)/1.963(4)	1.979(2)/1.981(5)	1.981(2)/1.988(5)	1.999(1)/1.987(4)	2.023(3)/2.020(8)
δ 13CCO/ppm	200.4/182.6	195.1/176.8	186.0/	185.0/163.8	171.5/	168.8/150.6
(CO)av/cm−11	-/-	2103/2095	2120/2115	2135/2132	2153/2150	2220/2216
Δ (COfree)/cm−		−40/−48	−23/−27	−8/−11	+10/+7	+77/+73
k CO/N m−1	1728ax & 1653eq/-	1767/1754	1843/1845	1846/1842	1981/2039	2048/2059
q CO (QTAIM)	−0.157/−0.180	−0.090/−0.125	−0.022/−0.046	−0.008/−0.026	+0.055/+0.030	+0.150/+0.128
q M (QTAIM)	0.787/0.900	M cen = 0.610/0.668	M av = 0.771/0.883	M out = 0.851/0.990		1.099/1.231

Conclusion

In this report we investigated the reactions of the trimetal dodecacarbonyls 1a and 1b with the inorganic oxidants [NO]⁺, Ag⁺ and Ag⁺/0.5 I₂. The reaction of 1a with [NO]⁺ leads to a mixture, which contains the cationic butterfly complex [2]⁺ and remarkably breaks the N–O bond in [NO]⁺. The treatment of 1a and 1b with silver cations yields the respective metal-only Lewis pairs [3a]⁺ and [3b]⁺ quantitatively. However, upon increase of the oxidation power of the silver cation through formation of the elemental diiodine complex [Ag₂I₂]²⁺, this only led to a mixture of [4]⁺ and [5]⁺, which is the result of iodonium additions, formally as in [Ag–I–I]⁺ → AgI + I⁺. Consequently, we looked for an innocent deelectronator able to ionize the carbonyls without competing side reactions. Because the only known innocent deelectronator, perfluorinated “phenazine^F”,¹⁰ has a tedious and time consuming synthesis, we developed an alternative, which can be directly generated from a commercially available chemical. The anthracene derivative 6 has a half-wave potential of 1.42 V vs. Fc^0/+ and can be deelectronated by [NO]⁺[WCA]⁻ in TFB to its radical cation salt [6]⁺˙[WCA]⁻. The easy access to the innocent deelectronator [6]⁺˙[WCA]⁻ will ease the access to known and unknown TMCCs, but also other cations in the future (cf. our work on the organic cations in⁶⁷). Two equivalents of this arenium cation are able to deelectronate the trimetal dodecacarbonyls 1a and 1b twice under CO pressure, which yields the first homotrimetallic TMCCs [7a]²⁺ and [7b]²⁺, respectively. The trimetal tetradecacarbonyl dications have been analysed by NMR as well as vibrational spectroscopy and show very different binding interactions between the carbonyl ligands and the metal centre within the complexes: while the carbonyl ligands in the central –M(CO)₄– fragment CO_cen,eq are closely related to the respective zero-valent metal pentacarbonyls M(CO)₅, the equatorial carbonyl ligands of the terminal fragments CO_out,eq have a similar force constant to free carbon monoxide. The axial carbonyl ligands, on the other hand, are predominantly σ-bound to the metal centres.

Data availability

Data available on request.

Author contributions

MS performed most of the syntheses, characterizations, performed the DFT calculations and analyses and wrote together with IK the manuscript. CF helped actively with all electrochemical measurements. MM and SR performed the EPR measurements/simulations and wrote and reviewed the respective passages for the manuscript. IK supervised and conceptionally devised the project.

Conflicts of interest

The authors declare no conflict of interest.