Information theory: A foundation for complexity science

Abstract

Modeling and inference are central to most areas of science and especially to evolving and complex systems. Critically, the information we have is often uncertain and insufficient, resulting in an underdetermined inference problem; multiple inferences, models, and theories are consistent with available information. Information theory (in particular, the maximum information entropy formalism) provides a way to deal with such complexity. It has been applied to numerous problems, within and across many disciplines, over the last few decades. In this perspective, we review the historical development of this procedure, provide an overview of the many applications of maximum entropy and its extensions to complex systems, and discuss in more detail some recent advances in constructing comprehensive theory based on this inference procedure. We also discuss efforts at the frontier of information-theoretic inference: application to complex dynamic systems with time-varying constraints, such as highly disturbed ecosystems or rapidly changing economies.

During the past several decades, technological advances have led to explosive growth along two axes of science: the acquisition of data and the computational capacity to process data. Paralleling these advances, scientists have become increasingly aware that civilization now depends upon our capacity to understand the structure and predict the future behavior of enormously complex systems, such as economies and ecosystems. The task of marshaling the fruits of the new technologies toward that goal poses a grand challenge to society.

A combination of huge datasets and fast computers coupled with advances in artificial intelligence, machine learning, deep learning, and data science in general might conceivably achieve that goal. Indeed, there has been progress in their application to chess, Go, computer vision, and robotics, as well as to improvements in text generation, facial and speech recognition, motion detection, and other tasks. In addition to “big data,” in the last few decades there have been numerous mathematical discoveries and new theorems that opened the way for a more theoretical analysis of certain complex systems. However, truly complex systems, such as ecosystems, economies, and climate, appear especially refractory to analysis by merely processing big datasets with these advanced tools and new mathematical discoveries. The available information for studying and modeling such systems is insufficient to determine outcomes. Such problems are greatly underdetermined. Moreover, myriad poorly understood mechanisms, including a web of feedbacks that masks causal interconnections, operate. Additionally, boundary conditions in space and time may not uniquely determine trajectories.

Understanding such systems requires theory and models spun off from theory, as well as big data. However, what kind of theory or models is needed? In the search for the answer, bottom-up, reductionist, and agent-based models are natural candidates. If these could be combined with identified laws analogous to Newton’s, then predictive theory might be obtainable. Unfortunately, the above-mentioned problems generally render such systems opaque to traditional mechanistic modeling. There are multiple theories and models that are consistent with the information we have about such systems; these are massively underdetermined problems.

Nearly four decades ago, John Skilling (1) suggested an answer to the fundamental question: How do we predict the behavior of incompletely characterized systems? His answer was to turn to information theory and in particular, to the maximum entropy (MaxEnt) inference procedure (2). The basic idea is to use the information and knowledge we do possess about a complex system as constraints and then, use well-established mathematical procedures to infer additional knowledge by maximizing a certain objective (decision) function subject to these constraints. The objective function is derived from information theory, and its maximization ensures that we have made optimal use of prior knowledge.

MaxEnt is a powerful inferential tool for modeling and theory construction. Each application is different and demands its own information and structure, but MaxEnt is a general logical foundation for solving a huge range of problems. Here, we briefly review the historical development of this procedure, provide an overview of the many applications of MaxEnt and its extensions to complex systems that have appeared since the Skilling article was published, and discuss in more detail some recent advances in constructing comprehensive theory based on this inference procedure. We also discuss efforts at the frontier of information-theoretic inference (application to complex dynamic systems with time-varying constraints, such as highly disturbed ecosystems or rapidly changing economies) and argue that information-theoretic inference, hybridized with more conventional mechanistic modeling, may provide the greatest insight. We conclude with thoughts on open questions and potential new directions.

A Brief Historical Perspective

The original principles of information-theoretic inference can be traced to Jacob Bernoulli’s work in the late 1600s. He established the mathematical foundations of decision-making under uncertainty and is recognized as the originator of probability theory. His work is summarized in Ars Conjectandi (3). Bernoulli introduced the “principle of insufficient reason,” although the principle is also attributed to Laplace. It states that absent relevant information about the probability of a particular outcome, we must treat all possible outcomes as equally likely. Following Bernoulli’s work, Simpson (4), Bayes (5), and de Moivre (6) independently established more mathematically sound tools of inference. However, it was Laplace (7), with his deep understanding of the notions of inverse probability and “inverse inference,” that finally laid the foundations for statistical and probabilistic reasoning or logical inference under uncertainty. The basics of MaxEnt and information-theoretic inference grew out of that work.

Jumping forward almost two centuries takes us to Shannon (8) and Jaynes (2). Shannon’s work on communication theory and in particular, on what he called information entropy became the foundation of modern information theory. Building on this foundation, Jaynes recognized that Shannon’s information entropy provided the key to unbiased inference under uncertainty. In particular, Jaynes generalized Bernoulli’s and Laplace’s principle of insufficient reason and formulated his classic work on the method of MaxEnt.

MaxEnt selects the flattest and therefore, least informative, probability distributions compatible with constraints imposed by prior knowledge. Bias, in the form of assumptions about the distribution that are not compelled by prior knowledge, is thereby eliminated (2, 9). The MaxEnt form of a probability distribution, $p\left(n\right)$, is obtained by maximizing its Shannon information entropy (8), $-{\displaystyle {\sum }_{n}p\left(n\right)}\log \left(p\left(n\right)\right)$, under imposed constraints. As Skilling (1) noted, Jaynes’ MaxEnt provides a systematic and optimal approach to inference from incomplete information. Methodological advances have subsequently been made by a large number of researchers across many disciplines (10–18).

To understand the motivation for the use of the MaxEnt inference principle, consider the following four premises, which comprise a logical foundation for knowledge acquisition.

• 1)In science, we begin with prior knowledge and seek to expand that knowledge.
• 2)Knowledge is nearly always probabilistic in nature, and thus, the expanded knowledge we seek can often be expressed mathematically in the form of probability distributions.
• 3)Our prior knowledge—including the information we have—can often be expressed in the form of constraints on those distributions.
• 4)To expand our knowledge, the probability distributions that we seek should be “least biased” in the sense that the distributions should not implicitly or explicitly depend upon any assumptions other than the information contained in our prior knowledge.

The key, of course, is how to implement step 4 above. Fortunately, there is a rigorously proven mathematical procedure (13, 19, 20) to do so, and it is precisely the maximization of Shannon entropy that Jaynes had earlier proposed. Thus, acceptance of these four premises entails acceptance of a specific information-theoretic process of inference, MaxEnt. A quick overview of the mathematical machinery of MaxEnt is given in Box 1 (13, 19, 21).

Box 1. The MaxEnt procedure.

To illustrate the basic structure of a MaxEnt inference, we use the simplest example of a single-variable, discrete probability distribution, $P(n)$, the form of which we seek to infer. Assume our prior knowledge consists of the mean values, over $P(n)$, of each of $K$ functions, $f_k\left(n\right)$, where $k$ can be $1, 2, \dots , K$. Our knowledge of these mean values may arise from measurements or by deduction from general principles, such as conservation laws and symmetries. Denoting these mean values as $F_k$, we have the following $K$ constraints on $P\left(n\right)$:

$${\displaystyle \sum }_n{f}_k\left(n\right)P\left(n\right)=F_k.$$

An additional constraint is that $P\left(n\right)$ is normalized to one.

If $n$ can take on any value from, say, 1 to $N$ and $N>K+1$, then these constraints do not uniquely determine $P\left(n\right)$. Maximizing the Shannon entropy of $P\left(n\right)$ subject to these constraints, however, does yield the unique MaxEnt solution:

$$P\left(n\right)=Z^{-1}{e}^{-{\displaystyle {\sum }_k{\lambda }_k{f}_k}(n)}.$$

Here, $Z$ is a normalization constant, and the ${\lambda }_k$’s are Lagrange multipliers, which along with $Z$, are uniquely determined functions of the $F_k$’s. A straightforward application of the calculus of variations (21) is used to derive this result. The same framework is easily extended to more complex problems, where the distribution is multivariable, continuous, and conditional on other factors.

Of all distributions that are consistent with the information used—the constraints—the MaxEnt solution for $P\left(n\right)$ can be shown (13, 19) to be closest to the uniform distribution, and thus, it captures a state of maximum uncertainty. In that sense, the derived probability distribution is unbiased; any other distribution, resulting from a different objective function, would implicitly embody assumptions that are not warranted by prior knowledge.

An Aside on the Interpretation of Probability

In applications of MaxEnt, we are not concerned about the distinction between frequencies and pure probabilities; constraints on the probability distribution, which are the input to MaxEnt inference, may arise from any combination of empirical (frequentist) data, Bayesian inferences, or symmetries and conservation laws. Probabilities are never observed; they are always theoretical expectations or inferred likelihoods based on observed frequencies or on laws of nature. Some argue that probabilities are objectively grounded in these laws [e.g., Keynes (22)], while others, such as Ramsey (23), consider them to be subjective degrees of belief, known also as “Bayesian probabilities.”

Regardless of the interpretation, we assert that there is a unique, most rational way to assign degrees of belief to the states of the system. Theoretical expectations of objective frequencies of occurrence are the goal of MaxEnt inference. MaxEnt updates probabilities, whether based on frequencies or subjective belief, using the information we have (ref. 23; a recent discussion is in ref. 16, box 2.1). Prior information may be noisy, imperfect, and subject to interpretational and processing errors, but within the MaxEnt inference framework, uncertainty and imperfections in our prior information can be readily accommodated.

In summary, the MaxEnt approach is an objective inference procedure in the sense that different analysts possessing the same prior knowledge, however obtained and however imperfect, will reach the same conclusions about inferred distributions.

Recent Applications: An Overview

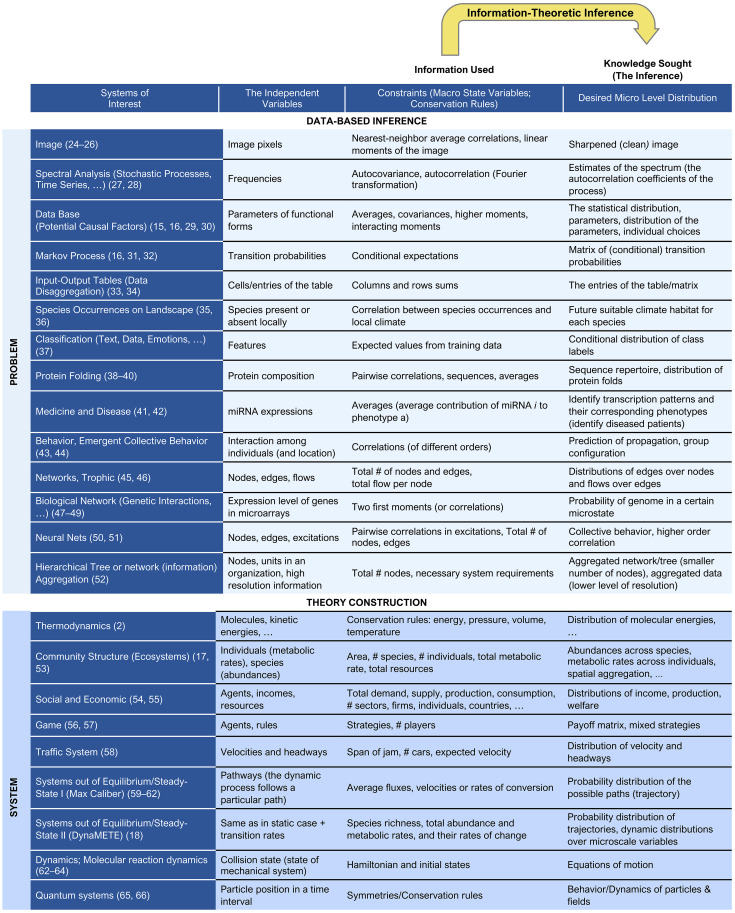
The use of information-theoretic inference and MaxEnt in particular blossomed within many disciplines in the last few decades. Fig. 1 summarizes representative applications from different disciplines. We divide them into two broad categories: data-based inference and theory construction, although that distinction is not always definitive; some applications may belong in both. In each example, we define in column 2 the entities that are the arguments of the probability distributions we wish to infer, in column 3 the information used as constraints, and in column 4 the new information we obtain from MaxEnt.

Fig. 1.

Overview of representative applications of information-theoretic MaxEnt inference.

Applications to data-based inference, emphasized in ref. 1, began with Bernoulli and Laplace and are distinguished from applications to theory construction by their focus on answering specific questions about, or resolving ambiguous or missing and imperfect information in, a specified dataset. Examples include improving the resolution of a fuzzy image, filling in missing data in an economic input–output table, and inferring the future range, under climate change, of a species. An example of creating an input–output table from aggregated data is shown in Box 2.

Box 2. An input–output and social accounting matrix (SAM) example.

Economists often work with regional or economy-wide equilibrium models. Such models require the use of multisectoral economic data to estimate a matrix of expenditure, trade, and/or income flows. Such detailed data become available only after a long delay (about a decade). However, the aggregated data—the totals of each row and column—are always available. Hence, the underdetermined problem is to infer, from the incomplete aggregated data, a new matrix that satisfies a number of linear restrictions. This is shown in the table below, where the observed information is the row and column sums (uppercase) and the desired information is the matrix entries (lowercase).

To put this within an economic context, consider the Leontief input–output model for an economy with $K$ sectors, each producing a single good. The sectors buy nonnegative amounts of each other's products to use as intermediate inputs. An input–output table also includes rows of payments to primary factors of production and columns of categories of final demand. An SAM expands the input–output accounts, adding accounts that map from factor payments (value added) to final demand for goods. An input–output table is rectangular, while an SAM is always square, with row sums equaling column sums $X=Y$ and $AX=Y$. In a $K\times K$ SAM matrix, call it $A$, the column sums of $A$ equal one, and the matrix is not invertible.

In this example, we show how to utilize the MaxEnt approach to fill up the cells of a $3\times 3$ SAM.

	$X_1$	$X_2$	$X_3$
$Y_1$	$a_{11}$	$a_{12}$	$a_{13}$
$Y_2$	$a_{21}$	$a_{22}$	$a_{23}$
$Y_3$	$a_{31}$	$a_{32}$	$a_{33}$

The table is a toy $3\times 3$ SAM matrix with elements $a_{ij}$. We want to infer these quantities from the observed row and column sums ($Y$ and $X$).

Although the $X$, $Y$, and $A$ are in units of dollars (flows), the observed $X$’s and $Y$’s can be normalized, so the matrix $A$ can be viewed as a set of $K$ probability distributions. To solve the problem, we maximize the entropy $-{\displaystyle {\sum }_{ij}{a}_{ij}}\text{log}{a}_{ij}$ subject to the $K$ linear constraints ${\displaystyle {\sum }_j{a}_{ij}}{x}_j=y_i$ and the $K$ normalizations ${\displaystyle {\sum }_i{a}_{ij}}=1$. The solution is $a_{ij}^{*}=\frac{1}{{\text{Z}}_{\text{j}}({\lambda }_i^{*})}\exp \left({\lambda }_i^{*}{x}_j\right)$, where ${\lambda }_i^{*}$’s are the $K=3$ Lagrange multiplier associated with each one of the three linear constraints and ${\text{Z}}_j\left({\lambda }_i^{*}\right)$ is a normalization factor. If any additional information is known, such as $a_{21}=0$, it can be incorporated into the model as well. That approach is used often in economics (15, 34) as well as other related matrix-balancing problems. The Markov example discussed below is a generalization of this simple model.

The goal of MaxEnt-based theory construction, in contrast, is to infer probability distributions that comprise a unified and comprehensive predictive understanding for a wide range of phenomena in a wide class of systems, such as thermodynamic systems, ecosystems, or economies. The first example, Jaynes’s (2) derivation of statistical mechanics, opened the floodgates to many recent applications shown in the figure. Because theory construction is more ambitious yet less familiar to many, we discuss this in more detail below (2, 15–18, 24–66).

MaxEnt for Theory Development

Many complex physical, biological, and social systems can be usefully, albeit approximately, described at two well-differentiated levels: the microscale and the macroscale. In the classical statistical mechanics of an ideal gas, we distinguish kinetic energies of individual gas molecules, which are microscale variables, from macroscale variables, often termed state variables, such as pressure, volume, and temperature. In ecology, we distinguish growth rates of individual organisms and abundances of each species from state variables, such as total productivity and the total number of individuals in the system. In economics, we distinguish the production and consumption of individuals from aggregate demand and supply or total Gross Dometic Product (GDP) of the economy.

Bottom-up models and theories of such systems begin with choices of dominant driving mechanisms operating among microscale components of the system and then, predict macroscale behavior from microscale drivers. This approach, although at times instructive, builds on assumptions about mechanisms and parameter values that can rarely be validated.

MaxEnt-based theory takes a top-down approach to infer probability distributions, describing the details at the microscale from prior knowledge specified in the form of macroscale constraints. Without MaxEnt, the problem is underdetermined because the low-dimensional macroscale constraints cannot uniquely determine the shape of high-dimensional distributions over microscale variables.

Example of Ecological Theory.

The ecological theory referred to in Fig. 1 (theory construction, row 2) is designated METE (Maximum Entropy Theory of Ecology). Over spatial scales ranging from small plots to large landscapes, for a wide variety of habitat types, and within broad groups of species, such as plants, birds, insects, or microbes, METE predicts the functions describing patterns in the abundance, spatial distribution, and energetics of species and individuals. Consider, for example, the community of trees in a designated area of a forest. In METE, the state variables are the area ($A_0$) of the system, the total number of tree species ($S_0$) and individuals ($N_0$) in the community, and the total productivity or metabolic rate ($E_0$) of the trees. These play a role loosely analogous to pressure, volume, temperature, and number of molecules in thermodynamics, although in thermodynamics, each state variable is either extensive or intensive, whereas in ecology, $S_0$ is neither.

At the core of METE are two probability distributions: an ecological structure function that describes the allocation of individuals across species and metabolism across individuals and a spatial distribution that describes the spatial clustering of individuals within species. The structure function is a joint probability distribution, $R(n,\epsilon |S_0, N_0,E_0)$, conditional on three state variables, giving the probability that a randomly selected species has abundance $n$ and a randomly selected individual from the species with abundance $n$ has a metabolic rate $\epsilon .$ The spatial distribution, $\mathrm{\Pi }(n|n_0,A,A_0)$, is the probability that if a species has abundance $n_0$ in an area $A_0$, then it has abundance $n$ in an area, $A$, randomly located in $A_0$. Ratios of the state variables $S_0$, $N_0$, and $E_0$ comprise the constraints that determine the structure function, and $n_{0}A/A_0,$ the mean value of $n$ in $A$, is the constraint on the spatial distribution. The MaxEnt solutions for these two distributions have no adjustable parameters if the constraints are specified. If their actual measured values are not available, we can indirectly infer them from other data and general principles. The metabolic rates of the insects in a patch of meadow, for example, are not readily measured, but if a metabolic scaling law relating mass and metabolism is assumed, then metabolism can be inferred (67).

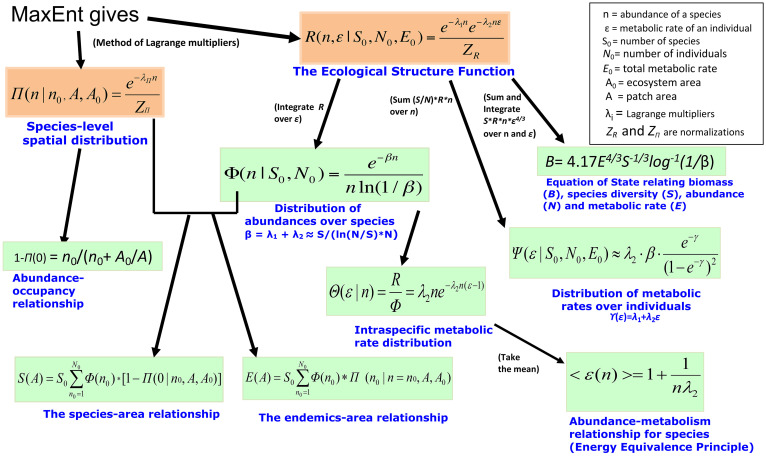
From the structure function and the spatial distribution, numerous testable ecological predictions flow, including the distribution of abundances over the species and metabolic rates over the individuals (68); a measure of intraspecific spatial aggregation of individuals (68); the dependence of species diversity on area sampled (69); a relationship between the abundance of a species and the average metabolic rate of its individuals (68); and an equation of state relating biomass, metabolic rate, abundance, and species diversity (18). Fig. 2 shows the mathematical structure of METE, illustrating how predictions for multiple patterns flow from the application of MaxEnt.

Fig. 2.

The mathematical architecture of the METE. Empirically testable metrics, such as the distributions of abundances over species and metabolic rates over individuals, the species–area and endemics–area relationships, and an energy-equivalence principle derive from specified mathematical operations on the two fundamental distributions in the theory: an ecological structure function, $R$, and a spatial distribution, $\mathrm{\Pi }$, which in turn, are derived using MaxEnt under the constraints specified in the text. Adapted from ref. 53.

Empirical tests provide support for the theory (69–72). An extension of the original theory with an additional state variable for the number of genera, or families, successfully predicts the distribution of species over these higher taxonomic categories as well as the dependence of the abundance–metabolism relationship on the structure of the taxonomic tree (53, 73).

Examples of Economic Theory.

In Fig. 1 (theory construction, rows 3 and 4), we refer to MaxEnt-based economic and social science theories. Depending on context, the entities of interest may be individual preferences, beliefs, strategies, strategic behavior, or even decision processes. Ambiguity arises because we do not observe, for example, individuals’ preferences and thus, the relationship between preference and action. Therefore, the specification of the constraints may be complicated and problem specific.

In an early application, Golan (54, 74) used MaxEnt to derive a multivariable stochastic theory of size distributions of firms in an economy. It is a statistical model of agents’ production subject to some resources and technological constraints. An extension of this theory to a general equilibrium model of a complex economy composed of consumers and producers is developed in refs. 16 and 75. Foley (55) developed a statistical equilibrium theory of markets. Market analysis begins with agents’ offer sets that reflect their desired and feasible transactions, which are conditional on agents’ information, technical possibilities, endowments, and preferences. The market distributes agents over offer sets to maximize the entropy of the market transaction distribution. This is the most decentralized allocation possible given the preferences of agents. Such top-down theories are based on minimal macroscale information and require less structure and fewer assumptions than in classical bottom-up economic modeling.

Information-theoretic inference also elegantly connects game theory with empirical evidence. McKelvey and Palfrey (76) took a statistical approach to modeling quantal (discrete) choice within a game-theoretic setup. Players choose strategies based on their preferences (expected utility), with choices based on a quantal choice model, and assume that all other players are doing the same. Given a specific error structure, a quantal response equilibrium (QRE) is a fixed point of this process. The resulting response functions are probabilistic; better responses are more likely to be observed than worse responses. They look at a specific parametric class of quantal response functions, which is the traditional way of analyzing empirical choice models to yield a logit equilibrium. The maximum likelihood logit model is exactly the MaxEnt model for all unordered discrete choice problems (77). The QRE can be developed directly via this approach. This, in turn, combines the two branches of literature coming from statistics and information theory for modeling a game, and it provides a simple way for doing empirical studies. More recently, Scharfenaker and Foley (78) built on the above work and employed the MaxEnt approach to develop a quantal response statistical equilibrium in a model of economic interactions.

Criticisms and Failures of MaxEnt-Based Theory

One criticism of MaxEnt-based theory is that the choice of state variables appears arbitrary, as does the choice of the sought-after probability distributions, such as the structure function in METE. Is theory construction just a trial and error search for suitable constraints and objective functions to accurately predict patterns in nature? In response, we note that a similar concern applies to bottom-up models, which often contain arbitrary choices of functional forms, individual’s behavior, and parameter values describing microscale interactions. Scientific theories, we reply, never derive purely from logic; the selection of the elements of theory is often guided in part by intuition and data availability.

If specified correctly, constraints are sufficient statistics and capture the information needed to describe a system’s behavior. They and Shannon’s entropy objective function provide a falsifiable means of characterizing the system in the simplest way.

Another criticism of MaxEnt-based theory is that, lacking explicit mechanisms, no causal insight is gained. One response is that when MaxEnt-based theory is successful, then whatever the mechanisms are that determine the values of the state variables, those mechanisms are sufficient to explain the probability distributions at the microscale; to predict the observed patterns, there is no need for added complexity. In that sense, the role of mechanism is identified, even if the actual mechanisms that determine the state variables are unknown. Below, we provide an example where MaxEnt allows us to infer causal relationships.

An important connection between MaxEnt and mechanism stems from the observation that if the set of state variables used in building a MaxEnt-based theory is insufficient to make accurate predictions, the nature of the discrepancy can point the way to identifying important mechanisms. In thermodynamics, for example, the failure of the ideal gas law under extreme values of the state variables led to the discovery of Van der Waals’s forces between molecules.

In ecology, if additional flow resources, such as water, nitrogen, etc., are allocated among individuals along with energy flow expressed as total metabolic rate, then the predicted distribution of abundances, $n$, over the species is altered. METE in its original form predicts a log-series abundance distribution, which varies as $1/n$ at small $n$. However, if $r$ additional resource constraints are added, then the abundance distribution varies as $1/n^{r+1}$ (17), thereby increasing the predicted fraction of species that are rare. This makes sense according to the niche concept in ecology; a greater number of limiting resources provides more specialized opportunities for rare species to survive. Thus, METE relates the degree of rarity in a community to the number of resources driving macroecological patterns. METE, a seemingly nonmechanistic theory, can inform us about what mechanisms might be driving these patterns.

A dramatic example of statistical theory failure arises when a MaxEnt theory derived using static constraints is applied to a dynamic system in which the values of the state variables are changing in time. However, if MaxEnt is specified correctly, dynamic systems can be modeled as well (Fig. 1, theory construction, bottom rows). As an example consider maximum caliber (MaxCal) (Fig. 1, theory construction, row 6). Applying the same principles as in MaxEnt, MaxCal (59–62) gives the probability distribution of the different potential pathways of a dynamical system or a network. While MaxEnt deals with equilibrium states and relatively stationary populations, MaxCal applies to systems far from equilibrium. The idea is to maximize the path entropy (defined over the probability that the dynamical process evolves in a specific path) over all possible pathways subject to dynamical constraints. This yields the probability distribution over the possible pathways: the relative probability that a system will move from one state to another. In most practical cases, that approach was applied for discrete probability distributions, which are in fact characterized by a first-order Markov process. Technically, although MaxCal deals with dynamical systems, the underlying logic is that these dynamics, or paths, are actually fixed throughout the period analyzed, and the constraints are averages over the different paths. In that way, the connection with MaxEnt is easy to see. In what follows, we provide new ways to model dynamic systems.

Extension of MaxEnt Methods to Dynamic Systems

If the state variables are changing in time, such as in a nonequilibrium thermodynamic system, a disturbed ecosystem, or a transitioning economy, the constraints imposed by instantaneous values of the dynamic state variables may fail to accurately predict instantaneous microscale distributions. In ecology, there are many examples of such failure (72, 79–82).

From METE to DynaMETE.

To extend MaxEnt-based ecological theory from the static to the dynamic domain, Harte et al. (18) proposed a theoretical framework, called DynaMETE, that hybridizes the MaxEnt inference procedure with explicit processes that perturb the system and generate time-dependent state variables. DynaMETE is an extension to far from steady-state ecosystems of METE, which was applicable only to systems with time-independent state variables. The list of state variables now includes both the instantaneous values and the first-time derivatives of the static-theory macrovariables, $S$, $N$, and $E$. In that circumstance, a purely top-down approach does not suffice; DynaMETE is a hybrid theory that combines mechanisms at the microscale with top-down MaxEnt inference.

The general structure of DynaMETE should apply to any system with clearly distinguishable macrostates and microstates, in which the time evolution of the microvariables can be written as transition functions of the instantaneous values of the microvariables and the macrovariables. The time evolution of the system is calculated in an iterative process in which the macrovariables are updated by averaging transition functions over probability distributions that in turn are updated by MaxEnt imposed instantaneously using the full set of state variables as constraints. A consistent iteration procedure for solving the theory was proposed in ref. 18 and is summarized in SI Appendix, Box S1 using a simple toy model realization of the more general DynaMETE framework.

The dynamics of disturbed two-tiered systems are especially complex and rich in possibilities if the microscale and the macroscale are entwined in the sense that the mechanisms governing the dynamics of the microscale variables are partially governed by the values of the macroscale variables (83). Although originally posited as a property unique to living systems, we see no reason why such entwining of the microscale and macroscales might not arise in any complex system. For example, in economics, changes in an individual’s wages or a firm’s profits can be influenced by the changing state of the macroeconomy and by changes in the number of firms and workers. In ecology, the reproductive rates and growth rates of individuals in any particular species might be influenced by a changing total number of individuals in the ecosystem as well as by the population density of that particular species. Such entwined dynamics are readily incorporated in the DynaMETE framework (SI Appendix, Box S1).

In the static limit, in which the state variables are relatively constant in time, DynaMETE reduces to the static METE. However, following an ecological disturbance, such as a wildfire or the introduction of exotic species, it makes new predictions for patterns of interest to ecologists, such as species–area relationships or abundance distributions. It also predicts the future time trajectory of the state variables. These new predictions will depend upon the nature of the disturbance. Hence, from observed transitions in patterns, we may be able, in the future, to attribute specific combinations of mechanistic causes of disturbance in our rapidly changing ecosystems in the Anthropocene.

Data-Based Extensions to Dynamics: A Conditional Markov Example.

Markov processes (referred to in Fig. 1, data-based inference, row 4) describe the time evolution of a system when the current state of the system is conditional on the state in the previous period. A simple Markov model yields a probability distribution describing the transition from state $k$ to state $j$ within a well-defined time period $\mathrm{\Delta }t \equiv \left(t+1\right)-t$, where “$\equiv$” stands for definition. It is also known as a “short memory” process.

Across disciplines, Markov processes are used to model dynamic processes from population growth of species to the progression of securities in financial markets to promotions within hierarchical organizations. To calculate the state of the system (or an individual in the system), the usual rule of conditional probability is used (SI Appendix, Box S2, Eq. S7). In a generalized and more realistic version of such a process, the transitions are also conditional on environmental, economic, physical, or other conditions, allowing inference of the causal effect of exogenous forces on the transition probabilities. However, for complex and evolving systems, such as behavioral, social, and ecological systems, that is a tough problem to solve because we do not know the details of the underlying processes that generate the observed information. In addition to the usual uncertainty, there is model ambiguity. This example shows that MaxEnt opens the way for modeling conditional Markov processes of complex systems with continuously evolving data. In SI Appendix, Box S2, we provide a detailed mathematical formulation of that model (16, 34).

To infer the steady-state transition probability matrix, we use time series data. The difficulty is that such data emerge from a constantly evolving complex system, and thus, there is no unique steady-state transition matrix. However, if we accommodate for possible ambiguity and uncertainty in the constraints, we can derive an approximate steady-state transition matrix. It is the most probable data-based transition matrix, conditional on all our information and consistent with all of the observed complex time series data.

The information used is time series data about each entity’s state at period $t$, as well as information on exogenous variables that may affect the entity’s transition probabilities. We capture the relationship between the observed data $Y$, the unknown probabilities $P$, and the exogenous information $X$ by multiplying each element of $X$ by the elements on both sides of the core equation, defined in SI Appendix, Box S2, Eq. S7, and sum over the entities and time periods (16). That is, the constraints are specified in terms of moment conditions. Due to model ambiguity and the complexity of the data, we also allow for some additive uncertainty in the constraints. We call it “flexible constraints.”

Given these flexible constraints (and the usual normalizations), our objective is to simultaneously infer the transition probabilities and the uncertainty (noise) given the observed information $Y$ and $X$. If we do not assume anything about the uncertainty or construct a likelihood function, the problem is underdetermined, but MaxEnt gives the desired solution. To do so, we need both the $P$’s and the uncertainty to be probability distributions so that we can define their Shannon entropy. To transform the uncertainty associated with each constraint into a probability distribution ($W$), we follow refs. 15, 16, and 77 and view the uncertainty as the expected value of a random variable (with mean zero) with probability distribution $W$ (SI Appendix, Box S2, step 1). With this transformation, we maximize the joint entropy of $P$ and $W$ subject to the constraints (SI Appendix, Box S2, Eq. S8) to obtain the solution. The transition probabilities ($P$), the uncertainty probabilities ($W$), and the Lagrange multipliers are inferred simultaneously in the optimization.

We can then evaluate the transition at each period $t$. Moreover, the effect of each exogenous variable on each one of the inferred transition probabilities has a direct causal interpretation: the effect of a change in some exogenous factor on the transition probability. Causal effects can be calculated for both continuous and discrete exogenous variables. Importantly, the generalized MaxEnt Markov problem is of the same dimension (the number of constraints and Lagrange multipliers) as the MaxEnt. The generalization discussed opens the way for solving more complex problems without increasing the model’s complexity. As with the DynaMETE and METE, if there is no uncertainty and the system is at a steady state, the generalized approach discussed here reduces to the classical MaxEnt or MaxCal. In fact, the MaxCal is a special case of the Markov framework we present here. If there is no ambiguity and uncertainty over the exact dynamic and the paths (or transitions) are not conditioned on other external factors and complex data, both converge to the same outcome (16, 61).

This example demonstrates one of the major advantages of the information-theoretic framework for data-based inference with a system that is constantly evolving. The inferred solution—transition matrix in this case—is the best data-based approximate theory of the unknown true process. It also allows us to perform predictions and to understand the forces driving this system. That framework is computationally efficient and easy to apply.

In both the Markov and the DynaMETE approaches to extending MaxEnt inference to dynamics, transition functions govern the time evolution of the probability distributions of interest. In the Markov example, MaxEnt is used to infer the transition matrix using observed time series data as constraints. In DynaMETE, on the other hand, the dependence of the transition functions on micro-level and macro-level variables is assumed as input, transition function averages over certain probability distributions give the time dependence of the state variables, and the state variables and their time derivatives provide the constraints under which MaxEnt inference updates the probability distributions. It is thus an iterative process in time. In both approaches, the transition functions can be functions not only of the micro-level entities but also, of the state variables or other exogenous factors.

Open Questions

Information theory has contributed much to the advancement of modeling and inference, yet it has much more to offer. One possible future advance in applying MaxEnt is to a class of systems that we have not discussed here. As emphasized above, applications of MaxEnt have generally been for the study of systems in which a clear separation of macro and micro levels of description is natural. Yet, some complex systems cannot be easily reduced to such a bipartite structure. Turbulence in Earth’s climate system, for example, is intrinsically a multiscale phenomenon. One open question, then, is how can we apply MaxEnt to infer distributions at any scale in such systems?

Another question is how to extend the framework to improve capacity to identify misspecification of constraint information and to better identify the nature of flexible constraints for data-based models. Related to this, improving the ability to identify the most useful constraints arising from huge datasets, which potentially could result in an overwhelming number of constraints, is likely to become more important in the future. This will likely entail developing optimal aggregation procedures.

Finally, we observe that the two approaches we have described above for using information theory to solve dynamical problems are complementary. DynaMETE assumes knowledge of the transition functions, whereas the Markov approach infers those functions. Might a synthesis of the two methods provide a powerful method for studying systems far from steady state?

Summary and Conclusion

With all problems in science, the more information we have, the better will be the models and theories we can construct. However, for hugely complex systems, like the ones we confront in economics and ecology, we never will have enough information to unambiguously predict outcomes. For such systems, theory and model construction are an underdetermined inference problem. If, however, we specify available information as constraints and build directly on the MaxEnt principle, we ensure that out of all possible models that are consistent with the information we have, the chosen one is least biased.

Both within each of us and surrounding all of us are systems of immense complexity. Critical to our survival and well-being is understanding those systems sufficiently well so that we can make reliable predictions and design effective interventions. MaxEnt, an information-theoretic method of inference, provides a powerful foundation for the study of complex and continuously evolving systems. It is a powerful method for extracting insight from sparse, uncertain, and heterogeneous information and is also a foundation for complex systems theory construction. We expect applications of MaxEnt inference to continue expanding the frontiers of complexity science within and across disciplines.

Data Availability

There are no data underlying this work.