Abstract
In multicellular organisms, nucleosomes carry epigenetic information that defines distinct patterns of gene expression, which are inherited over multiple generations. The enhanced capacity for information storage arises by nucleosome modifications, which are triggered by enzymes. Modified nucleosomes can transfer the mark to others that are in proximity by a positive-feedback (modification begets modification) mechanism. We created a generic polymer model, referred to as 3DSpreader, in which each bead, representing a nucleosome, stochastically switches between unmodified (U) and modified (M) states depending on the states of the neighbors. Modification begins at a specific nucleation site (NS) that is permanently in the M state, and could spread to other loci that is dictated by chromatin dynamics. Transfer of marks among the non-nucleation loci occurs stochastically as chromatin evolves in time. If the spreading rate is slower than the chromatin relaxation rate, which is biologically pertinent, then finite-sized domains form, driven by contacts between nucleosomes through a three-dimensional looping mechanism. Surprisingly, simulations based on the 3DSpreader model result in finite bounded domains that arise without the need for any boundary elements. Maintenance of spatially and temporally stable domains requires the presence of the NS, whose removal eliminates finite-sized modified domains. The theoretical predictions are in excellent agreement with experimental data for H3K9me3 spreading in mouse embryonic stem cells.
Significance
Epigenetic spreading and maintenance play an important role in cellular differentiation and disease. A number of factors contribute to spreading mechanisms, which makes it difficult to enumerate all the possibilities using experiments alone. We created a generic computational model, accounting for chromatin dynamics and stochastic enzyme-catalyzed modifications of the epigenetic states. The enzyme reactions that modify and erase the epigenetic marks on the nucleosomes are modeled using reversible two-state kinetics. We find that discrete epigenetic domains are formed around the nucleation sites, which act as a source of epigenetic modifications. Surprisingly, finite heterochromatin domains form spontaneously by a looping mechanism without the need for boundary elements. We reproduce several experimental findings, including domain sizes in mouse embryonic stem cells.
Introduction
The inheritance of distinct phenotypes that are not encoded in the DNA sequence has been demonstrated in multicellular organisms. The resulting distinct morphological characteristics are maintained over multiple cellular divisions (1,2). Alterations in the epigenome, leading to distinct gene expression and subsequent phenotype variations, without any change to the underlying DNA sequence, are referred to as epigenetic modifications, which are carried over multiple cell divisions. As a consequence, some aspects of cellular memory are often associated with the term epigenetics (3, 4, 5). The study of the establishment and inheritance of genetic patterns is a burgeoning field, especially because epigenetic misregulation is implicated in aging and cancer. In eukaryotes, DNA condenses to form chromatin by wrapping around histone proteins. The physicochemical mechanisms governing genetic activity constitute a myriad of strategies that change the structure and organization of chromatin. These include chemical tagging of DNA (6,7) and histones (8), as well as regulation of transcription factors (9), RNA interference (10), chromatin remodeling proteins (11), and nuclear architecture (12). The epigenetic landscape emerging from these alterations enables the storage of more information than is possible using sequence alone and represents a powerful force in cellular differentiation and environmental adaptation (13).
The intricacies of initiation, spreading, and maintenance of histone modifications are unclear because of the involvement of several factors whose roles have not been quantitatively elucidated. Upon DNA replication, histones are re-distributed in roughly equal proportions to the template and nascent DNA (14). Subsequently, nascent histones must re-establish the appropriate epigenetic attributes acquired before cell division (“memory”). Studies on chromatin inactivation have revealed important elements necessary for gene silencing, such as nucleation elements, which are specific DNA segments that bind protein complexes either directly or via RNA interference, and histone-modifying proteins, such as methyltransferases, which covalently modify histone tails (1). Although molecular identities of these mediators differ across eukaryotic species, certain unifying principles seem to underlie the observed homology between proteins that moderate them in yeasts, humans, mice, and flies (15,16). Experiments and theoretical studies suggest that a positive-feedback allosteric mechanism is important for the spreading of modifications, whereby the molecular complex binding to the nucleation site (NS) has an enhanced propensity to bind to nucleosomes that are already marked by an appropriate enzyme. The bivalent binding is thought to be the basis of the cooperative effect in spreading of the modifications (1).
Because of the involvement of several molecular components and inherent stochasticity in the modification process, a variety of mathematical models, which have provided insights into the formation of epigenetic domains and their self-perpetuation, have been proposed (2,17, 18, 19, 20, 21, 22, 23, 24, 25, 26). Some models may be classified as one-dimensional (1D), in which spreading occurs along a lattice representing the chromatin with built-in implicit positive-feedback mechanism (21,22). Other models consider the possibility of spreading beyond near neighbors of a modified nucleosome, which implicitly accounts for long-range contacts (19,20) along the genomic length. More recently, models that consider the polymeric characteristics of chromatin explicitly (17,18,25,26) or implicitly (20) have been investigated.
We surmise that chromatin organization is strongly related to the spreading of histone modification, as shown by the strong correlation between the epigenetic states and the compartments observed in the Hi-C contact maps (27). To explore the interplay between chromatin structure and dynamics on the spreading of epigenetic marks, we introduce a polymer-based model that accounts for the kinetics of modifications, thereby coupling chromatin dynamics with stochastic chemical kinetics. The model captures the conformational dynamics of chromatin as well as the biochemical mechanism of spreading, implemented through distinct rules under which the enzyme reactions take place. The aim is to test the extent to which conformational dynamics influence the formation of epigenetic domains, and whether the spreading of epigenetic marks is achieved along the chromatin thread, or is controlled by non-adjacent nucleosomes (see Fig. 1). Our model, with a minimal number of parameters, shows that stable epigenetic domains emerge without explicit boundaries when the conformational rearrangement of chromatin dictates the spreading of epigenetic modifications.
Figure 1.
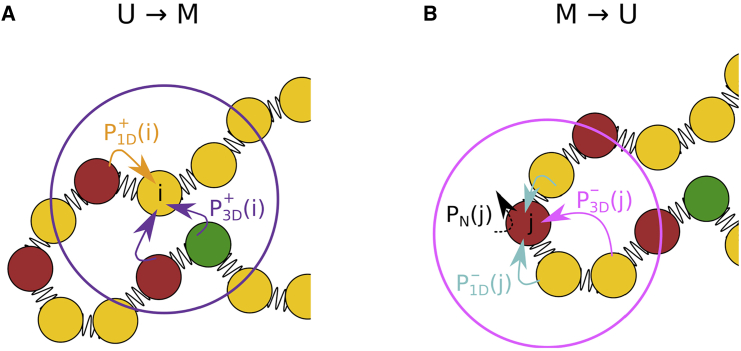
Transitions in the kinetic model. (A) The forward and backward reactions are shown on the left and right, respectively. The left depicts the enzyme-induced modification, , at the ith nucleosome. The right sketches the removal of the mark, , from the jth nucleosome. Modifications to unmarked (U) nucleosomes and removal of marks from the M-type nucleosomes are shown by arrows. Important mediators relevant to the spreading processes are shown in color: the nucleation site (NS) is in green, and U (M) nucleosomes are shown in yellow (red). Some or all elementary transitions are considered simultaneously, representing four separate spreading mechanisms (see Fig. S1). The forward reaction occurs if an unmarked nucleosome i has a neighbor nucleosome in the modified state with a probability (orange arrow) or with a probability if it is in the spatial vicinity of an NS/modified nucleosome (purple arrow). The backward reaction can always proceed with a probability PN(j), indicated by a black dashed arrow. The reaction may also depend on the presence of other unmarked nucleosomes. In such cases, neighbor nucleosomes might induce the transition in nucleosome j with a probability (cyan arrow), while U nucleosomes in the spatial vicinity of j may induce the reverse reaction with probability, (magenta arrow). (B) Asymmetric spreading from the NS (green) and non-NS sites (red). The forward rate for the non-NS sites is scaled by a factor of α compared with that for the NS site. Typically, we use in this study, which means that the ability of spreading of a non-NS site is much smaller than that of the NS site. To see this figure in color, go online.
We find that the NS acts as a positional signal that facilitates spreading to its surroundings. The bi-directional spreading from the NS was previously explored without considering chromatin conformation explicitly (20) or under conditions in which the formation of an epigenetic domain relies on attractive interactions between similarly modified loci (18,26). As a consequence, partial collapse of chromatin is required for epigenetic spreading. In our model, the cooperative effect of the writing and erasing processes, by which the probability of modification of a locus depends on epigenetic states of the neighbors, provides the sole positive reinforcement for spreading without the need for global conformational change of the chromatin. We show that finite modified domains cannot form without a looping mechanism, which brings nucleosomes that are well separated along the genome into proximity. The excellent agreement between the simulations and experiments on H3K9me3 spreading in mouse embryonic stem cells validates the proposed mechanism.
Methods
Model
Based on the modification mechanisms sketched in Fig. 1, we used a polymer with N = 300 nucleosomes to probe epigenetic spreading. Each monomer of size σ represents 200 base pairs (bp), modeling one nucleosome and a linker DNA. Following our previous study (28), we choose the simplest bead on string model. Although features such as DNA linker length, nucleosome shapes, and orientations are important for the chromatin fold (29), we concentrate on the interplay between chromatin dynamics and enzyme kinetics on epigenetic spreading. The 300-monomer chain models 60 kb of DNA. The choice of chain length allows us to efficiently explore the spreading mechanism for a range of parameters. The effects of changing N are discussed in the supporting material. The modified and unmodified states of the nucleosome are denoted as M and U, respectively. The present model is a generalization of the chromatin copolymer model (CCM), which successfully predicted the organization and dynamics of interphase chromosomes (28).
The energy function used to simulate chromatin dynamics is described in the supporting material. The connectivity of the chain is modeled using the harmonic potential (see Eq. 1, Section 1 in the supporting material). A Kratky-Porod angular term (Eq. 2 in Section 1 in the supporting material) is used to define an angle potential between three successive nucleosomes. The persistence length lp is defined through the parameter lk = 2lp. The non-bonded interactions are described using Lennard-Jones potential (Eq. 3 in Section 1 in the supporting material), where the parameter ε determines the strength of non-bonded interactions. The parameters in the model are given in Table S1 in the supporting material.
Physical properties of the chain
The value of ε determines whether the polymer adopts a random coil or is collapsed (see Section 6 in the supporting material for a detailed discussion). We first simulated chromatin in a good solvent using a fixed ε value that does not depend on the modification state of the nucleosome. This scenario, with , explores the case where chromatin dynamics directly affects spreading but not vice versa. To explore the two-way coupling of chromatin dynamics and epigenetic spreading, we also simulated the spreading process by taking .
Of particular relevance for epigenetic spreading is the persistence length of lp, because it affects the kinetics of loop formation, which in turn controls three-dimensional (3D) spreading through the looping mechanism (25). The persistence length could vary depending on many parameters, including the organism type, chromatin length scale, and the epigenetic state. Flexible polymer models have been successful in reproducing experiments (30, 31, 32). We explored the impact of varying lp on the spreading process (see the supporting material for details). Note that the chromatin dynamics and looping is not only determined by the lp but also by ε. The results shown in this study is focused on the case that lp = σ because we aim to create a generic model, not adapted to a particular organism, but rather one that is used to explore different scenarios.
Epigenetic modifications
We denote the U state to represent the active chromatin, which transitions to the marked M state, inactive chromatin, in a single-step reaction , where k+ and k− are forward and backward enzyme rates, respectively. The forward reaction is a caricature of chemical modifications of histone 3 (H3) lysine 9 (K9) with methyl groups (me2/3), referred to as H3K9me2/3, a hallmark of inactive chromatin (15). The modification is catalyzed by Clr4 in Schizosaccharomyces pombe and Suv39h in humans (15,16). The reverse reaction takes into account the removal of markers corresponding to histone turnover. In addition, U can reverse the state of M nucleosomes in their vicinity, thus introducing the cooperative effect in the reverse reaction. The latter process may mimic the activity of enzymes that remove histone modifications (for example, Epe1 in S. pombe (33)). Both the two-state model (20,24) and three-state models (active, inactive, and unmarked) (17, 18, 19,26) have previously been used to study transitions between epigenetic states.
The modifications achieved by specific DNA binding enzymes are modeled as stochastic events. We evaluate the transition probabilities between the two states at each time step (see Section 2 in the supporting material). The important parameters that determine the probability of spreading are r = k+/k− and , where τr, the relaxation time of the chromatin is a characteristic time that is used to measure the spreading rate. In addition, we introduce the parameter α (Eq. 7 in supporting material), which rescales the forward rate. We use α = 1 for spreading from the NS (Fig. 1). The α parameter is introduced to account for the possibility that spreading from the NS and from modified nucleosomes does not represent the same sequence of molecular events. A transition can occur only if at least one of the following five conditions is satisfied, shown schematically in Fig. 1:
-
1.
1D: transition may occur only if at least one nucleosome at is in the M state.
-
2.
3D: transition may occur only if there is a minimum of one nucleosome, j, in state M that satisfies the criteria and the distance rij to ith nucleosome is less than the threshold, rc.
-
3.
Noise: transition could occur at any nucleosome independent of the identity of all others.
-
4.
1D: transition may occur only if least one nucleosome at is in the U state.
-
5.
3D: transition may occur only if there is a minimum of one nucleosome, j, in state U that satisfies and rij < rc.
Because we are interested in epigenetic spreading, we do not consider the spontaneous stochastic transition (the analog of the third transition listed above). These transitions are allowed with probabilities given in Eq. 7 in the supporting material. Since multiple elementary steps could contribute to an epigenetic transition at each time step on a single nucleosome, the overall probability of changing the epigenetic state depends on the epigenetic states of its neighbors, except for the elementary transition 3, whose contribution is constant. We specifically explore two cases: 1) Scheme I: linear spreading model that includes elementary transitions 1, 3, and 4; and 2) Scheme II: linear and 3D spatial spreading model that includes all the listed elementary transitions 1–5. The details of the schemes are in Fig. S1 a and we mathematically formalize the overall forward (P+(t)) and backward (P−(t)) probability at each time step in Fig. S1 b.
At t = 0, all the nucleosomes are unmarked, except for the NS (shown in green in Fig. 1), chosen arbitrarily to be in the middle of the polymer. We also investigated the effects of altering the location of the NS (see Section 11 in the supporting material). Spreading starts at the NS, which enables bi-directional spreading along the nucleosomes, emanating outward from its location. A spreading trajectory is generated by stochastic changes in the nucleosome states, as outlined above in the five steps.
Since we consider only two epigenetic states, the nucleosome states can be characterized using Ising spin variables, s(U) = −1 and s(M) = 1 (34), except that the spin variables change stochastically with time depending on the instantaneous chromatin conformation. In such a system, there could be a cooperative transition in the spin states as chromatin evolves. The positive feedback, as the basis of cooperativity, arises because the probability of modifying a nucleosome increases if nucleosomes in the vicinity are already modified. This mimics the “reader-writer” model associated with the epigenetic spreading process, where modifying enzymes such as methyltransferases has a reader domain that binds to the previously modified nucleosome, and subsequently write the same modification to another nucleosome (35).
Epigenetic clock
The probabilities associated with epigenetic transitions in the model are coupled to the chromatin dynamics. The time that determines 3D spreading is associated with the lifetime of contact between two nucleosomes i and j with |i−j|≥2. There is a spectrum of lifetimes associated with loop formation depending on |i−j|. Our goal is to elucidate how chromatin dynamics are coupled to the enzyme-catalyzed reactions that modify the U state or erase the mark in the M state. Therefore, we chose the polymer relaxation time, τr, calculated from the time-dependent decay of the structure factor F(q,t), evaluated at the wave vector q = 2π/rc (see Section 5 in the supporting material), to set the overall time scale (time unit of the epigenetic clock). We show in Fig. S5 that τr is a reasonable surrogate for the mean contact lifetimes during which modifications could occur by the looping mechanism. The dependence of the spreading on lp and chain length N are described in the supporting material (Sections 9 and 10, respectively). Note that, in contrast to previous polymer models, there is an explicit connection between chromatin relaxation time (τr) and the dynamics of spreading. We set τr as the unit of time, and all other times are measured relative to τr.
Spreading rates
The limit of slow spreading (SS) is achieved by choosing . In the SS limit, chromatin undergoes multiple cycles of relaxation, which implies that nucleosomes separated by large genomic distance have a substantial probability of being in proximity for spreading to occur by the looping mechanism. With our choice of β = 0.01, we find numerically that spreading by the 1D mechanism is not as important. We introduce the parameter γ in order to control the contribution of 1D spreading mechanism. In this case, the probability of spreading is given by . In the steady-state limit, the value of γ has no bearing on the results of the simulations because it is a 3D dominated mechanism. Thus, by changing β, one can examine a range of possibilities for epigenetic spreading. Based on the estimation provided in the discussion section below, we believe that the SS limit is biologically relevant, and we show these results in the main text.
For completeness, we also explore the opposite limit, fast spreading (FS). The results are shown in the supporting material. In the FS limit, , which implies that modification occurs on time scales that are much shorter than τr, the chromatin relaxation time. In this limit, spreading occurs predominantly by a linear or 1D mechanism with the looping mechanism playing a less significant role. To achieve this limit in the simulations, γ (Fig. S1) is chosen so that is large. In the FS limit, this is achieved by choosing .
Implementation
We start from an equilibrated conformation of the chromatin polymer with all the nucleosomes in the U state at t = 0. The simulations were also repeated with all nucleosomes in the M states in order to show that the steady-state behavior is independent of the initial conditions, which is assured because the chromatin is epigenetically ergodic (see Section 8 in supporting material for details). In addition, the simulations were performed for times that exceed τr by several orders of magnitude, so that the chromatin conformation is well sampled.
The conformation of the polymer is evolved by integrating the Langevin equations by choosing a suitable time step (described in Section 3 in the supporting material). At each time step, marking or unmarking of all the nucleosomes is attempted with probabilities given in Fig. S1 b. A graphical representation of the modification algorithm is provided in Fig. 2 in the supporting material. A pictorial representation of the simulated trajectories for FS and SS limits are shown in Fig. S2, and in Videos S1 and S2.
Figure 2.
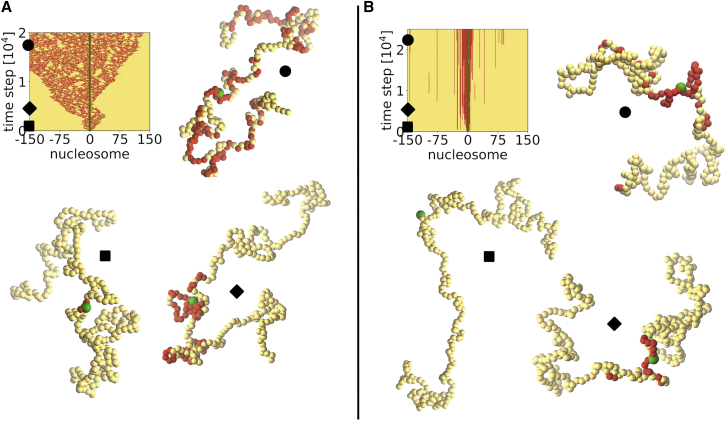
Visualization of single trajectories in the fast (A) and slow (B) spreading regimes. In the former case, the spreading occurs fast and independently of chromatin configuration, while in the latter case, the pattern of spreading may be determined by the dynamic rearrangement of the chromatin, as explained in the main text. The kymographs show the epigenetic identity of each nucleosome (marked/M/red, unmarked/U/yellow, NS/green) for a single trajectory, in both (A) and (B). Three distinct simulation time steps are chosen, marked with a symbol on the kymograph, and we extract polymer conformations with epigenetic identities of the nucleosomes to graphically represent them. For clarity, the size of the NS is enhanced. Accompanying Videos S1 and S2 are available online. To see this figure in color, go online.
Global epigenetic state
We use simple measures to characterize the global epigenetic state of chromatin as well as the modification state of the individual nucleosomes for both the FS and SS scenarios. By examining the dynamics in detail, we can quantitatively assess the contributions from 1D and 3D spreading separately for the two extreme cases. We determine the epigenetic state of chromatin using,
| (1) |
where () is the number of modified (unmodified) nucleosomes at time t in the jth trajectory, and N is the total number of nucleosomes. The quantity is averaged over time T and Ntraj. Unless otherwise stated, all the relevant quantities are calculated using Ntraj = 10, where each trajectory starts with a different initial chromatin conformation.
Average epigenetic state of the nucleosomes
We also determined the average, , of each nucleosome, which is calculated using,
| (2) |
where is the epigenetic state of locus i in trajectory j at time t.
The fraction of time each nucleosome is modified is measured by fim,
| (3) |
where counts the number of occurrences of nucleosome i in state M in trajectory j, while T is the total number of simulation snapshots taken into account.
Results
Chromatin topology drives domain formation
We explored the SS case by choosing . In this limit, the chromatin polymer could form the allowed contacts through the looping process multiple times on the time scale , which would allow for 3D as well as 1D spreading. Consequently, the inactivation profile would be determined by the contact probability between the nucleosomes separated by |i−j|≥2 (Fig. S6).
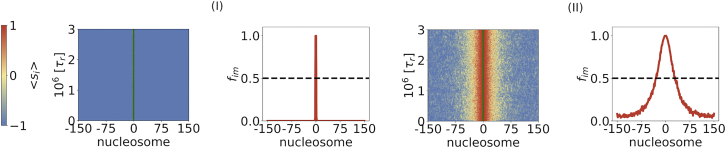
These expectations are tested by computing the epigenetic states of the nucleosomes as well as the associated inactivation profiles. We fixed k+ and varied k− to improve the odds of spreading, deciding finally on the choice k− = k+/10,000. For the chosen parameters, domain formation by the linear mechanism does not occur (Fig. 3, Scheme I). This is because the probability of linear spreading to neighboring nucleosomes, even away from the NS, is extremely low () at each time step. Thus, we surmise that spreading must occur exclusively through the formation of 3D contacts. This is borne out in the panels for Scheme II in Fig. 3, which show clearly that the 3D spreading mechanism results in the formation of stable domains around the NS. It is worth noting that stable domain formation ( 60 nucleosomes centered around the NS) does not require collapse (17) or partial collapse (18) of the chromatin polymer.
Figure 3.
The formation of the epigenetic domain is determined by SS kinetics with for Scheme I, where spreading occurs only through 1D, and Scheme II, where 3D spreading dominates. (Left) Average (over an ensemble of trajectories) states of nucleosomes as a function of time. (Right) Mean values of the spin states of the nucleosomes. These are the profiles that show the extent of inactive domain formation. The value of k+/k− = 10,000 in all simulations, while α(I) = 2.23⋅10−4 and α(II) = 2⋅10−4. To see this figure in color, go online.
The spreading profile in the right panel of Fig. 3 for Scheme II shows that the peak in the fim profile is localized around the NS. The boundary (or the interface) between the active and inactive domains is relatively soft (36), indicated by a continuous decrease of fim, rather than by a step-like drop to 0, which would occur if the boundary were sharp. Thus, the percentage of inactive loci in the interface region between the active and inactive nucleosomes could indicate whether the boundary is efficient in preventing modified nucleosomes from spreading distally of its position.
An important finding in our work, with potential biological importance, is that, even without an explicit boundary element, the epigenetic domain size is finite, and is localized around the NS. The distribution of modifications around the NS is governed by the contact probability of the NS with surrounding residues, which depends on the chromatin conformational dynamics. Furthermore, the shape of the epigenetic domain shown in the right panel of Fig. 3 and the boundary formation is due to the asymmetry in the spreading rates from the NS (k+) and the modified nucleosomes (αk+ with α less than unity). This asymmetry is required for the formation of discrete domains without explicit boundary elements to halt the spreading process, and points to the importance of the NS that we explore further (see below).
DNA replication and the NS
Next, we address the role of the NS in a pre-formed epigenetic domain and the impact of DNA replication. In our model, the NS is the only element whose epigenetic identity is unchanged, and functions as a reservoir for modifications. We performed simulations in which the conditions change over time. First, we performed simulations with NS present. At t = 301,205τr, we removed the NS by changing it to a non-NS nucleosome in the M state, and continued running simulations in this condition for another t = 301,205τr. With this alteration, the identity of the M state could change stochastically as the chromatin evolves. At t = 602,410τr, we mimic DNA replication by randomly assigning the active state to half of the nucleosomes, repeating this assignment every 150.6τr. Note that the end-to-end distance of the polymer relaxes in about 602.4τr, indicating that the DNA replication time (150.6τr) is shorter than the polymer relaxation time. We note parenthetically that the time for finite domain formation is roughly 50 times greater than the replication time (see Fig. 3). This implies that in our model it takes roughly 50 generations to establish finite domains. Experiments have shown that, in certain species, establishment of stable domains occurs in about 20 generations (37,38). We could have altered the DNA replication time in our simulations to reduce the number of generations needed for establishing stable domains. Nevertheless, our results are in qualitative agreement with experiments.
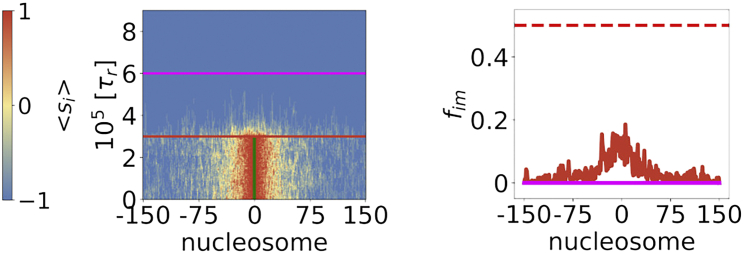
We follow the epigenetic identities of all the nucleosomes at all time steps and show them as a kymograph in the left panel of Fig. 4. We also calculate the inactivation profile of the chromatin for two distinct parts of the trajectory: 1) portion of the trajectory without NS (red curve in the right panel of Fig. 4), and 2) portion of the trajectory where DNA replications are repeated periodically (magenta curve in the right panel of Fig. 4). We define epigenetic domain to exist in the region above the level fim>0.5. Fig. 4 shows the results for Scheme II in the SS regime. The figure shows that the finite-sized domain cannot be maintained once the NS is deleted (red curve). Stable, bounded domains that are maintained during DNA replication would only occur if the looping mechanism for modification is allowed and the NS does not change. Thus, the results in Fig. 4 show that the NS is required for domain maintenance, and even more so if DNA replication is permitted (magenta curve). Experimental evidence on S. pombe (39) does suggest that some nucleation events needed for heterochromatin formation are triggered at each cell cycle, indicating that maintenance requires the nucleation event.
Figure 4.
Role of nucleation in establishing and maintenance of epigenetic spreading for Scheme II in the SS regime. (Left) The state of each nucleosome in a trajectory, (Eq. 2 in section “methods”). The trajectory is divided into three parts with distinct simulation conditions, whose transition is marked by two horizontal lines. Initially, the simulation starts with the NS present. Subsequently, the NS is removed (marked by a red horizontal line). After removing the NS, a new steady state is achieved. Thereafter, we introduce DNA replication (marked by magenta horizontal line) by stochastically replacing approximately 50% of M marks with U marks, mimicking equal redistribution of parent histones to both strands upon replication. Replications are repeated every 150.6τr. (Right) The presence of epigenetic domains provided the fraction of trajectory in the marked state for each locus is > 0.5. The red curve is computed from the trajectory between the NS removal and DNA replication. The magenta curve is computed from the trajectory after the DNA replication. The horizontal dotted red line represents the 50% mark. k+/k− = 10,000 and . To see this figure in color, go online.
Finite domain formation in an initially condensed or partially condensed chromatin
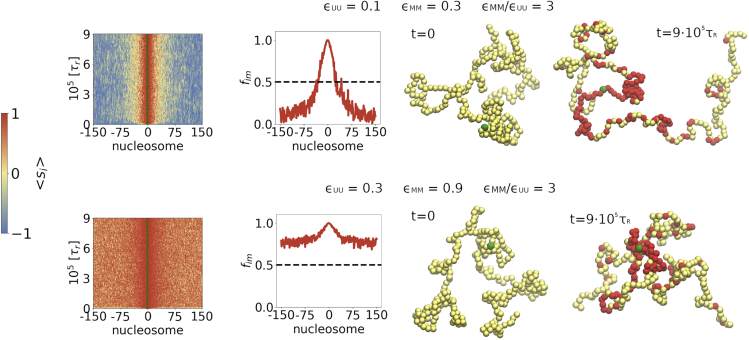
The results presented so far were obtained by setting . This choice places the chromatin in a good solvent, which could mimic the behavior in fission yeast (40). However, in some other eukaryotes, the heterochromatin is denser than euchromatin. In the context of our model, it would imply that the effective interaction . To account for the higher chromatin density, we set the interaction strength , which implies that, due to dynamical changes in the epigenetic landscape, the effective interactions between the nucleosomes are modified as in the previous polymer-based studies (17,18,26). We set to the geometric mean, . Since linear spreading does not depend on the solvent quality, we only explored Scheme II, where looping determines the outcome of the spreading process. We simulated the SS case ().
To fully explore the range of solvent conditions, we considered two cases. In both, we chose . Let us first consider and . For a homopolymer, is close to but slightly below the point (see Fig. S4 in Section 6 in the supporting material), whereas for chromatin behaves as disordered random coil. With this particular choice, we find (upper panels in Fig. 5) that the results are qualitatively similar to the case with (Fig. 3). In particular, the domain size is bounded, as discovered in experiments on mouse stem cells and fibroblasts (36). This is outlined both by the pattern formed around the NS on the kymograph (upper left panel) as well as in the activity profile of the domain (upper right panel). Since the epigenetic spreading in this regime is mostly due to contacts between the NS and spatially nearby nucleosomes, spreading is localized.
Figure 5.
Effect of solvent quality on the spreading of epigenetic modifications using Scheme II, in which looping affects the spreading process. The and values of each are shown. For all simulations, k+/k− = 10,000 and k+ = 0.01/τr. The initial and the final conformations from a single trajectory are displayed on the right. To see this figure in color, go online.
The with corresponds to a mixed case in which a fraction of modified nucleosomes experience moderately poor solvent conditions, whereas the U nucleosomes are in good solvent (see Fig. S4 in Section 6 in the supporting material). We then investigated the case when the modified nucleosomes are in bad solvent conditions and unmodified nucleosomes are close to but slightly below the condition by choosing while keeping the ratio as before. The results in the lower panels in Fig. 5 are dramatically different from those in the upper panels. The spreading of the marks is centered around the NS as before. However, modification occurs without bound with the probability of the ith nucleosome to be in the M state is as the genomic length increases or decreases from the NS. In contrast to the results in Fig. 4, which shows that probabilities of being in the M or U state away from the NS are (except for the ends), the results in the lower panels demonstrate a substantially higher probability of being in the M state. Taken together, the results in Fig. 5 suggest that is not as important as the solvent quality for predicting the outcome of the spreading dynamics. Although in Fig. 5, the initial conformation of the chromatin is a disordered coil in the upper panel, whereas in the lower panels it is more compact. The final epigenetic state of chromatin can be anticipated by the quality of the solvent that the chromatin is in at the initial state, especially in the SS limit, where spreading occurs predominantly by the 3D mechanism.
Comparison with experiments on mouse embryonic stem cells
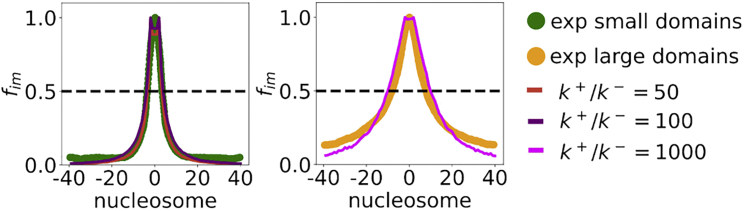
We explored the biological pertinence of our results by comparing them with the H3K9me3 enrichment profiles reported elsewhere (see Fig. 6 in (36)). In this study, the authors investigated the propagation of HP1α-induced H3K9me3 modification in the 10-kb Oct4 locus in embryonic stem cells (36), and found that H3K9me3 propagated symmetrically to produce finite spatial domains. To rationalize the observations, they proposed a 1D model (24,36) in which spreading occurs with finite probability to the neighboring sites from an already modified nucleosome. The enrichment in H3K9me3 marks can be partitioned into two groups by using clustering (41); small domains that encompass 77.1% of the data (Fig. 6, left panel) and large domains that account for the rest (Fig. 6, right panel) (36). Since the enrichment profiles are equivalent to inactivation profiles reported throughout this paper, we make a comparison between the two in Fig. 6.
Figure 6.
Comparison between simulations performed using Scheme II in the SS regime at different k+/k− values with experimental data for H3K9me3 domains in embryonic stem cells (41). The experimental data were divided into small and large domains by clustering. These domains differ in the size of the genomic length they cover, and we fit them using different k+/k− ratios that control the spreading process. We show that the small experimental domains correspond to a range of k+/k− parameters in our model (left), while a higher (k+/k− = 1000) value is needed to account for the larger domain size shown on the right. The parameters are chosen to be and α = 2k−/k+. To see this figure in color, go online.
To assess if our model, which involves an interplay of 1D and 3D spreading, could be used to reproduce the reported H3K9me3 enrichment profiles described above, we performed calculations using Scheme II. Using , we find that, for a range of k+/k− values, we obtain good agreement with the enrichment profiles (Fig. 6) for both small and large domains. The excellent agreement between our predictions and experiments shown in Fig. 6 allows us to draw a few pertinent conclusions. 1) The competition between the forward and the backward rate remains crucial (36) when accounting for epigenetic domain width, even when 3D spreading is possible. For example, if k+/k− is large, domains without bound form. 2) The experimental data compare well with a model where the NS is situated in every epigenetic domain. In our model, the spreading rate from the NS is greatly enhanced compared with spreading from non-NS-modified nucleosomes. NSs are sequence-defined DNA fragments to which enzymes bind with high specificity and different conformational changes might arise by binding to different sequences, thus modulating the enzyme activity. 3) Although a linear spreading model can also reproduce the experiment curve (36), our results show that 3D contacts are not inconsistent with the experimental observation. Different mechanisms might be operative in heterochromatin formation in different species. The combination of 1D and 3D models, which integrates the rates of spreading and chromatin dynamics created here, could be a step toward fulfilling this goal. Indeed, there is experimental evidence pointing to the importance of both linear (nearest-neighbor) (42) spreading of H3K9me3 marks, as well as spatial spreading (43) of H3K27 marks, showing that chromatin silencing could proceed by both mechanisms, as accounted for in Scheme II of our model.
Discussion
We developed a minimal polymer model to explore different scenarios for epigenetic domain formation with a focus on the coupling between chromatin dynamics and stochastic switching in individual nucleosome states. In our model, the interplay of the structural relaxation rate and the modification rates determines the efficacy of the spreading process. However, by setting our work in the context of the modeling literature on epigenetic spreading, we conclude that multiple scenarios for heterochromatin spreading are possible because the domain formation is an interplay of several time, length, and energetic scales. A similar picture emerges from experimental studies, encompassing different organisms and epigenetic modifications. It is only by exploring various scenarios and analyzing their validities against experimental data that we can determine the physics underlying epigenetic spreading, initiated by the complex enzymatic chemical reactions.
The main findings in our work are:
-
•
In the SS limit, with the modification rate that is much smaller than the relaxation rate of the polymer, finite domains are established on the time scales of . This time translates to about 50 generations, which is big, but is in qualitative accord with experimental results for silencing in certain species (37). The domain size is about 60 nucleosomes or roughly 12 kb. The width of the interface between the active and inactive domains is soft, involving a small number of nucleosomes (Fig. 3).
-
•
The presence of the NS is essential for the formation of the modified domains. An already established domain cannot be maintained if NS is removed. It should be noted that there is evidence for the NS in experiments (36). We should add that one can envision other mechanisms where finite domains could be established without explicitly having NS in the model (25,26). However, it is gratifying and maybe surprising that we are able to predict finite domain spreading purely from SS of the marks in conjunction with looping as a way to transfer the epigenetic marks.
-
•
An important finding in our work is that, in the limit of SS, finite modified domains form without boundary elements that are known to stop the spreading process. We find that finite domains form by mechanism II, which predominantly involves 3D chromatin looping. If the relaxation time associated with chromatin dynamics is shorter than the spreading time, then finite domains form. The formation of the finite domain does not depend on the spreading cutoff, because the rate is determined by the relaxation times associated with chromatin dynamics. It is possible to form finite domains using polymer models (interactions between modified nucleosomes are attractive), which have many genomic bookmarks (GBMs) that, in effect, are the boundary elements, which stop epigenetic spreading (26). In this model, it was found that finite-sized domains, with spacing that is given by the genomic distance between the GBMs, form only if the linear density of the GBMs exceeds a critical value. The presence of a large number of GBMs is tantamount to using many boundary elements, which we find is unnecessary in the present model. It is only by quantitatively analyzing specific experiments that we can assess the validity of various models. We provide such experimental validation of our model in this paper by showing quantitative agreement with experiments.
-
•
In an insightful article (25), it has been shown using a polymer model that, once formed, finite domains can be passed on to multiple generations upon DNA replication. In their model, the initial methylation patterns were taken from chromatin immunoprecipitation sequencing (ChiP-seq) data, and the maintenance of the silencing pattern is driven by heterochromatin protein 1 (HP1). Informed by experiments that HP1 preferentially binds to methylated tails in the histones, they showed the initial methylation pattern from the ChiP-seq data is not only maintained over nine generations but also spreads without having an NS. The HP1-mediated silencing is not unrelated to the GBM used elsewhere (26). In the present study, we were interested in exploring mechanisms for the establishment of finite domains. We do find, however, that the NS is necessary to maintain the finite domain upon DNA replication. We believe that if we imposed boundary elements, which would be the analog of preferentially binding of HP1 to methylated regions (25) or the use of GBM (26), there would not be a need to introduce the NSs. The present and previous studies are exploring different possibilities for spreading and maintenance of epigenetic marks, and only future experiments can differentiate between them.
-
•
A major determinant of spreading is the solvent quality of the initial (fully unmarked) epigenetic state, rather than the relative strength of the U−U and M−M interactions. If the initial epigenetic state of the chromatin is a coil, contacts rarely form, resulting in localized spreading around the NS, which leads to a discrete bounded domain (upper panel in Fig. 5). If, initially, chromatin is poised to be just below the point, we find that stable finite domains form (upper panel in Fig. 5) even if the interactions between the modified nucleosomes are attractive. On the other hand, if the initial chromatin state is such that it is partially condensed, we find that epigenetic domains form without bound (lower panel in Fig. 5). Because the propagation of heterochromatin without bound is biologically untenable, our results suggest that either there ought to be multiple boundary elements that stop the spreading of the epigenetic marks or the environmental conditions for the unmodified nucleosomes should poise them close to the conditions.
The data can be generated using the in-house computer code that has been deposited in Github. The URL is https://github.com/Katamar/epigenetic.
Experimental prospects
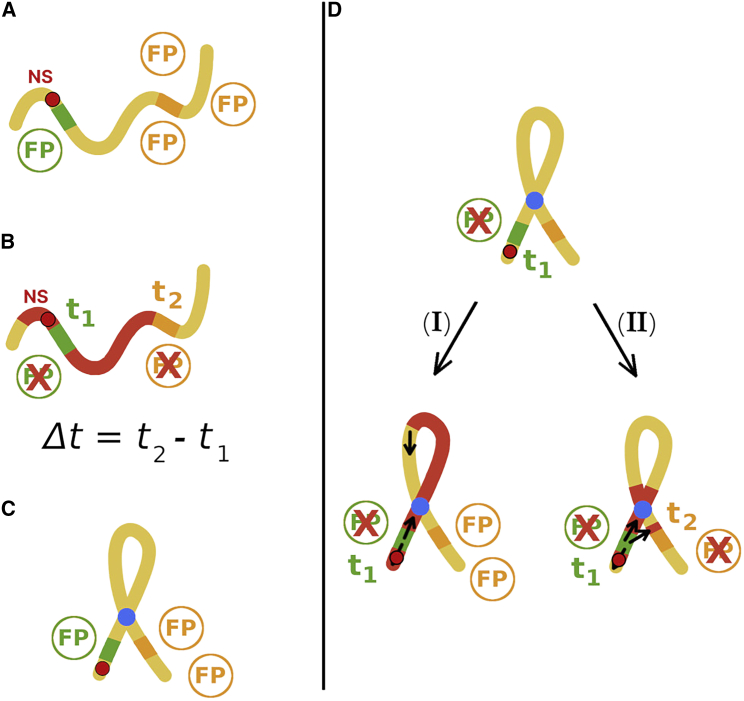
To test the prediction that stable finite domains can be driven by the 3D organization of chromatin without boundary elements, we propose an experiment based on fluorescent probes, similar to the one previously reported (44). The difference would be that the nucleation element and position-dependent fluorescent probe are placed within a permanent artificially engineered loop. The proposed experiment, shown schematically in Fig. 7, would help elucidate the extent to which chromatin looping plays a role in the formation of epigenetic domains. More generally, it could clarify whether epigenetic domain formation occurs by linear or spatial spreading or a combination of both these mechanisms, as is likely the case.
Figure 7.
Scheme for the proposed experiment. (A) The gene for the orange fluorescent protein (OFP, in orange) is expressed if chromatin is unmarked (yellow). The repression of the green fluorescent protein gene (GFP) acts as a proxy for the binding of epigenetic spreading initiators to the NS, shown in a red circle with a black border. Because the nucleation event has not occurred, the GFPs and OFPs are produced. The presence of fluorescent proteins (FPs) could be detected by measuring fluorescence intensity at a given wavelength. (B) The binding of epigenetic spreading initiators to the NS represses the GFP expression at time t1, which could be measured. Subsequently, epigenetic markers (red) spread until the OFP gene is inactivated, resulting in the disappearance of orange fluorescence at t2, which is measurable. During spreading, chromatin can form loops but need not have a permanent structure. The time difference, Δt = t2−t1, could be measured for many single cells to obtain the distribution P(Δt). This represents the control experiment; a similar experimental setup has been employed in (44). (C) A permanent loop (blue) in chromatin structure may be constructed so that the spatial proximity of the NS and OFP gene is decreased for a given genomic NS-FP distance. (D) Using the FPs as reporters for spreading, only cells that lack green fluorescence are taken into account, as it marks the successful initiation of epigenetic spreading from the NS. If the heterochromatin spreading from the NS is strictly 1D, then P(Δt) should not differ from the result in the control experiment. If 3D spreading is relevant, P(Δt) would differ compared with the control experiment. The same conclusions should be achieved by placing the OFP gene at different genomic distances from the NS, for a given loop length. To see this figure in color, go online.
Author contributions
M.K. created the model. M.K. and G.S. implemented the model. M.K. performed the simulations. M.K.,G.S., and D.T. interpreted the findings. D.T. supervised the work. All authors discussed the results and contributed to the writing of the final manuscript.
Acknowledgments
We thank Bassem Al-Sady and Ilya Finkelstein for advice and useful discussions. This work was initiated while M.K. was a postdoctoral fellow at the University of Texas. We acknowledge the National Science Foundation (CHE 19-00093) and the Collie-Welch Regents Chair (F-0019) for supporting this work.
Declaration of interests
The authors declare that there is no conflict of interest.
Editor: Yi Qin Gao.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.07.001.
Supporting material
References
- 1.Moazed D. Mechanisms for the inheritance of chromatin states. Cell. 2011;146:510–518. doi: 10.1016/j.cell.2011.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cortini R., Barbi M., et al. Victor J.M. The physics of epigenetics. Rev. Mod. Phys. 2016;88:25002. [Google Scholar]
- 3.Ptashne M. On the use of the word ‘epigenetic’. Curr. Biol. April 2007;17:R233–R236. doi: 10.1016/j.cub.2007.02.030. [DOI] [PubMed] [Google Scholar]
- 4.Ptashne M. Epigenetics: core misconcept. Proc. Natl. Acad. Sci. USA. 2013;110:7101–7103. doi: 10.1073/pnas.1305399110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ringrose L., Howard M. Dissecting chromatin-mediated gene regulation and epigenetic memory through mathematical modelling. Curr. Opin. Syst. Biol. 2017;3:217–314. [Google Scholar]
- 6.Holliday R., Pugh J.E. DNA modification mechanisms and gene activity during development. Science. 1975;187:226–232. [PubMed] [Google Scholar]
- 7.Compere S.J., Palmiter R.D. DNA methylation controls the inducibility of the mouse metallothionein-i gene in lymphoid cells. Cell. 1981;25:233–240. doi: 10.1016/0092-8674(81)90248-8. [DOI] [PubMed] [Google Scholar]
- 8.Bannister A.J., Kouzarides T. Regulation of chromatin by histone modifications. Cell Res. 2011;21:381–395. doi: 10.1038/cr.2011.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Todeschini A.L., Georges A., Veitia R.A. Transcription factors: specific DNA binding and specific gene regulation. Trends Genet. 2014;30:211–219. doi: 10.1016/j.tig.2014.04.002. [DOI] [PubMed] [Google Scholar]
- 10.Holoch D., Moazed D. RNA-mediated epigenetic regulation of gene expression. Nat. Rev. Genet. 2015;16:71–84. doi: 10.1038/nrg3863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Becker P.B., Workman J.L. Nucleosome remodeling and epigenetics. Cold Spring Harb. Perspect. Biol. 2013;5:a017905. doi: 10.1101/cshperspect.a017905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dekker J., Misteli T. Long-range chromatin interactions. Cold Spring Harb. Perspect. Biol. 2015;7:a019356. doi: 10.1101/cshperspect.a019356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Heard E., Martienssen R.A. Transgenerational epigenetic inheritance: myths and mechanisms. Cell. 2014;157:95–109. doi: 10.1016/j.cell.2014.02.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Alabert C., Groth A. Chromatin replication and epigenome maintenance. Nat. Rev. Mol. Cell Biol. 2012;13:153–167. doi: 10.1038/nrm3288. [DOI] [PubMed] [Google Scholar]
- 15.Beisel C., Paro R. Silencing chromatin: comparing modes and mechanisms. Nat. Rev. Genet. 2011;12:123–135. doi: 10.1038/nrg2932. [DOI] [PubMed] [Google Scholar]
- 16.Grewal S.I., Moazed D. Heterochromatin and epigenetic control of gene expression. Science. 2003;301:798–802. doi: 10.1126/science.1086887. [DOI] [PubMed] [Google Scholar]
- 17.Michieletto D., Orlandini E., Marenduzzo D. Polymer model with epigenetic recoloring reveals a pathway for the de novo establishment and 3d organization of chromatin domains. Phys. Rev. X. 2016;6:041047. [Google Scholar]
- 18.Jost D., Vaillant C. Epigenomics in 3d: importance of long-range spreading and specific interactions in epigenomic maintenance. Nucleic Acids Res. 2018;46:2252–2264. doi: 10.1093/nar/gky009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dodd I.B., Micheelsen M.A., et al. Thon G. Theoretical analysis of epigenetic cell memory by nucleosome modification. Cell. 2007;129:813–822. doi: 10.1016/j.cell.2007.02.053. [DOI] [PubMed] [Google Scholar]
- 20.Erdel F., Greene E.C. Generalized nucleation and looping model for epigenetic memory of histone modifications. Proc. Natl. Acad. Sci. USA. 2016;113:E4180–E4189. doi: 10.1073/pnas.1605862113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Berry S., Dean C., Howard M. Slow chromatin dynamics allow polycomb target genes to filter fluctuations in transcription factor Activity. Cell Syst. 2017;4:445–457.e8. doi: 10.1016/j.cels.2017.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Angel A., Song J., et al. Howard M. A Polycomb-based switch underlying quantitative epigenetic memory. Nature. 2011;476:105–108. doi: 10.1038/nature10241. [DOI] [PubMed] [Google Scholar]
- 23.Dodd I.B., Sneppen K. Barriers and silencers: a theoretical toolkit for control and containment of nucleosome-based epigenetic states. J. Mol. Biol. 2011;414:624–637. doi: 10.1016/j.jmb.2011.10.027. [DOI] [PubMed] [Google Scholar]
- 24.Hodges C., Crabtree G.R. Dynamics of inherently bounded histone modification domains. Proc. Natl. Acad. Sci. USA. 2012;109:13296–13301. doi: 10.1073/pnas.1211172109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sandholtz S.H., MacPherson Q., Spakowitz A.J. Physical modeling of the heritability and maintenance of epigenetic modifications. Proc. Natl. Acad. Sci. USA. 2020;117:20423–20429. doi: 10.1073/pnas.1920499117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Michieletto D., Chiang M., et al. Marenduzzo D. Shaping epigenetic memory via genomic bookmarking. Nucleic Acids Res. 2018;46:83–93. doi: 10.1093/nar/gkx1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lieberman-Aiden E., van Berkum N.L., et al. Dekker J. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. October 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shi G., Liu L., et al. Thirumalai D. Interphase human chromosome exhibits out of equilibrium glassy dynamics. Nat. Commun. 2018;9:3161. doi: 10.1038/s41467-018-05606-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Grigoryev S.A. Chromatin higher-order folding: a perspective with linker DNA angles. Biophys. J. 2018;114:2290–2297. doi: 10.1016/j.bpj.2018.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Socol M., Wang R., et al. Bancaud A. Rouse model with transient intramolecular contacts on a timescale of seconds recapitulates folding and fluctuation of yeast chromosomes. Nucleic Acids Res. 2019;47:6195–6207. doi: 10.1093/nar/gkz374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Langowski J. Polymer chain models of DNA and chromatin. Eur. Phys. J. E Soft Matter. 2006;19:241–249. doi: 10.1140/epje/i2005-10067-9. [DOI] [PubMed] [Google Scholar]
- 32.Knoch T.A. Simulation of different three-dimensional polymer models of interphase chromosomes compared to experiments–an evaluation and review framework of the 3d genome organization. Semin. Cell Dev. Biol. 2019;90:19–42. doi: 10.1016/j.semcdb.2018.07.012. [DOI] [PubMed] [Google Scholar]
- 33.Ragunathan K., Jih G., Moazed D. Epigenetic inheritance uncoupled from sequence-specific recruitment. Science. 2015;348:1258699. doi: 10.1126/science.1258699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Garel T., Orland H., Orlandini E. Phase diagram of magnetic polymers. Eur. Phys. J. B. 1999;12:261–268. [Google Scholar]
- 35.Zhang K., Mosch K., et al. Grewal S.I. Roles of the clr4 methyltransferase complex in nucleation, spreading and maintenance of heterochromatin. Nat. Struct. Mol. Biol. 2008;15:381–388. doi: 10.1038/nsmb.1406. [DOI] [PubMed] [Google Scholar]
- 36.Hathaway N.A., Bell O., et al. Crabtree G.R. Dynamics and memory of heterochromatin in living cells. Cell. 2012;149:1447–1460. doi: 10.1016/j.cell.2012.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu E.Y., Zawadzki K.A., Broach J.R. Single-cell observations reveal intermediate transcriptional silencing states. Mol. Cell. 2006;23:219–229. doi: 10.1016/j.molcel.2006.05.035. [DOI] [PubMed] [Google Scholar]
- 38.Obersriebnig M.J., Pallesen E.M.H., et al. Thon G. Nucleation and spreading of a heterochromatin domain in fission yeast. Nat. Commun. 2016;7:11518. doi: 10.1038/ncomms11518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen E.S., Zhang K., et al. Grewal S.I. Cell cycle control of centromeric repeat transcription and heterochromatin assembly. Nature. 2008;451:734–737. doi: 10.1038/nature06561. [DOI] [PubMed] [Google Scholar]
- 40.Matsuda A., Chikashige Y., et al. Hiraoka Y. Highly condensed chromatins are formed adjacent to subtelomeric and decondensed silent chromatin in fission yeast. Nat. Commun. 2015;6:7753. doi: 10.1038/ncomms8753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bilodeau S., Kagey M.H., et al. Young R.A. SetDB1 contributes to repression of genes encoding developmental regulators and maintenance of ES cell state. Genes Dev. 2009;23:2484–2489. doi: 10.1101/gad.1837309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Müller M.M., Fierz B., et al. Muir T.W. A two-state activation mechanism controls the histone methyltransferase suv39h1. Nat. Chem. Biol. 2016;12:188–193. doi: 10.1038/nchembio.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Leicher R., Ge E.J., et al. Liu S. Single-molecule and in silico dissection of the interaction between polycomb repressive complex 2 and chromatin. Proc. Natl. Acad. Sci. USA. 2020;117:30465–30475. doi: 10.1073/pnas.2003395117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Greenstein R.A., Jones S.K., et al. Al-Sady B. Noncoding RNA-nucleated heterochromatin spreading is intrinsically labile and requires accessory elements for epigenetic stability. eLife. 2018;7:e32948. doi: 10.7554/eLife.32948. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.