Estimating the localization spread function of static single-molecule localization microscopy images

Abstract

Single-molecule localization microscopy (SMLM) permits the visualization of cellular structures an order of magnitude smaller than the diffraction limit of visible light, and an accurate, objective evaluation of the resolution of an SMLM data set is an essential aspect of the image processing and analysis pipeline. Here, we present a simple method to estimate the localization spread function (LSF) of a static SMLM data set directly from acquired localizations, exploiting the correlated dynamics of individual emitters and properties of the pair autocorrelation function evaluated in both time and space. The method is demonstrated on simulated localizations, DNA origami rulers, and cellular structures labeled by dye-conjugated antibodies, DNA-PAINT, or fluorescent fusion proteins. We show that experimentally obtained images have LSFs that are broader than expected from the localization precision alone, due to additional uncertainty accrued when localizing molecules imaged over time.

Significance

Single-molecule localization microscopy (SMLM) is a class of imaging methods that resolve fluorescently labeled structures beyond the optical resolution limit of visible light. SMLM detects stochastically blinking labels over minutes and localizes each blink with precision of order 10 nm. We present a method to evaluate the accuracy of localizations in a way that is analogous to the point spread function of a conventional light microscope. The LSF estimate explicitly observes time-dependent factors that degrade image resolution and provides an objective tool to both optimize imaging and guide image analysis. The estimate is robust on useful timescales for a range of SMLM probes.

Introduction

Single-molecule localization microscopy (SMLM) is a powerful tool to image structures in cells with dimensions ranging between tens of nanometers to tens of microns. Methods such as (d)STORM (1,2), (F)PALM (3,4), and PAINT (5) exploit the stochastic blinking of single fluorophores to localize emitting molecules with a localization precision much smaller than the diffraction limit of visible light, by imaging only a small subset of probes in any given image frame. These samples are then imaged over time, and acquired localizations are typically assembled into a single reconstructed superresolved image.

Assessing the quality of reconstructed images can be challenging as numerous factors can contribute. These factors can include the labeling density, the types of structures being imaged, the brightness and blinking dynamics of the fluorophore, the finite size of labeling antibodies, motions of the stage or labeled molecules during acquisition, and the analytical methods used in postprocessing. One important measure of the quality of a measurement is the localization precision of single fluorophores, which is influenced by many of the factors listed above. Many localization algorithms directly return estimates of the localization precision of single fits, and similar information can be extracted directly from the localizations themselves through the use of pair-correlation functions or nearest neighbor analyses that extract the distribution of positions of molecules detected in adjacent frames (6,7). However, these methods are not sensitive to errors introduced on timescales longer than a few image frames. Other metrics of image quality have been developed that integrate both precision and spatial sampling. One widely used method, called Fourier ring correlation (FRC) (8,9), effectively captures the impact of factors that degrade quality over the entire span of image acquisition. The FRC curve depends on the types of structures imaged, how well they are sampled, and the specific regions of interest used. The resolution value it reports indicates the length scale below which the signal to noise ratio falls below a specified limit. This value is useful for comparing imaging conditions for a particular sample, but hard to compare across sample types, making its use highly context dependent.

Here, we present a simple method to estimate the average localization spread function (LSF) of an SMLM data set as a way to evaluate its resolution. The LSF is analogous to the point spread function (PSF) of a conventional microscopy measurement and can aid the interpretation of acquired images. The LSF reports on how accurately distances can be measured between labeled objects within images, and can be used when constraining the structure of a multiprotein complex or when estimating the statistical codistribution of labeled components. The LSF can also be used to evaluate optimizations all along the image acquisition and processing pipelines. The method presented exploits temporal correlations in the blinking dynamics of single fluorophores commonly used for localization microscopy (10, 11, 12). This enables the method to report on errors accumulated over time that do not typically impact the accuracy of single-molecule fitting but impact how accurately a molecule’s position is determined relative to others (13,14). Here, we derive a method to isolate the LSF directly from acquired localizations, validate it through simulation and images of DNA origami rulers, and apply it to several images of labeled structures in cells. In all of the experimental examples interrogated, the LSF width increases over timescales at and below that of drift correction.

Materials and methods

Simulations

Simulations mimicking DNA origami rods were accomplished by randomly placing pairs of fluorophores positioned 50 nm apart within a 40 by 40 μm region of interest (ROI) at an average density of 1 pair per μm². A total of 20,000 individual image frames with an effective frame time of 0.1 s were simulated by sampling a subset of molecular positions with a localization precision of 10 nm in each lateral dimension. The dynamics of individual fluorophores were governed by a continuous time Markov process involving five states: one on state (1), three dark states (0, 01, 02), and an irreversible bleached state (B), following the procedure described previously (12,15). The on state was accessible from any of the dark states, while dark state 0 was accessible only from the on state, and dark states 01 and 02 were accessible only from the previous dark states, 0 and 01, respectively. We used the following parameters (using the notation described in (12,15)) to capture essential elements of our experimental observations: $\lambda \left(0\to 1\right)=$ 1.2 Hz; $\lambda \left(0\to 01\right)=$ 0.05 Hz; $\lambda \left(01\to 02\right)=$ 0.0033 Hz; $\lambda \left(01\to 1\right)=$ 0.02 Hz; $\lambda \left(02\to 1\right)=$ 0.0005 Hz; $\lambda \left(1\to 0\right)=$ 5 Hz; $\mu \left(1\to B\right)=$ 0.05 Hz. The continuous time Markov process was simulated in MATLAB (MathWorks, Natick, MA) using File Exchange code “simCTMC.m” (16). When present, drift was applied to all molecular positions with a constant rate of 0.3 nm/s in the x direction along with diffusive drift characterized by a diffusion coefficient of D = 2.5 nm²/s. Drift was corrected using the mean shift algorithm described previously (17) using 1000 frames per alignment (10 s).

Experimental sample preparation

DNA origami “gatta-STORM” nanorulers were purchased from Gattaquant (Grafelfing, Germany) and a sample was prepared following the manufacturer’s instructions. In brief, biotinylated bovine serum albumin (biotin-BSA; Thermo Fisher, Waltham, MA, USA; 1 mg/mL) was absorbed to a clean 35 mm no. 1.5 glass bottom dish (MatTek well; MatTek Life Sciences, Ashland, MA, USA) for 5 min then washed. Streptavidin was then applied (1 mg/mL) for 5 min, then washed with a solution of phosphate-buffered saline (PBS) plus 10 mM MgCl₂. A solution containing the biotinylated DNA origami was then applied. Samples were then washed and imaged in an imaging buffer supplemented with 10 mM MgCl₂. “gatta-PAINT” 80RG nanorulers in a sealed sample chamber were purchased from Gattaquant and imaged in the Atto655 color channel following the manufacturer’s recommendations.

Mouse primary neurons were isolated from P0 mouse pups as described previously and cultured on MatTek wells (17). On day 10 of culture (days in vitro 10), neurons were rinsed with sterile Hanks’ balanced salt solution and fixed for 10 min with prewarmed 4% PFA (Electron Microscopy Sciences, Hatfield, PA, USA) in PBS. The fixed neurons were rinsed three times with PBS and permeabilized in 0.2% Triton X-100 (MilliporeSigma, St. Louis, MO, USA) in PBS for 5 min. Neurons were then incubated in blocking buffer containing 5% BSA for 30 min, and labeled with Nup210 polyclonal antibody diluted in PBS (1:200; Bethyl Laboratories, Montgomery, TX, USA; A301-795A) overnight in 4°C. The following day, neurons were washed three times in PBS and stained with goat anti-rabbit AlexaFluor647 Fab Fragment (1:800; Jackson ImmunoResearch, West Grove, PA, USA; 111-607-003) for an hour, washed three times with PBS, then imaged.

CH27 B cells (mouse, MilliporeSigma, St. Louis, MO, USA); cat. no. SCC115, RRID:CVCL_7178), a lymphoma-derived cell line (18) were acquired from Neetu Gupta (Cleveland Clinic, OH). CH27 cells were maintained in culture as described previously (19). Cells were adhered to MatTek wells coated with VCAM following procedures described previously (20). In brief 0.1 mg/mL IgG, Fcγ specific was adsorbed to a plasma cleaned well for 30 min at room temperature. Wells were rinsed with PBS, then nonspecific binding was blocked with 2% BSA at room temperature for 10 min, followed by incubation with 0.01 mg/mL recombinant human VCAM-1/CD106 Fc chimera protein (R&D Systems, Minneapolis, MN, USA) and 0.01 mg/mL ChromPure Human IgG, Fc fragment (Jackson ImmunoResearch) for 1 h at room temperature or overnight at 4°C. VCAM-1-coated dishes were stored up to 1 week in VCAM-1 and Fc at 4°C. Immediately before plating, dishes were blocked at room temperature in 2% goat serum (Gibco, Thermo Fisher, Waltham, MA, USA) for 10 min, then cells were allowed to adhere for 15 min in medium before chemical fixation in 2% PFA and 0.2% glutaraldehyde (Electron Microscopy Sciences). F-Actin was stained by permeabilizing cells with 0.1% Triton-X-100 before incubation with 3.3 μM phalloidin-AlexaFluor647 (Thermo Fisher, Waltham, MA, USA) for at least 15 min. Phalloidin-stained cells were imaged immediately after removing label. Cells transiently expressing Clathrin-GFP were permeabilized after fixation with 0.1% Triton-X-100 followed by labeling with a single domain anti-GFP antibody (MASSIVE-TAG-Q ANTI-GFP) from Massive Photonics (Grafelfing, Germany) for 1 h at room temperature, then imaged in 0.5 nM of imaging strand in the imaging buffer supplied by the manufacturer.

Cells expressing the membrane label Src15-mEos3.2 were prepared by transiently transfecting 10⁶ cells with 1 μg of plasmid encoding Src15-mEos3.2 (N′-MGSSKSKPKDPSQRRNNNNGPVAT-[mEos3.2]-C′), which was derived from a GFP-tagged version by replacing GFP with mEos3.2 (21,22). Transfection was accomplished using Lonza Nucleofector electroporation (Lonza, Basel, Switzerland) with program CA-137 and cells were grown in flasks overnight before plating and fixation as described above.

Single-molecule imaging and localization

Imaging was performed using an Olympus IX83-XDC inverted microscope. TIRF laser angles were achieved using a 100× UAPO TIRF objective (NA = 1.50), and active Z-drift correction (Olympus America, Center Valley, PA, USA). AlexaFluor647 was excited using a 647 nm solid-state laser (OBIS, 150 mW, Coherent, Santa Clara, CA, USA) and mEos3.2 was excited using a 561 nm solid-state laser (Sapphire 561 LP, Coherent), both coupled in free space through the back aperture of the microscope. Fluorescence emission was detected on an EMCCD camera (Ultra 897, Andor, Belfast, Northern Ireland). Samples containing AlexaFluor647 were imaged in a buffer containing 100 mM Tris, 10 mM NaCl, 550 mM glucose, 1% (v/v) β-mercaptoethanol, 500 μg/mL glucose oxidase (Sigma, St. Louis, MO, USA), and 40 μg/mL catalase (Sigma), with 10 mM MgCl₂ for the DNA origami sample. Samples with mEos3.2 or DNA PAINT Atto655 probes were imaged in imaging buffer from Massive Photonics. Single-molecule positions were localized in individual image frames using custom software written in MATLAB. In most cases, peaks were segmented and fit from background corrected images, where the background was estimated as the median signal over 500 acquisition frames. Peaks were segmented using a standard wavelet algorithm (23) and segmented peaks were then fit as single emitters on GPUs using previously described algorithms for 2D (24), or as multiemitters on a CPU using the ThunderStorm ImageJ plugin (25). After localization, points were culled to remove outliers before drift correction (17). Images were rendered by generating 2D histograms from localizations followed by convolution with a Gaussian for display purposes. Rendering parameters are included in captions and typically images showing larger regions are reconstructed with large pixels and Gaussian filters (10–50 nm) while small regions are rendered with small pixels and Gaussian filters (1 and 4–10 nm, respectively). For the nanoruler samples, localizations were assigned to single fluorophores using a home-built implementation of DBSCAN (26), with $\epsilon =$ 12 nm and minPts = 15.

Evaluation of space-time autocorrelations

Space-time autocorrelations were obtained by first tabulating space and time displacements between all pairs of localizations within a specified ROI detected in a given data set. This was accomplished using a crosspairs function based on the one from the R package spatstat (27), but used here as a C routine with a MATLAB interface, as described previously (17). Lists of displacements were converted into space-time autocorrelation functions by binning in both time and space within the C routine for improved performance, followed by a normalization implemented in MATLAB that produces a value $g(r,\tau )=1$ when localizations are randomly distributed in both space and time within the specified ROI. A derivation of the form of this normalization and an explanation of how it is computed are presented in supporting material Note S1.

Estimation of $g_{LSF}\left(r,\tau \right)$ and ${\sigma }_{xy}\left(\tau \right)$

The core computations of the LSF estimation are gathered in a single MATLAB function. First, $g\left(r_i,{\tau }_j\right)$ is computed as described above, for a range of distance and time separation values. By default, $r_i,i=1,\dots ,N_r$ represent bins with bin edges from 0 to 250 nm with equal spacing of 5 nm, resulting in bin centers ranging between 2.5 and 247.5 nm, and ${\tau }_j,j=1,\dots ,N_{\tau }$ represent bins with edges that are log spaced. The lower edge of the final time-separation bin is determined by identifying the lowest τ that satisfies $g\left(r<25\text{nm},\tau \right)/g\left(r<25\text{nm},\frac{3}{4}T<\tau \le T\right)\le 1.5$, where T is the time of the image acquisition. The ${\tau }_{\max }$ reported in figures is the bin center of this final time-separation bin.

Then, $\text{Δ}g\left(r,{\tau }_j\right)=g\left(r,{\tau }_j\right)-g\left(r,{\tau }_{max}\right)$ are computed for each $\tau$, normalized by their first spatial points ($r<5\text{nm}$), and fitted to a Gaussian of the form $A\exp \left(-r^2/4{{\sigma }_{xy,j}}^2\right)$, using MATLAB’s nonlinear least-squares fitting routing fit. ${\sigma }_{xy,j}$ is reported as the estimate of ${\sigma }_{xy,j}\left({\tau }_j\right)$. Bootstrapped standard errors are determined by choosing eight subsamples of the points, each containing one quarter as many points as the full data set, and estimating ${\sigma }_{xy}{\left({\tau }_j\right)}_k$ for each subsample $k$, in the same way as for the full data set. The standard error is reported as $\frac{1}{2}std.dev.\left({\sigma }_{xy}{\left({\tau }_j\right)}_k\right)$, where the $\frac{1}{2}$ accounts for the overestimate of errors due to using 4 times fewer points.

Estimating $g_{LSF}\left(r,\tau \right)$ by grouping localizations with molecules

In simulations and DNA origami samples, localizations imaged at $x_i,y_i,t_i$ are associated with the molecules that produced them. For the nanoruler samples, localizations were assigned to single fluorophores using a home-built implementation of DBSCAN (26), with $\epsilon =$ 12 nm and minPts = 15.

We tabulate displacements between all pairs associated with the same molecule $\text{Δ}{r}_{ij}=\sqrt{\text{Δ}{x_{ij}}^2+\text{Δ}{y_{ij}}^2}$ and $\text{Δ}{t}_{ij}$. The list of all pairs is binned into 2D histograms following the same r and τ bin-edges as described for computing $g(r,\tau )$ above and are normalized by the number of pairs contributing to each bin. Distributions at each τ bin are fit to the same Gaussian form as applied to the $g_{LSF}\left(r,\tau \right)$ estimated from $\text{Δ}g\left(r,\tau \right)$.

Measuring distances between distinct molecules on the same ruler

In simulations, all localizations were associated with the molecules and rulers that produced them. In DNA origami samples, DBSCAN segmented molecules on the same ruler were identified as segments whose average localization position was within 10 nm of the expected displacement between probes on rulers specified by the manufacturer (40–60 nm for 50 nm STORM origami and 70–90 nm for 80 nm PAINT origami). We then tabulate displacements between all pairs of localizations associated with different molecules on the same ruler $\text{Δ}{r}_{ij}=\sqrt{\text{Δ}{x_{ij}}^2+\text{Δ}{y_{ij}}^2}$.

Determining the resolution with FRC

The resolution of each data set was assessed with FRC (8). To produce the FRC curves, localizations were divided into consecutive blocks of 500 frames, and these blocks were randomly placed into one of two statistically independent subsets. For the simulated and experimental DNA origami data sets, as well as the nuclear pore complex (NPC) data set, the pixel size for the FRC calculation was taken to be 5 nm, and square regions (10 μm on each side) were used as a mask. For the actin and Src15 data sets, the pixel size was 10 nm, with the mask 20 μm on each side. Twenty randomly determined repetitions of the calculation were performed for each data set.

Determining localization precision using nearest neighbor distributions

Nearest neighbors were identified in adjacent image frames using the crosspairs algorithm using a time interval of 1 frame and a distance cutoff of 100 nm. The closest nearest neighbor was identified for each molecule and included in the distribution $P\left(r_{NN}\right)$. This distribution was then fit using the MATLAB function fit to extract the localization precision (${\sigma }_{NN}$) using the functional form (7) $P\left(r_{NN}\right)=\frac{A{r}_{NN}}{2{\sigma }_{NN}^2}\exp \left\{-\frac{r_{NN}^2}{4{\sigma }_{NN}^2}\right\}+\frac{B}{\sqrt{2\pi w^2}}\exp \left\{-\frac{{\left(r_{NN}-r_o\right)}^2}{2w^2}\right\}+C$.

The second and third term correct for pairs of localizations not originating from the same molecule.

Results

Derivation of the estimated LSF

The spatial autocorrelation function describing a distribution of static molecules is given by $g_{molecules}\left(r\right)$ and is tabulated as described in Materials and methods and supporting material. This function can be divided into two components:

$$g_{molecules}\left(\overrightarrow{r}\right)=\frac{1}{\rho }\delta \left(\overrightarrow{r}\right)+g_p\left(\overrightarrow{r}\right).$$ (1)

The first term in Eq. 1 comes from counting single emitters and is a Dirac delta function ($\delta \left(\overrightarrow{r}\right)$) with magnitude equal to the inverse average density of molecules ($\rho$) over the ROI. The second term in Eq. 1 comes from correlations between distinct pairs of molecules and reports on the sample-dependent detailed structure present in the image. In the special case of complete spatial randomness, $g_p\left(\stackrel{\rightharpoonup }{r}\right)=1$. In SMLM, single emitters labeling molecules have dynamics governed by the probe photophysics, which can be described with the temporal autocorrelation function $g_e\left(\tau \right)$. Probes can remain on for multiple sequential image frames and can blink on again at a later time before eventually bleaching irreversibly (10, 11, 12). As a result, $g_e\left(\tau \right)$ is highly correlated (>1) at short time intervals and decays sharply on timescales describing the average on-time of fluorophores. This function continues to decay slowly at long τ, both because some probes tend to flicker over medium to long timescales and because some fluorophores eventually bleach. Including $g_e\left(\tau \right)$ produces the following spatiotemporal autocorrelation function for the emitting molecules:

$$g_{emitters}\left(\overrightarrow{r},\tau \right)=\frac{1}{\rho }\delta \left(\overrightarrow{r}\right)g_e\left(\tau \right)+g_p\left(\overrightarrow{r}\right).$$ (2)

In other words, the central peak due to the same fluorophore being “on” at different times inherits the dynamics of the probe, while the contributions from pairs of different molecules remains time independent. Equation 2 assumes the blinking statistics of fluorophores labeling different molecules are uncorrelated, which is why $g_e\left(\tau \right)$ multiplies only the first term.

When fluorophores are localized with finite spatial resolution, the distribution of localization errors can be described as a probability density function that characterizes the resolution of the image. This distribution induces a characteristic blurring of the true locations of the molecules, just as a conventional microscope can be thought of as convolving a true image with a PSF. By analogy, we instead call this distribution the LSF. The autocorrelation function of localizations, $g\left(\overrightarrow{r},\tau \right)$, is the autocorrelation of the emitters, $g_{emitters}\left(\overrightarrow{r},\tau \right)$, blurred (convolved) by the autocorrelation of the LSF, or $g_{LSF}\left(\overrightarrow{r},\tau \right)$. Including this factor, $g\left(\overrightarrow{r},\tau \right)$ becomes:

$$g\left(\overrightarrow{r},\tau \right)=\frac{1}{\rho }{g}_{LSF}\left(\overrightarrow{r},\tau \right)g_e\left(\tau \right)+g_{LSF}\left(\overrightarrow{r},\tau \right)\ast g_p\left(\overrightarrow{r}\right),$$ (3)

where $\ast$ indicates a convolution. The first term in Eq. 3 describes multiple observations of the same molecule and is exactly proportional to the LSF at time interval τ.

The goal of subsequent steps of this derivation is to isolate $g_{LSF}\left(\overrightarrow{r},\tau \right)$ from the first term of Eq. 3 by comparing $g\left(\overrightarrow{r},\tau \right)$ tabulated from pairs of localizations acquired at different time intervals τ. In particular, we choose a long time interval ${\tau }_{\max }$ and consider differences:

$$\text{Δ}g\left(\overrightarrow{r},\tau \right)=g\left(\overrightarrow{r},\tau \right)-g\left(\overrightarrow{r},{\tau }_{\text{max}}\right).$$ (4)

First consider the simple case where the LSF is independent of τ, $g_{LSF}(\overrightarrow{r},\tau )=g_{LSF}\left(\overrightarrow{r}\right)$. In this limit, the second term of Eq. 3 is independent of τ, so $\Delta g(\overrightarrow{r},\tau )$ is exactly proportional to $g_{LSF}\left(\overrightarrow{r}\right)$:

$$\text{Δ}g\left(\overrightarrow{r},\tau \right)=\frac{1}{\rho }\left(g_e\left(\tau \right)-g_e\left({\tau }_{max}\right)\right)g_{LSF}\left(\overrightarrow{r}\right)\propto g_{LSF}\left(\overrightarrow{r},\tau \right).$$ (5)

Thus, the difference $\text{Δ}g\left(\overrightarrow{r},\tau \right)$ can be taken as a direct measurement of $g_{LSF}\left(\overrightarrow{r},\tau \right)$.

In practice, the above assumption does not hold exactly, so we must consider the effects of time-varying $g_{LSF}\left(\overrightarrow{r},\tau \right)$. In this more general case, the above equality becomes an approximation. However, under reasonable experimental conditions, the approximation often remains quite accurate. In the following, we discuss the potential sources of error, and relevant limits under which the errors become negligible.

The first source of error in Eq. 5 under time-varying $g_{LSF}\left(\overrightarrow{r},\tau \right)$ arises because the second term of Eq. 3 is no longer independent of τ. The resulting error is given by

$$g_{LSF}\left(\overrightarrow{r},\tau \right)\ast g_p\left(\overrightarrow{r}\right)-g_{LSF}\left(\overrightarrow{r},{\tau }_{\text{max}}\right)\ast g_p\left(\overrightarrow{r}\right).$$

Note that $g_{LSF}\left(\overrightarrow{r},\tau \right)$ is a PDF, so the magnitude of this error can be at most $g_p\left(\overrightarrow{r}\right)$. As a result, the approximation is likely to be valid when $\frac{1}{\rho }\left(g_e\left(\tau \right)-g_e\left({\tau }_{\max }\right)\right)\gg g_P\left(r\right)$. In practice, we find that even samples with relatively strong structure satisfy this assumption for short $\tau$, where $g_e\left(\tau \right)$ decays rapidly. In addition, this source of error can be negligible if $g_p\left(\overrightarrow{r}\right)$ is nearly constant, as is the case in a sample with weak interactions between labeled molecules. Similarly, if the LSF only broadens slightly, so $g_{LSF}\left(\overrightarrow{r},\tau \right)\approx g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$ the error will also be negligible. This condition often holds for accurately drift-corrected images, where we find the width of the LSF to be within a few nm of the localization precision even at ${\tau }_{\max }$.

A second source of error in Eq. 5 under time-varying $g_{LSF}\left(\overrightarrow{r},\tau \right)$ comes from the first term of Eq. 3. In particular, assuming that the first source of error is negligible, Eq. 4 yields:

$$\text{Δ}g\left(\overrightarrow{r},\tau \right)\approx \frac{1}{\rho }\left(g_{LSF}\left(\overrightarrow{r},\tau \right)g_e\left(\tau \right)-g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)g_e\left({\tau }_{\max }\right)\right).$$ (6)

In principle, Eq. 6 could be used to extract $g_{LSF}\left(\overrightarrow{r},\tau \right)$ and $g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$ through fitting. In practice, we make the further approximation that $\left(g_{LSF}\left(\overrightarrow{r},\tau \right)g_e\left(\tau \right)-g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)g_e\left({\tau }_{\max }\right)\right)\approx g_{LSF}\left(\overrightarrow{r},\tau \right)\left(g_e\left(\tau \right)-g_e\left({\tau }_{\max }\right)\right)$ yielding the simple relation:

$$\text{Δ}g\left(\overrightarrow{r},\tau \right)\propto g_{LSF}\left(\overrightarrow{r},\tau \right).$$ (7)

This applies in the limit of $g_e\left(\tau \right)>>g_e\left({\tau }_{\max }\right)$ or $g_{LSF}\left(\overrightarrow{r},\tau \right)\approx g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$, but introduces some practical limitations that are discussed in detail in the next section.

Equation 7 can be used to estimate the full $g_{LSF}\left(\overrightarrow{r},\tau \right)$ from acquired localizations. To summarize the LSF using a single number, we further assume that $g_{LSF}\left(\overrightarrow{r},\tau \right)$ takes on a Gaussian form:

$$g_{LSF}\left(\overrightarrow{r},\tau \right)\propto \exp \left\{-x^2/4{\sigma }_x^2\left(\tau \right)-y^2/4{\sigma }_y^2\left(\tau \right)\right\},$$

where ${\sigma }_x\left(\tau \right)$ is the standard deviation in the $x$ direction of the distance between the true position of the molecule at time $t$ and a localization at time $t+\tau$. The extra factor of 2 in the denominator accounts for the fact that $g_{LSF}$ reports on the distribution of distances between pairs of localizations, resulting in twice the variance compared with the error in a single localization. Typically, the LSF is isotropic in the lateral dimensions, so we take ${\sigma }_{xy}:={\sigma }_x={\sigma }_y$ and compute angularly averaged correlation functions resulting in:

$$g_{LSF}\left(r,\tau \right)\propto \exp \left\{-\frac{r^2}{4{\sigma }_{xy}{\left(\tau \right)}^2}\right\}.$$ (8)

It is convenient to also define the mean-squared displacement ${\sigma }_r^2\left(\tau \right)={\sigma }_x^2\left(\tau \right)+{\sigma }_y^2\left(\tau \right)=2{\sigma }_{xy}^2\left(\tau \right)$, which accounts for errors in both dimensions. When localizations are acquired in three dimensions, the axial resolution often differs from the lateral resolution, and this component can be considered independently:

$$g_{LSF}\left(z,\tau \right)\propto \exp \left\{-\frac{z^2}{4{\sigma }_z{\left(\tau \right)}^2}\right\}.$$

We have implemented this method as MATLAB code, which is available online (28).

Practical limitations of the LSF estimate

The derivation above mathematically demonstrates why it is possible to simply isolate the autocorrelation of the LSF from the full autocorrelation of the image by tabulating the differences between measured autocorrelations obtained at different time intervals (Eq. 7). This simple method works because repeated observations of the same molecule are typically correlated in time while repeated observations of pairs of distinct molecules are uncorrelated in time. Because of this, simply subtracting observations at different time intervals results in isolating the average contribution from multiple observations of the same molecule. As mentioned above, this simple view requires a few assumptions that limit the applicability of this approach.

The main assumption used to arrive at Eq. 7 is that individual molecules on average produce localizations that are correlated in time. These correlations are expected to extend out to some finite time interval beyond which the method no longer applies because repeated observations become uncorrelated. Past studies document surprisingly long correlation times for many (d)STORM and (f)PALM probes (10, 11, 12) under a range of imaging conditions, suggesting that Eq. 7 should apply even at extended time intervals for images generated using these methods and probes. PAINT probes, which produce localizations through binding and unbinding of a probe fluorophore to a target molecule, only produce temporal correlations up until the off-rate of the specific binding interaction, since the binding of new probes from solution does not depend on the history of probe binding to a specific site (5,29). These reduced correlations contribute to the more uniform appearance of FLM images acquired using PAINT, and will also limit the applicability of this method. Conveniently, plots of $g\left(r<{\sigma }_r,\tau \right)$ capture the time interval dependence of correlated observations from single molecules ($g_e\left(\tau \right)$) up to a numerical offset, and examples showing this decay for several experiments with different fluorophores are shown in Fig. S1. These curves can be used to guide the range of $\tau$ over which Eq. 7 is expected to apply.

For the case where $g_{LSF}\left(\overrightarrow{r},\tau \right)=g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$, Eq. 7 will correctly estimate $g_{LSF}\left(\overrightarrow{r},\tau \right)$ as long as $g_e\left(\tau \right)>g_e\left({\tau }_{\max }\right)$, since the two LSFs will have the same shape in space and subtraction will not lead to distortion even when both components have similar amplitudes ($\text{Δ}{g}_e\left(\tau \right)\ll g_e\left(\tau \right)$). When $g_{LSF}\left(\overrightarrow{r},\tau \right)$ does not have exactly the same shape as $g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$, distortions can arise for small $\text{Δ}{g}_e\left(\tau \right)/g_e\left({\tau }_{\max }\right)$ that can lead to systematic errors in estimates of $g_{LSF}\left(\overrightarrow{r},\tau \right)$. These systematic distortions are demonstrated in Fig. S2 for the example of a Gaussian LSF with a standard deviation that varies with $\tau$. For cases where $g_{LSF}\left(\overrightarrow{r},\tau \right)$ broadens slightly with increasing time interval, our approach will produce a systematically narrow estimate of $g_{LSF}\left(\overrightarrow{r},\tau \right)$ for small $\text{Δ}{g}_e\left(\tau \right)/g_e\left({\tau }_{\max }\right)$. This occurs, for example, when labeled molecules diffuse over length scales comparable to the localization precision over the acquisition time, and is demonstrated on the simulated example of Fig. S3. For the purposes of this report, we do not include estimates $g_{LSF}\left(\overrightarrow{r},\tau \right)$ that may be subject to this systematic bias, using a cutoff of$\text{Δ}g\left(r<5\text{nm},\tau \right)/g\left(r<5\text{nm},{\tau }_{\max }\right)<0.5$. In principle, a user could extend the applicability of this method to larger τ by instead fitting to Eq. 6 which independently models $g_{LSF}\left(\overrightarrow{r},\tau \right)$ and $g_{LSF}\left(\overrightarrow{r},{\tau }_{\max }\right)$ or could instead tabulate $\text{Δ}g\left(\overrightarrow{r},\tau \right)$ for closely spaced τ where changes in $g_{LSF}\left(\overrightarrow{r},\tau \right)$ are expected to be more subtle.

The decay of $g_e\left(\tau \right)$ means that the signal to noise ratio of $\text{Δ}g\left(\overrightarrow{r},\tau \right)$ will degrade at longer time intervals, over which fewer correlated pairs are observed. To increase statistical stability, we group time intervals into increasingly large disjoint τ bins and estimate $g(r,\tau )$ as a weighted average. In this report, τ bin edges are log spaced to account for the exponential decay inherent in $g_e\left(\tau \right)$ and we report the average τ value of the bin, but occasionally show the full range of τ values included in the bin. We typically use the back quarter of the data set to initially tabulate $g\left(\overrightarrow{r},{\tau }_{\max }\right)$, meaning that $\frac{3}{4}{T}_{\max }<{\tau }_{\max }<T_{\max }$, where $T_{\max }$ is the acquisition time. We then identify the cutoff by finding the $\tau$ where $\text{Δ}g\left(r<5\text{nm},\tau \right)/g\left(r<5\text{nm},{\tau }_{\max }\right)$ first falls below 0.5. We then recalculate $g\left(\overrightarrow{r},{\tau }_{\max }\right)$ using this cutoff as the low $\tau$ edge of the ${\tau }_{\max }$ bin. Statistical confidence is estimated through bootstrapping and we estimate the statistical power of $\text{Δ}g\left(\overrightarrow{r},\tau \right)$ directly from $g\left(\overrightarrow{r},\tau \right)$, as described in Materials and methods.

Validation through simulation

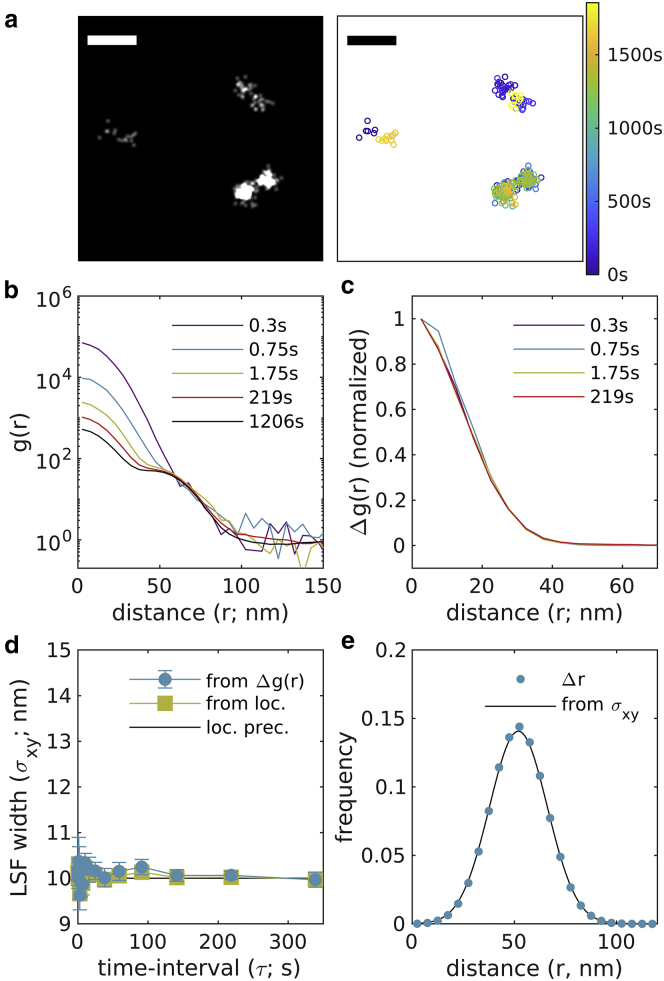
To validate this approach, we generated simulated data sets of DNA origami nanorulers in which fluorophores are separated by a fixed distance of 50 nm. Fluorophore blinking was subject to a photophysical model based on (12,15). In brief, fluorophores could exist in an “on” state, one of three dark states, or a bleached state. Transitions between states were governed by a continuous time Markov process, with transition rates roughly based on those measured in (12) but modified to reflect the experimental conditions used to obtain experimental images in this work. Nanorulers were placed randomly and uniformly with an average density of 1/μm² across a 40 by 40 μm field of view with the molecules having a localization precision of 10 nm in each lateral dimension. A total of 20,000 image frames were simulated with a frame time of 0.1 s. Fig. 1 a illustrates a small field of view containing 3 nanorulers, both as a reconstructed image and with localizations colored by time. An image showing a larger subset of the field of view is shown as Fig. S4.

Figure 1.

Validation of approach through simulation. (a) Simulations consist of randomly positioned pairs of molecules positioned 50 nm apart in random orientations. Reconstructed image (left; 1 nm pixels, 3 nm Gaussian blur) and scatterplot of localizations with color representing the observation time (right) for a small subset of the simulated plane. Scale bar, 100 nm. A reconstructed image showing a larger field of view is shown in Fig. S4. (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from simulations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=1206s\right)$ for the examples shown in (b). (d) $\text{Δ}g\left(r,\tau \right)$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the width of the LSF in each lateral dimension, which in this case is the same as the LSF width deduced by grouping localizations with their associated molecules (from loc.) and the simulated localization precision (loc. prec.) at all time intervals. Error bars represent estimates of the standard error obtained through bootstrapping. (e) The distribution of displacements between different molecules on the same ruler are well described by a model incorporating the localization precision (10 nm) and the separation distance (50 nm). To see this figure in color, go online.

Simulated localizations were subjected to a spatiotemporal autocorrelation analysis as described in Materials and methods and representative plots of the spatial component of $g(r,\tau )$ are shown in Fig. 1 b. This family of curves contains two major features: an initial peak at short displacements (r < 40 nm) arising from multiple localizations from the same molecule, and a second feature at wider radii (40 nm < r < 100 nm) arising from displacements between localizations from different molecules on the same ruler. The amplitude of the initial peak decreases with increasing τ, while the second feature is largely independent of τ. The τ-dependent component is isolated by subtracting $g(r,\tau )$ at long τ from those arising from shorter τ to obtain $\text{Δ}g\left(r,\tau \right)$ as shown in Fig. 1 c. In this simulation, there are no τ-dependent effects that would impact resolution, resulting in $\Delta g(r,\tau )$ having the same width for all τ. This is summarized by fitting $\Delta g(r,\tau )$ to the Gaussian function of Eq. 8 to extract the LSF width, ${\sigma }_{xy}$, reported in Fig. 1 d. Representative $\Delta g(r,\tau )$ with Gaussian fits are shown in Fig. S5. In this simulated example, we can associate all localizations with the molecules that produced them and can directly compute $g_{LSF}\left(r,\tau \right)$ from the relative positions of localizations originating from the same molecule as described in Materials and methods. This is followed by fitting to Eq. 8 to obtain ${\sigma }_{xy}$, which is also reported in Fig. 1 d. Finally, we tabulate displacements between all localizations originating from distinct molecules on the same ruler. The distribution of these displacements is shown in Fig. 1 e, and its properties are described by simulation parameters. The line in Fig. 1 e has a Gaussian shape with the form: $P\left(r\right)\propto \exp \left\{-{\left(r-⟨r⟩\right)}^2/4{\sigma }_{xy}^2\right\}$, where ${\sigma }_{xy}$ is the localization precision (10 nm) and $⟨r⟩$ is the average displacement between localizations originating at the ruler endpoints (52 nm). The slight bias in $⟨r⟩$ toward a value larger than the actual separation between molecules (50 nm) arises from the components of localizations that fall perpendicular to the ruler axis and always contribute positive values to the measured displacements ($\sqrt{{50}^2+2{{\sigma }_{xy}}^2}$ = 52 nm).

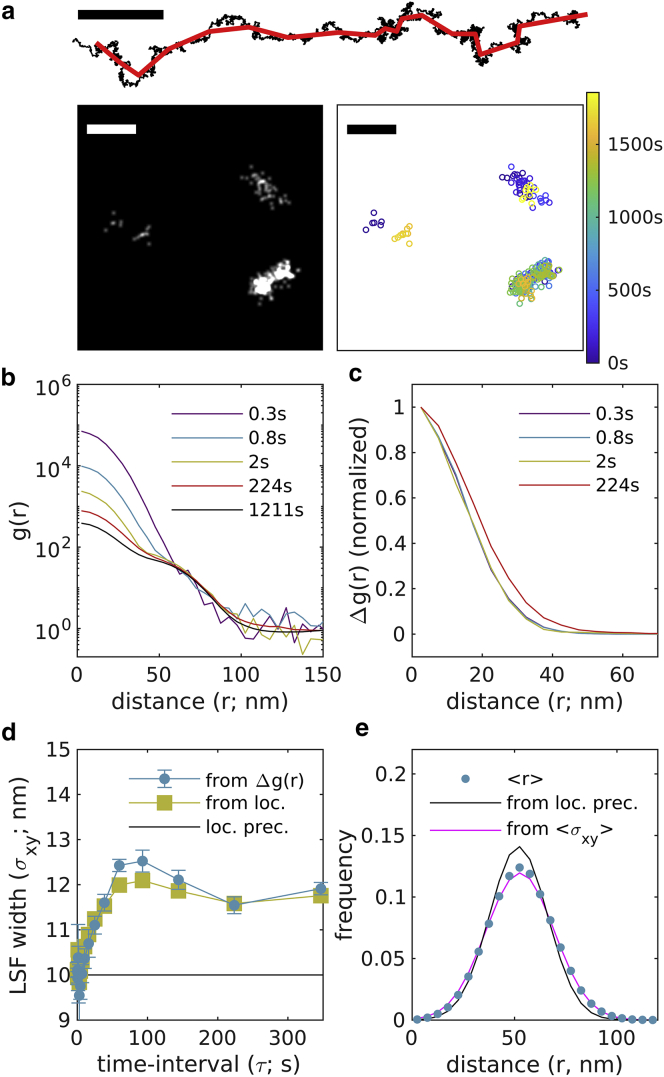
The simulation of Fig. 1 does not contain any factors that degrade image resolution over time. In Fig. 2, the same simulation is subjected to a directed drift in the x direction as well as diffusive drift in both x and y. Drift is corrected using a mean shift algorithm (17) that works by evenly dividing localizations into time-bins, then finding the displacement that minimizes the mean distance between localizations across all time-bins. The applied drift and the calculated drift correction are shown in Fig. 2 a along with the resulting image reconstruction. $g(r,\tau )$ curves over different windows in time interval (Fig. 2 b) closely resemble those shown in the static simulation, but $\Delta g(r,\tau )$ now broadens with increasing τ (Fig. 2 c). This broadening reflects a degradation of the LSF beyond the localization precision at all but the shortest time intervals and plateaus near the timescale of drift correction (Fig. 2 d). Here, the measured LSF width reaches a local maximum at a time separation somewhat smaller than the drift correction timescale, which we attribute to the drift correction algorithm itself as it is also apparent in the LSF width obtained by associating localizations with their originating molecules. Deviations from the expected distribution of pairwise distances between localizations of molecules from opposite ends of the same nanoruler also exceed those of the static case (Fig. 2 e) and are better described by a model that incorporates the measured LSF width, $⟨{\sigma }_{xy}⟩=11.8$ nm, which is determined by averaging over estimated ${\sigma }_{xy}\left(\tau \right)$ weighted by the number of pairs associated with each time interval window.

Figure 2.

Validation of approach through simulation with drift and drift correction. (a) The simulation from Fig. 1 with applied drift (black) and drift correction (red) as shown in the trajectory above. Reconstructed image (left; 1 nm pixels, 3 nm Gaussian blur) and scatterplot of localizations with color representing the observation time (right) for a small subset of the simulated plane. Scale bar, 100 nm. (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from simulations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=1211s\right)$ for the examples shown in (b). (d) $\Delta g(r,\tau )$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the width of the effective LSF in each lateral dimension. In this case, the LSF width varies with time interval, closely following the LSF width measured by grouping localizations with molecules (from loc.). Error bars represent estimates of the standard error obtained through bootstrapping. (e) The distribution of displacements between different molecules on the same ruler are well described by a model incorporating the average LSF width ($⟨{\sigma }_{xy}⟩=11.8\text{nm}$) and the known separation distance (50 nm). To see this figure in color, go online.

Observing a plateau in plots of ${\sigma }_{xy}\left(\tau \right)$ is a good indicator that the LSF estimator is generating reliable estimates, since drift correction is designed to stabilize localization error on long timescales. Fig. S3 shows an example of the same simulation with drift and drift correction, but where individual molecules are also allowed to diffuse slowly such that $g_{LSF}\left(r\right)$ broadens substantially with τ in a way that is not accounted for through drift correction. In that case, ${\sigma }_{xy}\left(\tau \right)$ increases with τ and is underestimated by$\text{Δ}g\left(r,\tau \right)$. This is a case where the approximations needed to estimate $g_{LSF}\left(r\right)$ as $\text{Δ}g\left(r,\tau \right)$ are not appropriate.

The simulated blinking dynamics of fluorophores includes a chance of photobleaching, or an irreversible transition into a dark state. In this example and in our experience in general, we find that this analysis is largely independent of photobleaching rates. This is because the normalization used to tabulate $g(r,\tau )$ accounts for any systematic reduction in the number of localizations over time. Photobleaching does reduce the number of pairs observed at large separation times, and therefore the statistical performance of the measurement.

Estimating the LSF of DNA origami data sets

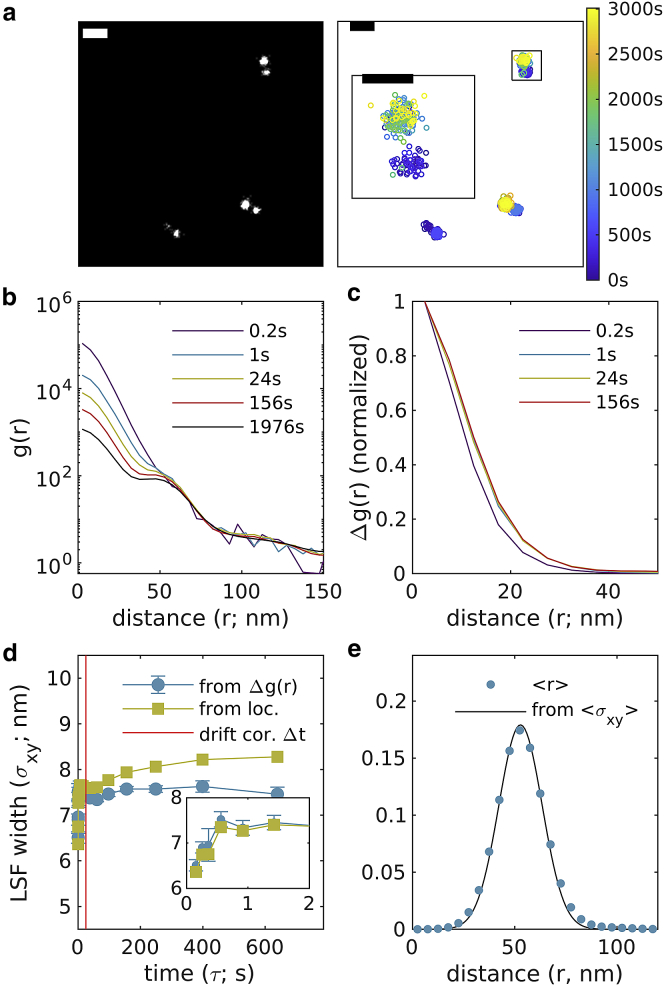
Fig. 3 demonstrates this approach on an experimental data set of DNA origami nanorulers that resemble the simulated rulers with AlexaFluor647 labeling sites separated by 50 nm. Fig. 3 a shows a small subset of the field of view of the acquired image, that was reconstructed from 29,000 image frames acquired over 53 min at a frame rate of 0.1 s, with a total of over 126,000 individual localizations. In postprocessing, a drift correction was applied with a time-window width of 25 s or 250 image frames. As in the simulated case, $g(r,\tau )$ decays at short r with increasing $\tau$ (Fig. 3 c), and $\text{Δ}g\left(r,\tau \right)$ is roughly Gaussian (Fig. 3 d). Fitting $\text{Δ}g\left(r,\tau \right)$ yields the resolution ${\sigma }_{xy}\left(\tau \right)$. As in the simulated example, the estimated LSF width is lowest at short time intervals (6.5 ± 0.1 nm) and plateaus at timescales somewhat shorter than the frequency of the applied drift correction.

Figure 3.

Experimental observations of DNA origami rulers labeled with AlexaFluor647. (a) Reconstructed image (left; 1 nm pixels, 3 nm Gaussian blur) and scatterplot of localizations with color representing the observation time (right) for a small subset of the observed plane. Scale bars, 100 nm and 50 nm (inset). A larger field of view from this image is shown in Figure S6. (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=1976s\right)$ for the examples shown in (b). (d) $\text{Δ}g\left(r,\tau \right)$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the width of the LSF in each lateral dimension which varies with time interval, closely following the LSF width measured by grouping localizations with DBSCAN segmented molecules (from loc.). Error bars represent estimates of the standard error obtained through bootstrapping. The resulting average LSF width for this image is $⟨{\sigma }_{xy}⟩=$ 7.48 ± 0.07 nm. (e) The distribution of displacements between pairs of fluorophores on the same ruler. Fitting to a Gaussian shape with width given by the measured $⟨{\sigma }_{xy}⟩$ produces $⟨r⟩=$ 52.2 ± 0.2 nm. To see this figure in color, go online.

Since the localization clouds from individual Alexa Fluor 647 molecules were visually distinct, we applied a DBSCAN segmentation algorithm (26) to associate localizations with individual molecules. From this segmentation, we tabulated the LSF width within segmented molecules (Fig. 3 d) and find good general agreement with estimates of the LSF width obtained from $\text{Δ}g\left(r,\tau \right)$ at short $\tau$, further validating this approach. At longer $\tau$, the LSF width differs somewhat by these two methods. We attribute this to inaccurate segmenting of localizations to molecules by the DBSCAN algorithm, which is expected to become more prominent at longer $\tau$ due to reduced temporal correlations of emitters. The segmented localizations are also used to tabulate the distribution of pairwise distances between different molecules on the same origami (Fig. 3 e). This distribution is well described by a model applying the measured $⟨{\sigma }_{xy}\left(\tau \right)⟩=7.5$ nm with $⟨r⟩=52.2\pm 0.2$ nm, where the error is dominated by uncertainty in the sample magnification at the camera. This yields a separation distance of 51.1 ± 0.2 nm between labels on individual rulers, which is within the manufacturer’s specifications.

We have conducted this same analysis on a similar DNA origami sample that was imaged using DNA PAINT, this time using rulers containing three collinear docking sites separated by 80 nm and summarized in Fig. 4. In contrast to the dSTORM fluorophores of Fig. 3, molecules imaged by DNA PAINT do not exhibit long timescale correlations, limiting the applicability of this method. The DNA PAINT probes used for this image do remain correlated over timescales relevant for drift correction (∼15 s), which is long enough to provide a useful estimate of image resolution. In this example, drift correction was applied with a time-window width of 11 s or 110 image frames. Pairwise distances between labels on the center and ends of the origami were measured after applying DBSCAN to segment localizations from distinct docking sites and are well described by a model applying the measured $⟨{\sigma }_{xy}\left(\tau \right)⟩=8.7\text{nm}$ with$⟨r⟩=82.5\pm 0.3\text{nm}$. This yields a separation distance of 81.6 ± 0.3 nm between the center and endpoint labels on individual rulers. Since temporal correlations of the PAINT probes used in this example only extend for a small fraction of the acquisition time (20 min), the average ${\sigma }_{xy}$ is given primarily by the value determined in the largest time interval bin ($\tau =15s$). This is because the vast majority of pairs are detected at time intervals grouped into ${\tau }_{\max }$, where we do not estimate ${\sigma }_{xy}$ but instead apply the value estimated at the previous time-window bin. The good agreement between the model and measured distributions in Fig. 3 e validates this approach, at least for this specific example where drift correction was accomplished on a shorter timescale.

Figure 4.

Experimental observations of DNA origami rulers imaged with DNA PAINT, using an Atto655 imaging strand. (a) Reconstructed image (left; 1 nm pixels, 3 nm Gaussian blur) and scatterplot of localizations with color representing the observation time (right) for a small subset of the observed plane. Scale bar, 100 nm. A larger field of view from this image is shown in Figure S7. (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=609s\right)$ for the examples shown in (b). (d) $\text{Δ}g\left(r,\tau \right)$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the width of the LSF in each lateral dimension, which varies with time interval, closely following the LSF width measured by grouping localizations with DBSCAN segmented molecules (from loc.). Error bars represent estimates of the standard error obtained through bootstrapping. The resulting average LSF width for this image is$⟨{\sigma }_{xy}⟩=$ 8.8 ± 0.2 nm. (e) The distribution of displacements between different molecules on the same ruler. Fitting to a Gaussian shape with width given by the measured $⟨{\sigma }_{xy}⟩$ produces $⟨r⟩=$ 82.5 ± 0.3 nm. To see this figure in color, go online.

Estimating the LSF from data sets of labeled structures in chemically fixed cells

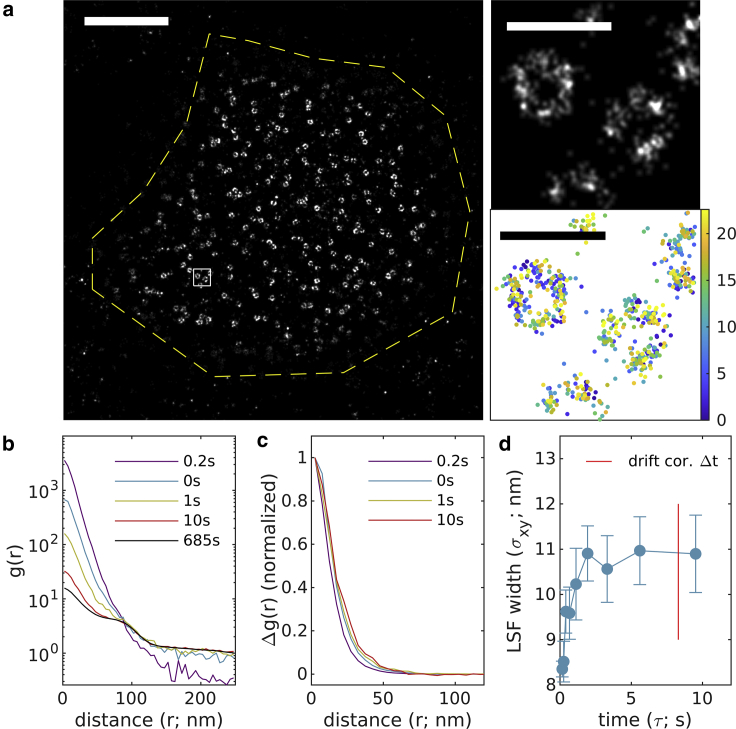
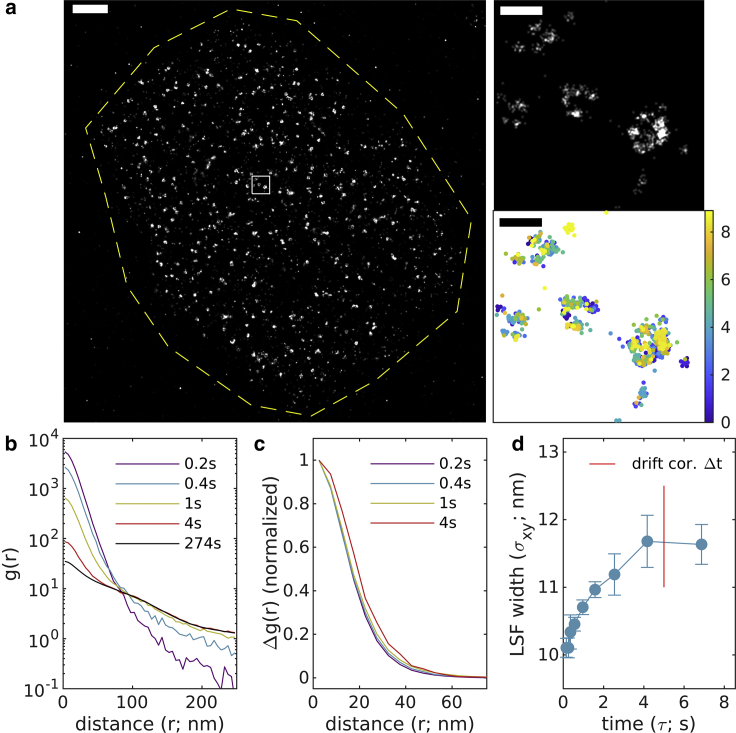
We next apply this method to image labeled structures in cells. Fig. 5 shows the method applied to NPCs within the nuclear envelope of chemically fixed primary mouse neurons. In these images, a protein component of NPCs, NUP210, was labeled with a conventional primary antibody and a Fab secondary directly conjugated to AlexaFluor647. A total of 12,500 images were acquired over 23 min with an integration time of 0.1 s and a total of 178,873 localizations detected within the masked ROI at the nuclear envelope. Drift correction was accomplished with a time-window of 8.3 s or 83 image frames. Reconstructed images of the entire nucleus and single pores are shown in Fig. 5 a along with a scatter plot demonstrating that individual NPC subunits are sampled at times throughout the observation $g(r,\tau )$ (Fig. 5 b). Curves extend to beyond 100 nm reflecting the extended structure of individual labeled NPCs, but extended structure is effectively removed by examining $\Delta g(r,\tau )$ (Fig. 5 c). Fitting $\Delta g(r,\tau )$ to a Gaussian shape quantifies image LSF width over time, which is smallest at short $\tau$ (8.3 ± 0.3 nm) and increases at larger time intervals. We estimate $⟨{\sigma }_{xy}⟩$ to be 10.9 ± 0.8 nm.

Figure 5.

Experimental observations of nuclear pore complexes within primary mouse neurons, antibody-labeled with AlexaFluor647. (a) (Left) Reconstructed image (10 nm pixels, 10 nm Gaussian blur) with yellow dashed line indicating the region of interest interrogated. (Right) A magnified subset from the white square region of larger image (1 nm pixels, 4 nm Gaussian blur) along with a scatterplot of localizations with color representing the observation time. Scale bars, 2 μm (left) and 200 nm (right top and bottom). (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=685s\right)$ for the examples shown in (b). (d) $\Delta g(r,\tau )$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the LSF width in each lateral dimension. Error bars represent estimates of the standard error obtained through bootstrapping. The average LSF width for this image is $⟨{\sigma }_{xy}⟩=$ 10.9 ± 0.8 nm. To see this figure in color, go online.

Fig. 6 shows a similar class of cellular structure imaged using DNA PAINT. In this example, clathrin-gfp is transiently expressed in CH27 cells then labeled post fixation with an anti-GFP nanobody conjugated to an ssDNA docking strand. Cells are then imaged in the presence of a complementary imaging strand labeled with Atto 655. Similar to the origami DNA PAINT sample of Fig. 4, temporal correlations from single molecules remain for short to medium timescales (∼8 s), allowing for accurate estimation of LSF broadening due to drift and drift correction. Here, we estimate the average LSF width $⟨{\sigma }_{xy}⟩$ to be 11.6 ± 0.3 nm.

Figure 6.

Experimental observations of clathrin-coated pits within CH27 B cells, imaged using a nanobody-coupled Atto655 DNA-PAINT scheme. (a) (Left) Reconstructed image (16 nm pixels, 20 nm Gaussian blur) with yellow dashed line indicating the region of interest interrogated. (Right) A magnified subset from the white square region of larger image (1 nm pixels, 4 nm Gaussian blur) along with a scatterplot of localizations with color representing the observation time. Scale bars, 2 μm (left) and 200 nm (right top and bottom). (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=274s\right)$ for the examples shown in (b). (d) $\Delta g(r,\tau )$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the LSF width in each lateral dimension. Error bars represent estimates of the standard error obtained through bootstrapping. The average resolution for this image is $⟨{\sigma }_{xy}⟩=$ 11.6 ± 0.3 nm. To see this figure in color, go online.

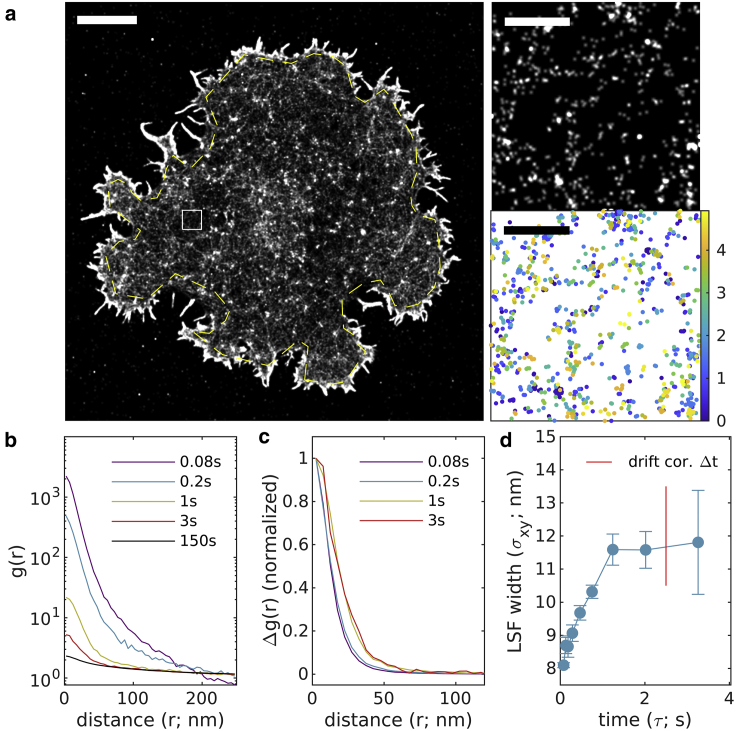
Fig. 7 shows the method applied to an image of F-actin staining by phalloidin-AlexaFluor647 in chemically fixed CH27 B cells adhered to a glass surface decorated with VCAM. For this sample, 5000 images were acquired over 4.9 min with an integration time of 0.05 s and a total of 302,681 localizations within the masked ROI. Drift correction was accomplished with a time-window of 2.5 s or 50 image frames. Unlike Figs. 5 and 6, where labels decorate isolated structures scattered over a surface, this reconstructed image of F-actin is more space filling, making up a web of fibers that extend across the entire ventral cell surface (Fig. 7 a). This extended structure can be detected in $g(r,\tau )$ (Fig. 7 b) as increased intensity in the tail that extends to large separation distances for curves generated at all τ. This large-scale structure is effectively removed in $\text{Δ}g\left(r,\tau \right)$ (Fig. 7 c) allowing for a determination of the LSF width over a range of timescales as shown in Fig. 7 d. In this example, the ROI was drawn within the cell boundary to minimize the intensity of $g_p\left(r\right)$ which allows for accurate estimation of $g_{LSF}\left(r,\tau \right)$ out to longer time intervals. This is because the amplitude of $g\left(r,{\tau }_{\max }\right)$ includes contributions from $g_p\left(r\right)$, while the amplitude of $\text{Δ}g\left(r,\tau \right)$ only depends on $g_e\left(r\right)$, therefore $\text{Δ}g\left(r<25\text{nm},\tau \right)/g\left(r<25\text{nm},{\tau }_{\max }\right)$ will remain larger than the cutoff over a wider range of $\tau$. The estimate for $⟨{\sigma }_{xy}⟩$ is 11.8 ± 1.5 nm.

Figure 7.

Experimental observations of F-actin on the ventral surface of a CH27 B cell using phalloidin-AlexaFluor647. (a) (Left) Reconstructed image (50 nm pixels, 50 nm Gaussian blur) with yellow dashed line indicating the region of interest interrogated. (Right) A magnified subset from the white square region of larger image (1 nm pixels, 10 nm Gaussian blur) along with a scatterplot of localizations with color representing the observation time. Scale bars, 5 μm (left) and 500 nm (right top and bottom). (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=150s\right)$ for the examples shown in (b). (d) $\text{Δ}g\left(r,\tau \right)$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the LSF width in each lateral dimension. The timescale of the drift correction is shown in red. Error bars represent estimates of the standard error obtained through bootstrapping. The average resolution for this image is $⟨{\sigma }_{xy}⟩=$ 11.8 ± 1.5 nm. To see this figure in color, go online.

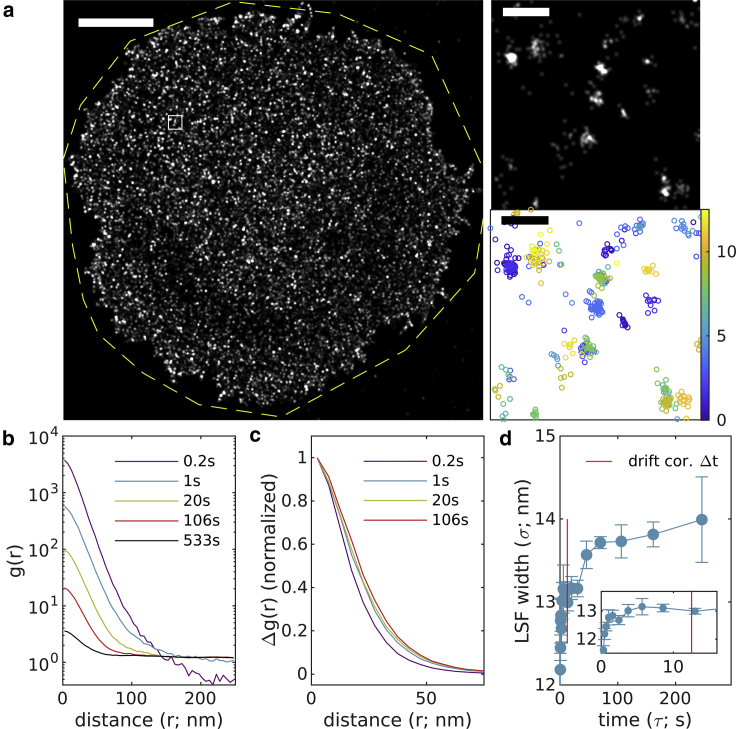
As a final demonstration, Fig. 8 shows the method applied to an image of Src15-mEos3.2, a myristoylated peptide bound to the inner leaflet of the plasma membrane and directly conjugated to the photoswitchable protein fluorophore mEos3.2. This peptide uniformly decorates the ventral surface of a chemically fixed CH27 B cell adhered to a glass surface decorated with VCAM, as seen in the reconstructed image of Fig. 8 a. For this sample, 7000 images were acquired over 12.7 min with an integration time of 0.1 s and a total of 240,503 localizations. Drift correction was accomplished with a time-window of 12.5 s or 125 image frames. mEos3.2 exhibits different blinking dynamics than AlexaFluor647, with some probes exhibiting correlated blinking on long timescales. This can be seen in plots of $g(r,\tau )$ that take long timescales to decay (Fig. 8 b). Again, $\text{Δ}g\left(r,\tau \right)$ curves isolate the initial peak, allowing for the quantification of the LSF width. In this example, the slow decay of $g\left(r<25\text{nm},\tau \right)$ with τ allows for estimation of ${\sigma }_{xy}$ out to large time intervals. The estimate for $⟨{\sigma }_{xy}⟩$ is 13.7 ± 0.2 nm.

Figure 8.

Experimental observations of membrane anchor peptide Src15-mEos3.2 on the ventral surface of a CH27 B cell. (a) (Left) Reconstructed image (50 nm pixels, 50 nm Gaussian blur) with yellow dashed line indicating the region of interest interrogated. (Right) A magnified subset from the white square region of larger image (1 nm pixels, 6 nm Gaussian blur) along with a scatterplot of localizations with color representing the observation time. Scale bars, 5 μm (left) and 200 nm (right top and bottom). (b) Autocorrelations as a function of displacement $g(r,\tau )$, tabulated from localizations for time interval windows centered at the values shown. (c) $\text{Δ}g\left(r,\tau \right)=g\left(r,\tau \right)-g\left(r,{\tau }_{\max }=533s\right)$ for the examples shown in (b). (d) $\text{Δ}g\left(r,\tau \right)$ are fit to $\text{Δ}g\left(r,\tau \right)\propto \exp \left\{-r^2/4{\sigma }_{xy}^2\right\}$ to extract the LSF width in each lateral dimension. The timescale of the drift correction is shown in red. Error bars represent estimates of the standard error obtained through bootstrapping. The average resolution for this image is $⟨{\sigma }_{xy}⟩=$ 13.7 ± 0.2 nm. To see this figure in color, go online.

Comparison with other measures of image resolution

The data sets interrogated in Figs. 1, 2, 3, 4, 5, 6, 7, and 8 were also subjected to other methods that report on image resolution and results are summarized in Table 1. These include the FRC (8,9), errors returned directly from fitting localizations (Cramer-Rao lower bound or CRLB of the variance of a maximum likelihood estimator (24,30)), and using the nearest neighbor distribution in adjacent frames (nearest neighbor-based analysis, or NeNA (7)).

Table 1.

Summary of values obtained for several resolution measures for the data sets shown in figures

Data set	LSF (from $\Delta g(r,\tau )$)		LSF (from segments)		FRC	CRLB		NeNA
	${\sigma }_{xy}\left({\tau }_{frame}\right)$	$⟨{\sigma }_{xy}⟩$	${\sigma }_{xy}\left({\tau }_{frame}\right)$	$⟨{\sigma }_{xy}⟩$		Peak	Avg
Fig. 1	10.1 (0.2)	10.02 (0.08)	10.1	10.0	30 (1)	N/A		10.0
Fig. 2	10.1 (0.1)	11.79 (0.07)	10.1	11.5	35 (1)	N/A		10.0
Fig. 3	6.5 (0.1)	7.48 (0.07)	6.4	8.1	20 (1)	6.3	9.0	6.7
Fig. 4	6.78 (0.02)	8.8 (0.2)	6.8	9.7	27 (1)	6.8	7.8	6.8
Fig. 5	8.3 (0.3)	10.9 (0.8)	N/A N/A N/A N/A		35 (1)	5.6	9.5	7.8
Fig. 6	10.1 (0.1)	11.6 (0.3)			48 (2)	10.9	14.1	9.3
Fig. 7	8.1 (0.1)	11.8 (1.5)			285 (6)	N/A		7.5
Fig. 8	11.0 (0.1)	13.7 (0.2)			59 (6)	9.9	14.2	9.9

All units are nm and errors, when evaluated, are included in parenthesis. LSF widths are estimated from $\text{Δ}g\left(r,\tau \right)$ and by associating localizations with molecules (from segments, not possible for cellular images). ${\sigma }_{xy}\left({\tau }_{frame}\right)$ is the LSF width for $\tau$ close to the frame time (${\tau }_{frame}$) and $⟨{\sigma }_{xy}⟩$ is the LSF widths averaged over all $\tau$. FRC are values obtained using the FRC. Full FRC curves are included in Fig. S8. CRLB values describe features of the distribution of Cramer-Rao lower bounds returned by the fitting procedure for data sets processed without background subtraction. Full distributions and ${\sigma }_{xy}\left(\tau \right)$ estimated from these differently processed images are included in Fig. S9. NeNA are obtained by fitting nearest neighbor distributions from localizations in adjacent frames. Distributions and fits are included in Fig. S9.

The FRC method involves reconstructing images and quantifying them in Fourier space, identifying the highest frequency signals that exceed some predetermined noise threshold, as illustrated in Fig. S8. As a result, the resolution values returned by the FRC algorithm depend on the localization accuracy of single emitters but also the structure present in images and the spatial sampling of that structure. Because of this, the FRC resolutions reported in Table 1 do not trend systematically with LSF widths extracted through $\text{Δ}g\left(r,\tau \right)$, as these report on the localization accuracy alone. The FRC method is sensitive to factors that erode the LSF over time, as indicated by the larger value generated from the simulated data set with drift and imperfect drift correction (Fig. 2; 35 nm) as compared with the simulation without drift (Fig. 1; 30 nm). The FRC is also highly dependent on the types of structures imaged, returning a very large value for the data set containing F-actin localizations (Fig. 7; 285 nm) even though the LSF width estimate from $\text{Δ}g\left(r,\tau \right)$ is similar to the other samples imaged (11.8 nm). This is because this data set contains the most space-filling structure so there is less signal at high spatial frequencies, and because this structure is less spatially sampled than the other data sets shown. We also note that long blinking time correlations can lead to artificially low FRC resolution values (8), whereas the LSF width estimate is dependent on these time correlations to achieve accurate results.

The fitting algorithms used return estimated localization precisions for each fit, known as the CRLB. These error estimates are obtained by applying a model that incorporates photon counting statistics, the Gaussian shape of the PSF, and specifics of the camera, such as its gain and offset. The accuracy of the error estimates depends in turn on the accuracy of the assumptions used to build the fitting model. While it is possible to achieve accurate error estimates with CRLBs (24), we find that factors, such as imperfect gain calibration, read noise, and nonuniform background fluorescence, frequently lead to imperfect error estimates in realistic experimental conditions. Our typical imaging processing pipeline involves a preprocessing step in which the image background is estimated then subtracted from raw image frames. The mean of the background on each fitting region is added back to that region, to approximately reproduce the appropriate counting statistics. Since this background subtraction is not incorporated into the model used to estimate errors, the values returned by the fitting algorithm are inaccurate. The values reported in Table 1 are obtained by re-fitting the data set without background subtraction, leading to somewhat different values of ${\sigma }_{xy}\left(\tau \right)$ as shown in supporting material Fig. S9. For each data set, there is a broad distribution of errors peaked at a value close to the LSF width estimated from $\text{Δ}g\left(r,\tau \right)$ at the shortest time interval interrogated (${\sigma }_{xy}\left({\tau }_{frame}\right)$). This distribution extends asymmetrically to larger errors, biasing the average error to larger values. We speculate that the average error from fits differs from that estimated by $\text{Δ}g\left(r,\tau \right)$ at short $\tau$ due to simplifying or inaccurate assumptions in the model employed by the fitting algorithm. It is also possible that larger errors originate from localizations that are not correlated in time and therefore do not contribute to the estimate from $\text{Δ}g\left(r,{\tau }_{frame}\right)$.

A third method uses the distribution of nearest neighbor distances between probes imaged in adjacent frames to estimate the average localization precision through fitting (supporting material Fig. S10) (7). This method makes the often valid assumption that the vast majority of neighbor localizations in adjacent frames arise from the same labeled molecule, therefore this distribution reports on the accuracy of localization at short time intervals. As expected the localization precision reported by the nearest neighbor distribution method is in good general agreement for the LSF width estimated from $\Delta g(r,\tau )$ at the shortest time interval interrogated (${\sigma }_{xy}\left({\tau }_{frame}\right)$), especially for data sets of well-separated molecules (Figs. 1, 2, 3, and 4). For images of cellular structures, we find a slight bias of the NeNA estimate toward smaller values than those estimated from $\Delta g(r,\tau )$. In these samples, a larger fraction of nearest neighbors originate from different molecules, and we speculate that the correction terms used to fit these additional neighbors contribute to this bias. Finally, we note that the NeNA estimates do not capture broadening of the LSF by factors that erode localization precision over time. This is expected since only nearest neighbors from adjacent frames are incorporated in the analyzed distributions.

Conclusions

Here, we present a method to estimate the LSF of an SMLM measurement directly from acquired localizations, relying on a few reasonable assumptions. The basic method is validated through simulations and demonstrated using experimental data of three commonly used localization microscopy probes. The described method performs best when used alongside fluorophores that exhibit blinking dynamics that remain correlated in time out to timescales relevant to sources of error present in the imaging experiment. The width of the LSF, here reported by fitting to a Gaussian shape, directly reports on how accurately the positions of molecules are recorded at the end of an experimental and analytical pipeline, and can be used to optimize imaging protocols or assist in the interpretation or further processing of imaged structures.

Directly measuring the LSF allows experimenters to validate and optimize imaging and processing methods, which can be difficult to accomplish using existing metrics of image resolution. For example, while commonly used fitting algorithms return localization precisions, these estimates are only valid when raw image frames are fit, prohibiting the use of preprocessing steps, such as filtering or background subtraction. In contrast, the FRC resolution metric can be used to compare processing steps accomplished on the same set of observations, but variation across samples can be hard to interpret since this measure depends on the LSF, the sampling of the image, and the types of structures being imaged. A distinct advantage of the LSF estimate described here is that it directly reports on how accurately one can measure distances between localized molecules in an image. We expect this method to be useful when interpreting experiments that involve the measurement of distances between localizations in images, for example, in nanometer precision distance measurement methods (31), where an accurate estimate of the localization error is essential. We also expect it to be useful in the interpretation of spatial auto- or cross-correlation analysis, which reports on the statistical distribution or codistribution of labeled components (6,32,33).

The values obtained using the described method depend on long timescale correlations of fluorescent probes used for imaging. For the examples shown, we find that it is most important to characterize resolution lost on timescales shorter than the timescale of drift correction, which appears to be the most important source of time-dependent degradation of the LSF in these cases. Fortunately, numerous methods exist to correct for rigid drift on timescales relevant to the temporal correlations of many SMLM probes (34, 35, 36, 37, 38, 39, 40, 41), suggesting that the method presented in this report is broadly applicable for a range of experimental conditions. Apart from drift, the estimated LSF is also sensitive to other time-dependent sources of error (or their absence). For example, a recent report observes residual motions of fluorescent labels in fixed samples, which would appear in the LSF as a degradation of LSF width over the timescale of the relevant motions (14).

The reported method estimates resolution by fitting the estimated LSF at each time interval probed to a Gaussian shape, followed by a weighted average to extract the estimated error of the average localization in an image. This approach is convenient because the resolution is summarized as a single number. However, it is possible to extract more detailed information about the LSF by not averaging over angles, or by loosening the assumption of a Gaussian shape. Fig. S11 shows the autocorrelation of the LSF, $g_{LSF}\left(\overrightarrow{r},\tau \right)$, for the NPC data set of Fig. 5, expanded in x, y, and $\tau$. Fig. S12 shows the weighted time average $⟨g_{LSF}⟩:={⟨g_{LSF}\left(\overrightarrow{r},\tau \right)⟩}_{\tau }$ for the six data sets of Figs. 3, 4, 5, 6, 7, and 8, with weights given by the observed number of localization pairs separated by each time delay $\tau$. Beyond quantifying resolution, we anticipate that the LSF could prove useful for other purposes, such as deconvolution of reconstructed images or spatial correlation functions, or as an input to clustering algorithms or other analysis tools.

Author contributions

T.R.S., F.J.F., and S.L.V. developed the method. T.R.S. and S.L.V. developed the analysis code and performed the analyses, with help from F.J.F. T.R.S., F.J.F., and S.L.V. developed the simulated data. S.L.V. imaged the nanoruler samples, and the clathrin, actin, and Src15 samples. The Src15 and clathrin samples were prepared by E.R.S. and the actin sample was prepared by J.C.F.-N. NPC sample preparation and imaging was carried out by S.K. S.L.V. and T.R.S. wrote the text in consultation with the other authors.

Editor: Amy Palmer.

Supporting citations

References (8,42, 43, 44) appear in the supporting material.