Abstract
Scattering-assisted synthesis of broadband optical pulses is recognized to have a cross-disciplinary fundamental and application importance. Achieving full-waveform synthesis generally requires means for assessing the instantaneous electric field, i.e., the absolute electromagnetic phase. These are generally not accessible to established methodologies for scattering-assisted pulse envelope and phase shaping. The lack of field sensitivity also results in complex indirect approaches to evaluate the scattering space–time properties. The terahertz frequency domain potentially offers some distinctive new possibilities, thanks to the availability of methods to perform absolute measurements of the scattered electric field, as opposed to optical intensity-based diagnostics. An interesting conceptual question is whether this additional degree of freedom can lead to different types of methodologies toward wave shaping and direct field-waveform control. In this work, we theoretically investigate a deterministic scheme to achieve broadband, spatiotemporal waveform control of terahertz fields mediated by a scattering medium. Direct field access via time-domain spectroscopy enables a process in which the field and scattering matrix of the medium are assessed with minimal experimental efforts. Then, illumination conditions for an arbitrary targeted output field waveform are deterministically retrieved through numerical inversion. In addition, complete field knowledge enables reconstructing field distributions with complex phase profiles, as in the case of phase-only masks and optical vortices, a significantly challenging task for traditional implementations at optical frequencies based on intensity measurements aided with interferometric techniques.
Keywords: THz imaging, scattering media, THz wave control, spatiotemporal focusing, coherent transfer matrix
Introduction
The propagation of waves in a scattering medium results in complex space–time interference patterns, i.e., in a complex time- and position-dependent response at the output.1,2 These phenomena are ubiquitous features in the physics of random wave propagation and significantly impact applications in several domains ranging from electromagnetic to acoustic, mechanical, and matter waves.2,3 For instance, in optical imaging, random propagation of light rapidly reduces the image fidelity in deep biological tissue characterization.4 As such, the performance of state-of-the-art microscopes is traditionally affected by the ineliminable dynamical turbidity in the samples.5,6
Although light scattering is usually considered an impediment, it is not necessarily accompanied by an irreversible loss of information.7 By leveraging this principle, researchers have recently developed a broad range of wavefront-shaping techniques to control complex light propagation through a scattering medium.8,9 The basic principle is to spatially modulate the wave impinging onto the medium to harness the scattering-induced amplitude and phase distortions. Recently, various approaches toward optical wavefront compensation based on feedback,10 guide stars,11 and memory effect12 have been demonstrated in different disciplines. These methodologies have enabled the manipulation of scattered waves for refocusing and imaging applications. Although approaches based on the iterative optimization of the scattered field rely on technically simple implementations, they fundamentally operate without direct knowledge of the scattering medium. As such, a specific optimization process provides little clues for a different one, and convergence is usually established solely by the inability to reduce an error function further. Deterministic approaches overcome this limitation. They rely on the knowledge provided by measuring the optical transfer matrix of the medium.13,14 Deterministic methods first measure the scattered light field corresponding to different sets of amplitude15,16 or phase17,18 illumination patterns (preferably forming an orthogonal set). The measurements are then combined to achieve a single-step illumination retrieval for a desired optimized wavefront through numerical inversion.
Challenges of Field-Wave Synthesis Using Random Media
Within the process of exploiting random media for space–time wave synthesis, one can argue that the knowledge of the transmission matrix is insufficient. While the transmission matrix components can be retrieved via complex spectral interferometry approaches, a full spatiotemporal synthesis requires prior knowledge of the source. If the absolute phase profile of the source pulse is not known, its effect on the scattered field is also unknown.
Interestingly, when the detection can resolve the instantaneous field dynamics for a large set of spatially modulated fields, one can trivially target a new scattered waveform as a simple combination of the field scattered by different illuminations without directly referring to the scattering matrix. Indeed, powerful wave-synthesis approaches in optics do not generally rely upon absolute phase knowledge.18 This rationale, for example, is one of the critical accelerating factors for optical frequency combs technology.19 Conversely, persuasive, popular nonlinear pulse diagnostics (e.g., FROG or SPIDER) do not provide access to the instantaneous field.20−22
Full Time-Domain Field Approach
The ability to perform a complete time-domain detection brings a conceptual difference: by introducing a sparse-light modulation (as in the practice of random media functionalization) for each spatially orthogonal illumination pi, one can detect the corresponding space–time waveform Ei+ (xo,t). These independently transmitted waveforms can, in principle, be used to decompose any desired space–time waveform ET+ (xo, t) at the output as a linear superposition
| 1 |
where ci are complex-valued expansion coefficients. Once one determines the set of ci, experimentally achievable, this can provide access to the spectrum of available waveforms. While this approach does not require specific access to the source waveform, the latter is, however, trivially accessible via time-sensitive detection and would grant access to the scattering matrix.
In this context, terahertz time-domain spectroscopy (THz-TDS) is a mature and established technique capable of fully resolving the electric-field oscillations in a broadband pulse,23 i.e., providing full knowledge of the complex spectral field.24 The scientific question is whether THz-TDS can be exploited to develop a deterministic approach to waveform synthesis (closely related to time-reversal methods,25−27 ultrasound, or radiofrequency approaches28,29). The idea is to extract sufficient information to obtain access to any scattering-allowed output field. The large relative THz bandwidth available in TDS embodiments (normally exceeding a decade) allows easily spanning a wide range of single and multiple scattering regimes for a given sample.30,31 On the practical side, the relatively large wavelength of THz waves (spanning from roughly 30 μm to 3 mm) suggests that the typical subwavelength scales of scattering phenomena are significantly more accessible in experimental platforms when compared to optical embodiments.32−34
A general downside in implementing THz wavefront control methods is, however, the limited availability of wavefront-shaping devices.35,36 In addition, the use of diffraction-limited systems at long wavelengths (which fixes the pattern resolution37,38) is undesirable because the experimental setting usually does not involve samples several orders of magnitude larger than the wavelength, trivial conditions in optics. This results in a relatively small number of modes that can be independently excited in a scattering structure with far-field illumination.39 Very recently, the nonlinear conversion of structured optical beams has emerged as a promising approach toward deeply subwavelength spatial light modulation (SLM) of THz waves.40,41 The combination of nonlinear THz pattern generation and time-resolved field detection, in particular, has enabled the development of hyperspectral THz imaging with deep subwavelength imaging resolution.42 In essence, placing an object in the near-field of a nonlinear optical-to-THz converter makes it possible to produce terahertz illumination patterns with fine spatial features approaching the optical (i.e., the pump) diffraction limit.
In this work, we explore this framework in connection with scattering-assisted waveform synthesis, introducing the field equivalent of the traditional spatiotemporal focusing and image retrieval. We explore scenarios extremely challenging in optics, which include retrieval of field distributions with complex phase profiles, such as phase-only masks and optical vortices. In our approach, we expand the complex-valued, coherent transfer matrix of the scattering medium using an orthogonal Walsh–Hadamard decomposition of near-field THz illumination.43 We leverage this knowledge to perform a direct single-step inversion using a constraint least-square optimization approach compatible with realistic experimental conditions.44
Methods
Model Definition and Simulation Setup
We define the input/output field relation in terms of an impulse response Tx (xo, x′, t, t′),45 as
| 2 |
where E– and E+ denote the spatiotemporal electric-field distribution just before and after the scattering medium. To lighten the notation, we define xo and x′ as the one-dimensional representation of the input and output planes, respectively. In the frequency domain ω, eq 2 reads
| 3 |
where Ẽ+ (xo, ω) and Ẽ– (x′, ω) are the time-Fourier transforms of the input and output fields.
Following
standard approaches, we rewrite eq 3 in a discrete scalar transfer matrix formalism, where
the response of the scattering medium for each incident frequency
is described by an M × N field-based,
random transmission matrix Tmn ∈  M×N.46 We divide the output and input
planes into M and N spatial independent
segments (corresponding, e.g., to the physical pixels on the input
wavefront-shaping and output imaging devices) and K spectral modes, a representation that is well-suited for experiments.
In the discrete coordinates, the transfer matrix is an N × M × K three-dimensional
matrix defined as Tmnk = Tmn(ωk). For a given kth frequency ωk, the
relationship between the THz fields Em+ (ωk) and En (ωk) at the nth input and mth output pixels reads
M×N.46 We divide the output and input
planes into M and N spatial independent
segments (corresponding, e.g., to the physical pixels on the input
wavefront-shaping and output imaging devices) and K spectral modes, a representation that is well-suited for experiments.
In the discrete coordinates, the transfer matrix is an N × M × K three-dimensional
matrix defined as Tmnk = Tmn(ωk). For a given kth frequency ωk, the
relationship between the THz fields Em+ (ωk) and En (ωk) at the nth input and mth output pixels reads
| 4 |
where we considered a coherent transfer matrix defined as
| 5 |
with amn(ω) and bmn(ω) random Gaussian variables with zero mean, and standard deviation σ = 1/2.47 The 1/N normalization factor ensures that, on average, the power transmitted by the TM is roughly half of the incident power. To introduce a controllable spectral correlation in the new model, we applied a Gaussian filter of width Δωc to the real and imaginary part of the transfer matrix.46,48−50 As illustrated in Figure S1, we verified that the introduction of a spectral correlation does not affect the statistical properties of the transfer matrix elements for each individual frequency. The spectral correlation is directly associated with the sample properties and inversely proportional to the Thouless time (corresponding to the average confinement time of the field in the medium).49,50 In the presence of broadband illumination, the spectral correlation bandwidth Δωc is of critical importance, as it determines the total number of accessible spectral modes within the illumination bandwidth.9,39,51 In our case, we convolve a white-noise distribution with a Gaussian filter with a standard deviation of Δνc = Δωc/2π = 150 GHz along the frequency axis to impose a desired spectral correlation in the transfer matrix elements. Further details on our particular choice of parameters are included in Supporting Information Note 1.
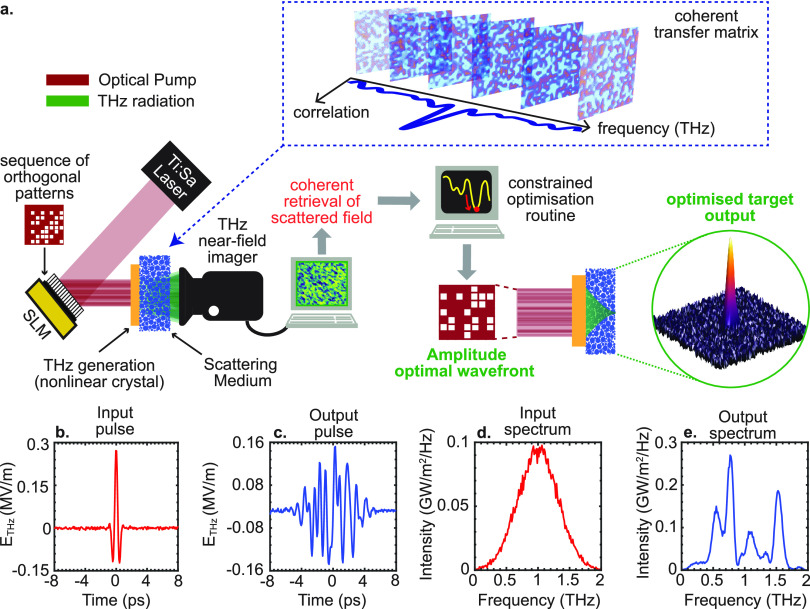
Figure 1a provides a conceptual overview of the THz-TDS experimental configuration we referenced in our modeling. An optical spatial light modulator (SLM) impressed a desired spatial pattern on an ultrafast optical field (λ = 800 nm). The optical pattern is converted to a THz structured field via a nonlinear crystal, as discussed in ref (41). Without loss of generality, we assume a quadratic χ(2) optical rectification process (e.g., ZnTe) that converts the optical intensity wavefront Ioptical (x′) to a THz wavefront ETHz (x, t) as follows
| 6 |
where χ(2) is the second-order susceptibility of the nonlinear crystal. With this position, the THz field impinging on the scattering medium is defined in the frequency domain as Ẽ– (x′, ω) = Ioptical (x′) f(ω), where f(ω) is the spectrum of the THz pulse. Our scheme requires controlling the optical intensity distribution impinging on the nonlinear crystal. This could be easily achieved in experiments through an amplitude SLM (e.g., a Digital Micromirror Device or DMD)41,52 or phase-only SLMs combined with interferometric techniques.53 The THz pattern impinges upon the scattering medium and produces a complex, time-dependent interference pattern at the output. Finally, a TDS image of the scattered THz wave is collected through a parallel, near-field imaging scheme based on electrooptical sampling.54 To assess the robustness of our numerical approach to experimental noise, we performed the theoretical analysis in this manuscript by assuming a 40 dB signal-to-noise ratio (SNR) per pixel at the detection. With this assumption, the THz pulse contains a white-noise term that is compatible with the experimental conditions. Such a relative low noise can be easily achieved in experiments based on electrooptic detection using balanced detectors of the THz field-induced birefringence in a nonlinear crystal.55 In Figure 1b–e, we show an illustrative THz transmitted field as a function of the spatial and spectral coordinates as obtained for plane wave illumination and detected in a single pixel at the output. The temporal profile of the pulse is significantly broadened (Figure 1c), and the peak field is attenuated. When moving to the spectral domain (Figure 1e), the transmitted THz field is characterized by a random modulation of its spectrum as a consequence of interference and dispersion effects induced by multiple scattering.
Figure 1.
Schematic of experimental-driven methodology (a) Conceptual overview of methodology, including the nonlinear conversion of optical patterns to THz structural waves and the retrieval of transmission properties of the scattering medium defined in terms of a coherent transfer matrix. The full knowledge of the coherent transfer matrix retrieved using an orthogonal set of patterns can be used to achieve scattering-assisted focusing at the output of the scattering medium. (b) Input THz pulse electric-field profile. (c) Scattered THz pulse collected at a generic mth output pixel. (d) Intensity spectral density of the input THz field. (e) Intensity spectral density of the scattered THz pulse as collected at a generic mth pixel. In our simulations, we considered a 1 nJ THz pulse of duration 250 fs at the input with 40 dB SNR per pixel. The 6.4 × 6.4 mm2 sample illumination area is spatially sampled at 200 μm resolution, corresponding to a number of pixels of 32 × 32.
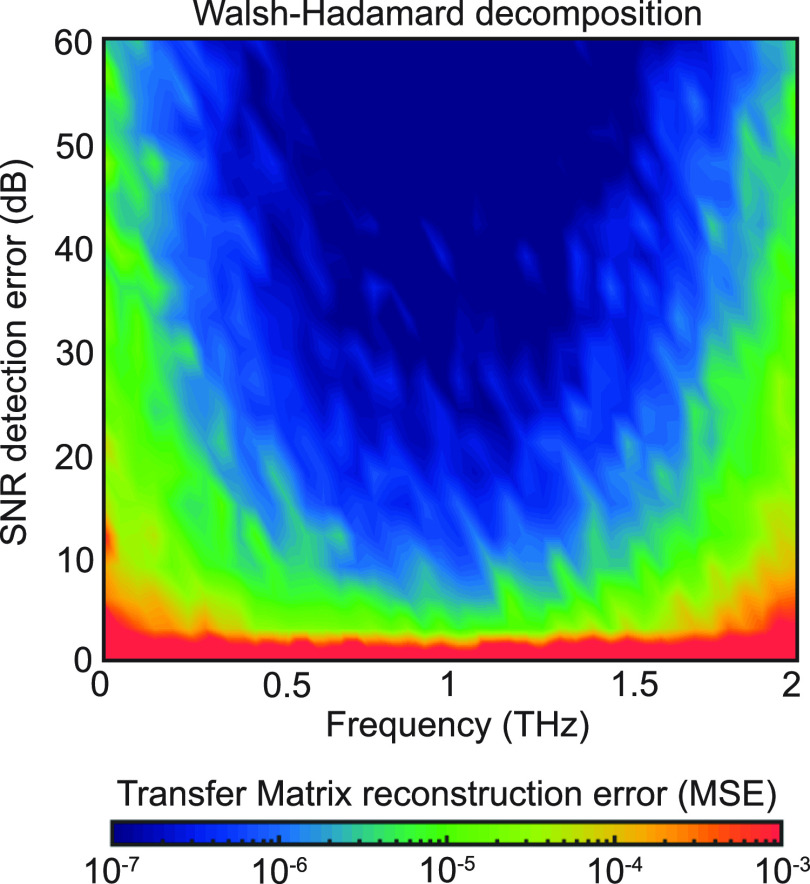
In close analogy with the traditional experimental approaches, we simulated the reconstruction of the coherent transfer matrix by computing the TDS output images corresponding to a predefined set of illumination patterns. In our simulations, we employed a Walsh–Hadamard decomposition scheme, i.e., we determined the full-wave responses corresponding to each column of an N × N Walsh–Hadamard matrix. We then extracted the frequency-dependent elements of the coherent transfer matrix through a linear inversion of the Walsh–Hadamard response (Figure 2). The detailed reconstruction method is described in Supporting Information Note 2.
Figure 2.
Transfer Matrix reconstruction. Mean squared error (MSE) of the coherent transfer matrix elements as reconstructed through a Walsh–Hadamard decomposition. The input and output planes are divided into 16 × 16 pixels, corresponding to a scattering matrix composed of 256 × 256 entries.
The identification of an optimized optical spatial pattern Iopt (x′) that produces a given field profile of interest Z̃target (xo, ω) carries a few significant challenges. First, as can be easily evinced from eq 6, in optical rectification, the THz field phase cannot be controlled through the incident optical phase, i.e., we can only control the THz amplitude distribution by varying the intensity distribution of the optical pump. Second, the spatial distribution of the optical intensity pattern is bound to be the same for all of the different frequencies carried by the THz pulse. Due to these two constraints, we cannot invert the coherent transfer matrix directly as the solution pattern is likely a frequency-dependent amplitude and phase distribution. On the contrary, we must identify a single, amplitude-only field distribution that best approximates the desired field distribution at the output. It is essential to stress that this is a post-measurement process, as opposed to the case of typical optimization techniques relying on feedback loops between illumination and measurement.
To this end, we cast our inversion problem in terms of a constraint least-square minimization of the following fitness function
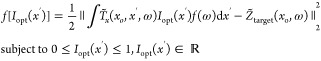 |
7 |
where ∥···∥2 is the Euclidean norm. In the discrete coordinate system, eq 7 reads
| 8 |
where Tmnk = 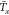 (xm, xn′, ωk), In = Iopt (xn), fk = f(ωk), and Zmk = Z̃target (xm, ωk), and where we replaced the Euclidean norm with
the Frobenius norm. The constrained convex optimization problem defined
in eqs 7 and 8 can be solved using various techniques. We use the
Trust-Region-Reflective algorithm, a well-established method capable
of rapidly solving relatively large-scale problems with low memory
requirements.56 The ability to optimize
the full-field properties of the transmitted field is a distinctive
feature of this approach; eqs 7 and 8 are, indeed, an absolute phase-sensitive
optimization, corresponding to a field-driven best fit rather than
an intensity-driven fit.
(xm, xn′, ωk), In = Iopt (xn), fk = f(ωk), and Zmk = Z̃target (xm, ωk), and where we replaced the Euclidean norm with
the Frobenius norm. The constrained convex optimization problem defined
in eqs 7 and 8 can be solved using various techniques. We use the
Trust-Region-Reflective algorithm, a well-established method capable
of rapidly solving relatively large-scale problems with low memory
requirements.56 The ability to optimize
the full-field properties of the transmitted field is a distinctive
feature of this approach; eqs 7 and 8 are, indeed, an absolute phase-sensitive
optimization, corresponding to a field-driven best fit rather than
an intensity-driven fit.
Results and Discussion
Spatiotemporal Focusing of THz Waves through a Scattering Medium
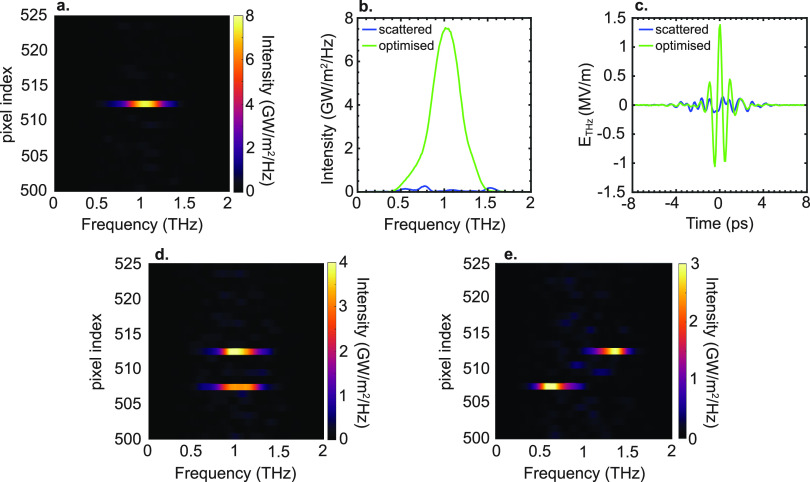
Our first objective is to invert the coherent transfer matrix to obtain a spatiotemporal localized focus spot at the output of the scattering medium, a classical state-of-the-art scenario. Such a task has been explored in the optical and infrared domain both for monochromatic15,52 and ultrafast pulses,25,50,57−59 but never tackled for THz fields. In our approach, the realization of a spatiotemporal focus corresponds to imposing the following target field profile in eq 7
| 9 |
where xa is the desired focus position, and Eafa (ω) is the spectrum of the incident THz pulse. Equation 9 targets an output field localized in one spatial point with the same spectral profile as the incident pulse. The results are shown in Figure 3a–c and effectively predict the formation of a sharp focus at the output. Quite remarkably, our amplitude-only optimized wavefront yields a spectral intensity enhancement η (defined as the ratio between the optimized and incident intensity spectral density at a specific frequency) of 78.43 (at 1 THz) at the focus spot (Figure 3b). The field peak (Figure 3c) is enhanced by a factor of 5.10, whereas the field-temporal standard deviation (the transient duration) is compressed by a factor of 4 with respect to the unoptimized case. It is worth stressing that, by observing Figure 3c, not just the pulse is recompressed. As expected from a full-field function reconstruction, the field dynamics are reconstructed locally, similar to Figure 1b. As illustrated in Figure S3, the performance of the optimal pattern is virtually identical to those obtained with standard iterative optimization techniques.60,61
Figure 3.
Spatiotemporal focusing of THz field: (a) optimized intensity spectral density distribution showing the focus spot in THz band. (b) Comparison between intensity spectral density profiles of the perturbed THz spectrum (blue) and optimized spectrum (green) at the mth pixel. (c) THz pulse profile of scattered field (blue) and optimized field (green) from the mth pixel of the output plane. (d) Intensity spectral density distribution of the output THz field showing two simultaneous focus spots at mth pixel and m′th pixel. (e) Intensity spectral density distribution of optimized THz field for two simultaneous focus spots at mth and m′th pixel with two different spectra centered around 0.7 and 1.3 THz. SNR per pixel: 40 dB. The 6.4 × 6.4 mm2 sample illumination area is spatially sampled at 200 μm resolution, corresponding to a number of pixels of 32 × 32.
Our approach is easily extendable to more challenging conditions, including the formation of separate spatial foci with different spectral profiles. To this end, we generalized eq 7 to the case of two foci by imposing
| 10 |
where xa and xb correspond to two different focus locations, and Eafa(ω) and Ebfb(ω) denote two distinct spectral profiles, respectively. Our results are shown in Figure 3d,e. When considering identical spectral profiles at the output (Figure 3d, fa (ω) = fb (ω)), we achieved the THz intensity spectral densities of 4.087 GW/m2/Hz (η = 43.10) and 3.17 GW/m2/Hz (η = 33.43) at 1 THz and THz peak field enhancements of 3.64 and 3.73, respectively. When considering two different spectral profiles, centered at around 1.3 and 0.7 THz, respectively (Figure 3e), the two foci exhibit intensity spectral densities of 2.74 GW/m2/Hz (η = 28.94) and 2.43 GW/m2/Hz (η = 25.63), respectively. For the sake of clarity, we stress here that the two spectral profiles included in eq 10 are different from the incident pulse spectrum.
Deterministic Coherent Control without Previous Knowledge of the Source
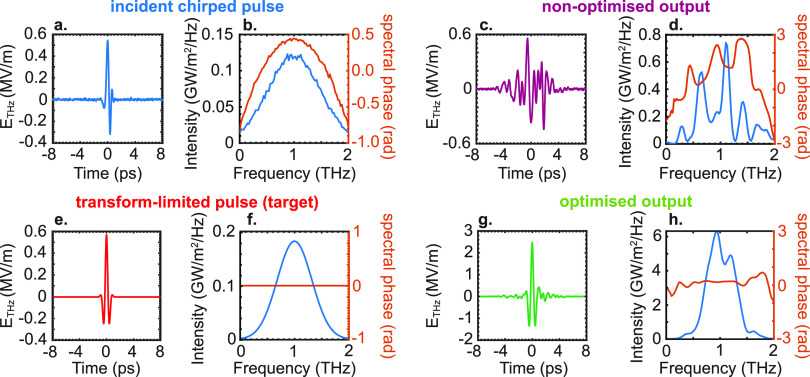
The loss function defined in eq 7 targets the spatial distribution of the incident spatial distribution Iopt (x′) (corresponding to the optical intensity distribution) producing a desired spatiotemporal electric-field distribution Z̃target (xo, ω) at the output. However, one could easily perform waveform synthesis using the experimental measurements of the nonnormalized transfer matrix T̃exp (xo, x′, ω) that contains the (generally unknown) incident pulse information (see eq 1). In this approach, the optimization function simply reads as follows
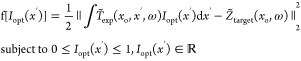 |
11 |
We stress that the optimization routine set by eqs 7 and 11 is field sensitive, and it simultaneously optimizes the amplitude and absolute phase of the transmitted field. This is a radically different scenario from the optical domain, where accessing the absolute phase with arbitrary precision is extremely challenging, and waveform synthesis can be attempted only if the absolute phase profile of the input is known beforehand (e.g., in the case of a transform-limited pulse).50 To illustrate this point, in Figure 4, we report the recompression of a chirped THz pulse obtained without any knowledge of the incident field. As shown in Figure 4g,h, the fitness function from eq 11 is well-suited to convert the initially chirped pulse (Figure 4a,b) into a good approximated version of the transform-limited pulse chosen as a target (Figure 4e,f). Analogous to the case in Figure 3a–c, the electric field is measured in the desired focal spot on the output face of the scatterer.
Figure 4.
Deterministic coherent control without previous knowledge of the source. (a) Input field-temporal profile corresponding to a chirped pulse. The temporal profile includes the 40 dB noise applied at the detection. (b) Intensity spectral density (blue line) and spectral phase (orange line) for the field profile in panel (a). (c, d) Same as panels (a) and (b) but for a nonoptimized incident pattern. (e, f) Same as panels (a) and (b) for the optimized profile targeted by our optimization routine. (g, h) Same as panels a and b for the optimized output field. The 6.4 × 6.4 mm2 sample illumination area is spatially sampled at 200 μm resolution, corresponding to a number of pixels of 32 × 32.
Time-Resolved Retrieval of Image Object Obscured by a Scattering Medium
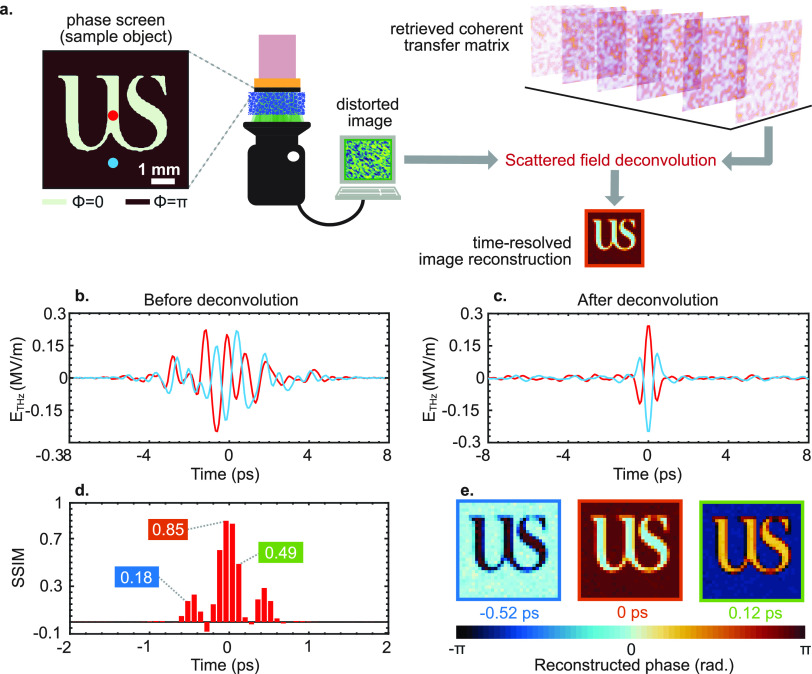
The reconstruction of the coherent transmission properties of the scatterer can be directly applied to reconstruct the image of an object concealed by the scattering medium.62−64 A particular possibility enabled by our full-field methodology is the possibility of performing phase-sensitive reconstruction, i.e., the reconstruction of samples characterized by complex phase profiles.
A numerical implementation of the image reconstruction process is shown in Figure 5a, where we place a phase mask U(x′) between the generating crystal and the scattering medium. In the frequency domain, the corresponding transmitted field reads as follows
| 12 |
where M̃(xo, ω) is the time-Fourier transform of space–time measurements. To retrieve the original image from the measurements, we perform a standard deconvolution of the retrieved coherent transfer matrix that yields the time-resolved image Eretrieved as
| 13 |
where (*) denotes a spatial
convolution, F–1 is the inverse
time-Fourier transform, and [...](−1) is the inversion
operator. As is customary in deconvolution problems, the main task
lies in finding the inverse of 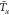 (xo, x′, ω). We applied the Moore–Penrose
pseudo-inversion method, implemented through a truncated singular-value
decomposition.65 As shown in Figure 5b, before applying the deconvolution
routine, the THz pulses corresponding to the two distinct pixels are
thoroughly perturbed, representing the multiplexing of waves due to
multiple scattering. Figure 5c shows the waves corresponding to two separate pixels (red
and cyan dots) after the deconvolution process. We calculated the
Structural Similarity (SSIM) index66 to
quantify the quality of the reconstruction process, as shown in Figure 5d. SSIM values obtained
at t = −0.52, 0, and 0.12 ps in our time reference
are 0.18, 0.85, and 0.49, respectively, showing high fidelity in the
time-resolved reconstruction of the image. The specific reconstruction
results shown in Figure 5e are the fixed-time reconstructed phase images of the transmitted
field at the same time values. Analogous results for an amplitude-only
object (i.e., a metallic mask) are included in Figure S4. As a final example, we extended our image reconstruction
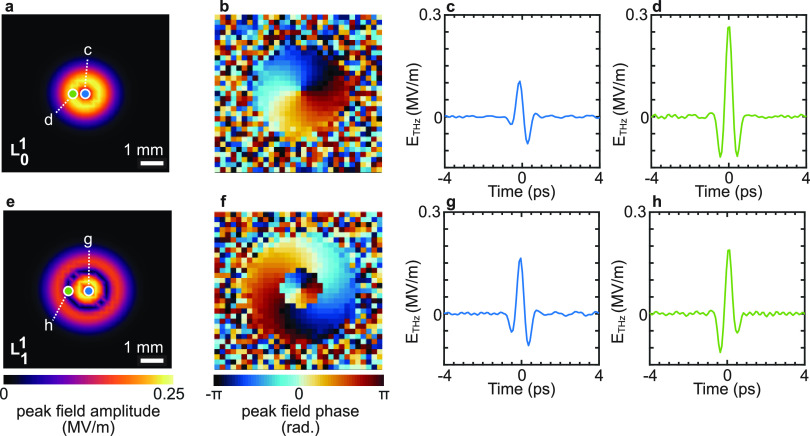
approach for the case of THz vortex beam67 and simulated the spatiotemporal field-phase profiles for the L01 and L1 beam profiles (see Figure S5).
We deconvolved the spatial field-phase information of L01 and L1 THz vortex beams with the complex scrambled output obtained from
propagation through the scattering medium. Figure 6 shows their retrieved spatial field-phase
profiles at t = 0 ps (Figure 6a,b,e,f). In Figure 6c,d,g,h, we report the temporal profile of
the retrieved THz field corresponding to the different pixels marked
in Figure 6a,b,e,f.
(xo, x′, ω). We applied the Moore–Penrose
pseudo-inversion method, implemented through a truncated singular-value
decomposition.65 As shown in Figure 5b, before applying the deconvolution
routine, the THz pulses corresponding to the two distinct pixels are
thoroughly perturbed, representing the multiplexing of waves due to
multiple scattering. Figure 5c shows the waves corresponding to two separate pixels (red
and cyan dots) after the deconvolution process. We calculated the
Structural Similarity (SSIM) index66 to
quantify the quality of the reconstruction process, as shown in Figure 5d. SSIM values obtained
at t = −0.52, 0, and 0.12 ps in our time reference
are 0.18, 0.85, and 0.49, respectively, showing high fidelity in the
time-resolved reconstruction of the image. The specific reconstruction
results shown in Figure 5e are the fixed-time reconstructed phase images of the transmitted
field at the same time values. Analogous results for an amplitude-only
object (i.e., a metallic mask) are included in Figure S4. As a final example, we extended our image reconstruction
approach for the case of THz vortex beam67 and simulated the spatiotemporal field-phase profiles for the L01 and L1 beam profiles (see Figure S5).
We deconvolved the spatial field-phase information of L01 and L1 THz vortex beams with the complex scrambled output obtained from
propagation through the scattering medium. Figure 6 shows their retrieved spatial field-phase
profiles at t = 0 ps (Figure 6a,b,e,f). In Figure 6c,d,g,h, we report the temporal profile of
the retrieved THz field corresponding to the different pixels marked
in Figure 6a,b,e,f.
Figure 5.
Time-resolved THz phase-sensitive imaging through the scattering medium. (a) Schematic of imaging methodology. Inset: time-resolved reconstruction of the image corresponds to the measurement at t = 0 ps in panel (e). (b) Temporal evolution of output speckles corresponding to two different pixels (red and cyan dots shown in panel (a)) before deconvolution. (c) Temporal evolution of reconstructed THz pulse (after deconvolution) for two different pixels (red and cyan dots shown in panel (a)). (d) Structural Similarity (SSIM) index in the time-resolved reconstruction of an image object. (e) Reconstructed phase images at t = −0.52, 0, and 0.12 ps. The 6.4 × 6.4 mm2 sample illumination area is spatially sampled at 200 μm resolution, corresponding to a number of pixels of 32 × 32 (see Video S1). Logo used with permission from the University of Sussex.
Figure 6.
Complex propagation of THz vortex beam through the scattering medium. (a, b) Retrieved spatial field and phase distribution of L01 vortex beam at t = 0 ps. (c, d) Temporal profile of the retrieved THz pulse corresponding to two different pixels for the L0 vortex beam in panels (a) and (b). (e–h) Same as panels (a–d) for an L11 vortex beam. The 6.4 × 6.4 mm2 sample illumination area is spatially sampled at 200 μm resolution, corresponding to a number of pixels of 32 × 32 (see Video S2).
Conclusions
In this work, we have theoretically demonstrated a deterministic approach toward the coherent spatiotemporal control of THz waves propagating through a scattering medium. Our methodology combines the nonlinear conversion of optical patterns to THz structured fields with field-sensitive THz field detection, as enabled by state-of-the-art TDS technology. We have shown how the full-wave detection of the scattered THz field enables retrieving the field-sensitive transfer function of the medium directly in a deterministic fashion, as described through a coherent transfer matrix modeling. We sample the complex time-domain elements of the coherent transfer matrix by projecting a sequence of orthogonal Walsh–Hadamard patterns. The TDS allows for a sufficient description of the coherent transfer matrix to enable spatiotemporal control through a direct inversion approach. We identified the spatial profiles that yield a desired output field distribution through a convex constraint optimization routine compatible with real-life experimental conditions. As relevant examples, we demonstrated the formation of single and multiple spatiotemporal foci and the retrieval of complex field distributions and phase-only images concealed by the scatterer. Our results suggest that it is still possible to investigate the scattering unaffected open path via a time-domain deterministic approach in an experimental-driven constrained scenario. Such control could have a profound impact, especially for THz imaging, where wave shaping is generally a challenge. In addition, we envision a role in time-resolved characterization techniques of complex media, including deep-tissue biological imaging.
Acknowledgments
V.K., V.C., and L.P. acknowledge the support from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme Grant No. 725046. J.S.T.G. acknowledges the support from the Leverhulme Trust (Early Career Fellowship ECF-2020-537).
Glossary
Abbreviations
- THz
terahertz
- TDS
time-domain spectroscopy
- FROG
frequency-resolved optical gating
- SPIDER
spectral phase interferometry for direct electric-field reconstruction
- SLM
spatial light modulator
- ZnTe
zinc telluride
- SNR
signal-to-noise ratio
- SSIM
structural similarity index
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.2c00061 The datasets for all figures are freely accessible at: http://doi.org/10.6084/m9.figshare.19447112.
Author Present Address
§ Emergent Photonics Research Centre and Dept. of Physics, Loughborough University, Loughborough, LE11 3TU, U.K
Author Present Address
⊥ Emergent Photonics Research Centre and Dept. of Physics, Loughborough University, Loughborough, LE11 3TU, U.K. email: m.peccianti@lboro.ac.uk
Author Contributions
All authors were engaged in the general discussion regarding the basic science of the paper. V.K. performed the calculations reported. All authors contributed to the general understanding of the results and drafting of the paper. J.S.T.G. and M.P supervised the general research activities.
This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme Grant No. 725046. The authors acknowledge financial support from the (UK) Engineering and Physical Sciences Research Council (EPSRC), Grant Nos. EP/S001018/1 and EP/T00097X/1 and the Leverhulme Trust (Early Career Fellowship ECF-2020-537).
The authors declare no competing financial interest.
Supplementary Material
References
- Laser Speckle and Related Phenomena, Dainty J. C., Ed.; Topics in Applied Physics; Springer-Verlag: Berlin, Heidelberg, 1975. [Google Scholar]
- Sheng P.Introduction to Wave Scattering, Localization and Mesoscopic Phenomena, 2nd ed.; Springer Series in Materials Science; Springer-Verlag: Berlin, Heidelberg, 2006. [Google Scholar]
- Ishimaru A.Electromagnetic Wave Propagation, Radiation, and Scattering: From Fundamentals to Applications, 2nd ed.; Wiley: Hoboken, New Jersey, 2017. [Google Scholar]
- Wax A.; Backman V.. Biomedical Applications of Light Scattering; McGraw-Hill Education, 2010. [Google Scholar]
- Hofer M.; Soeller C.; Brasselet S.; Bertolotti J. Wide Field Fluorescence Epi-Microscopy behind a Scattering Medium Enabled by Speckle Correlations. Opt. Express 2018, 26, 9866–9881. 10.1364/OE.26.009866. [DOI] [PubMed] [Google Scholar]
- Yoon S.; Kim M.; Jang M.; Choi Y.; Choi W.; Kang S.; Choi W. Deep Optical Imaging within Complex Scattering Media. Nat. Rev. Phys. 2020, 2, 141–158. 10.1038/s42254-019-0143-2. [DOI] [Google Scholar]
- Booth M. J. Adaptive Optics in Microscopy. Philos. Trans. R. Soc., A 2007, 365, 2829–2843. 10.1098/rsta.2007.0013. [DOI] [PubMed] [Google Scholar]
- Hsu C. W.; Liew S. F.; Goetschy A.; Cao H.; Douglas Stone A. Correlation-Enhanced Control of Wave Focusing in Disordered Media. Nat. Phys. 2017, 13, 497–502. 10.1038/nphys4036. [DOI] [Google Scholar]
- Mosk A. P.; Lagendijk A.; Lerosey G.; Fink M. Controlling Waves in Space and Time for Imaging and Focusing in Complex Media. Nat. Photonics 2012, 6, 283–292. 10.1038/nphoton.2012.88. [DOI] [Google Scholar]
- Vellekoop I. M.; Mosk A. P. Universal Optimal Transmission of Light Through Disordered Materials. Phys. Rev. Lett. 2008, 101, 120601 10.1103/PhysRevLett.101.120601. [DOI] [PubMed] [Google Scholar]
- Horstmeyer R.; Ruan H.; Yang C. Guidestar-Assisted Wavefront-Shaping Methods for Focusing Light into Biological Tissue. Nat. Photonics 2015, 9, 563–571. 10.1038/nphoton.2015.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judkewitz B.; Horstmeyer R.; Vellekoop I. M.; Papadopoulos I. N.; Yang C. Translation Correlations in Anisotropically Scattering Media. Nat. Phys. 2015, 11, 684–689. 10.1038/nphys3373. [DOI] [Google Scholar]
- Popoff S. M.; Lerosey G.; Carminati R.; Fink M.; Boccara A. C.; Gigan S. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys. Rev. Lett. 2010, 104, 100601 10.1103/PhysRevLett.104.100601. [DOI] [PubMed] [Google Scholar]
- Andreoli D.; Volpe G.; Popoff S.; Katz O.; Grésillon S.; Gigan S. Deterministic Control of Broadband Light through a Multiply Scattering Medium via the Multispectral Transmission Matrix. Sci. Rep. 2015, 5, 10347 10.1038/srep10347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H.; Lee K.; Park Y. Ultrahigh Enhancement of Light Focusing through Disordered Media Controlled by Mega-Pixel Modes. Opt. Express 2017, 25, 8036–8047. 10.1364/OE.25.008036. [DOI] [PubMed] [Google Scholar]
- Tao X.; Bodington D.; Reinig M.; Kubby J. High-Speed Scanning Interferometric Focusing by Fast Measurement of Binary Transmission Matrix for Channel Demixing. Opt. Express 2015, 23, 14168–14187. 10.1364/OE.23.014168. [DOI] [PubMed] [Google Scholar]
- Mariani F.; Löffler W.; Aas M.; Ojambati O. S.; Hong P.; Vos W. L.; van Exter M. P. Scattering Media Characterization with Phase-Only Wavefront Modulation. Opt. Express 2018, 26, 2369 10.1364/OE.26.002369. [DOI] [PubMed] [Google Scholar]
- Mounaix M.; Defienne H.; Gigan S. Deterministic Light Focusing in Space and Time through Multiple Scattering Media with a Time-Resolved Transmission Matrix Approach. Phys. Rev. A 2016, 94, 041802 10.1103/PhysRevA.94.041802. [DOI] [Google Scholar]
- Pasquazi A.; Peccianti M.; Razzari L.; Moss D. J.; Coen S.; Erkintalo M.; Chembo Y. K.; Hansson T.; Wabnitz S.; Del’Haye P.; Xue X.; Weiner A. M.; Morandotti R. Micro-Combs: A Novel Generation of Optical Sources. Phys. Rep. 2018, 729, 1–81. 10.1016/j.physrep.2017.08.004. [DOI] [Google Scholar]
- Trebino R.; DeLong K. W. K. W.; Fittinghoff D. N. D. N.; Sweetser J. N.; Krumbügel M. A.; Richman B. B. A.; Kane D. J. D. J.; Krumbügel M. Measuring Ultrashort Laser Pulses in the Time-Frequency Domain Using Frequency-Resolved Optical Gating. Rev. Sci. Instrum. 1997, 68, 3277. 10.1063/1.1148286. [DOI] [Google Scholar]
- Akturk S.; Kimmel M.; O’Shea P.; Trebino R. Measuring Pulse-Front Tilt in Ultrashort Pulses Using GRENOUILLE. Opt. Express 2003, 11, 491–501. 10.1364/OE.11.000491. [DOI] [PubMed] [Google Scholar]
- Iaconis C.; Walmsley Ia. Spectral Phase Interferometry for Direct Electric-Field Reconstruction of Ultrashort Optical Pulses. Opt. Lett. 1998, 23, 792–794. 10.1364/OL.23.000792. [DOI] [PubMed] [Google Scholar]
- Beard M. C.; Turner G. M.; Schmuttenmaer C. A. Terahertz Spectroscopy. J. Phys. Chem. B 2002, 106, 7146–7159. 10.1021/jp020579i. [DOI] [Google Scholar]
- Neu J.; Schmuttenmaer C. A. Tutorial: An Introduction to Terahertz Time Domain Spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101 10.1063/1.5047659. [DOI] [Google Scholar]
- Mounaix M.; Fontaine N. K.; Neilson D. T.; Ryf R.; Chen H.; Alvarado-Zacarias J. C.; Carpenter J. Time Reversed Optical Waves by Arbitrary Vector Spatiotemporal Field Generation. Nat. Commun. 2020, 11, 5813 10.1038/s41467-020-19601-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink M. Time-Reversal Acoustics. J. Phys.: Conf. Ser. 2008, 118, 012001 10.1088/1742-6596/118/1/012001. [DOI] [Google Scholar]
- Lerosey G.; de Rosny J.; Tourin A.; Derode A.; Montaldo G.; Fink M. Time Reversal of Electromagnetic Waves. Phys. Rev. Lett. 2004, 92, 193904 10.1103/PhysRevLett.92.193904. [DOI] [PubMed] [Google Scholar]
- Ulrich T. J.; Johnson P. A.; Sutin A. Imaging Nonlinear Scatterers Applying the Time Reversal Mirror. J. Acoust. Soc. Am. 2006, 119, 1514–1518. 10.1121/1.2168413. [DOI] [Google Scholar]
- Chen Q.; Song H.; Yu J.; Kim K. Current Development and Applications of Super-Resolution Ultrasound Imaging. Sensors 2021, 21, 2417 10.3390/s21072417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce J.; Mittleman D. M. Propagation of Single-Cycle Terahertz Pulses in Random Media. Opt. Lett. 2001, 26, 2002–2004. 10.1364/OL.26.002002. [DOI] [PubMed] [Google Scholar]
- Pearce J.; Mittleman D. M. Scale Model Experimentation: Using Terahertz Pulses to Study Light Scattering. Phys. Med. Biol. 2002, 47, 3823–3830. 10.1088/0031-9155/47/21/321. [DOI] [PubMed] [Google Scholar]
- Gentilini S.; Missori M.; Ghofraniha N.; Conti C. Terahertz Radiation Transport in Photonic Glasses. Ann. Phys. 2020, 532, 2000005 10.1002/andp.202000005. [DOI] [Google Scholar]
- Kaushik M.; Ng B. W.-H.; Fischer B. M.; Abbott D. Terahertz Scattering by Granular Composite Materials: An Effective Medium Theory. Appl. Phys. Lett. 2012, 100, 011107 10.1063/1.3674289. [DOI] [Google Scholar]
- Born P.; Holldack K. Analysis of Granular Packing Structure by Scattering of THz Radiation. Rev. Sci. Instrum. 2017, 88, 051802 10.1063/1.4983045. [DOI] [PubMed] [Google Scholar]
- Watts C. M.; Shrekenhamer D.; Montoya J.; Lipworth G.; Hunt J.; Sleasman T.; Krishna S.; Smith D. R.; Padilla W. J. Terahertz Compressive Imaging with Metamaterial Spatial Light Modulators. Nat. Photonics 2014, 8, 605–609. 10.1038/nphoton.2014.139. [DOI] [Google Scholar]
- Stantchev R. I.; Sun B.; Hornett S. M.; Hobson P. A.; Gibson G. M.; Padgett M. J.; Hendry E. Noninvasive, near-Field Terahertz Imaging of Hidden Objects Using a Single-Pixel Detector. Sci. Adv. 2016, 2, e1600190 10.1126/sciadv.1600190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y. C.; Gan L.; Stringer M.; Burnett A.; Tych K.; Shen H.; Cunningham J. E.; Parrott E. P. J.; Zeitler J. A.; Gladden L. F.; Linfield E. H.; Davies A. G. Terahertz Pulsed Spectroscopic Imaging Using Optimized Binary Masks. Appl. Phys. Lett. 2009, 95, 231112 10.1063/1.3271030. [DOI] [Google Scholar]
- Chan W. L.; Charan K.; Takhar D.; Kelly K. F.; Baraniuk R. G.; Mittleman D. M. A Single-Pixel Terahertz Imaging System Based on Compressed Sensing. Appl. Phys. Lett. 2008, 93, 121105 10.1063/1.2989126. [DOI] [Google Scholar]
- Lemoult F.; Lerosey G.; de Rosny J.; Fink M. Manipulating Spatiotemporal Degrees of Freedom of Waves in Random Media. Phys. Rev. Lett. 2009, 103, 173902 10.1103/PhysRevLett.103.173902. [DOI] [PubMed] [Google Scholar]
- Olivieri L.; Totero Gongora J. S.; Pasquazi A.; Peccianti M. Time-Resolved Nonlinear Ghost Imaging. ACS Photonics 2018, 5, 3379–3388. 10.1021/acsphotonics.8b00653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivieri L.; Gongora J. S. T.; Peters L.; Cecconi V.; Cutrona A.; Tunesi J.; Tucker R.; Pasquazi A.; Peccianti M. Hyperspectral Terahertz Microscopy via Nonlinear Ghost Imaging. Optica 2020, 7, 186–191. 10.1364/OPTICA.381035. [DOI] [Google Scholar]
- Totero Gongora J. S.; Olivieri L.; Peters L.; Tunesi J.; Cecconi V.; Cutrona A.; Tucker R.; Kumar V.; Pasquazi A.; Peccianti M. Route to Intelligent Imaging Reconstruction via Terahertz Nonlinear Ghost Imaging. Micromachines 2020, 11, 521 10.3390/mi11050521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harwit M.; Sloane N. J. A.. Hadamard Transform Optics; Academic Press: New York, 1979. [Google Scholar]
- Bertero M.; Boccacci M.; De Mol C.. Introduction to Inverse Problems in Imaging, 2nd ed.; CRC Press/Francis and Taylor: Boca Raton, 2021. [Google Scholar]
- van Beijnum F.; Putten E. G. van.; Lagendijk A.; Mosk A. P. Frequency Bandwidth of Light Focused through Turbid Media. Opt. Lett. 2011, 36, 373–375. 10.1364/OL.36.000373. [DOI] [PubMed] [Google Scholar]
- Rotter S.; Gigan S. Light Fields in Complex Media: Mesoscopic Scattering Meets Wave Control. Rev. Mod. Phys. 2017, 89, 015005 10.1103/RevModPhys.89.015005. [DOI] [Google Scholar]
- Goodman J. W.Statistical Optics; John Wiley & Sons, 2015. [Google Scholar]
- Garcia N.; Stoll E. Monte Carlo Calculation for Electromagnetic-Wave Scattering from Random Rough Surfaces. Phys. Rev. Lett. 1984, 52, 1798–1801. 10.1103/PhysRevLett.52.1798. [DOI] [Google Scholar]
- Berkovits R.; Feng S. Correlations in Coherent Multiple Scattering. Phys. Rep. 1994, 238, 135–172. 10.1016/0370-1573(94)90079-5. [DOI] [Google Scholar]
- Mounaix M.; Andreoli D.; Defienne H.; Volpe G.; Katz O.; Grésillon S.; Gigan S. Spatiotemporal Coherent Control of Light through a Multiple Scattering Medium with the Multispectral Transmission Matrix. Phys. Rev. Lett. 2016, 116, 253901 10.1103/PhysRevLett.116.253901. [DOI] [PubMed] [Google Scholar]
- Goodman P. J.Speckle Phenomena in Optics; W. H. Freeman: Englewood, Colo, 2010. [Google Scholar]
- Conkey D. B.; Caravaca-Aguirre A. M.; Piestun R. High-Speed Scattering Medium Characterization with Application to Focusing Light through Turbid Media. Opt. Express 2012, 20, 1733–1740. 10.1364/OE.20.001733. [DOI] [PubMed] [Google Scholar]
- Zhao J.; E Y.; Williams K.; Zhang X.-C.; Boyd R. W. Spatial Sampling of Terahertz Fields with Sub-Wavelength Accuracy via Probe-Beam Encoding. Light: Sci. Appl. 2019, 8, 55 10.1038/s41377-019-0166-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchard F.; Doi A.; Tanaka T.; Tanaka K. Real-Time, Subwavelength Terahertz Imaging. Annu. Rev. Mater. Res. 2013, 43, 237–259. 10.1146/annurev-matsci-071312-121656. [DOI] [Google Scholar]
- Naftaly M. Metrology Issues and Solutions in THz Time-Domain Spectroscopy: Noise, Errors, Calibration. IEEE Sens. J. 2013, 13, 8–17. 10.1109/JSEN.2012.2208624. [DOI] [Google Scholar]
- Moré J. J.; Sorensen D. C. Computing a Trust Region Step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. 10.1137/0904038. [DOI] [Google Scholar]
- McCabe D. J.; Tajalli A.; Austin D. R.; Bondareff P.; Walmsley I. A.; Gigan S.; Chatel B. Spatio-Temporal Focusing of an Ultrafast Pulse through a Multiply Scattering Medium. Nat. Commun. 2011, 2, 447 10.1038/ncomms1434. [DOI] [PubMed] [Google Scholar]
- Katz O.; Small E.; Bromberg Y.; Silberberg Y. Focusing and Compression of Ultrashort Pulses through Scattering Media. Nat. Photonics 2011, 5, 372–377. 10.1038/nphoton.2011.72. [DOI] [Google Scholar]
- Calba C.; Méès L.; Rozé C.; Girasole T. Ultrashort Pulse Propagation through a Strongly Scattering Medium: Simulation and Experiments. J. Opt. Soc. Am. A 2008, 25, 1541–1550. 10.1364/JOSAA.25.001541. [DOI] [PubMed] [Google Scholar]
- Bonyadi M. R.; Michalewicz Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. 10.1162/EVCO_r_00180. [DOI] [PubMed] [Google Scholar]
- Mitchell M.An Introduction to Genetic Algorithms: Complex Adaptive Systems; A Bradford Book: Cambridge, MA, USA, 1996. [Google Scholar]
- Satat G.; Heshmat B.; Raviv D.; Raskar R. All Photons Imaging Through Volumetric Scattering. Sci. Rep. 2016, 6, 33946 10.1038/srep33946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertolotti J.; van Putten E. G.; Blum C.; Lagendijk A.; Vos W. L.; Mosk A. P. Non-Invasive Imaging through Opaque Scattering Layers. Nature 2012, 491, 232–234. 10.1038/nature11578. [DOI] [PubMed] [Google Scholar]
- Kim K.; Somkuwar A. S.; Park Y.; Singh R. K. Imaging through Scattering Media Using Digital Holography. Opt. Commun. 2019, 439, 218–223. 10.1016/j.optcom.2019.01.080. [DOI] [Google Scholar]
- Penrose R. A Generalized Inverse for Matrices. Math. Proc. Cambridge Philos. Soc. 1955, 51, 406–413. 10.1017/S0305004100030401. [DOI] [Google Scholar]
- Wang Z.; Bovik A. C.; Sheikh H. R.; Simoncelli E. P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. 10.1109/TIP.2003.819861. [DOI] [PubMed] [Google Scholar]
- Lin Q.; Zheng S.; Song Q.; Zeng X.; Cai Y.; Li Y.; Chen Z.; Zha L.; Pan X.; Xu S. Generation of Terahertz Vortex Pulses without Any Need of Manipulation in the Terahertz Region. Opt. Lett. 2019, 44, 887–890. 10.1364/OL.44.000887. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.