Review and assessment of Boolean approaches for inference of gene regulatory networks

Abstract

Boolean descriptions of gene regulatory networks can provide an insight into interactions between genes. Boolean networks hold predictive power, are easy to understand, and can be used to simulate the observed networks in different scenarios.

We review fundamental and state-of-the-art methods for inference of Boolean networks. We introduce a methodology for a straightforward evaluation of Boolean inference approaches based on the generation of evaluation datasets, application of selected inference methods, and evaluation of performance measures to guide the selection of the best method for a given inference problem. We demonstrate this procedure on inference methods REVEAL (REVerse Engineering ALgorithm), Best-Fit Extension, MIBNI (Mutual Information-based Boolean Network Inference), GABNI (Genetic Algorithm-based Boolean Network Inference) and ATEN (AND/OR Tree ENsemble algorithm), which infers Boolean descriptions of gene regulatory networks from discretised time series data.

Boolean inference approaches tend to perform better in terms of dynamic accuracy, and slightly worse in terms of structural correctness. We believe that the proposed methodology and provided guidelines will help researchers to develop Boolean inference approaches with a good predictive capability while maintaining structural correctness and biological relevance.

Boolean network inference; Gene regulatory networks; Static validation; Dynamic validation; Systems biology

1. Introduction

One of the main goals of systems biology is to obtain a system-level understanding of a biological system, which can be regarded as a set of networks of interactions [1]. One of the main networks guiding the development and the dynamics of a biological system are gene regulatory networks (GRNs). Gene expression networks constitute fundamental cellular processes, such as cell proliferation [2], cell differentiation and tissue development [3], [4], stress response, metabolic stability [5], and apoptosis [6]. Their inference can provide a detailed insight into network dynamics and interactions between genes. While gene expression is a complicated multivariate process dependent on numerous factors, it can still be represented in a simplistic manner as a GRN. In this network, each node represents a gene and directed edges represent either activation or inhibition of a target gene.

When inferring gene regulatory networks, we are confronted with multiple challenges [7]. The number of measurements is typically much smaller than the number of genes, which directly affects the size of a solution space. In addition, the collected data contain noise due to intrinsic biological processes, external factors, and measurement errors [8]. The majority of network inference methods are focused on the reconstruction of a simple undirected or directed graph, Bayesian network, or a Boolean network [9], [10]. Graphs present a static representation of a biological network [11]. Bayesian networks allow us to model conditional probabilities among genes and their products and do not allow us to model the dynamics of the inferred gene regulatory network [12]. However, neither of these approaches is able to describe the dynamical aspects of the underlying networks [11]. They can be used as a basis for further development of more complex models, e.g., ODE systems [13], [14]. The latter require a precise assessment of kinetic parameter values, which are often hard or even impossible to obtain, especially when dealing with large networks. On the other hand, we can use Boolean networks to simulate the dynamics of gene regulatory networks even when the values of kinetic parameters are unknown [15]. Boolean genetic model presents a simple representation suitable for large scale gene regulatory networks [16], [17], [18]. Under a Boolean network model, each gene can either be active (1) or inactive (0). This property can be used to assess the accuracy of inferred networks, even if the underlying gene regulatory network is unknown and only time series data is provided.

Lack of ground truth models, i.e., gold standard networks, often represents a challenge in comparison and evaluation of inference methods [19]. In this work, we review fundamental and state-of-the-art Boolean inference methods, and apply a methodology for a thorough and robust evaluation of these methods. Our methodology includes the generation of test networks, selection of evaluation measures, and the analysis and visualisation of the obtained results. We demonstrate our methodology on five methods for the inference of Boolean networks from binarised time series data. The first two present two fundamental methods, i.e. REVEAL (REVerse Engineering ALgorithm) [20] and Best-Fit Extension [21]. While REVEAL can only solve problems with consistent and complete data, Best-Fit Extension presents a more general method. We examine how the inability to deal with incomplete and inconsistent data affects the inference of Boolean networks. Furthermore, we include three state-of-the-art methods, namely, MIBNI (Mutual Information-based Boolean Network Inference) [22], GABNI (Genetic Algorithm-based Boolean Network Inference) [23], and ATEN (AND/OR Tree ENsemble algorithm) [24]. MIBNI is able to model larger number of regulators for each gene in comparison to Best-Fit and REVEAL. GABNI increases the number of regulators even further. Both methods dedicate most of their computation time to the discovery of optimal regulation sets. On the other hand, ATEN focuses on inferring the best representation of a Boolean function. We apply the proposed evaluation process to compare two different philosophies, where the first focuses on finding the optimal regulators (e.g., by utilising information theory-based approaches [22]), while the second dedicates most of the resources to find the most accurate and compact Boolean representation of a GRN (e.g., by applying heuristic algorithms [24]).

The main contributions of this work are as follows. Firstly, we provide a comprehensive review of the fundamental and state-of-the-art methods used for Boolean inference of GRNs. Secondly, we provide a unified implementation of selected methods, which can be used in additional benchmarking experiments and to reproduce the results of this work as well as the results of other works reported in the literature. Finally, we apply a set of metrics, which can be used to systematically assess current and future implementations of Boolean inference methods. We discuss the obtained results in the context of possible extensions of observed methods to increase their performance and applicability.

2. Background

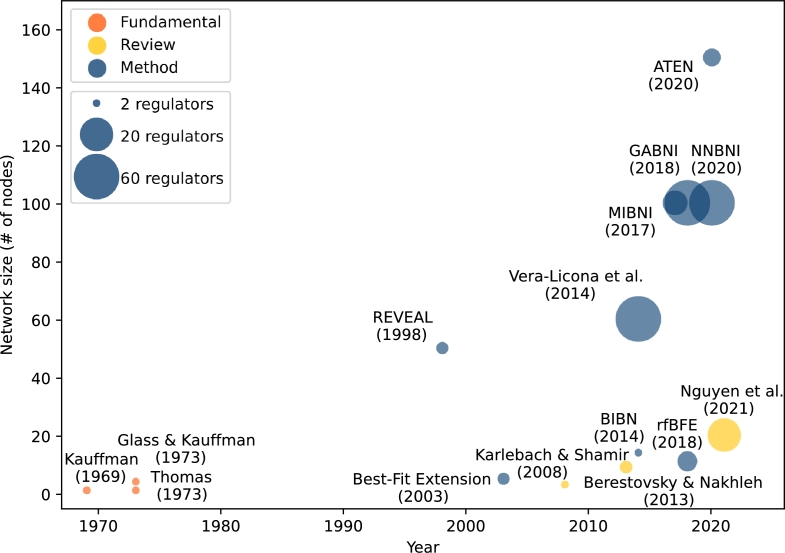
Even though Boolean networks reflect several benefits in comparison to alternative GRN representations, a minority of inference methods has been focused on Boolean network inference (the visual representation of these is presented in Fig. 1). Moreover, the survey [25] placed Boolean networks on the lower end of the expressiveness scale. Contrary to this classification, Berestovsky and Nakhleh [15] showed that iterative k-$means$ binarisation combined with network inference approaches, can capture the correct dynamics of Boolean networks and can provide enough predictive power in different applications.

Figure 1.

Visual representation of literature associated with the inference of Boolean networks. Axes correspond to the year of publication, and to the size of inferred networks in terms of number of nodes. Marker dot sizes correspond to the maximal number of regulators of each gene used by a given method. E.g., REVEAL and Best-Fit Extension can be applied to problems with maximal number of 3 regulators, while MIBNI uses at most 10 regulators.

When deriving large GRNs, the size of the solution space can drastically impede network inference, which is also the case when inferring large Boolean networks. The number of possible inputs for a single target gene equals $2^N$, where N is the number of genes, and the number of possible Boolean functions with k inputs equals $2^{2^k}$. The number of genes varies between species, e.g. the number of protein-coding genes in the human genome is approximately $20,000$ [26]. To reduce the size of the search space, some approaches infer regulatory dynamic only for meta-genes, i.e. groups of genes with similar expression profiles [27], [28]. It is also possible to reduce the search space of Boolean functions by considering only interactions with presumed biological relevance. Reconstruction strategies can focus on single pathways or sets of transcription factors [3], [29]. For example, Moignard et al. [3] analysed more than 40 genes in cells with blood-forming and endothelial potential to map the progression of a mesoderm toward blood in the development of the mouse embryo.

Other Boolean network inference approaches limit the number of inputs for a Boolean function [20], [21], [22]. REVEAL by Liang et al. [20] and Best-Fit Extension [21] by Lähdesmäki et al. search all possible $\left(\begin{array}{c}N\\ k\end{array}\right)$ combinations of input variables for a limited number of inputs, namely $k<K$, to determine a set of Boolean functions with limited error size. Since all possible combinations are considered, these methods suffer from a very high computational complexity. To mitigate this problem, K is usually low, e.g., the authors of REVEAL do not recommend more than 3 genes as an input for a Boolean function of a target gene. Similarly, Han et al. [30] limited the in-degree of a node to 2 in BIBN (full Bayesian Inference approach for a Boolean Network). While the selection of low K can be justified by the overall sparsity of GRNs, it may not be as appropriate when inferring networks with multiple hub genes, i.e., genes with a high degree of connectivity.

Recently, an effort has been made to utilise feature selection approaches to reduce the size of Boolean network inference search space [22], [31]. Barman and Kwon [22] introduced a Mutual Information-based Boolean Network Inference method MIBNI, which first identifies a set of initial regulatory genes that can best characterise the target variable. The method identifies an optimal subset with feature selection based on an approximated multivariate mutual information measure. The obtained subset is often not optimal, since the mutual information is only approximated. This method improves the prediction accuracy in the next step by iteratively swapping pairs of genes between sets of selected and unselected genes. In the end, MIBNI searches for the best fitting Boolean function that minimises the error. The limitation of MIBNI is that a Boolean function can consist of only two layers and one second layer operator, either a disjunction or a conjunction. All regulators, inverted or not, are therefore connected only to this operator. The limitation of this representation is that it is not functionally complete. This means it cannot be used to represent any possible Boolean function, despite utilising operators from a functionally complete set. Due to these limitations, Barman and Kwon proposed GABNI [23], a network inference algorithm that employs a genetic algorithm if MIBNI fails to provide an optimal Boolean function.

Latest Boolean inference approaches can be regarded as hybrid methods, which combine multiple different techniques to infer an accurate Boolean network. For example, Vera-Licona et al. [32] incorporated evolutionary algorithm as an optimisation procedure to infer Boolean functions represented as Boolean polynomial dynamical systems. NNBNI (Neural Network-based Boolean Network Inference) [33] combines mutual information feature selection, genetic algorithms as a global search technique, and a neural network to represent a regulatory rule. Similarly, RFBFE (Random Forest Best-Fit Extension) [31] employs random forest-based feature selection and Best-Fit Extension to infer large Boolean networks. Shi et al. introduced ATEN [24] an AND/OR Tree ENsemble algorithm for inferring accurate Boolean network topology and dynamics. A Boolean function in ATEN is represented by an AND/OR tree in three levels. The first level contains the logical operator OR (∨), second level nodes are labelled with AND (∧) operator, while nodes on the third level are labelled by a Boolean variable or its negation (¬). ATEN works by drawing bootstrap and out-of-bag samples from time series data to infer ensembles of trees and to compute the importance of prime implicants based on out-of-bag samples. Inferred trees are decomposed into prime implicants, and only essential prime implicants are used in the final AND/OR tree reconstruction with simulated annealing. Similarly, TaBooN [34] utilises tabu search algorithm to generate a Boolean representation of a GRN.

An effort has also been made in the development of graphical tools for reconstruction, analysis, and visualisation of GRN models from cell gene expression data [35] (e.g., see Cytoscape [36], VisANT [37], GeneNetWeaver [38] and GeNeCK [39]). In addition to tools with a graphical user interface that allow GRN visualisation and/or inference by utilising known methods and approaches, a number of tools are specialised for executable models in the Boolean domain [40], [41], [42]. BooleSim (Boolean network Simulator) [40] is an in-browser tool for simulation and manipulation of Boolean networks. ViSiBooL (Visualisation and Simulation of Boolean networks) [41] is a simulation and visualisation tool for the modelling of Boolean networks implemented in Java. ViSiBooL allows modelling, simulation, visualisation and organisation of Boolean networks through a graphical user interface. The Single Cell Network Synthesis toolkit (SCNS) [42] is a web-based graphical tool for reconstruction and analysis of executable Boolean models implemented in F# [43]. In addition, SCNS can display stable state attractors as a heatmap. In SCNS, gene expression profiles are represented with binary states. Regulatory rules are then extracted from a state transition graph. The search is limited only to functions with a form $f_1\wedge \neg f_2$, where $f_1$ and $f_2$ contain only AND or OR gates without negation. In this representation, regulators in $f_1$ represent activators while regulators in $f_2$ represent repressors. The algorithm searches for the shortest paths between all pairs of initial and final states with a breadth-first search and extracts transitions where the selected target variable changes. The procedure searches for a Boolean function that is compatible with discovered paths. This final step is encoded as a satisfiability (SAT) problem. For more information see [42], [44], [45]. One limitation of SCNS is its computational complexity. State transition graph with N variables can contain up to $2^N$ states with up to $N\cdot 2^{N-1}$ transitions. The size of a search space, combined with the fact that the SAT problem is NP-complete, makes SCNS an algorithm with high computational complexity.

Evaluation of Boolean inference approaches gives us an insight into how well does a specific method perform in a specific context. This allows us to select the most appropriate Boolean inference method for a given task. The evaluation of methods for inferring Boolean networks can be divided into two categories. Namely, dynamic and static evaluation. In dynamic evaluation, we focus on predicting the correct behaviour of a Boolean network. That is, how well does the simulation of an inferred model match the provided binarised time series data. On the other hand, in static evaluation we mainly focus on the structure of the predicted network, by assessing how similar it is to the underlying system by counting correctly and incorrectly inferred edges. In general, the estimated dynamic and static accuracy should be positively correlated. However, it is well known that different logical expressions can produce the same truth tables, therefore different network topologies can produce similar dynamical output [46]. When the underlying network is not known, reference networks with a similar structure can be used to approximate structural correctness. However, in this case, structural accuracy should be defined in a more general way in the terms of presence of motifs [47] and graphlets [48]. Motifs present partial subgraphs, whereas graphlets are defined as non-isomorphic induced subgraphs. Motifs are patterns of interconnections that occur significantly more frequently than expected when compared to random networks [47]. The same types of motifs emerged in organisms that are not related, since they introduce an evolutionary advantage due to their capability to execute various functions and process information. For this reason, motifs can be seen as building blocks of GRNs, and play a vital role in their general structure. Nonetheless, it is still not entirely clear in what degree can these basic building blocks be further simplified and mapped into Boolean domain. The question is, if inference approaches map similar motifs to the same Boolean functions with some high probability. For this reason, and to better understand the aspect of structural correctness in the domain of Boolean inference, we analyse the structural correctness of inference approaches on the data and networks extracted from the GRN of Escherichia coli (E. coli) [38], [49]. This way, the extracted networks should have similar structural properties as the initial network.

3. Methods

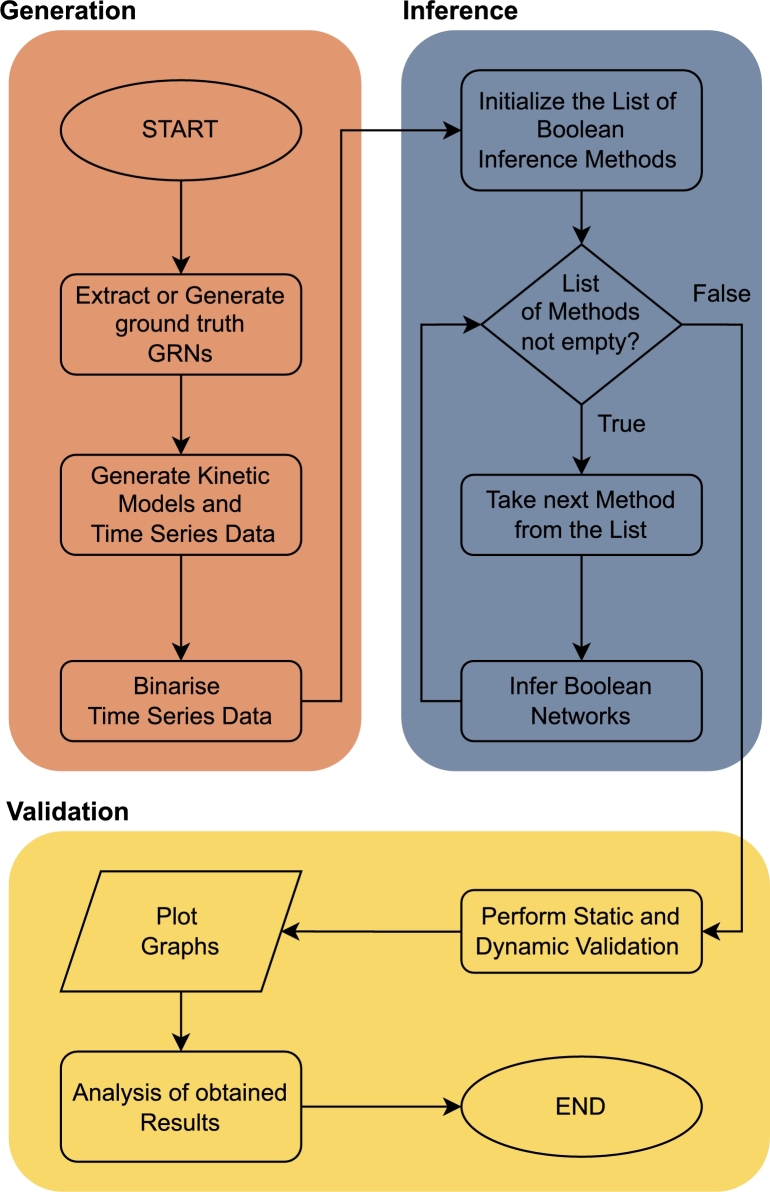
In the following section, we introduce a methodology for evaluation of Boolean network inference techniques. We demonstrate introduced methodology on five different inference methods, namely REVEAL [20], Best-Fit Extension [21], MIBNI [22], GABNI [23] and ATEN [24], which we describe in more detail. The methodology is depicted in Fig. 2.

Figure 2.

Flowchart depicting procedure for validation of methods for Boolean inference. The methodology consists of three main segments. In the first segment, we generate learning and validation datasets. More specifically, we extracted GRNs and produced corresponding kinetic models, which were used to generate a time series of gene expression data. Majority of the work in the first segment was achieved using GeneNetWeaver [38]. The second segment consists of the inference of Boolean networks with selected methods. In the final segment, we perform the static and dynamic validation, plot corresponding graphs and analyse the obtained results.

3.1. Computational methods for inference of Boolean networks

3.1.1. REVEAL

REVEAL is an information theory-based approach for the inference of genetic network architectures [20]. For each target gene, the algorithm exhaustively investigates all $\left(\begin{array}{c}N\\ k\end{array}\right)$ combinations of regulatory candidate sets, where k is a number of regulators and N is the number of nodes. The regulatory set $\mathcal{R}$ completely determines the target gene x if $\mathcal{R}$ accounts for all the entropy of x. I.e., if the amount of mutual information between $\mathcal{R}$ and x is the same as entropy of x. If such a set is found, a Boolean function is extracted from the predefined lookup table. If this set is not found, the function cannot be inferred. Mutual information (M) can be expressed by Equation (1) in terms of entropy (H) as

$$M(x,\mathcal{R})=H(x)+H(\mathcal{R})-H(x,\mathcal{R}),$$ (1)

and it is therefore not necessary to explicitly compute it, since if $M(x,\mathcal{R})=H(x)$ then $H(\mathcal{R})=H(x,\mathcal{R})$, making the computation faster.

For example, consider binarised time series data from Table 1. After we omit values of regulators from the last row and the initial value of the target gene, we get $H(D)=1$ and $M(D,\{A,B,C\})=0.5$. The Boolean function for D cannot be inferred, since the above condition is not satisfied. However, if we fix inconsistencies by changing target variable values in time points 2 and 5, we get $H(D)=M(D,\{A,B,C\})=1$. Nonetheless, the transition table is still incomplete. In order to infer a correct Boolean function, we would need to provide missing transitions, e.g. $D(t+1)=1$ for $A(t)=0,B(t)=0,C(t)=1$ (vector 001) and $D(t+1)=0$ for $A(t)=1,B(t)=0,C(t)=0)$ (vector 100). The complete transition table is given in Table 2. The function $f(A,B,C)=\neg A\wedge \neg B\vee B\wedge C$ now completely determines modified time series data.

Table 1.

Example of binarised time series data with regulators A, B, C, and target variable D.

t	A	B	C	D
1	0	1	0	0
2	0	1	1	1
3	1	0	1	1
4	0	1	1	0
5	0	0	0	0
6	0	1	0	1
7	1	1	1	0
8	1	1	0	1
9	0	1	0	0

Table 2.

Example of a state transition table with regulators A, B, C, and target variable D with a Boolean function f(A,B,C)=¬A∧¬B∨B∧C.

A(t)	B(t)	C(t)	D(t + 1)
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

The computational complexity of reveal is $O(N^{K+1}K{t}_n)$ for a fixed small maximal number of regulators K and $t_n$ time steps. Due to the high computational complexity and overall sparsity of GRNs, the authors do not recommend setting K to larger than 3. Liang et al. [20] evaluated REVEAL on 150 synthetic networks with at most 3 regulators. Furthermore, the authors showed that increasing the number of state transitions logarithmically decreases the number of misidentified functions.

3.1.2. Best-fit extension

Best-Fit Extension [21] is a Boolean inference algorithm based on finding Boolean functions with a minimal error size with respect to partially defined Boolean functions by solving the inconsistency problem. A partially defined Boolean function (pdBf) is a pair of sets T and F containing the vectors of all true and false examples, respectively. The function f is consistent if T is a subset of all examples where f is true, i.e. $T\subseteq T(f)$, and F is a subset of all examples where f is false, i.e. $F\subseteq F(f)$. A consistency problem, e.g. REVEAL, can be solved only if the intersect of sets T and F is an empty set, i.e. there are no input vectors in training data for which the output is 0 and 1. For a given target gene, Best-Fit Extension returns all Boolean functions with limited error size. More specifically, the error of a function f is defined as

$$\epsilon (f)=w(T\cap F(f))+w(F\cap T(f)),$$ (2)

where $w(S)$ is a summation of individual vector weights in the set of all training examples. Weights can be uniform or can depend on the training data, e.g., weights can be proportional to the occurrence of training examples.

For example, consider binarised time series data in Table 1 and a Boolean function $f(A,B,C)=\neg A\wedge \neg B\vee B\wedge C$ (see Table 2). From Table 1 we can extract a partially defined Boolean function pdbf($T,F$), where $T=\{010,011,000,111\}$ and $F=\{101,011,010,110\}$. Next, we assume equal weights $(w_i=1)$ of all examples in pdbf($T,F$). Then $w(T\cap F(f))=w(010)=1$ and $w(F\cap T(f))=w(011)=1$. When we consider uniform example weights, the error size (Equation (2)) is equal to the number of misclassifications.

Best-Fit Extension constructs a generalised truth table filled with symbols “0”, “1”, “?”, “⁎”. The symbol “⁎” represents a conflict, where a vector is both in T and F. If a vector does not appear in the training data, then its output is marked with a “do not care” value “?”. Best-Fit Extension generates a generalised truth table for all possible combinations $\left(\begin{array}{c}N\\ k\end{array}\right)$ of regulatory candidate sets and extracts functions with minimal error size. Computational complexity of the Best-Fit Extension is the same as in REVEAL, nonetheless, unlike REVEAL, Best-Fit Extension solves the inconsistency problem with a minimal error size. Best-Fit Extension was evaluated on the cdc15 yeast gene expression time series data set of cell cycle regulated genes [50]. Instead of the entire network, the authors focused only on a set of five genes, i.e. Cln1, Cln2, Ndd1, Hhf1, Bud3, and inferred all Boolean functions with up to three regulators and limited error size. The obtained results matched with other studies [51]. For example, the cyclin gene Cln1 was found to be regulated by the complex Swi4/Swi6 [51]. This was also predicted by the Best-Fit Extension, where the Boolean functions with regulators Swi4 and Swi6 achieved minimal error size.

3.1.3. MIBNI

To reduce the running time and improve the inference accuracy, Barman and Kwon [22] introduced MIBNI, a Mutual Information-based Boolean Network Inference method. MIBNI first identifies a set of initial regulatory genes that can best characterise the target variable. The method identifies an optimal subset $\mathcal{R}$ with a feature selection based on an approximated multivariate mutual information measure [52]. The problem is that the number of all possible subsets grows exponentially. Mutual information feature selection works incrementally under the assumption of independent features, or in our case independent gene expressions. In each iteration, a new variable v is added to an optimal candidate set $\mathcal{R}$ based on the following criterion

$$\arg \underset{v\notin \mathcal{R}}{\max }M(x,v)-\sum _{r\in \mathcal{R}}M(r,v),$$ (3)

where x represents the target gene.

Again, consider binarised gene expression data from Table 1. We first initialise the set $\mathcal{R}$ with a variable that maximises mutual information with the target variable D. In our case, we would select a regulator A with $M(D,A)=0.049$, $M(D,B)=0$ and $M(D,C)=0$. Now, we would apply mutual information feature selection based on Equation (3) and would consider two candidate regulators B and C. In our case, we would select B since $M(A,B)=0.016$ and $M(A,C)=0.049$.

MIBNI limits the maximal size of the set $\mathcal{R}$ to 10. The method then improves the prediction accuracy by iteratively swapping a pair of genes between the sets of selected and unselected genes. In the end, MIBNI searches for the best fitting Boolean function that minimises the error. By applying smart feature selection, MIBNI reduces the size of a search space of all possible Boolean functions. Nonetheless, the number of possible functions with 10 variables is still large, and MIBNI mitigates this by considering only disjunctive or conjunctive functions. This is biologically unrealistic. For example, two monomers $x_1$ and $x_2$ can form a dimer that activates a target gene, while a third protein $x_3$ represses the target gene independently. The Boolean function $f(x_1,x_2,x_3)=x_1\wedge x_2\vee \neg x_3$, which describes this system, cannot be expressed using only logical conjunction or disjunction. In general, every Boolean function can be expressed with two levels in disjunctive normal form (DNF).

MIBNI was evaluated on 300 random networks with different sizes, from 10 to 100 nodes and up to 10 regulators. These were extracted from E. coli GRN used in DREAM3 challenge [53]. In addition, the method was evaluated on a yeast cell cycle network used in [54] with 10 genes and 23 interactions, of which MIBNI correctly identified 14. Through extensive simulations, MIBNI showed better performance than other network inference methods, including REVEAL [20], BIBN [30] and Best-Fit Extension [21].

3.1.4. GABNI

The limitation of MIBNI is that only disjunction and conjunction functions are considered as Boolean functions. For this reason, Barman and Kwon introduced GABNI [23]. If MIBNI fails to find an optimal solution for a target gene, GABNI employs a genetic algorithm (GA) used to select an optimal set of regulatory genes. Each chromosome is composed of a binary vector of size N, where each element defines the presence or absence of i-th gene as a regulator of the observed gene. At each GA generation, a phenotype for each chromosome is defined on the basis of the gene expression data of regulatory gene $x(t+1)$ and its potential regulators $r(t)=r_1(t)r_2(t)...r_k(t)$ for all bit strings $\mathbf{\text{b}}=b_1{b}_2...b_k$ as $x^{\prime }(t+1)=\arg {\max }_{b\in \{0,1\}}Pr(x(t+1)=b|r(t)=\mathbf{\text{b}})$. Each chromosome is evaluated with the following fitness function

$$f=\frac{1}{(1-C(x,x^{\prime }))\cdot \gamma +k},$$ (4)

where k is a number of regulatory genes, and C is a gene-wise consistency (Equation (5)). Parameter γ is set such that $(1-C(x,x^{\prime }))\cdot \gamma \gg k$. Variant roulette wheel selection is then used to select two parent chromosomes for crossover with a small mutation probability to generate two offspring chromosomes. Each offspring replaces its parent in the next generation if it performs better in terms of its fitness, which is obtained with Equation (4). Barman and Kwon applied their GA over 1000 generations, with a population size of $N+10$. For more information, refer to [23]. A drawback of GABNI is that it identifies only the most suitable target genes and cannot be directly used for the inference of Boolean functions. Instead, GABNI generates a list of regulators and a truth table with the most probable outcome for all different input vectors extracted from binarised time series learning data. Therefore, this table can also be incomplete, if not all possible input vectors are present in the learning data. Nonetheless, GABNI can still identify the interaction types, i.e., activation or repression, between the target and its regulators based on the number of occurrences the regulator has the same value as the target gene, i.e. activation, or the regulator has the opposite value of the target gene, i.e. repression. GABNI was tested on artificial and real time series gene expression datasets and was evaluated on 300 random networks with different number of nodes, from 10 to 100. The method was also evaluated on the data from the past DREAM challenges [53], [55], [56]. More specifically, on two E. coli networks and three yeast networks. In addition, GABNI was validated on a budding yeast cell cycle network with 11 nodes and 29 interactions [57]. In all cases, GABNI performed well in terms of dynamical as well as in terms of structural accuracy, where the gold standard network was given.

3.1.5. ATEN

Instead of selecting the optimal subset of genes that can characterise a target gene, Shi et al. [24] focused on producing an accurate Boolean function in DNF by employing AND/OR Tree ENsemble algorithm (ATEN). A Boolean function in ATEN is represented by an AND/OR tree in three levels. The first level contains the logical disjunction (∨), second level nodes are labelled with conjunction (∧), while nodes on the third level are leaves. Leaves are labelled by a Boolean variable or its negation (¬). An example of a Boolean function depicted with an AND/OR tree is presented in Fig. 3.

Figure 3.

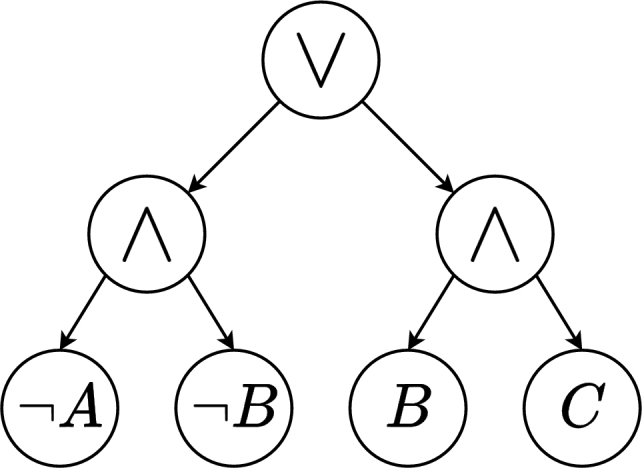
Representation of the Boolean function f(A,B,C)=¬A∧¬B∨B∧C with an AND/OR tree.

ATEN works by drawing bootstrap samples from time series data. Each sample is used to infer a Boolean function for a target gene using simulated annealing. Inferred trees are decomposed into prime implicants, and only essential prime implicants are used in the final AND/OR tree construction. For example, the Boolean function $f(A,B,C)=\neg A\wedge \neg B\vee B\wedge C$ is composed of prime implicants $\neg A\wedge \neg B$ and $B\wedge C$. ATEN first extracts a set of prime implicants by inferring AND/OR tree for each bootstrap sample drawn from time series data. Out-of-bag sample is then used to calculate the importance of prime implicants. The importance is measured based on how removing or adding a prime implicant to the tree reduces or increases misclassification. Important prime implicants are extracted with recursive procedure. In each iteration, only a percentage of prime implicants with the highest importance is kept and the duplicate of the time series dataset is extended based on the states of all remaining prime implicants for all the time steps. This extended dataset is then used in the next iteration of a recursive algorithm to update the set of important prime implicants. The procedure terminates when none of the newly constructed prime implicants is more important than the prime implicants from the previous iteration. Finally, the AND/OR tree is inferred by selecting the optimal input features, i.e. genes or prime implicants, with simulated annealing, where at each iteration a new tree is proposed based on the set of permissible moves, i.e. adding a leaf, removing a leaf, adding or removing prime implicants, etc. The new tree is then accepted with a certain probability based on the misclassification rates and the current temperature. By employing the same procedure for every gene, ATEN produces a full Boolean network. For a more detailed explanation of the algorithm and other information, see [24], [58].

ATEN was evaluated on artificial networks containing 50 or 150 nodes with at most 5 regulators for each node and different noise levels, i.e. 1% and 5% noise. The noise was introduced by random flipping of a state with a corresponding probability. In addition, ATEN was evaluated on a Drosophila segment polarity gene regulatory network [59]. Overall, ATEN outperformed MIBNI, Best-Fit Extension, and the inference approach described by Vera-Licona et al. [32] in terms of recall, false positive rate and F1 score.

3.2. Validation

3.2.1. Synthetic data generation

Generation of synthetic learning and validation data is composed of multiple steps. First, we generate a set of static ground truth GRNs from a reference network, e.g., from E. coli GRN [38], [49]. Networks extracted from realistic GRNs, at least to some degree, retain topological properties of the reference network such as sparsity, shallow paths, and frequently occurring network fragments and motifs [47], [60]. By including these properties in our datasets, we can get a better insight into how Boolean inference methods would perform in real world scenarios.

Generated networks act as a basis for generation of dynamical kinetic models, which are then simulated to produce a time course of gene expression data. Finally, we binarise the time series data using the iterative k-$means$ algorithm [15] with depth 3. Simple k-$means$ clustering with two classes can miss features in the data, such as fluctuations and oscillations. Iterative k-$means$ better addresses these shortcomings [15].

We generated synthetic data with an in silico benchmark generation and performance profiling tool GeneNetWeaver [38]. This tool allows us to import or extract networks from larger GRNs. In addition, GeneNetWeaver constructs dynamical kinetic models based on ODE systems and is able to simulate various types of experiments, i.e. wild-type data, knockdown and knockout data, multifactorial perturbations, and time series data. Examples of generated networks are presented in Appendix A (see Figure A.1, Figure A.2, Figure A.3).

Figure A.1.

Six examples of 16-node networks extracted from the gene regulatory network of E. Coli using GeneNetWeaver [38].

Figure A.2.

Six examples of 32-node networks extracted from the gene regulatory network of E. Coli using GeneNetWeaver [38].

Figure A.3.

Six examples of 64-node networks extracted from the gene regulatory network of E. Coli using GeneNetWeaver [38].

3.2.2. Dynamic validation

An important aspect of Boolean models is the capability to predict the dynamical response of a biological system. For this reason, the dynamic validation offers an important view into predicted model correctness. We evaluated each network based on its predicted dynamics. For each gene, we can define gene-wise consistency C (Equation (5)) as the absolute difference between the observed and predicted behaviour, x and $x^{\prime }$, averaged across $t_n-1$ time steps, excluding the initial state:

$$C=\frac{{\sum }_{t=2}^{t_n}|x(t)-x^{\prime }(t)|}{t_n-1}.$$ (5)

Dynamic error (Equation (6)) is a gene-wise consistency averaged across all N genes and is a quantitative measure for the whole model:

$$\mathit{\text{Dynamic error}}=\frac{{\sum }_{x\in \mathcal{N}}C(x,x^{\prime })}{N}.$$ (6)

Dynamic error can take a value between 0, perfect match, and 1, perfect mismatch. Dynamic error can be interpreted as a normalised Frobenius norm of the difference between the matrix containing the initial time series of all genes and a predicted time series ${\Vert X-X^{\prime }\Vert }_F/((t_n-1)N)$. It can also be written in a bilinear matrix form $a^T|{(X-X^{\prime })}_{ij}|b/((t_n-1)N)$, where a and b are column vectors containing ones. Two notations above offer different representations and means for calculating the dynamic error. Finally, we measure a model performance in terms of its dynamic accuracy (Equation (7)), which is an opposite of dynamic error:

$$\mathit{\text{Dynamic accuracy}}=1-\mathit{\text{Dynamic error}}.$$ (7)

3.2.3. Static validation

While dynamic validation is prevalent in the inference of dynamic models, e.g., Boolean networks, due to the lack of ground truth networks, static validation is more frequently used when the main goal of inference is to produce a structural representation of a gene regulatory network [9]. When performing the static validation of obtained Boolean networks, we applied and extended the measures as introduced in [61] and latter adapted in [24]. To evaluate the inferred networks from a static perspective, i.e. structural correctness, we compared a selected GRN structure with its inferred counterpart. We converted each Boolean network to a graph by replacing Boolean functions and their regulators with undirected edges for every target gene. Based on this comparison, there are four possible basic measures that can be observed, namely

• •TP: the number of correctly predicted edges,
• •TN: the number of correctly predicted non-edges,
• •FP: the number of falsely predicted edges,
• •FN: the number of falsely predicted non-edges.

Based on these measures, we evaluated Boolean network inference approaches based on standard classification measures, i.e., precision, recall, accuracy and F1 score, described in Equations (8), (9), (10) and (11), respectively. Precision is a fraction of correctly inferred edges among all edges in the inferred network, namely:

$$\mathit{\text{Precision}}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FP}}}.$$ (8)

On the other hand, recall presents a fraction of correctly inferred edges among all edges in the initial network:

$$\mathit{\text{Recall}}=\mathit{\text{TPR}}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}.$$ (9)

Precision and recall are important metrics, since we are more interested in edges than in non-edges. Accuracy is the proportion of all correct predictions, including edges and non-edges:

$$\mathit{\text{Accuracy}}=\frac{\mathit{\text{TP}}+\mathit{\text{TN}}}{\mathit{\text{TP}}+\mathit{\text{TN}}+\mathit{\text{FP}}+\mathit{\text{FN}}}.$$ (10)

F1 score is defined as a harmonic mean of the precision and recall:

$$\mathit{\text{F1}}=2\cdot \frac{\mathit{\text{Precision}}\cdot \mathit{\text{Recall}}}{\mathit{\text{Precision}}+\mathit{\text{Recall}}}.$$ (11)

In general, F1 score accounts for class imbalance, and is thus important for our analysis, since the number of non-edges in GRN is much greater than the number of edges. The same metrics can be applied to undirected and directed graphs. One can get even more exact and realistic measures from the perspective of biological context by applying the same metrics to a directed graph. In a sense, Boolean networks can even be seen as an extension of a directed graph. Additionally, if the Boolean inference method utilises edge probabilities or modifiable parameters that would directly affect true positive and true negative rates, AUC (area under the curve) can also be considered for different scenarios (e.g., see [62]).

Additionally to standard classification metrics, we extended our evaluation using the Matthews correlation coefficient (MCC) and bookmaker informedness (BM), described in Equations (12) and (13), respectively. MCC is a robust metric that summarises the classifier performance in a single value, if positive and negative cases are of equal importance [63]. MCC measures the correlation of the true classes with the predictions and ranges from −1 (perfect misclassification) to 1 (perfect classification). It yields a high score only if the predictor correctly predicts the majority of positive as well as the majority of negative cases [64]. MCC can be expressed as:

$$\mathit{\text{MCC}}=\frac{\mathit{\text{TP}}\cdot \mathit{\text{TN}}-\mathit{\text{FP}}\cdot \mathit{\text{FN}}}{\sqrt{(\mathit{\text{TP}}+\mathit{\text{FP}})(\mathit{\text{TP}}+\mathit{\text{FN}})(\mathit{\text{TN}}+\mathit{\text{FP}})(\mathit{\text{TN}}+\mathit{\text{FN}})}}.$$ (12)

Bookmaker informedness (BM) combines the prediction of false negatives and false positives in a single metric and ranges from −1 to 1 similarly as MCC [65]. It can be expressed as:

$$\mathit{\text{BM}}=\mathit{\text{TPR}}+\mathit{\text{TNR}}-1=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}+\frac{\mathit{\text{TN}}}{\mathit{\text{TN}}+\mathit{\text{FP}}}-1.$$ (13)

3.2.4. Running time

Running time is an important indicator that can give us an insight into the computational complexity of a method and its implementation. However, to assess the scalability of a method, we must take into account the increase in running time, as the complexity of the problem increases. In our case, we used three different network sizes. Even though it is not biologically realistic, we could also increase the maximal number of regulators or the number of training examples. Analysis of running time from the perspective of computational complexity also mitigates the problem of comparing algorithms on different systems with a varying number of cores and other computational resources. In our case, implementations of GABNI and ATEN are parallelised and can take advantage of multicore platforms. Nonetheless, parallelisation of an algorithm does not affect its computational complexity, only its running time, which is reduced by a constant factor.

3.3. Case study

We used GeneNetWeaver [38] to extract GRNs from the E. coli network and to generate gene expression datasets. We extracted 10 networks with 16 nodes and at least 5 regulators (see Appendix A, Fig. A.1), 10 networks with 32 nodes and at least 10 regulators (see Appendix A, Fig. A.2), and 10 networks with 64 nodes and at least 20 regulators (see Appendix A, Fig. A.3). For each network, we generated 10 time series with noise and 56 time steps. We believe that the number of time steps is low enough to maintain biological relevance, while at the same time providing enough data to inference methods to infer as accurate Boolean networks as possible. All parameters were the same as in in-silico network challenge DREAM4 [53], [55], [66]. To obtain data suitable for Boolean inference, we binarised the time series data with iterative k-$means$ with depth 3. To obtain representative and accurate results, we inferred 10 networks based on 10-fold cross validation for each network and inference method. We therefore inferred 1500 networks with 16, 32 and 64 nodes. Every performance measure was evaluated based on 10-fold cross validation and averaged across 10 networks for different sizes.

We implemented a Python 3 script to evaluate the selected Boolean network inference methods, namely, REVEAL, Best-Fit Extension, MIBNI, GABNI, and ATEN, from a static and dynamic perspective. The script utilises a module subprocess from the Python Standard Library to run methods in separate processes. This module also allowed us to evaluate approaches implemented with different programming languages and technologies. REVEAL and Best-Fit Extension are written in Python 2. Their implementations are available in the package published in [15]. Barman and Kwon provided us with the source code for methods MIBNI and GABNI written in Java. While GABNI was already fully implemented, we had to partially implement MIBNI, since only MIFS and SWAP routines were provided. ATEN is written in R and is available at https://github.com/ningshi/ATEN. Validation software with training data, results and implementations of methods for inference of Boolean networks is available within a Linux Docker image at https://hub.docker.com/r/zigapusnik/review_and_assessment_bn_inference.

4. Results

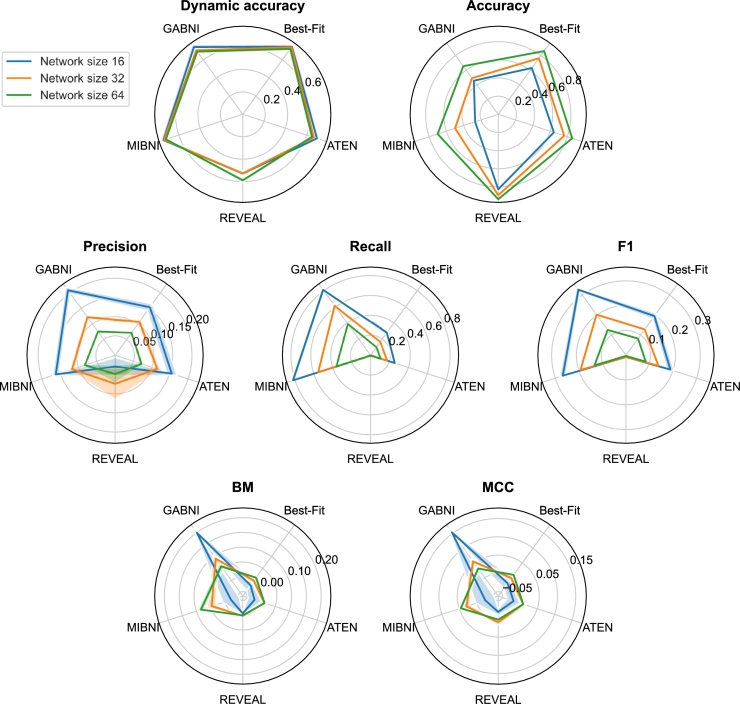
We evaluated methods REVEAL, Best-Fit Extension, MIBNI, GABNI and ATEN based on dynamic accuracy, structural accuracy, precision, recall, F1 score, BM, MCC (see Fig. 4) and running time (see Fig. 5). We ran the methods on NVIDIA DGX A100 system with 32 allocated CPU cores. Nonetheless, only GABNI and ATEN are parallelised and have the capability to take advantage of multicore platforms. In accordance with our expectations, dynamic accuracy decreases as the number of nodes in a network increases. Except for REVEAL, all methods achieve similar dynamic accuracy. REVEAL focuses on inferring Boolean functions with no inconsistencies and with all input vectors present in the learning examples. Inconsistencies in training examples are common and arise due to noise, which is a consequence of the stochasticity of biochemical reactions. For this reason, the majority of genes are not inferred with REVEAL, which consequently leads to a poor dynamic performance. GABNI does not infer a Boolean function for a target gene, and instead produces a truth table with the most probable outputs. We therefore mapped the output from the truth table if the current vector was present in the corresponding table. Otherwise, we set an output of a target gene to 0, i.e. False. In our case, GABNI achieved comparable results to other methods since we provided enough learning examples, i.e., 10 time series with 56 time steps for each GRN. In the case when only limited number of examples is available, GABNI performs worse. In the network inference stage, dynamic accuracy is typically the main metric that inference approaches try to maximise. This can also be the reason that all Boolean inference approaches achieved similar results in terms of dynamic accuracy.

Figure 4.

Dynamic accuracy, structural accuracy, precision, recall, F1, bookmaker informedness (BM) and Matthews correlation coefficient (MCC) for the evaluated Boolean inference methods for networks with 16, 32, and 64 nodes. Results were obtained with 10-fold cross-validation and averaged across 10 networks for each network size. Solid lines represent mean values. Shaded areas represent 95% confidence intervals.

Figure 5.

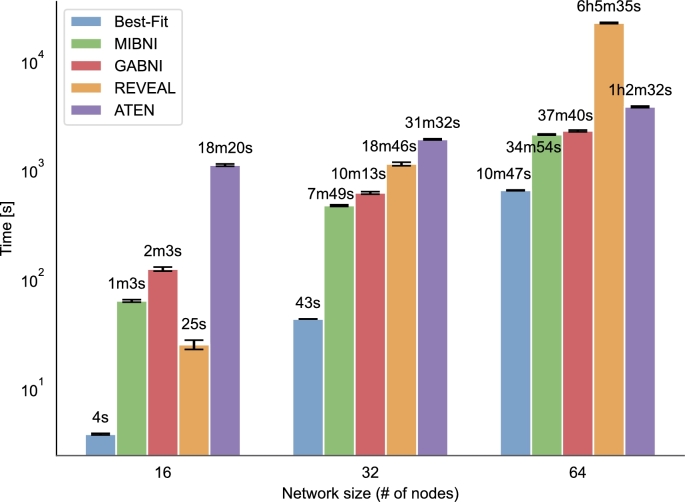
Running time for the evaluated Boolean inference methods for networks with 16, 32, and 64 nodes. Results were obtained with 10-fold cross-validation and averaged across 10 networks for each network size. Bars represent running time, and whiskers represent 95% confidence intervals. Values are displayed in a logarithmic scale.

The results of structural accuracy analysis are displayed in Fig. 4 (Accuracy). Opposite to dynamic accuracy, the structural accuracy increases as the number of nodes in a network increases. At first glance, this seems counter-intuitive, since the problem gets harder with larger GRNs. However, structural accuracy accounts for all correctly predicted edges and non-edges alike, and a majority classifier that always predicts a non-edge will achieve high structural accuracy. For this reason, REVEAL performs best in terms of structural accuracy. In addition, structural accuracy exhibits little or no deviation, since the majority of the variance is introduced with predicted edges being either true positives, false positives, or false negatives. For the above reasons, structural accuracy alone is not suitable as a performance metric in the domain of inferring gene regulatory networks. To gain better insight into structural correctness, one should consider precision and recall as well.

GABNI, MIBNI, Best-Fit Extension, and ATEN achieved comparable results in terms of precision, i.e., the ratio of correctly predicted edges among all predicted edges. Precision, recall, and F1 score also decrease when the number of nodes in a network increases. As opposed to the structural accuracy, REVEAL achieved the worst results, since it was unable to infer the majority of genes. MIBNI and GABNI performed best in terms of recall, i.e., the ratio between the correctly predicted edges and all true edges. However, MIBNI and GABNI performed the worst in terms of structural accuracy, which means that both methods infer a significantly larger number of regulators than necessary. MIBNI infers up to 10 regulators for a given target gene. GABNI can infer even more regulators for a target gene. More precisely, it can infer up to $0.6\cdot N$ regulators per gene, where N is a total number of genes in a network. In both cases, the maximal number of regulators is reached if the training examples contain inconsistencies and an optimal subset could not be determined. However, inconsistencies are almost ubiquitous due to noise in the training sets, which arises from the stochastic nature of biochemical reactions, other internal and external factors, and variability within experiments. A greater number of false positives affects the score of structural accuracy negatively, while it does not hinder precision and recall, since a greater number of inferred edges corresponds to a larger number of true positives. The F1 score is a harmonic mean of precision and recall, which can also be observed in Fig. 4 (F1). REVEAL, Best-Fit Extension, MIBNI and ATEN performed similarly in terms of BM and MCC scores. GABNI performed best for smaller networks. Both scores, in a sense, measure how similar is the predicted network to the one constructed with random guessing. Obtained results indicate that the observed inference methods performed poorly and do not substantially outperform random guessing in the context of static evaluation. Precision, recall, and F1 score alone are not as suitable as a performance metric and should be, to ensure unbiased evaluation, only taken into account together with the structural accuracy, BM and MCC scores.

In addition to the performance metrics, we also measured the required running time to infer a Boolean network for each method. Results are displayed in Fig. 5. In addition to the total running time, we should also consider the computational complexity, which can be estimated with the increase of running time as the number of nodes in a network increases. Results are displayed on a logarithmic scale, due to an exponential increase in running time. An exponential factor in computational complexity arises from the exponential number of possible regulators for a given target gene, and a double exponential increase in possible functions as the number of regulators increases. Best-Fit Extension and REVEAL have the lowest running times for small networks (16 nodes). Nonetheless, both methods have the steepest slope and are thus less suitable for larger networks. Despite the fact that both methods have a similar computational complexity, REVEAL requires significantly more time to infer a network. This indicates that the current implementation of REVEAL is not optimal, which can result from the use of inappropriate data structures or unnecessary recalculations of the required expressions. In addition to lower running time, Best-Fit Extension also outperforms REVEAL, since it can successfully deal with inconsistencies in the input data. Other approaches have a slightly more acceptable slope and are thus more suitable for larger networks. Overall, ATEN requires the largest amount of time to infer a network, however, it also has the best scalability.

5. Discussion

Since the static validation is usually performed on directed or undirected graphs obtained from a Boolean network, high metric values do not necessarily mean good prediction. Therefore, static validation needs to be used in a combination with the proposed dynamical validation to thoroughly investigate the predictive power of obtained Boolean networks. All methods performed well in terms of dynamic accuracy and slightly worse in terms of structural correctness. Poor performance of Boolean inference approaches in terms of structural correctness can also be observed in [10]. According to our experiments, all methods performed poorly in terms of precision. This indicates that dynamic accuracy should not be the only criterion when inferring gene regulatory networks in Boolean domain. Additional metrics, e.g. MC and BM, that explain how do the inference results compare to random guessing, should also be utilised. MCC and BM combine the prediction of false negatives and false positives in a single metric and give a more comprehensive view on the classifier performance. Even though MCC surpasses other conventional metrics for the assessment of classification, it may not represent a robust metric if the prevalence (ratio of positive cases in a dataset) significantly differs among datasets [63]. In the context of GRN inference, this might prove to be problematic for two reasons. Firstly, average connectivity within a network and thus prevalence of edges can differ significantly among different species [67]. Secondly, if we presume that the average connectivity is independent of a (sub)network size within the same species, the number of edges within the network will grow linearly with the network size. On the other hand, the number of all possible edges grows quadratically with the network size. This means that the prevalence will decrease in larger sub(networks) even within the same species. MCC could thus reflect different trends for the same method among different species, as well as within the same species for (sub)networks with different sizes. However, this is also the case for other conventional metrics as employed in this study. To make the assessment of inference methods more robust and transferable to different scenarios, one should opt to use a metric that reflects larger robustness to variable prevalence, such as BM [63], [65].

To increase structural as well as dynamical accuracy, a general structure of GRNs could also be considered. Gene regulatory networks are in general sparse, shallow and are composed of patterns that occur significantly more often than expected in random networks [47], [48]. This prior knowledge could be utilised to infer more accurate Boolean networks in terms of structural correctness [68]. It could either be defined as a set of predefined rules and guidelines, or could be extracted from the provided additional reference networks before the inference phase. Some inference methods can already, at least to some degree, rely on prior knowledge [69], [70], [71]. However, an automatic extraction of frequently occurring patterns and other network properties from reference networks is yet to be applied in the context of inferring Boolean networks.

Another reason for a slightly worse structural performance of inference methods, could be that multiple regulators with different descriptions of Boolean function produce the same results based on the same binarised learning data. In other words, for a given target gene, the system can be either underdetermined or overdetermined, where multiple solutions or no solutions are possible. In addition, binarisation of time series data can introduce a loss of information [72], [73], while different binarisation techniques can produce different results [15]. To mitigate this problem, Boolean inference methods could in addition to binarised learning data also consider data in continuous format (e.g. [74]). For example, to select a compact and accurate subset of potential regulators for a given target gene, an information theory-based approach could compute mutual information based on discrete and continuous data. Two obtained scores can then be directly compared based on their rank. This would give us additional insight and confidence into a selected subset of potential regulators. In addition to continuous time series data, Boolean network inference approaches could also utilise other data sources to improve their inference performance in terms of structural correctness (e.g., see [75], [76]). Gene expression depends on interactions between multiple biological processes. For instance, copy number variations, histone modifications, DNA methylations, etc., could also be incorporated. For example, Zarayeneh et al. [76] included copy number variations and DNA methylations in the process of network inference.

Other extensions to improve inference of Boolean networks could also be made. For example, Schwab et al. [77] developed a network reconstruction pipeline to infer an ensemble of Boolean networks from single-cell RNA-sequencing (scRNA-seq). The reconstruction pipeline generates pseudo-time series by exploiting the heterogeneity of single-cell populations, where the state of each single-cell measurement is assumed to be a potential predecessor or successor of the state of each other single-cell measurement from the same individual. Next, potential regulatory interactions are filtered with correlation-based screening. Finally, an ensemble of Boolean networks is inferred with the filtered Best-Fit approach. By applying this preprocessing step to filter potential dependencies, Schwab et al. [77] improved the computational time and robustness to noisy data. Biological systems are inherently stochastic and robust in the presence of noise. Therefore, the stochastic Boolean network model is potentially useful in the modelling of gene regulatory networks [78]. The inference methods included in our assessment produce Boolean network models, which can be applied using different updating schemes. Reconstruction of a deterministic network is a laborious process requiring significant computing resources. However, inference of stochastic networks presents an even more challenging problem.

Other formalisations of Boolean functions could be explored in the context of optimisation and inference. For example, the representation of Boolean functions with semi-tensor products offers additional algebraic principles that could be exploited in the domain of inference of Boolean genetic models. Nonetheless, recent advances in semi-tensor product based studies of Boolean networks have mostly been applied in the context of observability and controllability of logical control networks [79], [80].

Overall, none of the validated methods did not outperform others and there is no clear winner. However, REVEAL stands out negatively. It performed worse in terms of static as well as dynamic validation, since REVEAL cannot deal with inconsistencies in learning data. To mitigate this problem, one could preprocess the learning data and assign the most probable output to examples with conflicting outputs. On one hand, GABNI achieved the best F1 score and has good predictive power, while on the other hand it performed the worst in terms of structural accuracy. According to the obtained results, the methods that overestimate the number of regulators have higher precision and recall, while performing worse in terms of structural accuracy.

6. Conclusion

Accurate Boolean descriptions of gene regulatory networks can give us a detailed insight into the dynamics of GRNs. These descriptions can be obtained using different inference methods, which, as we showed, still have room for improvement. Better understanding of the interactions between genes would have a beneficiary impact in the field of synthetic as well as systems biology. However, the ability to reconstruct an accurate network with a given set of methods needs to be assessed before these are applied in relevant biological applications.

In this paper, we reviewed fundamental and state-of-the-art methods for Boolean inference of GRNs and applied a methodology for a thorough evaluation of these methods. We demonstrated our evaluation approach on five different inference methods, namely REVEAL, Best-Fit Extension, MIBNI, GABNI and ATEN. If needed, we reimplemented a given method. To perform a thorough evaluation of the selected methods, static and dynamic validation measures were proposed. We measured the static and dynamic performance on the networks extracted from the GRN of E. coli. To assess the scalability of each method, we validated these on different network sizes, i.e. networks with 16, 32 and 64 nodes.

Our results indicate, that the inference methods aimed at the reconstruction of Boolean networks could be further improved. Overall, all methods performed well in terms of dynamic accuracy and worse in terms of structural correctness. For this reason, we suggested guidelines for inferring Boolean rules in the domain of gene regulatory networks, which include learning from continuous as well as binarised data and incorporation of learning data from multiple sources as well as integration of prior knowledge. We strongly believe that these extensions would increase the performance of Boolean inference methods and should be incorporated in the inference process in the near future.

Declarations

Author contribution statement

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

This work was supported by Slovenian Research Agency [P2-0359; J1-9176], Ministry of Education, Science and Sport of the Republic of Slovenia [ELIXIR-SI RI-SI-2] and by European Regional Development Fund [ELIXIR-SI RI-SI-2].

Data availability statement

Data associated with this study [validation software with training data, results and implementations of methods for inference of Boolean networks] has been deposited within a Linux Docker image at https://hub.docker.com/r/zigapusnik/review_and_assessment_bn_inference.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.