BRIDGING RANDOMIZED CONTROLLED TRIALS AND SINGLE-ARM TRIALS USING COMMENSURATE PRIORS IN ARM-BASED NETWORK META-ANALYSIS

Abstract

Network meta-analysis (NMA) is a powerful tool to compare multiple treatments directly and indirectly by combining and contrasting multiple independent clinical trials. Because many NMAs collect only a few eligible randomized controlled trials (RCTs), there is an urgent need to synthesize different sources of information, e.g., from both RCTs and single-arm trials. However, single-arm trials and RCTs may have different populations and quality, so that assuming they are exchangeable may be inappropriate. This article presents a novel method using a commensurate prior on variance (CPV) to borrow variance (rather than mean) information from single-arm trials in an arm-based (AB) Bayesian NMA. We illustrate the advantages of this CPV method by reanalyzing an NMA of immune checkpoint inhibitors in cancer patients. Comprehensive simulations investigate the impact on statistical inference of including single-arm trials. The simulation results show that the CPV method provides efficient and robust estimation even when the two sources of information are moderately inconsistent.

1. Introduction.

Meta-analyses and network meta-analyses (NMAs) are fundamental tools to quantitatively and rigorously assess efficacy and cost-effectiveness of interventions in evidence synthesis (Welton et al., 2012), analyzing many studies at the same time. While standard pairwise meta-analyses can compare only two treatments, NMA was developed to compare multiple (≥ 3) interventions simultaneously. Both contrast-based NMA (CB-NMA) (Lu and Ades, 2004, 2006, 2009) and arm-based NMA (AB-NMA) (Zhang et al., 2014; Hong et al., 2016a; Zhang et al., 2017a) frameworks have been proposed, with the main difference lying in what they assume is exchangeable across studies: absolute treatment effects in AB-NMA, relative treatment effects (contrasts) in CB-NMA. Generally, randomized controlled trials (RCTs) with a blinded outcome assessment offer high-quality and reliable evidence for statistical analyses (Egger, Davey Smith and Altman, 2001) and are preferred for inclusion in meta-analyses. Partly because of strict screening processes, however, nearly half of the meta-analyses in the Cochrane Database of Systematic Reviews contain only two or three RCTs (Kontopantelis, Springate and Reeves, 2013). It is challenging to select an appropriate method for meta-analysis with only a few RCTs (≤ 5), balancing statistical power and nominal coverage probability (Mathes and Kuss, 2018). Similarly, in a survey of 186 NMAs, nearly 40% of treatments were included in four or fewer trials, and the median number of trials per comparison was 2 with an interquartile range of 1–4 (Nikolakopoulou et al., 2014; Wang et al., 2021). Because of this, variances of outcomes for individual treatments (absolute effects) in AB-NMA and variances for individual treatment comparisons (relative effects) in CB-NMA are difficult to estimate. Hence, it is natural to consider an extrapolation strategy in meta-analysis and NMA.

When information is sparse in a targeted population, information borrowing is a useful technique for incorporating an external data source to improve statistical estimation. It has been widely used in RCTs by incorporating historical controls when diseases are rare or patient populations are small (Chen et al., 2011; Hueber et al., 2012; Gamalo, Tiwari and LaVange, 2013; Gamalo-Siebers et al., 2017). While the history of borrowing external information in evidence synthesis dates back to the 1990s, when Begg and Pilote (1991) and Li and Begg (1994) tried to combine results from controlled and uncontrolled studies using a frequentist approach, only recently have we witnessed a surge of publications on this topic. For example, Zhang et al. (2019) proposed methods for a meta-analyses to adaptively combine RCTs and single-arm trials, while Röver, Wandel and Friede (2018) used Bayesian model averaging to borrow adult evidence in pediatric meta-analysis, which generally has fewer trials available. In CB-NMA, an approach to incorporate single-arm trial data by using aggregate-level covariate matching has been proposed and discussed (Jaff et al., 2017; Schmitz et al., 2018; Leahy et al., 2019; Phillippo et al., 2020). In addition, Efthimiou et al. (2017) recently proposed approaches to combining randomized and non-randomized evidence in CB-NMA, while Thom et al. (2015) proposed a method to conduct indirect comparisons in an incomplete network by including single-arm observational studies. Turner et al. (2019) introduced four different informative priors for multiple heterogeneity variances in CB-NMA. There are also AB-NMA methods to synthesize aggregate and individual patient data (Hong, Fu and Carlin, 2018).

So far, however, very little attention has been paid to including single-arm trials in an AB-NMA, partly because there is an ongoing debate about CB-NMA versus AB-NMA (Dias and Ades, 2016; Hong et al., 2016b; White et al., 2019). The AB approach has the potential to estimate marginal absolute risks, which are necessary to calculate the incremental cost effectiveness ratio for comparing the cost-effectiveness of health care interventions. As mentioned above, however, scant information is so prevalent in NMA that it is difficult to estimate the standard deviations of treatment-specific effects across trials (e.g., the log odds, if the logit transformation is used in AB-NMA with binary outcomes). Although a homogeneous variance assumption or variance shrinkage methods can help, these methods require some strong assumptions about variances (Wang et al., 2021). Hence, to provide better estimates it is necessary to develop methods that can incorporate extra evidence from single-arm trials in AB-NMA.

Several statistical methods have been developed for “information borrowing” using Bayesian methods, for instance, power priors (Chen and Ibrahim, 2000; Duan, Ye and Smith, 2005; Ibrahim et al., 2015), hierarchical commensurate priors (Hobbs et al., 2011; Hobbs, Sargent and Carlin, 2012; Murray, Hobbs and Carlin, 2015), and Bayesian model averaging (Schmidli et al., 2014; Kaizer, Koopmeiners and Hobbs, 2018; Kaizer, Hobbs and Koopmeiners, 2018). Motivated by these methods, we propose commensurate priors to adaptively incorporate variance information from single-arm trials into an AB-NMA. Although an AB-NMA naturally incorporates single-arm trials (Lin, Chu and Hodges, 2016), current methods do not explicitly account for the possibly lower quality of single-arm trials. Our new method, by contrast, has the advantage of downweighting single-arm trials when they appear to be inconsistent with two- or multi-arm RCTs in an NMA.

The rest of this article is organized as follows. Section 2 describes a motivating example, an NMA comparing safety of different immune checkpoint inhibitors for treating cancer. Section 3 introduces commensurate priors to combine RCTs and single-arm trials in an AB-NMA. Section 4 presents results from applying our method to the motivating example, followed by simulation studies in Section 5, comparing the performance of different commensurate priors. Section 6 summarizes our findings and discusses future research.

2. Motivating example.

Immune checkpoint inhibitors (ICIs) have recently emerged as a breakthrough in treating more than 14 cancers including melanoma, Hodgkin lymphoma, non-small cell lung cancer, and others (Johnson, Chandra and Sosman, 2018). To investigate the safety of ICIs, Xu et al. (2018) conducted a systematic review and NMA mainly on five ICIs, ipilimumab, tremelimumab, nivolumab, pembrolizumab, and atezolizumab. Only 3 out of 31 RCTs had an atezolizumab arm, making parameters related to this ICI (e.g., variance, absolute risk, and relative risk) difficult to estimate. Fortunately, Xu et al. (2018) identified not only the 31 RCTs but also found 36 single-arm trials. We collected all available data from these RCTs and single-arm trials for our analysis.

Table A1 in Appendix A presents a cleaned dataset of 27 RCTs and 28 single-arm trials comparing eight treatments: 1) nivolumab 3mg/kg every 2 weeks (NIV); 2) ipilimumab 3mg/kg every 3 weeks (IPI low); 3) ipilimumab 10mg/kg every 3 weeks (IPI high); 4) pembrolizumab (PEM); 5) atezolizumab 1200mg every 3 weeks (ATE); 6) one ICI drug plus investigator’s choice chemotherapy (ICI+ICC); 7) two ICI drugs together (2ICIs); and 8) investigator’s choice chemotherapy (ICC). The outcome is safety, specifically occurrence of any treatment-related grade 3–5 adverse events. Figure 1 intuitively shows the need to borrow information from single-arm trials to potentially improve estimation. For example, only 4 and 3 RCTs contain ipilimumab (high dose) and atezolizumab respectively, causing difficulty in estimating the variances of these two treatment-specific log-odds. Nevertheless, with the additional information from single-arm trials (3 for each of these two ICIs), we may be able to overcome this problem.

Fig 1.

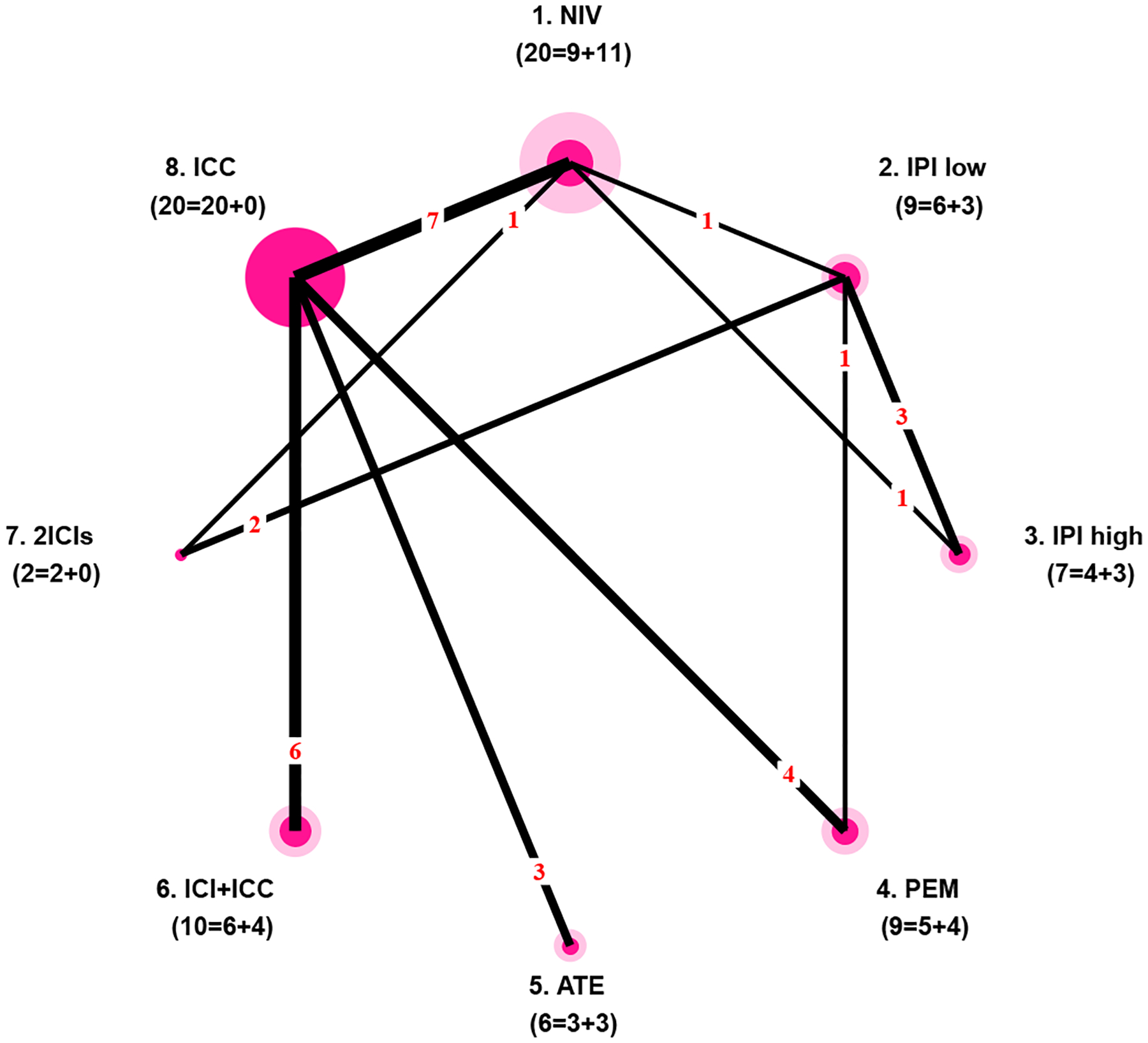
Network plot of the dataset about safety of ICIs in treating cancer. Each node represents a regimen, and each edge represents a direct comparison between two regimens. Node radius is proportional to the number of RCTs including the regimen (dark inner circle) plus the number of single-arm trials of the regimen (light outer circle). Edge thickness is proportional to the number of direct comparisons. Numbers in parentheses under a regimen name are the number of RCTs and the number of single-arm trials including the regimen. For example, 9 RCTs and 11 single-arm trials investigate nivolumab.

3. Statistical methods.

3.1. Notation.

Assume an NMA has K RCTs comparing a total of T treatments. Let ${\mathcal{A}}_k$ (k = 1, …, K) be the subset of treatments in the k^th trial. For most RCTs, the number of treatments in ${\mathcal{A}}_k$, denoted by $\left|{\mathcal{A}}_k\right|$, is 2 or 3. Let ${\mathcal{D}}_k$ be the data observed in the k^th RCT. For NMAs with a dichotomous outcome, ${\mathcal{D}}_k=\left\{\left(r_{kt},n_{kt}\right),t\in {\mathcal{A}}_k\right\}$, where r_kt and n_kt are the numbers of events and participants respectively for the t^th treatment in the k^th RCT. Assume that the NMA also includes J single-arm trials. Let ${\mathcal{D}}_j^{\text{s}}(j=1,\dots ,J)$ be the data collected in the j^th single-arm trial; ${\mathcal{D}}_j^{\text{s}}=\left\{\left(r_{jt}^{\text{s}},n_{jt}^{\text{s}}\right),t\in {\mathcal{A}}_j^{\text{s}}\right\}$, where ${\mathcal{A}}_j^{\text{s}}$ includes only one treatment with $\left|{\mathcal{A}}_j^{\text{s}}\right|=1$, and $r_{jt}^{\text{s}}$ and $n_{jt}^{\text{s}}$ are the numbers of events and participants for the t^th treatment in the j^th single-arm trial. We further define B_t to be the number of RCTs containing the t^th treatment, and $B_t^{\text{s}}$ to be the number of single-arm trials containing the t^th treatment. For instance, as shown in Figure 1, 9 RCTs and 11 single-arm trials contain nivolumab, so B₁ = 9 and $B_1^{\text{s}}=11$.

3.2. Arm-based network meta-analysis and model for single-arm trials.

This subsection briefly introduces the AB-NMA (Zhang et al., 2014; Hong et al., 2016a) and the model for single-arm trials, focusing on binary outcomes. The AB-NMA model for RCTs is:

$$\begin{gathered} r_{kt}~\text{Binomial}\left(n_{kt},p_{kt}\right),t\in {\mathcal{A}}_k,k=1,\dots ,K; \\ \text{logit}\left(p_{kt}\right)={\theta }_{kt}; \\ {\left({\theta }_{k1},\dots ,{\theta }_{kT}\right)}^{\prime }~MVN(\mu ,\Sigma ), \end{gathered}$$ (1)

where p_kt is the probability of an event (i.e., absolute risk) for the t^th treatment in the k^th trial and the latent log odds θ_k = (θ_k1, …, θ_kT)′ are assumed to follow the multivariate normal distribution with mean μ and covariance matrix Σ. Here, x′ denotes the transpose of the vector x. The vector of latent variables θ_k models all T treatments, even though only $\left|{\mathcal{A}}_k\right|$ treatments t are actually observed in trial k. The vector μ = (μ₁, …, μ_T)′ contains the overall logit event probability for each treatment. If we denote the between-trial standard deviation of treatment t by σ_t, we can decompose Σ as ΔPΔ, where P = {ρ_ij} is the correlation matrix and Δ is a diagonal matrix with σ_t being its t^th diagonal element. We further define μ^RCT = (μ₁, …, μ_T)′, and σ^RCT = (σ₁, …, σ_T)′. This model is exactly the same as Model 4 in White et al. (2019) though with slightly different notation. We call this original method no borrowing (NB) because it does not incorporate any information from single-arm trials.

Similarly, the model for single-arm trials is:

$$\begin{gathered} r_{jt}^{\text{s}}~\text{Binomial}\left(n_{jt}^{\text{s}},p_{jt}^{\text{s}}\right),t\in {\mathcal{A}}_j^{\text{s}},j=1,\dots ,J; \\ \text{logit}\left(p_{jt}^{\text{s}}\right)={\theta }_{jt}^{\text{s}}; \\ {\theta }_{jt}^{\text{s}}~N\left({\mu }_t^{\text{s}},{\left({\sigma }_t^{\text{s}}\right)}^2\right), \end{gathered}$$ (2)

where $p_{jt}^{\text{s}}$ is the probability of an event for the j^th single-arm trial, ${\mu }_t^{\text{s}}$ represents the overall fixed effect of treatment t from single-arm trials, and ${\sigma }_t^{\text{s}}$ is the standard deviation of the t^th treatment for single-arm trials. Unlike Equation (1), which contains some latent variables corresponding to unobserved treatment arms, the variables in Equation (2) all correspond to observed treatment arms. We further define ${\mu }^{\text{s}}={\left({\mu }_1^{\text{s}},\dots ,{\mu }_T^{\text{s}}\right)}^{\prime }$ and ${\sigma }^{\text{s}}={\left({\sigma }_1^{\text{s}},\dots ,{\sigma }_T^{\text{s}}\right)}^{\prime }$.

3.3. Connecting NMA and single-arm trials.

Based on the models above for an NMA and single-arm trials, we consider several methods to adaptively integrate information from the single-arm trials into the NMA.

3.3.1. Existing methods: full borrowing.

The AB-NMA model in Equation (1) could naturally incorporate information from single-arm trials about means and variances by assuming ${\mu }_t={\mu }_t^{\text{s}}$ and ${\sigma }_t={\sigma }_t^{\text{s}}(t=1,\dots ,T)$. We call this method fully borrowing on means and variances (FBMV). However, this assumption may be too strong and unrealistic. Instead, we can take a step back and only borrow information about variances from single-arm trials by assuming ${\sigma }_t={\sigma }_t^{\text{s}}$ while ${\mu }_t\ne {\mu }_t^{\text{s}}$. We call this method fully borrowing on variances (FBV). We could also borrow mean information only by assuming ${\mu }_t={\mu }_t^{\text{s}}$ while ${\sigma }_t\ne {\sigma }_t^{\text{s}}$, but this article will not discuss this fully borrowing on mean (FBM) method in detail as it might be less useful in practice.

3.3.2. Commensurate prior on mean.

Although a full-borrowing approach naturally integrates single-arm trials, it may also cause large biases if the reliability of single-arm trials may be doubtful. Instead, a commensurate prior on the means, introduced by Hobbs, Sargent and Carlin (2012), is a simple, flexible way to borrow from and downweight single-arm trials:

$${\mu }_t~N\left({\mu }_t^{\text{s}},{\eta }^{-1}\right);$$ (3)

that is, μ_t has a normal prior with mean ${\mu }_t^{\text{s}}$ and precision η. The precision η characterizes how commensurate the two sources of information (μ_t and ${\mu }_t^{\text{s}}$) are with each other. Hobbs, Sargent and Carlin (2012) proposed a “spike-and-slab” prior for η, but estimation of η is still difficult with this prior. Instead, Murray, Hobbs and Carlin (2015) proposed a modified commensurate prior:

$$\begin{gathered} {\mu }_t~{\left[N\left({\mu }_t^{\text{s}},{\left({\tau }_t^{\text{m}}\right)}^{-1}\right)\right]}^{1-{\kappa }_t^{\text{m}}}{\left[N\left({\mu }_t^{\text{s}},{\left(R^{\text{m}}\right)}^{-1}\right)\right]}^{{\kappa }_t^{\text{m}}}; \\ {\kappa }_t^{\text{m}}~\text{Bern}\left(p^{\text{m}}\right)\text{ and }{\tau }_t^{\text{m}}~U\left(s_1^{\text{m}},s_{\text{u}}^{\text{m}}\right),t=1,\dots ,T, \end{gathered}$$ (4)

where Bern(p^m) denotes a Bernoulli distribution with $\text{Pr}\left({\kappa }_t^{\text{m}}=1\right)=p^{\text{m}}$, and the prior distribution on the precision ${\tau }_t^{\text{m}}$ is uniform from $s_1^{\text{m}}$ to $s_{\text{u}}^{\text{m}}$ with $0\le s_1^{\text{m}}<s_{\text{u}}^{\text{m}}\ll R^{\text{m}}$ and 0 ≤ p^m ≤ 1 pre-specified. With this prior, μ_t follows a two-part mixture normal distribution consisting of a highly concentrated component, i.e., $N\left({\mu }_t^{\text{s}},{\left(R^{\text{m}}\right)}^{-1}\right)$, and a relatively diffuse component, i.e., $N\left({\mu }_t^{\text{s}},{\left({\tau }_t^{\text{m}}\right)}^{-1}\right)$. This distribution imitates a “spike-and-slab” prior by putting probability p^m at a point (i.e., the ‘spike’ part) to encourage borrowing information from single-arm trials (i.e., ${\mu }_t^{\text{s}}$) and the remaining probability 1 − p^m on a ‘slab’ of values close to the original information from the NMA. We call this method commensurate prior on mean (CPM).

3.3.3. Commensurate prior on variance.

Similarly, we propose a commensurate prior on variances to borrow only variance information from single-arm trials. Specifically, we assume:

$$\text{log}\left({\sigma }_t/{\sigma }_t^{\text{s}}\right)=c_t;c_t~N\left(0,{\eta }^{-1}\right),$$ (5)

so the log of the standard deviation ratio follows a normal distribution with mean zero and precision η. Like Murray, Hobbs and Carlin (2015), we can modify this prior as follows:

$$\begin{gathered} \text{log}\left({\sigma }_t\right)~{\left[N\left(\text{log}\left({\sigma }_t^{\text{s}}\right),{\left({\tau }_t^{\text{v}}\right)}^{-1}\right)\right]}^{1-{\kappa }_t^{\text{v}}}{\left[N\left(\text{log}\left({\sigma }_t^{\text{s}}\right),{\left(R^{\text{v}}\right)}^{-1}\right)\right]}^{{\kappa }_t^{\text{v}}}; \\ {\kappa }_t^{\text{v}}~\text{Bern}\left(p^{\text{v}}\right)\text{ and }{\tau }_t^{\text{v}}~U\left(s_1^{\text{v}},s_{\text{u}}^{\text{v}}\right),t=1,\dots ,T, \end{gathered}$$ (6)

where Bern(p^v) is a Bernoulli distribution with $\text{Pr}\left({\kappa }_t^{\text{m}}=1\right)=p^{\text{v}}$ and the prior distribution on the precision ${\tau }_t^{\text{v}}$ is uniform from $s_1^{\text{v}}$ to $s_{\text{u}}^{\text{v}}$ with $0\le s_1^{\text{v}}<s_{\text{u}}^{\text{v}}\ll R^{\text{v}}$ and 0 ≤ p^v ≤ 1 pre-specified. We call this method commensurate prior on variance (CPV). Unlike the FBV method, this prior borrows variance information from single-arm trials adaptively. More specifically, this model encourages borrowing variance information (i.e., ${\sigma }_t^{\text{s}}$) from single-arm trials if p^v approaches 1, while it tends to ignore single-arm trials if p^v approaches 0.

3.3.4. Double commensurate prior.

We can borrow both mean and variance information adaptively by applying both the CPV and CPM methods in Equations (4) and (6). We call this method commensurate prior on mean and variance or double commensurate prior (DCP); it is an adaptively borrowing version of the FBMV method.

3.3.5. Summary of prior specifications and models.

Table 1 lists model names, assumptions, and prior specifications in detail. For all these models, we specify a prior on the covariance matrix Σ using the separation strategy proposed by Barnard, McCulloch and Meng (2000). Specifically, we first decompose Σ into separate parts as Σ = ΔPΔ and then set priors independently on the correlation matrix P and the standard deviations σ_t (t = 1, …, T), which are the diagonal elements of Δ. Here, we focus on the exchangeable correlation prior for the correlation matrix P (Lin et al., 2017; Wang et al., 2020a): we assume all correlation coefficients ρ_ij are equal, i.e., ρ_ij = ρ for any i ≠ j, and assign a uniform prior $U\left(-\frac{1}{T-1},1\right)$ to ρ so P is positive-definite. For models in which mean or variance information is not shared between the RCTs and single-arm trials in specific models, we also assign a vague N(0, 100²) prior to μ_t and ${\mu }_t^{\text{s}}$, and a uniform prior U(0, 5) to σ_t and ${\sigma }_t^{\text{s}}$. On the other hand, if information is shared fully or adaptively between the RCTs and single-arm trials, we assume ${\mu }_t={\mu }_t^{\text{s}}$ and ${\sigma }_t={\sigma }_t^{\text{s}}$ for fully borrowing, or for adaptively borrowing we follow Equations (4) and (6) with pre-specified values (0.5, 2500, 0, 2) for (p^m, R^m, $s_1^{\text{m}}$, $s_{\text{u}}^{\text{m}}$) and (p^v, R^v, $s_1^{\text{v}}$, $s_{\text{u}}^{\text{v}}$).

Table 1.

Summary of prior specifications and assumptions for μ_t, σ_t, ${\mu }_t^s$, ${\sigma }_t^s$, and the correlation matrix P in six different models.

Model	Parameter
	μt, t = 1,…,T	σt, t = 1,…,T	${\mu }_t^{\text{s}},t=1,\dots ,T$	${\sigma }_t^{\text{s}},t=1,\dots ,T$	P = {ρij}
NB	μt ~ N (0,1002)	σt ~ U (0,5)	NA	NA	ρij = ρ (i ≠ j) and $\rho ~U\left(-\frac{1}{T-1},1\right)$ for all models
FBMV	μt ~ N (0,1002)	σt ~ U (0,5)	${\mu }_t={\mu }_t^{\text{s}}$	${\sigma }_t={\sigma }_t^{\text{s}}$
FBV	μt ~ N (0,1002)	σt ~ U (0,5)	${\mu }_t^{\text{s}}~N\left(0,{100}^2\right)$	${\sigma }_t={\sigma }_t^{\text{s}}$
CPM	Equation (4) with pm = 0.5, Rm = 2500, $s_1^{\text{m}}=0$, and $s_{\text{u}}^{\text{m}}=2$	σt ~ U (0,5)	${\mu }_t^{\text{s}}~N\left(0,{100}^2\right)$	${\sigma }_t^{\text{s}}~U(0,5)$
CPV	μt ~ N (0,1002)	Equation (6) with pv = 0.5, Rv = 2500, $s_1^{\text{v}}=0$, and $s_{\text{u}}^{\text{v}}=2$	${\mu }_t^{\text{s}}~N\left(0,{100}^2\right)$	${\sigma }_t^{\text{s}}~U(0,5)$
DCP	Equation (4) with pm = 0.5, Rm = 2500, $s_1^{\text{m}}=0$, and $s_{\text{u}}^{\text{m}}=2$	Equation (6) with pv = 0.5, Rv = 2500, $s_1^{\text{v}}=0$, and $s_{\text{u}}^{\text{v}}=2$	${\mu }_t^{\text{s}}~N\left(0,{100}^2\right)$	${\sigma }_t^{\text{s}}~U(0,5)$

3.4. Likelihood and posterior estimation.

The likelihood functions are provided in Appendix B. We used NIMBLE (de Valpine et al., 2017) to fit the proposed models both for the real dataset on ICI safety and for simulated datasets, with each fit consisting of four independent Markov chain Monte Carlo (MCMC) chains sampling from the joint posterior distribution. We first sample posterior distributions of the parameters μ and Δ and then use the following equations to compute samples from the posterior distributions of the log odds ratio between treatments i and j, and the marginal event rate of treatment t (Zeger, Liang and Albert, 1988):

$$\begin{gathered} {\text{LOR}}_{ij}={\mu }_i-{\mu }_j; \\ {p}_t=E\left[p_{kt}\mid {\mu }_t,{\sigma }_t\right]\approx {\left[1+\text{exp}\left(-{\mu }_t/\sqrt{1+\frac{256}{75{\pi }^2}{\sigma }_t^2}\right)\right]}^{-1}. \end{gathered}$$ (7)

Convergence of chains was assessed by trace plots, sample autocorrelations, and effective sample sizes. Finally, we can make statistical inference using posterior medians, and 95% equal-tailed credible intervals (CrIs) calculated from the posterior samples.

We chose NIMBLE for computations because it is much faster than JAGS (de Valpine, 2016). NIMBLE code, which is very similar to WinBUGS or JAGS code, is given online in the Supporting Information section.

3.5. Model comparison.

The deviance information criterion (DIC) (Spiegelhalter et al., 2002) and the logarithm of the pseudo marginal likelihood (LPML) (Geisser and Eddy, 1979; Hanson, Branscum and Johnson, 2011) are two popular criteria for comparing Bayesian models. Because estimates of single-arm trials are much less meaningful, we focus on the NMA part of the joint model. Appendix B describes procedures to estimate LPML. DIC can be calculated following the steps in Dias et al. (2013). A larger DIC value is less favorable, while larger values of LPML are more favorable. We use the rule of thumb that only differences larger than 5 in DIC indicate a considerable improvement (Lunn et al., 2010).

4. Data analysis.

We applied the six models in Table 1 to the motivating example of the ICI data and compared the results. (We also applied two CB-NMA models to this dataset. Appendix F gives the results, which are discussed below in Section 6.) This dataset does not have single-arm trials for treatments 7 (2ICIs) and 8 (ICC), so the model settings are slightly different from those described above. To demonstrate the differences differences between the model settings described above and used for this dataset, Figure 2 presents the directed acyclic graph (DAG) for the DCP model applied to the ICI data. In this DAG, square nodes represent observed data or fixed quantities, circle nodes with white background are intermediate unknown parameters, and circle nodes with gray background are unknown parameters with pre-specified prior distributions, e.g., μ_t ~ N(0, 100²) for t = 7, 8, ${\mu }_t^{\text{s}}~N\left(0,{100}^2\right)$ for t = 1, …, 6, σ_t ~ U(0, 5) for t = 7, 8, and ${\sigma }_t^{\text{s}}~U(0,5)$ for t = 1, …, 6.

Fig 2.

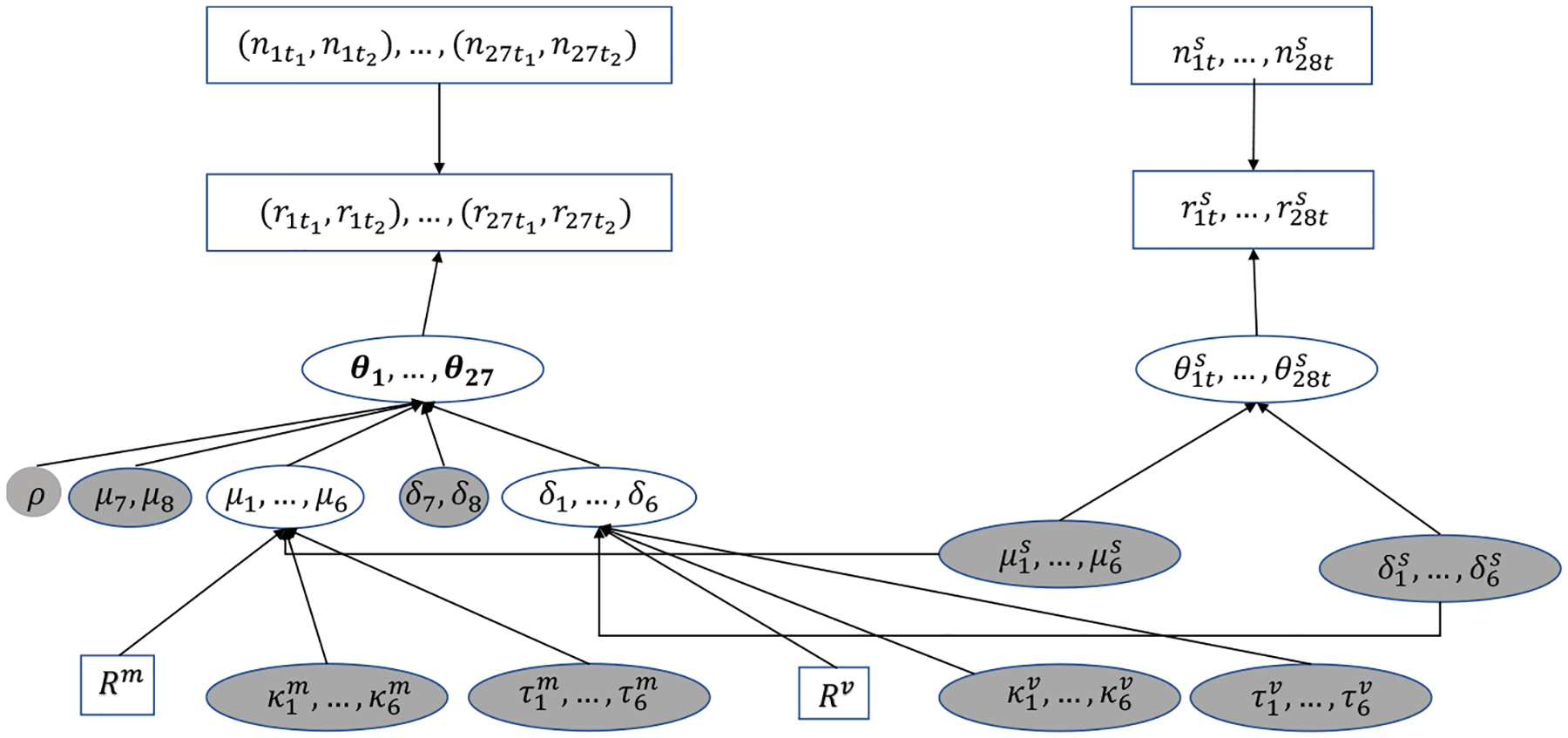
Directed acyclic graph of the DCP model for the motivating example. □, observed data or fixed quantities; ◯, intermediate unknown parameters; , unknown parameters with pre-specified prior distributions.

To summarize rankings of the treatments in terms of safety, we use the surface under the cumulative ranking (SUCRA) proposed by Salanti, Ades and Ioannidis (2011). Let prob_ti be the probability that treatment t has the i^th rank, where i = 1 represents the safest treatment; the SUCRA of the t^th treatment is

$${\text{SUCRA}}_t=\frac{1}{T-1}\sum _{k=1}^{T-1}\sum _{i=1}^k{\text{prob}}_{ti},$$

where the posterior mean of prob_ti is easily calculated using MCMC samples. The SUCRA ranges from 0% to 100%; a higher SUCRA value implies a better treatment.

Table 2 presents the results for absolute risk of events for the t^th treatment (p_t), fixed effect of log-odds for the t^th treatment (μ_t), standard deviation of log-odds for the t^th treatment (σ_t), selected log odds ratios LOR_ij, LPML, and DIC. These models did not differ notably in LPML or DIC. Some differences, however, appear in the estimates and intervals.

Table 2.

Analysis of ICI safety in cancer treatment: posterior medians and 95% credible intervals by 6 different models (NB, CPV, FBV, CPM, DCP, and FBMV). The estimated parameters include absolute risk of events for the t^th treatment (p_t), fixed effect of log-odds for the t^th treatment (μ_t), standard deviation of the log-odds for the t^th treatment (σ_t), and selected log odds ratios LOR_ij comparing treatments i and j. Treatment labels: 1) NIV; 2) IPI low; 3) IPI high; 4) PEM; 5) ATE; 6) ICI+ICC; 7) 2ICIs; and 8) ICC.

Parameter	Posterior median (95% credible interval)
	NB	CPV	FBV	CPM	DCP	FBMV
p 1	0.14 (0.11, 0.18)	0.14 (0.12, 0.17)	0.14 (0.12, 0.17)	0.15 (0.12, 0.19)	0.15 (0.12, 0.18)	0.16 (0.14, 0.19)
p 2	0.19 (0.13, 0.27)	0.19 (0.14, 0.27)	0.19 (0.13, 0.27)	0.20 (0.14, 0.28)	0.20 (0.15, 0.27)	0.21 (0.15, 0.28)
p 3	0.38 (0.25, 0.56)	0.37 (0.27, 0.50)	0.37 (0.27, 0.50)	0.36 (0.27, 0.49)	0.36 (0.28, 0.47)	0.36 (0.28, 0.45)
p 4	0.16 (0.12, 0.26)	0.16 (0.13, 0.22)	0.16 (0.13, 0.22)	0.16 (0.13, 0.22)	0.16 (0.13, 0.20)	0.16 (0.13, 0.20)
p 5	0.16 (0.09, 0.41)	0.16 (0.11, 0.25)	0.16 (0.11, 0.24)	0.16 (0.12, 0.30)	0.16 (0.12, 0.21)	0.16 (0.12, 0.21)
p 6	0.47 (0.42, 0.53)	0.47 (0.41, 0.54)	0.48 (0.39, 0.57)	0.48 (0.42, 0.54)	0.48 (0.41, 0.55)	0.49 (0.42, 0.57)
p 7	0.54 (0.14, 0.73)	0.54 (0.14, 0.75)	0.54 (0.16, 0.75)	0.55 (0.16, 0.75)	0.55 (0.16, 0.75)	0.55 (0.17, 0.78)
p 8	0.38 (0.31, 0.46)	0.38 (0.31, 0.46)	0.38 (0.31, 0.46)	0.39 (0.32, 0.46)	0.39 (0.32, 0.46)	0.39 (0.32, 0.47)
μ 1	−1.84 (−2.19, −1.58)	−1.82 (−2.11, −1.60)	−1.82 (−2.09, −1.59)	−1.75 (−2.08, −1.51)	−1.74 (−2.03, −1.54)	−1.71 (−1.90, −1.52)
μ 2	−1.48 (−2.06, −1.07)	−1.48 (−1.99, −1.08)	−1.49 (−2.03, −1.06)	−1.44 (−1.93, −1.05)	−1.42 (−1.87, −1.06)	−1.40 (−1.82, −1.04)
μ 3	−0.53 (−1.36, 0.33)	−0.53 (−1.10, 0.01)	−0.54 (−1.10, −0.01)	−0.59 (−1.11, −0.03)	−0.58 (−1.00, −0.14)	−0.60 (−0.99, −0.22)
μ 4	−1.67 (−2.18, −1.22)	−1.67 (−2.00, −1.34)	−1.66 (−1.99, −1.34)	−1.69 (−2.02, −1.38)	−1.68 (−1.94, −1.42)	−1.67 (−1.93, −1.43)
μ 5	−1.75 (−3.52, −0.59)	−1.69 (−2.36, −1.22)	−1.69 (−2.31, −1.23)	−1.75 (−2.33, −1.25)	−1.71 (−2.09, −1.40)	−1.72 (−2.06, −1.42)
μ 6	−0.10 (−0.34, 0.14)	−0.11 (−0.38, 0.17)	−0.10 (−0.47, 0.32)	−0.09 (−0.31, 0.16)	−0.09 (−0.36, 0.19)	−0.04 (−0.32, 0.30)
μ 7	0.16 (−4.09, 1.59)	0.18 (−3.84, 1.86)	0.19 (−3.55, 1.92)	0.20 (−3.41, 1.84)	0.21 (−3.37, 1.85)	0.24 (−3.36, 2.23)
μ 8	−0.52 (−0.86, −0.18)	−0.52 (−0.86, −0.19)	−0.52 (−0.86, −0.18)	−0.50 (−0.83, −0.17)	−0.51 (−0.84, −0.17)	−0.49 (−0.82, −0.15)
σ 1	0.36 (0.15, 0.83)	0.31 (0.15, 0.59)	0.31 (0.16, 0.56)	0.35 (0.13, 0.81)	0.31 (0.14, 0.58)	0.32 (0.16, 0.57)
σ 2	0.43 (0.14, 1.24)	0.41 (0.14, 1.02)	0.45 (0.18, 1.07)	0.42 (0.14, 1.20)	0.40 (0.13, 0.96)	0.44 (0.17, 1.00)
σ 3	0.53 (0.18, 2.30)	0.41 (0.16, 1.22)	0.41 (0.18, 1.17)	0.49 (0.18, 1.87)	0.39 (0.16, 1.01)	0.39 (0.18, 0.95)
σ 4	0.41 (0.12, 1.38)	0.29 (0.06, 0.75)	0.29 (0.08, 0.71)	0.38 (0.12, 1.11)	0.27 (0.02, 0.66)	0.26 (0.06, 0.63)
σ 5	0.65 (0.12, 3.87)	0.32 (0.05, 1.33)	0.31 (0.07, 1.20)	0.49 (0.10, 2.79)	0.27 (0.05, 0.89)	0.27 (0.08, 0.82)
σ 6	0.18 (0.04, 0.57)	0.21 (0.04, 0.66)	0.35 (0.10, 0.91)	0.19 (0.04, 0.58)	0.22 (0.05, 0.66)	0.35 (0.11, 0.83)
σ 7	0.59 (0.02, 4.52)	0.60 (0.02, 4.49)	0.59 (0.02, 4.47)	0.59 (0.02, 4.46)	0.60 (0.02, 4.44)	0.65 (0.03, 4.52)
σ 8	0.73 (0.51, 1.11)	0.71 (0.50, 1.07)	0.72 (0.51, 1.08)	0.72 (0.51, 1.10)	0.71 (0.51, 1.06)	0.71 (0.51, 1.07)
LOR14	−0.17 (−0.72, 0.38)	−0.16 (−0.57, 0.23)	−0.16 (−0.56, 0.23)	−0.07 (−0.50, 0.33)	−0.07 (−0.44, 0.26)	−0.03 (−0.34, 0.28)
LOR15	−0.08 (−1.26, 1.66)	−0.13 (−0.67, 0.55)	−0.14 (−0.65, 0.51)	−0.01 (−0.57, 0.60)	−0.04 (−0.44, 0.38)	0.01 (−0.34, 0.39)
LOR45	0.09 (−1.18, 1.88)	0.03 (−0.55, 0.75)	0.03 (−0.52, 0.71)	0.06 (−0.52, 0.70)	0.04 (−0.37, 0.48)	0.04 (−0.34, 0.46)
LOR23	−0.97 (−1.90, −0.11)	−0.95 (−1.63, −0.30)	−0.96 (−1.63, −0.30)	−0.87 (−1.53, −0.23)	−0.85 (−1.41, −0.32)	−0.80 (−1.33, −0.29)
LOR53	−1.25 (−3.20, 0.23)	−1.17 (−2.01, −0.40)	−1.15 (−1.97, −0.42)	−1.16 (−1.99, −0.43)	−1.13 (−1.71, −0.61)	−1.11 (−1.63, −0.63)
DIC	15970.4	15971.0	15970.3	15970.7	15971.4	15970.5
LPML	−224.4	−226.3	−222.4	−221.7	−224.3	−226.3

Figure 3a is a forest plot of the posteriors for the standard deviations σ_t. Clearly, because of lack of information about treatments 3 (IPI high), 5 (ATE), and 7 (2ICIs), the estimates of σ₃, σ₅, and σ₇ under the NB method were dominated by prior information, i.e., U(0, 5), with wide CrIs. By fully (the FBV method) or adaptively (the CPV method) incorporating variance information from single-arm trials for treatments IPI high and ATE, we may have better estimates for σ₃ and σ₅ with much narrower CrIs. However, when the RCTs provided a good deal of information, e.g., for treatment 6 (ICI+ICC with B₆ = 6 > 5) and the variances in the RCTs and single-arm trials differed, the FBV method had a much stronger effect on the posterior of σ₆ than the adaptive (CPV) method; the posterior median and 95% CrI of σ₆ were 0.18 (0.04, 0.57) for NB, 0.21 (0.04, 0.66) for CPV, and 0.35 (0.10, 0.91) for FBV. Similar results were obtained when mean information was adaptively or fully borrowed, e.g., the posterior median and 95% CrI of μ₁ were −1.84 (−2.19, −1.58) for NB, −1.75 (−2.08, −1.51) for CPM, and −1.71 (−1.90, −1.52) for FBMV. Posterior medians of the μ_t’s were generally quite similar among the NB, CPV, and FBV methods because the CPV and FBV methods shared only variance information. The CPM method also narrowed the CrIs of σ₃ and σ₅ a bit by sharing mean information from single-arm trials.

Fig 3.

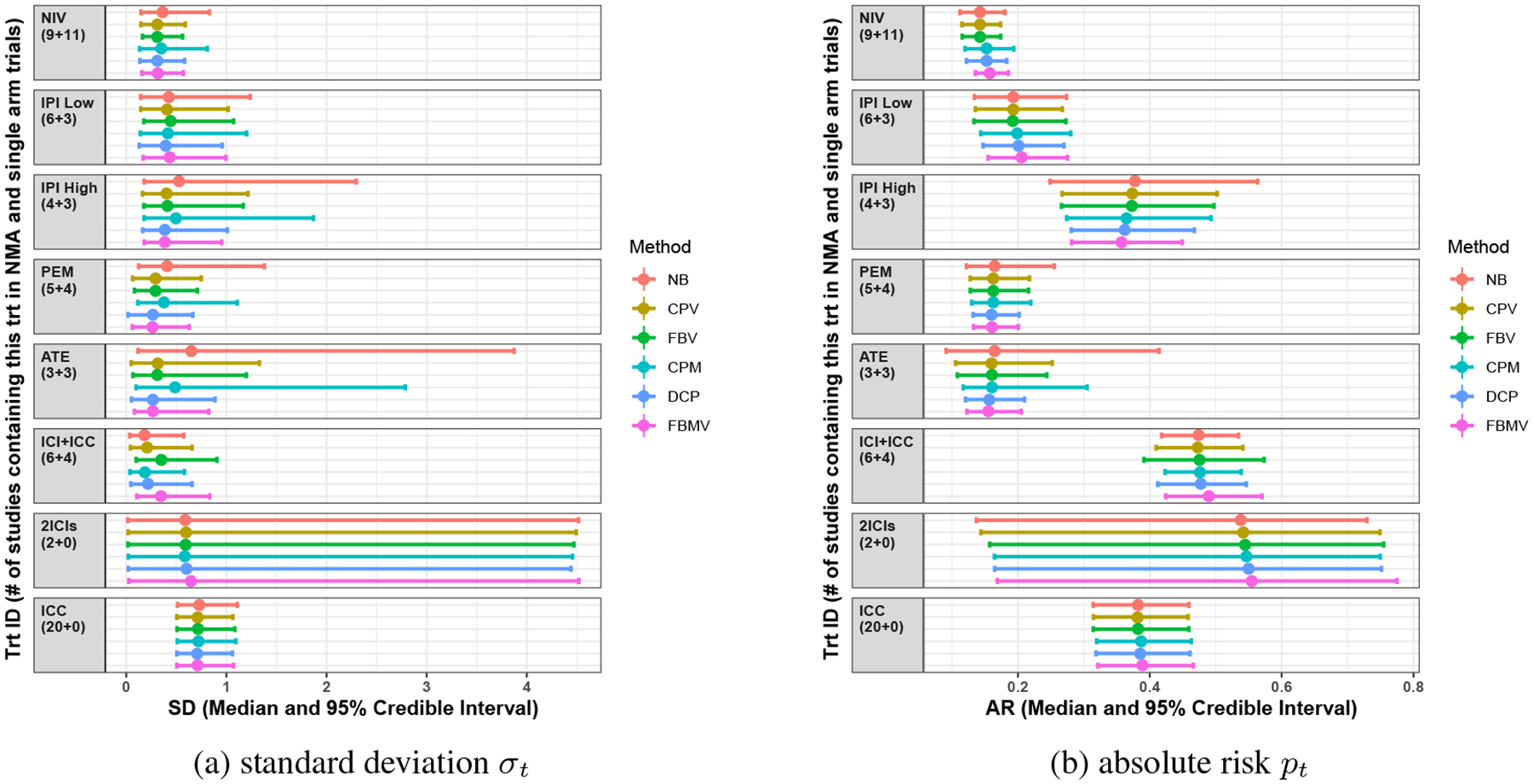
Results for the dataset of the safety of ICIs in cancer treatment: forest plot of posterior estimates of standard deviations σ_t and absolute risks p_t (posterior medians with 95% credible intervals). Different colors indicate different methods. The y-axis represents regimen abbreviations, with the number of RCTs (B_t) and single-arm trials $\left(B_t^s\right)$ in parentheses.

The differences between methods in mean and variance estimates can affect the estimates of absolute risks, as shown in Figure 3b. The NB method yielded a much wider CrI for treatments IPI high dose and ATE than the CPV and FBV methods because those treatments had few RCTs. On the other hand, the FBV method gave wide CrIs for treatment 6 (ICI+ICC) because it fully incorporated variance information from the single-arm trials, while the CPV method gave estimates more similar to the NB method by adaptively downweighting variance information that was inconsistent between the RCTs and single-arm trials. The posterior median and 95% CrI of p₆ were 0.47 (0.42, 0.53) for NB, 0.47 (0.41, 0.54) for CPV, and 0.48 (0.39, 0.57) for FBV. The CPV and FBV methods provided almost the same posterior medians of p_t for all treatments as the NB method, while the other three methods (CPM, DCP, and FBMV) gave rather different point estimates of p_t because of incorporating potentially inconsistent results from single-arm trials. The posterior median and 95% CrI of p₂ were 0.19 (0.13, 0.27) for NB, 0.19 (0.14, 0.27) for CPV, 0.20 (0.14, 0.28) for CPM, and 0.21 (0.15, 0.28) for FBMV.

Figure 4, known as the plate plot (Wang et al., 2020b), visualizes the estimated log odds ratios (with results for NB shown above the diagonal and CPV below the diagonal) and SUCRAs (shown as a percent). Specifically, the radius of the gray circle represents the point estimate of LOR_ij, with the radius of the inner white circle (not shown if P > 0.05 for testing the difference between two treatments) and outer colored circle representing the 95% CrI. The coloration on the scale is determined by the P-value, with blue indicating that the upper-left treatment is better than the lower-right treatment in terms of lower drug-related grade 3–5 adverse events (AEs). The largest difference between NB and CPV methods in estimating LOR_ij and SUCRA_t was for the log odds ratio between ATE and IPI high dose; the posterior median and 95% CrI of LOR₅₃ were −1.25 (−3.20, 0.23) for NB and −1.17 (−2.01, −0.40) for CPV. Such differences arose because the CPV method incorporated more variance information than the NB method, which narrowed the CrI.

Fig 4.

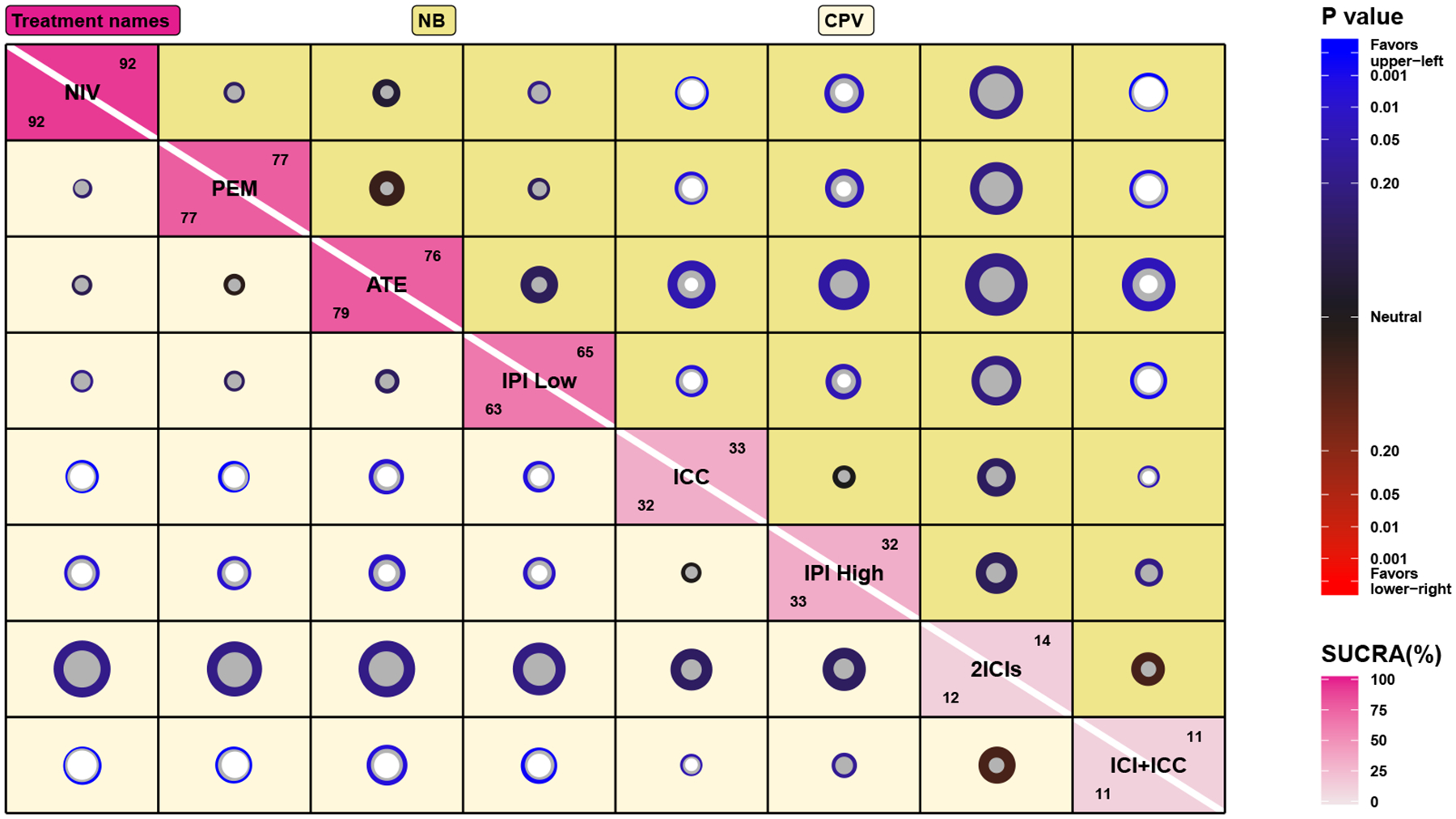
Estimated log odds ratios LOR_ij for grade 3–5 adverse events of ICIs in cancer patients using the NB (upper right) and CPV (lower left) methods. The LOR information is visualized as a plate plot, with the gray circle representing the posterior median of LOR_ij and the inner white circle (not shown if P-value > 0.05) and outer colored circle representing the 95% CrI. The coloration is determined by the P-value of LOR, with blue indicating the upper-left treatment is safer than the lower-right treatment. The diagonal of the plot displays SUCRA of treatments under the NB (upper right number) and CPV (lower left number) methods.

These analyses confirmed that drug-related grade 3–5 AEs were dose-dependent with ipilimumab; the posterior median and 95% CrI of LOR₂₃ were −0.97 (−1.90, −0.11) for NB, and −0.95 (−1.63, −0.30) for CPV. Also, drug-related grade 3–5 AEs were less frequent for all ICIs (NIV, PEM, ATE, and IPI low) than for traditional chemotherapy or combination therapy of ICI and ICC. We found no significant differences between anti–PD-1 monotherapy (nivolumab, or pembrolizumab), anti–PD-L1 monotherapy (atezolizumab), and anti–CTLA-4 monotherapy (ipilimumab 3mg/kg every 3 weeks) in drug-related grade 3–5 AEs, with appropriate dose. Based on SUCRA, however, nivolumab (SUCRA₁ = 0.92 for the CPV method) may be the ICI drug with the lowest frequency of drug-related grade 3–5 AEs among the drugs that were investigated.

In summary, when results from single-arm trials are potentially unreliable, the CPV method can provide better estimates than other methods that borrow mean information. Meanwhile, unlike the NB or FBV methods, the CPV method allows treatments with limited data to adaptively incorporate variance information from single-arm trials to improve estimates related to these treatments.

5. Simulation studies.

5.1. Simulation settings.

These simulation studies compared five methods (NB, CPV, FBV, CPM, and DCP) defined in Section 3. Each simulated dataset contained K = 14 RCTs, J = 30 single-arm trials, and T = 5 treatments (indexed from 1 to 5). The number of participants in each treatment arm in each RCT, n_kt, was fixed at 150. The 30 single-arm trials were allocated to treatments with the pre-specified partition scheme of $B_1^{\text{s}}=14$, $B_2^{\text{s}}=5$, $B_3^{\text{s}}=4$, $B_4^{\text{s}}=4$, and $B_5^{\text{s}}=3$. The number of participants in each single-arm trial was 75, 38, 75, 150, and 113 for treatments 1 to 5 respectively. The number of simulated datasets in each simulation setting was 1000.

In simulated datasets, we considered four scenarios with different levels of reliability of mean and variance information from single-arm trials. In scenario EM-EV (equal mean and equal variance), we first generated a complete dataset for the RCTs under the AB model with binary outcomes as in Equation (1), with μ^RCT = (μ₁, …, μ₅)′ = (−2, −3, −2.5, −2, −1.5)′ and (θ_k1, …, θ_k5)′ ~ MV N(μ, Σ). In the covariance matrix Σ = ΔPΔ, the correlation matrix P had all off-diagonal entries ρ_ij = 0.5 for i ≠ j, and standard deviations (i.e., diagonal entries) σ^RCT = (σ₁, …, σ₅)′ = (0.4, 1.0, 1.0, 0.3, 0.3)′. In this complete dataset for the RCTs, each trial had 5 arms with $\left|{\mathcal{A}}_k\right|=5$. To generate the 30 single-arm trials, we used Equation (2) with ${\mu }^{\text{s}}={\left({\mu }_1^{\text{s}},\dots ,{\mu }_5^{\text{s}}\right)}^{\prime }={(-2,-3,-2.5,-2,-1.5)}^{\prime }$ and ${\sigma }^{\text{s}}={\left({\sigma }_1^{\text{s}},\dots ,{\sigma }_5^{\text{s}}\right)}^{\prime }={(0.4,1.0,1.0,0.3,0.3)}^{\prime }$. In these single-arm trials, each trial only had one arm with $\left|{\mathcal{A}}_j^s\right|=1$. The only difference between EM-EV and the other three scenarios was the pre-specified values for μ^RCT, σ^RCT, μ^s, and σ^s as follows. The UM-EV (unequal mean and equal variance) scenario had μ^RCT = (−2, −3, −2.5, −2, −1.5)′, μ^s = (−1, −2.5, −2, −2.5, −2)′, and σ^RCT = σ^s = (0.4, 1.0, 1.0, 0.3, 0.3)′. The EM-UV (equal mean and unequal variance) scenario had μ^RCT = μ^s = (−2, −3, −2.5, −2, −1.5)′, σ^RCT = (0.4, 1.0, 1.0, 0.3, 0.3)′, and σ^s = (1.2, 0.5, 0.5, 0.9, 0.9)′. The UM-UV (unequal mean and unequal variance) scenario had μ^RCT = (−2, −3, −2.5, −2, −1.5)′, μ^s = (−1, −2.5, −2, −2.5, −2)′, σ^RCT = (0.4, 1.0, 1.0, 0.3, 0.3)′, and σ^s = (1.2, 0.5, 0.5, 0.9, 0.9)′.

Once the complete dataset of RCTs was generated, we excluded treatment arms to create a realistic (partially missing) NMA dataset as illustrated in Figure 5, with two types of missingness: missing completely at random (MCAR) and missing at random (MAR). Under the MCAR mechanism, we kept all treatment 1 data (all 14 RCTs) and then randomly kept data for treatments 2 to 5 data in blocks of 3, 4, 2, and 5 trials respectively, where the blocks did not overlap. Under the MAR mechanism, we kept all treatment 1 data and ranked the RCTs in descending order by the rough estimates of event rates r_k1/n_k1; then we made treatment 5 available only in the first 5 trials, treatment 4 available in next 2, and so on as in Figure 5.

Fig 5.

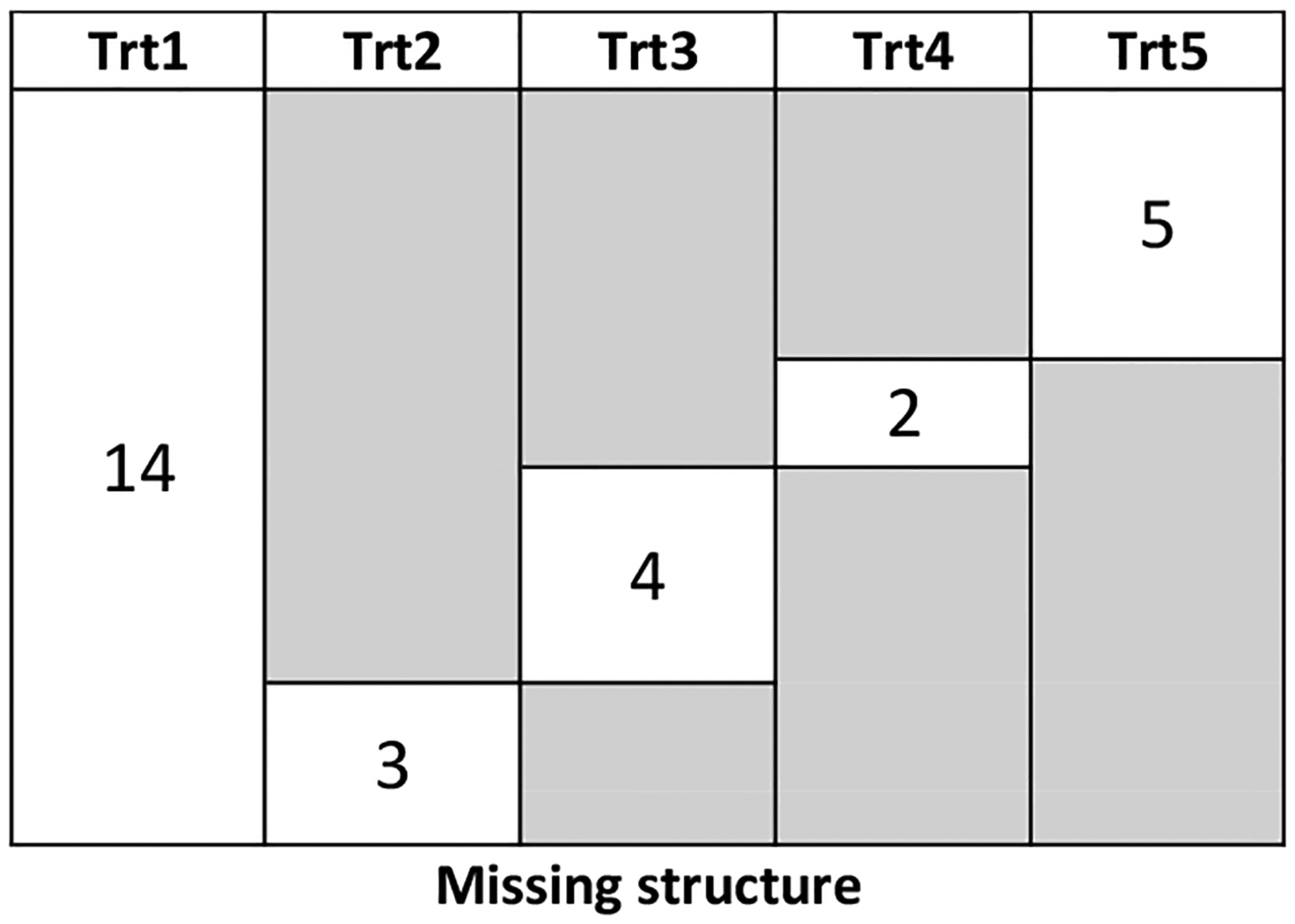
Missing data structures for the simulation study under MCAR and MAR. The number in the white-background boxes is the observed number of RCTs for the treatment in the corresponding column, while the gray background indicates that the corresponding treatment is not observed in these trials.

We used the prior specifications in Table 1 for all models and obtained posterior medians and 95% equal-tailed CrIs for these estimands: event risk for the t^th treatment (p_t), fixed effect of treatment-specific log-odds (μ_t), standard deviation of treatment-specific log-odds (σ_t), and log odds ratio between the i^th and j^th treatments (LOR_ij). To measure the methods’ performance, we followed the instructions provided by Morris, White and Crowther (2019). In particular, we used bias, mean squared error (MSE), and the 95% CrI’s coverage probability (CP) and length (CrIL). Detailed simulation results for the different performance measures and corresponding Monte Carlo standard errors are in Appendix C, as well as the effective sample size, which describes the amount of information in the MCMC samples.

5.2. Simulation results.

Table 3 summarizes the bias and MSE of the posterior median and the coverage probability of the 95% CrI for the five methods in four different simulation scenarios under MAR. Due to space limits, instead of presenting the results for each treatment or each treatment comparison, we summarized overall measures across all treatments or across all pairs of comparisons for each of bias, MSE, and CP. For example, the entry with bias as the column and LOR_ij as the row was calculated as ∑_i≠j |bias(LOR_ij)|. The formula was similar for MSE: ∑_i≠j MSE(LOR_ij). To summarize the CPs, the corresponding value in column CP and row p_t was calculated as ${\sum }_{t=1}^5{\left(0.95-\text{CP}\left(p_t\right)\right)}_{+}$, where x₊ = x if x ≥ 0 and x₊ = 0 if x < 0. Table D1 in Appendix D presents the same summaries of simulation results under MCAR. Figure D1 in Appendix D displays the log of CrIL ratio for four methods (NB, FBV, CPM, and DCP) compared to the CPV method, using box plots with whiskers representing the 1st and 99th percentiles. Each sub-figure presents one of the four estimands: μ_t, σ_t, p_t, and LOR_ij. Also, each panel shows one of the four scenarios (EM-EV, UM-EV, EM-UV, and UM-UV in columns) under the different missingness structures (MCAR and MAR in rows).

Table 3.

Simulation results comparing data generated under four different scenarios (EM-EV, UM-EV, EM-UV, and UM-UV) with MAR missingness of treatment arms. Bias and mean squared error of the posterior median and the coverage probability of the 95% credible interval are summarized for the five methods (NB, CPV, FBV, CPM, and DCP). The value in the column for bias and the row for LOR_ij is calculated as ∑_i≠j |bias(LOR_ij)|; the value in the column for coverage probability and in the row for LOR_ij is calculated as ∑_i≠j(0.95 − CP(LOR_ij))₊.; the value in the column for coverage probability and in the row for LOR₂₅ is CP(LOR₂₅).

Parameter	Truth	Bias					Mean squared error					Coverage probability
		NB	CPV	FBV	CPM	DCP	NB	CPV	FBV	CPM	DCP	NB	CPV	FBV	CPM	DCP
Scenario EM-EV
LORij	.	1.82	0.35	0.48	0.60	0.25	4.84	3.85	3.83	2.06	2.05	0.00	0.00	0.00	0.00	0.00
μ t	.	0.40	0.17	0.22	0.18	0.17	1.18	1.01	1.00	0.53	0.54	0.00	0.01	0.02	0.00	0.00
p t	.	0.10	0.04	0.05	0.07	0.03	0.01	0.01	0.01	0.01	0.00	0.00	0.02	0.03	0.00	0.00
σ t	.	1.83	0.53	0.69	1.22	0.38	2.17	0.82	0.87	1.37	0.55	0.07	0.05	0.11	0.02	0.05
LOR25	−1.50	−0.41	0.03	−0.05	−0.13	0.01	0.68	0.35	0.38	0.25	0.23	1.00	0.98	0.98	1.00	0.99
p 5	0.19	0.03	−0.01	−0.00	0.01	−0.01	0.00	0.00	0.00	0.00	0.00	0.99	0.99	0.99	0.99	0.99
σ 5	0.30	0.32	−0.01	0.01	0.16	−0.04	0.21	0.03	0.03	0.08	0.02	0.93	0.99	0.98	0.96	0.99
Scenario UM-EV
LORij	.	1.81	0.36	0.46	2.21	2.11	4.83	3.82	3.80	2.63	2.60	0.00	0.00	0.00	0.00	0.03
μ t	.	0.40	0.17	0.20	0.75	0.71	1.17	1.00	0.99	0.66	0.65	0.00	0.02	0.04	0.00	0.09
p t	.	0.10	0.04	0.04	0.11	0.09	0.01	0.01	0.01	0.01	0.01	0.00	0.03	0.04	0.03	0.06
σ t	.	1.83	0.45	0.63	1.13	0.25	2.17	0.76	0.76	1.28	0.51	0.07	0.07	0.18	0.00	0.07
LOR25	−1.50	−0.41	0.03	−0.05	0.34	0.39	0.67	0.35	0.37	0.34	0.36	1.00	0.98	0.99	0.99	0.96
p 5	0.19	0.03	−0.00	−0.00	−0.01	−0.02	0.00	0.00	0.00	0.00	0.00	0.99	0.99	0.99	1.00	0.95
σ 5	0.30	0.32	0.01	0.03	0.17	−0.02	0.21	0.03	0.03	0.09	0.03	0.93	0.98	0.98	0.96	0.99
Scenario EM-UV
LORij	.	1.81	0.39	0.69	0.93	0.28	4.83	3.75	3.56	1.57	1.93	0.00	0.02	0.03	0.00	0.00
μ t	.	0.40	0.11	0.24	0.23	0.08	1.17	0.97	0.92	0.39	0.50	0.00	0.02	0.04	0.00	0.00
p t	.	0.10	0.04	0.11	0.08	0.02	0.01	0.01	0.01	0.01	0.00	0.00	0.02	0.10	0.00	0.00
σ t	.	1.83	0.63	1.85	1.26	0.65	2.17	0.86	1.65	1.36	0.65	0.07	0.03	1.82	0.02	0.02
LOR25	−1.50	−0.41	−0.03	−0.01	−0.21	−0.07	0.67	0.36	0.35	0.26	0.23	1.00	0.99	0.99	1.00	0.99
p 5	0.19	0.03	0.01	0.03	0.02	0.01	0.00	0.00	0.00	0.00	0.00	0.99	1.00	0.99	0.99	0.99
σ 5	0.30	0.32	0.23	0.48	0.22	0.19	0.21	0.12	0.37	0.12	0.09	0.93	0.94	0.55	0.95	0.95
Scenario UM-UV
LORij	.	1.82	0.46	0.94	2.03	1.83	4.84	3.64	3.47	1.74	2.23	0.00	0.03	0.06	0.00	0.03
μ t	.	0.40	0.14	0.29	0.70	0.64	1.17	0.94	0.91	0.47	0.58	0.00	0.04	0.09	0.00	0.04
p t	.	0.10	0.04	0.10	0.11	0.04	0.01	0.01	0.01	0.01	0.01	0.00	0.04	0.13	0.09	0.05
σ t	.	1.83	0.70	1.83	1.10	0.77	2.17	0.82	1.61	1.27	0.61	0.07	0.02	1.73	0.01	0.03
LOR25	−1.50	−0.41	0.02	0.08	0.26	0.33	0.68	0.34	0.32	0.23	0.28	1.00	0.99	0.99	1.00	0.99
p 5	0.19	0.03	0.01	0.03	0.00	−0.01	0.00	0.00	0.00	0.00	0.00	0.99	1.00	1.00	1.00	0.99
σ 5	0.30	0.32	0.23	0.49	0.20	0.17	0.21	0.13	0.42	0.11	0.08	0.93	0.95	0.58	0.95	0.96

Under the MAR mechanism (Table 3), the CPV method was much better than the NB method with less biased estimates, smaller MSE, and comparable CP in all scenarios. Although the CPV method produced the second largest MSE (smaller only than that of the NB method), the other three methods did not perform well in some situations. For example, DCP was better than CPV in terms of bias when mean information from single-arm trials was reliable (EM-UV and EM-EV); however, when this information was not reliable (UM-EV and UM-UV), the biases of DCP and CPM were even worse than that of NB. Similarly, FBV’s performance was worse than CPV’s when variance information from single-arm trials was not reliable (EM-UV and UM-UV). Similar performance patterns were present under the MCAR mechanism (Table D1 in Appendix D), though the difference between methods was much smaller.

Compared to the NB method, the CPV and FBV methods greatly reduced CrI length for all estimates under all scenarios (Figure D1 in Appendix D). Compared to CPV, the relative length of CrI for CPM varied depending on simulation scenario and estimand. The DCP method produced the smallest CrI length for all estimates under all scenarios; hence, when we believe in the reliability of mean information from single-arm trials, the DCP method would be the first choice.

Overall, the CPV method provided better estimates of log odds ratios and absolute risks than the NB method even when true variances in the single-arm trials differed from true variances in the RCTs, e.g., the elementwise ratios were σ^RCT/σ^s = (1/3, 2, 2, 1/3, 1/3)′. The performance of the other three borrowing strategies depended largely on the reliability of the single-arm trials.

6. Summary and discussion.

This paper has proposed and discussed different strategies to incorporate single-arm trials into AB-NMA to mitigate the prevalent “lack of information” problem. We have performed extensive simulation studies to explore whether it is preferable to choose a full borrowing strategy or one of the adaptive borrowing methods (commensurate prior), and whether to borrow mean information, variance information, or both. The simulation studies considered scenarios when information from single-arm trials could be unreliable. Our proposed CPV method delivered the most robust estimates of relative and absolute risks in all four simulation scenarios. Specifically, CPV could improve efficiency even in the presence of modestly discordant variance information, by facilitating partial pooling of variance information from single-arm trials, rather than fully borrowing as in the FBV method. Also, unlike the CPM and DCP methods, ignoring mean information from the supplemental source could help the CPV method produce more reliable point estimates with reduced CrI lengths. Although we did not examine FBM in our paper, it could be expected that FBM would perform even worse than CPM if mean information from single-arm trials was biased. To the best of our knowledge, this is the first proposal in Bayesian extrapolation analyses to borrow only variance information. The application to safety of ICIs in cancer research also illustrated potential gains of the CPV method for estimates related to the treatments IPI high dose and ATE, by adaptively incorporating variance information from single-arm trials.

Some researchers have reservations about the AB-NMA approach because it includes random study intercepts, which may lead to bias when differences exist between trials with different designs (White et al., 2019). Hence, we compared our proposed approach (CPV) with the classic CB-NMA model and the CB-NMA with random study-specific baseline intercepts (CB-2) in the case study. Appendix F presents the results. Overall, the point estimates of LOR and p_t from the CPV method were consistent with those from the classic CB and CB-2 models, except for estimands related to treatments 6 (ICI+ICC) and 7 (2ICIs). This was expected because of substantial differences in the ICI drug or the dose of the drug used in clinical trials that compared ICI+ICC or 2ICIs with other treatments, which led to large uncertainties in safety profile. On the other hand, by including additional information from single-arm trials, the CPV method delivered overall smaller CrILs for LORs and p_ts compared with the classic CB and CB-2 methods. In summary, our proposed method was compatible with the CB-NMA approaches on point estimation and achieved more certainty by borrowing information, at least in this case study.

We have focused on commensurate priors to synthesize RCTs and single-arm trials in the AB-NMA; many future studies are possible. First, selecting pre-specified values for p^v, R^v, $s_1^{\text{v}}$, and $s_{\text{u}}^{\text{v}}$ in the commensurate prior might lead to some problems (Murray, Hobbs and Carlin, 2015). We did a sensitivity analysis to assess how much importance should be placed on the single-arm trials (see Appendix E) and found that any value between 0.1 to 0.5 would be suitable for p^v in the CPV method, while the choice of p^m is quite sensitive in the CPM method. Future research is needed specifically for different combinations of (p^v, R^v, $s_1^{\text{v}}$, $s_{\text{u}}^{\text{v}}$) for AB-NMA. Also, existing methods cannot assess the importance of single-arm trials in AB-NMA. We need to develop methods that separately assess each component of the joint model, of the NMA dataset and the supplemental source, e.g., by decomposing DIC or LPML into two parts (Zhang et al., 2017b), with one part for the supplemental source and the other part for the NMA dataset conditional on the supplemental source.

Second, empirical studies should evaluate the reliability of mean and especially variance information from single-arm trials that may be eligible for use in NMAs. Such a study could help experts to judge whether incorporating variance is reasonable in general or in specific subject-matter areas.

Third, alternative Bayesian methods could be used to adaptively incorporate information from single-arm trials into AB-NMA. For example, the extrapolation strategy for meta-analyses proposed by Röver, Wandel and Friede (2018) is to express the posterior distribution as a weighted average of posterior components from four simple models: NB, FBM, FBV, and FBMV. Although not mentioned by Röver, Wandel and Friede (2018), it is possible to borrow only variance information by averaging just two models: NB and FBV. Another method is power priors (Ibrahim et al., 2015; Zhang et al., 2019) that incorporate supplemental information by raising the likelihood of the single-arm trials to a power α ∈ [0, 1]. This may be problematic, however, because mean and variance information is included in the likelihood as a whole and cannot easily be separated, as in the CPV and CPM methods. Zhang et al. (2019) used simulation studies to compare the hierarchical power prior (HPP) and hierarchical commensurate prior (HCP) in meta-analysis of binary data. They concluded that the performance of HCP was better in terms of relative bias and stable throughout all their simulation scenarios. Also, by building on the design-by-treatment interaction model (White et al., 2012; Jackson et al., 2014), we could treat the single-arm trials as inconsistent with the RCTs, and set up the following random inconsistency effects model:

$$\begin{gathered} \text{logit}\left(p_{kt}\right)={\mu }_t+{\beta }_{kt},k=1,\dots ,K; \\ \text{logit}\left(p_{jt}^{\text{s}}\right)={\mu }_t+{\beta }_{jt}^{\text{s}}+{\omega }_t,j=1,\dots ,J; \end{gathered}$$ (8)

where μ_t is the overall logit event probability for each treatment, ω_t is a design-by-treatment interaction effect reflecting inconsistency between single-arm trials and RCTs, and β_kt and ${\beta }_{jt}^{\text{s}}$ are trial-by-treatment interaction effects to reflect between-trial heterogeneity. The ω_t’s could be treated as fixed effects or random effects. In the random-effects approach, these ω_t {t = 1, …, T} could be independent or dependent with correlations representing the similarity across different treatments of inconsistency between single-arm trials and RCTs.

Fourth, Turner et al. (2019) proposed to incorporate external evidence in CB-NMA by using informative priors specified based on previously published evidence describing between-trial heterogeneity. A similar idea could be used in AB-NMA by first obtaining a posterior distribution for ${\sigma }_t^{\text{s}}$ from single-arm trials, then using this as an informative prior for σ_t. However, small $B_t^{\text{s}}$ or B_t may still provide little improvement in estimation. Another widely used approach in CB-NMA to borrow information from single-arm trials or observational studies is aggregate-level covariate matching (ALCM), which was thoroughly discussed in Leahy et al. (2019). In short, covariate information is first used to match single-arm trials to form constructed RCTs; when analyzing the existing network of RCTs, these constructed RCTs are also incorporated by various statistical methods. One advantage of this method over our approach is that it can fill the gap between two disconnected evidence networks (Schmitz et al., 2018), while CPV cannot. Currently, the CB-NMA approach is also more widely accepted by health technology assessment agencies than the AB-NMA approach. However, the CPV method only incorporates variance information of absolute effects from single-arm trials; in contrast, the ALCM method borrows both mean and variance information of constructed contrast effects, which may cause potentially larger bias. Also, incorporating variance information from single-arm trials in the CPV method, even though this method may be subject to potential bias of variance information from the perspective of randomized clinical trial designs, could help us understand the variability of absolute treatment effects in the real world applications. Results based on CPV method may serve as a supplementary source of evidence to make better decisions. Moreover, we could also use covariate information to match single-arm trials and treatment arms from RCTs to determine how much information we should borrow in the CPV method.

Finally, we could also develop power priors, commensurate priors, or Bayesian model averaging methods to incorporate supplemental information under the framework of the CB-NMA. The triangle inequalities on between-trial standard deviations could make prior specifications more complicated (Lu and Ades, 2009).