Abstract
Accurate inference of population structure is important in many studies of population genetics. Here we present HaploNet, a method for performing dimensionality reduction and clustering of genetic data. The method is based on local clustering of phased haplotypes using neural networks from whole-genome sequencing or dense genotype data. By using Gaussian mixtures in a variational autoencoder framework, we are able to learn a low-dimensional latent space in which we cluster haplotypes along the genome in a highly scalable manner. We show that we can use haplotype clusters in the latent space to infer global population structure using haplotype information by exploiting the generative properties of our framework. Based on fitted neural networks and their latent haplotype clusters, we can perform principal component analysis and estimate ancestry proportions based on a maximum likelihood framework. Using sequencing data from simulations and closely related human populations, we show that our approach is better at distinguishing closely related populations than standard admixture and principal component analysis software. We further show that HaploNet is fast and highly scalable by applying it to genotype array data of the UK Biobank.
Understanding population structure is a cornerstone in population and evolutionary genetics as it provides insights into demographic events and evolutionary processes that have affected a population. The most common approaches for inferring population structure from genetic data are using principal component analysis (PCA) (Patterson et al. 2006) and clustering algorithms such as STRUCTURE (Pritchard et al. 2000), or derivations thereof. PCA infers continuous axes of genetic variation that summarize the genetic relationship between samples, whereas clustering algorithms assign samples to a fixed or variable number of ancestral sources while allowing for fractional membership. The inferred axes of PCA are very useful to account for population or cryptic structure in association studies or even to simply visualize the genetic data. A limitation for most PCA and clustering algorithms is that they assume all single-nucleotide polymorphisms (SNPs) to be independent, and they do therefore not benefit from the information of correlated sites or they may be biased thereof in their global estimates (Tang et al. 2005; Patterson et al. 2006). A notable exception is ChromoPainter (Lawson et al. 2012), which uses the Li and Stephens (2003) hidden Markov model for haplotype sampling in order to model and use correlations between SNPs, by letting samples be a mosaic of each other's haplotypes. This has improved the fine-scale resolution, and ChromoPainter has become state of the art for inferring fine-scale population structure.
Gaussian mixture models and k-means are other commonly used methods for performing unsupervised clustering (Saxena et al. 2017). However, these methods suffer from the curse of dimensionality in which relative distances between pairs of samples become almost indistinguishable in high-dimensional space (Zimek et al. 2012). A popular approach to overcome the curse of dimensionality is to perform dimensionality reduction, for example, using PCA, and then perform clustering in the low-dimensional space that still captures most of the variation in the full data set (Ding and He 2004). Recently, deep autoencoder methods have been very successful for large-scale data sets as they perform dimensionality reduction and clustering either sequentially or jointly to benefit from induced nonlinearity and scalability of deep learning architectures using neural networks (NNs) (Xie et al. 2016; Yang et al. 2017). Deep autoencoders have also been introduced in generative models, for example, variational autoencoders (VAEs), in which the unknown data generating distribution is learned by introducing latent random variables, such that new samples can be generated from this distribution (Kingma and Welling 2013; Rezende et al. 2014).
Most studies in population genetics using NNs for parameter inference have mainly focused on supervised learning through simulations from demographic models (Sheehan and Song 2016; Chan et al. 2018; Schrider and Kern 2018; Flagel et al. 2019; Gower et al. 2021). Here, an overall demography is assumed, based on previous literature, and a lot of different data sets are simulated using small variations in model parameters, for example, selection coefficient or recombination rate, with evolutionary simulators (e.g., msprime [Kelleher and Lohse 2020] or SLiM [Haller and Messer 2019]). The studies usually convert a simulated haplotype matrix into a downscaled fixed sized image with rows and/or columns sorted based on some distance measure. The network is then trained on the simulated data sets to learn the specified model parameters with feature boundaries in convolutional layers, and in the end, the model is tested on a real data set. However, recently, more studies have instead focused on deep generative models for data-driven inference or simulation using unsupervised learning approaches, which will also be suitable for the growing number of unlabeled large-scale genetic data sets (Montserrat et al. 2019; Battey et al. 2021; Wang et al. 2021; Yelmen et al. 2021; Ausmees and Nettelblad 2022). There has also been a recent interest in the application of the nonlinear dimensionality reduction method UMAP in population genetics (Diaz-Papkovich et al. 2019).
We here present HaploNet, a method for inferring haplotype clusters and population structure using NNs in an unsupervised approach for phased haplotypes of whole-genome sequencing (WGS) or genotype data. We use a VAE framework to learn mappings to and from a low-dimensional latent space in which we will perform indirect clustering of haplotypes with a Gaussian mixture prior. Therefore, we do not have to rely on simulated training data from demographic models with a lot of user-specified parameters but are able to construct a fully data-driven inference framework in which we can infer fine-scale population structure. We locally cluster haplotypes and exploit the generative nature of the VAE to perform PCA and to build a global clustering model similar to NGSadmix (Skotte et al. 2013), which we fit using an accelerated expectation–maximization (EM) algorithm to estimate ancestry proportions, as well as frequencies of our NN-inferred haplotype clusters.
Results
Simulation scenarios
We performed a simulation study of five populations inspired by the simple demography by Lawson et al. (2012) and applied HaploNet to four different scenarios. The demography used for simulation is displayed in Figure 1A. We simulated three different scenarios of various population split times with a constant population size of 10,000, as well as another scenario with a constant population size of 50,000, to counteract the increased genetic drift in an increase of population split times. In all scenarios, we simulated 500 diploid individuals with 100 from each of the five populations. We compare the estimated ancestry proportions from our HaploNet clustering algorithm against results from ADMIXTURE based on signal-to-noise ratio measures (Supplemental Table S1) and their ability to separate ancestry sources. We further compare the inferred population structure from our PCA approach to the PCA from ChromoPainter and standard PCA using PLINK based on signal-to-noise ratio measures of the inferred top principal components that capture the population structure (Supplemental Table S2). The results of the ancestry estimation of all simulation scenarios are shown in Supplemental Figure S2.
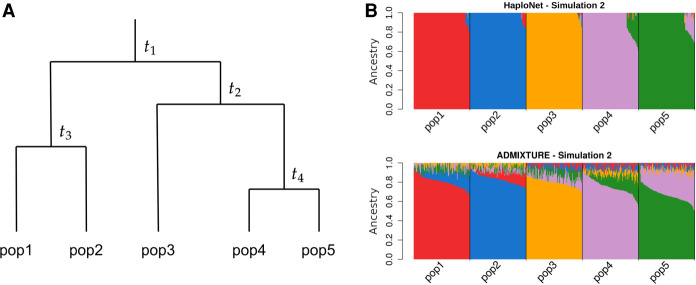
Figure 1.
Inference of population structure in different simulation configurations. (A) Overview of simulation configuration of four splits into five populations with equal population sizes at all times. The time of population splits are designated t1, t2, t3 and t4, measured in generations. (B) Estimated ancestry proportions in one of the four simulation scenarios (Simulation 2) with t1 = 200, t2 = 120, t3 = 80, and t4 = 40 using HaploNet (top) and ADMIXTURE (bottom).
Simulation 1 is the hardest scenario in which the split times measured in generations between populations are very recent, t1 = 100, t2 = 60, t3 = 40, and t4 = 20, with a constant population size of 10,000. Here, we see HaploNet capturing more structure and able to better separate the five populations than ADMIXTURE, as also seen in the signal-to-noise ratio measures. As expected owing to the recent split between them, pop4 and pop5 have not had time to become two distinct homogeneous populations, and we are not able to perfectly separate them into homogeneous clusters. For the PCAs, visualized in Supplemental Figure S3, we see that all three methods are able to split the five populations with only small overlap between a few individuals of pop4 and pop5 on PC4.
In Simulations 2 and 3, the split times are, respectively, two and 10 times longer than in Simulation 1, and in these easier scenarios, the admixture proportion estimates from ADMIXTURE are still very noisy, whereas HaploNet has better separation of the populations (Fig. 1B; Supplemental Fig. S2). All methods are able to infer distinct clusters of the populations using PCA (Supplemental Figs. S4, S5), with ChromoPainter having the best signal-to-noise ratio for scenario 2 and a similar performance to HaploNet in scenario 3 (Supplemental Table S2).
Simulation 4 has the same split times as Simulation 3 (t1 = 1000, t2 = 600, t3 = 400, and t4 = 200) but with a constant population size of 50,000, which lowers the effect of genetic drift that makes the populations less distinct and thus makes the scenario harder than Simulation 3. We observe that HaploNet is still capable of perfectly separating the ancestry sources, whereas ADMIXTURE has noisy estimates for all individuals. We note that ChromoPainter was prematurely terminated owing to memory error for 13.4 million SNPs by exceeding the available memory on the test machine (128 GB), and the expected runtime would have been approximately 1.5 months. HaploNet and PLINK are able to perfectly split and cluster the populations in PC space as visualized in Supplemental Figure S6. In all scenarios, we performed the ADMIXTURE analyses and the PLINK PCA with and without LD pruning. For all analyses, the method performed slightly better with LD-pruned data (Supplemental Table S1, S2).
1000. Genomes Project
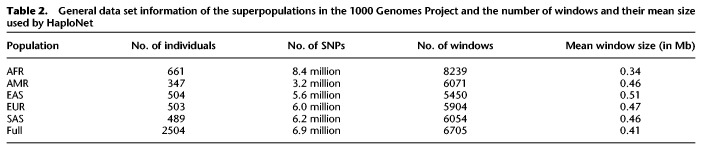
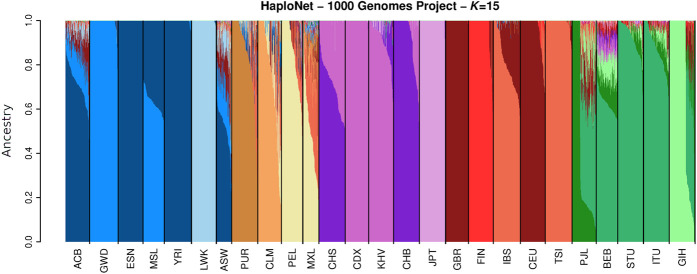
We applied HaploNet to the entire 1000 Genomes Project and separately to each of its five superpopulations (African [AFR], American [AMR], East Asian [EAS], European [EUR], and South Asian [SAS]). Each superpopulation had between 347 and 661 individuals and 3.2–8.4 common (MAF > 5%) SNPs (Table 2). We compare the estimated individual ancestry proportions from our clustering algorithm with results from ADMIXTURE based on signal-to-noise ratio measures (Supplemental Table S3), and we compare the inferred population structure from our PCA approach with the PCA from ChromoPainter and standard PCA using PLINK, as well based on signal-to-noise ratio measures of the inferred principal components (Supplemental Table S4) for each of the superpopulations. We only use the principal components capturing the population structure as displayed in Supplemental Figure S23 for the EUR superpopulation. Additionally, we compare the runtimes of HaploNet and ChromoPainter for Chromosome 2 in each of the five superpopulations using both GPU and CPU for training HaploNet, which is summarized in Table 1. Overall illustrations of ancestry estimations for the full data set (K = 15) and for each superpopulation are depicted in Figures 2 and 3, respectively. The application of HaploNet on the full data set has been performed to validate the fine-scale structure in the superpopulation applications. Another visualization of ancestry estimations in the full data set is shown in Supplemental Figure S24 for K = 14, which was the highest K for which ADMIXTURE has reached convergence.
Table 2.
General data set information of the superpopulations in the 1000 Genomes Project and the number of windows and their mean size used by HaploNet
Table 1.
Runtimes for Chromosome 2 in the five superpopulations of the 1000 Genomes Project using HaploNet and ChromoPainter
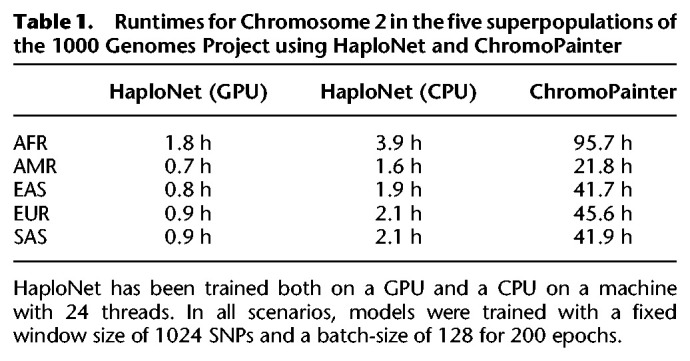
Figure 2.
Estimated ancestry proportions in the full 1000 Genomes Project using HaploNet for K = 15. ADMIXTURE was not able to converge to a solution in 100 runs for this scenario.
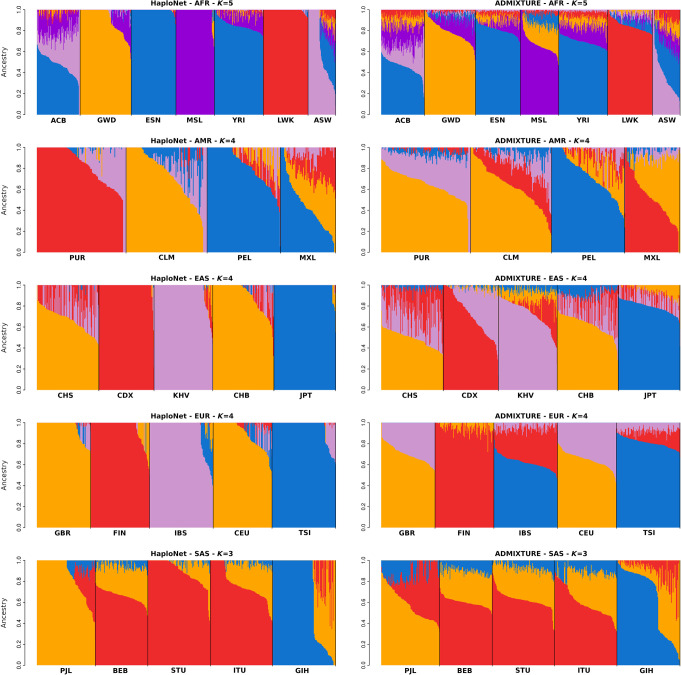
Figure 3.
Estimated ancestry proportions in the superpopulations of the 1000 Genomes Project using HaploNet (left column) and ADMIXTURE (right column) for African (AFR), American (AMR), East Asian (EAS), European (EUR), and South Asian (SAS), respectively.
The AFR superpopulation includes 661 individuals from seven populations with two populations also having European ancestry (African Caribbean [ACB] and African American [ASW]). The inferred population structure for different Ks and PCs is shown in Supplemental Figures S7 and S8. The benefit of using haplotype information is immediately clear, as the estimated ancestry proportions from HaploNet are much better at separating the populations as also seen by the signal-to-noise ratio measure in comparison to ADMIXTURE. This is clearly visible for K = 5 (Fig. 3), where the Mende in Sierra Leone (MSL) population is represented by its own component and its ancestry is also seen in the GWD and YRI populations, which makes sense from a geographical viewpoint. For PCA (Supplemental Fig. S8), the beneficial effect of using the haplotype-based methods is not apparent as the large-scale structure from the European ancestry within ACB and ASW makes it hard to distinguish fine-scale structure within the African ancestry. This European ancestry is correctly inferred in the full data set with K = 15 (Fig. 2), where both ASW and ACB have substantial north European ancestry (British in England and Scotland [GBR] and Utah residents with Northern and Western European ancestry [CEU]).
The results of the AMR superpopulation containing 347 individuals are visualized in Supplemental Figures S9 and S10. These populations consist of many individuals with both European and Native American ancestry. We observe that HaploNet and ADMIXTURE cluster the individuals differently: HaploNet splits the Puerto Rican in Puerto Rico (PUR) and Colombian in Medellin (CLM) populations, which could correspond to two different European ancestry sources, whereas ADMIXTURE splits the Native American ancestry within the Peruvian in Lima (PEL) and Mexican Ancestry in Los Angeles (MXL) populations, for K = 3, 4. In K = 4, we see that HaploNet captures an African ancestry signal in PUR and to a lesser degree in CLM. This is consistent with previous studies (Gravel et al. 2013) and validated from running on the full data set (Fig. 2). In the full data, we can also see that the European ancestry in the Mexican population (MXL) is mainly from southern European (Toscani in Italy [TSI] and Iberian populations in Spain [IBS]), whereas the PUR and CLM European ancestry gets its own component. In the PCA plots (Supplemental Fig. S10), we see that HaploNet and ChromoPainter are clustering the populations slightly better than standard PCA by making them more separable and by separating the signal captured by PC3 and PC4.
We next analyzed the 504 individuals in the EAS superpopulation (Fig. 3; Supplemental Figs. S11, S12). From the estimated ancestry proportions, HaploNet performs much better than ADMIXTURE and is able to cleanly separate the Vietnamese ancestry (KHV) from the ancestry signal of the Dai people (CDX) for K = 4. We see a very similar pattern on the PCA plots, where the haplotype-based methods are able to separate the two populations as well, whereas the standard PCA approach cannot.
The results of the EUR superpopulation are visualized in Supplemental Figures S13 and S14 for ancestry proportions and PCA, respectively. For K = 4 (Fig. 3), we observe that HaploNet is able to distinguish between the two Southern European populations (IBS and TSI), which is not the case for ADMIXTURE. We also see from the signal-to-noise ratio measures that HaploNet is much better at separating the five populations. A similar pattern is observed in the population structure inferred using PCA for HaploNet and ChromoPainter, where they are able to separate the Southern European populations on PC3 as also verified with their signal-to-noise ratio measures.
Finally, the results of the SAS superpopulation are visualized in Supplemental Figures S15 and S16. We see that the complex population structure of the SAS superpopulation makes it hard for the haplotype-based methods to separate the populations on a finer scale than the standard approaches.
The presented analyses were run on computer clusters and in order to benchmark the runtimes, we timed the analyses of Chromosome 2 on a single machine with both CPU and GPU. HaploNet was about twice as fast using the GPU compared with CPU and ChromoPainter was 10–30 times slower (Table 1), and we were not able to run it on the full 1000 Genomes Project data.
Robustness
To test the robustness of HaploNet in terms of hyperparameters, model, and data type, we applied it to the European superpopulation under various scenarios and compared the performance to the results above. The performances are summarized in Supplemental Table S5.
We varied window sizes and evaluated its performance on inferring population structure based on both ancestry proportions and PCA. The results are displayed in Supplemental Figures S17 and S18. HaploNet estimates very similar ancestry proportions for each of the window sizes where we are able to separate the Southern European populations. However, we see a decreasing degree of resolution in the ancestry proportions as the window size becomes larger. For the PCA plots, we observe that all windows sizes are able to separate the Southern European populations and have similar performances in terms of signal-to-noise ratio measures.
We investigated the effectiveness of the Gaussian mixture prior model by only having a model with a categorical latent variable and a linear decoder. The model would then perform amortized haplotype clustering with the decoding process directly modeling haplotype cluster frequencies. The results are shown in Supplemental Figure S19, where we see a decrease in the model's sensitivity to separate the Southern European populations in comparison to our full model.
We also verified the model's dependency on LD structure to infer fine-scale population structure. Here, we permuted SNP positions of all chromosomes to distort and remove the LD structure in the data. The results are visualized in Supplemental Figure S20, where the model is not able to infer any meaningful population structure further than on PC1.
Lastly, we analyzed only the SNPs found on the high density genotype chip of the Omni platform (The 1000 Genomes Project Consortium 2015) to test how well HaploNet would perform on SNP array data. After filtering, the data set contained 1.3 million SNPs, and we have used a window size of 256 in HaploNet. The results are visualized in Supplemental Figures S21 and S22, where HaploNet has similar performance in comparison to when it is used on the full data set and is also fully able to split the two Southern European populations, which was not possible for ADMIXTURE with the full data set.
UK Biobank
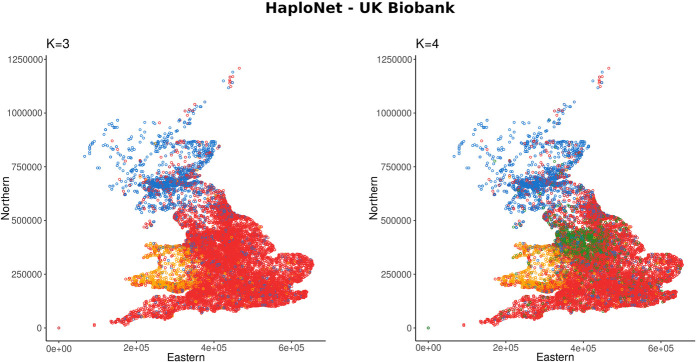
We further applied HaploNet to SNP array data of the UK Biobank data set and infer population structure on a subset of 276,732 unrelated with self-reported ethnicity as “white British” with a total of 567,499 SNPs after quality control and filtering. It took 7.3 h to train HaploNet on the Chromosome 2 with a window size of 256 and a batch-size of 8196 for 100 epochs. The results are displayed in Figure 4 and Supplemental Figure S26 for estimating ancestry proportions and inferring population structure using PCA, respectively. For K = 3, HaploNet infers three clear ancestral components that reflect English, Scottish, and Welsh sources, whereas for K = 4, we infer an additional ancestral component capturing a signal in Northwest England. We have visualized the distributions of ancestry proportions stratified by country of birth for K = 4 in Supplemental Figure S25. For the population structure inferred using our PCA method, we capture similar structure in the top PCs, where we additionally see a component capturing the variation between North and South Wales. On PC6, we capture structure that does not reflect population structure but instead captures variation that could be owing to SNP ascertainment or strong LD structure as previously observed for the UK Biobank (Privé et al. 2020). The signal is caused by a single genomic region as shown by the SNP loadings in Supplemental Figure S27. Similar cluster patterns in the Northwest England have previously been observed before (Saada et al. 2020) in the “white British” subset of the UK Biobank.
Figure 4.
Estimated ancestry proportions in the subset of unrelated self-identified “white British” of the UK Biobank using HaploNet for K = 3 and K = 4, respectively. Individuals are plotted by their birthplace coordinates and colored by their highest associated ancestry component.
Discussion
We have presented our new framework, HaploNet, which performs dimensionality reduction and clusters haplotypes using NNs. We explored its capability to infer population structure based on local haplotype clusterings, which are performed in windows along the genome, as well as its generative properties for estimating NN likelihoods. We show the benefits of merging machine learning with traditional statistical frameworks, as we developed a novel method for estimating ancestry proportions from NNs in a likelihood model. We tested HaploNet in simulation scenarios and data from the 1000 Genomes Project and compared its results to commonly used software for inferring population structure based on ancestry proportions or PCA. We show that HaploNet is capable of using haplotype information for inferring fine-scale population structure that outperforms ADMIXTURE with respect to signal-to-noise ratio. On real data sets, HaploNet infers similar population structure to ChromoPainter using PCA, while being much faster. However, in several simulations, ChromoPainter separated the populations better than HaploNet. It was not computationally feasible to run ChromoPainter for larger data sets in terms of both speed and memory usage. We further showed the scalability of HaploNet by applying it to genotype data of the UK Biobank with hundreds of thousands of individuals, which is not possible with ADMIXTURE or ChromoPainter, and we are able to infer four ancestry sources for individuals born within the United Kingdom.
We have also reported the performances of ADMIXTURE and PLINK on a LD-pruned version of all data sets for ancestry estimation and PCA, respectively. In all cases, we observed similar or slightly better performance in comparison to using the full nonpruned data set. However, the consequence of LD pruning in a heterogeneous data set with population structure besides losing information is not fully understood because the population structure will increase the LD between SNPs. LD pruning can greatly decrease FST values between populations Li et al. (2019) and thus affects the distribution of eigenvalues because they are proportional to FST (McVean 2009). Therefore, we have measured the accuracy of PCA (PLINK) and ADMIXTURE with and without pruning for each of the superpopulations. However, for computational reasons, we have only used a LD-pruned version when analyzing the full 1000 Genomes Project data with ADMIXTURE. Another factor that can affect measures of population structure is minimum minor allele frequency cutoffs. We have chosen the standard 5% cutoff for most analyses, including ADMIXTURE and PCA in PLINK. Rare alleles can reduce the performance of these methods (Ma and Shi 2020) and are harder to phase, which can be a problem for HaploNet and ChromoPainter. On the other hand, they can also be informative about a more recent population structure. However, we have not explored the effect of including the more rare alleles in this study.
The number of clusters, C, is usually a nontrivial hyperparameter to set in a Gaussian mixture model or in a genetic clustering setting. Multiple runs of varying C are usually performed and evaluated based on some criteria. In our study, we saw that HaploNet seemed capable of inferring the optimal number of haplotype clusters to use by setting C to a high fixed number (C = 32 in all analyses). HaploNet will then only use a subset of the possible haplotype clusters to model the haplotype encodings, which has also been observed in a different application of the Gaussian mixture VAE (GMVAE) model (Bozkurt Varolgüneş et al. 2020). At a lower C, for example, 20, we observed slightly worse performances for all superpopulations in the 1000 Genomes Project (Supplemental Table S6). The decrease in performance appears to be related to the number of evaluated windows and, therefore, the genetic diversity in each superpopulation.
A limitation of our model and other deep learning models is that usually only relatively small genetic data sets are available to researchers, which introduces problems with training convergence and overfitting. To combat these issues, we kept the number of parameters low and used an autoencoder architecture that naturally regularizes its reconstruction performance. Another advantage of having a small model configuration is observed for the low training times on both GPU and CPU setups that broadens the application opportunities of HaploNet. However, the difference between the GPU and CPU runtimes will be larger when running chromosomes in parallel. For all analyses in this study, including the UK Biobank data, we have been using the entire data for training our NNs to model all available haplotypes, whereas with larger labeled data sets, one could have a separate training data. We have also limited ourselves to using fixed window lengths across chromosomes for the matter of simplicity and ease of use, where we instead could have included external information from genetic maps to define windows of variable size. We show that HaploNet is somewhat robust to changes in window size when inferring global population structure, either using PCA or ancestry proportions; however, for fixed-size windows, there is a trade-off in resolution and training time that is a subject for future research. We further show that we are able to capture fine-scale structure when only evaluating variable sites available on a common genotype chip that allows for broader applications of our method.
Our model serves as a proof of concept and an exploration for how nonlinear NNs and specialized architectures can be used to learn haplotype clusters and encodings across a full genome in a very scalable procedure. We hypothesize that as the number of large-scale genetic data sets are growing, we will see the increasing importance of deep learning in population genetics, as deeper models can be trained and more bespoke architectures will be developed. As shown in our study, we can even use learned mappings together with standard statistical frameworks to further improve our understanding of genetic variation. Future developments of our framework are to use the haplotype clusters in sequential models to, for example, infer local ancestry and IBD tracts in hidden Markov models, as well as investigate its potential integration into imputation based on haplotype reconstruction and association studies.
Methods
The method is based on phased haplotype data from diallelic markers. We define the data matrix X as a 2N × M haplotype matrix for a given chromosome, where N is the number of individuals and M is the number of SNPs along the chromosome. The entries of the matrix are encoded as either zero or one, referring to the major and minor allele, respectively.
For each chromosome, we divide the sites into W windows of a fixed length of L SNPs, which we assume is much smaller than M. The windows are nonoverlapping, and we will further assume that the parameters estimated in a window are independent from parameters estimated in adjacent windows. The length of the genomic windows can also be defined by a recombination map; however, we have kept it fixed for the sake of generalizability and ease of application in this study. For each defined window along a chromosome, we independently train NNs in a VAE framework to learn haplotype clusters and encodings using a Gaussian mixture prior. We define haplotype clusters as a collection of haplotypes that cluster together based on similarities in their encodings. In the model, they are identified by their latent state (y) whose mean structure predicts a distribution of similar haplotypes. We are then able to calculate a likelihood for an observed haplotype given an inferred haplotype cluster that resembles calculating genotype likelihoods in WGS data from the trained networks.
Variational autoencoder
An autoencoder is a state-of-the-art approach for performing dimensionality reduction by learning a mapping of the space of the input data, , to a low-dimensional space, , and a mapping back to the input data (Rumelhart et al. 1985; Baldi 2012). More formally, we can describe the two mapping functions as and , which are commonly called the encoder and the decoder, respectively. Both the encoder and the decoder are parameterized by (deep) NNs to learn the mappings, as multilayer feed-forward NNs are universal function approximators (Hornik et al. 1990).
A probabilistic variant of this NN architecture is introduced in the VAE, where the unknown generating process of the input data is modeled by introducing latent variables and the joint probability is approximated through variational inference. As an optimization method, variational inference is often used to approximate the posterior distribution of a set of latent variables, z, , by fitting a function that describes a chosen family of distributions, . Thus, variational inference turns it into an optimization problem, where the objective is to maximize the evidence lower bound (ELBO) of the marginal log-likelihood of the data, , iteratively. In contrast, Monte Carlo Markov chain methods approximate the joint probability of the data and the latent variables by sampling from the posterior distribution (Blei et al. 2017). The function approximating the posterior distribution is parameterized with variational parameters ϕ. Kingma and Welling (2013) introduced the stochastic gradient variational Bayes (SGVB) estimator of the ELBO for approximate posterior inference in a VAE framework (as well as Rezende et al. 2014), where a set of parameters, (θ, ϕ), are optimized with amortized inference using mappings parameterized by NNs. Here, the marginal log-likelihood of the data, , is parameterized with parameters θ. This amortization means that the number of parameters does not depend on sample size as in traditional variational inference but depends on the network size (Shu et al. 2018). The VAE can be seen as an autoencoder with its latent space being regularized by a chosen prior distribution to make the inferred latent space more interpretable and to preserve global structure. A standard Gaussian prior is the most common choice; however, it is often too simple, and a lot of effort has been made to make the approximate posterior richer with normalizing flows and additional stochastic layers (Rezende and Mohamed 2015; Kingma et al. 2016; Sønderby et al. 2016).
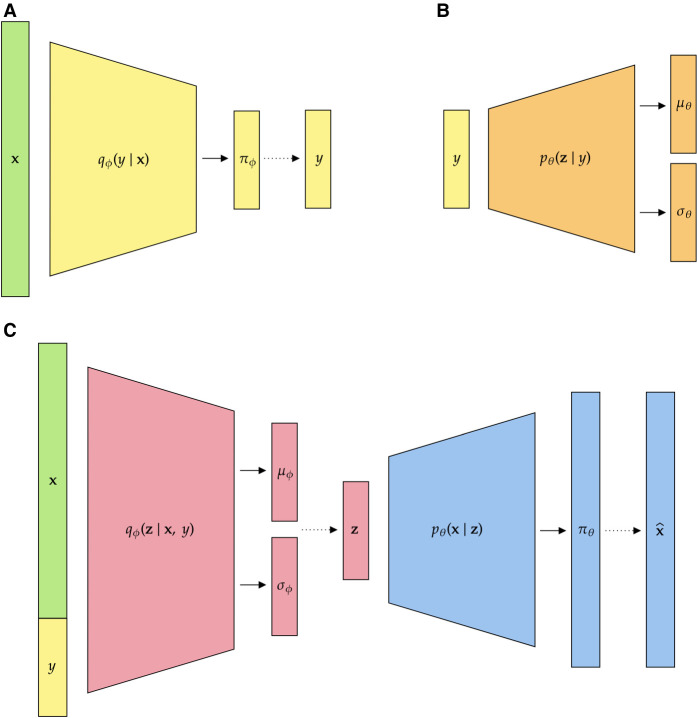
In our proposed method, HaploNet, we construct a generative model and use a VAE framework to learn low-dimensional encodings of haplotypes in windows along the genome. However, we also introduce an additional categorical variable, y, to represent haplotype clusters as mixture components such that we assume a Gaussian mixture prior in the generative model. In this way, we are able to jointly perform dimensionality reduction and cluster haplotypes in a highly scalable approach for a given genomic window. In the following model descriptions, we will follow the mathematical notation used in the machine learning literature and by Kingma and Welling (2013), where and are probability functions that define the decoder and encoder part, respectively. θ and ϕ are the parameters (biases and weights) in the NNs. We have provided a visualization of our overall network architecture, including descriptions of the major substructures, in Figure 5A–C. We define the following latent variable model for a single haplotype in a single genomic window with data x ∈ {0, 1}L, Gaussian latent variables , and categorical latent variable y ∈ {0, 1}C (one-hot encoded) such that x is conditionally independent of y:
| (1) |
with generative processes defined as
| (2) |
| (3) |
| (4) |
Here z is a D-dimensional vector representing the latent haplotype encoding, and C is the number of haplotype clusters, whereas , and are mapping functions parameterized by NNs with network parameters θ. In this case, is a vectorized notation of Bernoulli distributions, and each of the L sites will have an independent probability mass function. We assume that the covariance matrix of the multivariate Gaussian distribution is a diagonal matrix that will promote disentangled factors. We assume the following inference (encoder) model that constitutes the approximate posterior distribution:
| (5) |
| (6) |
| (7) |
where , and again are mapping functions parameterized by NNs with network parameters ϕ. Therefore, the marginal posterior distribution and marginal approximate posterior distribution of z will both be a mixture of Gaussians. Thus, and will constitute the probabilistic encoder and decoder, respectively, in comparison to the deterministic encoder and decoder of the standard autoencoder.
Figure 5.
The NN architecture of HaploNet split into three major substructures. Here the solid lines represent the estimation of distribution parameters, and the dashed lines represent sampling of latent variables. (A) The NN parameterizing the distribution , for sampling the haplotype cluster; (B) the network parameterizing the regularizing distribution of the sampled encoding, ; and (C) the network parameterizing the distribution , for sampling the haplotype encoding, as well as the network decoding the sampled encoding to reconstruct our input. Note that the colors of the network blocks are coherent across substructures such that the sampled y in A is used in both B and C.
From the marginal log-likelihood of the data, we derive the following ELBO (Blei et al. 2017) of our VAE model for haplotype i,
| (8) |
where the marginal log-likelihood of the full data in a window is given by
| (9) |
The full derivation of this ELBO is described in the Supplemental Material, as well as reparameterization tricks that are needed to approximate and optimize it through Monte Carlo samples of the latent variables. We immediately see that the first term in Equation 8 describes the reconstruction error of mapping from the latent space back to the input space as in an autoencoder framework. The next two terms act as regularization on the learned latent spaces, where the second term encourages the variational Gaussian distributions to be close to the estimated prior distributions, whereas the last term encourages anticlustering behavior to prevent all haplotypes to cluster in one component. This is a modification of the unsupervised loss of the M2 model (Kingma et al. 2014), as described by Shu (2016), where information of the haplotype cluster is also propagated through . However, we further approximate the categorical latent variable with samples from a Gumbel–Softmax distribution (Jang et al. 2016; Maddison et al. 2016) instead of the categorical distribution. The Gumbel–Softmax distribution is a continuous approximation to the categorical distribution that can be easily reparameterized for differentiable sampling and gradient estimations (Supplemental Fig. S1). In this way, we can avoid an expensive computational step of having to marginalize over the categorical latent variable in the SGVB estimator of the ELBO as is performed in the original model. A lot of different interpretations and implementations of the GMVAE have been proposed (Dilokthanakul et al. 2016; Jiang et al. 2016; Collier and Urdiales 2019; Bozkurt Varolgüneş et al. 2020), and a similar architecture to ours has been implemented (Figueroa 2019).
NN likelihoods
We can exploit and use the generative nature of our GMVAE model based on the parameters of the trained NNs for a window to construct likelihoods from the mean latent encodings of the estimated haplotype clusters through reconstruction. We define , with yi,a being one-hot encoded, as the NN likelihood that the data are generated from the cth haplotype cluster, for the ath haplotype of individual i in window w. The NN likelihoods are calculated as follows using the probability mass function of the Bernoulli distribution and the properties, and :
| (10) |
for c = 1, …, C (one-hot encoded) and are the data of the ath haplotype of individual i in window w with L being the number of SNPs. Here describes the learned mean latent encoding of a given haplotype cluster, y, in the generative model, and is the learned mean reconstruction of the mean latent encoding.
Ancestry proportions and haplotype cluster frequencies
A widely used approach for inferring population structure is estimating ancestry proportions. We propose a model for estimating ancestry proportions and haplotype cluster frequencies assuming K ancestral components based on the model introduced in NGSadmix (Skotte et al. 2013), as an extension to the ADMIXTURE model (Alexander et al. 2009), where instead of latent states of unobserved genotypes, we have latent states of haplotype clusters. We can then construct the following likelihood model of the data X using the above-defined NN likelihoods given the genome-wide ancestry proportions Q and window-based ancestral haplotype frequencies F:
| (11) |
with k describing the ancestral state, for Q ∈ [0, 1]N×K with constraint and F ∈ [0, 1]W×K×C with constraint . Here W is the total number of windows across chromosomes, N is the number of individuals, and C is the number of haplotype clusters. Maximum likelihood estimates of F and Q are obtained using an EM algorithm. The full description of the EM algorithm is detailed in the Supplemental Material. We use the S3 scheme of the SQUAREM methods (Varadhan and Roland 2008) for accelerating our EM implementation, such that one large step is taken in parameter space based on the linear combination of two normal steps.
Inference of population structure using PCA
We can also use the NN likelihoods to infer population structure using PCA; however, the approach is not as straightforward as for the model-based ancestry estimation. We use a similar approach as in microsatellite studies in which we assume that all clusters are an independent marker, and we simply sum the cluster counts for each individual in each window by taking the most probable cluster for each haplotype to construct a N × W × C tensor, Y.
| (12) |
| (13) |
We can now treat the task as a standard PCA approach in population genetics based on a binomial model (Patterson et al. 2006) such that the pairwise covariance is estimated as follows for individual i and j:
| (14) |
where is the frequency of the cth haplotype cluster in window w. We can finally perform eigendecomposition on the covariance matrix to extract principal components.
Implementation
We have implemented HaploNet as a Python program using the PyTorch library (v.1.10) (Paszke et al. 2019), and it is freely available at GitHub (https://github.com/rosemeis/HaploNet). We have used the NumPy (Harris et al. 2020) and scikit-allel (https://doi.org/10.5281/zenodo.4759368) libraries for preprocessing the data from variant call format (VCF) into data structures to be used in HaploNet. The EM algorithm for estimating ancestry proportions and the algorithm for performing PCA have been implemented in Cython (Behnel et al. 2011) for speed and parallelism.
An overall detailed description of the network architectures used in different scenarios can be found in the Supplemental Material. We have used fully connected layers throughout the network, and for all inner layers in our NNs, we are using rectified linear unit (ReLU(x) = max (0, x)) activations to induce nonlinearity into the networks, followed by batch normalization (Ioffe and Szegedy 2015), whereas all outer layers are modeled with linear activations. The usage of linear activations means that the networks are estimating the logits of the probabilities instead the probabilities directly in and for computational stability, as well as for and that represent logσ2 in inner computations.
We are training our networks with the Adam optimizer (Kingma and Ba 2014) using default parameters with a learning rate of 1.0 × 10−3, β1 = 0.9, and β2 = 0.999. The batch sizes and number of epochs are detailed in the Supplemental Material for each of the different data sets. We have used a fixed temperature in the sampling from the Gumbel–Softmax distribution of τ = 0.1 to approximate and encourage a categorical sampling, and we use one Monte Carlo sample of the latent variables to approximate the expectation in Equation 8.
Simulations
We have simulated five populations from a simple demography with four population splits (t1, t2, t3,t4) using msprime (Fig. 1A; Kelleher and Lohse 2020). We have simulated 500 diploid individuals in four different scenarios with various changes to the chosen population split times and the population sizes. A uniform recombination rate of 1.0 × 10−8 has been assumed in all simulations as well as a mutation rate of 2.36 × 10−8 (Tennessen et al. 2012) for a sequence of 1.0 × 109 bases.
Simulation 1 has the following population split times: t1 = 100, t2 = 60, t3 = 40, and t4 = 20 with an assumed constant population size of 10,000 at all points. After filtering for minor allele frequency threshold of 0.05, the data set consists of 2.8 million SNPs.
Simulation 2 has the following population split times: t1 = 200, t2 = 120, t3 = 80, and t4 = 40 with an assumed constant population size of 10,000 at all points. After filtering for minor allele frequency threshold of 0.05, the data set consists of 2.7 million SNPs.
Simulation 3 has the following population split times: t1 = 1000, t2 = 600, t3 = 400, and t4 = 200 with an assumed constant population size of 10,000 at all points. After filtering for minor allele frequency threshold of 0.05, the data set consists of 2.7 million SNPs.
Simulation 4 has the following population split times: t1 = 1000, t2 = 600, t3 = 400, and t4 = 200 with an assumed constant population size of 50,000 at all points. After filtering for minor allele frequency threshold of 0.05, the data set consists of 13.4 million SNPs.
In all simulation scenarios, we have used a fixed window size of 1024 SNPs, corresponding to a mean window size of 0.37 Mb in scenario 1, 2, 3, and 0.08 Mb in scenario 4.
1000 Genomes Project
We have applied HaploNet to the phase 3 data of the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015). The entire data set consists of phased genotype data of 2504 unrelated individuals from 26 different populations that are assigned to five superpopulations, which are AFR, AMR, EAS, EUR, and SAS, and we inferred local haplotype structure and global population structure for each superpopulation. The information of the data set and each superpopulation is summarized in Table 2.
For each of the superpopulations, we have filtered their SNPs with a minor allele frequency threshold of 0.05. The AFR data set consists of 661 individuals and 8.4 million SNPs from the following seven populations: African Caribbean in Barbados (ACB), Gambian in Western Division (GWD), Esan in Nigeria (ESN), Mende in Sierra Leone (MSL), Yoruba in Ibadan (YRI), Luhya in Webuye (LWK), and African Ancestry in Southwest US (ASW). The AMR data set consists of 347 individuals and 6.2 million SNPs from the following four populations: Puerto Rican in Puerto Rico (PUR), Colombian in Medellin (CLM), Peruvian in Lima (PEL), and Mexican Ancestry in Los Angeles (MXL). The EAS data set consists of 504 individuals and 5.6 million SNPs from the following five populations: Han Chinese South (CHS), Chinese Dai in Xishuangbanna (CDX), Kinh in Ho Chi Minh City (KHV), Han Chinese in Beijing (CHB), and Japanese in Tokyo (JPT). The EUR data set consists of 503 individuals and 6 million SNPs from the following five populations: British in England and Scotland (GBR), Finnish in Finland (FIN), Iberian populations in Spain (IBS), Utah residents with Northern and Western European ancestry (CEU) and Toscani in Italy (TSI). The SAS data set consists of 489 individuals and 6.2 million SNPs from the following five populations: Punjabi in Lahore (PJL), Bengali in Bangladesh (BEB), Sri Lankan Tamil in the UK (STU), Indian Telugu in the UK (ITU), and Gujarati Indians in Houston (GIH). We have used a fixed window size of 1024 SNPs for all superpopulations.
We have additionally used the EUR superpopulation to evaluate various aspects of our proposed method. We have applied HaploNet to a filtered SNP set that overlap with the SNP set of the high-density genotype chip data of the 1000 Genomes Project to explore our capabilities on genotype chip data sets, while using a lower window size of 256. We have applied HaploNet on haplotype matrices with permuted SNPs to ensure that our model captures and uses the LD information in the haplotypes. We have also tested different window sizes (L = {512, 1024, 2048}) to evaluate their effect on the inference of global population structure. Lastly, we have also tested a simpler version of our model architecture in which we only use the categorical latent variable with a linear decoder to investigate the importance of the flexible Gaussian mixture prior. This version can be seen as amortized haplotype clustering in which the decoder learns allele frequencies for each haplotype cluster.
The 1000 Genomes Project phase 3 data used in this study are publicly available at https://www.internationalgenome.org/category/phase-3/.
UK Biobank
To test the scalabilty of HaploNet, we have also applied it to array data of the UK Biobank using unrelated individuals who are self-reported as “white British” as well as having similar genetic ancestry based on PCA from genotype data. We only use SNPs from the UK Biobank Axiom array, where we have filtered the SNPs based on available QC information, a minor allele frequency threshold of 0.01, and a maximum missingness rate of 0.1 and additionally removed variants in located known high LD regions. The final data set consists of 276,732 individuals and 567,499 SNPs. We perform phasing on the genotype data using SHAPEIT4 without using a reference panel. Further details of the sample and variant filtering are described in the Supplemental Material. We have used a fixed window size of 256 SNPs, corresponding to a mean window size of 0.6 Mb.
The genotype data from the UK Biobank (https://www.ukbiobank.ac.uk/) can be obtained by application.
Computational comparisons
All models of HaploNet, as well as other analyses, presented in this study have been run on a machine with a NVIDIA GeForce RTX 2080 Ti GPU (11GB VRAM), using CUDA v.10.2 and cuDNN v.7.6.5, and an Intel Core i9-10920X CPU (3.5 GHz, 24 threads). We compare HaploNet with widely used software based on performance as well as runtime.
We have compared the estimated ancestry proportions of HaploNet with the results of the widely used software ADMIXTURE (v.1.3) (Alexander et al. 2009), which uses unphased genotypes, in the simulation scenarios and in each of the superpopulations in the 1000 Genomes Project. Both methods have been run at least five times using different seeds and determined convergence with three runs being within 10 log-likelihood units of the highest achieved log-likelihood. We evaluate their performances to distinguish populations based on a signal-to-noise ratio measure using the available population labels. We use the average within-population distance of ancestry proportions in comparison to the average between-population distance as a measure of how well populations are separable, similarly to the approach of Lawson and Falush (2012). We included code and scripts for the signal-to-noise ratio measure in the GitHub repository, and in the Supplemental Material (S3).
For estimating the covariance matrix and performing PCA, we have compared HaploNet to ChromoPainter (v.4.1.0) (Lawson et al. 2012) and standard PCA in PLINK (v.2.0) (Chang et al. 2015) on unphased genotypes. We have used ChromoPainter to estimate the shared genome chunks between individuals in an unsupervised manner such that no population information is given and all individuals can be used as donors of each other. We are using their linked model that uses pre-estimated recombination rates from genetic maps of the human chromosomes to model the correlation between SNPs using default parameters. We have used their own R library for performing PCA on the estimated chunk-count matrix. As well as for the ancestry estimations, we also evaluate the population structure inferred using PCA based on the signal-to-noise ratio measure with the principal components. We further compare the computational runtime of HaploNet and ChromoPainter on Chromosome 2 for each of the superpopulations.
Software availability
HaploNet is freely available at GitHub (https://github.com/rosemeis/HaploNet) and as Supplemental Code.
Supplementary Material
Acknowledgments
The study was supported by the Lundbeck Foundation (R215-2015-4174). This research was conducted using the UK Biobank Resource under application 32683.
Author contributions: J.M. and A.A. conceived the study and derived the methods. J.M. implemented the methods and performed the analyses. J.M. and A.A. discussed the results and contributed to the final manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276813.122.
Competing interest statement
The authors declare no competing interests.
References
- The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander DH, Novembre J, Lange K. 2009. Fast model-based estimation of ancestry in unrelated individuals. Genome Res 19: 1655–1664. 10.1101/gr.094052.109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ausmees K, Nettelblad C. 2022. A deep learning framework for characterization of genotype data. G3 12: jkac020. 10.1093/g3journal/jkac020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldi P. 2012. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of ICML Workshop on Unsupervised and Transfer Learning. PMLR27: 37–49. [Google Scholar]
- Battey C, Coffing GC, Kern AD. 2021. Visualizing population structure with variational autoencoders. G3 11: jkaa036. 10.1093/g3journal/jkaa036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behnel S, Bradshaw R, Citro C, Dalcin L, Seljebotn DS, Smith K. 2011. Cython: the best of both worlds. Comput Sci Eng 13: 31–39. 10.1109/MCSE.2010.118 [DOI] [Google Scholar]
- Blei DM, Kucukelbir A, McAuliffe JD. 2017. Variational inference: a review for statisticians. J Am Stat Assoc 112: 859–877. 10.1080/01621459.2017.1285773 [DOI] [Google Scholar]
- Bozkurt Varolgüneş Y, Bereau T, Rudzinski JF. 2020. Interpretable embeddings from molecular simulations using Gaussian mixture variational autoencoders. Machine Learning: Science and Technology 1: 015012. 10.1088/2632-2153/ab80b7 [DOI] [Google Scholar]
- Chan J, Perrone V, Spence J, Jenkins P, Mathieson S, Song Y. 2018. A likelihood-free inference framework for population genetic data using exchangeable neural networks. Adv Neural Inf Process Syst 31: 8594–8605. [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, Lee JJ. 2015. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience 4: 7. 10.1186/s13742-015-0047-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collier M, Urdiales H. 2019. Scalable deep unsupervised clustering with concrete GMVAEs. arXiv:1909.08994 [cs.LG].
- Diaz-Papkovich A, Anderson-Trocmé L, Ben-Eghan C, Gravel S. 2019. UMAP reveals cryptic population structure and phenotype heterogeneity in large genomic cohorts. PLoS Genet 15: e1008432. 10.1371/journal.pgen.1008432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dilokthanakul N, Mediano PA, Garnelo M, Lee MC, Salimbeni H, Arulkumaran K, Shanahan M. 2016. Deep unsupervised clustering with gaussian mixture variational autoencoders. arXiv:1611.02648 [cs.LG].
- Ding C, He X. 2004. K-means clustering via principal component analysis. In Proceedings of the 21st International Conference on Machine Learning, p. 29. Banff, Alberta, Canada, Association for Computing Machinery. [Google Scholar]
- Figueroa JGA. 2019. Gaussian mixture variational autoencoder. https://github.com/jariasf/GMVAE [accessed January 18, 2022].
- Flagel L, Brandvain Y, Schrider DR. 2019. The unreasonable effectiveness of convolutional neural networks in population genetic inference. Mol Biol Evol 36: 220–238. 10.1093/molbev/msy224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gower G, Picazo PI, Fumagalli M, Racimo F. 2021. Detecting adaptive introgression in human evolution using convolutional neural networks. eLife 10: e64669. 10.7554/eLife.64669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravel S, Zakharia F, Moreno-Estrada A, Byrnes JK, Muzzio M, Rodriguez-Flores JL, Kenny EE, Gignoux CR, Maples BK, Guiblet W, et al. 2013. Reconstructing native American migrations from whole-genome and whole-exome data. PLoS Genet 9: e1004023. 10.1371/journal.pgen.1004023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, Messer PW. 2019. SLiM 3: Forward genetic simulations beyond the Wright–Fisher model. Mol Biol Evol 36: 632–637. 10.1093/molbev/msy228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, et al. 2020. Array programming with NumPy. Nature 585: 357–362. 10.1038/s41586-020-2649-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornik K, Stinchcombe M, White H. 1990. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw 3: 551–560. 10.1016/0893-6080(90)90005-6 [DOI] [Google Scholar]
- Ioffe S, Szegedy C. 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning. PMLR37: 448–456.
- Jang E, Gu S, Poole B. 2016. Categorical reparameterization with Gumbel–Softmax. arXiv:1611.01144 [stat.ML].
- Jiang Z, Zheng Y, Tan H, Tang B, Zhou H. 2016. Variational deep embedding: an unsupervised and generative approach to clustering. arXiv:1611.05148 [cs.CV].
- Kelleher J, Lohse K. 2020. Coalescent simulation with msprime. Methods Mol Biol 13: 191–230. 10.1007/978-1-0716-0199-0_9 [DOI] [PubMed] [Google Scholar]
- Kingma DP, Ba J. 2014. Adam: a method for stochastic optimization. arXiv:1412.6980 [cs.LG].
- Kingma DP, Welling M. 2013. Auto-encoding variational Bayes. arXiv:1312.6114 [stat.ML].
- Kingma DP, Mohamed S, Rezende DJ, Welling M. 2014. Semi-supervised learning with deep generative models. In Advances in Neural Information Processing Systems 27 (NIPS 2014, Montreal, Canada). NeurIPS Proceedings, pp. 3581–3589. [Google Scholar]
- Kingma DP, Salimans T, Jozefowicz R, Chen X, Sutskever I, Welling M. 2016. Improved variational inference with inverse autoregressive flow. In Advances in Neural Information Processing Systems 29 (NIPS 2016, Barcelona, Spain). NeurIPS Proceedings, pp. 4743–4751. [Google Scholar]
- Lawson DJ, Falush D. 2012. Population identification using genetic data. Annu Rev Genomics Hum Genet 13: 337–361. 10.1146/annurev-genom-082410-101510 [DOI] [PubMed] [Google Scholar]
- Lawson DJ, Hellenthal G, Myers S, Falush D. 2012. Inference of population structure using dense haplotype data. PLoS Genet 8: e1002453. 10.1371/journal.pgen.1002453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Stephens M. 2003. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165: 2213–2233. 10.1093/genetics/165.4.2213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Löytynoja A, Fraimout A, Merilä J. 2019. Effects of marker type and filtering criteria on QST-FST comparisons. R Soc Open Sci 6: 190666. 10.1098/rsos.190666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma S, Shi G. 2020. On rare variants in principal component analysis of population stratification. BMC Genet 21: 34. 10.1186/s12863-020-0833-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison CJ, Mnih A, Teh YW. 2016. The concrete distribution: a continuous relaxation of discrete random variables. arXiv:1611.00712 [cs.LG].
- McVean G. 2009. A genealogical interpretation of principal components analysis. PLoS Genet 5: e1000686. 10.1371/journal.pgen.1000686 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montserrat DM, Bustamante C, Ioannidis A. 2019. Class-conditional VAE-GAN for local-ancestry simulation. arXiv:1911.13220 [q-bio.GN].
- Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, et al. 2019. PyTorch: an imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019, Vancouver, Canada). NeurIPS Proceedings, pp. 8026–8037. [Google Scholar]
- Patterson N, Price AL, Reich D. 2006. Population structure and eigenanalysis. PLoS Genet 2: e190. 10.1371/journal.pgen.0020190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. 2000. Inference of population structure using multilocus genotype data. Genetics 155: 945–959. 10.1093/genetics/155.2.945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privé F, Luu K, Blum MG, McGrath JJ, Vilhjálmsson BJ. 2020. Efficient toolkit implementing best practices for principal component analysis of population genetic data. Bioinformatics 36: 4449–4457. 10.1093/bioinformatics/btaa520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rezende DJ, Mohamed S. 2015. Variational inference with normalizing flows. In Proceedings of the 32nd International Conference on Machine Learning. PMLR 37: 1530–1538.
- Rezende DJ, Mohamed S, Wierstra D. 2014. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the 31st International Conference on Machine Learning. PMLR32: 1278–1286.
- Rumelhart DE, Hinton GE, Williams RJ. 1985. Learning internal representations by error propagation. ICS Report 8506. Institute for Cognitive Science, University of California, San Diego, La Jolla, California.
- Saada JN, Kalantzis G, Shyr D, Cooper F, Robinson M, Gusev A, Palamara PF. 2020. Identity-by-descent detection across 487,409 British samples reveals fine scale population structure and ultra-rare variant associations. Nat Commun 11: 6130. 10.1038/s41467-020-19588-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxena A, Prasad M, Gupta A, Bharill N, Patel OP, Tiwari A, Er MJ, Ding W, Lin C-T. 2017. A review of clustering techniques and developments. Neurocomputing 267: 664–681. 10.1016/j.neucom.2017.06.053 [DOI] [Google Scholar]
- Schrider DR, Kern AD. 2018. Supervised machine learning for population genetics: a new paradigm. Trends Genet 34: 301–312. 10.1016/j.tig.2017.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheehan S, Song YS. 2016. Deep learning for population genetic inference. PLoS Comput Biol 12: e1004845. 10.1371/journal.pcbi.1004845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu R. 2016. Gaussian mixture VAE: lessons in variational inference, generative models, and deep nets. http://ruishu.io/2016/12/25/gmvae/ [accessed January 18, 2022].
- Shu R, Bui HH, Zhao S, Kochenderfer MJ, Ermon S. 2018. Amortized inference regularization. In Advances in Neural Information Processing Systems 31 (NeurIPS 2018, Montreal, Canada). NeurIPS Proceedings, Vol. 31, pp. 4393–4402. [Google Scholar]
- Skotte L, Korneliussen TS, Albrechtsen A. 2013. Estimating individual admixture proportions from next generation sequencing data. Genetics 195: 693–702. 10.1534/genetics.113.154138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sønderby CK, Raiko T, Maaløe L, Sønderby SK, Winther O. 2016. Ladder variational autoencoders. In Advances in Neural Information Processing Systems 29 (NIPS 2016, Barcelona, Spain). NeurIPS Proceedings, pp. 3738–3746. [Google Scholar]
- Tang H, Peng J, Wang P, Risch NJ. 2005. Estimation of individual admixture: analytical and study design considerations. Genet Epidemiol 28: 289–301. 10.1002/gepi.20064 [DOI] [PubMed] [Google Scholar]
- Tennessen JA, Bigham AW, O'Connor TD, Fu W, Kenny EE, Gravel S, McGee S, Do R, Liu X, Jun G, et al. 2012. Evolution and functional impact of rare coding variation from deep sequencing of human exomes. Science 337: 64–69. 10.1126/science.1219240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan R, Roland C. 2008. Simple and globally convergent methods for accelerating the convergence of any EM algorithm. Scand J Stat 35: 335–353. 10.1111/j.1467-9469.2007.00585.x [DOI] [Google Scholar]
- Wang Z, Wang J, Kourakos M, Hoang N, Lee HH, Mathieson I, Mathieson S. 2021. Automatic inference of demographic parameters using generative adversarial networks. Mol Ecol Resour 21: 2689–2705. 10.1111/1755-0998.13386 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J, Girshick R, Farhadi A. 2016. Unsupervised deep embedding for clustering analysis. In Proceedings of The 33rd International Conference on Machine Learning. PMLR 48: 478–487. [Google Scholar]
- Yang B, Fu X, Sidiropoulos ND, Hong M. 2017. Towards k-means-friendly spaces: Simultaneous deep learning and clustering. In Proceedings of the 34th International Conference on Machine Learning. PMLR 70: 3861–3870. [Google Scholar]
- Yelmen B, Decelle A, Ongaro L, Marnetto D, Tallec C, Montinaro F, Furtlehner C, Pagani L, Jay F. 2021. Creating artificial human genomes using generative neural networks. PLoS Genet 17: e1009303. 10.1371/journal.pgen.1009303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimek A, Schubert E, Kriegel H-P. 2012. A survey on unsupervised outlier detection in high-dimensional numerical data. Stat Anal Data Min 5: 363–387. 10.1002/sam.11161 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.