Optimal transport and control of active drops

Significance

Transportation, in its broadest sense, is an important task in many fields, including engineering, physics, biology, and economics, and a great deal is known about optimal and efficient strategies to move matter, energy, and information around. But can we craft similar optimal protocols to transport autonomously moving (active) matter, such as self-propelled drops or migrating cells? We develop an optimal control framework to transport active fluid drops with the least amount of energy dissipated, by manipulating the spatio-temporal profile of its internal active stresses. By combining numerical solutions and analytical insight, we uncover simple principles and characteristic trade-offs that govern the optimal policies, suggesting general strategies for optimal transportation in a wide variety of synthetic and biological active systems.

Abstract

Understanding the complex patterns in space–time exhibited by active systems has been the subject of much interest in recent times. Complementing this forward problem is the inverse problem of controlling active matter. Here, we use optimal control theory to pose the problem of transporting a slender drop of an active fluid and determine the dynamical profile of the active stresses to move it with minimal viscous dissipation. By parametrizing the position and size of the drop using a low-order description based on lubrication theory, we uncover a natural “gather–move–spread” strategy that leads to an optimal bound on the maximum achievable displacement of the drop relative to its size. In the continuum setting, the competition between passive surface tension and active controls generates richer behavior with futile oscillations and complex drop morphologies that trade internal dissipation against the transport cost to select optimal strategies. Our work combines active hydrodynamics and optimal control in a tractable and interpretable framework and begins to pave the way for the spatiotemporal manipulation of active matter.

In recent years, active fluids composed of internally driven units have emerged as a powerful platform to manipulate and morph matter far from equilibrium (1–3). Such fluids have been assembled from a variety of biological and synthetic constituents, including self-propelled colloids, driven biofilaments, and living cells (4–7). These systems often exhibit complex spatiotemporal dynamics and pattern formation that have been the focus of intense research efforts in the past two decades or so.

While a great deal is now understood about the emergent collective dynamics in active fluids (8), much less is known about how we can control or harness such collective phenomena to achieve functional goals. Recent experimental advances in microfabrication and optogenetic techniques have allowed the development of novel bacterial and synthetic reconstituted systems to begin addressing this question in different contexts, such as active engines for efficient work extraction (9, 10), the dynamic control of reconfigurable density patterns (11, 12), and the targeted creation and transport of localized structures such as defects (13, 14). On a different scale, the collective control of migrating and proliferating cellular monolayers through patterned substrates (15, 16) or external fields (17, 18) also presents new possibilities for the control of active biological matter.

The capacity for spontaneous and autonomous motion in active fluids raises a natural question: What are the optimal strategies to spatially transport active materials? The general problem of optimal mass transport—i.e., finding the easiest or cheapest way to move mass from one place to another—has been explored for over two centuries (19, 20) with deep connections to economics, hydrodynamics, machine learning, etc. (20–22). But much less is known about how to optimally transport physical materials, such as active fluids, that obey complex spatiotemporal dynamics, leading us to ask: How can we construct and understand optimal transport policies to move active matter?

Here, we pose this question in the simplest setting of transporting an active drop by dynamically controlling its internal activity in space–time. By incorporating the dynamical constraints of droplet motion using the lubrication approximation and expressing the cost of transport in terms of the dissipation rate, we ask if we can determine the internal activity to move the drop from one place to another while minimizing the total dissipation, thus bringing it within the framework of optimal control theory.

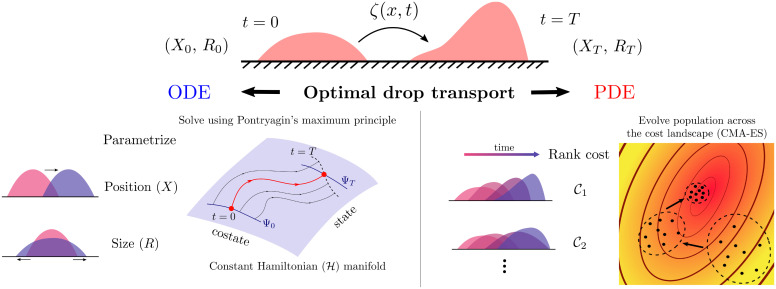
By projecting the continuum description of droplet motion onto a finite-dimensional slow manifold, we derive a reduced system of ordinary differential equations (ODEs) for the position and size of the droplet. Interestingly, for a range of parameters, an intuitive “gather–move–spread” style strategy emerges naturally as an optimum within our framework. Numerical simulations of the continuum equations using an evolutionary algorithm to determine the optimal activity profile confirm the qualitative nature of the results obtained from the reduced order model. Together, these solutions provide a comprehensive, yet interpretable, framework (Fig. 1) to understand the optimal solutions obtained and highlights the resulting trade-offs between cost, transport precision, and efficiency that can be tuned by the interplay of passive and active stresses in the system.

Fig. 1.

Optimal transport of an active drop. A schematic illustrating our framework to solve the problem of transporting an active drop by minimizing a specified cost function, such as the mechanical work. The spatiotemporal profile of activity $\zeta (x,t)$ is the control variable, and the transport task involves moving the drop from position X₀ and size R₀ to a final position X_T and size R_T in a finite time T. We employ two complementary approaches: 1) finite-dimensional optimal control using Pontryagin’s maximum principle on an ODE-based reduced order model that captures parametrized features of the drop; and 2) constrained numerical optimization of the nonlinear continuum PDE using a gradient-free evolutionary algorithm, such as CMA-ES (see PDE Control main text).

Mathematical Model for Optimal Droplet Transport

Lubrication Dynamics of an Active Drop.

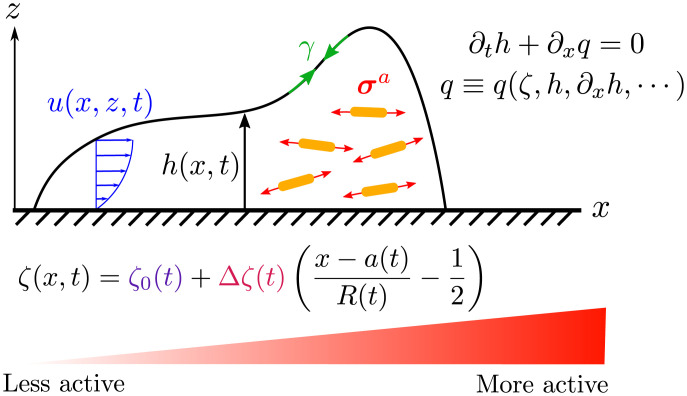
We describe the dynamics of a slender drop of an active suspension on a solid surface in the asymptotic limit exemplified by viscous lubrication theory (23, 24, 25). For simplicity, we consider a two-dimensional (2D) drop moving in the x direction (see Fig. 2) and neglect gravity by assuming the drop size to be smaller than the capillary length. Fluid incompressibility requires that $\mathbf{\nabla }·\mathbf{u}={\partial }_{x}u+{\partial }_{z}v=0$, where $\mathbf{u}=(u(x,z,t),v(x,z,t))$ is the local flow velocity. Upon depth integrating the incompressibility equation, and noting the free surface boundary condition $v{|}_{z=h}={\partial }_{t}h+u{\partial }_{x}h{|}_{z=h}$, where h(x, t) is the height profile of the drop, we obtain the conservation law

$${\partial }_{t}h+{\partial }_{x}q=0.$$ [1]

Fig. 2.

Model of an active drop moving on a substrate. The horizontal flow velocity $u(x,z,t)$ driven by active internal stresses (${\mathit{\sigma }}^a$) and surface tension (γ) adopts a Poiseuille-like profile in the drop interior, characteristic of lubrication theory. The drop height h(x, t) obeys the continuity equation (Eq. 1) with a flux q that encodes the constitutive relation (Eq. 3) for how activity drives fluid flow. The spatial profile of activity ($\zeta (x,t)$) is a simple linear ramp with a constant offset, allowing for both drop translation and size change (Eq. 7).

Here, the mass flux $q=h\langle u\rangle$, with the average horizontal velocity $\langle u\rangle =(1/h){\displaystyle {\int }_0^h\text{d}}z\hspace{0.17em}u$. Assuming that there is no addition or loss of mass of the drop, we can write this as a global condition

$${\displaystyle \int \text{d}}x\hspace{0.17em}h(x,t)=1,$$ [2]

to fix our units of length.

In the low-Reynolds-number regime appropriate for small viscous drops, we operate in the Stokesian limit, wherein force balance implies $\mathbf{\nabla }·\mathit{\sigma }=\mathbf{0}$, where the total stress $\mathit{\sigma }=-p\mathbf{I}+\eta [\mathbf{\nabla }\mathbf{u}+{(\mathbf{\nabla }\mathbf{u})}^T]+{\mathit{\sigma }}^a$ is the sum of the pressure p, a viscous stress (in a liquid with shear viscosity η), and an active stress. We assume that the active stress ${\mathit{\sigma }}^a=\zeta h(\widehat{\mathbf{n}}\widehat{\mathbf{n}}-\mathbf{I}/2)$ (8, 26) is proportional to the local density $\sim h$, while depending on the local orientation $\widehat{\mathbf{n}}$ of anisotropic active agents.* The activity $\zeta (x,t)$ depends on space and time and originates from the density of force dipoles exerted by elongated active units, which can be of either sign, with $\zeta >0$ for contractile systems and $\zeta <0$ for extensile systems. This form of the active stress is applicable to drops of coherently swimming dense bacterial suspensions or ordered collections of motor-protein-driven cytoskeletal filaments present in synthetic drops or living cells (23, 24). For simplicity, we shall assume strong ordering along the horizontal direction and neglect any rapid orientational relaxation to set $\widehat{\mathbf{n}}\simeq \widehat{\mathbf{x}}$ to lowest order in gradients ($\left|{\partial }_{x}h\right|\ll 1$). The active forcing nonetheless survives in this limit, as the active stress directly depends on the local density of the drop ($\sim h$), unlike previous models (23, 24) that rely on splay–bend deformations of orientational order.

In the lubrication limit corresponding to a slender drop, $|{\partial }_{x}h{|}^2\ll 1$, so that we can neglect longitudinal flow gradients as $\left|{\partial }_x^{2}u\right|\ll \left|{\partial }_z^{2}u\right|$ and $\left|{\partial }_{x}v\right|\ll \left|{\partial }_{z}u\right|$. Then, the stress in the fluid is dominated by the pressure, which is determined by the capillary boundary condition on the drop surface ${\sigma }_{zz}{|}_{z=h}=\gamma {\partial }_x^{2}h$, where γ is the interfacial tension and yields $p=-(\zeta /2)h-\gamma {\partial }_x^{2}h$. Using this in the horizontal force-balance equation, along with the no-slip ($u{|}_{z=0}=0$) and free surface (${\partial }_{z}u{|}_{z=h}=0$) boundary conditions, yields the horizontal velocity profile $u=z((2h-z)){\partial }_x\sigma /2\eta$, where $\sigma =\zeta h+\gamma {\partial }_x^{2}h$ is the effective uniaxial stress. Averaging the velocity through the thickness of the drop shows that the net flux is

$$q=h\langle u\rangle =\frac{h^3}{3\eta }{\partial }_x(\zeta h+\gamma {\partial }_x^{2}h).$$ [3]

Eqs. 1 and 3 complemented by boundary and initial conditions on the height of the film and its derivatives completely describe the macroscopic dynamics of an active drop on a substrate, once the activity field $\zeta (x,t)$ is specified. For finite drops, in the neighborhood of the contact line, the boundary conditions associated with partial slip, prewetting films, and/or finite contact angles have to be accounted for (26, 27) (SI Appendix). In our formulation, the passive surface tension γ serves to regulate the drop curvature, while the (controllable) activity $\zeta (x,t)$ enters as an unknown spatiotemporally varying nonlinear diffusivity, but is analogous to gravity (26).

Optimal Transport.

The optimal transport of an active drop requires finding an actuation protocol for the activity profile $\zeta (x,t)$ that moves the drop at a minimal cost. We choose a physically motivated cost $\mathcal{C}=\mathcal{W}+\mathcal{T}$, which includes two terms, an integrated bulk cost that tracks the total mechanical work ($\mathcal{W}$) done by the active and passive forces and a terminal cost ($\mathcal{T}$) that penalizes any discrepancy between the final and desired state of the drop. Within the lubrication approximation, the viscous dissipation in the drop $\sim \eta {({\partial }_{z}u)}^2$ is dominated by shear, so that the total mechanical work is given by

$$\mathcal{W}={\displaystyle {\int }_0^T\text{d}}t{\displaystyle \int \text{d}}x\hspace{0.17em}\frac{h^3}{3\eta }{({\partial }_x\sigma )}^2.$$ [4]

As expected, the total amount of energy expended and lost via dissipation by the system is always nonnegative ($\mathcal{W}\ge 0$). We note that this is equivalent to stating that the effective mechanical energy in the drop $E=(1/2){\displaystyle \int \text{d}}x[\gamma {({\partial }_{x}h)}^2-\zeta h^2]$ satisfies the condition $\text{d}E/\text{d}t=-{\displaystyle \int \text{d}}x(h^3/3\eta ){({\partial }_x\sigma )}^2<0$ if ${\partial }_t\zeta =0$ and boundary fluxes are absent—i.e., the system is dissipative. The work done by the active stress alone (${\mathcal{W}}_a={\displaystyle {\int }_0^T\text{d}}t{\displaystyle \int \text{d}}x\hspace{0.17em}h\langle u\rangle {\partial }_x(\zeta h)$), on the other hand, is not guaranteed to be a well-behaved cost function, as ${\mathcal{W}}_a$ can be of either sign in general (though ${\mathcal{W}}_a=\mathcal{W}\ge 0$ when γ = 0), reflecting the possibility of both energy consumption and extraction from the nonequilibrium system (28). Here, we have not included the energy cost required to maintain the active machinery (29); in the simplest setting, this is proportional to the total amount of the active fluid, which, in our case, is a constant.

For simplicity, we have assumed that the total time duration T is fixed, though other strategies, such as minimal time control, are possible. However, we do account for a terminal cost to minimally capture the intent of the task, which is to translate the drop by a fixed distance and control its final spread as well. We incorporate this in a simple quadratic term

$$\mathcal{T}={\mu }_X{\left(\frac{X(T)-X_T}{X_T}\right)}^2+{\mu }_R{\left(\frac{R(T)-R_T}{R_T}\right)}^2\text{},$$ [5]

where X_T and R_T are the desired values for the drop center of mass and the drop size at the end of the transport. The corresponding penalties are μ_X and μ_R for the terminal position and size terms. As mentioned previously, the drop has compact support and finite size, which is denoted by R(t), and its position is given by the center of mass, namely,

$$X(t)={\displaystyle \int \text{d}}x\hspace{0.17em}xh(x,t),$$ [6]

both of which can be evaluated at the final time t = T to compute $\mathcal{T}$ (Eq. 5). We will always set the initial position of the drop to be at the origin, $X(0)=0$, without loss of generality.

It is worthwhile to pause here to compare our formulation of optimal droplet transport with the classical Monge–Kantorovich formulation of optimal transport (19–22). Unlike the conventional formulation, where the sole constraint is global mass conservation (Eq. 2), here, we constrain the dynamics to account for both local mass and momentum conservation. The latter is a direct consequence of the physics of fluid motion that dictates how the material responds to local actuation of active stresses, as specified by Eqs. 1 and 3. As a result, our transport plan does not simply rely on a registration solution of a static Monge–Ampère equation (20). A further salient feature worth emphasizing is the parabolic (diffusive) nature of our dynamics, where the control (activity) enters as a nonlinear diffusivity by virtue of the geometric reduction intrinsic to drops and thin films. This is distinct from the hyperbolic (advective) setting present in Benamou–Brennier-style formulations (22) that employ a hydrodynamic analogy between optimal transport and inviscid fluid flow, where the velocity field is the control variable.

Protocol for Optimal Droplet Transport

With this minimal physical framework in hand, how can we compute the optimal transport policies? We choose two different routes of solving the problem (Fig. 1). First, we project our nonlinear partial differential equation (PDE) for the drop dynamics (Eqs. 1 and 3) onto a finite number of low order modes that correlate with the location, size, and shape of the droplet. We propose a strategy that minimizes or eliminates drift terms in the reduced description by considering the active controlled dynamics within a low-dimensional slow manifold that is approximately invariant to the passive (noncontrolled) forces. The resulting ODEs can then be handled using standard optimal control theory (30), which we solve both analytically and numerically. We then compare this reduced order description to the full PDE model, for which we analyze the optimal control problem numerically. However, unlike conventional forward problems that are solved with initial values in time, the controlled dynamics requires the solution to a much harder boundary-value problem in time. One way to solve this problem is to stochastically search for different initializations using a large number of forward runs to find an appropriate solution satisfying the required boundary condition. We implement this using a gradient-free covariance matrix adaptation evolution strategy (CMA-ES) (31), as explained later and in SI Appendix.

ODE Control.

For simplicity, we consider a minimal setting, where the spatial variation of the activity is fixed, but its time variation is arbitrary. As we are primarily interested in controlling the position and size of the drop, the simplest spatial variation of activity that can accomplish both is a linear profile,

$$\zeta (x,t)={\zeta }_0(t)+\mathrm{\Delta }\zeta (t)\left(\frac{x-a(t)}{R(t)}-\frac{1}{2}\right)\text{},$$ [7]

where ${\zeta }_0(t)$ is a time-varying mean activity and $\mathrm{\Delta }\zeta (t)$ is a time-varying gradient in activity (Fig. 2). We choose this specific form, which depends explicitly on the drop size R(t) and the position of the left edge of the drop a(t), so that the (spatial) average activity in the drop is $(1/R(t)){\displaystyle {\int }_{h>0}\text{d}}x\hspace{0.17em}\zeta (x,t)={\zeta }_0(t)$. We note that while ζ₀ essentially controls the size of the drop, with ${\zeta }_0>0$ leading to contraction and ${\zeta }_0<0$ leading to expansion, the linear gradient in activity $\mathrm{\Delta }\zeta$ controls the drop translation, the direction of which is determined by the sign of $\mathrm{\Delta }\zeta$. In contrast with recent works that have explored bulk contractility driven crawling of cells (25, 32) and shown how it optimizes the mechanical efficiency of steady motion (29), here, we address the unsteady dynamics and its control problem.

The relative importance of the active drive versus surface tension is quantified by a dimensionless active capillary number

$${\text{Ca}}_{\zeta }={\langle \frac{|\mathrm{\Delta }\zeta (t)|R{(t)}^2}{\gamma }\rangle }_T,$$ [8]

where the time average ${\langle A\rangle }_T=(1/T){\displaystyle {\int }_0^T\text{d}}t\hspace{0.17em}A$. As will be clear later, Eq. 8 is akin to the conventional definition of a capillary number (27), only now with the velocity scale set by the activity gradient ($\mathrm{\Delta }\zeta$), which is essential to drive drop motion.^† For large Ca${}_{\zeta }\gg 1$, active forcing dominates surface tension, and we can safely neglect boundary effects, while for Ca${}_{\zeta }\sim 1-\mathcal{O}(10)$, active and passive forces compete, and the equations have to be generalized to include the dynamics of the contact lines, as detailed in SI Appendix.

We project the nonlinear PDE (Eqs. 1 and 3) onto a truncated set of modes that we choose so that the resulting ODE system is as drift-free as possible—i.e., the system lacks dynamics in the absence of the controls (here, activity). This is achieved by noting that the flux due to capillary forces vanishes when ${\partial }_x^{3}h(x,t)=0$, and the drop adopts a parabolic profile. This permits a simple parametrization of the drop profile via two modes of deformation—a translation in the center of mass X(t) and a change in the size R(t), which, along with Eq. 2, gives

$$h(x,t)=\frac{6}{R{(t)}^3}\left[\frac{R{(t)}^2}{4}-{\left(x-X(t)\right)}^2\right]\text{}.$$ [9]

Note that $h(x,t)=0$ at the two ends of the drop, $x=X(t)\pm R(t)/2$, and vanishes outside this region. While translation is a genuine zero mode of capillarity, size change of the drop is only an approximate zero mode that is violated near the boundaries where wetting and contact-angle physics become important (27). Nonetheless, by focusing on the bulk dynamics, we obtain a 2D manifold spanned by X(t) and R(t) that remains approximately invariant under the action of capillary forces.

Employing a Galerkin approximation (i.e., projecting onto a local polynomial basis) allows us to compute spatial moments of the flux q(x, t) and project the continuum equations onto this manifold to obtain a pair of nonlinearly coupled ODEs (SI Appendix)

$$\dot{X}(t)=\frac{18\mathrm{\Delta }\zeta (t)}{35\eta R{(t)}^4},\hspace{1em}\dot{R}(t)=-\frac{24{\zeta }_0(t)}{7\eta R{(t)}^4}.$$ [10]

As expected, the mean (ζ₀) and gradient ($\mathrm{\Delta }\zeta$) components of the active stress independently control the drop size and position, respectively. By construction, surface tension γ is absent in Eq. 10, and the equation is drift-free. The existence of optimal controls is predicated on an important property of the dynamics, namely, controllability (33, 34)—i.e., the existence of a path connecting any two points in the state or configuration space, spanned here by X and R (see SI Appendix for a more detailed explanation). As the two controls (${\zeta }_0,\mathrm{\Delta }\zeta$) enter linearly and independently, and the dynamics has no fixed points for nonvanishing controls, one can easily confirm that Eq. 10 is controllable, allowing us to guarantee the ability to steer the system from any state to any other state within the space of drop configurations labeled by (X, R). The absence of any drift (control-independent) terms presents a technical advantage, as the system permits a global, rather than local, notion of controllability, even when the dynamics is nonlinear (SI Appendix), thereby justifying our mode-reduction strategy.

For simplicity, we consider the fixed end point problem where the terminal conditions are imposed strictly ($X(T)=X_T,\hspace{0.17em}R(T)=R_T$), in which case the total cost reduces to the net dissipation ($\mathcal{C}=\mathcal{W}$). The drop parametrization (Eq. 9) allows us to easily compute the dissipation rate to be

$$\mathcal{L}=\frac{1}{\eta R^6}\left[\frac{72}{35}{\zeta }_0^2+\frac{54}{77}\mathrm{\Delta }{\zeta }^2\right]\text{},$$ [11]

whose time integral gives the cost ($\mathcal{W}={\displaystyle {\int }_0^T\text{d}}t\hspace{0.17em}\mathcal{L}$). As expected, we obtain a simple sum of squares in terms of the two active drives, along with a strong size dependence arising from the geometry of the drop. To solve the optimal control problem, we employ Pontryagin’s Maximum Principle that provides the necessary conditions for optimality (35) (see SI Appendix for a brief summary). Upon introducing the costates (Lagrange multipliers) $p_X(t)$ and $p_R(t)$ to enforce the dynamical constraints in Eq. 10, a necessary condition for optimality is the maximization of the control Hamiltonian

$$\mathcal{H}=p_X\frac{18\mathrm{\Delta }\zeta }{35\eta R^4}-p_R\frac{24{\zeta }_0}{7\eta R^4}-\mathcal{L},$$ [12]

with respect to the controls (SI Appendix). This gives ${\zeta }_0^{*}=-5p_R{R}^2/6$ and $\mathrm{\Delta }{\zeta }^{*}=11p_X{R}^2/30$, which, when substituted back into Eq. 12, gives the conserved Hamiltonian $H=\mathcal{H}({\zeta }_0^{*},\mathrm{\Delta }{\zeta }^{*})$. The candidate extremals for the optimal control problem satisfy Hamiltonian dynamics in terms of the state variables ($\dot{X}={\partial }_{p_X}H,\hspace{0.17em}\dot{R}={\partial }_{p_R}H$) and corresponding costates (${\dot{p}}_X=-{\partial }_{X}H,\hspace{0.17em}{\dot{p}}_R=-{\partial }_{R}H$). For the state variables, this gives back Eq. 10 driven now by the optimal controls $({\zeta }_0^{*},\mathrm{\Delta }{\zeta }^{*})$; translational invariance enforces that ${\partial }_X\mathcal{H}=0$; hence, p_X is conserved along the optimal trajectory.

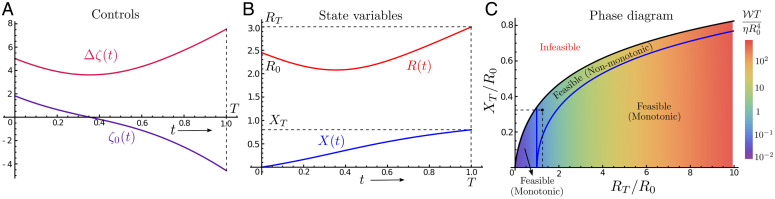
These coupled dynamical equations along with the initial and terminal conditions can be solved analytically to obtain the optimal transport protocols (SI Appendix) to displace an active drop by a distance X_T and change its size from R₀ to R_T in a finite time interval T. A representative solution is plotted in Fig. 3A and B for $X_T=0.8,\hspace{0.17em}{R}_0=\sqrt{6}$ and R_T = 3. The first-order necessary conditions generally allow for nonuniqueness of the candidate extrema, but we only show the global optimizer in Fig. 3. For the chosen parameters, the optimal protocol leads to a nonmonotonic change in drop size (Fig. 3B), first decreasing and later increasing to reach the final size R_T. This is reflected in the sign change of the mean active stress ζ₀ (Fig. 3A), which switches from being contractile initially (${\zeta }_0>0$) to extensile at later times (${\zeta }_0<0$). The drop translates smoothly with a maximal velocity precisely when the drop size is the smallest, even though the drive ($\mathrm{\Delta }\zeta$) is minimal at this point (Fig. 3A). Hence, the drop executes a continuous version of an intuitive gather–move–spread-like strategy that naturally emerges as an optimal transport plan in our framework. A simple concentration effect that enhances the active drive in smaller drops underlies this phenomenon by allowing for faster transport at lower activity. Our solution reveals a further striking result—for certain values of the target parameters (set by X_T and R_T) with strict terminal constraints, no continuous optimal policies for the transport problem exist! This does not contradict the fact that the dynamical system (Eq. 10) is controllable, but, rather, highlights a subtlety. While controllability guarantees the presence of a trajectory in configuration space that steers the drop to its desired final state, and hence the existence of optimal controls, it does not, in general, guarantee that this transport is either continuous or achievable in finite time.

Fig. 3.

ODE optimal control. (A and B) Sample trajectories for the globally optimal mean (ζ₀) and gradient ($\mathrm{\Delta }\zeta$) activity are shown in A, and the associated controlled dynamics for the drop position (X) and size (R) are shown in B. The parameters chosen are $X_T=0.8,\hspace{0.17em}{R}_0=\sqrt{6}$, R_T = 3, T = 1, and $\eta =0.1$. Note that as η sets a time scale, only the ratio $T/\eta$ is important. For these parameter values, we see that the size change is nonmonotonic, which is reflected in the sign change in the mean activity ${\zeta }_0(t)$. The initial contractile activity (${\zeta }_0>0$) causes the drop to shrink and consequently accelerate its translation, and, later, the activity switches over to become extensile (${\zeta }_0<0$) to allow the drop to reach its larger final size R_T. (C) The phase diagram here represents the feasibility region for optimal transport of a parabolic active drop, as a function of the nondimensionalized drop displacement ($X_T/R_0$) and its size disparity ($R_T/R_0$). The black curve is the maximum achievable displacement X_T for a given relative change in size ($R_T/R_0$), beyond which no smooth optimal controls exist. Below the black curve is the feasible region, with the shaded color representing the total work done [nondimensionalized as $\mathcal{W}T/(\eta R_0^4)$] by the globally optimal policy, with the cost increasing from blue to red. The blue curves in the shaded region demarcate the parameter space where the global optimizer has a monotonic or nonmonotonic size dependence as a function of time. Nonmonotonic changes in size are favored in the region bordered by the blue and black curves and only occur when $R_T>R_0$. For $R_T<R_0$, the optimal policies have a monotonic size dependence. The black dot corresponds to the solution shown in A and B.

As shown by the colored region bounded by the black curve in Fig. 3C, we have a feasible or reachable regime, where smooth optimal solutions exist and the net dissipation is finite (shown in the heat map, with the cost increasing from blue to red), while in the infeasible region, no smooth solution satisfies the terminal conditions. The blue curve in Fig. 3C further demarcates the parameter regime where the global optimum corresponds to polices with a monotonic change in drop size, where the mean activity (ζ₀) maintains a fixed sign. These appear either for sufficiently small displacements or when the final drop size is smaller than the initial one ($R_T<R_0$). Nonsmooth protocols can be constructed to access points in the infeasible region in Fig. 3C, but they lack a natural parametrization. As a result, the search for an optimal policy in this larger function space is analytically intractable, and we focus only on smooth protocols for simplicity. The feasibility curve can alternatively be viewed as solving a maximin problem, where we maximize the minimum dissipation protocol over the translation X_T for a fixed change in drop size ($R_T/R_0$), the solution for which roughly equipartitions the transport cost (black curve in Fig. 3C; see SI Appendix for further details).

Keeping surface tension γ = 0, we can extend this analysis to include simple variations in drop shape via a spatial asymmetry of the height profile and numerically solve the optimal control problem using CasADi (36) and numerical continuation schemes (see SI Appendix for details). Our results show that while small variations in the drop asymmetry result in smooth optimal policies, similar to those in Fig. 3A, larger values of drop asymmetry lead to short-wavelength numerical instabilities, as expected when the surface tension vanishes. Thus, while the dynamics of drop position and size are captured by the simple ODE model (Eq. 10), the dynamics of drop shape requires us to account for the inclusion of capillary effects for stability. To accomplish this, we switch to solving the full PDE model.

PDE Control.

As the PDE model permits complex shape change of the drop, we lift the restriction of the controlled dynamics on the slow manifold selected by capillarity and allow arbitrary shape variations by tuning γ (conversely, Ca${}_{\zeta }$; Eq. 8). In order to select smooth control policies, we generalize the cost function $\mathcal{C}=\mathcal{W}+\mathcal{T}+\mathcal{R}$ (SI Appendix) to include a regularizing term $\mathcal{R}$ in addition to the total dissipation ($\mathcal{W}$; Eq. 4) and a finite terminal cost ($\mathcal{T}$ with ${\mu }_X,{\mu }_R<\infty$; Eq. 5). The regularization cost $\sim {\displaystyle \int \text{d}}t{\displaystyle \int \text{d}}x\hspace{0.17em}{({\partial }_t\zeta )}^2$ penalizes large temporal variations in activity (SI Appendix), and it implements a version of minimal attention control (37). In the presence of a finite surface tension γ, we must also correctly implement contact-line motion at the boundary of the drop, which we do by simply introducing a thin precursor film that coats the entire surface and a disjoining potential (26) that sets both the film thickness and the equilibrium contact angle of a sessile drop (see SI Appendix for details). These additional terms are negligible in the bulk of the drop, but are dominant near the contact lines, which will become important when active and capillary forces are comparable (Ca${}_{\zeta }\lesssim \mathcal{O}(10)$), similar to recently explored scenarios the context of steady migration of cells (25) in the absence of any dynamic control.

We numerically integrate the dynamical equations using a finite element method implemented using the FEniCS open-source package (38, 39) and perform constrained optimization using a gradient-free CMA-ES (31) (see SI Appendix for details). Multiple runs are sequentially minimized with independent initializations for the activity profile, and we choose the lowest-cost solution as an estimate for the optimum. As before, the drop is initially at the origin ($X_0=0$) with a size $R_0=\sqrt{6}$, which corresponds to an equilibrium contact angle of ${\varphi }_{\text{eq}}=\pi /4$. The viscosity $\eta =0.1$ and total time T = 1 are fixed in all the runs. To probe the caliber of the optimal policies obtained across tasks of increasing difficulty, we vary the imposed drop translation X_T along with the surface tension γ.

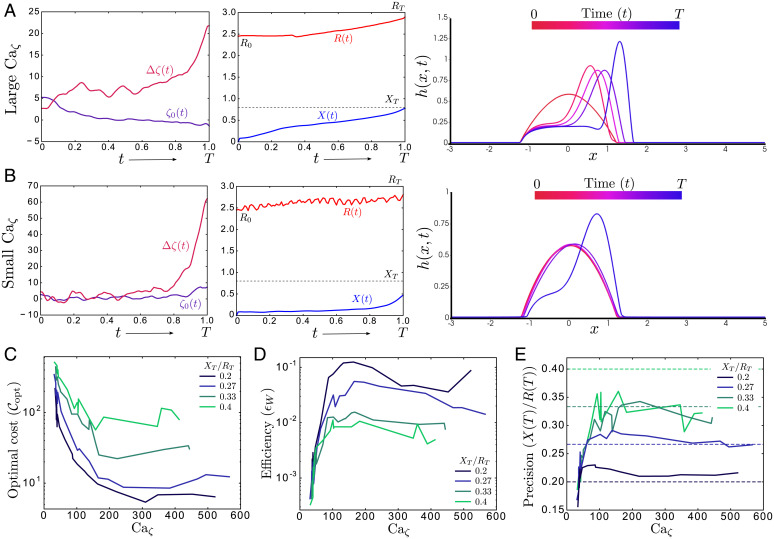
For small surface tension or strong active driving (large Ca${}_{\zeta }$), the dynamics of the drop is dominated by bulk dissipation. A typical trajectory of the drop profile (Movie S1) and the controls is shown in Fig. 4A, for $X_T=0.8$ and Ca${}_{\zeta }\sim 383$. The drop develops a prominent advancing peak and a thin receding tail (Fig. 4 A, Right and Movie S1), similar to steadily translating drop shapes recently obtained in ref. 25. The optimal controls and the drop motion vary smoothly (Fig. 4 A, Left and Center) and successfully accomplish the transport task. Although the drop undergoes dramatic shape changes, the optimal controls are qualitatively consistent with our ODE results (Fig. 3 A and B). In particular, we note that the mean activity (ζ₀) changes sign, switching from contractile to extensile activity, as predicted by our reduced order description (Fig. 3A). For further comparison, we also simulate the continuum drop dynamics (Movie S2), using the optimal activity profile supplied by the ODE solution (Fig. 3A) for the same parameters. In the regime of applicability of the reduced order model (corresponding to low values of the surface tension or, equivalently, large Ca${}_{\zeta }$), the resulting drop trajectory (Movie S2) is qualitatively consistent with the solution obtained from the PDE optimization (Fig. 4A and Movie S1); larger values of surface tension (smaller Ca${}_{\zeta }$) lead to a qualitatively different scenario. As shown in Fig. 4B and Movie S3, for $X_T=0.8$ and Ca${}_{\zeta }\sim 31$, the drop remains nearly stationary for a finite time period, after which it advances by a small amount. This is reminiscent of “waiting-time” solutions (40) that are present in nonlinear diffusion equations of the form we have here. The drop performs rapid small-scale oscillations of its shape and size (Fig. 4 B, Center and Right and Movie S3) that arise from a competition between the active and passive (capillary) forces. While the active controls drive droplet motion, surface tension and substrate wetting resist variations in the drop shape and the contact angle, thereby limiting the translation achieved by the drop. The resulting “futile” oscillations wastefully dissipate large amounts of energy, performing poorly in the transport task (Fig. 4 B, Left and Center). We note that in all the examples studied, only the final drop position (X(T)) and size (R(T)) are constrained, but the final shape is not. Nonetheless, upon cessation of the activity protocol, surface tension will cause the drop to round up into a parabolic shape (just as it started out) without any additional energy injection. This allows for a simple way to recover the sessile drop shape at the end. Although this passive relaxation will inevitably incur drop translation due to its asymmetric shape, by extending the control protocol (and, hence, expending additional energy), it should be possible to compensate for this passive drop recoil.

Fig. 4.

PDE optimal control. (A) The optimal activity controls (${\zeta }_0(t),\hspace{0.17em}\mathrm{\Delta }\zeta (t)$; Left) and corresponding trajectories for the state variables ($X(t),\hspace{0.17em}R(t)$; Center) and the full drop profile (h(x, t); Right), obtained by numerical optimization for small surface tension or large active capillary number ($\gamma =0.15$, Ca${}_{\zeta }=383.66$). The drop adopts a strongly asymmetric shape, with an advancing peak and receding tail, like in ref. 25. (B) Similar plots with the optimal activity controls (${\zeta }_0(t),\hspace{0.17em}\mathrm{\Delta }\zeta (t)$; Left), and corresponding drop trajectory ($X(t),\hspace{0.17em}R(t)$, Center; h(x, t), Right), now obtained for large surface tension or small active capillary number (γ = 2, Ca${}_{\zeta }=30.91$). The transport plan fares poorly as the drops fails to reach the desired final position and size and wastes a significant amount of energy in futile size oscillations (R(t); Center) that don’t aid in transport. Both A and B are computed by using $X_T=0.8$ and R_T = 3 ($X_0=0$ and $R_0=\sqrt{6}$ is kept fixed throughout), though similar policies are obtained for other values of $X_T/R_T$ as well. (C–E) The total cost (${\mathcal{C}}_{\text{opt}}$; C), efficiency (ϵ_W [Eqs. 13 and 14]; D), and precision ($X(T)/R(T)$; E) of the numerically computed optimal transport protocol plotted against Ca${}_{\zeta }$, for different tasks labeled by increasing $X_T/R_T$ (blue to green). Remarkably, the performance curves present an optimal trade-off in balancing active forces against passive ones to attain improved drop transport plans at intermediate values of Ca${}_{\zeta }$.

The varied optimal strategies obtained upon tuning surface tension suggests a potential trade-off between active and passive forces. While large Ca${}_{\zeta }$ allows for robust and efficient transport, it also generates dramatic shape changes, which dissipate excessive energy. Smaller Ca${}_{\zeta }$ restricts shape change, but consequently dissipates energy into futile oscillations that fail to complete the transport task. This suggests that an intermediate surface tension or Ca${}_{\zeta }$ would serve as the best choice to tune the optimal transport plan by balancing active and passive forces. To quantify this trade-off, we employ three different performance metrics as a function of Ca${}_{\zeta }$ and the task difficulty characterized by increasing $X_T/R_T$. The first is simply the total cost of the optimal solution (${\mathcal{C}}_{\text{opt}}$), plotted in Fig. 4C. Second, we use a simple measure of efficiency (ϵ_W) to quantify the excess dissipation in the optimal solution (Fig. 4D). We note that, for any arbitrary drop trajectory starting at the origin, there is a minimal amount of work that must necessarily be expended, given by (see SI Appendix for a derivation)

$${\mathcal{W}}_{\text{min}}=\frac{3\eta }{2T\Vert h{\Vert }_{\infty }^2}\left[X{(T)}^2+\frac{{(\mathrm{\Delta }(T)-\mathrm{\Delta }(0))}^2}{4{\langle \mathrm{\Delta }\rangle }_T}\right]\text{},$$ [13]

where $\Vert h{\Vert }_{\infty }={\sup }_{x,t}h(x,t)$ is the maximum value of the drop height attained throughout its trajectory and $\mathrm{\Delta }(t)={\displaystyle \int \text{d}}x\hspace{0.17em}{(x-X(t))}^{2}h(x,t)$ is the variance in the drop height, which is related to the size of the drop ($\mathrm{\Delta }\propto R^2$). Note that Eq. 13 is independent of the rheology and constitutive law for the fluid stress and simply relies on the existence of a flux q(x, t) that directly determines the dissipation (SI Appendix). As the work done in the optimal solution is bounded below by construction (${\mathcal{W}}_{\text{opt}}\ge {\mathcal{W}}_{\text{min}}$), we define the mechanical efficiency for the optimal solution

$${ϵ}_W=\frac{{\mathcal{W}}_{\text{min}}}{{\mathcal{W}}_{\text{opt}}}\le 1,$$ [14]

which quantifies the extent to which energy is dissipated in internal modes rather than transporting the drop (Fig. 4D). Finally, we also use the coefficient of variation of the height—i.e., the ratio of the final displacement to size achieved by the drop, $X(T)/R(T)$, as a measure of transport precision (Fig. 4E, solid) and compare it against the prescribed value $X_T/R_T$ for a given transport task (Fig. 4E, dashed). Interestingly, the optimal solutions for $X_T/R_T=0.2,\hspace{0.17em}0.27$ achieve a higher precision (solid curves, Fig. 4E) than required by the task (dashed lines, Fig. 4E) across a large range of Ca${}_{\zeta }$, but this enhanced performance degrades for larger $X_T/R_T=0.33,\hspace{0.17em}0.4$. As anticipated, all three performance metrics are nonmonotonic and display an optimal trade-off at intermediate values of Ca${}_{\zeta }$ (Fig. 4 C–E), with both the efficiency and the precision being maximized around Ca${}_{\zeta }\sim 100$ to 200, while the optimal cost is minimal at a slightly higher Ca${}_{\zeta }\sim 250$ to 380. Qualitatively similar trends appear as we vary the transport task via $X_T/R_T$ (Fig. 4 C–E), though for larger values of $X_T/R_T=0.33,0.4$ (in the infeasible region of the symmetric ODE optimal transport; Fig. 3C), the performance curves exhibit more kinks, perhaps suggestive of a rougher cost landscape with many nearly degenerate local minima when the task difficulty increases.

Discussion

Complementing classical optimal transportation and its hydrodynamic analogies that use a very specific form of the cost (22), we have formulated a framework to address questions of optimal mass transport in physical continua obeying complex dynamical constraints and illustrated its utility in a simple, yet rich, problem of transporting a drop of an active suspension by dissipating the least amount of energy. Our strategy combines a finite-dimensional (ODE) description based on a physically motivated mode-reduction scheme, along with the full infinite-dimensional (PDE) model, both of which we couch within optimal control theory to obtain a tractable and interpretable characterization of the resulting optimal transport policies. An important outcome is the prediction of intuitive gather–move–spread-style strategies and simple trade-offs between active and passive forces that emerge naturally within our formulation of optimal drop transport, with implications for a wide range of synthetic and living active matter.

In active physical systems, magnetically controlled ferrofluid drops (41–43), digital microfluidic platforms (44), and bicomponent volatile liquids (45) might provide an immediate platform to deploy our framework. As an example, for ferrofluid droplets, the active stress would be replaced by a magnetic stress given by ${\sigma }^m\approx {\mu }_0{M}_{s}H$, where ${\mu }_0=4\pi \times {10}^{-7}$ N/A² is the vacuum permeability, $M_s\sim {10}^4$ A/m is the ferrofluid saturation magnetization, and $H\sim {10}^3$ to 10⁴ A/m is the magnetic field strength. Dimensional considerations suggest that small drops (size $R\sim 1$ to 3 mm and height $h\sim 1$ mm) with a typical viscosity $\eta \sim 0.4$ Pa ⋅s and surface tension $\gamma \sim {10}^{-2}$ N/m can easily achieve rapid movement with speeds $\sim 0.1$ to 1 mm/s (41–43) and also change shape by varying the magnetic capillary number ${\text{Ca}}_m\sim {\sigma }^m{R}^2/\gamma h\sim 10$ to 100.

In bio-hybrid contexts, our work is directly relevant to the control of self-propelled drops composed of microtubule-kinesin nematic gels (4), swimming bacteria (46), and isolated motile cells (47, 48) that are often viewed as active drops (25, 32, 49, 50). Our results could also be tested by using optogenetically controlled living motile cells (51) or in reconstituted active drops (4, 52). Since the cortical tension of individual cells varies in the range of $\gamma \sim 0.1$ to 1 mN/m (53) and the characteristic active stress $\zeta h\sim 1$ kPa (49), Ca${}_{\zeta }\sim {10}^2$ to 10³ for a $R=10 \text{μ}$m size cell (assuming an average height $h\sim 1 \text{μ}$m), allowing for an exploration of the transport cost versus internal dissipation trade-off at intermediate Ca${}_{\zeta }\sim \mathcal{O}(100)$ that we have uncovered here. This suggests that contractility driven cellular motility may be optimal, even beyond steady translation (29), by harnessing dynamic optimal protocols and internally regulating differential contractility against surface tension. Extensions of our framework can also easily be used to address the control and patterning of localized structures, such as defects in active fluids, which has been the focus of much research in recent years (13, 14, 54, 55).

More broadly, beyond the control of active systems, our formulation of optimal transport offers an alternative choice of transport metrics that are physically motivated and potentially richer than the conventional ones (like the L²-Wasserstein norm) used in standard optimal transport (20), yet their mathematical properties remain to be uncovered. A tantalizing possibility is to exploit thermodynamic analogies connecting minimum dissipation protocols in stochastic systems to optimal transport (56). In this regard, a generalization of our framework to include fluctuations within stochastic optimal control (57) would be a promising future direction.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.