Confidence Intervals for Difference in Proportions for Matched Pairs Compatible with Exact McNemar’s or Sign Tests

Summary

For testing with paired data (for example, twins randomized between two treatments), a simple test is the sign test, where we test if the distribution of the sign of the differences in responses between the two treatments within pairs is more often positive (favoring one treatment) or negative (favoring the other). When the responses are binary, this reduces to a McNemar-type test, and the calculations are the same. Although it is easy to calculate an exact p-value by conditioning on the total number of discordant pairs, the accompanying confidence interval on a parameter of interest (proportion positive minus proportion negative) is not straightforward. Effect estimates and confidence intervals are important for interpretation because it is possible that the treatment helps a very small proportion of the population yet gives a highly significant effect. We construct a confidence interval that is compatible with an exact sign test, meaning the 100(1 − α)% interval excludes the null hypothesis of equality of proportions if and only if the associated exact sign test rejects at level α. We conjecture that the proposed confidence intervals guarantee nominal coverage, and we support that conjecture with extensive numerical calculations, but we have no mathematical proof to show guaranteed coverage. We have written and made available the function mcnemarExactDP in the exact2x2 R package and the function signTest in the asht R package to perform the methods described in this paper.

1 |. INTRODUCTION

Consider a matched pair study of some disease where one member of each pair gets a new therapy and one member gets standard therapy. Let the response for each pair be either: new therapy is preferred (1), standard therapy is preferred (−1), or no preference (0). In deciding which therapy is better for more people, it is reasonable to condition on the pairs that had a preference, and the resulting test is a sign test. If the individual responses within each pair are binary, one popular version of such a conditional test is McNemar’s test. The sign test is based on a conditional statistic which is binomial, so it is straightforward to get exact p-values and compatible exact confidence intervals on the conditional parameter, where the conditional parameter is the probability of preferring new therapy conditioned on having a preference. The issue is that the conditional parameter may not be the most appropriate parameter for a public health interpretation. For example, we can get a highly significant sign test and a large estimate of the conditional parameter, but if the proportion of pairs with a preference is small, the public health impact of the therapy may be small. For example, if only 6% of the population has a preference, and the other 94% of the matched-pairs there is no preference, then even if the new therapy is substantially better than standard therapy in that 6%, the therapy may not have a large public health impact, especially if we cannot identify the specific ones in the 6% of the population that will benefit prior to introduction of therapy. It is useful to have an effect estimate that measures the potential effect of the new therapy on the population, for example, Δ, the proportion of the population that prefer new therapy minus the proportion that prefer the standard therapy. The aim of this paper is to develop exact confidence intervals for Δ from matched-pair studies that are compatible with the exact sign test. By compatibility, we mean that the 100(1 − α)% confidence interval excludes Δ = 0 if and only if the exact sign test rejects Δ = 0 at level α. What makes this problem difficult is that although the sign test conditions on the pairs that have a preference, the parameter Δ is not conditional in that way but refers to the entire population.

There are many versions of the sign test. Of theoretical interest is the exact randomized sign test, which has type I error rate exactly equal to its α level and is the uniformly most powerful unbiased test, but has the unsatisfying property that two statisticians correctly analyzing the same data may disagree on the accept/reject decision because of the randomized decision rule¹. Asymptotic versions of the sign test are available, but may have inflated type I error rate for small sample sizes. In this paper, we focus on the non-randomized exact sign test and the compatible confidence intervals, which are exact in the sense that for all situations the type I error rate is no more than α and the confidence intervals have at least nominal coverage.

The sign test only uses the preference information for each pair, regardless of whether the individual responses within a pair are binary, ordinal, or numeric. Thus, the review of Fagerland et al² on different parameters for paired binomial proportions, applies equally to parameters for sign tests as for McNemar-type tests. Fagerland et al² study difference in proportions, ratio of proportions, and odds ratios of proportions, but in this paper we study only the difference in proportions. Fagerland et al² reviews 7 different confidence intervals on Δ, an exact unconditional method, and 6 other methods. Unlike exact methods, those 6 other methods are not guaranteed to achieve nominal coverage. In general, unconditional exact tests for pair matched binary studies have better power than the exact sign test, which is a conditional exact test². The improved power likely comes from having less discreteness, since the unconditional test allows the number of mismatched pairs (say M) to change. There are ways to improve the power for unconditional exact tests^3,4. For example, Lloyd and Moldovan⁴ describe several methods including an unconditional exact test based on a method of Berger and Boos⁵, that depends on using a 100(1 − γ)% confidence interval for a nuisance parameter. One can invert a series of unconditional exact tests to create exact confidence intervals, but not all such inversions are straightforward. For example, one can invert a Berger-Boos⁵ adjusted test for independent binomials because the difference in proportions in that case is increasing in one parameter and decreasing in the other⁶, but the lack of that type of monotonicity makes the application to matched-pair binary data difficult. Further, the Berger-Boos adjustment requires specifying γ, and no such parameter specification is needed in the method we propose. Nevertheless, there are several developed methods to create unconditional exact confidence intervals^7,8. A main issue with the unconditional exact tests is that they are relatively difficult to calculate compared to the exact conditional one (i.e., the exact sign test). Similar computational difficulties arise with exact unconditional confidence intervals. Another issue is that the confidence sets created from inverting the p-value functions may include more than one disjoint interval⁹, and this means that the associated confidence intervals cannot be compatible¹⁰. A similar compatibility issue arises when we start with confidence intervals that have optimal widths, and examine their compatibility with their associated tests. Wang⁸ developed an exact one-sided interval for Δ that is smallest one within a class of unconditional exact tests. Although the Wang interval is typically smaller than our proposed one, the Wang interval has no compatible test associated with it.

Fagerland et al² states that “no simple exact conditional interval is possible for the difference between proportions. The only option for an exact interval is an exact unconditional interval.” This paper fulfils that need. We develop confidence intervals compatible with the exact sign test, and show by extensive computer calculations that the intervals guarantee coverage in a wide variety of situations. We create those confidence intervals using a modification of melded intervals¹¹. Fay et al¹¹ developed melded confidence intervals designed to give guaranteed coverage for an effect parameter for the two sample problem, by melding together the two confidence intervals from two independent samples. For example, melded one-sided (or central) confidence intervals on a difference in proportion for a two sample independent binomial study were developed that are compatible with one-sided (or central) Fisher’s exact tests¹¹. Melding uses confidence distributions (see¹²), which are closely related to fiducial methods (see¹³ and references therein). To avoid problems of fiducial inferences, melding as described in Fay et al¹¹, has three restrictions on its application. First, it applies to two independent samples. Second, it builds on confidence distributions from each sample created from nested confidence interval procedures, where a nested confidence interval procedure requires that if two confidence intervals with different levels are calculated on the same data set, the interval with the larger level completely contains the other interval (e.g., the 96% confidence interval completely covers the 95% interval). Third, the parameter of interest is a function of two parameters (one from each sample), and the function is required to be increasing in one parameter and decreasing in the other, while holding the other parameter constant (within the range of allowable values of those parameters). This work expands the application of melding as described in¹¹ in two ways. First, it allows for matched pair sampling. Second, it allows the parameter of interest (in this case, Δ), to be a more complicated function of parameters.

Our method is an extension of the melded confidence intervals for independent two-sample tests as described in Fay, et al.¹¹. In Section 2 we introduce notation and review the melded confidence interval for the difference in proportions for the two sample binary response problem without matched-pairs. In Section 3 we develop the confidence interval for Δ from the matched-pair problem, and show that it is compatible with the exact sign test. In Section 4 we present calculations that support the proposition that our proposed confidence interval procedure gives intervals with at least nominal coverage. We show that over a fine grid covering the full range of possible parameters, and for all sample sizes up to n = 100 pairs, our proposed 95% two-sided confidence intervals and 97.5% one-sided intervals cover with at least the nominal level (up to computer rounding error) in every case. In Section 5 we compare our proposed confidence interval to the exact confidence intervals of Wang⁸, discussing how although the Wang intervals have typically smaller width than our proposed intervals, they do not have a compatible test associated with it. Finally, in Section 6 we demonstrate our proposed confidence interval in an application, and Section 7 ends with a discussion.

2 |. TWO SAMPLE BINOMIAL MELDED INTERVALS

We start by reviewing lower and upper confidence distributions for a single binomial sample, and then show how those can be used to get a confidence interval for the difference in proportions. This section is a review and was previously covered in Fay, et al.¹¹.

Let X₀ ~ Binomial(m₀, β₀) and independently X₁ ~ Binomial(m₁, β₁), and suppose we are interested in a confidence interval on β₁ − β₀. First, we write the exact central (i.e., Clopper-Pearson) confidence intervals for β_a for a = 0, 1 using lower and upper confidence distributions. Let $L_{{\beta }_a}(1-\alpha /2;x_a,m_a)$ be the lower confidence limit associated with the one-sided 100(1 − α/2)% exact confidence interval for β_a, and similarly let $U_{{\beta }_a}(1-\alpha /2;x_a,m_a)$ be the upper confidence limit associated with the other one-sided 100(1 − α/2)% exact confidence interval for β_a. Then the exact 100(1 − α)% central confidence interval (i.e., the one that bounds the error on each side at α/2) for β_a, is

$$\left\{L_{{\beta }_a}\left(1-\frac{\alpha }{2};x_a,m_a\right),U_{{\beta }_a}\left(1-\frac{\alpha }{2};x_a,m_a\right)\right\}.$$ (1)

Both L_βa and U_βa can be used to create nested one-sided exact confidence intervals, hence may be used for melding. An equivalent way to write the Clopper-Pearson interval is to use lower and upper confidence distributions. Let $B_{aL}=L_{{\beta }_a}(A;x_a,m_a)$ be a random variable, specifically the lower confidence distribution random variable (CD-RV), where the randomness comes from A (since x_a and m_a are fixed), where A is uniformly distributed. Similarly, define the upper CD-RV for β_a as $B_{aU}=U_{{\beta }_a}(A^{\ast };x_a,m_a)$, where A* is also uniformly distributed and is independent of A. Let q(a, W) be the ath quantile for any random variable W. Then we can rewrite equation 1 as

$$\left\{q\left(\frac{\alpha }{2},B_{aL}\right),q\left(1-\frac{\alpha }{2},B_{aU}\right)\right\}.$$ (2)

For the binomial situation, because of the relationship between the cumulative distributions of the binomial and the beta distributions (see Appendix A), we can write the 100(1 − α)% Clopper-Pearson confidence interval for β_a in terms of quantile functions of slightly generalized beta random variables. Specifically, that interval is

$$\{F_{beta}^{-1}(\alpha /2;x_a,m_a-x_a+1),F_{beta}^{-1}(1-\alpha /2;x_a+1,m_a-x_a)\},$$ (3)

where $F_{\mathit{beta}}^{-1}(\cdot ;a,b)$ is the quantile function of a generalized beta random variable with parameters a and b, and the generalization defines Beta(0, c) and Beta(c, 0) for c > 0 as point mass distributions at 0 and 1, respectively. Therefore the lower and upper CD-RVs are

$$\begin{gathered} B_{aL}=F_{\mathit{beta}}^{-1}(1-A;x_a,m_a-x_a+1) \\ \text{and} \\ {B}_{aU}=F_{\mathit{beta}}^{-1}(A^{\ast };x_a+1,m_a-x_a). \end{gathered}$$ (4)

Since A is a uniform random variable, then 1 − A is also uniform, and using the probability integral transformation (see e.g.,¹⁴, p. 54), we get $B_{aL}\sim \mathrm{Beta}(x_a,m_a-x_a+1)$ and $B_{aU}\sim \mathrm{Beta}(x_a+1,m_a-x_a)$, where both are generalized beta random variables. The lower CD-RV, B_aL, has a mean of $x_a/(m_a+1)$ and is stochastically smaller than the upper CD-RV, B_aU, which has a mean of $(x_a+1)/(m_a+1)$. In order to guarantee coverage for discrete distributions, we need to use those two different CD-RVs for the exact central confidence interval, with the stochastically lower RV on the lower limit. In contrast, only one CD-RV is needed for continuous distributions (see¹²).

Equation 2 seems like a convoluted way to write the exact central confidence interval for β_a, but the notation and ideas are useful for describing the 100(1 − α)% so-called “melded” confidence interval for β₁ − β₀, which is

$$\left\{q\left(\frac{\alpha }{2},B_{1L}-B_{0U}\right),q\left(1-\frac{\alpha }{2},B_{1U}-B_{0L}\right)\right\}.$$ (5)

In order to guarantee that the lower error is not more than α/2, for the lower limit we use the lower CD-RV for β₁, but we use the upper CD-RV for β₀ because of the minus sign in the parameter of interest, β₁ − β₀. Analogously for the upper limit, we use the upper CD-RV for β₁ but the lower CD-RV for β₀. See Fay et al¹¹ for computational details and for showing that the interval of equation 5 is compatible with the central Fisher’s exact test. Besides the difference function, g(β₀, β₁) = β₁ − β₀, we can also apply the melding method to other functions. For the binomial case where 0 ≤ β_a ≤ 1, we can also apply the method to the ratio, $g({\beta }_0,{\beta }_1)={\beta }_1/{\beta }_0$ and the odds ratio, $g({\beta }_0,{\beta }_1)=\{{\beta }_1(1-{\beta }_0)\}/\{{\beta }_0(1-{\beta }_1)\}$, giving a 100(1 − α)% confidence interval for $g({\beta }_0,{\beta }_1)$ as

$$\left\{q\left[\frac{\alpha }{2},g\left(B_{0U},B_{1L}\right)\right],q\left[1-\frac{\alpha }{2},g\left(B_{0L},B_{1U}\right)\right]\right\}.$$

A key restriction presented in Fay et al.¹¹ on the function g(·, ·) is that for the range of the parameters allowed, $g({\beta }_0,{\beta }_1)$ must be decreasing in β₀ for all allowable values of β₁ and increasing in β₁ for all allowable values of β₀. In this paper, we expand the melding method, by working with a parameter function that violates this restriction in a specific way, and by working with matched-pair samples.

3 |. PROPOSED CONFIDENCE INTERVAL FOR Δ

Now consider the matched-pair data. Within the ith pair let the observed responses be y_i0 and y_i1 representing the two groups of interest. For example, in a study of twins randomized to new therapy or standard therapy, the response from the twin randomized to new therapy is y_i1 and the response from the twin randomized to standard therapy is y_i0. The responses may be numeric or binary. Let the associated random variables be Y_i0 and Y_i1. In this section, assume that [Y_i0, Y_i1] for i = 1, …, n are independent random variables coming from the bivariate distribution F₀₁. In other words, there may be correlation within a pair of responses, but the vectors of paired responses are independent. Let S_i = Y_i1 − Y_i0 be the sign of the difference for the ith pair. Let ${\sum }_{i=1}^{n}I(S_i=1)=X$ and ${\sum }_{i=1}^{n}I(S_i=1\text{or}{S}_i=-1)=M$, where I(A) = 1 if A is true, and 0 otherwise. Because of the independence of the paired responses, this implies that the S₁, …, S_n are independent as well. Let the distribution of S_i for each i = 1, …, n be a trinomial distribution, with parameters defined as follows:

s	Pr[Si = s]	# {Si = s}
−1	θ(1 − β)	M − X
0	1 − θ	n − M
1	θβ	X

In terms of these parameters, $\text{Δ}=E(S_i)=\theta (2\beta -1)$. Let d(t, b) = t(2b − 1), so that d(θ, β) = Δ. We have

$$\begin{gathered} M\sim Binomial(n,\theta ) \\ \text{and} \\ X\mid M\sim Binomial(M,\beta ). \end{gathered}$$

with β ∈ (0, 1) and θ ∈ (0, 1). The parameter function d(t, b) does not follow the typical restriction required for melding; it is increasing in t when b > 0.5, but decreasing in t when b < 0.5 and constant when b = 0. Thus, we must modify the usual construction of the melding intervals.

We are interested in testing hypotheses about Δ. We begin with a one-sided hypotheses:

$$\begin{gathered} H_0:\text{Δ}\ge 0 \\ {H}_1:\text{Δ}<0. \end{gathered}$$

Because Δ = θ(2β − 1) and θ ∈ (0, 1), these hypotheses are equivalent to

$$\begin{gathered} H_0:\beta \ge 0.5 \\ {H}_1:\beta <0.5. \end{gathered}$$

Let p_U(x, m) be the p-value for the exact sign test of those one-sided hypotheses, and

$$p_U(x,m)=\mathit{Pr}[X\le x\mid m,\beta =0.5].$$

We use CD-RVs to rewrite the p-value, and to define the associated one-sided confidence interval. We use the lower and upper confidence distribution random variables (CD-RVs) associated with the binomial parameters. Let the lower and upper CD-RVs for θ be

$$\begin{gathered} T_L\equiv T_L(m,n)=F_{\mathit{beta}}^{-1}(1-A;m,n-m+1)\sim Beta(m,n-m+1) \\ {T}_U\equiv T_U(m,n)=F_{\mathit{beta}}^{-1}(A^{\ast };m+1,n-m)\sim Beta(m+1,n-m) \end{gathered}$$

and let the lower and upper CD-RVs for β be

$$\begin{gathered} B_L\equiv B_L(x,m)=F_{\mathit{beta}}^{-1}(1-C;x,m-x+1)\sim Beta(x,m-x+1) \\ {B}_U\equiv B_U(x,m)=F_{\mathit{beta}}^{-1}(C^{\ast };x+1,m-x)\sim Beta(x+1,m-x), \end{gathered}$$

where A, A*, C and C* are independent uniform random variables. Recall, these distributions are interpreted as point masses when x=0 or x=m.

In terms of CD-RVs, we can rewrite p_U(x, m) for the exact sign test of either H₀ : Δ ≥ 0 or H₀ : β ≥ 0.5, as

$$p_U(x,m)=\mathit{Pr}\left[X\le x\mid m,\beta =\frac{1}{2}\right]=\mathit{Pr}\left[B_U(x,m)\ge \frac{1}{2}\right]$$ (6)

which does not depend on n (see Appendix A). In equation 6, x and m are fixed constants that define the CD-RV, B_U(x, m), whose randomness comes from an independent uniform random variable, C*.

We define our proposed melded one-sided 100(1 − α)% upper confidence limit for Δ as:

$$U_{\text{Δ}}(1-\alpha ;x,m,n)=\{\begin{array}{c}q\{1-\alpha ,d(T_U,B_U)\}\text{if}{p}_U(x,m)>\alpha \\ q\{1-\alpha ,d(T_L,B_U)\}\text{if}{p}_U(x,m)\le \alpha .\end{array}$$ (7)

(Recall that d(θ, β) = Δ.) Figure 1 helps motivate U_Δ. When β > 0.5 then Δ increases with θ, while if β < 0.5 then Δ decreases with θ. So if 1 − α of the distribution of B_U is less than 1/2, then p_U(x, m) ≤ α, and we use T_L to get a larger (and conservative) value for U_Δ, otherwise we use T_U to get the larger, conservative, value for U_Δ.

FIGURE 1.

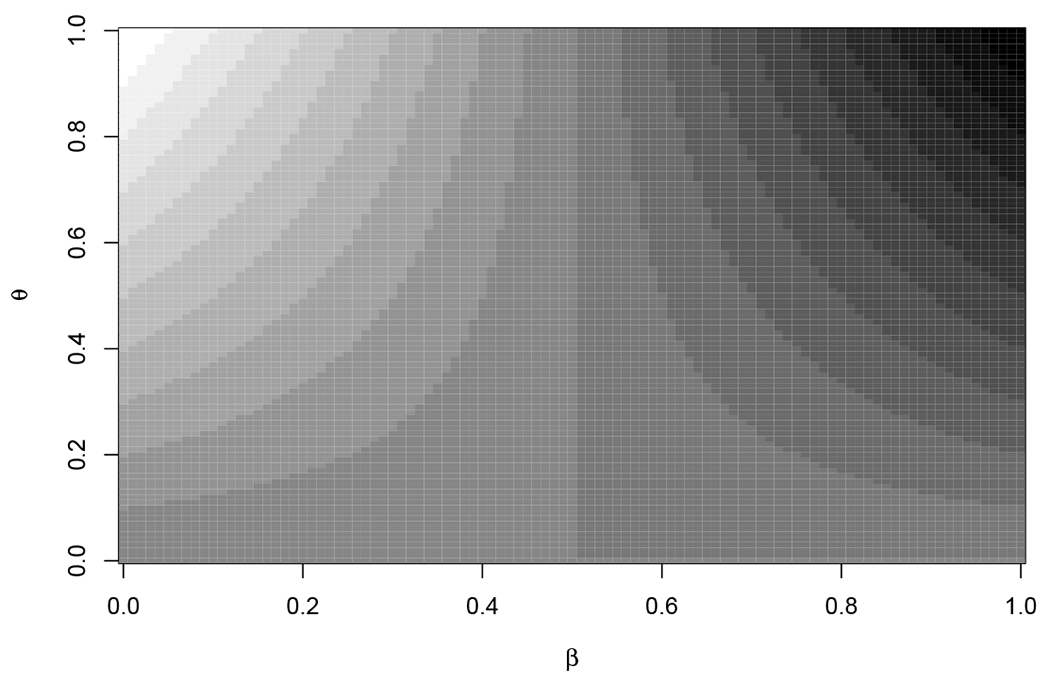
Contour plot of $\text{Δ}=\theta (2\beta -1)$ as β by θ. Δ goes from −1 (white) to 1 (black).

Now consider the other one-sided hypotheses for Δ,

$$\begin{gathered} H_0:\text{Δ}\le 0 \\ {H}_1:\text{Δ}>0. \end{gathered}$$

Denote the associated exact sign test p-value as p_L(x, m). Analogous to equation 6,

$$p_L(x,m)=Pr\left[B_L(x,m)\le \frac{1}{2}\right].$$ (8)

Following analogous reasoning to the motivation of U_Δ, we define the lower limit. Let the one-sided lower 100(1 − α)% confidence limit be $L_{\text{Δ}}(1-\alpha ;x,m,n)$, given by

$$L_{\text{Δ}}(1-\alpha ;x,m,n)=\{\begin{array}{c}q\{\alpha ,d(T_L,B_L)\}\text{if}{p}_L(x,m)\le \alpha \\ q\{\alpha ,d(T_U,B_L)\}\text{if}{p}_L(x,m)>\alpha .\end{array}$$ (9)

We define a two-sided 100(1 − α)% central confidence interval by taking the intersection of the two 100(1 − α/2)% one-sided intervals, to get

$$\left\{L_{\text{Δ}}\left(1-\frac{\alpha }{2};x,m,n\right),U_{\text{Δ}}\left(1-\frac{\alpha }{2};x,m,n\right)\right\}.$$ (10)

The associated exact central two-sided p-value for the sign test for testing H₀ : Δ = 0 versus H₁ : Δ ≠ 0 is

$$p_C(x,m)=\min \{1,2p_L(x,m),2p_U(x,m)\}.$$ (11)

Expanding the definition of Fay, et al¹¹, we call these proposed intervals melded confidence intervals for Δ. We now state some properties of the confidence intervals and the associated exact sign test p-values.

Theorem 1 (Compatibility). The upper limit $U_{\text{Δ}}(1-\alpha ;x,m,n)$ (equation 7) is compatible with p_U(x, m) (equation 6), the lower limit $L_{\text{Δ}}(1-\alpha ;x,m,n)$ (equation 9) is compatible with p_L(x, m) (equation 8), and the central confidence interval given in equation 10 is compatible with p_C(x, m) (equation 11).

See Appendix B for proof.

Proposition 1 (Validity). The one-sided 100(1 − α)% confidence intervals $\{-1,U_{\text{Δ}}(1-\alpha ;x,m,n)\}$ and $\{L_{\text{Δ}}(1-\alpha ;x,m,n),1\}$, as well as the two-sided 100(1 − α)% central confidence interval (equation 10) are valid (i.e., the coverage for each is at least 1 − α).

This proposition is not yet proven, but we support it with calculations in Section 4.

4 |. VALIDITY CALCULATIONS

To check the coverage of the melded confidence intervals, we did some numeric calculations using the mcnemarExactDP function in the exact2x2 (version 1.6.4) R package. For n = 1, 2, …, 100, we calculate the 95% melded confidence interval for Δ for all possible values (m = 0, 1, …, n and within each m the values x = 0, 1, …, m). Then we checked the lower error (i.e., Pr[Δ < L_Δ]) and upper error (i.e., Pr[Δ > U_Δ]) for all values (θ, β) with θ ∈ {0, 0.01, 0.02, …, 1} and β ∈ {0, 0.01, 0.02, …, 1}. In all cases, none of the errors were greater than the nominal 0.0250, within computer rounding error. (For each of n = 71 and n = 72, two of the (θ, β) values gave errors greater than 0.025 by less than 3.2 × 10⁻⁵, probably due to computer numerical integration rounding error). For each n > 5 the maximum calculated one-sided error over the entire parameter space was greater than 0.024, so the maximum error is close to the ideal 0.025. The R code for the calculations is available in the demo directory of the exact2x2 (version 1.6.4) R package. As an example, Figure 2 plots the lower and upper errors from the melded confidence intervals when n = 26.

FIGURE 2.

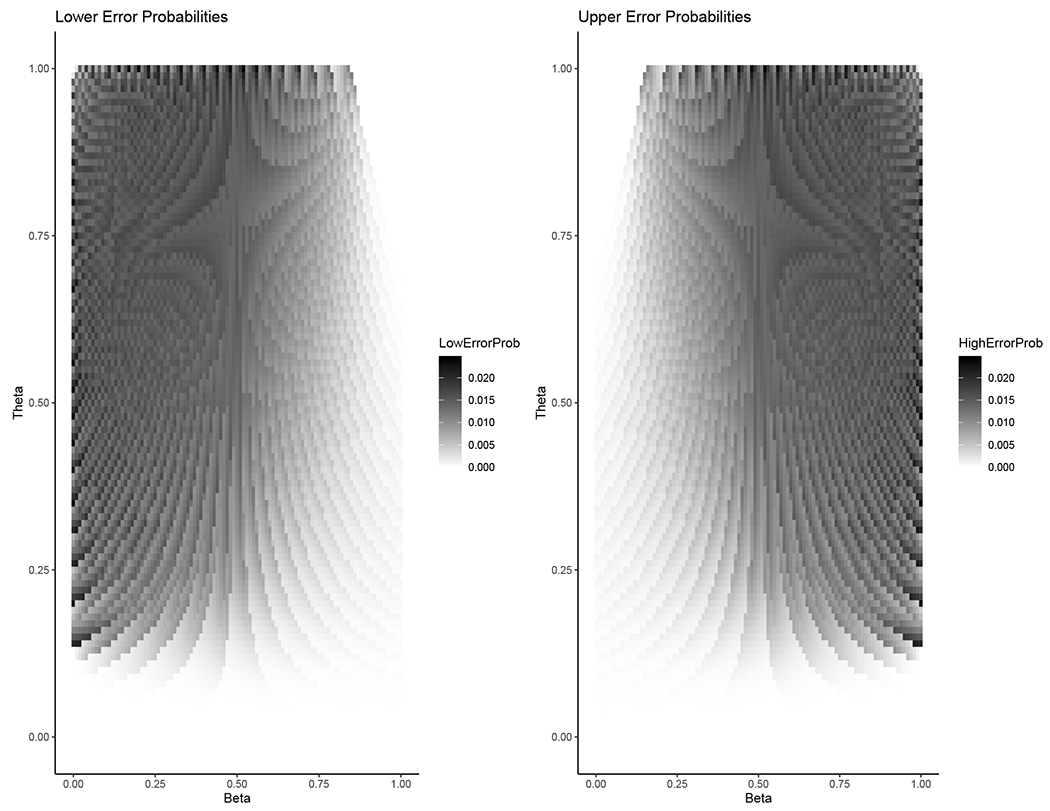
Lower and upper errors from the 95% central melded confidence interval for Δ (equation 10) when n = 26 for all values of β, θ ∈ {0, 0.01, 0.02, …, 1}. The maximum of all the calculated errors for both the lower and upper errors was 0.0242, less than the nominal 0.025.

5 |. AN ALTERNATIVE EXACT INTERVAL WITHOUT A COMPATIBLE TEST

We have proposed melded confidence intervals for Δ that are compatible with the exact McNemar’s test and the exact sign and given numerical calculations showing that they have at least nominal coverage for the two-sided 95% level or one-sided 97.5% level. For completeness we compare the melded intervals with the confidence intervals of Wang⁸. Wang⁸ derived exact one-sided intervals that are proven to have the smallest width among intervals with a specific sample space ordering, an inductive method designed to give smallest width confidence intervals; however, there is no explicit proof that there is not some other (as yet unknown) ordering that may give smaller width intervals. A central 95% two-sided exact interval can be created as the intersection of two 97.5% one-sided Wang intervals. These properties of the Wang intervals depend on ideal computer implementation, but the algorithm is a double grid search algorithm, so depending on the parameters of the grid searches, the resulting intervals may not be the smallest width. Despite these caveats, the Wang exact central intervals are expected to have smaller width than the (suspected to be exact) central melded interval. In Figure 3, we give the 95% confidence intervals for Δ using both methods for all 378 possible outcomes when n = 26. The graph has a sawtoothed pattern because of the way we sorted the data (first by $\widehat{\text{Δ}}$, then by L_Δ(0.975)), and because there are many sets of tied values of $\widehat{\text{Δ}}=\frac{x-(m-x)}{n}$, so that among each set there are different m values giving different confidence intervals. For n = 26, the Wang method always has smaller width (within computer error, ≈ 10⁻⁴) than the melded method, and on average the melded method confidence interval width is only 9.9% larger. The lower and upper error for the 95% central intervals of Wang are plotted in Supplemental Figure S1. Here the maximum lower and upper errors are both 2.499%, within rounding error of the target 2.5%.

FIGURE 3.

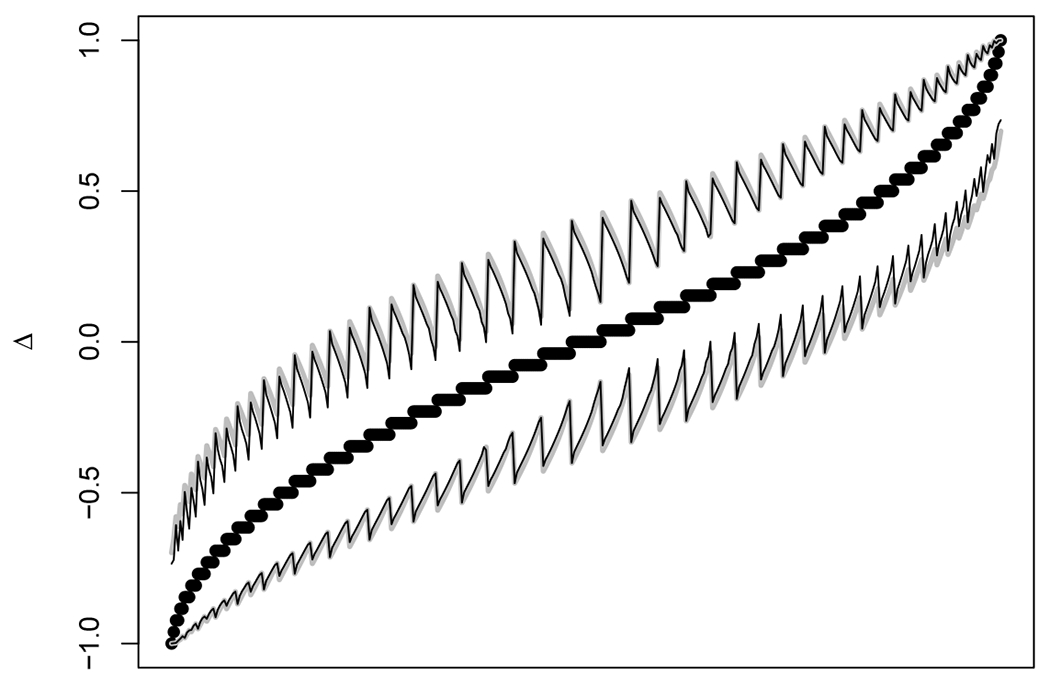
For the case n = 26, we plot $\widehat{\text{Δ}}$ and the two confidence intervals for all possible 378 outcomes, sorted by $\widehat{\text{Δ}}$, then within tied values of $\widehat{\text{Δ}}$, sorted by L_Δ(0.975). The thick gray lines define the 95% confidence intervals by the proposed melded method, and the thin black lines define the 95% confidence intervals by the Wang method. The x-axis only represents the rank of each of the 378 estimates, so it is not labeled.

An advantage of the proposed melded intervals are that they are faster to calculate. The calculation time on a PC (64 bit processor, 3 GHz, 16 GB RAM) for the 378 confidence intervals of Figure 3 averaged about 0.1 second for each melded confidence interval, compared to averaging 17 seconds for each Wang interval. For Figure 4 (described later) that has n = 67 the difference is even larger: the melded intervals averaged about 0.1 seconds again, but Wang’s interval averaged about 3 minutes per interval.

FIGURE 4.

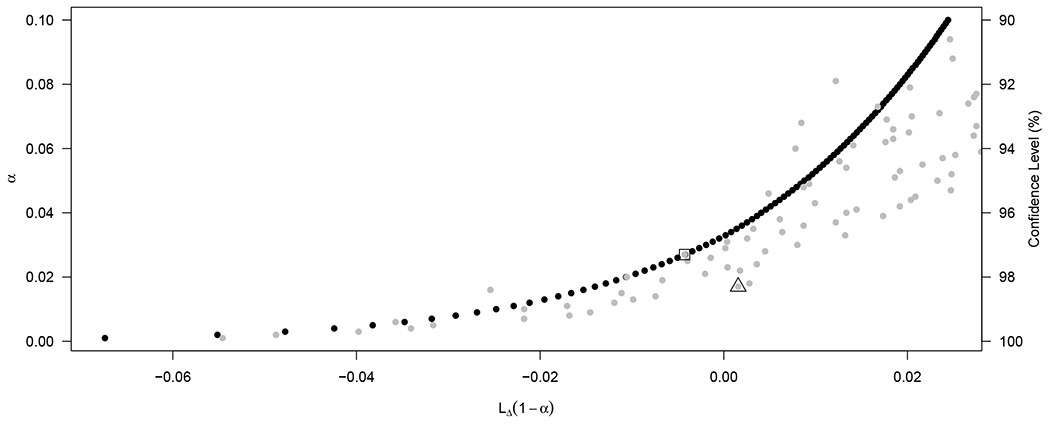
Lower 100(1 − α)% confidence limits by α ∈ {0.001, 0.002, …, 0.100} for the data x = 9, m = 11 and n = 67. Black dots are the lower limit for the melding interval, L_Δ(1 − α), and gray dots are the lower limit for the Wang interval, $L_{\text{Δ}}^W$ (1 − α). The point outlined by a square is Wang’s one-sided 97.3% limit, $L_{\text{Δ}}^W$ (0.973; 9, 11, 67) = −0.0043, and the point outlined by a triangle is the one-sided 98.3% limit, $L_{\text{Δ}}^W$ (0.983; 9, 11, 67) = 0.0016.

The major advantage of the melded method is its compatibility with McNemar’s exact test. The Wang interval has no compatible associated test, because its one-sided confidence intervals are not nested. Fay and Hunsberger¹⁰ show (Theorem 4.1) that exact confidence intervals that are not nested cannot be compatible with their associated test.

We show this with a counterexample. Let $L_{\text{Δ}}^W(1-\alpha ;x,m,n)$ be the 100(1 − α)% one-sided confidence interval of Wang. Consider the one-sided test, H₀ : Δ ≤ 0 versus H₁ : Δ > 0. Suppose there is a p-value associated with H₀ that is from a test compatible with the Wang interval, and let that be $p_L^W(x,m)$. Then compatibility means that whenever $L_{\text{Δ}}^W(1-\alpha ;x,m,n)>{\text{Δ}}_0$ then we reject H₀ at level α, meaning $p_L^W(x,m)\le \alpha$, and whenever $L_{\text{Δ}}^W(1-\alpha ;x,m,n)\le {\text{Δ}}_0$ then we fail to reject H₀ at level α, meaning $p_L^W(x,m)>\alpha$. Consider the case when x = 9, m = 11, and n = 67. We calculate two one-sided confidence intervals using Wang’s method using the ExactCIdiff R package (version 1.3, R version 4.0.0, using default arguments), one with α = 0.017 and one with α = 0.027. In the first case the 100(1 − 0.017)% = 98.3% lower limit is $L_{\text{Δ}}^W$ (0.983; 9, 11, 67) = 0.0016 > 0, and we reject H₀ at level α = 0.017, implying $p_L^W$(9, 11) ≤ 0.017. This implies that we reject at the traditional one-sided 2.5% level as well. In the second case the 100(1 − 0.027)% = 97.3% lower limit is $L_{\text{Δ}}^W$ (0.973; 9, 11, 67) = −0.0043 < 0, and we fail to reject H₀ at level α = 0.027, implying $p_L^W$(9, 11) > 0.027 and we fail to reject at the traditional one-sided 2.5% level. This implies that 0.027 < $p_L^W$(9, 11) ≤ 0.017, which is impossible and shows that there cannot exist a compatible test of H₀ with Wang’s confidence interval procedure. In Figure 4 we plot the 100(1 − α)% one-sided lower limits for Δ by α for the counterexample case: x = 9, m = 11 and n = 67. The melded limits (black dots) are typically lower than the Wang limits (gray dots), but notice the non-nestedness of the Wang limits.

The counterexample was chosen to highlight that there is not compatible associated test with the Wang intervals. For other examples (e.g., x = 9, m = 11, n = 26), many of the data points have intervals that are closer to monotonic in the confidence level for parts of the range (see Supplemental Figure S2). The Wang intervals are based on a double grid search algorithm and may change slightly if the number of elements in the grid searches in the maximization algorithm are changed, but we kept the default to mimic the typical user.

A similar lack of a compatible test may arise when using unconditional exact tests. An unconditional exact test may be formulated using any “ordering function”, a function that orders the sample space (see e.g.,¹⁰). The lack of a compatible test may occur if the ordering function depends on Δ₀ (i.e., the parameter value that is on the boundary between the null and alternative hypotheses). This is an issue when using score test statistics to order the sample space, as in the example in Fagerland et al². For analogous examples in the independent two-sample binomial case see¹⁵ and¹⁰. We did not explore those unconditional exact tests further, because we could not find an R package to do these calculations, and because the unconditional exact test using the score statistic is not straightforward to define (e.g., there is not a clear definition of the ordering function when the squareroot term in the denominator is negative).

6 |. APPLICATION

For illustration we consider data comparing low versus high dose of an analgesic for the treatment of dysmennorrhea given in Table 1 (reproduced from¹⁶, Table IV). In the trial, each individual was given both a low dose and a high dose of an analgesic at different times, and for the purposes of illustration only we assume no period effects and no crossover effects (see Jones and Kenward¹⁷ a more complete description and analysis that does not make these assumptions).

TABLE 1.

Low dose versus high dose analgesic for treatment of dysmennorrhea in a crossover trial. Success is pain relief, and failure is no pain relief.^16,17.

		High Dose
		Success	Failure
Low	Success	53	8	61
Dose	Failure	16	9	25
		69	17	86

The exact two-sided sign test gives a p-value of p = 0.15. The effect is not significant at the two-sided α = 0.05 level. To get a more complete picture we look at effect estimates and confidence intervals. We first look at the confidence interval on β. Conditional on a preference, we have $\widehat{\beta }$= 16/(8+16) = 0.667 prefer the high dose, and the 95% exact central confidence interval (i.e., the Clopper-Pearson interval) on β is (0.447, 0.844). So it looks like there is a possibility of a fairly strong effect, since we cannot rule out as high as 84% of those with a preference preferring the high dose. If we define the net benefit for those with a preference as

$$(\text{proportion who prefer high dose})-(\text{proportion who prefer low dose})=\beta -(1-\beta ),$$

then there is a net benefit of 33.3% with 95% confidence interval of (−10.6%, 68.7%).

Another related question is: what is the net benefit to the entire study population (not just those with a preference)? In other words, what if we used Δ, and defined the net benefit for the population as Δ? For the calculation of the proposed melded confidence interval (equation 10), we use the mcnemarExactDP function in the exact2x2 R package, and we get $\widehat{\text{Δ}}$= 0.093 as our estimate of the proportion who prefer the high dose over the low dose minus the proportion who prefer the low dose over the high dose, with 95% confidence interval (−0.030, 0.214). In other words, there is a net benefit of high dose over low dose of 9.3%, with 95% confidence interval (−3.0%, 21.4%). Because there is a high proportion of the pairs with no preference, the net benefit of the entire study population is much smaller from the net benefit of those that have a preference.

7 |. CONCLUSION

We have developed a confidence interval procedure for Δ, the difference in proportions (proportion with positive sign minus proportion with negative sign) from a matched-pair study. We have shown that our proposed melded confidence interval is compatible with the exact sign test (for both one-sided versions as well as the central version). This ensures that when the exact sign test is used, a researcher may present a useful confidence interval for Δ that will not contradict the test. Thus, for example, our proposed 95% confidence interval will always exclude 0, whenever the exact test shows a significant difference from 0 at the 5% level. The exact sign test and these compatible confidence intervals are easy to calculate for any sample size.

We have provided extensive numerical calculations suggesting that our confidence interval is valid (i.e., exact). These calculations cover the parameter space with a fine grid for all samples sizes up to n = 100. Thus, the calculations are much more than the typical set of simulations of a small subset of possible situations. Nevertheless, we have not proven the validity of our confidence intervals, and this essential mathematical proof is left to future work.

Although there are simpler asymptotic methods that do not guarantee coverage, and more complicated exact methods that can have better power² or smaller confidence intervals⁸, our proposed confidence intervals have a compatible test and are easier to calculate than the exact ones, and like the other exact ones, our intervals are designed to guarantee coverage for all sample sizes. Although we have shown that the Wang⁸ interval has no compatible test, there are other exact unconditional confidence intervals^2,7 which may possibly have a compatible associated test, but because they are unconditional there is no expectation that they will be compatible with the exact sign or McNemar’s tests.

We have expanded the definition of melding to allow paired data and functions of parameters that have a special kind of monotonicity (see e.g., Figure 1). The melding method uses two nested confidence intervals associated with two parameters (e.g., θ and β), that combine through a function of those parameters to define a parameter of interest (e.g., Δ = θ {2β − 1}). There were two ways we expanded the original definition. First, we no longer require the random variables that estimate the two parameters to be independent. Specifically, M, which estimates θ, is not independent of X, which estimates β given M. Second, we now allow that the function of the two parameters to create the parameter of interest only needs to be monotonic within the two different partitions of the parameter space (e.g., when β < 0.5 and when β > 0.5). We leave to future work the full extent to which the definition of melding may be expanded to other applications.

We provide R functions for these methods on CRAN. For binary data, use the mcnemarExactDP function of the exact2x2 R package (available at https://CRAN.R-project.org/package=exact2x2), and for orderable data, use the signTest function of the asht R package (available at https://CRAN.R-project.org/package=asht).

Supplementary Material

Supplement

Figure S1. Lower and upper errors from the 95% central Wang confidence interval for Δ using the ExactCIdiff R package when n = 26 for all values of β, θ ∈ {0, 0.01, 0.02, …, 1}.

Figure S2. Lower 100(1 − α)% confidence limits by α ∈ {0.001, 0.002, …, 0.100} for the data x = 9, m = 11 and n = 26.

Abbreviations:

CD-RV

confidence distribution random variable

APPENDIX

A. EXPRESSIONS OF THE CLOPPER-PEARSON CONFIDENCE INTERVALS

Let X ~ Binomial(m, β). The 100(1 − α)% Clopper-Pearson confidence interval on β is $\{L_{\beta }(1-\alpha /2;x,m),U_{\beta }(1-\alpha /2;x,m)\}$, where

$$L_{\beta }(1-\alpha /2;x,m)=\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}x=0\hfill \\ \{\beta :\mathrm{Pr}[X\ge x\mid m,\beta ]=\alpha /2\}& \hfill \text{if}x>0\hfill \end{array}$$

By using integration by parts, one can show (see e.g., Casella and Berger¹⁴, p. 82) that for x > 0,

$$\mathrm{Pr}[X\ge x\mid m,\beta =b]=F_{beta}(b;x,m-x+1)$$

where $F_{beta}(b;x,m-x)$ is the cumulative distribution function (cdf) of a beta random variable (RV) with parameters x and m−x+1 evaluated at b. Therefore when x > 0 we can write $L_{\beta }(1-\alpha /2;x,m)=F_{beta}^{-1}(\alpha /2;x,m-x+1)$, where $F_{\mathit{beta}}^{-1}(q;x,m-x+1$ is the qth quantile of a beta RV with parameters x and m − x + 1. The upper limit is defined analogously, to get equation 3. This is not a new result, and in fact, this is the way that the Clopper-Pearson confidence interval is calculated in the binom.test function in R¹⁸.

B. COMPATIBILITY PROOF

Proof of Theorem 1. First we prove the result for the p_U and U_Δ.

Step 1, show $p_U\le \alpha \Rightarrow U_{\text{Δ}}\le 0$: If $p_U(x,m)\le \alpha$ then m > 0 and by definition $\mathit{Pr}[B_U\ge 0.5]\le \alpha$. Further $\mathit{Pr}[T_L(m,n)>0]=1$ for all m > 0. Thus,

$$\begin{gathered} \mathit{Pr}[B_U\ge 0.5]\le \alpha \Rightarrow \mathit{Pr}[T_L\left(2B_U-1\right)\ge 0]\le \alpha \\ \Rightarrow \mathit{Pr}[d(T_L,B_U)\ge 0]\le \alpha \\ \Rightarrow \mathit{Pr}[d(T_L,B_U)<0]\ge 1-\alpha \\ \Rightarrow 0\ge q\{1-\alpha ,d(T_L,B_U)\} \\ \Rightarrow 0\ge U_{\text{Δ}}. \end{gathered}$$

Step 2, show $U_{\text{Δ}}\le 0\Rightarrow p\le \alpha$: First consider the case when m = 0. When m = 0 then p_U(0, 0) = 1 and $U_{\text{Δ}}=q(1-\alpha ,d(T_U,B_U))$. Also, B_U is a point mass at 1 so that d(T_U, B_U) = T_U, but when m = 0 then Pr[T_U > 0] = 1 so q(1 − α, T_U) > 0 and U_Δ > 0. Now consider when m > 0. Let T be either T_L or T_U, since both T_L and T_U will always be positive because neither will be a point mass at 0 when m > 0.

$$\begin{gathered} U_{\text{Δ}}\le 0\Rightarrow q(1-\alpha ,d(T,B_U))\le 0 \\ \Rightarrow 1-\alpha \le \mathit{Pr}[d(T,B_U)\le 0] \\ \Rightarrow \alpha \ge 1-\mathit{Pr}[d(T,B_U)\le 0] \\ \Rightarrow \alpha \ge \mathit{Pr}[T(2B_U-1)>0] \\ \Rightarrow \alpha \ge \mathit{Pr}[B_U>0.5] \\ \Rightarrow \alpha \ge \mathit{Pr}[B_U\ge 0.5]=p_U(m,n). \end{gathered}$$

where the last step comes because B_U is continuous unless it is a point mass at 1.

Proof for the lower limit is analogous and is not given.

Now we prove the compatibility in the central case. Let the central confidence interval be given by

$$C_{\text{Δ}}(1-\alpha )=\{L_{\text{Δ}}(1-\alpha /2),U_{\text{Δ}}(1-\alpha /2)\}.$$

Step 1, show $p_C\le \alpha \Rightarrow 0\notin C_{\text{Δ}}(1-\alpha ):$ Since α < 1,

$$\begin{gathered} p_C\le \alpha \Rightarrow \min \left(2p_L,2p_U\right) \\ \Rightarrow \text{either}\{\begin{array}{c}\text{Case}1:p_L\le \alpha /2,\text{or}\hfill \\ \text{Case}1:p_U\le \alpha /2.\hfill \end{array} \end{gathered}$$

Case 1 implies that $L_{\text{Δ}}(1-\alpha /2)>0$ by the compatibility of L_Δ with p_L, and that implies that $0\notin C_{\text{Δ}}(1-\alpha )$ by the definition of $C_{\text{Δ}}(1-\alpha )$. Analogously, Case 2 implies that $U_{\text{Δ}}(1-\alpha /2)<0$ by the compatibility of U_Δ with p_L, and that implies that $0\notin C_{\text{Δ}}(1-\alpha )$ by the definition of $C_{\text{Δ}}(1-\alpha )$.

Step 2, show $0\notin C_{\text{Δ}}(1-\alpha )\Rightarrow p_C\le \alpha$: The statement $0\notin C_{\text{Δ}}(1-\alpha )$ implies either Case 1: $L_{\text{Δ}}(1-\alpha /2)>0$ or Case 2: $U_{\text{Δ}}(1-\alpha /2)<0$. So by the definition of C_Δ and the compatibility of the one-sided intervals, we have either Case 1: $p_L\le \alpha /2$ or Case 2: p_U ≤ α/2, which means that $p_C=\min (1,2p_L,2p_U)\le \alpha$.

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.