Abstract
In [Fogelson and Keener, Phys. Rev. E, 81 (2010), 051922], we introduced a kinetic model of fibrin polymerization during blood clotting that captured salient experimental observations about how the gel branching structure depends on the conditions under which the polymerization occurs. Our analysis there used a moment-based approach that is valid only before the finite time blow-up that indicates formation of a gel. Here, we extend our analyses of the model to include both pre-gel and post-gel dynamics using the PDE-based framework we introduced in [Fogelson and Keener, SIAM J. Appl. Math., 75 (2015), pp. 1346–1368]. We also extend the model to include spatial heterogeneity and spatial transport processes. Studies of the behavior of the model reveal different spatial-temporal dynamics as the time scales of the key processes of branch formation, monomer introduction, and diffusion are varied.
Keywords: kinetic gelation, blood clotting, fibrin branching, gel front, generating function, polymer diffusion
AMS subject classifications. 92C05, 92C45, 82C26, 82D60
1. INTRODUCTION.
The formation of a fibrin gel, or fibrin clot, is an important component of the blood clotting process; it complements the other major part of the clotting process, platelet aggregation [11]. Together, clumps of platelets and a fibrin mesh between and around the platelets constitute the bulk of many blood clots. The structure of the fibrin clot (branch points per unit volume, fiber thickness, pore sizes, etc.) is sensitive to the conditions under which the gel is formed. Both the mechanical properties of the clot and the efficacy of clot degradation by the fibrinolytic system [21] are very sensitive to its structure. Variations in clot structure are correlated with bleeding or thrombotic disorders [6, 8, 24].
Fibrin clots are assembled from fibrin protofibrils which are in turn composed of fibrin monomers produced by the action of the enzyme thrombin on the plasma protein fibrinogen (as reviewed [23]). Briefly, fibrinogen is an elongated, trinodular molecule with a central E region connected by coiled-coil chains to two D regions. As illustrated in Fig. 1, a fibrin monomer is produced when thrombin cleaves two short protein fragments, called fibrinopeptides, from the E region on fibrinogen. This uncovers two “A” sites, each of which can bind to a constitutively-exposed complementary “a” site in the D region of another fibrin(ogen) molecule. Through this binding process, fibrin monomers spontaneously polymerize into long double-stranded protofibrils that are half-staggered through middle to end binding. When sufficiently long, the double-stranded protofibrils can bind side by side to form thicker fibers in a process known as lateral assembly. Somewhere during the formation of a protofibril and/or during lateral assembly branches form and, eventually, a three-dimensional fibrin gel results.
Fig. 1:
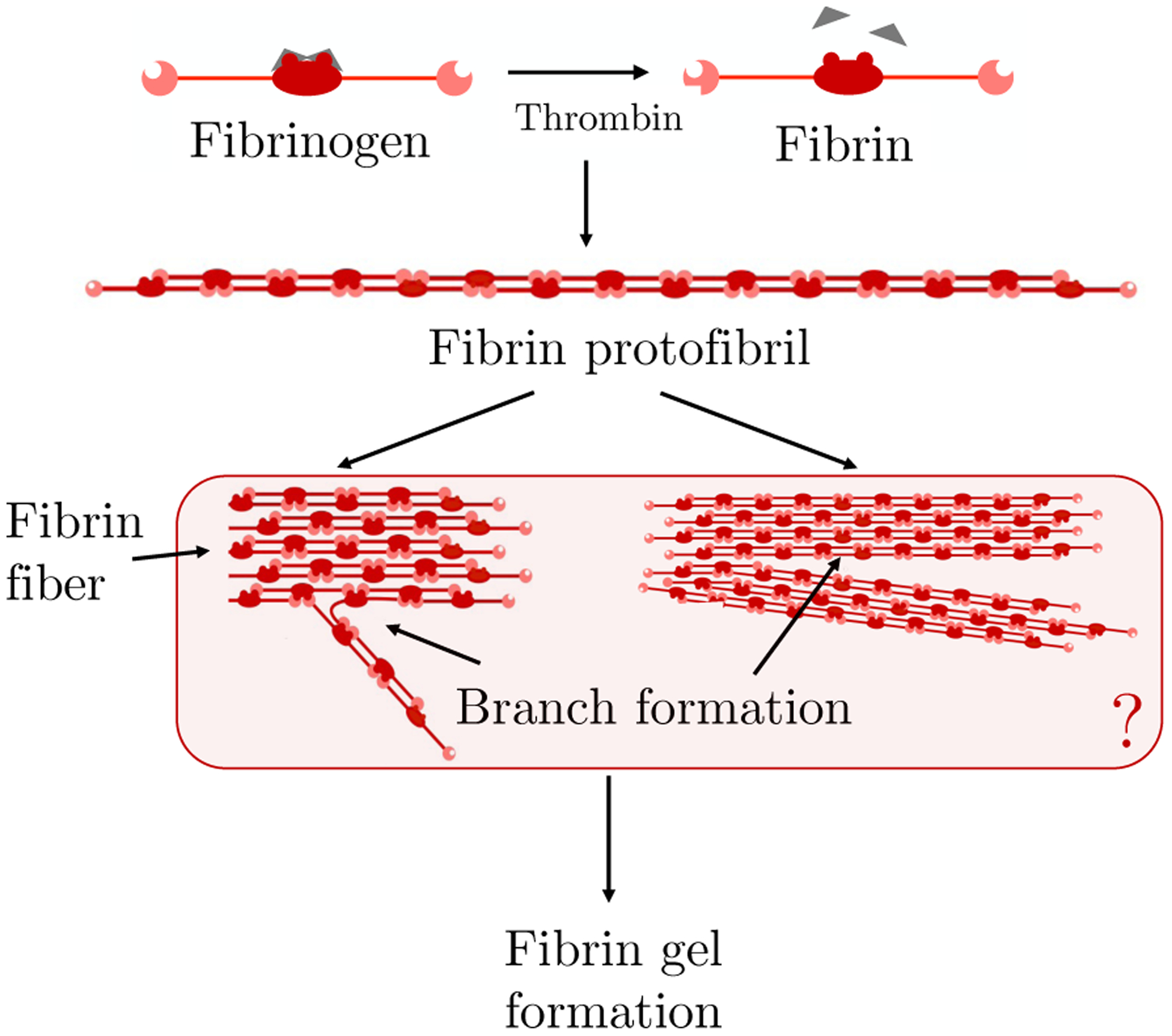
Schematic of fibrin polymerization showing thrombin-mediated fibrinopeptide release (top), protofibril formation (middle), and hypothesized [23] modes of branch formation (bottom).
The fibrin branching is not well understood. There is no specific molecule responsible for nucleating branch formation; in fact, a three dimensional gel can develop in vitro in a solution in which the only proteins present are fibrinogen and thrombin [20]. Experimental results indicate that the thrombin concentration strongly influences the structure of the gel that forms [1, 20]. High thrombin concentrations result in “fine” clots, with relatively thin fibers, a high volume density of branch points, and small pore size. Low thrombin concentrations produce “coarse” clots: thicker fibers, lower branch point density, and larger pores [20]. During clotting in vivo, thrombin is produced on the surfaces of platelets in the platelet aggregates and is then released into the surrounding fluid where it can convert fibrinogen to fibrin monomers. In in vitro studies in which thrombin is produced by reactions on cellular surfaces [2, 3, 21], the structure of the resulting fibrin clots varies with distance from the cell surfaces. A fine gel is seen close to the surfaces and a coarser gel more distally, consistent with the expected drop in thrombin concentration with distance from the cells on which it is made. Studies of the early stages of fibrin polymerization [1, 4, 5] suggest that much, but not all, of the final gel architecture (branch point density and pore size) is determined by the time of gelation, and that most fiber thickening occurs later.
One of the factors that influences the structure of a fibrin clot is the concentration of thrombin which, as described above, converts molecules of fibrinogen into fibrin monomers, and does so at a rate that depends on the thrombin concentration. Hence the thrombin concentration influences the rate of fibrin monomer supply during fibrin polymerization and gelation. In this paper, we do not explicitly include thrombin, and instead we use variations in the specified rate of supply of fibrin monomers as a surrogate for variations in thrombin concentration. The model we presented in [9] provided a plausible mechanism of fibrin branch formation and showed that it could account for sensitivity of the resulting gel to the rate of monomer supply (i.e., to the concentration of thrombin in the system) as seen experimentally. Using a small set of ordinary differential equations (ODEs) for moments of the polymer distribution, we studied the behavior of the model up to the time that a gel formed. Gel formation in the model corresponds to a finite time blow-up of a second moment of the oligomer size and structure distribution functions (concentrations). The ODE model in [9] does not hold after a gel forms. In the context of a simpler kinetic model of polymerization (discussed below) studied by Ziff and Stell [26], we provided a framework for extending polymerization studies past gel time [10]. In the current paper, we extend that framework to our fibrin branching model in order to study its behaviors both before and after gel formation occurs. Other kinetic models have been developed to study fibrin polymerization [13, 19, 22], but they do not account for branch formation.
Ziff and Stell [26] studied a kinetic polymerization model with gelation which tracks concentrations ck of k-mers made from k identical monomers each with f functional units or binding sites. Binding reactions between functional sites on different molecules lead to formation of larger polymers, with the restriction that no loop formation is allowed. In the Ziff–Stell model, gelation is guaranteed to occur for any nonzero initial concentration of monomers only if the number of functional sites per monomer f > 2. In our model of fibrin polymerization [9], we track concentrations cmb of clusters with b branches and comprised of m + 2b monomers. The model allows two types of reactions: bimolecular “linking” reactions lead to oligomer elongation and trimolecular “branching” reactions result in new branch formation. Monomers in our model have f = 2 functional sites, and so gelation is possible only because of branching reactions which result in clusters with three or more functional sites. As reactions proceed, the average number of functional sites per oligomer, which we refer to as fA, evolves at a rate determined by the relative numbers of linking and branching reactions that occur. The time required for a gel to form depends on the relative numbers of these two types of reactions, and the resulting gel structure is sensitive to the rate at which monomers are supplied to the system (a surrogate for the thrombin concentration). In [9] we looked only at well-mixed systems from the start of polymerization until a gel formed.
In the current paper, we look also at how polymerization proceeds after the gel has formed. To extend our model [9] beyond the gel time, we must make assumptions about the types of reactions in which the gel can participate. In their analysis, Ziff and Stell [26] considered three distinct post-gelation scenarios in which (i) reactive sites in the gel do not react at all; (ii) reactive sites in the gel react with other reactive sites on the gel as well as those on finite-size oligomers; or (iii) reactive sites on the gel react only with sites on finite-sized oligomers. In this paper, we present results only for the third scenario because only it produces results that agree with those from stochastic simulations involving large numbers of fibrin monomers (also see [10]).
We also investigate the effects of spatial heterogenity and diffusive transport on the evolution of the fibrin gel structure, because conversion of fibrinogen depends on the concentration of thrombin, which itself is likely to be spatially heterogeneous. Because thrombin production is localized to activated platelet surfaces, and, when released into the plasma, can be rapidly inactivated by antithrombin and other inhibitors [7] its concentration is likely to be large only near the activated platelets on which it is produced. Similarly, in some in vitro experiments thrombin is produced by reactions on cellular surfaces and then released [2, 3, 21]. In both situations, conversion of fibrinogen to fibrin is believed to occur predominantly in the neighborhood of the cells on which thrombin is made. These situations therefore correspond to the spatially localized sources of fibrin that we explore in this paper.
2. FIBRIN POLYMERIZATION MODEL.
2.1. Basic Model.
As in [9], we regard a fibrin monomer as a long, linear molecule comprised of two half-monomer domains denoted S (see Fig. 2). The monomer has two kinds of binding sites, those at its ends (depicted by a square) and those in the middle (depicted by a circle), so each half-monomer has one of each type of binding sites. A circle of one molecule can bind to a square of another molecule and this allows for staggered polymerization. Because of the staggering, a linear polymer always has two free ends, each of which consists of the half-monomer S. We refer to such a free end as an active site. Two distinct bonds have to form for linear polymerization, end to middle and middle to end. We do not consider the intermediate state (denoted by Z in Fig. 2a) in which one bond has formed, but instead only the overall process of linear polymerization which we assume occurs at rate kl[S]2, see Fig. 2a. We call this process “link formation”. Fibrin linear polymerization is a two step process, so the possibility exists that the second step is prevented by binding with other free ends, creating a structure we refer to as a branch (see Fig. 2b). Again we consider only the overall reaction of “branch formation”, which we assume occurs at rate kb[S]3.
Fig. 2:
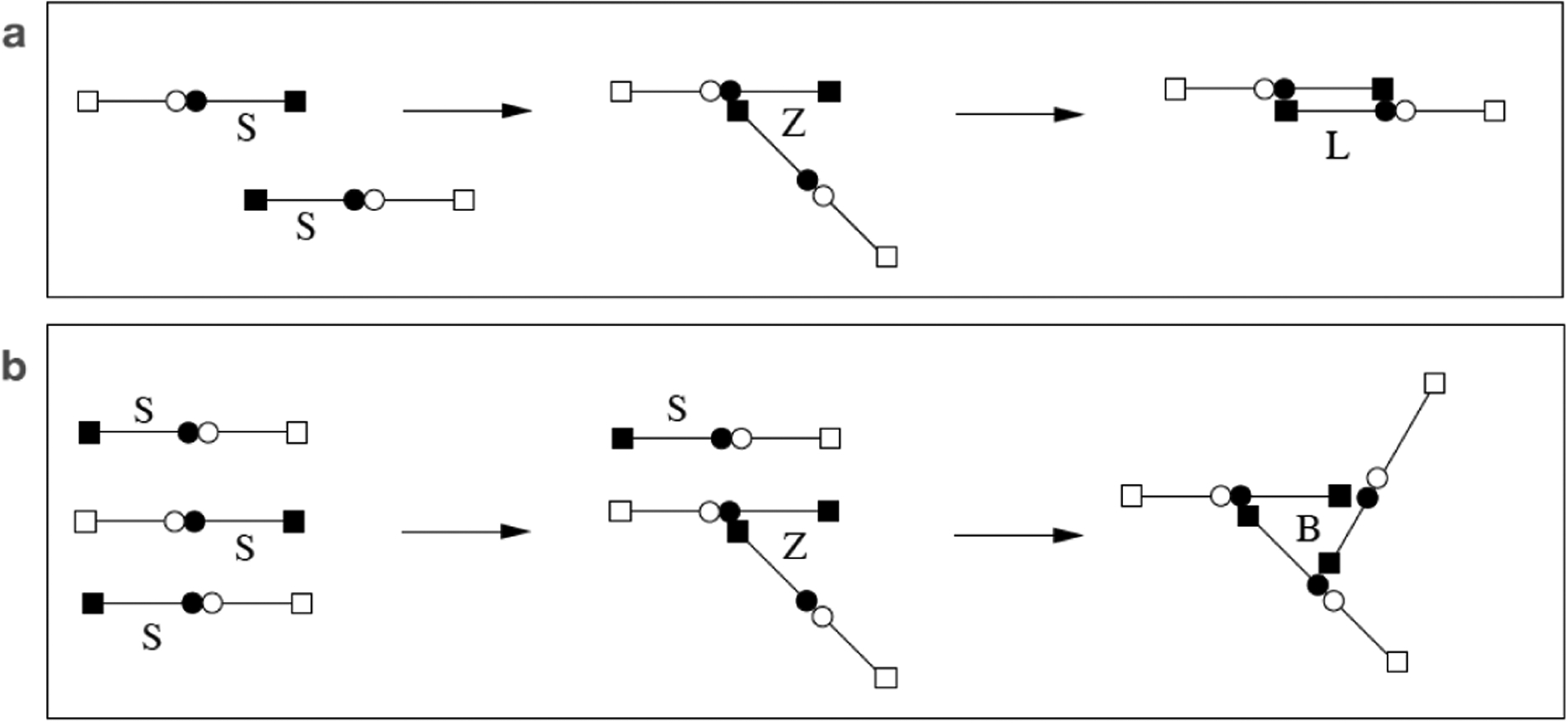
(a) Linear polymerization to form a link. (b) Branch formation.
With linear polymerization and branch formation as the only two possible reactions, we examine the formation of clusters. We describe a cluster using two indices, m and b, where b is the number of branch points, and m + 2b is the total number of monomers in the cluster. We denote such a cluster by Cmb and its concentration at location x at time t by cmb(x, t). With this notation, a single monomer has m = 1, b = 0, and a simple branch (shown in Fig. 2b) has m = 1, b = 1.
We allow two types of reactions between clusters. The first is the combination of two clusters to form a new link
| (2.1) |
and the second is the formation of a new branch point by a trimolecular reaction combining three active sites
| (2.2) |
For mathematical tractability, we also assume that there are no self interactions between the active sites in a single cluster, i.e., no loops, so that the number of active sites in a cluster is b + 2.
In [9], we assumed that the dynamics of the cluster concentrations cmb, m = 1, 2,…, b = 0, 1, 2…, were described by the system of ordinary differential equations
| (2.3) |
The first two terms on the right hand side of Eq. 2.3 describe the bimolecular reactions and use reaction rates that are the same as used by Ziff and Stell [26]. The next two terms describe the trimolecular reactions and are based on the same fundamental principle. These rates follow the law of mass action when reacting clusters are all different, but deviate from it when two or more of the reacting clusters are the same. The final term Smb in the equation represents the source of clusters of type m, b. Below, we make the assumption that only S10 may be nonzero.
2.2. Up to Gel Time.
In [9], we generalized an idea of Ziff and Stell in introducing a generating function
and used Eqs. 2.3 to derive a single nonlinear partial differential equation for g:
| (2.5) |
where Rs(t) is defined below and . Since we allow only S10 to be nonzero, P(t, y, z) = yz2S10(t). Quantities of interest can be expressed in terms of the distribution of oligomers {cmb(t)}:
| (2.6) |
| (2.7) |
| (2.8) |
(In [9], we referred to these as R, B, and M, respectively.) We refer to finite-sized oligomers that are in the solution phase as “sol” and denote sol quantities with subscript “s”. Rs, Bs, and θs are the concentration of available reaction sites, the concentration of branches, and the total concentration of monomers in the sol. Analogous quantities in the gel are denoted with subscript “g”. We define the average number of monomers in an oligomer, which we call the average cluster size, as
| (2.9) |
Gelation occurs if As(t) → ∞ at a finite time tgel. Each of the quantities of interest can be expressed in terms of low-order moments of the oligomer distribution,
for j ≤ 2 and k ≤ 2. Using Eq. 2.5, we derived ODEs for these moments and from those we derived ODEs for the quantities of interest.
| (2.10) |
| (2.11) |
| (2.12) |
| (2.13) |
| (2.14) |
where a = kl + kbRs. The function U has initial values U(0) = 1 and . It was derived from an expression related to As by a Riccati transformation [9], (specifically ) and provides a convenient indicator of gelation because U → 0 as t → tgel if and only if As(t) → ∞ as t → tgel. The moment M00(t), which gives the total concentration of all molecules, is also of interest because fA(t) = Rs(t)/M00(t) is the average number of available reaction sites per molecule at time t. M00 satisfies the ODE
| (2.15) |
For use in discussing post-gel dynamics, we introduce quantities R, B, and θ, which are the total reactive site concentration, total branch concentration, and total mass density, and we define Rg = R − Rs, Bg = B − Bs, and θg = θ − θs. These are the reaction site concentration, branch point concentration, and mass density of the gel. Equations for these quantities are derived below.
In [9], we showed that for any positive initial quantity of monomer c10(0) > 0 or any positive constant source of monomer S10 > 0, As(t) → ∞ at a finite time tgel we refer to as the gel time. By solving Eqs. 2.10–2.14, we studied the development of the average oligomer size and branch concentration up to gel time and characterized the dependence of these quantities at that time on the rate of supply of monomer. The gel time itself depends on the size of the initial monomer concentration and/or the rate of monomer supply, as well as on the rate constant kb. We showed that the branch concentration at tgel is significantly affected by the rate of monomer supply.
To facilitate our discussions below, we use Rs to rewrite Eqs. 2.3 as
| (2.16) |
and, for convenience, we repeat the ODE for Rs here,
| (2.17) |
Eqs. 2.16 and 2.17 form a closed system, but they hold only until gel time.
2.3. Beyond Gel Time.
2.3.1. Modified dynamics.
To go beyond tgel, we must postulate the post-gel dynamics. Our assumption in this paper is that gel reactive sites can react with those on finite-sized oligomers but not with other gel reactive sites as in the third scenario considered by Ziff and Stell [26]. This is consistent with the assumption underlying Eqs. 2.16 that formation of cycles is not permitted. To implement this assumption, we first modify Eqs. 2.16–2.17 by replacing each occurence of Rs by the total concentration of reactive sites R. Then, we subtract terms that describe interactions involving two or more reaction sites on the gel. Since R = Rs + Rg, we note that and . The expressions and arise from reactions between pairs or triplets of gel reactive sites, respectively, and so we remove them from the equations. Specifically, we modify Eq. 2.16 by replacing Rs by R in the second term and by replacing by in the fourth term on the right hand side. We modify Eq. 2.17 by replacing by and by .
We also extend the model by allowing oligomer and gel concentrations to vary in space (x), and finite-sized oligomers, but not gel, to move. In this paper we consider only diffusive movement, but it is straightforward to also include advective motion of oligomers as we did in [25]. Taking into account our assumptions about post-gelation reactions and diffusive movement of oligomers, the equations for cmb(x, t) and R(x, t) are the infinite set of partial differential equations
| (2.18) |
and
| (2.19) |
and we assume that they hold for all t ≥ 0 and for x in a specified domain with boundary conditions discussed below. Until the time a gel forms, R = Rs and Rg = 0, and these equations represent a spatial extension of Eqs. 2.16–2.17. After a gel forms, and Rg(x, t) = R(x, t) − Rs(x, t).
2.3.2. Reformulation using generating function.
To study Eqs. 2.18–2.19 before and after gel time, we again introduce a generating function
| (2.20) |
and find that
| (2.21) |
In these equations, z and y are “dummy” variables from the generating function, they do not refer to the spatial coordinates which are denoted x. In the derivation of Eq. 2.21, we made use of the assumptions that all oligomers have the same diffusion coefficient D. It is not possible, in general, to reduce equations 2.18 to a single PDE for g if the oligomer diffusivities depend on the oligomer size and structure, i.e., if D is replaced by Dmb in 2.18. However, it is straightforward to allow a finite-number of oligomer species to have larger diffusion coefficients than other oligomers. If this is done for monomers only, then we must solve a separate PDE for the monomer concentration as well as make a small modification to the equation for g above. For details, see Supplement section S1.2 and [10]. Further discussion of our assumptions in modeling oligomer diffusion is given in Section 4.
Following its successful use by Ziff and Stell [26], we make the change of variables
| (2.22) |
It follows from the PDEs for g and R that satisfies the equation
| (2.23) |
This equation describes diffusion of a quantity related to with respect to the spatial variable x and “transport” of in the variable z with flux function . Because of the presence of in the diffusion term, the equation for is nonlocal in the variable z.
As we show below, to calculate the quantities of interest to us requires and . To obtain an evolution equation for W, we simply set y = 1 in Eq. 2.23. To obtain an evolution equation for V, we use Eq. 2.23 to derive a PDE for and then set y = 1 in that PDE. The resulting equations are
| (2.24) |
| (2.25) |
The concentration of reactive sites in the gel, Rg(x, t), can be obtained from W, in fact,
| (2.26) |
To see this, note that Rg = R − Rs, , and W|z=1 = R − gz|y=1,z=1 = R − Rs. Hence, using Eq. 2.26, we see that Eqs. 2.19 and 2.24–2.25 form a closed system. Values of V are used to calculate quantities of interest (see below) but do not affect the dynamics of W and R.
2.3.3. Other Physical Quantities.
Recall that the sol mass density, branch concentration, reactive site concentration, and total concentration of oligomers are , , , and , respectively. These can be expressed in terms of W(x, t, z) and V (x, t, z):
| (2.27) |
| (2.28) |
| (2.29) |
and
| (2.30) |
The first three of these relations are derived in Supplement section S1.1, and the fourth follows immediately from the definitions of the quantities involved. θg and Bg can be computed from Eqs. 2.27–2.29 and the total mass density θ and branch concentration B as θg(x, t) = θ(x, t) − θs(x, t) and Bg(x, t) = B(x, t) − Bs(x, t) provided we know θ and B. To determine them, we solve the PDEs
| (2.31) |
| (2.32) |
Eq. 2.31 follows from the facts that in the domain interior, mass is produced only through the supply of monomers, and that the mass can be redistributed in space by diffusion of finite-size clusters. The rate of branch production in Eq. 2.32 is one third of the rate of disappearance of reactive sites when branches form (see Eq. 2.19) because three reactive sites disappear whenever a branch is formed. Like mass, branches can be redistributed in space by the diffusion of branches on finite-sized clusters.
2.3.4. Boundary Conditions.
When we consider the PDE model, Eqs. 2.19, 2.24–2.29, and 2.31–2.32, in a bounded region Ω, we require boundary conditions. We restrict ourselves to situations in which monomer is produced at the rate F10(x, t) at a point x ∈ ∂Ω. The boundary conditions for cmb are
| (2.33) |
where n is the unit normal pointing into Ω at x. In Supplement section S1.4, we use Eq. 2.33 to derive boundary conditions for R, W, V, θs, and Bs, valid for any F10(x, t), but in the results of this paper, we consider only F10(x, t) = 0, and give the corresponding boundary conditions here.
| (2.34) |
| (2.35) |
| (2.36) |
In this paper, we consider the one dimensional domain Ω = −L ≤ x ≤ L, assume that D is constant, and we set F10(−L) = F10(L) = 0. To determine the monomer distribution c10, we also solve the m = 1, b = 0 instance of Eqs. 2.18 and 2.33.
3. RESULTS.
In this section we consider a series of computational “experiments” in which we solve the equations of the model under various conditions to explore its behavior. As in [9], we nondimensionalize our variables by scaling all concentrations using a typical concentration C0, scaling time by (C0kl)−1, and defining nondimensional monomer supply rate and branching rate as and kbC0/kl, respectively. We use the numerical method sketched in section S1.5 in the Supplement and described in more detail in [10] except when we solve the moment equations Eq. 2.10–2.14, in which case we use Matlab’s ode23 ODE solver.
3.1. Spatially-uniform initial monomer distribution.
Consider a spatially-uniform initial monomer concentration with no source or boundary flux. In this example, we omit reference to the spatial variable x. The corresponding initial conditions are W(0, z) = 0, , , and B(0) = Bs(0) = 0. Fig. 3a shows curves of W as a function of z ∈ [0, 1) at several times before and after gelation, in red and blue respectively. Before gel time, the curves steepen towards z = 1 as time progresses. Gelation occurs when Wz(t, 1−) → −∞. After that time, W(t, 1) > 0 and, in this simulation, W(t, 1) = Rg(t) continues to grow with time (Fig. 3b) until no finite size oligomers remain (not shown). Fig. 3cd show the time dependence of quantities (c10, Rs, θs, and Bs) associated with finite-size oligomers and quantities (Rg, Bg, and θg) associated with gel. Early in the simulation, monomers combine to produce oligomers, which combine with other oligomers or monomers to produce larger oligomers, so c10 steadily decreases and θs − c10 grows. Reactive sites are “consumed” during each interaction, so Rs decreases. Some of the interactions result in branch formation and Bs increases. Beginning at tgel, θs and Bs suddenly start to decrease and Rs decreases at a faster rate than earlier, as sol mass, branches, and reactive sites become incorporated into the growing gel. The solution curves in Fig. 3c match those of the ODE system Eqs. 2.10–2.14, studied in [9], up to tgel, but it is not possible to solve Eqs. 2.10–2.14 past tgel when Rg, θg, and Bg start to grow from zero, and kinks appear in θs, Bs, and Rs. Note that Bg(t) = Rg(t) for all t, as shown in Supplement section S1.3.
Fig. 3:
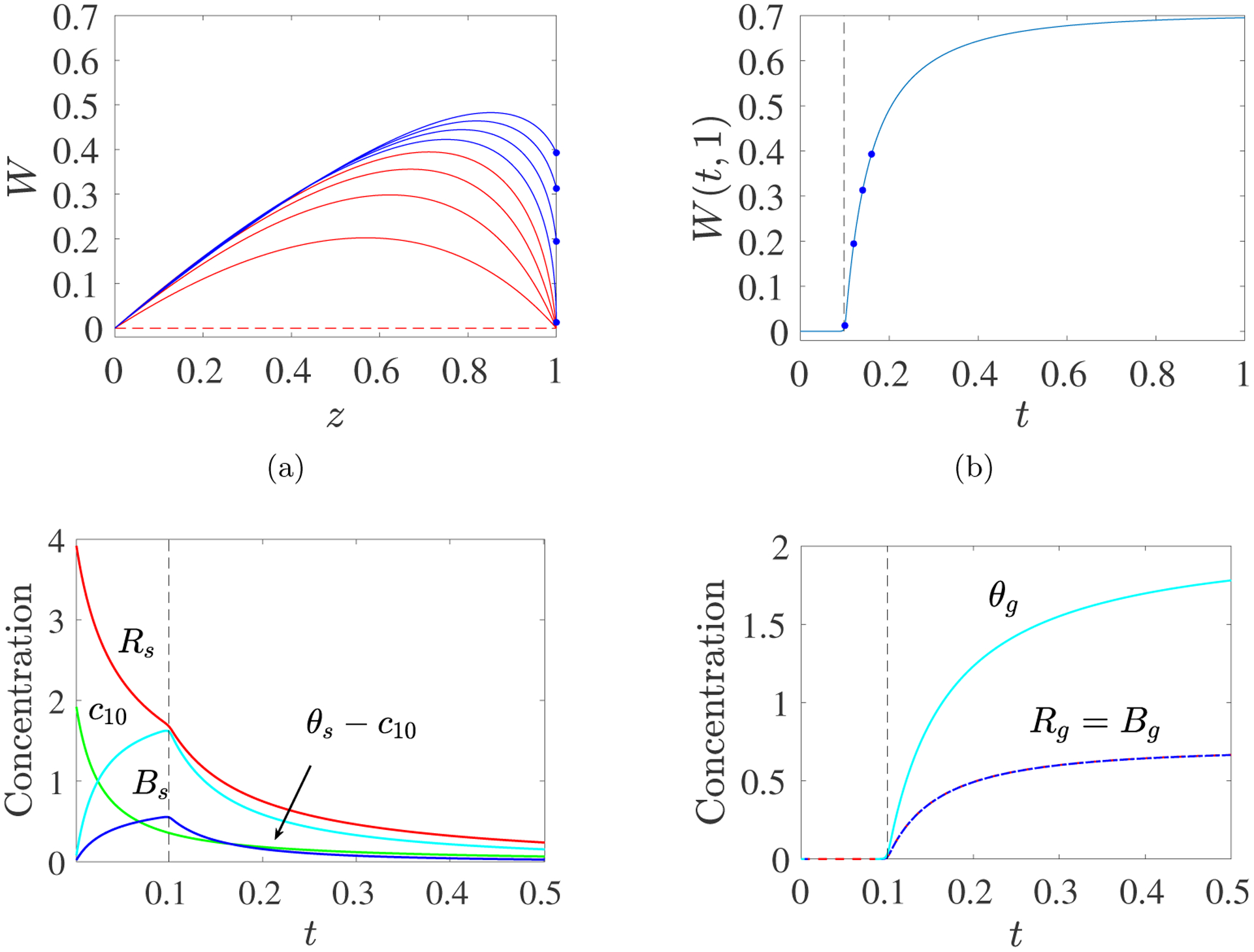
PDE Model with Spatially-uniform Initial Monomer Concentration: c10(0) = 2, kl = 1, kb = 2. (a) Time snapshots of profiles W(t, z) vs z. The curves move upward with time and are colored red before gel time and blue afterward. Values of W(t, 1) for t > tgel are shown with dots. (b) Plot of W(t, 1) vs t. Dots show (t, W(t, 1)) values corresponding to the dots in panel (a). (c) Time dependence of the concentrations of monomer c10, sol reactive sites Rs, sol branches Bs, and mass in finite size oligomers larger than monomers θs − c10. (d) Time dependence of the concentrations of gel reactive sites Rg, gel branches Bg, and gel mass θg. Note different concentration scales in panels (c) and (d). Dashed black line indicates gel time.
3.2. Spatially-uniform constant rate monomer source.
Next, we assume that there is no monomer initially and that monomer is supplied uniformly in space at a constant rate S10. The results shown in Fig. 4 up to tgel, match those shown in Fig. 4 of [9], which were obtained by solving the system Eqs. 2.10–2.14.
Fig. 4:
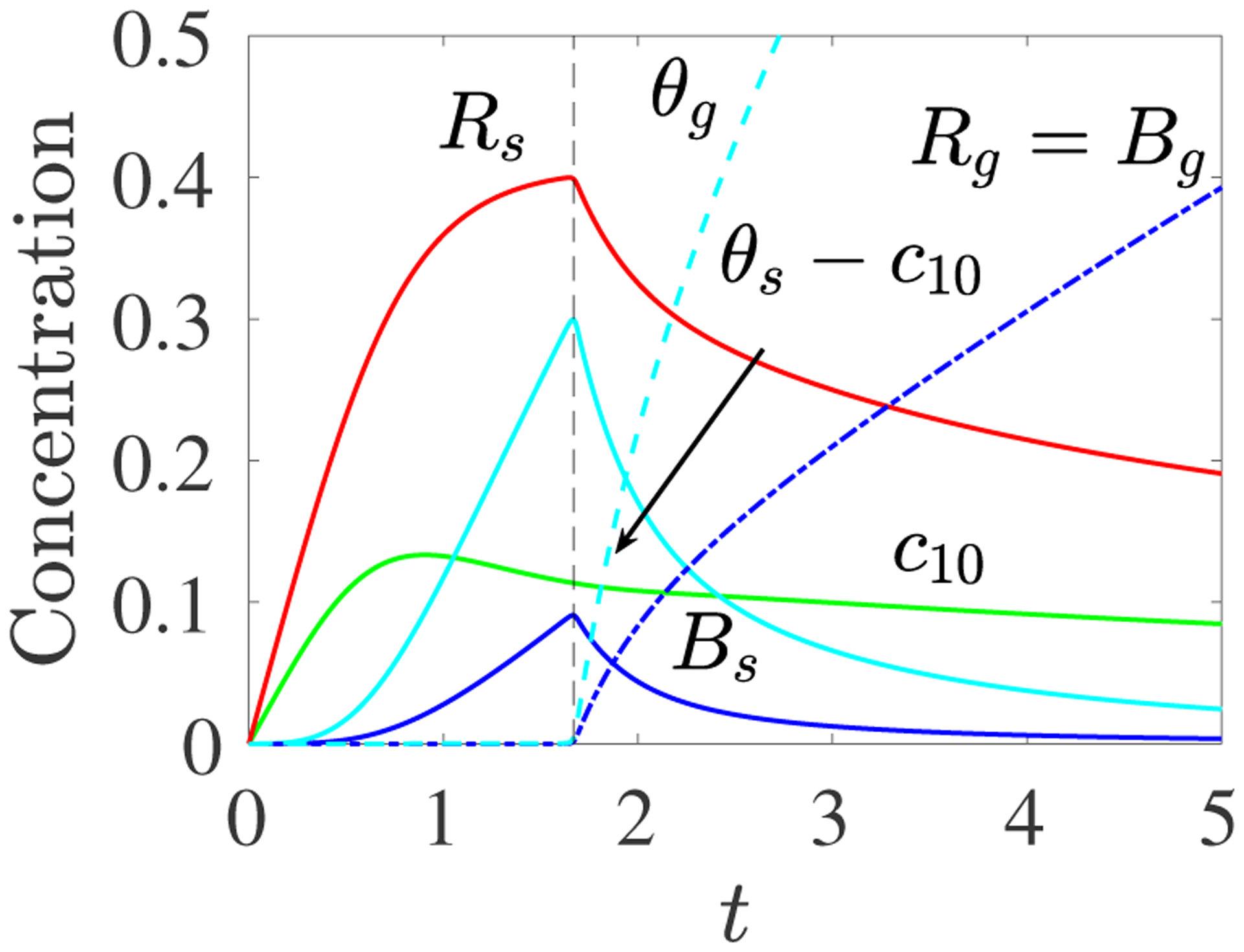
PDE Model with Spatially-uniform Monomer Source: c10(0) = 0, S10(t) = 0.25, kl = 1, kb = 10. Plots of c10(t) (green), Rs(t) (red), Bs(t) (blue), θs(t) − c10(t) (cyan), Rg(t) = Bg(t) (dashed red and blue) and θg(t) (dashed cyan).
To assess our assumptions about post-gelation reactions, we performed stochastic simulations of the reactions in Eqs. 2.1–2.2 in a volume v with no monomers initially and with monomers introduced at a constant average rate of S10v. Oligomers and form a link during an infinitesimal time interval dt with probability if (m1, b1) is different from (m2, b2), where nmb is the number of oligomers of type Cmb. If (m1, b1) and (m2, b2) are the same, the probability is . Oligomers , , and form a branch with probability if (m1, b1), (m2, b2) and (m3, b3) are distinct, with probability if (m1, b1) is the same as (m2, b2), but different from (m3, b3), and with probability if (m1, b1), (m2, b2), and (m3, b3) are the same. The larger the volume v, the more monomers the source introduces before substantial linking or branching reactions occur.
We implemented the simulation using the Gillespie alogorithm [12]. In the stochastic simulations, the average oligomer size cannot “blow up” because there are only a finite number of monomers in total. However, the average oligomer size and the size of the largest oligomer both begin to rise sharply starting at the gel time predicted by the deterministic PDE system, as shown in Fig. 5ab. Fig. 5c shows plots of R, B, θ, and c10 from the Gillespie (solid color curves) and PDE model (dashed black curves) simulations based on the assumption that gel reaction sites can bind with those on finite-sized oligomers, but not with other reaction sites on the gel. We see excellent agreement, which is similar to the behavior we saw with the Ziff–Stell gelation model [10]. To further compare dynamics after gelation, we partitioned each of R, B, and θ from the stochastic simulation into a part, denoted Rg, Bg, and θg, respectively, corresponding to the largest oligomer and a part corresponding to all of the smaller oligomers. Fig. 5d shows excellent agreement between these Rg, Bg and θg as well as Bs and θs − c10 and the corresponding PDE model variables from the simulation shown in Fig. 4. This suggests that regarding the gel in the PDE model as approximating the largest oligomer in a large finite system is reasonable.
Fig. 5:
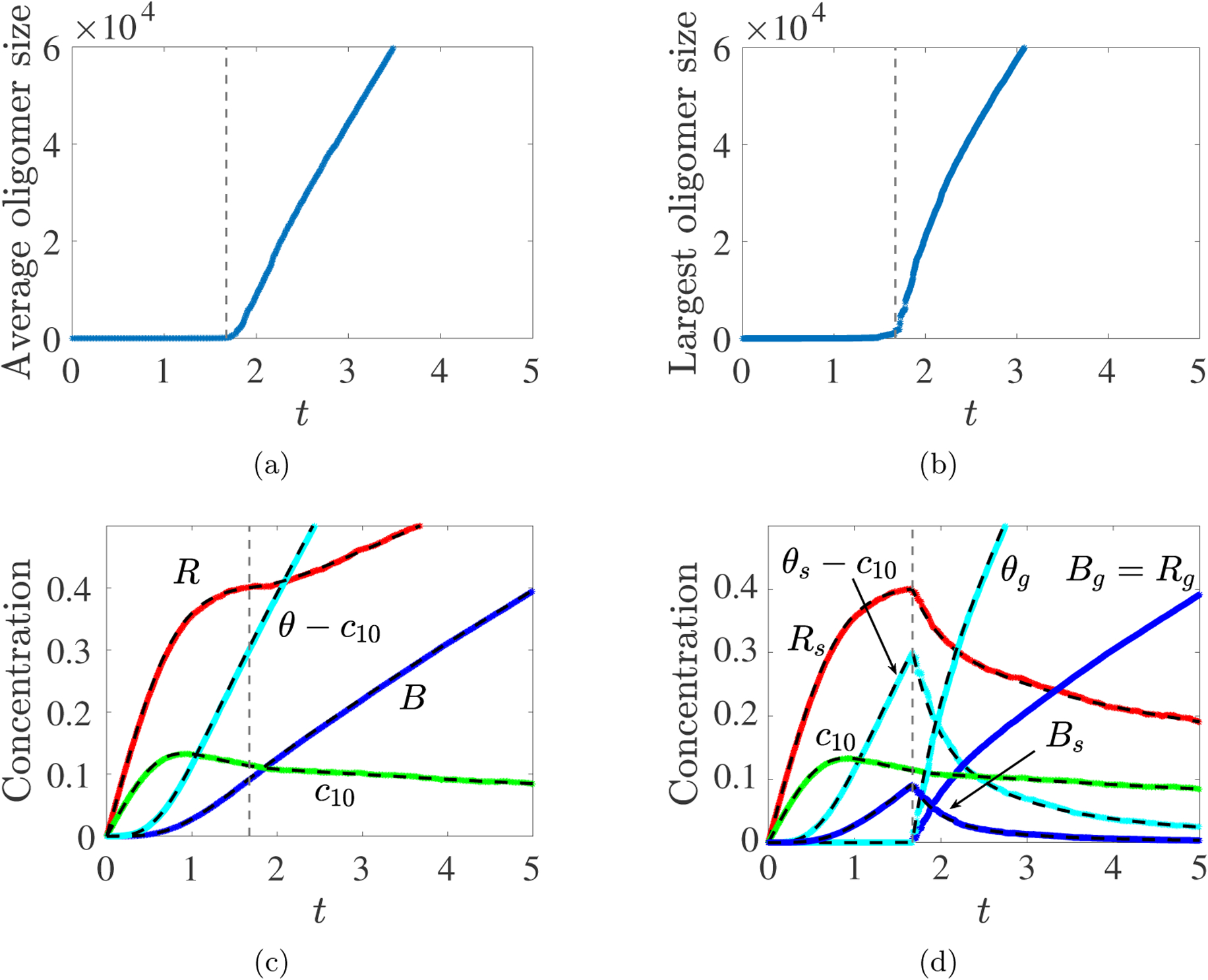
Gillespie Simulations. Rate constants kl = 1, kb = 10, source rate S10 = 0.25, and volume v = 105. (a) Average oligomer size vs. t, (b) Largest oligomer size vs. t, (c) R(t), B(t), θ(t) and c10(t) from Gillespie Simulation (colors) and ODE model (dashed black) show excellent agreement up to tgel. (d) After tgel, the mass density (θg), branch point density (Bg) and reaction site density (Rg) of the largest oligomer (colors) agree well with the corresponding gel variables (dashed black) from the PDE model.
This is support for the particular choice we made for post-gel kinetics as described in section 2.3.1.
3.3. Spatially-uniform time-varying monomer source.
In these simulations, the spatially-uniform, time-varying source of monomer is given by
| (3.1) |
This source is motivated by experiments in which fibrinogen and thrombin are put in solution at specified concentrations [20], and thrombin proteolytically converts fibrinogen to fibrin. The source term corresponds to that from conversion of fibrinogen to fibrin according to the linearized Michaelis–Menten equation
| (3.2) |
where G(t) is the fibrinogen concentration, G(0) = m0 is its initial value, E is the thrombin concentration, and kcat and KM are the catalytic rate constant and Michaelis–Menten constant for thrombin’s conversion of fibrinogen to fibrin. Setting λ = kcatE/KM gives the formula in Eq. 3.1.
We report on simulations run for a range of m0, λ, and kb values. Each simulation is run to a time tfinal by which 99% percent of the supplied monomer has been incorporated into the gel. Fig. 6 shows how tgel varies with the changes in m0, λ, and kb. For each m0 value, tgel is smallest when both λ and kb are large, and for fixed (λ, kb), tgel decreases with increasing m0. The observed gel times span up to 5 orders of magnitude moving from the lower left to upper right of a heatmap.
Fig. 6:
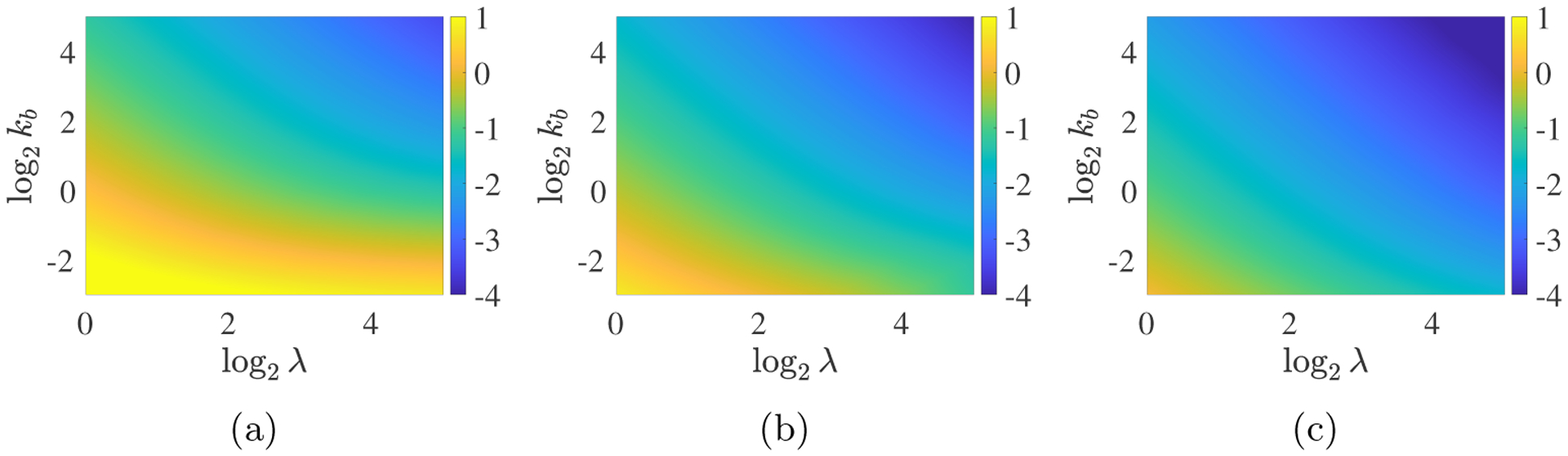
PDE Model – Gel time as a function of m0, λ, and kb with the spatially-uniform time-varying monomer source S10 = m0λ exp(−λt). The heatmaps show log10(tgel) as a function of log2(λ) and log2(kb). (a) m0 = 2, (b) m0 = 4, (c) m0 = 8.
For the same simulations, Fig. 7abc show parametric plots of the branch point density at the final time Bg(tfinal) versus that at gel time Bs(tgel), as λ and kb are varied for a fixed value of m0 (the lowest point on each curve corresponds to the smallest kb). Several features of these plots noteworthy. For each m0, Bs(tgel) is monotone increasing in λ, but non-monotone in kb, while Bg(tfinal) is monotone increasing in both λ and kb. For given m0 and λ values, two different kb values can yield very similar values of Bs(tgel) and very different values of Bg(tfinal). In many cases, one of these Bg(tfinal) values is only a little greater and the other is much greater than Bs(tgel). The heatmaps of the ratio Bs(tgel)/Bg(tfinal) in Fig. 7def show this more clearly. For each m0, there is a range of λ and kb values for which Bs(tgel) is at least 80% of Bg(tfinal), in agreement with recent experimental results [4, 5]. These λ and kb values seem to satisfy a condition log2 kb/log2 λ ≤ f(m0), where f(m0) decreases with m0. Hence, our model can capture this important experimental observation, but only in certain parameter value ranges.
Fig. 7:
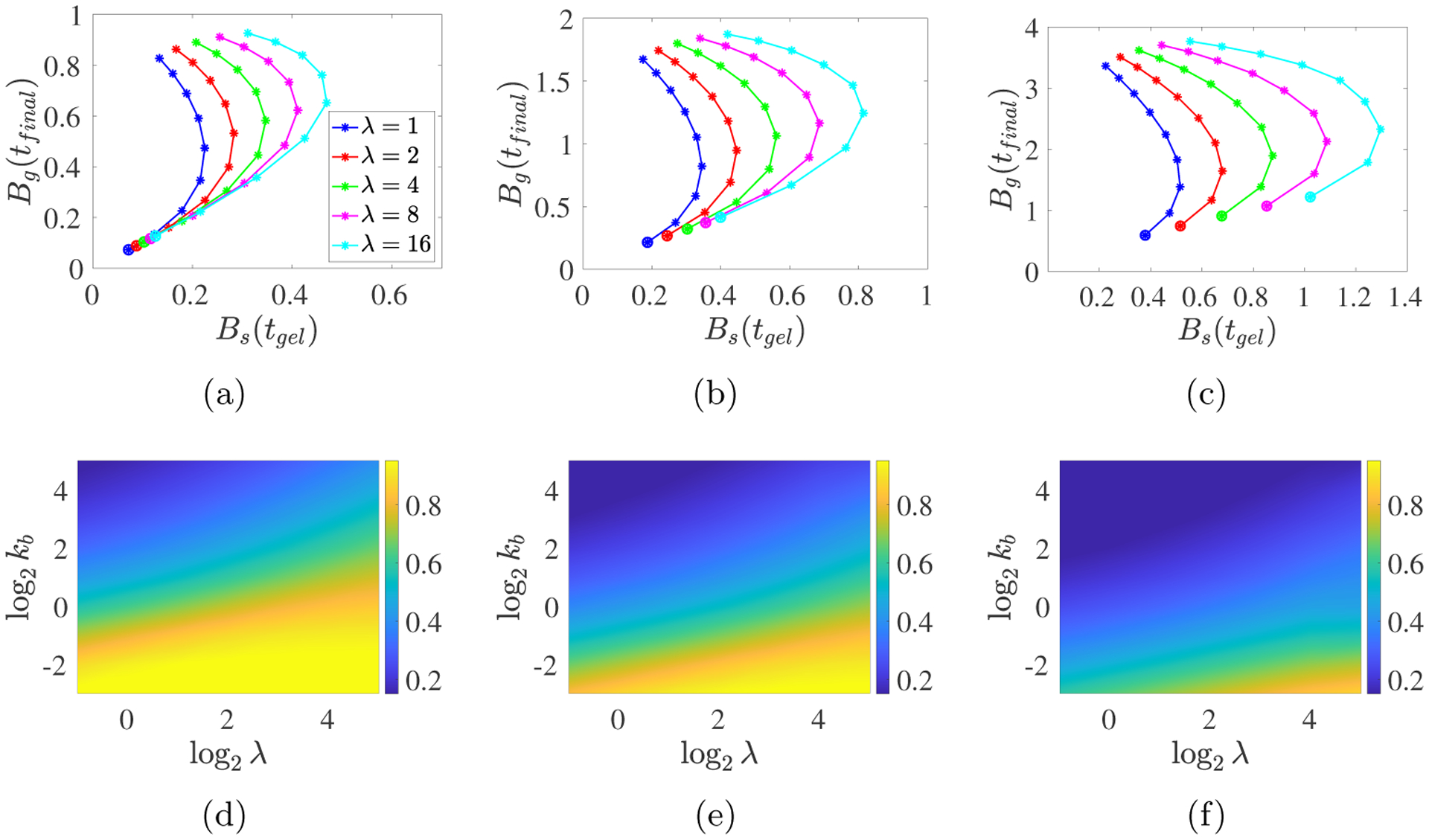
PDE model simulations with a spatially-uniform time-varying monomer source S10 = m0λ exp(−λt) for (a,d) m0 = 2, (b,e) m0 = 4, and (c,f) m0 = 8. (a-c) Each curve corresponds to a specific λ value as indicated in the legend, and the points along each curve are for the different kb values with the large dots indicating kb = 1/8 and the kb values increasing from that point to kb = 32 at the other end of the curve. Note the different vertical scales. (d-f) The heatmaps show Bs(tgel)/Bg(tfinal).
The curves in Fig. 8 show how tgel and Bs(tgel) vary with kb, for five values of λ. Unsurprisingly, tgel decreases and Bs(tgel) increases as λ increases. The gel time also decreases as kb increases (moving from right to left along each curve), but strikingly, there is a peak in Bs(tgel) for an intermediate value of kb close to 1 for each λ and m0 value. In Fig. 9 we look at time course data to understand how these behaviors arise.
Fig. 8:
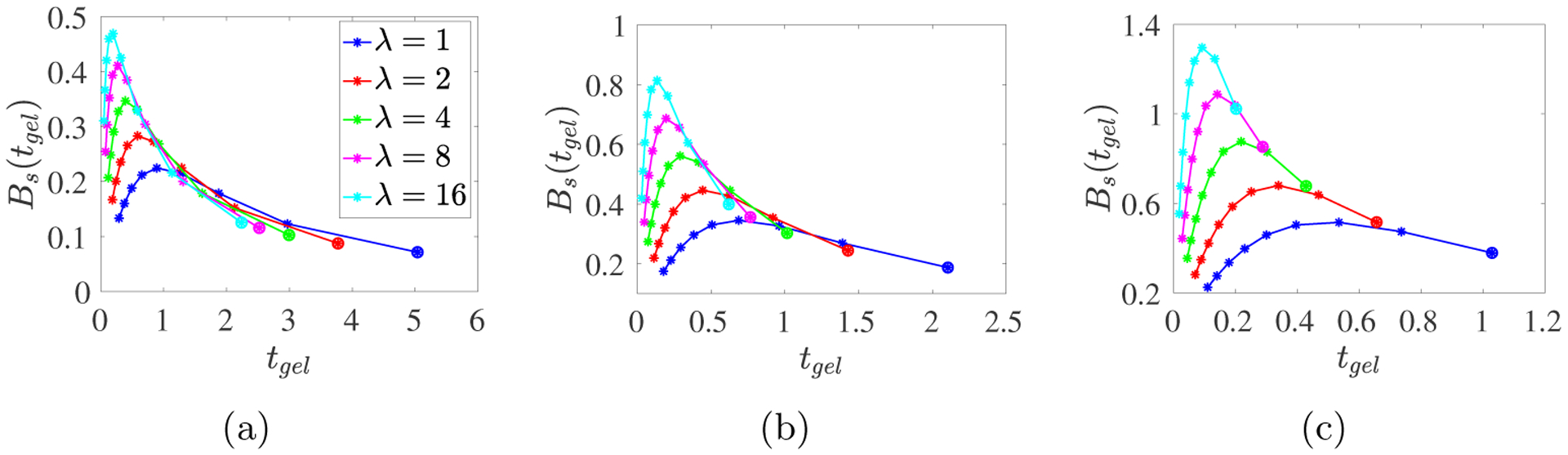
PDE model simulations with a spatially-uniform time-varying monomer source S10 = m0λ exp(−λt) for (a) m0 = 2, (b) m0 = 4, and (c) m0 = 8. Each curve corresponds to a specific λ value as indicated in the legend, and the points along each curve are for the different kb values with the large dot indicating kb = 1/8 and the kb values increasing from that point to kb = 32 at the other end of the curve.
Fig. 9:
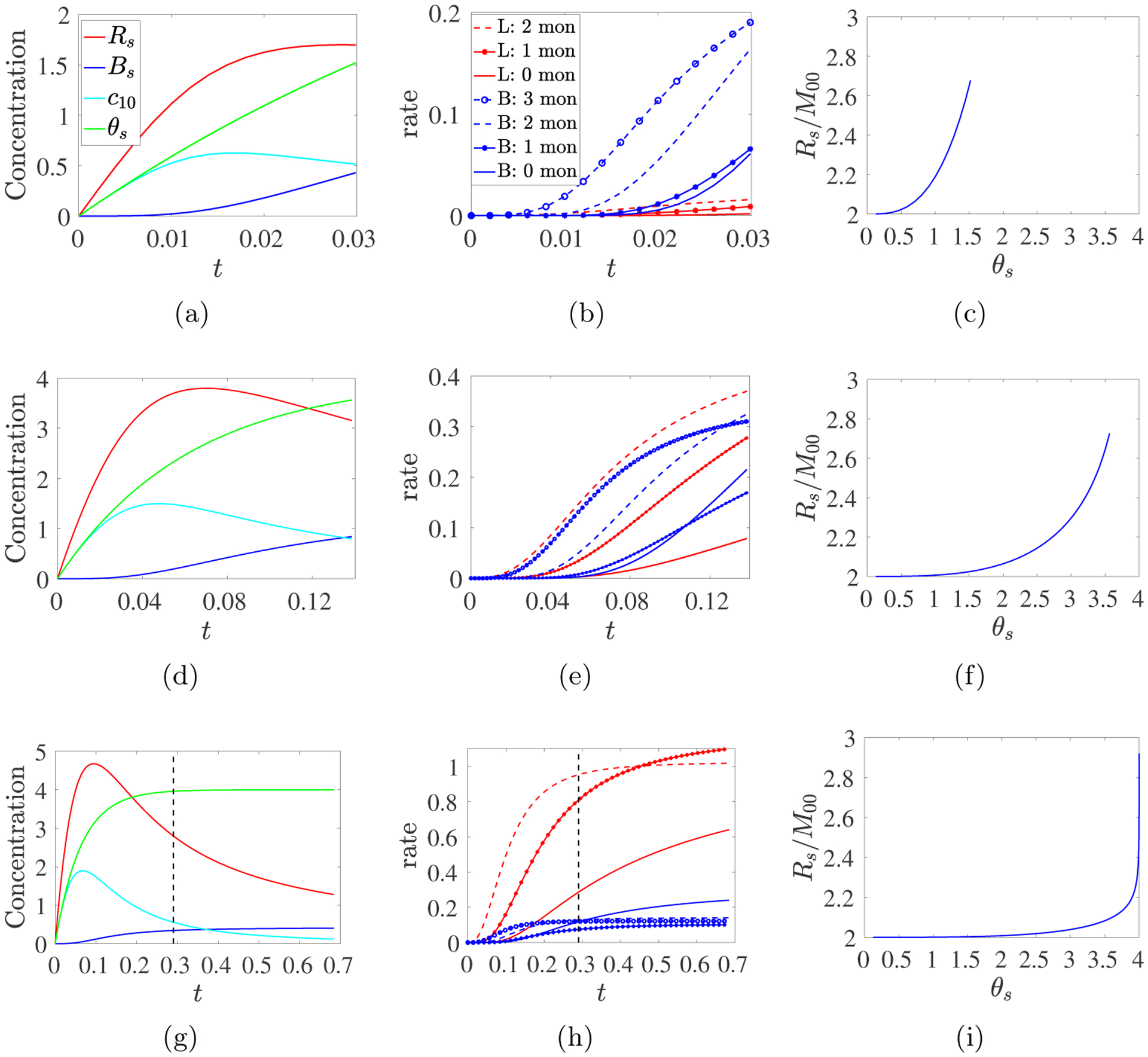
ODE model simulations with a time-dependent source S10(t) = m0λ exp(−λt) with m0 = 4 and λ = 16, and (abc) kb = 32, (def) kb = 1, (ghi) kb = 1/8. (Left) Plots of Rs(t), Bs(t), c10(t), and θs(t) until t = tgel. (Middle) Rates of link and branching formation reactions involving different numbers of monomers. (Right) Average functionality f(t) = Rs(t)/M00(t) vs. cumulative monomer sourced θs(t). Dashed black lines indicate when 99% of the monomer has been sourced.
Fig. 9 shows results up to tgel from the ODE model (Eqs. 2.10–2.14) for simulations run with the three sets of parameters (m0 = 4, λ = 16, and kb = 32, 1, or 1/8) which produced the leftmost, peak, and rightmost points on the cyan curve in Fig. 8b. Fig. 8b shows that Bs(tgel) is approximately the same for kb = 32 and kb = 1/8, and that the peak value of Bs(tgel) at kb ≈ 1 is approximately twice that at the kb values at the endpoints of the curves. Fig. 9adg show the different time courses of Rs, Bs, θs, and c10 for the three kb values. To understand them, we look in more detail at how links and branches are formed in these simulations. The overall link formation rate can be broken down as
| (3.3) |
into the rates at which links form through interactions involving 2, 1, or 0 monomers (i.e., only oligomers), respectively. The overall branch formation rate can be split as
| (3.4) |
into the rates of branch formation through reactions involving 3, 2, 1, or 0 monomers. These rates are plotted in Fig. 9beh. In Fig. 9cfi, we show the average functionality fA(t) = Rs(t)/M00(t) plotted as a function of the total mass density of monomer θs(t) that has been injected by time t. Recall that in the Ziff–Stell model, each monomer has f functional reactive sites and that it is necessary that f > 2 in order for a gel to form. In our model, fA = 2 for monomers and, thus, fA(t) depends on the extent of branch formation prior to time t. The concentration and reaction rate curves in Fig. 9 for the different values of kb are strikingly different.
Fig. 9abc show that with kb = 32, the total monomer concentration θs increases throughout the simulation, and it closely tracks the concentration of monomers, c10, up to a time at which Bs(t) noticeably rises. Bs(t) then increases at an accelerating rate until tgel. The branching reaction rates far exceed those for the linking reactions, and branch formation is dominated by reactions involving 2 or 3 monomers. θs(tgel) ≈ 1.5 compared to the maximum m0 = 4 that the source can inject. fA increases monotonically from 2 to ≈ 2.68.
Fig. 9def show results with kb = 1. The curves for θs and c10 first diverge and Bs first noticeably rises at a later time than for kb = 32. Bs continues to increase until tgel while Rs begins to decline about mid-way to tgel in concert with the decreasing rate of monomer supply. The link and branch formation rates are similar; most early reactions involve only monomers. As time progresses, the rates of reactions involving one oligomer increase, followed later by the rates of reactions involving multiple oligomers. While some types of branching reactions slow later in the simulation, others accelerate, and Bs(t) is approximately linear for much of the simulation. Here, tgel is more than 4-fold greater than with kb = 32. By tgel, θs reaches ≈ 88% of its possible maximum m0. fA increases monotonically from 2 to ≈ 2.75. It remains close to 2 longer than for kb = 32 because linking reactions involving only unbranched oligomers cannot cause fA to increase.
Fig. 9ghi show that with kb = 1/8, a gel forms substantially later than for kb =1 or 32. Almost all of the potential monomer source has been injected by t = 0.29. At this time, Rs and c10 are decreasing quickly and Bs is increasing slowly. Much of the branch formation occurs after monomer injection is essentially complete, and so draws on a rapidly decreasing pool of monomers and small oligomers. Link formation outpaces branch formation and primarily comprises reactions involving 2 monomers. Early branch formation primarily involves 2 or 3 monomers, but after the source is exhausted, branch formation by 3 oligomers dominates. Because linking reactions involving 2 monomers predominate for much of the simulation, fA increases very slowly during the first half of the simulation; it increases from below 2.2 to over 2.9 after monomer injection is essentially complete.
Bs(tgel) is also not monotonic in kb for constant source rates. Because these observations pertain to t < tgel, we can use Eqs. 2.10–2.14, with a constant source S10, to investigate the origin of the intriguing non-monotonicities shown in Fig. 8. The colored curves in Fig. 10a show Bs(tgel) for such simulations for a large range of S10 and kb values. For each S10, there is a well-defined peak for an intermediate value of kb. It occurs at kb = O(1), kb ≪ 1 and kb ≫ 1 for intermediate, large, and small values of S10, respectively. Bs(tgel) scales like for small kb and like for large kb. The peak occurs during the transition between these two behaviors.
Fig. 10:
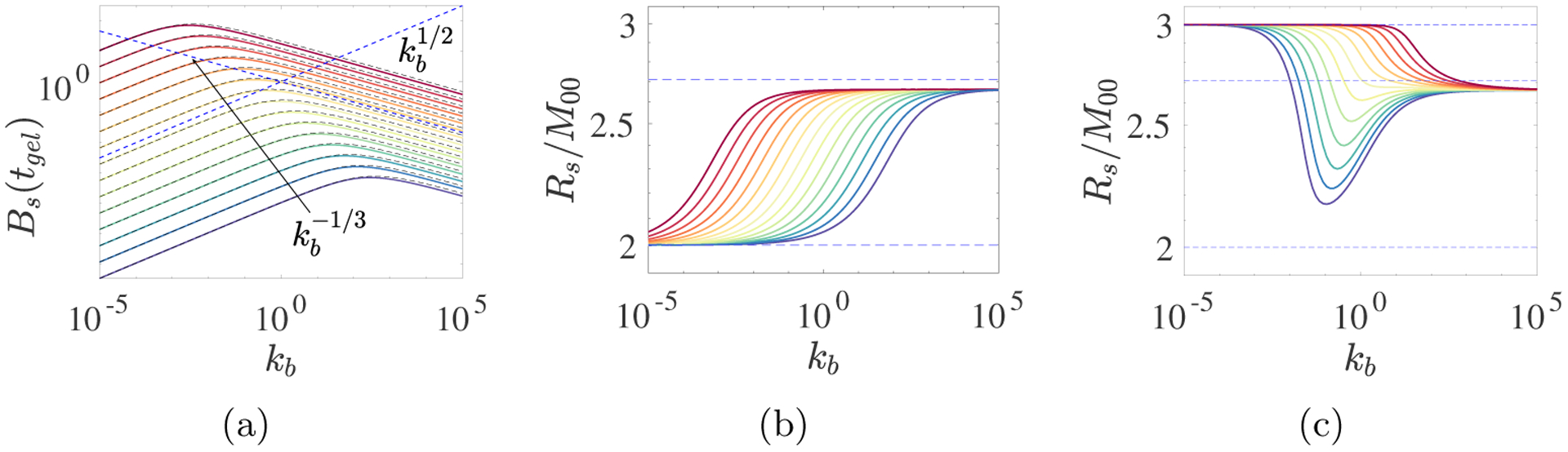
ODE model calculations for various branching rates kb and various (a,b) constant source rates S10 and (c) time-varying source rates. (a) Colored curves show Bs(tgel), blue dashed lines show its scaling behaviors, and black curves show approximate Bs(tgel) from Eq. 3.10 using rss values computed by solving Eq. 3.5 numerically; (b) Colored curves show average functionality fA = Rs/M00 at tgel. In (a) and (b), S10 decreases from 105 (deep red curve) to 10−5 (deep blue curve). Dashed blue line in (b) and (c) is 2/(1 − Bs/Rs) ≈ 2.7093 (see text). (c) Average functionality for time-varying source rate S10(t) = m0λ exp(−λt) m0 = 4 and λ decreases from 105 (deep red curve) to 10−5 (deep blue curve). Branching rates kb vary as indicated.
To understand the origin of these scaling behaviors, suppose that Rs is in quasisteady state, so that from Eq. 2.10, Rs = rss where rss satisfies
| (3.5) |
Then, Eq. 2.14 simplifies to the constant-coefficient linear equation
| (3.6) |
The solution to this equation which satisfies U(0) = 1 and U′(0) = 0 is
| (3.7) |
where . Since, U(tgel) = 0, we find that
| (3.8) |
under the assumption that Rs(t) ≡ rss. From Eq. 2.11, with Rs = rss constant, we see that
| (3.9) |
When kb ≫ 1, S10 is at least of moderate size, and we assume that the terms and 2S10 in Eq. 3.5 balance, and . When kb ≪ 1 and we assume that the terms and 2S10 balance, rss ≈ (2S10/kl)1/2 and . Using the limiting expressions for rss in Eq. 3.9, we find that
| (3.10) |
Substituting the numerical solution of Eq. 3.5 into Eq. 3.10 yields the black curves in Fig. 10a, which are in excellent agreement with the corresponding colored curves.
In the examples in Fig. 9, average functionality fA(tgel) increases monotonically in t from 2 at t = 0 towards a value between 2.6 and 3 at tgel. In Fig. 10b, we see that, for a wide range of S10, fA(tgel) approaches 2 from above as kb approaches 0, and it approaches a value close to 2.7 as kb becomes very large. The transition between these behaviors shifts leftward as S10 increases. To understand the asymptotic results, we first note that the relation Rs = Bs + 2M00 implies that
| (3.11) |
Then, using the asymptotic values of Bs(tgel) and rss from Eq. 3.10 and the text above it, respectively, we find that for kb ≪ 1, and therefore fA(tgel) → 2+ as kb → 0. For kb ≫ 1, Eq. 3.10 implies that and so , which is the height of the dashed blue horizontal line in Fig. 10b. The origin of the gap between the dashed blue line and the colored curves is explored in Supplement section S1.6. Fig. 10c shows plots of fA(tgel) for the source S10(t) = m0λ exp(−λt) with m0 = 4 and λ ∈ [10−5, 105]. For each λ, fA seems to approach the same limit as for the constant source case for kb → ∞, while for kb → 0, it asymptotes to 3. As shown in Supplement section S1.7, fA → 3 as t → tgel for any positive branching rate kb when starting with an initial supply of monomer and 0 source. Here, with kb ≪ 1, the source is essentially depleted after a time of order λ−1 that is much shorter than the branch formation time scale . Therefore, the system behaves much like one with an initial supply of monomer.
3.4. Temporally and spatially varying monomer source.
We next look at the PDE system’s behavior before and after gelation when there is no monomer initially and monomer is supplied at the temporally and spatially varying rate
| (3.12) |
where s(x) = 1 + cos(π · x/h) for |x| < h = 0.1 and s(x) = 0 otherwise. In the following sections we look at the effects of variations in the source rate λ, branching rate kb, and diffusion coefficient D.
3.4.1. Variations in Source Rate λ.
We begin with m0 = 8, kb = 4, and λ = 1/4, 1, or 4, so the rate, but not the amount of monomer supplied varies. Fig. 11a shows the contour Rg(x, t) = 0.001 for each λ. Since Rg(x, t) first becomes nonzero when a gel forms at location x, these contours show the propagation of the gel front toward the domain boundary. The front propagates quickly across the support of the source, slows for intermediate values of x, and speeds up when approaching the no-flux boundary at x = 0.5. Gel formation within the source’s support occurs sooner for larger λ, but the gel front for λ = 1 “catches” that for λ = 4 about midway across the domain and reaches the boundary sooner.
Fig. 11:
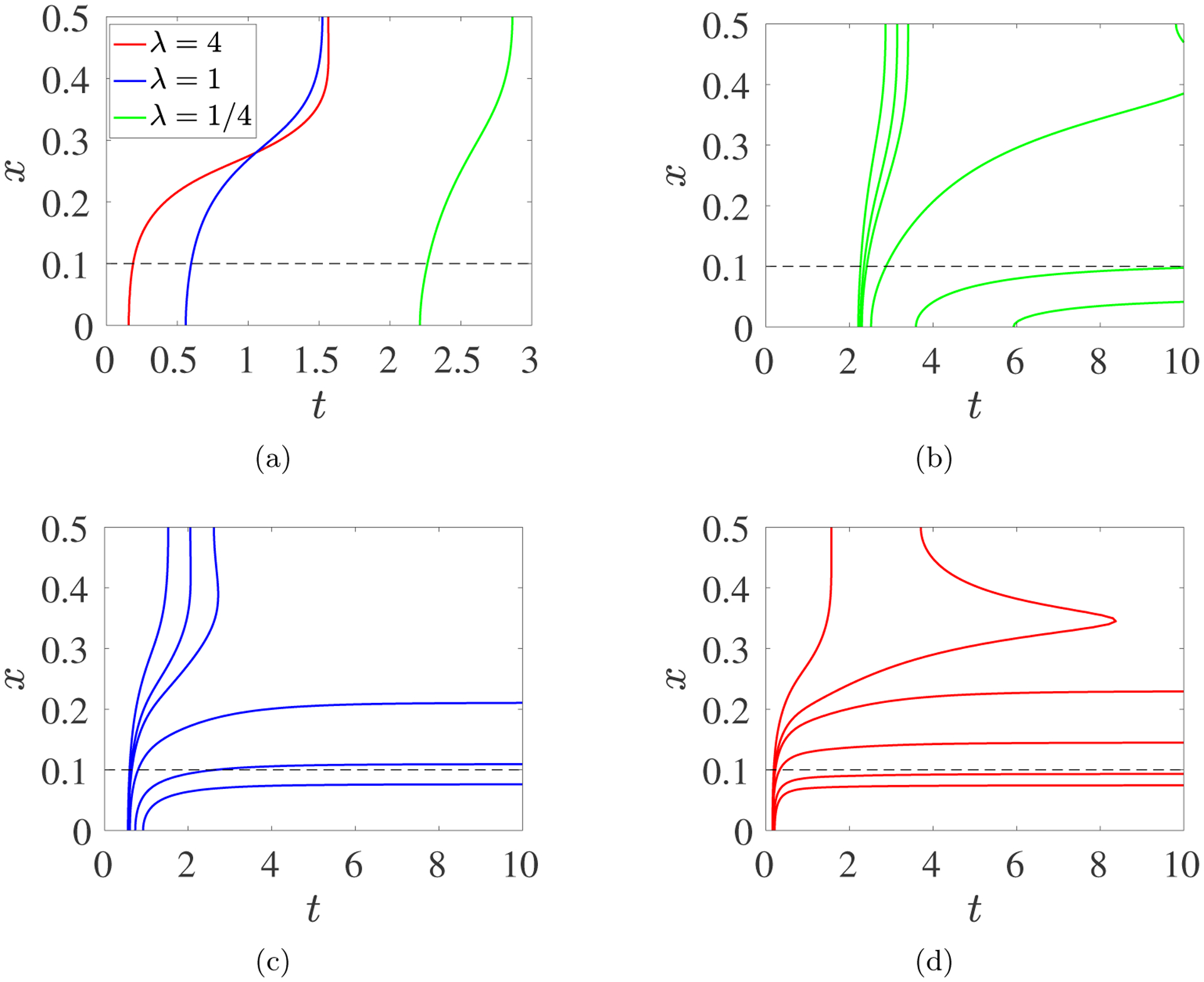
PDE model simulations with source rate S10(x, t) given in Eq. 3.12, with m0 = 8, kb = 4, λ = 0.25, 1.0, 4.0, contours of Rg in the xt–plane. (a) Contour Rg(x, t) = Bg(x, t) = 0.001 for λ = 4.0 (red), 1.0 (blue), and 0.25 (green). Each contour defines the gel front location xgel(t) vs t. (b,c,d) Contours Rg(x, t) = Bg(x, t) = 0.001, 0.005, 0.01, 0.05, 0.25, and 0.50 (increasing from left to right) for (b) λ = 0.25, (c) λ = 1.0, and (d) λ = 4.0. The black dashed lines show the upper edge of the monomer source’s support. Note the different time interval in (a).
Fig. 11bcd show contours of Rg(x, t) for λ =1/4, 1, and 4. For λ = 1/4, the lowest value contours rapidly cross the domain, and there is a long delay between the start of gelation at x = 0 and Rg(0, t) reaching 0.5. For λ = 1, this delay is much shorter, while propagation of higher values of Rg toward the domain boundary is slower. For λ = 4, there is very little delay between the onset of gelation at x = 0 and Rg(0, t) reaching 0.5. In contrast, Rg grows much more slowly than for the smaller λ values at locations midway between the source and the boundary. For λ = 4, Rg reaches 0.005 at x = 0.5 much earlier than it does at x = 0.35. These observations reflect the relative extent to which monomers introduced in the source region become part of the gel there as opposed to diffusing toward the boundary. With λ = 4, the rapidly cascading growth of oligomers near x = 0 “absorbs” much of the monomer before it can diffuse away. For λ = 1/4, diffusion keeps up with the introduction of monomer, and the gel develops more slowly at x = 0 and faster at locations near the boundary.
For λ = 1, Fig. 12 shows snapshots of the spatial evolution of the sol and gel variables and of two derived indicators of oligomer and gel structure: the structure parameter, B(x, t)/θ(x, t), which is the ratio of the total branch point density in both the sol and gel to the total mass density, and the average functionality fA(x, t) = Rs(x, t)/M00(x, t). Fig. 12 shows the base case to which other results, presented in the Supplement, should be compared. Recall that fA(x, t) > 2 is required for gelation to occur, and that monomers in our model have functionality 2. The first four rows show the situation at times by which 18, 39, 63, and 86% of the monomer has been delivered by the source. At the earliest times, the peak sol densities occur at x = 0. At t = 0.2, θs is only moderately larger than c10 at x = 0 indicating that most molecules there are monomers. At the boundary x = 0.5, c10 ≈ θs > 0, signifying that monomer has reached the domain boundary but that few larger oligomers are present there. fA(0, t) has increased somewhat from its base value 2. By t = 0.5, θs and Bs at x = 0 have grown significantly, while c10 is lower there despite the continued activity of the source. fA ≈ 2.4 within the source region and is above 2 throughout the rest of the domain.
Fig. 12:
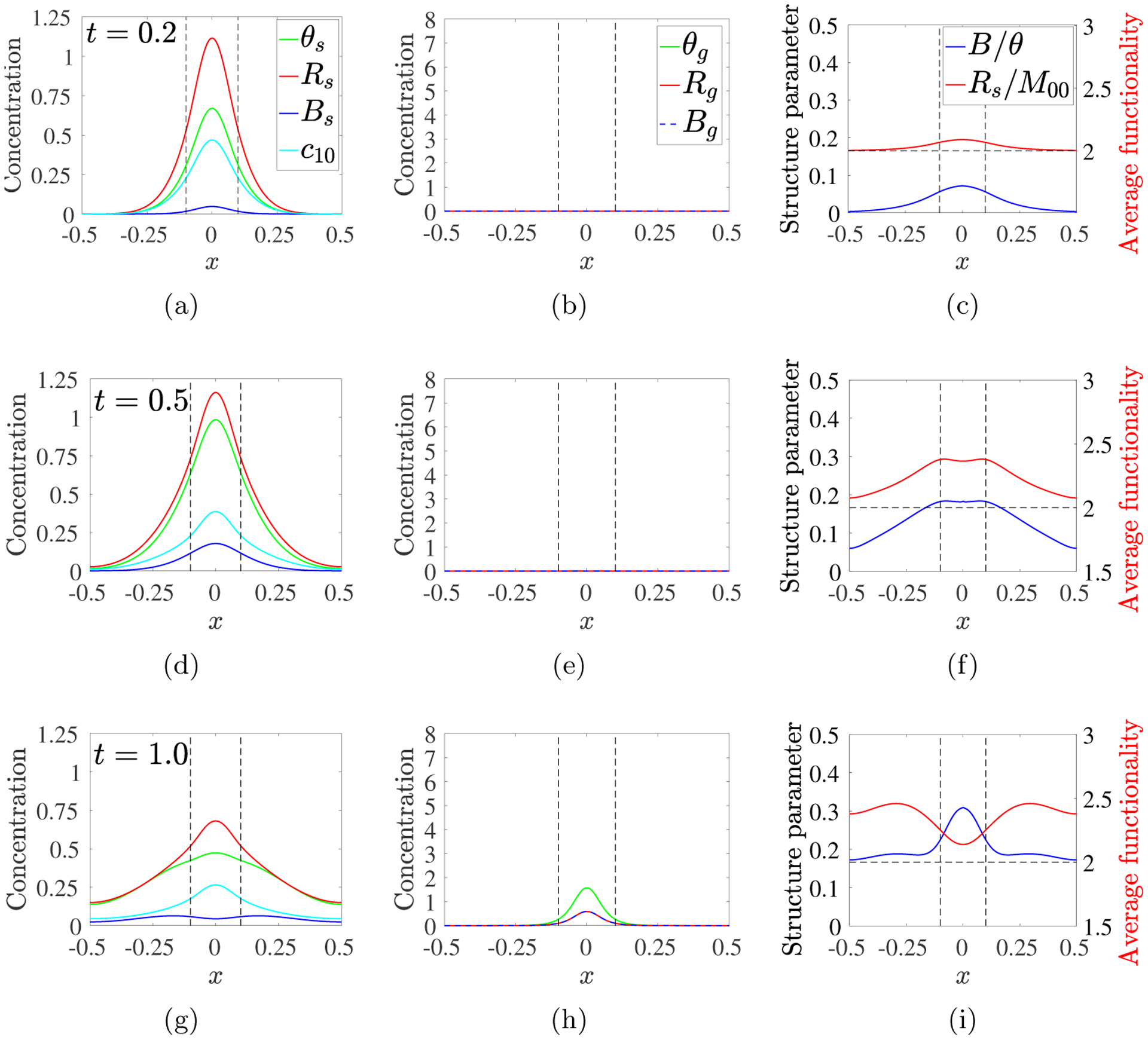
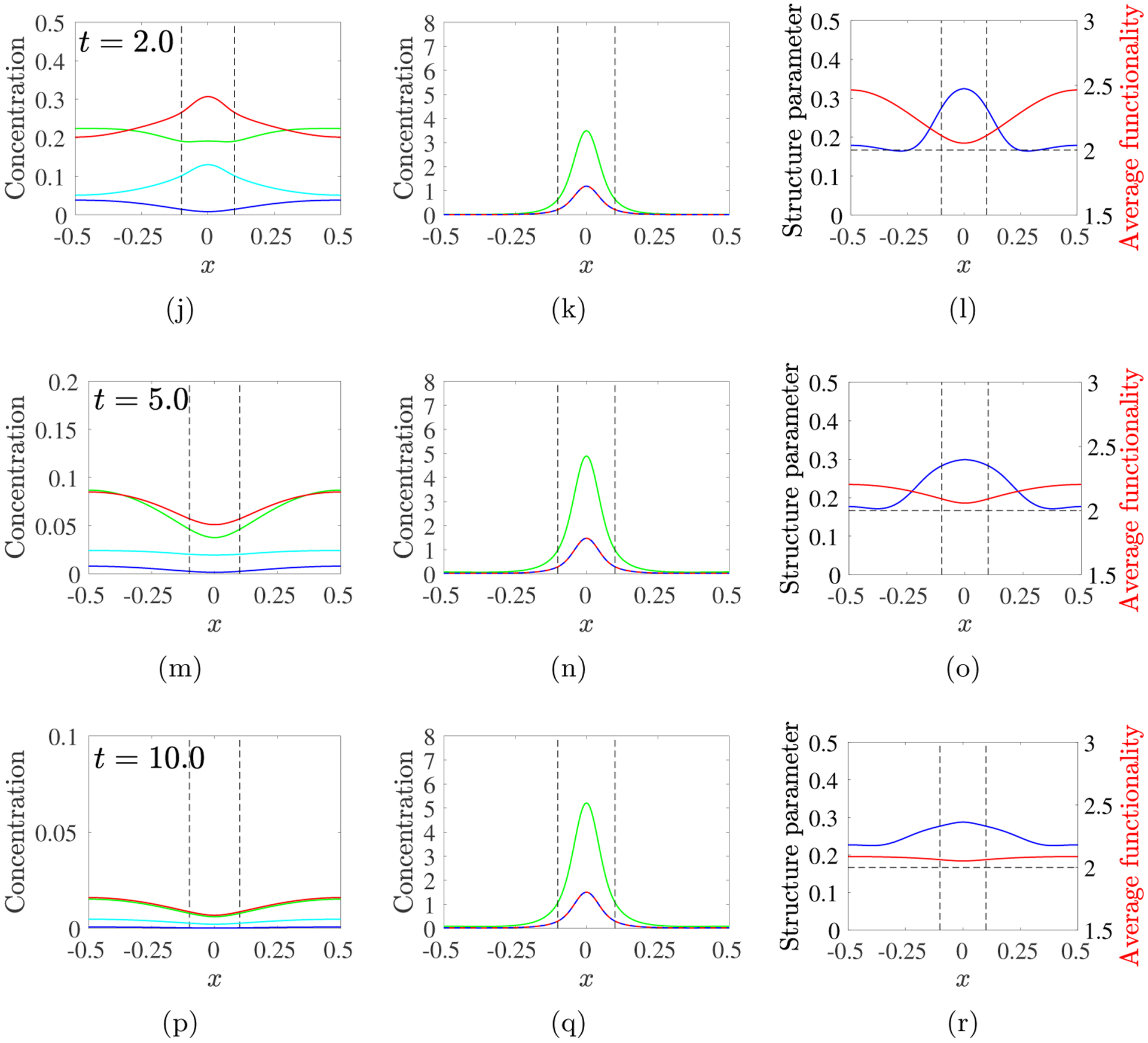
PDE model simulations with source rate S10(x, t) given in Eq. 3.12, with m0 = 8, kb = 4, λ = 1, D = 0.04. Snapshots of sol variables (left) gel variables (middle), and structure variables (right) at the times indicated for each row. Note change in vertical scale in left column. Black dashed vertical lines show extent of source’s spatial support.
By t = 1.0, gel covers the source region, but is most prominent near x = 0. Values of θs, Bs, and c10 are lower there than earlier because finite-size oligomers have been incorporated into the gel. Gel has formed throughout the domain, but θg(0.5, 1) is 5 · 104-fold smaller than θg(0, 1). fA is lower within the source’s support and higher for |x| > 0.25. B/θ is significantly higher near x = 0 than outside of the source region. The trends continue through t = 5, with θg and Bg increasing mainly within the source region. fA drops back towards 2 throughout the domain, as multi-branched oligomers are incorporated into the gel, while B/θ is relatively high over a much broader region. So much finite-sized oligomer within the source region becomes part of the gel that a “reverse” diffusive gradient in θs develops, particularly for intermediate |x|, and finite-size oligomers diffuse from this region toward x = 0. Between t = 5 and t = 10, θg increases a little throughout the domain and at t = 10, over 98% of the total sourced monomer is in the gel. B/θ is higher throughout the domain than earlier and fA is now uniformly ≈ 2.1.
Supplement Fig. S2 shows similar snapshots for the slower source rate λ = 1/4. The salient differences from the λ = 1 results are that oligomer and branch formation, and the onset of gelation are slower within the source region. Sol variables are more homogeneous in space as are gel variables later in the simulation. At t = 10, most branches are in the gel and so fA ≈ 2 for all x. No reverse gradient in sol concentrations is present, so sol species continue to diffuse toward the boundaries. At x = 0.5, θg reaches a value almost three times that for λ = 1. Supplement Fig. S3 shows results with λ = 4. This larger source rate leads to faster early gelation in the support region and also wider spread of oligomers outside of this region because of steep concentration gradients. At times t ≥ 2, with the source largely exhausted, continued gelation within the source region depletes oligomers there and results in substantial reverse diffusion. The result at t = 10 is a taller gel profile that is almost entirely contained within the source region.
3.4.2. Variations in Branching Rate kb.
Here, we fix λ = 1 and consider kb = 1, 4, and 16. Fig. 13a shows the propagation of the gel front for these values of kb. Gelation within the source region occurs earliest for kb = 16 and latest for kb = 1. As for simulations with different source rates λ, the early occurence of gelation near x = 0 for a particular kb does not imply that the gel front reaches the boundary first for that kb. Here, the gel front for kb = 4 crosses that for kb = 16 and reaches the boundary significantly sooner than for the larger kb.
Fig. 13:
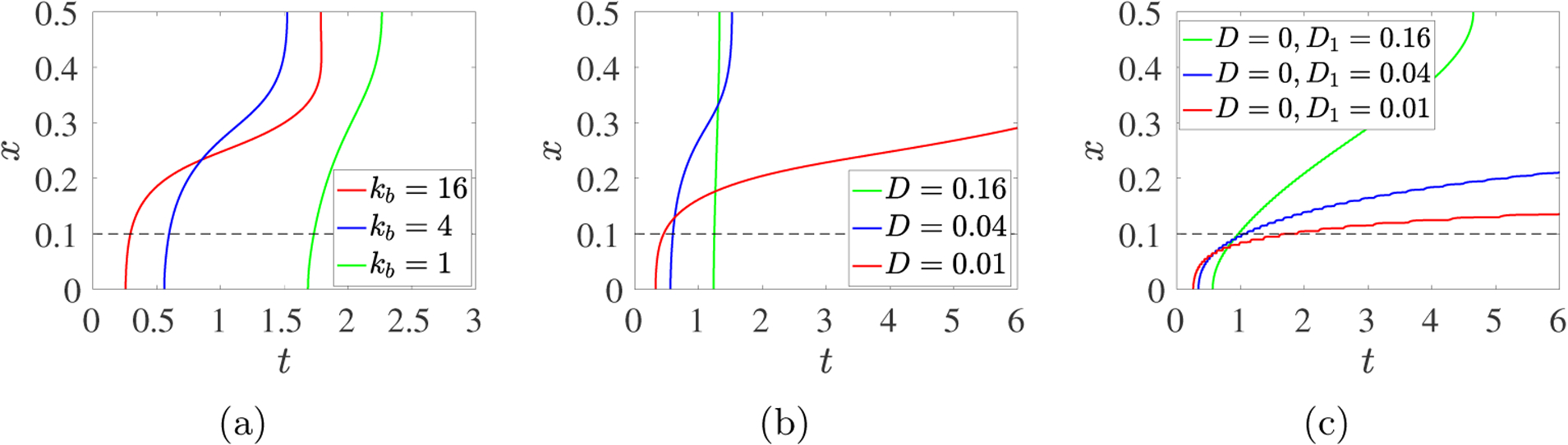
PDE model simulations with source rate S10(x, t) given in Eq. 3.12, with m0 = 8 and λ = 1 contours of Rg = 0.001 in the xt–plane for (a) D = 0.04 and kb = 1, 4, 16, (b) kb = 4 and D = 0.16, 0.04, 0.01, (c) kb = 4, D = 0, and D1 = 0.16, 0.04, 0.01, The black dashed lines show the upper edge of the monomer source’s support.
Fig. S4 and Fig. S5 in the Supplement show snapshots of simulations with kb = 16 and kb = 1, respectively. They can be compared to those in Fig. 12 for which kb = 4. Gelation near x = 0 occurs earliest for kb = 16, and later gel growth is also much more rapid than for smaller kb. The spatial extent of significant gelation is narrowest for kb = 16 and broadens progressively as kb decreases. At t = 10, the values of θg at x = 0 increase approximately four-fold and those at the boundary decrease by more than 16-fold as kb increases from 1 to 16. Similarly Bg at x = 0 increases substantially as kb increases. The reverse gradients in Bs and θs are more pronounced for kb = 16 than for kb = 4, and are nonexistent or weak for kb = 1. At t = 10, fA is a little above 2 throughout the domain for all kb, and as kb increases, the structure parameter B/θ increases for all x and it has a higher “bump” for smaller |x|, where the gel is concentrated, for large kb.
3.4.3. Variations in Diffusivity D and D1.
Fig. 13b shows gel front propagation for simulations in which monomers and oligomers diffuse and D was varied over the values D = 0.16, 0.04, 0.01, while λ = 1 and kb = 4. Near x = 0, gelation occurs earlier for smaller D, and the front propagates towards larger |x| much more rapidly for D = 0.16 and D = 0.04 than for D = 0.01. The solution snapshots in Supplement Figs. S6–S7 for D = 0.16 and D = 0.01, respectively, can be compared to those in Fig. 12 for which D = 0.04. No gel formation is apparent up to t = 0.5 for D = 0.04 and D = 0.16, while θg(0,0.5) > 1 for D = 0.01. For D = 0.16, sol has spread throughout the domain by t = 0.5, and there is little sign of reverse gradients at this or later times. When gelation does ensue, it does so over the entire domain with only moderately higher θg and Bg levels near x = 0 than near the boundary. In contrast, for D = 0.01, reverse gradients in sol quantities develop near the source by t = 2 and throughout the domain by t = 10, and gelation is confined to a narrow region around x = 0 during the entire simulation. The sturcture variables vary notably in space. Due to the rapid growth of the gel near x = 0 by t = 0.5, the average functionality fA there has already begun to drop. It is highest in locations adjacent to the gel to which sol has spread but not yet gelled; it remains high where little gelation occurs.
Next, we consider simulations in which only monomer diffuses. The necessary modifications to the PDEs are described in Supplement section S1.2. Fig. 13c shows gel front propagation for monomer diffusion coefficient D1 = 0.16, 0.04, 0.01 with D = 0. Comparing these gel fronts to those in Fig. 13b, we see earlier gelation at x = 0, slower movement of the gel front across the source region, and much slower propagation of the front from the edge of the source to the boundary. In fact, only for D1 = 0.16 does the front come close to the boundary by the end of the simulation. These behaviors are all due to the immobility of the oligomers, which allows faster progression in oligomer size near x = 0 while hindering this progression elsewhere.
Supplement Figs. S8 and S9 show snapshots of the dynamics for D1 = 0.04 and D1 = 0.16, respectively. For D1 = 0.04, gelation is underway near x = 0 before t = 0.5. By t = 10, the gel peak has grown and the spatial extent of the gel has widened somewhat, but is confined to |x| < 0.25. For the simulation in Fig. 12, in which oligomers also diffuse, the peak is a little lower and the gel front has reached the boundary by t ≈ 1.5. With only monomer diffusing, θs and Rs are much higher immediately adjacent to the gel front (see Fig. S8d) than farther away or than when oligomer also diffuses (see Fig. 12djp). fA in Fig. S8cfi drops to near 2 within most of the gel but is high adjacent to it, exceeding 3 at t = 10. The sol concentrations there are low, but high fA suggests that further branch formation will occur there. For D1 = 0.16 (Fig. S9, compare with Fig. S6), the gel grows faster and to a higher peak near x = 0 than when oligomers also diffuse, but at t = 2 it is confined to the region |x| < 0.25, whereas it reaches the boundary shortly after t = 1 if oligomers also diffuse. By t = 10, gelation has spread all the way to the boundary, but θg near the boundary is only about 40% of that when oligomers diffuse. At t = 10, fA and B/θ are distributed heterogeneously when D = 0 and D1 = 0.16 compared to their almost uniform distribution when D = D1 = 0.16.
4. Discussion.
In this paper, we consider a model of fibrin polymerization that investigates the spatial and temporal behavior of the polymers both pre- and post-gelation. Using the framework we introduced in [9], we study the early behavior of the system using moment equations derived from a doubly-infinite set of ODEs that describe the oligomer concentrations. The moment equations are valid only until gel time which is when a second moment, tracked by these equations, blows up. As we did in [10] for a simpler kinetic gelation model, we develop an alternative approach, based on the generating function of the oligomer concentrations, in order to extend our studies past gel time. To do this, we make assumptions about the types of reactions in which the gel can particpate, and use them to derive a closed system consisting of a PDE for the generating function and an ODE for the reaction site density. We find that the new system produces behaviors that agree with the moment system prior to gel time and it lets us continue our studies after gelation. We examine our assumptions about post-gelation reactions using the Gillespie method to carry out stochastic simulations beginning with a large, but finite, set of discrete monomers. These simulations agree with the solutions to the original differential equation system before gelation and with the new PDE system after gelation, giving support to our assumptions about post-gelation reactions. Finally, we extended the PDE system by incorporating spatial heterogenity and transport in space by diffusion.
The essential kinetic processes in our model are linking reactions, in which two oligomers join together without formation of a new branch, and branching reactions, in which three oligomers join together to form a new branch. These processes have timescales 1/(klC0) and , respectively, that are determined from their respective rate coefficients and a characteristic concentration C0. Another time scale λ−1 comes from the monomer source Eq. 3.1, which models the conversion of fibrinogen by thrombin into fibrin monomers. In problems with diffusion, a fourth time scale is L2/D where L is the half-width of the physical domain, and D is the diffusion coefficient. We use the linking timescale to non-dimensionalize the model equations and investigate the effects of varying the other times scales by changing λ, kb, and D.
An important quantity in kinetic gelation models is the functionality, f. In the Ziff–Stell model, each monomer has f reactive sites and it is necessary that f > 2 in order for a gel to form. In our model, f = 2 for fibrin monomers and the number of available reaction sites in an oligomer is always two more than the number of branches in that oligomer. Since the average number of branches per oligomer is a dynamic quantity, the average oligomer functionality, fA, is also dynamic and can increase only through branch formation. How rapidly fA grows from its initial value influences the time until gelation and the structure of the resulting gel, and is itself affected by the relative time scales of the linking, branching, source, and diffusion processes.
We used the PDE model first in a spatially homogeneous situation and investigated the system’s behavior, for different initial fibrinogen concentrations, m0, as the rates of conversion of fibrinogen to fibrin, λ, and branching, kb, were varied. We saw that gels form sooner for larger values of any of these parameters and that there are ranges of λ and kb values for which the branch point density at tgel is a large fraction of the gel’s branch point density after reactions have ceased, as seen experimentally [1, 4, 5]. For other values of these parameters, the branch point densities at tgel and the final time are very different. A possible explanation for this is the absence from the model of fiber thickening reactions after tgel which would remove oligomers from the pool that can form new branches, and thus reduce post-gel branch formation.
We then looked at how Bs(tgel) and fA(tgel) vary with λ and kb and saw that both are non-monotonic functions of kb. To understand this behavior we turned to the moment system since the behavior of interest here occurs before gel time, and we simplified the investigation by using a source rate that is constant in time. Numerically, we found that, for each source rate, Bs(tgel) scaled like for kb ≫ 1 and like for kb ≪ 1. The cross-over in these scaling behaviors for intermediate kb values explains the non-monotonicity we observed. We presented an asymptotic explanation of the two scaling behaviors, in which the reaction site density Rs, governed by Eq. 2.10, was taken to be in steady-state with a balance between source rate and link formation rate for kb ≪ 1 and between source rate and branching rate for kb ≫ 1.
Next we looked at the model in a one-dimensional spatial domain [−L, L] with a time-dependent source, Eq. 3.12, limited to a narrow interval around x = 0. A higher value of λ or kb or a value of D led to earlier gelation at x = 0, but not necessarily faster propagation of the gel front from the source to the boundary. We also see cases in which the gel’s final branch point density at a particular location is lower than the earlier peak sol branch point density at the same location. These behaviors can be ascribed to diffusion carrying oligomers away from that location to other locations closer to the source, before they can become part of the gel. The “reverse gradient” driving this flux is set up when extensive gelation at locations closer to the center of the source reduces the soluble oligomer density to a sufficiently low value.
Two distinct patterns of spatial-temporal gel development are seen. For large λ or kb or small D (see Fig. S3, S4, S7) the gel is highly peaked and largely confined to a narrow region surrounding the center of the source. In these cases, we see early reverse diffusion of oligomers, average functionality fA that decreases towards 2 within the narrow gel while remaining high (> 2.5) adjacent to it, and structure parameter B/θ that is substantially higher within the gel than outside of it. For small λ or kb or large D (see Fig. S2, S5, S6), we see a wide gel with a low peak, fA that rises and then decreases towards 2 approximately uniformly in space, and a uniformly low structure parameter. Thus, a relatively large source rate or branching rate leads to a tightly confined gel, while a relatively large diffusivity leads to a dispersed one.
Our current model of fibrin polymerization model does have limitations. We make specific simplifying assumptions about diffusion of oligomers of different sizes. This is done (i) to produce a mathematically tractable treatment of diffusion and (ii) because for the in vivo situations to which we will ultimately apply the model (after we couple it to our existing models of platelet deposition and coagulation under flow [7, 15, 17]), there are two cases of particular interest, in both of which diffusion of large oligomers is expected to be of limited importance. If a clot forms inside a blood vessel, advection is generally dominant over diffusion and we would expect many small fluid-phase oligomers to be washed away before they combine into large oligomers, and it may be that only the fibrin strands which are anchored to platelets remain at the injury site. On the other hand, if a clot forms in the complex milieu of the extravascular space (in the presence of cells and extracellular protein matrices), the spatial gaps in which molecules can diffuse are likely to be small, and this would reduce the importance of diffusion of large oligomers. Another limitation of the current model is that it does not treat fiber thickening after gel time, which is seen to be important experimentally [22, 21] and extending the model to treat thickening is an open question. The model also does not account for the fact that fibrinogen can bind to a fibrin oligomer and, until that fibrinogen is converted to fibrin, reduce the ability of that oligomer to bind with other oligomers. In [18], we present our preliminary work on analyzing models of polymerization that involve two types of monomers. A paper using similar ideas to include fibrinogen binding in the fibrin branching model is forthcoming. An open issue is the coupling of our fibrin polymerization model with our existing non-spatial [14, 7, 15, 17] and spatial [16] models of coagulation biochemistry and platelet deposition under flow. Fibrinogen will be converted to fibrin by thrombin at the concentrations that emerge from the calculations, fibrinogen and fibrin in the plasma will be transported with the flow, and we expect that the binding of fibrinogen and fibrin to the surfaces of platelets in the clot will play an important role in the dynamics.
Supplementary Material
Acknowledgments.
This work was supported in part by NSF grant DMS-1716898 and NHLBI grant R01HL151984 to ALF and by a grant to ACN from BioFire Diagnostics.
Footnotes
Submitted to the editors September 20, 2021.
REFERENCES
- [1].Blombäck B, Carlsson K, Fatah K, Hessel B, and Procyk R, Fibrin in human plasma: Gel architectures governed by rate and nature of fibrinogen activation, Thromb Res, 75 (1994), pp. 521–538. [DOI] [PubMed] [Google Scholar]
- [2].Campbell RA, Overmyer KA, Bagnell CR, and Wolberg AS, Cellular procoagulant activity dictates clot structure and stability as a function of distance from the cell surface, Arter Thromb Vasc Biol, 28 (2008), pp. 2247–2254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Campbell RA, Overmyer KA, Selzman CH, Sheridan BC, and Wolberg AS, Contributions of extravascular and intravascular cells to fibrin network formation, structure, and stability, Blood, 114 (2009), pp. 4886–4896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Chernysh IN, Nagaswami C, and Weisel JW, Visualization and identification of the structures formed during early stages of fibrin polymerization, Blood, 117 (2011), pp. 4609–4614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Chernysh IN and Weisel JW, Dynamic imaging of fibrin network formation correlated with other measures of polymerization, Blood, 111 (2008), pp. 4854–4861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Collet J, Park D, Lesty C, Soria J, Soria C, Montalescot G, and Weisel J, Influence of fibrin network conformation and fibrin fiber diameter on fibrinolysis speed: dynamic and structural approaches by confocal microscopy, Arter Thromb Vasc Biol, 20 (2000), pp. 1354–1361. [DOI] [PubMed] [Google Scholar]
- [7].Elizondo P and Fogelson A, A model of venous thrombosis initiation, Biophys J, 111 (2016), pp. 2722–2734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Fatahl K, Silveiro A, Tornval P, Karpeo F, Blomböck M, and Hamsteno A, Proneness to formation of tight and rigid fibrin gel structures in men with myocardial infarction at a young age, Hypertension, 7 (1996), p. 2. [PubMed] [Google Scholar]
- [9].Fogelson AL and Keener JP, Toward an understanding of fibrin branching structure, Physical Review E, 81 (2010), p. 051922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Fogelson AL and Keener JP, A framework for exploring the post-gelation behavior of Ziff and Stell’s polymerization models, SIAM J Appl Math, 75 (2015), pp. 1346–1368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Fogelson AL and Neeves KB, Fluid mechanics of blood clot formation, Ann Rev Fluid Mech, 47 (2015), pp. 377–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Gillespie DT, A general method for numerically simulating the stochastic time evolution of coupled chemical reactions, J Comput Phys, 22 (1976), pp. 403–434. [Google Scholar]
- [13].Guy R, Fogelson A, and Keener J, Fibrin gel formation in a shear flow, Math Med Biol, 24 (2007), pp. 111–130. [DOI] [PubMed] [Google Scholar]
- [14].Kuharsky AL and Fogelson AL, Surface-Mediated Control of Blood Coagulation : The Role of Binding Site Densities and Platelet Deposition, Biophysical Journal, 80 (2001), pp. 1050–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Leiderman K, Chang W, Ovanesov M, and Fogelson A, Synergy between Tissue Factor and Factor XIa in initiating coagulation, Arter Thromb Vasc Biol, 36 (2016), pp. 2334–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Leiderman K and Fogelson AL, Grow with the flow: A spatial-temporal model of platelet deposition and blood coagulation under flow, Mathematical Medicine and Biology, 28 (2011), pp. 47–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Link K, Stobb M, Sorrells M, Bortot M, Ruegg K, Manco-Johnson M, Paola JD, Sindi S, Fogelson A, Leiderman K, and Neeves K, A mathematical model of coagulation under flow identifies factor V as a modifier of thrombin generation in hemophilia A, J Thromb Hemost, 18 (2020), pp. 306–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Nelson AC, Keener JP, and Fogelson AL, Kinetic model of two-monomer polymerization, Physical Review E, 101 (2020), p. 022501. [DOI] [PubMed] [Google Scholar]
- [19].Rukhlenko O, Dudchenko OA, Zlobina KE, and Guria1 GT, Mathematical modeling of intravascular blood coagulation under wall shear stress, PLOS One, 10 (2015), p. e0134028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Ryan EA, Mockros LF, Weisel JW, and Lorand L, Structural origins of fibrin clot rheology, Biophys J, 77 (1999), pp. 2813–2826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Weisel J, Structure of fibrin: Impact on clot stability, J Thromb Haemos, 5 (2007), pp. 116–124. [DOI] [PubMed] [Google Scholar]
- [22].Weisel J and Nagaswami C, Computer modeling of fibrin polymerization kinetics correlated with electron microscope and turbidity observations: clot structure and assembly are kinetically controlled, Biophys J, 63 (1992), pp. 111–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Weisel JW, Fibrinogen and fibrin, in Adv Prot Chem, vol. 70, Elsevier, 2005, pp. 247–299. [DOI] [PubMed] [Google Scholar]
- [24].Wolberg AS and Campbell RA, Thrombin generation, fibrin clot formation and hemostasis, Transf Apher Sci, 38 (2008), pp. 15–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Zapata-Allegro CL, Mathematical Modeling of Fibrin Gelation Dynamics and Structure Formation Under Flow, PhD thesis, The University of Utah, 2018. [Google Scholar]
- [26].Ziff RM and Stell G, Kinetics of polymer gelation, J Chem Phys, 73 (1980), pp. 3492–3499. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


