Detecting critical transition signals from single-cell transcriptomes to infer lineage-determining transcription factors

Abstract

Analyzing single-cell transcriptomes promises to decipher the plasticity, heterogeneity, and rapid switches in developmental cellular state transitions. Such analyses require the identification of gene markers for semi-stable transition states. However, there are nontrivial challenges such as unexplainable stochasticity, variable population sizes, and alternative trajectory constructions. By advancing current tipping-point theory-based models with feature selection, network decomposition, accurate estimation of correlations, and optimization, we developed BioTIP to overcome these challenges. BioTIP identifies a small group of genes, called critical transition signal (CTS), to characterize regulated stochasticity during semi-stable transitions. Although methods rooted in different theories converged at the same transition events in two benchmark datasets, BioTIP is unique in inferring lineage-determining transcription factors governing critical transition. Applying BioTIP to mouse gastrulation data, we identify multiple CTSs from one dataset and validated their significance in another independent dataset. We detect the established regulator Etv2 whose expression change drives the haemato-endothelial bifurcation, and its targets together in CTS across three datasets. After comparing to three current methods using six datasets, we show that BioTIP is accurate, user-friendly, independent of pseudo-temporal trajectory, and captures significantly interconnected and reproducible CTSs. We expect BioTIP to provide great insight into dynamic regulations of lineage-determining factors.

Graphical Abstract

Graphical Abstract.

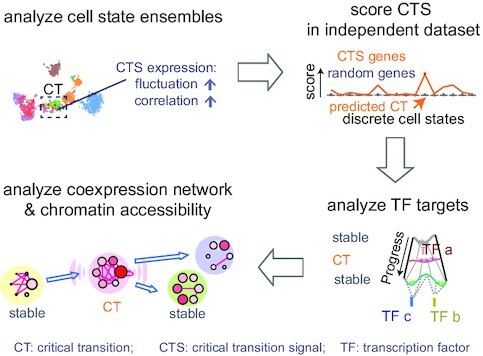
BioTIP: identifying CTS genes; characterizing CT state’s reproducibly; predicting lineage-determining factors; disclosing gene-regulatory dynamics.

INTRODUCTION

Developmental fate decisions involve transient bifurcations between stable cell states (1). Before a bifurcation, multilineage progenitor cells undergo priming when preparing for distinct cell identities (2–5). Besides epigenetic priming, transcriptional priming has been described using single-cell transcriptomes (6–10). The transcription factors (TFs) that orchestrate transcriptional priming have been evaluated in early cardiogenesis (11). However, assuming there exist smooth and continuous transitions marked by the progressive activation and silencing of molecular hallmarks (12), mainstream analyses are unable to identify gene markers that characterize these semi-stable transition events. Therefore, it is crucial to identify when bifurcations occur, what characterizes them, and what drives their onset.

Cell clusters in a single-cell transcriptomic snapshot represent cellular states along a trajectory. These discrete clusters allow us to characterize bifurcations using tipping-point theory (reviewed by (3)). In this theory, a bifurcation is an abrupt, non-linear, and often irreversible critical transition (CT) between stable state (13). A CT occurs when perturbations in gene interactions cause the cell to cross a certain threshold that had been maintaining an equilibrium (11,14). Then, in the cluster composed of CT-occurring or CT-impending cells, a set of interconnected genes gain covariance due to the loss of the preexisting equilibrium and the onset of a new state (3,15–17). By applying tipping-point theory, two types of CT events have been described from gene expression profiles: saddle-node and pitchfork bifurcations. Saddle-node bifurcations occur when a cell approaches an irreversible commitment toward a new stable state (7,18); pitchfork multifurcations happen before a choice among multiple new stable state (1,11,17) (e.g. Figure 1A, embedded panel).

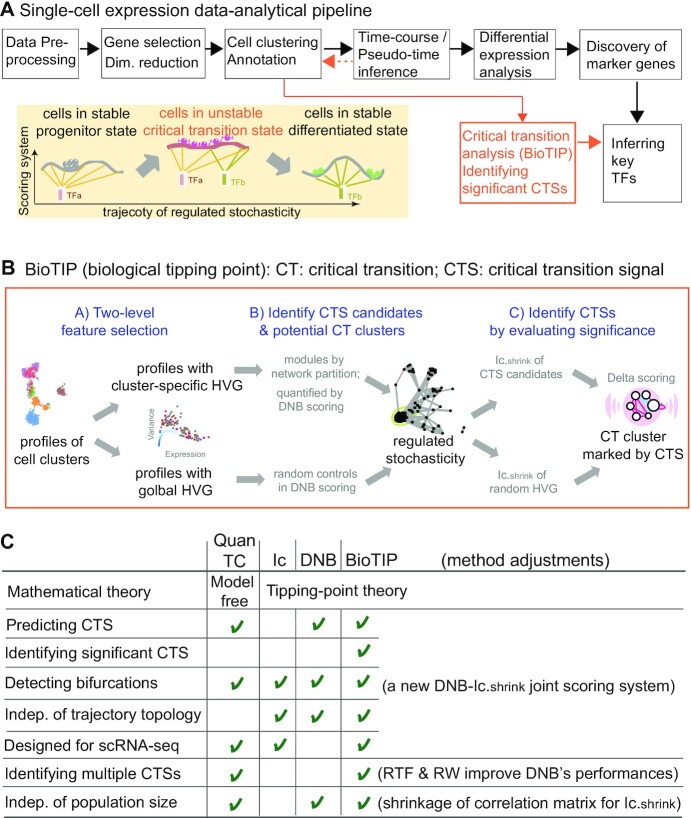
Figure 1.

Overview of BioTIP. (A) Analytic pipeline of single-cell RNA-seq analysis, with BioTIP as an alternative focusing on transition states. Solid orange arrows show how BioTIP differs from the typical pipeline while the dashed line shows optional optimizing inputs. The embedded panel illustrates TF-regulated stochasticity during developmental bifurcation. The flat brown line shows the effect of multiple decayed attractions at the tipping point, representing a vulnerable regulation. Then, this unstable state is resolved into distinct cellular states and phenotypes, shown by the green balls. (B) Overview of BioTIP’s three analytical steps. ScRNA-seq profiles with cell cluster IDs are inputted. The outputs are significant CT states and their characteristic CTSs which can infer CT-driven transcription factors. HVG: highly variable genes. DNB: dynamic biomarker network; Ic: index of criticality. (C) Table view comparing the functionality of BioTIP with three current methods. Ic.shrink: a redefined Ic using the ‘shrinkage of correlation’ method (32); RTF: relative transcript fluctuation; RW: random walk. See Figure 5 to compare BioTIP with DNB, Ic and QuanTC.

Index of criticality (Ic) is the first tipping-point theory-based mathematical model to detect CT states using single-cell RNA-sequencing (scRNA-seq) data (7,18). However, Ic assumes that stochastic fluctuation (including unexplainable stochasticity) in transcription prescribes abrupt cell-fate transitions. Ic therefore is not designed to identify gene markers associated with cell-state transitions.

To infer what drives a CT event, one must identify its significant signal (CTS). This computational work must be done at the level of the single cell (18). This is because the heterogeneity of single cells is absent in bulk samples. The identification of CTS is inspired by a ‘regulated stochasticity’ assumption (reviewed by (3)). The assumption comes from the fact that temporal TF activities determine distinct cell fates (19–22). Under this assumption, dynamic network biomarker (DNB) is the first tipping-point theory-based mathematical model to detect CTS (16). DNB and recent methods model gene co-expression networks to probe intercellular communications (16,23). Intercellular communications responding to bidirectional signals may drive cellular heterogeneity, and therefore is a powerful metric to characterize regulated state transitions (24–26). However, DNB was designed to analyze bulk transcriptomes, requiring modifications to analyze comprehensive cellular states. So far, DNB has been only applied to single-cell datasets with either a small number of cells (n = 389) (18), a simple trajectory topology of one bifurcation (17), or a linear process from normal to disease (3–4 states) (27,28).

Bifurcations have been described by transcriptional entropy-based approaches, such as MuTrans (29) and QuanTC (30). MuTrans applies stochastic differential equations to detect smooth or abrupt transition cells that present energy barriers at transitions. However, without considering intercellular communications, MuTrans is not designed to infer TF regulators or the regulated stochasticity. QuanTC is the first transition-signal-focused scRNA-seq method and has succeeded in characterizing the epithelial-to-mesenchymal transition. QuanTC is model-free by detecting transition cells that portray multiple stable state. A prerequisite for detecting transition markers by QuanTC is choosing a trajectory-starting point, making its application difficult for large datasets (e.g. >10 clusters). Therefore, new user-focused methods are required to study transition states using single-cell transcriptomes.

Rooted in the same tipping-point theory to model an increased oscillatory expression at a CT state, DNB and Ic provide each other a technical valuation in detecting bifurcations. Therefore, we introduce BioTIP (biological tipping point): a computational toolset that adapts the DNB algorithm to scRNA-seq data and technically evaluates the model's multiple outcomes using a redefined Ic score (Figure 1b). We evaluate BioTIP’s performance on two benchmark single-cell datasets with previously validated CT states, transition-marker genes, or transition-driving TFs. We demonstrate that BioTIP can not only recapture evaluated transition events, but also it can assess the significance of its predictions—thus enabling the inference of fate-deciding TFs. BioTIP is then applied to mouse gastrulation data on which tipping point analyses had never been conducted before. Multiple CTSs are identified and evaluated using independent cells from the same developmental stages of mouse gastrulation. We compare BioTIP with three existing tools in six real or simulated data analyses; we show these tools’ consistency in identifying and characterizing state transitions. Additionally, we show the user-friendliness of BioTIP since there is no requirement of a trajectory, a starting point, nor a 5k size limit of cells. We also present BioTIP’s advantage in capturing interconnecting transition markers that are conserved across independent datasets. Most importantly, we demonstrate how interconnecting CTS genes provide insight into cell-fate decisive transcription factors. These results open a way for characterizing CT events from dynamic expression profiles of developmental biology.

MATERIALS AND METHODS

Overview of BioTIP

BioTIP’s use of single-cell transcriptomes satisfies the assumptions of tipping-point theory that a cell system has a dissipative structure (i.e. having discrete states including the one showing semi-stability); each state is an ensemble of the individual replicates; and that each state has a characteristic gene expression profile and presents a distinct molecular phenotype.

BioTIP is a new toolset that complements the mainstream scRNA-seq analytical pipeline by modeling cell clusters, thus being independent of the trajectory topologies among states (Figure 1A). The goal of BioTIP is to identify multiple significantly interconnecting and technically reproducible CTSs.

BioTIP has three analytical steps to identify significant CTSs with practical considerations (Figure 1B). The first step enhances the feature (gene) selections for oscillations in expression that are subtle across all cells but prominent in one or more subpopulations. Without this step, transient CT states will be overlooked. This step outputs two gene lists. The first list, made of highly variable genes (HVG) across all clusters, is used for downstream permutation-based statistics. The second list, called cluster-specifical HVG, is used as the input for CTS predictions and is made of the subset of the global HVG. The second step detects CTS candidates from many gene modules per state, by coupling the DNB model with optimization and network partition algorithms. A module — interconnecting genes with similar expression profiles in a cellular state — tends to be functionally related and co-regulated (31). This step outputs multiple CTS candidates (gene modules significant in the DNB-scoring system) rather than only the highest-scoring one. Given that each CTS indicates one CT state, our last step considers the common CT states recaptured by both DNB and redefined Ic models. Such technically reproducible results will ensure significance in analyzing noisy scRNAseq data. The feasibility is supported by the observed agreements between both tipping-point theory-based models in the same system (18). To further correct Ic's inaccuracy, we introduce an improved estimation of the true correlation matrices (32). This improved estimation was called ‘shrinkage of correlation’ because it calculates a weighted average of the original correlation matrix and a target matrix that is to be shrunken towards. We name our newly defined score to be Ic.shrink. To assess the empirical significance, we designed a Delta score based on where the maximum Ic.shrink score occurs and its distance from the second maximum Ic.shrink score. Together, each significant CTS meets all the following quantitative criteria:

• A significantly high DNB score, indicating increased gene-gene interconnections at the cluster from which this CTS was identified.

• A significantly high Ic.shrink score of this CTS, indicating that critical transition happens at the same cluster.

• And a significantly high Delta score at the same state, distinguishing the CTS from other randomly selected genes to characterize regulated stochasticity during this transition.

These designs enable BioTIP to identify multiple CTSs significantly and robustly and be independent of the predicted trajectory topology (Figure 1C).

Three analytical steps

Measured at single-cell levels, a cells’ state can be stable or semi-stable (i.e. the transition state). BioTIP analyzes cell-state ensembles (clusters of transcriptionally similar cells) and will characterize clusters of transition cell states. What follows is a description of the analytical methods within these three steps.

• Step A: Two-level features/genes preselection

Let 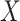denote the 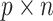matrix of the expression levels of P genes ({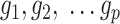}) in rows and 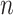cells (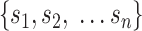) in columns. When the 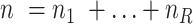cells are clustered into 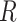distinct states, we can group the columns of 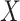to have 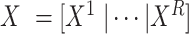, where 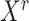denotes the 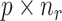submatrix for cells in a state 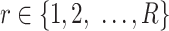and 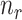denotes the number of cells observed in the 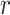-th state.

To remove lowly-expressed transcriptional noise and reduce the downstream calculation burden, we first select global HVG that express above a certain threshold in 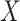. We recommend keeping about 3k or more HVG to retain cluster-specific variable genes that may not have been selected by a more restricted cutoff. Hereafter, let us denote the number of HVG as .

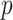To pre-select CTS-informative transcripts and minimize the intrastate dispersions caused by sample outliers, we estimate the variation of a gene 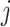in state r relative to the rest of cells in other states (-r) using a relative transcript fluctuation (RTF) score for each state r:

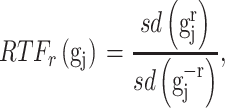(1)

where 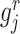denotes the expression vector for gene 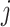among samples in the state (i.e. the 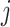-th row of the normalized expression matrix 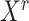) for a given state 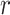, and sd(.) takes the standard deviation of the vector.

We use saturation (i.e. statistical resampling) based approaches to optimize the RTF estimation. To optimize the RTF estimation given the heterogeneity of single cells within each state (cluster), we first randomly bootstrap of the number of samples in the -th state 100 times to estimate the distribution of 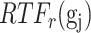. Then, we select the 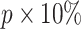genes that have top RTF scores in the state and repeat this selection for each state. By adjusting the parameter b, we allow 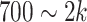genes per state for the analysis of comprehensive data (Supplementary Table S1). In the following steps, we detect CTSs from the pool of these cluster-specific HVG and conduct random simulations using the global HVG.

• Step B: Identification of CTS candidates

The goal is to identify a subset of genes that ‘drive’ or respond to the between-state transitions. For the expression profiles of cluster-specific HVG, we define gene-modules, followed by an application of the DNB algorithm (16).

Network partition

Between-gene correlation reveals gene regulatory networks. For clusters of stable states, these networks were kept at equilibrium, as perturbations are contained within an attractor's potential. CT events happen when the perturbation passes a threshold of equilibrium (33). It is essential to uncover which genes are most influential within these co-expressed networks. Therefore, for each cluster, we first build a network graph in which cluster-specific HVG are nodes and edges connect genes whose expression is correlated (e.g. FDR of Pearson correlation < 0.1). To find strongly connected components (or gene modules) within a cluster-specific graph, we used the random walk (RW) algorithm (S Methods). We choose RW because of its high accuracy and performance in network decomposition (31). As a result, we partition co-expressed cluster-specific HVG into modules per state which will serve as the inputs of the next CTS-searching goal.

Identification of CTS candidates

This calculation adapts the DNB model to quantify each gene module in each cell state 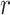(16). This score compares expressional deviation, the connectivity and homogeneity in this module 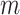relative to its complement set 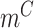. Let PCC refer to the Pearson correlation coefficient between any two genes (g_i and g_j). Let |.| take the absolute value. This gives:

(2)

A putative CTS is a module 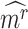that has the higher-than-expected score in the state 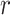. We therefore estimate the expected DNB scores from 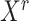by bootstrapping 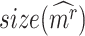genes from the transcriptomic background 1000 times. We keep significant modules in the DNB-scoring system as CTS candidates.

• Step C: Technical evaluation of the significance

We are interested in the reproducible tipping points captured by both Ic and DNB scoring systems because both are based on the tipping-point theory. To this end, there are two following analytical goals:

Goal 1: Redefine the Ic.shrink score using the Schafer–Strimmer method

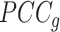refers to the Pearson correlation coefficient matrix between 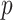genes; 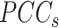refers to the Pearson correlation coefficient matrix between 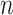samples. For each state, the original Ic is the ratio of average 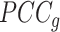to average 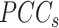(7). At a critical transition (CT) state, the average 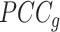increases and the average 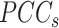decreases, resulting in an overall increase in Ic.

To resolve Ic's limitation in its tipping-point prediction towards states with a small sample size, we introduce 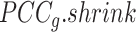, a regularized 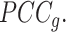To obtain improved estimates of the co-expression matrix, 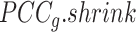shrinks the observed correlation matrix 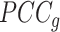to a target matrix 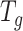and then weights the 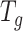to get an improved estimation (32). By introducing a small amount of bias (i.e. decrease accuracy), the estimator 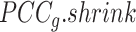can greatly reduce its variance (i.e. increase stability). This gives per state r that:

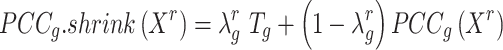(3)

We apply the ‘Target D’ in (32) where 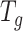is the identity matrix (a square matrix with ones on the diagonal and zeros elsewhere), and the weight 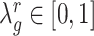is a value to be optimized from 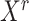and 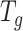. The optimization of follows the method outlined in (32), in which an approximation to the mean squared error (MSE), 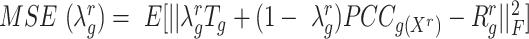, is minimized. Here, 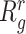is the true (unknown) underlying gene-gene correlation matrix for samples in state 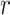, 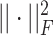is the squared Frobenius norm, and 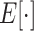is the expectation operator.

Consequently, when the sample size 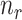is small (i.e. 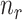<< number of genes) the optimal value for 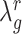will be large (close to 1), indicating a strong level of shrinkage of the correlations for that state towards 0. When the sample size is large, the optimal value of 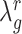will be small (close to 0), and the shrinkage towards zero will be minor so that the 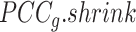is close to the observed 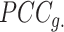The bias observed in Ic towards small sized states is due to the increased variability of the Pearson correlation matrix estimate, leading to more extreme magnitudes of estimated correlations. By shrinking the estimate of the correlation matrix, we drastically reduce that variance (at the cost of some bias), which resolves Ic's bias.

Similarly, we shrink the 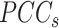to get an improved approximation  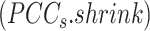of the true but unknown between-sample correlation matrix (‘Target F’ in (32) which additionally estimates 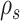, the average of sample correlations as a new parameter). Here, we set the target matrix 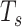with 1 on the diagonal and 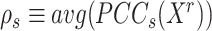elsewhere, so that for each state, we shrink the correlations towards the average value. The choice of average not only reflects the steady expression pattern in a stable state but also preserves the pattern difference across states.

Thereby, we introduce 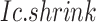, the refined Ic model with 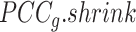and 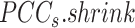estimates. 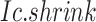remains robust regardless of sample sizes (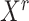denotes the 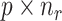submatrix of 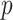genes for 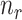samples in a state ).

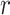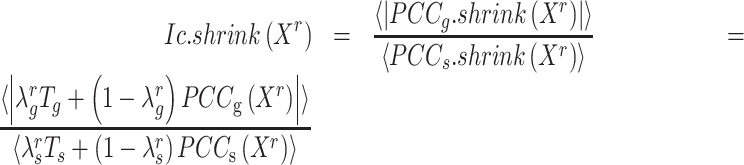(4)

Goal 2: Identify CTSs significant in the 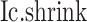scoring system

To evaluate the significance of the CTS candidates, we design a Delta score to quantify abrupt changes in 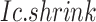between states. Given a CTS candidate, the 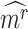detected in state 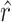, calculating its 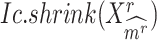per state gives a vector 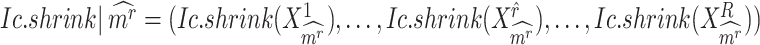, which should peak at the state 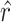significantly. The Delta score measures the distance between the largest and the second-largest scores in :

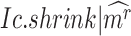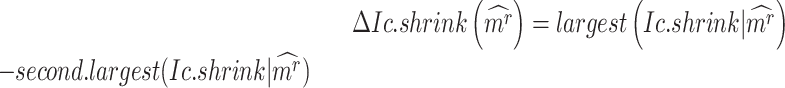(5)

Given a CTS identification, comparing the observed Delta score of the observed 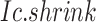to the simulated Delta scores (of random 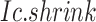scores using randomly selected genes) delivers an empirical p-value. From the transcriptome 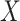, the random Delta scores are calculated from the Ic.shrink scores of random 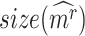genes. The candidates significant in the Ic.shrink-scoring system are the final CTSs identified.

Additionally, for a CTS-indicated CT state, comparing the observed Delta score to randomly simulated Delta scores gives another empirical p-value. These random Delta scores are calculated by fixing the CTS genes but randomly permuting the state labels.

Note that in complex systems, the identified signal may be a mix of CTS of TF regulation and epigenetic effects (e.g. the haemato-endothelial bifurcation). Therefore, we recommend additional biological validations using independent samples of concordant states on the same trajectory.

Data, biological gold standard, and statistical analysis

Six datasets

We demonstrate the utility of BioTIP using six independent single-cell gene expression datasets. The human embryonic stem cells (hESCs) dataset consists of 96 selected genes in 929 cells with predefined nine clusters (11). The lung dataset consists of 10.3k genes in 131 mouse alveolar type (AT2) cells (34). The E8.25 2019 dataset consists of 10.9k genes of 7.2k developing mesoderm cells collected at embryonic day (E) 8.25 (35). The E8.25 2018 dataset contains 12.7k genes in 11k E8.25 cells, with 16 predefined sub-cell types (36). The embryoid bodies (EB) dataset contains 15.2k genes of 1.5k developing mesoderm cells (6). The epithelial-to-mesenchymal transition (EMT) dataset was simulated from an established 18-gene regulatory network of 5.4k cells, consisting of four stable states and between-state transition cells (30). For each dataset, cell-type biomarkers or cluster identities are given from the original publications. Then, scRNA-seq data quality control (e.g. removing doublet cells and mitochondria genes), normalizing distinct sequencing depths, global feature selections, and cell clustering are performed following the corresponding manuscripts and described in S Methods.

Proxy gold standard (GS) per dataset

For CT detection, the established transition state and the state identified by both BioTIP and QuanTC serve as a proxy GS. For CTS identification per CT cluster, the co-identified transition markers by BioTIP running on variable sets of clusters or by QuanTC serve as a proxy GS (Supplementary Figure S1).

BioTIP’s stability is evaluated by the similarity between each prediction from down-sampled data and its proxy GS, per dataset. We sample 95% of the cells and 95% of global HVG randomly and apply BioTIP, doing 10–20 iterations. For each run 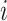, CT-detection accuracy is measured by Jarcard score as described (37). For CTS identification, we calculate the F1 score for two sets of transition markers: 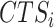and the GS markers (37). Meanwhile, a negative control of F1 score compares 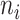random genes and the GS markers, where 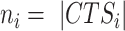observed. To ensure that easy and difficult datasets have equal influence when comparing methods, we normalize all the F1 scores of each dataset as previously described (37) (S Methods). After iterating, all normalized F1 scores are compared to all normalized controls using the unequal-variance t-test. Additionally, we evaluate the consistency of BioTIP predictions under two key-parameter settings: minimum DNB cutoff and minimum gene-module size.

BioTIP’s robustness is evaluated after applying different clustering pipelines and varying the key parameters that result in different numbers of clusters. We apply Leiden, consensus, and nearest-neighbor graph, using R packages Seurat v4, SC3, and scran. Also, we apply soft clustering using the MATLAB pipeline QuanTC (30,38–40). Each output is compared to the GS per dataset. We evaluate CT detection by Jarcard similarity and evaluate CTS identification by a normalized F1 score which is modified from previous benchmarking work (37) (S Methods).

To compare methods per dataset, we calculate the Jarcard score and normalized F1 score between the outputs of a method and the GS of that dataset (S Methods).

Prediction of upstream regulators is a crucial aspect in inferring regulated stochasticity from BioTIP’s outputs. We examine four pieces of evidence—the curated repository IPA (41), TF-binding motif, published ChIP-seq data, and evaluated TF targets in comparable systems—to predict the upstream regulatory TFs of identified CTS genes (S Method).

QuanTC (30) is applicable to sample sizes smaller than 5k cells; all five datasets except the E8.25 2018 dataset are below 5k. We use the default parameters, except we increase the cutoff to prioritize high-scoring transition cells when analyzing lung and EB datasets. For the E8.25 2019 dataset, 19 clusters are beyond the range of QuanTC’s analytical design (13 states). We therefore apply it to cells belonging to six clusters that are related to the HEP multifurcation (19% of all profiled cells). We optimize the number of stable states (clusters) as suggested by choosing the largest gap from the sorted eigenvalues (30). This strategy resulted in an optimal number (4 stable states) in the hESC and lung datasets but two numbers in the E8.25 2019 dataset (4 or 6 stable states, respectively).

MuTrans analysis (29) is applied to the hESC dataset, using MATLAB version R2020b downloaded from Github. We analyze the same 929 cells collected during days 0–3 plus 299 cells collected at day 4 (the cluster 12 (C12), next to the C10 cells on the trajectory shown in Figure 2a). The addition of day-4 cells verifies if the transition at day 3 is detectable with MuTrans (29).

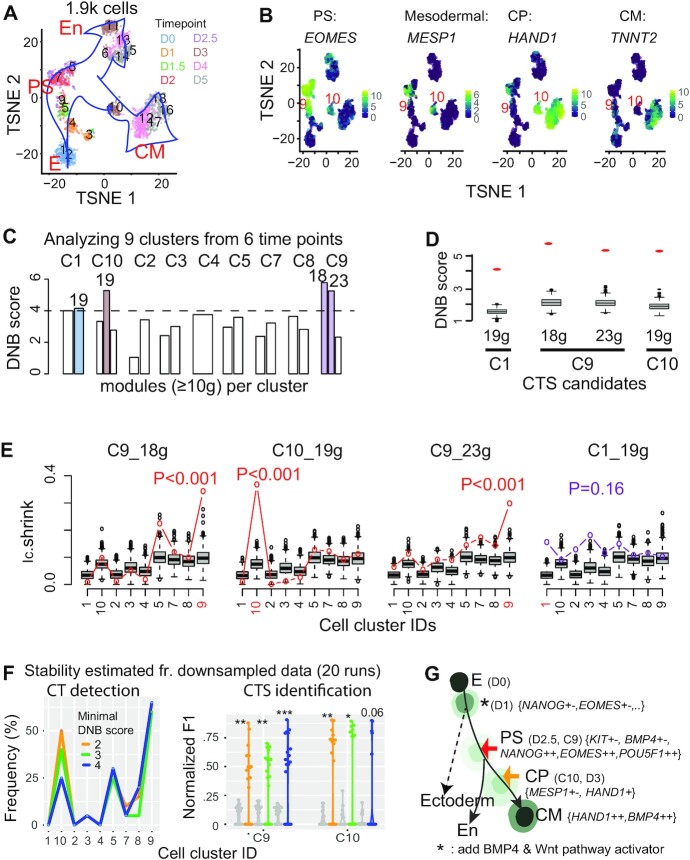
Figure 2.

Applying BioTIP to the hESC dataset identified significant CTSs characterizing the verified bifurcations, being independent of the trajectory topologies. (A) TSNE plot for all cells colored by eight collection days (D) and labeled by 18 predefined clusters. Blue arrows indicate the developmental trajectory. E: epiblast, PS: primitive streak; CM: cardiomyocyte, En: endoderm. (B) TSNE plot for the 1.9k cells, colored by the expression levels of four genes marking PS, mesoderm, cardiomyocyte progenitor (CP), and CM. Clusters of PS and CP cells are labeled. See Supplementary Figure S2a for details. (C) Bar plots showing DNB scores in nine clusters (C) of 929 cells along the CM trajectory with cells collected before day 4. The horizontal dashed line indicates a cutoff, resulting in four gene modules with the module sizes listed atop (colored bars). See Supplementary Figure S2b for details. (D) Comparing the observed (red dot) versus simulated (box) DNB scores of the 4 resulting CTS candidates that were significant in the DNB-scoring system (P <0.001). Gene numbers are given at bottom. (E) Technical evaluation of the four CTS candidates, labeled by the cell-cluster identity from which the CTS was identified (highlighted red in axis). Observed Ic.shrink (colored line) is compared to the gene-size-controlled random scores (boxes, 1000 runs). Also shown is the P-value of Delta of the observed Ic.shrink at the CTS-indicated CT state, resulting in three significant CTSs (red p-values). See Supplementary Table S1 for parameters. (F) Stability of BioTIP estimated from 929 cells of predefined clusters and 96 genes after down-sampling 95% genes and 95% cells (20 runs). Left: frequency of identifying each cluster as a significant CT state. Right: Normalized F1 score compares each run and the identified CTSs from the whole dataset, at two CT clusters. For C9, the union of two identified CTSs (see panel e) served as the proxy gold standard. The grey violin plots present negative control scores. Color represents the minimal DNB score to prioritize gene modules. *P< 0.05, **P< 0.01, ***P< 0.001 in t-test. (G) Tipping points (TPs) along the trajectory from early stem cell to CM differentiation (adapted from (11) and (29)). Each cell state (stable or transitional) has specific markers. The states are colored by energy values estimated by MuTrans. Lighter colors represent higher energy (Detailed in Supplementary Figure S5a). Colored arrows distinguish the verified tipping point (red) or the BioTIP-identified one (orange); both are verified by QuanTC and MuTrans. See Supplementary Figure S5 for MuTrans results, Supplementary Figure S4 for QuanTC results.

RESULTS

Following, we test and validate BioTIP’s advancements in simulated and sequencing data analyses. We further demonstrate BioTIP’s ability to detect TF-regulated stochasticity in both benchmark and high-throughput scRNA-seq datasets.

BioTIP identifies multiple significant CTSs accurately, and it is independent of the trajectory topologies

To demonstrate BioTIP’s accuracy, we used the benchmark hESC dataset with experimentally and computationally validated bifurcations (11). Cells at day 2–2.5 exhibit the experimentally verified pitchfork bifurcation from multipotent primitive streak (PS)-like progenitor cells to the mesoderm cardiomyocyte (CM, marked by Hand1) or to the endoderm (En, marked by Sox17) lineages (Figure 2, a-b, Supplementary Figure S2a). Then on day 3, major CM lineage commitments took place (11). KIT is a verified early-warning marker because its expression level at day 1 to 2.5 in a cell indicates future fate choices at day 3. Another bifurcation marker DKK1 is highly correlated with KIT expression levels in the cKIT^Medium population that can be induced into both lineages (11). 1.9k cells were collected from eight timepoints. We inputted the published consensus clusters of 929 cells (days 0–2.5, and mesoderm-specific day 3) into BioTIP for two reasons: they were previously analyzed by Ic (11) and allows for a fair comparison, and we will demonstrate the ability to detect a cluster at day 3 without subsequently collected cells.

To set up a proxy gold standard, we use the common predictions from three computational methods: Ic (11), QuanTC (30) and MuTrans (29). Cells of cluster 9 (C9) have an abundant level of NANOG and EOMES, representing the earlier PS state (Supplementary Figure S2a). The highest Ic score at C9 suggests increased transcriptomic stochasticity (Supplementary Figure S3a). In the model-free QuanTC analysis, cells of day 2.5 stand the highest cell plasticity indexes (CPI) (Supplementary Figure S4, S Methods). In the energy landscape predicted by MuTrans, cells of day 2.5 present the highest energy barrier (Supplementary Figure S5, a-b). These results suggest that the reported true development bifurcation at PS state (11) is detectable with different computational approaches.

Cells of cluster 10 (C10) have high expression of the PS marker EOMES, the mesoderm marker MESP1, and the cardiac precursor marker HAND1, but not the differentiated cardiac myocyte marker TNNT2 (11) (Figure 2b), indicating C10 to be a mesoderm progenitor state. C10 cells were collected at day 3. Interestingly, day 3 mesoderm-fate cells stand the 2^nd highest CPI with QuanTC. 22% of these cells also approach an increased energy barrier in an expanded energy landscape covering day 4 mesoderm cells (Supplementary Figure S5a, b). Both analyses indicate a topological saddle-node bifurcation happening at C10 before cells committed to cardiomyocytes.

Applying BioTIP to this dataset, we identified both evaluated bifurcations. Among four CTS candidates identified by the DNB scores (Figure 2C, D), we found three of them to be significant in the Ic.shrink-scoring system: two at C9 and one at C10 (Figure 2E). The detection of C10, a topological saddle-node bifurcation, is independent of pseudo-order construction because it doesn't require subsequently collected cells. This result demonstrates BioTIP’s accuracy in analyzing complex and noisy data.

Stability and robustness of CT detection and CTS Identification

By subsampling the hESC dataset (95% global HVG and 95% cells) iteratively and analyzing the predefined clusters, we first estimated BioTIP’s stability in detecting both bifurcations at C9 and C10. Among 20 runs, the most frequently significant CT cluster was C9 (>60%), followed by C5 and C10 (Figure 2F, left, blue line). A key parameter for significant CTS identification is the minimal DNB score to prioritize gene modules per state. We expect a random DNB score to be around 1 (Formula 2), however due to the small size of well-selected genes (96), the random scores ranged from 1 to 3 (Figure 2D). Therefore, we set this parameter to 4 (Figure 2C). When decreasing this parameter, C9 and C10 had the highest frequency to be detected (Figure 2F, left).

We then estimated BioTIP’s stability in identifying CTSs, using the same down-sampled data. Comparing CTS genes derived from the whole dataset for C9 to observed CTS genes or equally sized random genes, the observed CTS genes presented significantly higher F1 scores (Figure 2F, right). We observed the same pattern for C10. Our results thus depict the stability of BioTIP’s predictions in the hESC dataset.

We next evaluated the robustness to different clustering pipelines. We used cells of the predefined C9 (PS-like progenitor) and C10 (cardiac progenitor) to represent the two bifurcation states. BioTIP accurately detected both bifurcations when analyzing the clusters defined by consensus, nearest-neighbor graph, or soft-clustering approaches with proper clustering parameters (Supplementary Figure S1a, green bars). Furthermore, we successfully identified two established bifurcation markers (KIT and DKK1) at PS, regardless of the choice of five clustering pipelines (Supplementary Figure S1a, blue bars). In this example, BioTIP reached a comparably high performance with three clustering pipelines (AUC ≥ 0.89, Supplementary Figure S1a, right).

Significant CTSs disclosed experimentally validated transition marker and fate-deciding transcription factors

In this benchmark dataset, we identified two distinct CTSs for C9, with 18 and 23 genes in each. The CTS of 18 genes contained the verified bifurcation markers KIT and DKK1 (11). The co-expression of its members NKX2-5 and TBXT has been reported to bring about the completion of cardiac progenitor specification (42). These genes gained variance in expression among C9 cells (Supplementary Figure S5c, purple bars). Therefore, BioTIP characterizes the mesoderm-endoderm bifurcation by known bifurcation markers and their inter-cellular communications.

Our results exemplify a model that CTS genes are regulated by competing TFs (reviewed in (3)). The 18 CTS genes of C9 are the enriched targets of two groups of TFs. One group is the established PS regulators: NANOG, and EOMES. Another group is the established CM-inducing regulators: BMP4 and CTNNB1 (β-catenin) (IPA analysis, P < 1e–8, ≥5 genes, Supplementary Figure S2c) (reviewed by (42)). Similarly, the 23 CTS genes for C9 were the enriched targets of not only the highly expressed pluripotency factor POU5F1 but also the CM-inducing factor BMP4 (43) (Supplementary Figure S2d). These results fit the hypothesis of bidirectional forward and reverse regulators causing transcriptional priming (2,3). We conclude that a significant CTS can contain targets of lineage-determining TFs at the bifurcation (Figure 2G).

Compared to traditional markers, a CTS member gene that fluctuates at the transition state can be highly-expressed markers (e.g. TBXT at PS, Supplementary Figure S5c). A CTS can also contain the ‘transition driver’ markers reported by MuTrans (29) that vary significantly between two stable states. For example, the established mesodermal markers MESP1/2 that express in PS (C7), silence in later CM (C12) and fluctuate in the transition C10 (Supplementary Figure S5D, E).

Overall, this case study using the hESC dataset demonstrates BioTIP’s ability to find verified CTS genes that are covariables during the transition. These unique CTS genes disclose known and potentially new bifurcation-driving TFs that are prominent for further investigations. Therefore, we propose that BioTIP is broadly applied in analyzing single-cell gene expression profiles to characterize critical cellular state transitions.

Application to lung development data identifies new critical transition at E16.5 characterized by The second highest DNB score

During mouse lung epithelium development, morphological and molecular separation of AT1/AT2 bipotent cells occurred at E18.5 (34,44) (Figure 3A). Cells collected at E16.5 presented the highest plasticity when analyzed by QuanTC (Supplementary Figure S6). This result is in line with a previous Ic analysis of cell-collection days (7). Therefore, E16.5 cells represent a gold-standard CT event.

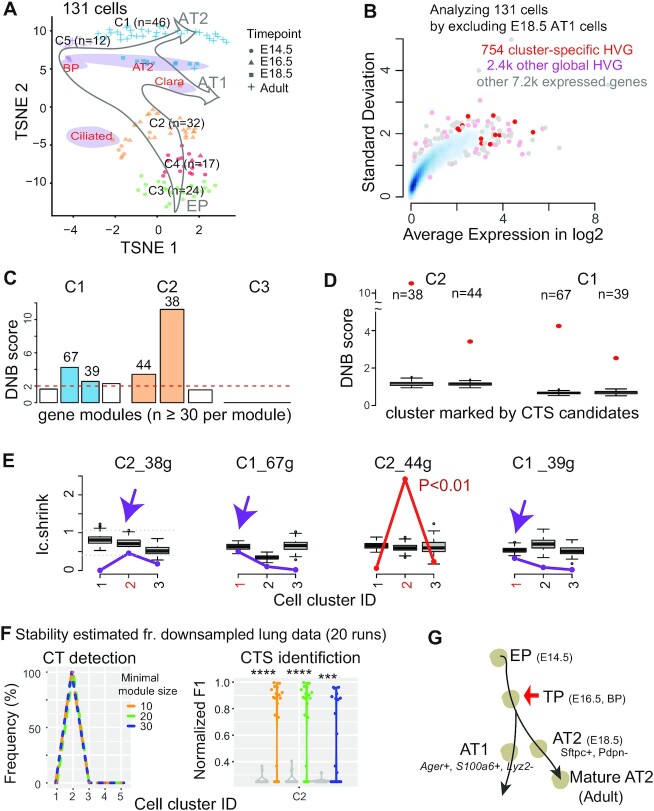
Figure 3.

Applying BioTIP to lung epithelial developmental data identified a CTS for the known critical transition, which shows a significant but not the highest DNB score. (A) TSNE plot of 131 lung epithelium cells shaped by collection days. It is colored and numbered by five clusters detected from the transcriptomes. Purple ovals highlight four subpopulations of E18.5 cells with published cell identities. Grey hollow arrows illustrate the knowledge-based pseudo-orders. EP: early progenitor; BP: biopotential progenitor. (B) Smooth color density scatter plot of 10.3k expressed genes. The blue dots represent a high density while the grey dots represent a low density. Highlighted in pink or red are the global HVG selected to conduct simulation statistics and the cluster-specific HVG (red) from which CTS candidates are identified. (C–G) Similar to Figure 2C–G, showing results for three clusters having 20 or more cells. Panel E has purple arrows pointing to when the observed score falls into the range of random scores at the intended cluster, and the CTS candidate is rejected. Panel f uses a proxy gold standard of 16 genes characterizing E16.5 cells by at least three out of five predictions (detailed in Supplementary Figure S1b). ****P< 0.0001 in t-test. Panel G points to the known tipping point at E16.5 which is verified by QuanTC (See also Supplementary Figure S6).

Applying BioTIP to this benchmark dataset of the known alveolar-type bifurcation, we identified a set of 44 genes to characterize E16.5 (C2) as a developmental tipping point (Figure 3B–E, S Methods). Notably, the Ic.shrink-scoring system validated the significance of only this one out of four CTS candidates predicted by the DNB-scoring system (Figure 3e).

We verified BioTIP’s stability in detecting the known bifurcation at E16.5 (C2), using iteratively down-sampled data (n = 20). Another key parameter of the BioTIP application is the minimal module size of CTS candidates per state. We set this parameter to 10 in the small hESC data (96 measured gene) and 30 in the large lung data (3.2k global HVG). When tuning this parameter between 10 and 30, BioTIP consistently detected C2 (Figure 3F, left). Compared to a proxy gold standard of 6 inferred transition markers (Supplementary Figure S1b), the normalized F1 scores for the down-sampled predictions were significantly higher than random genes (P <1e–4, Figure 3F, right). Our results thus depict the stability of BioTIP’s predictions in the lung dataset.

Again, by trying commonly used cell-clustering methods and varying their parameters, we found that BioTIP worked equally well among three cell-clustering methods (Supplementary Figure S1b).

Note that the identified CTS of 44 genes exhibited the 2nd highest DNB score at C2 (Figure 3D), suggesting the need to check more candidates besides the highest-scoring one in the DNB system. Applied to the same cell clusters but with 50 random global HVG, Ic predicted the C5 at E18.5 (Supplementary Figure S3b). This result suggests increased transcriptomic stochasticity concurring with the reported AT1/AT2 separation (34,44). However, Ic failed to detect transcriptional priming prior to such morphological and molecular separation. Therefore, this case study exemplifies BioTIP’s accuracy over Ic for CT detection and over DNB for CTS identification.

Application to the developing mesoderm data identifies four significant and reproducible CTSs

To demonstrate BioTIP’s applicability, we studied bifurcations at mouse E8.25 when precursor cells of major organs have been formed (35). We hypothesize that the significantly regulated stochasticity identified in one dataset can indicate the same bifurcation events in independent samples along the same developmental paths. The branches of cardiac mesoderm and muscle mesenchymal from early mesoderm were followed by a bifurcation between the hematopoietic and endothelial lineages (Figure 4A). Note that clusters C13, C10 and C15 in the E8.25 2019 data were three haemato-endothelial progenitor (HEP) clusters sequentially in pseudo-order (35). They also have notable differences in the expression levels of classic lineage markers (Supplementary Figure S8a, Supplementary Table S2). The early C13 has the highest average expression of Kdr which marks the hematoendothelial and cardiac lineage (Supplementary Figure S7a) (45), suggesting a multifurcation state.

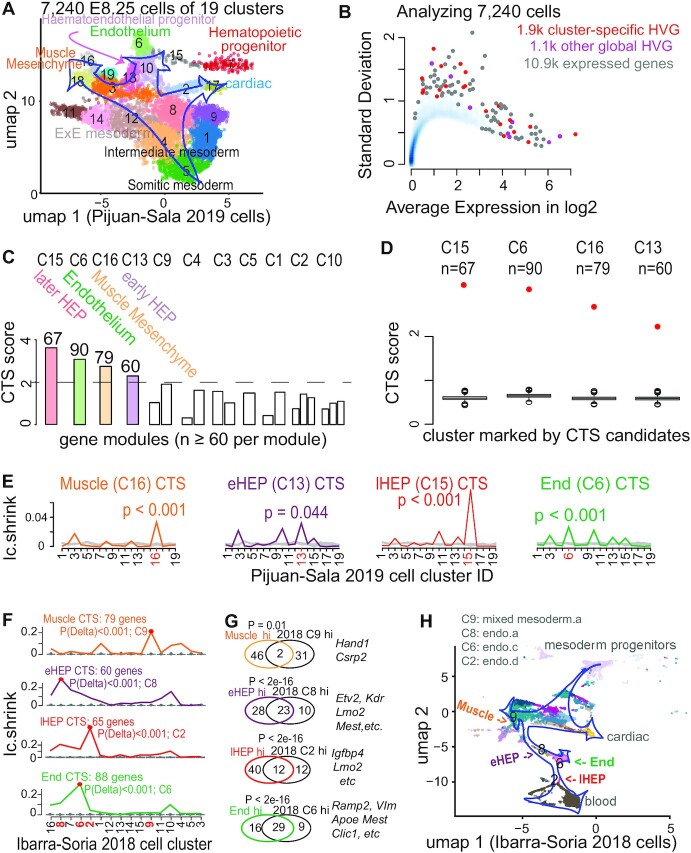
Figure 4.

Applying BioTIP to data of developing mesoderm identified four significant and reproducible CTSs. (A) Uniform manifold approximation and projection (umap) plot of 15.9k developing mesoderm cells (E8.25, GSE87038, published in 2019) colored and numbered by 19 clusters of transcriptionally similar cells (See Supplementary Figure S7a, b). Blue hollow arrows illustrate the knowledge-based pseudo-orders. ExE: extra-embryonic. (B) Similar to Figure 3b, showing the smooth scatter plot of 10.9k expressed genes. (C–E), Similar to Figure 2C–E. Each illustrates the results in 11 of 19 clusters that have module identifications. See Supplementary Figure S7d for stability. (F) Validating the four CTSs in independent profiles of 11 039 E8.25 cells of 16 pre-defined sub-cell types (published in 2018). Ic.shrinks of each CTS across these sub-cell types (line) were compared to their empirically simulated scores (box, 1000 runs). Calculation was conducted after mapping all CTS genes (n = 79, 60, 67, 90) to this profiling, extracting >98% of CTS genes (n = 79, 60, 65, 88, respectively) measured. The sub-cell type with the highest Ic.shrink is highlighted with a red dot, and the p-value for the Delta is shown. The red number on the x-axis indicates ‘CTS-mapped’ states of bifurcation. (G) Venn-diagram comparing the up-regulated biomarkers of each bifurcation state (in 2019 profiles) with the biomarkers of the mapped sub-cell types (in independent 2018 profiles). The numbers in the Venn count the up-regulated biomarkers (See Supplementary Figure S8). Circle color represents the four CTSs. Fisher's Exact tested P value. Some shared markers are displayed to the right. (H) Umap showing 2018 E8.25 cells, colored and indexed by 16 unique sub-cell types. Blue hollow arrows illustrate the knowledge-based pseudo-orders. Colored text indicates four CTS-mapped states of bifurcation.

Applying BioTIP to 19 cell clusters and 4k HVG, we first selected 1.9k cluster-specific HVG (Figure 4B). From these 19 clusters, we then detected four CTS candidates, each presented significant DNB scores at one state (Figure 4C, D). Note that among the three HEP states, multiple clusters intermingled only at C10 in the expression space (Supplementary Figure S7b), but BioTIP identified the other two multifurcation states. This demonstrates BioTIP’s ability to detect true CT events rather than a simple mixture of cell identities.

The significance of these CTSs was supported by the Ic.shrink simulation (P <0.05, Figure 4E). These CTSs revealed four bifurcation events in four states. Only the early C13 (eHEP) sits before a pitchfork bifurcation of the constructed trajectory; the other three clusters sit either along or at the end of a lineage branch, which are the later HEP (lHEP, C15), endothelial (C6), and muscle progenitors (C16) (Figure 4A, Supplementary Figure S7c). QuanTC detected the transition from EMT to the endothelial fate after assembling four stable states (Supplementary Figure S9). However, QuanTC also assembled cells into six states, which alternatively captured the transition from EMT to the hematopoietic lineage (Supplementary Figure S10). These alternative predictions suggest QuanTC’s outputs are dependent on the parameter setting and the chosen trajectories of interest. Because we can only partially snapshot the overall differentiation trajectories, BioTIP’s ability to identify multiple significant CTSs independent of the constructed trajectory topologies creates an easy understanding of the dynamic processes of gastrulation.

We assessed the robustness and stability, using the same subset of cells that we conducted QuanTC analysis (Materials and Methods). This allowed us to evaluate three hematopoietic-endothelial bifurcation-involving CT clusters (C13, C13, C6). These clusters were stably significant in the down-sampled data analysis, and their characterizing CTSs significantly overlapped their inferred gold-standard markers (Supplementary Figure S7d). Again, BioTIP was robust against four tested clustering pipelines in this dataset (Supplementary Figure S1c).

We then verified the biological reproducibility of these identified CTSs in an independent mouse gastrulation transcriptome, the E8.25 2018 dataset (36). For each above-identified CTSs, its Ic.shrink scores in the new dataset peaked at one sub-cell type significantly, thus pairing this sub-cell type to the above-detected bifurcation state (P of Delta < 0.001, Figure 4F).

Each state pairing was supported by their shared classic biomarkers (Supplementary Figure S8). Three out of four pairs shared the top-10 up-regulated biomarkers (12–29 shared markers from 10k common background genes, Fisher's exact test P <2e–16, odds ratio >250, Figure 4G). One pair with moderate overlap is also significant (P= 0.01, OR = 15). All four CTS-mapped sub-cell types resembled the pseudo-order of the four CTS-indicated bifurcations (Figure 4H versus A). These concordances suggest that the four CTSs are biologically reproducible in characterizing multiple bifurcations in the developing mesoderm.

In summary, we identified four significant CTSs as the readout of imminent developmental bifurcations and validated their significance in independent cells. These CTSs reveal the plastic and transcriptional regulatory mechanisms in early mesoderm development.

Comparing BioTIP with other methods for the detection or characterization of CT events

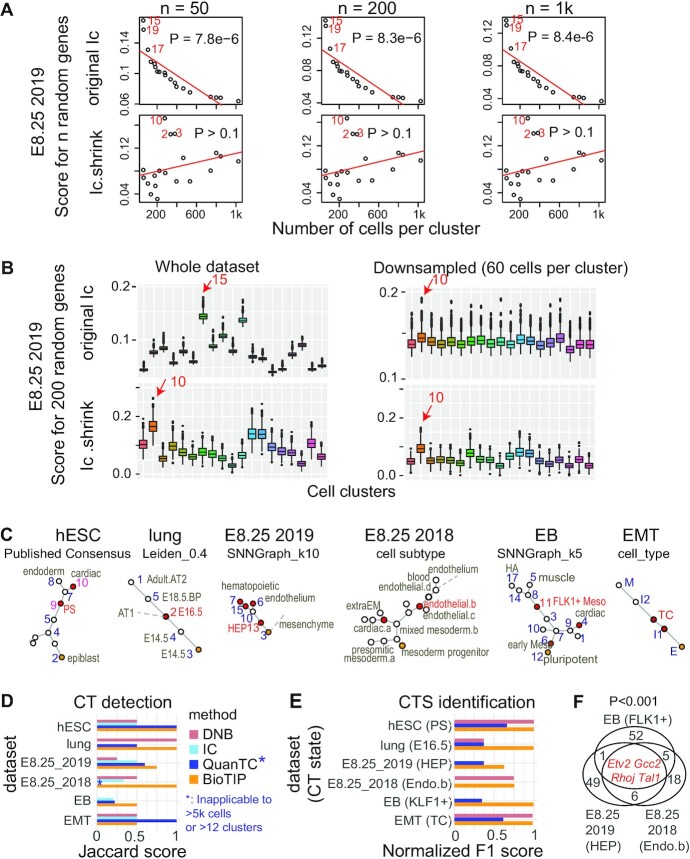
We first detailed how BioTIP corrects Ic's problem using the E8.25 2019 data (35). A higher Ic score indicates a CT state (7). However, there exists a positive correlation between the Ic scores calculated with random genes and the cell-population sizes (P= 8e–6); and the three smallest-sized clusters presented the highest Ic scores. This bias is consistent regardless of the number of genes tested (from 50 to 1000) (Figure 5A, top). We then asked if the Ic's bias causes trouble in predicting CT events. Cells have been bootstrapped to generate simulation data with variable or equal cell-population sizes, allowing an easy validation of methods. Tested with 200 random genes, C10 exhibited the highest Ic in the down-sampled simulation, making the highest score at C15 in the full dataset irreproducible (Figure 5B, top).

Figure 5.

Comparing BioTIP with three current methods. (A) Comparing Ic.shrink to Ic using the E8.25 2019 data (GSE87038). Each dot represents one cell cluster. The top 3 scoring clusters are labeled by cellular cluster IDs in red. Ic scores significantly decrease with large state sizes (top); Ic.shrink is not correlated with cell size (bottom). Both scores are calculated using different numbers of random genes (50, 200 and 1000). A P-value of Pearson Correlation is calculated between cell-population sizes (x) and the scores (y). See Supplementary Figure S11a for another example. (B) Comparison of the Ic scores on the simulated dataset of variable subpopulation sizes (left) with that of down-sampled equal subpopulation sizes (right). Boxplot shows the simulation of 1000 scores based on 200 random genes. Box color represents 19 unique cell clusters. In each subpanel, a red arrow labels the top-scoring cluster with its cluster ID. Ic scores output different clusters with the highest scores (top); Ic.shrink outputs consistent results (bottom). See Supplementary Figure S11b for another example. (C) Cellular cluster pseudo-trajectory constructed using the minimum-spanning-tree algorithm, labeled with its clustering method. Each dot is a cluster. Orange represents the developmental starting point and red represents the established (hESC, lung, EMT) or robustly detected (E8.25 2019, E8.25 2018, EB) transition states. For the CT cluster labeled in red, we inferred a proxy gold standard for CTS identification (See Supplementary Figure S1). HA: hemangiogenic, FLK1+: FLK1–expressing mesoderm. (D) Bar plot comparing the CT predictions using four methods in six datasets. DNB predicts one cluster with the highest DNB score per dataset. Supplementary Figure S3 details the Ic applications in six datasets. See Supplementary Figures S12, S13, S15 for BioTIP applications in the E8.25 2018, EB and EMT datasets, respectively. See Supplementary Figures S4, S6, S10 and S14 for QuanTC applications. (E) Bar plot comparing the CTS identification of three methods (same colors as panel D) in six datasets. F1 score is normalized per dataset and compares the CTS predicted by each method and the marker used as the gold standard for the known transition states (See Supplementary Figure S1). (F) Venn diagram comparing three sets of transition marker genes, each is the CTS identified by BioTIP for the haemato-endothelial bifurcation from one dataset. Four consistently identified CTS genes are listed in red. Empirical P is estimated by iteratively sampling the same number of genes (n = 1000) from the global HVG of each dataset and counting the overlaps. See Supplementary Figure S16a for the same comparison for DNB or QuanTC.

By contrast, using Ic.shrink to analyze the same dataset removed the unwanted bias (Figure 5A, bottom). The benefit of Ic.shrink over Ic exists regardless of the number of random genes tested (from 50 to 1000). Additionally in the simulation study, the highest Ic.shrink stayed at C10, regardless of cell-population sizes per state (from 60 to 1025) (Figure 5B, bottom). Although the C10 cluster is a branching point in the constructed trajectory, the cell cluster C13 (early HEP) prior to C10 is the most interesting—it is predicted by both BioTIP and QuanTC for the coming haemato-endothelium branching event (Supplementary Figures S7f, S9, S10). We conclude that when using Ic.shrink instead of Ic, BioTIP has no longer a risk of confounding predictions when working with data sets of variable population sizes. Similarly, we illustrated how Ic.shrink corrects Ic's bias in the EB dataset (Supplementary Figure S11).

We then compared BioTIP with three other methods for detecting one or more CT states, using the same six datasets. These datasets present linear, bifurcation, or complex tree topology in their developmental trajectories (Figure 5C). Each dataset has one best-studied bifurcation event (Figure 5c, the red labeled cluster) among its robustly predicted gold-standard bifurcations (Materials and Methods, Supplementary Figure S1). Both QuanTC and BioTIP reached the highest similarity between their CT predictions and the gold standard in two datasets (Figure 5D), in line with a report that 92% of transition-cell subpopulations exhibited higher Ic scores than the cells in stable states (30). We observed that QuanTC was more accurate for data with a small set of selected genes and simple trajectory (e.g. the EMT dataset), while BioTIP was more accurate for data with high-dimension genes and complex trajectory (e.g. the E8.25 2018 dataset).

Next, we compared BioTIP with two methods—DNB and QuanTC—for CTS identifications at each best-studied transition state. In four of the six datasets, BioTIP’s output recaptured the proxy gold standard (i.e. the highest F1 per dataset) (Figure 5E). We observed a higher F1 score with BioTIP rather than DNB in half of the case studies. This is expected because BioTIP can detect multiple significant CTSs per bifurcation and multiple bifurcations per datasets, while the one CTS predicted by the DNB model alone do not always mark the best-studied transition (e.g. in the E8.25 2019 and EB datasets). However, in the extreme case of only 18 selected genes, BioTIP functions only without the assessment of empirical significance (Supplementary Figure S15), suggesting global HVG is a requirement in assessing significance. Compared to QuanTC, we found more biologically meaningful CTS genes with BioTIP. For example, in the hESC data with two known bifurcation markers, we detected one with QuanTC (Supplementary Figure S1a, red boxes), while both were detected with BioTIP.

Additionally, we compared these methods by the ability to identify conserved markers across datasets, e.g. for haemato-endothelial bifurcation from the three developing mesoderm datasets. Applying DNB alone with the highest score, we found significantly shared markers between two E8.25 datasets but not the EB dataset (P <0.001, Supplementary Figure S16a). QuanTC also reported a common marker (Kdr, P= 0.001) across two datasets but failed to analyze the E8.25 2018 profiles over 5k cells. In contrast, BioTIP is unique in discovering significantly recurring markers across all three datasets (P <0.001, Figure 5F). Intercellular communications among these markers include prominent Etv2-Rhoj and Etv2-Tal1 coactivations that may drive heterogeneity during haemato-endothelial bifurcation (46–50).

Overall, BioTIP presents broad applications to variable scales of scRNA-seq data, consistency with other tools in CT detection, and a unique ability to identify conserved transition markers. Therefore, we anticipate BioTIP to be useful for characterizing developmental critical bifurcations.

Significant CTS discloses an Etv2-centred transcriptional and epigenetic regulatory dynamics during haemato-endothelial bifurcation

We have shown that a significant CTS contains or is the target of TFs marking or driving the bifurcation, using the benchmarking hESC dataset. Here, we asked whether the identified CTSs disclose fate-decisive TF activities in the complex E8.25 2019 dataset. From four identified CTSs, we isolated three upstream-regulatory TFs whose fluctuation in expression most likely impacts other genes’ fluctuation in two CTSs (Figure 6A, Supplementary Figure S7e). They were Gata1 at the more blood-committed later HEP, Etv2 and its direct target Ets1 (51) at early HEP (C13). These agree with the literature that Gata1 drives stem cells toward blood fates (52); and transient Etv2 activation specifies HE lineages, which is required until HE bifurcation (51,53). We are interested in how the mRNA variance of Etv2 explains the expression changes of other CTS genes, given that C13 sits just before the HEP branching point (Figure 4A).

Figure 6.

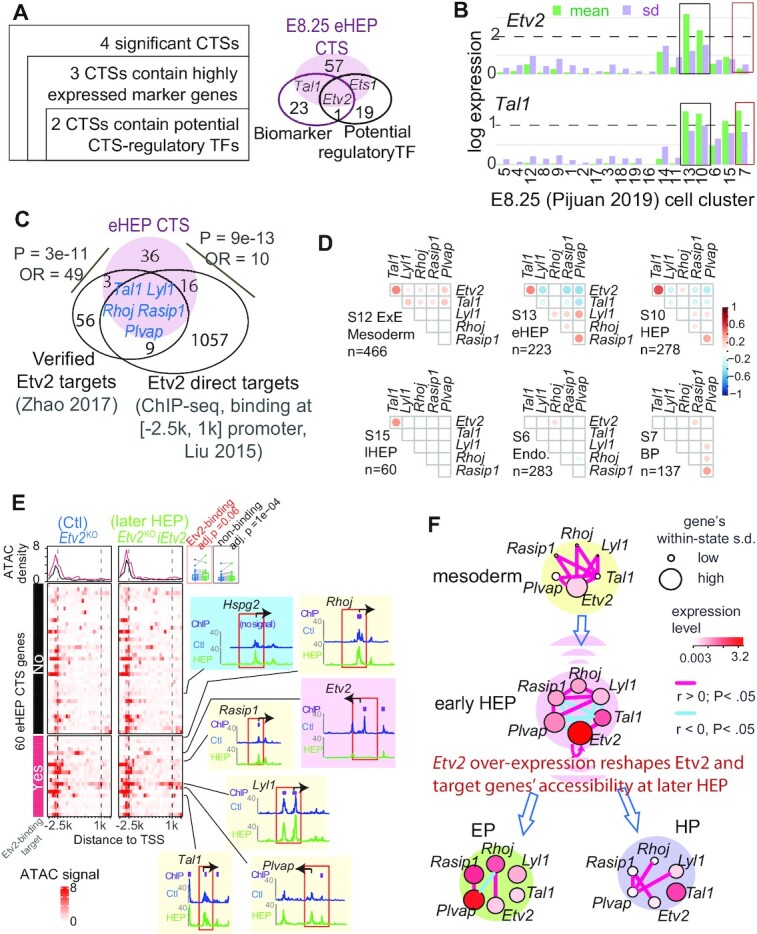
ETV2-centred transcriptional and epigenetic dynamics during haemato-endothelial bifurcation. (A) Disclosing fate-deciding TFs from two CTSs (left) (See Supplementary Figure S7e). We used differential-expression analysis to define highly expressed biomarkers; we used the union of IPA and motif enrichment analyses to infer potential regulatory TFs. The Venn-diagram compares the 60 eHEP CTS genes, eHEP biomarkers, and potential CTS-regulatory TFs. (B) Bar plot displaying the log2-scaled expression of Etv2 and Tal1 across cell states. Colored boxes highlight the HEP (black) or HP (red) state, respectively. (C) Venn-diagram shows the overlap among eHEP CTS genes, 73 previously validated Etv2 targets that are important for the hemangiogenic program, and the Etv2 direct targets from a published ChIP-seq dataset. Five evaluated direct targets are identified. (D) Pairwise gene-correlation among Etv2 and its five direct targets in six clusters (See Supplementary Figure S16c for the results for a biological validation). Significant Pearson coefficients (P <0.05) are shown as proportionally sized circles. We observe distinct patterns for many gene pairs, such as Etv2-Tal1 (gaining correlation during Extra-embryonic (ExE) mesoderm → HEP but not after the HEP bifurcation). (E) Heatmaps showing chromatin accessibility for 60 CTS genes with signal density atop. For each gene, the ATAC-seq signal in a 5.2k bp window around its transcription start site (TSS) is normalized into 20 ranges. The overall signals are stronger in the Etv2-induced Etv2^KOiEtv2 cell (right) than the control Etv2^KO cell (left). Two boxes in the top-right corner compare the signal between these two cell types (red for Etv2-binding and black for non-binding genes). Shown is the pairwise multiple-testing adjusted Wilcox-tested P-value. For the majority of 60 CTS genes, the signal aggregated at around 2.5k bp upstream of the TSS suggests enhancer activity (top boxes). The TSS accessibility of Etv2, Hspg2, and five Etv2-binding targets are checked (colored embeds), each highlighting a window of [-2500, 1000] bp around the TSS (red box). (F) A model of Etv2 expression mastering the dynamics of gene regulatory network during HE bifurcation. Each colored ball is a unique cell state. Within each state, each dot is a gene, colored and sized according to its average expression abundance fluctuation. s.d.: standard deviation.

To inspect the driver role of Etv2 fluctuation during the well-studied HE bifurcation, we checked the two key features of a tipping point (33): threshold-dependence and autoactivation. First, the variance and mean value of Etv2 expression peaked at HEP clusters (C13 or C10) (Figure 6B). This is consistent with the report that an expression threshold of Etv2 is required for HE bifurcation (50,53). Second, Etv2 autoactivation in hematoendothelial specification has been reported (54). Here, the variance and mean value of Tal1 expression peaked at early HEP and then maintained its value for blood progenitors. These temporal activations are consistent with the data in a time-resolved experiment (1) and go along with the literature that Etv2 activation induces a positive Etv2-Tal1 loop (50). Therefore, we reason that Etv2 fluctuation in expression is a new transcriptional feature for HE bifurcation.

We then verified Etv2’s central role in this CTS for C13 in two steps. First, we confirmed Etv2 as an upstream regulator of the 60 CTS genes with three pieces of evidence (S Methods). (a) An enrichment of ETS motifs presented at the proximal promoters (Supplementary Figure S16b). (b) There was a significant overlap with Etv2 direct targets derived from ChIP-seq binding data of differentiated embryonic stem cells (51) (P= 3.8e–7, Figure 6C). (c) Another significant overlap was observed with 73 previously verified Etv2 targets during haemangiogenic differentiation (50) (P= 3.2e–11, Figure 6C). Second, we investigated the gene co-expression changes impacted by Etv2 fluctuation during the transition, focusing on five CTS members that are verified Etv2 direct targets: Tal1, Lyl1, Rhoj, Rasip1 and Plvap. Along the developmental path from the extraembryonic mesoderm to HE bifurcations, the pairwise correlations among these six genes change (Figure 6d). A transient anti-correlation between Etv2 and its three target genes exhibits only at the CT state, which is also observed before the HE bifurcation in the E8.25 2018 dataset (Supplementary Figure S16c). This data suggests that there exists an Etv2-coordinated transcriptional priming.

Etv2 induction-dependent chromatin remodification (48) could be one mechanism underlying the transient gene covariance of the identified CTS. To test this hypothesis, we compared the published ATAC-seq data between Etv2-overexpressed (Etv2^KOiEtv2) cells and its control Etv2^KO cells at the EB differentiation day 4.75 (55). This Etv2^KOiEtv2 EB cells mimic a normal later HEP state because Etv2 expression ceases around EB day 5 (55,56). For the 60 CTS genes, most Etv2-binding sites gain chromatin accessibility in Etv2^KOiEtv2 than Etv2^KO cells (adjusted P= 0.06, Figure 6E, comparing two red lines atop). This pattern is consistent with our recent in-vitro observation (57), and holds true at the promoters of all the five Etv2 targets (Figure 6E, yellow embeds). Even without evidence of Etv2 binding, most CTS genes gain accessibility in the Etv2-overexpressed Etv2^KOiEtv2 cells (adjusted P= 1e–4, Figure 6e, comparing two black lines atop, shown at Hspg2, blue embed). This data suggests Etv2 overexpression itself impacts chromatin remodeling. Interestingly, an Etv2-binding proximate (<1k bp upstream from TSS) promoter of Etv2 is accessible in the Etv2^KO control but inaccessible in Etv2^KOiEtv2 (Figure 6E, pink embed). Because Etv2 binds to this region for autoactivation (54), we reason there is an instrumental epigenetic control terminating Etv2 autoactivation at the later HEP state. This instrumental epigenetic control might underlie the reported expression threshold of Etv2 during HE bifurcation, thus coordinating the CTS expression changes.

Based on changes in co-expression, the observed chromatin remodeling, and literature, we propose an Etv2-induced HE bifurcation (Figure 6F). In this transcriptional and epigenetic co-modification model, Tal1 and other Etv2 targets are co-activated before the bifurcation. At the transition state, the Etv2-autoactivation and onset of several positive feedback loops amplified the oscillations of Etv2 and its five targets. Cells continue to differentiate into distinct stable states after Etv2 expression reaches a threshold. Then, the inaccessibility to its promoter region terminates Etv2-autoactivation. Consequently, Etv2 expression decreases, coinciding with gene regulatory network changes. After entering a stable cellular state, some oscillating CTS genes gain lineage-specific expressions, such as Tal1 in hematopoietic progenitor (46), and Plvap, Rasip1 and Rhoj in the endothelium (47–49). The fate specification is also under the control of chromatin remodeling driven by Etv2-induction (48). Across these states, four pairs of instant Etv2-target correlations disappear or switch the directionality, while Etv2-Rhoj correlation appears in endothelial lineages.

In summary, our efforts to detect significantly interconnecting CTS genes from a noisy background bring us one step closer to understanding the dynamic TF regulation, in which the transient induction of TFs concur with or drive critical state changes. The above results provide an impetus to adopt tipping-point models to uncover the roles of transcriptional oscillation using single-cell transcriptomes.

DISCUSSION

In this study, we developed BioTIP to characterize transcriptional priming before cells transition from one stable state to another. The major challenge we overcome is that cells may also determine their fate by taking developmental cues from stochastic fluctuations. Using BioTIP, we identified multiple significant, reproducible, and trajectory topology-independent CTSs. We achieve this by parsing out regulated stochastic signals from the transcriptional background. For example, in the lung, E8.25 2018, and EB datasets (Figure 3e, Supplementary Figure S12e, Supplementary Figure S13e), the results show that the identified CTS (the colored line rather than background gene signals) is the only readout of the best-known lineage bifurcation. In contrast, Ic alone was able to capture some CT events in the hESC, E8.25 2019, and EMT datasets, showing how random gene signals can be indicative of a tipping point (Supplementary Figure S3a, c, f). In both cases, we showcase our significant CTSs consist of or are targets of fate-determining TFs (Figure 6C, Supplementary Figure S2c, d).

To exploit the regulated stochasticity via single-cell gene expression data, BioTIP adapts the tipping-point theory and high-throughput data analytical algorithms. Compared to existing works on transition states, the methodological contributions of this work are:

• BioTIP allows a fair comparison among cellular states with variable population sizes in high-throughput datasets. The between-state comparison of Ic is biased towards small-sized states. Given that the sizes of cellular clusters vary in a scRNA-seq dataset, this bias results in Ic being inaccurate. We corrected Ic's inaccuracy by introducing an improved approximation of the true correlation matrixes and designed Ic.shrink (Figure 5A, B). Therefore, BioTIP detects small-sized transition states more accurately than Ic.

• BioTIP advances DNB’s application in identifying multiple, significant, and reproducible CTSs from high-throughput scRNA-seq profiles. Due to the increased number of cell states detectable, a subset of module genes can interact in multiple states. Therefore, by modeling gene co-expression alone, the DNB scores of a module detected from one state might be undesirably high at other states. Knowing this drawback, current applications of DNB identify only one CTS with the highest score in a system (16,17,28,58–60). By overcoming this restriction, BioTIP can detect multiple modules per dataset then discover conserved transition markers across multiple datasets (Figure 5F).

• Compared to transcriptional entropy-based methods, for example QuanTC (30) and MuTrans (29), BioTIP does not assume a smooth activation or silencing of markers during a transition. Therefore, BioTIP predicts more transition markers rejected by this stable-state-central assumption. Additionally, BioTIP models gene-gene interconnections, thus enabling the divination and understanding of transition-driver TFs.

These methodological contributions can potentially help understand transcriptional priming at transition states in three angles:

• A significant CTS is not only reproducible across independent datasets but also informs key TF regulations that could be valuable for investigating cellular engineering.

• By realizing the independence of the CTS identifications from cellular states’ trajectory topologies, we can uncover previously undetectable multiplications (e.g. the saddle-noddle bifurcation before fate commitment and the transition states at the branch end of a snapshotted trajectory).

• BioTIP is a unique toolset for identifying significant CTSs from given single-cell transcriptomes. It provides versatile functions with a user-focused tutorial, thus warranting more biological applications.

The CTSs identified from mouse gastrulation data may serve as the initial attempt to bridge transition-marker identifying to investigate lineage-determining TFs at the transition. For example, the cooperated expressional dynamics between Tal1 and Lyl1 has been observed during the endothelial-to-hematopoietic transition of cells originating in endothelial lineages (61). Our results show that these two Etv2-targets are co-expressed only in the CT cluster before HE-bifurcation but not in later differentiated states. The results elaborate on the coordination of competing regulatory factors’ alternative fate potentials in transition cells that has been noted in other tissues (14). Second, our inference of Etv2 as a CTS driver suggests its potential in reprogramming the plastic cells at the transition. ETV2 reactivation was reported to reset the chromatin and transcriptome of human endothelial cells to become adaptable, vasculogenic cells (47). We found exciting evidence to suggest Etv2-overexpression remodels CTS genes’ chromatin accessibility (Figure 6E). Both suggest an Etv2-governed cell plasticity via transcriptional and epigenetic remodeling, potentially explaining the notion that transition cells can undergo a ‘temporal switch’ (back towards a more plastic progenitor) (1). Such reprogramming factors are promising as cell-based therapeutic reagents for treating diseases, during an unstable, plastic state.

Compared with standard gene signatures, CTSs were reported to be depleted with differentially-expressed genes (62). We found they are unrelated. Four CTSs of developing-mesoderm were either distinguished from or recaptured 8–21% of the up-regulated genes of their CT clusters (Supplementary Figure S7e, colored cycles). This independence suggests that CTSs (modeling variance and correlation) detect new features of dynamics, regardless of traditional analysis relying on group means.

As an alternative approach to estimating critical transitions in silico from their RNA-Seq profile, transcriptional entropy could be used rather than tipping-point theory. Transcriptional entropy-based approaches (QuanTC, MuTrans) have inferred subpopulations that undergo transitions and exhibit higher entropy than stable populations (29,30). Despite different underlying theories, QuanTC and BioTIP converged at the same best-studied bifurcations in six datasets (Figure 5D). Of note, transcriptional entropy should not be confused with signaling entropy measure. Signaling entropy estimates cell's overall differentiation potencies and thus decreases continuously during developmental differentiation (23,63). In contrast, transcriptional entropy exhibits a local peak before a critical cell-fate transition occurs (29,30).

Both transcriptional entropy and signaling entropy reveal TFs important for state transitions (23,30). TFs identified by these entropy-based approaches should not be confused with those inferred from BioTIP. In entropy-driven approaches, the TF drivers significantly change from one to another stable state along the pseudotime. In contrast, BioTIP considers that TFs can be responsible for state transitions by propagating intercellular communications to downstream target genes (23,30) and therefore infers transition-driver TFs from CTS genes identified. We found overlaps between these two types of TFs (e.g. EOMES in the hESC data, Supplementary Figures S2c, S4b). We interpret this co-identification as a fluctuating TF that responds to bidirectional forward and reverse signals and also changes significantly after the transition. However, inferring transition-driver TFs from CTS genes remains challenging. We recommend checking different levels of evidence, including manually curated repositories, interactions, and TF-promoter binding derived from ChIP-seq data in a related system (64,65).

There are three suggestions for a biologically meaningful BioTIP application. First, we recommend removing unwanted artifacts of expression variance following a standard scRNA-seq analytical pipeline before applying BioTIP. Second, cell clustering is a prerequisite. While different cluster resolutions may affect BioTIP’s prediction, a reasonable clustering method (with reasonably chosen parameters) will not have a major impact on the CTSs identified (Supplementary Figure S1). We designed BioTIP for the case where local transition cells can be assembled as a cluster and therefore had no prediction from only the stable cells nor from some clustering procedures (Supplementary Figure S1). Third, applications to the cell populations of interest will likely present high stability. For example, the outputs of 6 clusters connecting on the developmental trajectory recaptured the gold standard better than those of all 19 clusters of the E8.25 2019 data (Supplementary Figure S1c). In general, proper data procession and confidently inferred clusters are required by BioTIP; and an established trajectory topology should enhance computational sensitivity and biological interpretation.

In conclusion, we present the BioTIP approach for identifying CTSs from noisy, large-scale, and heterogeneous cellular gene expression profiles. We use identified CTSs to infer lineage-determining TFs and provide computational validation of these CTSs in independent profiles. Our CTS identifications reflect regulated oscillations in gene expression at critical transition states and offer hypotheses about the transcriptional or epigenetic priming related to early biases in cell fate choices. We anticipate that transcriptomic tipping-point analysis will be widely applicable for a deeper understanding of the plasticity, heterogeneity, and phenotypic changes in dynamical biological systems.

DATA AVAILABILITY

Published data used in this paper include the following already deposited data sets: scRT-PCR from publication (11) (hESC), GEO: GSE52583 (lung), GSE87038 (developing mesoderm at E8.25 published in 2019), GSE130146 (EB), GSE59402 (ChIP-seq signal for Etv2 binding in-vitro-differentiated ES cells), GSE92537 (ATAC-seq signal for Etv2-deficient Etv2^KO cells, ArrayExpress: E-MTAB-6153 (developing mesoderm at E8.25 published in 2018), as well Etv2^KOiETV2 cells with induced Etv2 expression), and github.com/yutongo/QuanTC (EMT).

The code for the BioTIP algorithm, its applications to six datasets, the quantitative evaluations, and a detailed tutorial are available at https://github.com/xyang2uchicago/BioTIP.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NIH [5R21LM012619 to X.Y. and Z.W.]; Micro-Metcalf Program Project at the University of Chicago (to Y.S.). Funding for open access charge: Department of Pediatrics, University of Chicago.

Conflict of interest statement. None declared.